岩溶地面塌陷是岩溶地区典型的地质灾害类型,严重威胁其影响范围内群众的生命及财产安全,造成巨大的经济损失,每年国内外都有大量针对此类灾害的报道。有研究表明[1-3],多数塌陷都受人类工程活动的影响,如地下水开采、隧洞施工、水库修建及矿坑抽水等。随着人类工程活动的加剧,岩溶地区可能发生更多的地面塌陷,阻碍人类社会和经济发展。为此,进一步梳理塌陷区的基础地质条件,分析塌陷形成原因,揭示岩溶地面塌陷机理,具有显著的理论意义和工程价值。覆盖层是岩溶地面塌陷的主体,地下水是诱发岩溶地面塌陷的重要动力因素[4],剖析地下水位下降对覆盖层的影响,能进一步深入理解诱发塌陷的机理。岩溶区工程建设会改变地下水流场,导致地下水向下伏岩溶管道漏失,还会改变覆盖层的物理性质,改变土壤的含水率[5]。除此之外,地下水位下降会间接对覆盖层产生作用力,造成覆盖层变形失稳,从而形成塌陷[6-7]。在地下管道泄露或地下水位下降过程中,地下水的排放量及地下水位下降速率控制着覆盖层土体渗透变形,甚至塌陷[8-10]。物理模型试验能直观地模拟岩溶塌陷形成的全过程,探查不同影响因素对覆盖层的影响及其响应情况。XIAO等[11-12]使用物理模型对水-气相互作用过程进行了模拟,分析了盖层变形演化行为和塌陷的内在机理。SHI等[13]对突水引起的土洞的形成、扩大和变化过程进行了研究,指出土洞的扩大和塌陷是由剪切应力对土洞拱脚的集中作用引起的。在塌陷发生之前,地下水流场会形成位于塌陷坑位置分布的降落漏斗,该现象可在早期阶段用于预测塌陷发生的潜在位置,这也是由实验室构建的致塌模型观察而来的[14-15]。当应力条件超过了周围环境的的材料强度,覆盖层的强度决定了是否会出现塌陷[16]。此时对于覆盖层的稳定性,定量分析不失为探讨盖层失稳机制的更好办法。HE等[17]建立了致塌力学模型,并用模型对枣庄市的岩溶塌陷进行了验证分析与评价。针对正压和负压作用下触发塌陷的统一模型的缺失这一问题,WEI等[18]根据塌陷阶段的不同特征,基于波义尔定律分别建立关键综合力学模型。不可忽略的是,力学模型的建立与覆盖层结构及影响因素密不可分。自然界中,阻-透型盖层具有上部为阻水类土而下部为透水性土的二元结构特征,是一种典型的盖层结构类型[19],但当前学者们对地下水位升降下该类盖层受力状态及变形特性的认识尚不够深入,相关的研究成果较少。因此,本文以曲靖市马龙区岩溶地面塌陷为研究对象,在充分认识研究区地质环境条件的基础上,构建了地质物理模型,开展了符合实际多组室内试验,从而分析地下水位下降速率与盖层塌陷的关系,探讨阻-透型岩溶塌陷的致塌机理,并在此基础上,利用力学模型对其进行验证。本研究一定程度上可为岩溶塌陷地区预测预报、防灾减灾提供技术支撑。
1 岩溶塌陷地质原型
曲靖市马龙区内的车马碧水库输水隧洞自2018年11月开始疏排水后,导致周边地区地下水位快速下降,由此引发了位于隧洞东南侧约1.6 km处的杨官田地区发生了22次塌陷,并伴随有建筑物墙体、道路开裂,河流、泉点干涸等不良现象。杨官田地区塌陷具有数量多、规模大、群发性强的特点。
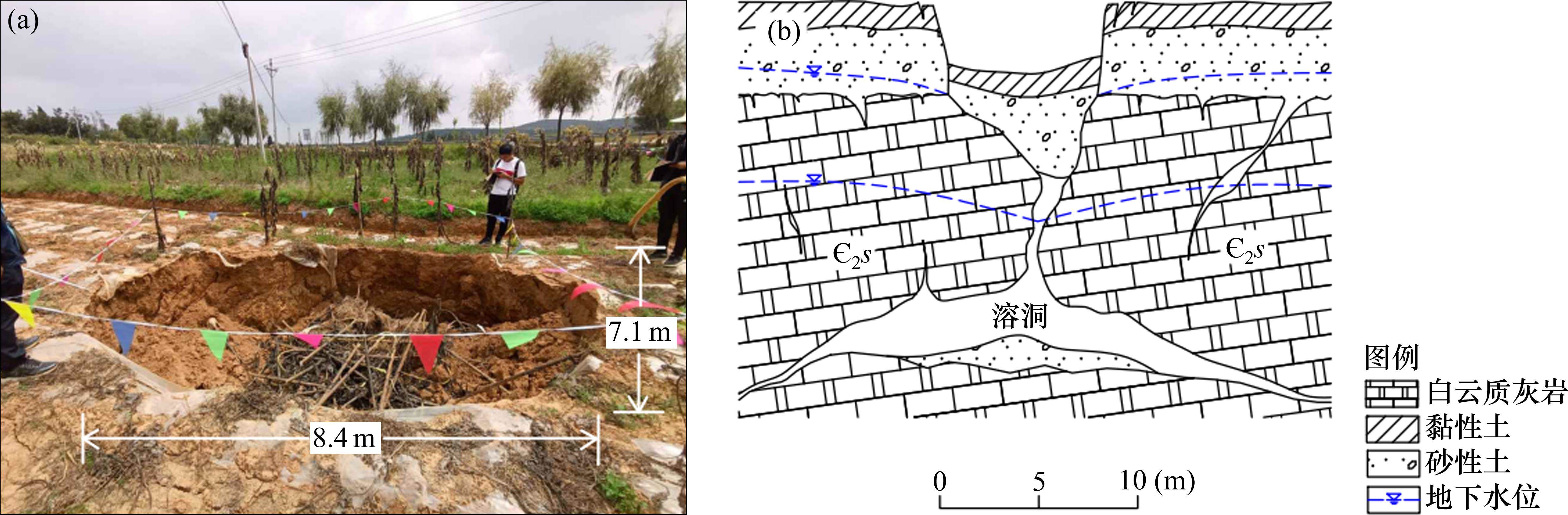
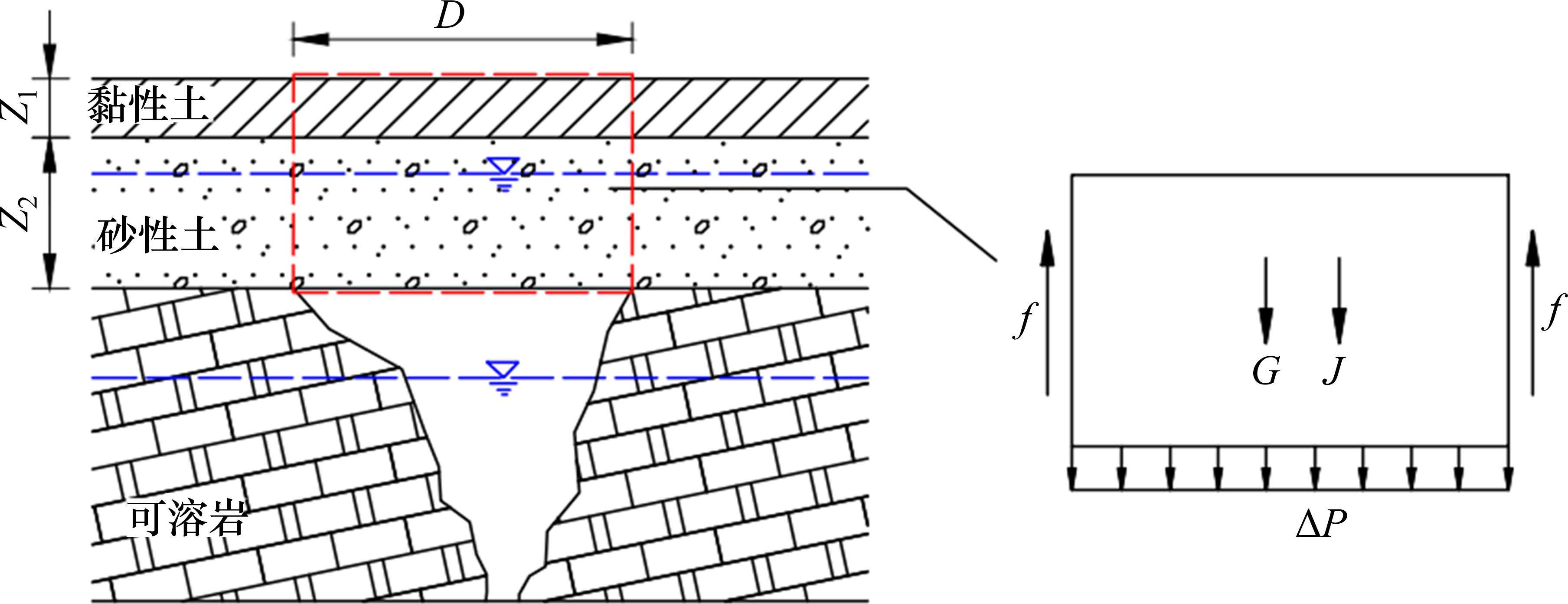
为此,本文以杨官田地区的典型塌陷坑为原型(图1(a)),分析研究地下水位下降触发岩溶塌陷的过程与机理。野外调查发现,该塌陷坑平面上呈亚圆状,长轴8.4 m,短轴7.1 m,可见深度2.1 m。其覆盖层结构从上到下大致可分为2层,第1层为厚约2.2 m的黏性土层,第2层为厚约4.6 m的砂性土层,下伏基岩为寒武系中统双龙潭组地层(Є2s)的白云质灰岩。从盖层结构特征来看,黏性土层具有透气性差、渗透性低、强度低等特点,而第2层砂性土层具有透水(气)性相对强,含砂量高的特点,属于典型的上阻下透结构。塌陷坑底部存在岩溶空腔开口,推测为溶洞或溶蚀管道(图1(b))。据资料显示,塌陷发生前,塌陷区内存在双水位情况,孔隙水水位位于砂性土层内,埋深约2.8 m,岩溶水水位埋深约10 m。在塌陷发生后,塌陷区的岩溶地下水位埋深约57 m。初步分析认为,塌陷发生前,由于溶洞中地下水位下降,在溶洞中产生了真空负压,盖层下层的砂性土中产生了渗透力,从而形成了该塌陷坑。
在此基础上,通过取样实验和野外现场试验,获取了覆盖层的相关参数(表2),选择该塌陷坑为地质原型,根据相似理论在室内构建地质物理模型,开展地下水位下降导致塌陷的过程试验。
| 土层名称 | 粒径质量百分比/% | ||||
|---|---|---|---|---|---|
| <0.075 mm | 0.075~0.25 mm | 0.25~0.5 mm | 0.5~1 mm | >1 mm | |
| 黏性土层 | 41 | 26 | 11 | 9 | 13 |
| 砂性土层 | 30 | 22 | 13 | 12 | 23 |
| 土层名称 | 类型 | 厚度 Z/m | 物理力学性质参数 | 水理性质参数 | ||||
|---|---|---|---|---|---|---|---|---|
含水率 ω/% | 黏聚力 c/kPa | 内摩擦角 φ/(°) | 天然重度 γ/(kN∙m-3) | 渗透系数 k/(cm∙s-1) | 给水度 μ/% | |||
| 黏性土层 | 原型 | 2.2 | 23.8 | 19.7 | 23.3 | 19.1 | 0.001 1 | 0.034 |
| 模型 | 0.022 | |||||||
| 砂性土层 | 原型 | 4.6 | 35.5 | 8.3 | 19.2 | 18.7 | 0.015 2 | 0.073 |
| 模型 | 0.046 | |||||||
2 物理模型试验
2.1 相似理论及试验平台
物理模型试验设计总体遵循相似理论[20-21],满足盖层材料相似、盖层物理性质相似、几何尺寸相似、水动力条件相似等相似条件。本模型的相似比Ci为100,即原型与模型比例系数为100。试验盖层用土根据土体的粒径质量百分比(表1)进行配比,配制成含水量、重度等与野外盖层总体相同。为了保证原型与模型材料的相似性,开展了室内土工试验,得到了模型材料的物理力学性质参数和水理性质参数,如表2所示。
试验平台由地质体模拟箱、供排水系统及数据监测装置组成(图2)。地质体模拟箱分为上下2个区域,上部区域模拟第四系覆盖层,尺寸为长×宽×高=1 m×0.5 m×0.9 m。下部区域模拟可溶岩中发育的溶洞,尺寸为1 m×0.5 m×0.5 m。2个区域用2 cm厚的透明有机玻璃板隔开,玻璃板中央有直径为10 cm的圆孔,用于模拟溶洞开口。由于试验装置的限制性,与溶洞相连接的岩溶管道将不做模拟。模拟溶洞下端设置排水管,装有控制排水速率的阀门,可将试验后的水排入下侧储水箱。地质体模拟箱两侧设置可升降溢流箱,并通过软管与模拟溶洞及储水箱相连,模拟溶洞内水位可通过两侧溢流箱进行调节。
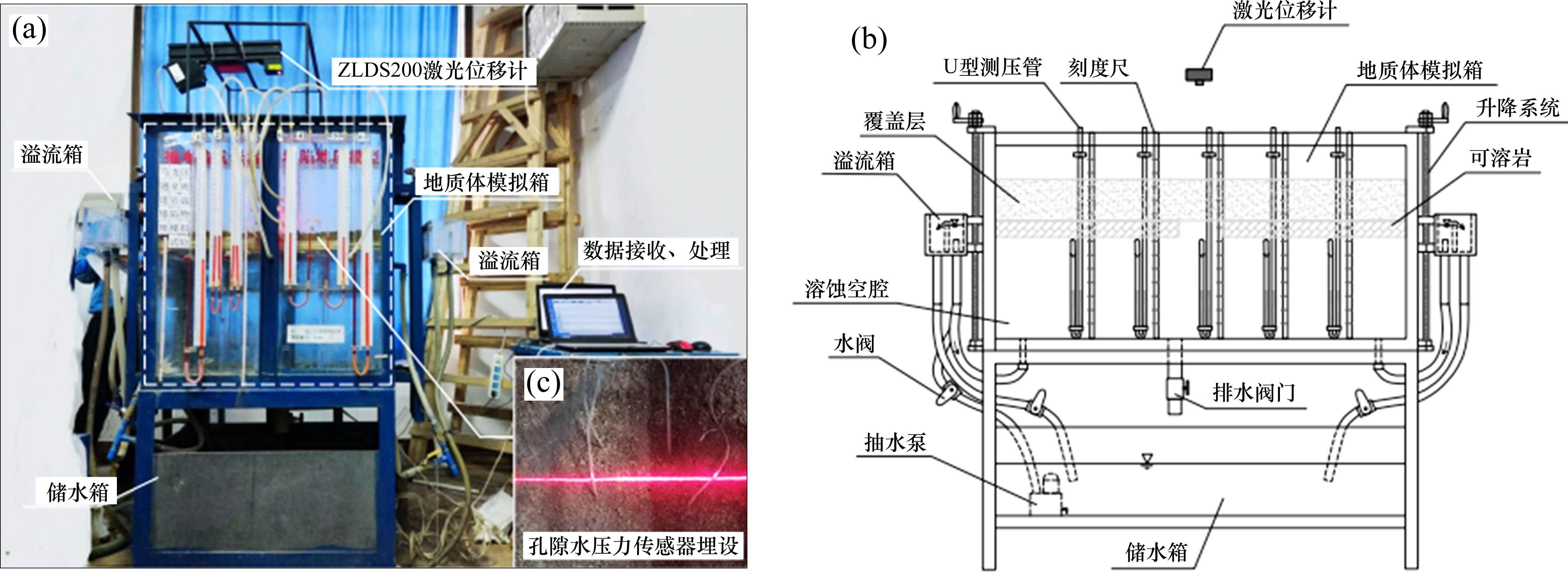
对于数据监测装置,本试验采用ZLDS200激光位移计来实时监测并传输第四系覆盖层表面高度数据,能达到Z轴0.1%的高精度。采用4根孔隙水压力传感器监测孔隙水水压力变化,其量程为-100~20 kPa,均匀埋在塌陷坑四周(图2(c))。采用与模拟溶洞相连接的U型测压管内的液位差来反映模拟溶洞内气压大小,用式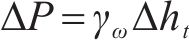
2.2 试验方案及步骤
试验共进行5组,这些方案中,其他因素不变,仅改变地下水位下降速率。由于原型塌陷坑的地下水位降幅约47 m,根据相似关系,设计的5组试验中地下水下降速率分别为:8×10-5、1×10-4、1.2×10-4、1.4×10-4和1.8×10-4 m/s。
试验按如下步骤。
1) 关闭排水阀门,往模拟溶洞内注水,当水位距有机玻璃板3.2 cm(地下水位埋深10 cm)时,停止注水。
2) 铺设盖层。将配置好的土体材料从下到上按顺序铺设,并根据原型所得重度值计算体积和称重,保证模型中的土体容重与原型完全相同,模型箱中覆盖层自下到上2层厚度分别设计为4.6 cm、2.2 cm。初始条件下,孔隙水位面与基覆界面高差设计为4.0 cm(孔隙水水位埋深2.8 cm)。
3) 在U型管内注入蒸馏水(加红色指示剂以方便测量数据),保持U型管两侧液面持平。
4) 架设监测仪器。均匀在土层内埋设4根孔隙水压力传感器后,将激光位移计架设在塌陷坑正上方,连接计算机,调整位置保证激光线经过塌陷坑中心。
5) 调节排水阀门,控制排水速率,开始排水。在排水过程中,记录U型测压管液位变化及模拟溶洞内水位下降速率。利用计算机直接记录和处理盖层表面变形数据及盖层内孔隙水压力变化。录像并观测盖层表面裂缝发育和分布情况。
6) 结束实验。
2.3 试验结果及分析
1) 溶洞内真空压强变化
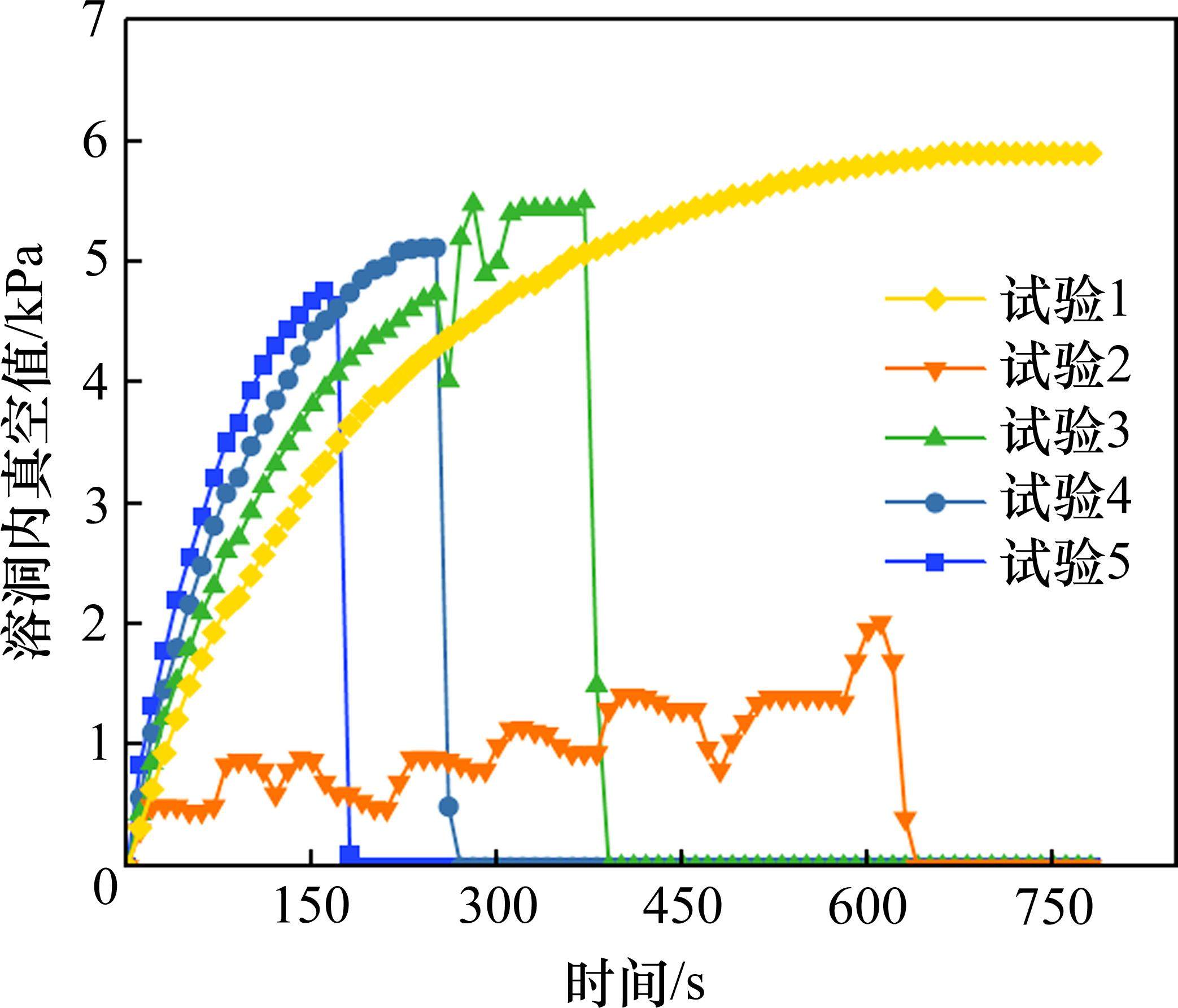
不同排水速率下,5组试验的真空值随时间变化曲线如图3所示。除实验1外,其他4组实验均能产生塌陷,但塌陷时间不同,真空值的峰值不同。塌陷所需时间随排水速率的增大逐渐缩短,试验2~试验5塌陷所需时间分别为612、391、273和170 s。试验数据显示,在试验1中,真空值不断增大至5.9 kPa后保持不变,塌陷并未发生。试验2在塌陷发生之前,真空值呈波动上升的趋势,真空值的峰值为1.96 kPa,远低于试验3~试验5的真空值的峰值,经分析发现在塌陷前盖层内部已逐渐产生了一些细微裂缝或通道,使得外界大气能更快速地补给到溶洞内。试验3~试验5的数据表明,排水速率越大,溶洞内真空值上升也越快,真空值的峰值越小,这是因为出现了速率快,早塌陷的现象。塌陷发生后,溶洞内得到外界大气压的补给,真空值急剧降为0,发生塌陷时对应的真空峰值分别为5.50、5.12和4.78 kPa。
据5组试验的真空值变化速率曲线(图4)分析发现,在塌陷发生前均表现为逐渐下降的趋势。其中试验2真空值变化速率波动较大,而其余4组试验变化较为规律,表现为排水速率越大,初始真空值变化速率越大。总体上整个实验过程中,真空值变化速率呈逐渐减小的态势,并在塌陷前逐渐趋近于0。
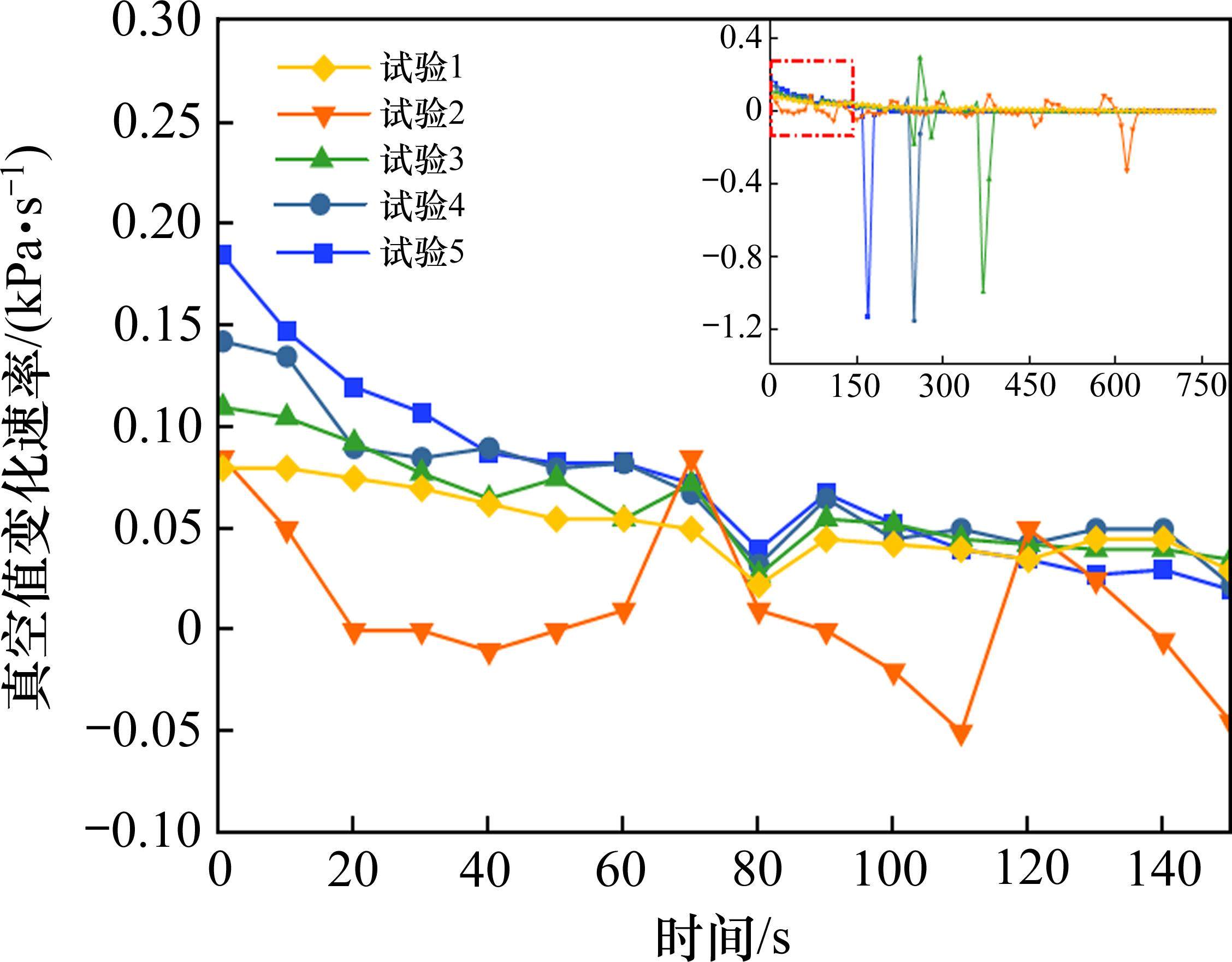
2) 地下水位下降速率
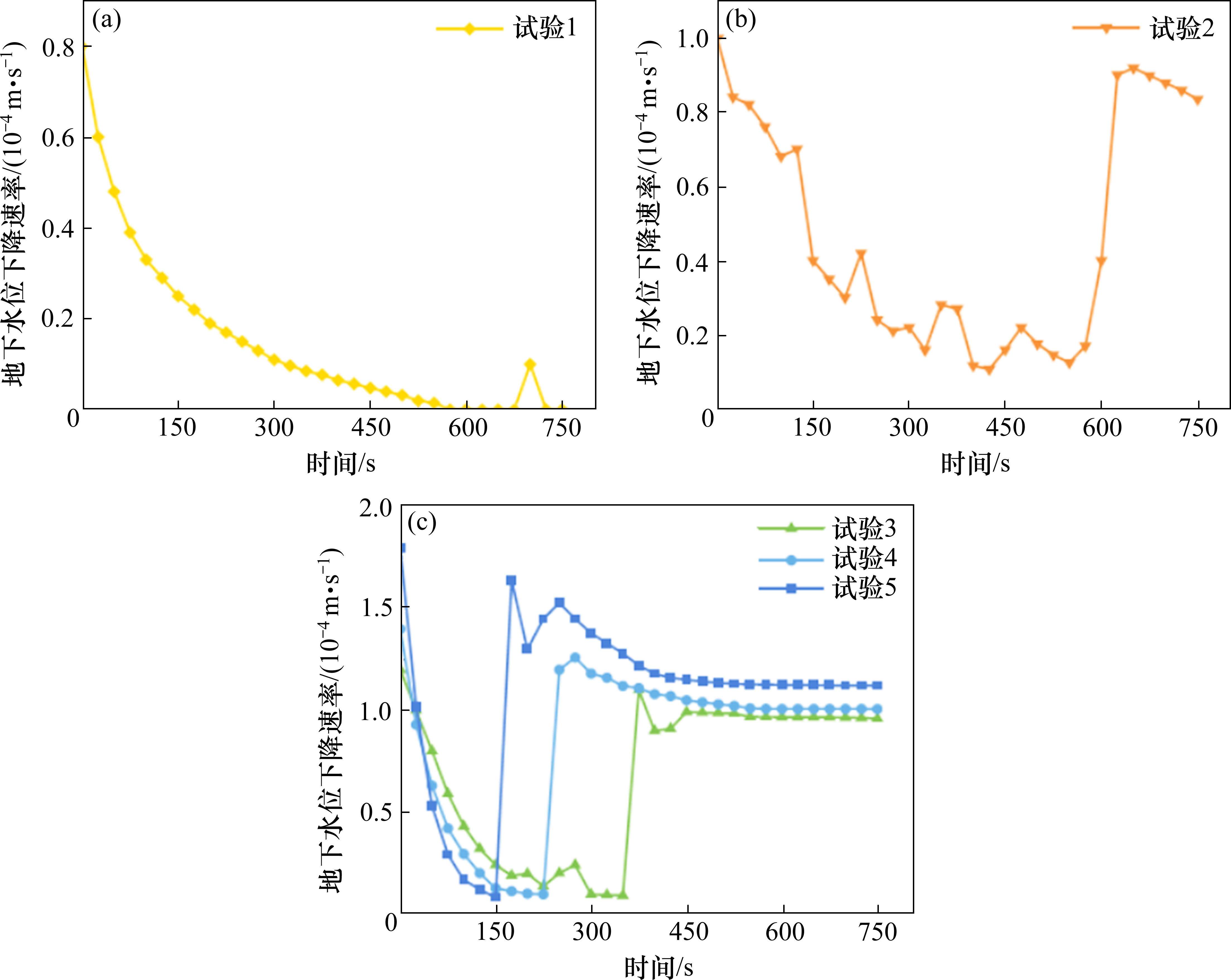
在每组实验中,地下水位下降速率并不等同于排水速率。地下水位下降所产生的真空负压会阻止地下水的垂向排泄,导致地下水位下降速率并不是一个定值。如图5所示,地下水位下降速率的曲线变化趋势与真空值变化相反。试验1盖层未塌陷,地下水位下降速率在真空负压的影响下逐渐减小直到排水停止。由于盖层并不是完全不透气材料,因此在排水停止后,偶尔会出现突然的排水现象。对于发生塌陷的试验2~试验5,地下水位下降速率均存在3个阶段。第1个阶段是在塌陷发生前,地下水位下降速率呈逐渐减小的趋势,并且减小趋势逐渐变缓。在第2阶段盖层破坏发生塌陷,这一阶段历时较短,水位下降速率从谷值开始急剧增大。第3阶段由于盖层完全破坏,溶洞内真空负压消失,地下水位在自然重力及大气压条件下恢复下降的趋势。
3) 盖层内孔隙水压力变化
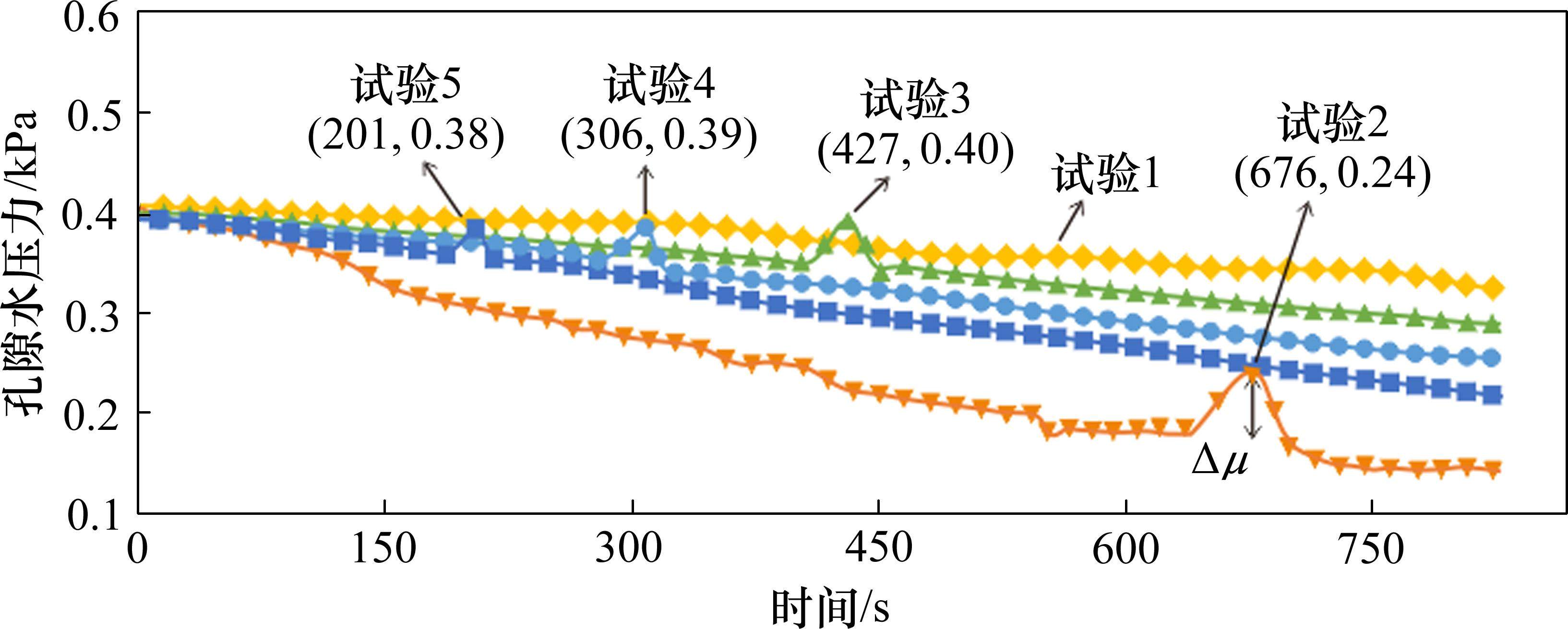
如图6所示,初始孔隙水压力约为0.4 kPa。随着排水开始,盖层内的孔隙水压力逐渐减小。在塌陷阶段,试验2~试验5的孔隙水压力表现为先突增后突减,该曲线段呈“倒V形”,随后孔隙水压力又恢复逐渐减小的趋势。试验2~试验5“倒V形”曲线段的增幅Δμ分别为0.06、0.05、0.04和0.03 kPa,发现该增幅随排水速率的增大而减小。“倒V形”曲线段的峰值时间分别为676、427、306和201 s,与塌陷发生时间相比较,明显看出盖层内的孔隙水压力变化具有滞后性。
4) 盖层表面变形特征
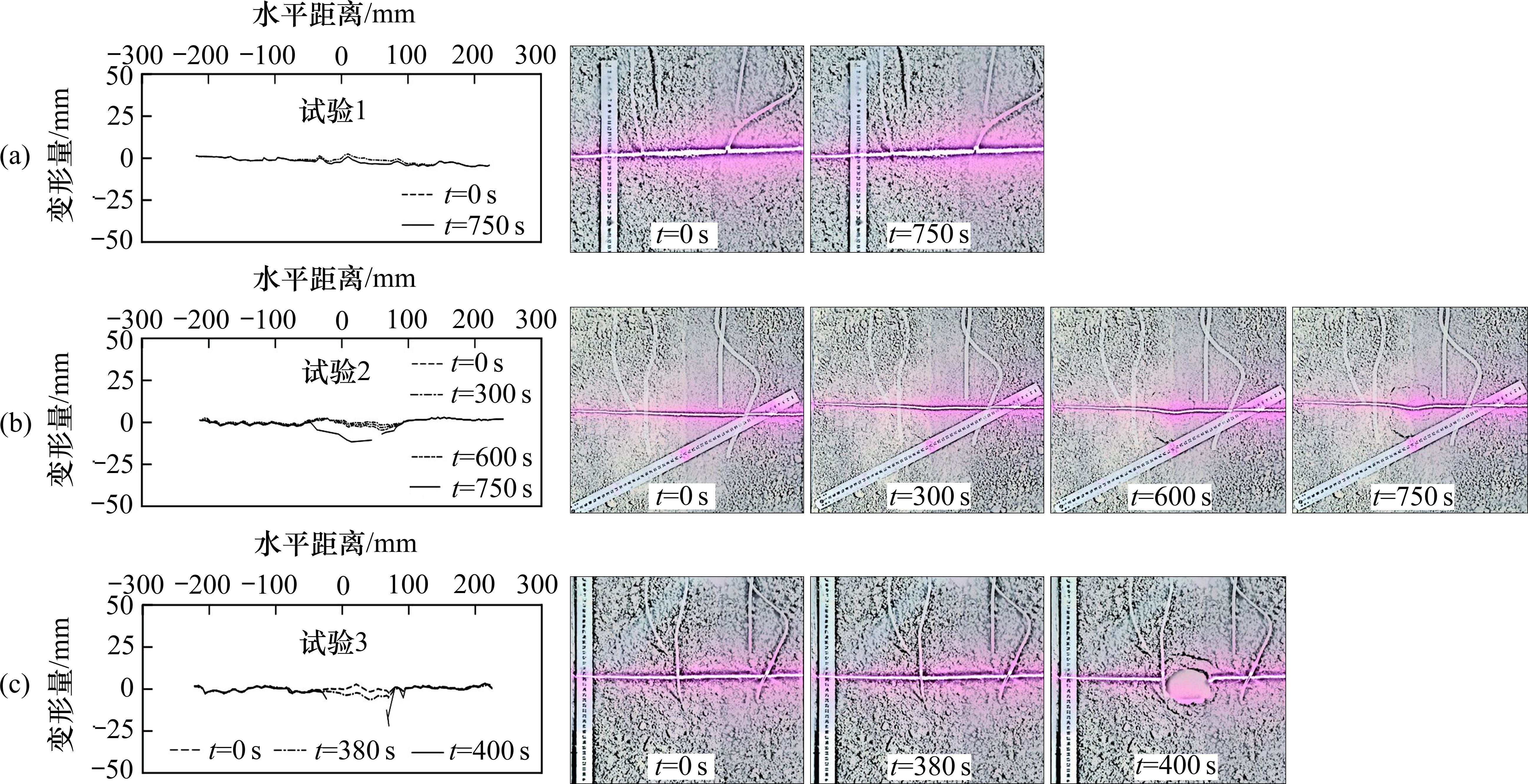
水位下降引起的真空负压会对盖层产生向下的真空吸蚀力,盖层由此变形下凹。以盖层表面为基准面,即盖层的初始变形量为0,观察地下水位下降过程中盖层的变形或塌陷情况。试验1盖层产生了约2.6 mm的累计变形量,但其表面并未观察到明显破坏或变形现象(图7(a))。试验2随着时间的增加溶洞开口上方的盖层逐渐产生一圆形裂缝。在时间t=612 s塌陷发生前,裂缝逐渐加宽但变形不明显。在塌陷发生后,盖层并未陷落,产生了最深约12.4 mm的累计变形量(图7(b))。试验3~试验5盖层的变形情况类似。如图7(c)所示,试验3在塌陷前仪器监测到盖层向下的垂向变形明显,达5.4 mm。当溶洞内真空负压足够大时,盖层无征兆突然坍塌,并形成一圆形塌陷坑。塌陷坑周围可能会出现拉伸裂缝。
3 基于盖层稳定性判别模型的试验结果验证
3.1 盖层稳定性判别模型
为了进一步验证实验结果的可靠性,对阻-透型盖层的受力状态进行分析(图8)。当溶洞内地下水位下降时,取溶洞开口上方盖层(潜在塌陷体)为研究对象,假设上层土体厚度为Z1,下层土体厚度为Z2,上下2层土体的总重力为G、溶洞内的真空吸蚀力为P、砂性土层中因水位下降引起的渗透压力为J、盖层土体侧向摩擦力为f。
根据莫尔-库伦强度理论,极限平衡条件下盖层土体达到破坏时其主应力满足下列方程
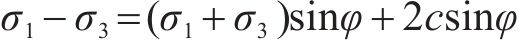
式中: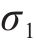
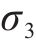
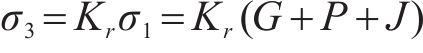
式中: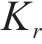
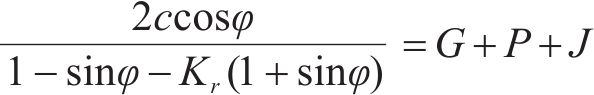
式(3)左侧为摩阻力f。可见,公式左侧项为抗塌力,用

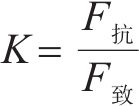
显然,当K>1时,盖层土体处于稳定状态;当K=1时,盖层土体处于极限平衡状态;当K<1时,盖层土体破坏,塌陷发生。
1) 抗塌力(F抗)
大量试验表明,含水量对土的强度影响较大,且在一定含水量范围内,非饱和土的强度随含水率的降低而增加[22-23]。因此,在地下水位下降过程中,盖层抗塌力可表述为
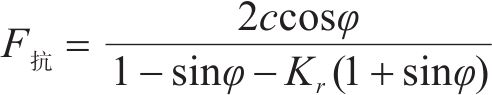
其中
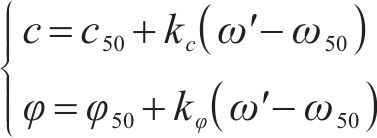
式中:
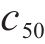
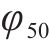
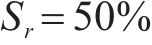
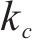
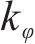
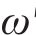
2) 致塌力(F致)
盖层内存在地下水时,盖层土体的自重为
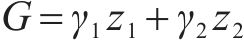
式中: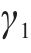
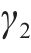
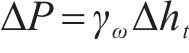
式中: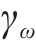
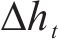
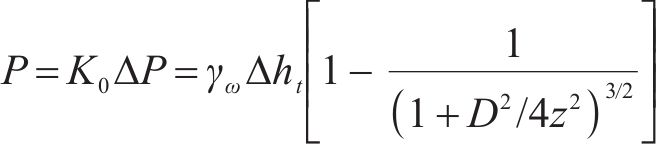
式中: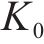
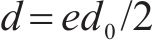
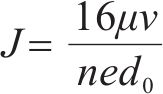
式中:v为平均渗透流速,m/s;μ为水的动力黏度,取值1.01×10-6 kPa∙s;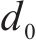
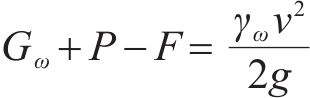
式中: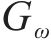
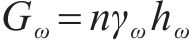
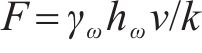
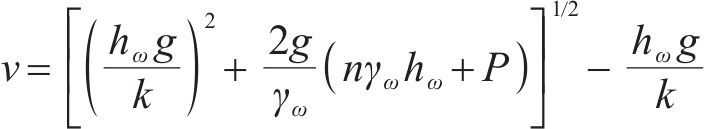
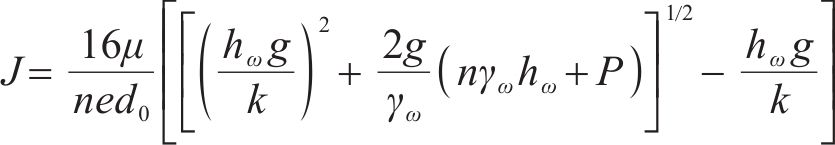
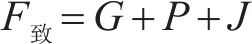
其中
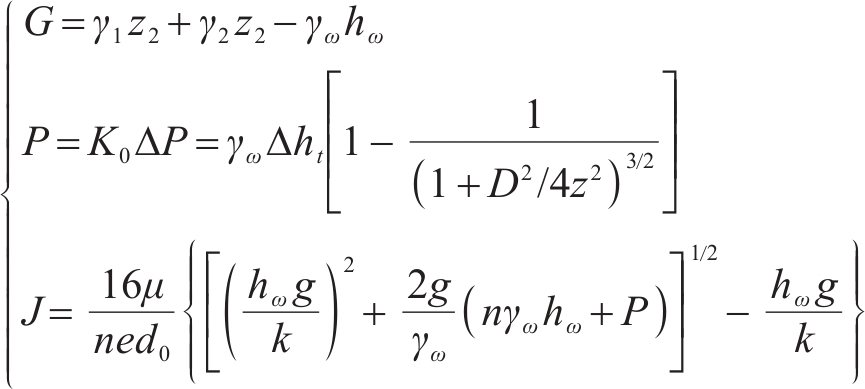
3.2 判别模型计算结果
根据前述基于极限平衡法所提出的盖层稳定性判别模型,对塌陷与否进行判别,并结合物理模拟试验结果进一步验证。根据工程地质手册(第4版)查询黏性土及砂性土的经验值,结合土工实验数据代入式(5)~(6),计算出两盖层抗塌力,黏性土层抗塌力较小并取其值,其中黏性土经验值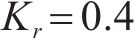
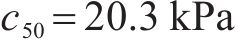
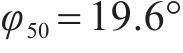
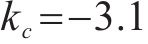
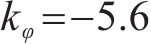
| 试验方案 | 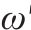 | G/kPa | P/kPa | J/kPa | 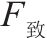 | 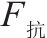 | 塌陷与否 | |
|---|---|---|---|---|---|---|---|---|
| 判别模型 | 物理模型 | |||||||
| 试验1 | 10.3 | 128.0 | 193.8 | 1.6 | 323.4 | 329.8 | 否 | 否 |
| 试验2 | 17.7 | 64.4 | 0.6 | 193.0 | 302.5 | 否 | 是 | |
| 试验3 | 23.3 | 180.7 | 1.5 | 310.2 | 284.3 | 是 | 是 | |
| 试验4 | 25.6 | 168.2 | 1.4 | 297.6 | 277.5 | 是 | 是 | |
| 试验5 | 30.5 | 157.0 | 1.3 | 286.3 | 263.6 | 是 | 是 | |
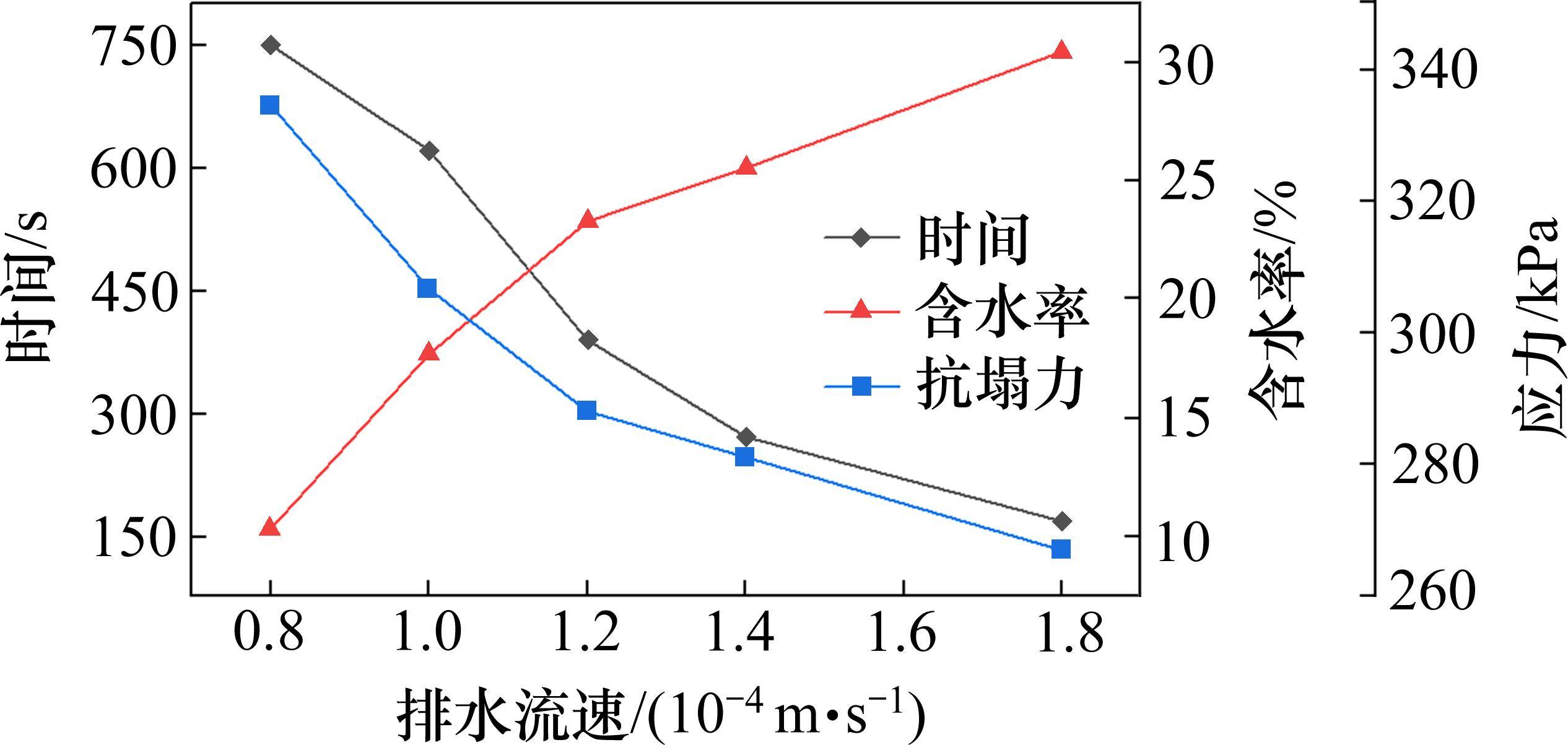
判别模型数据显示,致塌力主要由盖层自重和真空吸蚀力组成,渗透压力可忽略不计。如图9所示,排水速率、塌陷所需时间、盖层含水率以及抗塌力之间存在联系。在抗塌力的计算过程中,含水率作为唯一变量,与抗塌力呈反比。而盖层的含水率随塌陷时间的减小逐渐增大。这是因为塌陷所需时间越短,越不利于盖层地下水的排泄。因此排水速率越大,抗塌力越小。
3.3 验证及分析
如表3所示,物理模型与判别模型两者结果相比较,发现除试验2外,其余结果总体都较吻合。试验2地下水位下降过程中,渗透压力的存在将促使地下水迁移,携带盖层细颗粒并冲刷,使得盖层内部产生结构性破坏,盖层自身强度大大减小。同时外界大气也会不断补给到溶洞内,导致溶洞内不能形成较高的负压吸蚀力,因而致塌力相对较小。抗塌力来源于盖层自身强度,由于抗塌判别模型为解析模型,其计算结果为未破坏盖层时的抗塌力,使得计算结果与物理模型结果相反。
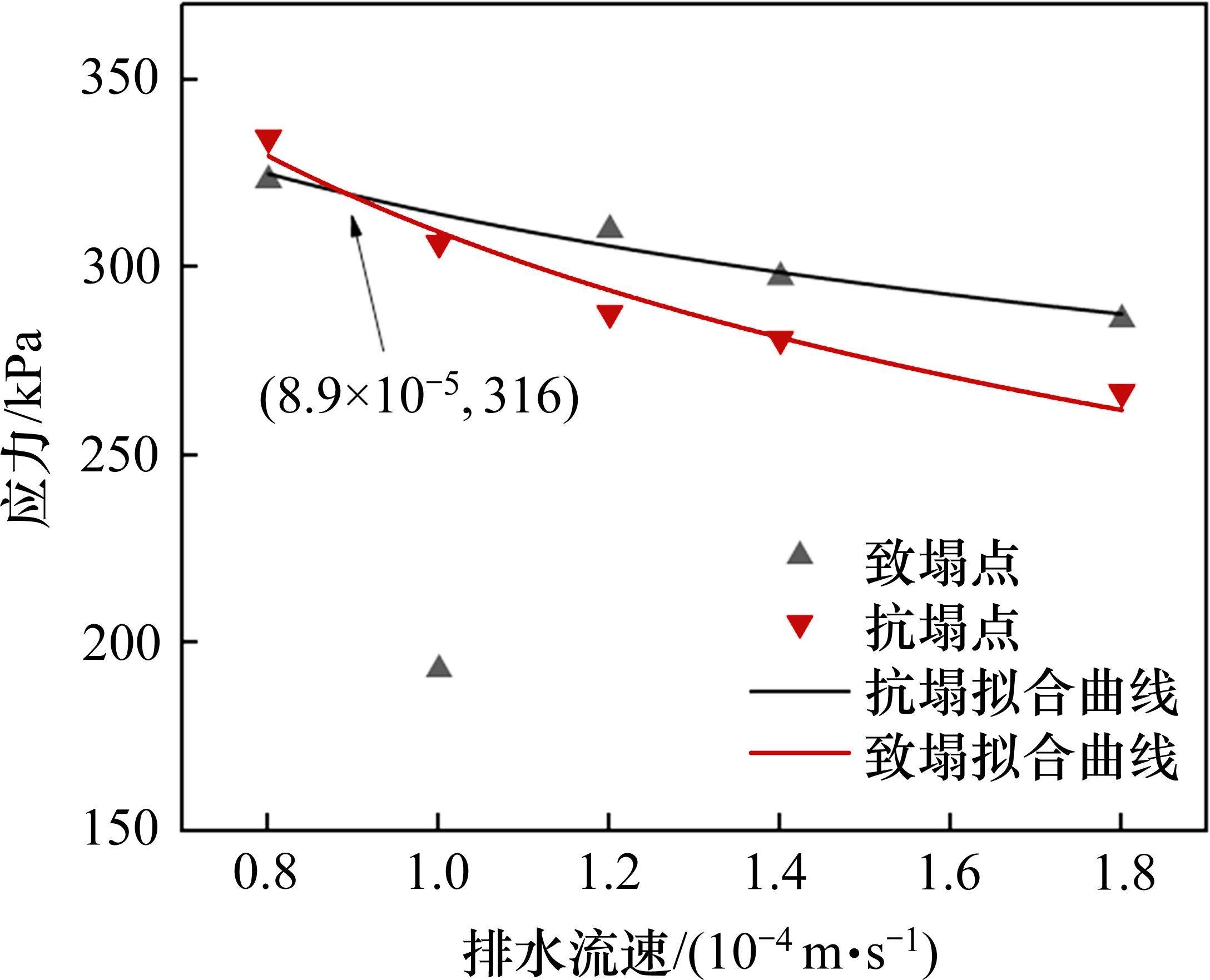
对5组试验进行拟合分析发现(图10),抗塌、致塌拟合曲线交点的临界排水速率为8.9×10-5 m/s。当排水速率大于该临界值时,致塌拟合曲线位于抗塌拟合曲线上方,塌陷能够发生。致塌、抗塌拟合曲线均随着排水速率的增大而减小,但在实际情况中,由于下伏可溶岩层的透水性、裂隙溶隙发育程度等因素的影响,排水速率并不能无限增大或减小。在致塌力计算过程中,渗透压力虽然较小,但渗透压力可能导致覆盖层产生结构性破坏,如试验2,这在图中表现为致塌点偏离致塌拟合曲线。
4 岩溶塌陷成因机理探讨
从力学的角度来看,阻-透盖层会出现什么样的变形行为,塌陷什么时候发生,这取决于作用在盖层上的致塌力以及盖层本身的抗塌力两者之间的大小关系。由判别模型的分析可知:1) 本文中盖层的强度是指抵抗破坏和过度变形的能力,在数值上可看做是抗塌力(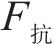

溶洞内地下水位的初始下降速率对塌陷的形成及演化起关键作用。根据相似关系,可知在实际工程中地下水位下降速率的临界值为8.9×10-3 m/s。当地下水位下降时,存在2种情况:1) 初始下降速率小于临界值时,溶洞内的真空负压随水位的下降不断增大,但其增长速率在不断减小,直到减小到与外界大气的补给速率持平后,真空负压保持不变,但此时的致塌力仍小于抗塌力,因此盖层可能发生变形,但将一直处于相对稳定状态,塌陷不会发生。2) 初始下降速率大于临界值时,当地下水位开始下降,孔隙水位同时也在缓慢下降,但此时致塌力的增长速率远大于抗塌力的增长速率,为了抵抗快速增大的致塌力,溶洞开口上方盖层表现为变形下凹,并可能在塌陷坑周围产生裂缝,这一变形阶段往往持续时间较长。随着地下水位持续下降,盖层变形不断增加,当致塌力增大到等于抗塌力时,覆盖层将处于临界状态,之后塌陷急剧发生。这一过程可总结为盖层逐渐向下变形和突然失稳塌陷2个阶段。
5 结论
1) 物理模型试验表明,排水速率不同,盖层的变形、塌陷情况明显不同。排水速率越大,溶洞内真空值上升越快,真空峰值越小,塌陷发生所需时间越短,盖层越容易发生变形或塌陷。盖层内的孔隙水压力在塌陷阶段出现“倒V形”曲线段,且该变化具有滞后性。地下水位下降速率与溶洞内真空负压相互响应,其变化与真空值相反。
2) 利用判别模型对物理模拟试验结果进行检验,两者总体吻合。除盖层本身的自重外,地下水位下降产生的渗透压力、真空吸蚀力是触发岩溶地面塌陷的关键因素。若盖层内部产生结构性破坏,则计算结果与物理模型结果相反,此时判别模型失效。
3) 开展的物理模型试验及提出的判别模型基本能反映地下水位下降条件下阻-透型岩溶塌陷的致塌机理。致塌力和抗塌力均随着地下水位的下降而增大,当地下水位的初始下降速率大于临界值8.9×10-3 m/s时,致塌力的增长速率才能大于抗塌力的增长速率,从而赶超抗塌力,形成塌陷。在致塌力和抗塌力相互抗衡的过程中,盖层将经历盖层逐渐向下变形和突然失稳塌陷2个阶段。在隧洞抽排水过程中,为防治塌陷发生或保护含水层的可持续性,应控制地下水位下降速率小于该临界值。
Land deformation and sinkhole occurrence in response to the fluctuations of groundwater storage: an integrated assessment of GRACE gravity measurements, ICESat/ICESat-2 altimetry data, and hydrologic models
[J]. GIScience & Remote Sensing, 2021, 58(8): 1518-1542.王英,肖先煊,许模.基于模型试验的阻-透型岩溶塌陷演化过程与机理研究[J].铁道科学与工程学报,2024,21(11):4815-4826.
WANG Ying,XIAO Xianxuan,XU Mo.Development process and mechanism of sinkhole with upper clayey and lower sandy layer cover based on model tests[J].Journal of Railway Science and Engineering,2024,21(11):4815-4826.

