桩承式路堤结构体系因施工速度快、路堤沉降变形小、相对经济合理等优点在软土路基工程中应用广泛。该路堤体系荷载传递过程中,因桩土刚度差异引起桩土差异沉降,以致路堤填土中土拱效应存在。国内外学者在各自假定的基础上,相继提出各种土拱模型以分析土拱效应。目前,较为常用的土拱模型有Terzaghi土柱模型[1]、北欧地区的三角形模型[2]以及HEWLETT等[3]提出的圆拱模型等。其中,Terzaghi土柱模型假定土拱滑移面为竖直面,推导简单,应用尤为广泛。国内外不少学者修正Terzaghi土柱模型,并将其应用于桩承式路堤的设计计算。例如,刘吉福等[4-6]基于Terzaghi土柱模型,将桩顶上方填土视为内土柱,桩间土上方填土视为外土柱,内外土柱交界面即滑移面上各点土体达到摩尔库仑极限状态,然后根据路堤-桩-土变形和应力协调,得到路堤下复合地基桩土应力比计算公式。但实际上,滑移面剪应力的发挥应与桩土差异沉降及填土高度等因素有关,内外土柱相对位移自桩顶平面往等沉面应是逐渐向上发展,且当桩土差异沉降较小,内外土柱相对位移较小时,土拱滑移面上各点的剪应力并非都能达到其极限值。刘吉福[4]引入摩擦力发挥程度系数β考虑这一因素影响,但计算时仍取β=1。俞缙等[7-8]在Terzaghi土柱模型基础上,假定滑移面上剪应力在等沉降面为0,然后沿竖向线性增加,在桩顶平面处达到极限值。Terzaghi土柱模型分析计算时,剪切面上剪应力大小的确定是关键,而其又与侧向土压力系数密切相关,但目前侧向土压力系数的取值尚无统一标准。俞缙等[7]使用主动土压力系数,ZHANG等[8]认为在该点竖向应力、水平应力、剪应力满足摩尔库仑强度准则,推导得到侧向土压力系数。亦有学者采用静止土压力系数[6-7]、被动土压力系数[3]等。而实际上,活动门下移伴随着土体应力的偏转,引起应力转移,导致竖向应力减小,水平应力增大,这意味着侧向土压力系数的取值应与主应力偏转相关。由于不同深度处土体的位移沿深度应该逐渐递进,更合理的侧向土压力系数应该随深度变化。此外,上述研究[4-8]均假定土拱区填土竖向应力沿水平向均匀分布,而实际上,由于土拱效应、路堤-桩-土相互作用等影响,路堤填土竖向应力沿水平向非线性变化。由上述分析可见,土拱效应的本质是土体产生不均匀变形,使得土体中的主应力发生偏转[9],滑移面剪应力从主应力偏转的角度分析确定更为合适。目前,采用主应力偏转理论分析土拱效应主要集中于挡土墙土拱[9-14]、抗滑桩土拱[15]和隧道土拱[16-19]。然而,桩承式路堤土拱有其自身特点,且土拱的发展与桩土差异沉降密切相关[5-8],需考虑路堤-桩-土变形和应力协调,以及滑移面深度范围内土体侧向土压力系数和主应力偏转的过渡和连续。为此,本文在Terzaghi土拱土柱模型的基础上,考虑主应力偏转的影响,结合路堤-桩-土应力位移协调条件,对桩承式路堤土拱效应进行分析,进而得到相应的桩土应力比和土拱高度,以期为桩承式路堤设计计算提供参考。
1 计算模型与基本方程的建立
1.1 模型建立
在路堤中线取相邻两桩间的填土为研究对象,建立如图1所示土拱分析模型,其中路堤高度H,桩径a,桩间距s,桩间净距2b。同Terzaghi土柱模型,假定滑移面竖直。因桩土刚度差异,桩间土上方路堤填土的沉降大于桩顶上方填土沉降,该沉降差随填土高度的增加不断减小,在距桩顶h处沉降差为0,即为等沉面。本文假定路堤高度H>等沉面高度h,即保证路堤填高下有完整土拱形成。以等沉面为z轴的O点,向下为正。在桩间土上方土柱内取一dz厚度的水平薄层单元进行受力分析,其竖向应力沿水平向非线性分布。
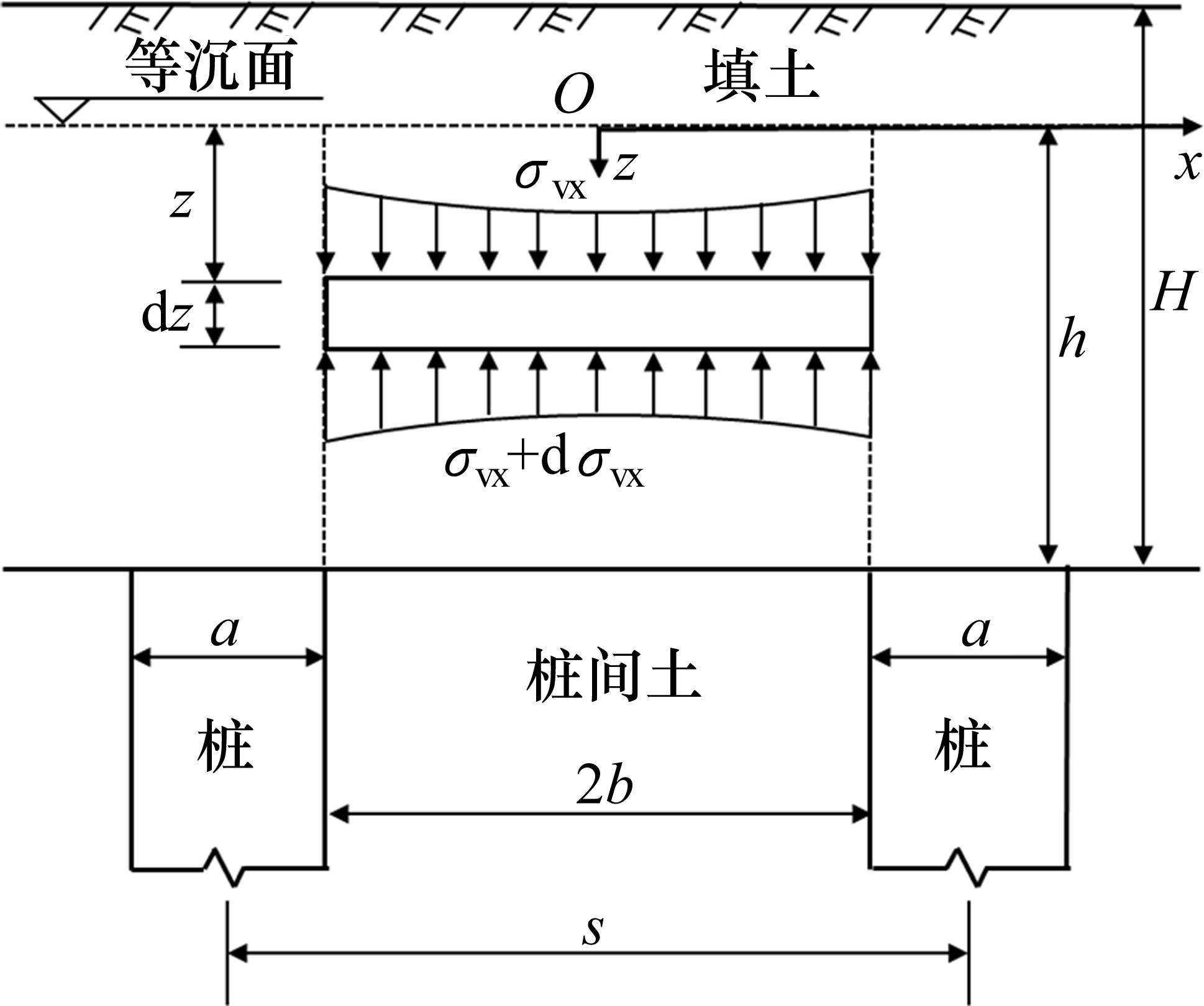
滑移面处的剪应力τ(z)使水平薄层单元的小主应力σ3方向发生偏转,假定所形成的小主应力轨迹为如图2所示的圆弧,其上任一点的切线代表该单元相应点的小主应力方向,大、小主应力(σ1与σ3)互相垂直。由于对称性,中点处小主应力方向为水平,且τ(z)仅在桩顶平面(z=h)处达到极限平衡状态。
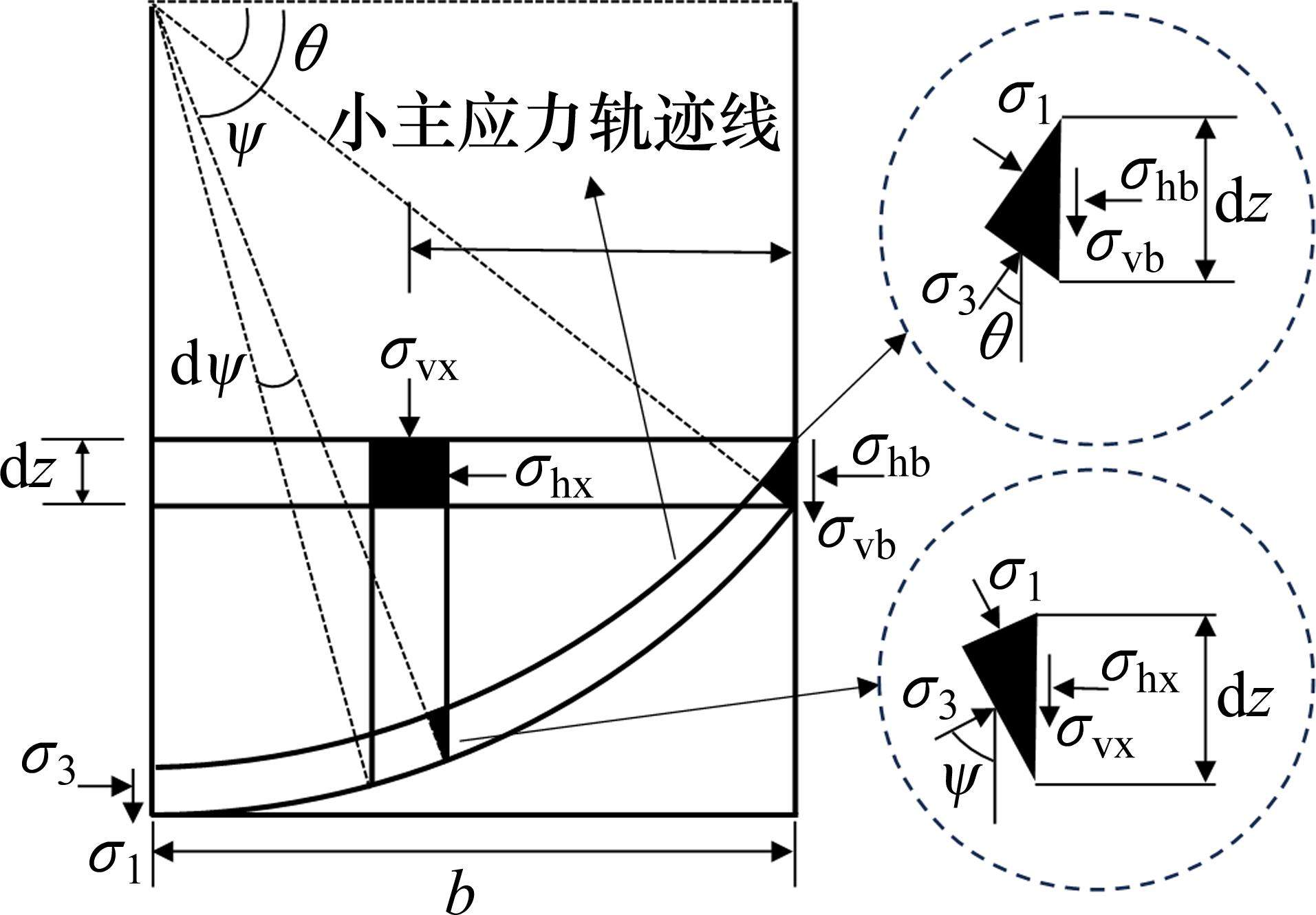
1.2 水平薄层单元受力变形分析
滑移面上的水平和竖向应力为:
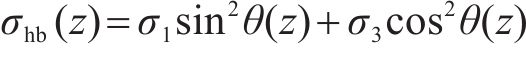
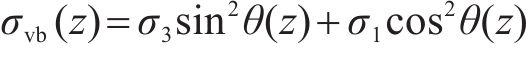
式中:θ为滑移面上小主应力偏转角,假定θ沿深度z线性变化。当z=0时,滑裂面上无剪应力,小主应力σ3不偏转,θ=0°;当z=h时,根据前面假定,剪应力达到其极限值,θ=(45°+φ/2),φ为土体内摩擦角。
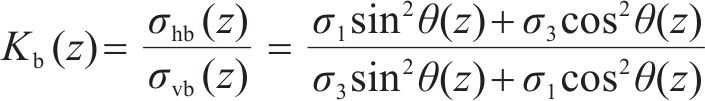
距滑移面x处的竖向应力σvx为:
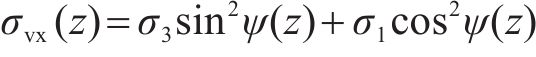
式中:ψ为计算点距滑移面x处小主应力迹线与竖直方向的夹角,且
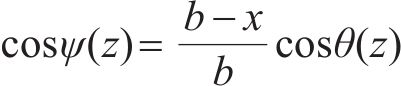
当x∈[0, b]时,ψ∈[θ,π/2]。
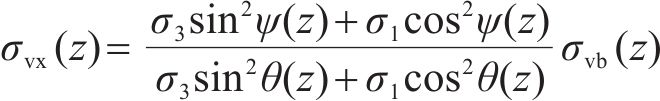
将应力σvx沿宽度b积分并除以宽度b可得到作用在桩间土薄层单元上的平均竖向应力(图3):
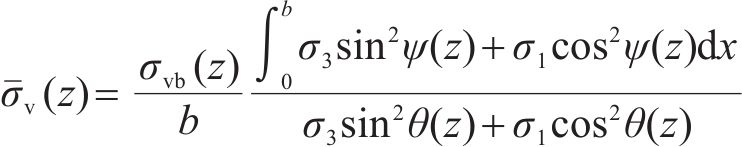

联立式(5)~式(7)求解可得z深度平均应力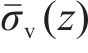
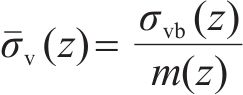
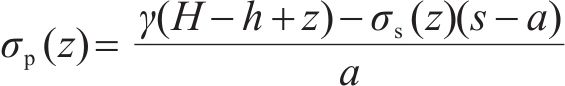
式中:m为小主应力轨迹线形状系数;Kp为被动土压力系数,Kp=tan2(45+φ/2)。
根据薄层单元竖向力平衡条件可得:
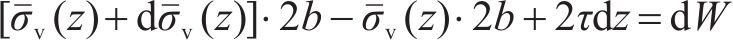
其中:
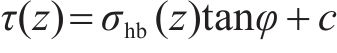
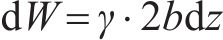
式中:c、W、γ分别为土体的黏聚力、自重和重度。
将式(4)、式(9)、式(11)、式(12)代入式(10)求解得:
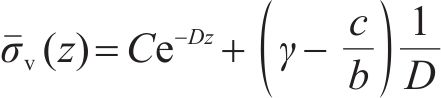
式中: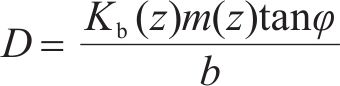
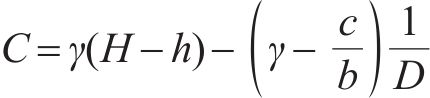
桩间土上填土平均应力σs(z)即为:
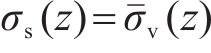
再根据z平面处桩间距范围内填土的竖向力平衡可得桩顶上方填土平均应力σp(z):
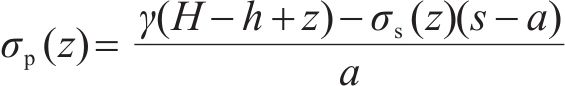
定义桩顶平面处桩上和桩间土上平均应力为σpt和σst,桩土应力比n为:
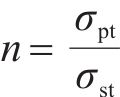
式中:σpt和σst分别由式(13)和式(16)取z=h得到。
等沉面处各点沉降相等,即有:
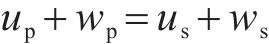
式中:up和us分别为等沉面至桩顶范围内桩上和桩间土上土柱的压缩量;wp和ws分别为桩顶平面桩、土沉降。
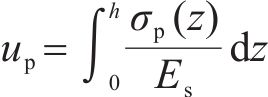
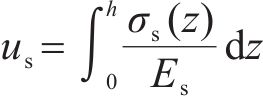
式中:Es为路堤填土压缩模量。
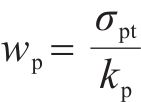
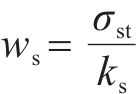
式中:kp为桩体刚度,可由基桩载荷试验确定;ks为桩间土基床系数,亦可由载荷试验确定,若无实测资料,可参照文献[20]并结合工程实际取值。
1.3 方程求解
由上述分析可见,拱高h难以直接求解,故本文采用试算法,反复迭代计算得到。具体计算步骤如下。
1) 初步计算时取h=4b。
2) 为便于分析,将h范围内土层平均分成N层,每一层的层厚为Δh=h/N(N不宜太小,以σs(zN-1)/σs(zN)<0.01为判断标准),等沉面到第i层土的计算深度为:
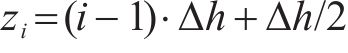
3) 将zi代入式(3)和式(9),计算相关系数Kb(zi)和m(zi),再由式(16)~式(17)计算得σp(zi)、σs(zi)及ni。
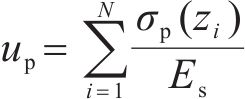
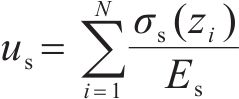
5) 将σpt和σst代入式(21)和式(22)求得桩wp和桩间土沉降ws。
6) 将up、us、wp、ws代入式(18)判断等式是否成立。若不成立,则根据桩土差异沉降调整土拱高度h,重复步骤1~步骤6,直至桩、土位移协调,式(18)成立,此时得到唯一土拱高度h以及最终的桩土应力比n等参数。
2 工程实例验证
2.1 工程实例1
为验证本文方法的可行性及编制程序的正确性,对文献[21-22]上海某工程桩承式路堤方案进行分析。计算参数如下:路堤高度H=5.6 m,黏聚力c=10 kPa,内摩擦角φ=30°,重度γ=18.5 kN/m3,压缩模量Es=7 MPa;桩体为现浇混凝土环形桩,桩间距s=3.0 m,桩径a=1 m,桩长=16 m,桩身刚度kp=56 790 kN/m3由实测的P~s曲线反算得到;桩间土为软塑粉质黏土,根据参考文献[20],桩间土体刚度取ks=400 kN/m3。
表1对比了不同计算方法所得该工程的桩土应力比以及土拱高度情况。表1中土拱高度的实测值是根据现场试验所得的桩间土对应的填土区域应力折减系数对应的转折点位置确定,详见文献[21]。由表1可见,本文方法求得的桩土应力比和土拱高度更接近实测值,其主要原因是本文的侧向土压力系数和随之引起的剪应力与其他方法不同(见图4和图5)。Terzaghi方法的计算结果偏大,主要原因是Terzaghi方法计算时假定摩阻力完全发挥,从而高估了滑裂面剪应力荷载传递的作用。刘吉福[4]以主动土压力系数作为侧向土压力系数(图4),但忽略了土体在等沉面至桩顶的不同深度处的应力变化(图5),因此结果较Terzaghi方法更接近实测值。俞缙等[7]通过考虑剪应力在不同深度处的线性分布,使计算得到的桩土应力比偏小。
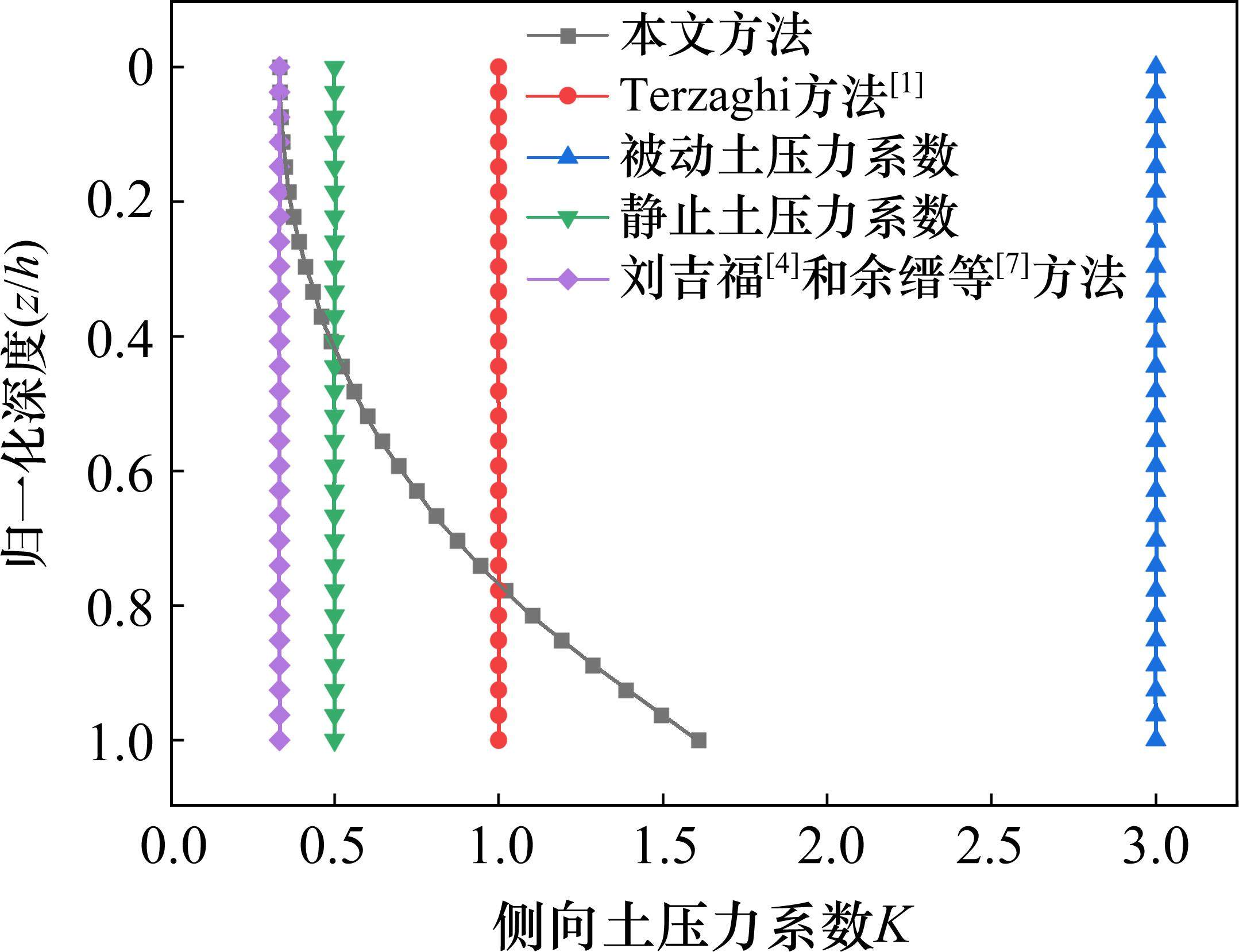
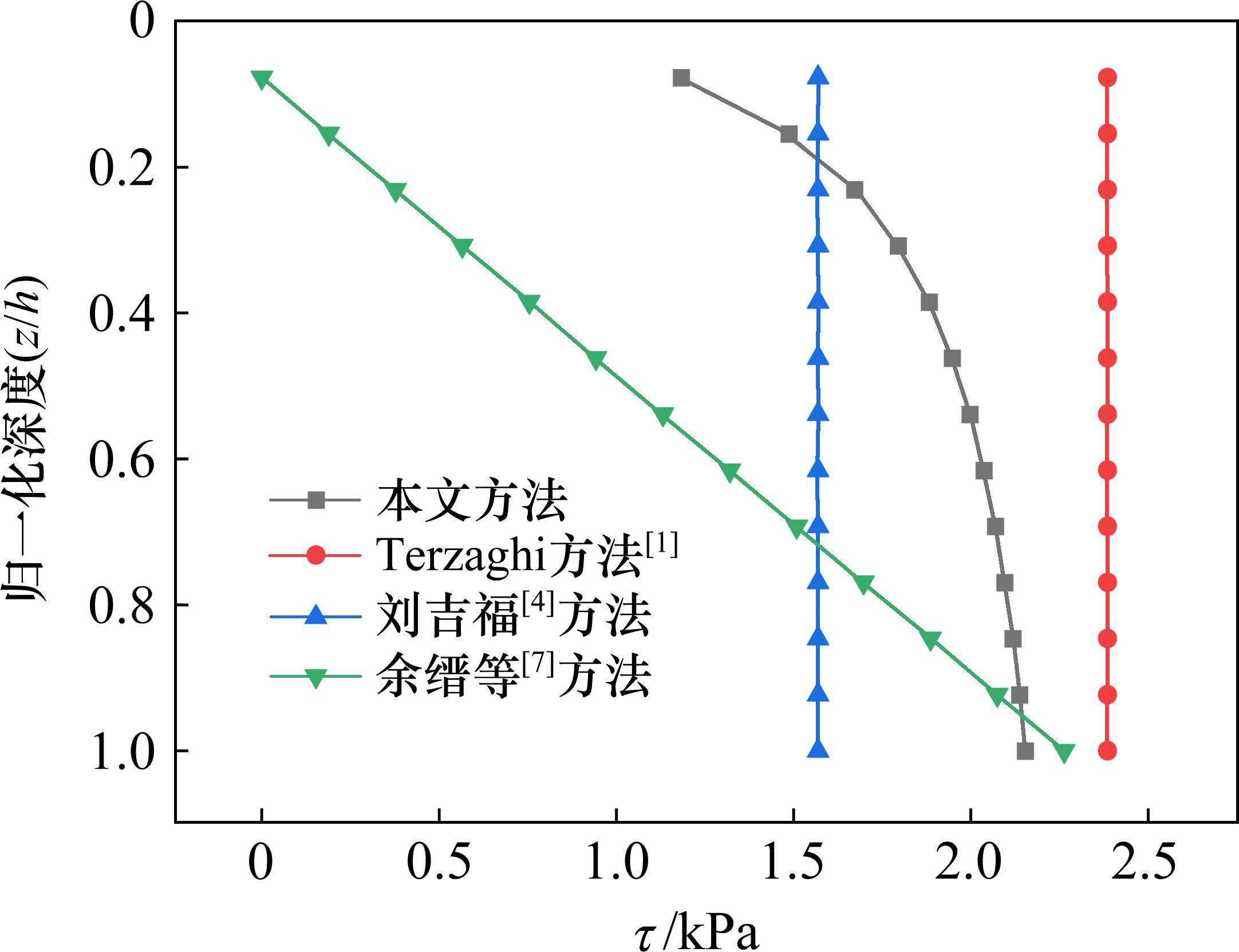
图4为不同方法侧向土压力系数随归一化深度(z/h)的变化,从图中可以看出,由于应力偏转角随深度发生改变,随着深度的增大,本文方法的侧向土压力系数逐渐增大。图5展示了不同计算方法下剪应力值随深度的变化趋势。Terzaghi方法[1]与刘吉福[4]方法均假定在滑裂面处剪应力达到极限值。其中,Terzaghi方法的剪应力值相对较大,这一差异主要源于Terzaghi方法在侧向土压力系数假定上采用了较大的值。
2.2 工程实例2
为进一步验证,采用本文方法对徐正中等[23-24]5个断面的现场实测结果进行对比分析。其中,D1、D2断面位于申苏浙皖高速公路,路基填高H=4 m,填料黏聚力c=10 kPa,内摩擦角φ=35°,平均重度γ=22 kN/m3,压缩模量Es=5 MPa,桩土刚度系数分别取为ks=400 kN/m3,kp=4 745 kN/m3。D1断面桩间净距1.1 m,桩帽0.9 m;D2断面桩间净距1.5 m,桩帽1.0 m。D3、D4和D5断面位于台缙高速公路,路基填筑高度H=4.5 m,填料黏聚力c=10 kPa,内摩擦角φ=35°,平均重度γ=22 kN/m3,压缩模量Es=5 MPa,取ks=400 kN/m3,kp=4 667 kN/m3。D3断面桩间净距1.2 m,桩帽1.3 m;D4断面桩间净距1.4 m,桩帽1.6 m;D5断面桩间净距1.0 m,桩帽1.0 m。
采用本文方法可得上述各断面处土拱高度、桩土差异沉降及桩土应力比,分别见表2和表3。
| 断面 | 桩土差异沉降/mm | 桩土应力比 | ||
|---|---|---|---|---|
| 计算值 | 实测值 | 计算值 | 实测值 | |
| D1 | 7.4 | 5.0 | 9.8 | 10.1 |
| D2 | 14.6 | 9.0 | 8.7 | 9.9 |
| D3 | 6.5 | 5.0 | 9.9 | 10.8 |
| D4 | 8.7 | 10.0 | 9.5 | 10.5 |
| D5 | 5.5 | 7.0 | 10.3 | 11.0 |
如表2所示,D1~D3、D5断面的土拱高度计算值均在实测值范围内,仅有D4断面的土拱高度计算值与实测值略高于实测值。此外,D1~D5断面的桩土差异沉降与桩土应力比计算值与实测值接近(表3),再次验证了本文方法的可行性。
3 影响参数分析
进一步探讨分析不同路堤高度、桩土刚度比及桩间净距等条件下主应力偏转对桩土应力比的影响,并与经典Terzaghi方法进行对比分析。计算过程中基本参数的取值与上述工程实例1保持一致。
3.1 路堤高度的影响
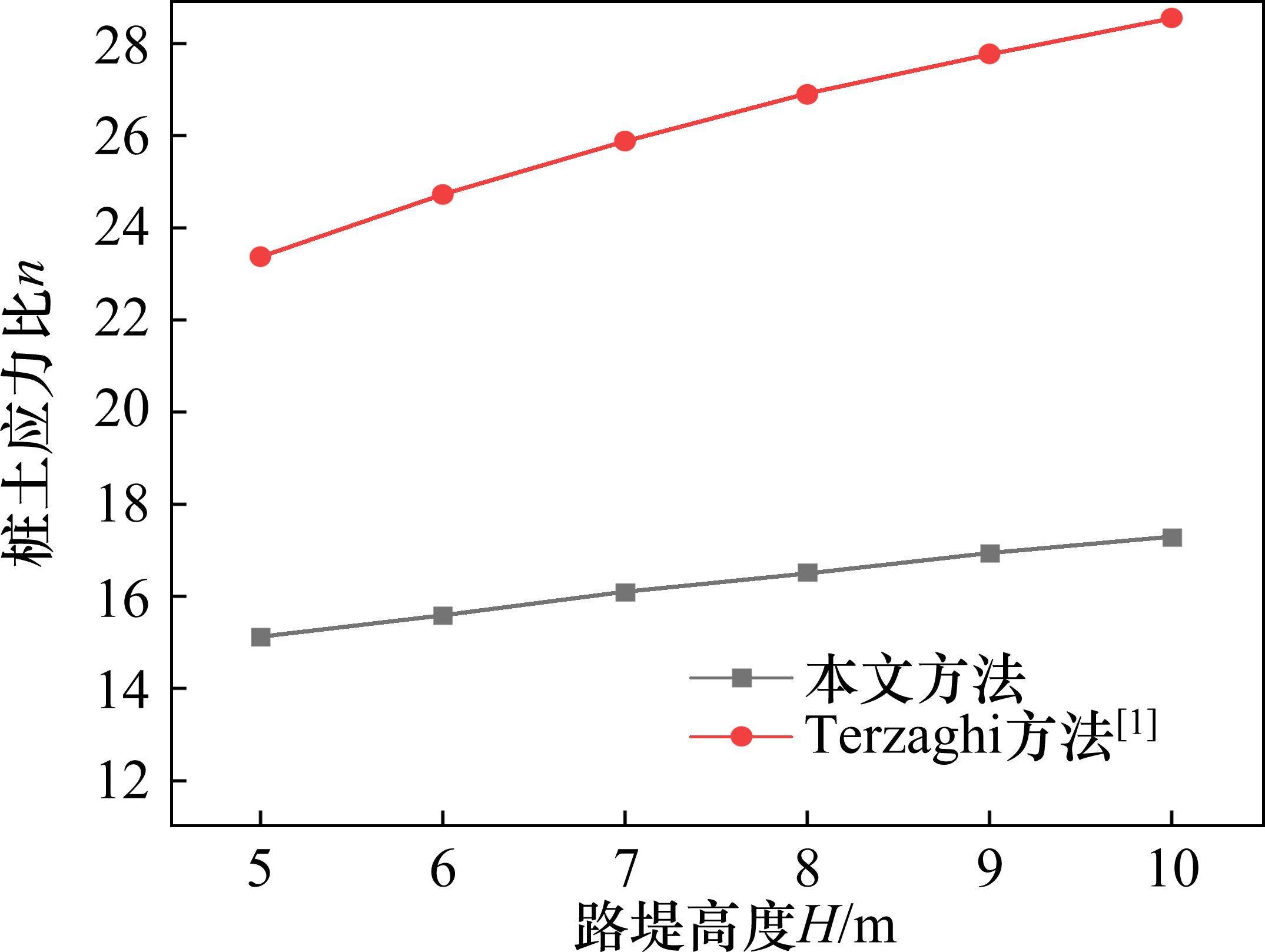
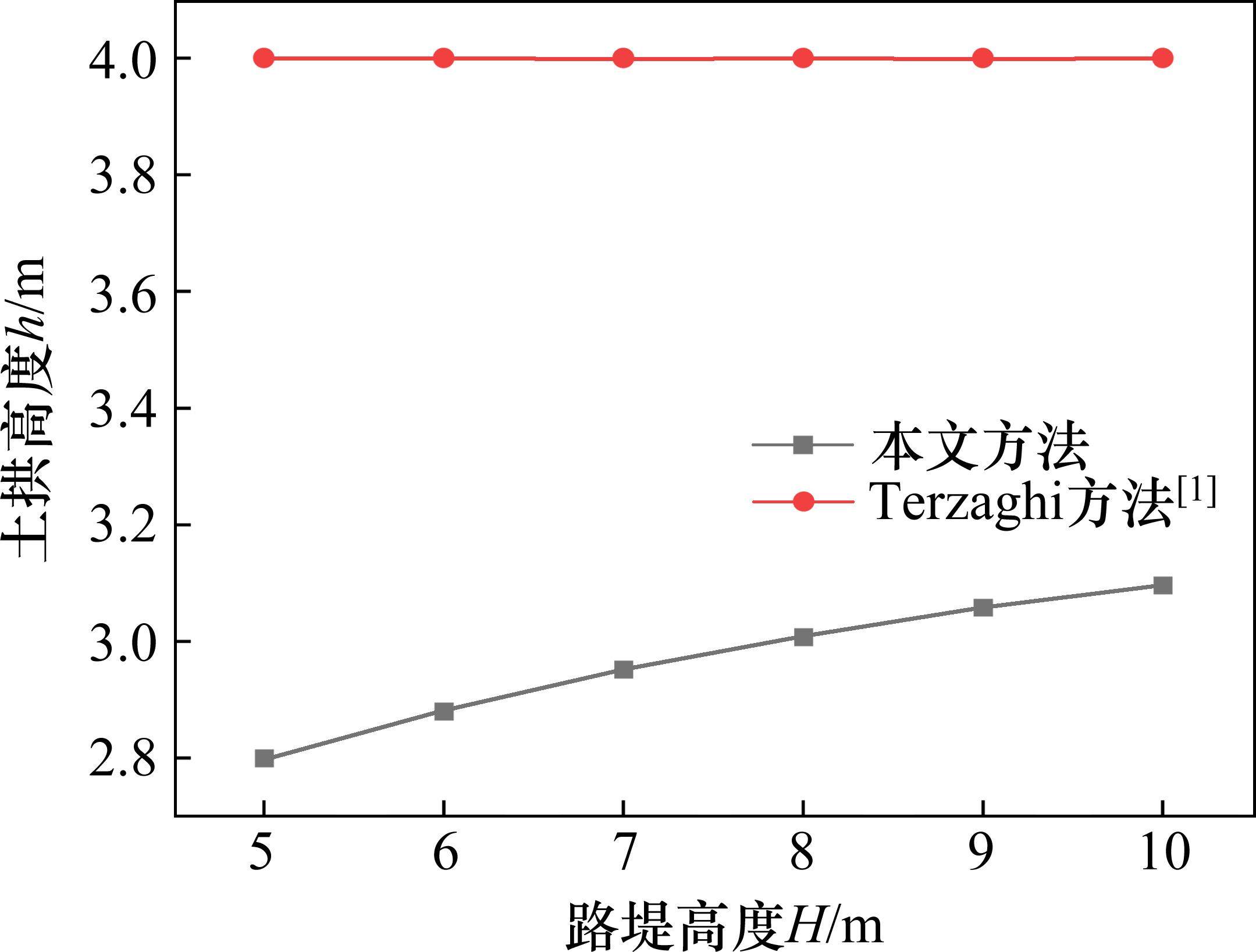
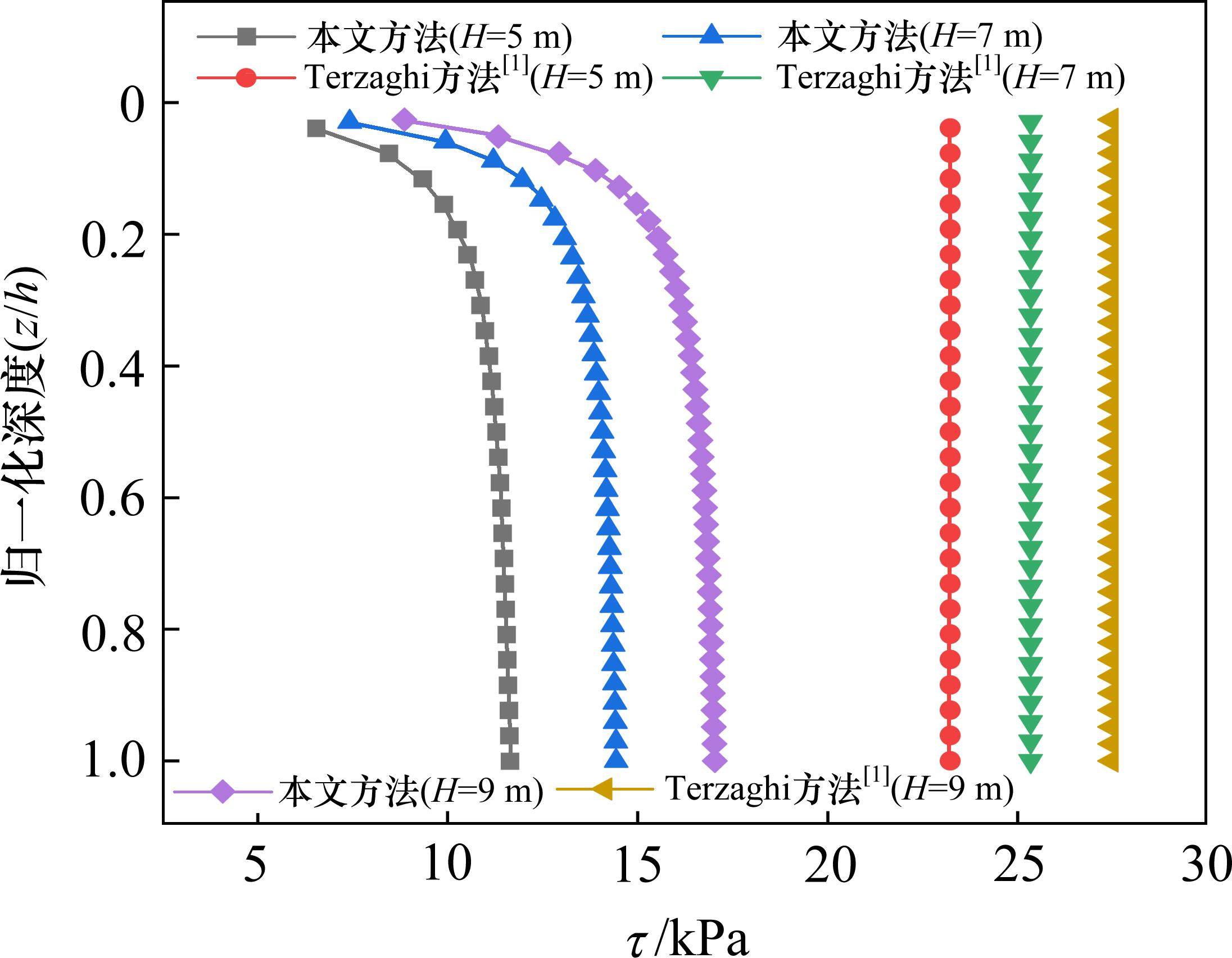
图6为路堤高度H=5~10 m,其他参数不变时,桩土应力比n随路堤高度H的变化情况。由图6可见,n随H的增大呈上升趋势,但增长速率逐渐减缓。考虑应力偏转(本文方法)较不考虑应力偏转(Terzaghi方法)所得桩土应力n偏小,且2种方法所得n的差异随着填土高度的增大而增大。例如,当H从5 m增大到10 m时,本文方法所得n从15.12增至17.28,增加了14.28%,而Terzaghi方法所得n从23.37增至28.55,增加了22.17%。原因主要在于本文方法(考虑应力偏转)所得的土拱高度随填土高度逐渐增加(图7),且滑裂面上剪应力随着深度逐渐发挥(图8),而Terzaghi方法对应的土拱高度与填土高度不相关,且滑裂面上剪应力完全发挥。
3.2 桩土刚度比的影响
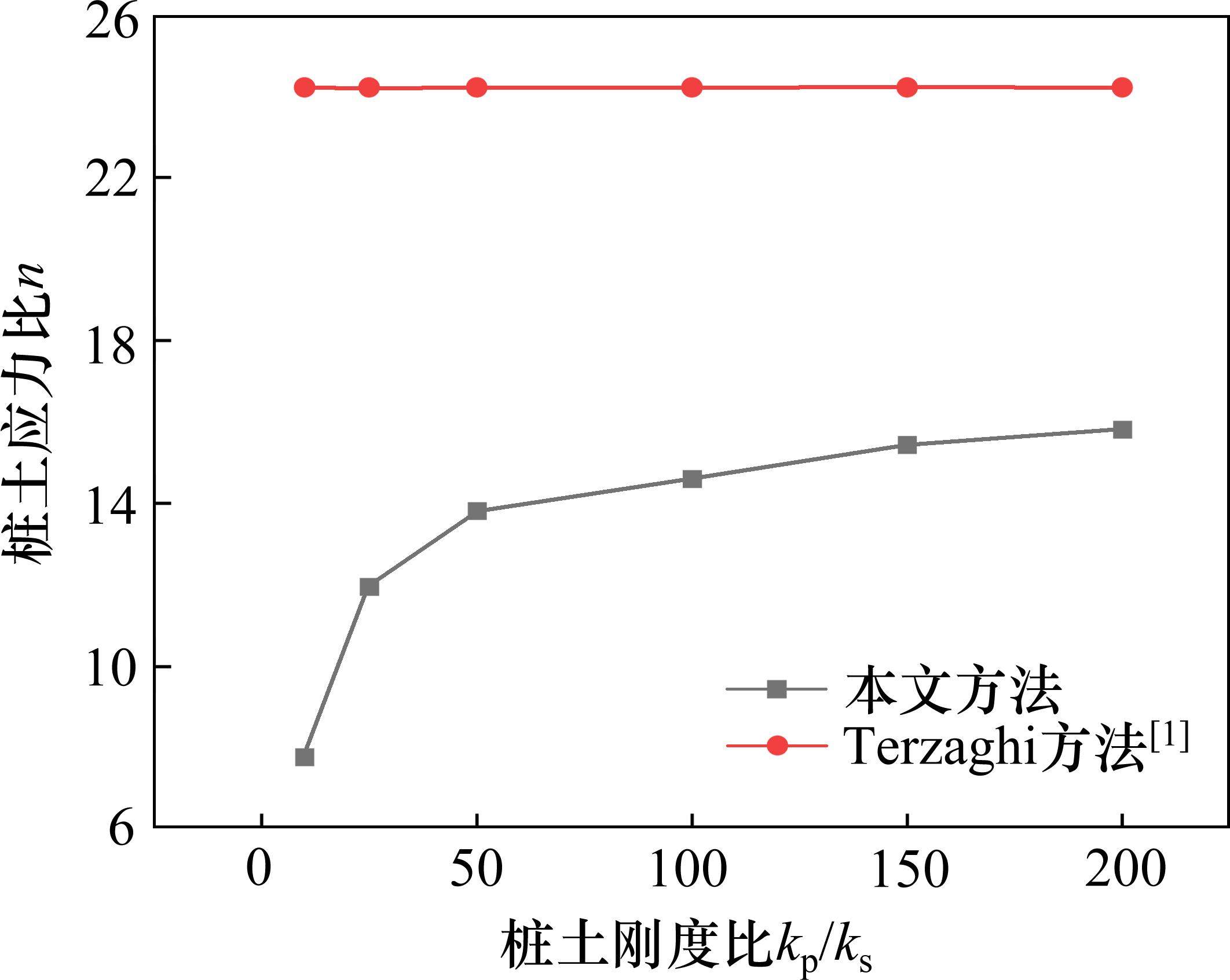
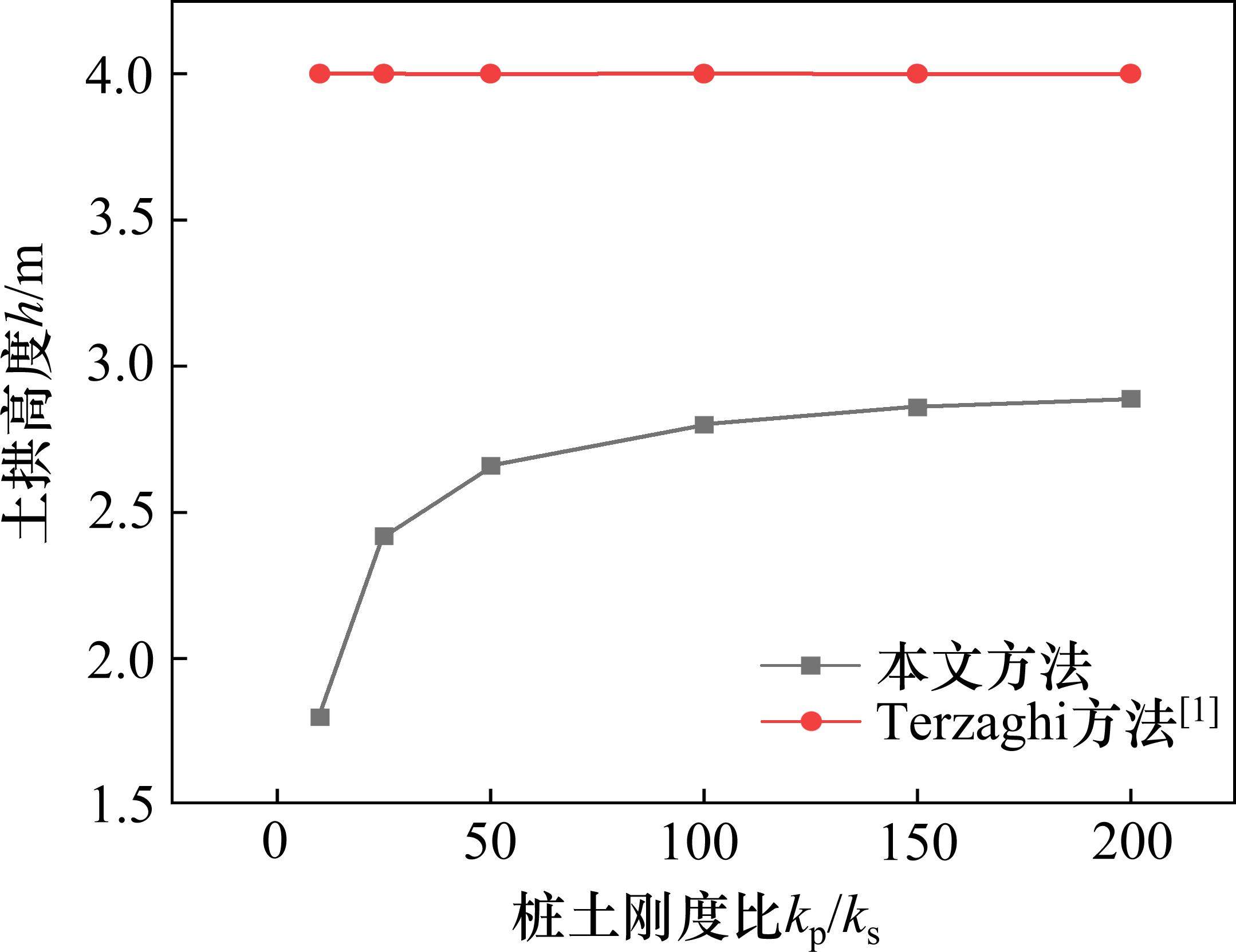
图9展示了桩土刚度比kp/ks=10~200,其他参数不变时,桩土应力比n随kp/ks的变化情况。如图9可见,当kp/ks小于50时,n随kp/ks增大而呈增大趋势;当kp/ks超过50时,土拱高度的增加趋势明显放缓,并逐渐趋于平稳。考虑应力偏转(本文方法)较不考虑应力偏转(Terzaghi方法)所得桩土应力n偏小,且差异随着桩土刚度比的增大而减小。例如,当kp/ks从10增大至200时,本文方法所得n从7.78增至15.82,增加了103.34%,而Terzaghi方法所得n与桩土刚度比不相关。原因主要在于本文方法(考虑应力偏转)所得的土拱高度随桩土刚度比逐渐增加(图10),且滑裂面上剪应力随着深度逐渐发挥(图11),而Terzaghi方法对应的土拱高度和滑裂面上剪应力均与桩土刚度比不相关。
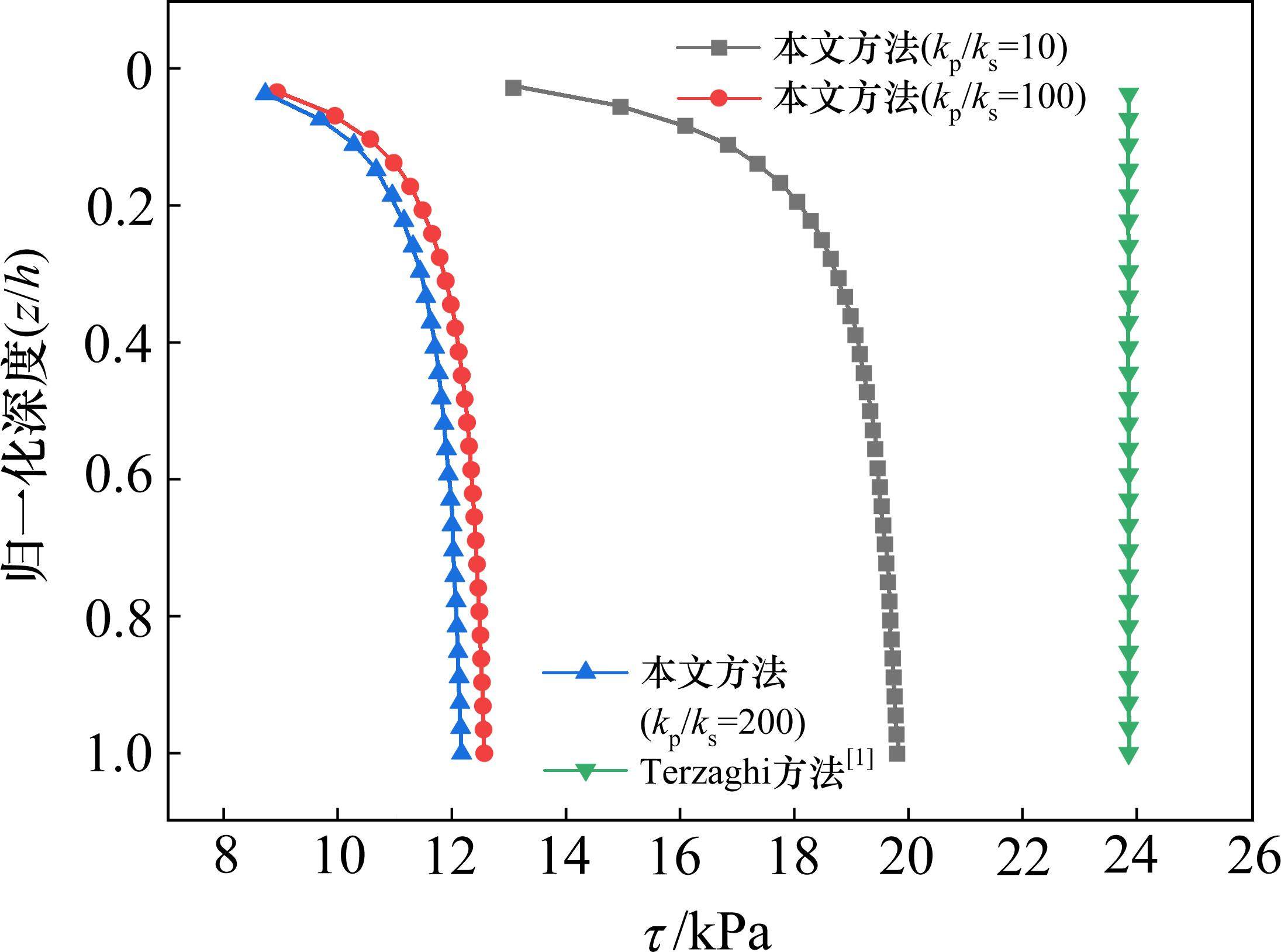
3.3 桩间净距的影响
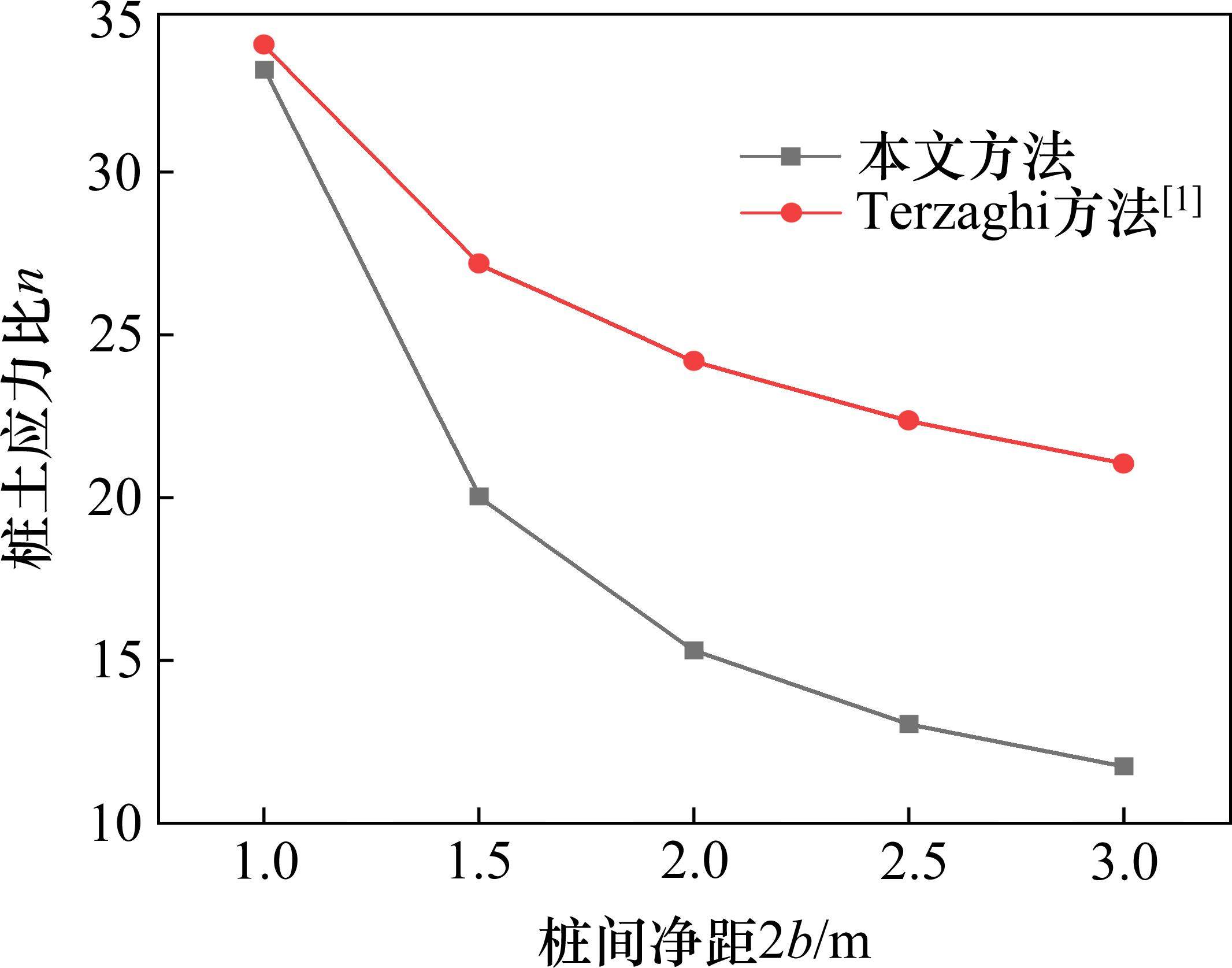
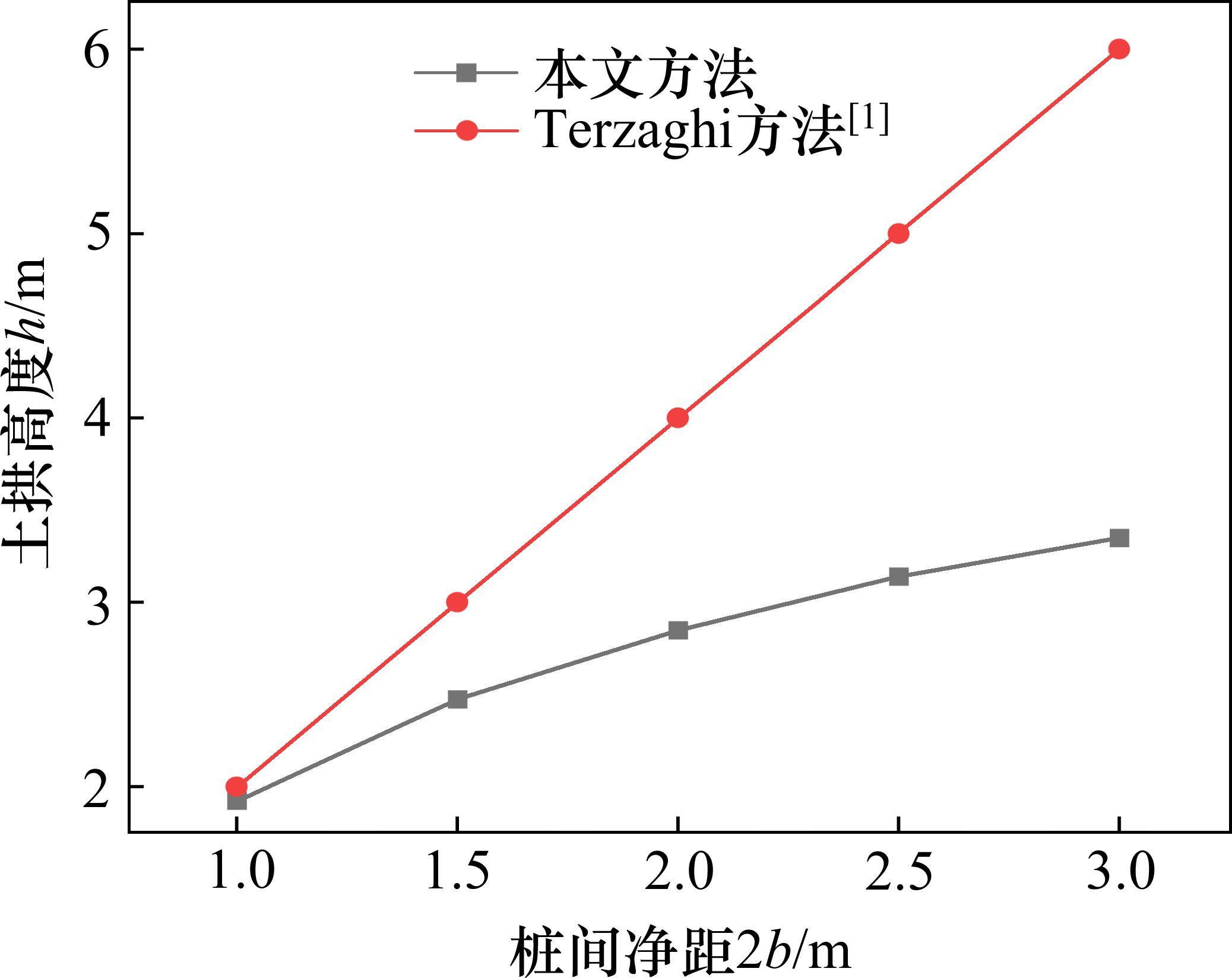
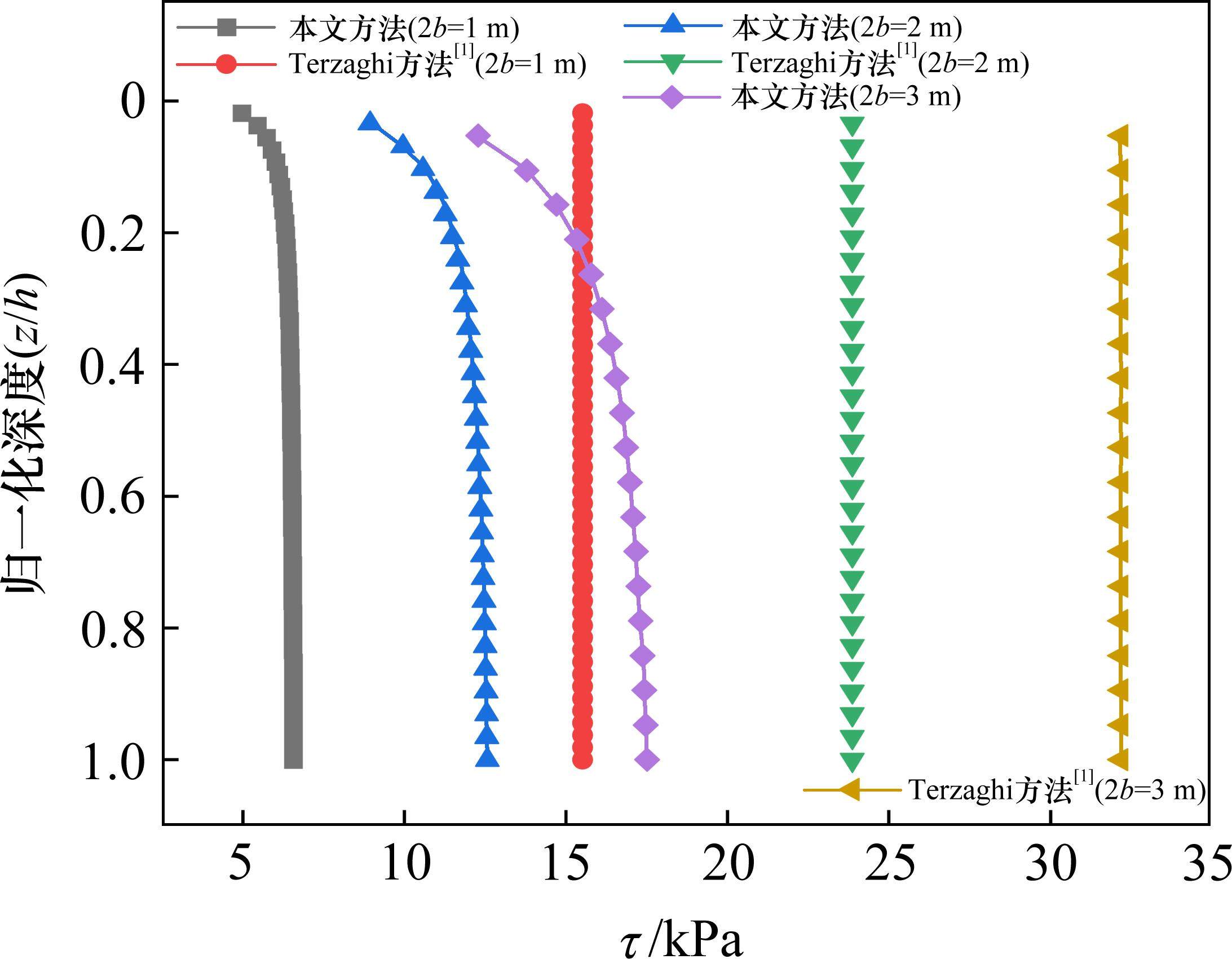
图12为桩间净距2b=1.0~3.0 m,其他参数不变时,桩土应力比n随桩间净距的变化情况。如图12所示,随着桩间净距的增加,桩土应力比逐渐减小,趋势逐渐放缓。考虑应力偏转(本文方法)较不考虑应力偏转(Terzaghi方法)所得桩土应力n偏小,且差异随着桩间净距的增大而增大。例如,当2b从1.0 m增加至3.0 m,本文方法所得的n从33.15降至11.76,降低了64.52%,而Terzaghi方法所得的n从33.91降至21.04,降低了37.95%。原因主要是在较小的桩间净距下,应力偏转的幅度相对较小(图13),此时剪应力(图14)变化也较小。随着桩间净距的逐渐增大,应力偏转效应逐渐增强,从而导致Terzaghi方法与本文方法在预测桩土应力比上的差异显著。此外,由图13可见,考虑主应力偏转后,土拱高度随桩间净距的增加逐渐增大,但趋势逐渐放缓。
4 结论
1) 本文方法考虑了滑移区域内土体主应力偏转的影响,有效优化了滑移面上侧向土压力系数及剪应力的分布模式。相较于传统Terzaghi方法,本文方法剪应力随深度递增,土拱高度则随路堤填土高度、桩土刚度比及桩间净距的变化而动态调整,且桩土应力比的变化趋势与Terzaghi方法相符,考虑主应力偏转的桩土应力较传统Terzaghi方法所得结果偏小,在工程设计中应考虑主应力偏转以避免高估桩的荷载分担作用。
2) 在考虑主应力偏转的情况下,对桩土应力比和土拱高度的影响进行了分析。结果显示,路堤填土高度对桩土应力比和土拱高度的影响相对较小,桩间净距对桩土应力比和土拱高度的影响最为显著。
3) 桩土刚度比的增加会导致滑移面上剪应力的下降。随着桩土刚度比的增加,桩土应力比和土拱高度均显示出相似的变化趋势。当桩土刚度比超过50时,桩土应力比趋于稳定,工程实践中考虑桩体选型和承载效能时应考虑这一因素影响,即当桩土刚度比超过50后,继续盲目增大桩体刚度并不能充分发挥出桩体分担荷载的作用。
张玲,林炜,周帅等.考虑主应力偏转的桩承式路堤土拱效应分析[J].铁道科学与工程学报,2025,22(03):1064-1073.
ZHANG Ling,LIN Wei,ZHOU Shuai,et al.Soil arch effect of pile-supported embankment considering principal stress deflection[J].Journal of Railway Science and Engineering,2025,22(03):1064-1073.

