能源桩具有承担上部结构荷载和地热交换两大重要功能,是一种经济高效的建筑节能解决方案。与普通桩基相比,能源桩在实际工作中受到循环温度变化的影响。周期性的温度变化引起桩体的反复膨胀和收缩,导致桩-土界面的循环加卸载,从而改变能源桩的热力响应。因此,对循环温变荷载作用下桩-土相互作用进行研究具有重要意义。
针对能源桩的热力学响应,国内外学者开展了大量的研究。LALOUI等[1-4]的试验结果表明,温度变化引起的桩体胀缩变形将影响桩-土相对位移,从而改变桩-土界面的轴力和侧阻力分布。NG等[5]采用离心机试验分析了有、无外部荷载及不同温度增量下能源桩的承载特性。STEWART等[6]采用离心机试验研究了粉土中端承型能源桩 桩-土界面的相互作用机理。GOODE等[7]根据离心机试验结果,探究了桩端约束条件对能源桩承载性能的影响。NGUYEN等[8-9]通过模型槽试验,研究了能源桩在多次温度循环作用下的桩顶位移变化规律。以上结果表明,在进行能源桩设计时,需合理考虑温度对桩身应力和变形的影响。
目前,针对能源桩承载性能的研究大多是在5次以内温度循环的条件下进行的,针对长期温度循环的研究一般采用有限元方法。如OLGUN等[10]利用有限元软件分析了30次温度循环作用下桩身温度与桩顶位移变化规律。NG等[11]研究了摩擦型能源桩在循环温度荷载作用下桩周土体的水平土压力变化。SAGGU等[12]根据建立的有限元模型,分析了能源桩在砂土中的应力、应变特征并验证了循环温度荷载作用下土体会对桩体产生负摩阻力。费康等[13]采用可反映土体循环力学特性的边界面模型,研究了干砂地基中能源桩单桩的长期工作特性。总体来看,有限元方法能够较合理地反映材料本构关系、相互作用、荷载和边界条件,但建模和计算较复杂。因此,研究数值分析方法显得尤为重要。
荷载传递法避免了计算量大、数值模型复杂的缺点,是能源桩设计中最常用的数值方法。KNELLWOLF等[14]采用分段折线形式的传递函数来模拟能源桩的热力学行为,通过与现场实测结果比较,发现该方法能较好地评估单调温度变化对桩热力响应的影响。PLASEIED等[15-16]将荷载传递函数取为双曲线进行参数敏感度分析并校准模型参数。黄胤培等[17]基于桩侧-土荷载传递的指数模型进行了相似研究。以上方法都没有考虑循环温变荷载的影响且计算中需要预先假定温度位移零点的位置,分析结果可能不易收敛。PASTEN等[18]假设桩-土相互作用关系为线弹性-完全塑性,考虑了循环温变荷载的影响,但没有进行实验验证。SURYATRIYASTUTI等[19]开发了一个可以描述桩轴阻力软化机制的循环桩-土相互作用函数,但仅适用于假设情况。费康等[20]基于双曲线模型建立的简化分析方法克服了上述缺点,但由于加卸载函数曲线分支形成的滞回圈闭合,还需引入土体刚度折减系数来模拟循环加载下土体的剪切应变软化特性。罗喆等[21-22]分别选用三折线模型和指数模型作为荷载传递循环加卸载曲线中的骨干曲线,模型不需引入折减系数,但计算较为复杂。
本文在前人工作基础上,将桩-土荷载传递函数取为双曲正切曲线,利用改进的Masing准则构建桩侧和桩端的荷载传递循环加卸载曲线,进而基于热力荷载传递原理来模拟循环温变荷载作用下能源桩的工作特性,无需预先假定温度位移零点的位置和引入土体刚度折减系数。结合现场试验实例,验证方法的可靠性,并分析能源桩不同冷热循环方式和上部结构荷载对能源桩长期响应的影响。
1 循环温变荷载下的荷载传递法
1.1 荷载传递循环加卸载曲线
1.1.1 桩侧荷载传递骨干曲线
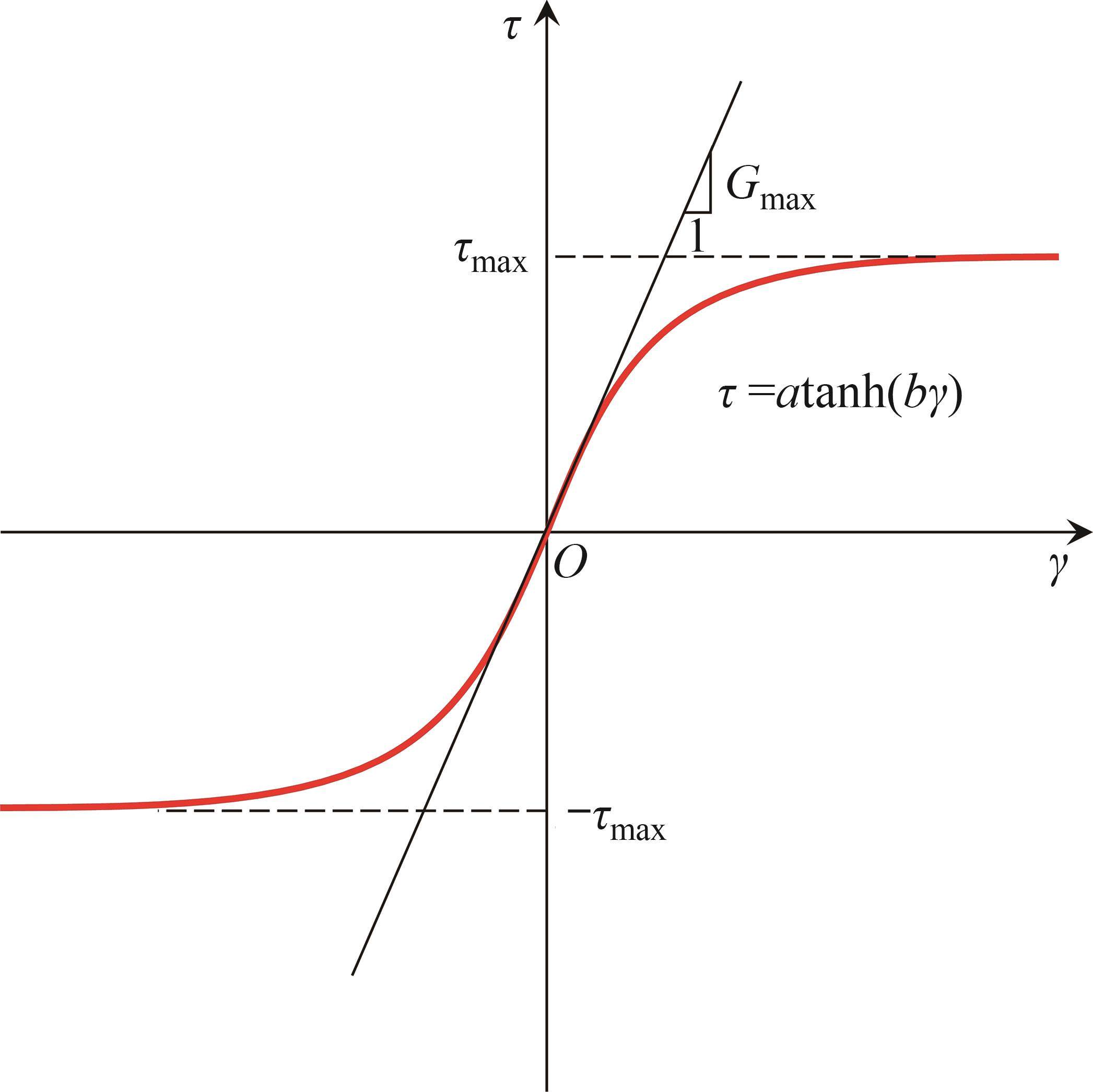
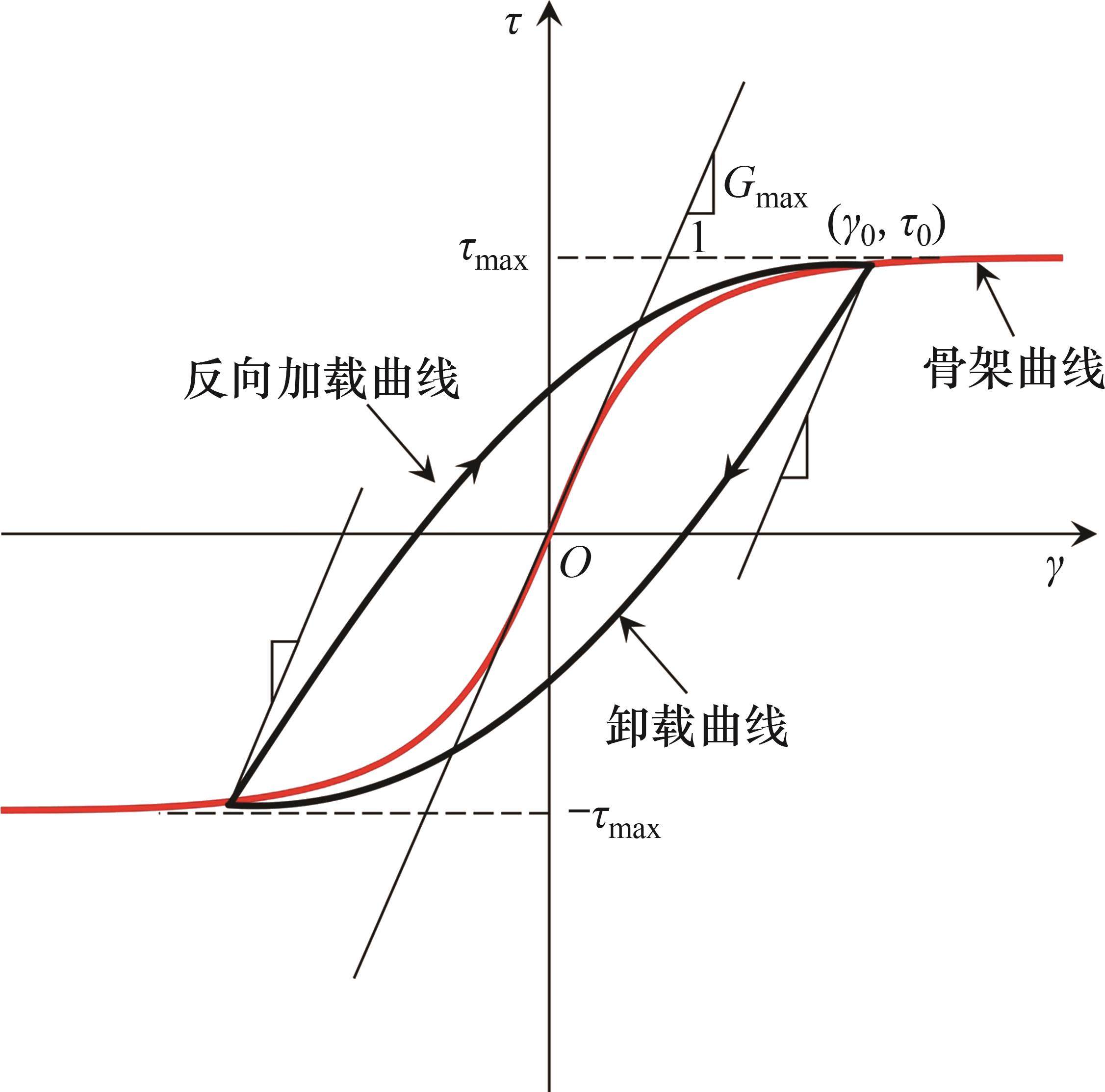
选用形式简单且物理意义明确的双曲正切模型[23]作为荷载传递循环加卸载曲线中的骨架曲线(见图1)。桩侧骨架曲线表示为
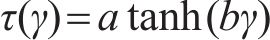
式中:
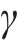
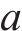
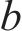
1.1.2 桩侧荷载传递循环加卸载曲线
改进的Masing准则可归纳为[23]:1) 在初始加载过程中,动应力-应变关系曲线骨架曲线相符;2) 滞回曲线与骨架曲线有相同的函数形式,但模型拟合参数不同;3) 模型卸载及反向加载应力应变关系曲线趋近于骨架曲线的极限应力点;4) 骨架曲线与滞回曲线上的剪应力不能超过土体的极限应力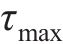
与常规桩相比,能源桩的循环响应机理更复杂。在循环轴向荷载作用下,常规桩整体向下或向上位移。然而,在循环温变荷载作用下,除非桩的顶部或底部受到完全约束,否则桩的上部和下部会反向膨胀和收缩。因此,由于能源桩的独特性,一部分桩可以处于加载或再加载阶段,而另一部分桩同时处于卸载阶段。卸载和再加载曲线可以根据改进的Masing准则,以剪应力的极限值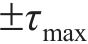
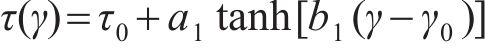
式中,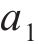
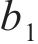
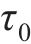
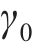
反向加载应力-应变曲线的构造与卸载应力应变曲线的构造方法类似。假定模型反向加载的起点为(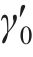
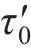
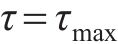
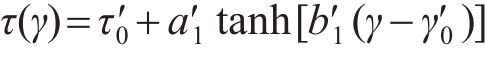
式中,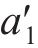
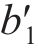
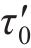
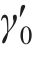
1.1.3 桩端荷载传递曲线
桩端受到的压应力是影响能源桩整体性最显著的因素,因此,只考虑桩端受到压应力的情况。当桩端受到循环荷载作用时,桩端土体的应力-应变曲线是非线性的,因此,仍用双曲正切模型模拟桩端阻力和桩端位移的荷载传递关系,即
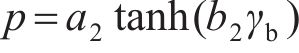
式中,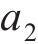
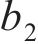
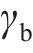
桩端阻力与位移之间的加卸载关系同样采用改进的Masing准则构建,不考虑桩端受拉应力的情况。
1.1.4 参数确定
荷载传递参数可按现场原位试验结果的剪应力-应变曲线数据拟合后获得,也可按相关理论公式确定。丁玉琴[23]建议骨架曲线的模型拟合参数a和b由桩-土界面初始剪切刚度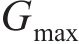
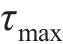
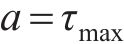
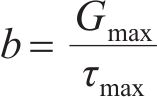
式中: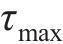
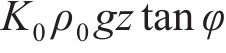
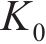
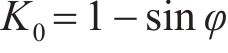
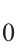
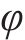
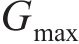
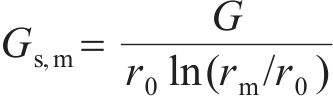
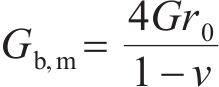
式中,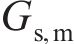
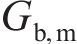
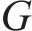
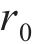
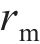
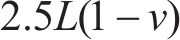
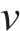
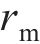
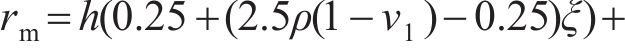
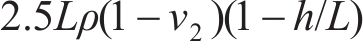
式中:h为第一层土层厚度;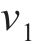
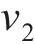
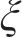
滞回曲线函数中的参数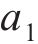
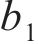
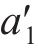
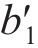
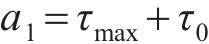
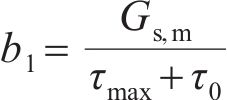
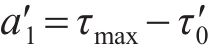
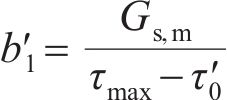
对于桩端荷载传递曲线中的模型拟合参数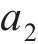
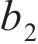
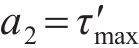
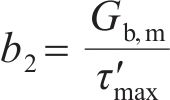
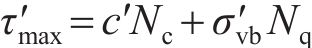
式中: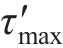
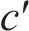
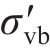
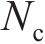
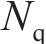
1.2 热-力耦合作用下的荷载传递计算模型
采用费康等[20]提出的考虑循环温变荷载的荷载传递模型,研究热-力耦合作用下能源桩的长期工作特性。
1.2.1 基本假设
1) 桩体的弹性模量E和热膨胀系数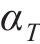
2) 桩侧、桩端土体性质和荷载传递函数不受温度影响,桩身变形始终处于热弹性状态。
3) 在热-力耦合作用下,桩身仅考虑一维轴向变化。
4) 桩身单元位移向下,温度增加及压应力为正。
1.2.2 控制方程
将桩长为L的能源桩离散为N个单元,每个单元及节点由上至下依次编号,选用非线性界面弹簧来描述桩-土界面行为。能源桩离散示意图如图3所示。图3中,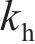
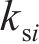
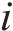
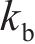
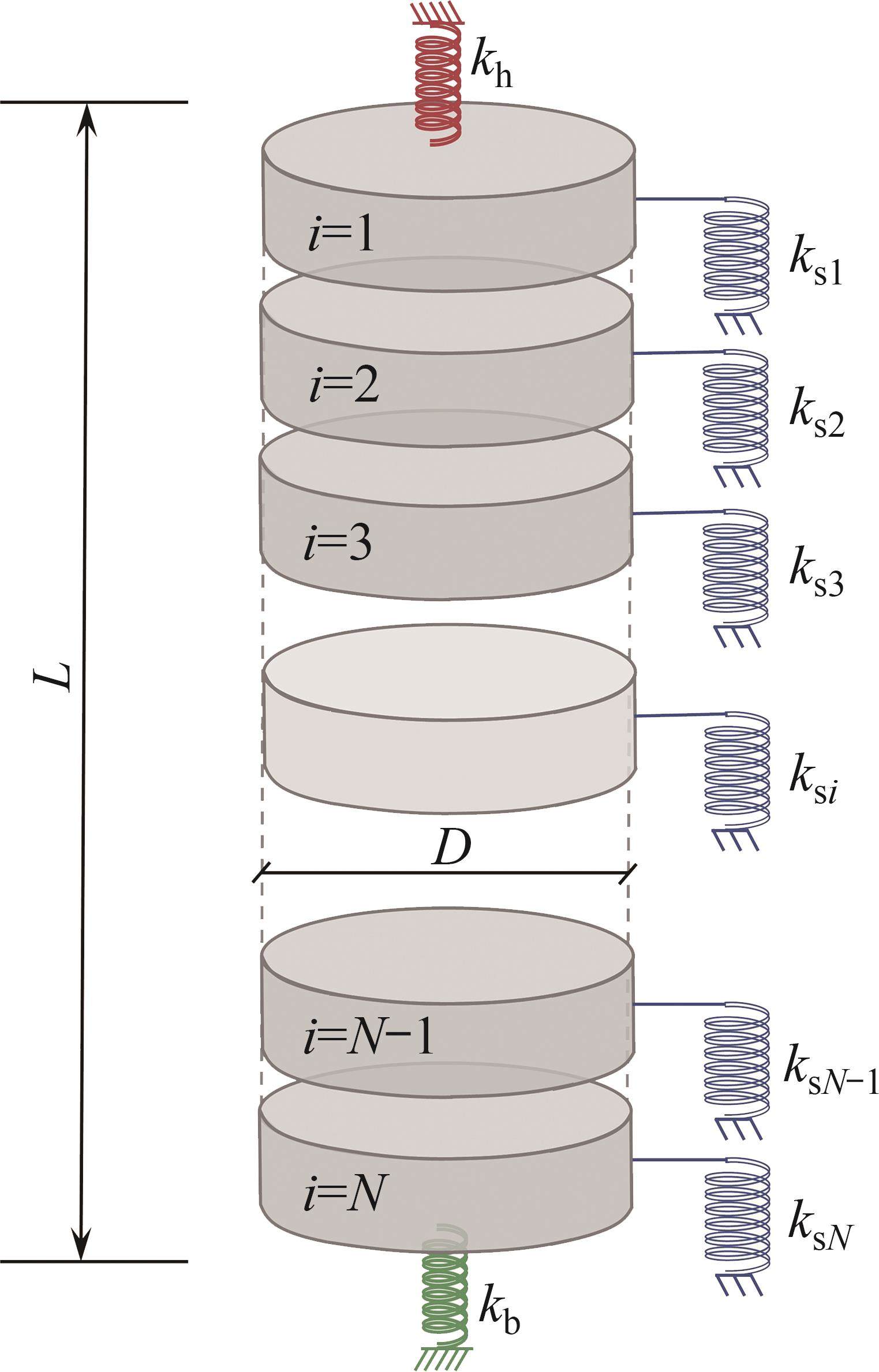
当仅施加机械荷载时,桩整体向下移动,单元i受到轴向应力、桩侧摩阻力以及端部反力作用。若再施加一个温度荷载,则单元i会增加一个由温度引起的轴力,桩单元受力分析如图4所示。图4中,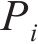
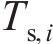
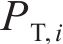
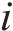
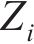
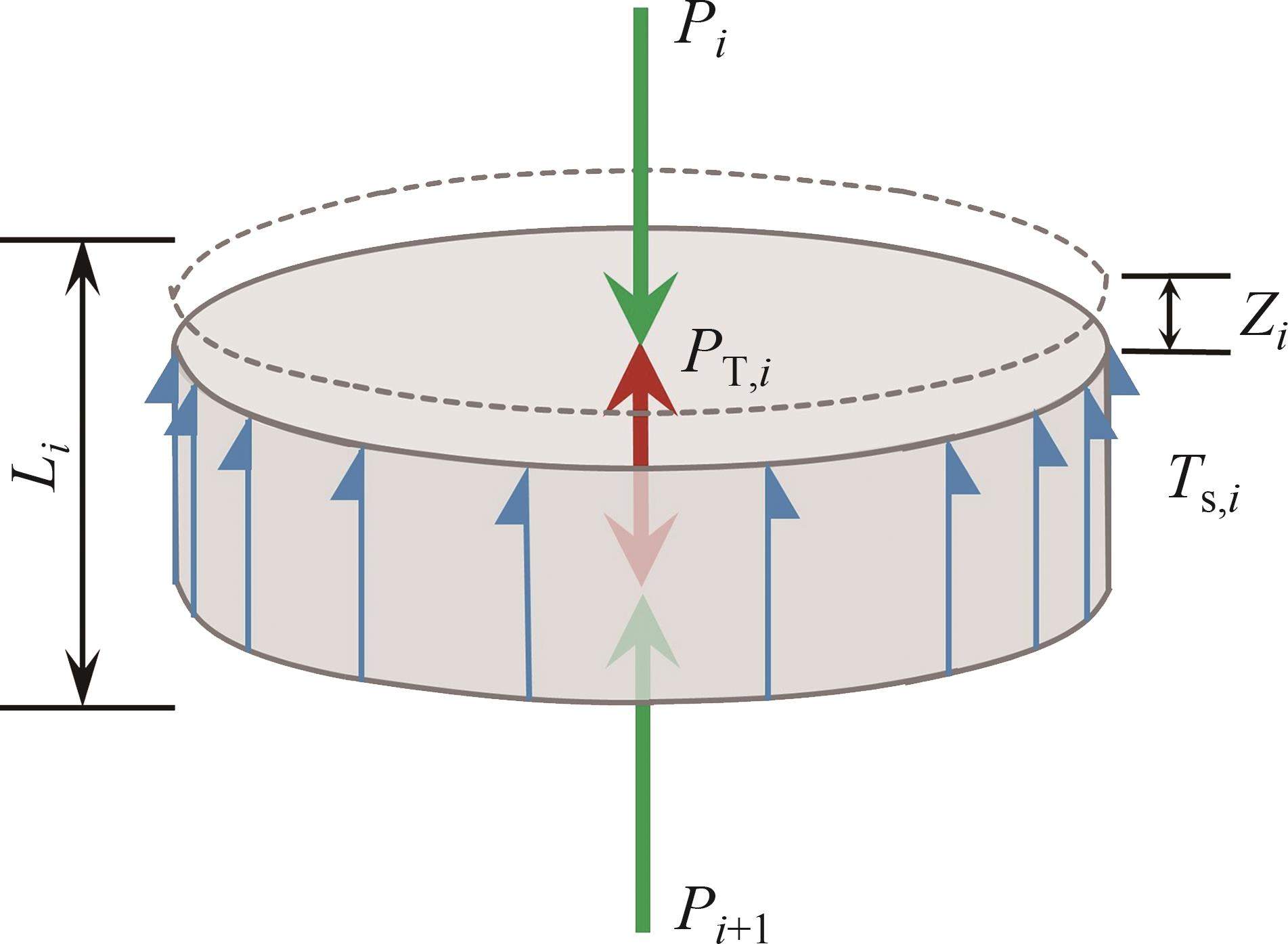
考虑热-力耦合作用,单元i的局部平衡方程可以表示为
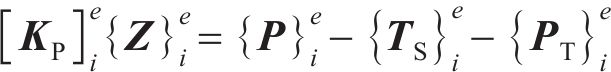
每个桩基单元的行为由一个刚度为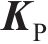
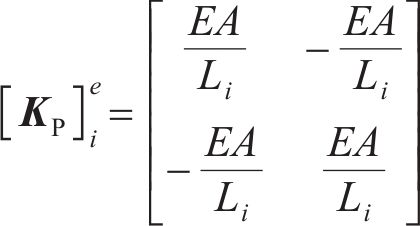
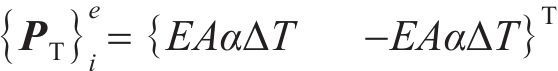
式中: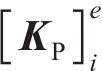
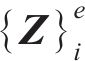
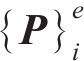
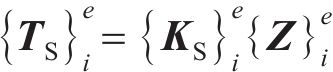
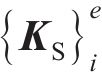
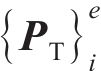
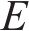
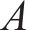
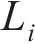
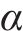

作用于单元i周围、处于节点i和i+1间的桩侧剪应力用等效节点力代替,再结合桩头及桩底边界条件,即可构造出矩阵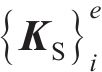
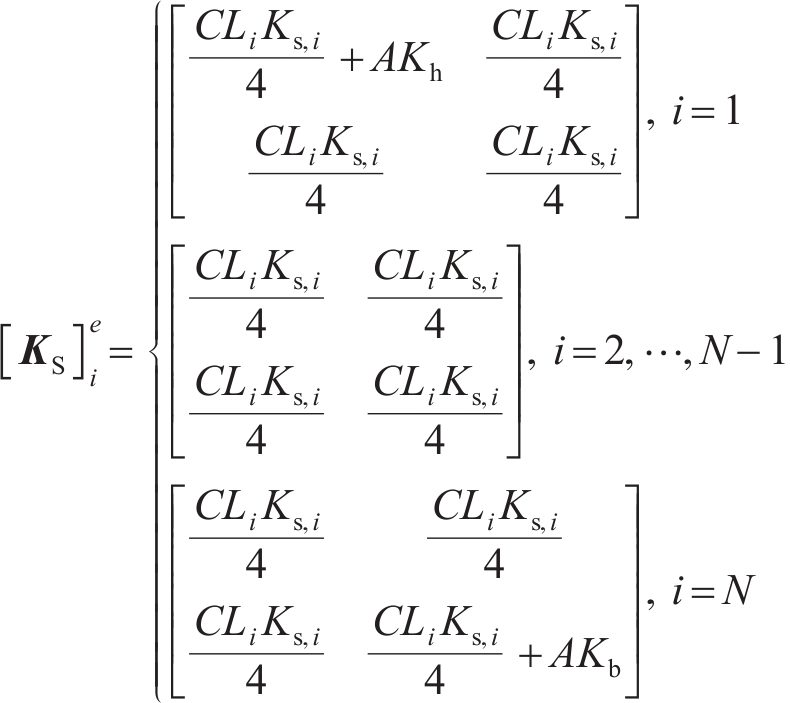
式中,C为桩周长;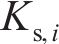
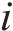
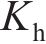
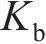
联立式(17)~(20),将单元刚度组合成整体刚度矩阵,移项后得到桩节点位移增量的求解矩阵为
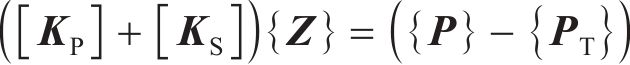
式中: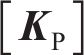
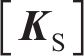
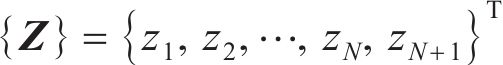
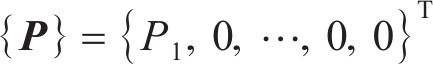
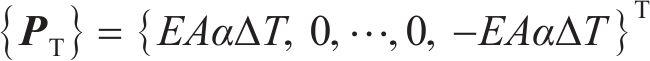
由各节点的位移增量可以得到能源桩的桩侧摩阻力增量、桩身轴力增量和桩端阻力增量。
1.2.3 数值实现
考虑到能源桩的实际工作特性,传力后再传热,基于Matlab软件将热力耦合作用下桩的响应计算分为力学加载和循环温度加载2个阶段,如图5所示。
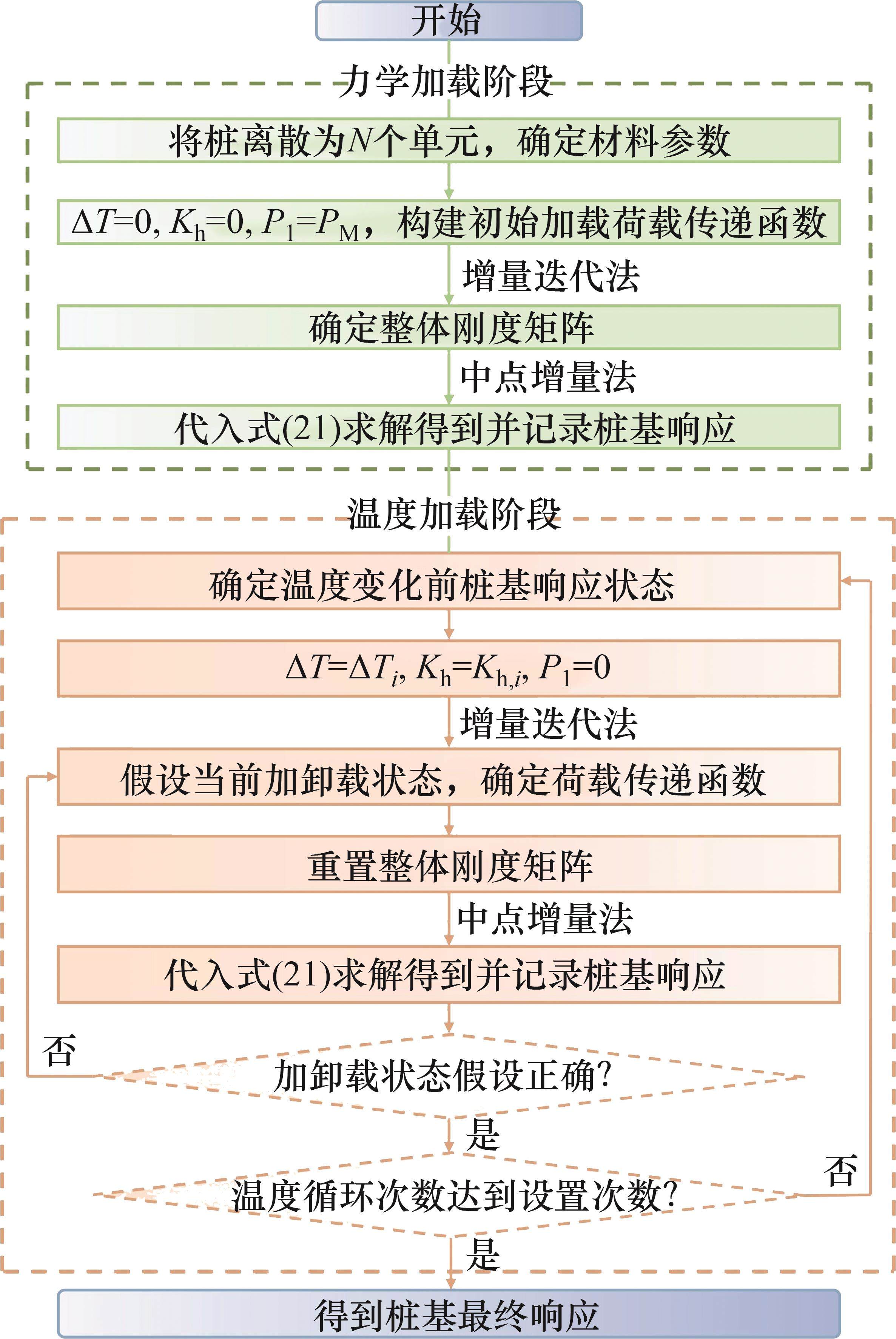
在力学加载阶段,首先将桩划分为N个单元,确定能源桩及周围土体的材料参数。令温度增量
在循环温度加载阶段,以力学加载结束时的状态作为温度变化前的桩基响应状态。将温度变量
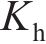
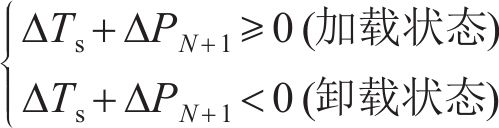
2 模型验证
桩体弹性模量为29.2 GPa,热膨胀系数为10-5 ℃-1。根据现场试验的土体参数求得桩-土荷载传递参数,如表1所示。选取桩顶自由(T1桩)和上部结构施工完成后(T7桩)的试验结果进行对比,并与费康等[20]和董龙龙等[22]的计算解进行比较,从而对荷载传递双曲正切模型进行验证。
| 土层 | 厚度/m | a/kPa | b/m-1 | a2/MPa | b2/m-1 |
|---|---|---|---|---|---|
| 冲积土1 | 5.5 | 114 | 324.8 | — | — |
| 冲积土2 | 6.5 | 78 | 307.4 | — | — |
| 砂砾冰碛土 | 10 | 83 | 485.8 | — | — |
| 冰碛土 | 3 | 179 | 1 506.2 | — | — |
| 磨砾层 | 0.8 | 179 | 1 506.2 | 12.3 | 120 |
对于T1桩,桩顶无结构荷载处于自由状态,因此,将桩顶结构接触刚度设置为零。对于T7桩,桩顶荷载约为1 088 kN,并增温15 ℃,上部建筑物对桩顶变形约束系数为1 GPa/m。
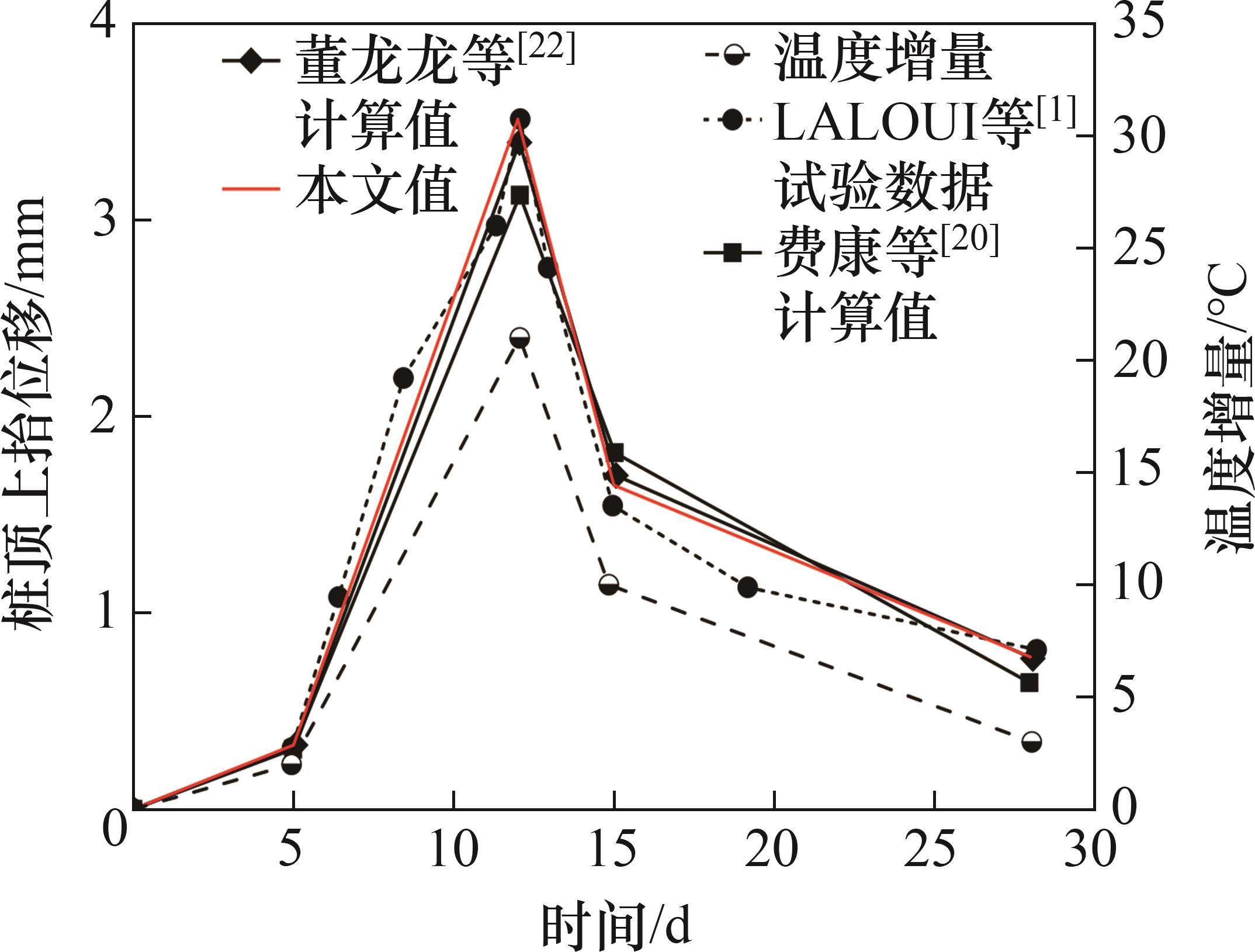
图6所示为由温度荷载引起的桩顶上抬位移曲线(T1桩),温度变化路径为0 ℃→2 ℃→21 ℃→10 ℃→3 ℃。从图6可见:随着温度的升高,桩顶隆起,当桩体温度达到21 ℃时,其抬升位移达到3.5 mm,之后温度逐渐下降,但最终桩温仍比初始温度高3 ℃,故桩顶依然存在上抬位移。计算值与实测值变化规律一致。
选取3 ℃和21 ℃进行比较分析,由温度荷载导致的竖向热应变沿T1桩桩身分布的实测和计算结果如图7所示。从图7可见:由于没有施加结构荷载,在桩头处几乎没有约束,实测和计算热应变分别为-193×10-6和-205×10-6,接近热自由膨胀应变的理论值-210×10-6。桩端支承于较为坚硬的磨砾层上,致使桩端存在较大的约束力,因此,当温度变化为21 ℃时,桩身最小应变增量出现在桩端附近,实测值与计算值分别为-144×10-6和-155×10-6,相当于无约束热膨胀应变的68.6%和73.8%。费康等[20]预测的轴向应变与实测值有所偏差,而本文计算值与董龙龙等[22]的预测值基本重合,更加接近于实测结果。
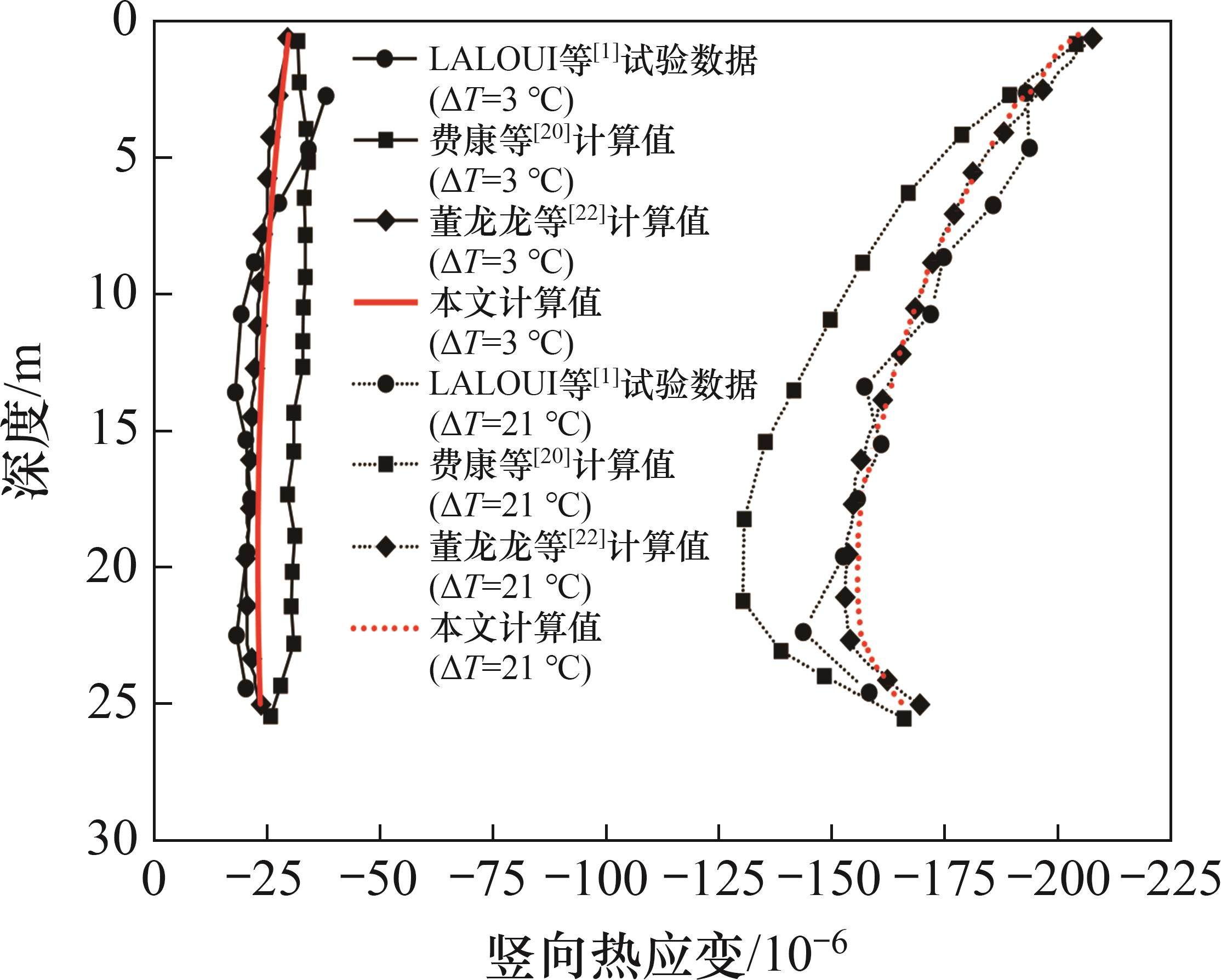
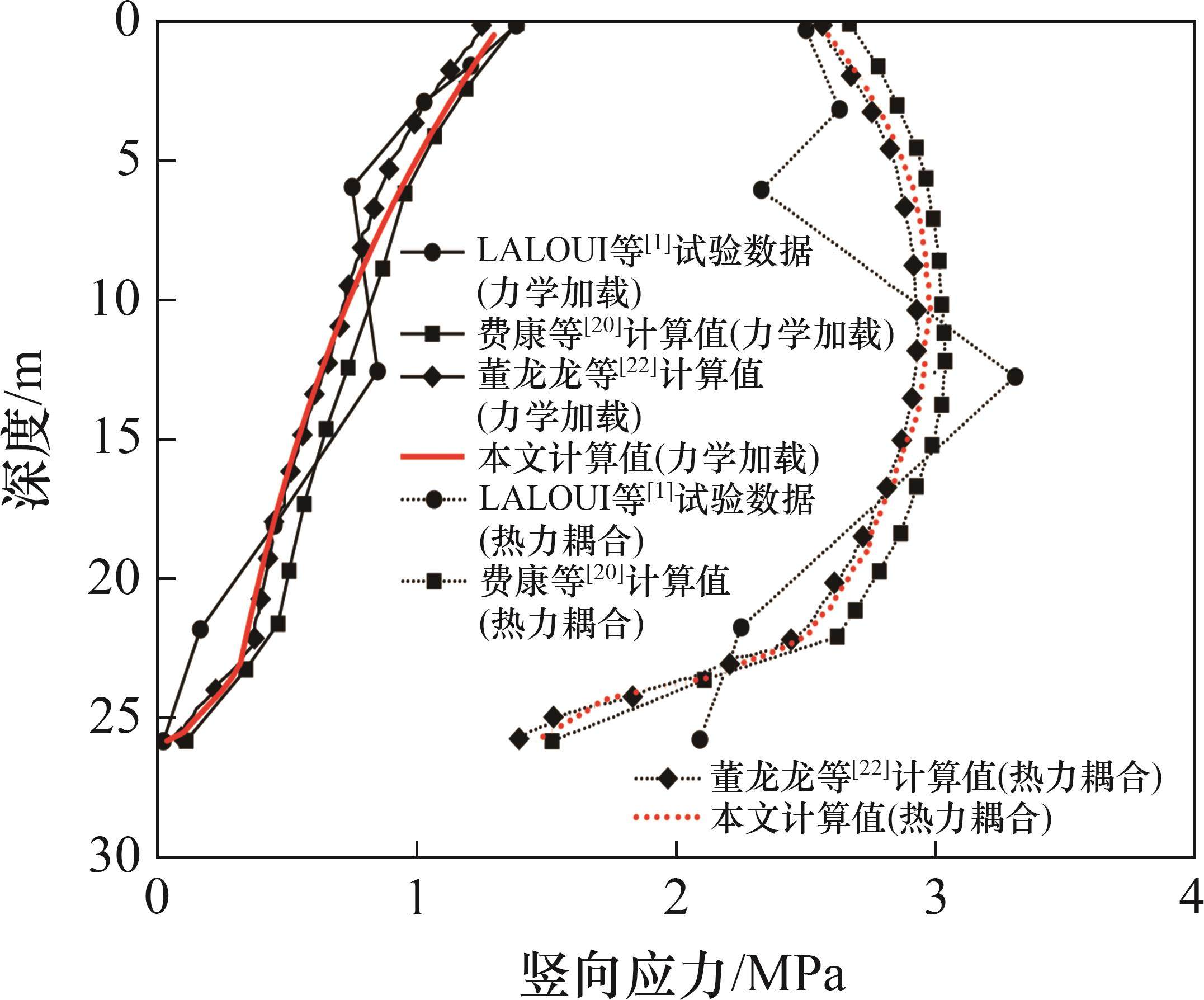
图8所示为T7桩身竖向应力分布的实测和计算结果。从图8可见:在桩顶荷载1 088 kN作用下,桩身竖向应力随深度增加而不断减小,桩端应力接近于零,桩顶荷载主要由桩侧承担;当温度增加15 ℃时,由于桩顶结构、桩周与桩端土体的约束作用,桩身中出现明显的附加热应力,造成桩身竖向应力显著增大,竖向应力最大值仅为力学加载时的2~3倍。在热力耦合作用下,桩身竖向应力最大值出现在桩体中部,这是由于在升温过程中,温度位移零点以上侧阻力减小,温度位移零点以下侧阻力增大,故零点位置附加热应力最大,而在桩体两端约束作用下,零点趋近于桩体中部。由图8可知:本文模型计算的桩身轴力分布与试验实测值拟合较好,说明本文建立的荷载传递双曲正切模型可以较真实地模拟能源桩的热力耦合承载特性。
3 能源桩长期响应影响因素
3.1 计算工况
本文计算工况与董龙龙等[22]假设工况一致,需要注意的是,假设能源桩位于单层黏性土中,桩体及土体荷载传递假设参数见表2,荷载传递模型参数可以通过式(5)~(16)确定。
| 参数 | 取值 |
|---|---|
| 桩长/m | 25 |
| 桩径/m | 1 |
| 桩身弹性模量/GPa | 30 |
| 热膨胀系数/℃-1 | 1×10-5 |
| 结构荷载/kN | 3 000 |
| 桩侧极限摩阻力/kPa | 80 |
| 桩侧初始剪切刚度/(MPa·m-1) | 30 |
| 桩端极限抗力/MPa | 10 |
| 桩端初始剪切刚度/(MPa·m-1) | 0.001 5 |
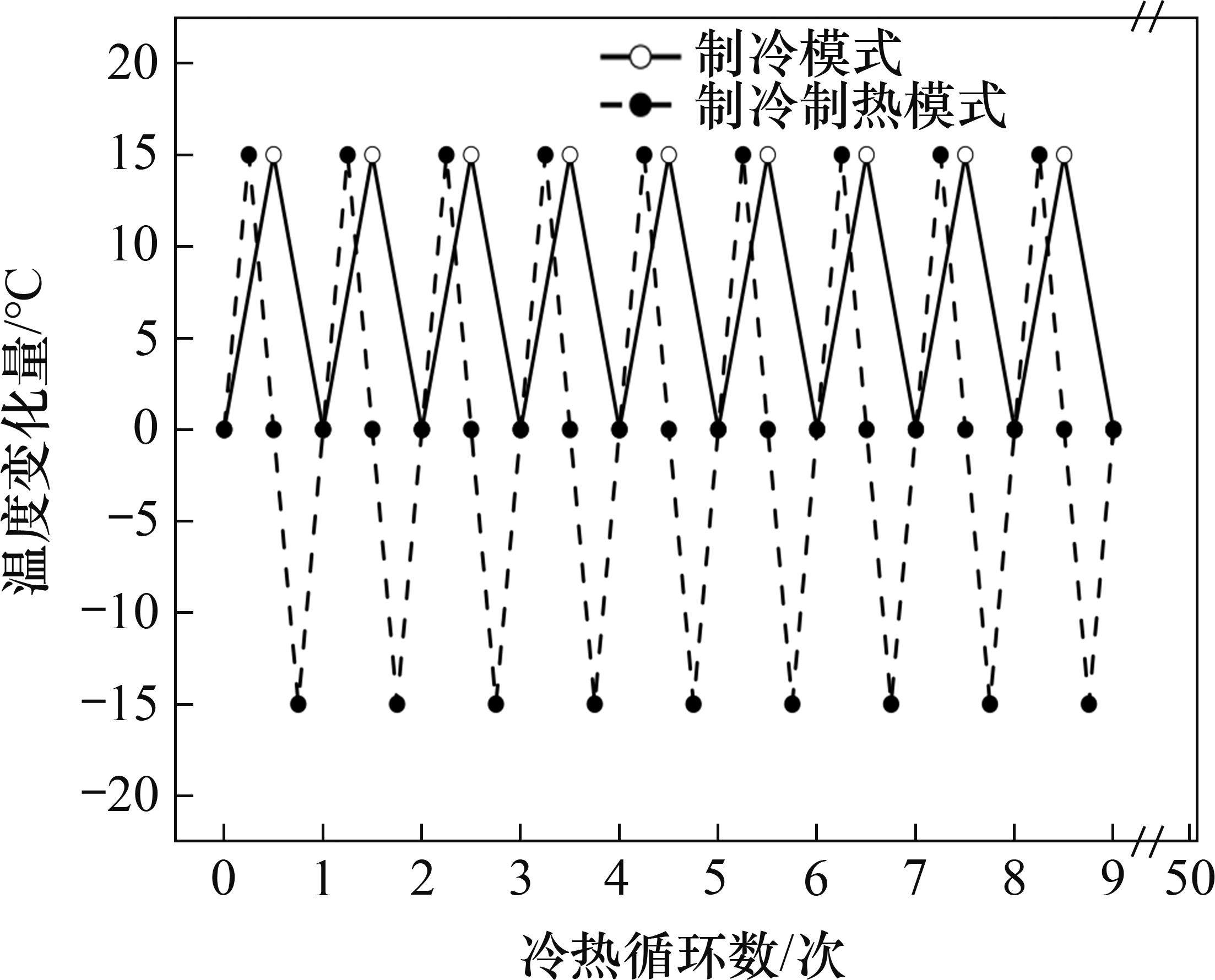
假设桩体最大温度增量为15 ℃,温度循环为50个周期,利用双曲正切荷载传递模型,研究能源桩冷热循环方式、上部结构荷载对桩头沉降和桩头轴力的影响。能源桩普遍在夏季和冬季运行。在夏季运行期间,冷却土壤通过沿桩身循环较热的流体,流体中的热量会被逐渐释放到地下,使得周围地面温度升高,此时桩体膨胀。在冬季运行时,向桩中注入较冷的流体以从温度较高的土壤中提取热能,桩体收缩。为研究这2种运行模式下能源桩的长期工作特性,将1个周期内的冷热循环方式简单分为制冷和制冷制热模式,如图9所示,其中,在制冷模式下,1个周期内冷热循环方式为增温→回温;在制冷制热模式下,1个周期内冷热循环方式为增温→回温→降温→再回温。
3.2 冷热交替方式对能源桩长期响应的影响
3.2.1 桩头沉降
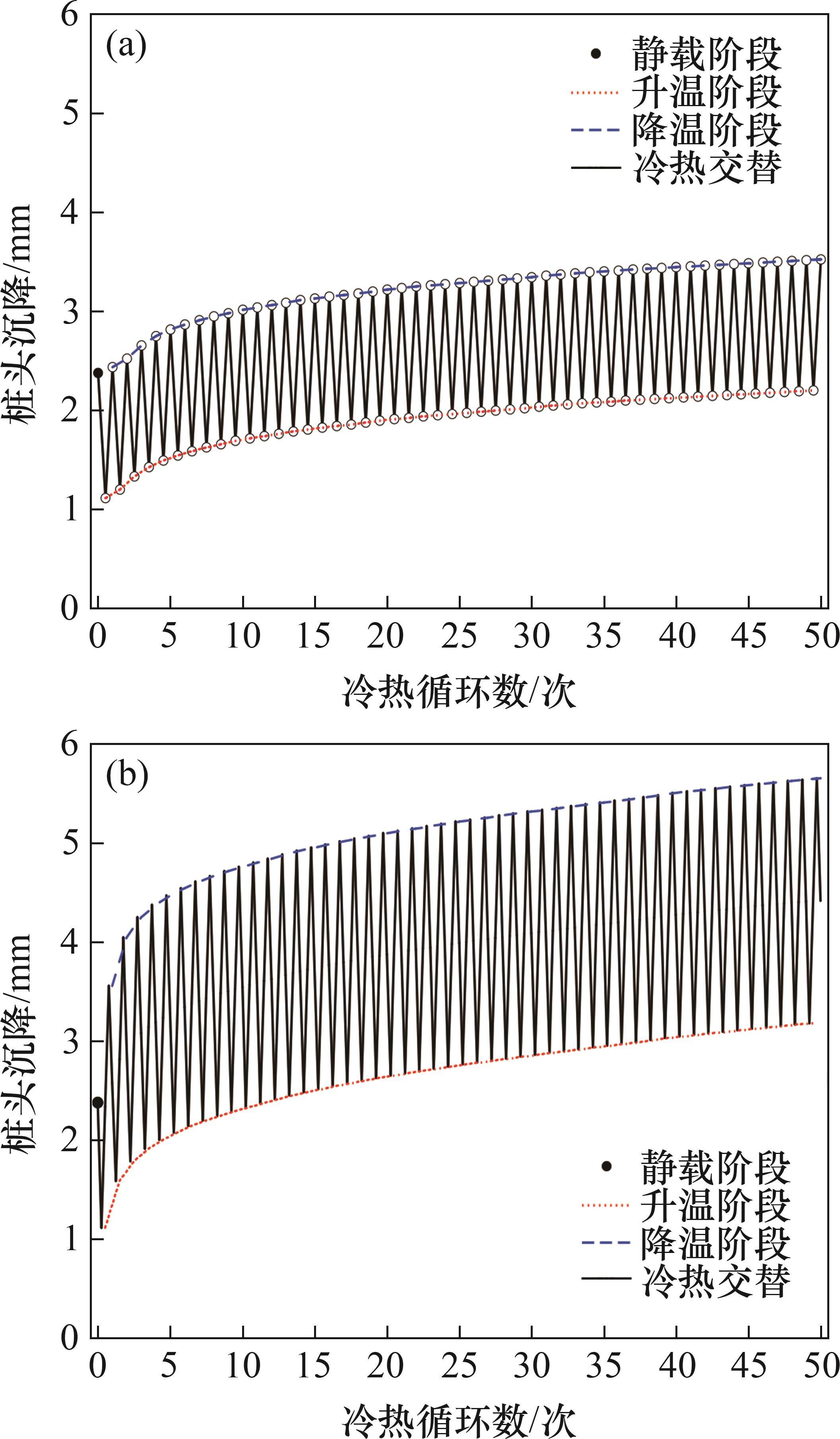
基于2种不同的冷热循环方式,根据50个周期的能源桩响应结果,总结分析循环温变荷载对能源桩桩头沉降的影响,结果如图10所示。从图10可以看出:能源桩在升温阶段桩头沉降减小,这是因为加热引起桩体膨胀,桩头隆起导致沉降降低;而在降温阶段,桩头沉降迅速增大甚至超过了静载时的沉降,这是因为降温时,能源桩上部处于卸载状态,即冷却收缩,导致桩头沉降增大;随着冷热循环次数的增加,桩头沉降会逐渐变大,这是由于桩体具有残余沉降的累积效应。除此之外,还观察到制冷制热模式的桩头沉降增长速率比制冷模式的更快,且桩头沉降约为制冷模式的1.5倍;随着冷热循环次数的增大,增长速率会逐渐变缓并趋于稳定。需要注意的是,桩头沉降更易受降温影响,在制冷制热模式下能源桩的长期运行更容易导致桩头产生累积沉降,降低桩的承载性能,进而影响上部结构的正常使用。
3.2.2 桩头轴力
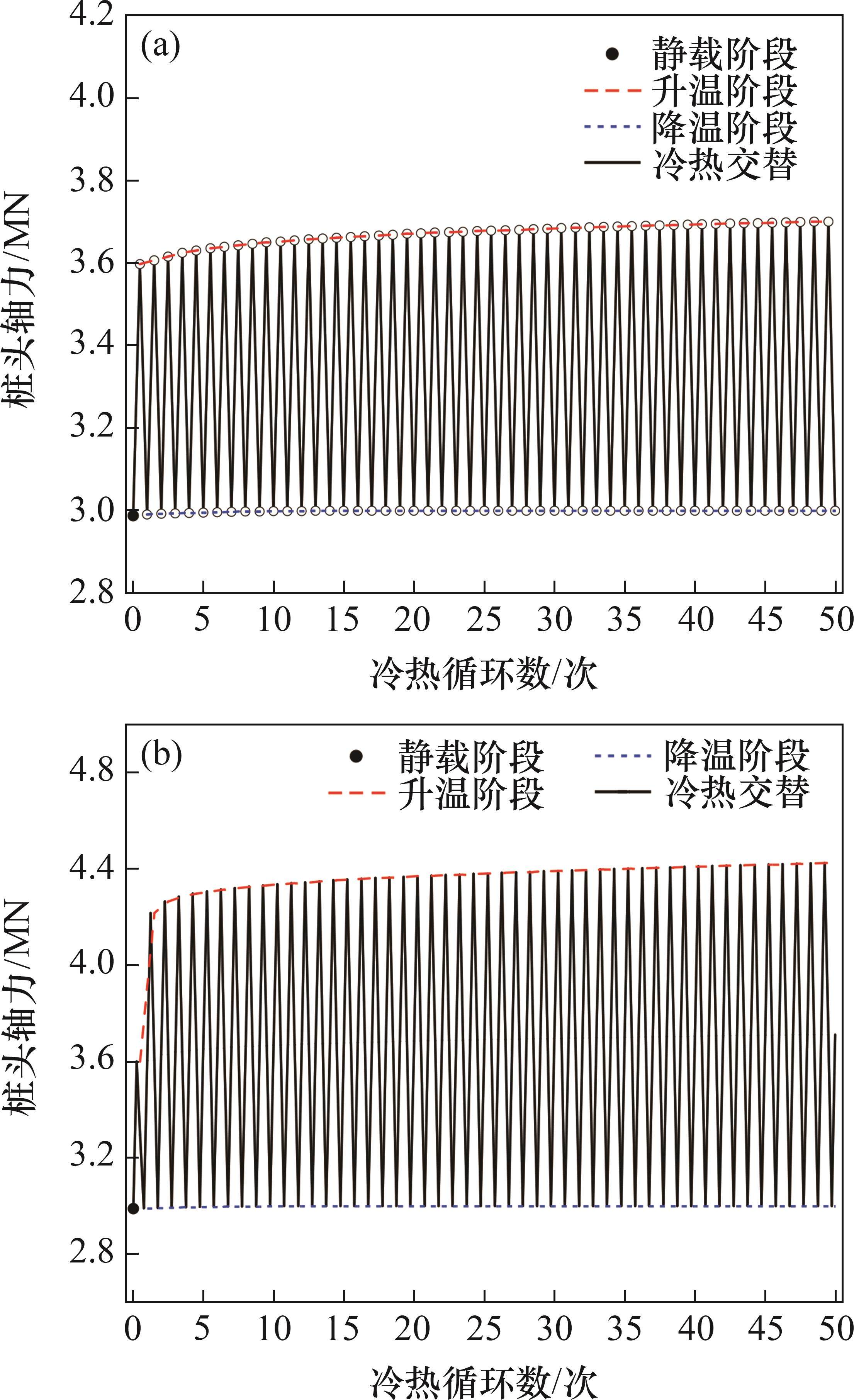
图11所示为50个温度循环周期内不同冷热循环方式下桩头轴力与冷热循环次数间的关系曲线。从图11可以看出:在升温阶段,随冷热循环次数的增加,桩头轴力不断增大,这是因为在上部结构的约束下,升温会导致桩体产生附加热应力,且随着冷热循环次数的增加,温度应力会逐渐累积;而在降温阶段,桩头轴力基本上与静载阶段的一致,这是由于能源桩上部处于卸载状态,基本不会产生轴向温度应力;此外,在制冷制热模式下,能源桩在升温阶段的桩头轴力增量明显比制冷模式下的高,且增长速率更快,稳定得更慢,与桩头沉降规律一致。需要注意的是,桩头轴力主要受升温影响,制冷制热模式下能源桩的长期运行更容易引起残余温度应力累积。
3.3 上部结构荷载对能源桩长期响应的影响
3.3.1 桩头沉降
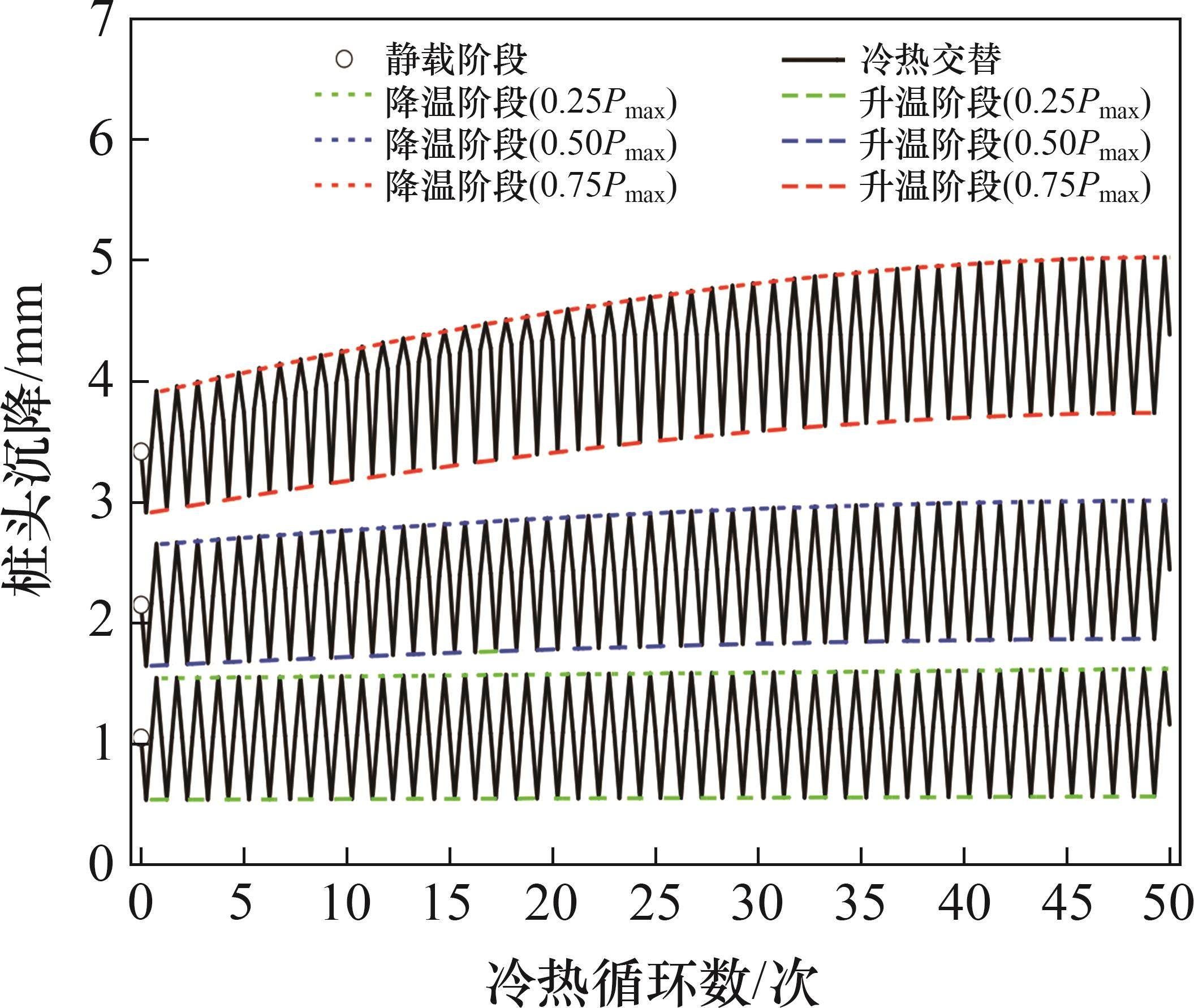
由表2中土层参数可得本假设桩基极限承载力Pmax=6 000 kN,为研究上部载荷对长期运行下能源桩桩头沉降的影响,以制冷制热模式为例,选取3个典型工况(0.25Pmax、0.50Pmax、0.75Pmax)进行分析,并对其进行归一化处理,桩头结构接触刚度为5 GPa/m。图12所示为不同上部荷载水平下桩头沉降与冷热循环次数的关系曲线。从图12可以看出:随着上部结构荷载的增大,静载阶段的桩头沉降增大;当结构荷载为0.25Pmax和0.50Pmax时,循环温变荷载对桩头沉降的影响并不明显,桩头沉降很快趋于稳定,而当结构荷载为0.75Pmax时,桩头沉降随冷热循环次数的增加而迅速增大,降温阶段的桩头沉降甚至达到了初始沉降的1.5倍,且稳定得更慢.因此,在能源桩基设计时,需妥善考虑上部结构荷载与桩基极限承载力的比例关系。
3.3.2 桩身轴力
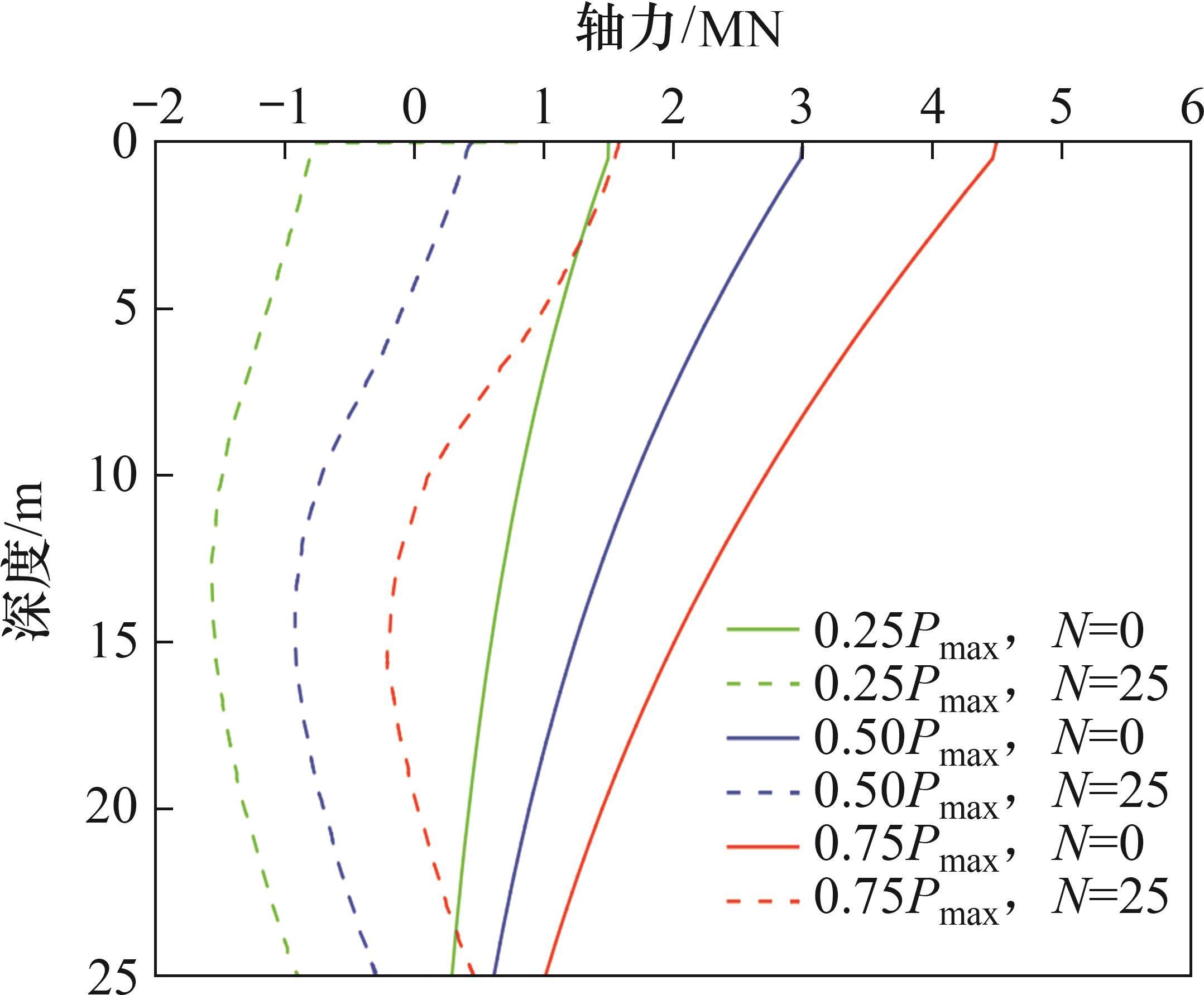
图13所示为在制冷制热模式下上部结构荷载对桩身轴力的影响规律,桩头结构接触刚度取为 5 GPa/m,桩头半固定。以桩体降温15 ℃温度加载前和循环25次时的桩身轴力分布为例,可以看出:当结构荷载为0.25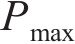
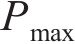
4 结论
1) 温度循环会造成能源桩桩头沉降和桩头轴力不断累积,并逐渐趋于稳定。相较于制冷模式,制冷制热模式运行时更容易引起桩头残余沉降和残余温度应力的累积效应。
2) 上部结构荷载与桩基极限承载力的比值过大容易引起桩头残余沉降累积,过小则会导致桩体产生拉应力,影响桩基性能。在本模拟工况中,结构荷载为0.75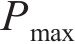
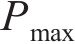
3) 本文方法忽略了周围土体的热体积变化,当周围土壤是随温度变化的软黏土或膨胀黏土时,可能会遇到明显的体积变化和循环效应,使用随温度和加载路径变化的荷载传递函数可以解决这一问题,但有待进一步研究。
王桐, 张云鹏, 郑君, 等. 基于双曲正切模型的能源桩长期响应研究[J]. 中南大学学报(自然科学版), 2024, 55(12): 4593-4603.
WANG Tong, ZHANG Yunpeng, ZHENG Jun, et al. Long-term responses of energy piles based on hyperbolic tangent model[J]. Journal of Central South University(Science and Technology), 2024, 55(12): 4593-4603.

