膨润土泥浆具有良好的流变特性,早期在地基工程和石油勘探领域被用于钻井泥浆[1]。自1967年以来,膨润土泥浆开始广泛应用于泥水盾构施工[2-3]。盾构机在地层中掘进时,泥浆在泥水舱与地层的压力差作用下压入前方,随后在开挖面表层形成透水性较小的泥膜[4]。由泥浆颗粒堆积形成的泥膜能够将大部分泥水压力转化为地层有效应力,为开挖面提供支护压力。但是,在颗粒粒径较大的粗砂、砾石地层,泥浆成膜时间较长。若盾构机掘进速度大于泥膜生成速度,则泥膜无法在掌子面生成,开挖面无法得到有效支护。饱和地层中易导致大量水体涌入,甚至发生开挖面主动失稳现象。因此,泥浆成膜时间判定对于泥水盾构开挖面稳定研究至关重要。
已有研究表明渗滤效应是泥膜形成的主要原因[4]。在泥浆渗透过程中,部分泥浆颗粒会被土颗粒骨架所阻拦,使得泥浆颗粒逐渐沉积、淤堵土体孔隙,泥浆浓度降低。一般认为土体对泥浆的渗滤作用越强,泥浆成膜时间越短。泥浆颗粒在土体内部迁移-沉积的微观过程十分复杂,渗滤效应的强弱受惯性力、物理拦截、重力、水动力、电荷作用和布朗扩散和等诸多因素影响[5-11]。在泥浆渗透沉积过程的宏观分析中,渗滤系数常常作为表征土体对泥浆中悬浮固相颗粒过滤效率的关键物理量。然而,已有渗滤系数计算方法中参数众多[12-14],且物理量难以与实际工程参数对应。目前对于渗滤系数的取值仍以经验为主[15-17]。
探明泥膜生成机理及其类型是成膜时间判定研究的前提。WHITE[18]通过室内试验总结了砂土地层泥浆支护要素:1) 泥浆需要具备一定屈服强度以维持土骨架的力系平衡;2) 泥水压力与静水压力的差值与土压力相等,两者相互抵消。MÜLLER-KIRCHENBAUER[19]通过试验和理论分析对泥浆在土体中的渗透现象进行了初步研究,认为泥浆渗透将改变泥水压力传递方式,土体颗粒尺寸分布对渗透行为影响较大,并将泥浆-土体相互作用模式分为两类:1) 泥浆无法渗入土体内部,只在土体表层形成泥皮;2) 泥浆持续渗入土体,在土体表层无任何沉积。此后,THIENERT等[20]提出了泥浆-土体相互作用的第三种模式,即土体中存在泥浆渗透区,土体表层有泥皮形成。TALMON等[21]对第三种类型泥膜生成机制进行了研究。泥浆渗透过程被分为2个阶段:1) 泥浆快速渗入土体深层孔隙;2) 泥浆中固相颗粒逐渐沉积,渗透速度减慢,土体表层出现泥浆失水固结现象。MIN等[22-23]根据土体平均孔径和泥浆颗粒粒径的比值将泥膜分为泥皮型、泥皮+渗透带型和渗透带型3种类型。对于泥皮型泥膜和泥皮+渗透带型泥膜,土体表层孔隙被泥浆中固相颗粒堆积至渗流通道堵塞是泥膜形成的根本原因。而渗透带型泥膜因土体骨架粒径过大,泥浆与土体适配性较差,仅有部分泥浆颗粒在土体深层孔隙中堆积,土表生成泥膜需使用大量泥浆持续加压,与实际工程应用不符。因此,本研究不考虑渗透带型泥膜。上述研究虽然对泥膜形成机制和泥膜表观类型进行了区分,但未采用成膜时间判定方法,无法与实际工程相结合。
在此,本文对泥浆成膜时间判定方法进行研究。首先,研发泥浆多层渗滤试验装置,测定泥浆在多种粒径土体渗滤后固相颗粒含量变化,以泥浆质量浓度、土体与泥浆颗粒粒径比为自变量,拟合生成渗滤系数计算公式;然后,通过孔隙中固相颗粒沉积质量与渗滤系数、泥浆流速、泥浆质量浓度相对关系,结合泥浆成膜判据,提出泥浆固相颗粒渗透成膜时间计算公式;最后,探究了泥水压力、泥浆质量浓度、土体渗透系数、隧道半径及粒径比等参数对成膜时间的影响。
1 多层渗滤试验
1.1 试验材料
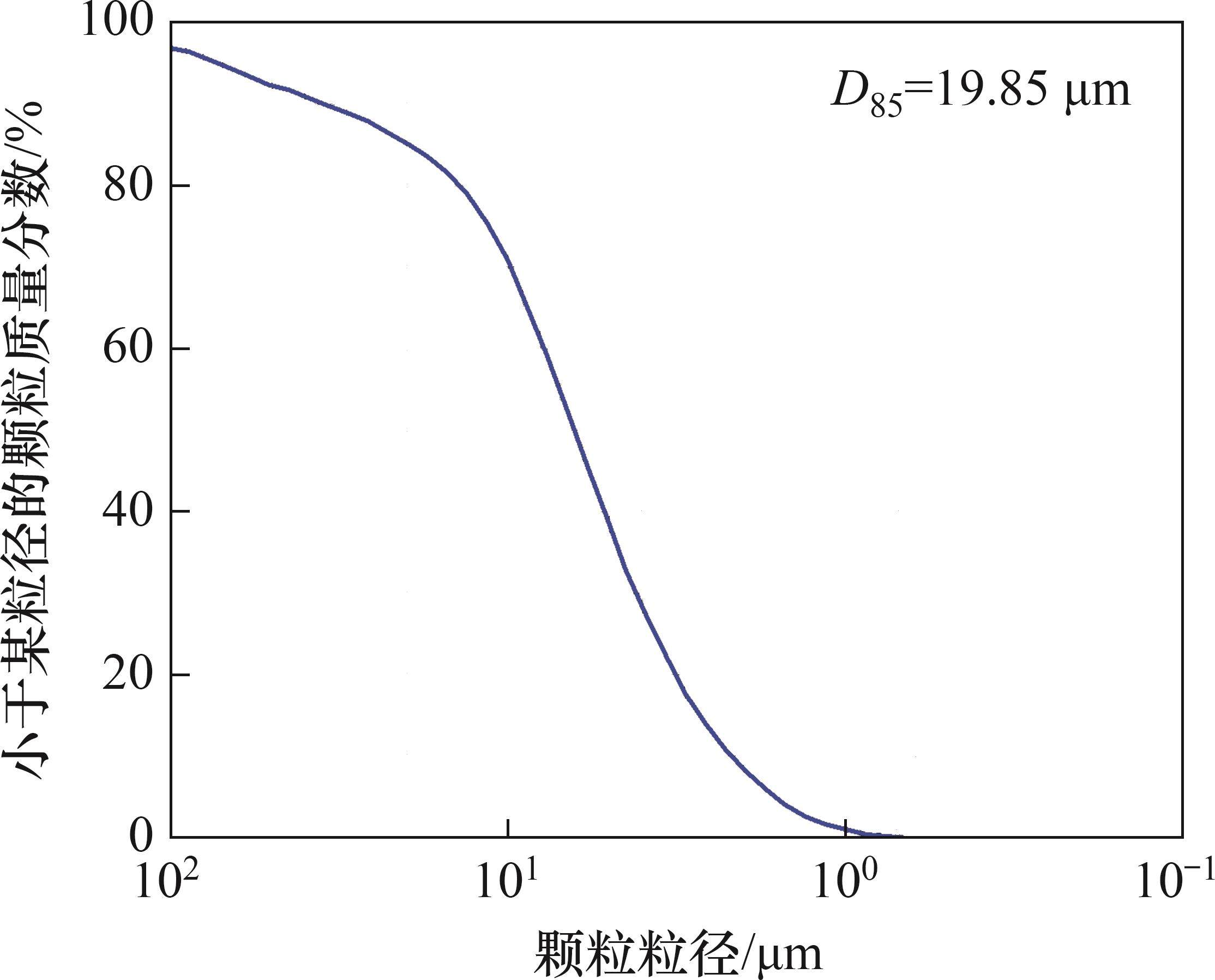
泥浆材料由钠基膨润土、水和羧甲基纤维素钠(CMC)溶液组成。其中,膨润土采用BAROID品牌系列膨润土(美国Halliburton公司生产),在1 000 ℃时烧失量为5.1%,松铺孔隙率为0.501,干密度为 2 620 kg/m3。试验用膨润土颗粒粒径分布如图1所示。试验用水为搅拌至无气泡的自来水,其pH为7.1。CMC是纤维素醚类产品中需求量最大和应用最广泛的产品,主要用于调节泥浆的黏滞性能。试验开始前,需将CMC溶于水中,以溶液形式加入膨化好的泥浆中。在静置状态下,泥浆黏度具有时变性,本研究中膨润土泥浆膨化时间均为24 h。试验通过调节膨润土质量浓度制备了5种泥浆,其中,CMC质量分数均为0.05%,泥浆参数见表1。测量温度为(20±1) ℃。
| 泥浆 | 膨润土质量浓度CL0/(kg·m-3) | 密度ρ/(g·cm-3) |
|---|---|---|
| SL1 | 30 | 1.008 |
| SL2 | 40 | 1.015 |
| SL3 | 50 | 1.022 |
| SL4 | 60 | 1.036 |
| SL5 | 70 | 1.042 |
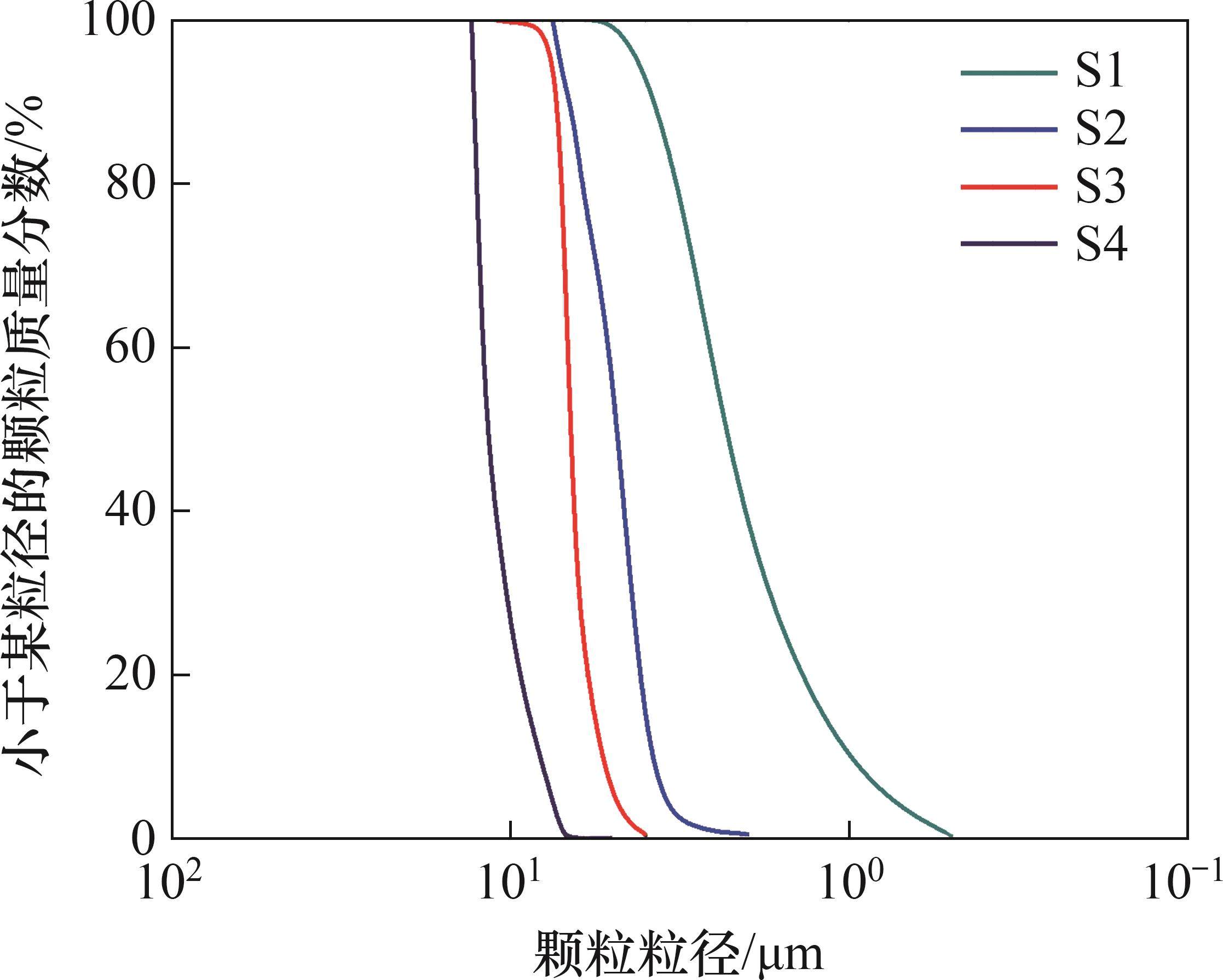
图2所示为试验选用的4种砂土试样粒径分布曲线。砂土试样均为筛分后的河砂,代表粒径d10为1.18~8.76 mm。在试验前洗净各砂土试样,然后在烘干箱中于110 ℃干燥24 h,以排除细颗粒粉土对滤液质量浓度测定的影响。土样干密度为2 670 kg/m3,采用恒水头渗透试验测定砂土试样的渗透系数,砂土试样的基本参数见表2。
| 砂土试样 | 孔隙率φ | 渗透系数k/(cm·s-1) | 粒径d10/mm |
|---|---|---|---|
| S1 | 0.47 | 2.48 | 1.09 |
| S2 | 0.44 | 5.22 | 4.07 |
| S3 | 0.42 | 8.96 | 5.35 |
| S4 | 0.41 | 12.63 | 8.13 |
1.2 试验装置
为探究泥浆在多种粒径土体中的渗透行为,研发了多层渗滤试验系统。该系统由多层渗透柱和辅助装置(包括自主开发的试验控制程序、空压机、储浆桶、电子天平、电炉等)组成,如图3所示,其中,多层渗透柱由4个有机玻璃渗透柱单元、进浆口和出水阀门组成。各单元间通过螺栓连接,且隔有放水橡胶垫以防止泥浆逸出。各渗透柱单元由盖板和双层柱构成,上层粗柱和下层细柱内径分别为10 cm和3 cm,高度均为3 cm,上层和下层盖板中心处均有内径为1 cm的圆形开口。下层细柱侧壁中心位置开有内径为0.5 cm、长度为7 cm的导管,导管外侧连接手动阀门以排出渗透柱单元内的滤液。

压力控制由试验控制程序中的调节器和空气压缩机组成,通过软件设定加压压力后,空压机将空气压入储浆桶,泥浆通过多层柱顶部的进浆孔注入多层渗透柱。需要说明的是,本试验装置尺寸远小于真实盾构尺寸,忽略重力对泥浆颗粒渗滤的影响。为便于泥浆压入土体试样,单元1不填充土样,且手动阀门始终保持关闭状态。在各渗透柱上层粗柱与下层细柱间均放置孔径为0.09 mm单层滤网,以保证泥浆中膨润土颗粒过筛率为100%而细砂过筛率为0。此外,各单元细柱中均填充直径为5 mm的玻璃珠以降低滤液流速,便于从侧口处提取。细柱底部放置孔径为0.425 mm单层滤网以防止玻璃珠通过底部圆形开口运移至下一单元。经测定,泥浆通过细柱前后质量浓度差值<0.1 kg/m3,玻璃珠对滤液质量浓度测量的影响基本可以忽略。填砂时控制各单元盖板和砂样表面之间有5 mm的高度余量,以保证浆液在上层粗柱的截面上均匀渗透。填土完成后,首先自下而上对土样进行饱和。滤液通过量筒收集,测量其体积,而后将滤液倒入烧杯。对量筒内壁附着的膨润土进行多次洗涤,将滤液倒入烧杯。为避免液体飞溅,滤液以60 ℃恒温加热至水分完全蒸发,称膨润土颗粒质量后计算滤液质量浓度。
1.3 试验流程
滤液质量浓度测量步骤如下。
1) 组装试验装置。按照试验设计方案,在各渗透柱单元上安装手动阀门并使其处于关闭状态。用塑料软管将装置底部阀门与用于试样饱和的集水罐连接。
2) 试样制备及饱和。将一渗透柱单元与带有出水阀门的托盘通过螺栓连接为整体。首先在单元细柱底部放置孔径为0.425 mm滤网,填充直径为3 cm的玻璃珠,而后放置孔径为0.09 mm滤网。为使泥浆在所有土样中完全渗透,土样在多层渗透柱中自上而下填充粒径依次减小,采用雨淋法使砂样达到设计高度(2.5 cm)。待所有渗透柱单元填充及连接工作完成后,将带有进浆口的盖板与顶部渗透柱单元相连,在集水罐中加适量的水并提升至适当高度,打开装置底部阀门,控制集水罐内水面高度,使试样由下而上缓慢饱和,以排出土样内部的空气。饱和结束后,关闭装置底部的阀门。
3) 泥浆制备。根据试验设计工况,使用螺旋搅拌机将膨润土与水搅拌30 min,使膨润土与水充分混合,而后将CMC溶液与泥浆混合后继续搅拌10 min,搅拌结束后密封泥浆筒,以防止杂质进入泥浆。试验所用泥浆试样需保证膨化时间为24 h,并在使用前搅拌5 min,使膨润土颗粒分布均匀。待砂样饱和完成后,将泥浆倒入储浆桶内,连接空压机,此时,装置底部的出水阀门处于关闭状态。
4) 滤液质量浓度测量。试验前分别准备3个量程50 mL的量筒和烧杯并编号,用量筒测得渗透柱单元侧口滤液体积,而后将滤液转入烧杯中。为提升测量结果的准确性,对量筒洗涤2~3次,将少量黏附在烧杯侧壁上的膨润土颗粒也倒入烧杯中。为防止加热后的膨润土颗粒吸收空气中的水分,同时保证滤液不飞溅,烧杯中溶液经电炉加热至无水蒸气逸出后立即置入电子天平内,而后关闭天平玻璃盖板,测得滤液试样中膨润土颗粒质量,进而计算滤液中膨润土颗粒的质量浓度。
5) 泥浆渗透测试。打开气泵和装置底部的出水阀门,将压力设置为恒定值40 kPa。泥浆缓慢填充顶部单元1后并向下渗滤,待泥浆流经单元2土样至泥浆充满细柱后立即打开手动阀门,用量筒自上而下依次对滤液取样,取样时间为5 s。当有泥浆从装置底部出水阀门滤出后停止加压,一次泥浆渗透结束。
6) 预试验。为确定土样是否满足滤液差浓度测定要求,采用高浓度泥浆试样SL5进行预试验。试验现象表明,在S4土样中泥浆在填满整个渗透柱断面前已经大量渗透,滤液质量浓度与泥浆初始质量浓度差值低于0.5 kg/m3,不能排除温度、湿度等环境因素对浓度测量的影响。因此,正式试验中仅采用S1~S3土样。
2 渗滤系数测定方法
2.1 测定原理
在渗滤过程中,泥浆的性质变化与土体孔隙结构特征均密切相关。本研究中,渗滤系数定义为在单位长度的多孔介质中沉积的颗粒质量与流入颗粒质量的比值[23],其表达式为:
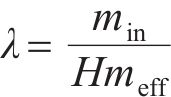
式中:min和meff分别为沉积在单位体积土体骨架中的颗粒质量和流入土体单元的泥浆颗粒总质量;H为多孔介质长度,本试验中,H为渗透柱内土样填充高度,泥浆在膨润土颗粒的沉积质量通过滤液浓度差测量。
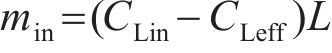
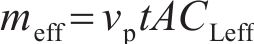
式中:CLin和CLeff分别为泥浆的流入质量浓度和流出质量浓度,在试验中分别对应两相邻渗透柱单元侧口滤液质量浓度;L为流入泥浆体积;vp为孔隙流速,vp=L/(φ0At),t为渗流时间;φ为土体试样孔隙率;A为渗透柱单元截面积,A=πRd2,Rd为渗透柱单元上层粗柱内径。
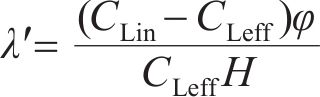
2.2 渗滤系数回归分析
泥浆渗透测试验共设置15组工况,对各工况均进行3次重复试验。各渗透柱土样单元的进浆质量浓度和滤液质量浓度、土体渗滤系数见表3。总体而言,CLin和CLeff的差值随土体泥浆粒径比减小而增大。
| 序号 | 泥浆 | 土样 | 泥浆质量浓度/(kg·m-3) | 渗滤系数/m-1 | |
|---|---|---|---|---|---|
| CLin | CLeff | ||||
| 1 | SL1 | S3 | 27.13 | 26.15 | 0.78 |
| 2 | S2 | 26.15 | 24.54 | 1.29 | |
| 3 | S1 | 24.54 | 22.33 | 1.86 | |
| 4 | SL2 | S3 | 38.03 | 35.97 | 1.19 |
| 5 | S2 | 35.97 | 33.15 | 1.67 | |
| 6 | S1 | 33.15 | 29.55 | 2.29 | |
| 7 | SL3 | S3 | 48.86 | 45.55 | 1.51 |
| 8 | S2 | 45.55 | 41.23 | 2.06 | |
| 9 | S1 | 41.23 | 36.10 | 2.67 | |
| 10 | SL4 | S3 | 58.87 | 54.10 | 1.83 |
| 11 | S2 | 54.10 | 48.32 | 2.34 | |
| 12 | S1 | 48.32 | 41.99 | 2.84 | |
| 13 | SL5 | S3 | 67.97 | 61.75 | 2.09 |
| 14 | S2 | 61.75 | 54.30 | 2.69 | |
| 15 | S1 | 54.30 | 46.57 | 3.12 | |
为便于将提出的渗滤系数λ求解方法应用于实际工程,选用泥浆质量浓度CL、土体有效粒径与泥浆颗粒粒径的比值d10/D85作为独立设计变量,以λ作为响应值,应用试验设计与分析软件SPSS中的非线性分析模块建立多元回归方程。渗滤系数随泥浆质量浓度和粒径比变化如图4所示。渗滤系数实测值在平面上的投影显示λ与CL呈线性相关,d10/D85与λ呈指数关系。
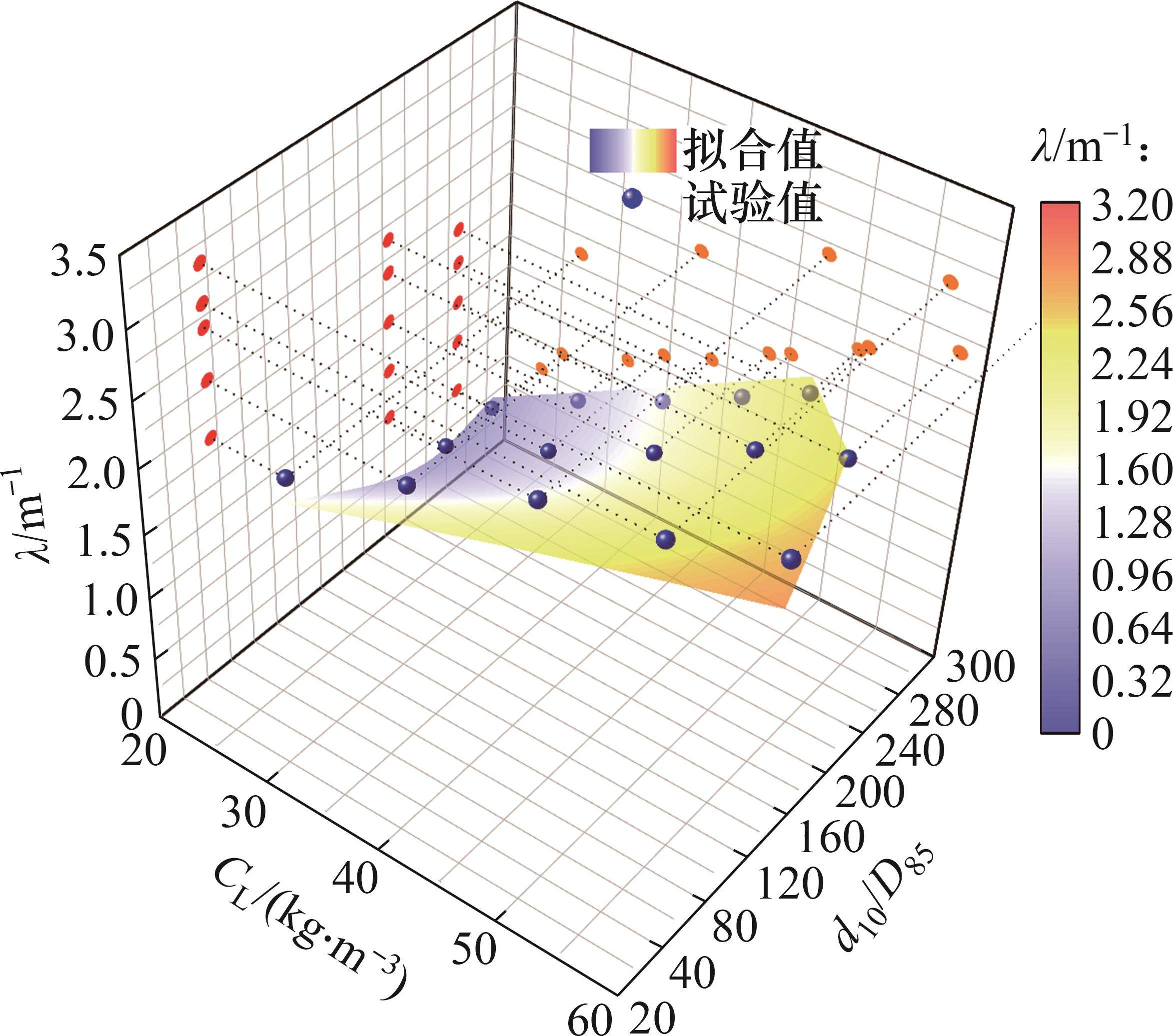
应用SPSS软件中非线性模块进行分析。对渗滤系数试验值进行拟合,得到土体渗滤系数的回归方程λreg:
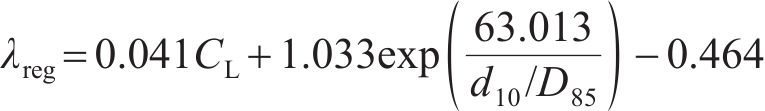
该回归方程的相关系数R2=0.960,接近于1,方程的显著性概率P=0.006(远小于0.05)。拟合值与试验值的平均相对误差为18.96%。从图4可见,渗滤系数拟合值随各影响因素的变化规律与试验结果较一致,该求解方法可以用于预测不同条件下的渗滤系数。
3 成膜时间判定方法
BEZUIJEN等[25]提出了一种适用于饱和砂层中因泥浆入渗导致超孔隙水压力的计算方法,其示意图如图5所示。该方法假定地层为均一粒状土体,舱内泥水在掌子面上均匀渗透,超孔隙水压力消散距离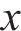
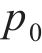
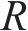
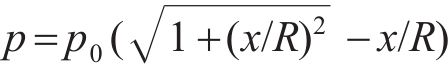
式中:p为掌子面前方dx处超孔隙水压力。
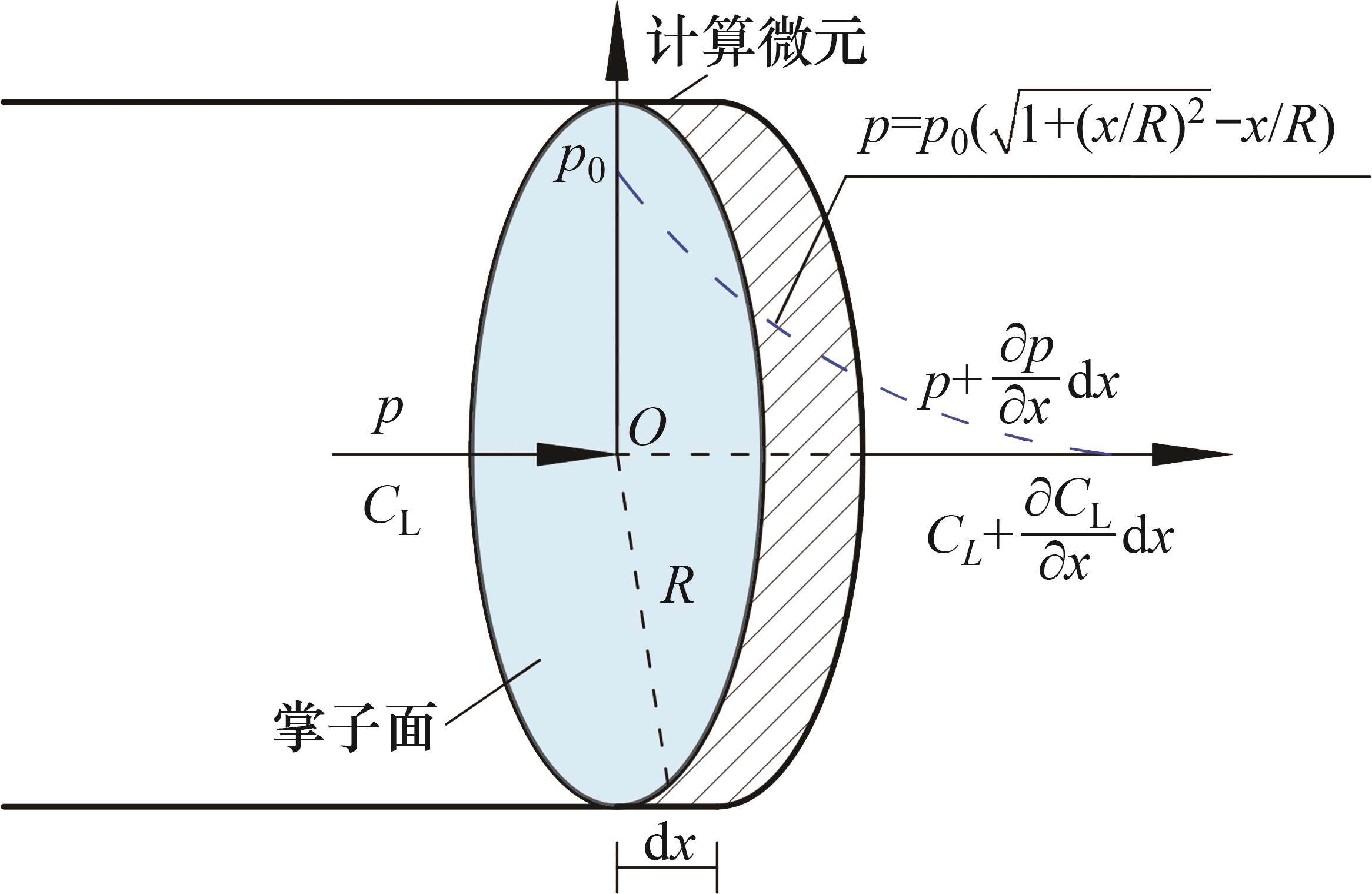
则开挖面处超孔隙水压力水力梯度i0可表示为:
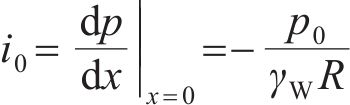
式中:γW为水的重度。
土体中赋存的孔隙水内因泥浆渗透向前驱替,开挖面表明浆液流速v为:
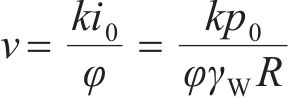
式中:k为土体渗透系数;φ为土体孔隙率。
BAI等[26]通过研究发现泥浆中固相颗粒沉积是泥膜形成的主要原因。随着泥浆入渗,泥浆颗粒逐渐沉积-淤堵土体孔隙,导致浆液质量浓度降低。一般认为土体对泥浆的渗滤作用越强,泥浆成膜时间越短。泥浆颗粒沉积质量浓度
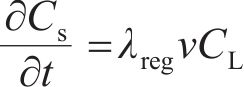
式中:t为渗流时间;CL为泥浆质量浓度。
相关研究表明,单位体积孔隙中沉积的膨润土颗粒达到泥浆颗粒的松铺孔隙率即可判定泥皮生成,此时,土体孔隙中表层沉积的泥浆颗粒临界质量浓度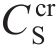
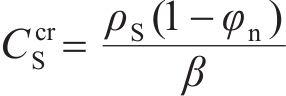
式中:φn为膨润土颗粒的松铺孔隙率;ρS为膨润土颗粒干密度;β为浆体颗粒膨胀系数。假设膨润土颗粒是均匀球体,排列成立方体,β=6/π[28],则成膜时间t可表示为
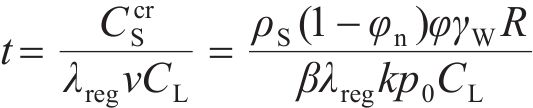
4 模型验证
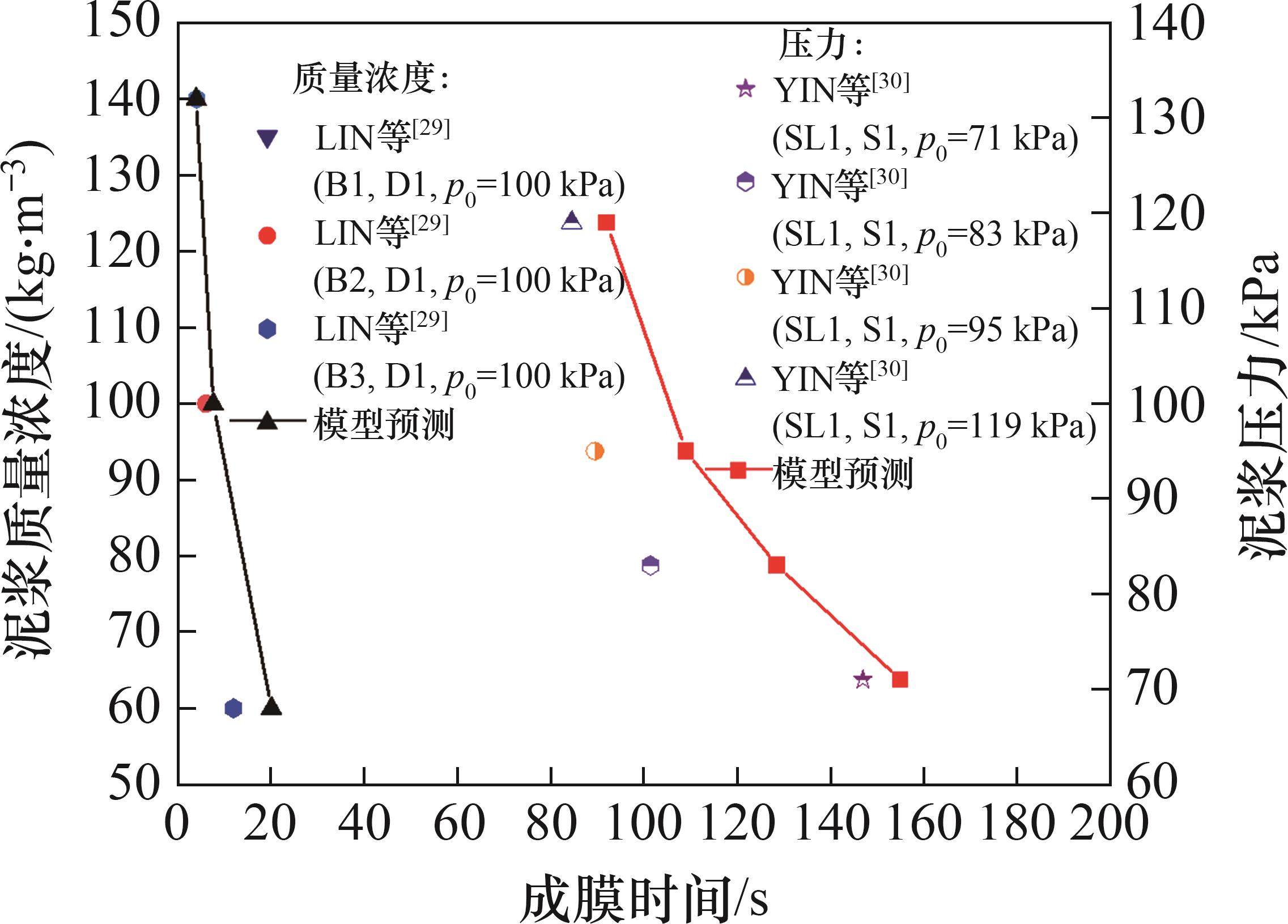
为验证本文提出的成膜时间判定方法,根据已有研究中多种泥浆配比及土体粒径组合试验结果进行验证。模型所需泥浆、土体和泥水压力输入参数见表4。试验研究中成膜时间通常为滤水量明显降低时的时间。成膜时间模型预测结果与试验结果对比如图6所示。LIN等[29]的研究表明,成膜时间随泥浆质量浓度的增高逐渐增加,与本文预测结果较一致;YIN等[30]试验结果显示,增加泥水压力能有效降低泥膜生成时间,符合式(11)预测趋势。证明了本文提出泥浆成膜时间判定方法的合理性。
| 模型 | 泥浆 | 泥浆质量浓度CL/(kg·m-3) | 泥浆代表粒径D85/μm | 土体 | 土体有效粒径d10/mm | 孔隙率 | 土体渗透系数k/(m·s-1) | 不均匀系数Cu | 泥水压力p0/kPa |
|---|---|---|---|---|---|---|---|---|---|
| 1 | B1 | 60 | 12.5 | D1 | 0.309 | 0.41 | 3×10-4 | 1.15 | 100 |
| 2 | B2 | 100 | 12.5 | ||||||
| 3 | B3 | 140 | 12.5 | ||||||
| 4 | SL1 | 50 | 80 | S1 | 0.137 | 0.39 | 2×10-4 | 1.25 | 71 |
| 5 | 83 | ||||||||
| 6 | 95 | ||||||||
| 7 | 119 |
5 参数分析
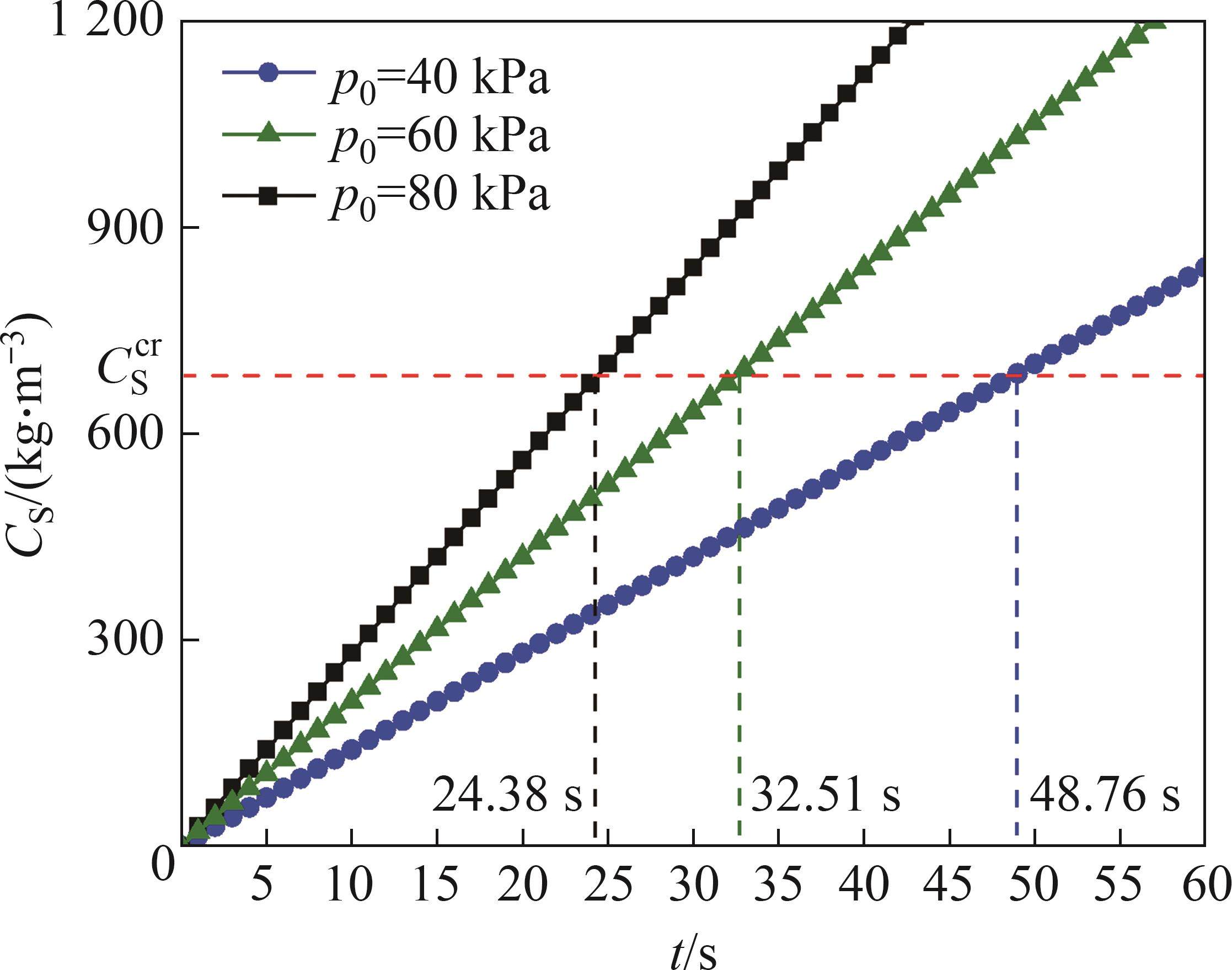
隧道半径设为3 m,以泥浆SL2和土体S1为例计算不同泥水压力下土体表层孔隙中膨润土颗粒沉积量随渗透时间的变化,结果图7所示。由式(10)计算可得,土体临界沉积泥浆颗粒质量浓度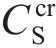
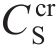
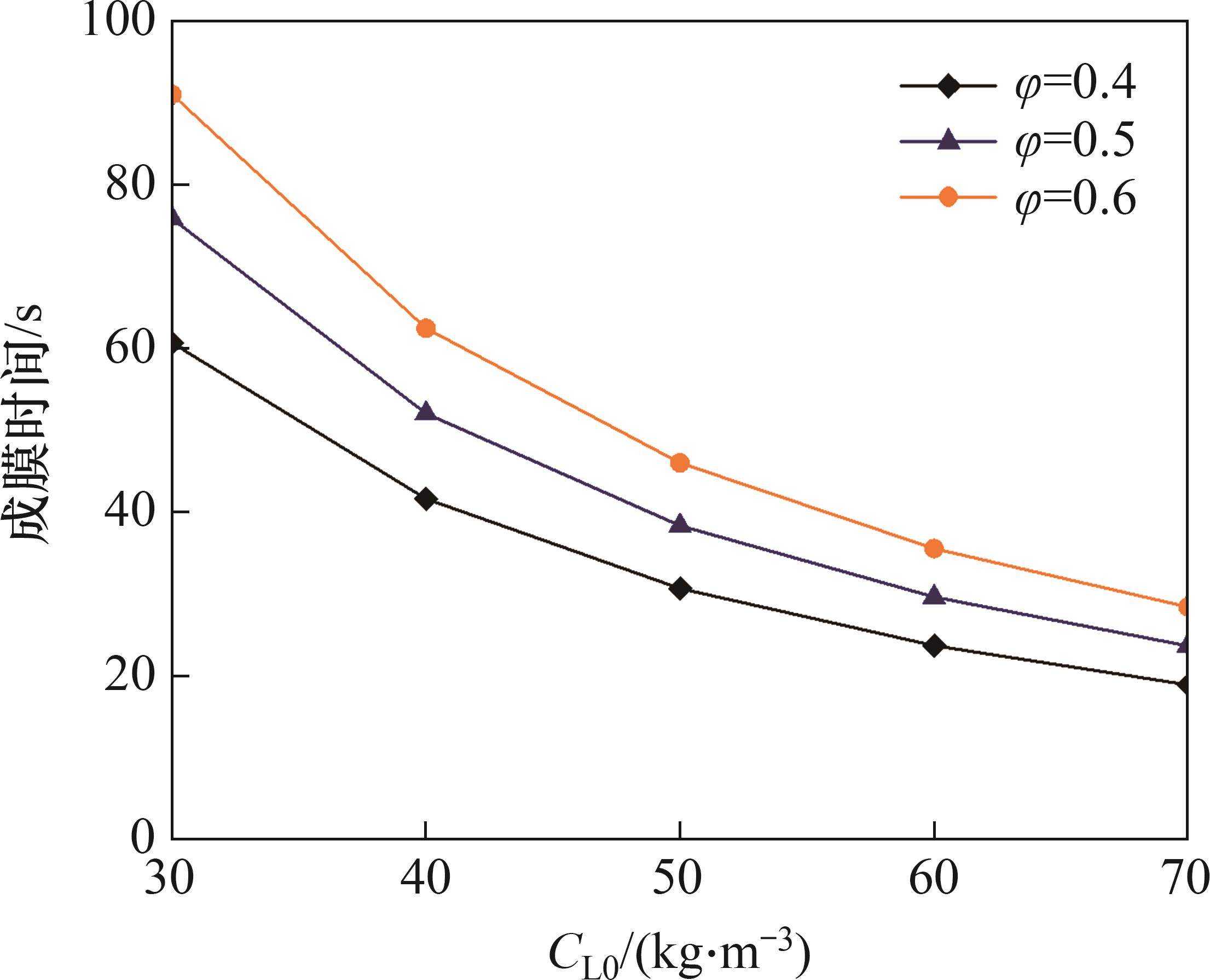
泥膜生成时间与泥浆参数和地层孔隙率也有较强的相关性,设泥水压力为40 kPa,隧道半径为3 m,根据泥浆SL2和土体S1参数研究泥浆质量浓度和土体孔隙率对成膜时间的影响,结果如图8所示。从图8可见:成膜时间随泥浆质量浓度的增大而减小,成膜时间与土体孔隙率呈正相关,这意味着在粗砂、砾石等粗粒径地层中,增大泥浆中固相颗粒含量有利于泥膜生成,发挥泥浆的支护作用。
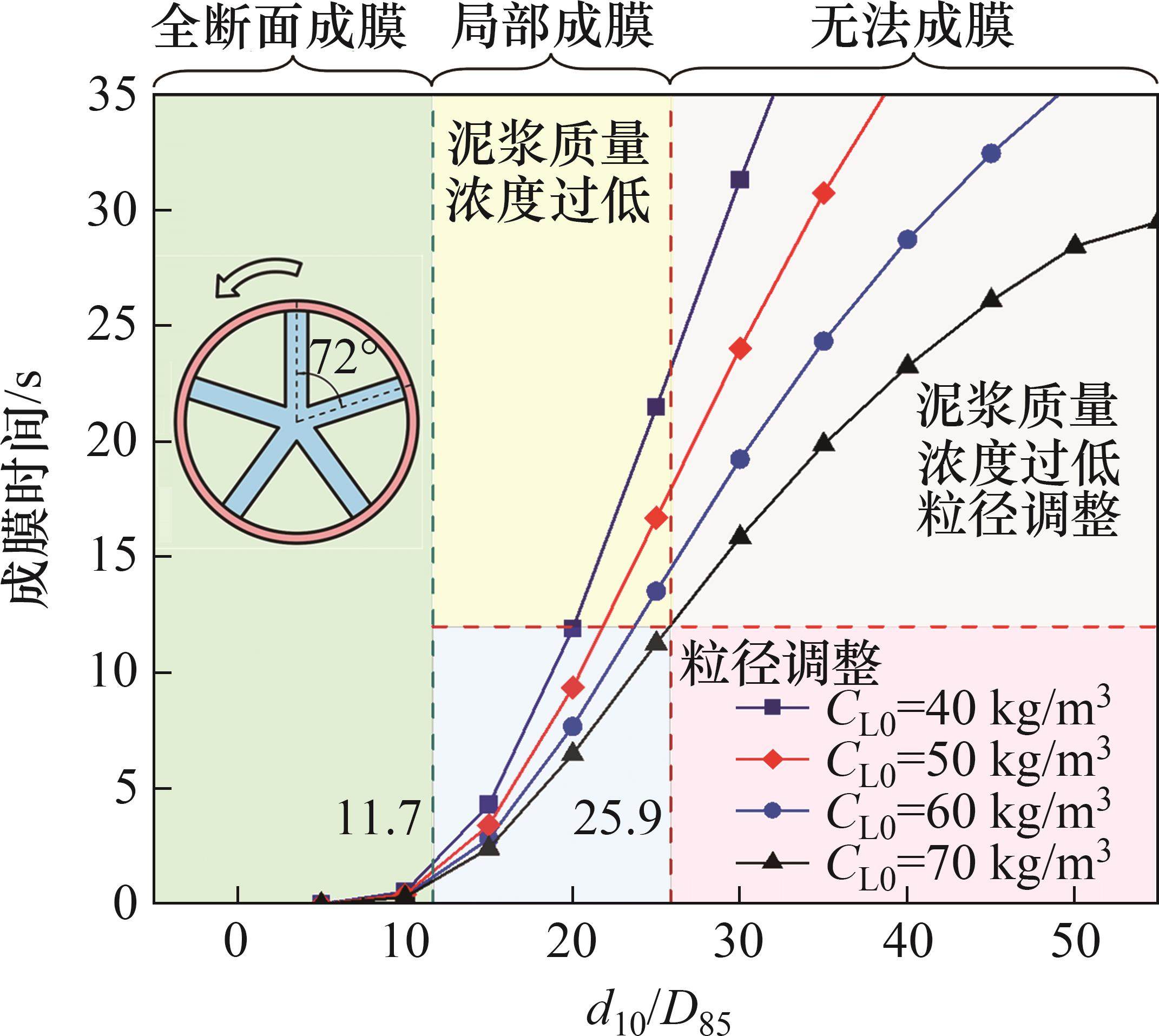
结合刀盘转速分析土体与泥浆粒径比(d10/D85)对成膜时间及泥膜分布状态的影响。在实际掘进中,泥膜处于切削-生成循环过程中,因此,只有当成膜时间低于相邻刀具切削时间时,掌子面才有泥膜生成。以五辐条式刀盘为例,刀盘转速设为1 r/min,相邻刀具切削周期Tn为12 s,泥水压力为40 kPa,SL2泥浆质量浓度为40~70 kg/m3,成膜时间随粒径比d10/D85的变化如图9所示。从图9可见:成膜时间随粒径比d10/D85呈指数增加;当d10/D85



6 结论
1) 渗滤系数与泥浆性质和土体孔隙特征均密切相关,其数值与泥浆质量浓度呈正相关,与地层渗透系数、土体与泥浆粒径比呈负相关。这表明粗粒地层中土体骨架对泥浆颗粒的吸附能力更低,泥浆滤失量更高,提高泥浆中固相颗粒含量有利于泥膜生成,发挥泥浆的支护作用。
2) 当土体表层孔隙内泥浆颗粒孔隙率达到松铺孔隙率时即可判定泥膜生成,成膜时间与泥水压力呈正相关。在实际工程中,适当增加泥水压力有利于泥浆颗粒迅速堆积成膜,也应同时考虑泥浆与地层的适配性以免造成浆液大量滤失。在粗砂、砾石等粗骨架地层中,泥浆滤失量远大于细颗粒地层滤失量,采用高质量浓度泥浆更易生成泥膜,有利于维持掘进过程中开挖面稳定。
3) 随土体与泥浆中固相颗粒粒径比d10/D85增加,成膜时间呈指数增加。当粒径比较低时,掌子面处泥膜可完整或局部生成,泥膜可有效发挥支护作用;当粒径比较大时,成膜时间高于相邻刀具切削周期,泥膜无法生成。当盾构穿越粗粒径地层时,可在泥浆中加入粉细砂等细颗粒以降低粒径比,或适当提升泥浆质量浓度,促使泥膜快速生成。
金大龙, 杨引尊, 袁大军, 等. 砂土地层泥浆成膜时间判定方法[J]. 中南大学学报(自然科学版), 2024, 55(12): 4583-4592.
JIN Dalong, YANG Yinzun, YUAN Dajun, et al. Computing method of filter cake formation time in sandy stratum[J]. Journal of Central South University(Science and Technology), 2024, 55(12): 4583-4592.

