预应力空间结构体系主要由索(包括斜拉索与悬索)与空间钢结构杂交而成。经过多年的发展与应用,已形成了张弦梁、弦支穹顶、索穹顶、索桁架等结构体系[1-4]。而预应力空间结构的关键在于通过预应力索的张拉来提高结构刚度,主要分为2个途径,即预应力作用时对结构产生的预变形以及结构在受荷载过程中预应力索对结构刚度的贡献[5]。
预应力空间结构分析的首要问题是预应力水平的确定[6],即找力分析,常用的方法有动力松弛法、力密度法等。文献[7]提出一种基于叠加原理的弦支穹顶结构找力方法,最大计算误差达到1.16%,但仅适用于几何非线性不明显的预应力结构。文献[8]基于平衡矩阵理论,提出一种简化的基于节点平衡的自内力模态的确定方法,针对弦支穹顶结构常用的Levy索系和Giger索系提出了其自内力模态的解析解,但并未考虑施工过程的影响。文献[6]将BP神经网络算法引入找力分析问题中,基于大量的数据集,建立BP神经网络模型,以初始态下的环向索内力为输入数据,以零状态下主动索的初应变为输出数据,并结合遗传算法GA对BP神经网络算法的权重及阈值进行优化,进一步提高找力分析预测的精度及稳定性,但该方法针对不同的工程结构均需建立大批量的结构数据模型。
上述找力分析只是确定拉索的实际内力,但对于拉索的预应力模拟及张拉分析,预应力的模拟计算是通过以初应变或温度作用等方式施加在拉索单元上的非平衡力即拉索的等效预张力来实现的。预应力结构通过分步张拉建立预应力,根据图纸的初始态预设各施工步的索力分布,然后在施工模拟中推导各步骤的等效预张力,以确保各施工步的索力在预设范围之内。在大多数情况下,拉索等效预张力与拉索的实际内力并不一致[9],因此,拉索等效预张力的确定问题为:已知某种荷载态下的拉索实际索力,求解所应施加在拉索上的等效预张力的问题[10]。这是预应力空间结构形态分析理论中的关键问题之一,也是预应力空间结构施工仿真分析的基础[11-12]。
目前对预应力空间结构拉索等效预张力确定问题的研究相对较少。文献[13]采用张力补偿法的思想,进行弦支穹顶结构拉索等效预张力的计算求解;文献[14]提出差值迭代法进行斜拉桥施工索力的计算分析,与补偿法的思路较为相似;文献[15]借鉴Newton法的思路,采用差分的形式代替函数的一阶导数,即采用弦截法来进行拉索等效预张力的迭代求解;文献[9-10, 16]提出了基于设计初始态确定拉索等效预张力的增量比值法、定量比值法、补偿法和退化补偿法,并基于退化补偿法提出弦支穹顶预应力施工过程的正算法。对于简单的张弦结构,上述方法具有较高的计算效率,但对于拉索索力之间耦合影响较大的复杂预应力空间结构存在一定不足:增量比值法和定量比值法收敛不稳定,且限制条件较多;定量比值法要求索力在迭代过程中不为零且不变号;而补偿法的收敛速度取决于补偿因子λ,λ较小则收敛较慢,λ较大则容易发散,迭代不稳定,对补偿因子λ有较强的依赖性[9];而Newton法由于无法进行求导运算,其收敛阶次仅为1.618阶,同时也存在不稳定问题[15, 17]。
鉴于目前拉索等效预张力确定方法的局限性大、稳定性差、计算效率低等不足,本文首先基于数学推导和表达,将复杂的拉索等效预张力确定问题转化为多个相对独立的非线性隐式方程求解问题,为拉索等效预张力确定问题的求解提供理论支撑,同时大大降低了求解的难度;然后,将数值分析理论与实际工程问题相结合,引入Steffensen迭代法,提出基于Steffensen迭代法的拉索等效预张力确定方法,大大提高了其计算效率、稳定性及适用性,为拉索等效预张力确定问题提供了一种高效、可靠的求解方法。
1 拉索等效预张力确定问题的数学表达
无论是采用初始应变还是等效温差的方式模拟施加等效预张力,其核心均是通过索长的变化引起索内力的变化[18]。
对于两端固定且无其他外荷载作用下的单根拉索,其等效预张力与索长变化的关系可表达为
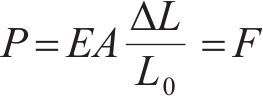
式中:P为拉索的等效预张力;E为拉索的弹性模量;A为拉索的截面积;
而对于整体结构中的某一索段,在结构外荷载及拉索等效预张力的共同作用下,整体结构发生变形及内力重分布,拉索的索长变化不仅包括等效预张力引起的索长变化,而且包括外荷载引起的索长变化,即
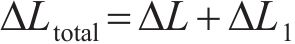
其中: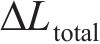

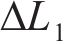
根据胡克定律,拉索的内力即索力与拉索总的索长变化值的关系如下:
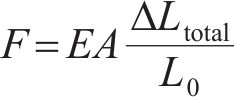
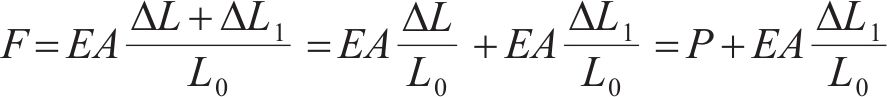
1.1 单索结构
基于线性叠加原理,对于有且仅有1根施加等效预张力拉索的结构(如单榀张弦梁),其拉索总的索长变化值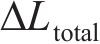
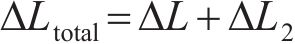
其中,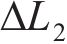
当结构荷载恒定时,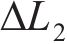
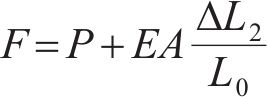
因此,拉索的索力F可表达为与P有关的函数,且近似为一元线性函数:
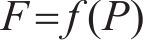
1.2 多索结构
对于有n根施加等效预张力拉索的结构,第i根拉索总的索长变化值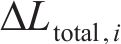
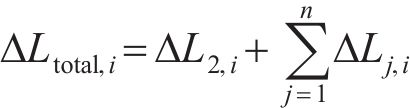
式中,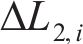
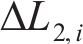
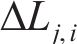
与式(6)和(7)类似,第i根拉索的索力Fi为
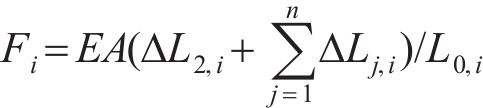
式中: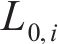
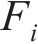
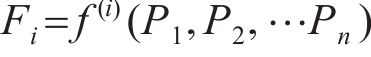
n根施加等效预张力的拉索的索力F可表达为
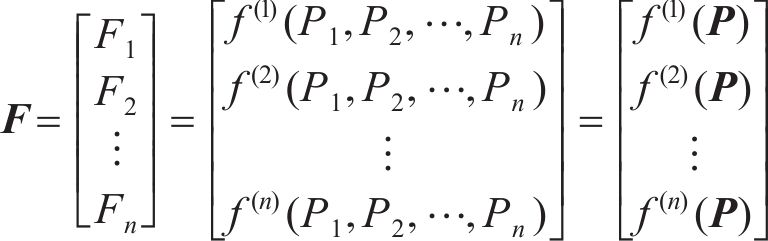
式中:P为n根施加等效预张力拉索的等效预张力列向量,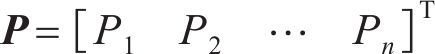
综上,已知某种预应力态或荷载态下的拉索实际索力,求解所应施加在拉索上的等效预张力的问题,其数学表达为已知索力列向量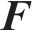
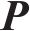
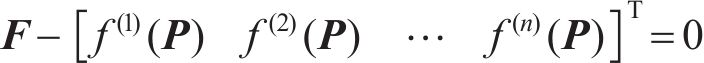
因此,拉索等效预张力的确定问题可转化为非线性方程的求解问题。
对于简单的张弦结构或者相互之间拉索索力影响不大的空间张弦结构,拉索的索力主要与结构荷载及等效预张力有关,因此,可进一步将式(10)进行简化,将第i根拉索的索力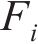
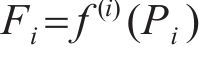
单索结构的拉索索力与等效预张力近似呈线性关系,即式(13)为线性函数;而对于简单的多索结构,其余拉索等效预张力会对该根拉索的索力产生一定的影响,式(13)由线性函数转变为非线性函数,鉴于工程结构的复杂性及拉索之间的耦合影响,该非线性函数难以显式表达,无法进行函数的求导运算,其拉索索力与拉索的等效预张力呈隐式非线性关系。
对于上述非线性隐式方程的求解,鉴于现有算法的不足,本文引入数值分析中的Steffensen迭代法,对拉索等效预张力的确定问题进行求解。
2 基于Steffensen迭代法的拉索等效预张力确定方法
2.1 Steffensen迭代法的原理
在数值分析的非线性方程求解中,最经典的迭代法是Newton迭代法,它具有较高的收敛阶和计算效率,但在其迭代求解中,需要进行求导计算,对于较复杂的非线性方程,其求导计算难以进行。而Steffensen迭代法不需要进行求导运算,且其收敛阶数至少为平方阶,因此,具有较高的收敛阶和计算精度,被广泛应用于各种数值计算[19-21]。根据Steffensen迭代法,对于求f (x)=0的问题,第n+1次迭代的解xn+1为
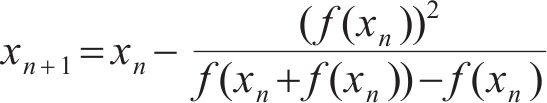
其中,xn为第n次迭代的解。
Steffensen迭代法基本原理如下。
1) 根据一般迭代法的原理,对于求解f(x)=0的问题,首先构造一个新的函数φ(x):
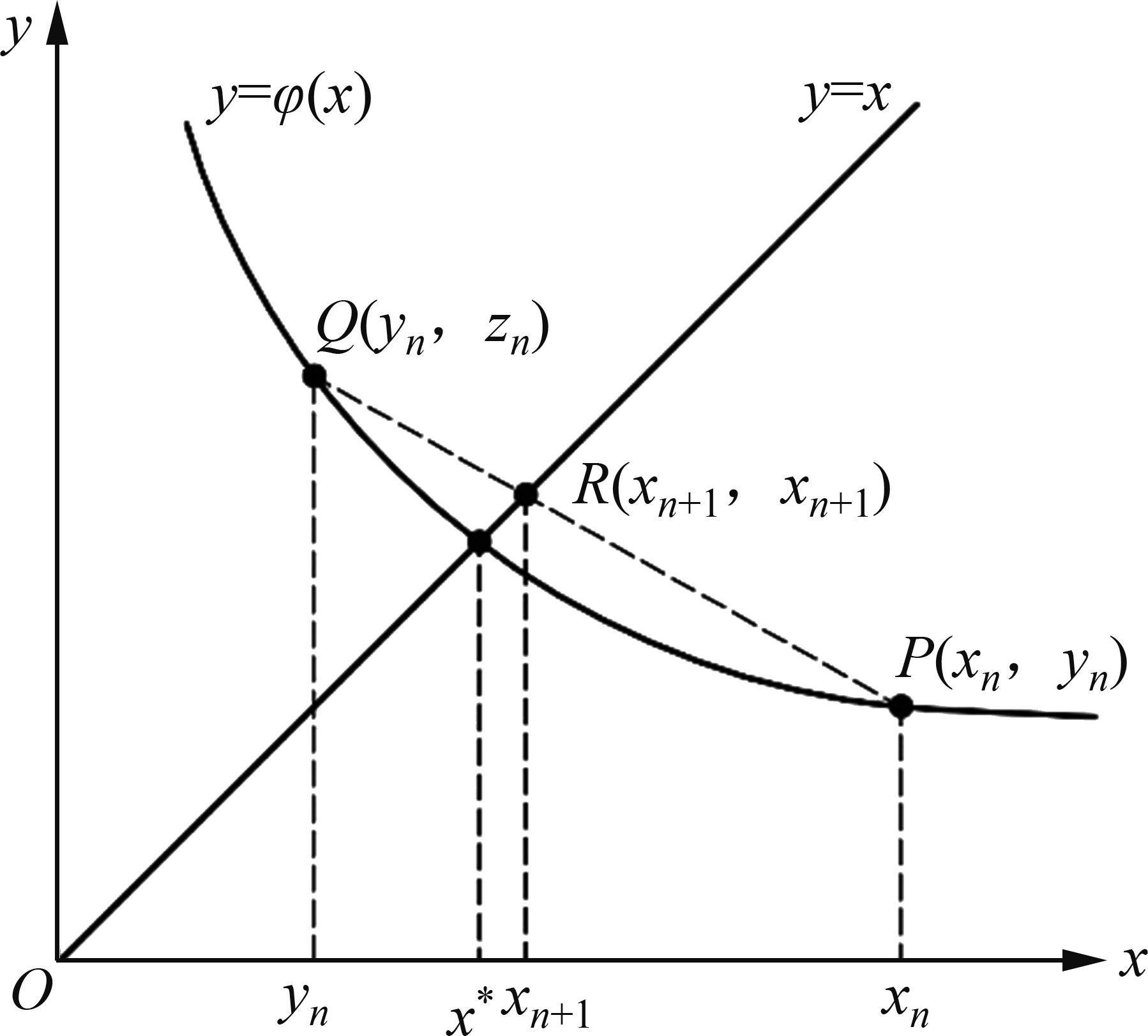
将求解f (x)=0的问题转换为求解φ(x)=x的问题,即寻找曲线y=φ(x)与y=x交点对应的值,记为x*,x*即为方程f (x)=0的解,如图1所示。
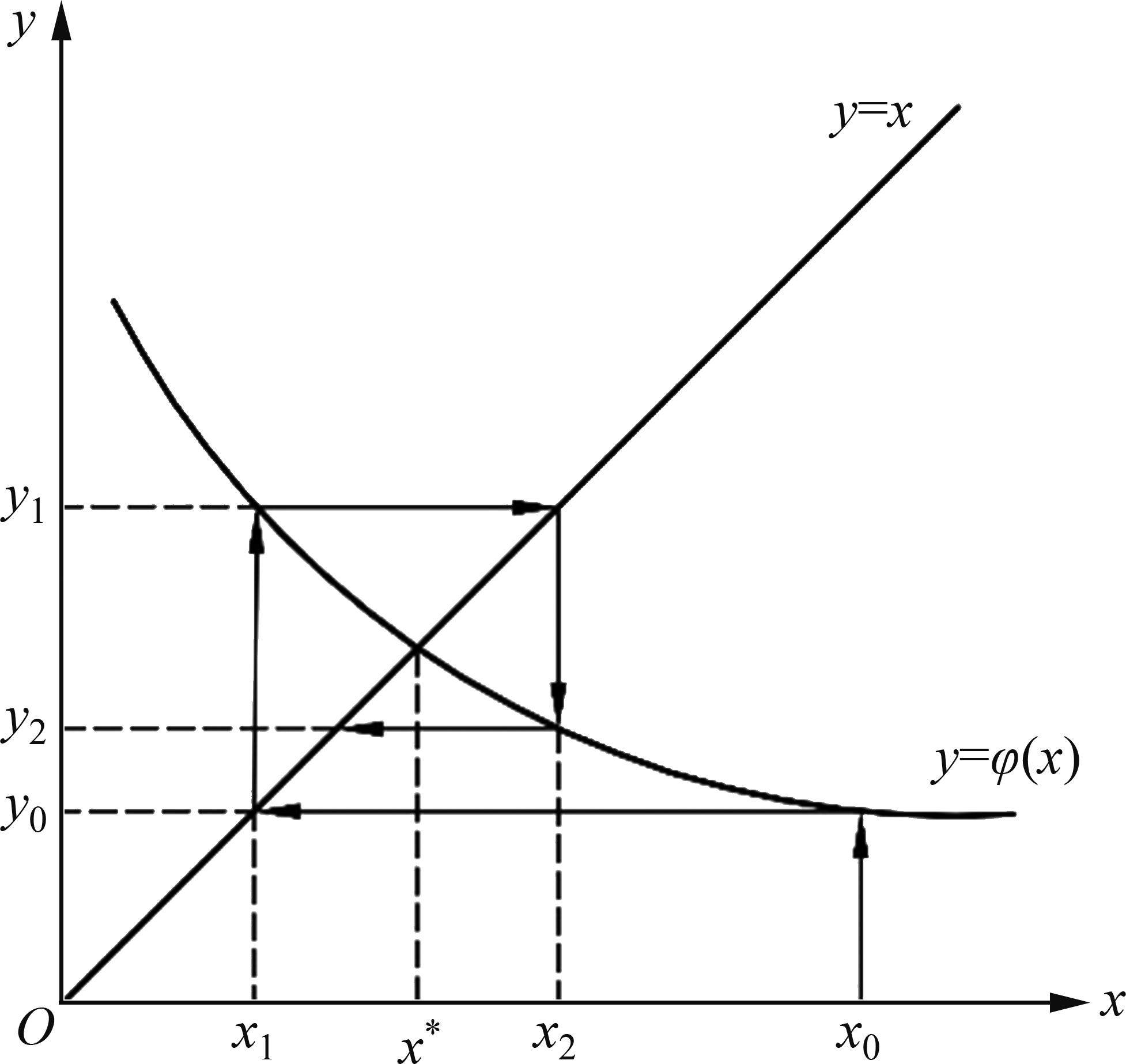
2) 结合式(15),用φ(x)替换f (x),则式(14)可修改成
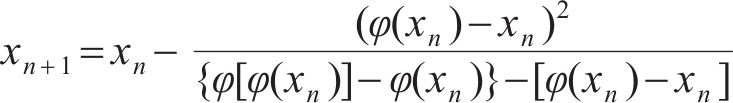
3) 令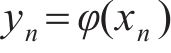
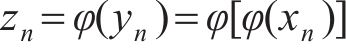
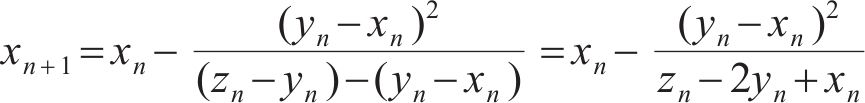
5) 对于Steffensen法的迭代式(18),其几何意义如下:对于曲线y=φ(x)上的两点P(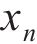
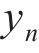
Q(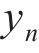
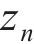
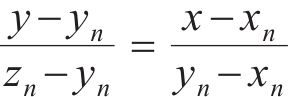
因此,令y=x,则有
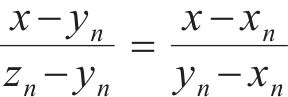
求解式(20)可得
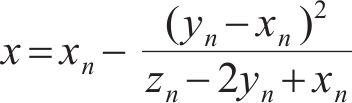
结合式(18)和式(21)可知,直线QP与直线y=x的交点的横坐标为xn+1,即直线QP与直线y=x的交点坐标为(xn+1,xn+1)。
因此,Steffensen法的几何解释为:从xn出发,找到曲线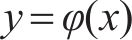
2.2 基于Steffensen迭代法的拉索等效预张力确定方法
根据式(12)和(13),拉索等效预张力确定问题可转化为多个近似相对独立的非线性方程的求解问题,因此,可应用Steffensen迭代法进行非线性方程的求解。
基于Steffensen迭代法的拉索等效预张力确定方法的主要原理如下。
1) 所需求解的问题。根据式(13)和Steffensen迭代法的原理,拉索等效预张力确定问题表达为
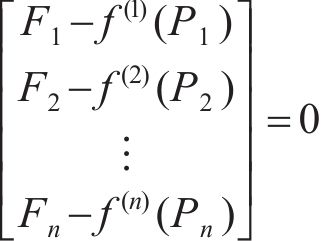
令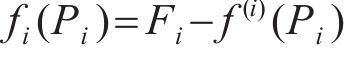
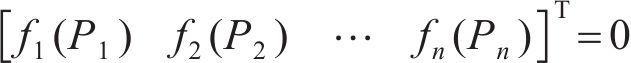
因此,拉索等效预张力确定问题转化为n个独立的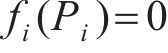
2) 构造一个新的函数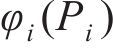
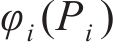
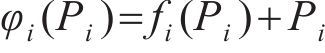
因此,式(23)可转化为
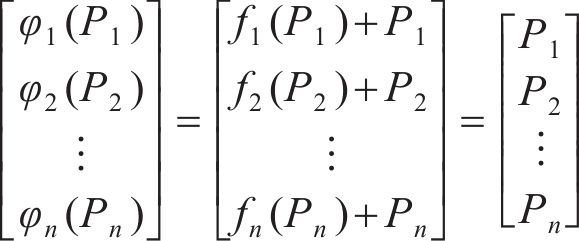
3) 定义迭代公式。对于第n次迭代的第i根拉索的等效预张力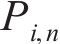
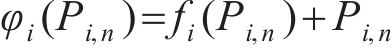
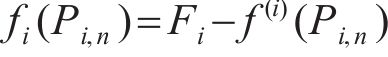
式中: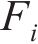
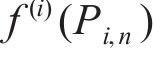
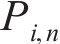
令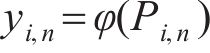
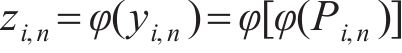
根据式(18)可得迭代公式为
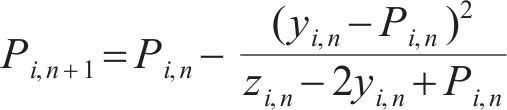
4) 迭代终止机制。对于迭代法,其终止机制一般为前后两次迭代的自变量差值小于容许误差,即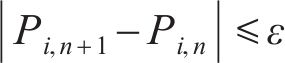
根据预应力钢结构技术规程[22],预应力的误差不应超过设计值的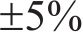
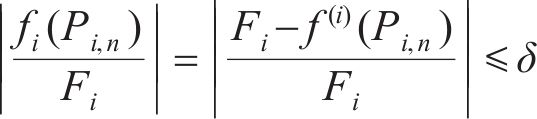
其中,δ为容许相对误差(简称容差)。
2.3 实现流程
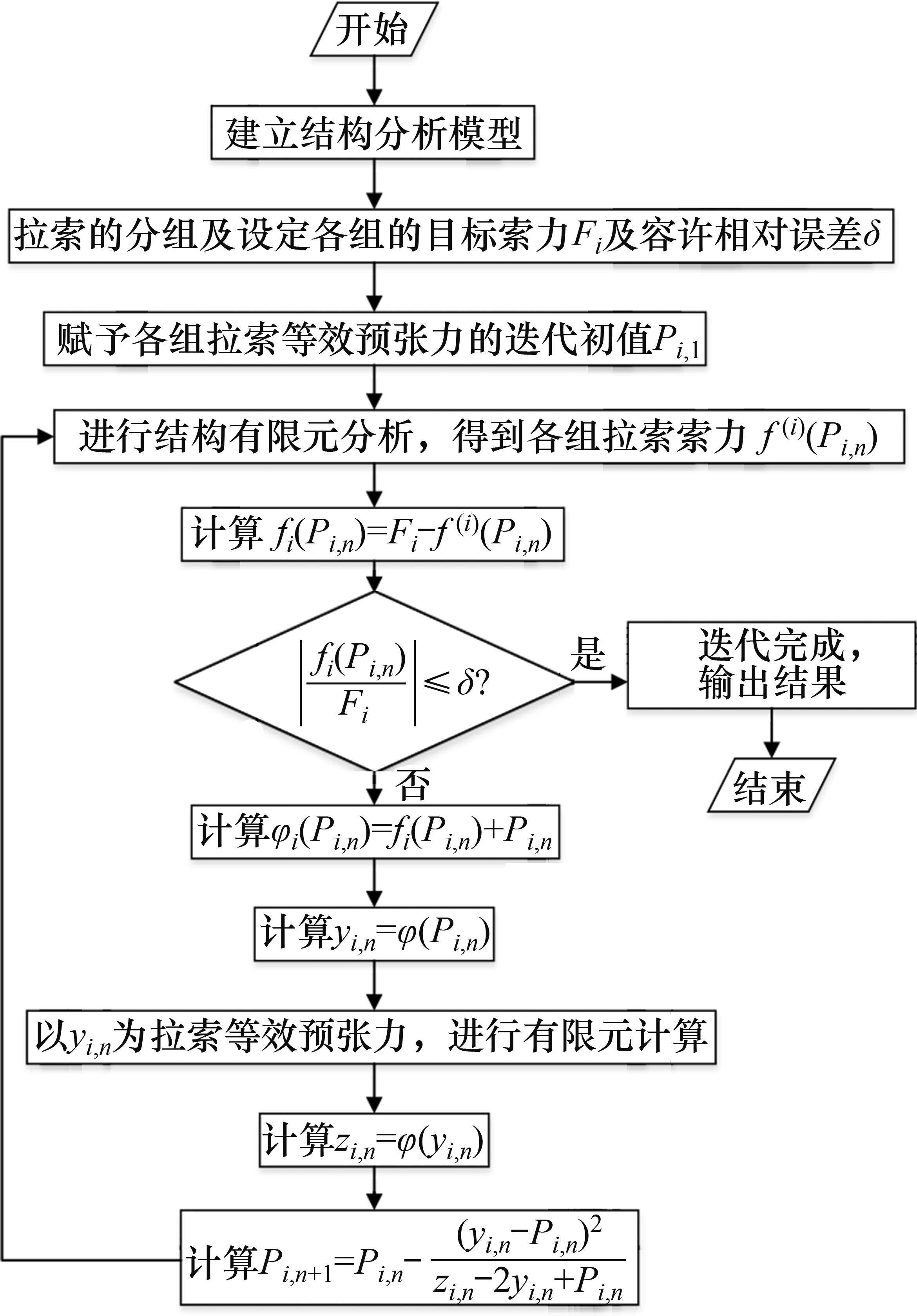
根据上述基本原理,基于Steffensen迭代法的拉索等效预张力确定方法流程如下。
1) 建立结构分析模型,对拉索进行分组,设定各组拉索的目标索力Fi以及索力的容差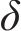
2) 赋予各组拉索等效预张力的迭代初值Pi,1;
3) 进行结构有限元分析计算,得到各组拉索内力重分布后的索力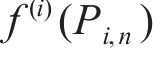
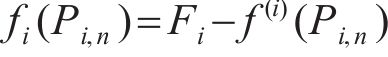
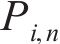
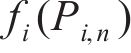
4) 判断各组拉索索力与目标索力的差值是否小于容差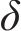
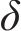
5) 根据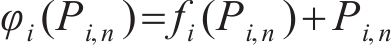
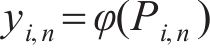
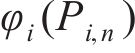
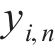
6) 以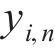
7) 根据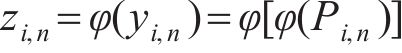
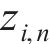
8) 根据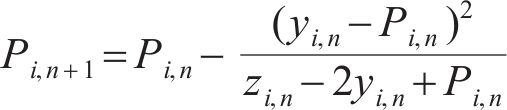
基于Steffensen迭代法的拉索等效预张力迭代流程如图3所示。
3 计算效果分析
以实际的工程算例对Steffensen法的计算效果,包括不同方法、不同求解精度、不同迭代初值下的计算效率及稳定性等进行分析,并对其在预应力张拉施工模拟、多变量耦合高精度问题下的应用效果进行分析,从而全面验证该方法在各类拉索等效预张力问题中的效率、适用性和可靠性。
3.1 不同求解精度下的计算效果分析
以贵阳奥林匹克体育中心(二期)主体育馆超大跨度肋环型弦支穹顶屋盖结构为例(如图4所示)进行分析。屋盖净跨度为117 m,最高处标高为 42 m,整体结构主要包括上部肋环型单层网壳、下部5圈levy索杆体系、环桁架结构和外墙面网壳结构,环桁架结构底部及外墙面网壳结构底部由下部混凝土结构柱支承,肋环型单层网壳采用箱形截面,最大高度为600 mm,最大宽度为400 mm,最大腹板厚度为25 mm,最大翼缘板厚度为 25 mm;每圈布置16根撑杆,材质均为Q355B,最大高度为6 500 mm,最大管径为273 mm,最大壁厚为20 mm;每圈布置32根径向钢拉杆,径向钢拉杆为E650级,最大直径为120 mm;环向索为1 670 级高钒密闭索,最外圈为4根并排的80 mm直径密闭索。
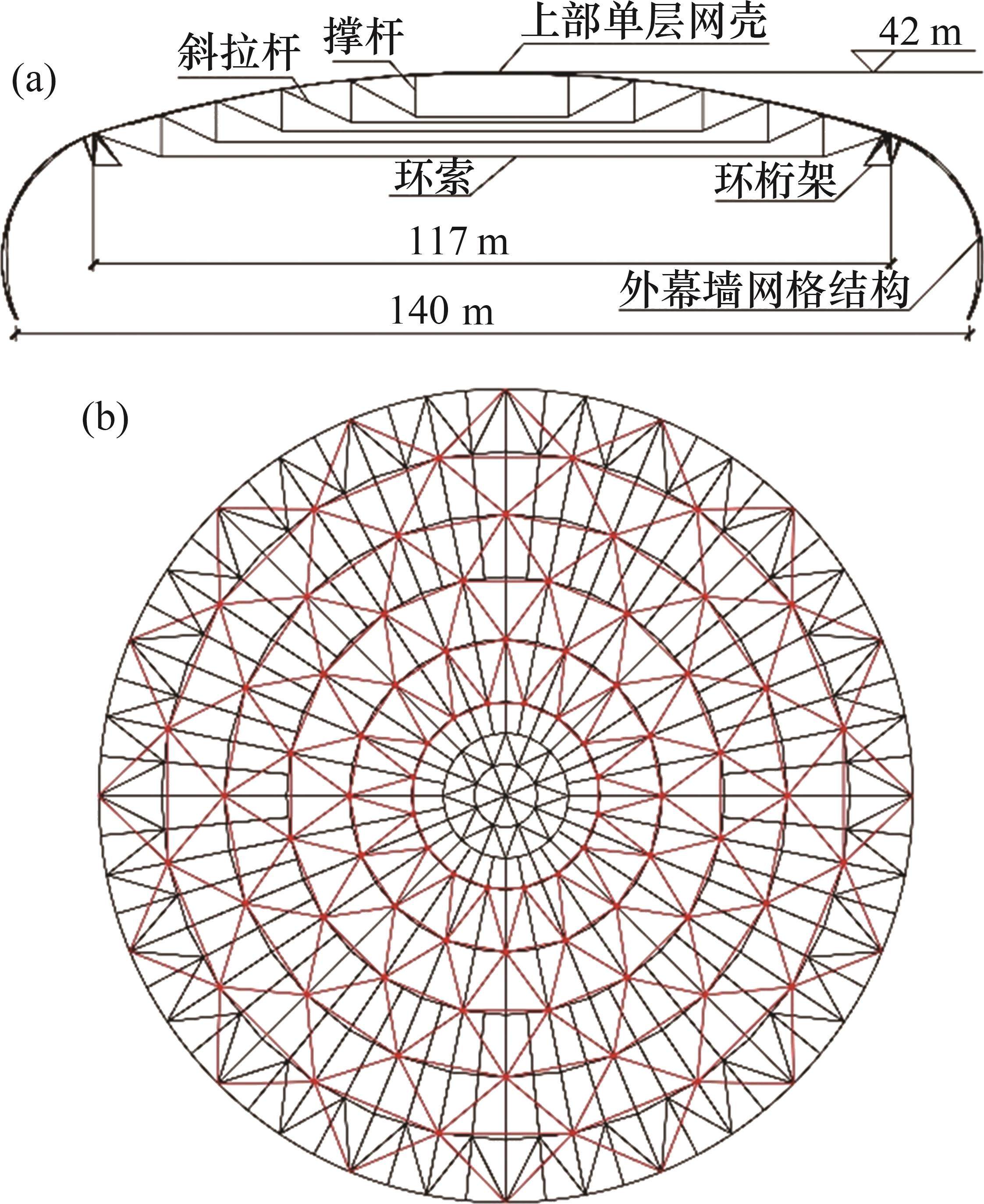
本算例中将每圈环向索作为1组拉索,针对载荷为1.0倍自重+1.0倍预应力的基本工况,各组环向索的已知索力(即目标索力)Fi如表1所示。
| 分组 | 目标索力Fi/kN |
|---|---|
| 第一圈 | 133 |
| 第二圈 | 364 |
| 第三圈 | 1 070 |
| 第四圈 | 2 660 |
| 第五圈 | 6 060 |
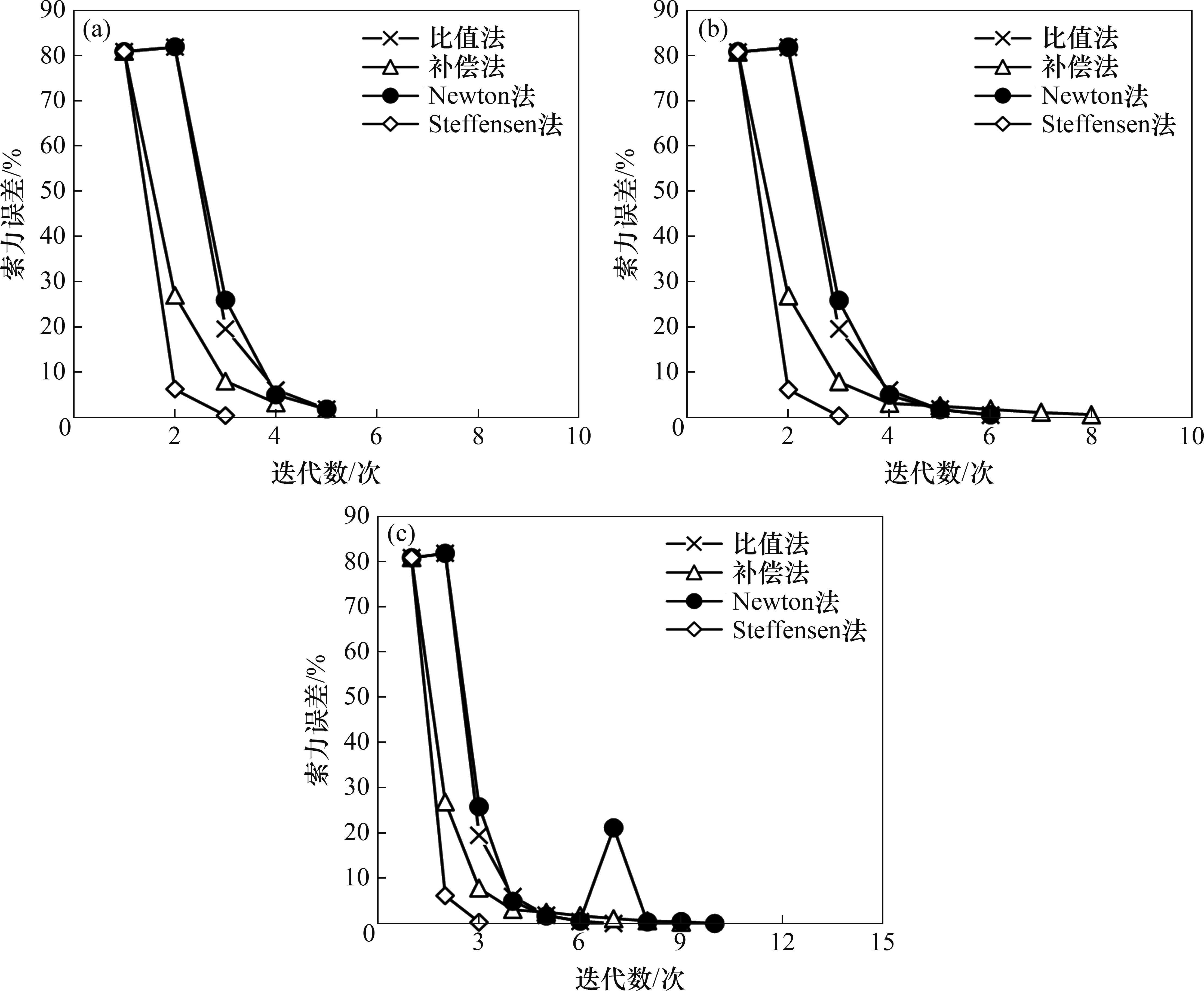
针对索力的容差δ分别为5%、1%和0.5%这3种情况,以目标索力作为等效预张力的迭代初值,分别采用比值法、补偿法、Newton法以及Steffensen法确定环向索等效预张力,以研究不同求解精度下各方法的计算效果,结果如图5和表2所示,其中,索力误差为所有各圈环向索的最大索力误差。
| 分组 | 比值法 | 补偿法 | Newton法 | Steffensen法 |
|---|---|---|---|---|
| 第一圈 | 294.8 | 290.5 | 294.9 | 289.0 |
| 第二圈 | 526.1 | 529.0 | 524.6 | 528.7 |
| 第三圈 | 1 668.0 | 1 673.4 | 1 665.6 | 1 677.1 |
| 第四圈 | 4 115.6 | 4 120.8 | 4 112.6 | 4 132.2 |
| 第五圈 | 9 718.2 | 9 700.5 | 9 723.0 | 9 682.7 |
从图5可知,Steffensen法的计算效率最高,仅经过3次迭代即将索力误差降低至0.4%;对于比值法,当索力容差为5%、1%和0.5%时,分别需要5次、6次、7次迭代,而且迭代过程中出现索力误差的浮动,计算过程不稳定,计算速度相对较快;对于补偿法,当索力容差为5%、1%和0.5%时,分别需要4次、8次、9次迭代,当计算精度要求较高时,补偿法的计算速度相对较慢。对于Newton法,当索力容差为5%、1%和0.5%时,分别需要5次、6次、10次迭代,与比值法相似地,计算速度相对较快,但迭代过程中索力误差存在浮动,迭代稳定性较差。
限于篇幅,表2仅列出索力容差为0.5%时的等效预张力对比。从表2可见:不同方法求解得到的等效预张力基本一致,说明本文Steffensen法的有效性。
3.2 高精度索力求解问题下的计算稳定性分析
为了进一步验证上述方法在高精度索力求解问题下的计算稳定性,以上述结构为例,选取不同迭代初值进行稳定性分析,结果如表3所示。
| 分组 | 迭代初值1 | 迭代初值2 | 迭代初值3 |
|---|---|---|---|
| 第一圈 | 100 | 100 | 100 |
| 第二圈 | 300 | 650 | 700 |
| 第三圈 | 1 000 | 2 100 | 1 300 |
| 第四圈 | 2 000 | 4 100 | 5 000 |
| 第五圈 | 6 000 | 9 700 | 6 000 |
索力的容差δ设置为0.5%,分别采用比值法、补偿法、Newton法、Steffensen法确定环向索等效预张力,对比结果如表4和图6所示,其中,索力误差为所有各圈环向索的最大索力误差。
| 分组 | 迭代初值1 | 迭代初值2 | 迭代初值3 |
|---|---|---|---|
| 第一圈 | 292.7 | 293.3 | 292.5 |
| 第二圈 | 529.3 | 526.1 | 525.6 |
| 第三圈 | 1 673.8 | 1 669.0 | 1 670.1 |
| 第四圈 | 4 098.6 | 4 113.1 | 4 119.6 |
| 第五圈 | 9 706.6 | 9 721.7 | 9 718.3 |
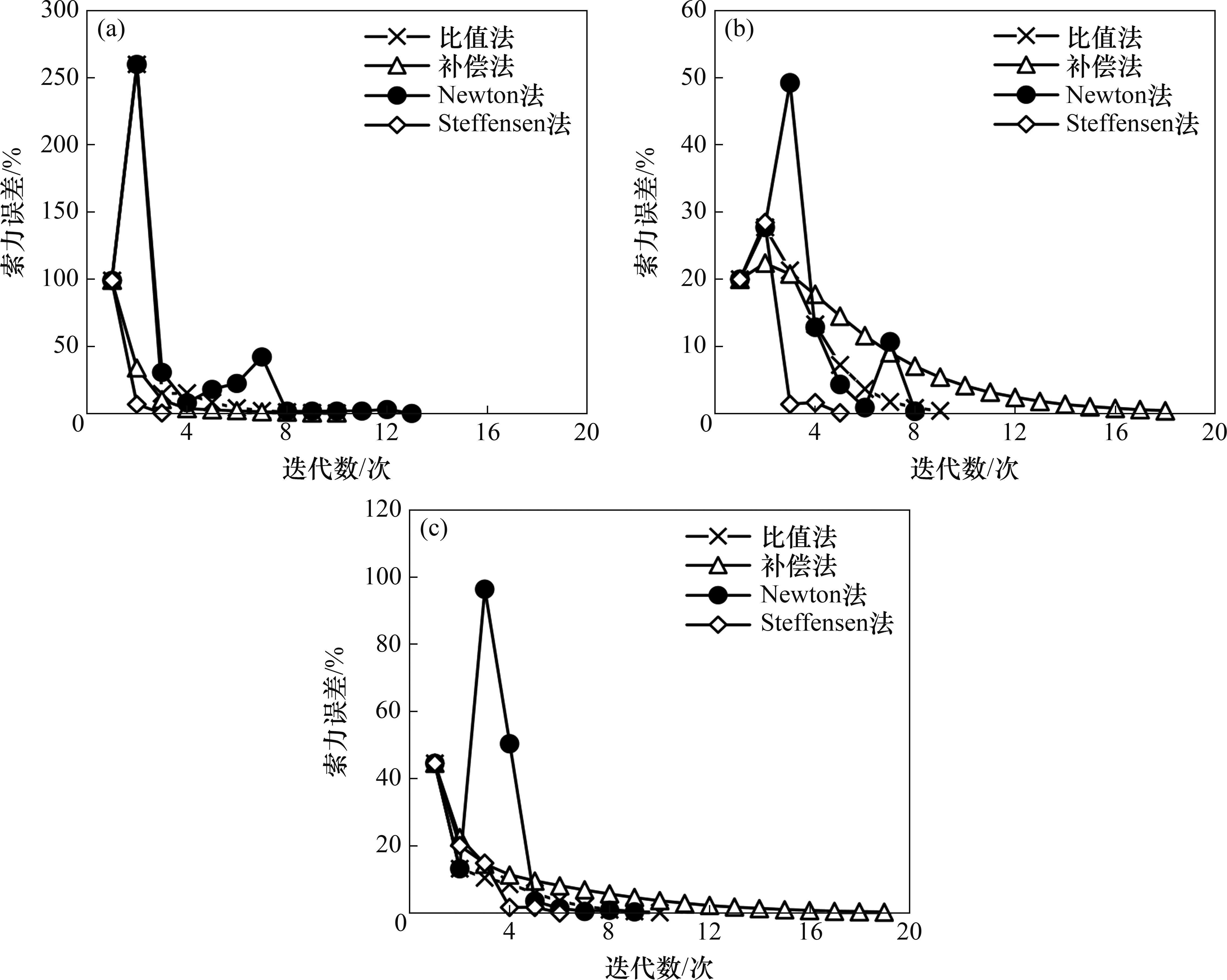
1) 对于各迭代初值,Steffensen法的计算效率均最高,迭代过程稳定,说明该方法对不同迭代初值的适应性较好。
2) 对于迭代初值为1的情况,比值法第二次迭代时误差高达260%,最终经过10次迭代,误差降低至0.3%,计算过程不稳定;此外,对于不同迭代初值,其迭代次数也相对较多。
3) 虽然补偿法的迭代过程较稳定,但其所需的迭代次数最多,且对于不同的迭代初值,迭代次数变化较大,计算效率不稳定。
4) 对于Newton法,不同迭代初值下均出现误差的较大浮动,计算过程不稳定,迭代次数也相对较多。
5) 在不同迭代初值下,Steffensen法求解得到的拉索等效预张力值基本保持一致,进一步说明了该方法具有较高的计算稳定性与可靠性。此外,当Steffensen法的迭代初值取为目标索力时,其计算效率较高。
3.3 在预应力张拉施工仿真分析中的应用效果分析
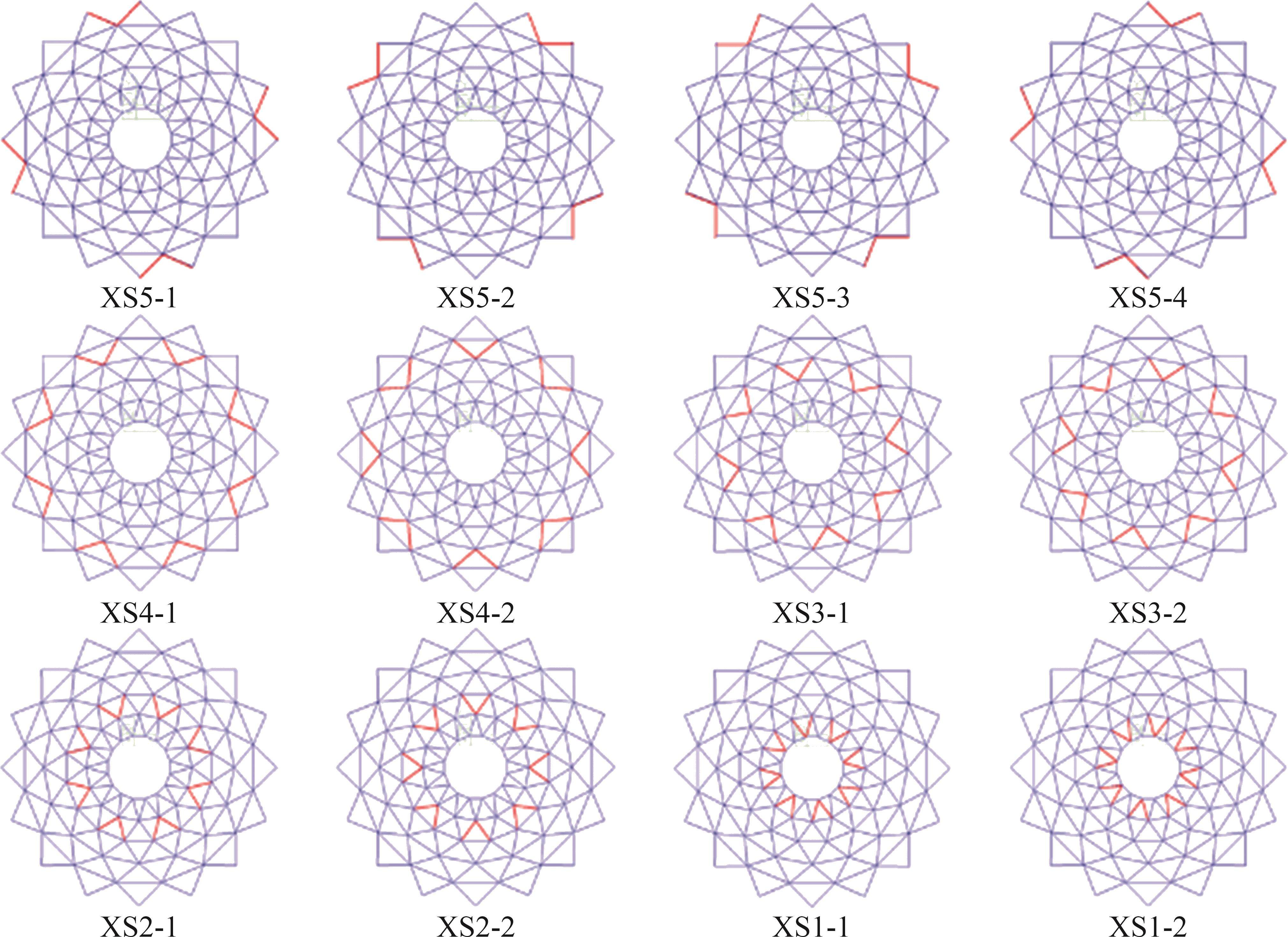
以3.1节中的贵阳奥林匹克体育中心(二期)主体育馆超大跨度肋环型弦支穹顶屋盖结构为例,采用径向钢拉杆张拉的方法,根据下部索杆体系的布置特点及张拉设备等因素,对其每圈32根钢拉杆进行分组,其中第五圈钢拉杆分成4组,其余圈每圈分成2组,如图7所示。预应力张拉采用分级分组张拉的方式进行,共分3级(40%→90%→105%超张拉)。拉索编号如图8所示。
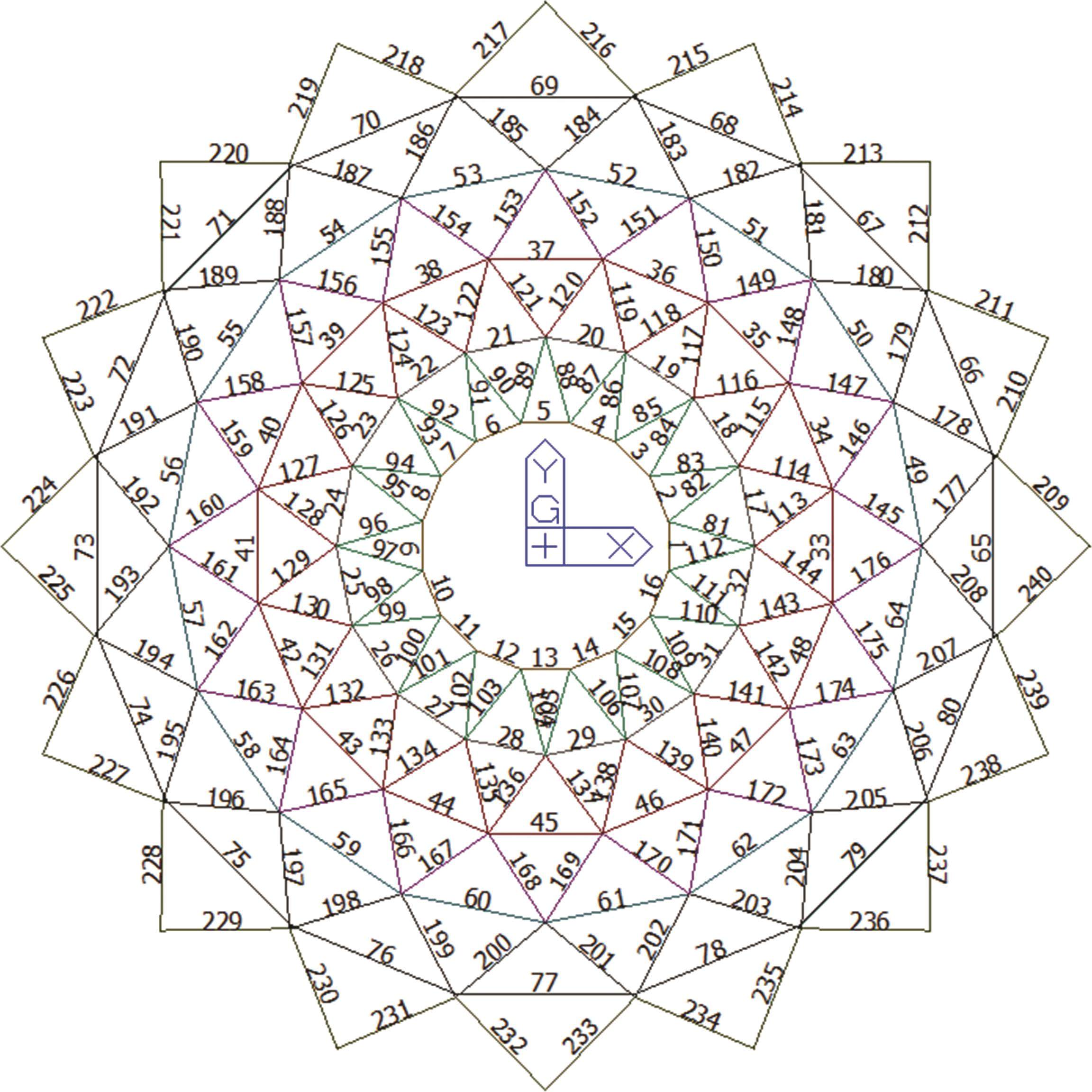
根据设计初始态的索力及张拉分级比例,计算每一级张拉完成状态各圈径向钢拉杆的索力,以此作为每一级张拉施工的索力目标值,在此基础上,采用上述Steffensen法分别求解每级每组钢拉杆的等效预张力。基于求解得到的等效预张力进行预应力张拉仿真分析,得到每级每组径向钢拉杆张拉后的结构状态及索力分布。
每级张拉完成状态的径向钢拉杆实际计算索力与目标索力的对比如表5和图9所示。
| 径向杆 | 张拉40% | 张拉90% | 超张拉105% | |||
|---|---|---|---|---|---|---|
| 索力实际值/kN | 索力目标值/kN | 索力实际值/kN | 索力目标值/kN | 索力实际值/kN | 索力目标值/kN | |
| XS1 | 52.7 | 51.8 | 114.8 | 116.6 | 140.7 | 136.0 |
| XS2 | 81.6 | 80.7 | 180.7 | 181.5 | 222.3 | 211.8 |
| XS3 | 182.4 | 182.0 | 408.5 | 409.5 | 485.9 | 477.8 |
| XS4 | 271.6 | 273.0 | 616.2 | 614.2 | 731.1 | 716.6 |
| XS5 | 664.8 | 665.5 | 1 496.0 | 1 497.3 | 1 744.6 | 1 746.9 |
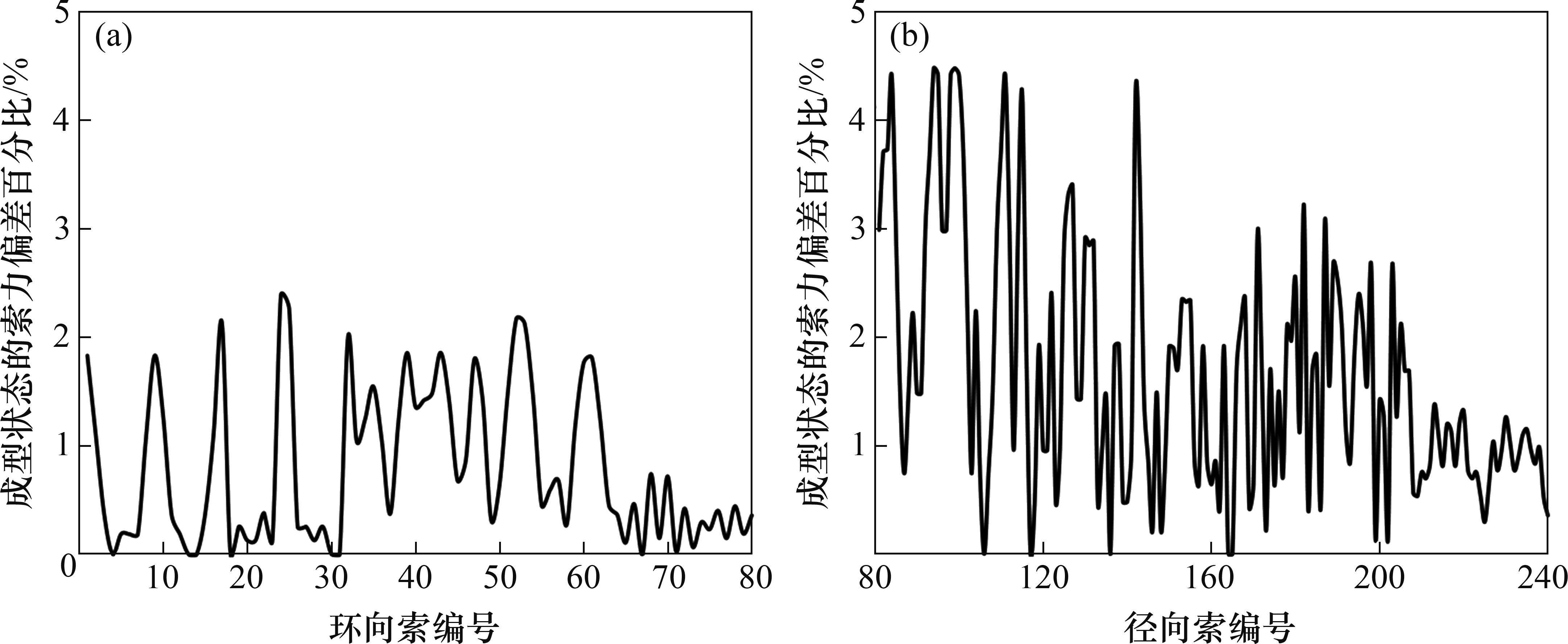
从表5可知,在载荷为1.0倍自重+1.0倍预应力的基本工况下,每级张拉完成状态的径向钢拉杆实际计算索力与目标索力基本一致。从图9可得:张拉完成状态实际计算索力与目标索力的偏差均在5%以内,满足预应力钢结构技术规程[22]的相关要求。
3.4 在多变量耦合的高精度问题下的计算效果分析
对于异形弦支穹顶结构,由于荷载、支承刚度、径向索角度、撑杆高度等不均匀分布,其同圈的拉索索力不尽相同,拉索的分组数量多,且拉索索力之间相互影响,因此,其拉索等效预张力确定问题是一个多变量耦合问题。
以大沙河文体中心项目异形弦支穹顶屋盖结构为例研究该方法在多变量耦合的高精度问题下的计算效果,其异形弦支穹顶结构组成如图10所示。该屋盖为异形曲面,其投影为类椭圆形,长轴跨度为50.4 m,短轴跨度为42 m,矢高为5.4 m,最高点标高为52 m,由悬挑桁架、环桁架、肋环型单层网壳及Giger型索杆体系组成,下部布置2圈索杆体系,每圈布置16根径向钢拉杆,荷载集中位置增加竖向稳定索以提高索杆体系的稳定性,环向拉索采用强度等级为1 670 MPa的密封索,径向钢拉杆采用强度等级为650级的等强钢拉杆,稳定索采用强度等级为1 670 MPa的钢丝束。
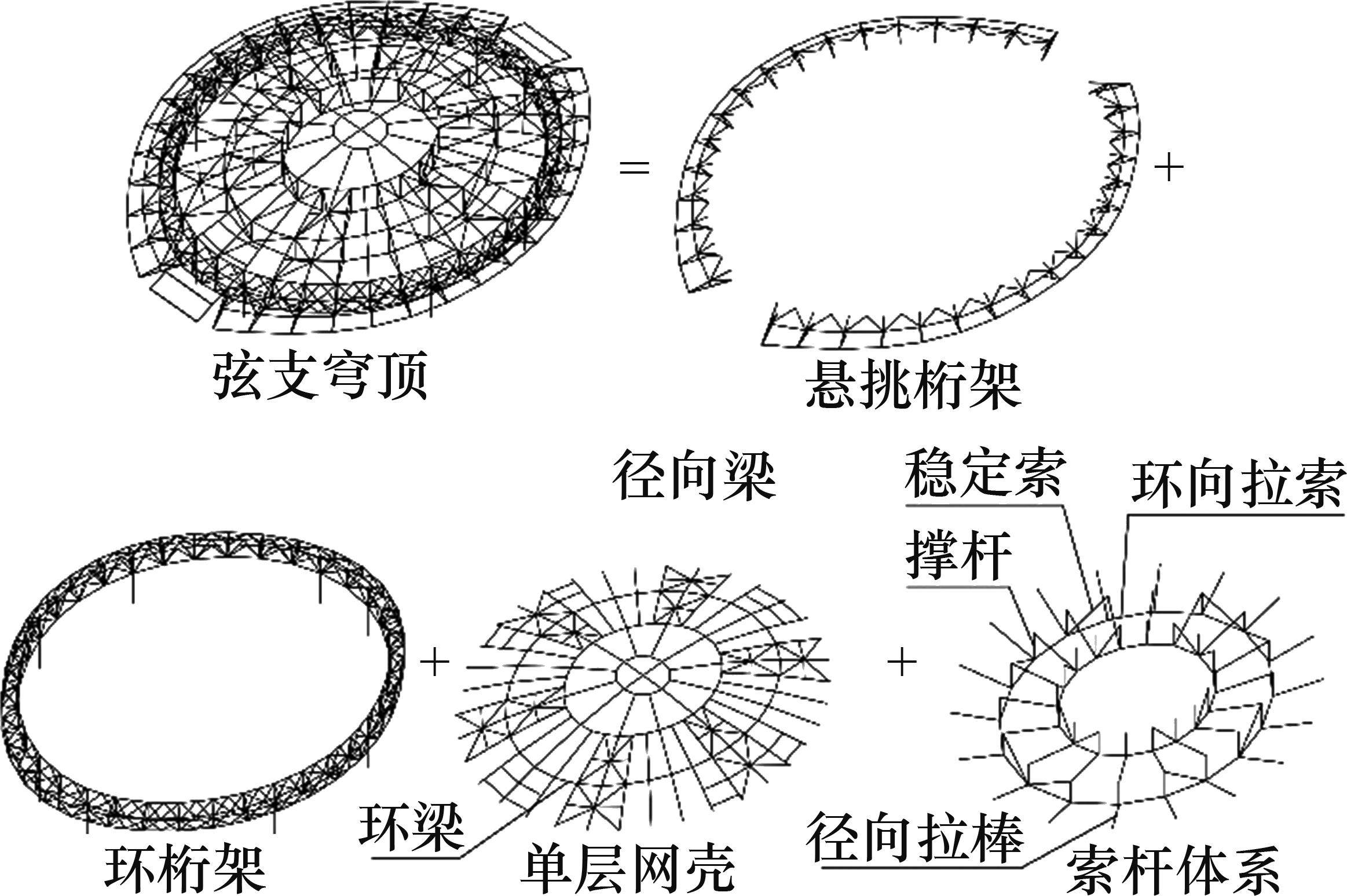
节点质量为预应力结构体系质量的15%,根据对称性及索力分布,将环向索和径向索分为20组,针对载荷为1.0倍自重+1.0倍预应力的基本工况,基于设计图纸得到各组拉索的已知索力(即目标索力)Fi如表6所示。
| 拉索 | 分组 | 目标索力/kN |
|---|---|---|
| 内圈环向索 | 1 | 181 |
| 2 | 196 | |
| 3 | 210 | |
| 4 | 218 | |
| 5 | 221 | |
| 外圈环向索 | 6 | 1 868 |
| 7 | 2 015 | |
| 8 | 2 159 | |
| 9 | 2 246 | |
| 10 | 2 279 | |
| 内圈径向索 | 11 | 96 |
| 12 | 90 | |
| 13 | 69 | |
| 14 | 61 | |
| 15 | 68 | |
| 外圈径向索 | 16 | 997 |
| 17 | 926 | |
| 18 | 706 | |
| 19 | 618 | |
| 20 | 685 |
以上述异形弦支穹顶结构为例,索力的容差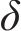
| 分组 | 比值法 | 补偿法 | Newton法 | Steffensen法 |
|---|---|---|---|---|
| 1 | 157.7 | 157.2 | 155.9 | 157.4 |
| 2 | 174.5 | 174.6 | 174.6 | 174.3 |
| 3 | 187.0 | 187.2 | 187.2 | 186.9 |
| 4 | 191.9 | 191.7 | 191.0 | 191.7 |
| 5 | 194.0 | 193.7 | 192.8 | 193.8 |
| 6 | 2 111.5 | 2 110.7 | 2 112.5 | 2 110.8 |
| 7 | 2 276.0 | 2 275.5 | 2 277.5 | 2 278.0 |
| 8 | 2 442.2 | 2 441.1 | 2 443.1 | 2 440.4 |
| 9 | 2 537.8 | 2 537.1 | 2 539.2 | 2 537.9 |
| 10 | 2 579.0 | 2 577.7 | 2 579.9 | 2 576.9 |
| 11 | 85.1 | 85.2 | 85.0 | 85.1 |
| 12 | 80.4 | 80.4 | 80.5 | 80.3 |
| 13 | 61.8 | 62.0 | 62.0 | 61.8 |
| 14 | 54.6 | 54.7 | 54.8 | 54.5 |
| 15 | 60.4 | 60.4 | 60.4 | 60.4 |
| 16 | 1 124.1 | 1 124.1 | 1 125.5 | 1 124.4 |
| 17 | 1 039.4 | 1 040.0 | 1 043.2 | 1 041.0 |
| 18 | 811.7 | 809.4 | 821.0 | 819.0 |
| 19 | 696.5 | 696.6 | 697.5 | 696.9 |
| 20 | 777.2 | 776.5 | 777.5 | 776.6 |
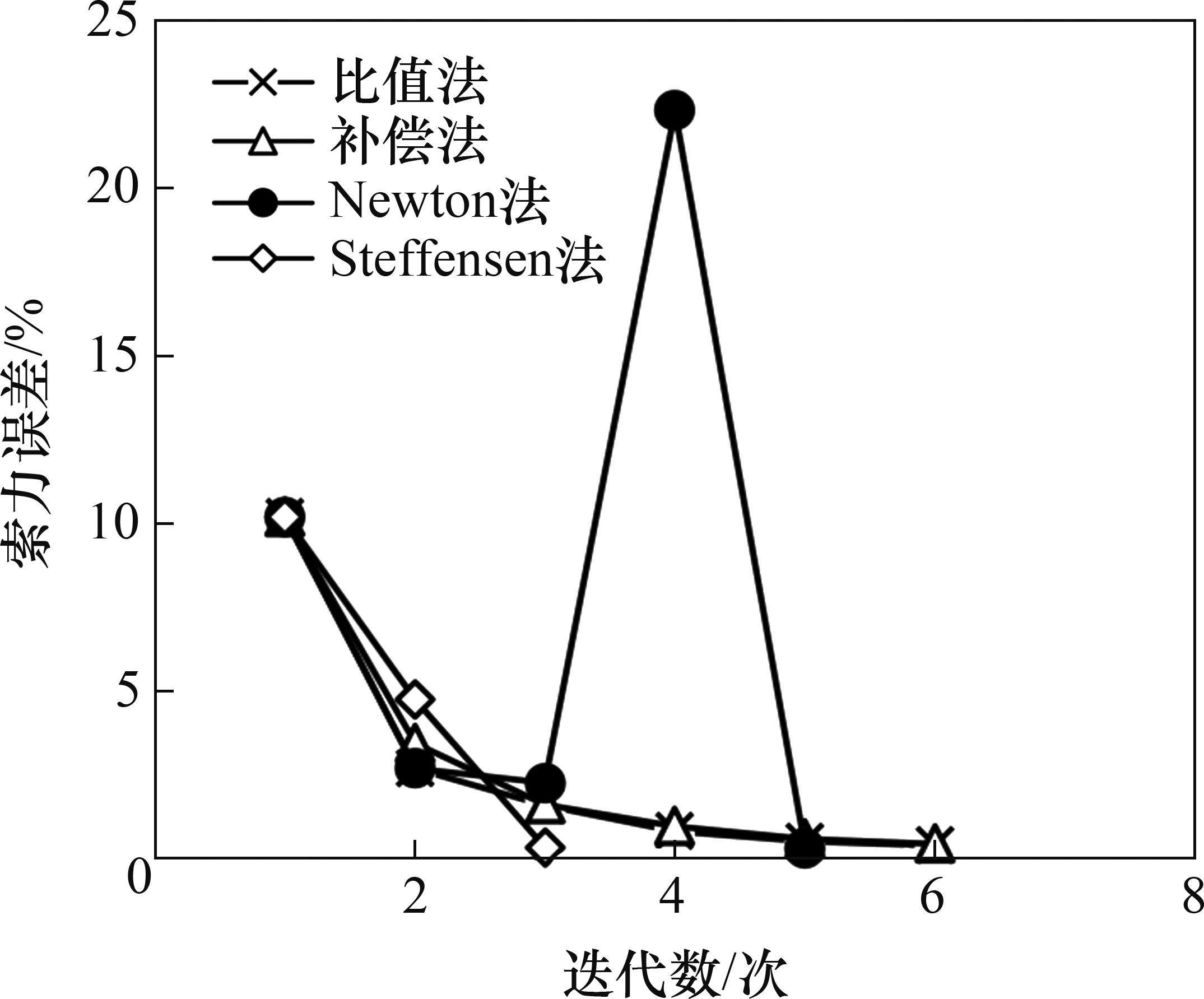
从图11可知:Steffensen法对多变量耦合的高精度问题依然具有较高的计算效率,仅需3次迭代即将误差降低到0.3%;而比值法、补偿法的迭代次数相对较多,且Newton法在迭代过程中出现较大的误差浮动,迭代过程稳定性较差。
从表7可见:不同方法求解得到的等效预张力基本一致,说明本文提出的Steffensen法在求解多变量耦合的高精度问题时的有效性。
4 结论
1) 基于对拉索等效预张力确定问题的数学推导及表达,将复杂拉索等效预张力确定问题转化为多个相对独立的非线性隐式方程求解问题,为拉索等效预张力确定问题的求解提供了理论支撑,大大降低了求解的难度。
2) 所提出的基于Steffensen迭代法的拉索等效预张力确定方法将数值分析理论与实际工程问题相结合,具有较高的计算稳定性及二阶以上的收敛效率,为拉索等效预张力确定问题提供了一种高效可靠的方法。
3) 相比于比值法、补偿法、Newton法等,Steffensen法在相同求解精度下具有更高的计算效率,对不同迭代初值均具有较好的适应性,迭代稳定性较强,且对多变量耦合的高精度问题依然具有较高的计算效率。
4) 以Steffensen法的迭代初值为目标索力时,其计算效率相对较高;对于一般项目,容差1%即可满足工程实际及研究需求。
5) 所提出的Steffensen法可适用于各类复杂预应力空间结构,可用于确定预应力张拉施工仿真中分级分组张拉等效预张力。
赵文雁, 潘文智, 查晓雄. 基于Steffensen迭代法的拉索等效预张力确定方法研究[J]. 中南大学学报(自然科学版), 2024, 55(12): 4570-4582.
ZHAO Wenyan, PAN Wenzhi, ZHA Xiaoxiong. Study on determination method of cable equivalent pre-tension based on Steffensen iteration method[J]. Journal of Central South University(Science and Technology), 2024, 55(12): 4570-4582.

