预应力锚杆作为隧道支护的一种手段,因其具有主动性强、施工快速、支护效果好等优点,在开挖建设过程中已被广泛使用[1],如木寨岭隧道[2]、青岛地铁[3]、岷县隧道[4]等成功应用预应力锚杆较好控制了围岩变形。预应力树脂锚杆作为一种永久支护形式,在隧道服役期间必然会产生预应力损失,如在张拉初期锚杆的应力松弛、岩体和树脂锚固剂的蠕变等均会引起预应力损失,其中锚杆应力松弛所占损失比重较小,损失量约为5%~10%[5],岩体的蠕变与岩性好坏有关[6],而树脂锚固剂的蠕变效应则会引起大量预应力损失。诸多学者对锚固体蠕变行为进行了大量试验研究。付文光等[7]针对蠕变曲线以及注浆黏结锚杆荷载试验进行了判稳机理的探讨。渠红霞[8]通过试验分析了第二锚固界面蠕变特性以及锚固体位移,同时对应力分布进行了研究。陈昌富等[9]针对锚-土界面蠕变特性,提出了一种试验方法与蠕变模型。伍国军等[10]开展锚固界面力学特性流变试验,提出一种非线性剪切流变模型,并通过数值仿真进行了验证。袁超等[11]开展室内试验针对第一锚固界面与第二锚固界面进行了剪切蠕变特性的研究。锚固段蠕变特性下将导致预应力的松弛,使整体支护结构存在潜在破坏的风险。王建松等[12]针对岩土锚索结构预应力损失问题,通过现场张拉试验发现采用多循环张拉可减少预应力损失,获得更好的长期锚固效果。覃荷瑛等[13]提出将多点准分布FGB耦合于混凝土梁预应力钢绞线中心丝技术,对不同线形的孔道进行预应力损失监测。由于预应力锚索在张拉锁定以及开挖过程中会产生较大损失,影响开挖过程中的稳定性和支护效果,刘明华[14]对边坡锚索预应力损失影响因素进行研究,提出了相关控制损失的施工建议。李英勇等[15]对边坡加固工况进行分析,研究了预应力锚索短期和长期预应力变化规律。针对预应力损失问题,边坡、大坝等岩土工程中采取的主要措施为补张拉和超张拉[16]。然而,在隧道工程中,补张拉因锚固系统端头被喷砼封闭难以进行,而超张拉则可能导致锚固系统在张拉过程中发生破坏。因此,上述方案并不能很好地解决隧道工程锚固系统预应力损失问题,亟待开展相关研究以保障预应力锚固系统下支护结构长期安全性。预应力树脂锚杆通过树脂锚固剂与深部围岩进行黏结,而作为端锚结构,因其材料性质在长期受力情况下不可避免地会产生蠕变,进一步发生锚固失效现象,引起预应力损失。为此,在普通预应力树脂锚杆基础上,后注浆+树脂锚固形式预应力锚杆[17]的提出可以有效地解决该问题,采用后注浆的形式避免了当出现锚固力失效而引起的支护系统整体破坏的问题。而当该形式锚杆锚固段产生损失后,注浆段承载特性以及力学行为还有待研究。本文对于后注浆+树脂锚固的新型锚固形式,提出一种力学模型,用以验证后注浆预应力树脂锚固系统在产生预应力损失后的力学行为,同时进行室内试验对模型准确性进行验证,并与普通预应力树脂锚杆对比,研究后注浆+树脂锚固形式的预应力锚杆在锚固段产生预应力损失后的支护效果,进一步地对该模型进行参数化分析,寻找敏感性参数,为隧道建设中后注浆式预应力树脂锚杆在预应力损失后注浆段力学行为提供相关理论依据。
1 理论解析
1.1 力学模型
后注浆预应力树脂锚杆由树脂锚固段(速凝段)和后注浆段(缓凝段)组成(图1(a)),其中,树脂锚固段的快速固化能力可保障预应力的快速施加,而后注浆段则可保障预应力的长期有效。从受力上而言,后注浆预应力树脂锚杆在前期预应力张拉时(浆液未凝结),预应力荷载由树脂锚固段承载,即锚杆支护力仍然由深部完整围岩所提供。而当树脂锚固段在长期作用下蠕变/松弛,注浆段与锚杆的黏结将阻碍锚杆向垫板方向的回缩,从而降低表层围岩处锚杆支护力损失。
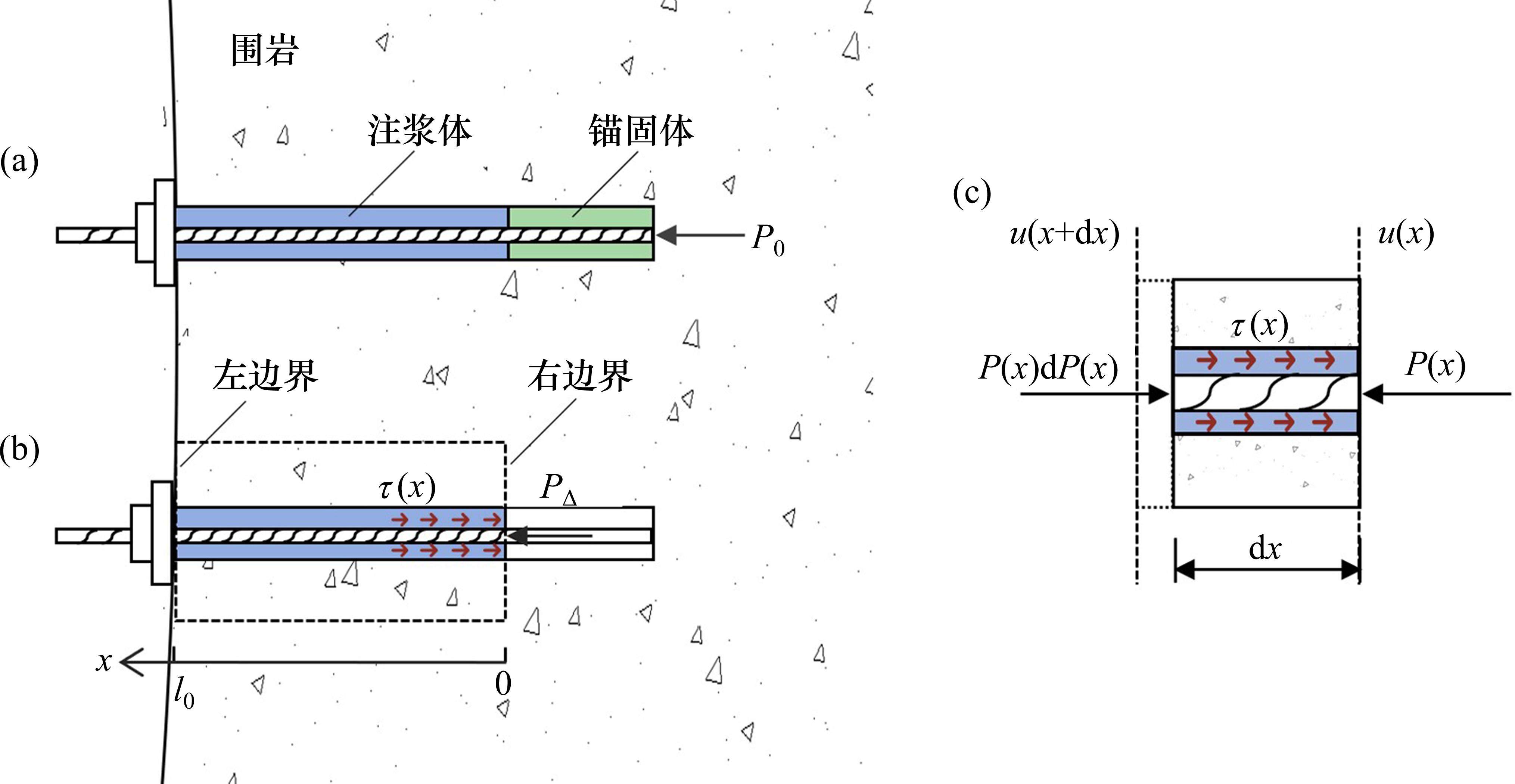
为研究锚固段长期蠕变/松弛下注浆段的力学响应,文中忽略锚固段与注浆段之间的相互作用,并忽略岩体在剪切荷载下的位移[18],建立如图1(b)所示的注浆段力学模型。
模型中锚杆直径为D,其初始受力如图1(a)所示,锚杆在张拉后初始预应力为P0,反力由锚固段上剪应力承担,在锚固体产生蠕变后,锚固段预应力会产生损失,锚杆回缩,对应的松弛荷载PΔ作用在注浆段右边界锚杆上,如图1(b)所示,取注浆段长度l0进行分析,坐标系以注浆段与锚固段分界面为起始点,向垫板端为x轴正方向。现对模型作出以下假设:1) 锚杆、注浆体均为弹性体,注浆-岩体边界处为刚性边界。2) 考虑垫板约束作用,模型左侧边界处注浆体与锚杆无相对位移。3) 模型右边界锚杆承受松弛荷载PΔ。4) 注浆-岩体界面上无滑移,注浆-锚杆界面上存在滑移,滑移量与界面剪应力τ(x)的关系满足式(1)[19]。
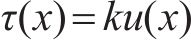
式中:k为注浆体与锚杆界面的剪切刚度系数。在图1(b)中取长度dx的锚杆微段进行分析,如图1(c)所示,根据平衡方程,以及锚杆应力应变关系,可以得到:
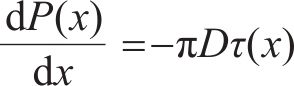
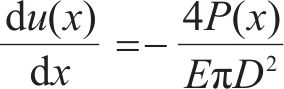
式中:P(x)为锚固段松弛荷载PΔ引起的锚杆x处的轴力;u(x)为锚杆在x处产生的位移;
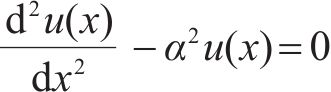
式(4)中: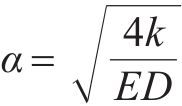
边界条件满足下式:
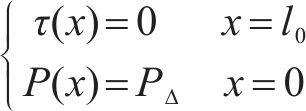
代入式(4)中,解得:
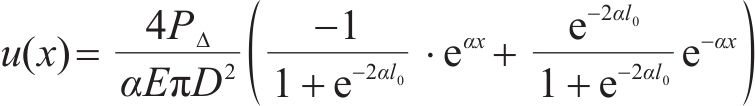
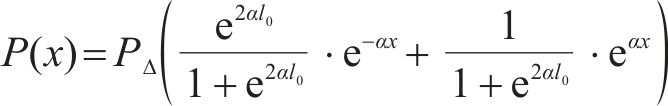
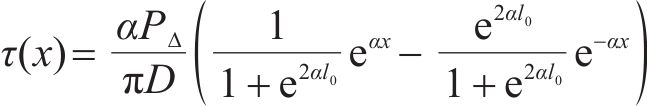
将式(7)得到的锚杆轴力与初始预应力进行叠加,可以得到后注浆段锚杆在产生预应力损失后的锚杆轴力分布:
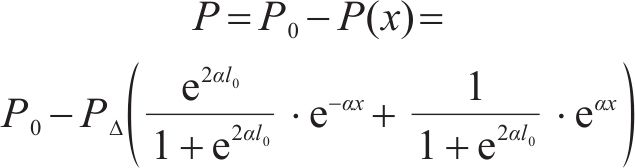
1.2 模型参数获取
根据力学模型,揭示后注浆预应力树脂锚杆力学行为需要确定的物理量包括:锚杆弹模E、锚杆直径D以及锚杆-注浆体界面剪切刚度系数k。根据式(6),在锚杆直径D、弹模E确定后,锚杆-注浆体界面剪切刚度系数k与模型右边界处锚杆位移u(0)满足式(10)。因此,通过室内测量u(0),可以计算得到锚杆界面剪切刚度k值,如式(11)。
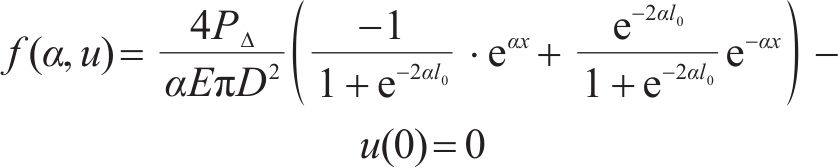
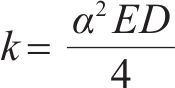
2 锚固段预应力损失力学试验方法
根据理论公式可以看出,注浆体的力学行为与本身材料参数、预应力量值等密切相关。为研究后注浆预应力树脂锚杆在锚固段预应力损失下,荷载从锚固段向注浆段的转移规律,现对理论模型进行试验验证,试验设置3种预应力水平(40,60和80 kN)。按照设定损失率进行损失,同时与纯树脂锚固不注浆情况下预应力损失情况引起的锚杆轴力作为对照分析,具体工况如表1所示。
试件 编号 | 注浆长 度/cm | 初始预应力量值/kN | 预应力损 失率/% |
|---|---|---|---|
| S1 | 60 | 40 | 20,40,60,80,100 |
| 不注浆 | 40 | ||
| S2 | 60 | 60 | |
| 不注浆 | 60 | ||
| S3 | 60 | 80 | |
| 不注浆 | 80 |
2.1 试验材料
试验以混凝土模拟围岩对注浆体的约束,混凝土配合比为水泥∶砂∶骨料∶水=1∶1.5∶3∶0.5,强度等级为C35,横截面尺寸30 cm×30 cm,长度60 cm,浇筑3块。为确保注浆层具有一定的厚度,截面中心预埋外径为40 mm的PVC管,以形成相同孔径的钻孔,同时在试件上表面中心预埋外径为20 mm的PVC管,形成注浆孔。待混凝土浇筑完成后,在标准环境(25 ℃,湿度≥90%)下养护28 d后用于试验。试件如图2所示。

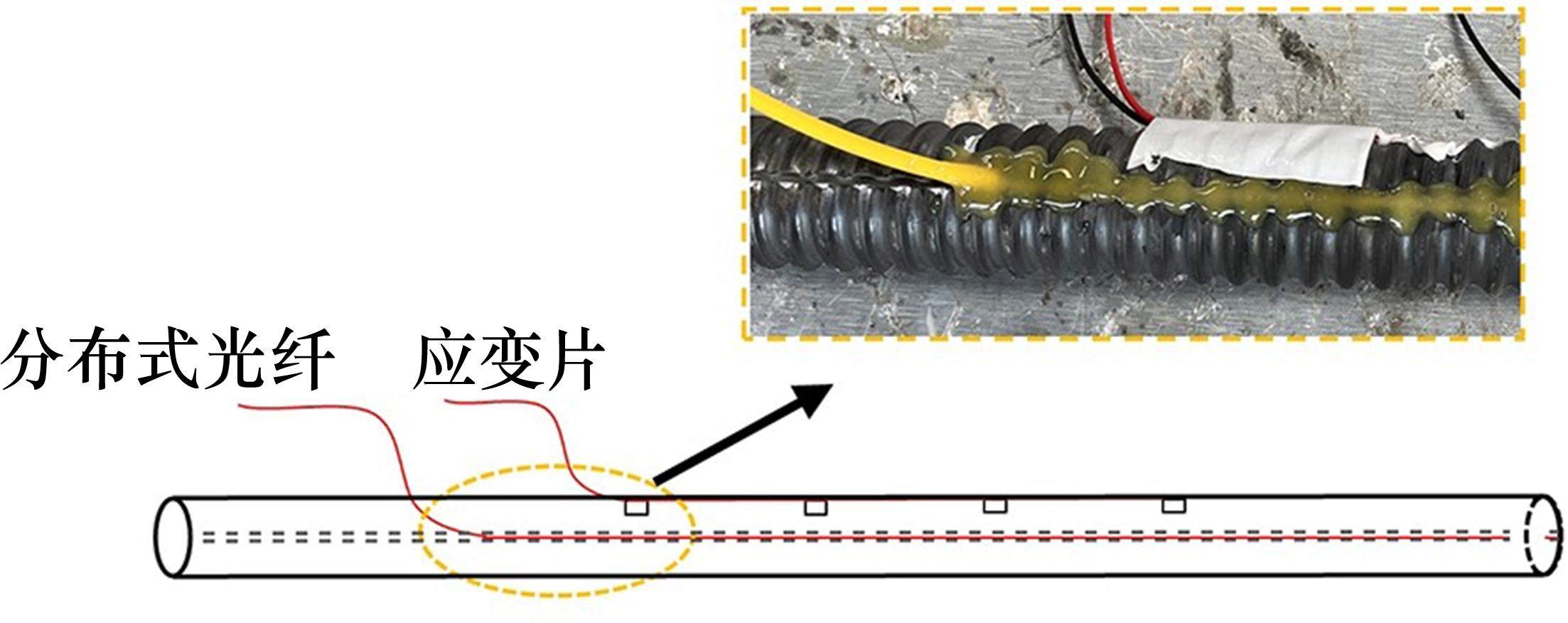
试验采用直径为25 mm的中空注浆锚杆,锚杆表面沿轴线方向对称刻有宽2 mm,深2 mm的槽口,利用502胶水以及环氧树脂AB胶,将分布式光纤紧贴槽内粘贴,同时粘贴应变片以验证分布式光纤的准确性(图3)。垫板为15 cm×15 cm的平板垫板,螺母与之配套,均由Q335钢材制作而成。注浆材料采用R∙SAC42.5硫铝酸盐快硬水泥,水灰比为0.35,减水剂掺量2.00%,缓凝剂掺量0.20%,混凝土、钢材及试验获得的注浆体力学性能均由表2给出。
| 规格 | 弹性模量/GPa | 泊松 比 | 屈服强度/MPa | 极限强度/MPa | |
|---|---|---|---|---|---|
| 混凝土 | C35 | 31.5 | 0.2 | — | 35 |
| 锚杆 | Q335 | 210.0 | 0.3 | 335 | 455 |
| 注浆体 | R∙SAC42.5 | 24.9 | 0.3 |
2.2 试验装置
试验装置及测量设备如图4所示,试块左侧为垫板端,2块垫板之间安装测力计进行锚杆预应力测量。试块右侧采用垫板-螺母-反力架-千斤顶代替锚固段,通过控制千斤顶的荷载以模拟锚固段蠕变引起的预应力损失,光纤与应变线从试块右侧表面的预留槽口引出,如图4虚线所示。

现对试验所用装置设备进行简单介绍。
1) 锚索测力计:试验采用振弦式锚索测力计进行垫板端轴力测量。
2) 扭矩扳手:通过扭矩扳手上的扭力调节器来控制扭矩大小,达到所要施加的预紧力。
3) 位移计:精度为0.01 mm,位移采集设备连接千斤顶油泵进行位移-力关系的实时读取,通过标定系数换算即可得到不同加载阶段对应的锚杆变形量。
4) 光纤解调仪:以普通光纤作为传感器,中心波长设置为1 cm、传感间距设置为0.5 cm后通过光纤解调仪(LUNA)设备进行光信号的采集、处理,利用OFDR技术对光纤中各个位置处的瑞利散射频移进行解调,即可获得锚杆沿长应变分布特征。
5) 应变箱:利用动静态应变测试分析系统进行应变采集,与同位置处光纤应变进行对比。
6) 油压千斤顶:控制预应力损失量值大小,利用千斤顶示数标定值与实际压力进行换算。
2.3 加载方案
待混凝土养护完成,先对试块进行不注浆预应力损失试验,以千斤顶模拟锚固段蠕变引起的预应力损失方法如下。
1) 为了防止锚杆安装时出现偏心问题,设置了锚杆居中装置,通过居中装置将锚杆放置在预留钻孔中,按照图4方式安装垫板、螺母、千斤顶等,通过扭矩扳手施加5 N∙M预紧扭矩,待安装完成后进行锚杆光纤、应变片初始值记录。
2) 通过千斤顶向锚杆施加张拉力,期间记录锚杆张拉过程中的荷载与位移值,张拉至设计荷载后,记录光纤、应变片、锚杆测力计等数据。向反力架内螺母施加(110 N∙M)的扭矩(由预实验确定该扭矩值下锚杆轴力会大于设计损失率下轴力),然后卸载千斤顶。
3) 将千斤顶加压至损失后的设计荷载,松掉反力架内螺母,锚杆轴力基本与千斤顶加载值相同,使锚固端轴力达到设计损失荷载并记录各数据。如此往复至预应力完全损失。
注浆试验过程同不注浆过程一样,安装试验装置,增添止浆材料,随后利用千斤顶张拉至设计荷载的120%,向反力架内螺母施加110 N∙M的扭矩锁紧锚杆,卸载千斤顶,待放置一天锚杆进行应力松弛后[20]记录测力计、光纤、应变计读数,之后利用注浆孔向钻孔进行注浆,注浆完成48 h后,再次记录各数据,随后同不注浆试验步骤进行注浆预应力损失试验。
3 试验研究与结果对比
3.1 后注浆式预应力锚杆支护效果分析
现对S1这2种工况,即在初始预应力为40 kN,树脂锚固端产生不同预应力损失后,纯预应力树脂锚杆与后注浆式预应力树脂锚杆垫板端支护力情况进行比对,从而得到如图5所示的注浆与不注浆支护力对比图。
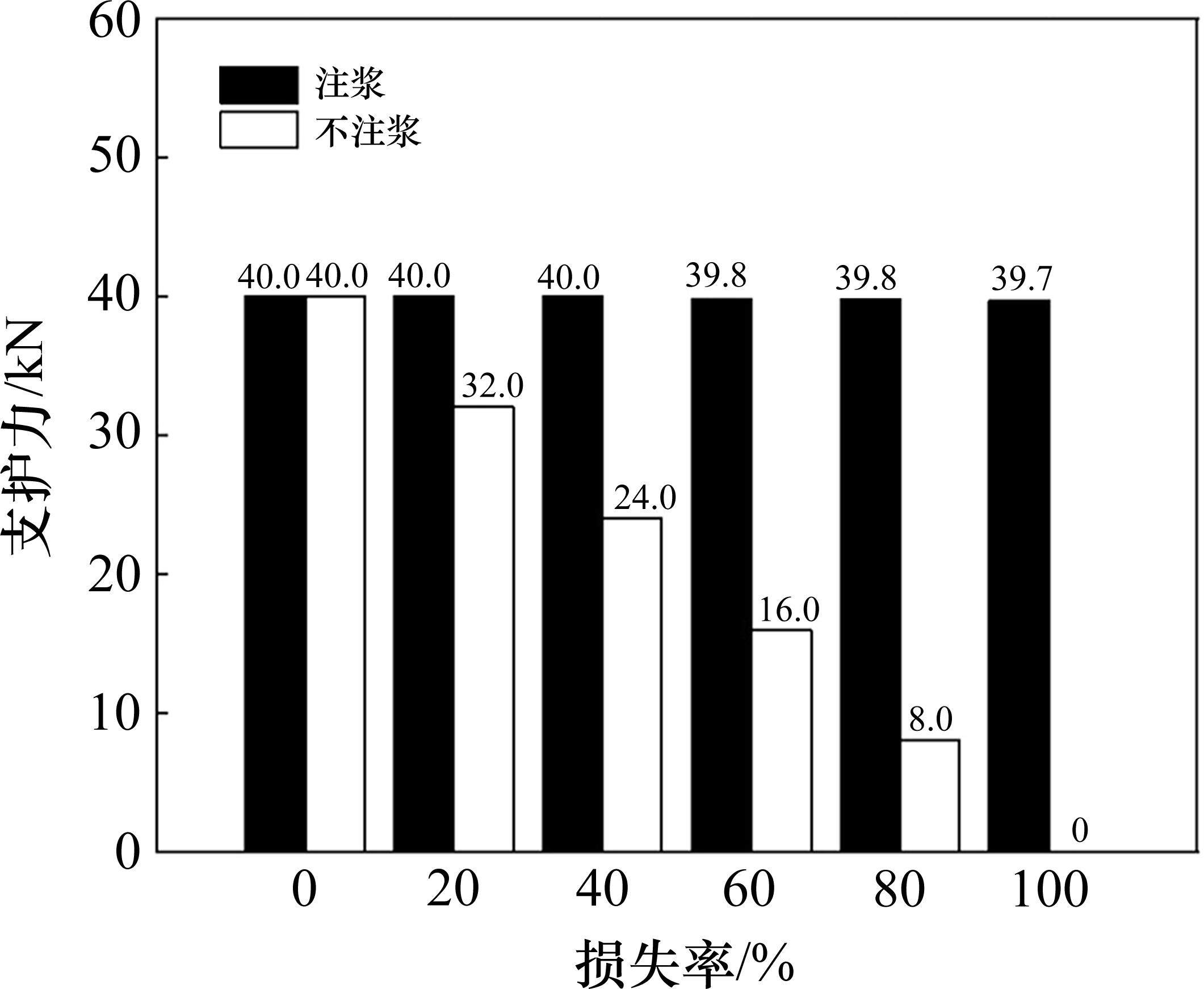
通过图5注浆与不注浆效果对比,发现后注浆+树脂锚固形式在不同损失率下注浆段均可以起到很好的效果,当锚固段产生预应力损失时,注浆段可以通过浆液很好地“锁住”预应力,保持垫板端对围岩的支护力,各损失阶段预应力上升效果显著,而不注浆情况下支护力则随着预应力损失的增大而增大。
3.2 后注浆式预应力锚杆轴力分布特征分析
通过分布式光纤传感器可以监测锚杆在注浆段轴力分布特征[21-23]。图6给出了松弛荷载下锚杆注浆段轴力分布特征。为消除光纤与锚杆黏结端部对测试结果的影响,去除了光纤0~0.05 m范围内数据,并将千斤顶实际加载荷载作为0 m处轴力,以虚线连接0 m和0.05 m处数据。此外,图中还给出了应变片的测试结果,以验证分布式光纤测试结果的准确性。
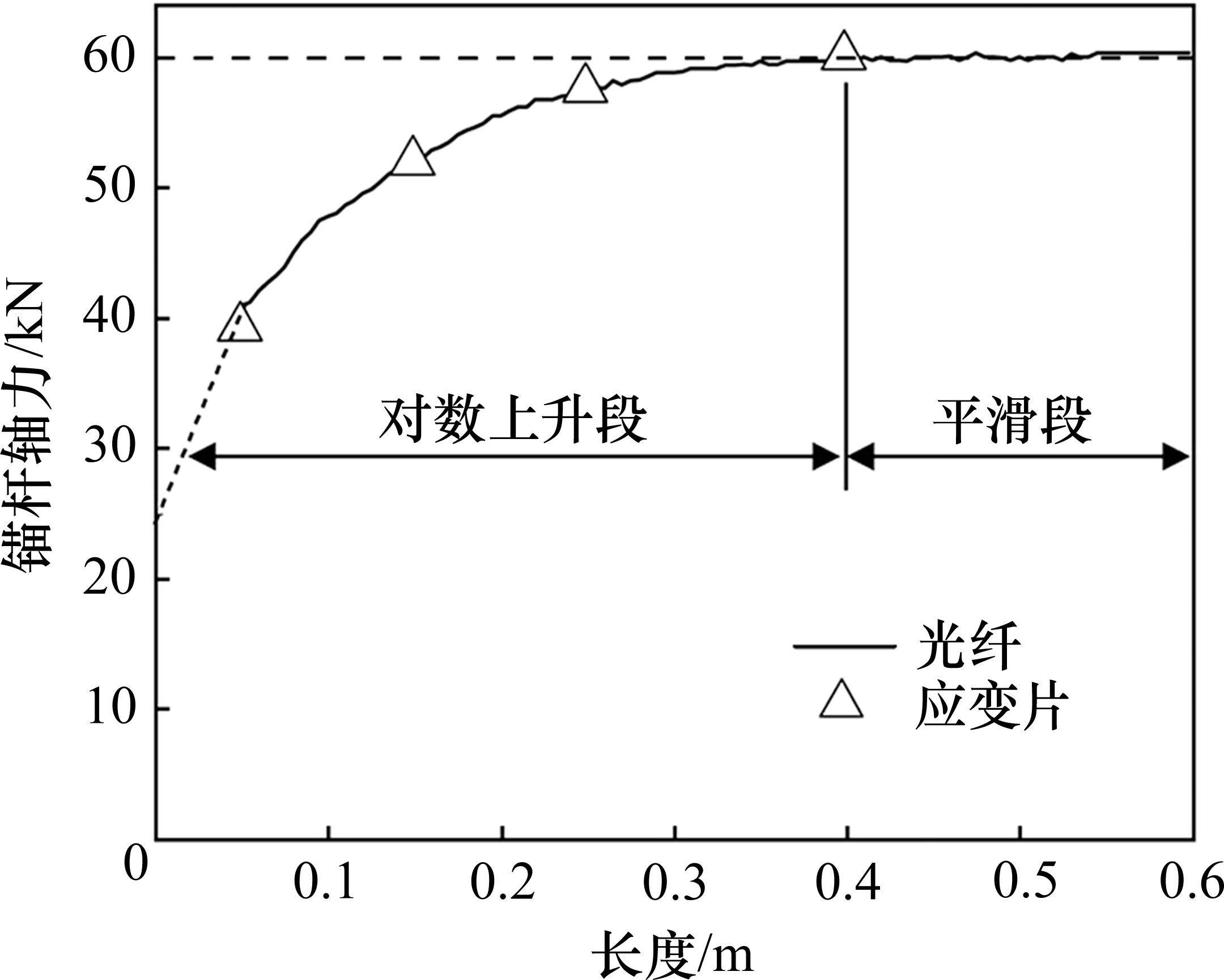
从图6可知,在锚固段松弛荷载下,注浆段锚杆轴力分布曲线为对数上升段和平滑段。具体地,锚固-注浆分界面(x=0)在预应力损失60%时锚杆轴力下降至24 kN,随着测点与锚固段的距离x逐渐增加,轴力呈现对数上升,当x增加至一定长度后,锚杆轴力基本保持原预应力量值(60 kN)。对比锚杆轴力分布可知,0.4~0.6 m内锚杆轴力几乎不受锚固段松弛荷载影响。上述现象表明注浆体与锚杆之间的黏结作用可以有效抑制锚杆在松弛荷载下的回缩,从而减小锚固段蠕变/松弛带来的预应力损失,使锚杆对围岩表层支护力维持在设计荷载值。
为对比不同损失率下注浆段支护力变化特征,现绘制损失20%、60%、100%工况下的锚杆轴力分布曲线,如图7所示。
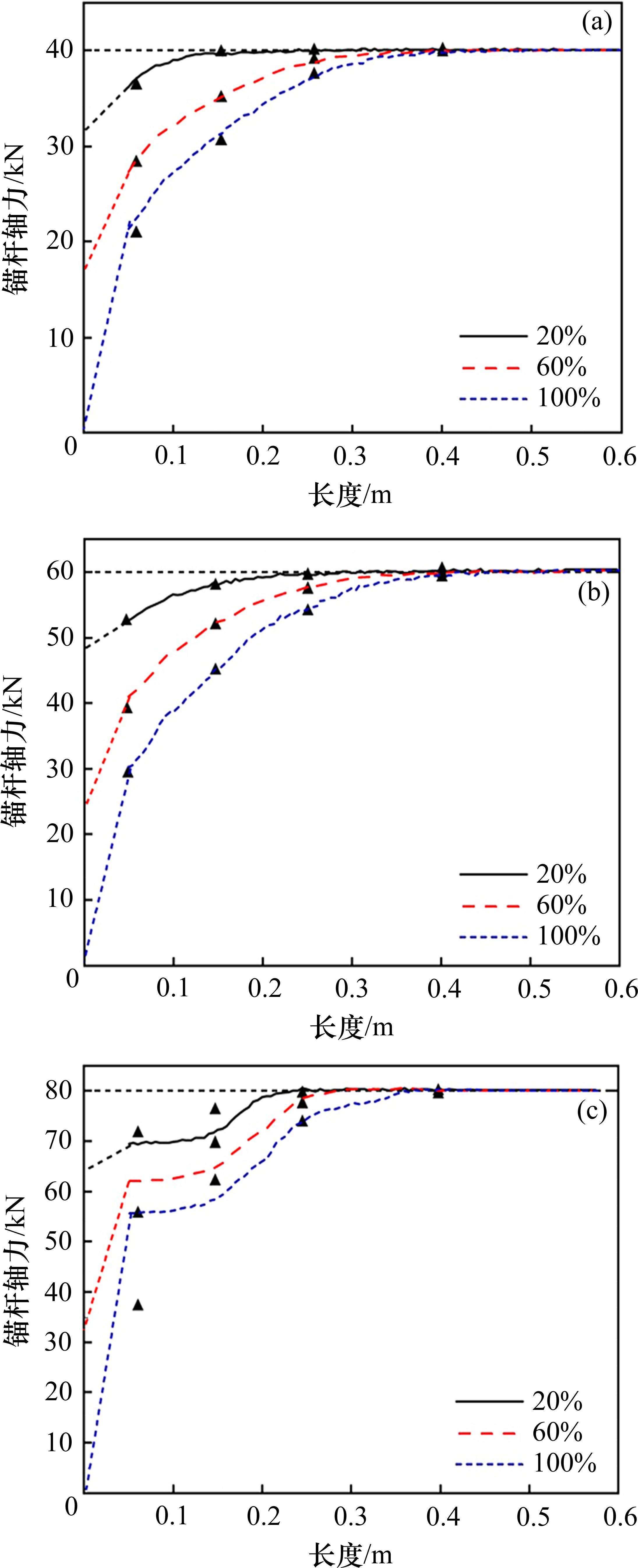
由图7可知,对比不同损失率下轴力沿长分布特征,各个曲线均呈抛物线趋势,且随着损失率增大,对数上升段长度增加,平滑段长度减小,支护力损失范围越大,且随着初始预应力量值的增大,损失量值相同,但对数上升段长度随之增大。图7(c)由于光纤粘贴以及锚杆预应力较高等问题产生部分脱黏,导致前端轴力分布与实际情况差异较大。
3.3 后注浆式预应力锚杆压缩区变化规律分析
当沿隧道周边以足够小的间距布置锚杆群时,各个锚杆产生的压应力圆锥体会相互重叠,从而在围岩中形成一个均匀的压缩带,这个压缩带即为承压拱,能够承担来自上方破碎岩石的径向荷载[24]。而锚杆施加预应力的范围即压缩区,压缩区可以表征岩体承载效应,随着锚固段预应力损失,锚杆预应力由锚固段逐渐转移到注浆段,压缩区范围随之发生改变,当损失率不同时,压缩区范围也不同,不同损失程度下压缩区示意图如图8所示。

现对3种工况下压缩区范围进行分析,以预应力初始量值95%作为压缩区基准,选取各工况不同损失率下轴力量值达到95%的点与垫板端的距离作为压缩区长度,作出不同损失率下压缩区范围图,如图9所示。随着损失率增加,注浆段压缩区长度会进一步减小,从初始0.6 m逐渐减小到0.3 m左右,减小趋势逐渐变缓,说明随着锚固段逐渐失效,压缩区由原来垫板-锚固段开始向注浆段转移,锚固段“前移”,压缩区虽然减小,但仍能维持支护作用。
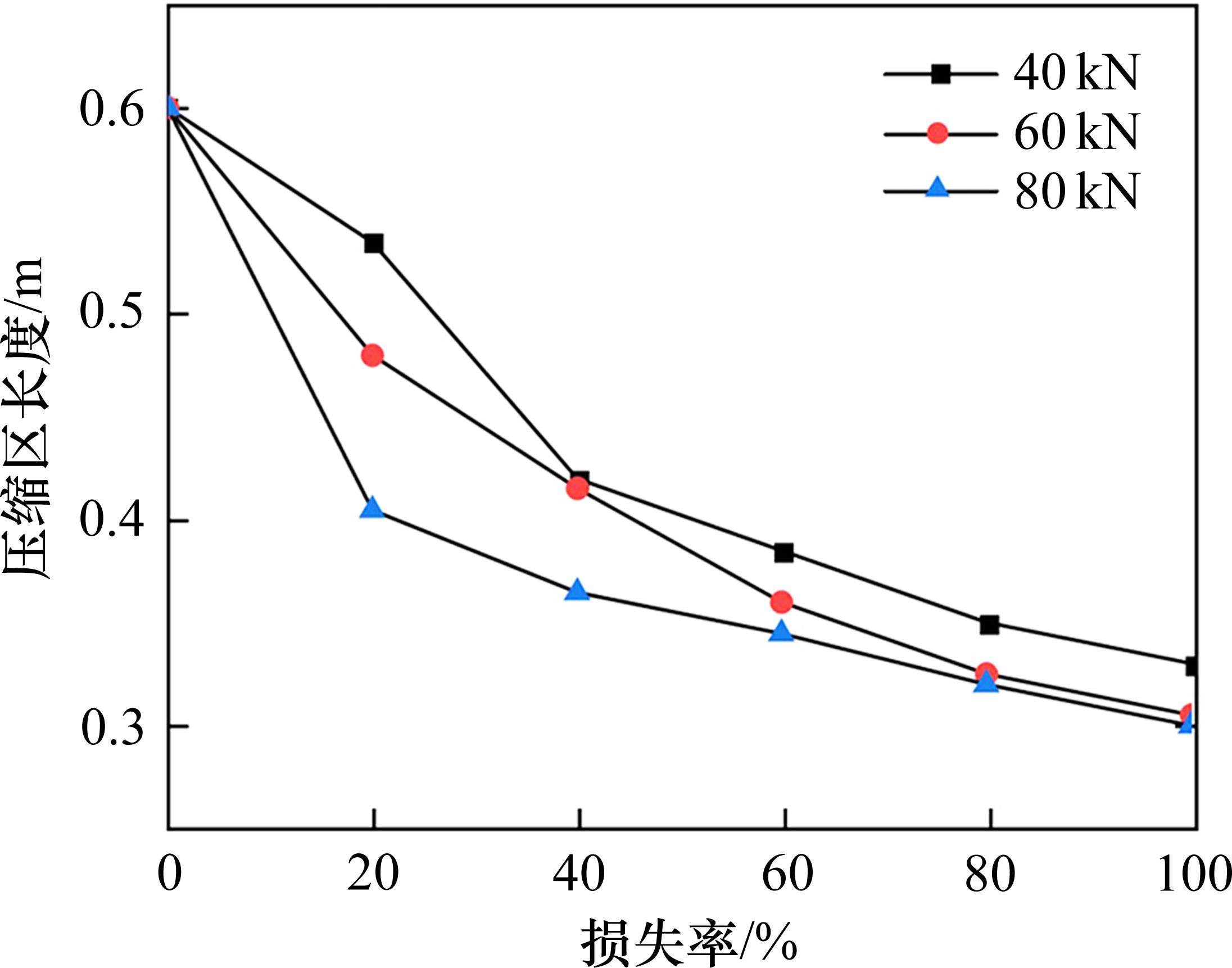
对比不同初始预应力工况,在同一损失率下,初始预应力大的压缩区长度降低显著,在损失率增加情况下,初始预应力大的压缩区长度降低缓慢,在损失初期压缩区便降低大部分。根据锚固段损失后注浆段压缩区范围,发现当锚固段100%损失后,预应力量值大小对最终压缩区范围影响不大,均在0.3 m左右,可见后注浆式预应力树脂锚固形式在锚固段预应力损失后对支护效果具有较大贡献。
4 模型验证及参数分析
4.1 理论模型验证
为验证所提注浆段力学模型的准确性,将S2工况下模型试验力学参数代入解析解,并根据所测锚杆轴力分布对其进行验证。取注浆段长度l0=0.6 m,锚杆弹模E=210 GPa,锚杆直径D=0.025 m,松弛荷载PΔ=60 kN。为计算力学模型中参数k的取值,首先根据试验中位移计测得变形,按式(12)计算端头处位移u(0)。
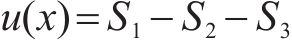
其中,S1为千斤顶端锚杆位移;S2为垫板端锚杆位移;S3为千斤顶端锚杆弹性变形。在损失20%时,对应的S1=0.451 mm,S2=0.190 mm,S3=0.250 mm。结合测得的位移以及式(10)和式(11),可解出注浆段界面滑移刚度k≈130 GPa。
根据上述物理量并结合式(9),可以绘制S2工况下损失分别为20%、60%、100%的理论与实际曲线,如图10所示,虚线为理论解析所得不同预应力损失下锚杆轴力沿长分布曲线,实线为分布式光纤所测曲线。
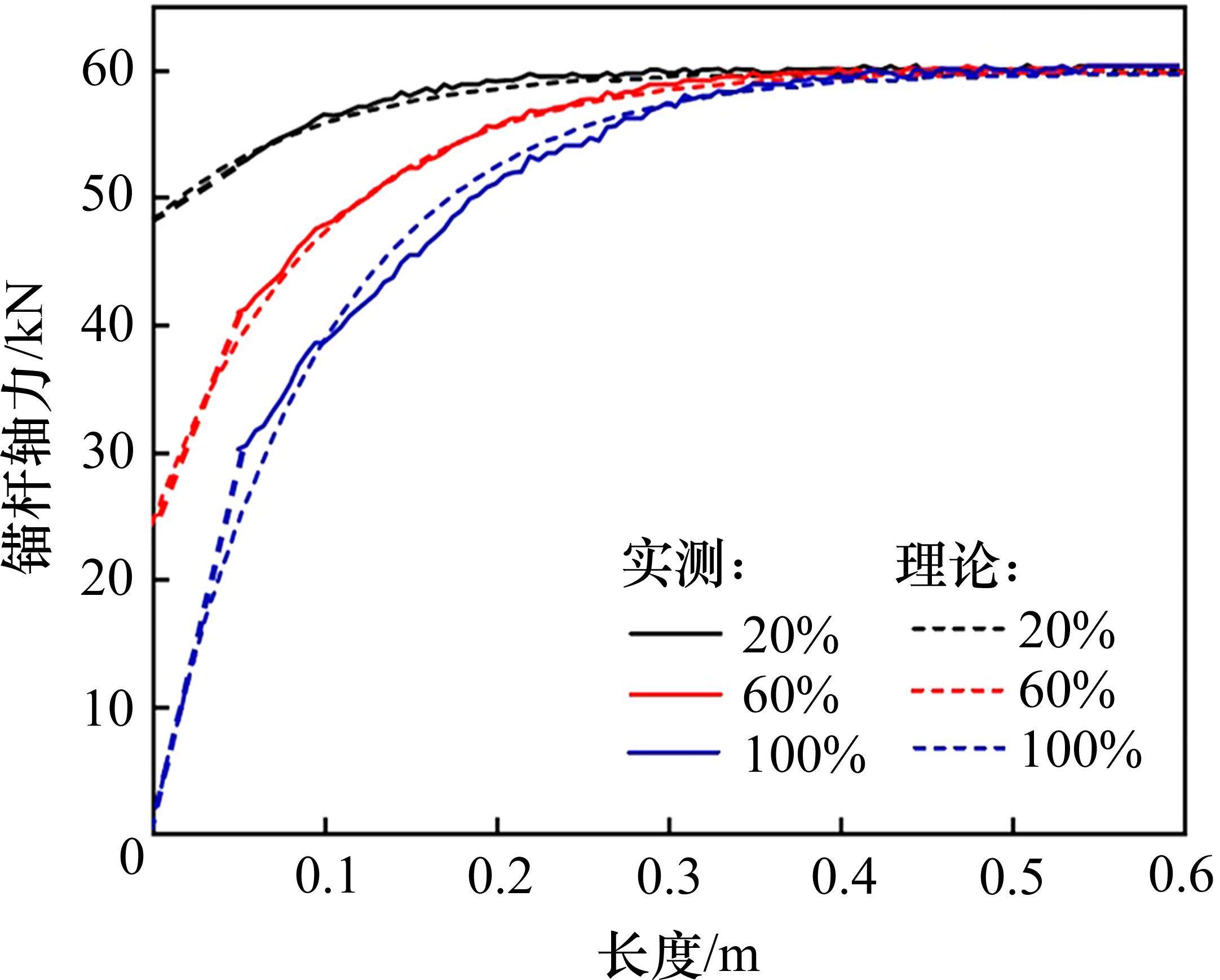
由图10可知,理论解析与实测数据曲线趋势相同,无论是解析值还是实测值,当产生预应力损失时,注浆段均可以发挥较好作用,在预应力损失100%时实测值较于理论值更为平缓,考虑到实际材料力学性能会随着受力与变形进行改变,所以与弹性理论解有一定差距。
4.2 后注浆式预应力锚杆参数分析
为研究注浆段力学参数对其在松弛荷载下力学响应的影响,基于已验证的理论模型研究了不同注浆长度l,锚杆弹性模量E,锚杆直径D,剪切刚度k下的锚杆轴力分布。具体地,将锚杆在60 kN初始预应力下,锚固段预应力损失20%作为研究工况。
4.2.1 注浆长度l
现对注浆长度l进行参数化分析,作出不同注浆长度与锚杆轴力关系图(图11)以及注浆长度对支护力影响图(图12)。
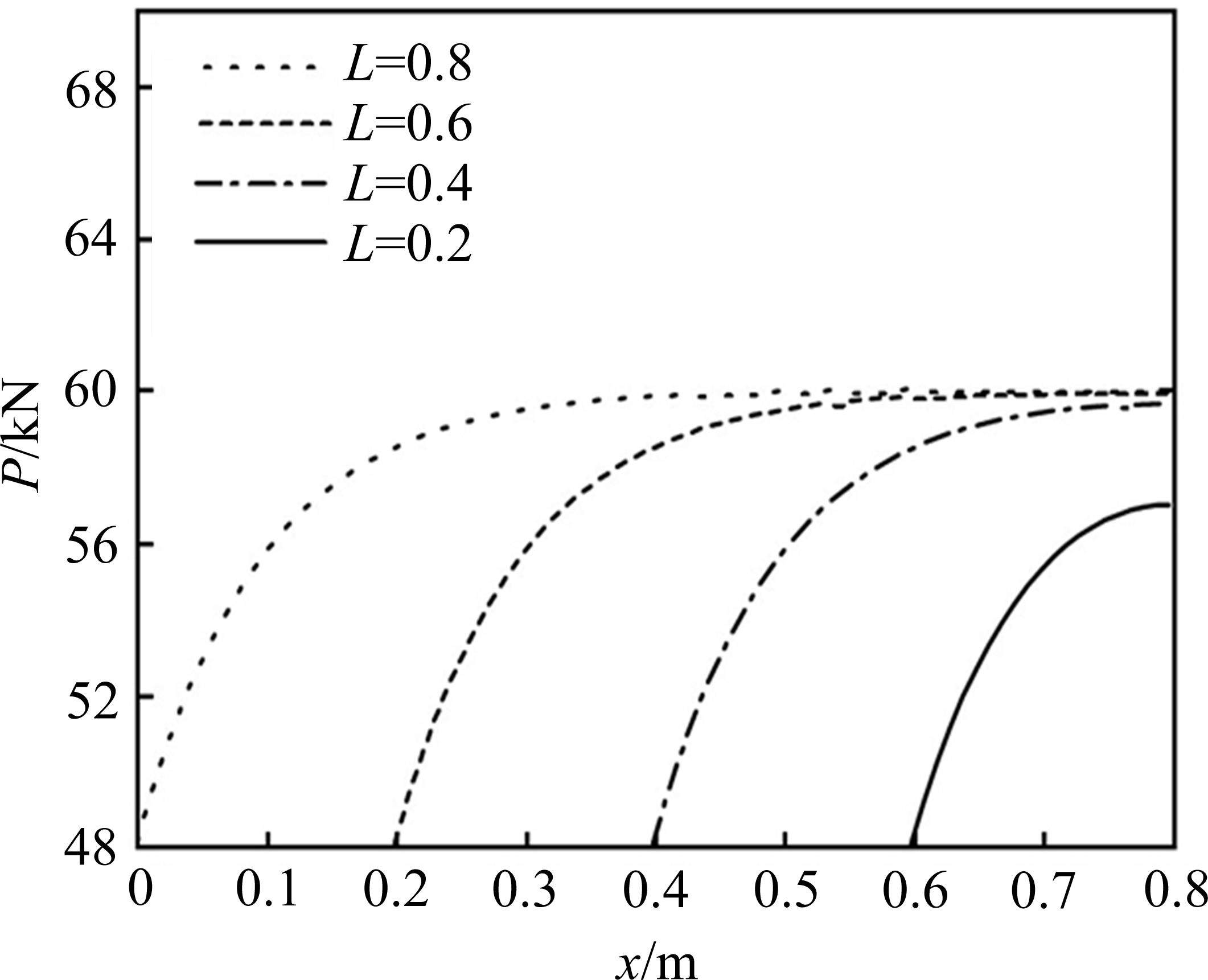
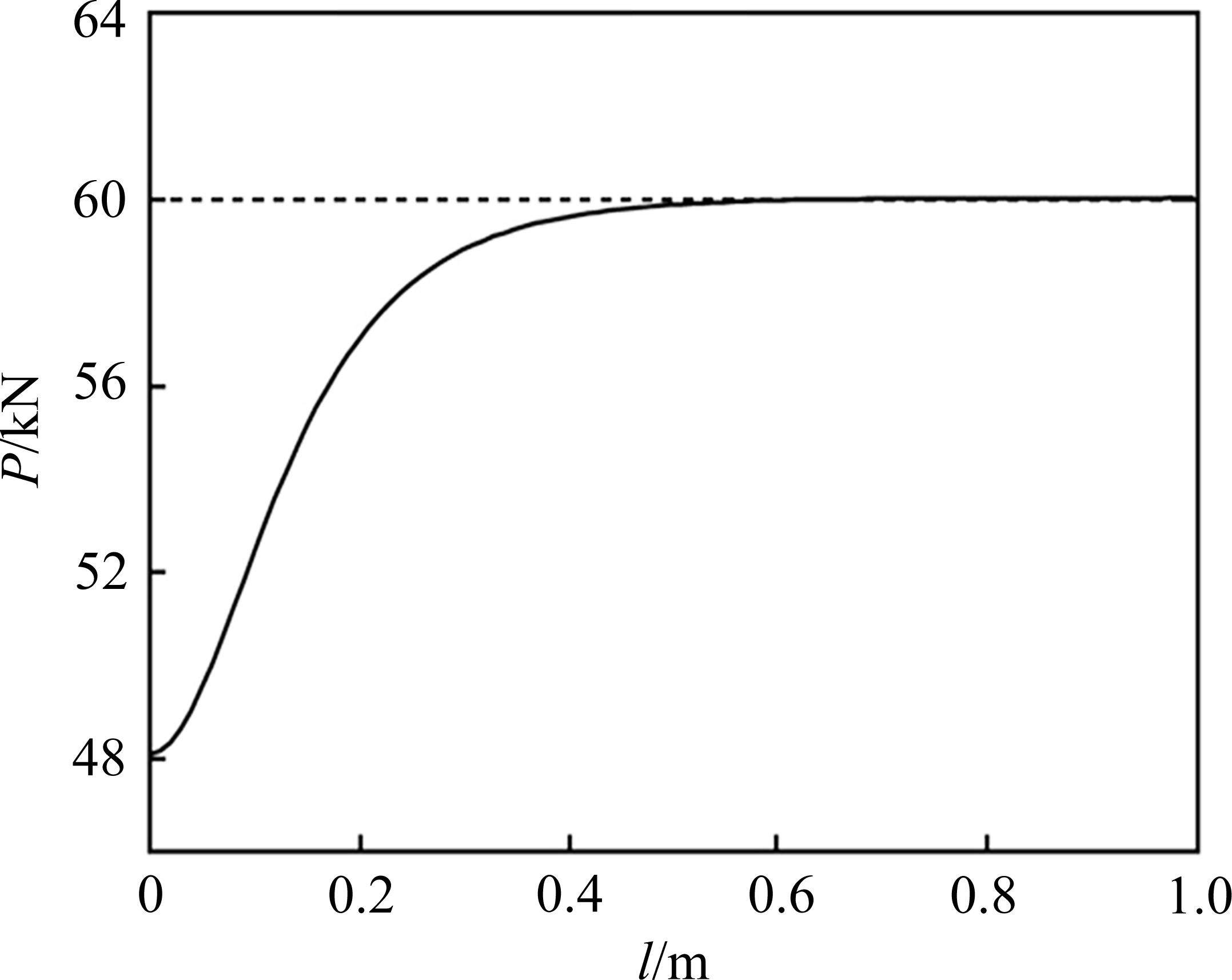
由图11可以看出,在端锚产生预应力损失后,随着注浆长度的增加,锚杆轴力能较好地保持,当注浆长度为0.2 m时,垫板端支护力为57 kN,而当注浆长度大于等于0.4 m时,垫板端支护力较好维持在60 kN附近,且压缩区范围较长,这点在图12中更为明显,当注浆长度超过一定范围时,认为能够在锚固段发生预应力损失时,较好地维持支护力,并不是随着锚固段产生预应力损失而一同减小。
4.2.2 锚杆弹模E
图13绘制了锚杆不同弹模对注浆段的影响,可见弹模越大,预应力损失对注浆段长度影响范围越大,取锚杆轴力为初始预应力98%时为对数上升段与平滑段分界处,当弹模为20 GPa时,对数上升段长度a=0.1 m,锚杆轴力随着弹模增大而降低,而当弹模为300 GPa时,对数上升段长度b=0.5 m。
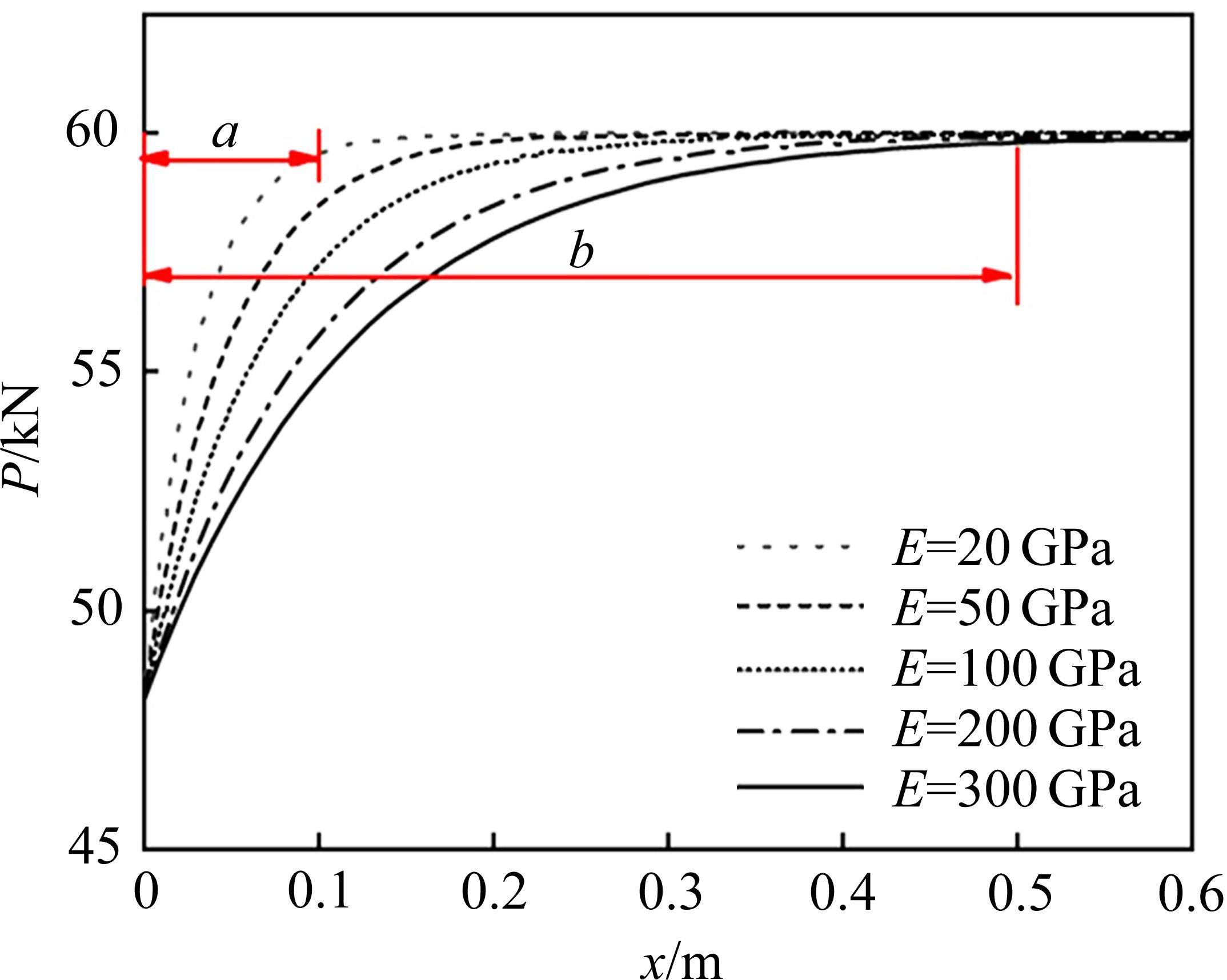
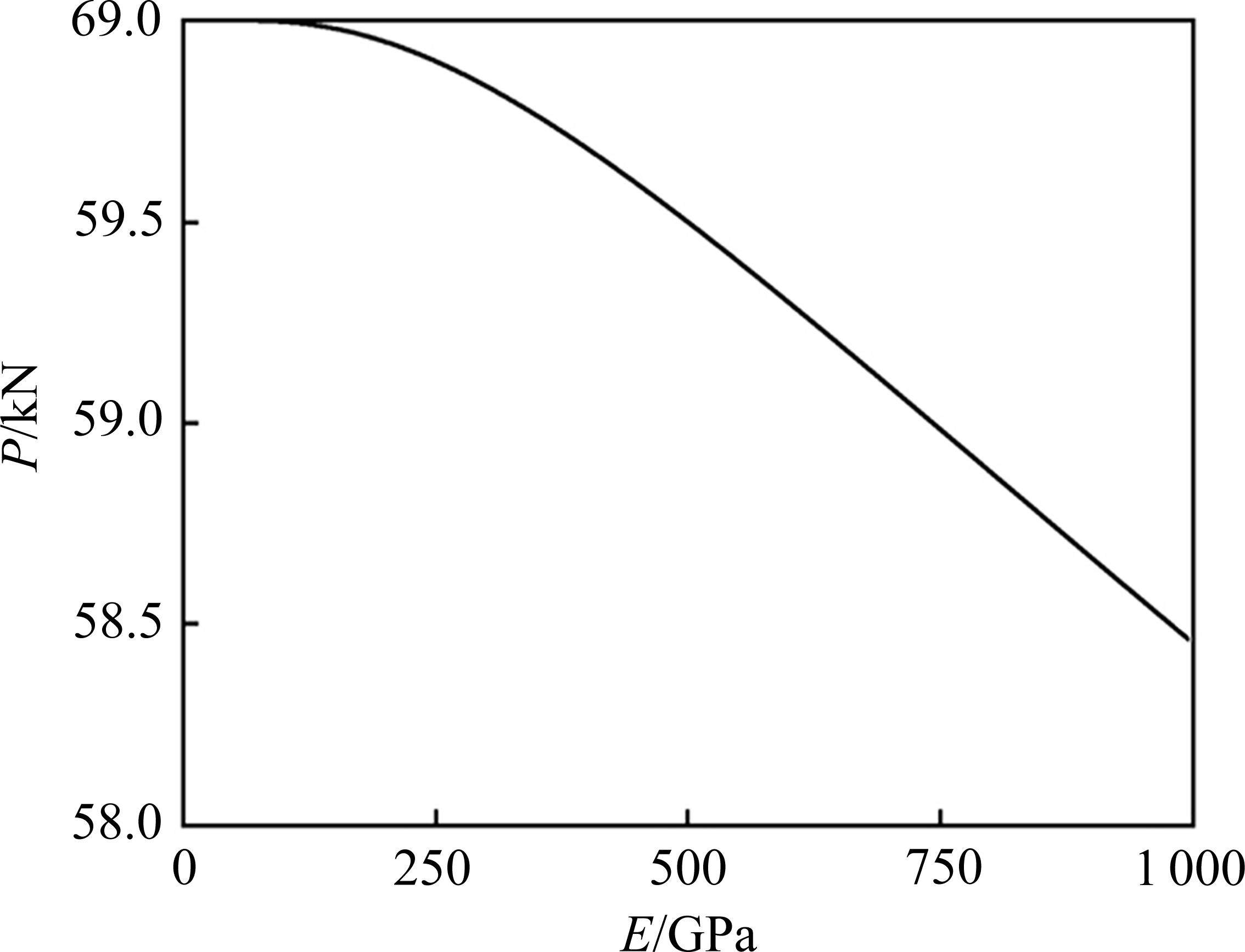
图14所示为锚杆弹模影响性分析,根据不同弹模所对应的围岩-垫板端支护力进行曲线作图,发现随着锚杆弹性模量的增大,锚杆支护力逐渐减小,但总体减少较少,当弹模为150 GPa时,支护力损失0.3%,当弹模为300 GPa时,支护力才损失0.33%。
4.2.3 锚杆直径D
根据《岩土锚杆与喷射混凝土支护工程技术规范》[25]中所给定的中空注浆锚杆直径建议值为25~52 mm,现研究不同锚杆直径对注浆段支护力的影响,不同直径锚杆支护力沿长变化如图15所示,垫板端锚杆直径参数化影响如图16所示。
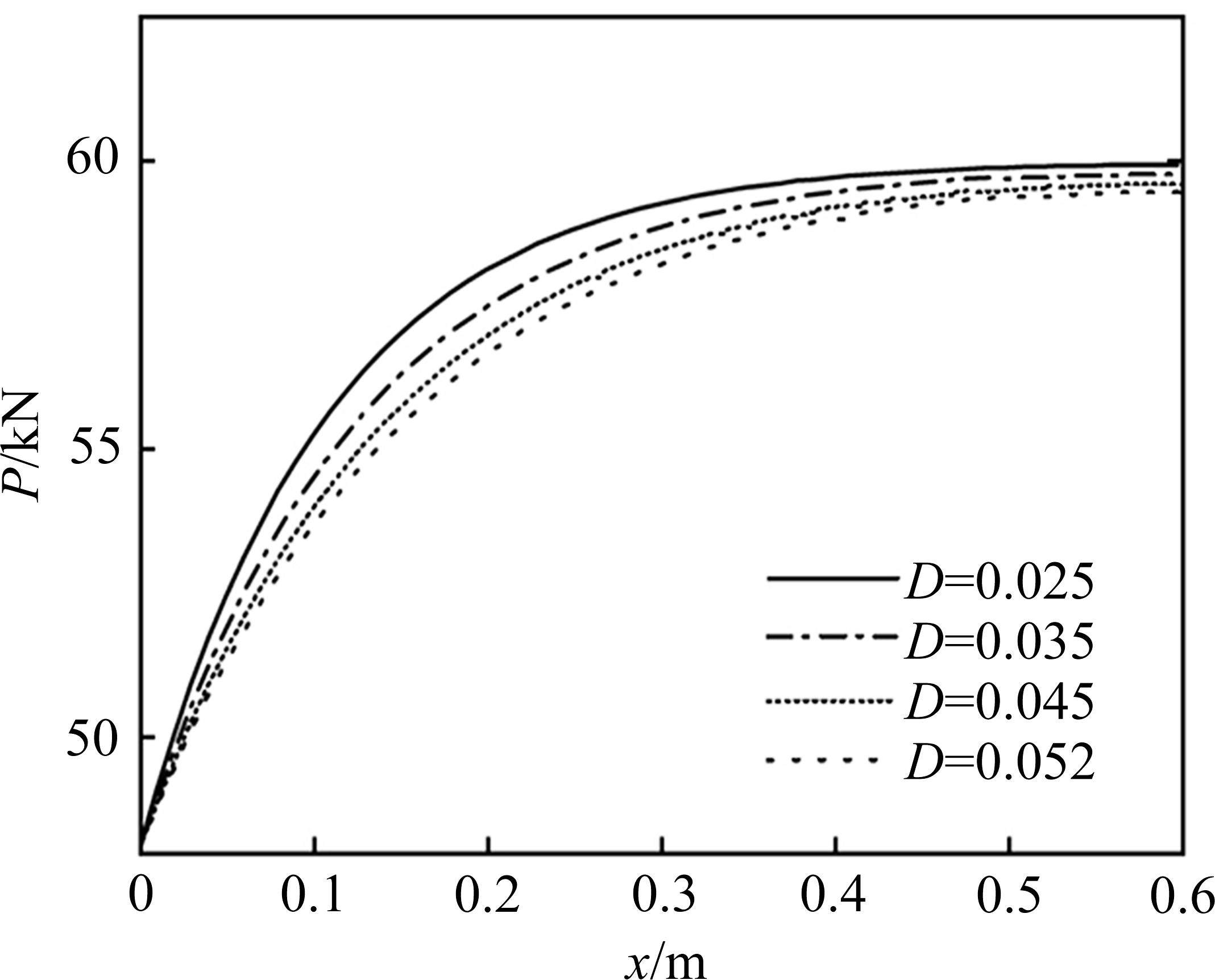
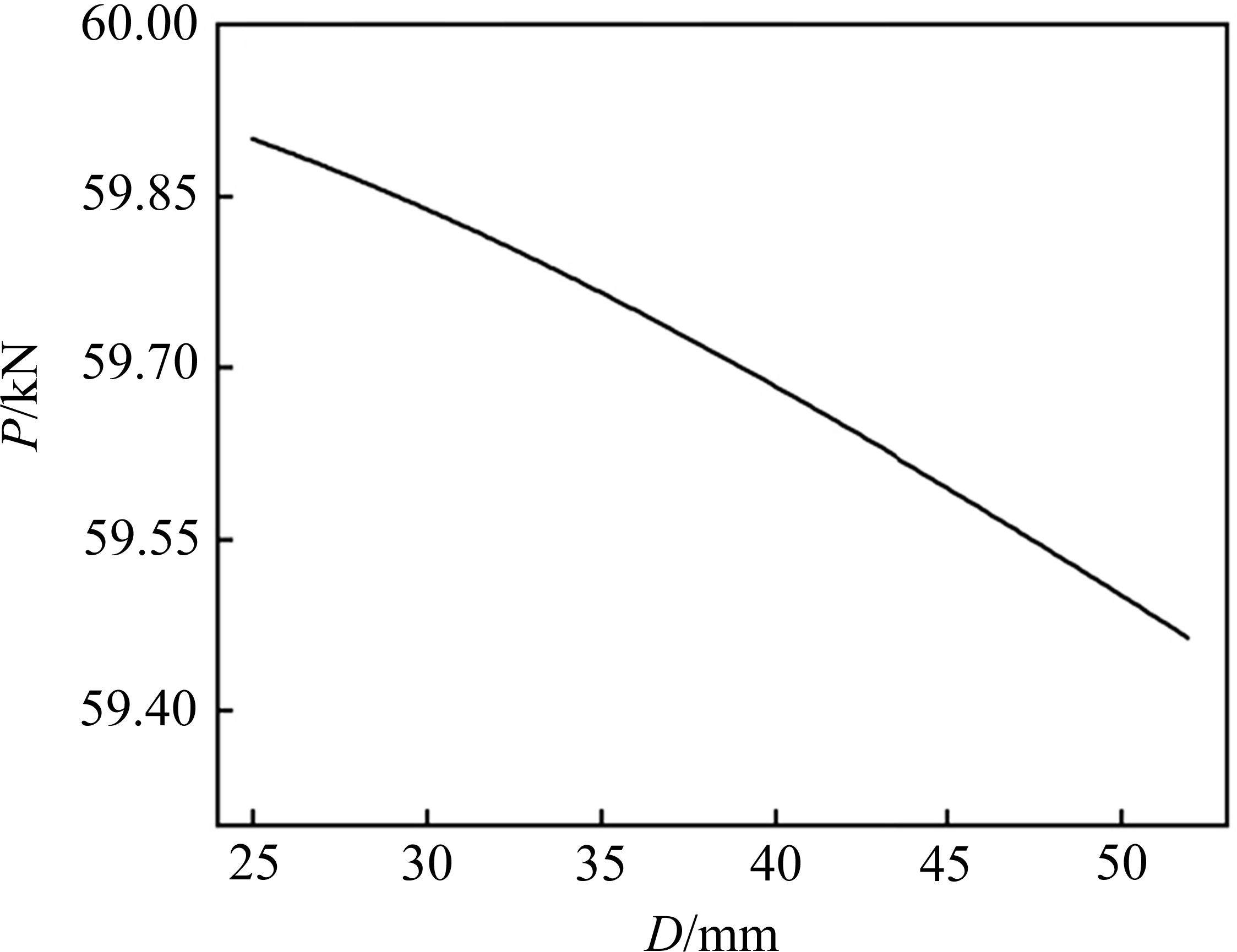
根据图15可以看出,锚杆直径的改变对支护力影响并不大,曲线斜率稍有改变,其预应力损失对注浆段的影响长度随着锚杆直径增大而增大,但幅度较小。图16可以更明显看出锚杆直径的改变对垫板端支护力的影响并不显著,呈负相关关系,当锚杆直径为25 mm时,垫板端支护力为59.90 kN,支护力损失0.17%,当锚杆直径为52 mm时,垫板端支护力为59.46 kN,支护力损失仅为0.9%,因此可以认为在规范给定范围内,锚杆直径的改变对垫板端的影响认为可以忽略不计。
4.2.4 剪切刚度k
为了研究剪切刚度对锚杆支护力的影响,作出不同剪切刚度k下锚杆支护力曲线(图17)和剪切刚度对垫板端支护力影响曲线(图18)。
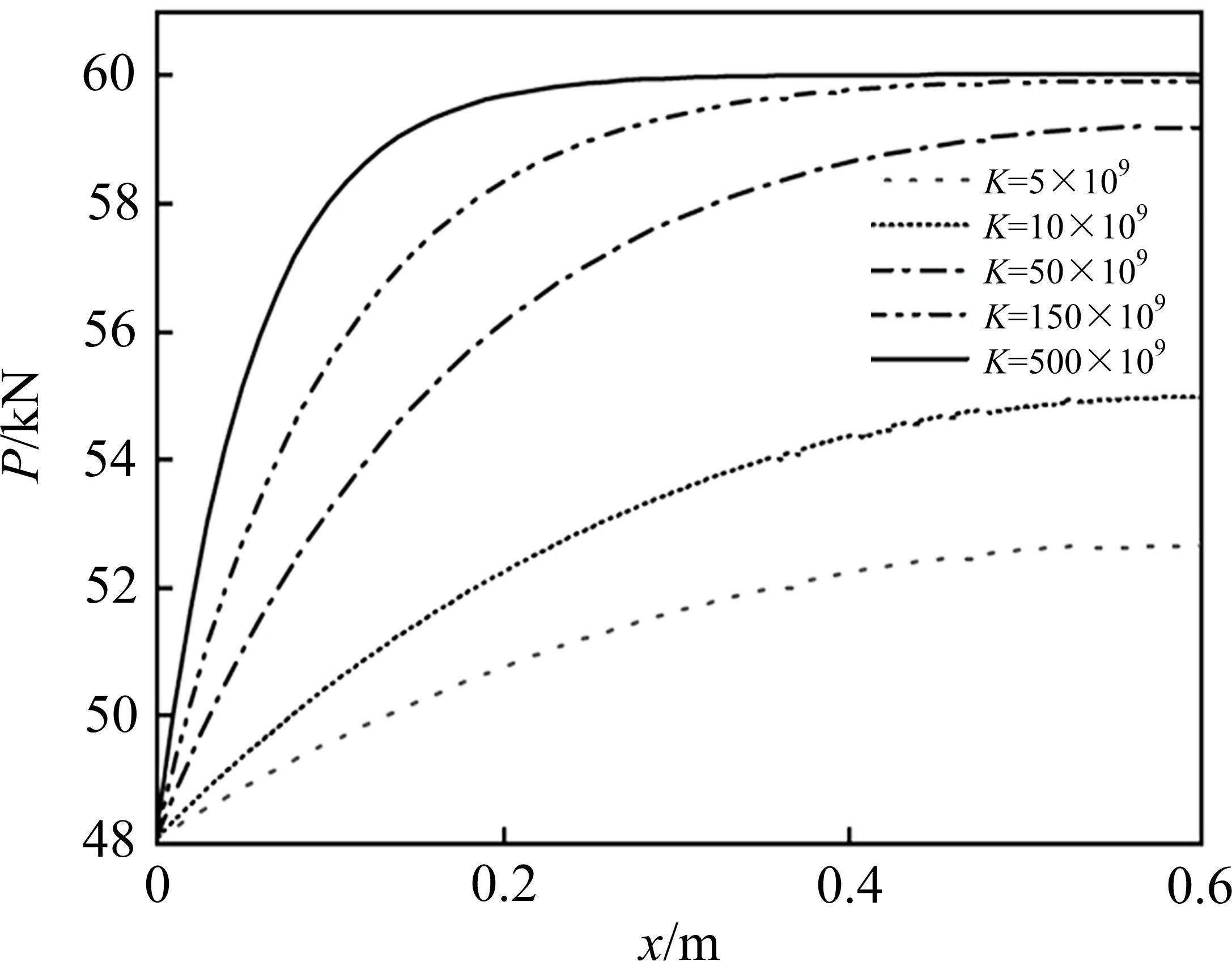
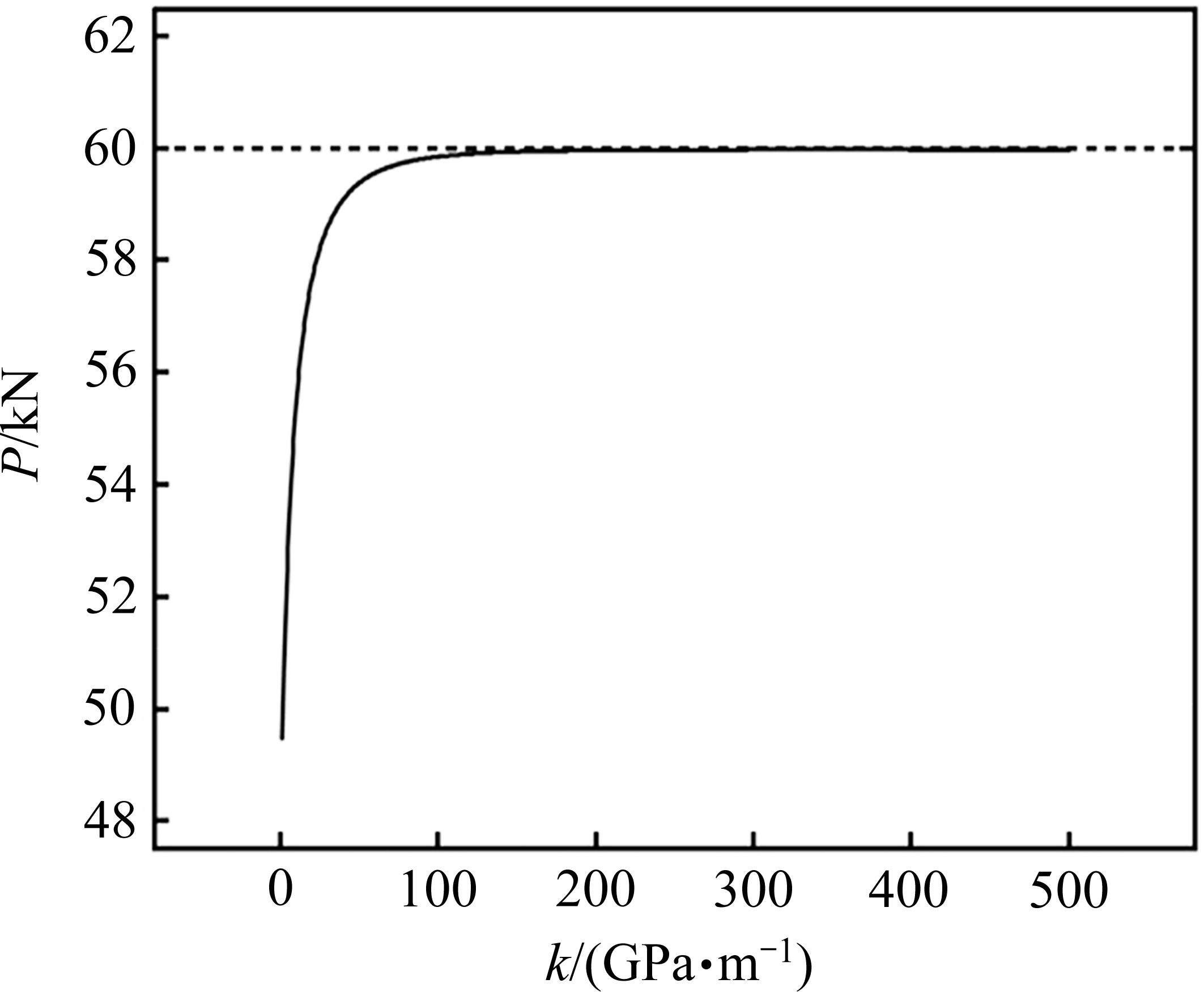
根据图17可以看出,剪切刚度的变化对锚杆支护力影响较为明显,随剪切刚度增加,支护力随之上升,曲线斜率也随之增加,对注浆段影响长度逐渐减小。由图18可以更直观地看出以上趋势,当剪切刚度在50 GPa前,认为剪切刚度对支护力影响较大,而超过该值时认为剪切刚度对支护力影响较小,即后注浆树脂锚固形式在锚固段产生预应力损失后能够更好保持其注浆段预应力。
5 结论
1) 建立了后注浆式预应力树脂锚杆在产生预应力损失后,注浆段受力力学模型,根据三线性本构关系以及锚杆轴力变形条件,推导出锚杆轴力沿长分布曲线表达式。
2) 对理论模型进行了室内试验验证,试验中通过千斤顶、反力架、垫板和螺母模拟锚固失效的效果。使用分布式光纤作为应变采集技术,测量了纯预应力树脂锚杆和后注浆式预应力树脂锚杆在注浆段的力学行为变化。结果表明,实验数据与理论分析解相吻合,进一步证实了注浆段力学模型的合理性。
3) 对锚固段产生预应力损失后压缩区长度进行分析,当锚固段预应力完全损失后,压缩区范围虽然减小但最终在0.3 m左右,表明后注浆式预应力树脂锚杆相较于纯预应力树脂锚杆在预应力完全损失后仍能起到支护作用。
4) 进一步对理论模型注浆段各参数进行分析,发现当注浆长度l达到一定范围时,在锚固段产生预应力损失后能够较好地维持支护力;锚杆的直径以及弹模对注浆段力学性能影响较小;而接触面剪切刚度对注浆段力学性能影响较大,当剪切刚度达到一定值时可以认为注浆段能够较好地维持锚杆支护力。
张子洋,汪波,刘锦超等.后注浆预应力树脂锚杆应力损失后注浆段效用分析[J].铁道科学与工程学报,2025,22(02):783-794.
ZHANG Ziyang,WANG Bo,LIU Jinchao,et al.Utility analysis of post grouting section after stress loss of post grouting prestressed resin bolt[J].Journal of Railway Science and Engineering,2025,22(02):783-794.

