随着我国基础建设的快速发展,地上建筑层高增加且逐渐趋向于饱和,地下建筑逐渐开发如地下城市、地下室和地铁车站等,尤其是我国的滨海城市中,抗浮建设较为普遍[1-3]。抗浮锚杆作为众多抗浮措施中的一种,因其具有施工工艺简单、结构受力合理和高性价比等优点[4-5],成为解决建筑结构抗浮问题的优先选择。钢筋具有较高的抗拉强度和弹性模量,成为现阶段抗浮锚杆工程中的主要材料,其在抗浮过程中的受力机理受到工程界和学术界的关注。
抗浮锚杆的承载性能与锚筋参数[6-7]、混凝土强度[8]和环境因素[9-10]等相关,其中,锚固长度对锚杆承载力产生的影响最为明显[11-12],且在不同的地质情况下,抗浮锚杆的锚固长度不相同。在室内锚杆拉拔模型试验下,冯君等[13-14]阐明了抗浮锚杆极限承载力与锚固长度成正比的规律以及抗浮锚杆杆体的轴力沿杆体呈单峰形式分布。SUN等[14]还发现抗浮锚杆的锚固长度存在临界值,当锚固长度超过该临界值时,抗浮锚杆的承载力与锚固长度不再相关。KON等[11]通过嵌入式光纤光栅传感技术证明抗浮锚杆锚固体系存在临界深度。匡政等[15]从理论推导的角度,结合荷载传递理论和Kelvin位移解,提出理想条件下抗浮锚杆杆体与锚固体的轴力、剪应力沿锚固深度的分布函数,并利用现场拉拔试验进行验证,在考虑不均匀性和脱黏效应后修正分布函数,极大程度地提高了其精度。白晓宇等[16]则基于钢筋抗浮锚杆的现场拉拔破坏试验,得到钢筋抗浮锚杆普遍产生拔断破坏的结论,证明了锚固长度是影响抗浮锚杆杆体-灌浆体界面黏结强度的最重要因素,且黏结强度与锚筋直径呈正相关。抗浮锚杆的承载性能主要由杆-浆界面、浆-岩界面的黏结锚固作用提供,锚固长度则直接影响两界面的接触面积。YOO等[6-7]利用试验发现较长锚固长度的抗浮锚杆承载性能明显增加,但锚筋的黏结强度较小。
合理的锚固长度可以在保证工程质量的前提下充分发挥锚杆杆体本身的力学性能,并可以最大程度地减少锚杆材料的浪费,符合绿色低碳的理念。因此,需要系统研究风化岩地层中抗浮锚杆的承载性能,明确抗浮锚杆的锚固长度,揭示抗 浮锚杆的承载机制。本文利用3组直径为28 mm,锚固长度分别为3、4、5 m的9根抗浮锚杆进行现场拉拔破坏性试验,研究相同地质条件下抗浮锚杆锚固长度对承载性能的影响,通过安装锚杆杆体表面的电阻应变传感器,实时测试试验过程中不同锚固深度抗浮锚杆的应变分布情况,揭示抗浮锚杆的荷载传递规律。
1 现场试验
1.1 工程概况
试验场区地质条件均为强风化片麻岩,其揭露厚度为2.00~11.00 m,平均厚度为8.44 m。在试验场地范围内,岩层主要为中风化花岗片麻岩,颜色呈灰绿色,矿物主要为钾长石、石英、黑云母,呈中粗粒、片麻状、块状。结构部分被破坏;沿节理面有次生矿物,裂隙较发育,岩芯呈碎块状、短柱状,岩芯节理密集发育带处较易击碎,遇水不易软化,无膨胀性,无崩解性。岩层的地基承载力特征值为500 kPa,重度为22 kN/m3,岩石饱和单轴抗压强度为28.5 MPa,灌浆体与岩石间黏结强度标准值为240 kPa,等效内摩擦角为40°,岩体较破碎,岩体完整性指数Kv为0.40,岩体基本质量等级为Ⅳ级,场区内地下水位埋深为6.50~9.70 m。
1.2 试验方案
本试验采用直径为25 mm的HRB400钢筋作为试验锚杆。锚杆的极限抗拉强度为570 MPa,屈服强度标准值为400 MPa、设计值为360 MPa,弹性模量为210 GPa。焊接式锚具由本课题组指定的工厂定制而成,锚具边长为200 mm,厚度为20 mm,中心开孔,孔直径为30 mm。利用3组不同锚固长度的抗浮锚杆进行现场极限抗拔试验,为保证试验结果的科学性,将每组试验锚杆设置3个平行试验。试验锚杆的具体参数如表1所示。
| 试验编号 | 杆体直径/mm | 锚固长度/m | 砂浆强度等级 |
|---|---|---|---|
| Z1-1、Z1-2、Z1-3 | 25 | 3 | M30 |
| Z2-1、Z2-2、Z2-3 | 25 | 4 | M30 |
| Z3-1、Z3-2、Z3-3 | 25 | 5 | M30 |
通过电阻式应变传感器测试试验过程中锚杆杆体的应变变化,根据匡政等[3]的研究发现,抗浮锚杆杆体的轴力和剪应力主要集中在浅部的岩土层,在锚杆前3 m加密布置传感器,间距为500 mm,锚杆3 m以下布置传感器,间距为 800 mm。应变传感器的具体布置方式如图1所示。
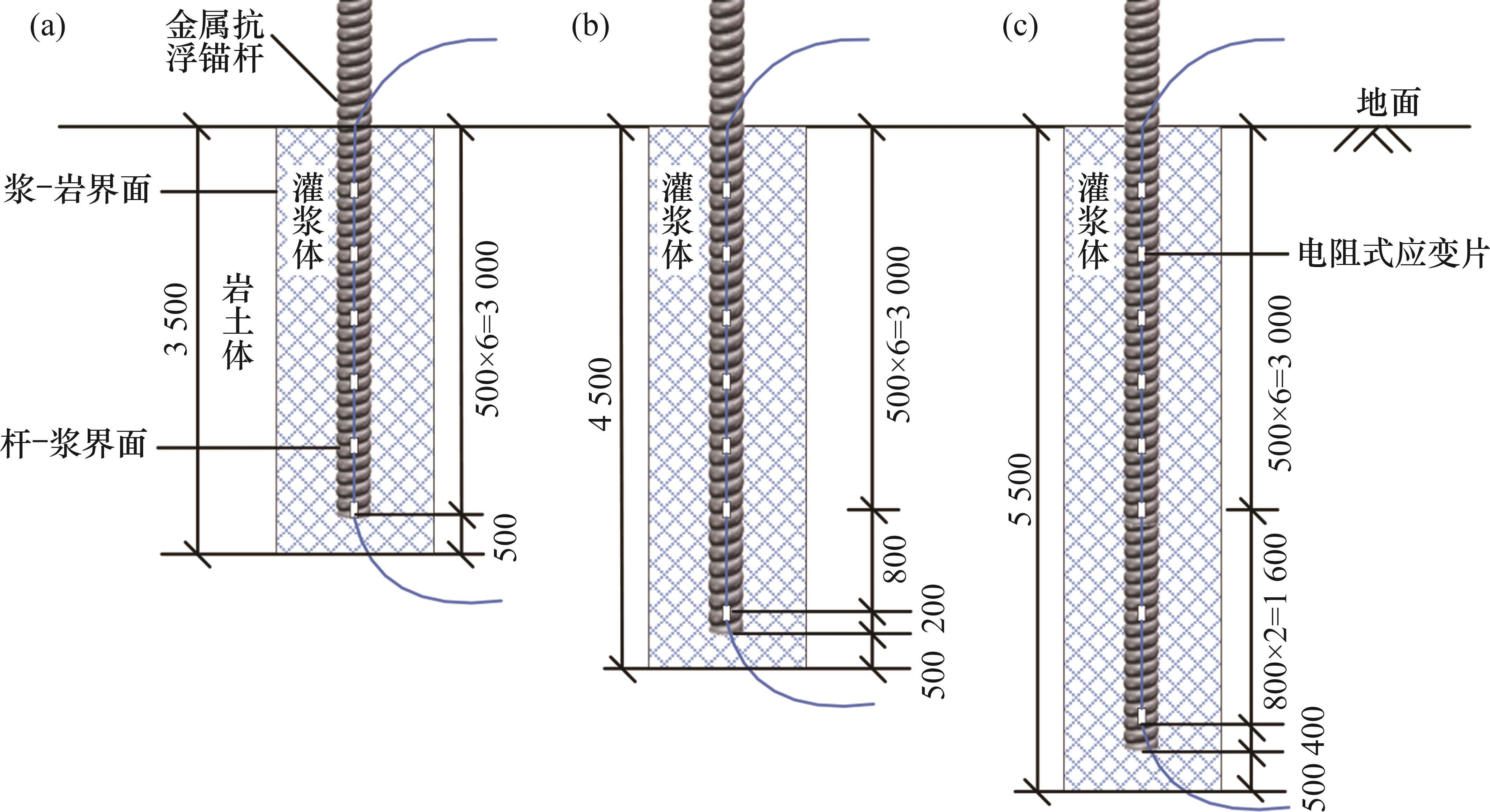
1.3 试验过程
依次进行锚杆定位、钻孔、试验锚杆制作、注浆、试验装置安装及试验加载,其中,锚孔直径为150 mm,采用M30水泥砂浆进行注浆。待砂浆养护28 d后,砂浆强度达到32.7 MPa,试验装置示意及实物图如图2所示。按图2所示的加载装置进行试验,具体安装步骤为:在距离锚杆杆体 0.5 m两端放置2个钢制支墩,在钢制支墩上依次安装格构式反力梁、穿心千斤顶、荷载传感器和焊接式锚具,各部件之间均安装20 mm厚的钢性垫板。在锚杆杆体外露处对称焊接2块光滑铁片,并在灌浆体表面对称放置2块光滑铁片,随后安装4个位移传感器,用于测量锚杆杆体与灌浆体的竖向位移。
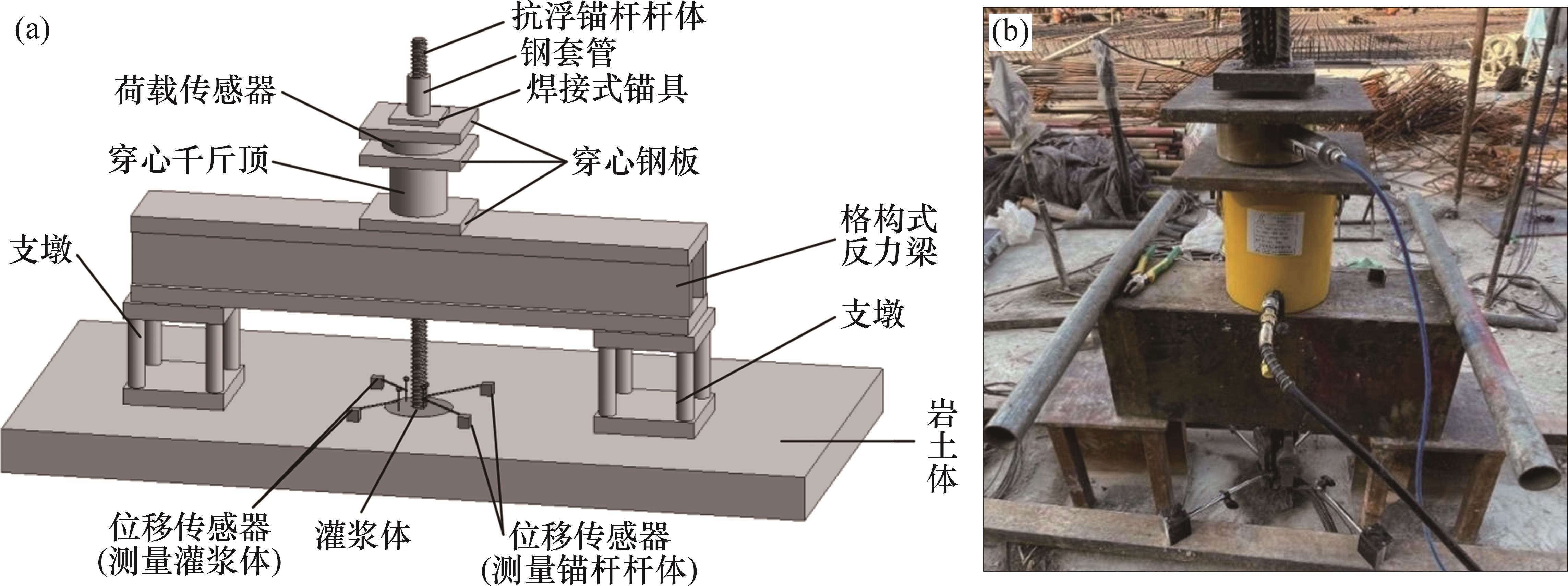
试验为破坏性拉拔试验,在试验过程中采用分级加载的方式。根据试验锚杆参数,计算抗浮锚杆的屈服强度约为200 kN(即Qmax),为了更详细地研究加载过程中锚杆杆体的内力变化情况,采用每级荷载1/8Qmax(即25 kN)的方式进行加载,即0→25 kN→50 kN→75 kN→100 kN→125 kN→…,以2 kN/s的速率匀速加载,直至试验锚杆发生破坏为止。当每级加载完成后,记录4个位移传感器的读数,相邻两级荷载之间的加载间隔为 15 min。根据JGJ120—2012《建筑基坑支护技术规程》[17]附录A规定,锚杆试验中从第2级荷载开始,后一级荷载产生的锚头位移增量达到或超过前一级荷载产生位移增量的5倍,或锚头位移不收敛,或锚杆杆体破坏或从灌浆体中拔出时,判定为锚杆破坏,终止继续加载。
2 试验结果及分析
2.1 试验现象及破坏特性分析
在通常情况下,抗浮锚杆锚固结构的破坏形式分为以下4种情况:锚杆自身强度不足,锚杆发生屈服破坏;锚杆杆体-灌浆体界面(杆-浆界面)发生剪切破坏,锚杆被拔出;灌浆体-岩土体(浆-岩界面)发生剪切破坏,灌浆体被拔出;砂浆强度不足,发生倒锥形拔出破坏。一般以前3种破坏形式为主[18]。本次试验为破坏性抗拔试验,抗浮锚杆试验情况统计如表2所示,表中锚杆破坏形态均为锚杆杆体屈服破坏。
| 锚杆编号 | 最大加载量/kN | 杆体位移/mm | 灌浆体位移/mm |
|---|---|---|---|
| Z1-1 | 210 | 6.95 | 1.76 |
| Z1-2 | 214 | 6.83 | 0.67 |
| Z1-3 | 209 | 7.18 | 1.46 |
| Z2-1 | 210 | 7.63 | 1.45 |
| Z2-2 | 212 | 8.59 | 0.82 |
| Z2-3 | 204 | 6.66 | 1.51 |
| Z3-1 | 210 | 11.15 | 0.39 |
| Z3-2 | 210 | 11.49 | 1.44 |
| Z3-3 | 204 | 9.85 | 0.75 |
记录加载过程中抗浮锚杆的试验现象发现:当试验荷载低于最大加载量的50%时,灌浆体几乎未发生变化,锚杆杆体与灌浆体呈现良好的协同变形状态。随着荷载的增加,位移百分表读数变化量较小;当加载量超过最大加载量的60%时,灌浆体出现开裂现象,且随着荷载量的增加,裂缝数量增多且长度增大,此时,位移传感器读数变化量增大;当荷载达到锚杆的最大加载量时,试验锚杆发生破坏,锚杆的持荷水平接近材料本身的屈服强度;随着荷载量的增加,荷载传感器读数在小范围内波动,位移传感器读数快速增加;锚杆杆体与灌浆体之间发生不同程度的滑移,但均未出现锚杆杆体被拔出、杆-浆剪切破坏或灌浆体被整体拔出的现象。锚杆Z2-3的破坏现象最为明显,如图3所示。

2.2 荷载-位移曲线分析
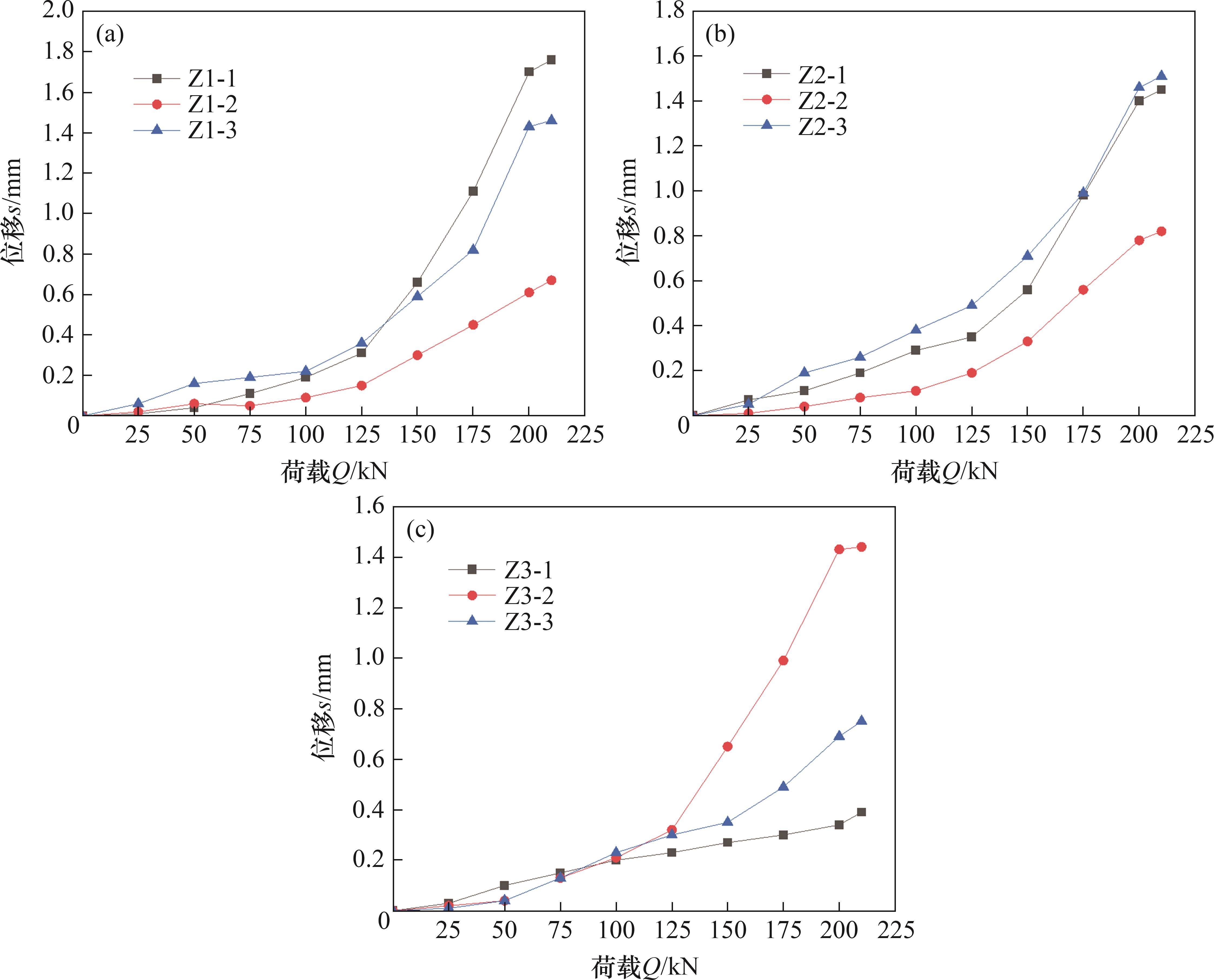
荷载-位移(Q-s)曲线可以直观反映抗浮锚杆在荷载作用下荷载与锚杆位移之间的关系,并且可以宏观反映荷载水平对抗浮锚杆锚固性能的影响,有助于后续对锚杆荷载传递性状的分析。试验中分别利用2组(4个)位移传感器测试锚杆杆体位移和灌浆体位移,使用高精度荷载传感器测量拉拔荷载,可在一定程度上减少偶然误差。不同荷载水平的抗浮锚杆杆体、灌浆体的荷载-位移曲线分别如图4、图5所示。
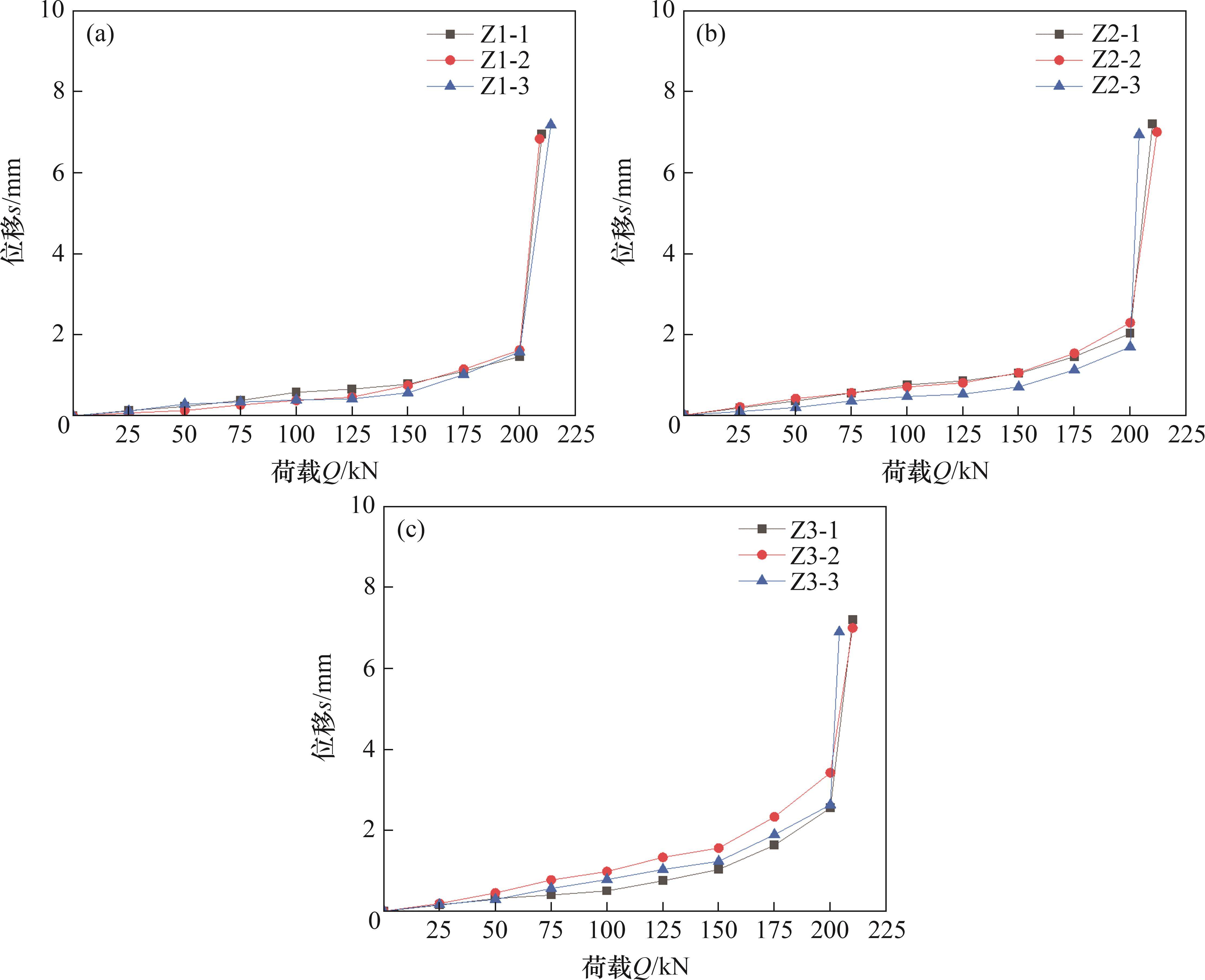
由图4可见:所有试验锚杆杆体荷载-位移曲线在0~200 kN时变化缓慢(缓变段),而后随着荷载继续增大,荷载-位移曲线陡然增大(陡升段),故整体曲线呈现为缓变-陡升形状,其中,缓变段可大致分为两个阶段;在加载至试验锚杆极限荷载的75%(150 kN)之前,锚杆杆体位移随荷载的增加匀速增加,称为缓和段;当加载量超过试验锚杆极限荷载的75%时,锚杆杆体的位移随着荷载的增加而加速增加,称为加速段。这两阶段之间存在转折点,对比3组试验锚杆发现该拐点与锚杆的锚固长度无明显关联,转折点并不随锚杆长度的增加而改变,缓和段承担的荷载约为缓变段承担荷载的75%,而缓和段位移仅为缓变段位移的50%左右;当加载量达到200 kN时,随着试验荷载的增加,3组试验锚杆的承载极限在210 kN左右波动,但锚杆杆体的位移持续增加。经计算可知锚杆杆体(钢筋)屈服时所需拉力为196.36 kN,此时,抗浮锚杆发生缩颈现象,导致锚杆杆体位移不断增加,锚杆杆体与灌浆体之间的黏结力大于抗浮锚杆杆体本身的极限承载力。
从锚固机理上分析,在荷载加载至锚杆极限荷载的75%之前,随着荷载的逐渐增加,浅层锚杆杆体与灌浆体产生相对位移,该位移沿深度方向逐渐增加。杆体通过形变承担应力而后传递给灌浆体,浅层灌浆体主要依靠机械咬合力承担荷载,深层灌浆体则主要通过摩擦力和化学黏结作用分担荷载。当荷载量超过锚杆极限荷载的75%时,灌浆体所受拉力超过砂浆的抗拉强度,发生开裂现象,而后将荷载传递至周围岩体,此时,灌浆体的劈裂阻力发挥重要作用。
由图5可见:所有灌浆体的Q-s曲线均为缓变型,曲线形式类似于锚杆杆体的Q-s曲线形式,也存在缓和段、加速段和转折点;与锚杆杆体相比,灌浆体位移转折点出现位置提前,在锚杆最大加载量的60%(即125 kN)左右,此时,锚杆杆体与灌浆体产生相对位移,在实际加载过程中,灌浆体裂缝也在此时出现。随着荷载量的增加,裂缝逐渐变大。在转折点之前,灌浆体位移随荷载量的增加呈匀速变化,在转折点之后,灌浆体位移加速变大,且荷载-位移曲线转折点之后灌浆体位移变化速度比锚杆杆体位移变化速度大。
图5中灌浆体在最后一级荷载(约为209 kN)作用下,位移变化速率明显减小,原因是在极限荷载的作用下,孔口附近的锚杆杆体进入屈服阶段,在后续的加载过程中,主要发生锚杆杆体的屈服变形,浅层灌浆体与锚杆杆体脱离,在荷载作用下,灌浆体的位移变化较小。对比3组灌浆体的Q-s曲线发现,锚固长度越长,灌浆体位移略小,但抗浮锚杆的锚固长度对灌浆体位移的影响并不显著,并且灌浆体的最终位移存在一定偶然性。
2.3 杆体轴力分布特征
采用电阻式应变传感器对加载过程中锚杆杆体的应变进行实时监测,使用DH3816N静态应变测试仪采集加载过程中锚杆杆体的应变。根据测得的应变计算锚杆杆体轴力随深度的变化曲线,如图6所示。
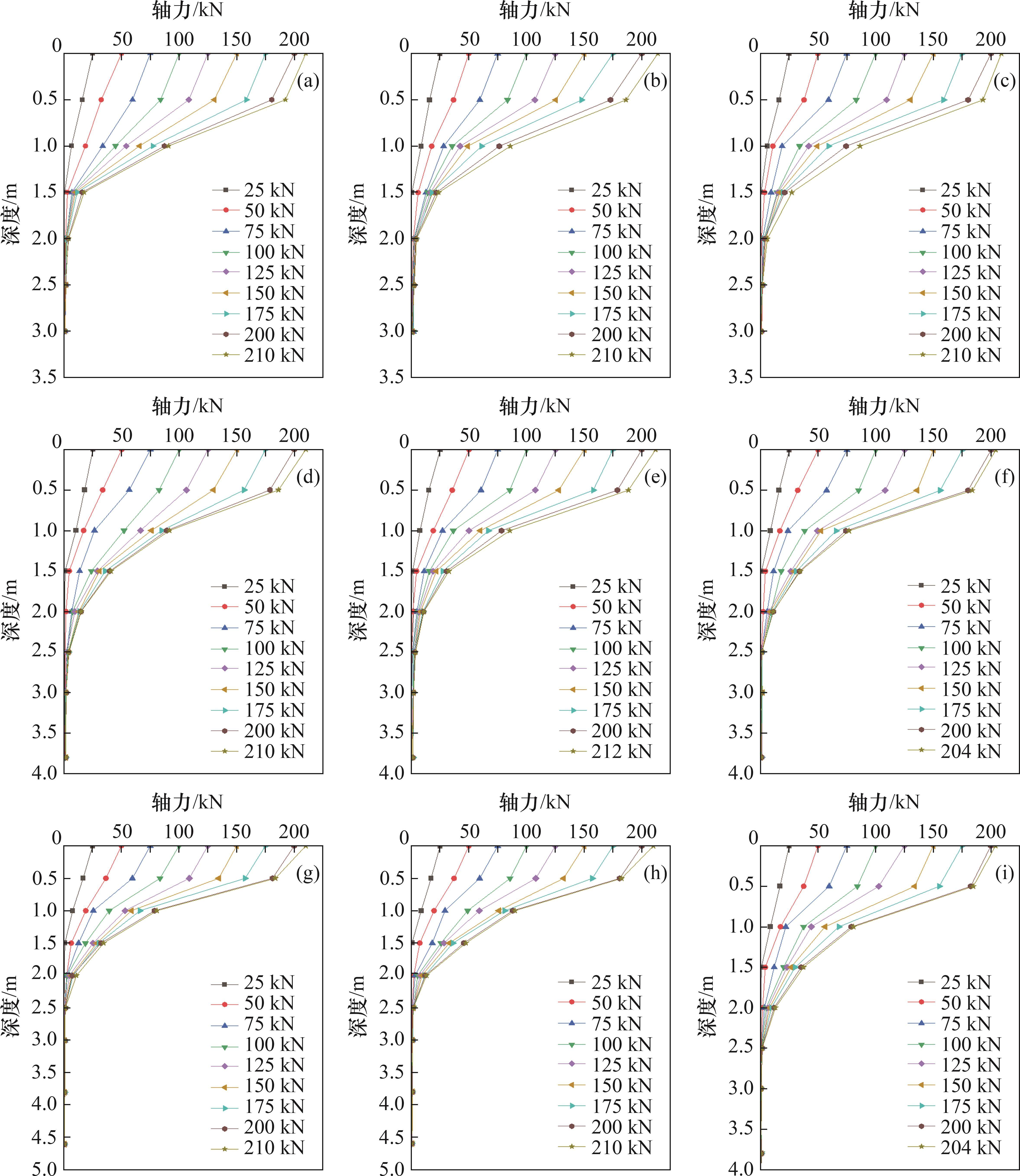
由图6可见:9根试验锚杆杆体轴力随深度变化的规律一致;随着荷载的增加,锚杆的轴力沿深度方向逐渐向下传递,由第1级荷载(25 kN)作用下的1.5 m发展为破坏荷载作用下的2.5 m;锚杆杆体各深度的轴力均增加,但不同深度处锚杆的轴力增幅不同,浅层锚杆轴力增长较大;随着深度的增加,锚杆轴力的增长幅度逐渐减小。从图6(a)可见:在同一荷载水平下,锚杆杆体的轴力随深度增加逐渐减小,且减小的速率逐渐降低;在孔口处出现应力集中的现象,且应力主要集中在距孔口深度2 m的区域内,随着锚杆锚固长度的变化,应力作用区域未出现明显的变化,锚杆末端几乎不产生轴力。综上所述,抗浮锚杆杆体轴力沿锚杆深度逐渐向下传递,且轴力传递呈衰减状态。
本试验9根锚杆的荷载传递深度均约为2.5 m,应力主要集中在深度约2 m的范围内。对比3组不同锚固长度的试验锚杆发现,锚杆轴力的传递深度未出现明显变化,说明在2 m深度以下的锚杆几乎不发挥作用。在其他参数(岩土层力学参数、灌浆体强度、锚杆的材料类型等)固定的情况下,当锚杆受到拉拔荷载时,锚杆的锚固长度存在一个临界值(即临界锚固长度[19]),超过这个临界值后,锚杆的承载力将不会随锚固长度的增加而增大。
2.4 杆-浆界面剪应力分布特征
在试验过程中无法直接获得杆-浆界面剪应力,为了研究抗浮锚杆在荷载作用下的杆-浆界面剪应力分布规律,利用式(1)将锚杆杆体轴力转化为杆-浆界面的平均剪应力,得到杆-浆界面剪应力随深度变化曲线如图7所示。
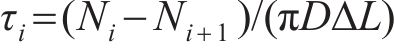
式中:Ni为锚杆上i点处的轴力;τi为杆体i与i+1间中点处的剪应力;D为锚杆杆体的直径,D= 25 mm;
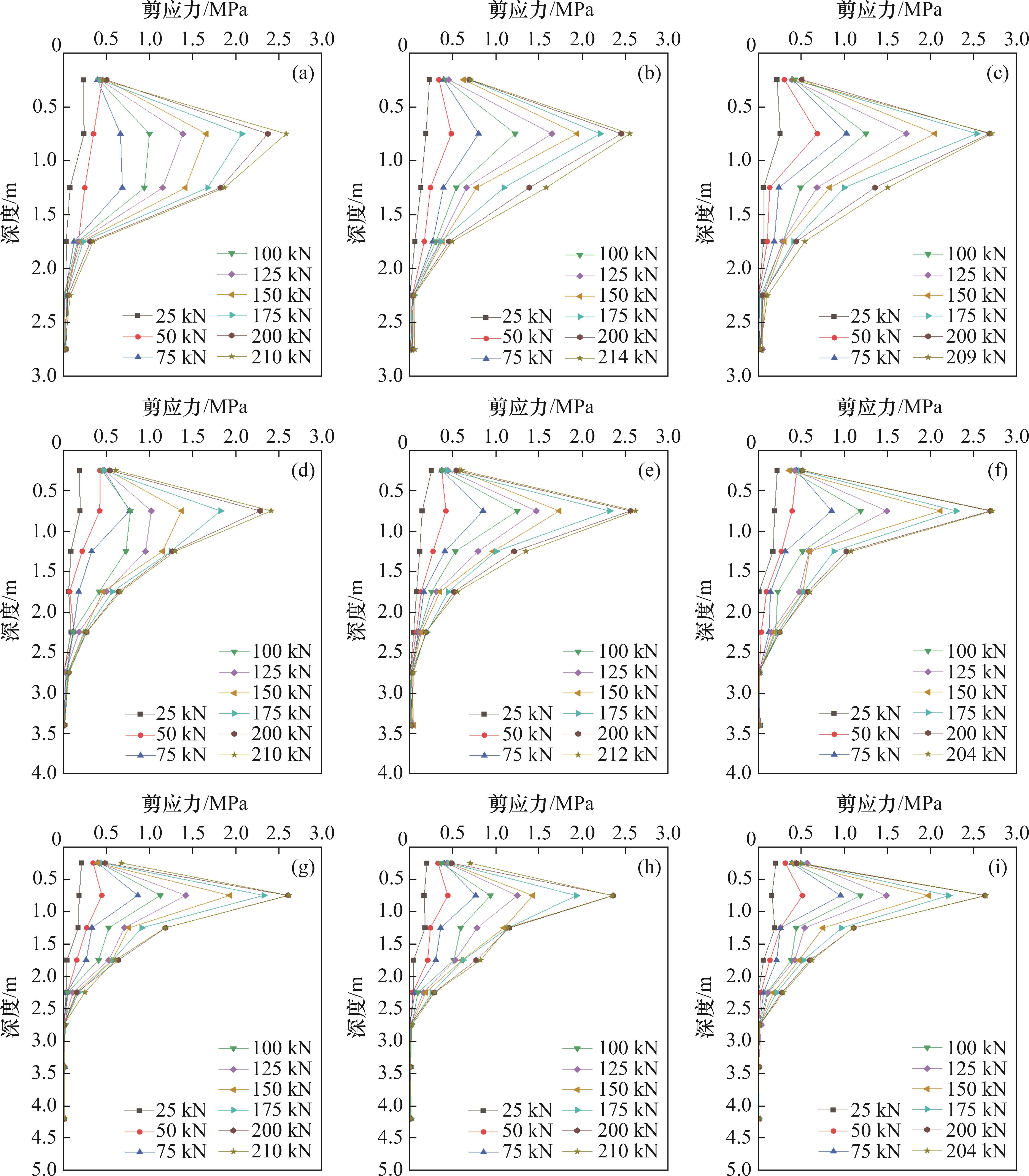
由图7可见:杆-浆界面剪应力在孔口处从0 MPa迅速增加到最大值(约为2.6 MPa),而后又迅速减小,在达到一定深度(2.75 m)时趋向于0 MPa;杆-浆界面最大剪应力出现在深度0.75 m处,随着荷载量的增加,剪应力峰值逐渐增大,作用的范围也随之加大,而锚杆的锚固长度对杆-浆界面剪应力产生的影响较小;对同一深度处锚杆杆体而言,随着荷载量的增加,锚杆杆体应力整体呈现增大趋势,存在部分减小现象,这可能是施工过程中砂浆强度不均匀导致;在锚杆杆体处于低应力状态(轴力<50 kN)时,部分杆-浆界面剪应力最大值出现在距孔口0.25 m处,其原因是荷载较小,沿深度方向传递的距离较小;对于抗浮锚杆而言,当杆-浆界面剪应力超过杆体材料本身的抗剪强度或杆-浆界面抗剪强度时,锚杆或杆-浆界面发生剪切破坏,表现为锚杆存在拔断破坏或拔出破坏。
对比所有试验锚杆杆-浆界面的剪应力,发现其作用的深度达到2.75 m左右时,主要作用在距孔口2.25 m范围内。对比不同锚固长度的试验锚杆发现,杆-浆界面剪应力的传递深度几乎不变,说明在杆体长度2.75 m以下的部分几乎不发挥作用,该结果与锚杆轴力分析的结果一致,进一步验证了在本试验条件下,抗浮锚杆的实际锚固长度超过其临界锚固长度,这与李国维等[20]的研究结果一致。
由图7(a)、7(c)和7(i)可见:在锚固深度0.25 m处,杆-浆界面剪应力出现先增大后减小的现象;锚杆Z1-1、Z1-3在200 kN荷载作用下剪应力最大,而锚杆Z3-3在125 kN荷载作用下剪应力最大,说明这3根试验锚杆在荷载作用下,浅层岩土层杆-浆界面出现不同程度的破坏,其中,锚杆Z3-3破坏程度最为严重,在150 kN荷载作用下锚杆发生破坏,且随着荷载的增加,杆-浆界面的破坏逐渐向深处发展,其余试验锚杆的杆-浆界面均未发展到锚固深度0.25 m处。
3 锚固机制分析
抗浮锚杆作为永久性地下抗浮结构,需要进行合理设计以确保建筑结构的安全。为了明确抗浮锚杆的承载机制,从细观角度分析荷载作用下杆-浆界面、浆-岩界面的变化。内锚固段锚杆与灌浆体之间的锚固作用主要由承载阻力(因本试验采用带肋锚筋,故又称承载阻力为机械咬合力)提供,化学黏结和摩擦阻力也起一定的作用[5]。
当地下水位产生浮动变化时,基础底板受浮力作用产生上浮现象,此时,抗浮锚杆开始工作,通过外锚固段并通过锚杆杆体将荷载传递至灌浆体,随后传递至岩土体,最终在各组成部分协同作用下,实现抗浮体系的稳定,由试验结果可知,抗浮锚杆内锚固段浅层承担大部分荷载。当地下水浮力作用较小时,杆-浆界面、浆-岩界面间的化学黏结作用和摩擦阻力起主要作用。随着地下水浮力作用增大,锚杆杆体所传递的荷载也随之增加,锚杆杆体与灌浆体之间产生相对错动的现象,此时,锚杆杆体与灌浆体之间的机械咬合力发挥作用(如图8(a)所示),阻止杆体向上位移。当地下水浮力作用继续增加时,表层灌浆体产生裂隙,并逐渐向深处发展,内锚固段浅层杆-浆界面的灌浆体在剪切作用下产生不同程度的破碎(如图 8(b)所示),锚杆杆体和灌浆体产生相对位移,此时,浅层灌浆体的劈裂阻力承担部分荷载,其余荷载将通过锚杆杆体向锚固深处传递。随着地下水浮力的不断增加,抗浮锚杆内锚固段深层重复发生以上3个过程,直至抗浮锚杆发生破坏,锚杆内锚固段的荷载传递方式如图8所示,其中,F为抗浮锚杆所受的荷载,τ1、τ2分别为杆-浆界面、浆-岩界面的作用力。
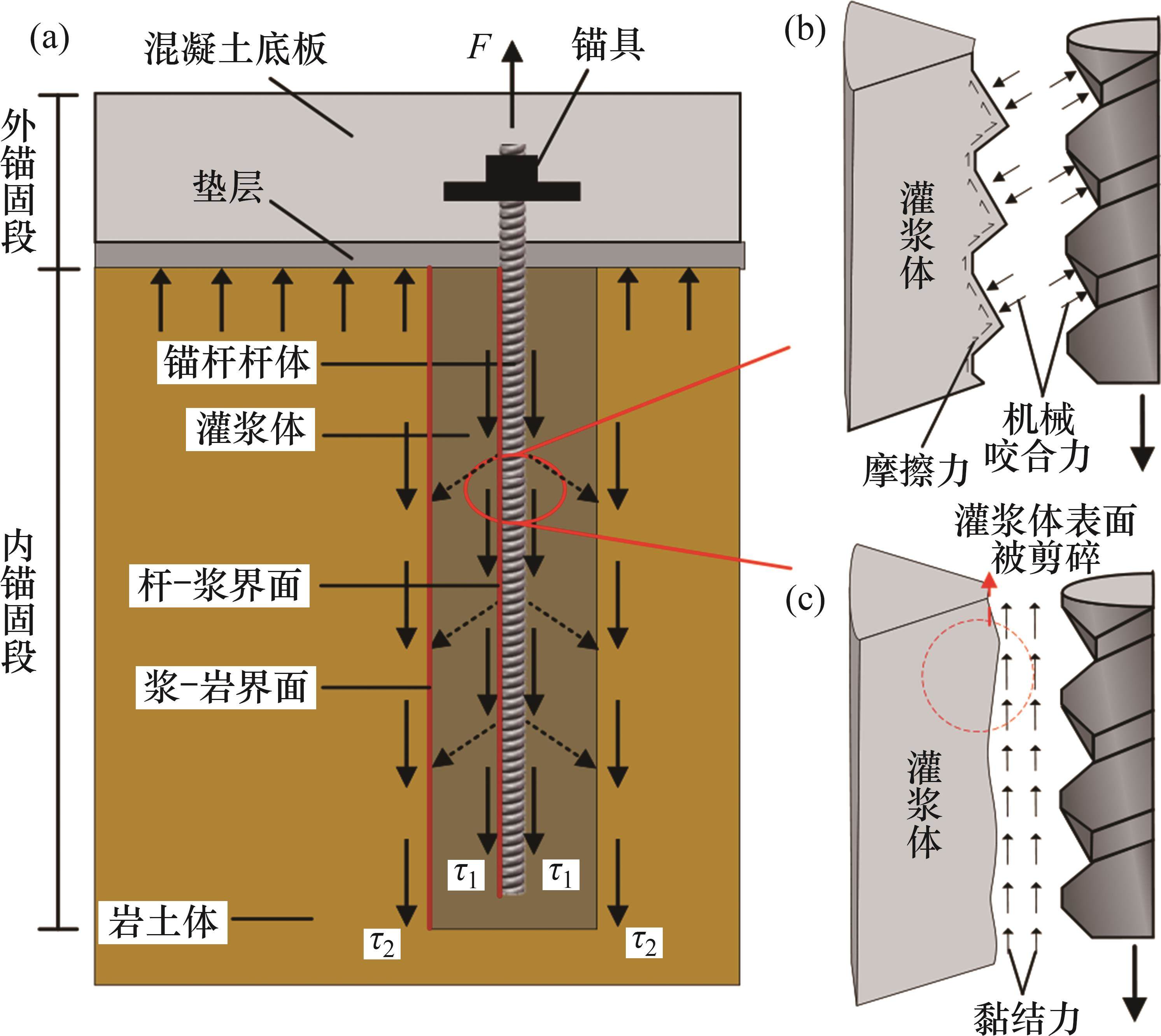
在试验中,岩土体强度较高,而锚杆杆体与灌浆体的强度存在明显差异,抗浮锚杆的杆-浆界面作用较明显。在基础底板受到浮力作用初期,锚杆所受荷载较小,锚固力主要由化学黏结作用和摩擦阻力提供;随着浮力作用增加,抗浮锚杆承担的荷载逐渐增大,浅层锚杆与灌浆体之间的机械合力开始发挥作用,如图8(a)所示;随着浮力进一步增大,浅层灌浆体表面被剪碎,如图8(b)所示,锚杆杆体与灌浆体发生相对位移,深层锚杆与灌浆体之间的机械咬合力开始发挥作用,锚杆杆体与灌浆体产生相对位移。如此往复,直至整个锚固长度内杆-浆界面的灌浆体表面被完全破坏,锚杆即发生拔出破坏。如果在此过程中锚杆受力达到材料的极限抗拔承载力,那么会发生拔断破坏。根据学者的研究及本试验结果可知:抗浮锚杆内锚固段主要发生拔断破坏,很少发生滑移破坏,这与锚筋抗剪强度高有一定关系。
4 基于Hoek-Brown准则的临界锚固长度计算
4.1 Hoek-Brown岩石破坏准则
HOEK和BROWN通过对大量的室内岩石试验及现场岩体研究,提出了可以反映岩石破坏时极限主应力间的非线性经验公式[21],经过不断地改进,使其可同时应用于岩石和岩体,被称为广义H-B岩体强度准则,其表达式为
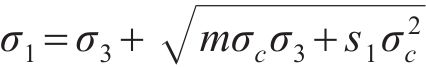
式中:σ1、σ3分别为岩体所受的最大、最小压应力,MPa;σc为完整岩体(即岩块)的饱和单轴抗压强度,MPa;m为反映岩石的软硬程度指标,其取值范围为0.001~25.000;s1为反映岩体破碎程度的指标,其取值范围为0~1.0。对于完整的岩体(即岩石),s1为1.0。参数m、s1可由岩体质量和经验常数之间关系查取[21],本试验条件下,结合工程地质情况,取m为23,s1为1.0。
当计算岩石地基中抗浮锚杆的极限抗拔承载力时,仅存在竖直向上的上拔力,即σ1=0,σ3=-σt(σt为岩体饱和单轴抗拉强度),岩石的饱和单轴抗压强度与岩体的抗拉强度关系为
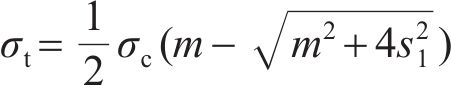
4.2 临界锚固长度计算
由于本试验锚杆安放在中风化片麻岩中,基于Hoek-Brown岩石破坏准则,根据极限平衡原理,提出锚杆抗拔承载力计算模型如图9所示。根据ASEM等[22]的研究成果,锚杆在拉拔荷载下,不同强度的岩石破坏体的圆锥角在60°~120°内,岩体破坏面与水平面的夹角α为30°~60°。为保证公式推导的可靠性,α取较大值,假设岩体破坏面与水平面间的夹角α=30°+φ/3(φ为岩石内摩擦角)。由图9可见:岩石锚杆的极限抗拔承载力一部分由倒锥形破坏体的重力W提供,一部分由岩体的抗力R提供,还有一部分由H-h段第二界面的黏结力F提供。
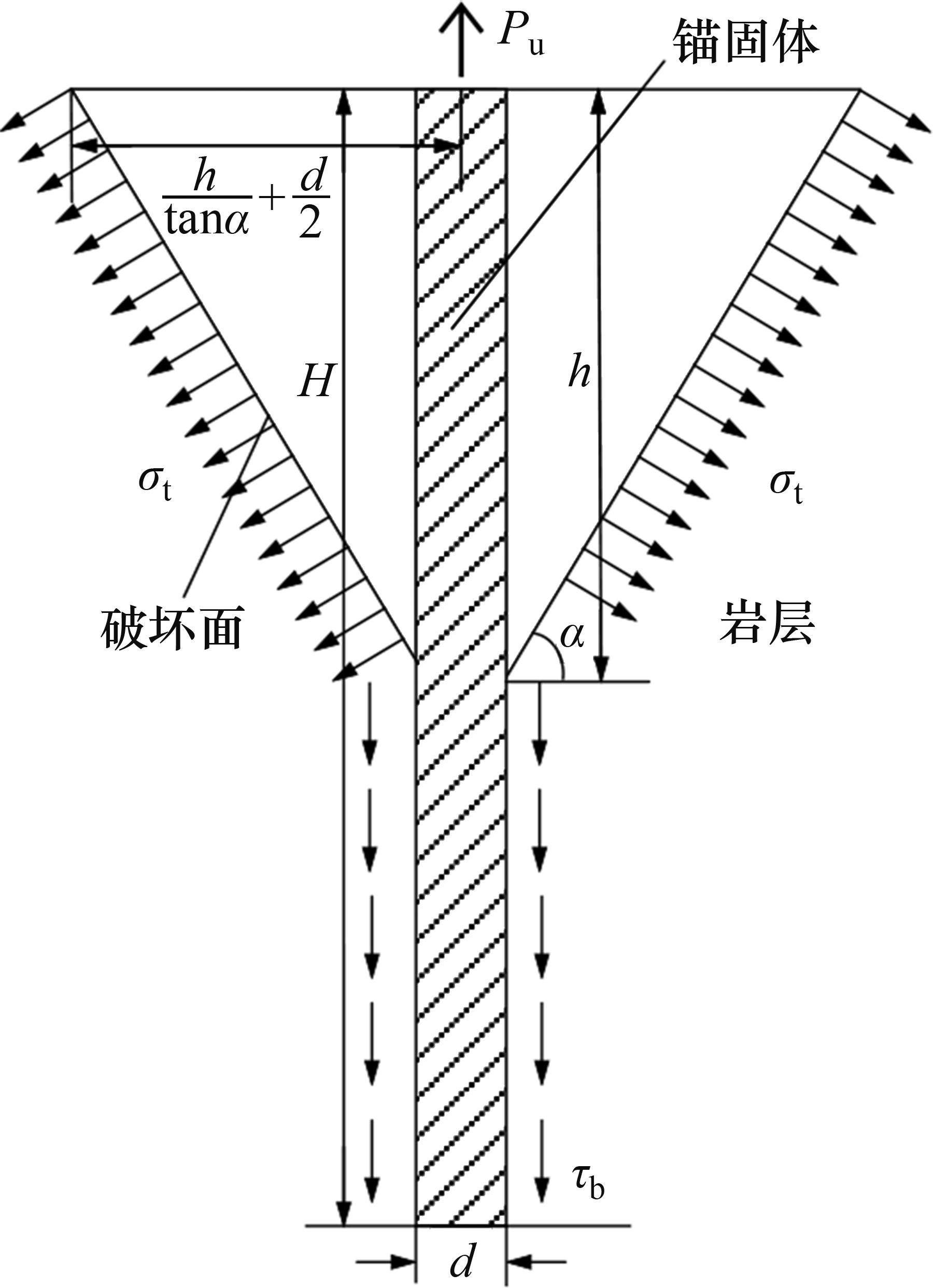
1) 倒锥形破坏体重力。由图9可知,破坏体的重力为倒锥形岩体的重力W,即不考虑锚杆重力的倒锥形破坏体重力W为
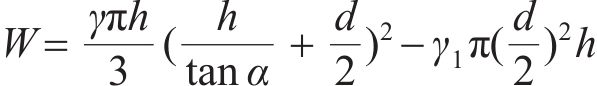
式中:γ为岩体平均重度;γ1为锚杆平均重度,本文取γ1=23 kN/m3;h为计算深度;α为30°+φ/3;d为锚孔直径。
2) 岩体所提供的承载力。由图9可知,岩体所提供的承载力为
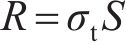
式中:S为岩体中破坏体的侧面积;σt为岩体饱和单轴抗拉强度。根据图9中的几何关系可得侧面积S为
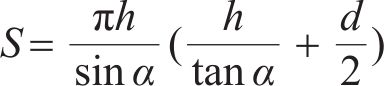
联立式(5)、式(6),并进行力的分解得到岩体竖直方向的抗力Rv为
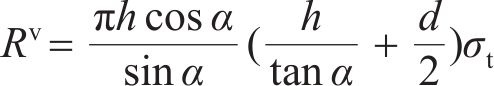
3) H-h段浆-岩界面的黏结力。由图9可得H-h段浆-岩界面的黏结力F为
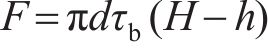
式中:τb为锚杆浆-岩界面处的黏结强度;H为锚固深度。
为保证计算结果的准确性,结合试验结果和白晓宇等[16]的研究结果,并确保计算模型更贴近实际工程情况,锚杆杆体的轴力主要集中在杆体前1/3处,即h=1/3H。
根据图9中受力关系,由静力平衡原理得到岩石抗浮锚杆的极限抗拔承载力为
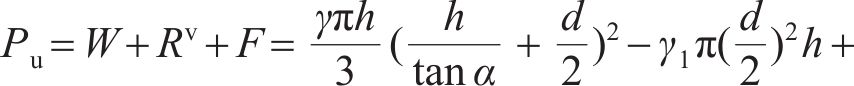
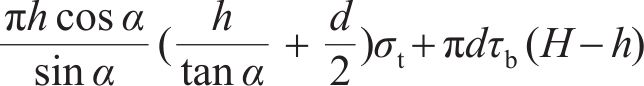
将抗浮锚杆的极限抗拔承载力200 kN代入 式(9),得到抗浮锚杆的临界锚固长度为2.78 m,与应变传感器的测试结果基本吻合,并进一步证明本试验条件下抗浮锚杆的锚固长度超过了试验条件下的临界锚固长度(2.78 m)。
5 讨论
为进一步验证式(9)在岩性地层中的实用性,选取中风化花岗岩地层中抗浮锚杆现场试验结果[23-25],结合抗浮锚杆破坏形态及试验结果进行综合分析。试验场地的岩石属性及试验锚杆参数如表3所示,抗浮锚杆临界锚固长度计算值如表4所示。
| 锚杆编号 | 锚杆极限承载力实际值/kN | 破坏形态 | 锚固长度计算值/m |
|---|---|---|---|
| a | 325 | 杆-浆界面剪切破坏 | 3.05 |
| b | 362 | 锚筋拔断破坏 | 3.33 |
| c | 372 | 锚筋拔断破坏 | 2.48 |
| d | 395 | 锚筋拔断破坏 | 3.21 |
由表4可见:锚杆a、b由于锚固深度的差异,抗浮锚杆的破坏形式也发生改变,说明抗浮锚杆的临界锚固长度介于3.0~4.5 m之间,由锚杆b求得的锚杆锚固长度为3.33 m,即为此试验下的抗浮锚杆临界锚固长度,且此长度与锚筋的杆-浆界面剪应力分布图中剪应力传递深度极其吻合。此外,由锚杆a所求得锚杆锚固长度为3.05 m,误差仅为1.7%,进一步证明了式(9)的准确性。由锚杆c、d所求得锚固长度与试验锚杆的轴力传递深度相近,说明式(9)对GFRP抗浮锚杆也具有较强的适用性。
6 结论
1) 抗浮锚杆主要发生锚杆杆体屈服破坏,且不同锚固长度的试验锚杆,其极限抗拔承载力无明显变化,在此试验条件下,锚杆的实际锚固长度超过其临界锚固长度。
2) 抗浮锚杆杆体与灌浆体的荷载-位移曲线均为缓变-陡升形,曲线均存在明显拐点,分别在抗浮锚杆极限承载力的75%、60%处,且拐点的位置与抗浮锚杆的锚固长度无关。抗浮锚杆灌浆体在曲线拐点处出现开裂现象。
3) 抗浮锚杆杆体轴力沿深度方向呈衰减状态传递,随深度的增加,轴力的衰减速度逐渐减小,轴力主要作用在距孔口深度2 m范围内,最大传递至深度2.5 m处。同一深度处锚杆轴力随荷载增加而增加,随深度增加轴力增幅逐渐减小,且在本试验条件下,锚杆杆体的轴力与锚固长度相关性较小。
4) 试验杆-浆界面剪应力呈现先快速增加而后减小的分布规律,剪应力峰值出现在锚固深度0.75 m处,且随锚固深度的增加,剪应力的减小速度逐渐降低,剪应力主要作用在距孔口深度2.25 m的范围内,最深传递至深度2.75 m处。
5) 根据Hoek-Brown岩石破坏准则,对本试验条件下的锚杆的临界锚固长度进行预测,在预留一定安全储备的前提下,计算模型所得的临界锚固长度为2.78 m,与现场应变传感器的测试结果相吻合。
闫楠, 孙淦, 白晓宇, 等. 嵌岩抗浮锚杆承载性能现场试验与机理分析[J]. 中南大学学报(自然科学版), 2025, 56(2): 730-743.
YAN Nan, SUN Gan, BAI Xiaoyu, et al. Field test and mechanism analysis of bearing capacity of rock-socketed anti-floating anchor[J]. Journal of Central South University(Science and Technology), 2025, 56(2): 730-743.

