随着我国交通建设不断向中西部推进,一大批软岩工程不断涌现。深部软岩具有复杂的力学特性和流变行为,其所引起的软岩大变形问题突出[1],研究深部软岩隧洞长期变形对于保障隧洞的安全施工具有重要意义。
围岩长期的蠕变变形由岩石流变本构关系描述。针对不同因素影响下的岩石蠕变特性,研究者基于大量试验提出了不同本构模型[2-4]。其中一种常见的模型是通过将Hooke体、Kelvin体、Maxwell体和黏塑性体元件进行全部或部分串联,构建出黏弹-黏塑性流变模型,该模型能有效描述深部岩体的蠕变特性[5-7],HUANG等[8]在该模型基础上考虑了开挖损伤和孔隙水压的影响。此外,为描述岩体加速蠕变阶段的非线性特征,周宏伟等[9]提出了基于分数阶理论的Abel黏壶元件,LIU等[10-13]在这基础上建立了众多非线性流变模型。尽管改良流变本构模型可以很好地模拟和预测岩体蠕变行为,但多数研究的运用对象为工程岩样,并不能直接进行隧洞变形预测。
隧洞变形的解析方法是变形预测的重要手段,计算应同时考虑蠕变变形和塑性变形的影响。经典的弹塑性解析仅考虑围岩破坏后的塑性变形,能得到不同空间坐标处的位移,但不能计算与时间相关的长期位移,为考虑蠕变变形,可将流变模型与弹塑性解析方法相结合,得到隧洞位移的时空解答。研究者对隧洞长期变形的解析计算进行了一些研究。TRAN等[14]基于Bugers模型和Mohr-Coulomb(M-C)准则,求解了蠕变影响的隧洞变形;ZHANG等[15]基于分数阶黏塑性流变模型和Hoek-Brown(H-B)准则,得到了分数阶变形解析解;LIU等[16]考虑湿度损伤和施工过程中的应力释放,讨论了支护和时间对变形的影响;夏才初等[17]基于经典西原模型和M-C准则,通过拉氏变换得到了黏弹-黏塑性解析解。
综上所述,当前已有研究基于不同流变本构和强度理论建立了隧洞长期变形解析。但由试验及理论研究可知,在深部软岩隧洞中,岩体破坏后有明显的应变软化行为[18-21],强度从峰值不断衰减至残余值。现有围岩流变解析研究较少考虑围岩在塑性破坏后的软化特性,并且在强度理论方面,现有解主要基于M-C准则、H-B准则等二维模型得到,不能反映深部岩体所处的三维应力状态[22]。ZHANG等[23-24]建立了考虑中间主应力的GZZ准则,CAI等[25]提出了非凸性改良后的光滑GZZ准则,三维准则在深部岩体中有较好适用性。
本文针对深部软岩隧洞长期变形解析问题,基于非线性黏弹-黏塑损伤流变模型和光滑GZZ准则,采用分数阶理论对流变模型进行非线性处理,考虑深部软岩的应变软化特性和中间主应力效应,建立软岩隧洞长期变形的有限差分计算方法,对比已有的解析研究和实际工程应用结果,验证该方法的正确性,分析蠕变特性对隧洞变形的影响,讨论不同参数对该解的敏感性。研究成果可为流变特性下的深部软岩隧洞变形预测提供理论参考。
1 软岩隧洞长期变形计算模型
1.1 力学模型及基本假定
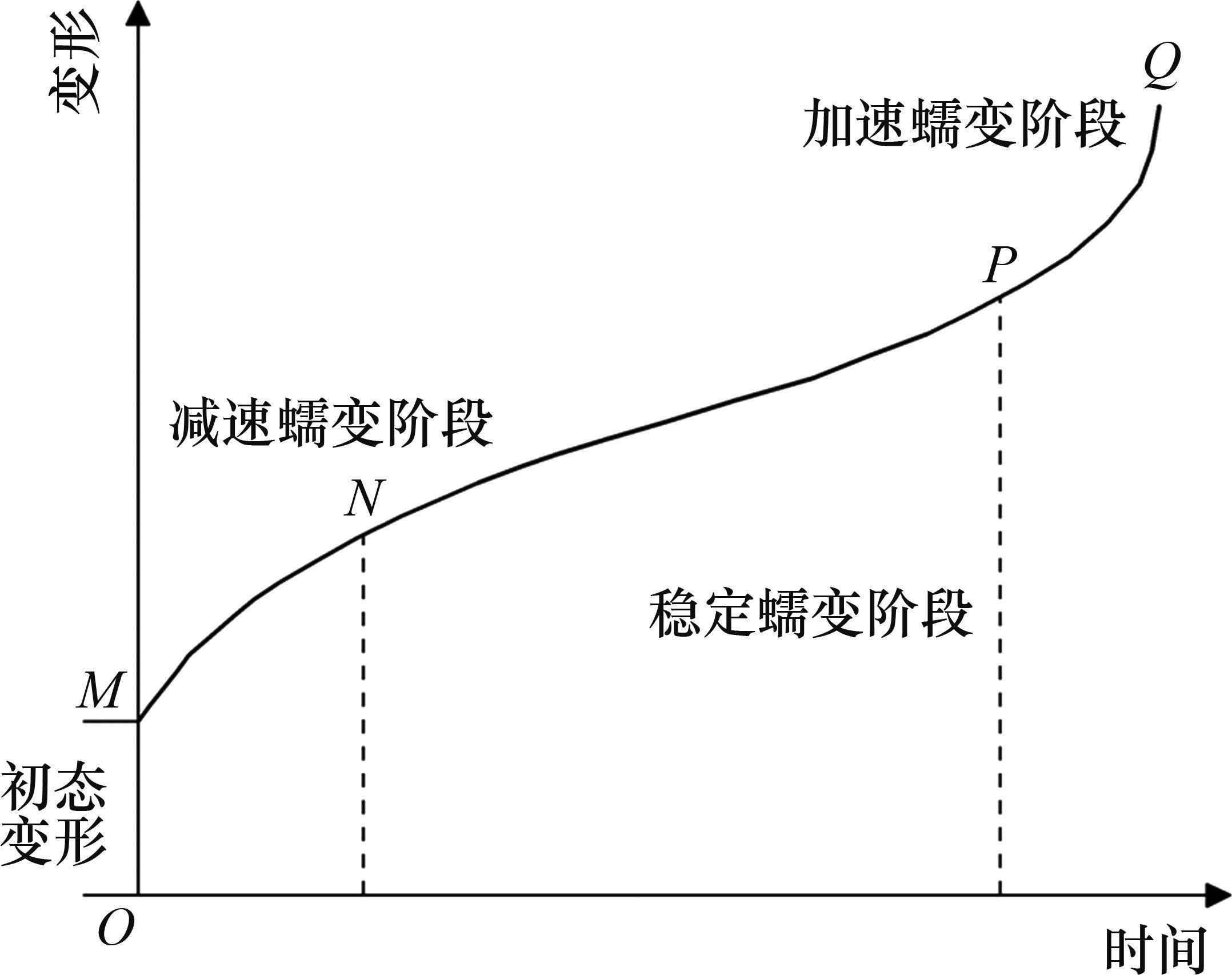
图1所示为软岩的蠕变曲线图,原点处于初始时刻,此时发生初态变形,随后围岩经历减速蠕变、稳定蠕变和加速蠕变共3个阶段。在初始时刻,隧洞开挖导致围岩应力重分布。假设应力变化和弹塑性变形是以弹塑性波的速度传递,在开挖成洞瞬间,围岩的应力变化和变形已经全部完成,形成初态应力场和初态变形,此时,围岩仅发生了瞬时弹塑性变形,未发生随时间积累的蠕变变形。若围岩变形只与半径r和时间t两个变量有关,则初始时刻的弹塑性变形仅与半径有关,蠕变变形与半径和时间均有关。
初态变形的求解可看作是平面应变问题下的弹塑性解析。围岩在洞内岩体被清除后存在应力集中现象,当应力超过临界应力时产生塑性屈服,在洞周形成黏塑性区。本文采用应变软化模型进行分析。隧洞力学模型如图2所示。黏塑性区被分为软化区和残余区,从软化区过渡到残余区的过程中,围岩质量参数从峰值降至残余值。图2中,r为极坐标半径,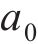
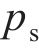
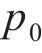
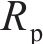
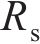
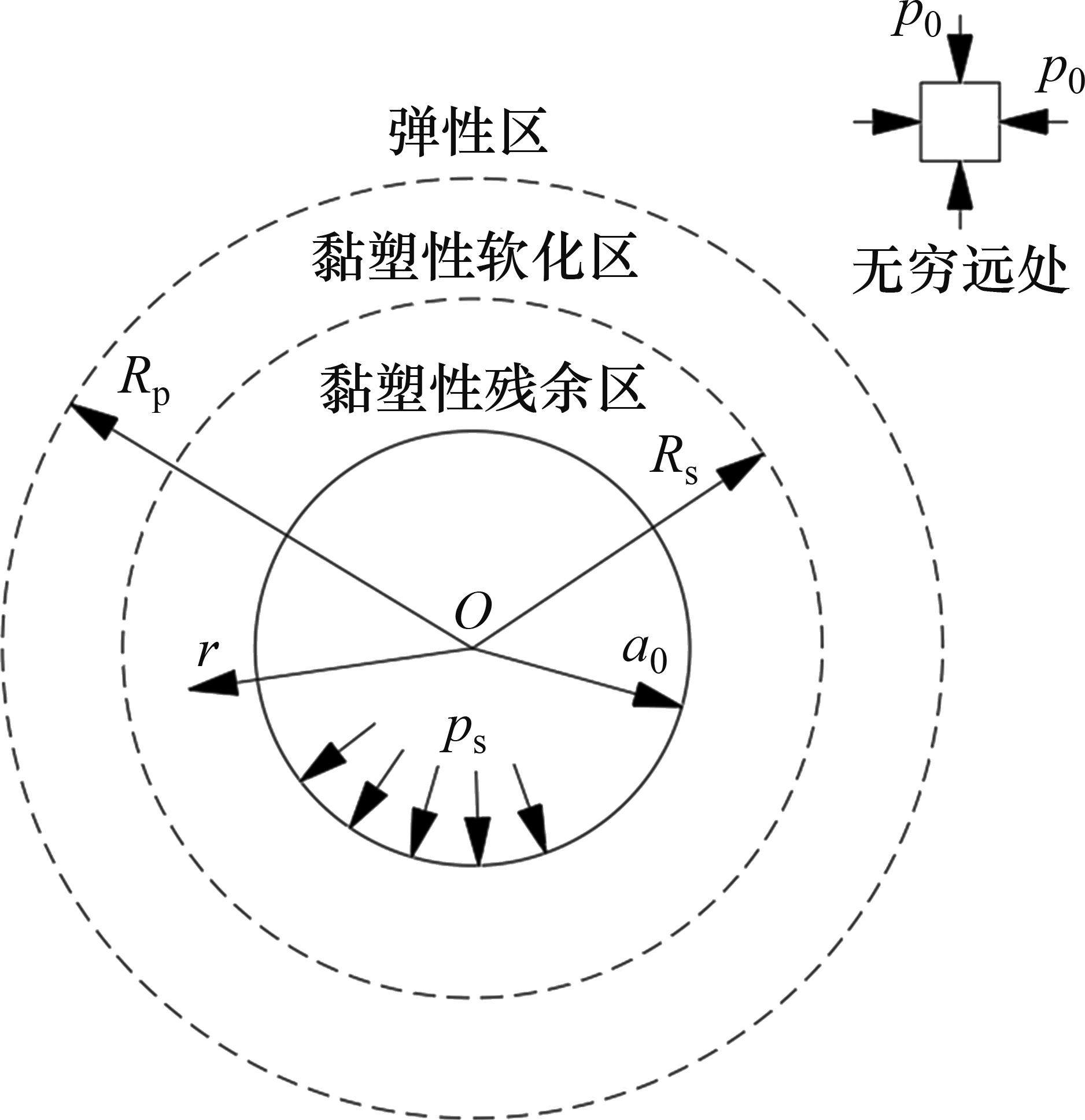
围岩发生蠕变变形后,用流变模型表征岩体的3阶段蠕变力学特征。基于HUANG等[8]建立的黏弹-黏塑性损伤流变模型,串联Kelvin体、考虑损伤的Maxwell体和黏塑性体,形成的黏弹-黏塑性流变模型如图3所示。模型包含黏弹和黏塑两部分,当黏塑性体不作用时,即为仅考虑黏弹性的流变模型。在图3中,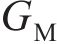
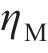
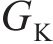
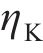
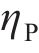
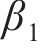
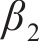
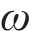
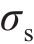
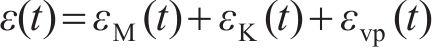
式中: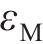
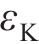
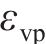
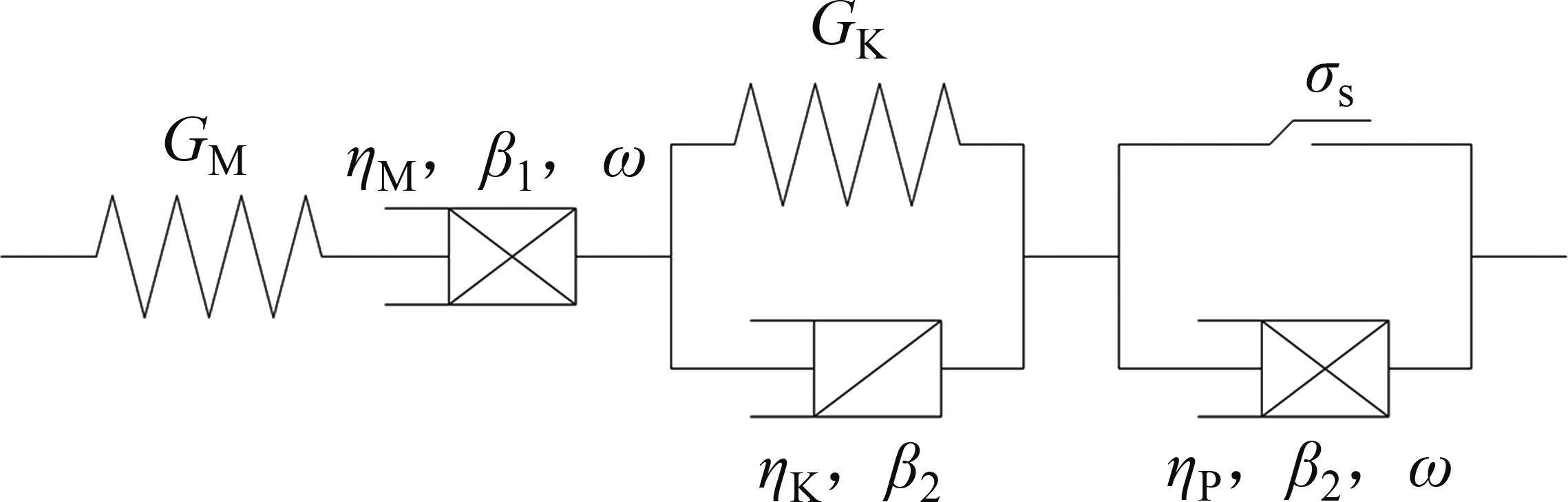
为了推导理论力学模型,进行以下假定:围岩是连续、均匀、各向同性的弹塑性材料;围岩的塑性屈服服从光滑GZZ准则,蠕变行为服从分数阶黏弹-黏塑性模型;隧洞形状为圆形,埋深远大于隧洞半径,轴向长度远大于横截面尺寸,纵向长度围岩岩性不变,可简化为平面应变问题。
1.2 分数阶黏弹-黏塑性损伤模型
岩土材料的流变特性介于理想弹性体和理想流体的流变特性之间,应变随时间非线性增大,分数阶形式的Abel黏壶对蠕变的非线性特征有较为完整的描述[9],其本构表达式为
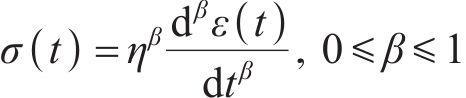
式中: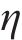
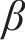
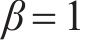
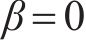
由分数阶积分,Abel黏壶的蠕变方程为
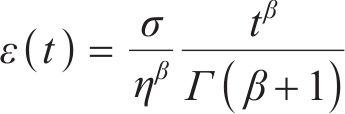
式中: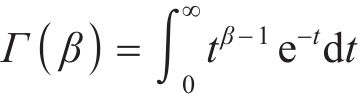
在蠕变过程中,岩体微观裂纹发展导致损伤不断积累,黏性系数不再恒定为常数,需对蠕变方程进行修正,定义蠕变损伤为时间相关函数[8],其表达式为
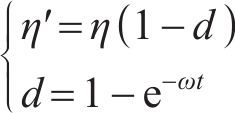
式中: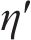
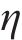
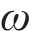
将式(2)中的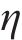
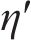
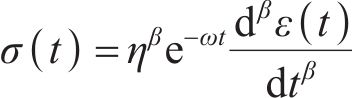
根据分数阶理论,考虑损伤的Abel黏壶蠕变方程为
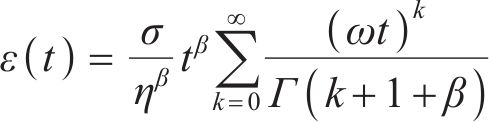
在黏弹-黏塑性模型中,用Abel黏壶替代Newton黏壶,非线性黏弹-黏塑性模型的一维蠕变方程为
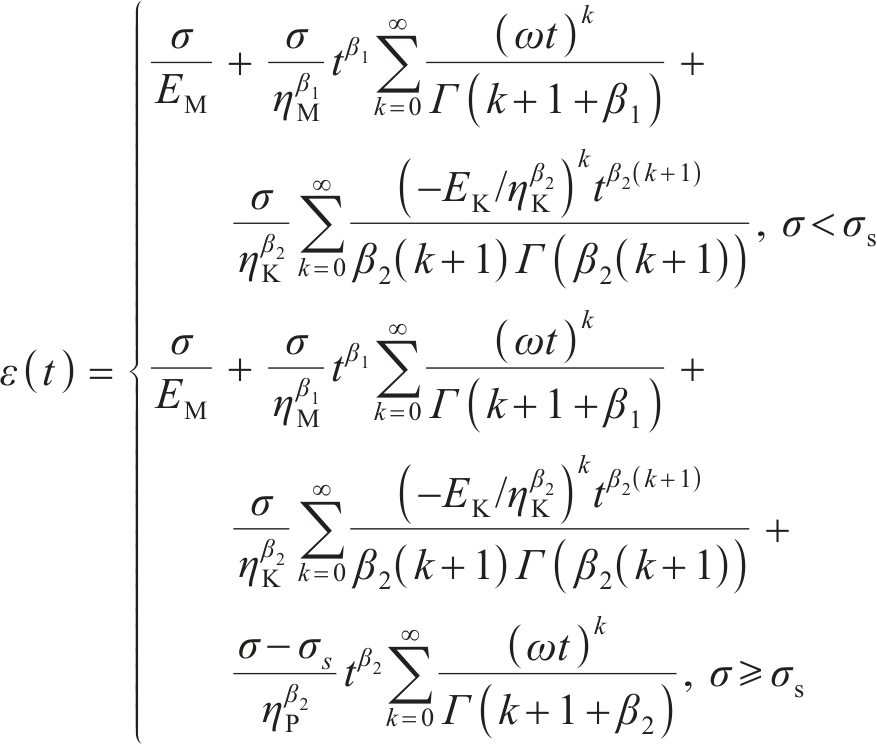
式中: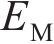
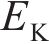
为求三维蠕变方程,引入Von Mises等效塑性应力-应变,用应变率来描述本构关系。应变率张量函数为
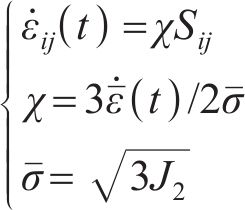
式中: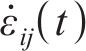
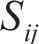
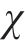
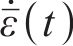
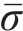
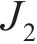
将式(7)中的应力
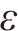
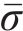
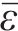
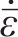
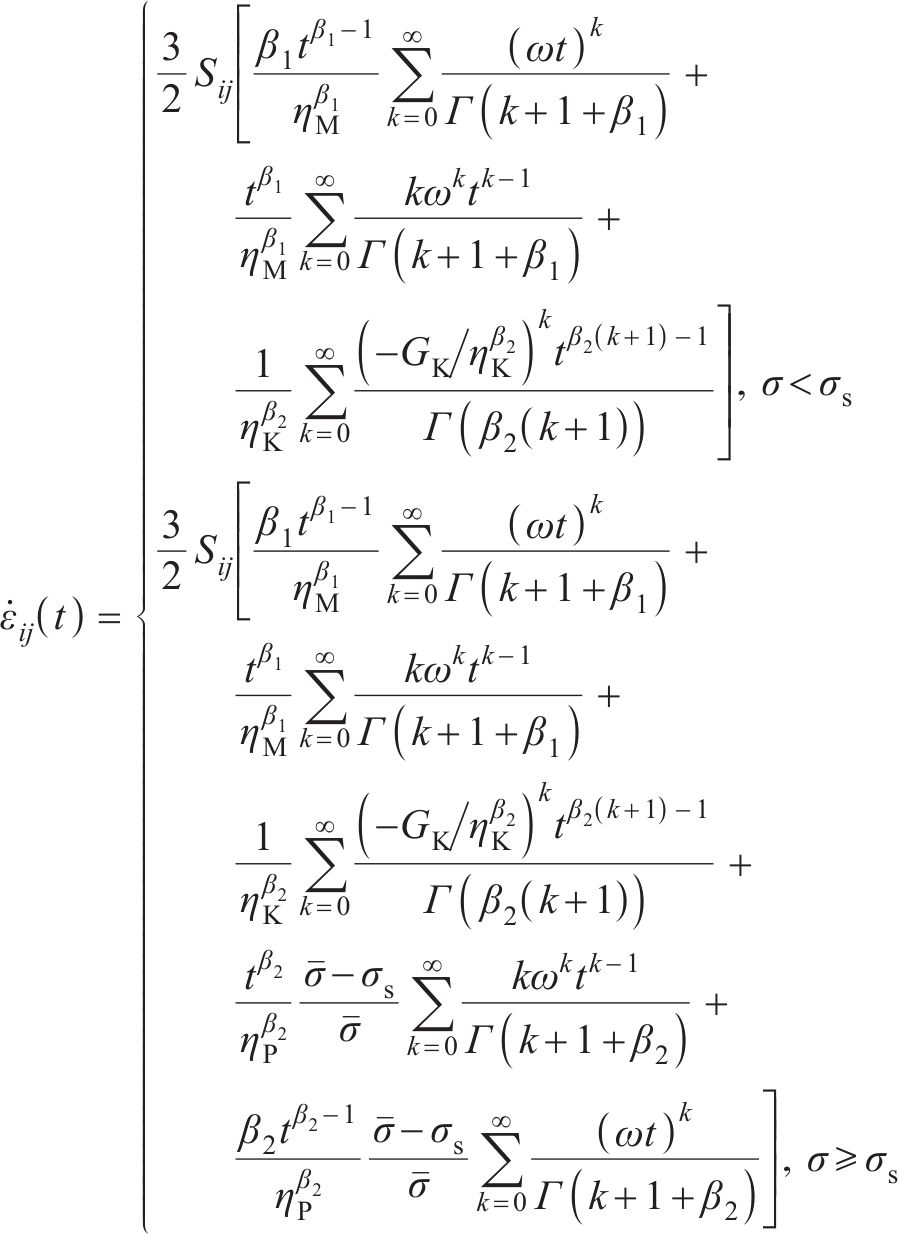
1.3 光滑GZZ强度准则
在三维应力状态下,岩体破坏后的极限应力服从光滑GZZ准则[25],其应力不变量形式的表达式为
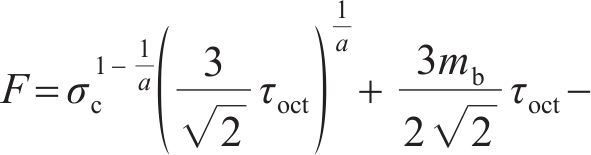
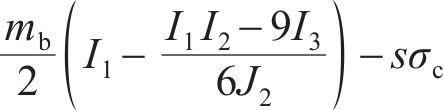
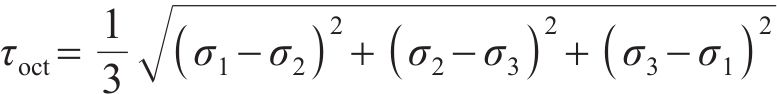
式中: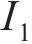
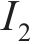
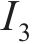
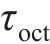
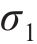
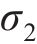
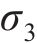
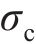
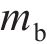
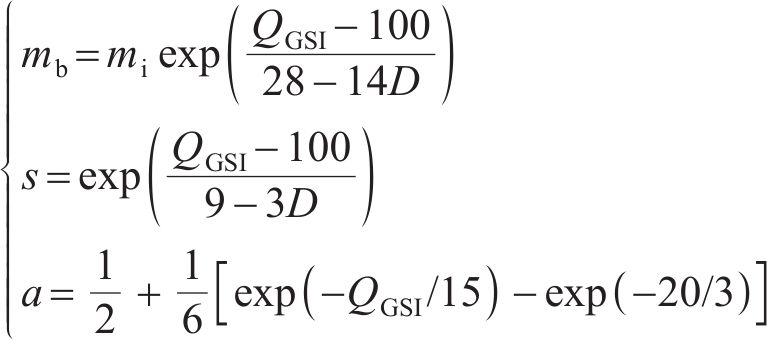
式中: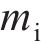

2 长期变形计算过程
2.1 黏弹性区位移
平面应变条件下围岩无剪应力,径向应力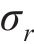
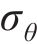
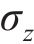
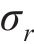
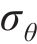
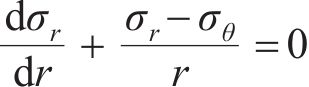
径向应变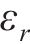
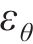
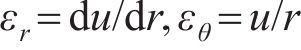
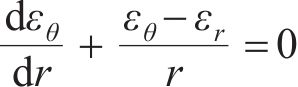
初始时刻只有Maxwell体的弹簧元件产生作用,弹性模量取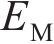
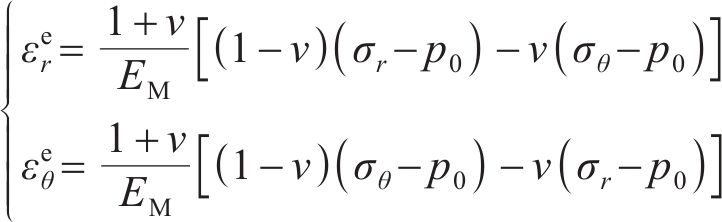
式中: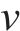
初始时刻黏弹性围岩的初态应力和位移采用经典Lame解答为:
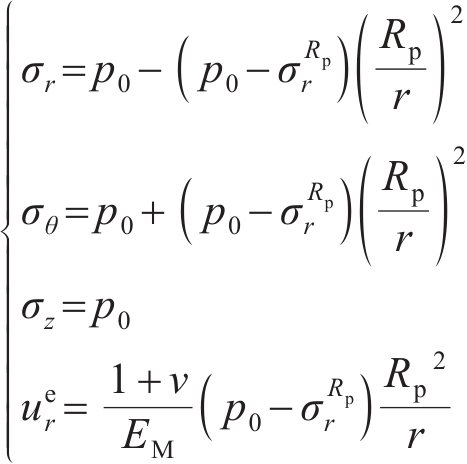
式中: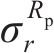
由式(17)可得弹塑性交界面处应力条件为
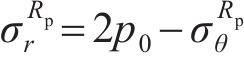
联立式(10)和(18),通过牛顿法求解弹塑性边界径向应力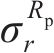
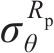
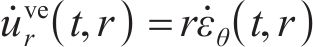
式中: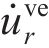
由式(17)可求出偏应力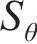
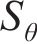
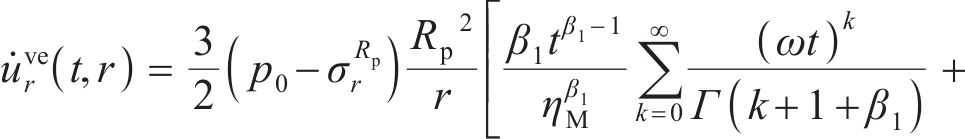
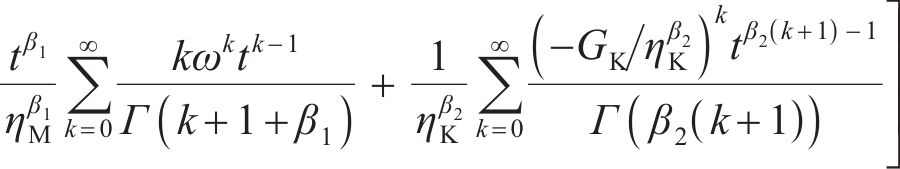
式(17)中的弹性变形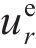
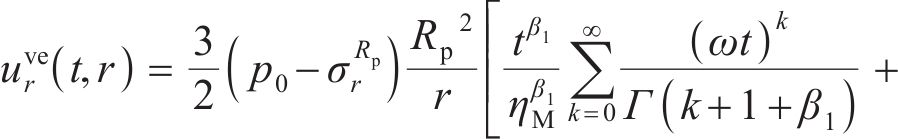
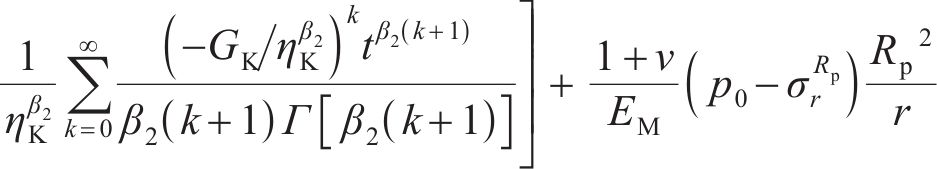
2.2 黏塑性区初态位移
黏塑性区初态应力场由光滑GZZ准则得出,为描述围岩塑性变形中的参数衰减过程,采用有限差分法求出半解析解[27]。将连续的位移函数在空间上离散,每个半径上有对应的初态应力和位移,黏塑性区分环示意图如图4所示。由图4可见:围岩被分成n个不等距的圆环,在计算时,由黏塑性区边界向洞壁处循环求解,第j环内外半径分别为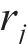
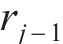
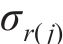
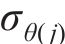
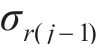
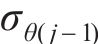
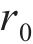
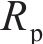
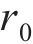
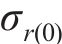
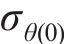
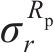
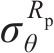
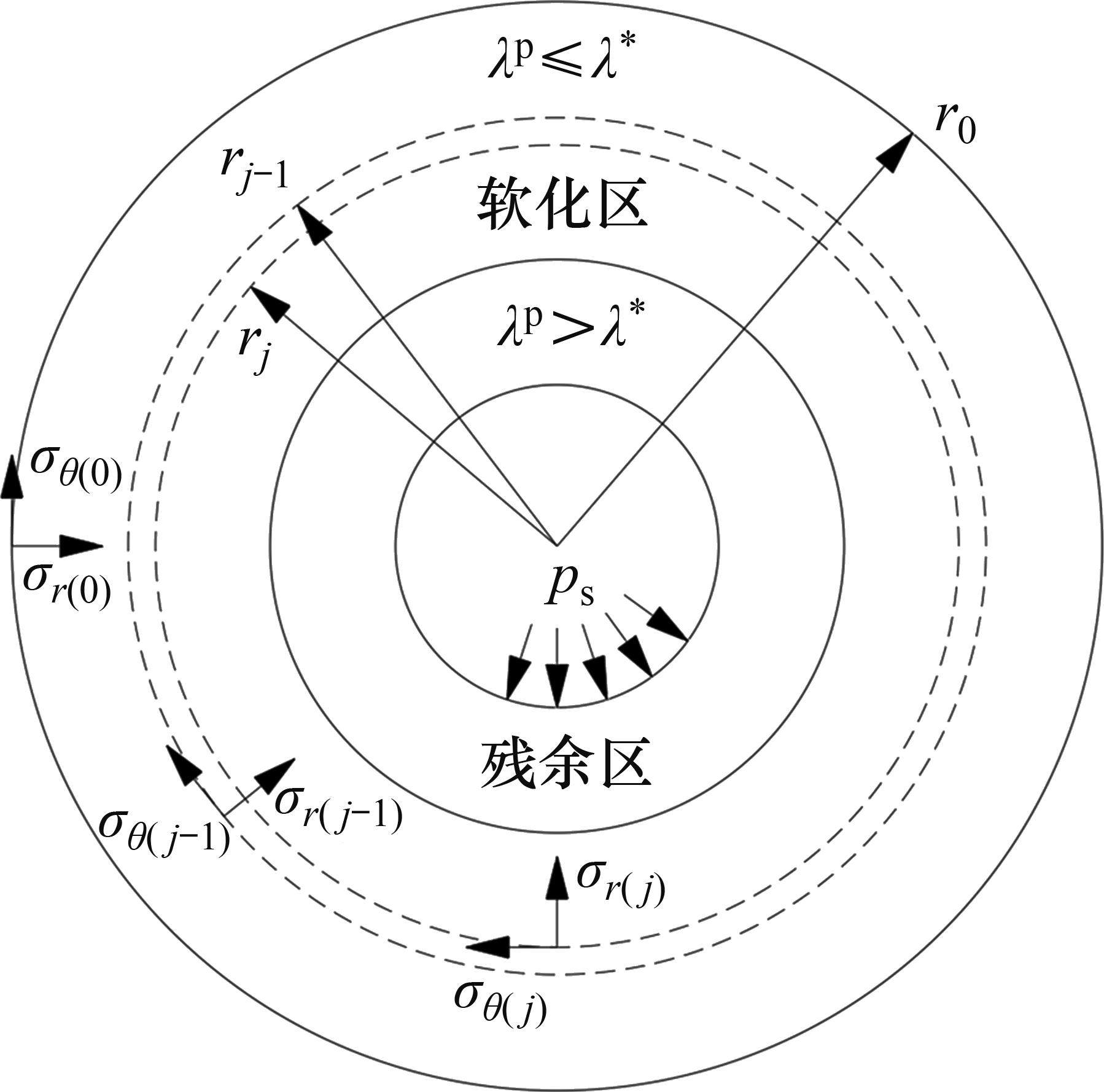
黏塑性区的应变软化行为用
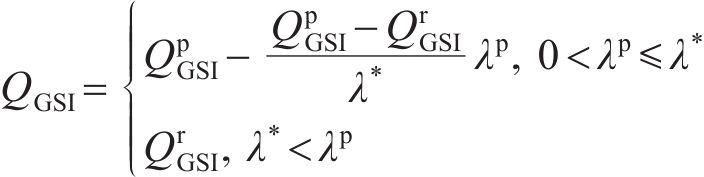
式中: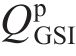
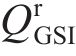
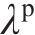
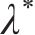
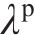
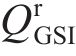
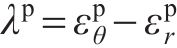
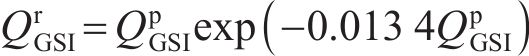
式中: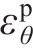
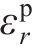
将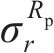
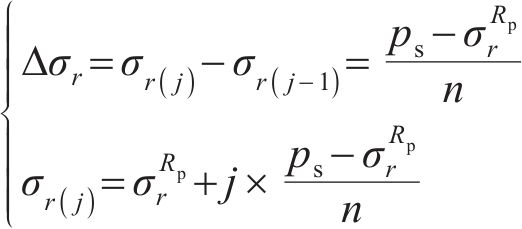
式中: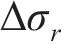
轴向应力表达式为
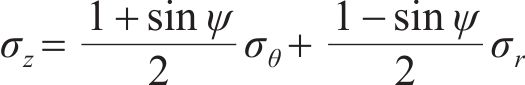
式中: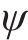
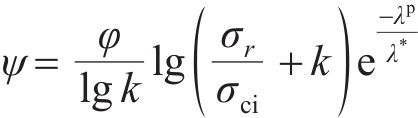
式中:k为围压影响系数,根据CAI等[28]的研究,软岩采用k=0.004 1;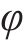
求解第j环环向应力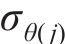
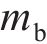
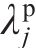
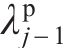
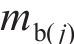
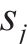
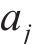
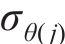
将式(13)写为差分形式,并进行变换可得圆环半径关系为
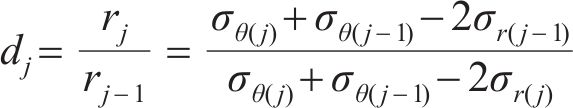
式中: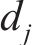
同样地,将式(15)改写成差分形式为
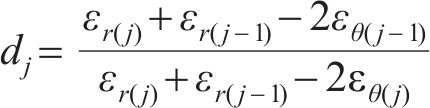
黏塑性区初态应变由弹性和塑性两部分组成,其增量形式为
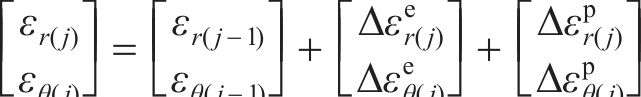
式中: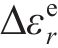
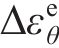
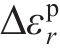
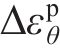
由式(16),弹性应变增量为
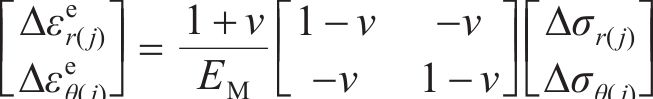
黏塑性区的剪胀行为满足非关联流动法则,其增量形式为
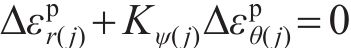
式中: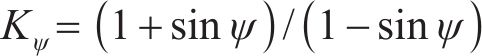
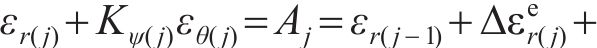
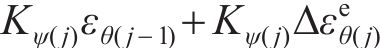
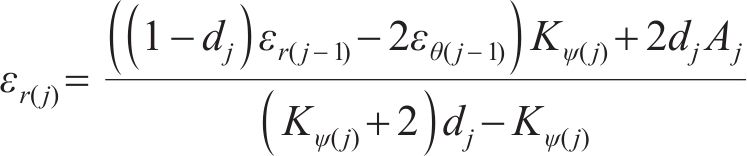
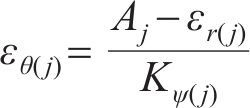
将j环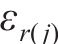
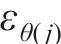
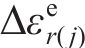
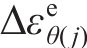
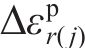
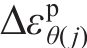
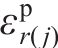
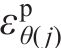
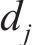
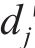
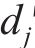
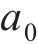
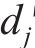
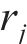
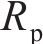
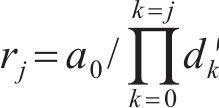
将每环环向应变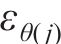
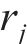
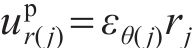
2.3 黏塑性区瞬态位移
黏塑性区围岩蠕变变形与时间和空间两个维度相关,采用与上节相同的有限差分法,将蠕变求解在时间上离散。将时间分为m个固定间隔的时间步,每个时间步有对应的蠕变变形,时间表示为
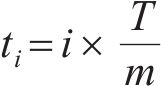
式中:T为目标时长;m为离散时间的数量。
黏塑性区围岩蠕变阶段同样伴随塑性剪胀,服从非关联流动法则,即
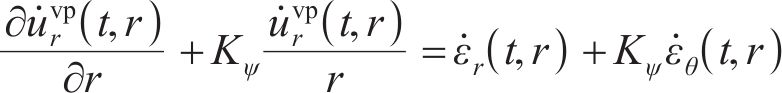
式中: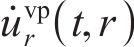
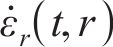
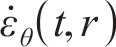
根据初态应力场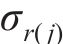
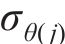
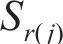
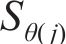
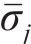
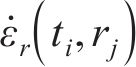
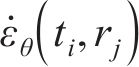
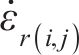
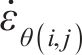
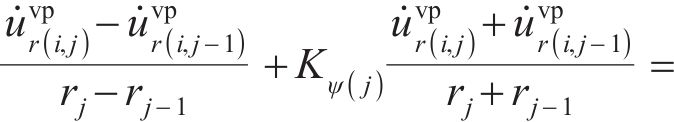
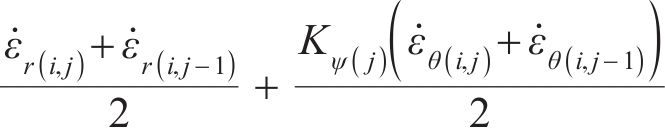
当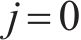
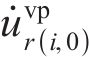
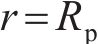
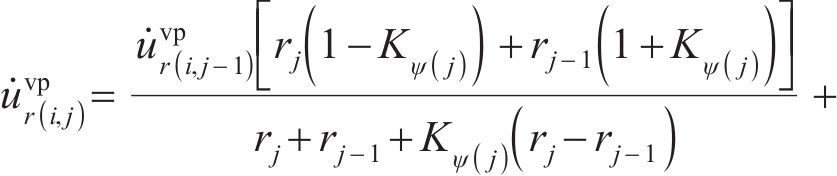
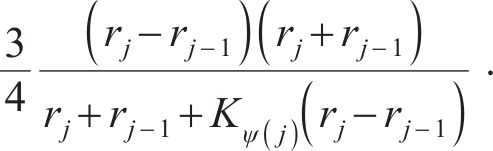
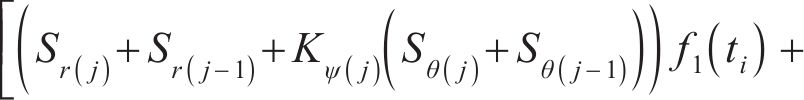
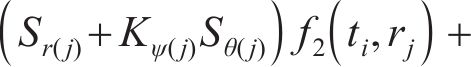
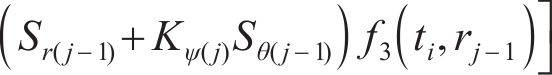
式(41)中的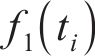
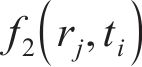
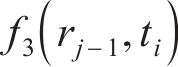
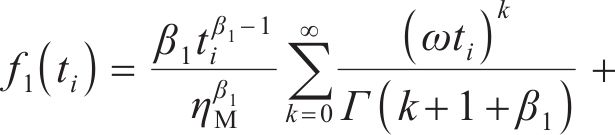
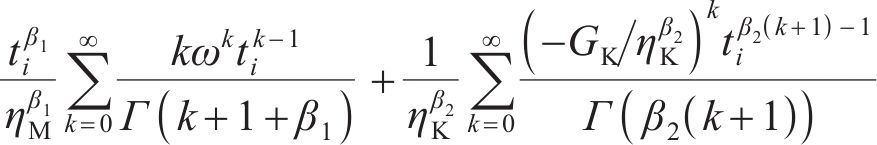
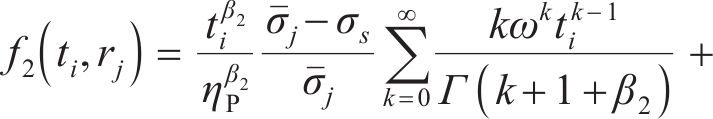
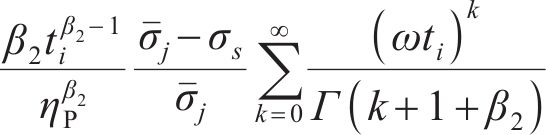
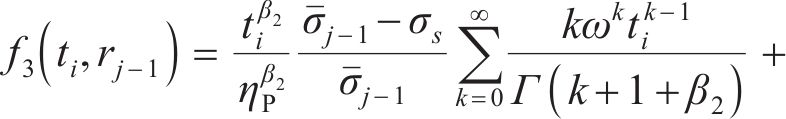
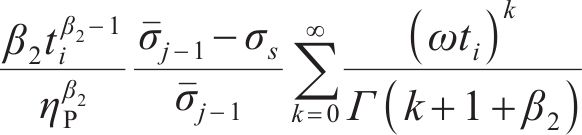
将位移率对时间积分得到黏塑性区位移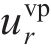
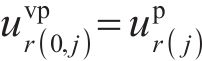
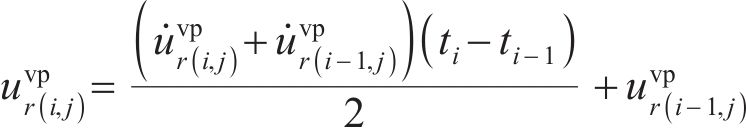
2.4 解析计算的数值实现
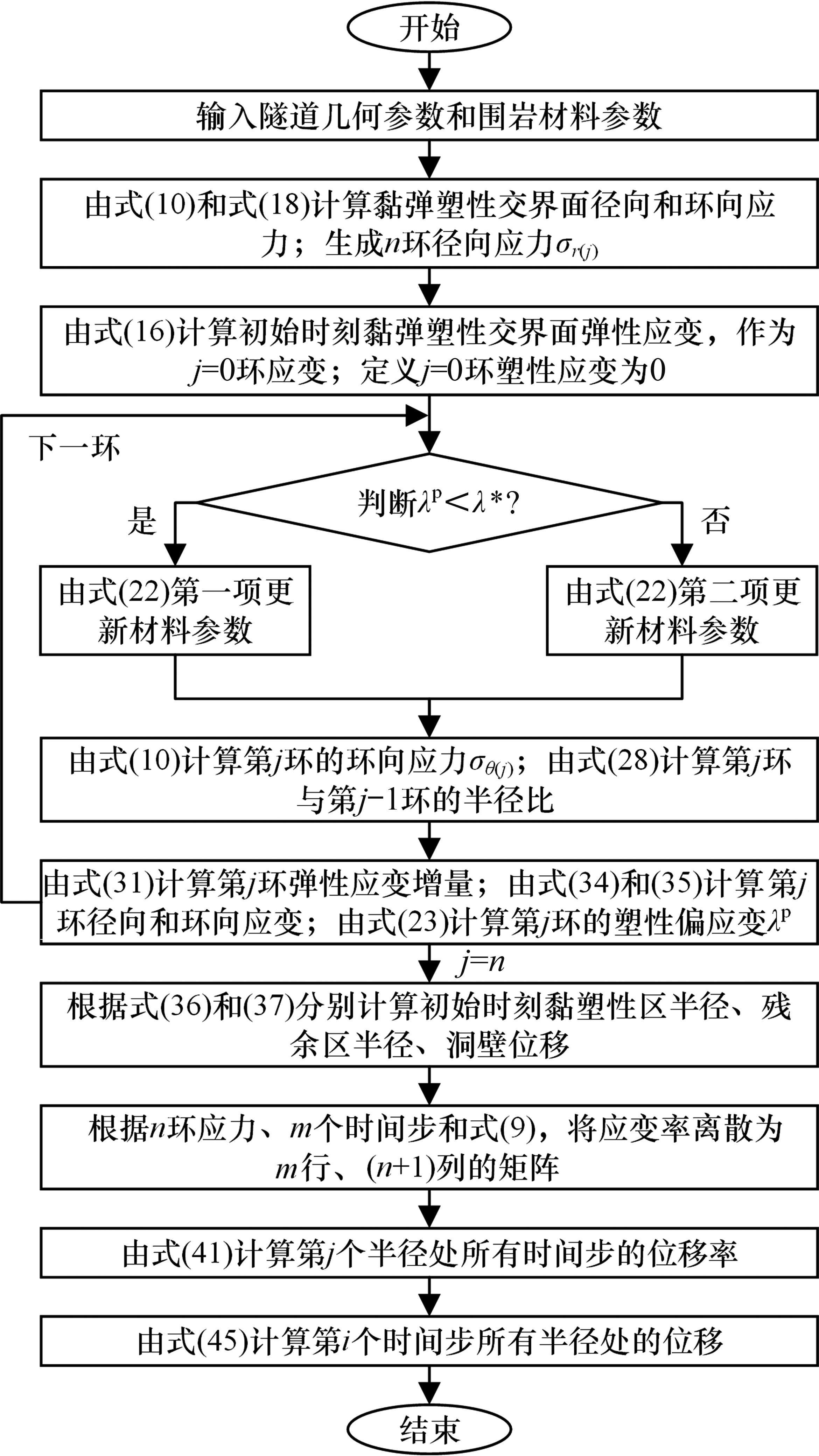
将黏塑性区计算过程编写为数值程序,计算流程如下。
步骤1:输入隧洞几何和材料参数。计算应力应变边界值,并将径向应力离散化。
步骤2:计算环向应力和半径比,再计算每环弹性应变增量和总应变,得到塑性应变增量和塑性剪切应变。
步骤3:比较塑性剪切应变是否大于临界值,判别岩体是否进到塑性残余阶段,并更新材料参数。重复步骤直到j=n,得到每环应力、应变和半径比值后,计算初始时刻每环半径和位移。
步骤4:编写应变率矩阵,计算蠕变开始后每环位移率,再计算每个时间步的位移。
数值计算流程如图5所示。在求解中,应力离散数量n和时间离散数量m会影响计算精度,两者取值越大,计算误差越小。表1所示为本文计算采用的几何和材料参数,算例1见文献[11]。使用算例1中参数,蠕变时长取100 d,分析n和m对洞壁变形的影响,计算结果如图6所示。从图6可见:变形随着n和m的增加而逐渐稳定,增量趋近于0;当n大于100、m大于300时,变形变化较小;当n从100增加到101时,变形增加了0.005%,当m从300增加到301时,变形增加了0.009%。综上可知,取n=100、m=300时,计算结果可满足工程要求。
| 参数 | 算例1 | 算例2 |
|---|---|---|
| a0/m | 3 | 3.68 |
| p0/MPa | 15 | 36.36 |
| ps/MPa | 0 | 0 |
| σc/MPa | 25 | 141.17 |
| σs/MPa | 21 | 130.1 |
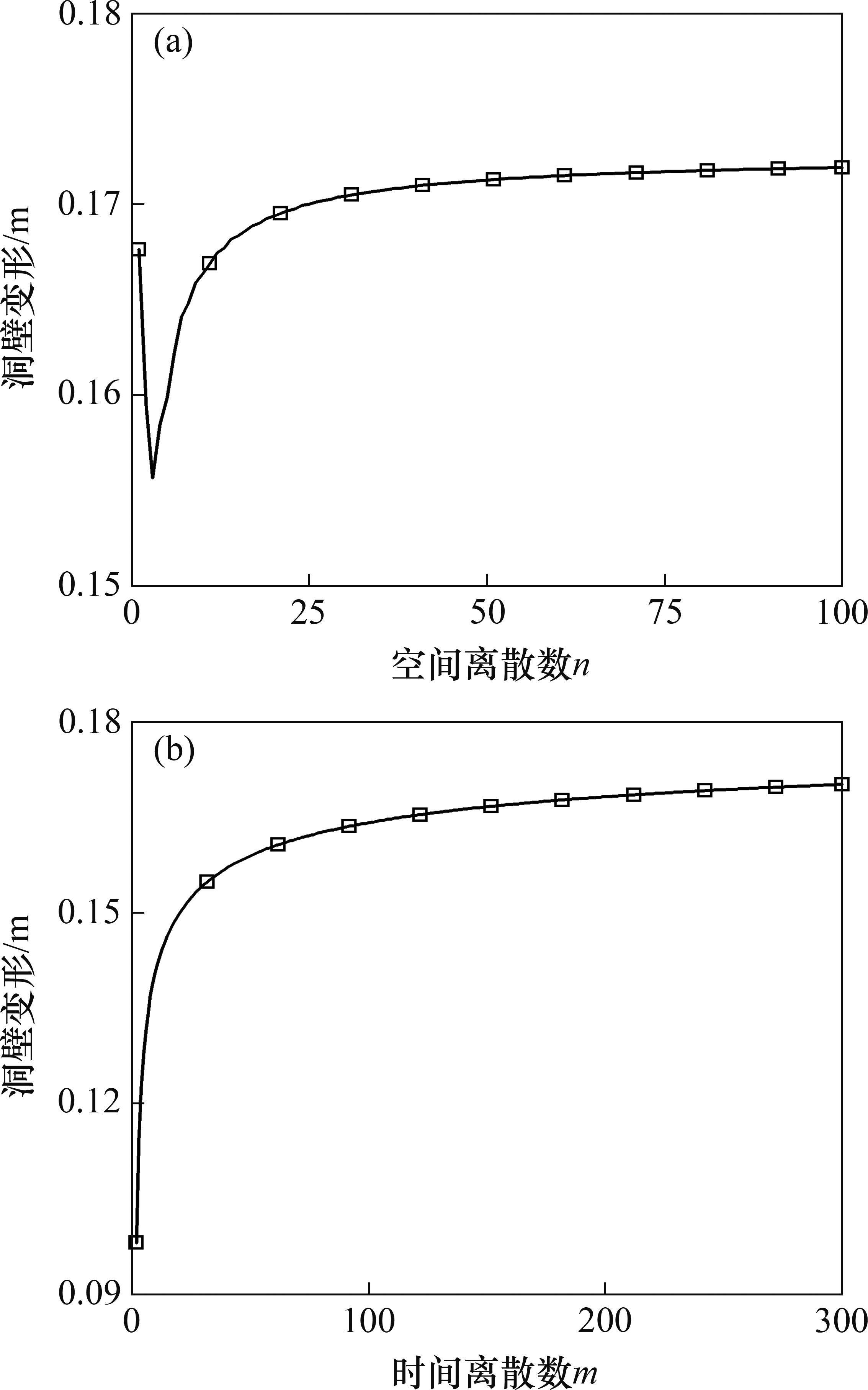
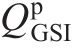 | 40 | 50 |
| mi | 6 | 9 |
| D | 0 | 0 |
| λ* | 0.025 | — |
| φ | 25 | — |
| ν | 0.25 | 0.25 |
| EK/GPa | 1.625 | — |
| ηK/(GPa·hγ) | 5.36 | — |
| EM/GPa | 1.183 | 129.25 |
| ηM/(GPa·hβ) | 88.87 | 192 0 |
| ηP/(GPa·hγ) | 1.2 | 354 5 |
| ω | 0.006 | — |
| β1 | 0.1 | 0.2 |
| β2 | 0.4 | 0.32 |
3 验证与讨论
3.1 算例验证
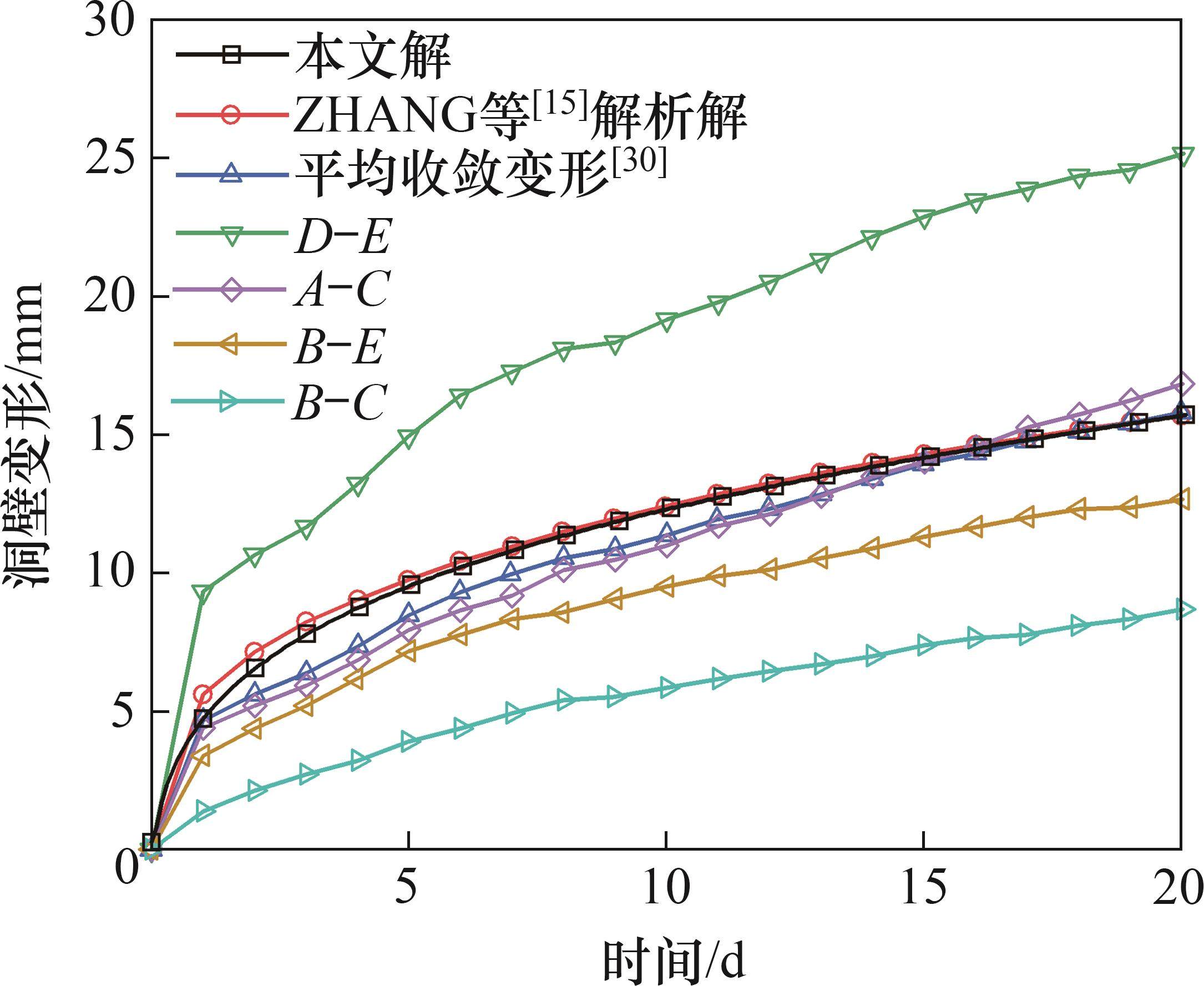
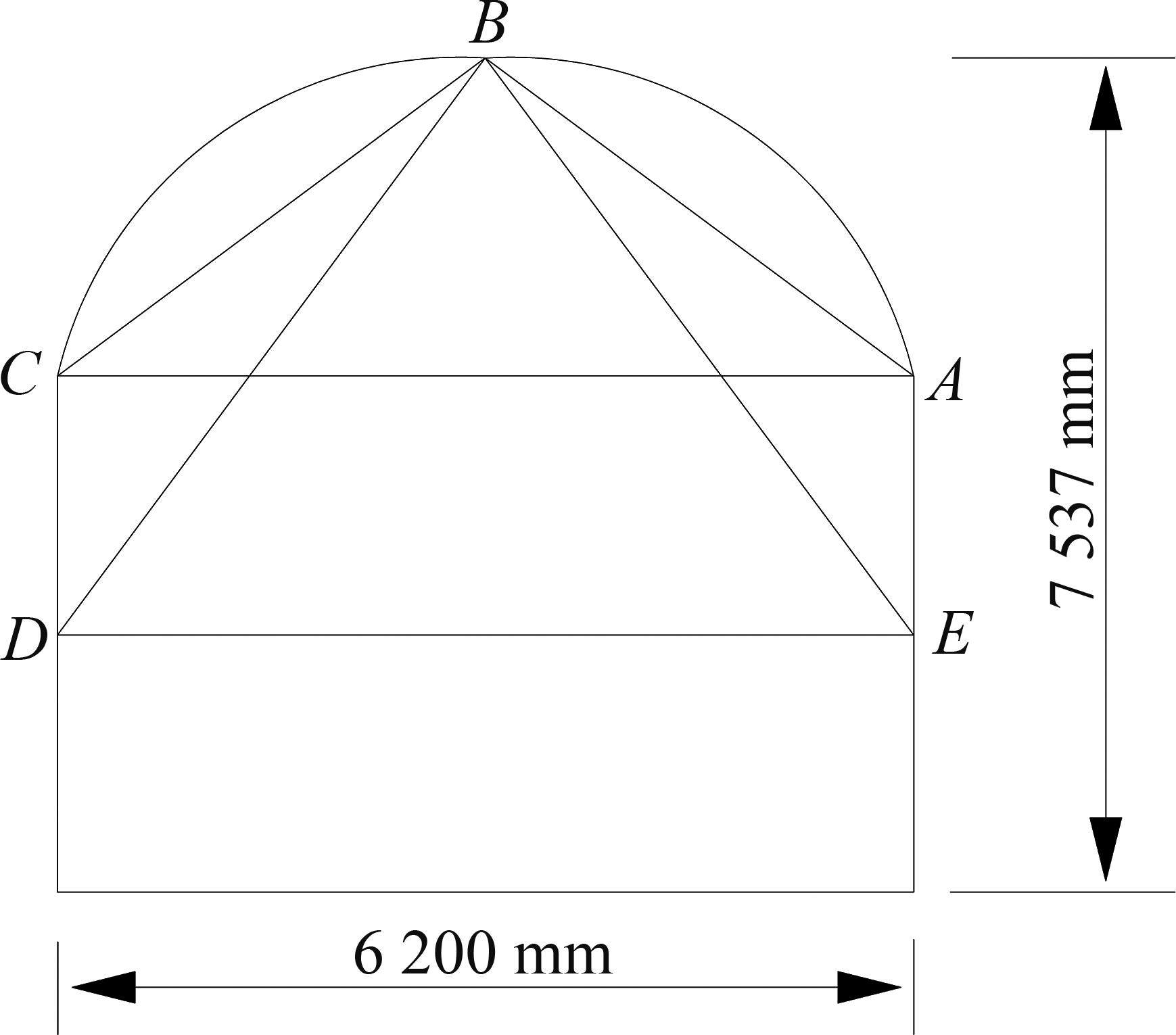
为验证本文解的正确性,将其与锦屏二级水电站排水隧洞工程的监测数据和解析解进行对比。该水电站的排水隧洞包括两条辅助洞和4条引水洞,其中,辅助洞开凿于白山组大理岩中。采用辅助洞断面BK14+190作为分析对象,辅助洞BK14+190断面监测点位布置如图7所示,等效半径为3.68 m。基于HUANG等[8]和CHEN等[29-30]的研究,得到大理岩的相关蠕变参数如表1算例2所示。
将本文解与ZHANG等[15]建立的基于分数阶黏塑性流变模型(FVP)的解析解及监测数据进行对比,结果如图8所示。图中A-C、B-C、B-E、D-E分别表示图7中A点与C点、B点与C点、B点与E点、D点与E点间的收敛变形,重点将变形解析结果与平均收敛变形进行比较。对比结果显示,本文解与监测值和解析解之间的误差较小,可以满足工程应用,验证了其正确性和实用性。与ZHANG等[15]的解析过程相比,本文解计算简便,能反映软岩的应变软化效应,考虑更多参数影响,且能灵活应用于不同流变模型和强度理论。
3.2 蠕变对围岩变形和支护措施的影响
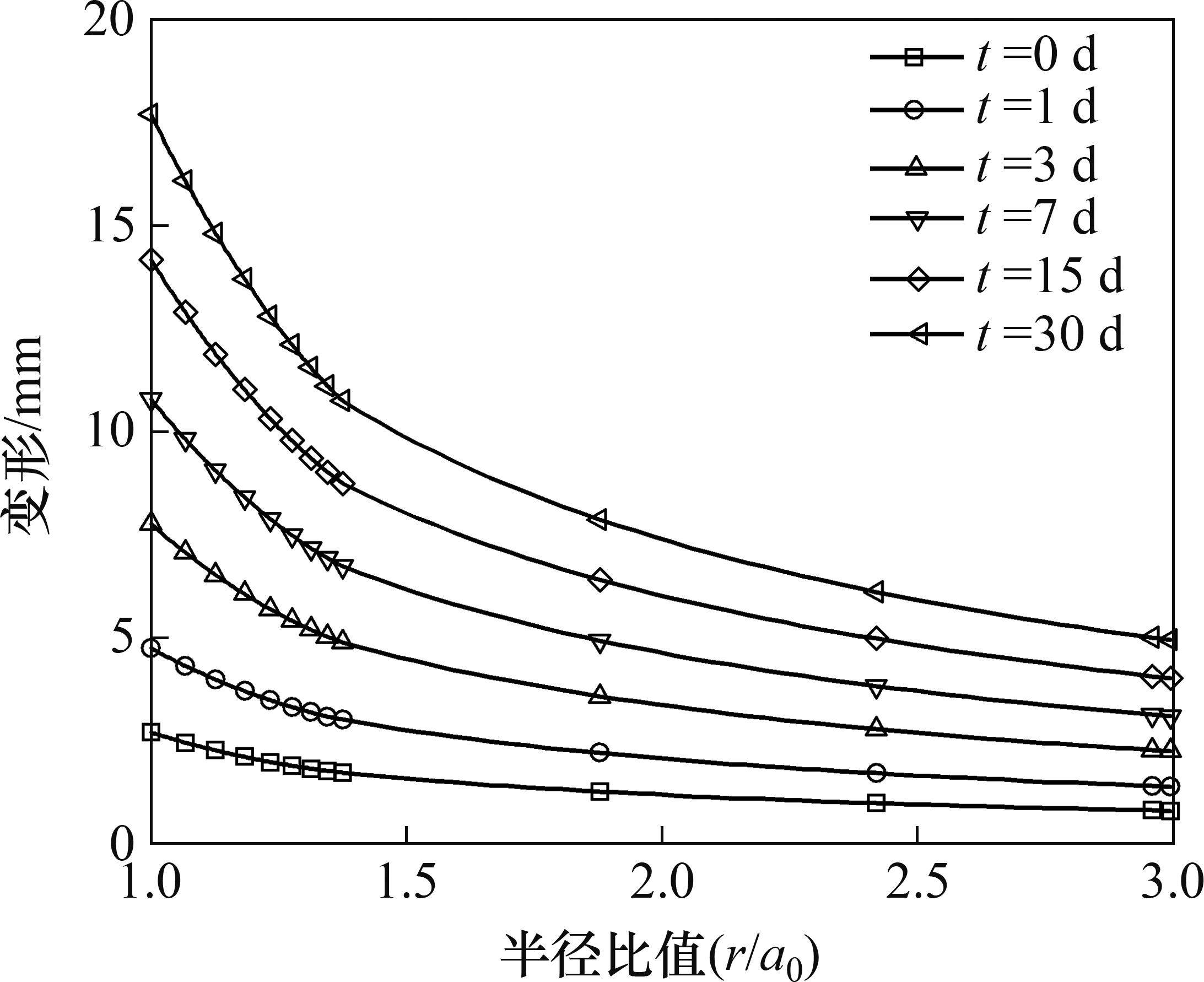
为分析蠕变时长对隧洞变形的影响,计算算例2在不同时间的围岩变形,蠕变时长取0、1、3、7、15 和30 d,径向变形曲线如图9所示。由图9可见:在初始时刻,变形在黏塑性区内快速增大,应变软化模型下的塑性区和残余区半径分别为4.13 m和3.59 m。岩体产生蠕变后,黏弹性区和黏塑性区变形均增大,蠕变初期变形的增幅较大,随着蠕变时长增加,变形增幅逐渐减小,变形增大过程体现了减速蠕变阶段应变率减小的特征。
围岩-支护特征曲线基于收敛-约束法得出,能反映支护对变形收敛的控制作用。算例2的蠕变时间对围岩-支护特征曲线如图10所示,其中,线段a-b、c-d和a-e-f-g分别为刚性支护、应力释放支护和让压支护的支护特征示意曲线。
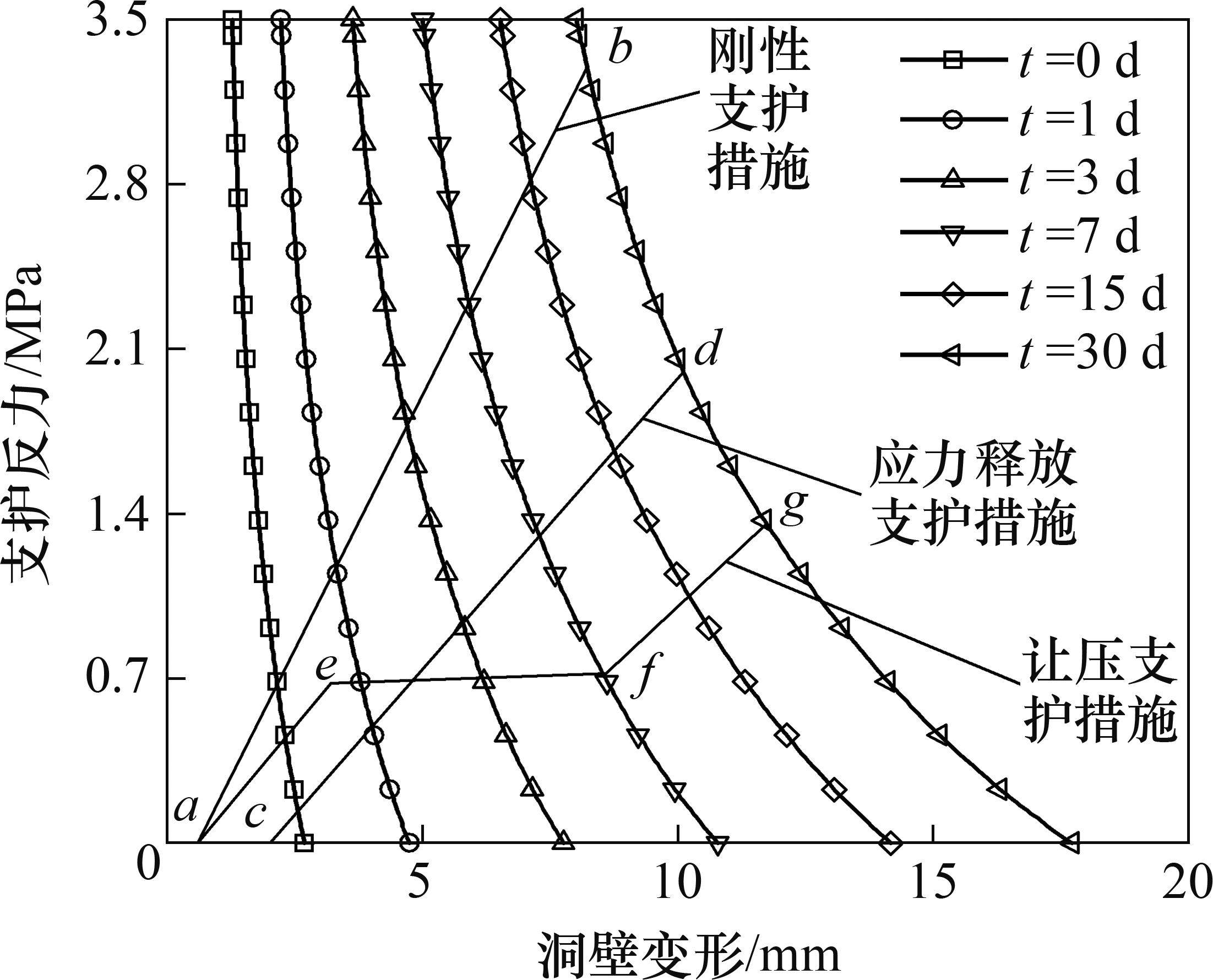
由图10可见:在初始时刻,围岩特征曲线最靠左,随着时间延长,特征曲线向右移动,曲线在初期右移的速率较快。假设围岩在开挖30 d后稳定,由支护特征曲线看出,采用刚性支护措施,支护力会随着时间增大,支护结构与围岩在b点即较小变形处取得平衡,该措施能限制围岩变形,但所受荷载较大,易导致支护失效和二衬开裂。采用应力释放支护措施时,支护前,围岩产生变形已释放应力;线段a-c即对应应力释放阶段,过度增加预留变形量会令围岩松动压力增大,软弱围岩变形难以控制,预留变形量较少会导致初支侵占隧道净空,即使未产生侵占,为保证支护的有效性和安全性,也需对损坏初支进行更换。采用让压支护措施时,a-e段表示支护在初期提供较低的支护力保持围岩稳定,在e-f段围岩进入非线性流变阶段,支护结构随围岩一起变形,通过可控变形构件控制围岩变形速率。变形增大期间,支护结构荷载变化较小,能够有效保护初支,在 f-g段实施刚性支护,将围岩变形控制在安全值内。让压支护措施具备足够支护力和一定可缩性,能够限制围岩变形,避免洞壁过度收缩,为初支提供较好的保护作用,避免返工。
4 参数敏感性分析
4.1 峰值剪胀角和损伤参数
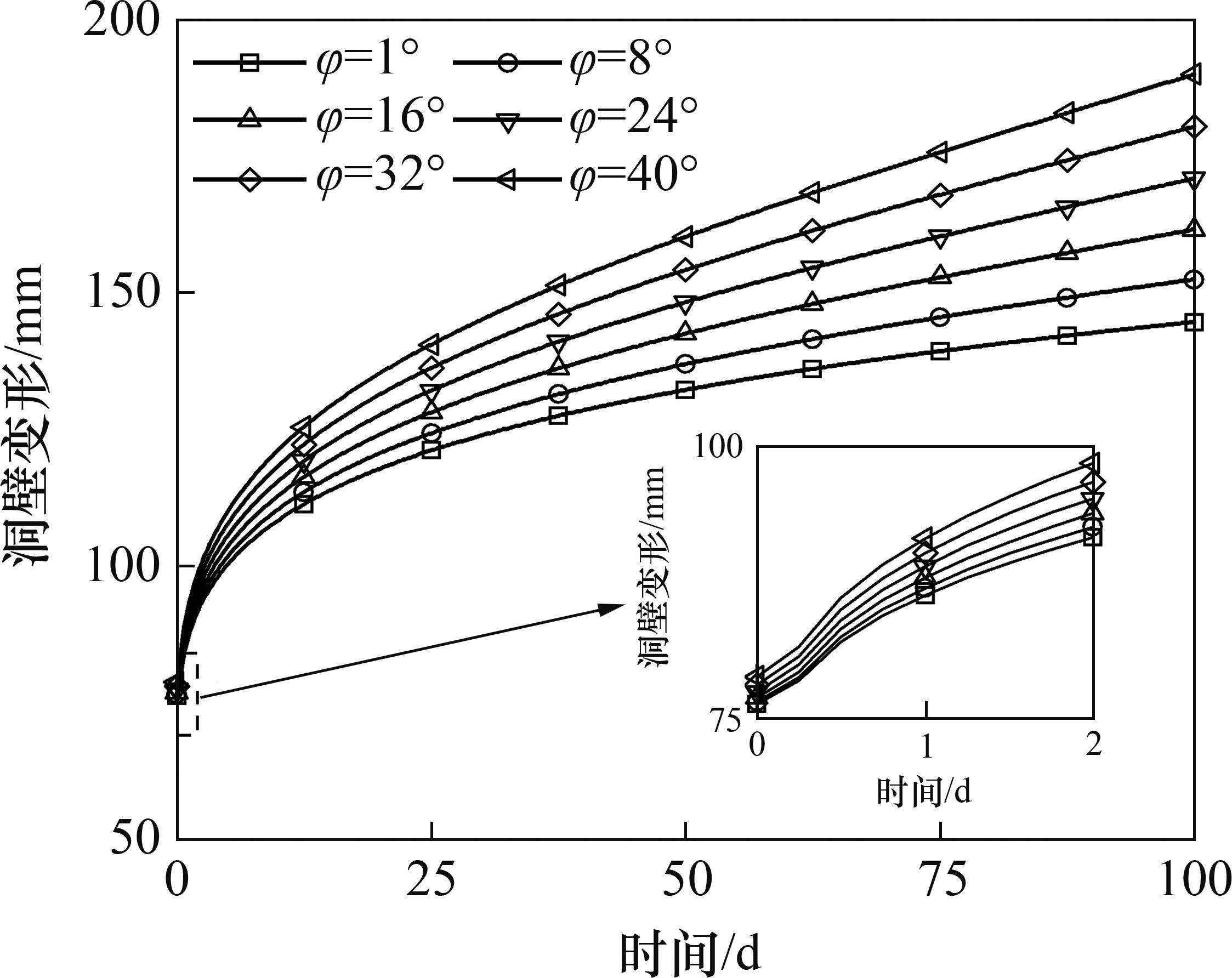
峰值剪胀角取值与M-C准则的内摩擦角相同,主要影响围岩的塑性体积应变,用算例1参数和不同峰值剪胀角(1°、8°、16°、24°、32°、40°)进行计算,得到随时间变化的洞壁变形曲线如图11所示。由式(32)和式(40)可知,黏塑性区初态和瞬态变形都会受到非线性剪胀角的影响。由图11可见:随着峰值剪胀角增大,洞壁变形曲线逐渐增大,表2所示为初始时刻和100 d后的洞壁变形以及相邻峰值剪胀角之间变形增大的百分比,可见初态变形的增幅小于100 d瞬态变形的增幅。峰值剪胀角增大会引起初态和瞬态变形增大,但初态变形的增幅较小。
| 参数 | 峰值剪胀角φ/(°) | |||||
|---|---|---|---|---|---|---|
| 1 | 8 | 16 | 24 | 32 | 40 | |
| 初态变形/mm | 76.24 | 76.46 | 76.84 | 77.35 | 78.02 | 78.79 |
| 初态变形增幅/% | — | 0.29 | 0.50 | 0.66 | 0.84 | 1.01 |
| 100 d变形/mm | 144.66 | 152.43 | 161.56 | 170.9 | 180.4 | 189.99 |
| 100 d变形增幅/% | — | 5.37 | 5.99 | 5.78 | 5.56 | 5.32 |
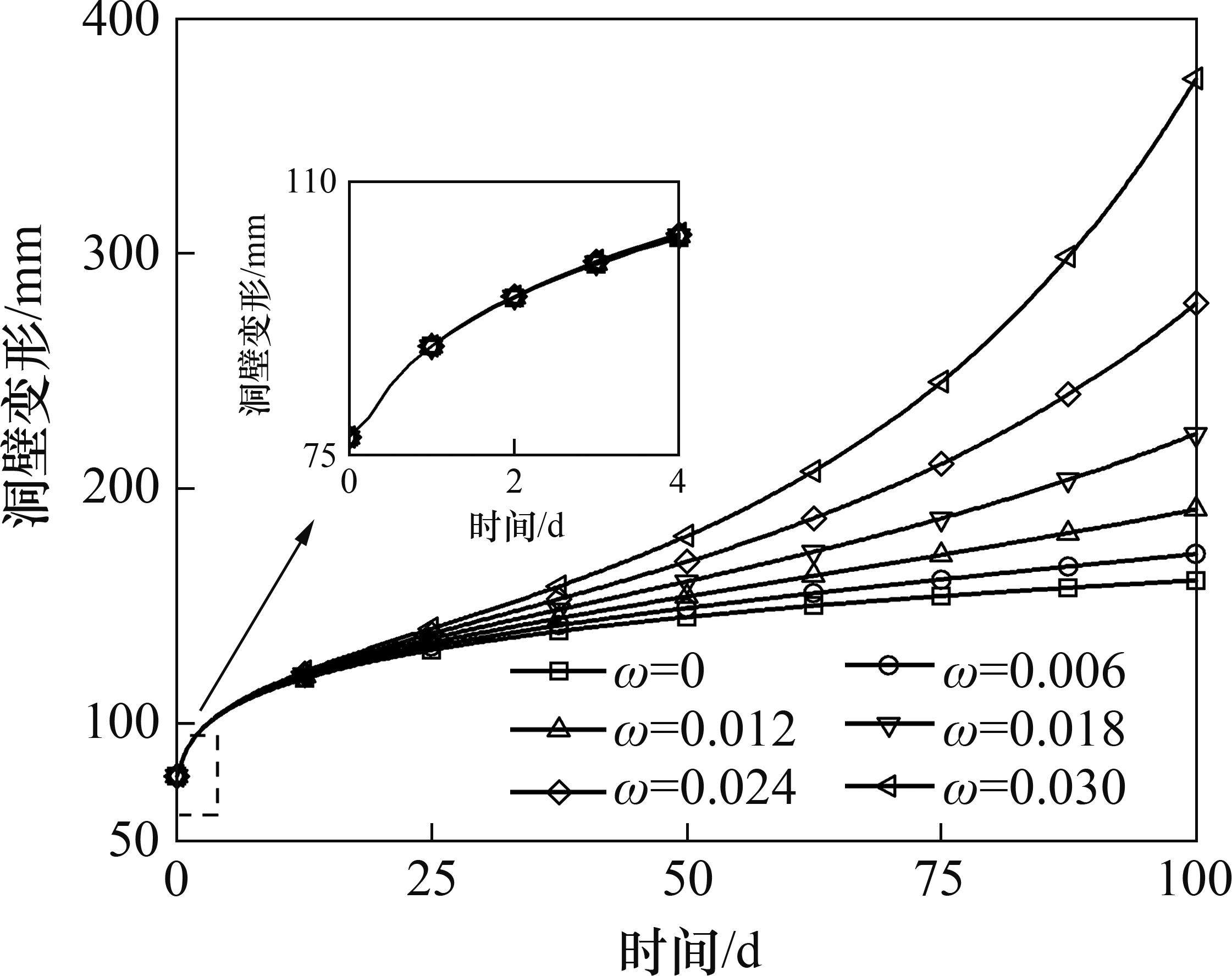
损伤参数量化材料内部缺陷演化,影响黏性系数的取值,用算例1中的参数和不同损伤参数(0、0.006、0.012、0.018、0.024、0.03)进行计算,洞壁变形曲线如图12所示。由图12可见:围岩变形初期表现出减速蠕变特征,此时,损伤参数增大对变形的影响较小;随着时间延长,变形增大逐渐明显;在蠕变时长较大时,较小损伤参数的位移率变化较小,变形曲线表现出稳定蠕变阶段特征,较大损伤参数的位移率增长更快,变形表现出加速蠕变阶段特征。损伤参数增大则洞壁变形增大,使围岩加快进入加速蠕变阶段。
4.2 蠕变参数
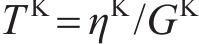
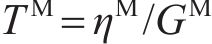
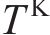
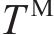
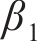
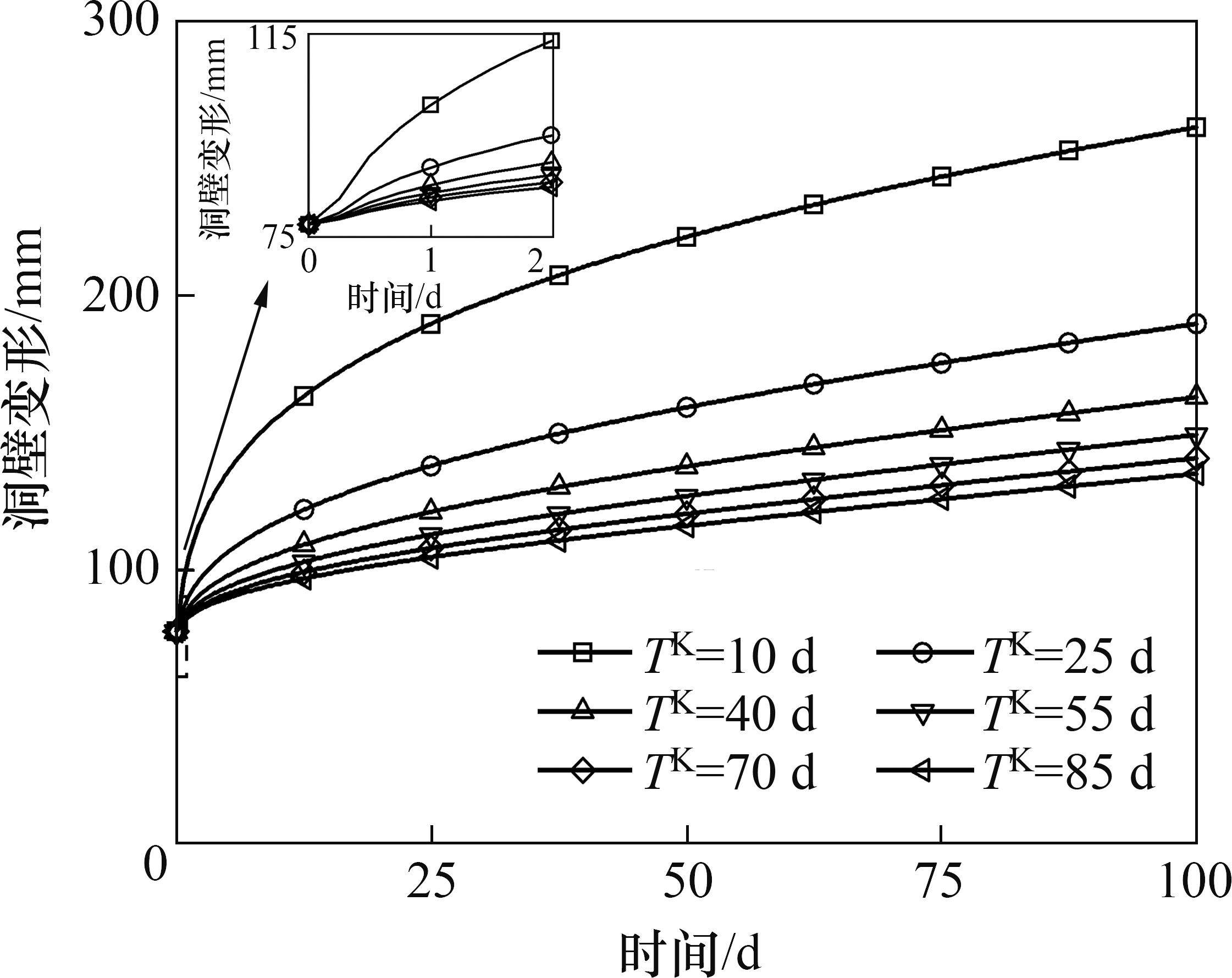
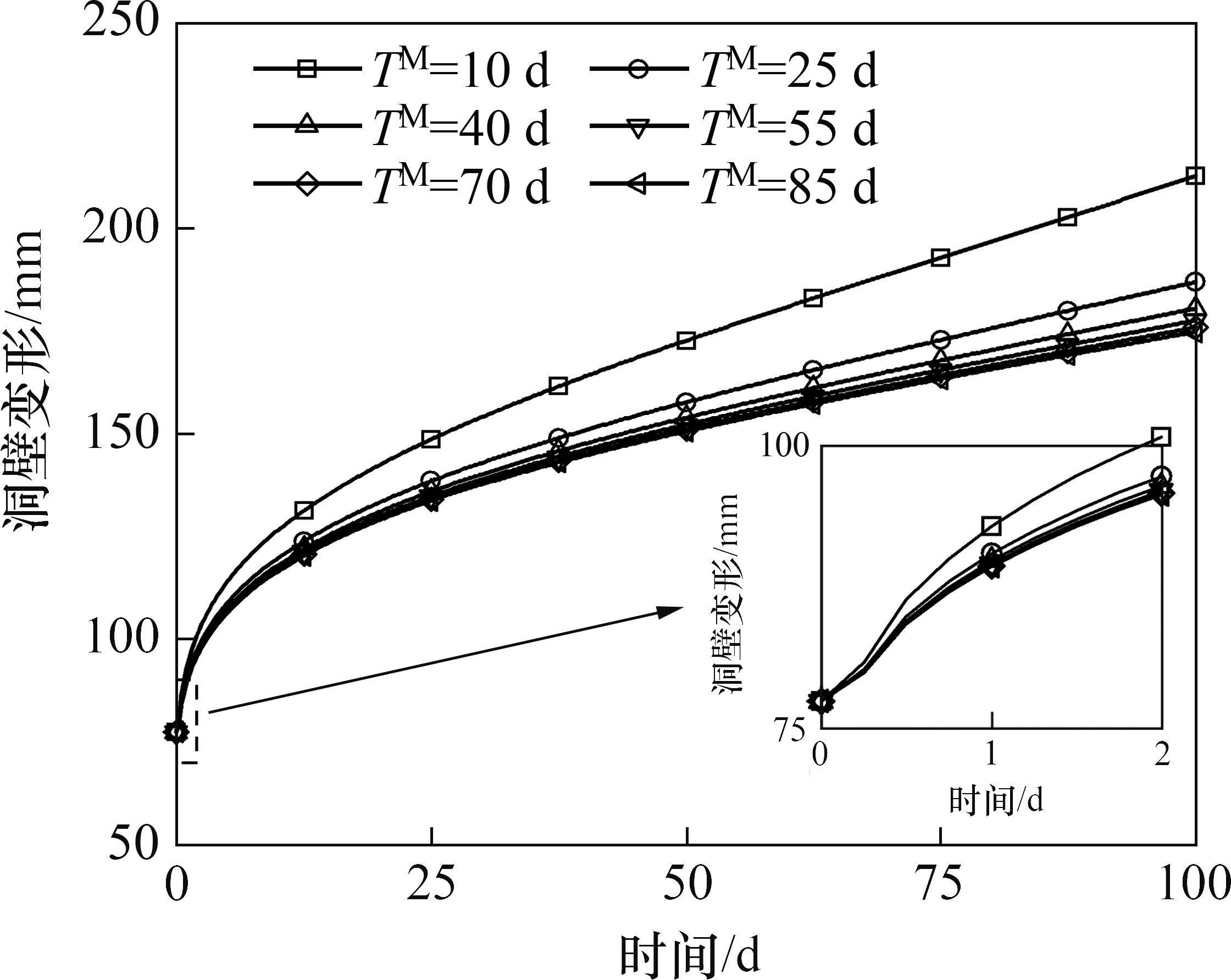
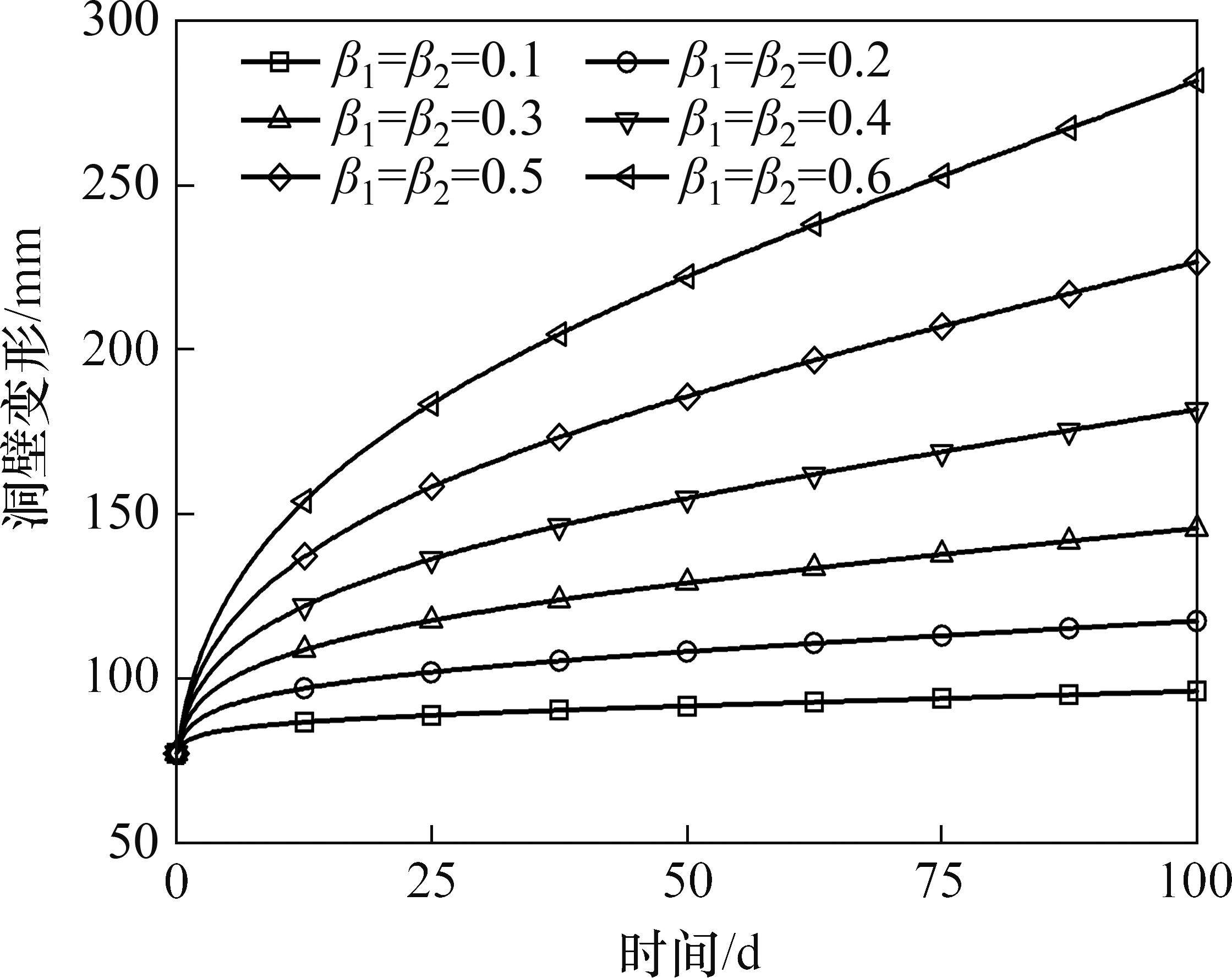
延迟时间对变形的影响如图13所示。由图13可见:延迟时间增加会导致洞壁变形减少,且降幅逐渐减小;在蠕变初期,较大延迟时间下的位移率快速减小,曲线非线性特征不明显。松弛时间对变形的影响如图14所示。由图14可见:松弛时间增长也会减少洞壁变形,降幅逐渐减小,但变形减小主要出现在蠕变中期。求导阶数对变形的影响如图15所示。由图15可见:当求导阶数较小时,变形总增量较小,求导阶数增加使变形增大,且变形曲线由线性增长过渡到呈非线性增长。延迟时间和松弛时间增大均使变形减小,但降幅逐渐递减,增大延迟时间主要减小蠕变初期位移率,增大松弛时间主要使蠕变中期位移率减小,求导阶数增大则变形增大,使变形曲线在蠕变初期的非线性特征更加明显。
5 结 论
1) 本文采用非线性黏弹-黏塑损伤流变模型描述围岩的减速、稳定和加速蠕变阶段,引入考虑中间主应力的光滑GZZ准则,得到了考虑应变软化特性的软岩隧洞长期变形有限差分计算方法,该解采用离散化方法,相比于解析解计算更简便。
2) 将该解与实际工程数据和解析解进行对比,本文解与监测结果、解析解结果之间的误差较小,证明了本文解的正确性和适用性;在该解下对工程支护措施进行讨论,让压支护措施能有效适应围岩长期蠕变,对流变性软岩建议采用让压支护措施。
3) 峰值剪胀角和损伤参数增大引起洞壁变形增大,且损伤参数增大使围岩加快进入加速蠕变阶段;增大延迟时间会减小洞壁变形和蠕变初期的位移率,增大松弛时间也会使洞壁变形减小,同时减小蠕变中期的位移率;增大求导阶数会使洞壁位移率和变形增大,使变形曲线在蠕变初期的非线性特征更加明显。
冯渠彰, 刘海明, 曹净, 等. 基于黏弹-黏塑性模型的软岩隧洞长期变形解析[J]. 中南大学学报(自然科学版), 2025, 56(2): 716-729.
FENG Quzhang, LIU Haiming, CAO Jing, et al. Analysis of long-term deformation in soft rock tunnels based on viscoelastic-viscoplastic creep model[J]. Journal of Central South University(Science and Technology), 2025, 56(2): 716-729.