天然层状岩石在油气开采、采矿工程、隧道工程、边坡工程以及地下工程中广泛存在[1-4]。层状岩石主要分为具有层理结构的沉积岩和具有片理结构的变质岩两大类[5-8]。各向异性是层状岩石的显著特征之一,包括弹性、强度、渗透率等均呈现各向异性特征[9-10]。岩石各向异性力学特征对钻孔稳定性[11-12]、水力裂缝起裂和扩展[13-14]、隧道稳定性及岩爆[15]等有显著的影响。因此,深入研究层状岩石的各向异性力学行为,对于岩土工程设计和施工具有重要的指导作用。
抗张强度是层状岩石最重要的力学参数之一,岩石抗张强度测试主要包括直接拉伸和间接拉伸两种方法。由于直接拉伸对试样制备和试验配置的要求较高,导致直接拉伸试验应用较少。许多学者开发了多种间接拉伸试验方法[16],巴西劈裂试验是应用最广泛的方法之一,其具有试样容易制备、试验配置简单、数据处理简便等特点,被广泛用于不同加载角度下各向异性巴西圆盘(BD)的间接抗张强度、破坏模式和裂纹起裂扩展行为的研究。TAVALLALI等[17]通过巴西劈裂试验研究了层理对砂岩峰值载荷、抗张强度和破坏模式的影响;CHO等[18]开展了Asan片麻岩、Boryeong页岩和Yeoncheon片岩巴西劈裂和单轴压缩试验,分析了层理对这3种岩石强度及破坏模式的影响;吴秋红等[19]开展了各向异性花岗岩单轴压缩和巴西劈裂试验,发现花岗岩具有显著的各向异性特征,而且单轴抗压强度与弹性模量、纵波波速呈负相关;侯鹏等[20]结合高速摄像机和声发射开展了不同加载角度下页岩巴西劈裂试验,分析了层理对页岩抗张强度、裂纹扩展及声发射特征的影响,讨论了加载角度对破坏模式的影响规律。马天寿等[21]开展了龙马溪页岩巴西劈裂试验,揭示了其抗拉强度的各向异性特征,并通过试验结果检验了CPA(critical plane approach)准则的准确性和适用性。
数值模拟不仅可以从宏观上分析岩石破坏过程和力学性质,而且能够从微观上分析岩石破坏的微观机理,从而为认识层状岩石力学特性提供更加明确的证据。CAI等[22]采用有限元-离散元混合方法(FDEM)研究了岩石各向异性对裂纹起裂与扩展的影响,指出各向异性对裂纹起裂与扩展的影响非常显著,最终影响岩石的破坏模式与抗张强度;TAN等[23]结合巴西劈裂试验和离散元法研究了层理对板岩破坏机理的影响,试验结果与数值结果吻合较好,均反映板岩具有显著的各向异性特征;MENG等[24]结合黏聚力模型和巴西劈裂试验研究了层理对砂质泥岩抗拉强度和破坏模式的影响;李德健等[25]结合FDEM和巴西劈裂试验研究了层理对煤岩抗张强度与破坏模式的影响;李二强等[26]开展了不同加载角度下炭质板岩巴西劈裂试验,利用黏聚力模型进行数值模拟研究,揭示了层理特性对炭质板岩强度及破坏模式的影响规律;乔兰等[27]基于FLAC3D开展了巴西劈裂二维及三维数值模拟,分析了BD的起裂模式与裂缝扩展规律。
虽然国内外研究者已经针对不同类型层状岩石开展了巴西劈裂试验和数值模拟研究,分析了层理特性对层状岩石力学行为的影响,但是,对于层状页岩巴西劈裂各向异性特征及其影响的研究并不深入,特别是对于层理对页岩抗张强度及破坏模式的影响没有形成统一的认识。因此,本文以龙马溪页岩巴西劈裂试验数据为基础,利用PYTHON对ABAQUS进行二次开发,通过全局嵌入零厚度黏聚单元法(cohesive element method),建立了层状页岩BD二维有限元模型,对比了数值模拟与巴西劈裂试验结果,并分析了层理间距和强度对页岩巴西劈裂力学行为及其各向异性的影响。研究结果可为油气开采、采矿工程、隧道工程、边坡工程以及地下工程的设计和施工提供依据和参考。
1 层状页岩巴西劈裂试验
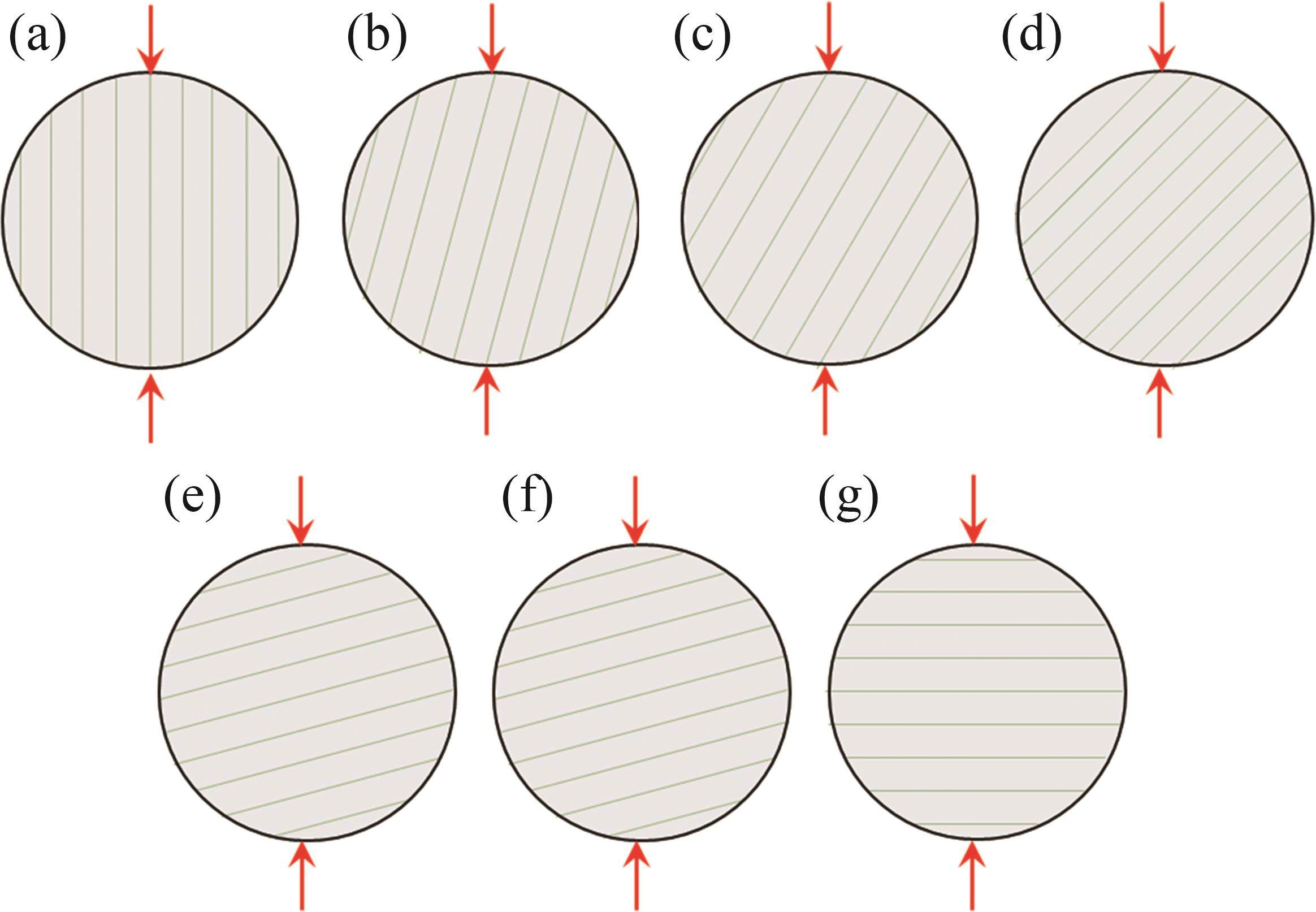
岩样取自重庆彭水区块龙马溪露头页岩(如图1所示),该页岩具有显著的定向层状结构,且层内颗粒粒度较为均匀,层理间距为4.0~7.0 mm,密度为2 340 kg/m3。根据X射线衍射和电镜扫描结果,该页岩富含石英、黏土、长石等矿物,发育较多的纳微米孔隙和一定的微裂隙。根据国际岩石力学学会建议方法,沿平行层理方向钻取直径为50 mm、厚度为25 mm的BD试样21块。加载角度β为层理面与加载方向之间的夹角,采用三轴岩石力学测试系统,开展了加载角度为0°、15°、30°、45°、60°、75°和90°时层状页岩巴西劈裂试验[21]。不同加载角度层状页岩巴西劈裂测试原理图如图2所示。
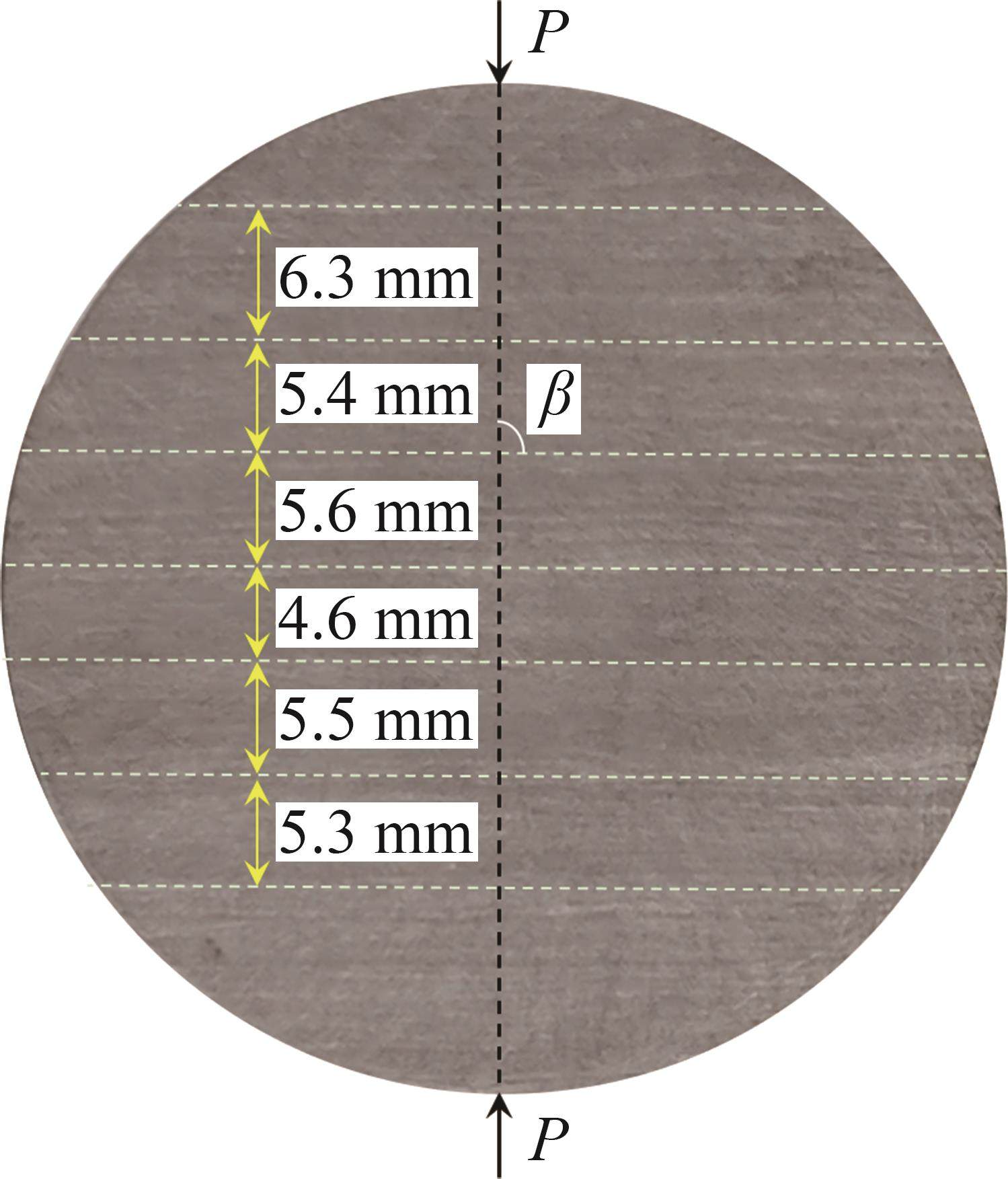
为了计算龙马溪层状页岩的巴西劈裂强度,采用CLAESSON等[28]提出的各向异性岩石间接拉伸强度模型进行计算。该模型考虑了加载角度和弹性各向异性的影响,其计算公式为
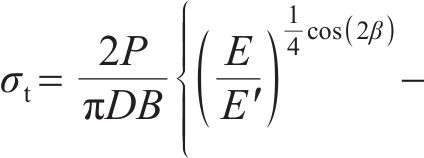
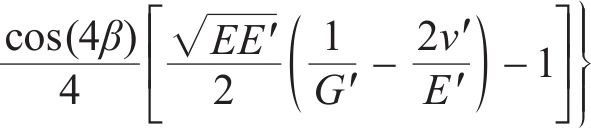
式中:σt为巴西劈裂强度,MPa;P为峰值载荷,kN;D为巴西圆盘直径,mm;B为巴西圆盘厚度,mm;β为加载角度,(°);E为平行于层理方向的弹性模量,GPa;E'为垂直于层理方向的弹性模量,GPa;v'为垂直于层理方向的泊松比;G'为垂直于层理方向的剪切模量,GPa。
对于试验测试的龙马溪页岩,式(1)中弹性参数由波速各向异性测试结果计算确定[21],得到E=20.53 GPa,E'=15.21 GPa,v=0.17,v'=0.19,G'=7.17 GPa。
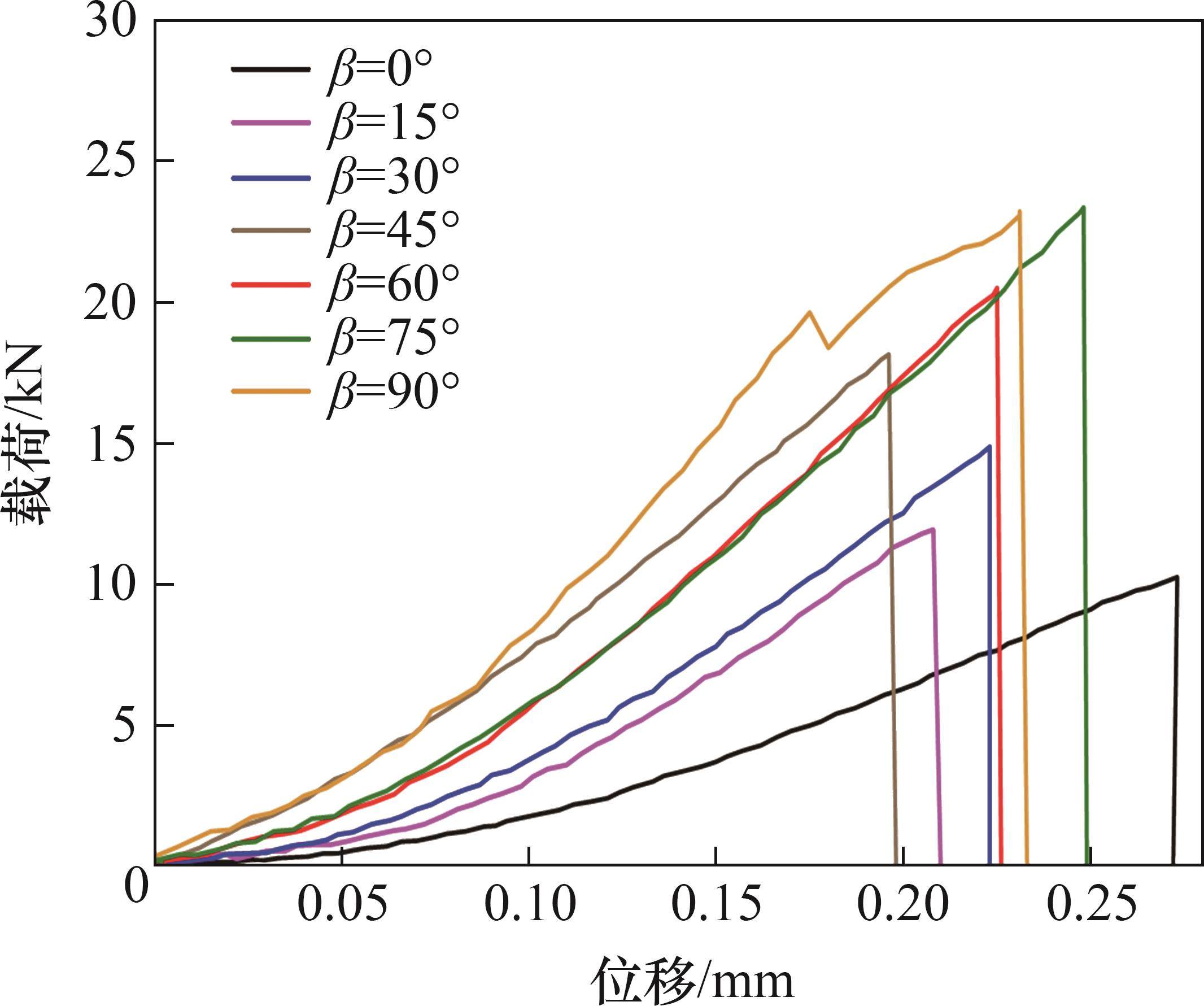
三轴岩石力学测试系统最大轴向载荷为 1 000 kN,测力精度达±0.5%,采用位移控制加载,加载速率为0.1 mm/min,并记录加载过程中的载荷-位移曲线。为了避免试验测试随机误差的影响,每一组试验重复测试3次,试验结果如表1所示。由于测试结果具有一定离散性,选取7种加载角度条件下最典型的载荷-位移曲线进行分析,如图3所示。从图3可见:不同加载角度下峰值载荷和巴西劈裂强度差异显著;整体上,随加载角度的增加,峰值载荷和巴西劈裂强度增大;在加载初期,层状页岩具有明显的压密阶段;在峰后阶段,载荷陡降,表现出明显的脆性破坏特征。
| 加载角度/(°) | 直径/mm | 厚度/mm | 峰值载荷/kN | 强度/MPa | 强度平均值/MPa |
|---|---|---|---|---|---|
| 0 | 50.07 | 25.32 | 10.44 | 5.63 | 5.24 |
| 50.03 | 25.13 | 10.32 | 5.62 | ||
| 50.01 | 25.01 | 8.16 | 4.47 | ||
| 15 | 49.89 | 24.98 | 13.91 | 7.57 | 6.27 |
| 50.01 | 24.91 | 11.90 | 6.48 | ||
| 49.92 | 25.05 | 8.77 | 4.76 | ||
| 30 | 50.28 | 24.94 | 16.73 | 8.83 | 7.63 |
| 50.00 | 24.96 | 14.84 | 7.87 | ||
| 50.02 | 24.92 | 11.66 | 6.19 | ||
| 45 | 49.96 | 25.03 | 21.69 | 11.08 | 9.63 |
| 49.94 | 25.05 | 18.18 | 9.28 | ||
| 50.14 | 25.04 | 16.78 | 8.53 | ||
| 60 | 50.04 | 25.15 | 25.19 | 12.29 | 10.57 |
| 50.01 | 24.93 | 20.46 | 10.08 | ||
| 50.08 | 24.96 | 19.00 | 9.34 | ||
| 75 | 50.00 | 25.01 | 29.45 | 14.03 | 11.90 |
| 49.73 | 25.27 | 23.14 | 10.97 | ||
| 49.98 | 25.02 | 22.47 | 10.70 | ||
| 90 | 50.09 | 24.91 | 32.65 | 15.41 | 11.83 |
| 49.86 | 25.00 | 23.44 | 11.07 | ||
| 49.92 | 24.88 | 19.01 | 9.01 |
2 基于黏聚单元的数值模拟方法
2.1 基本原理
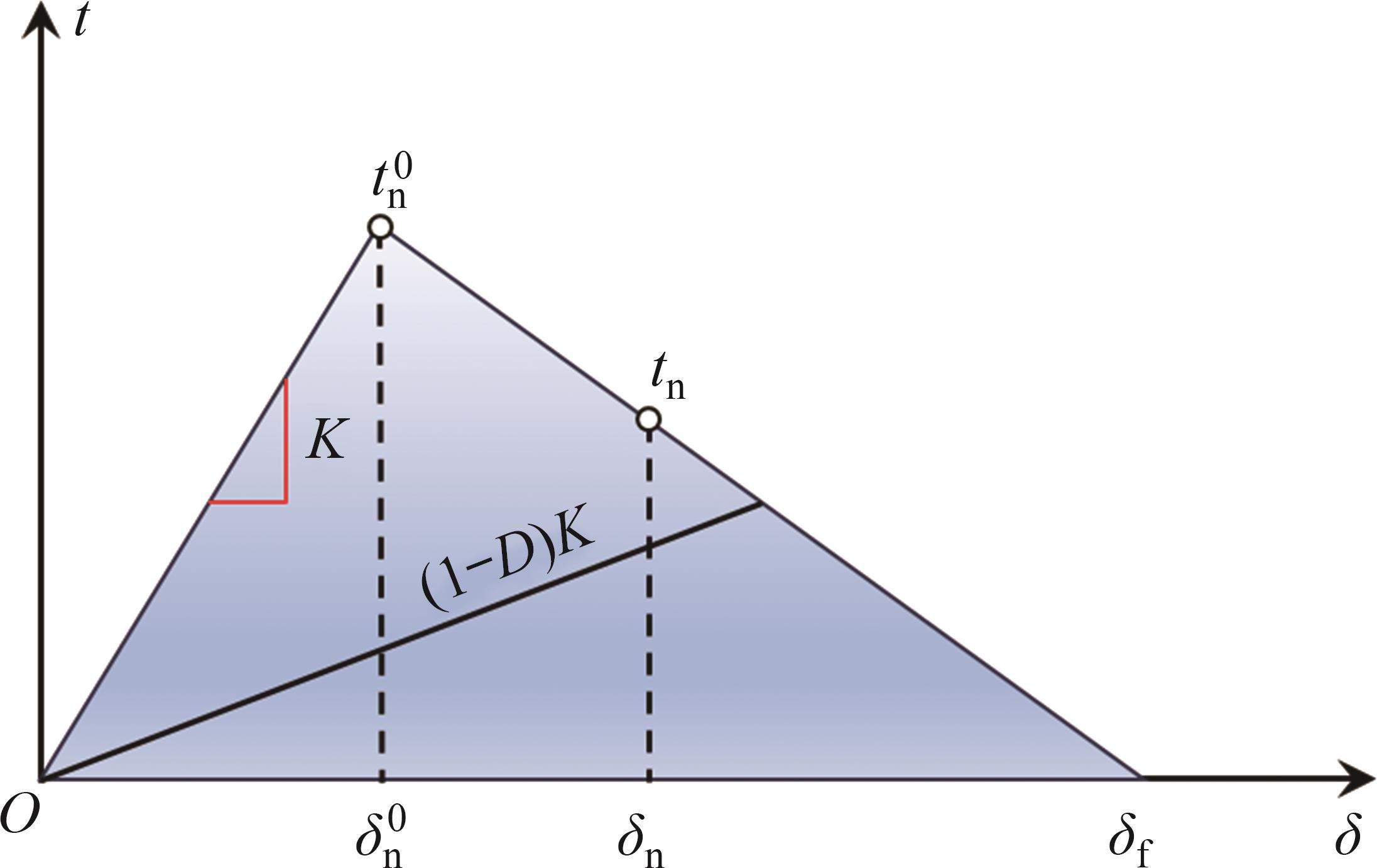
相较于扩展有限元法,黏聚单元模型[29-30]能够更有效地模拟复杂裂纹扩展行为与材料缺陷;相较于离散元方法,该模型计算时间少。黏聚单元以牵引-分离准则为基础,假设初始损伤和损伤演化前为线弹性,黏聚单元牵引-分离准则如图4所示,其中,t为黏聚单元应力矢量,其分量tn、ts、tt分别为法向应力张量、第一切向应力张量和第二切向应力张量,对应的位移分别为ẟn、ẟs、ẟt;tn0为变形完全垂直于黏聚单元面时的最大名义应力。结合黏聚单元初始厚度T0,黏聚单元的名义应变可表示为[31]:
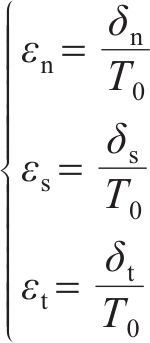
式中:ẟn为黏聚单元的法向位移,mm;ẟs为黏聚单元沿第一方向的切向位移,mm;ẟt为黏聚单元沿第二方向的切向位移,mm;ɛn为黏聚单元的法向应变;ɛs为黏聚单元沿第一方向的切向应变;ɛt为黏聚单元沿第二方向的切向应变。
在黏聚单元失效前,应力与应变满足如下线弹性关系[31]:
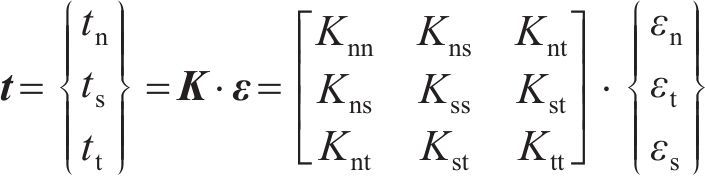
式中: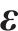
在数值模拟过程中,黏聚单元的牵引-分离特征受损伤起始准则和损伤演化准则控制。本文以最大名义应力准则作为损伤起始准则,假设黏聚单元损伤发生在法向或切向应力达到预设应力时[31],有
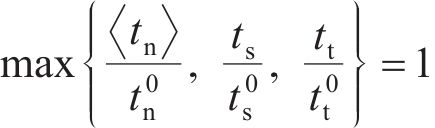
其中:
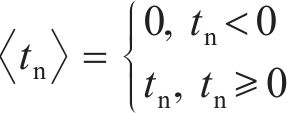
式中: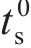
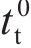
当黏聚单元满足损伤条件时,损伤演化方程主要用于计算材料的刚度退化速率。损伤变量D表征材料的整体损伤,并考虑了所有损伤演化的综合影响。随着加载的继续,D逐渐从0变为1。牵引-分离准则的应力分量受到以下损伤的影响[31]:
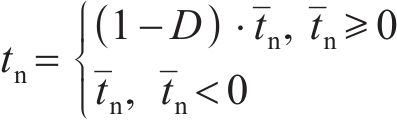
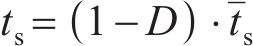
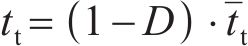
式中: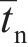
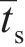
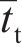
采用有效位移ẟm表征黏聚单元在法向变形和剪切变形共同作用下的损伤演化[31]:
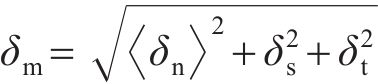
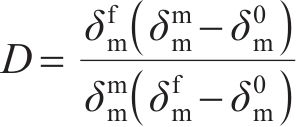
式中:ẟmf为材料破坏时黏聚单元的有效位移,mm;ẟm0为材料初始损伤时黏聚单元的有效位移,mm;ẟmm为加载过程中黏聚单元的最大有效位移,mm。
2.2 模型建立
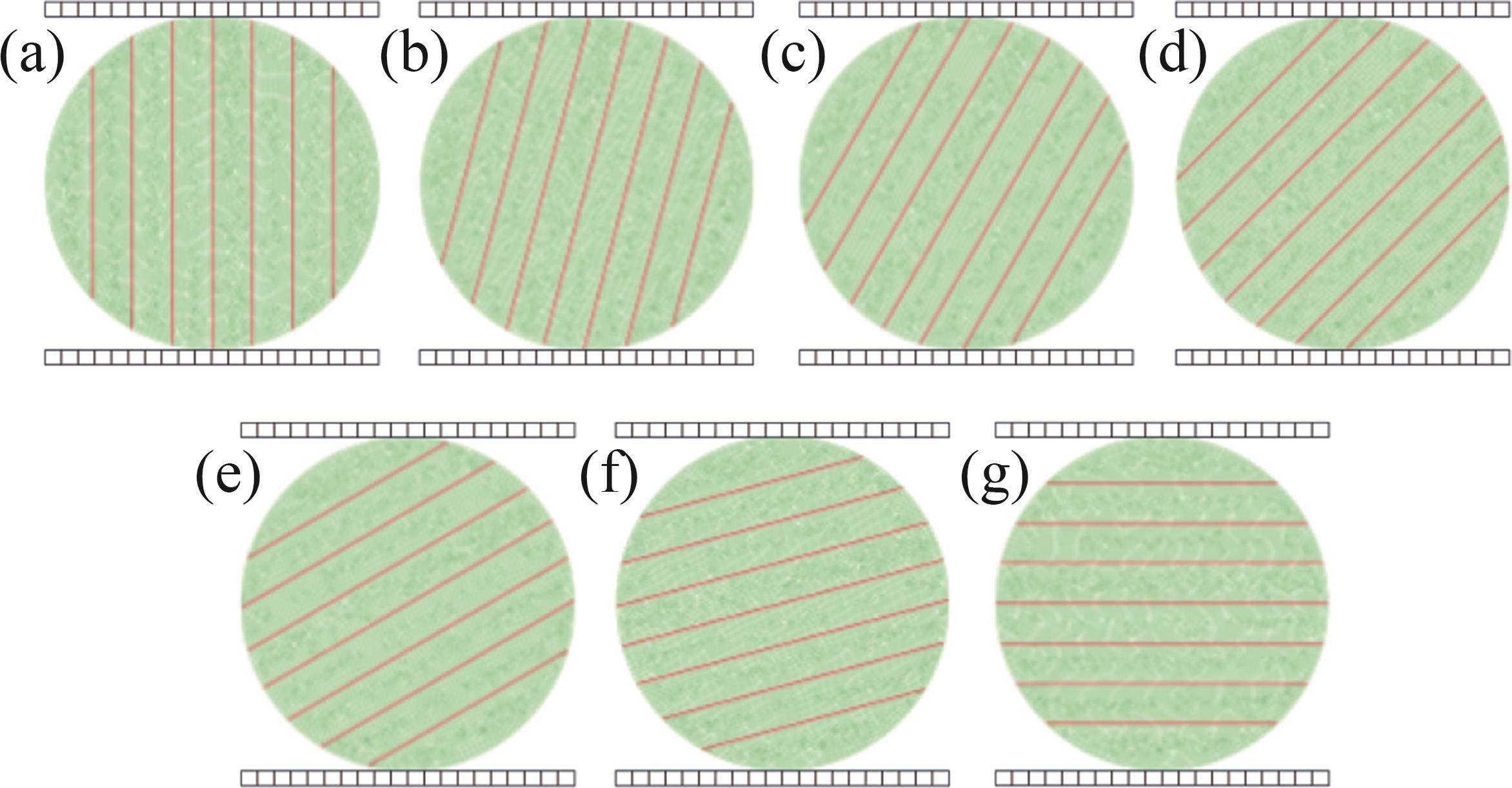
基于平面应变假设,采用全局嵌入零厚度黏聚单元法,建立了层状页岩BD试样二维模型,其几何尺寸与真实试样的一致,直径为50 mm、厚度为25 mm,层理间距根据真实试样设置为6 mm,不同加载角度的BD模型示意图如图5所示。由于层状页岩BD试样破坏模式复杂,为真实反映层状页岩裂纹起裂和扩展规律,采用PYTHON编程对ABAQUS软件进行二次开发,将基质黏聚单元和层理黏聚单元嵌入实体单元中,2种黏聚单元的类型相同,但力学性质不同。实体单元采用四边形网格自由划分,单元全局尺寸为0.001 mm,类型为平面应变单元,实体单元和黏聚单元总数约为43 000个。然后,将上下压板设置为刚体,对上压板设置垂直向下的位移边界条件,加载速率为 0.1 mm/min,对下压板设置完全固定的边界条件。在有限元分析过程中采用显式动力学算法,并利用GPU提高计算效率。
在一般情况下,黏聚单元的微观参数无法通过试验直接测定。因此,根据前人的方法和经验,假设第一和第二切向微观参数相同,基于不同加载角 度下BD试样的峰值载荷,采用试错法确定黏聚单元微观参数[21-22, 27]。实体单元密度为2 340 kg/m3、弹性模量为21 GPa、泊松比为0.17,而黏聚单元微观参数由β=90°时的试验结果确定,结果如表2所示。
| 单元类型 | Knn/(MPa·mm-1) | Kss/(MPa·mm-1) | Ktt/(MPa·mm-1) | tn/MPa | ts/MPa | tt/MPa | ẟn/mm |
|---|---|---|---|---|---|---|---|
| 层理单元 | 600 | 1 000 | 1 000 | 5 | 8 | 8 | 1×10-7 |
| 基质单元 | 900 | 1 200 | 1 200 | 10 | 15 | 15 | 2×10-7 |
3 数值模拟结果与试验结果对比
3.1 载荷-位移曲线
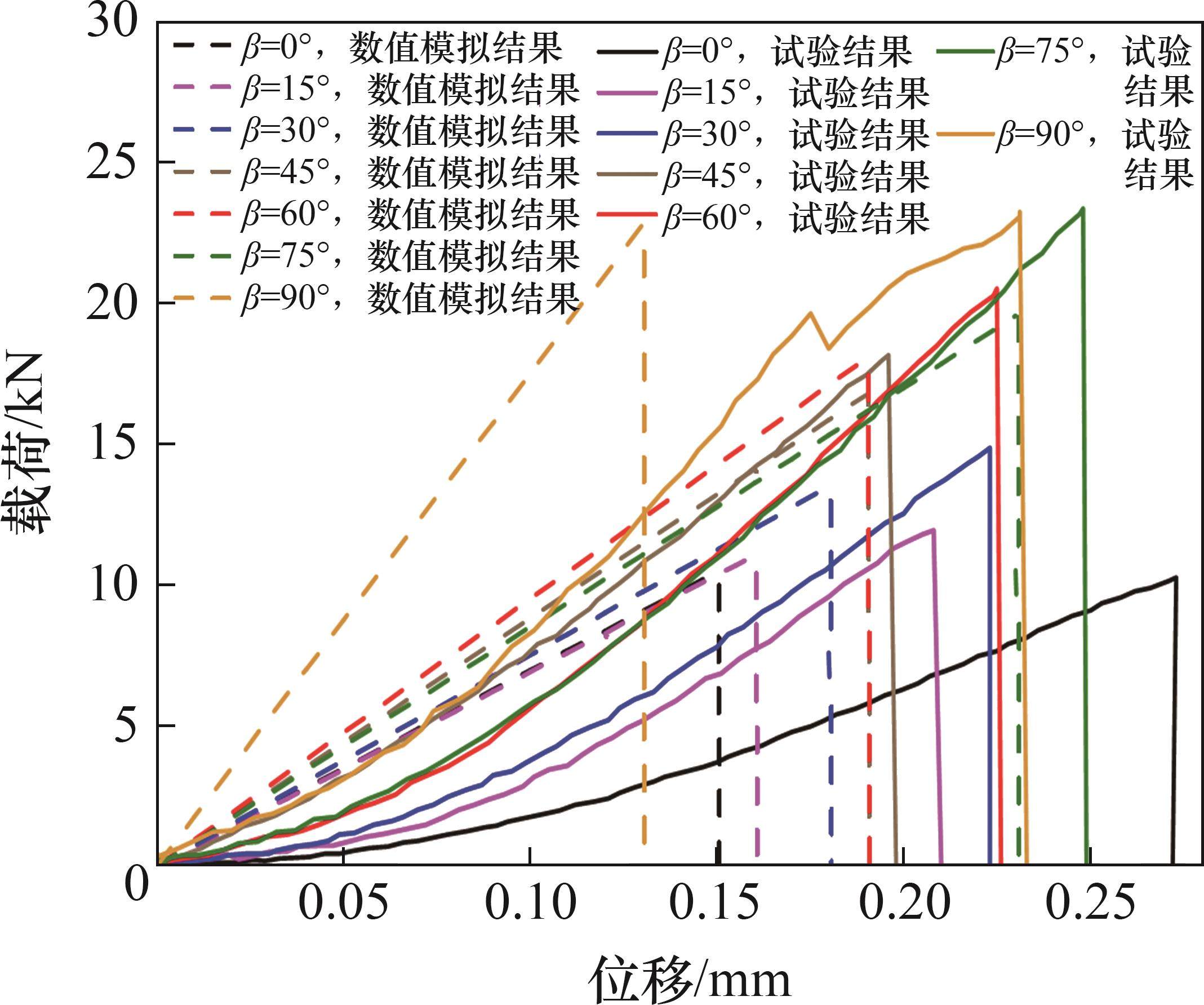
不同加载角度下数值模拟与试验载荷-位移曲线对比如图6所示。从图6可见:在不同加载角度下,试验和数值模拟的载荷-位移曲线吻合较好;模拟载荷在达到峰值后呈现陡降趋势,很好地表现了层状页岩的脆性破坏特征;峰值载荷均随着加载角度的增加逐渐上升,反映层状页岩具有显著的各向异性特征。然而,页岩的层状结构具有一定厚度,且发育有一定量的微孔隙和微裂隙,载荷-位移曲线加载初期表现为上凹的压密阶段,但由于数值模拟的局限性,无法考虑层理厚度等微观结构参数的影响,导致位移的试验结果和数值模拟结果存在一定差异。
3.2 巴西劈裂强度
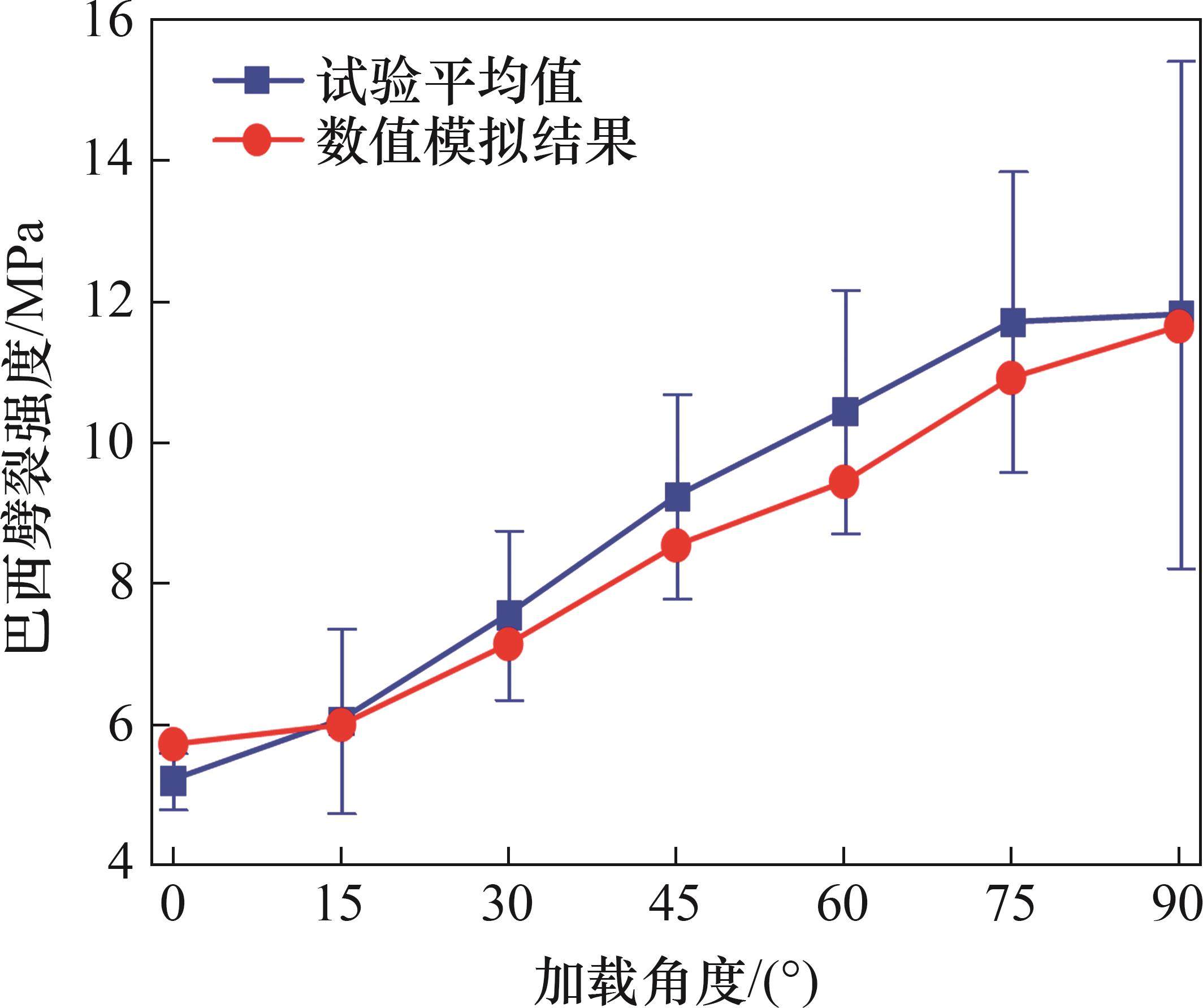
根据不同加载角度的峰值载荷,利用式(1)计算不同加载角度下BD试样的巴西劈裂强度,并与试验结果进行对比,结果如图7所示。从图7可见:巴西劈裂强度数值模拟与试验结果均随加载角度的增加近似呈线性增长;当加载角度为0°时,巴西劈裂强度最小,数值模拟结果与试验结果分别为5.32 MPa和5.62 MPa;当加载角度为90°时,巴西劈裂强度最大,数值模拟结果与试验结果分别为11.6 1MPa和11.07 MPa;数值模拟结果与试验结果的各向异性比值分别为2.18和2.00,均表现出显著的各向异性特征。此外,在不同加载角度下,巴西劈裂强度数值模拟结果与试验平均值间的相对误差<10%,验证了数值模拟的准确性和有效性。
3.3 破坏模式
图8所示为不同加载角度下数值模拟与试验试样的破坏模式对比,其中,红色线条为加载方向、蓝色线条为层理方向、绿色线条为裂纹破坏轨迹。从图8可见:破坏模式的数值模拟结果与真实破坏模式吻合较好,能够较真实地反映不同加载角度条件下破坏模式的差异性;当β=30°和β=45°时,数值模拟结果与试验结果存在一定差异,这是因为有限元模型没有考虑页岩层理的非均质性、非均匀层厚及其与页岩基质之间的摩擦力[32]。
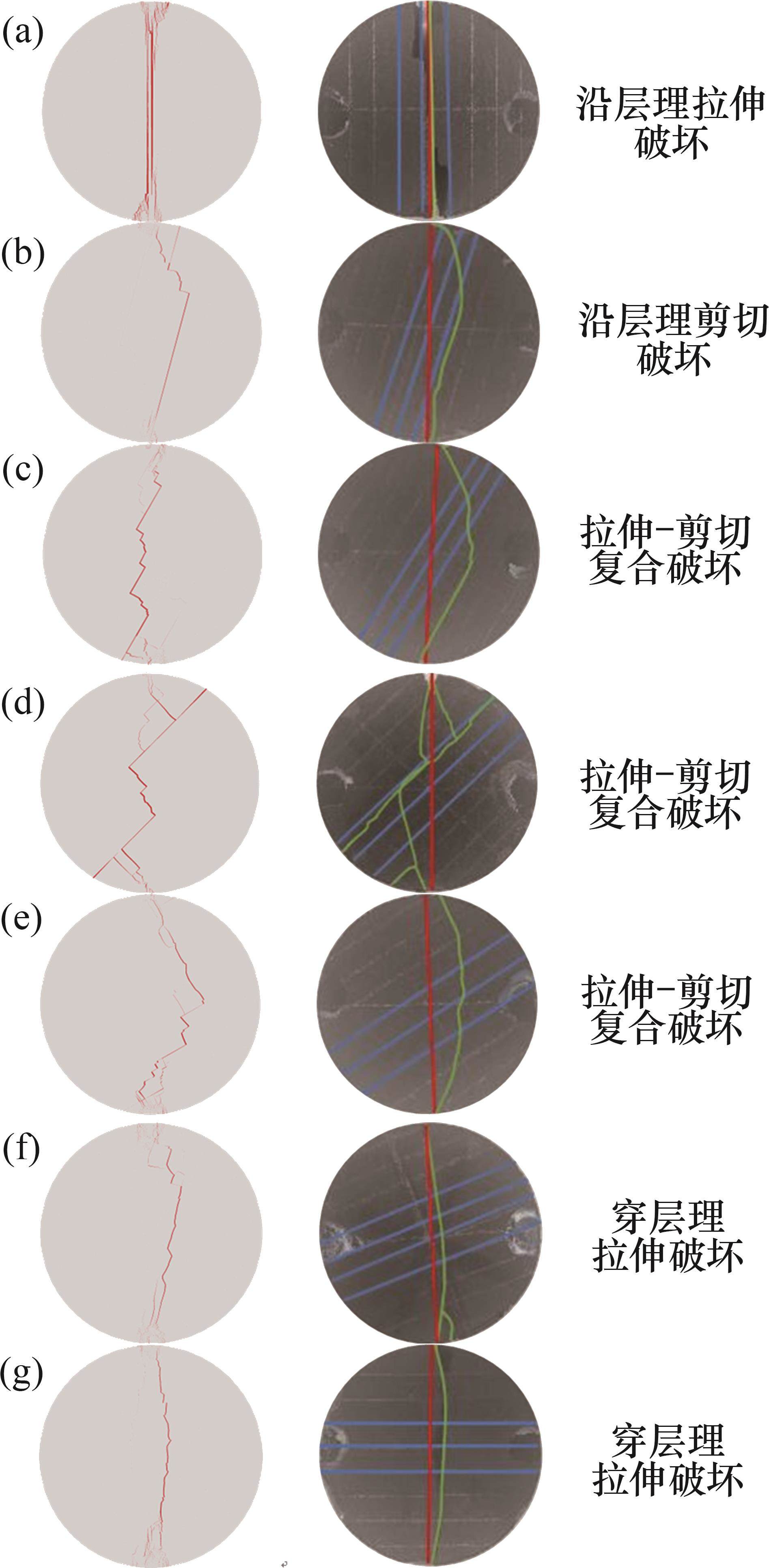
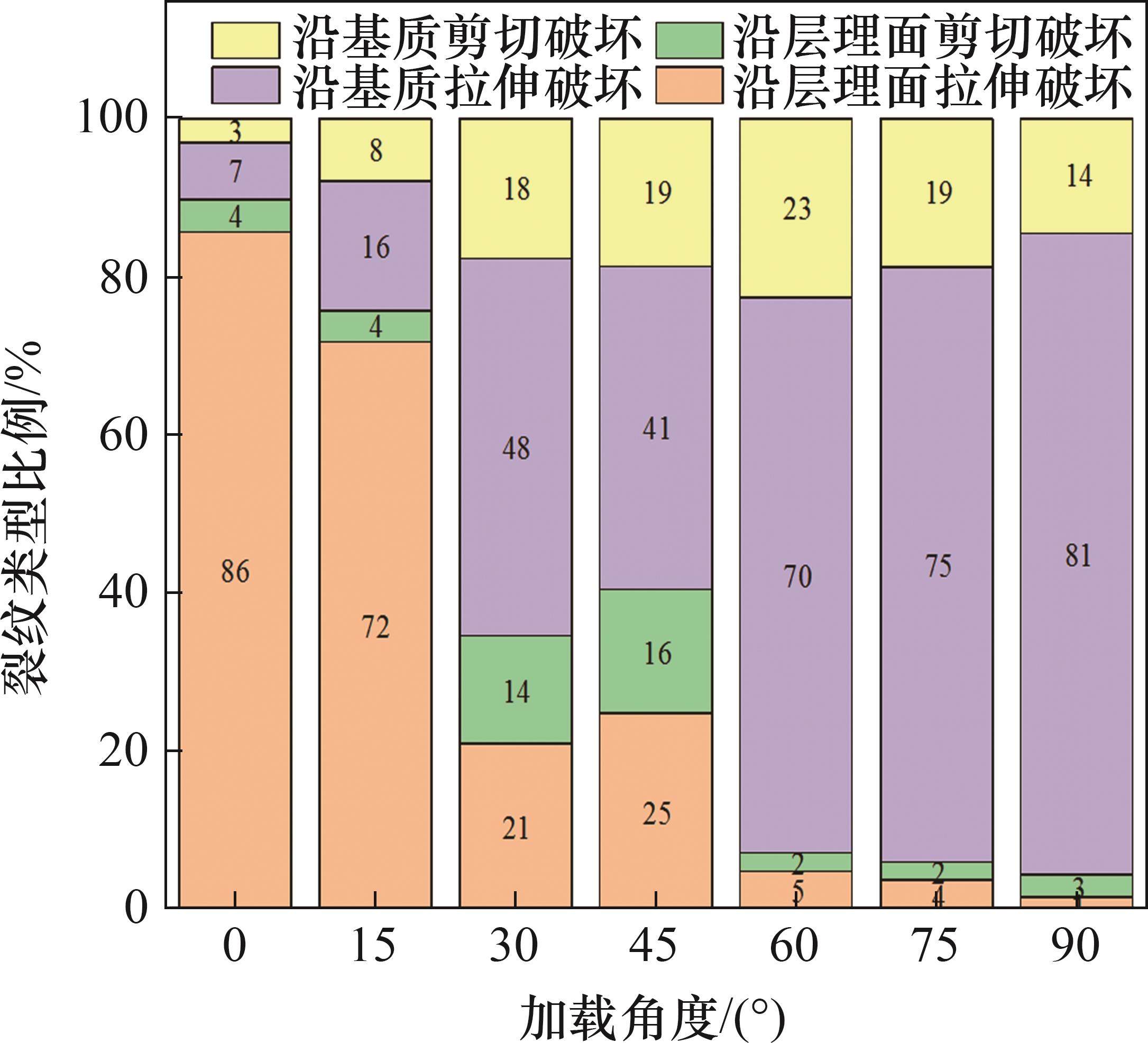
为了进一步分析不同加载角度下拉伸和剪切破坏的比例,采用PYTHON语言对ABAQUS软件进行二次开发,提取层理和基质黏聚单元的MMIXDME数据M(M=-1表示单元未破坏,0<M≤0.5表示单元以拉伸破坏为主,0.5<M<1表示单元以剪切破坏为主),结果如图9所示。从图9可见:当加载角度β=0°和15°时,破坏模式主要由层理控制,产生沿层理的拉伸破坏,其比例分别为86%和72%;当加载角度β=30°~60°时,岩石基质拉伸和剪切破坏比例大幅增加,岩石基质拉伸破坏比例大于40%,剪切破坏比例大于20%,破坏模式上表现为沿层理和基质的拉伸-剪切复合破坏;当β=45°时,沿层理破坏的比例最大,沿层理拉伸和剪切破坏的比例分别为25%和16%;当β=60°时,沿层理破坏的比例最小,沿层理拉伸和剪切破坏的比例分别为5%和2%;当加载角度β=75°和90°时,破坏模式主要由岩石基质控制,主要产生穿层理的基质拉伸破坏,其比例分别为75%和81%,而沿层理破坏的裂纹比例<6%。因此,随着加载角度的增加,破坏模式主要由沿层理拉伸破坏先转变为沿层理和基质的拉伸-剪切复合破坏,最终再转变为岩石基质拉伸破坏,而且剪切破坏的比例先升高再降低,层理的影响逐渐减弱。
4 层理对页岩巴西劈裂的影响
4.1 层理间距的影响
4.1.1 等间距层理的影响
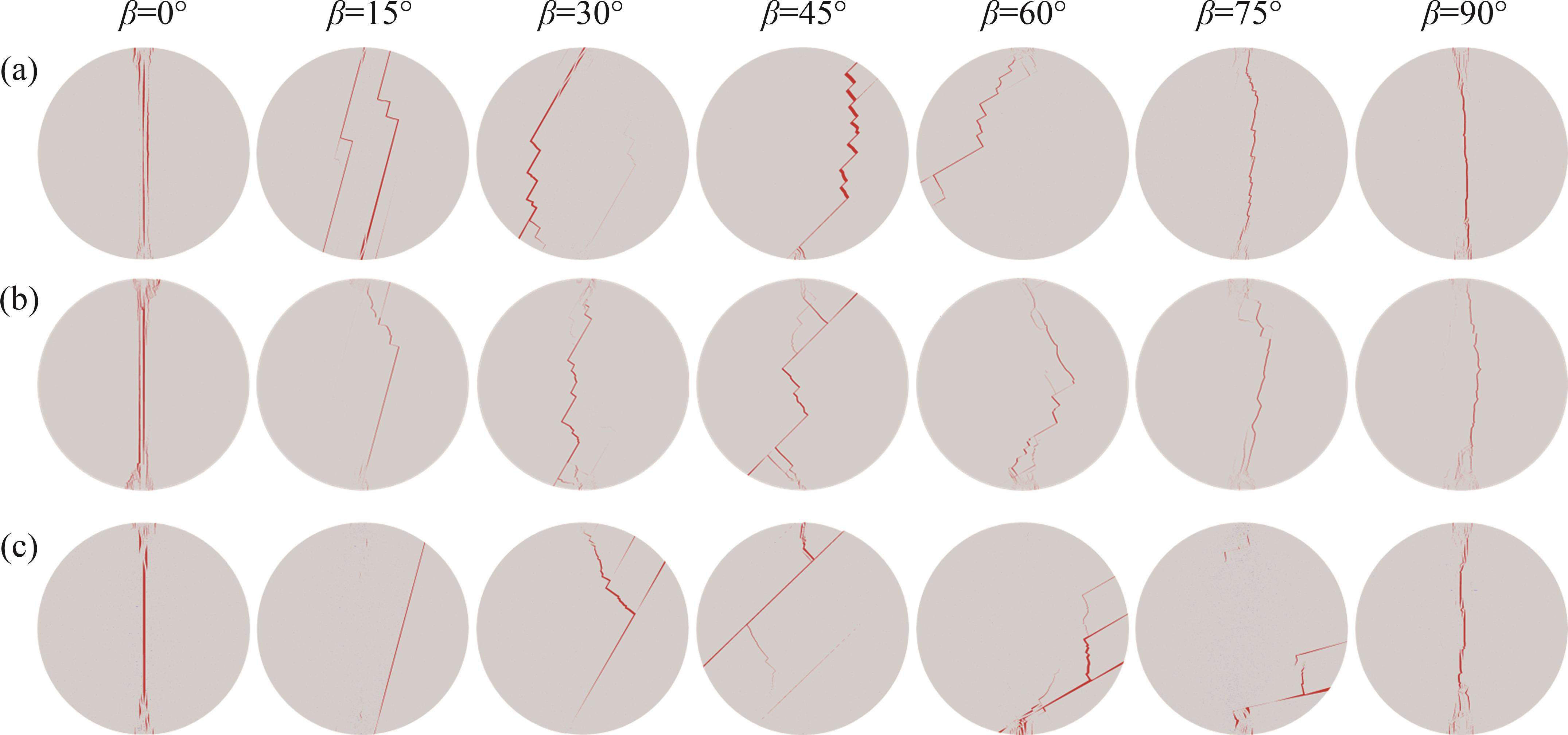
为了研究层理间距对层状页岩试样劈裂强度和破坏模式的影响,建立了层理面间距分别为3、6和9 mm的等间距模型,如图10所示,其中,s=6 mm为原模型。此外,模拟过程中选用相同类型的单元,通过优化网格数量,保证3种模型的单元数量差低于2%,从而最大程度地消除单元数量和类型对模拟结果的影响。

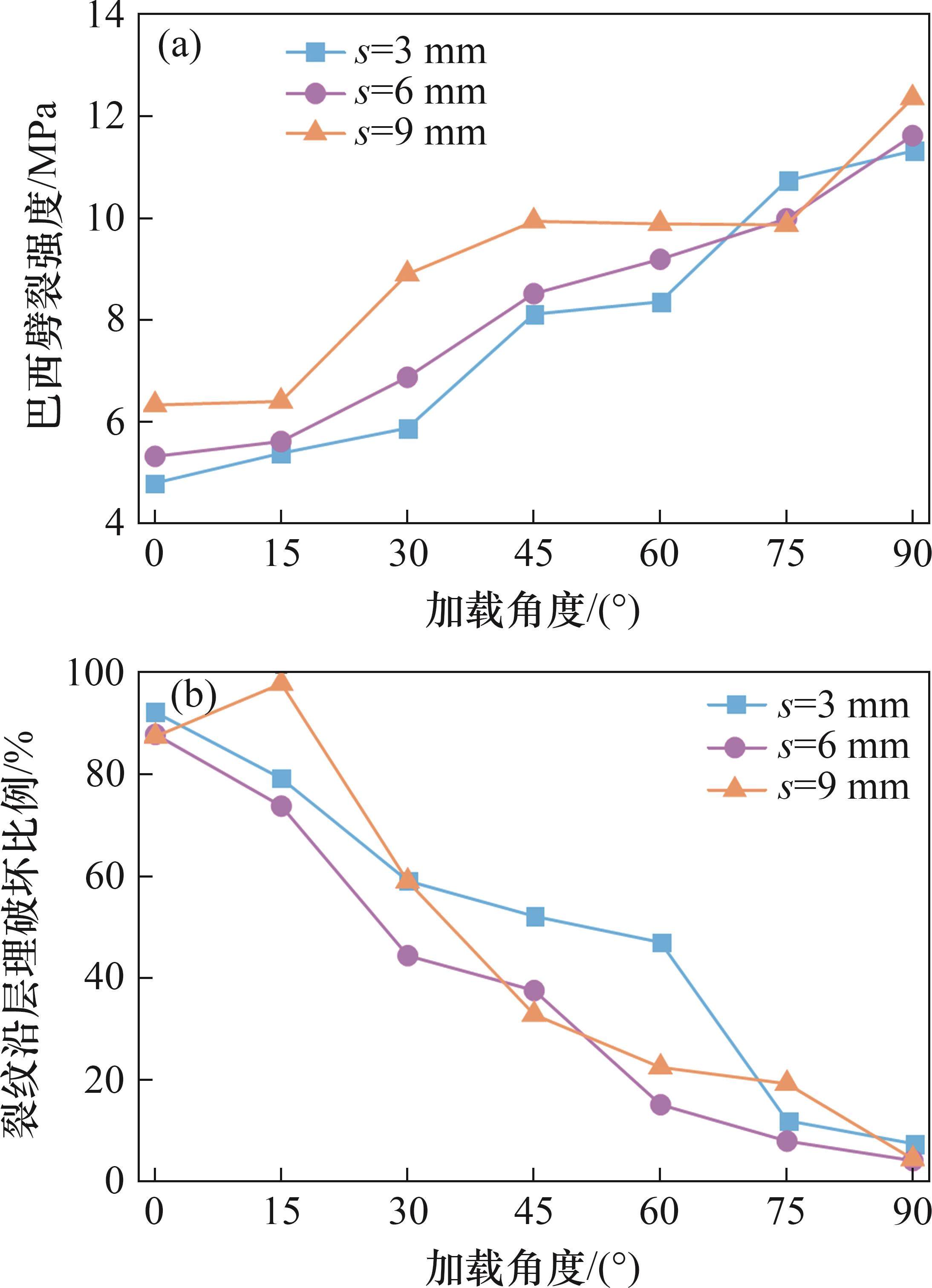
不同层理间距下的数值模拟结果如图11和图12所示,其中,图12(b)所示为不同加载角度下裂纹沿层理破坏的比例,其计算是通过PYTHON对ABAQUS进行二次开发,以材料刚度退化标量SDEG数据S为判断标准(S=1表示单元完全破坏,S<1表示单元未完全破坏),分别提取层理和基质黏聚单元的破坏数量,以便从微观角度分析层理间距对层状页岩裂纹扩展的影响。由图12可见:层理间距对不同加载角度下巴西劈裂强度影响较小,当加载角度β=30°和75°时,3种层理间距下巴西劈裂强度差异较大,最大差值分别为2 MPa和2.3 MPa;随着加载角度增加,当s=3 mm和6 mm时,巴西劈裂强度整体上保持逐渐增大的趋势;当s=9 mm时,巴西劈裂强度呈先上升再下降后再上升的趋势;层理间距对破坏模式的影响较为显著,当加载角度β=0°~15°时,层理间距对破坏模式的影响较小,3种层理间距条件下试样主要沿层理面拉伸破坏;当加载角度β=30°~75°时,试样的破坏模式存在一定的差异,但仍然表现为沿层理和基质的拉伸-剪切复合破坏;当加载角度β=90°时,试样的破坏模式几乎不受层理间距的影响,沿层理破坏的比例不超过10%,主要产生岩石基质的拉伸破坏。因此,在等间距层理条件下,层理间距对巴西劈裂强度的影响较小,仅对β=30°~75°试样的破坏模式有一定影响。
4.1.2 非等间距层理的影响
天然层状页岩的层理并不是等间距的,为了分析非等间距层理对页岩巴西劈裂强度和破坏模式的影响,通过随机生成不同厚度随机数,建立了2种非等间距模型,如图13所示。
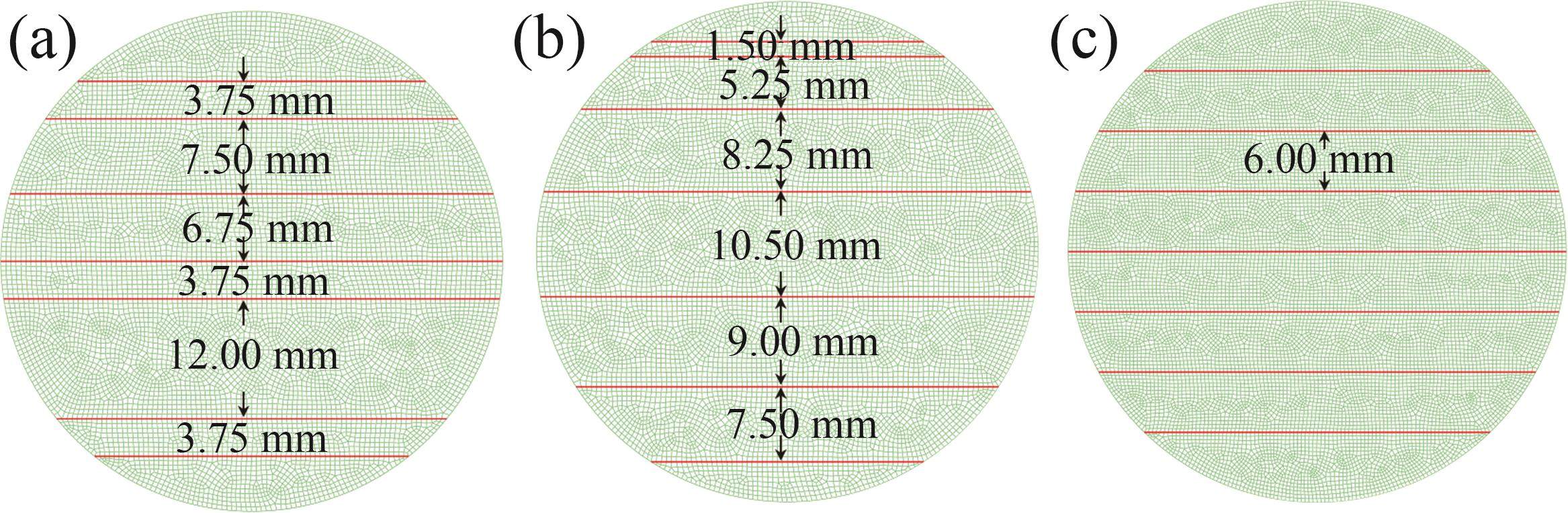
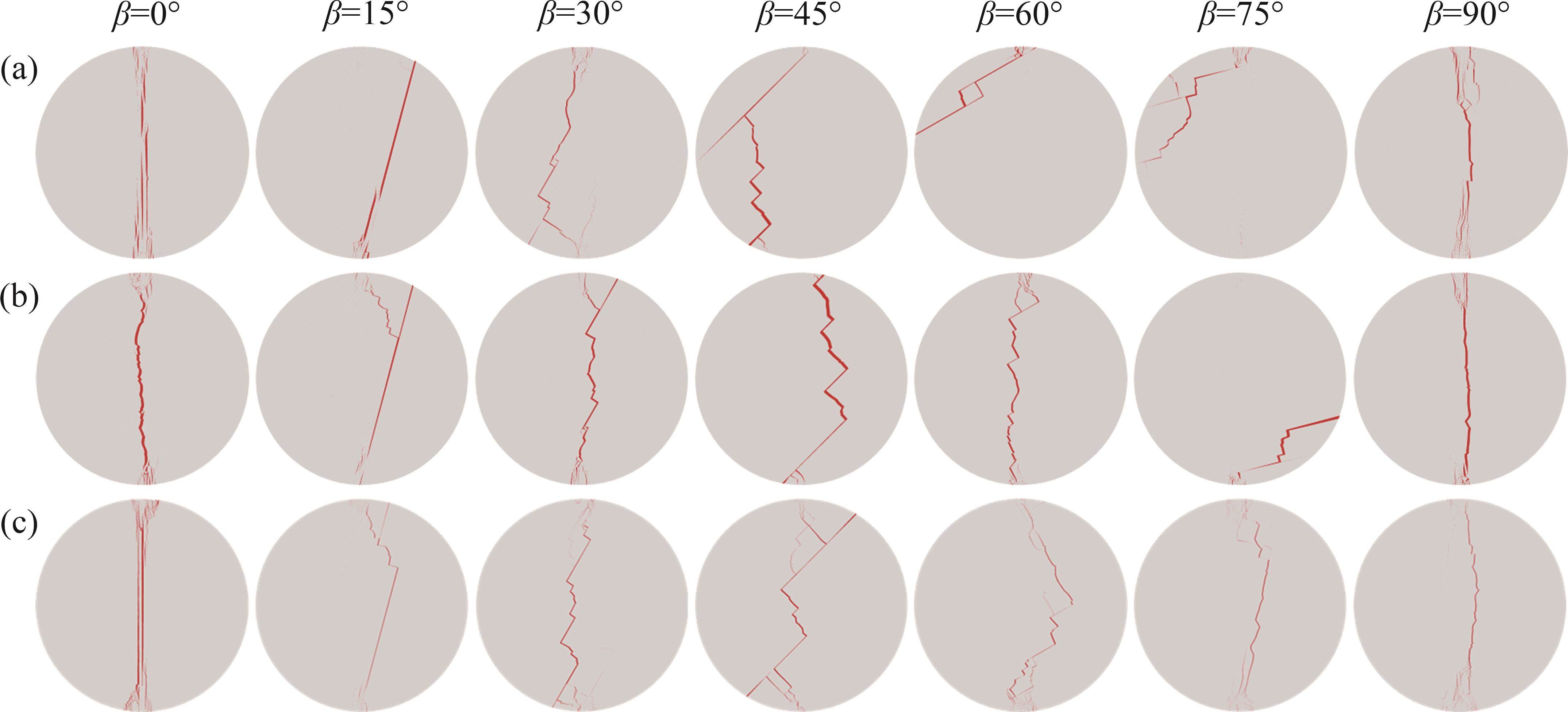
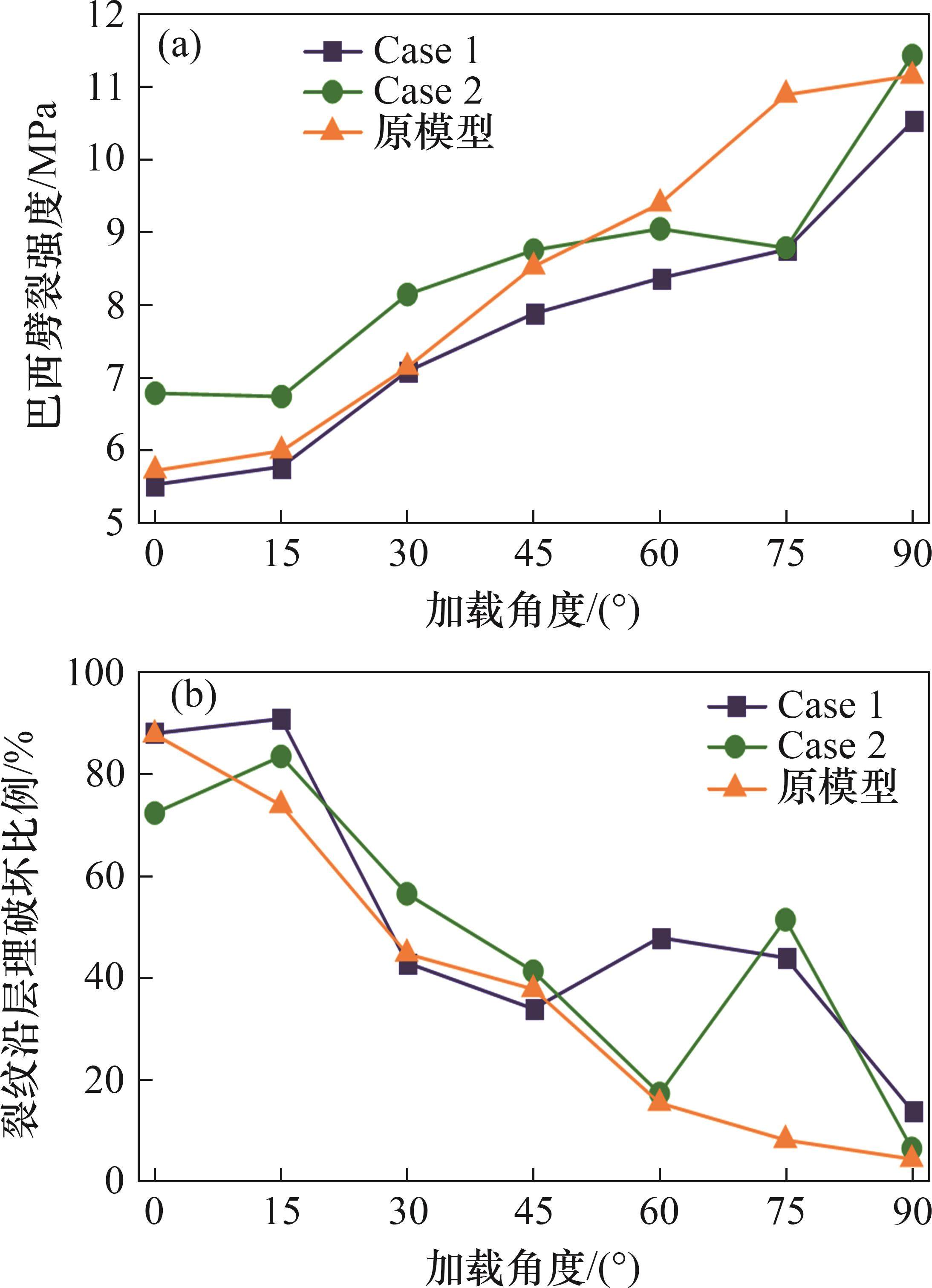
图14和图15所示为2种非等间距数值模型与原模型结果的对比。由图14和15可见:非等间距层理与等间距层理对BD试样力学行为的影响基本一致,二者之间无显著差异性;Case1和原模型的巴西劈裂强度随加载角度的增加而增大,而Case2的巴西劈裂强度在β=0°~60°时持续升高,但在β=75°时出现了巴西劈裂强度明显偏低的现象,这主要是裂纹被层理捕捉,裂纹沿层理破坏的比例增加所致,这种破坏模式不仅与层理分布有关,而且与层理强度有关。整体来看,非等间距层理对破坏模式的影响明显大于其对巴西劈裂强度的影响;在加载角度β=0°~15°时,3种模型的破坏模式主要是沿层理的拉伸破坏;当加载角度β=30°~75°时,非等间距层理主要影响裂纹的破裂轨迹,但并不会明显改变裂缝沿层理破坏的比例;当加载角度β=90°时,非等间距层理对破坏模式基本无影响。因此,等间距和非等间距层理对试样劈裂强度的影响较小,主要影响裂纹扩展轨迹和破坏模式,但并不会改变破坏机制和巴西劈裂强度随加载角度变化的规律。
4.2 层理面强度的影响
为研究层理强度对页岩试样的影响,保持原模型基质黏聚单元力学参数不变,强度参数选取原模型层理黏聚单元的0.50、0.75、1.25和1.50倍,建立4种不同层理强度的数值模型。不同层理强度下黏聚单元强度参数如表3所示。
| 序号 | 基质黏聚单元 | 层理黏聚单元 | ||||
|---|---|---|---|---|---|---|
| tn/MPa | ts/MPa | tt/MPa | tn/MPa | ts/MPa | tt/MPa | |
| Case 1 | 10 | 15 | 15 | 2.50 | 4 | 4 |
| Case 2 | 10 | 15 | 15 | 3.75 | 6 | 6 |
| Case 3 | 10 | 15 | 15 | 5.00 | 8 | 8 |
| Case 4 | 10 | 15 | 15 | 6.25 | 10 | 10 |
| Case 5 | 10 | 15 | 15 | 7.50 | 12 | 12 |
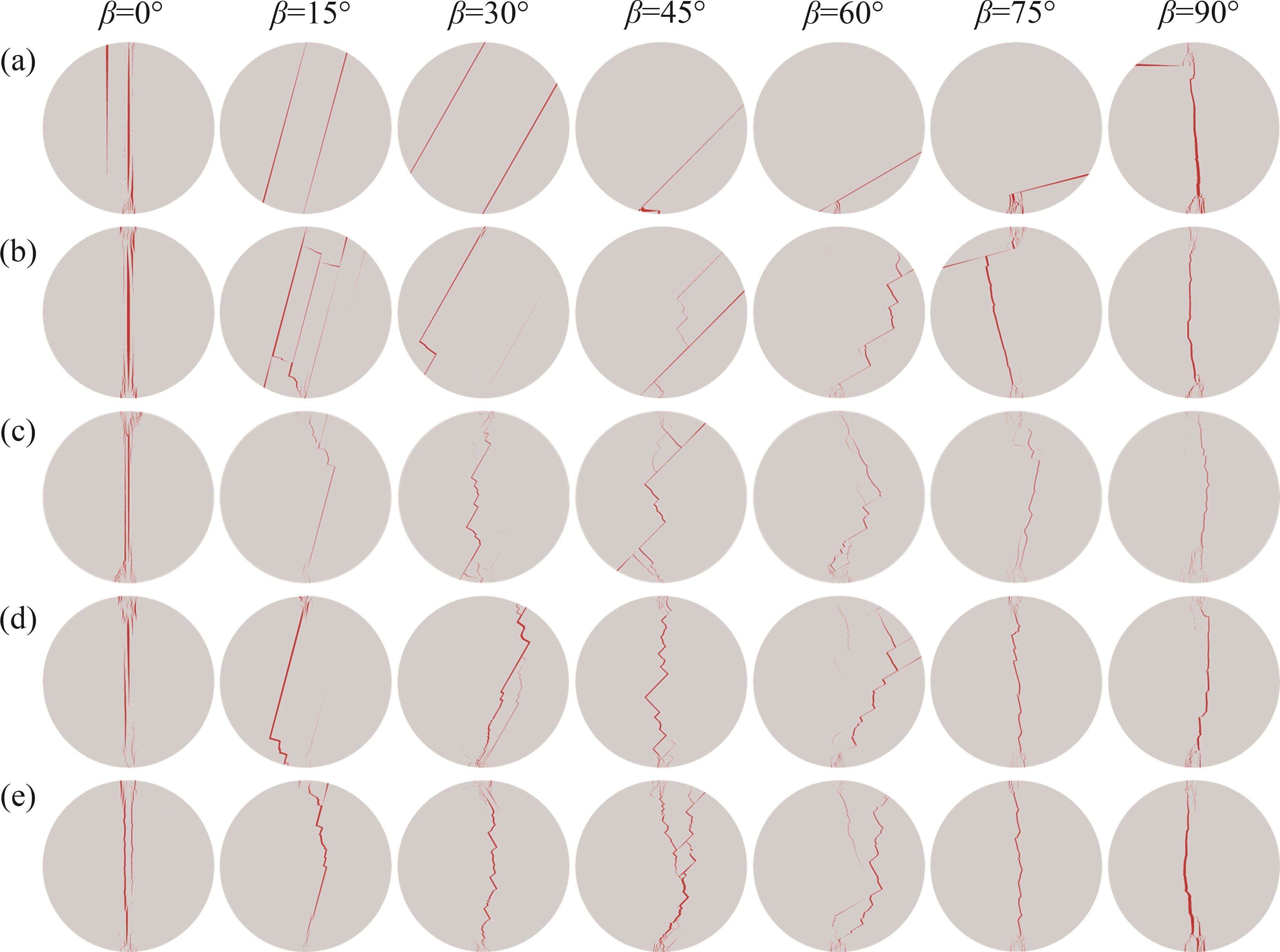
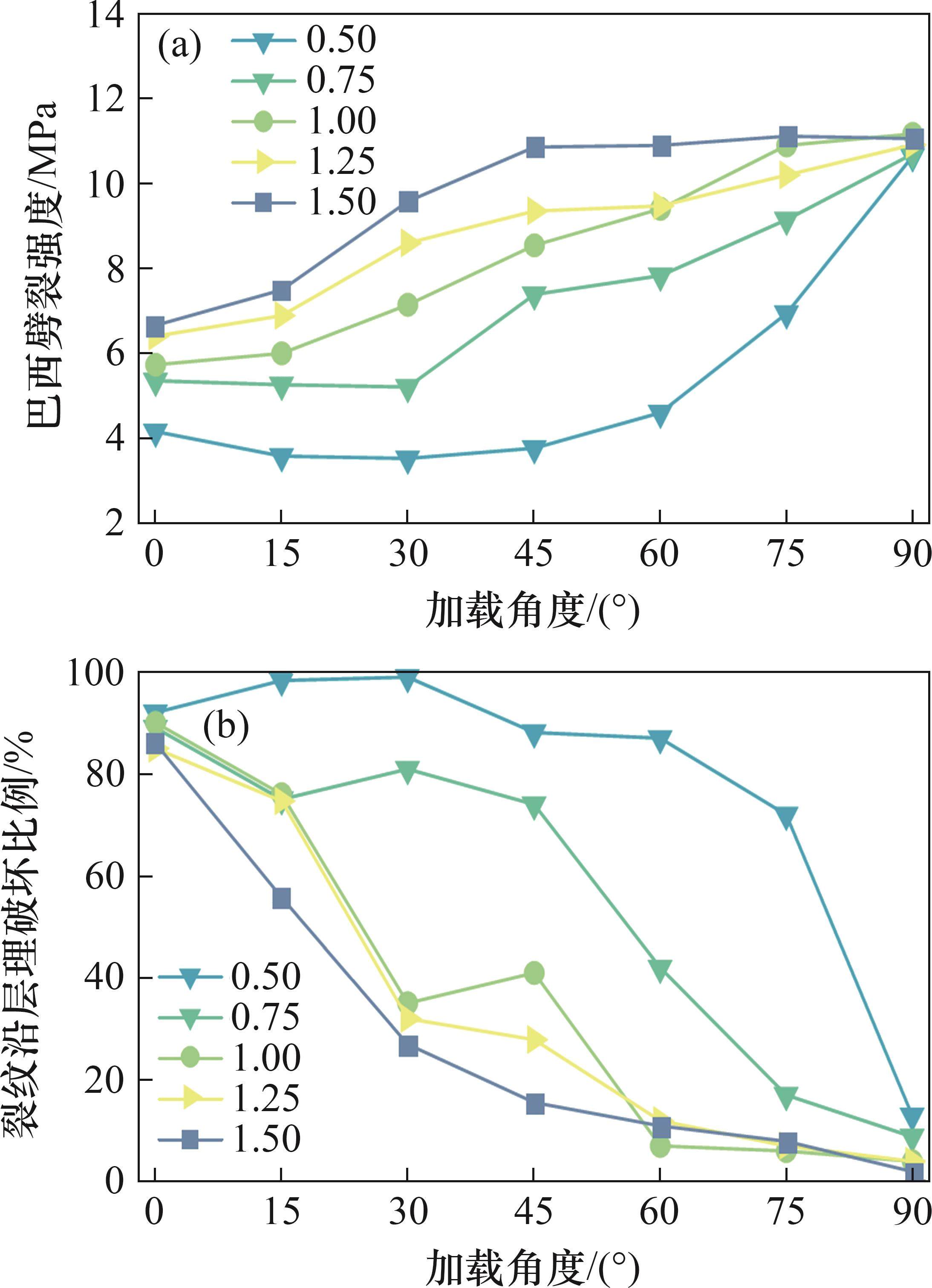
图16和图17所示为层理强度对页岩巴西劈裂的影响。从图16和17可见:层理强度对页岩巴西劈裂强度具有显著影响;随着层理强度降低,巴西劈裂强度显著降低,特别是当层理强度比为0.5꞉1.0时,加载角度β=0°~75°的试样主要产生沿层理的拉伸或剪切破坏,沿层理破坏的裂纹比例高达70%以上,与其他层理强度条件的巴西劈裂强度差值可达7.1 MPa;当加载角度β=90°时,层理强度对巴西劈裂强度和破坏模式的影响较小,不同层理强度的巴西劈裂强度差值低于0.6 MPa,且破坏模式主要由岩石基质强度控制;当层理强度比为0.75꞉1.00、1꞉1和1.25꞉1.00时,层理强度对巴西劈裂强度的影响开始减弱,巴西劈裂强度整体上随加载角度呈近似线性增大的趋势;当β=0°~15°时,产生沿层理的拉伸或剪切破坏;当β=30°~60°时,产生沿层理和基质的拉伸-剪切复合破坏;当β=75°~90°时,产生沿基质的拉伸破坏;当层理强度比为1.5꞉1.0时,层理强度与基质强度接近,层状页岩逐渐转变为各向同性材料,层理的影响大幅降低,除β=90°以外,其余加载角度的巴西劈裂强度均有不同程度增加,特别是当β=30°~60°时,巴西劈裂强度的增加幅度可达188%;在破坏模式方面,除β=0°和β=15°的试样仍以沿层理破坏为主外,其余加载角度试样均为岩石基质的拉伸-剪切复合破坏或拉伸破坏,平均裂纹沿层理破坏比例约12.6%。因此,层状页岩的巴西劈裂强度和破坏模式具有较强的层理强度依赖性,低层理强度会显著影响试样的力学行为,导致其巴西劈裂强度大幅降低,破坏模式主要受层理控制,产生拉伸或剪切破坏;而高层理强度会使试样逐渐转变为各向同性材料,导致其巴西劈裂强度大幅增加,破坏模式主要受岩石基质控制,产生拉伸或拉伸-剪切复合破坏。
5 讨论
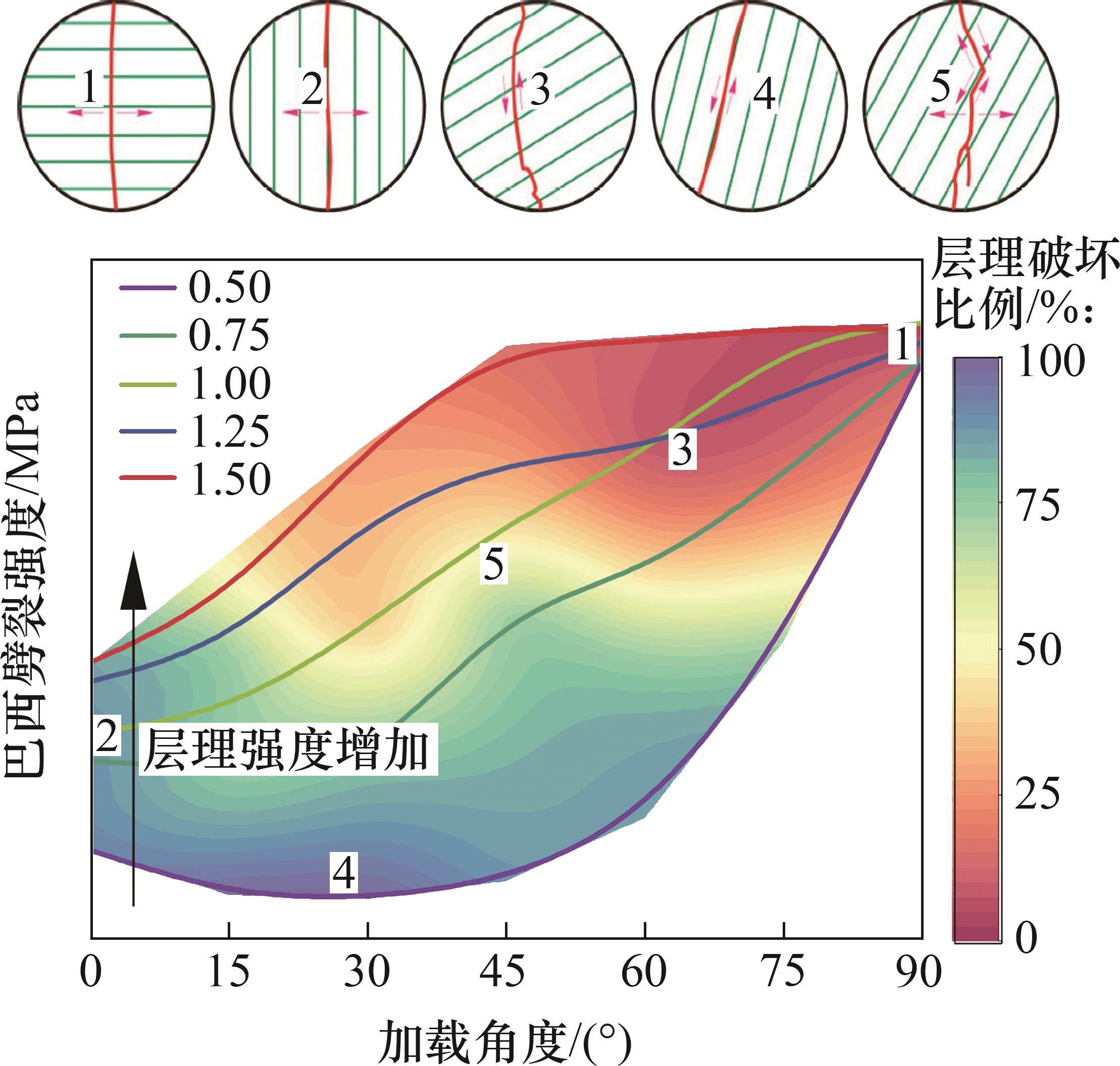
MA等[16]基于大量巴西劈裂试验结果,总结了5种类似的典型破坏模式,如图18所示[16],其中“模式1”表示穿层理面的拉伸破坏,“模式2”表示沿层理面的拉伸破坏,“模式3”表示穿层理面的剪切破坏,“模式4”表示沿层理面的剪切破坏,“模式5”表示沿层理面和岩石基质的拉伸-剪切复合破坏。崔壮等[33]进一步证实了这5种典型破坏模式。因此,根据不同层理强度的数值模拟结果,建立了层状页岩的破坏模式分类图,如图19所示。从图19可见:纯拉伸破坏仅发生在β=0°和β=90°时,纯剪切破坏发生在β=15°~45°或低层理强度时,而其他区域均随着层理强度的增加会发生更为复杂的拉伸-剪切复合破坏。由此可见,拉伸-剪切复合破坏是层状页岩试样破坏的主要形式,层状页岩试样强度、破坏模式主要受加载角度和层理强度所控制。

6 结论
1) 基于全局嵌入零厚度黏聚单元法,考虑页岩层理的影响,建立了层状页岩试样的二维黏聚单元有限元模型,数值模拟和试验得到的巴西劈裂强度和破坏模式均较吻合,巴西劈裂强度最大相对误差不超过10%。
2) 数值模拟和试验得到的巴西劈裂强度均随加载角度的增加呈线性增加,在β=0°时,巴西劈裂强度最小、在β=90°时,巴西劈裂强度最大,且二者各向异性比值分别为2.18和2.00,说明龙马溪页岩具有显著的各向异性特征。
3) 在不同加载角度下,龙马溪页岩试样的破坏模式受层理影响会产生不同类型的裂纹。随着加载角度的增加,破坏模式主要由沿层理的拉伸破坏先转变为沿层理和基质的拉伸-剪切复合破坏,最终再转变为基质的拉伸破坏,而且剪切破坏的比例先升高再降低,层理的影响随加载角度的增加逐渐减弱。
4) 层理间距对龙马溪页岩试样力学行为影响较小。在等间距条件下,层理间距对β=30°和
β=75°试样的劈裂强度有一定影响,对β=30°~75°的试样破坏模式影响显著,但对破坏机理并无显著影响;在非等间距条件下,层理间距的影响依然较小,主要体现为不同层理分布导致的裂纹扩展轨迹不同。
5) 层理强度对龙马溪页岩试样的影响非常显著。当β=30°~75°时,低层理强度会导致巴西劈裂强度大幅降低,破坏模式主要受层理控制产生拉伸或剪切破坏;高层理强度会使试样逐渐转变为各向同性材料,导致其巴西劈裂强度大幅增加,破坏模式主要受基质控制产生拉伸或拉伸-剪切复合破坏;当β为0°、15°和90°时,层理强度对试样的力学行为影响较小。
马天寿, 王浩男, FADHEL A M, 等. 基于黏聚单元法的层状页岩巴西劈裂数值模拟[J]. 中南大学学报(自然科学版), 2025, 56(2): 702-715.
MA Tianshou, WANG Haonan, FADHEL A M, et al. Numerical simulation of Brazilian splitting of layered shale based on Cohesive element method[J]. Journal of Central South University(Science and Technology), 2025, 56(2): 702-715.

