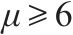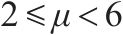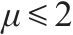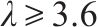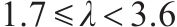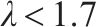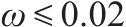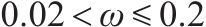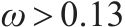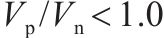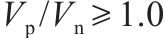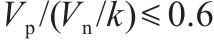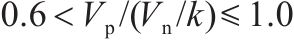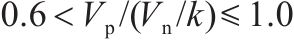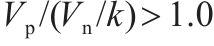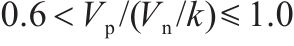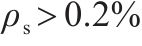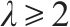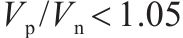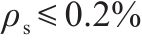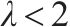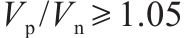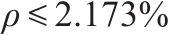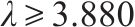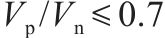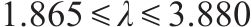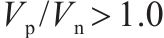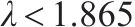我国许多西部铁路靠近断层,近断层地震会对铁路桥墩造成严重的破坏[1]。近断层重力式矮墩通常设置高配筋,其地震破坏模式表现为剪切与弯剪破坏。然而,现行的《铁路工程抗震设计规范》[2]并未给出此类桥墩的抗震设计方法,因此开展“高配筋”铁路矮墩在地震作用下的破坏模式及抗剪强度计算公式研究具有重要意义。目前,诸多学者已对铁路重力式桥墩进行了拟静力试验研究。赵冠远等[3]对6个圆端形桥墩进行了拟静力试验,指出剪跨比为2.4的桥墩会发生弯剪破坏。陈兴冲等[4]提出了低配筋(配筋率为<0.5%)混凝土重力式弯曲破坏型桥墩的抗震设计方法。邵光强等[5]针对高速铁路矮墩开展了4个模型桥墩的拟静力试验,指出高速铁路矮墩设计时需保证其在横桥向有足够的抗剪承载力。沈林白等[6]研究了不同配筋率和配箍率对小剪跨比铁路桥墩抗震性能的影响,并基于试验定义了桥墩5种损伤状态对应的位移延性比临界值。LU等[7]对配筋率为0.3%和0.4%的2个重力式桥墩进行试验,发现配筋率低的桥墩破坏时有明显的钢筋拉断现象。然而,上述研究主要侧重于低配筋铁路重力式桥墩顺桥向的抗震性能,很少涉及小剪跨比“高配筋”铁路重力式桥墩的地震破坏模式及抗剪强度计算公式方面的研究。本文以某近断层高原铁路桥梁为工程背景,设计并制作了5个剪跨比从1.4到3.2的高配筋铁路重力式桥墩缩尺模型,通过拟静力试验研究剪跨比对其横桥向破坏特征及抗震性能的影响,并基于试验结果给出了铁路重力式桥墩的地震破坏模式判别方法及抗剪强度计算公式。
1 拟静力试验设计
1.1 模型桥墩设计与制作
选取某近断层高原铁路桥梁的重力式桥墩为原型,设计了5个缩尺模型桥墩进行拟静力试验。原型桥墩纵筋率为0.58%,明显高于常见的铁路重力式桥墩[4-5, 7],其配置134根直径32 mm的HRB500钢筋。模型桥墩按剪跨比从小到大排列分别记为R1~R5,R1~R4和R5的长度相似常数SL分别为1/8和1/10,原型与缩尺模型之间的相似关系列于表1。模型尺寸及配筋见图1,构造参数列于表2,其中剪跨比λ为墩高与截面受力方向尺寸之比。模型材料的150 mm

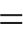
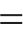
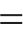
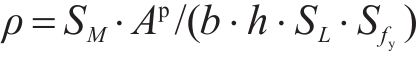
式中: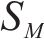
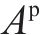
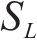
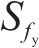
| 物理量 | 量纲 | 关系式 | 相似常数 |
|---|---|---|---|
| 长度/L | L | 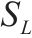 | 1/8(1/10) |
| 面积/A | L2 | 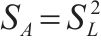 | 1/82(1/102) |
| 应力/σ | FL-2 | 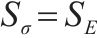 | 1 |
| 应变/ε | — | 1 | 1 |
| 弹性模量/E | FL-2 | 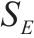 | 1 |
| 集中力/P | F | 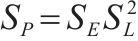 | 1/82(1/102) |
| 力矩/M | FL | 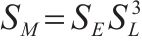 | 1/83(1/103) |
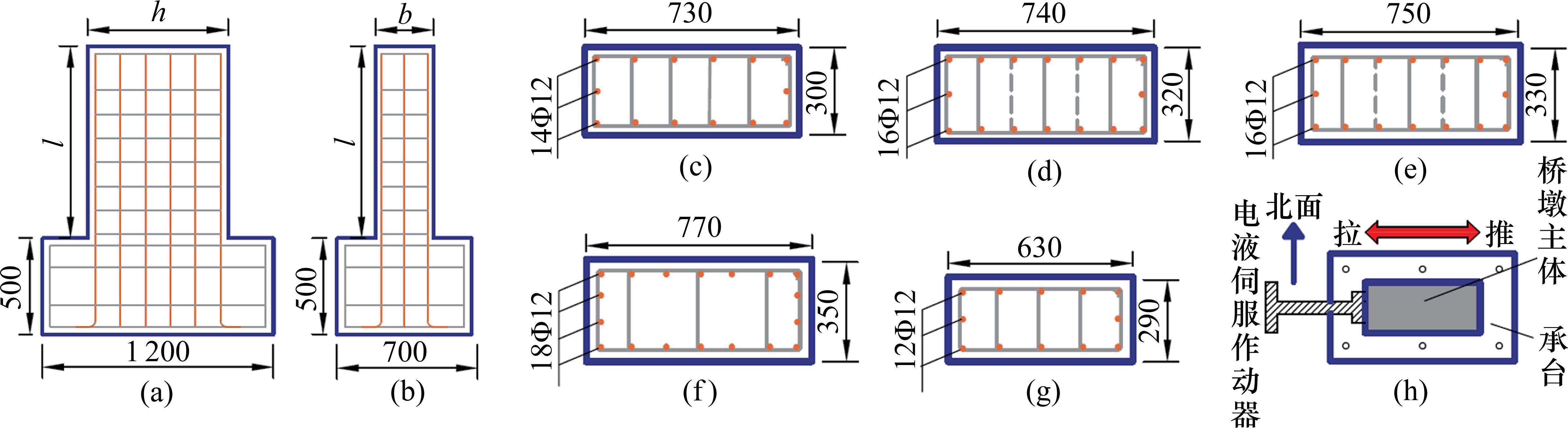
| 桥墩 | 墩高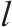 | 截面尺寸 | 配筋率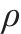 | 剪跨比 | 轴压比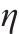 | 配箍率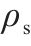 | 箍筋间距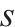 |
|---|---|---|---|---|---|---|---|
| R1 | 1 000 | 730×300 | 0.74 | 1.4 | 0.04 | 0.44 | 125 |
| R2 | 1 250 | 740×320 | 0.74 | 1.7 | 0.04 | 0.44 | 120 |
| R3 | 1 500 | 750×330 | 0.74 | 2.0 | 0.04 | 0.44 | 115 |
| R4 | 2 000 | 770×350 | 0.74 | 2.6 | 0.04 | 0.44 | 110 |
| R5 | 2 000 | 630×290 | 0.74 | 3.2 | 0.04 | 0.44 | 140 |
1.2 试验加载系统
试验加载装置见图2(a)、图2(b),模型桥墩使用锚杆穿过预留孔洞固定。竖向荷载通过固定在反力架上的千斤顶施加。电液伺服作动器最大水平推力为600 kN,量程为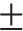
2 试验结果
2.1 试验现象
R1桥墩(λ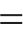
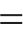
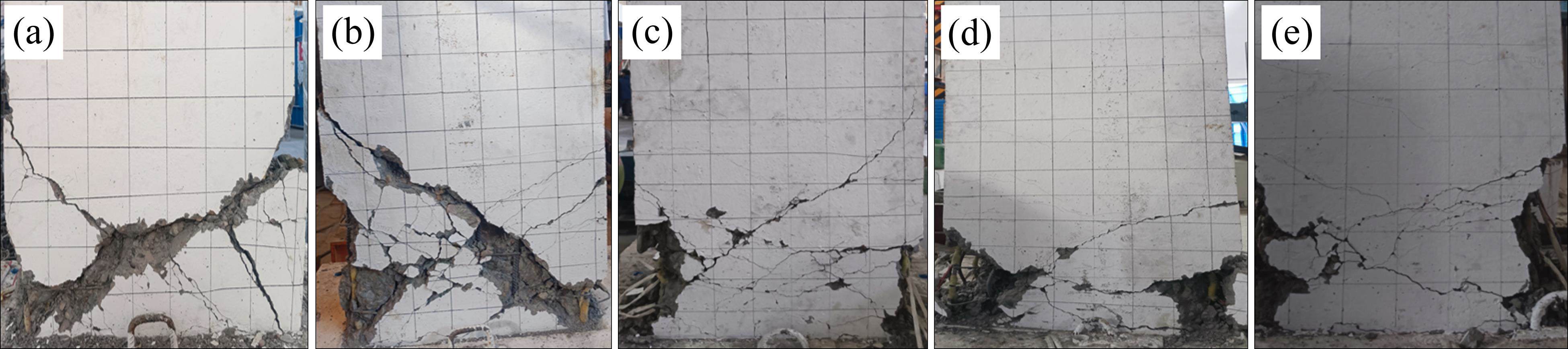
R3、R4及R5桥墩(λ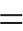
剪跨比从3.2减小到1.4,桥墩斜裂缝与桥墩纵轴线的夹角由60°减小到45°,斜裂缝占墩高的比值由20%增加到68%,破坏后“X”裂缝的宽度、深度均增大,而水平弯曲裂缝的数量和分布高度不断减少,桥墩破坏模式由弯剪破坏向剪切破坏转变。这表明剪跨比对铁路重力式桥墩的破坏模式有显著影响,鉴于剪切破坏的突然性,在工程中应尽量避免桥墩发生剪切破坏。
文中的桥墩由于纵筋率较高,其破坏时混凝土严重剥落,且由于剪跨比较小,斜裂缝发展明显。其破坏特征明显区别于纵筋突然拉断、混凝土基本没有压碎且墩底只有少量裂缝的低配筋重力式桥墩[4, 7]。因此,需要深入研究高配筋铁路矮墩的抗震性能及抗剪强度。
2.2 滞回曲线及骨架曲线
图4(a)~图4(e)给出了5个试件的墩顶荷载-位移滞回曲线,R4桥墩加载至35 mm时由于设备故障导致部分数据丢失,其形状在受推侧(正向)与其余4个略有不同。图4(f)给出了不同剪跨比下桥墩的骨架曲线。
由图4可知,在力控制加载阶段,5个桥墩的滞回曲线呈线性变化,滞回环面积小且基本没有残余变形,反映了桥墩处于弹性状态。进入位移控制阶段,由于混凝土开裂和钢筋变形,滞回曲线趋于饱满,残余变形逐渐增大,且因为强度退化,在同一加载位移下,后一循环的承载能力较前一循环低。水平力达到峰值荷载后,随着位移幅值的增加,纵筋或箍筋迅速屈曲甚至拉断及斜裂缝的迅速扩展,导致墩顶水平荷载骤降至峰值荷载的85%以下。所有桥墩的滞回曲线都出现不同程度的“捏拢”,这种现象主要是由墩身裂缝在循环荷载作用下不断张开、闭合引起的。对比5个桥墩的滞回曲线可以发现,剪跨比越大,滞回曲线越饱满,剪跨比越小,曲线“捏拢”效应越显著,这是因为剪跨比越小,桥墩的剪切变形越大[9],这与观察到的试验现象一致。
由图4(f)可以看出,所有桥墩的骨架曲线都经历了弹性阶段、强化阶段和退化阶段。在弹性阶段,墩顶水平力增长速度随着剪跨比的减小而增大,但进入退化阶段,剪跨比越小的桥墩承载力下降越快,原因是剪跨比小的桥墩在破坏时斜裂缝迅速扩展,导致截面抗剪面积减小,从而引起水平承载力骤降。
3 抗震性能分析
3.1 延性性能
根据骨架曲线得到的桥墩屈服点(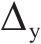
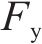
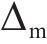
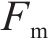
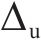
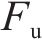
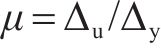
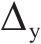
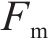
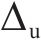
| 桥墩 | 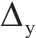 | 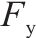 | 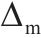 | 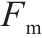 | 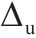 | 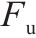 | 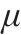 |
|---|---|---|---|---|---|---|---|
| R1 | 27.5 | 389 | 35.7 | 414 | 42.0 | 370 | 1.5 |
| R2 | 24.4 | 324 | 44.9 | 363 | 50.0 | 309 | 2.1 |
| R3 | 29.1 | 296 | 48.0 | 325 | 62.1 | 276 | 2.1 |
| R4 | 45.0 | 266 | 56.1 | 290 | 66.1 | 247 | 1.5 |
| R5 | 38.8 | 137 | 90.1 | 164 | 100.1 | 140 | 2.7 |
由表3可见,剪跨比为1.4~3.2的桥墩延性系数均较低,其值在1.5~2.7之间,体现出较差的延性性能。剪跨比从3.2减小到1.4,桥墩水平最大承载力从164 kN增加至414 kN、增加了约2.5倍,位移延性系数从2.7降低至1.5。这表明减小剪跨比可以显著提升桥墩的承载能力,但会降低其延性性能。
3.2 耗能能力
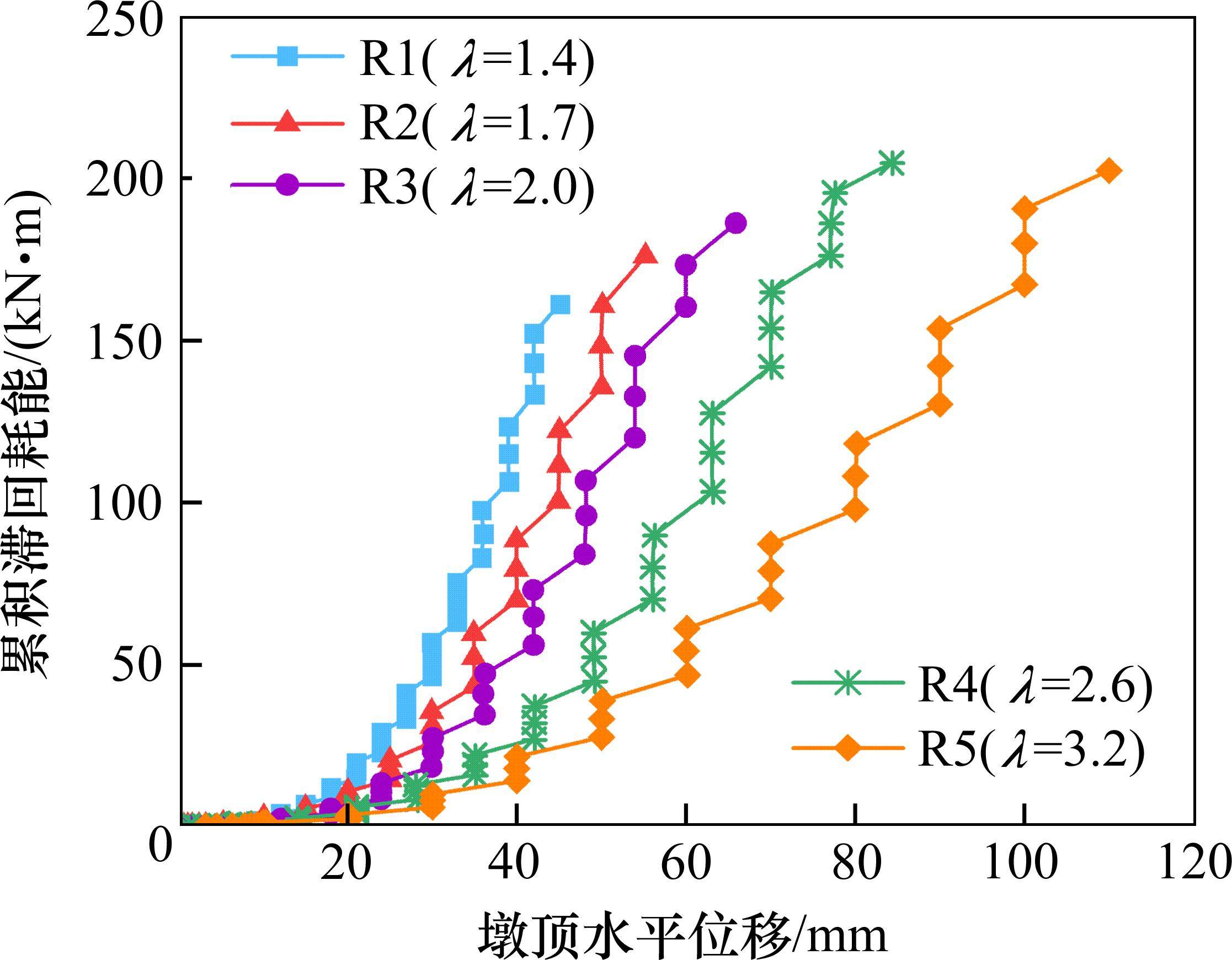
将各滞回环所包围的面积求和计算得到桥墩累积滞回耗能[11],5个模型桥墩的累积滞回耗能见图5。由图5可知,当位移幅值小于10 mm时,由于桥墩处于弹性状态,所以5个桥墩累积耗能几乎为0。随着位移幅值的增大,试件损伤加重,累积耗能呈指数增长。桥墩剪跨比越小,其水平承载力越大,所以在墩顶水平位移相同时,剪跨比越小的桥墩累积耗能越大。但由于剪跨比越小,桥墩的极限位移越小,所以减小桥墩的剪跨比,会降低其最终累积耗能。R5桥墩的最终耗能低于R4,原因在于R5的横截面面积仅为R4的68%。
3.3 刚度退化
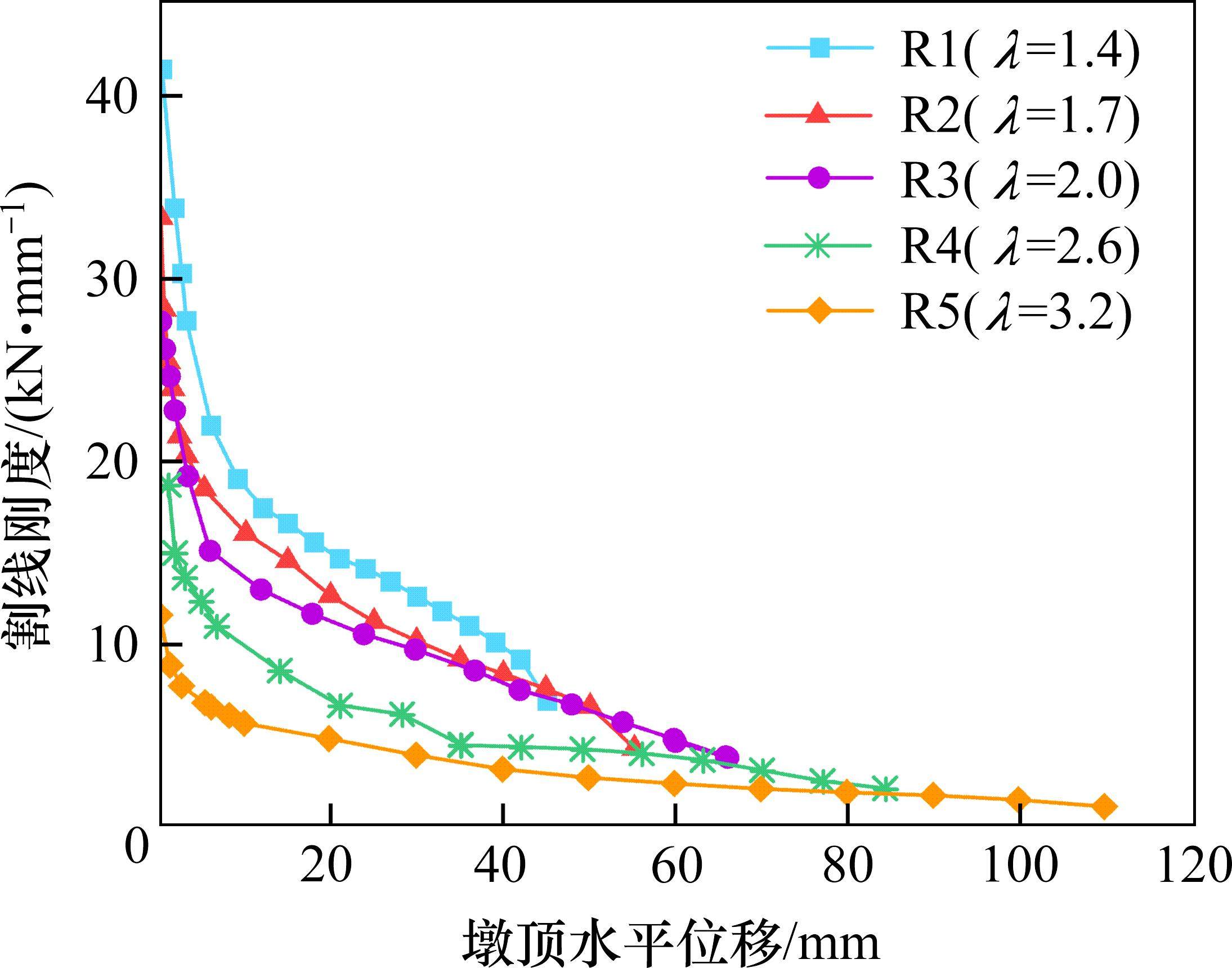
桥墩在拟静力试验中由于累积损伤,导致其刚度逐渐退化。本文引入《建筑抗震试验规程》(JGJ/T 101―2015)中的割线刚度来评估模型桥墩的刚度退化,割线刚度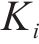
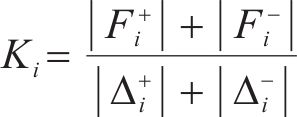
式中: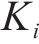
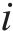
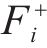
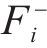
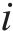
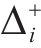
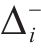
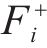
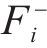
各模型桥墩刚度退化曲线见图6。由图6可以看出,加载初期,由于混凝土的开裂削减了试件的有效截面面积,所以各试件的刚度迅速下降。随着加载位移的增大,混凝土及钢筋的非线性耗能减缓了刚度退化的速率,但剪跨比为1.4和1.7的桥墩在最后破坏时由于箍筋拉断导致其刚度突然下降。此外,相较于剪跨比较大的试件R4和R5,剪跨比较小的试件R1、R2及R3在整个加载过程中展现出更大的刚度及更快的刚度退化速率,这是由于在同一加载位移下,剪跨比较小的试件损伤更严重。
4 重力式桥墩地震破坏模式判别方法
4.1 常用的桥墩破坏模式判别方法
桥墩在地震作用下可能出现弯曲、剪切或弯剪破坏模式[12]。弯曲破坏模式表现为纵筋屈服后,混凝土压碎,在墩底形成明显的塑性铰区,横向钢筋在整个过程中可能不会屈服,其表征出完全延性破坏特征。剪切破坏模式的特点是混凝土出现斜裂缝,破坏时箍筋屈服而纵筋未屈服,这种破坏模式是典型的脆性破坏,在设计中应避免。弯剪破坏模式为纵筋首先屈服,混凝土裂缝变宽后有效抗剪截面减小,导致桥墩抗剪能力退化,塑性铰区箍筋屈服,其体现出有限延性特征。
桥墩地震破坏模式受剪跨比、延性系数等参数的影响[13]。常用的桥墩地震破坏模式判别方法列于表4。GHEE等[14]认为延性系数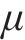

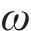
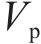
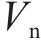
4.2 判别方法比较
采用上述判别方法对文中5个重力式桥墩的破坏模式进行判别,结果列于表5,其中S表示剪切破坏、FS表示弯剪破坏、F表示弯曲破坏、/表示无法判别。
由表5可见,GHEE方法错判了1个桥墩的破坏模式。MA错判4个桥墩的破坏模式,表明基于普通钢筋混凝土柱拟静力试验得出的概率模型不适用于高配筋重力式桥墩破坏模式的判别。ATC-06[16]、ASCE/SEI 41-06[17]、ZHU等[18]及刘鸣等[19]方法判错率均较高,是由于这4种方法都需要计算桥墩的抗剪强度。然而,桥墩的抗剪机理极为复杂,至今还未形成统一的抗剪强度计算公式。并且这4种判别方法使用的抗剪强度计算公式是基于公路钢筋混凝土桥墩提出的,而刚度大、小剪跨比、低轴压比的铁路重力式桥墩明显区别于普通钢筋混凝土桥墩,其能否直接用于重力式桥墩抗剪承载能力评估还有待验证。张永强[12]方法采用剪跨比作为判别桥墩地震破坏模式的依据,其成功鉴别5个铁路重力式桥墩的地震破坏模式,这是因为斜截面破坏模式与正应力和剪应力的比值密切相关,而剪跨比反映的正是剪压区平均正应力与剪应力的相对比值[20]。
5 重力式桥墩抗剪强度计算公式
5.1 国内外规范中钢筋混凝土桥墩抗剪强度计算公式
欧洲Eurocode 8[21]将混凝土抗剪贡献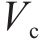
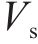
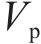
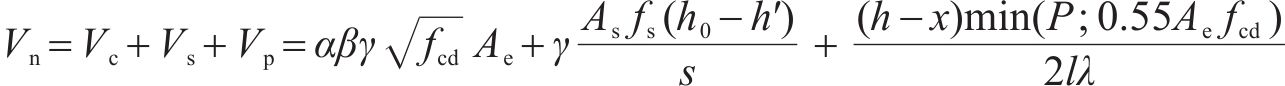
式中: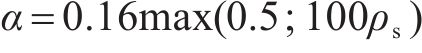
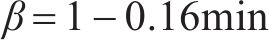
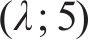
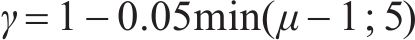
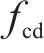
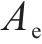
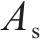
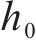
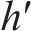
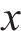
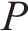
研究表明,轴力会提高混凝土的抗剪贡献[10],部分规范将轴力抗剪贡献纳入混凝土抗剪贡献中[22-24]。美国Caltrans[22]及AASHTO在混凝土抗剪贡献中考虑配箍率、位移延性及轴压力的影响,Caltrans中抗剪强度计算公式见式(4)。
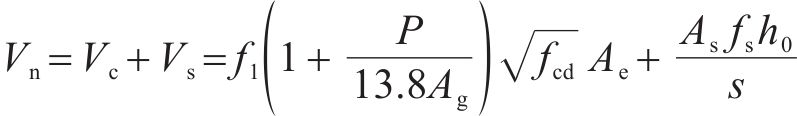
式中: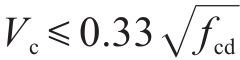
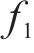
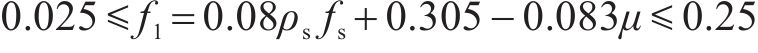
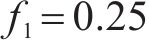
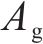

《公路桥梁抗震设计规范》(简称《公路规范》)[23]和《城市桥梁抗震设计规范》(简称《城市规范》)[24]均借鉴了美国AASHTO的抗剪强度计算公式,《公路规范》的抗剪强度计算公式见式(5)。
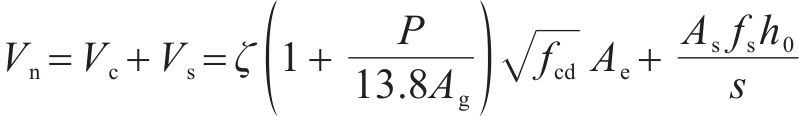
式中:当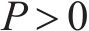
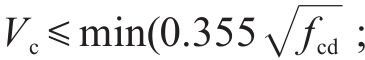
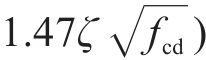
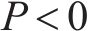
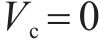

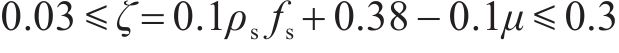
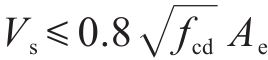
《城市规范》在2021年进行了修订,与未修订公式相比增加了塑性铰区外抗剪强度计算公式,本文采用修订稿中的公式,当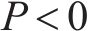
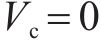
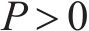
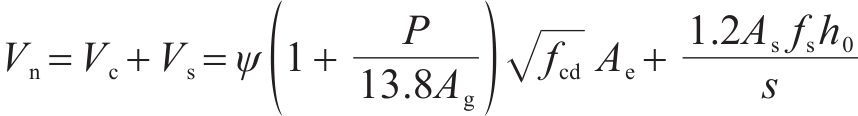
式中:塑性铰区内: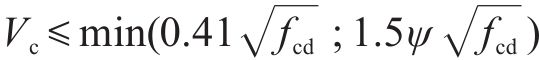
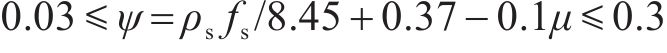
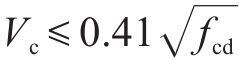
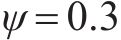
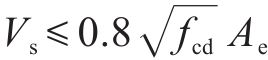
我国台湾省《铁路桥梁耐震设计规范》(简称《中国台湾规范》)在美国ATC-32抗剪公式基础上引入了ASCHHEIM等[25]提出的与位移延性相关的系数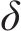
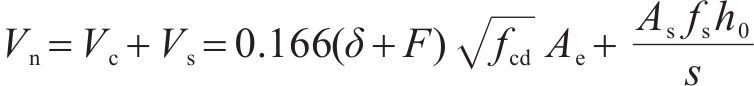
式中: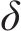
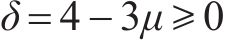
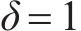
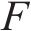
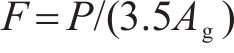
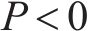
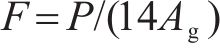
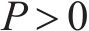
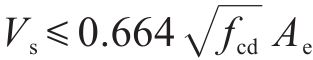
5.2 抗剪强度计算公式比较
对于发生剪切及弯剪破坏的桥墩,需要识别出桥墩的抗剪强度试验值
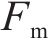

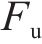

采用文中列出的抗剪强度计算公式对文中5个重力式桥墩进行抗剪强度计算。由于桥墩发生剪切破坏时墩底不形成塑性铰,剪切破坏桥墩的混凝土抗剪贡献按塑性铰区外公式进行计算[12],弯剪破坏桥墩则按塑性铰区内公式计算。抗剪强度试验值
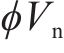
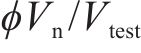
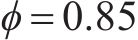
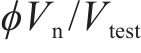
| 桥墩编号 | 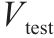 | 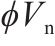 | ||||
|---|---|---|---|---|---|---|
| Eurocode 8 | Caltrans | 《公路规范》 | 《城市规范》 | 《中国台湾规范》 | ||
| R1 | 414 | 166 | 261 | 296 | 313 | 200 |
| R2 | 309 | 159 | 272 | 289 | 336 | 170 |
| R3 | 276 | 157 | 282 | 300 | 323 | 177 |
| R4 | 247 | 158 | 318 | 362 | 382 | 223 |
| R5 | 140 | 88 | 174 | 178 | 194 | 107 |
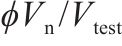 | 平均值 | 0.521 | 0.975 | 1.051 | 1.142 | 0.642 |
| COV | 0.170 | 0.240 | 0.220 | 0.216 | 0.198 | |
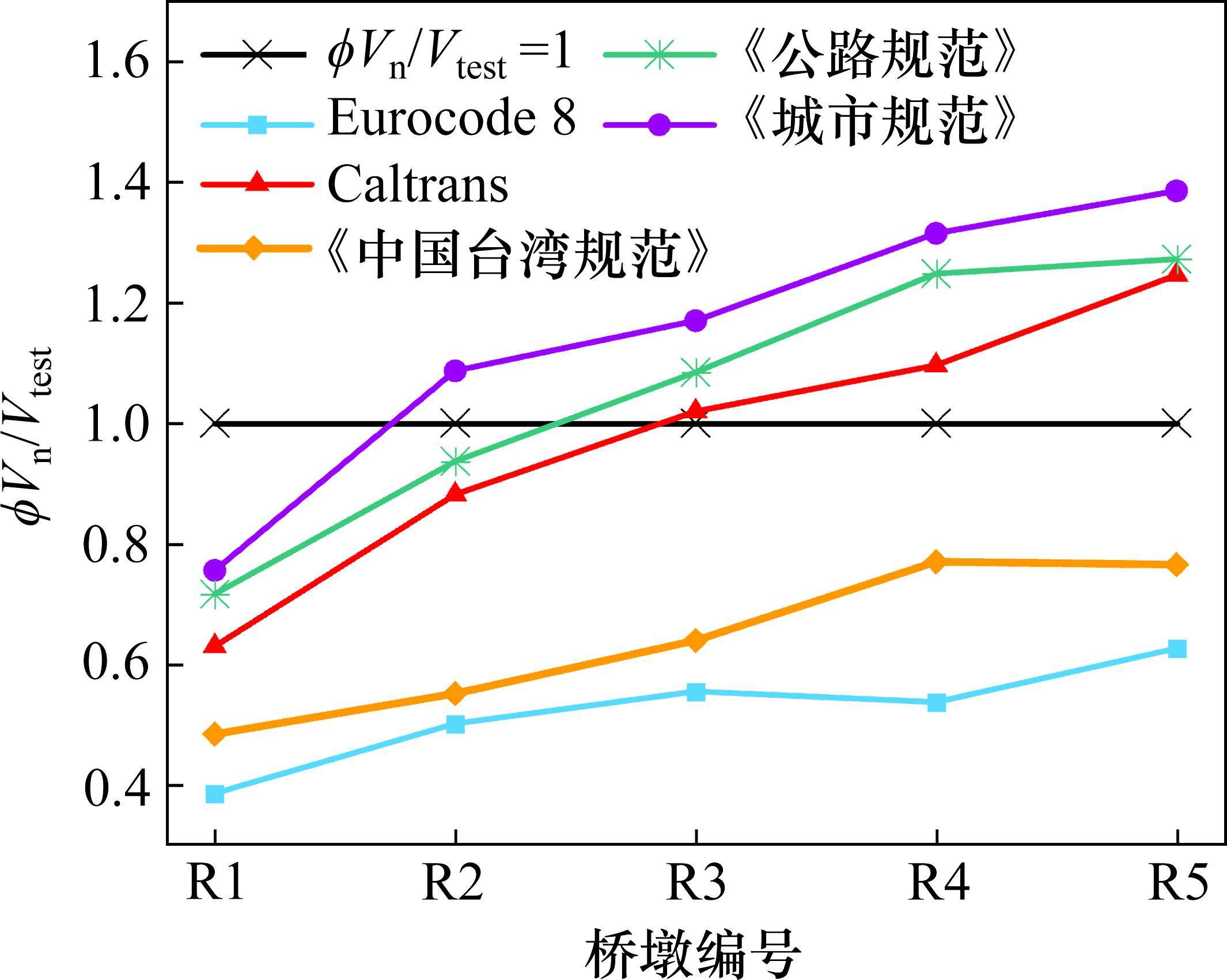
由表6和图7可知,总体上5个规范的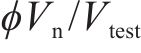
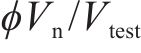
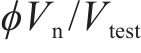
6 结论
1) 剪跨比为1.4的高配筋铁路重力式桥墩发生了剪切破坏,其破坏特征表现为墩底出现“X”形斜裂缝和箍筋拉断,并未形成塑性铰区,高配筋率的纵筋未起到抗剪作用。剪跨比为1.7~3.2的高配筋铁路重力式桥墩发生弯剪破坏,破坏时墩底同时出现斜裂缝和塑性铰区,其破坏形态与传统的低配筋重力式桥墩明显不同。
2) 高配筋铁路重力式桥墩最大水平承载力和等效刚度随剪跨比减小而增加,桥墩的位移延性系数和累积耗能随剪跨比减小而降低。剪跨比为1.4~3.2的桥墩位移延性系数在1.5~2.7之间,明显小于现行铁路规范的容许延性值4.8。
3) 当剪跨比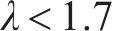
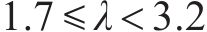
4) 铁路重力式桥墩弯剪破坏时可采用《公路桥梁抗震设计规范》(JTG/T 2231―01―2020)中抗剪强度计算公式;剪切破坏时可采用《城市桥梁抗震设计规范》(CJJ 166―2011)修订稿中塑性铰区外的抗剪强度计算公式。
杨钟仁,夏修身,钟亚伟等.高配筋铁路重力式桥墩地震破坏模式及抗剪强度公式研究[J].铁道科学与工程学报,2025,22(03):1154-1164.
YANG Zhongren,XIA Xiushen,ZHONG Yawei,et al.Seismic failure mode and shear strength formula of high reinforced railway gravity piers[J].Journal of Railway Science and Engineering,2025,22(03):1154-1164.