随着斜拉桥跨度的不断增长,其风致振动问题日益突出[1-2]。抖振作为一种限幅振动,虽然不会直接导致桥梁结构的损毁,但所导致的疲劳损伤不容忽视,且过大的抖振响应将会影响行人以及行车的舒适性与安全性。因此,大跨度桥梁抖振分析是其抗风设计的重要内容,采用有限元技术以及风洞试验对其进行深入研究是十分必要的。1952年,LIEPMANN[3]采用概率统计方法开展机翼的抖振分析,谱写了结构抖振响应研究的序章。而自从SCRUTON于1955年首次提出桥梁抖振的概念以来,学者们便开始了对桥梁抖振问题的研究。具体而言,抖振分析方法有频域法和时域法2种:频域法是通过傅里叶变换,直接计算结构的响应谱,但是无法考虑到结构的非线性和风的相关性[4];随着计算机算力的提升和有限元软件的普及,计算成本较大但精度较高的时域法逐渐在抖振分析中被采用。时域法是将结构的激励输入转化为时间序列,得到风荷载时程并施加到有限元模型中计算结构的瞬态响应,可计入非线性因素的影响,如气动力非线性以及几何非线性等。近年来,国内外学者围绕桥梁抖振时域分析进行了一系列深入研究。卢晓伟[5]通过山区某大跨度叠合梁斜拉桥开展了抖振响应时域分析,其在计算单元自激力时,采用集中法将自激力由Matrix27单元等效为节点力进行加载,研究了平均风速分布特性等因素对抖振响应的影响;陈建兵等[6]针对双边钢箱钢-混组合梁斜拉桥在不同风参数下的抖振响应进行时域分析,得出忽略气动导纳函数的抖振位移响应后进行桥梁设计是偏安全的结论;杨昊[7]运用ANSYS-MATLAB进行联合仿真,生成三维随机风场以及编制增量与内外两重迭代程序研究公轨两用斜拉桥抖振响应随跨度的非线性演变;刘忠敏[4]在ANSYS中采用时域分析的方法研究了考虑脉动风非平稳特性下的大跨度悬索桥抖振响应,同时利用颤振导数在ANSYS平台Matrix27单元中集成气动刚度矩阵以及气动阻尼矩阵,保证了计算结果的精度,但在前处理阶段增大了很大的工作量。尽管有限元方法具有较好的精度,但是风洞试验可以更为充分地模拟大气边界层的紊流,更为真实地反映桥梁结构在实际大气边界层中的气动稳定性和风致振动响应。雷永富等[8]通过制作1∶100全桥气弹模型,对武汉青山长江公路大桥(整体流线型钢箱梁斜拉桥)的抖振性能进行风洞试验研究,确保了其成桥状态和施工状态的抖振响应满足我国及多国的抗风规范;董锐等[9]在风洞试验的基础上,采用均匀设计以及回归分析的手段,针对大跨度斜拉桥抖振响应的多影响因素进行分析;何旭辉等[10]通过开展全桥气弹模型风洞试验对金海特大桥主桥在施工和运营期间的抗风安全性进行了研究,并发现增设抗风缆可以显著降低施工阶段主梁风致抖振响应和提高桥梁施工安全。综上,尽管围绕大跨度斜拉桥抖振分析的有限元方法已取得一定进展[11],但是现有的抖振有限元分析方法需要定义气动阻尼和气动刚度矩阵,这将在前处理部分增加较大的工作量,且计算时间和算力需求均会进一步增加。因此,本文提出了一种大跨度桥梁抖振响应有限元分析的简化方法,并以某大跨度斜拉桥为工程背景开展数值分析,通过ANSYS-MATLAB联合仿真分析程序进行抖振响应分析;最后通过开展全桥气弹模型试验,将风洞试验结果与数值模拟结果对比分析,以验证该方法的有效性。
1 理论分析
1.1 抖振力模型
对于离散为多自由度体系的大跨度桥梁,其承受风荷载的动力方程可写为:
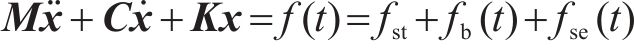
式中:M、C和K分别为结构的质量、阻尼和刚度矩阵;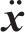
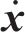
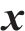
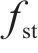
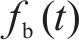
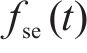
自激力是风场中因结构运动而诱发的作用在结构上的气动力,根据Scanlan提出的桥梁断面二维气动自激力公式,对于考虑主梁侧向位移的三维情况而言,桥梁断面单位展开上受到的气动自激力公式可以拓展为用18个颤振导数表示,如式(2)至式(4)所示:
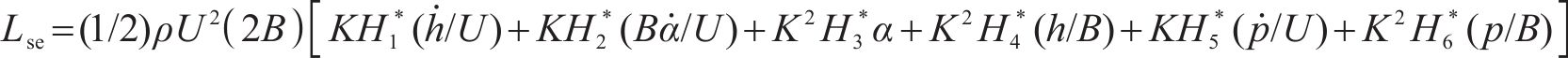
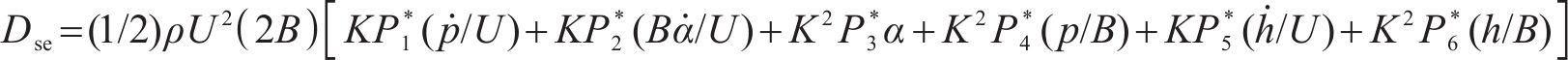
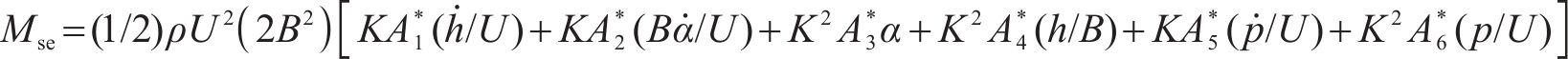
式中:ρ为空气密度;U是来流风速;B为桥宽;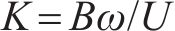

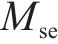
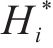
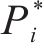
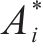
1.2 抖振简化分析方法
传统的抖振有限元分析方法[13-14]中自激力对于主梁的影响从形式上可以体现为阻尼特性以及刚度特性的改变,可以视为在主梁上作用了附加的阻尼和刚度[1];而使用气动刚度矩阵和气动阻尼矩阵的方式对自激力进行考虑,可以用式(5)来表达:
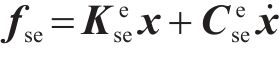
式中: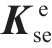

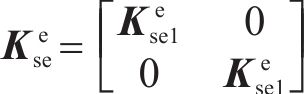
其中,
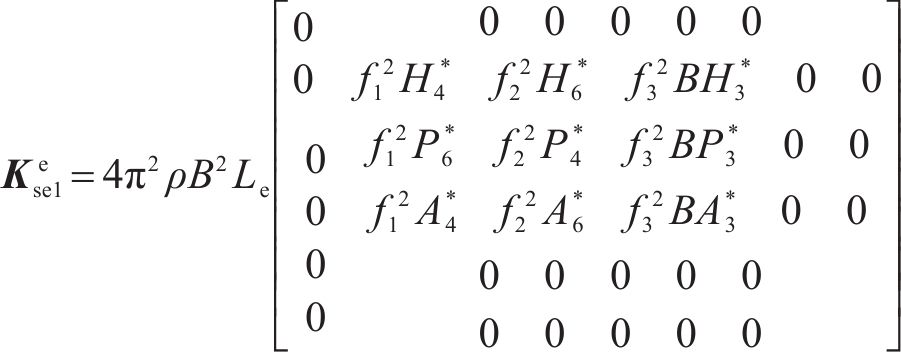
气动阻尼矩阵可以表示为:
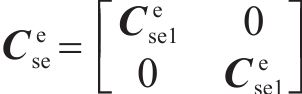
其中,
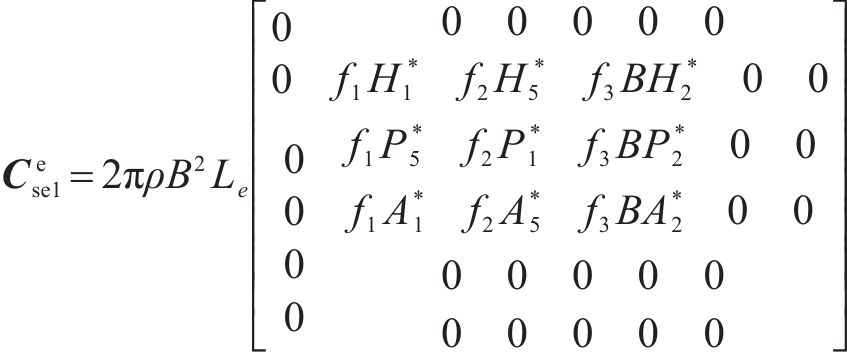
式中: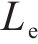
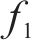
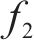
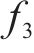
梁剑青等[17]指出,在自激力的计算中可不考虑气动导数耦合项的影响,进一步基于准定常假定,利用静力三分力系数推导流线型箱梁气动阻尼的表达式。LAROSE[16]指出,结构受到的每延米的升力可以表达为式(10):
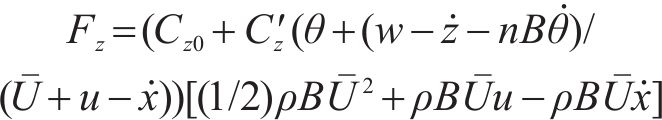
式中: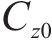
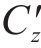
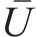
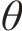
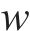
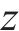
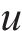
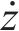
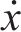
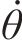
而忽略其中u、w、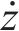
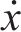
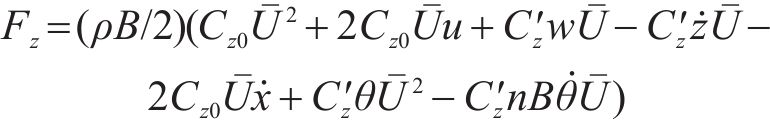
式中:第1项代表平均风荷载导致的升力;第2、第3项分别表示顺风向、竖向抖振风荷载导致的升力;第4项代表自激力导致的升力,并且如果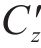
式(11)同样适用于计算结构的阻力和扭矩。协同考虑速度项和阻尼,则竖向气动阻尼可以表示为:
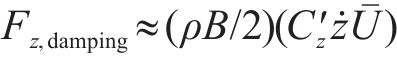
而临界阻尼比的定义是一个循环对升力所做的功与系统中储存的总能量之比,而升力与其作用的空间距离长短的乘积为其所做的功,即可表达为:
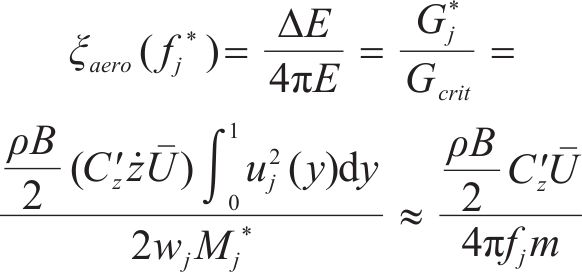
式中: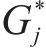
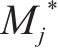
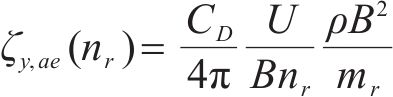
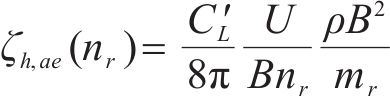
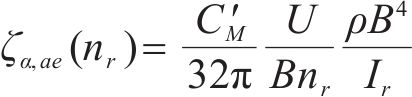
式中: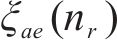
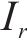
2 数值仿真
2.1 模型参数
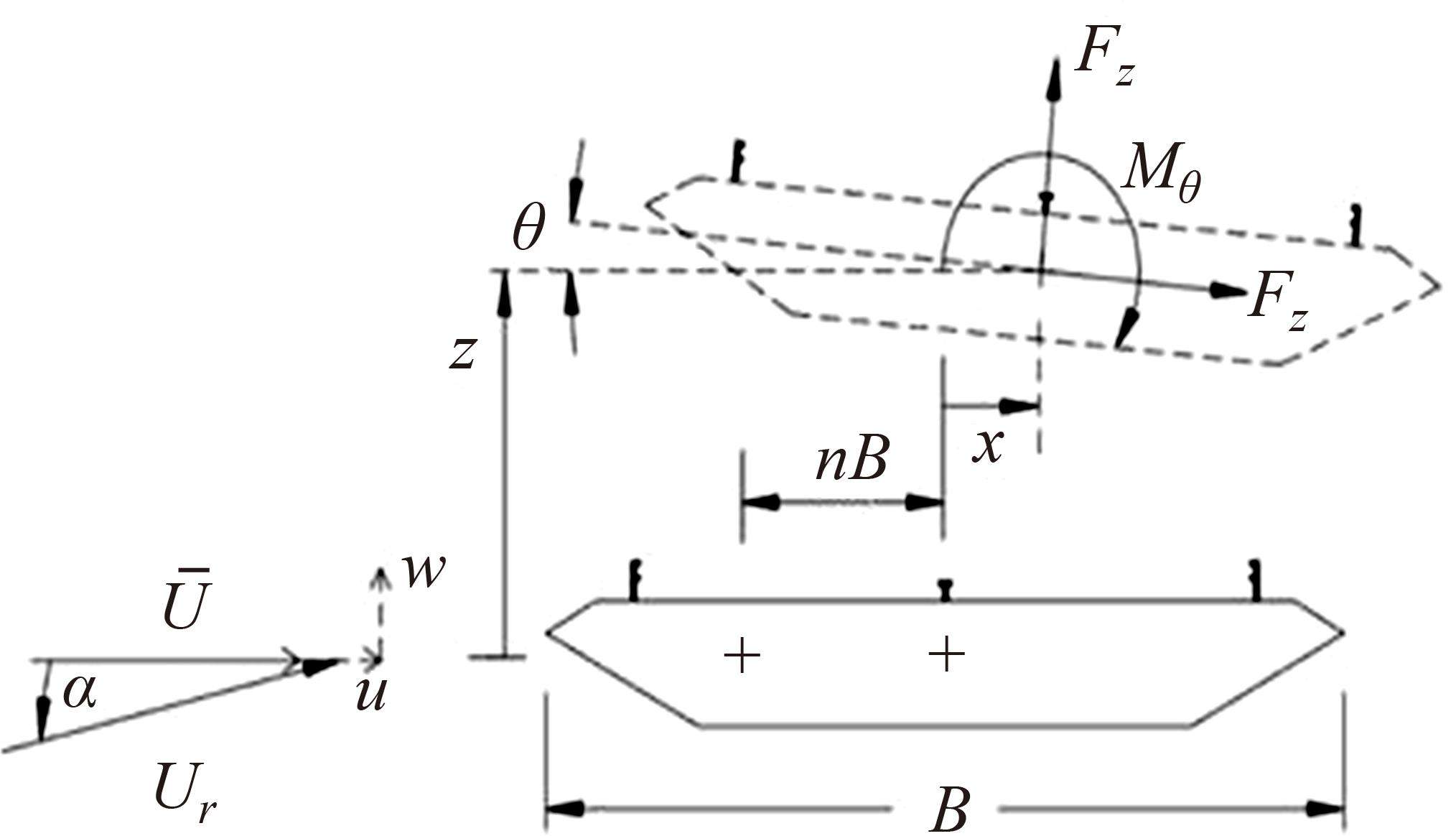
某大跨度斜拉桥全长约1 316.5 m,主桥采用主跨454 m双塔双索面斜拉桥。主梁采用流线型钢箱梁,梁宽33.95 m,梁高4 m。该桥主梁基准高度为56.135 m,根据规范[18]计算,基本风速为24.5 m/s,桥面处设计基准风速为32.3 m/s。
其立面布置图与主梁横断面示意图如图2所示。
鉴于该桥扭转刚度较大,在对该桥进行ANSYS有限元分析时,采用单主梁模型进行桥面系的模拟。主梁、桥塔、桥墩采用Beam188单元模拟;拉索采用杆单元Link10模拟;横隔板、压重和二期恒载采用质量单元Mass21模拟;主梁与拉索、桥塔与拉索之间的刚臂单元采用Beam4模拟。该桥成桥状态动力特性计算结果如表1所示。
| 振型阶数 | 频率/ Hz | 振型主 要特征 | 等效质量/(t∙m-1)/ 质量矩/(t∙m2∙m-1) |
|---|---|---|---|
| 1 | 0.335 8 | 1阶正对称竖弯 | 42.819 7 |
| 2 | 0.446 7 | 1阶正对称横弯 | |
| 3 | 0.474 2 | 1阶反对称竖弯 | |
| 6 | 0.681 6 | 2阶反对称竖弯 | |
| 9 | 0.757 8 | 2阶正对称竖弯 | |
| 10 | 0.887 7 | 1阶正对称扭转 | 4 522.280 0 |
| 11 | 0.956 1 | 3阶正对称竖弯 | |
| 12 | 1.003 1 | 4阶正对称竖弯 | |
| 15 | 1.146 9 | 3阶反对称竖弯 | |
| 16 | 1.158 9 | 1阶反对称横弯 | |
| 17 | 1.163 4 | 5阶正对称竖弯 | |
| 19 | 1.268 3 | 1阶反对称扭转 |
2.2 风谱模拟
谐波合成法是进行脉动风荷载模拟的常用手段,通过功率谱分解和三角级数叠加模拟风速时程,虽然计算量较大但模拟结果较为准确。本文在进行数值模拟时,首先采用谐波合成法模拟了顺风向脉动风速u和竖向脉动风速w。
顺风向脉动风谱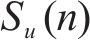
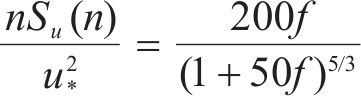
竖向脉动风速谱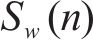
根据规范确定该桥位处风速模拟基本参数:地貌类型为B类地貌,平均风剖面指数α=0.16,地表粗糙高度为0.05 m。全桥一共选取了103个节点对风场进行脉动风速时程模拟,各节点之间的纵向间距为10.398 m。生成风速时程曲线的时间间隔为0.1 s,总时长为600 s。
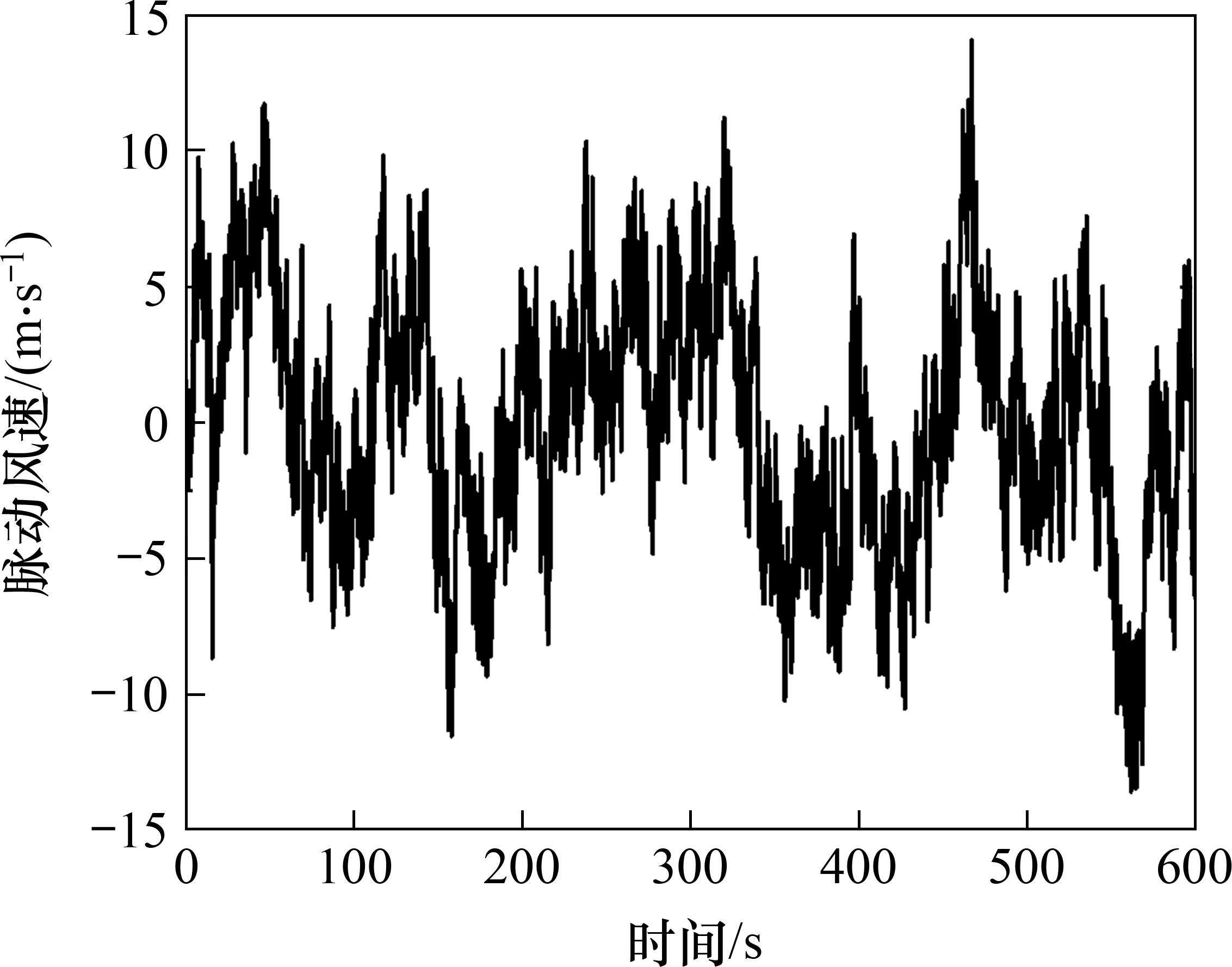
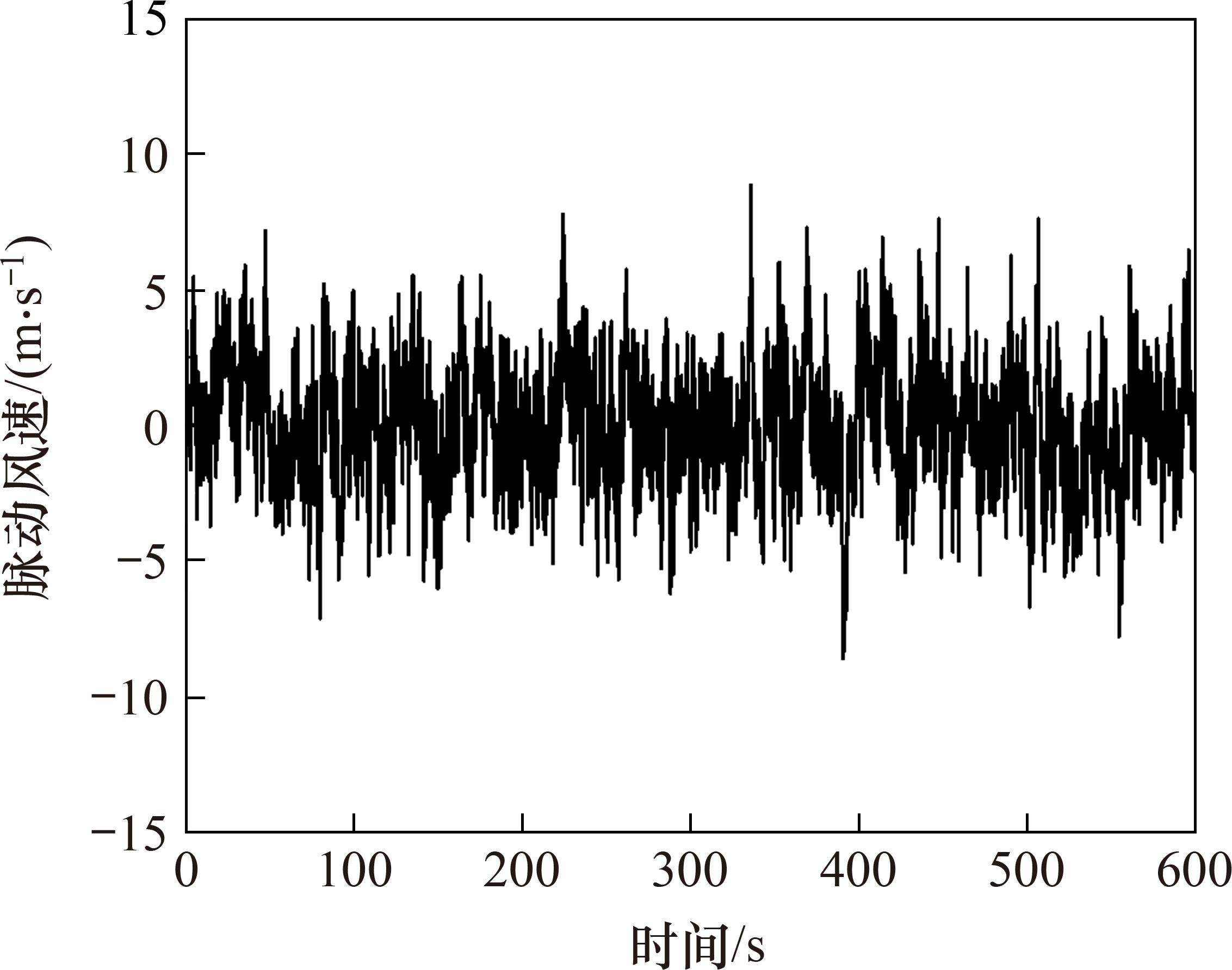
谐波合成法模拟的顺风向、竖向脉动风速时程图如图3和图4所示。由图可以得出谐波合成法生成的脉动风速时程均值在0附近,满足风荷载模拟的平稳性和各态历经性的要求。
为了验证生成风荷载的准确性,采用Matlab软件分别计算了模拟风谱和理论风谱,在2个方向分别采用上述提及的公式进行计算,最终模拟结果如图5和图6所示。风剖面风速及紊流度对比如图7和图8所示。
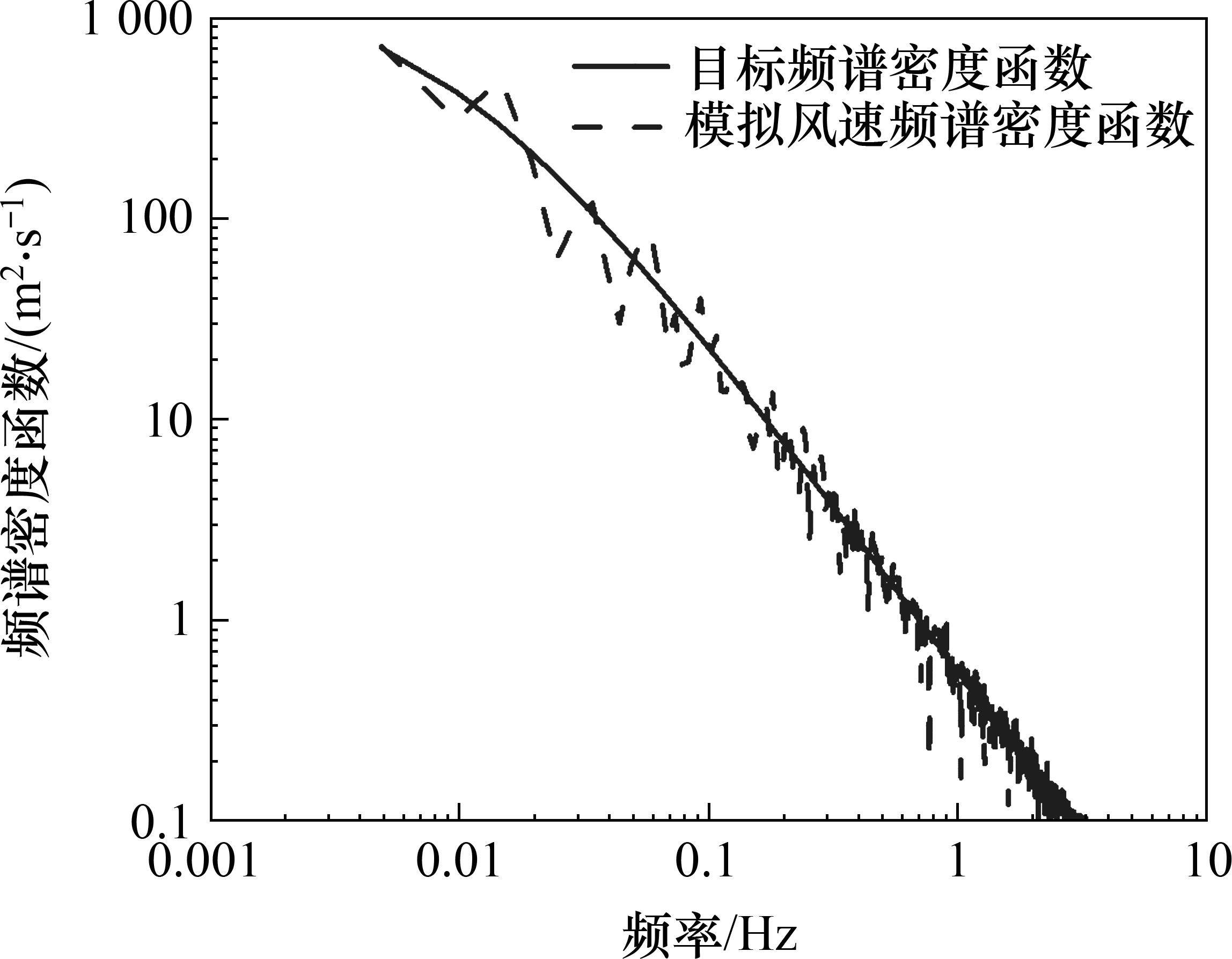
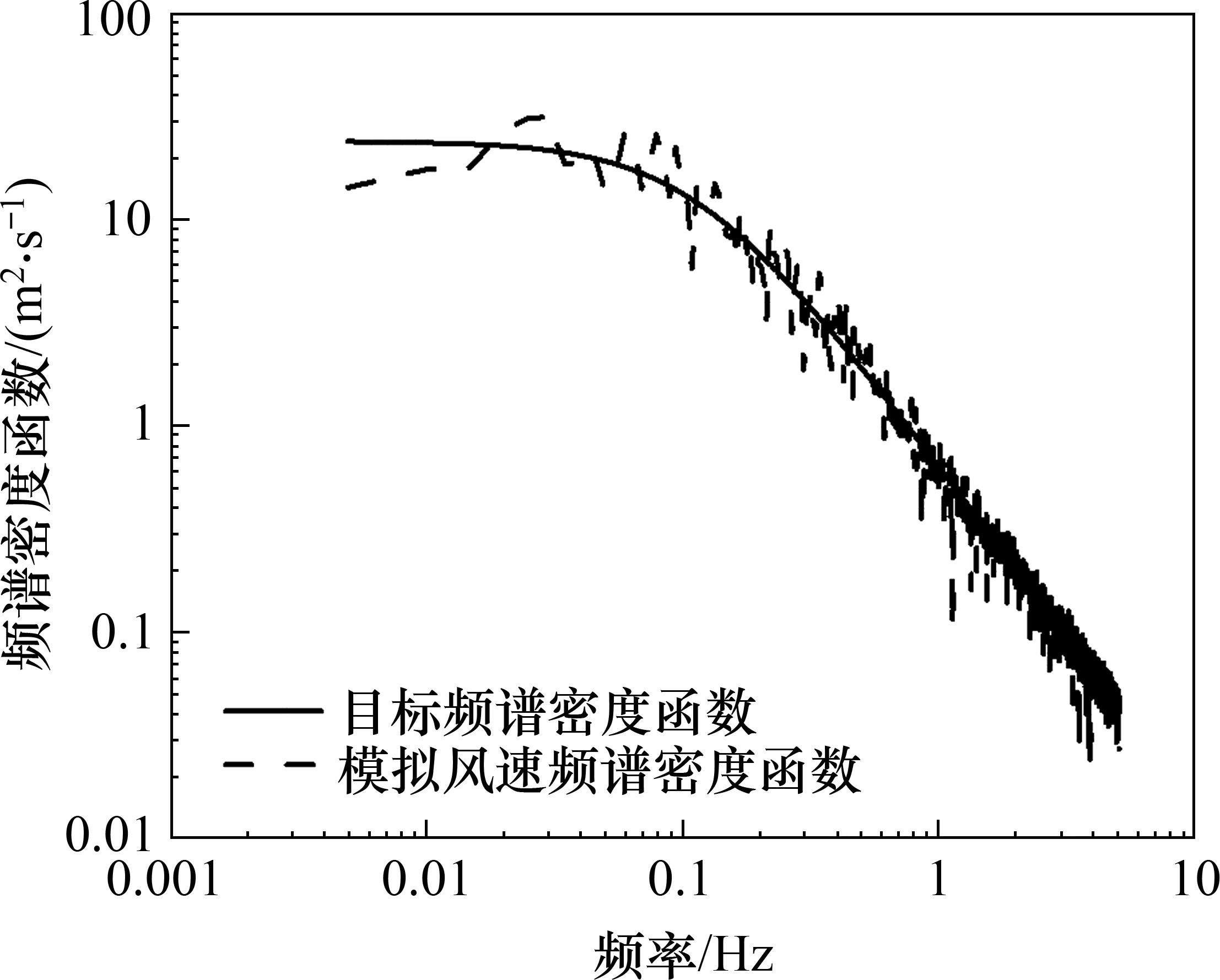
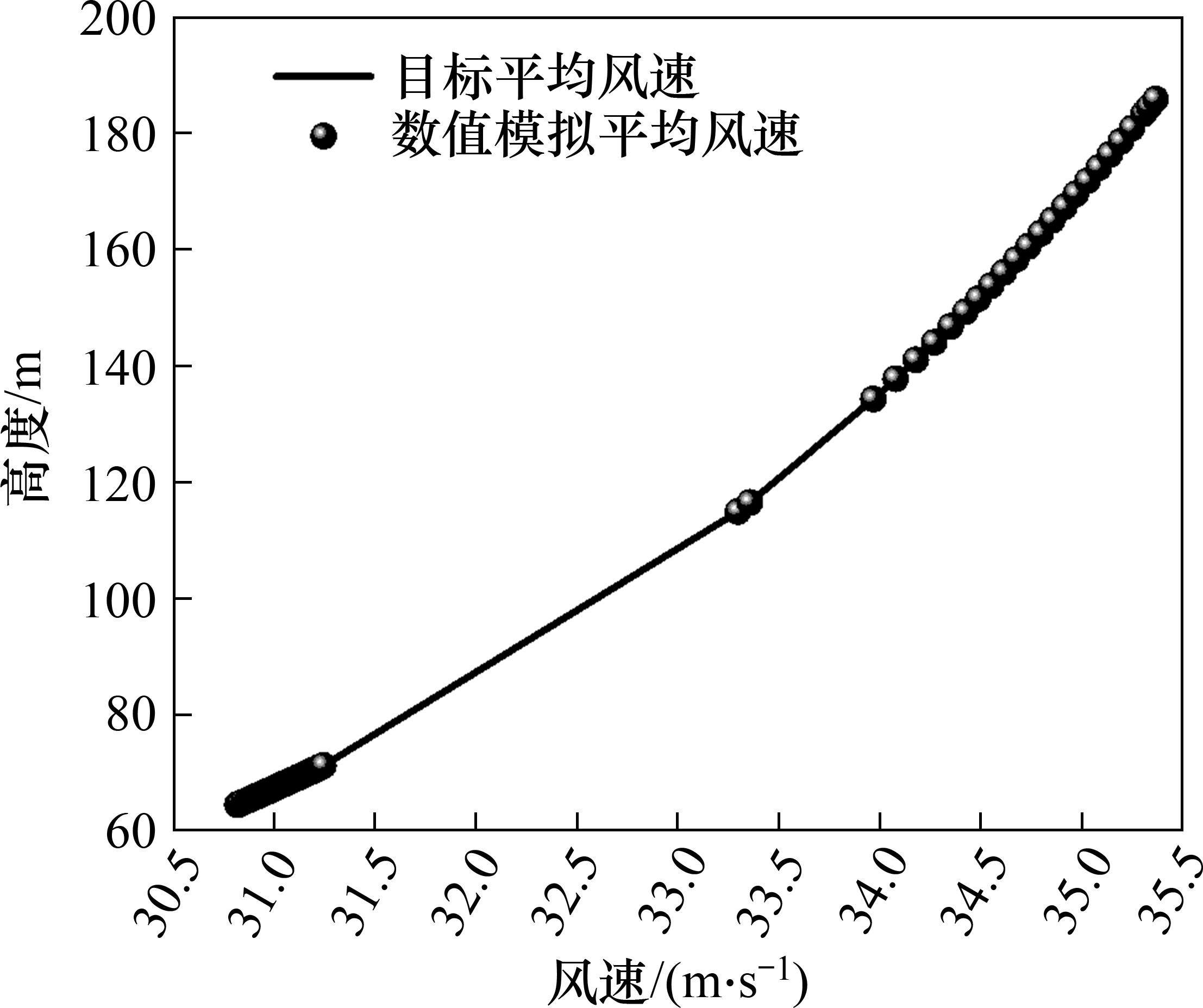
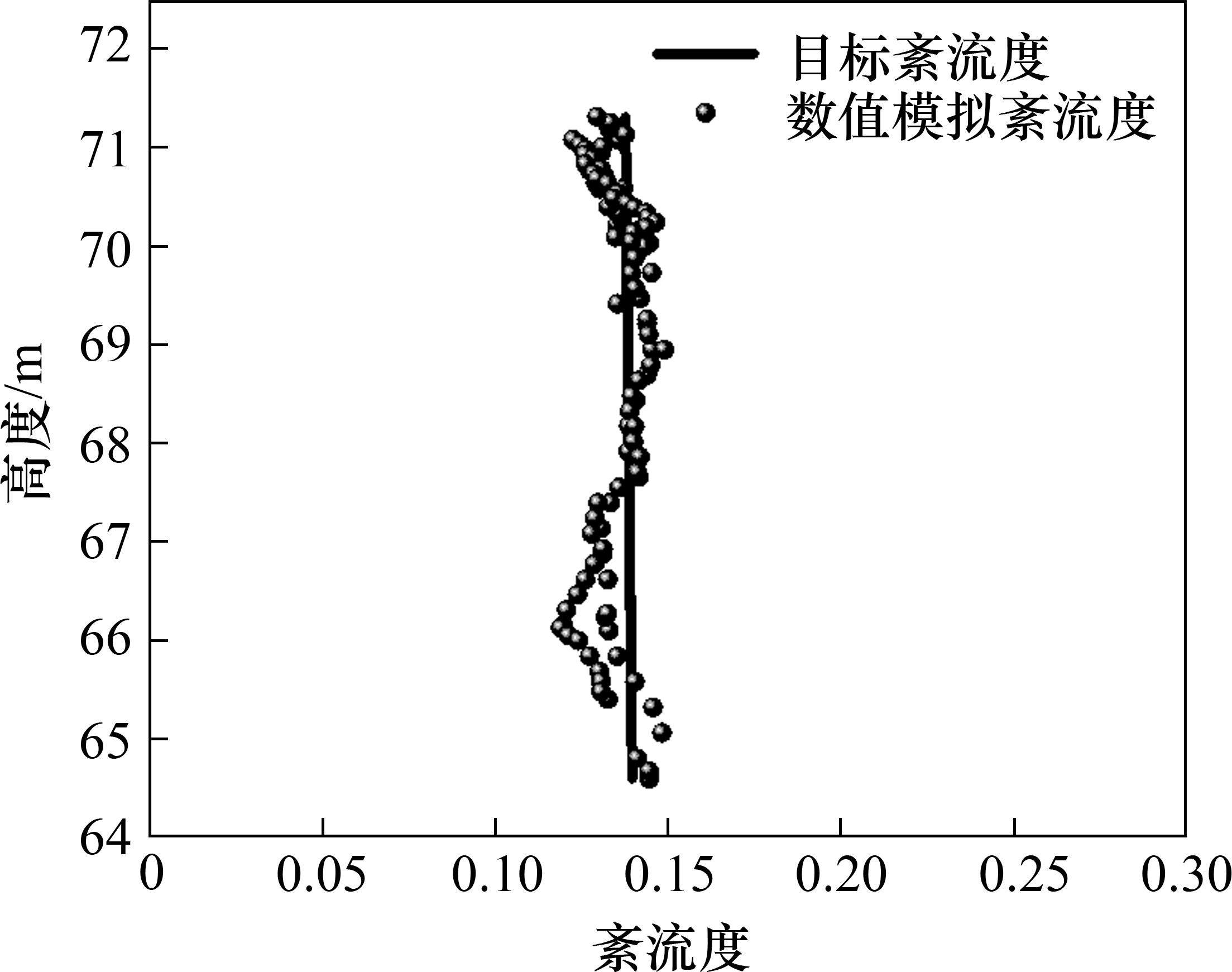
根据风速以及紊流度对比图可以看出:根据规范[18]计算距离地面高度为71.25 m处的风速为32.19 m/s,紊流强度为0.143;而采用谐波合成法模拟出来的风场于71.25 m处风速为31.25 m/s,紊流度为0.155,误差分别为2.92%、8.39%,根据图表显示情况可以得出,数值模拟模拟出的风场与目标风场较为吻合。
2.3 简化分析方法抖振响应计算
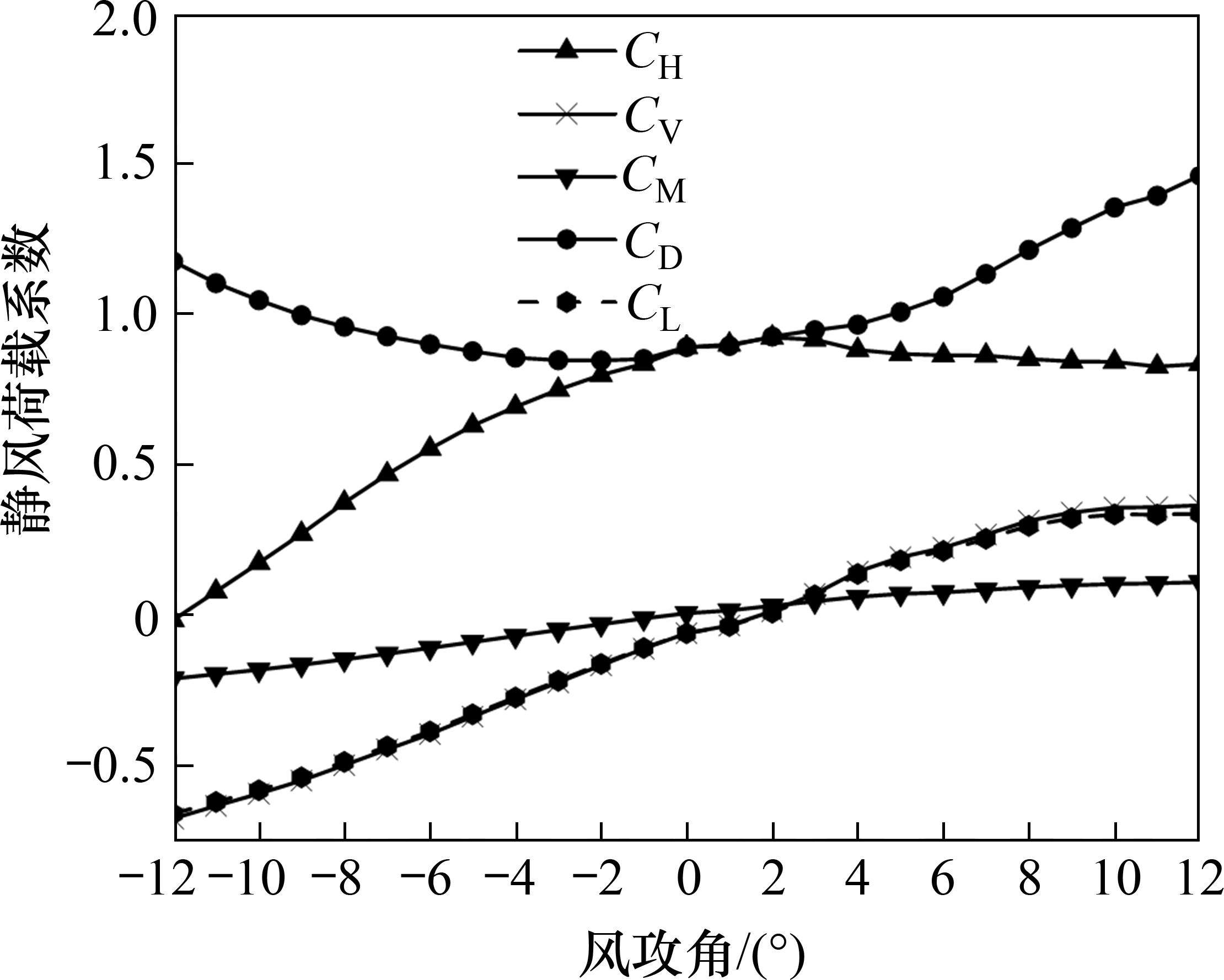
通过节段模型测力风洞试验,得到各工况下不同风攻角对应主梁断面的体轴阻力系数

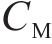
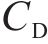

根据上述所阐述的气动阻尼计算公式(14)~(16),采用准定常气动力计算各模态的气动阻尼,该气动阻尼叠加结构固有阻尼即可得到结构的总阻尼。按准定常理论计算得到的与主梁振动有关模态的气动阻尼和总阻尼如表2所示。
| 模态号 | 频率/Hz | 单位长度等效质量/t | 振型描述 | 气动阻尼比/% | 总阻尼比/% |
|---|---|---|---|---|---|
| 1 | 0.335 8 | 42.819 5 | 1阶正对称竖弯 | 0.910 | 1.210 4 |
| 2 | 0.446 7 | 37.840 1 | 1阶正对称横弯 | 0.008 | 0.307 8 |
| 3 | 0.474 2 | 54.677 3 | 1阶反对称竖弯 | 0.505 | 0.804 9 |
| 6 | 0.681 6 | 91.059 3 | 2阶反对称竖弯 | 0.211 | 0.510 9 |
| 9 | 0.757 7 | 59.484 1 | 2阶正对称竖弯 | 0.290 | 0.590 4 |
| 10 | 0.887 7 | 4 522.11 | 1阶正对称扭转 | 0.335 | 0.635 3 |
| 11 | 0.956 1 | 43.764 8 | 3阶正对称竖弯 | 0.313 | 0.612 9 |
| 12 | 1.003 0 | 39.754 2 | 4阶正对称竖弯 | 0.328 | 0.628 3 |
| 15 | 1.146 8 | 40.079 7 | 3阶反对称竖弯 | 0.285 | 0.584 8 |
| 16 | 1.158 9 | 79 411.2 | 1阶反对称横弯 | 0.000 | 0.300 0 |
| 17 | 1.163 4 | 465 004 | 5阶正对称竖弯 | 0.000 | 0.300 0 |
| 19 | 1.268 2 | 15 914.1 | 1阶反对称扭转 | 0.067 | 0.304 7 |
在获得脉动风速后即可进行结构在模拟风场下的动力响应时程分析,再采用三维抖振时域分析方法对该桥在0°风攻角的抖振响应进行分析。图10和图11分别展示了主跨跨中和1/4跨位置处的竖向位移时程,图12给出了主梁竖向位移抖振均方根值,图13给出了主跨跨中竖向抖振加速度自功率谱。
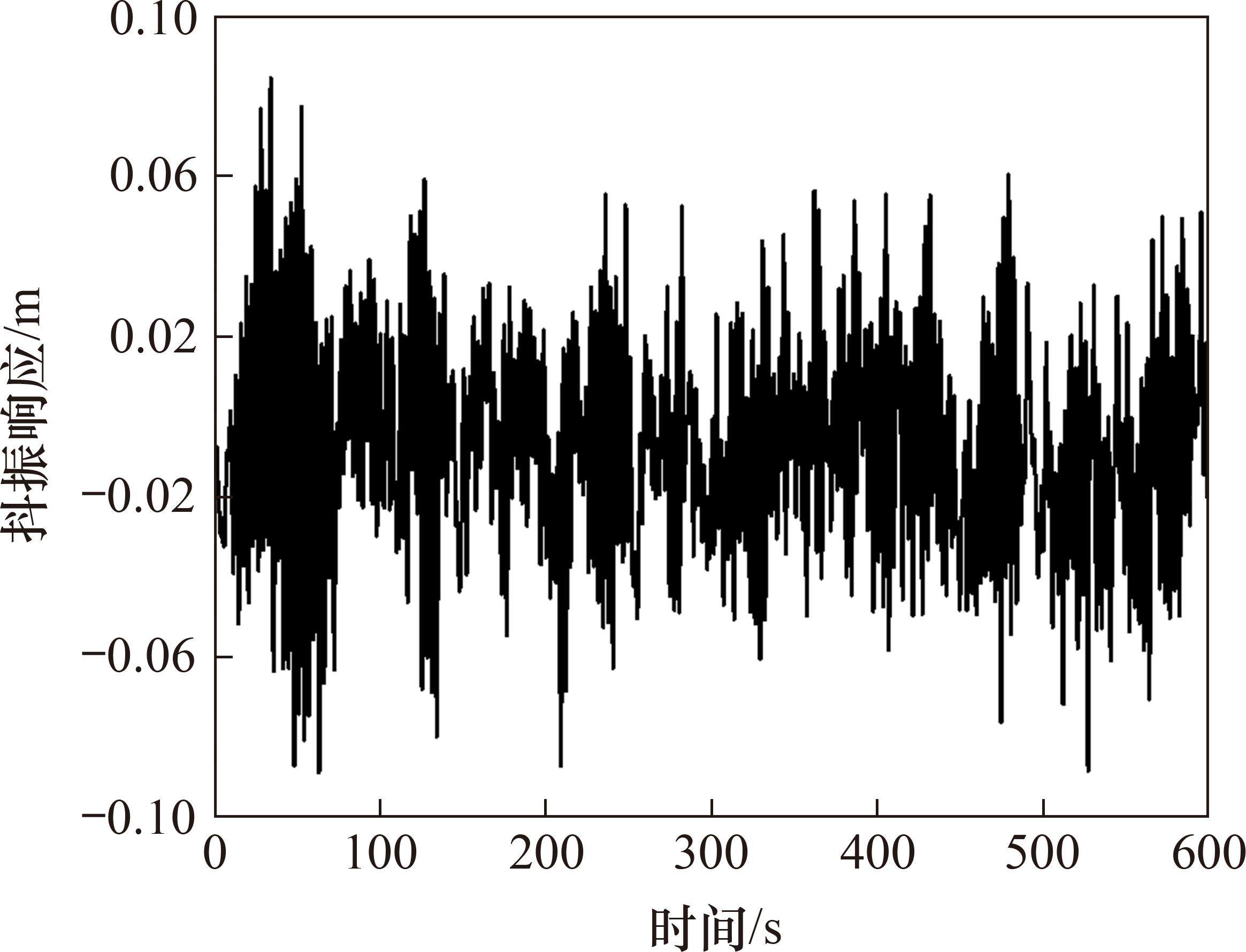
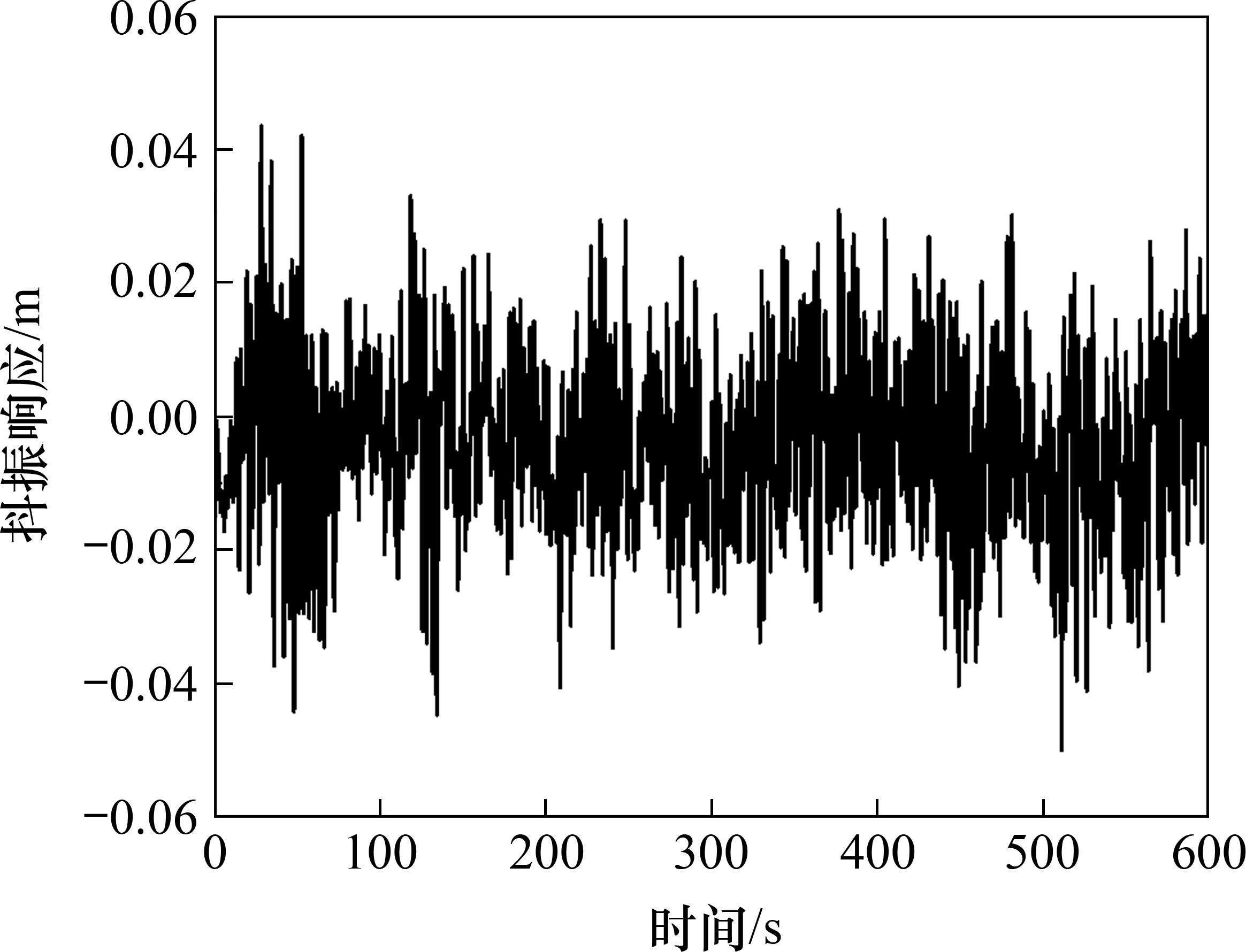
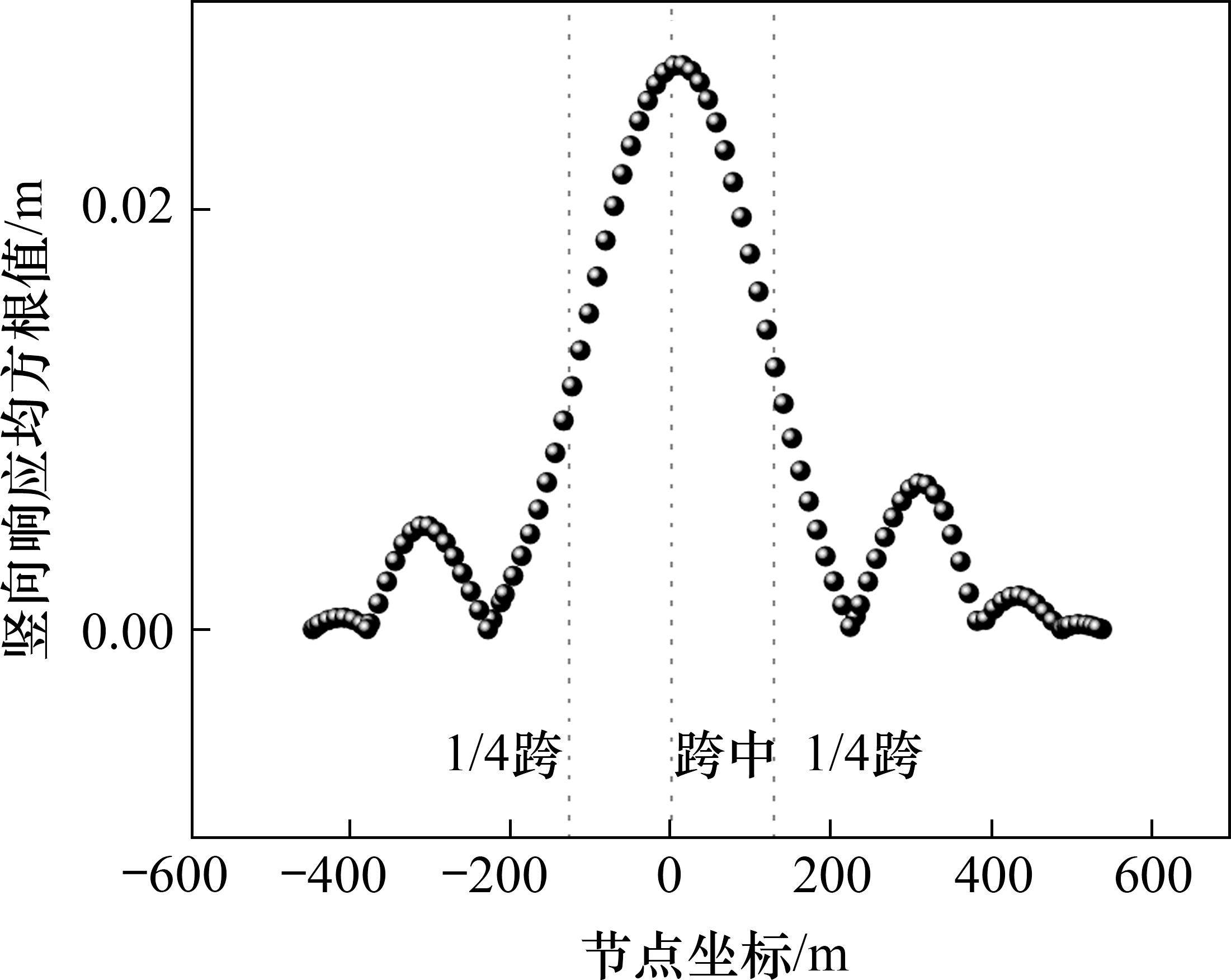
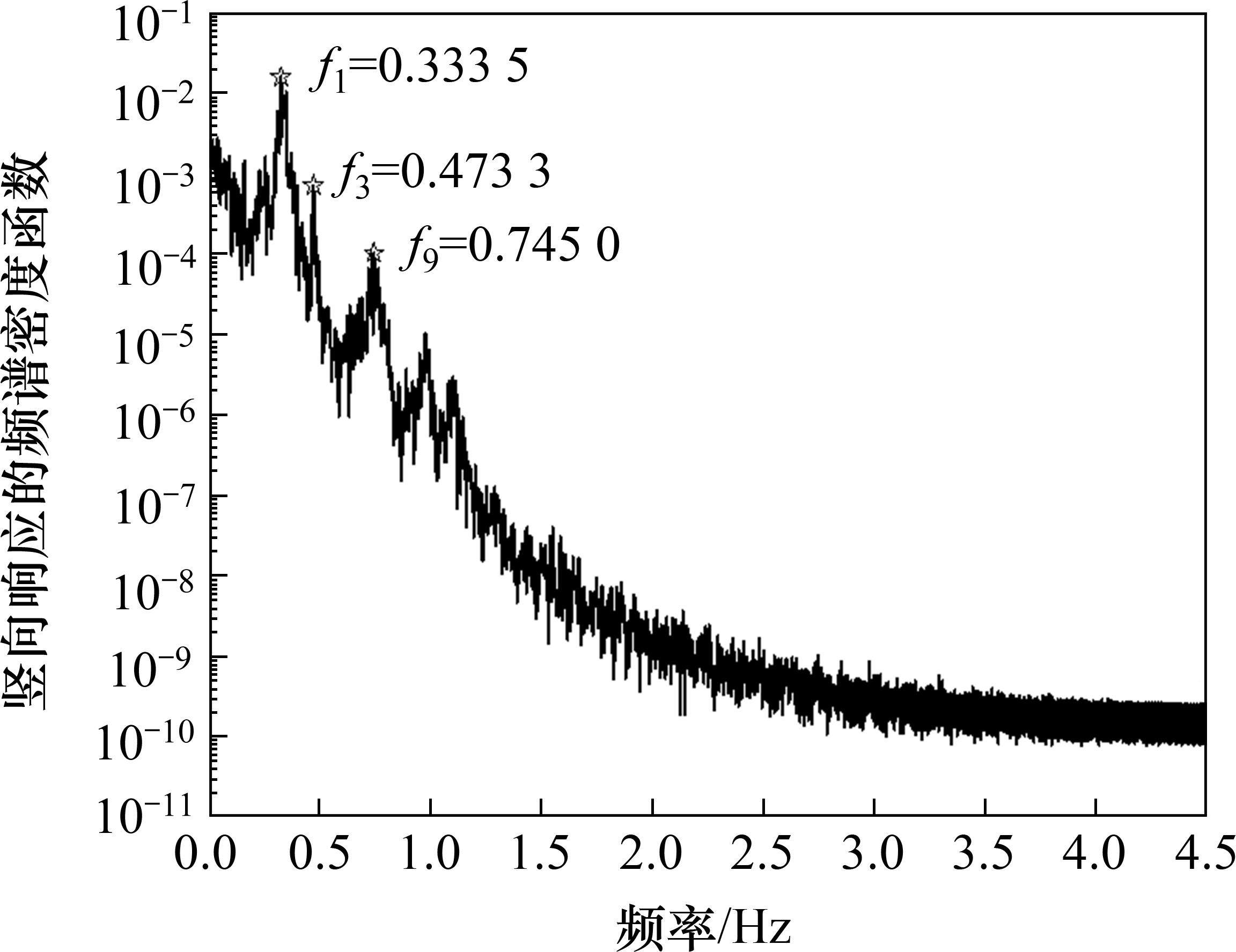
由于抖振是一个非平稳发展的过程,在进行响应分析时,选取风速发展完全阶段进行分析。由上述数值分析结果可得,在成桥状态设计基准风速32.3 m/s下,考虑气动阻尼影响时0°攻角下主梁跨中及四分点处的位移均方根值分别为0.028 8 m、0.015 3 m,换算得到竖向抖振位移响应分别为40.7 mm、21.6 mm。由结构响应谱图13可知,3个卓越频率分别为0.326 7、0.473 3和0.745 Hz,与有限元分析所得主梁第1、第3、第9阶自振频率0.335 8、0.474 2和0.757 7 Hz非常接近,相差均仅在3%以内。
2.4 传统分析方法抖振响应计算
为进一步确保本文所提出的简化分析方法的准确性,本文采用上述传统抖振响应分析方法,在ANSYS有限元分析软件中使用Matrix27单元在原模型上实现全桥气动自激力的加载,随后加载相同风荷载进行抖振响应分析。图14和图15展示了主跨跨中和1/4跨位置处的竖向位移时程,图16给出了主梁竖向位移抖振均方根值,图17给出了主跨跨中竖向抖振加速度自功率谱。
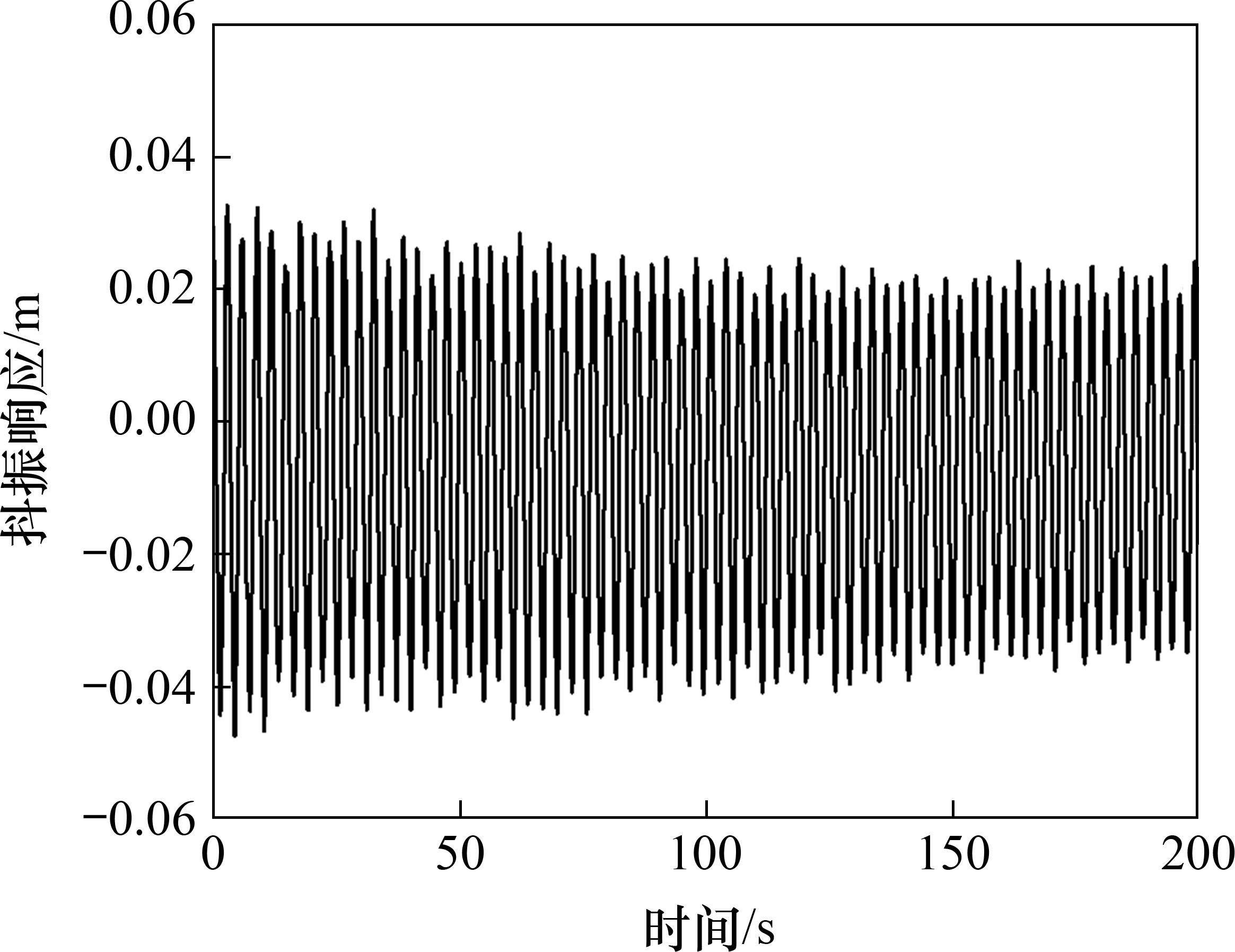
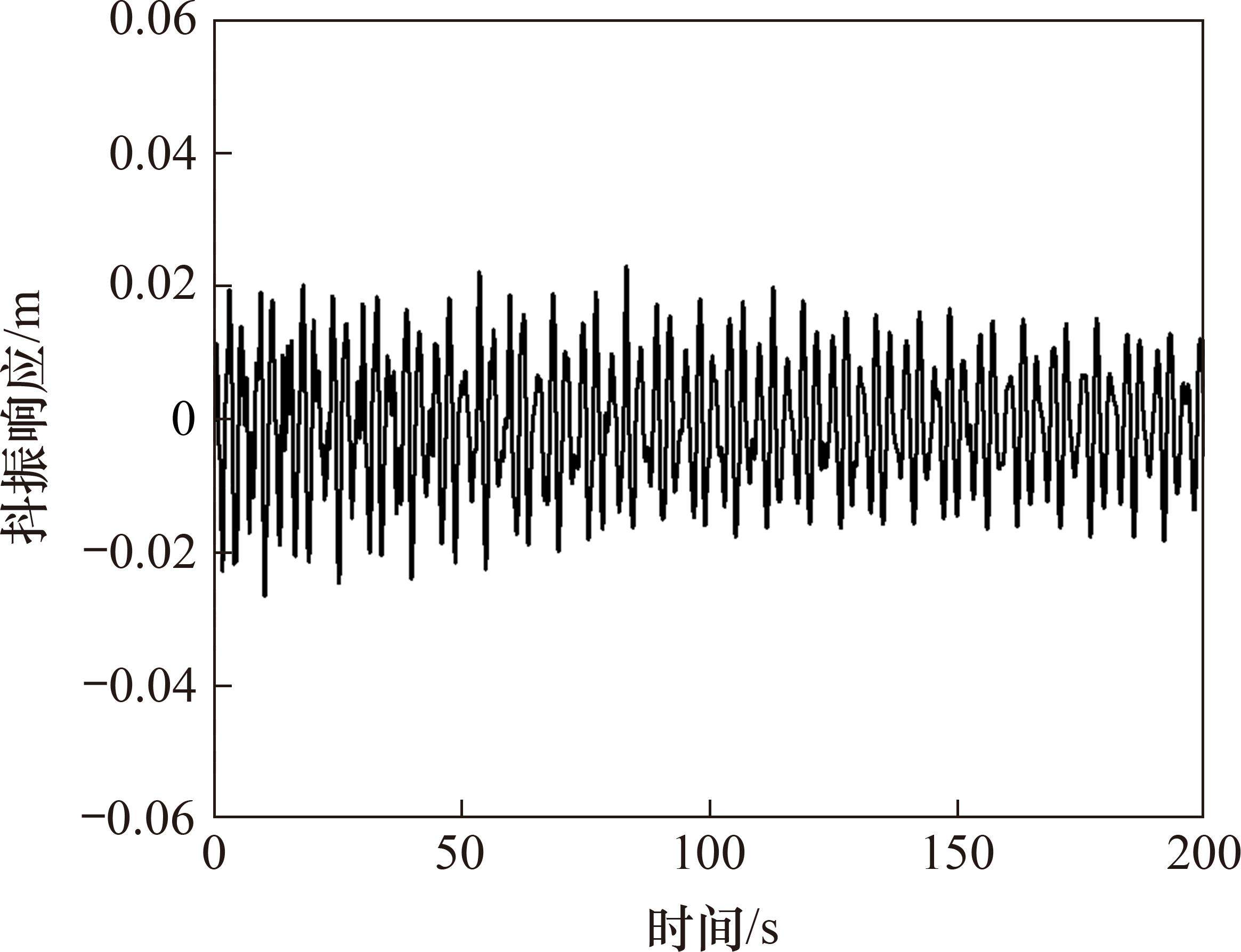
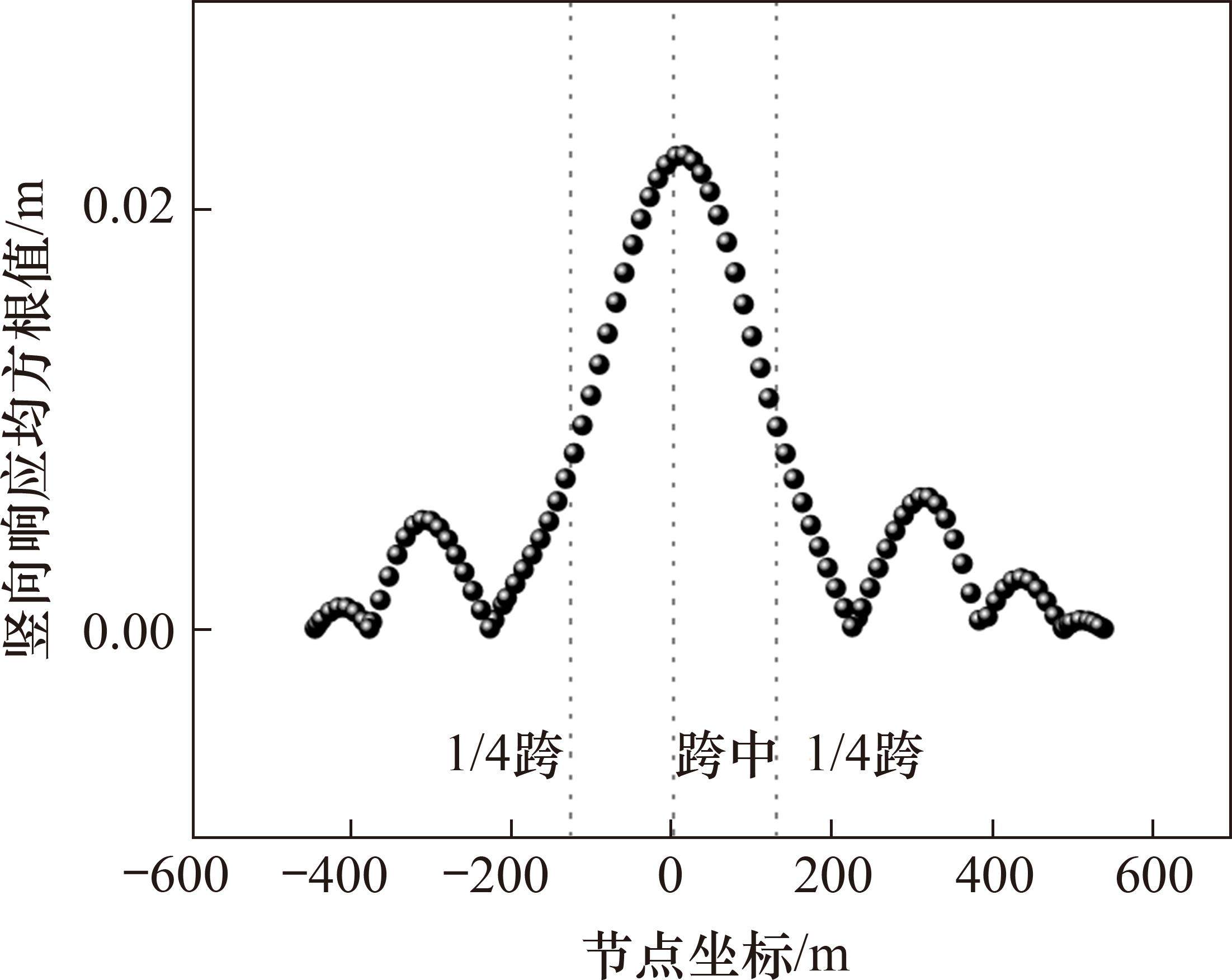
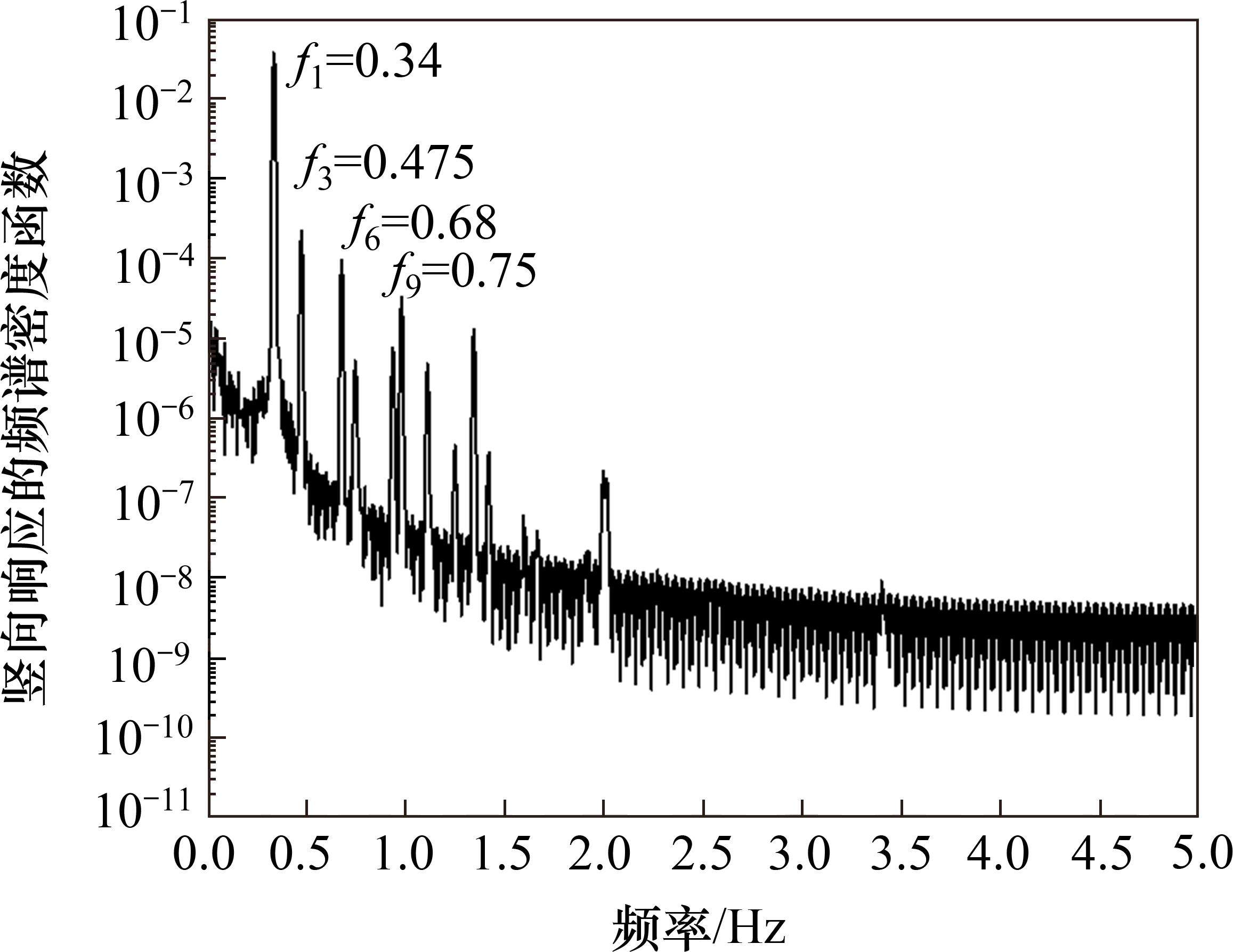
在使用传统方法进行抖振响应分析时,由于有限元模型的复杂性以及计算机性能的限制,计算时长无法达到600 s,实际计算时长只能达到200 s。分析传统抖振响应分析方法所得结果发现,在成桥状态设计基准风速32.3 m/s下,考虑气动阻尼影响时0°攻角下主梁跨中及四分点处的位移均方根值分别为0.026 m、0.012 6 m,换算得到竖向抖振位移响应分别为36.8 mm、17.8 mm。在相同风荷载作用下,200 s内响应并未完全发展,所得到的响应较简化分析方法所得结果相比偏小。由结构响应谱图17可知,3个卓越频率分别为0.34、0.475和0.75 Hz,与有限元分析所得主梁第1、第3、第9阶自振频率0.335 8、0.474 2和0.757 7 Hz非常接近。
3 全桥成桥状态紊流场气弹模型试验
为了进一步对比验证所提大跨度斜拉桥抖振响应简化分析方法的准确性,依托该斜拉桥设计了全桥气弹模型。
3.1 模型设计
综合考虑模型尺寸和试验风速,确定模型的缩尺比为λL=125,气弹模型试验的风速比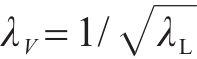
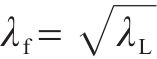

试验时采样频率为500 Hz,采样时间为60 s,试验时测得的主梁1阶正对称竖弯频率为3.808 6 Hz,与模型目标值3.754 4 Hz误差为1.44%,误差在规范范围内;主梁1阶横弯频率4.101 6 Hz以及1阶扭转频率11.274 2 Hz分别与模型标准值4.994 3 Hz、9.924 8 Hz存在10%以上的误差,其原因可能是主梁芯梁存在制造误差,导致芯梁横向抗弯惯性矩偏小而扭转抗弯惯性矩偏大,但针对本文关心的竖弯响应影响很小。
3.2 风荷载模拟
在进行全桥气弹试验之前,同样需要对该桥所处流场进行模拟,该桥位所处的紊流场为B类风场,采用矩形粗糙元加尖劈的形式布置风场,图21为风洞试验段内模拟紊流风场的布置情况。
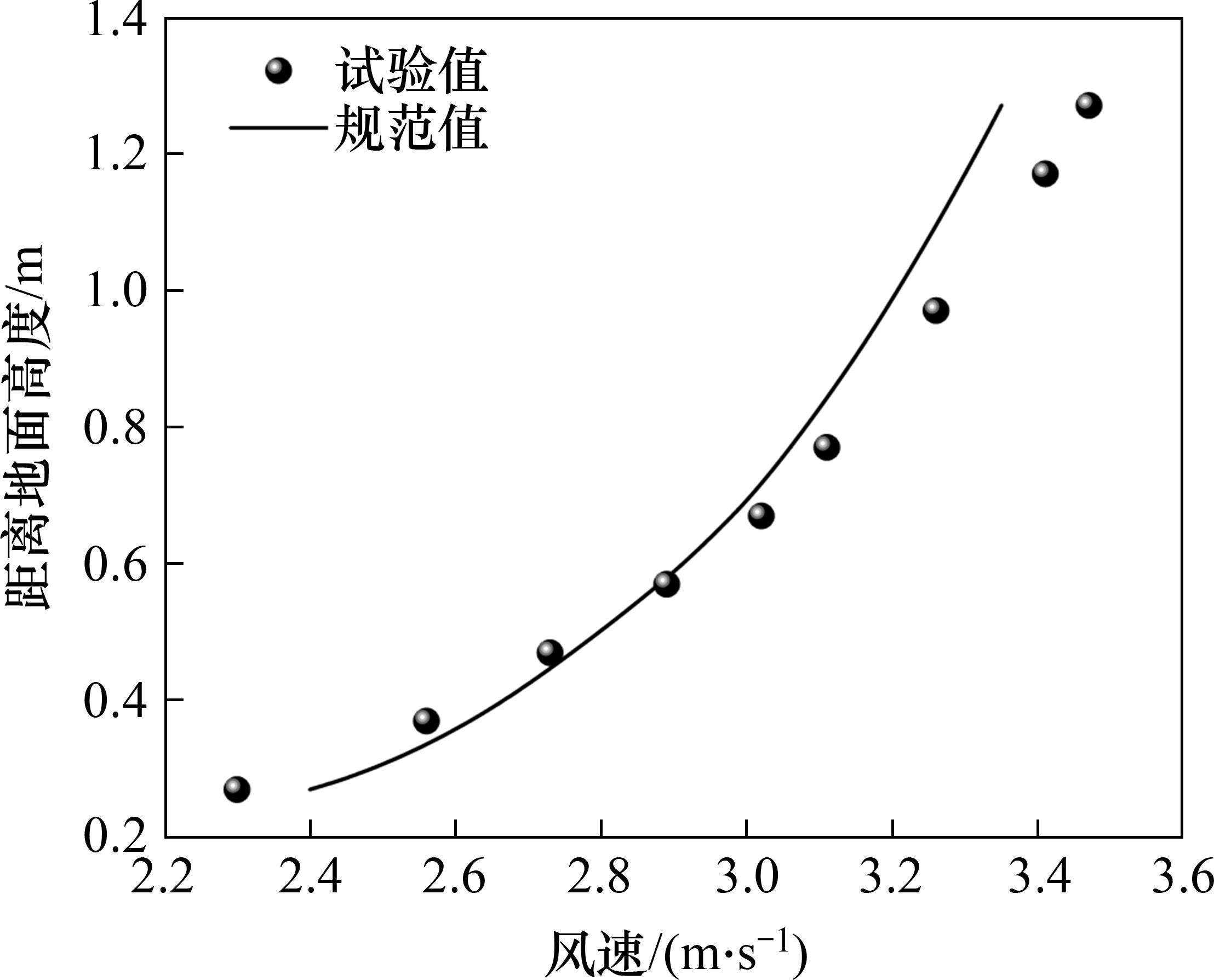
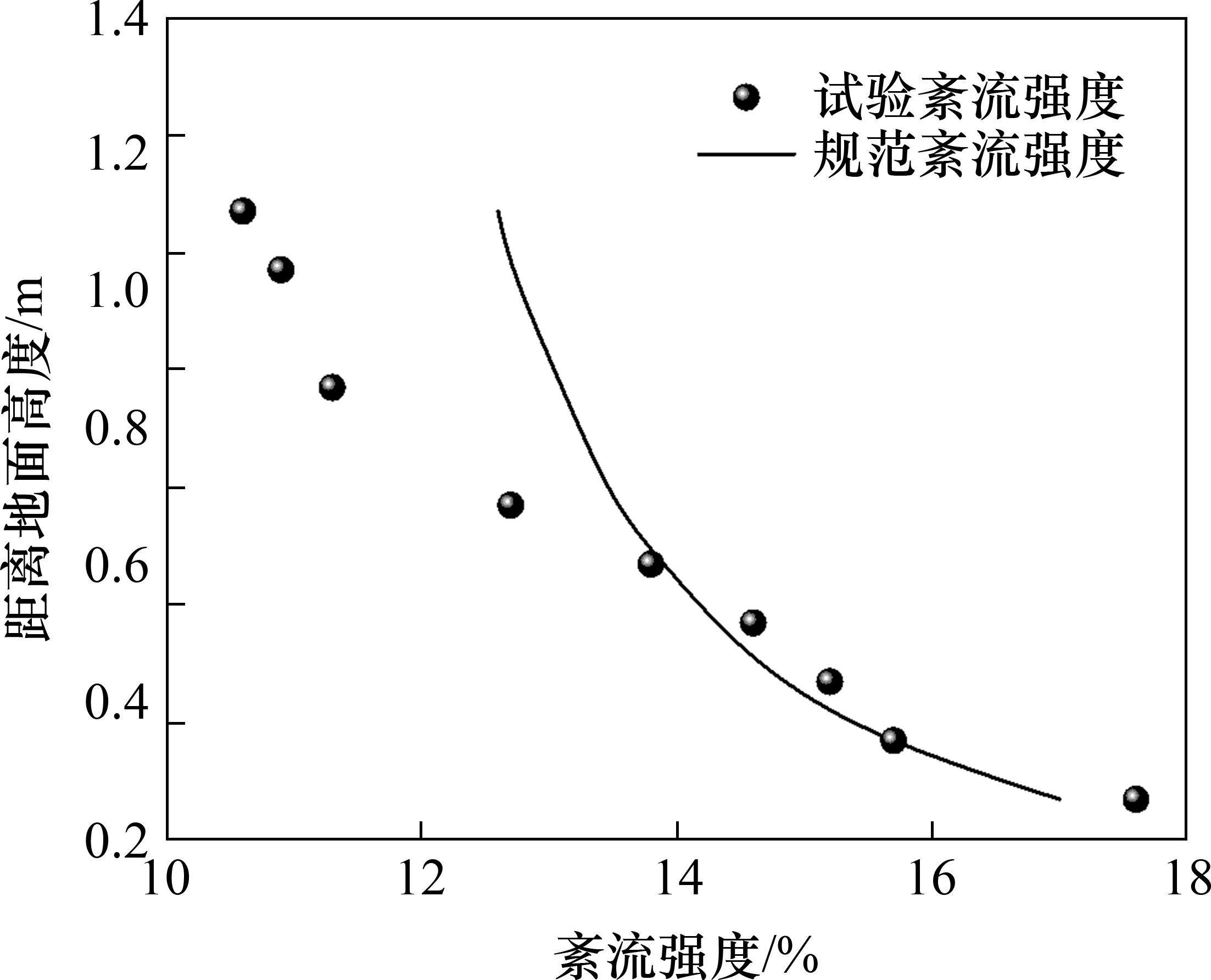

沿着试验段宽度方向选取3个测点测量该位置的风速剖面及紊流度剖面,每个测点分别测量9个离地高度处的风速和紊流度,其中离地高度570 mm为跨中桥面高度。试验测得3个测点的风速剖面及紊流度剖面基本一致,对3个测点的测量结果取平均值,得到风速及紊流强度模拟结果如表3、图19和图20所示。由图表均可看出,各测点平均风速与目标值的相对误差在±5%之内,紊流强度与目标值的绝对偏差在±0.02之内,满足规范要求。
| 离地高度/mm | 风速 | 紊流强度 | ||||
|---|---|---|---|---|---|---|
规范值/ (m∙s-1) | 模拟值/ (m∙s-1) | 误差/ % | 规范值 | 模拟值 | 偏差 | |
| 270 | 2.40 | 2.30 | -4.25 | 0.170 | 0.176 | 0.006 |
| 370 | 2.62 | 2.56 | -2.14 | 0.156 | 0.157 | 0.001 |
| 470 | 2.76 | 2.73 | -1.26 | 0.148 | 0.152 | 0.004 |
| 570 | 2.88 | 2.89 | 0.33 | 0.143 | 0.146 | 0.003 |
| 670 | 2.98 | 3.02 | 1.47 | 0.139 | 0.138 | -0.001 |
| 770 | 3.06 | 3.11 | 1.70 | 0.135 | 0.127 | -0.008 |
| 970 | 3.19 | 3.26 | 2.08 | 0.131 | 0.113 | -0.018 |
| 1 170 | 3.30 | 3.41 | 3.20 | 0.127 | 0.109 | -0.018 |
| 1 270 | 3.35 | 3.47 | 3.49 | 0.126 | 0.106 | -0.020 |
由试验测得在高度为570 mm,即跨中时,测得的风速为2.89 m/s,换算成实桥跨中的风速为32.31 m/s;而采用谐波合成法获得的风速在跨中为31.25 m/s,误差为3.28%。试验测得在跨中处的紊流度为0.146,数值模拟所得的紊流度为0.155,误差为6.16%,由此可以证明模拟所得风场与实际风场较为吻合,基于此风场获得的抖振响应结果也较为可靠。
3.3 抖振响应分析
全桥气弹模型试验在某大型边界层风洞第2试验段(低速试验段)进行,该试验段长15 m、模型试验区横截面宽5.5 m、高4.4 m,最大试验风速16 m/s。
为了与数值分析结果进行对比,在紊流B类风场中开展该桥成桥状态全桥气弹模型风洞试验,试验时最高风速为实桥风速65 m/s。试验时全桥气弹模型和传感器测点布置如图21所示。成桥状态紊流作用下,主梁跨中、1/4跨处竖弯的位移响应幅值随风速的变化如图22所示,图中的振幅和风速均已换算为实桥值。
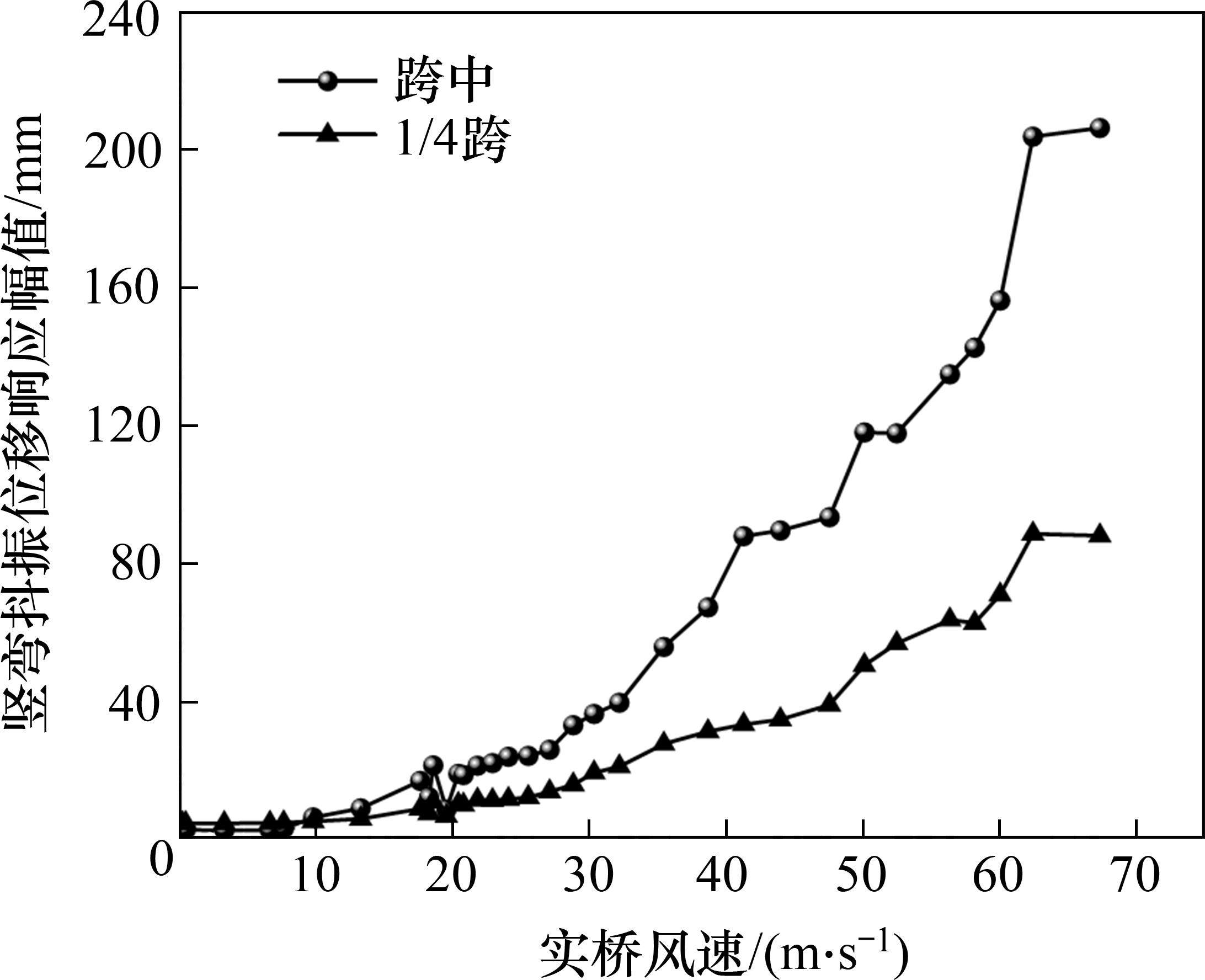
由结果可知,在紊流场中,成桥状态设计基准风速32.3 m/s下,0°攻角时主梁跨中及四分点的竖向抖振位移响应分别为39.6 mm和21.1 mm。
试验结果与采用简化分析方法以及传统分析方法的数值模拟结果对比情况如表4所示。
竖弯 响应 | 位置 | 全桥气弹试验结果/mm | 简化方法数值模拟结果/mm | 误差/% | 传统方法数值模拟结果/mm | 误差/% |
|---|---|---|---|---|---|---|
| 跨中 | 39.6 | 40.7 | 2.78 | 36.8 | 7.08 | |
| 1/4跨 | 21.1 | 21.6 | 2.37 | 17.8 | 15.64 |
4 结论
1) 数值模拟所得的紊流风场、全桥气弹风洞试验模拟风场与实际风场均吻合较好。基于此,数值模拟所得的斜拉桥竖弯抖振响应与全桥气弹风洞试验结果较为一致。因此,可以认为所提出的大跨度斜拉桥抖振响应简化分析方法是可行的,即在保证结果准确性的同时,为了简化前处理部分的工作量并减小计算代价,在进行大跨度斜拉桥抖振响应数值分析时可以忽略气动自激力引起的气动刚度。
2) 本文提出的大跨度斜拉桥抖振响应简化分析方法在对大跨度斜拉桥抖振响应进行预估分析时具有一定的准确性。该方法可以结合计算流体动力学(CFD)等软件,实现大跨度斜拉桥抖振响应的全过程数值仿真。
Π型主梁斜拉桥抖振响应多因素分析
[J/OL]. 振动工程学报, 1-11(甘泽鹏,邓佳逸,吴庆等.大跨斜拉桥抖振响应简化分析方法及试验验证[J].铁道科学与工程学报,2025,22(03):1165-1176.
GAN Zepeng,DENG Jiayi,WU Qing,et al.Simplified analysis method and experimental verification for buffeting response of long-span cable-stayed bridge[J].Journal of Railway Science and Engineering,2025,22(03):1165-1176.

