截至2023年底,我国共有55个城市开通运营城市轨道交通线路306条,运营里程10 165.7 km[1]。随着城市中心地带地铁线路路网系统日益稠密,其相伴而生的振动噪声问题日益突显,降低了沿线居民的生活质量,地铁环境振动分析已成为近年来铁路行业的研究热点[2-3]。在地铁线路设计时,基于减振降噪要求的线路设计和结构选型已成为目前需要重点关注的设计方案,因此亟待发展一种准确、高效的车致环境振动预测和数值评估方法,以期科学合理地获取地铁线路的最优匹配设计参数。在地铁环境振动预测方面,早期采用经典的隧道-土体二维解析模型[4]和PiP半解析模型[5],此类模型计算效率高,但对于隧道和土体进行了大量的假设和简化,适用范围受限;杨建近[6]提出了柱状层单元离散形式的隧道-土体半解析模型,研究隧道土体的动力响应。MA等[7]完整考虑隧道仰拱结构特点,建立了基于2.5D-FEM-PML理论的曲线段黏弹性隧-土模型,研究模拟地铁曲线段中振动波的辐射规律;LIU等[8]基于周期有限元-无限元理论研究准确预测地铁曲线隧道的地面振动;XU[9]建立了基于6~8节点等参元的车-线-隧-土耦合动力学模型,研究列车数和隧道数对地面振动的影响规律。目前地铁环境振动预测模型日趋完善,但在土体中大规模和复杂土质条件计算方面仍有进步空间,对特定土质条件可以结合经验公式大幅计算求解效率。在减振参数优化设计研究方面,冯青松等[10]研究了市域铁路过渡段轨道结构的动力响应,并设计了该段减振垫刚度阻尼匹配优化策略;张皓迪等[11]基于2.5D环境预测模型,探究了减振扣件和减振轨道的最优匹配策略;杨宜谦等[12]基于我国35个地铁断面振源的实测数据,分析了地铁的振动源机理和时频特性,总结出P2共振是城市轨道环境振动和二次噪声的主要原因之一。刘文武等[13]基于预制浮置板轨道结构,探究了剪力铰和浮置板隔振器排布方式的优化设计。然而以车线隧耦合模型为基础,开展地铁环境振动的预测及扣件、减振垫刚度阻尼最优匹配的综合性研究相对较少。本文基于车辆-轨道-隧道空间耦合时变动力学模型,引入环评经验预测公式,建立了地铁车致环境振动预测的数值模型,研究行车速度、扣件和减振垫刚度、阻尼等关键参数对车致隧道壁和地表Z振级的影响,给出了合理的结构设计参数范围和地铁线路选线时与不同功能区建筑结构的最小距离限值。
1 基于车-线-隧耦合振动模拟的地铁环境振动预测方法
本文将车辆-轨道-隧道耦合模型和环境振动评估与预测方法相结合,从数值模拟角度开展地铁车致环境振动预测方法研究。
1.1 车辆-轨道-隧道空间耦合时变动力学模型
基于车辆-轨道耦合动力学理论[14],将地铁列车、减振垫轨道结构、隧道视为整体系统,引入能量变分原理[15],建立了车辆-轨道-隧道空间耦合时变动力学模型[16](见图1),用下式表示:

式中:

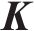
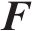
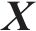
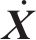
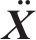

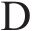

1.1.1 车辆-轨道耦合动力学模型
在车辆-轨道耦合动力学模型中,视车辆子系统为42自由度多刚体系统,钢轨由离散支撑的Euler-Bernouli梁单元模拟、轨道板由Mindlin中厚板单元模拟,扣件和减振垫填充层等层间结构用弹簧-黏性阻尼单元模拟,车辆子系统和轨道子系统通过轮轨单元矩阵法[16]进行耦合。
1.1.2 隧道模型
视隧道管片、仰拱、注浆层和周围土体为整体,将注浆层与土体简化为圆柱层均匀介质,隧道外层为黏弹性单元[18],隧道模型的横剖面见图2(a)。基于6~8节点空间等参元组合法[11],将隧道模型离散化,隧道模型单元划分方式见图2(b),具体描述如下:以仰拱隧道壁交点为界划分仰拱延伸区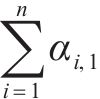
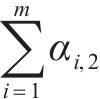
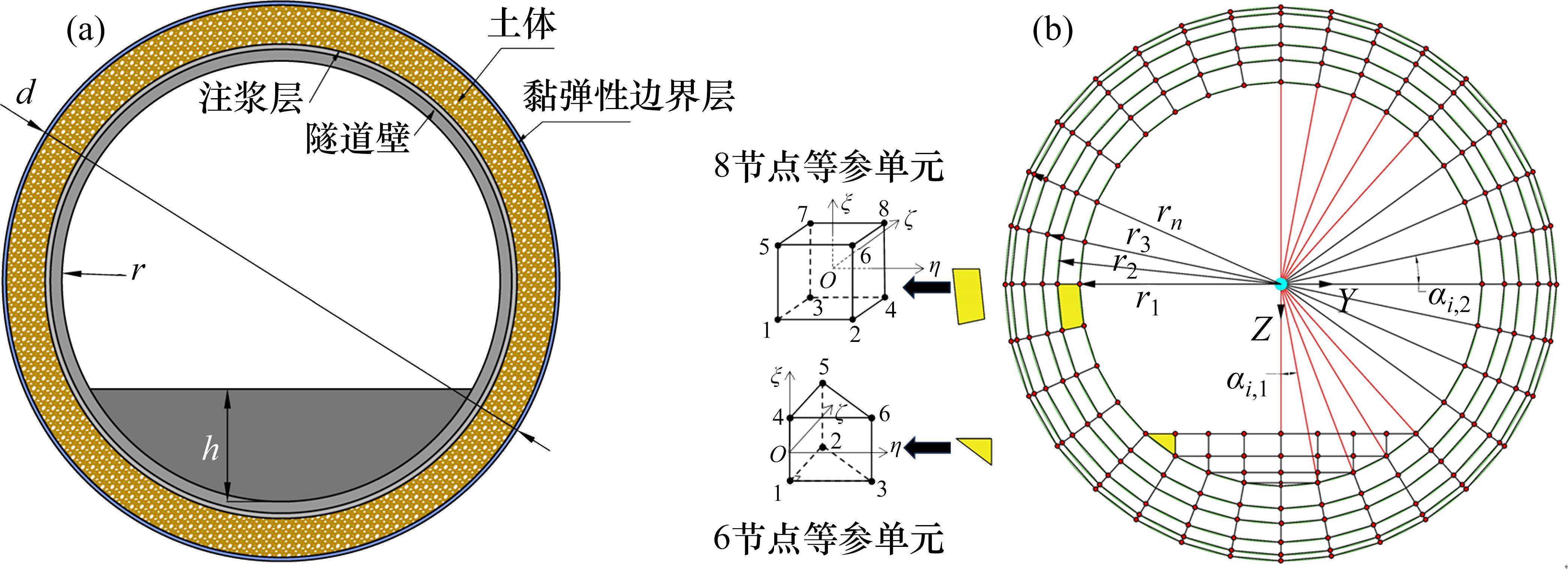
1.2 环境振动评估与预测方法
针对地铁列车引起的建筑振动噪声评估和预测,本文采用《城市区域环境振动标准》[22]规定的Z振级和标准限值评价各类区域建筑物室内振动噪声,以《环境评价影响技术导则 城市轨道交通》[21]中的环境振动影响预测方法预测地表以及建筑Z振级。
1.2.1 环境振动评估方法
城市轨道交通环境振动水平的评价指标宜采用Z振级和分频最大振级。垂向加速度时程信号以1 s为间隔计权,分为若干幅波形进行计算分析,先计算每一幅波形下的各1/3倍频程中心频率对应的分频振级,再通过下式计算Z振级[20]:
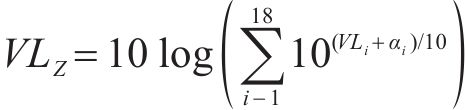
式中: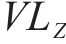
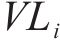
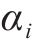
分频最大振级由计权因子修正1/3倍频程下的垂向加速度得到,采用常见的线性平均法计算分频最大振级:
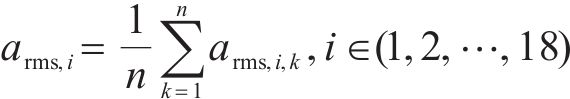
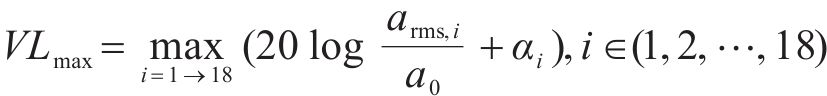
式中: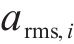
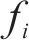
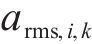
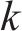
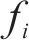
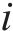
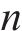
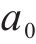
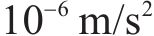
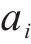
1.2.2 环境振动预测方法
本文选用模式预测法[21]计算列车运行引起的环境振动:
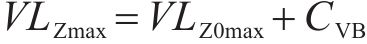
式中: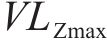

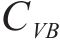
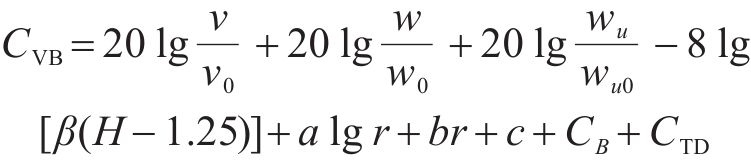
式中: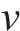
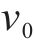

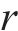
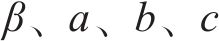
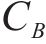

1.3 地铁车致环境振动预测评估框架
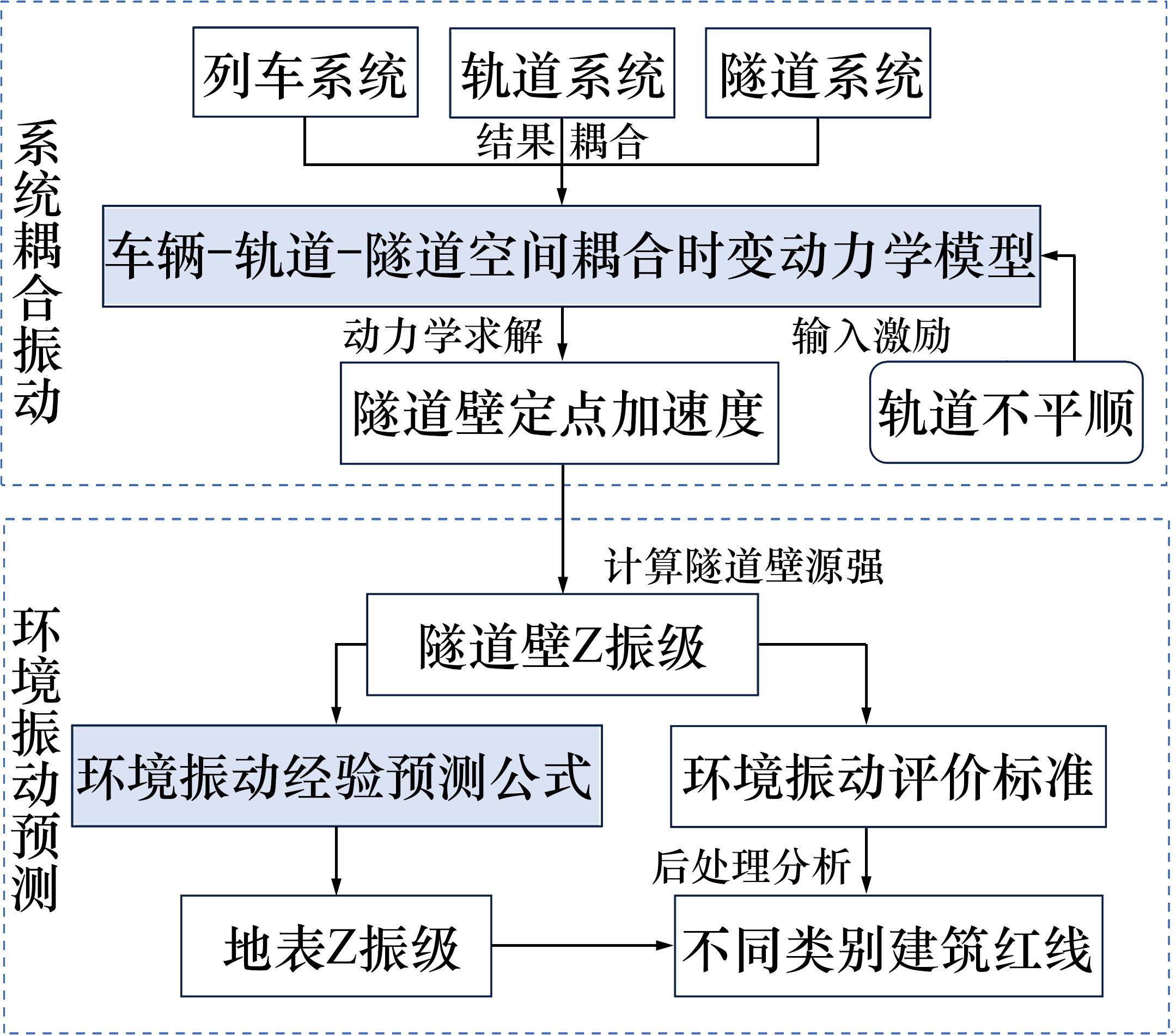
基于车辆-轨道-隧道耦合时变动力学模型和经验公式预测方法,采用循环计算[16]的策略高效组装系统动力学矩阵,实现地铁环境振动预测及评估。具体步骤如下:1) 基于车辆-轨道-隧道耦合时变动力学模型,输入轨道不平顺激励,通过时域积分方法计算得到隧道壁定点垂向加速度响应;2) 根据规范的环境评价经验公式预测地表Z振级;3) 根据环境振动评价标准对响应进行评估,划分不同类别建筑红线。
综上,地铁环境振动评估预测框架如图3所示。
1.4 实测结果及模型验证
为了验证车-线-隧耦合模型的可靠性,对某地铁直线段开展现场实测(见图4)。钢轨测点位于轨腰两相邻扣件跨中、道床测点位于距轨道中心线约1 m处,隧道壁测点位于距离钢轨顶面约1.25 m处,确保传感器安装方向的竖直[23]。测试采用东方所自研智能数据采集分析仪,型号INV,安装KSI加速度传感器采集振动信号,钢轨处布置的传感器量程为50g,道床和隧道壁处布置的传感器量程为20g。地铁线路工况剖面图见下图5,其中隧道结构为单线行车盾构隧道,采用6B编组地铁B型车,列车速度68 km/h;钢轨由间距为0.6 m的DTVI2-1型扣件支撑,轨道板尺寸为0.37 m×3 m×4.77 m(高×宽×长)。隧道顶部距地表20 m,隧道内径5.2 m,隧道壁、注浆层及土体参数见图5,土体参数根据勘测资料得到等效剪切波速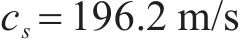
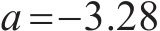
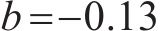
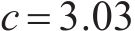
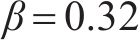

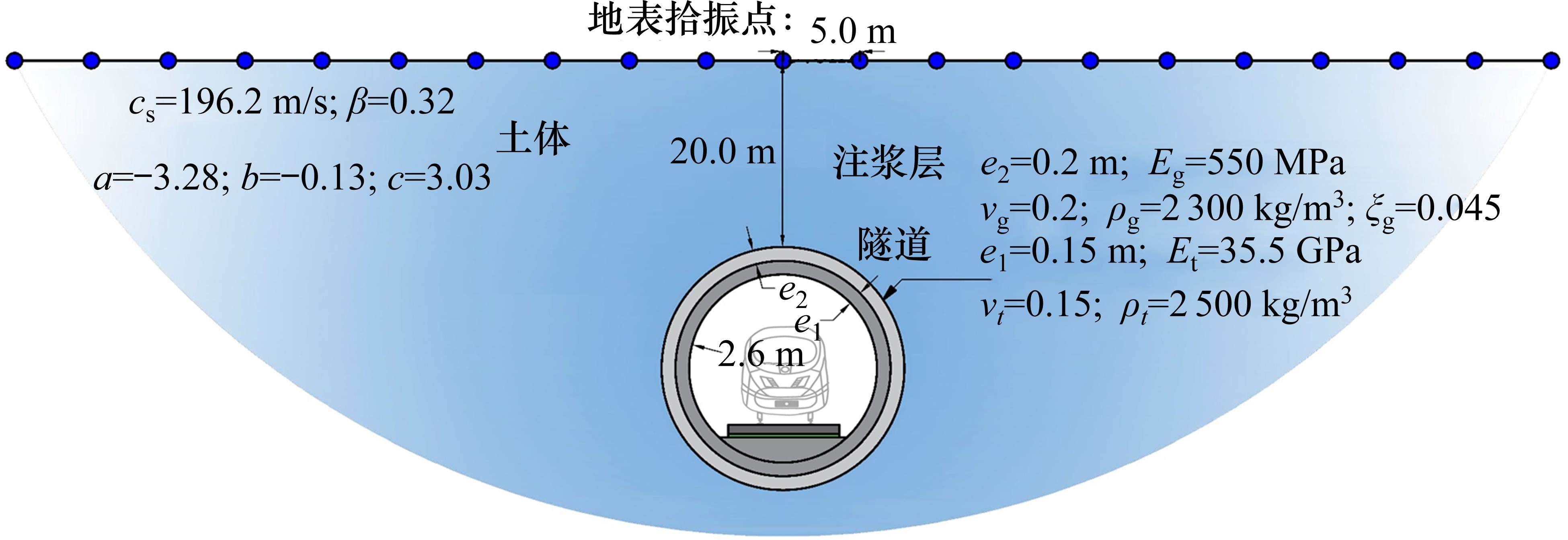
本文建立的地铁列车-减振垫浮置板-隧道动力学模型参数见表1和表2。
| 参数 | 数值 | 结构 | 参数 | 数值 | |
|---|---|---|---|---|---|
| 车重/kg | 2.192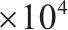 | 扣件 | 纵向刚度/(N∙m-1) | 6.7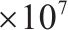 | |
| 车体侧滚惯性矩/(kg∙m2) | 6.173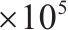 | 横向刚度/(N∙m-1) | 2.3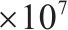 | ||
| 车体点头惯性矩/(kg∙m2) | 1.489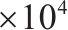 | 垂向刚度/(N∙m-1) | 5.6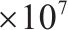 | ||
| 车体摇头惯性矩/(kg∙m2) | 6.173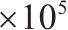 | 纵向阻尼/(N∙s∙m-1) | 3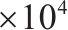 | ||
| 转向架重/kg | 2 550 | 横向阻尼/(N∙s∙m-1) | 3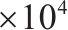 | ||
| 转向架侧滚惯性矩/(kg∙m2) | 1 050 | 垂向阻尼/(N∙s∙m-1) | 2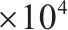 | ||
| 转向架点头惯性矩/(kg∙m2) | 1 750 | 轨道板 | 弹性模量/MPa | 3.25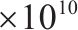 | |
| 转向架摇头惯性矩/(kg∙m2) | 1 980 | 密度/(kg∙m-3) | 2 500 | ||
| 轮对重/kg | 1 420 | 泊松比 | 0.2 | ||
| 轮对侧滚惯性矩/(kg∙m2) | 985 | 长/宽/高/m | 4.77/3/0.37 | ||
| 轮对点头惯性矩/(kg∙m2) | 97 | 板下刚度/(N∙m-3) | 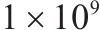 | ||
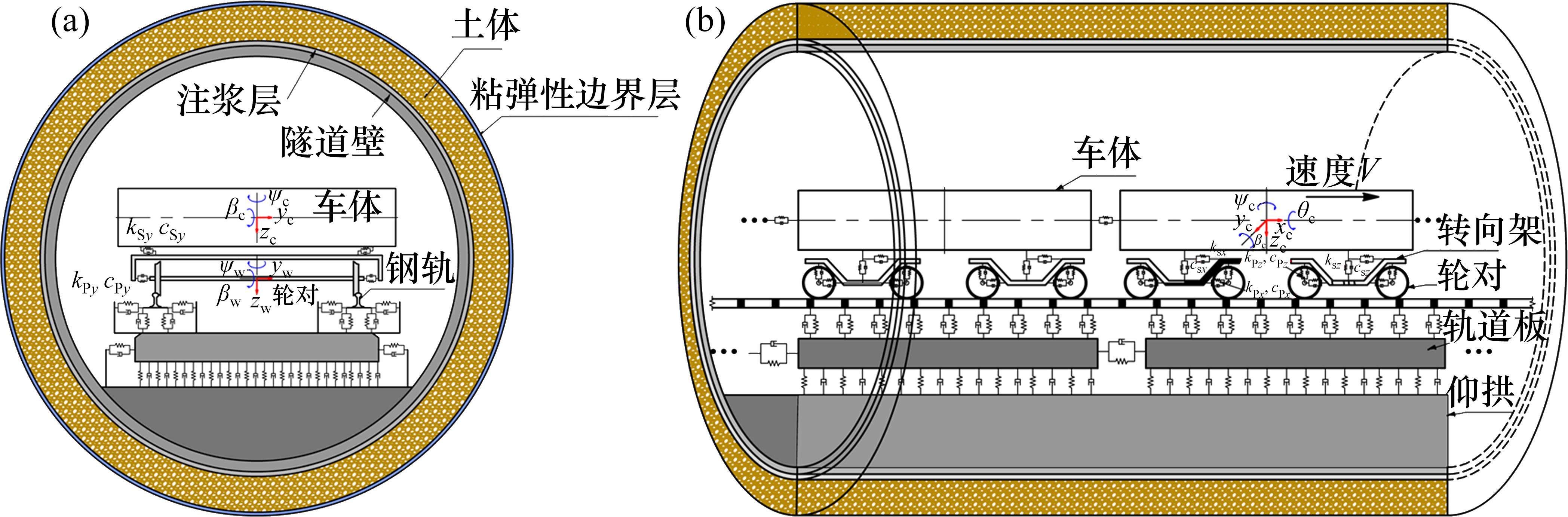
| 轮对摇头惯性矩/(kg∙m2) | 985 | 板下阻尼/(N∙s∙m-3) | 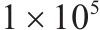 | ||
| 一系悬挂垂向刚度/(N∙m-1) | 1.7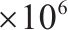 | 隧道 管片 | 密度/(kg∙m-3) | 2 500 | |
| 一系悬挂垂向阻尼/(N∙s∙m-1) | 5 000 | 弹性模量/MPa | 3.55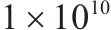 | ||
| 二系悬挂垂向刚度/(N∙m-1) | 2.75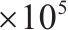 | 泊松比 | 0.15 | ||
| 二系悬挂垂向阻尼/(N∙s∙m-1) | 3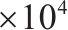 | 内/外径/m | 2.6/2.75 | ||
| 转向架间距/m | 12.6 | ||||
| 轮对内间距/m | 2.2 |
| 结构 | 参数 | 数值 | 结构 | 参数 | 数值 |
|---|---|---|---|---|---|
| 沙砾土 | 密度/(kg∙m-3) | 2 050 | 注浆层 | 密度/(kg∙m-3) | 2 300 |
| 弹性模量/MPa | 186 | 弹性模量/MPa | 550 | ||
| 泊松比 | 0.3 | 泊松比 | 0.2 | ||
| 厚度/m | 0.5 | 厚度/m | 0.2 | ||
| 阻尼比 | 0.045 | 阻尼比 | 0.045 |
本模型轨道不平顺激励由德国高干扰谱(波长1~200 m)、SATO谱(波长0.01~1 m)反演叠加得到,实测测点都取模型的纵向中点所在铅垂面,右轨腰、轨道板距中线1 m和隧道壁处(测点距离钢轨顶面约1.25 m)测点的1/3倍频程振动加速度级对比见图6。
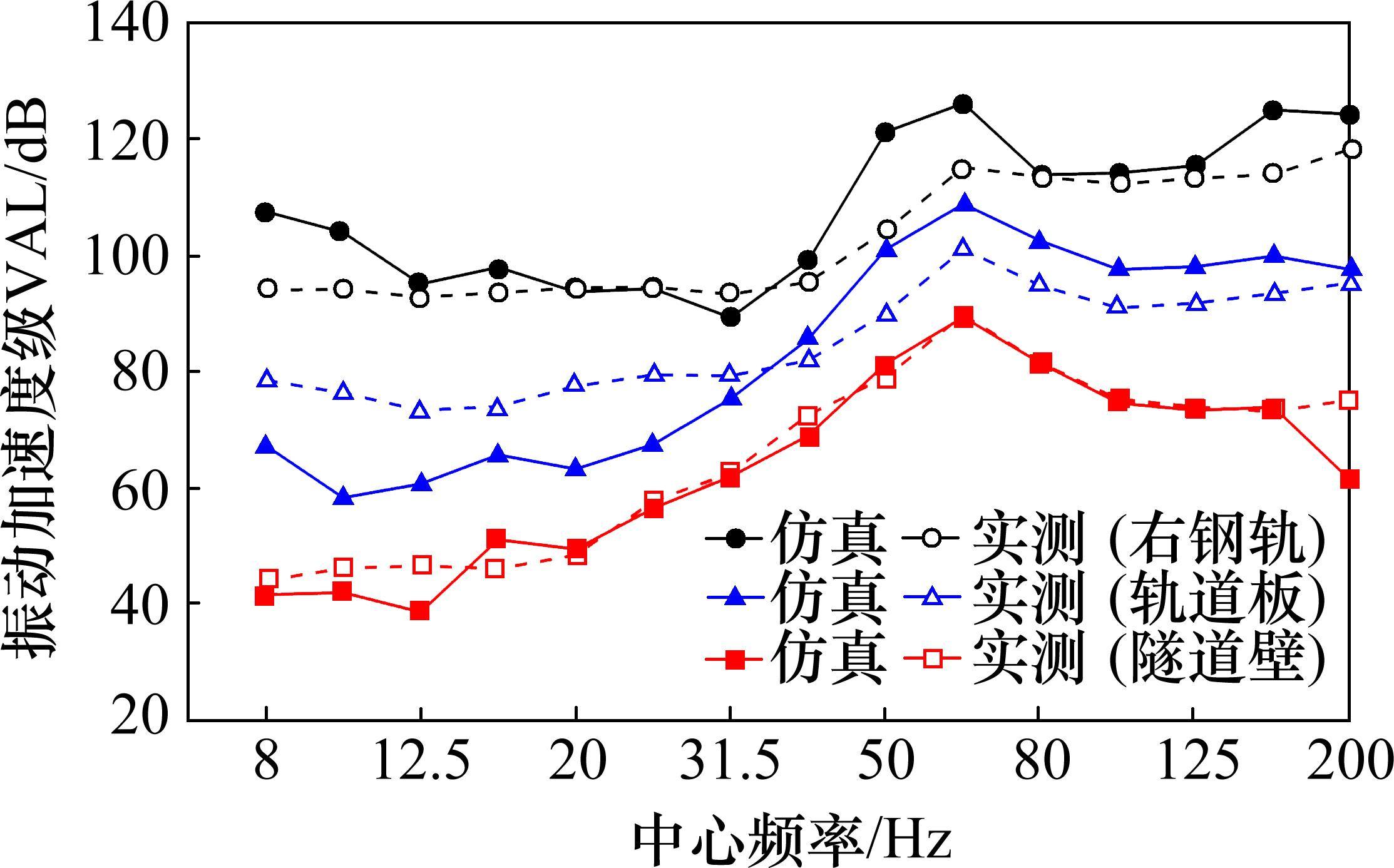
从图6可知,本文模型获得的右钢轨、轨道板和隧道壁加速度级与实测结果基本一致,尤其是主频62.5 Hz对应的幅值较为准确,道床板和钢轨的8~20 Hz的低频振级结果相比实测结果有差异,主要原因在于模型中轨道不平顺激励源、结构参数等与现场实际情况存在一定差异。总体来看,本文建立的车辆-轨道-隧道空间耦合时变动力学模型能够较好地反映地铁车致下部结构振动响应特性。
2 关键参数分析
根据文献[13]可知,低频振动的主要成分为列车和轨道各子结构间距引起的,而P2共振频率与减振垫1阶自振频率是影响环境振动的关键频率。其中减振垫隔振频率即为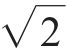
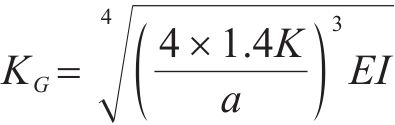
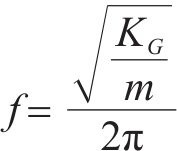
式中: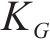
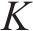
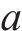
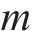
显而易见,扣件刚度是影响P2共振频率的主要因素。本文考虑列车速度、扣件刚度阻尼和减振垫刚度阻尼,研究扣件和减振垫参数组合对行车性能及隧道壁1/3倍频程分频振级影响规律,分析参数变化对地表Z振级分布的影响规律,并结合环评标准划定参数的合理取值范围。
2.1 列车速度对地表Z振级的影响
为了探明不同行车速度对车致结构振动响应的影响,研究了列车速度40~120 km/h(以20 km/h为间距)地表Z振级分布,结果见图7所示。
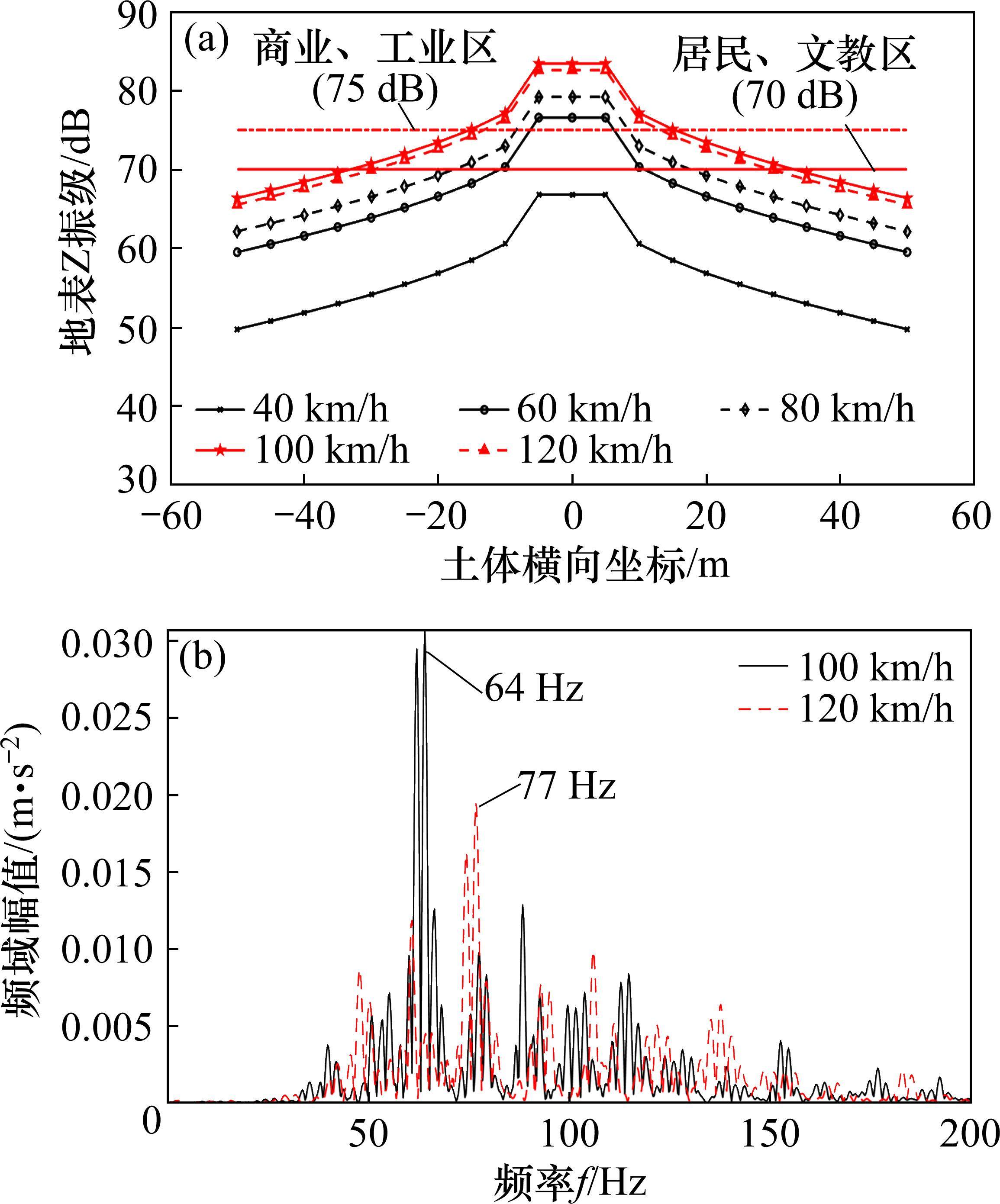
由图7(a)可知当车速由40 km/h增大到60 km/h时,地表Z振级大幅增大;40~100 km/h范围地表Z振级随车速的增大而增大,120 km/h时地表Z振级减小。根据GB10070-88城市各类区域垂向Z振级标准值[21]划分商业、工业区建筑室内Z振级不得超过75 dB,居民、文教区建筑室内Z振级为70 dB。规范定义的建筑室内Z振级测点布置在建筑一楼室内或建筑物外墙0.5 m范围内,可以认为与地表Z振级的大小一致。对于居民、文教区,距线路中心35 m外各车速对应室内Z振级都在标准值以下,车速在80 km/h以下时,距线路中心20 m外室内Z振级均低于标准值;对于商业、工业区,距线路中心18 m外各车速对应室内Z振级都在标准值以下;当车速在80 km/h及以下时,距线路中心10 m外室内Z振级都在标准值以下。
图7(b)对比了100 km/h和120 km/h隧道壁垂向加速度频谱幅值,可以得出在车速100 km/h下的峰值频率与隧道固有频率64 Hz重合,导致该主频远大于车速120 km/h下的峰值频率77 Hz。Z振级的计权频率范围为1~80 Hz,低频权重高而高频权重低,提高车速将使隧道壁峰值频率提高,从而使隧道壁峰值频率的权重降低或者将峰值频率移出80 Hz,导致隧道壁Z振级降低,从而使100 km/h的地表Z振级略大于120 km/h的地表Z振级。
2.2 扣件参数对地铁行车性能和地表Z振级的影响
为了分析扣件参数对建筑室内振动的影响,本文取列车速度80 km/h,6B编组,其他参数和轨道不平顺与验证时采用的模型参数相同。根据文献[11, 13]可知DTVI2-1型扣件型号的垂向刚度取值范围是20~60,扣件垂向阻尼系数取20 (kN∙s)/m,故本文设计了扣件刚度10~80 kN/mm(以10 kN/mm为间距,阻尼取20 (kN∙s)/m)和扣件阻尼20~30 (kN∙s)/m(以2 (kN∙s)/m为间距,刚度取40 kN/mm)分析沿地表横向距离分布的地表Z振级分布(见图8)。
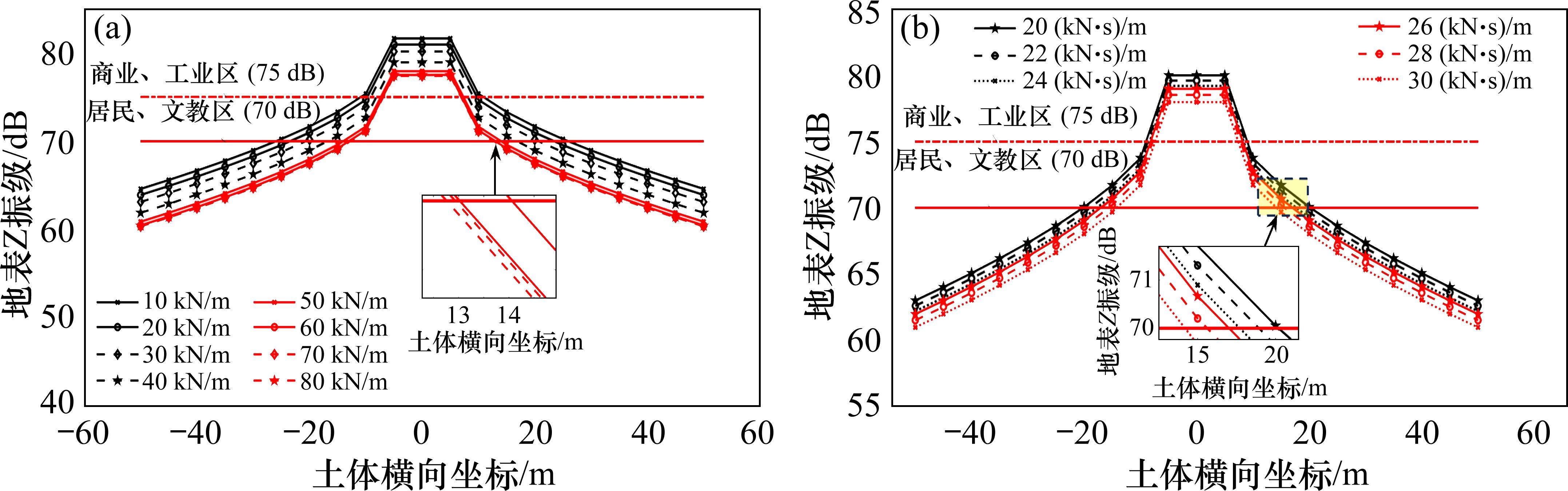
由图8(a)可知地表Z振级随着扣件刚度的增大而降低,在扣件刚度达到60 kN/mm后减振效果不明显,故扣件刚度最高只需要取60 kN/mm。对于居民、文教区,根据扣件刚度的由高到低,距线路中心13~28 m以外对应的建筑室内振动满足标准值要求,对于商业、工业区,由于该段地表Z振级随扣件刚度变化不大,距线路中心12 m以外对应的建筑室内振动满足标准值要求。由图8(b)可知地表Z振级随着扣件阻尼的增大而降低。对于居民、文教区,根据扣件阻尼的由高到低,距线路中心14~20 m以外对应的建筑室内振动满足标准值要求,对于商业、工业区,由于该段地表Z振级随扣件阻尼变化不大,距线路中心9 m以外对应的建筑室内振动满足标准值要求。
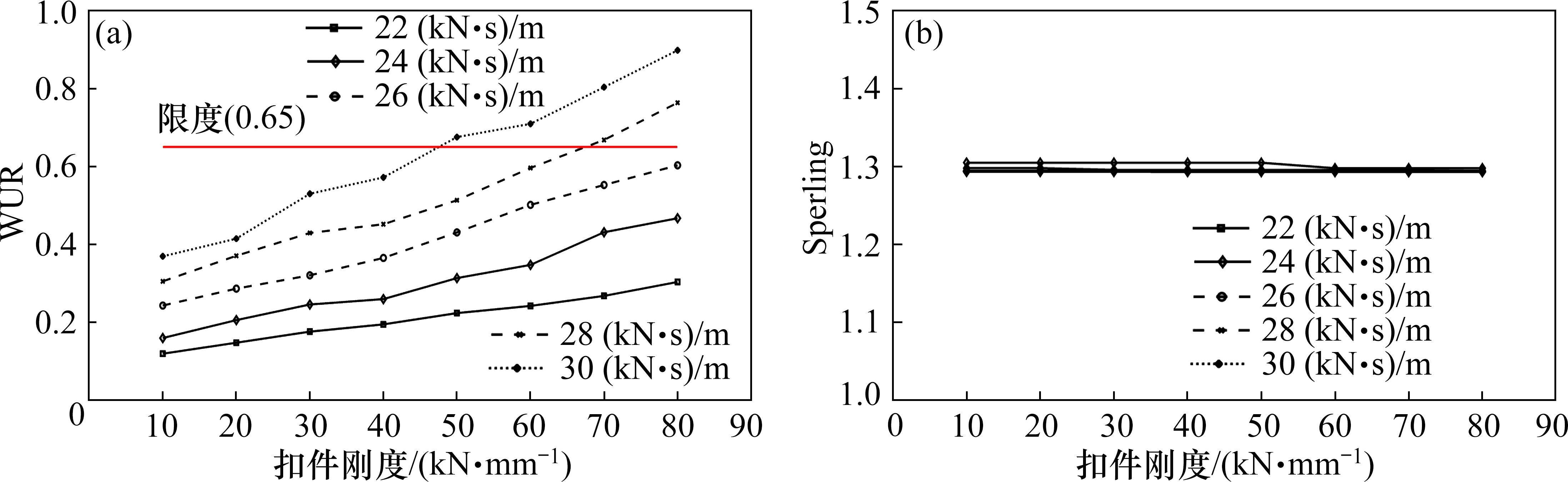
扣件刚度的改变会直接影响轮轨力的峰值和主频率,从而影响行车性能。行车性能包括行车安全性和行车舒适性,其控制指标分别为轮重减载率(WUR, Wheel unloading rate)和Sperling平稳性指标。根据《机车车辆动力学性能评定及试验鉴定规范》[24]规定,当行车速度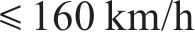
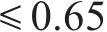
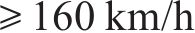
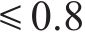
2.3 减振垫参数对隧道壁和地表Z振级的影响
本文选用减振垫刚度1、2、5、10、15和
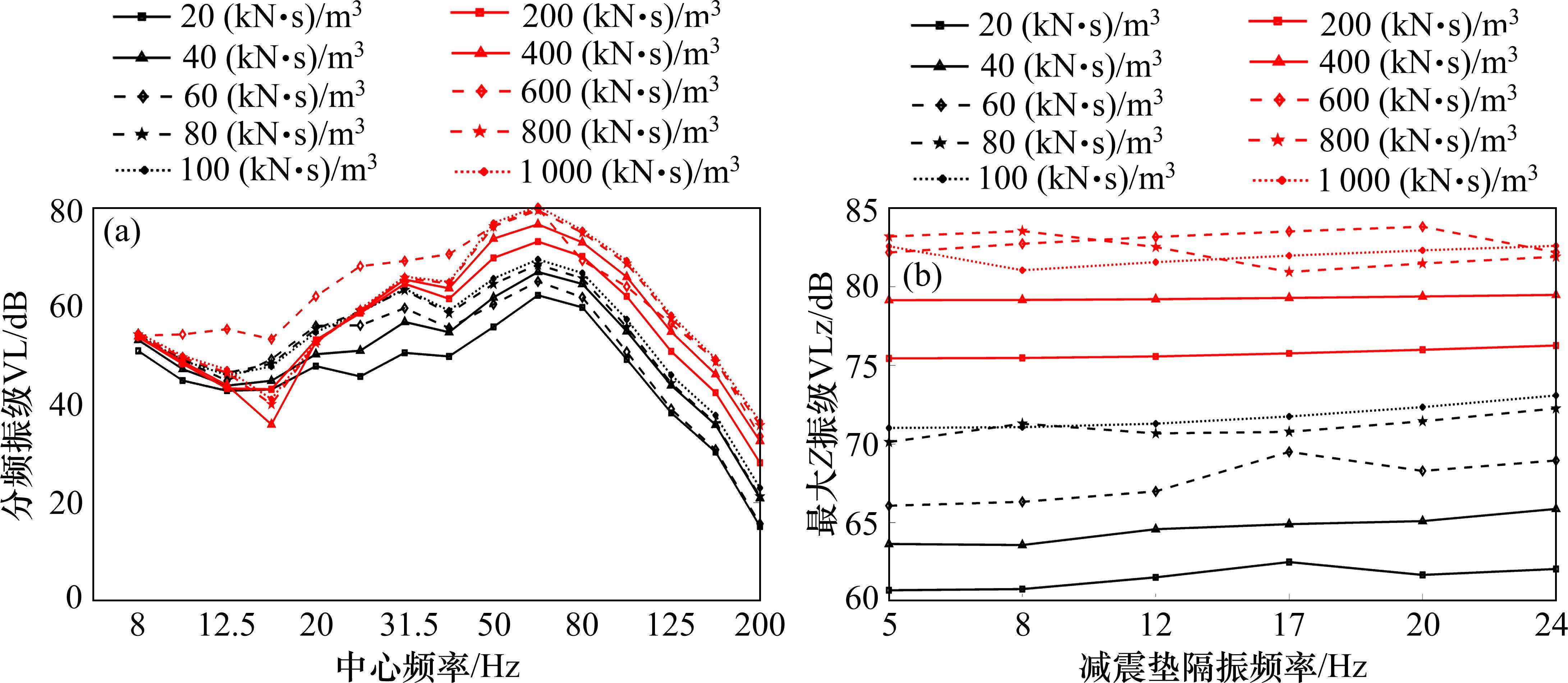
由图10(a),刚度为
为了分析减振垫频率对建筑室内振动的影响规律以及探明各类建筑的达标参数范围,本文减振垫频率选取了5、8、12、17、20和24 Hz共6种(减振垫阻尼取100 (kN∙s)/m3,与无隔振保持一致)和减振垫阻尼20~1 000 (kN∙s)/m3(考虑最不利情况,减振垫频率取24 Hz)分析沿地表横向距离分布的地表Z振级分布(见图11),并对比其与无隔振措施(阻尼100 (kN∙s)/m3,刚性连接)地表Z振级的差异。
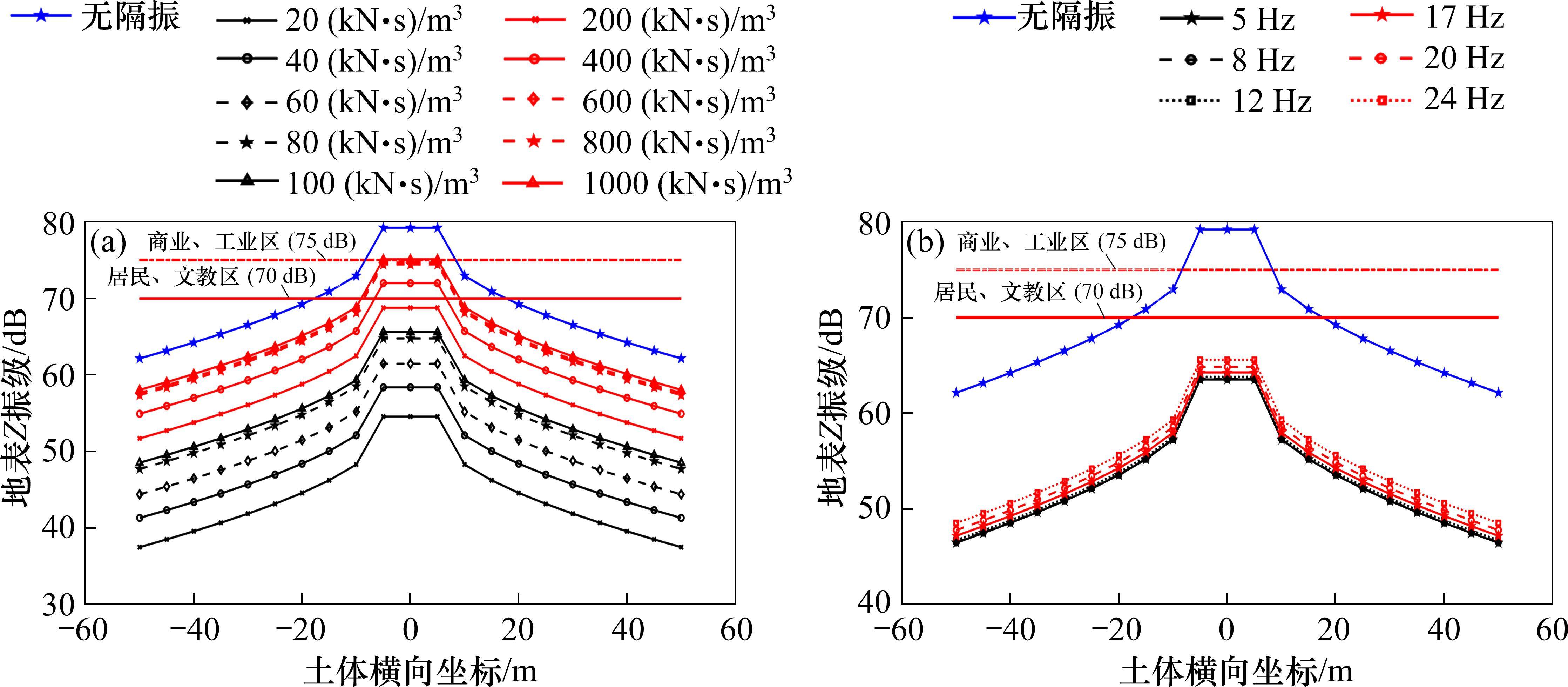
由图11可知采用减振垫浮置板能显著降低地表Z振级的大小。总体来看,地表Z振级随减振垫频率和减振垫阻尼的增大而增大,与文献[12]结果相一致。由图11(a)可知,对于居民、文教区,减振垫阻尼为400 (kN∙s)/m3时,距线路中心7 m以外的室内振级满足要求,减振垫阻尼达到及高于600 (kN∙s)/m3,距线路中心10 m以外的室内振级满足标准值要求。结合图11(a)和图11(b)可知,对于商业和工业区,各减振垫频率和阻尼对应建筑室内振级都满足标准值要求。
3 结论
1) 40~100 km/h车速范围内,地表Z振级随车速的增大而增大,120 km/h时地表Z振级减小。考虑GB10070―88城市Z振级标准值要求,地铁在车速80~120 km/h范围内,居民、文教建筑应距地铁线路中心35 m以外,商业、工业建筑应距地铁线路中心18 m以外;在设计车速80 km/h及以下,居民、文教建筑应距地铁线路中心20 m以上,商业、工业建筑应距地铁线路中心10 m以上。
2) 地表Z振级随着扣件刚度的增大而减小,随扣件阻尼的增大而增大,在扣件刚度大于60 kN/mm时减振效果不明显。地铁在扣件刚度10~80 kN/mm范围内,居民、文教建筑应距地铁线路中心28 m以外,商业、工业建筑应距地铁线路中心12 m以外。
3) 扣件刚度的改变会直接影响轮轨力的幅值和峰值频率,从而影响行车性能。轮重减载率随着扣件刚度的提高而增大,在22~30 (kN∙s)/m的阻尼区间内,轮重减载率随着扣件阻尼的提高而增大,扣件阻尼在26 (kN∙s)/m以下时轮重减载率满足限度(0.65);阻尼为28 (kN∙s)/m时,60 kN/mm以上刚度超过限度(0.65);扣件刚度、阻尼对Sperling指标基本没有影响。
4) 减振垫阻尼存在临界值。阻尼小于600 (kN∙s)/m3时隧道壁Z振级随着减振垫参数的增大而增大,阻尼高于600 (kN∙s)/m3时,转向架内轴距对应的特征频率段的隧道壁振级大幅降低,说明该部位引起的振动叠加效应减小,导致了隧道壁Z振级减小及出现局部峰值。隧道壁Z振级在隔振频率20 Hz、阻尼600 (kN∙s)/m3时达到最大值,在隔振频率5 Hz、阻尼20 (kN∙s)/m3达到最小值。
5) 采用减振垫浮置板能显著降低地表Z振级的大小。总体来看,地表Z振级随减振垫频率和减振垫阻尼的增大而增大。在减振垫阻尼达到及高于600 (kN∙s)/m3时,居民、文教建筑应距线路中心10 m以上。20~1 000 (kN∙s)/m3减振垫阻尼以及5~24 Hz隔振频率对应室内振级都能满足商业、工业区的要求。
6) 模式预测法适用于剪切波速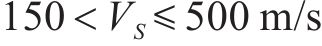
徐磊,胡逸宁,朱光楠等.基于车线隧系统的环境振动预测评估方法及参数影响研究[J].铁道科学与工程学报,2025,22(03):1177-1187.
XU Lei,HU Yining,ZHU Guangnan,et al.Environmental vibration prediction and evaluation method based on vehicle-track-tunnel system and key parameters impact[J].Journal of Railway Science and Engineering,2025,22(03):1177-1187.

