高速列车隧道空气动力学问题是当前中国高铁迫切需要解决的关键技术之一[1]。高速列车通过或者在隧道交会时,其强烈的“活塞效应”会引起复杂的压缩波和膨胀波,导致列车受到较大的气动载荷作用而影响结构的可靠性[2]。同时,列车在隧道中交会时产生的复杂压力波频率与高速列车整车低阶固有振动频率接近或一致时,导致列车振动加剧,严重影响行车安全及乘坐舒适性[3-4]。因此,研究高速列车隧道交会气动载荷及其对列车振动特性的影响,对于抑制列车异常振动和提高列车运行安全性具有重要意义。针对高速列车隧道空气动力学问题,国内外学者进行了广泛深入的研究,而气动载荷对列车的影响,尤其是对列车舒适性和振动特性的影响方面,尚没有开展系统的研究,对列车隧道会车工况下出现的晃车或者振动舒适性等问题无法从机理上解释其发生的原因。在高速列车隧道会车气动载荷数值模拟方面,梅元贵等[5]采用一维可压缩非定常不等熵流动模型对单车通过及隧道会车压力波进行了研究,发现列车在隧道内等速交会时压力波动范围约为单车通过隧道的2倍。王磊等[6]对横风下高速列车隧道洞口交会的气动效应进行了研究,结果发现有横风时列车交会开始与完成时,列车中部压力系数峰值分别较无横风情形增大7.8%和30.6%。钟沙等[7]对400 km/h不同编组的高速列车隧道交会气动效应进行了研究,结果表明16节车相较于3节车的车体表面峰值压力由12.05 kPa增加至15.18 kPa,涨幅约为25.98%。杨思涵等[8]对400 km/h的高速列车隧道交会气动效应进行了研究,结果表明车体变截面处压力幅值变化明显。LI等[9]采用三维可压缩非定常雷诺时均法(Reynolds- Average Navier-Stokes, RANS)对隧道交会工况下车体表面压力波的传播、形成机理及气动力特性进行研究。LIU等[10]采用RANS对隧道会车压力波的分布及振幅的变化规律进行了研究,结果表明同一截面的测点压力波变化趋势基本一致,仅幅值存在一定差异。综上,对隧道交会压力波特性及车外压力变化规律等进行了分析,但对气动载荷的频域特性及尾部涡流分析较少,且较少有对会车后气动载荷幅值和波动情况高于会车前的现象进行原因揭示。在分析隧道会车气动载荷的时域频域特性及尾部流场结构的基础上,采用顺序耦合的方法,将气动载荷作为列车振动激励,分析其对列车振动的影响。在气动振动的影响方面,LIU等[11]将隧道交会下的气动载荷作用在车体上,不考虑轨道激励的影响,结果发现气动载荷作用下车体和侧壁的横向以及垂向位移都有显著增加。周黎等[12]进一步对更高速度下复兴号动车组系统动力学进行了试验研究,结果表明高速列车明线会车气动压力波对车体的横向振动将产生影响。王亚朋等[13]研究了高速列车等速交会时对车-桥耦合系统的影响,结果发现列车交会风压对列车轮重减载率、车体竖向加速度及竖向Sperling影响较小,但对脱轨系数、轮轨横向力、车体横向加速度、横向Sperling及动态偏移影响较大。李红梅等[14]研究了高速列车在隧道内不同线间距等速交会时的气动力影响,并将结果应用于车辆动力学模型,发现交会对车辆安全性指标影响有限,但在交会瞬间可能引起车体横向振动。雷成等[15]通过实际线路试验和多体系统动力学仿真,对列车低频振动情况进行了深入研究,发现低频振动模态与车体固有横移模态之间容易发生耦合共振。目前同时考虑国内实测轨道不平顺与隧道会车气动载荷耦合激励,从气动载荷时域、频域角度分析其对车体振动特性影响,揭示气动载荷对隧道会车车体振动贡献度的研究较少。针对高速列车隧道会车工况,首先采用RANS数值模拟方法计算得到列车气动载荷和列车流场结构,分析列车气动载荷的时域频域特性,并通过分析列车交会时流场的时空演化规律,揭示气动载荷在会车后显著升高的原因;然后,建立列车系统动力学模型,分析整车振动模态特性和压力波频率特性之间的关系;最后,耦合轨道激励和气动激励,研究耦合激励对车体横向振动特性的影响,得到了气动载荷对车体横向振动的贡献度。
1 列车隧道交会气动载荷数值模拟
1.1 列车隧道会车CFD数值模型
隧道交会工况下高速列车的外部空气流动是三维的湍流运动。本文采用基于SST k-ω 的三维可压缩非定常雷诺时均法RANS对高速列车隧道交会的气动特性及外部流场进行数值模拟,该模型被广泛用于隧道气动效应的研究[16-18],足以验证其计算结果的可靠性。
SST k-ω的k方程为
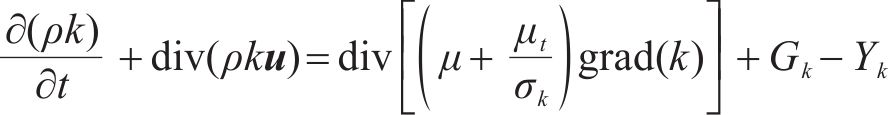
ω方程为
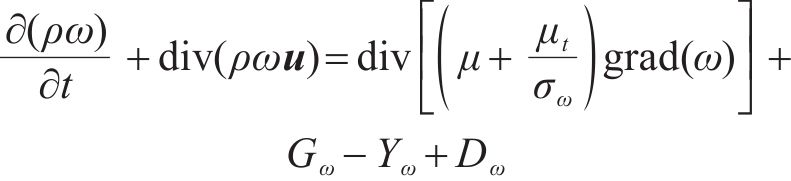
式中:
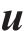
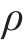
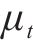
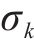
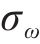
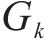
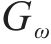
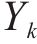
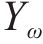
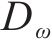
以某型高速列车为研究对象,建立其数值模型。本文假设列车表面光滑,忽略受电弓及悬挂设备等细节结构,考虑风挡及雨刮器区域,建立头-中-尾3节车编组模型,并根据实际尺寸建立转向架模型,采用3节车模型代替8节车模型是由于高速列车的中间各节车几何截面形状一致,中间各节车的气动载荷差距较小[19-21]。列车特征高度H=4.05 m,简化模型如图1所示,列车底部间隙0.2 m,头车26.85 m,中间车25 m。
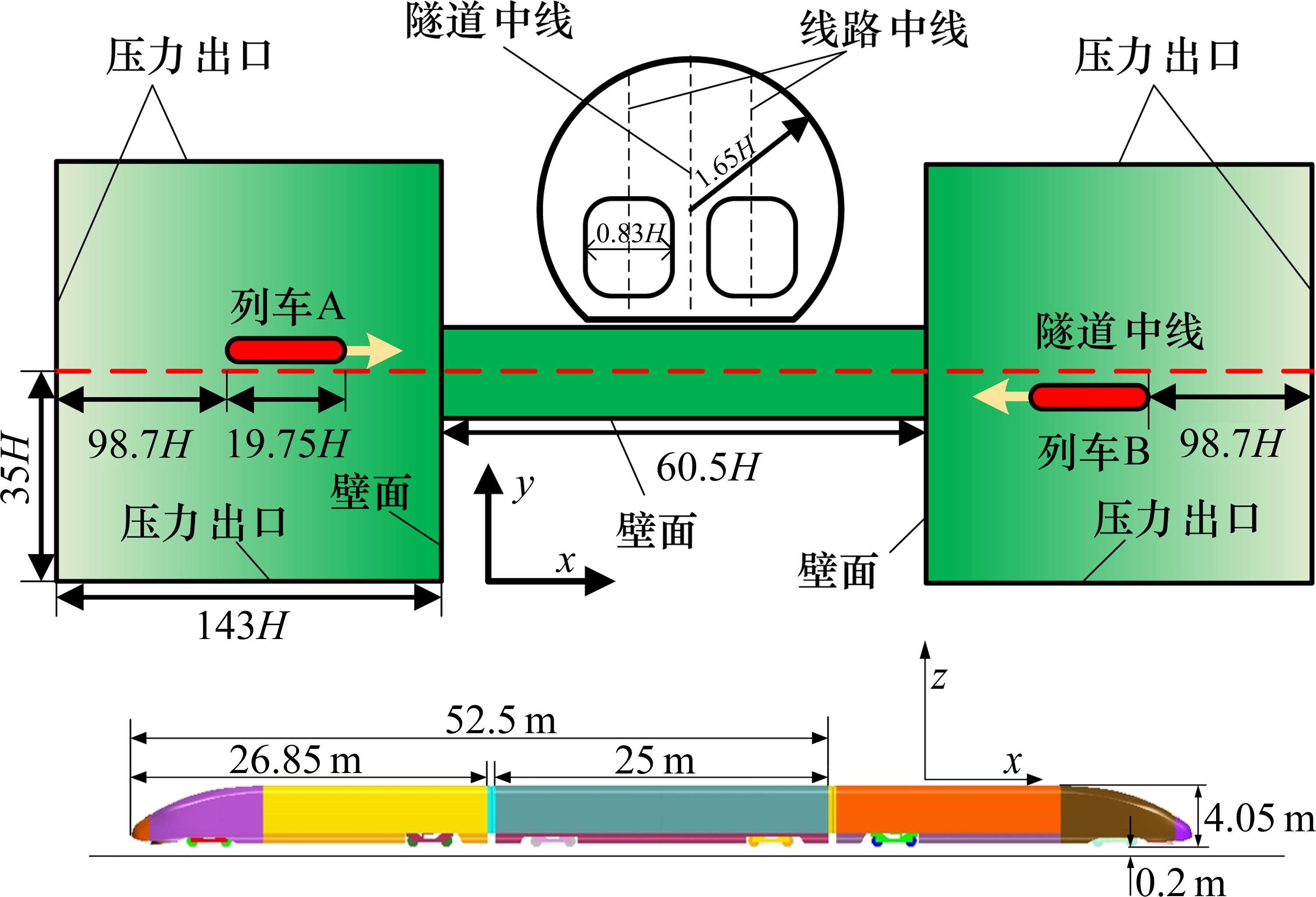
隧道采用《高速铁路设计规范》所规定的双线隧道,线间距5 m,隧道横截面积100 m2,阻塞比0.112,根据EN 14067-5标准提供的最不利隧道公式[22]计算得到隧道长度为60.5H,假设隧道内均为平直线路。计算域和边界条件如图1所示,初始时刻列车车头鼻尖距离隧道入口24.55H,隧道入口及隧道出口为明线区域,其计算域的尺寸均为143H×70H×35H。设置2列车的速度分别为x方向的111.1 m/s和-111.1 m/s。采用重叠网格方法来准确地模拟列车A与列车B、列车与隧道之间的相对运动。最不利隧道公式为
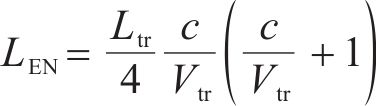
式中: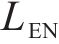
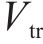
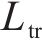
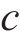
高速列车表面、隧道壁面、隧道入口和出口壁面、轨道以及地面均采用无滑移壁面边界,其余边界均为压力远场边界。
将计算域划分为背景区域和重叠区域2个部分,隧道及外部明线区域为背景区域,包含列车运动对象的为重叠区域,2个区域独立生成网格。采用Trimmer网格对2个区域进行离散,部分网格模型如图2所示。车身非流线型区域网格尺寸为0.22 m,并对转向架、车身流线型及风挡等区域进行局部加密,网格尺寸为0.025~0.05 m。y+值在30~50的范围内,重叠区域最外层网格尺寸为0.22 m。并设置3个加密区域B、C、D,加密区域的尺寸如图2所示,对应网格尺寸分别为0.22,0.44及0.88 m,最终整体计算模型离散后体网格总数约为1 524万。
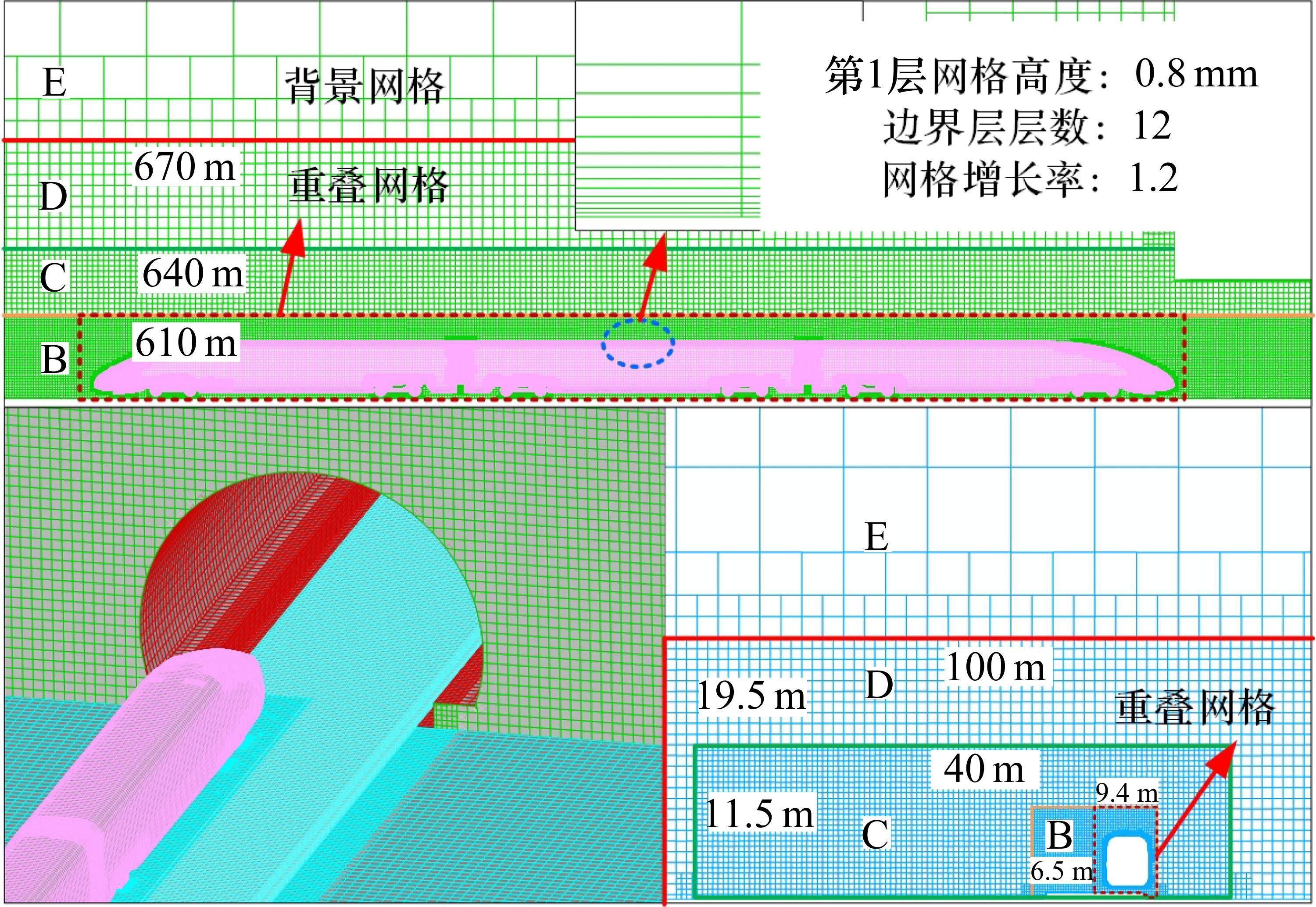
本文采用有限体积法将控制方程离散成代数方程,基于SIMPLE算法实现压力-速度耦合,对流项采用二阶迎风格式,扩散项采用中心差分格式,时间项采用二阶隐式格式。库朗数(Courant-Friedrichs-Lewy, CFL)根据反映的实际物理特性选择[22],本文为满足重叠网格的插值精度,使列车在每个时间步内移动的距离为一个网格长度,因此取CFL约为1,重叠网格与背景网格交界处网格尺寸为0.22 m,时间步长由式(4)计算得到为0.002 s,每个时间步迭代20次。

式中: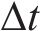
为验证网格无关性,划分了G-1、G-2、G-3这3套网格,如表1所示为列车进入隧道前明线行驶下的头车数值模拟结果,G-1的结果与其他结果有显著偏离。这是由于这组网格的分辨率较低,无法捕捉到细微的流动特征。另外2组网格结果非常接近,考虑到计算精度和计算资源,最终选择G-2来离散模型。将G-2的结果与其他研究人员的数据进行比较[24],结果误差在5%以内。
| Case | 网格总数/千万 | CD | CL |
|---|---|---|---|
| G-1 | 0.99 | 0.113 | -0.081 |
| G-2 | 1.52 | 0.118 | -0.074 |
| G-3 | 1.94 | 0.119 | -0.072 |
| 文献[24] | — | 0.124 | — |
为验证本文数值计算的准确性,将列车进入隧道前明线行驶下的数值模拟计算结果与风洞试验数据进行比较[25],仿真设置与风洞试验条件相同,计算模型仅在细节处存在细微不同,计算域按照标准[26]设置,使用上节网格参数进行网格划分。如图3所示为列车进入隧道前车身上表面中心线沿列车行驶方向表面压力分布,与风洞试验测试得到的数据基本一致,因模型细节有细微不同,压力幅值仅有很小的差异。
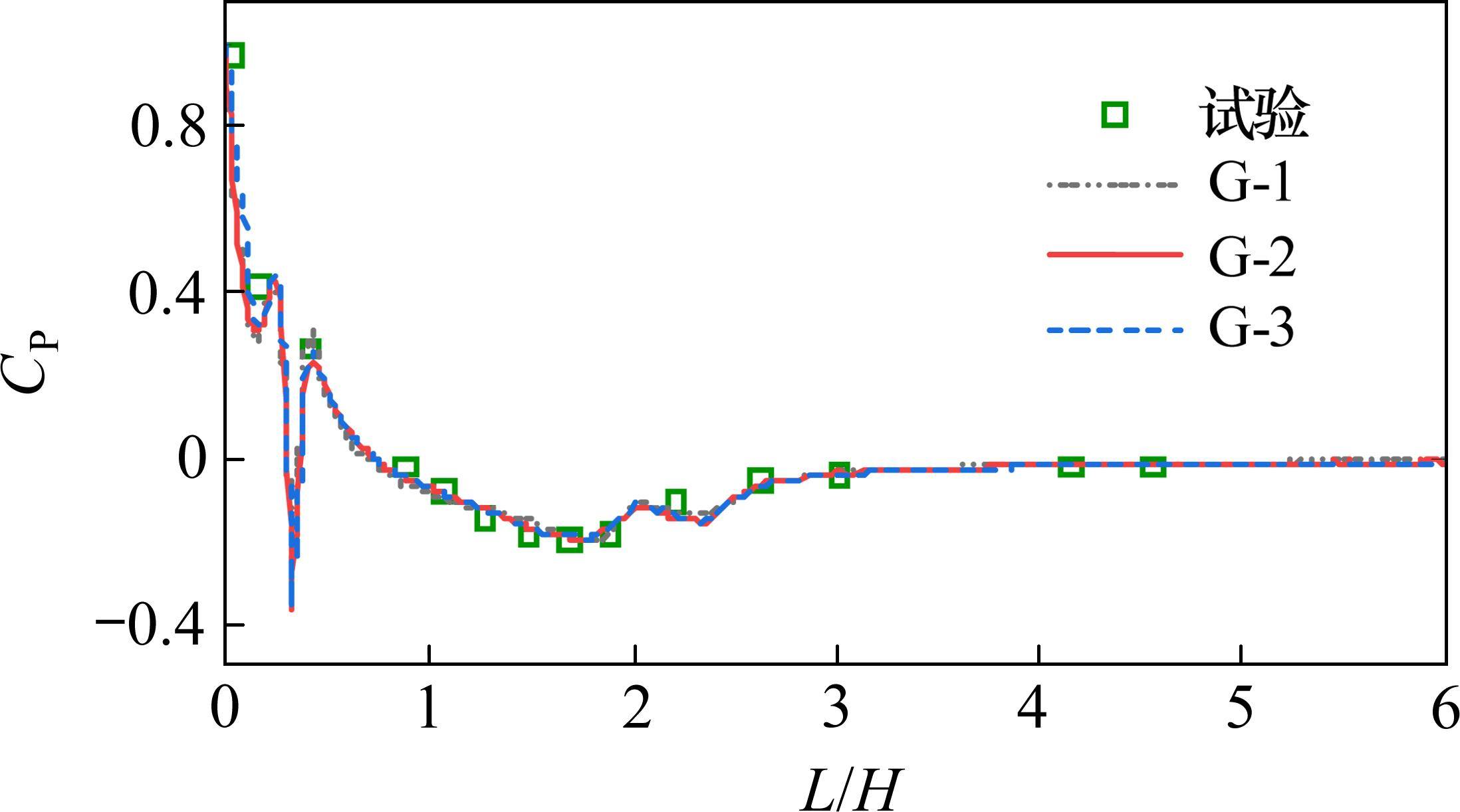
表2比较了数值模拟和风洞试验数据的阻力系数结果[25],结果表明,在不同的网格尺度下,CD偏差在0.8%到4.7%之间,可以认为本文的数值模拟结果是准确可靠的。
| G-1 | G-2 | G-3 | 试验[25] | |
|---|---|---|---|---|
| CD | 0.322 | 0.332 | 0.335 | 0.338 |
| 误差/% | 4.7 | 1.7 | 0.8 | — |
为进一步验证本研究所使用的算法和设置,采用Miyachi的动模型试验数据进行对比[27]。试验装置[28]如图5(a)所示,动模型试验基于2个压力传感器(P2和P3)得到了压力-时间历程曲线,测点1位置与试验中P2位置相同,测点2位置与试验中P3位置相同。根据文献中模型参数建立模型,网格划分策略和计算参数设置与上文相同。数值计算结果与试验数据对比如图5(b)、图5(c)所示,数值计算结果与实测数据波形基本一致,幅值接近,可以认为本文的数值计算方法具有准确性和可靠性。
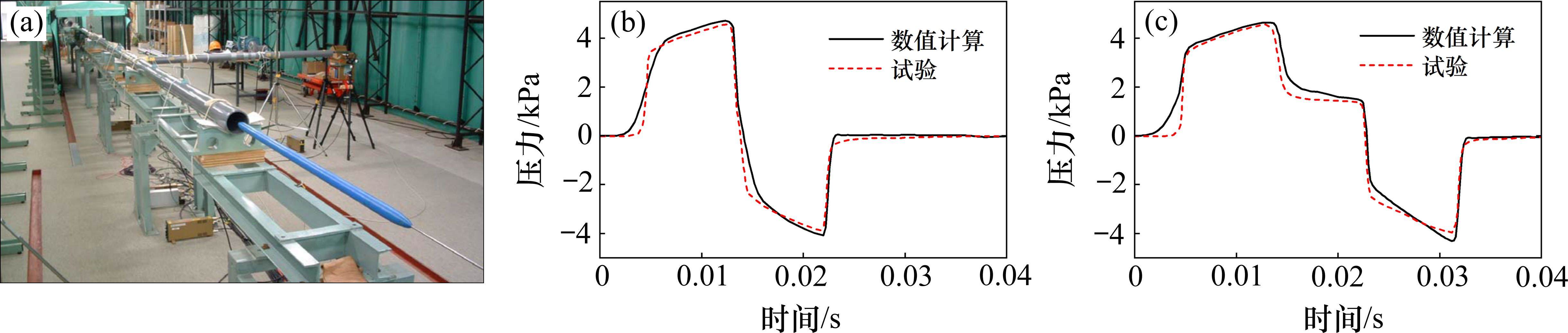
1.2 隧道会车气动载荷时域特性分析
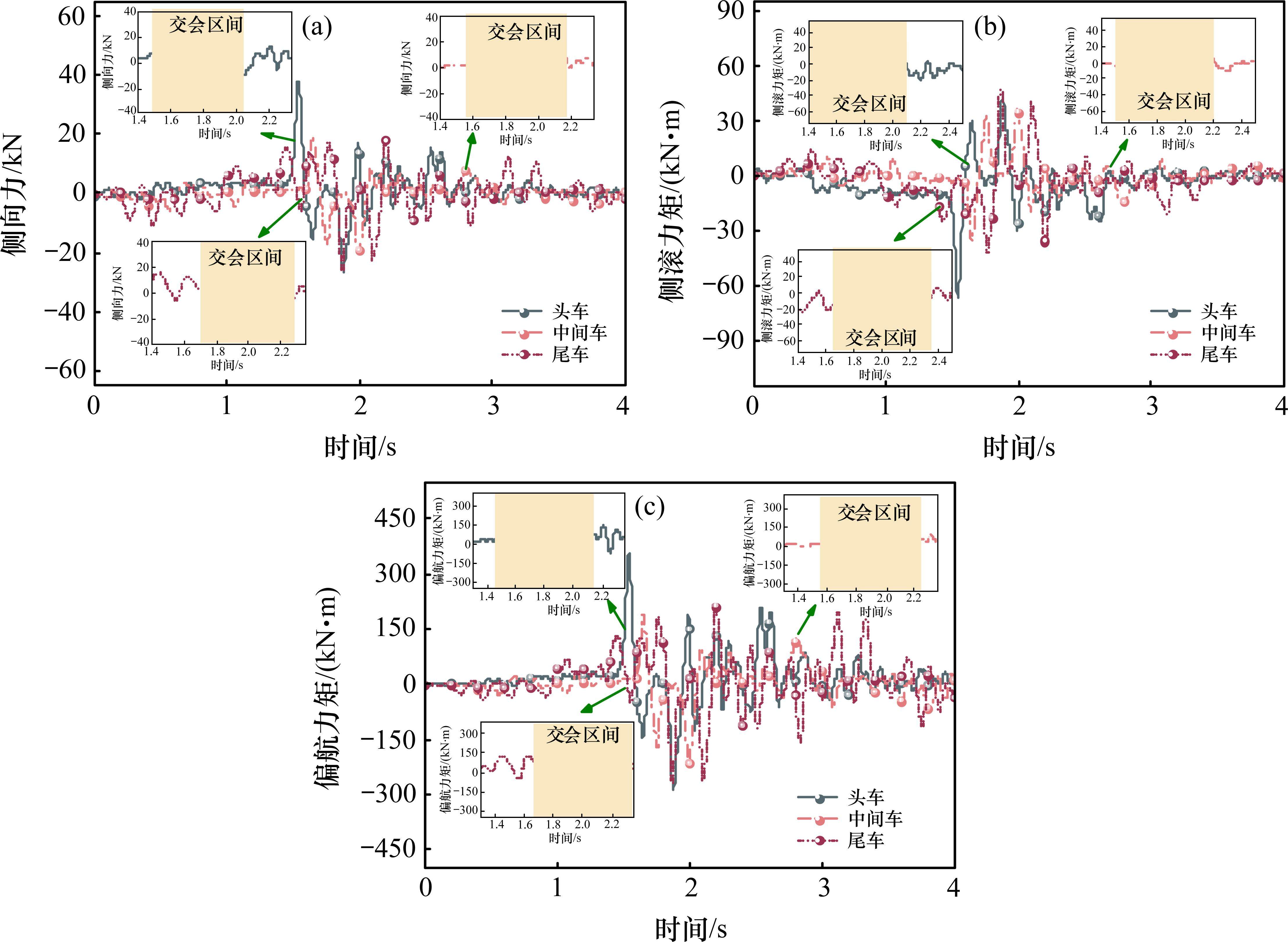
高速列车交会时气动载荷显著变化,尤其是当列车在最不利隧道内交会时,列车的“晃车”问题更加突出。气动载荷是导致列车会车时车体横向振动的主要原因,图5给出了头车、中间车和尾车的气动载荷时程曲线。在非会车时刻,尾车气动载荷波动的频率和幅值最大,头车最小,这主要在于列车尾部存在明显涡脱落现象,涡的周期性生成和脱落导致了越靠近车尾的车身压力波动越剧烈,进而导致气动载荷的波动。在隧道会车时刻,车体表面的气动载荷变化剧烈,头车、中间车、尾车的气动载荷均出现2个极大值和2个极小值,头车、中间车和尾车的气动载荷在时间尺度上存在明显的滞后性,且各节车的气动载荷的变化规律基本一致,列车会车后的气动载荷幅值及波动情况显著高于会车前。
为揭示隧道会车时气动载荷突变和会车后气动载荷同样显著波动的原因,图6给出了部分会车时刻下列车表面及周围流场结构。Q准则可用来确定涡旋的位置和强度,定义如下:

式中:Ω是涡度张量;S是应变率张量。

可以看出,由于列车并不位于隧道中心,尾涡并不对称,靠近隧道中心的涡旋会逐渐向隧道另一侧移动,涡旋逐渐增大,但强度衰减,最终消散。由t=2.1 s和t=2.3 s可知,列车会车部位呈现较大负压,且2列车尾部涡脱落互不干涉,列车的涡结构只受到隧道壁面的阻碍作用。由t=2.5 s和t=2.7 s可知,当列车A的车头与列车B的车尾相遇以后,列车B的尾部涡脱落受到列车A的阻碍作用,列车A的纵向涡脱落与列车B的纵向涡脱落产生严重的干涉现象,这种现象将持续一段时间直到2列车的涡全部脱落。因此,会车后,涡与涡之间、涡与地面之间、涡与隧道壁面之间的干涉现象是导致列车气动载荷幅值和波动情况高于会车前的主要原因。
列车交会时车体的气动载荷峰值如表3所示,在列车交会过程中,气动载荷的正负峰值显著增加,头车的峰值差异最大,尾车次之,中间车最小,正负峰值差异使得短时间内车体承受交变气动载荷而导致其出现明显的横向振动。尾车周围复杂的流场结构和涡不断地生成和脱落使得尾车气动载荷比中间车更大。
| 侧向力/kN | 侧滚力矩/(kN·m) | 偏航力矩/(kN∙m) | ||||
|---|---|---|---|---|---|---|
| 正峰值 | 负峰值 | 正峰值 | 负峰值 | 正峰值 | 负峰值 | |
| 头 车 | 38.23 | 26.47 | 44.55 | 66.35 | 351.12 | 284.32 |
| 中间车 | 19.34 | 19.81 | 36.01 | 36.24 | 188.87 | 221.33 |
| 尾 车 | 17.97 | 26.33 | 48.29 | 42.17 | 212.51 | 269.37 |
1.3 隧道会车气动载荷频域特性分析
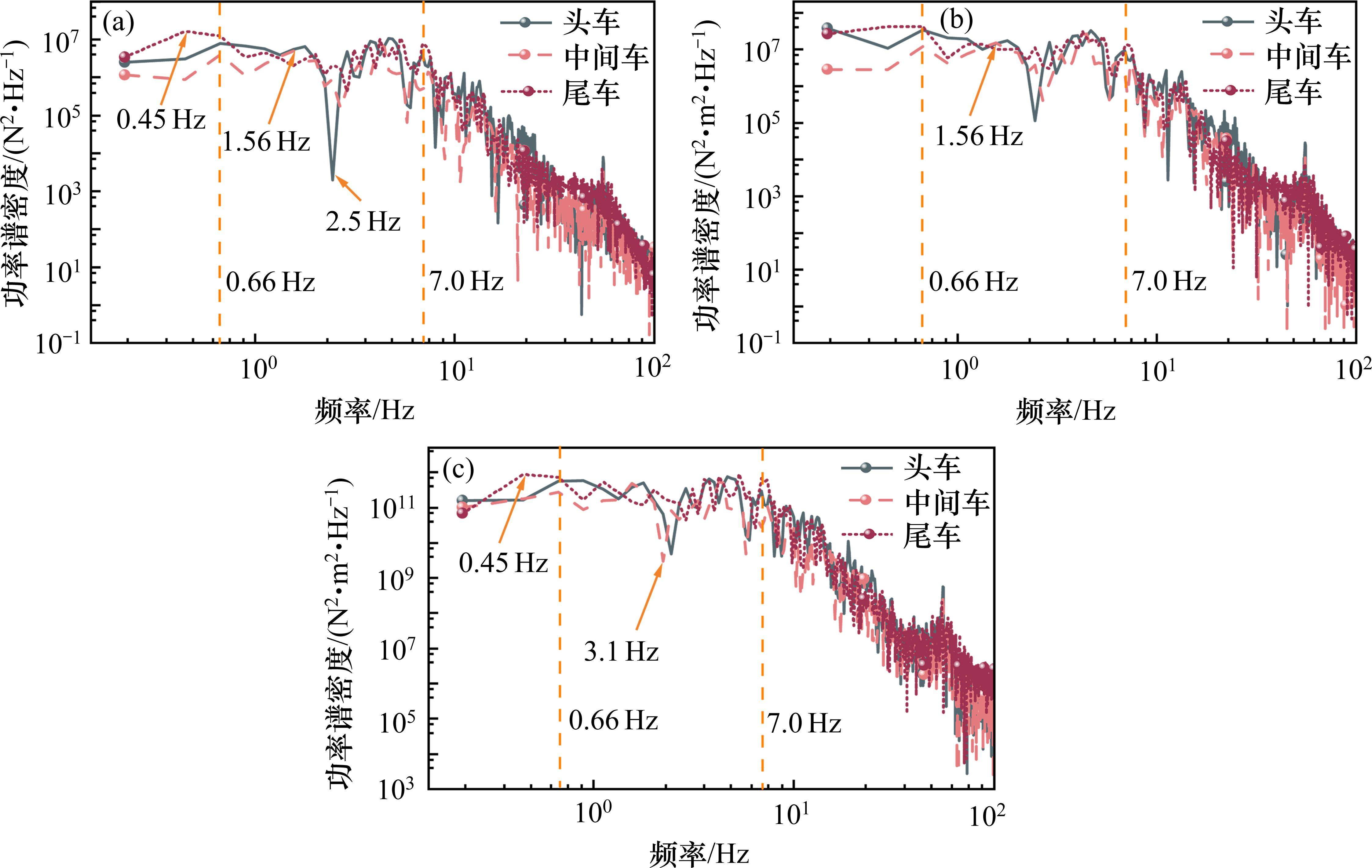
为探究高速列车隧道交会时车体受到的非定常气动载荷的频域特性,将车体的气动载荷数据进行频谱分析,采样样本数为2 000,采样频率为500 Hz,窗口函数使用汉宁窗口(Hanning Window)。不同车体的气动载荷功率谱密度如图7所示。车体气动载荷的频域特性总体上呈现为次声波特性,主要能量分布在低频区域,主要峰值频率出现在0~7.0 Hz范围内。头车气动载荷的第1主频均为0.66 Hz,中间车气动载荷的第1主频为1.56 Hz,尾车侧向力、侧滚力矩和偏航力矩的第1主频分别为0.45、0.66和0.45 Hz,从低频区域的能量分布来看,尾车的能量总体上高于中间车。列车气动载荷在0~7.0 Hz范围内能量基本下降缓慢,而当频率高于7.0 Hz后气动载荷的能量快速下降,低频高能量的频率易与车体悬挂模态频率接近或重叠。
2 气动载荷对车体振动的影响分析
2.1 车辆多刚体振动模态分析
车辆系统主要由车轮、构架、横梁、车体、主悬架和副悬架、减震器等组成,是一个多自由度非线性的振动系统。本文采用SIMPACK软件建立的高速列车系统动力学模型,将车体、轮对、构架、枕梁等假设为刚体,有6个自由度,转臂为单自由度。将横向/纵向减振器、空气弹簧、抗蛇形减振器、轴箱弹簧等处理为力元,并考虑垂向和横向运动的弱耦合,不同列车之间通过车间缓冲装置进行连接,高速列车系统动力学模型如图8所示。

自振频率是铁路车辆系统动态特性的重要参数,是系统的固有特性,由于轮轨关系的特殊性,有些模态参数与运行速度有较大关系。基于运行工况下的车辆系统动力学状态方程描述为
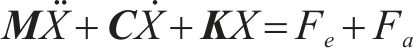
式中:X为动力学状态方程的状态变量;M、C和K分别为系统的惯量、阻尼和刚度矩阵;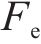
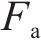
改写为状态方程的形式并令:
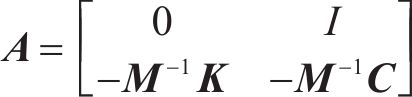
车辆系统的特征值和特征向量由式(8)求得:
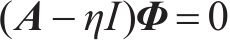
式中: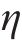

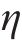
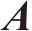
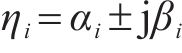
式中: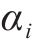
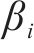
每对特征根(振动模态)对应的振动频率为:
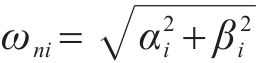
在高速列车垂向动力学模型中,车体固有的悬挂振动模态包括车体浮沉、点头;在横向动力学模型中,车体的侧滚和横移运动始终耦合在一起[29],表4为车体悬挂振动模态的5种固有振动的自振频率。
| 下心滚摆 | 摇头振动 | 上心滚摆 | 浮沉振动 | 点头振动 |
|---|---|---|---|---|
| 0.53 | 1.06 | 1.67 | 0.77 | 1.04 |
2.2 气动载荷频率与车体振动特性的关系分析
通过对高速列车气动载荷进行频域分析,发现气动载荷的频域较低,主要频段分布在低频区域。通过多体动力学计算得到列车车体5种振动频率分别为:下心滚摆0.53 Hz、上心滚摆1.67 Hz、摇头振动1.06 Hz、点头振动1.04 Hz、浮沉振动0.77 Hz。头车气动载荷主频0.66 Hz,尾车气动载荷主频0.45、0.66和0.45 Hz均与车体下心滚摆频率十分接近,而中间车气动载荷主频1.56 Hz与车体上心滚摆频率1.67 Hz十分接近。可见,车体气动载荷主频与车体固有频率十分接近,容易与车体共振而导致车体横向振动剧烈,会很大程度降低列车的横向平稳性和舒适性。
2.3 耦合载荷激励下车体的横向振动响应
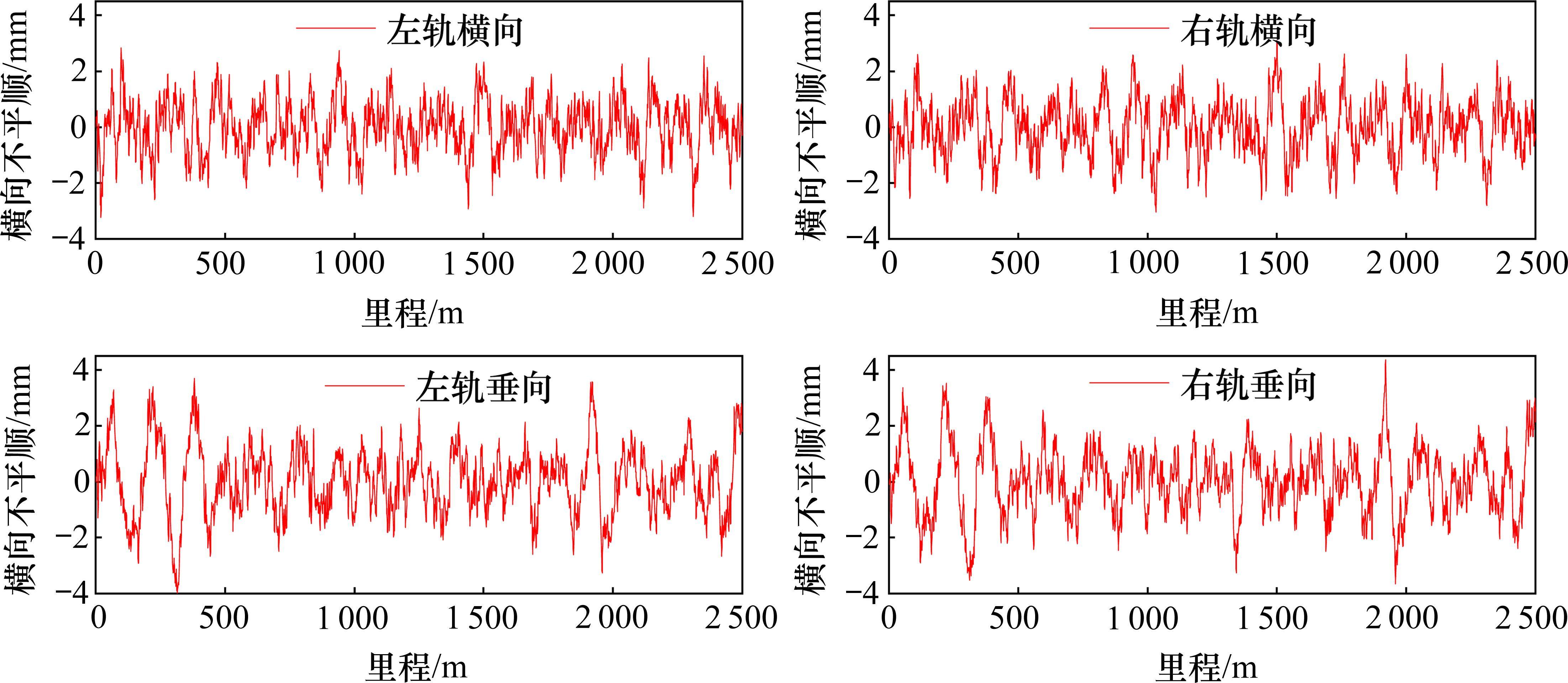
在前述建立的车辆系统动力学模型的基础上,考虑气动激励和轨道不平顺的耦合影响,分析车体的振动响应。采用中国实测的武广高速无砟轨道谱作为轨道不平顺激励[30],如图9所示。通过编写输入函数将CFD数值计算得到气动载荷导入到时间激励中,最后通过93号力元,将气动载荷加载到动力学模型中。
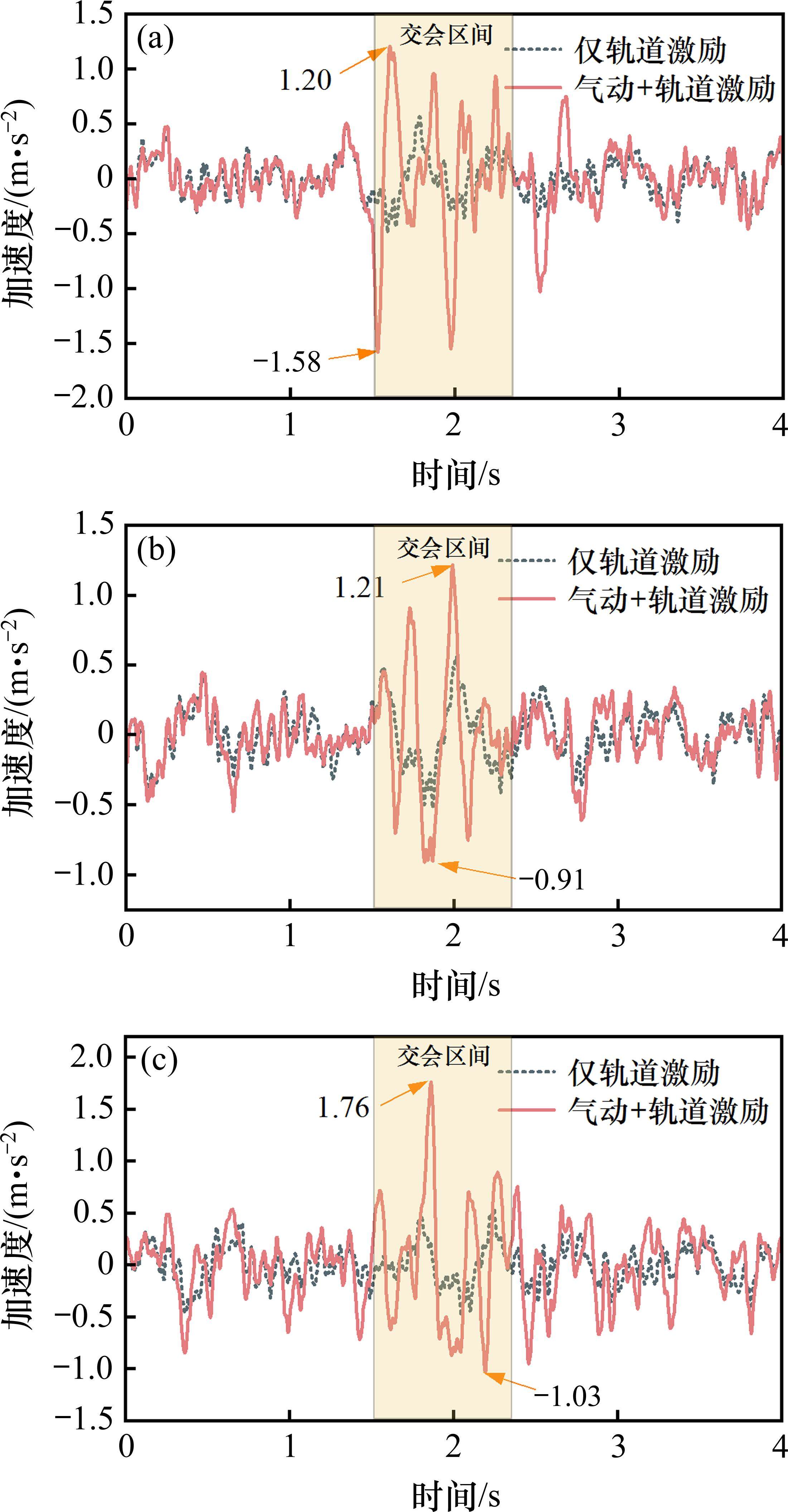
车体横向加速度响应如图10所示,在考虑耦合气动和轨道激励载荷作用下,在隧道会车瞬间车体的横向振动加速度显著增大。仅考虑轨道激励下车体横向加速度最大值为0.49 m/s2,头车在耦合载荷作用下车体最大横向加速度为1.58 m/s2,约为仅考虑轨道激励的3.22倍;中间车的最大横向加速度为1.21 m/s2,约为仅考虑轨道激励的2.47倍;尾车的最大加速度为1.76 m/s2,约为仅考虑轨道激励的3.59倍。在非会车时刻,头车和中间车的气动载荷对车体振动影响较小,而尾车在非会车时刻对车体的影响较大,主要原因在于,非会车时刻下尾车同样承受着较大的气动载荷。
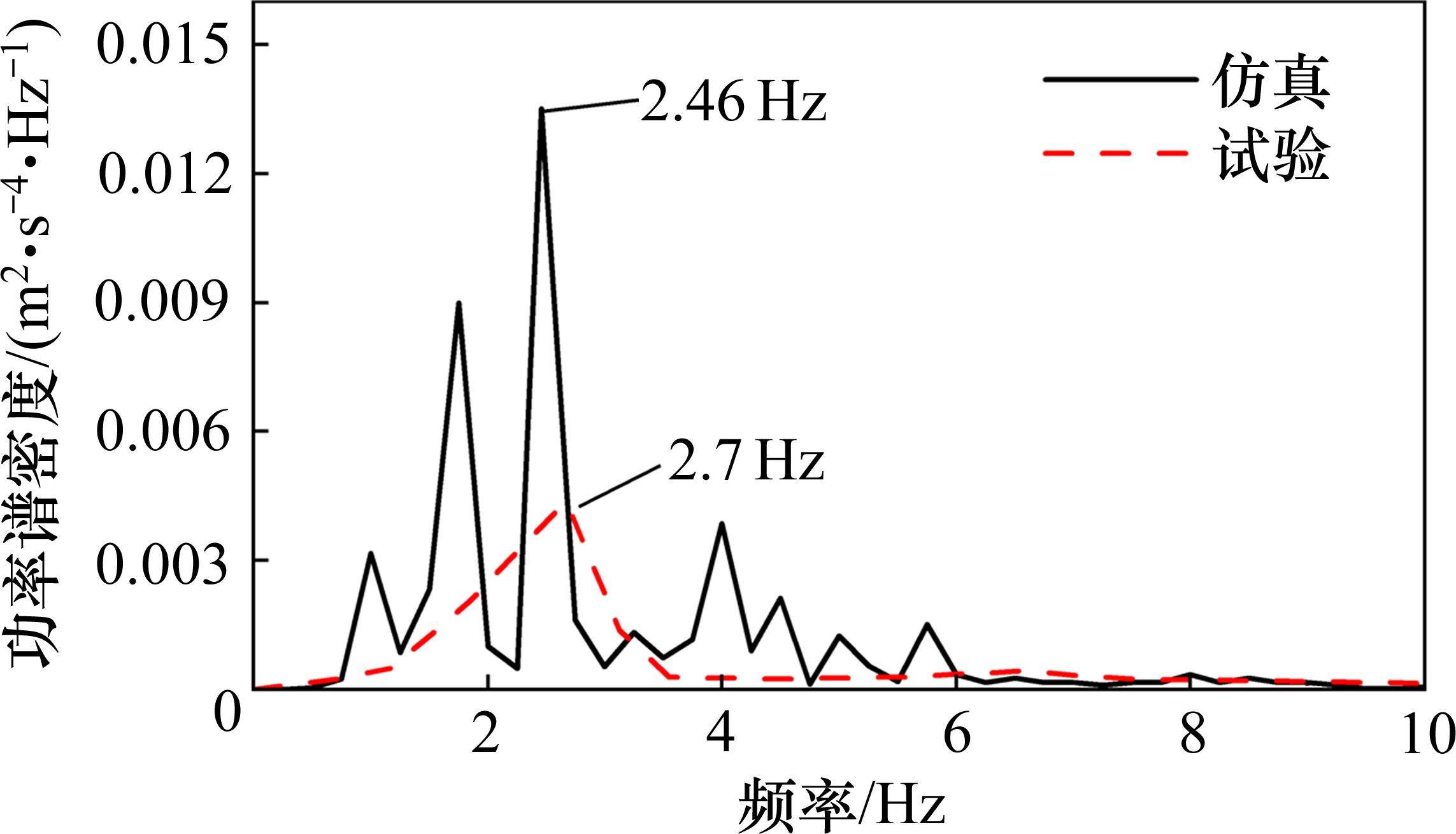
车辆系统动力学模型的准确性直接影响仿真结果的精度。在设计车体时,考虑到整车1阶弯曲模态的振动频率超过10 Hz,10 Hz以上包含车体的弹性振动,因此对图10所示的中间车的车体横向振动加速度数据进行10 Hz的低通滤波处理。如图11所示,对比滤波后的仿真和文献中[31]武广线的综合试验数据,发现车体横向加速度功率谱密度的幅值存在差异,这主要归因于车辆运行速度、轨道不平顺幅值以及车辆结构简化方式的不同。车体横向振动的主频率误差为8.8%,表明仿真模型较为准确。
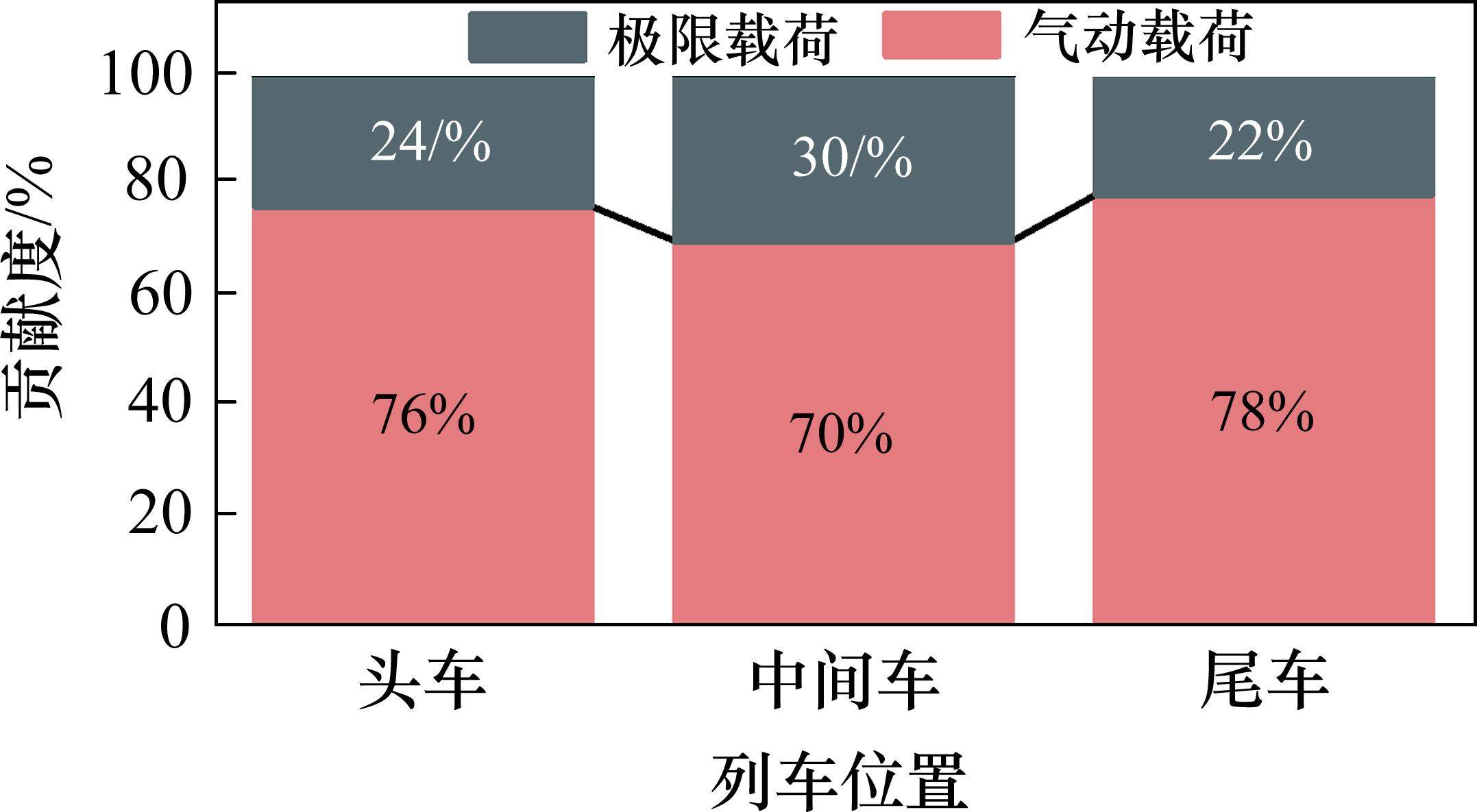
对列车隧道交会时车体横向加速度最大峰值进行分析,得到不同载荷对车体振动影响的贡献度,如图12所示。可以发现,气动载荷对车体振动影响的贡献度均超过70%,且尾车气动载荷对车体振动影响的贡献度最大,达到了78%。头车次之,中间车最小。可见,高速列车隧道交会时气动载荷是引起车体横向振动的最主要因素。
采用Sperling指标对车体的平稳性进行评价。
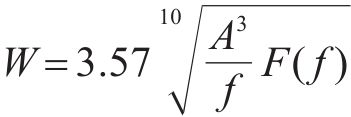
式中: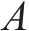
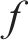
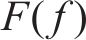
根据EN12999[32]标准,规定Sperling垂向平均平稳性指标低于2.5为乘坐舒适。分析显示,在单一轨道激励下,高速列车的垂向平稳性指标保持在2.01。然而,当考虑耦合轨道激励与气动载荷的联合作用时,车体的垂向平稳性出现不同程度的变化:头车指标上升至2.25,增幅达11.9%;中间车指标增至2.14,上升了6.4%;尾车则更为明显,达到2.27,增长了12.9%。尽管所有车体的平稳性指标均未超出舒适界限,但气动载荷的介入显著削弱了列车的垂向稳定性。结合图10所展示的列车横向加速度变化,可以明确看出,在隧道交会过程中,高速列车的整体晃动现象明显加剧。
3 结论
1) 隧道会车时列车气动载荷显著变化,头车气动载荷幅值最大,尾车次之,中间车最小。涡与涡之间、涡与地面之间、涡与隧道壁面之间的干涉现象是导致会车后列车气动载荷幅值和波动情况高于会车前的主要原因。
2) 隧道会车列车气动载荷主频位于低频段,头车气动载荷主频0.66 Hz,尾车气动载荷主频0.45、0.66和0.45 Hz均与车体下心滚摆频率0.53 Hz十分接近,而中间车气动载荷主频1.56 Hz与车体上心滚摆频率1.67 Hz十分接近,容易与车体共振而导致车体横向振动剧烈,会很大程度降低列车的横向平稳性和舒适性。
3) 隧道会车气动载荷对车体横向振动影响显著,头车、中间车和尾车的横向振动加速度峰值分别为仅考虑轨道激励的3.22倍、2.47倍和3.59倍。平稳性指标相对于单一轨道激励下,分别增加11.9%、6.4%和12.9%,气动载荷对车体横向振动的贡献度分别达到76%、70%和78%,气动载荷是导致会车时车体横向振动的主要原因。
Analysis of the aerodynamic pressure effect on the fatigue strength of the carbody of high-speed trains passing by each other in a tunnel
[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2019, 233(8): 783-801.时速400 km动车组最不利隧道交会气动效应分析
[J/OL]. 机械科学与技术, 1-11[王北昆,冯达,卢耀辉等.高速列车隧道交会对其振动特性的影响分析[J].铁道科学与工程学报,2025,22(03):930-941.
WANG Beikun,FENG Da,LU Yaohui,et al.Effect analysis of high-speed trains passing by each other in tunnel on its vibration characteristics[J].Journal of Railway Science and Engineering,2025,22(03):930-941.

