高速列车转向架作为列车重要的组成结构,其机械性能好坏直接影响列车运行的稳定性以及安全性,因此,高速列车转向架关键部件的故障诊断方法在实际应用中存在着重要意义[1]。目前,高速列车通过安装在各个位置的不同传感器来采集列车在运行过程中的振动信号,通过提取振动信号的数据特征,实现对高速列车的故障诊断。然而,由于高速列车在运行过程中产生的振动信号是典型的非线性以及非平稳性的信号,传统的信号分析方法往往难以有效提取出故障特征[2]。针对此问题,很多学者进行了研究。目前,常用信号处理的办法有谱峭度、时间序列分析、稀疏表示、包络调制、自适应信号分解(adaptive mode decomposition, AMD)等[3]被用来提取信号的故障特征。李亚兰等[4]提出了噪声辅助多元经验模态分解(noise assisted multivariate empirical mode decomposition, NAMEMD)的方法将振动信号分解成一系列固有模态函数,再选取与原始信号相关性较大的IMFs,并提取全矢样本熵作为故障特征,该方法很大程度上缓解了模态混叠问题。王清波等[5]提出一种基于IMF重构-SLLE的新的故障特征提取方法,该方法利用平均经验模态分解(ensemble empirical mode decomposition, EEMD)将振动信号分解得到的IMFs通过有监督局部线性嵌入算法(SLLE)进行降维重构,使其EEMD的自适应性有效抑制了模态混叠的问题。相较于以上几种特征提取的方法,变分模态分解(variational modal decomposition, VMD)可以将振动信号分解成一系列有限带宽的固有模态函数,并且自适应地将信号不同频率有效分离,克服了EMD分解时存在的模态混叠问题,适用于非线性非平稳性信号,并且效率高,在很多领域得到广泛应用。苟先太等[6]针对高速列车横向减振器故障特征提取相对困难的问题,提出了VMD和多尺度熵结合的特征提取方法,将原始振动信号通过VMD分解后得到的若干IMFs利用互信指标选取有效IMFs,求多尺度熵作为故障特征,实现了横向减振器故障的有效判别。LIU等[7]为实时监测不同磨削过程中颤振的检测问题,提出了基于VMD参数优化的新型监测方法,该方法利用局部均值经验模态分解(FLMEMD)对记录的颤振信号进行预处理,然后根据相似性系数准则估计模态数量,并通过综合评估因子的方法优化二次惩罚项,实验结果表明所提出的基于VMD参数优化和能量熵的颤振检测方法能够有效地检测凸轮轴高速磨削中的颤振特征,并且能够准确识别不同轮廓段的颤振状态。董俭雄等[8]利用麻雀搜索算法解决了VMD根据经验人为设置参数的问题。虽然,变分模态分解(variational modal decomposition, VMD)在处理非平稳、非线性信号方面有良好的表现,但是,VMD需要通过经验,人为观察中心频率对多个参数(分解层数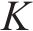
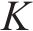
1 基本理论
1.1 变分模态分解
变分模态分解的基本思想是通过迭代优化的过程,将原始信号分解为多个模态。每个模态具有不同的频率和幅度特征,而且它们在频域上相互正交。VMD通过最小化信号与一组基函数之间的距离来实现,同时通过引入约束条件来确保分解结果的稳定性和物理可解性[14]。约束变分问题表达式如下:
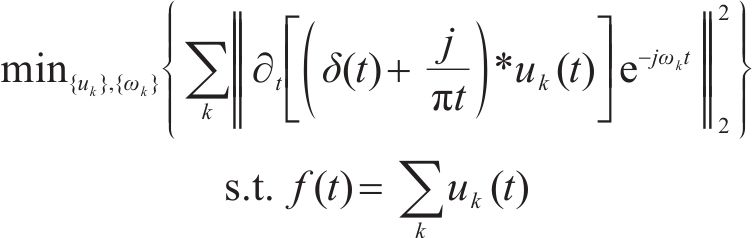
式中:原始信号
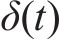
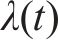
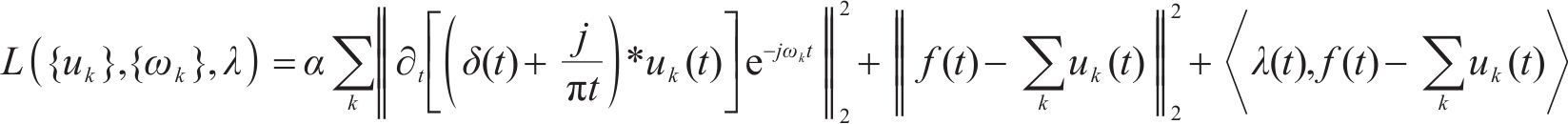
式中: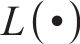
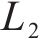
为了搜寻式(2)的最优解,需通过模式分量和中心频率依据交替方向乘子法不断地迭代更新,达到条件之后终止迭代,得到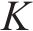
VMD在分解的过程中,分解模态数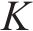
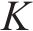
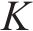
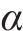
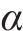
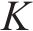
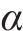
1.2 霜冰优化算法
RIME算法基于物理的优化器,利用模拟霜冰中软冰针和硬冰针生长过程,来实现优化方法的探索和开发行为,并通过改进的正向贪婪选择机制进行全局寻优。SU等[17]将该算法划分为初始化霜冰结晶点、引入软霜冰搜索策略和硬霜冰穿刺机制,并改进贪婪选择策略来建立数学模型。
RIME霜冰粒子种群
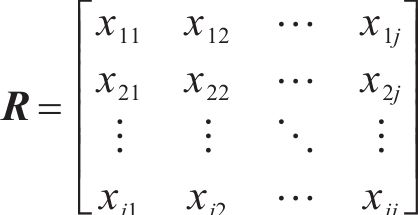
式中:霜冰粒子种群可通过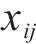
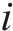
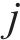
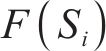
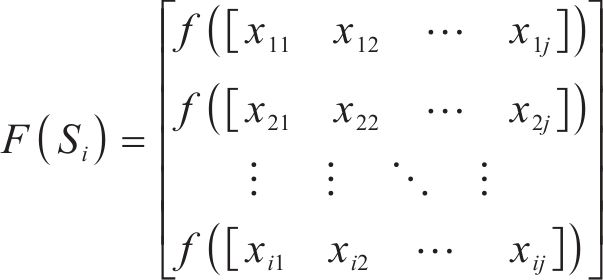
式中: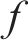
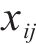
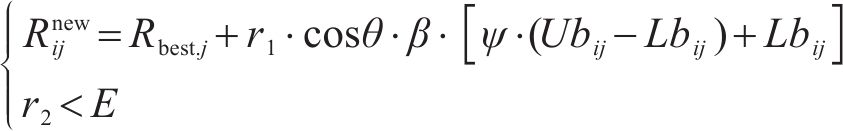
式中: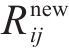


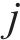
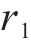
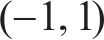
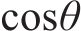

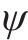
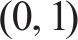
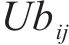
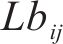
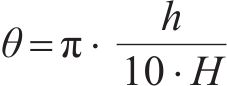
式中: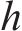

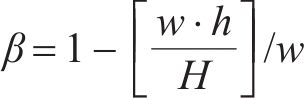
式中:
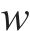
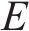
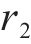
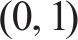
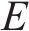
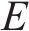
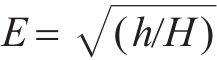
随软冰凝结面积增大,产生强随机性和覆盖范围广的特点,让算法能够快速覆盖全空间的搜索,从而在优化过程中兼顾了全局性和局部性。硬冰受外界因素影响会向着同一方向凝结,由于硬冰的增长方向一致,导致硬冰之间很容易交叉,实现普通粒子和最优粒子的维度交换,有利于提高解的精度。由于在迭代的过程中,粒子之间的交叉互换,避免了局部最优,提高了收敛性。随着硬冰的生长穿刺,粒子之间的交叉替换如下式所示:
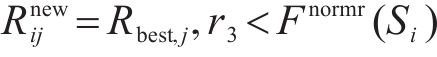
式中: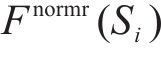
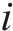
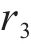
1.3 RIME-VMD
RIME-VMD利用RIME算法较强的全局搜索能力以及高效的参数更新机制搜寻出VMD分解层数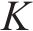
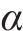
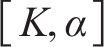
RIME-VMD算法其核心是通过最小包络熵作为优化算法的适应度函数,得出最优参数组合。RIME-VMD流程如图1所示,算法详细步骤如下。
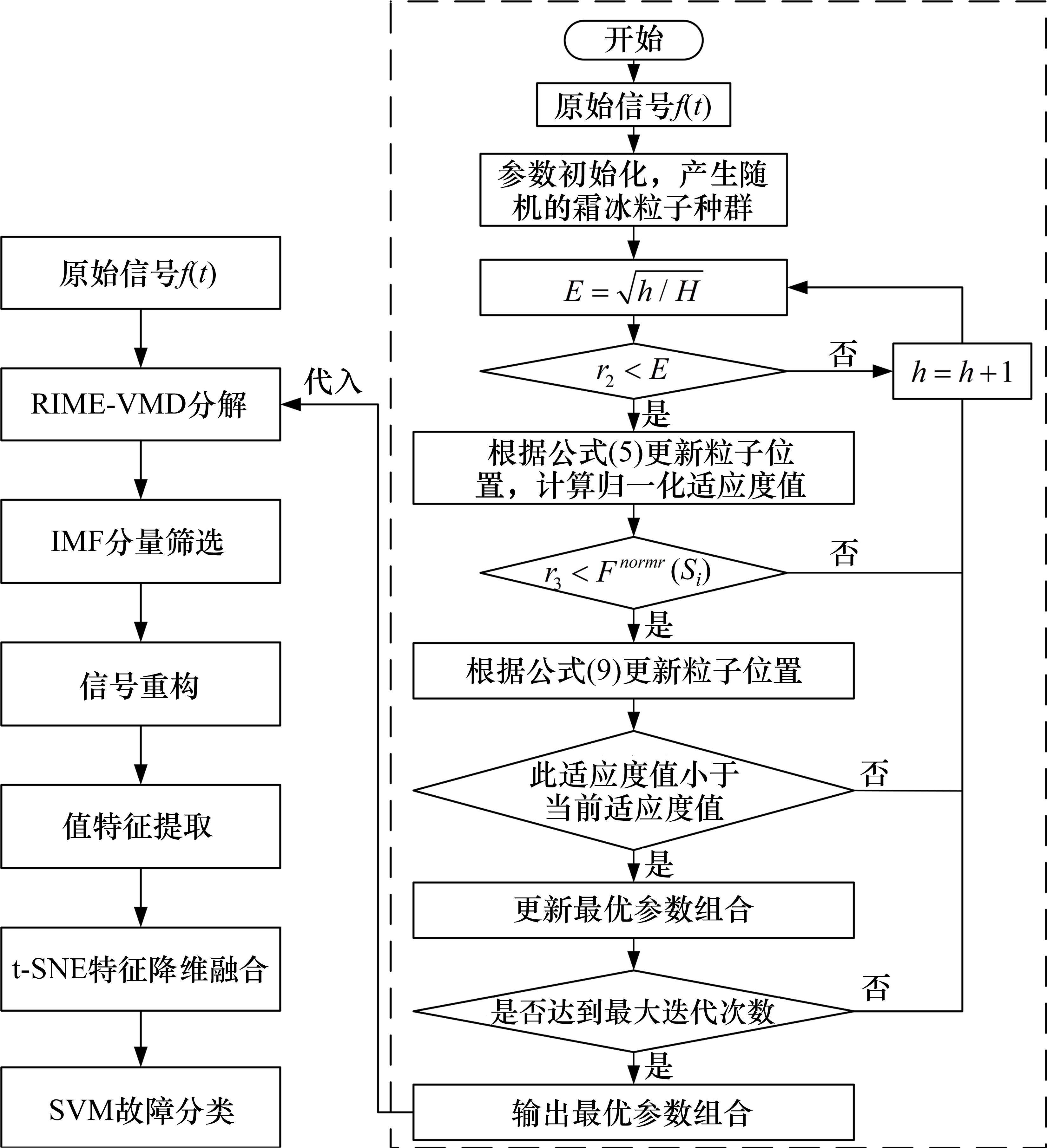
1) 对RIME及VMD各项参数初始化,设定RIME霜冰种群以及迭代次数
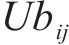
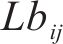
2) 输入原始信号;
3) 根据当前迭代次数

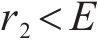
4) 根据归一化的适应度值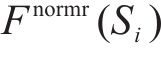
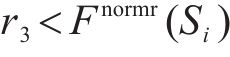
5) 通过比较每个新位置的适应度值与当前位置的适应度值来更新最优粒子位置和最优适应度值;
6) 若满足循环条件,且当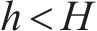
2 故障诊断流程
高速列车横向减振器振动信号具有非线性以及非平稳的特性,故障特征主要包含在低频部分[18]。首先通过RIME-VMD进行分解得到若干IMFs,并选取峭度值较大、相关系数较高的IMFs进行信号重构降噪;其次对重构后的信号提取多尺度奇异熵、多尺度样本熵和多尺度排列熵分别作为故障特征值;最后将求得的故障特征分别通过t-SNE降维融合,去除冗余特征[19-20],将降维后的特征矩阵逐一输入到SVM中,对高速列车横向减振器实现故障分类。具体实现步骤如图1所示。
3 仿真分析
3.1 仿真数据
实验数据通过基于多体动力学软件Simpack构建的某动车组车辆系统非线性动力学模型进行仿真获得。仿真模型如图2所示。该模型由1个车体、前后2个转向架、前后各2个横向减振器、前后各4个抗蛇形减振器以及前后各2个空气弹簧等组成。为模拟真实路况,仿真实验所加轨道激扰为武广线轨道谱,并分别在220、280和320 km/h的速度下运行3 min,故障信号通过分布在车体、构架和轴箱各个位置的传感器采集得到,采样频率为243 Hz,包括横向、纵向和垂向的振动加速度数据,共27个通道数据,每个故障选取样本共7 290个数据点,时间长度为30 s。横向减振器的6种故障类型如表1所示。
| 编号 | 故障类型 |
|---|---|
| 故障1 | 前转向架左侧横向减振器失效 |
| 故障2 | 前转向架右侧横向减振器失效 |
| 故障3 | 后转向架左侧横向减振器失效 |
| 故障4 | 后转向架右侧横向减振器失效 |
| 故障5 | 前、后转向架右侧横向减振器同时失效 |
| 故障6 | 后转向架左、右侧横向减振器同时失效 |
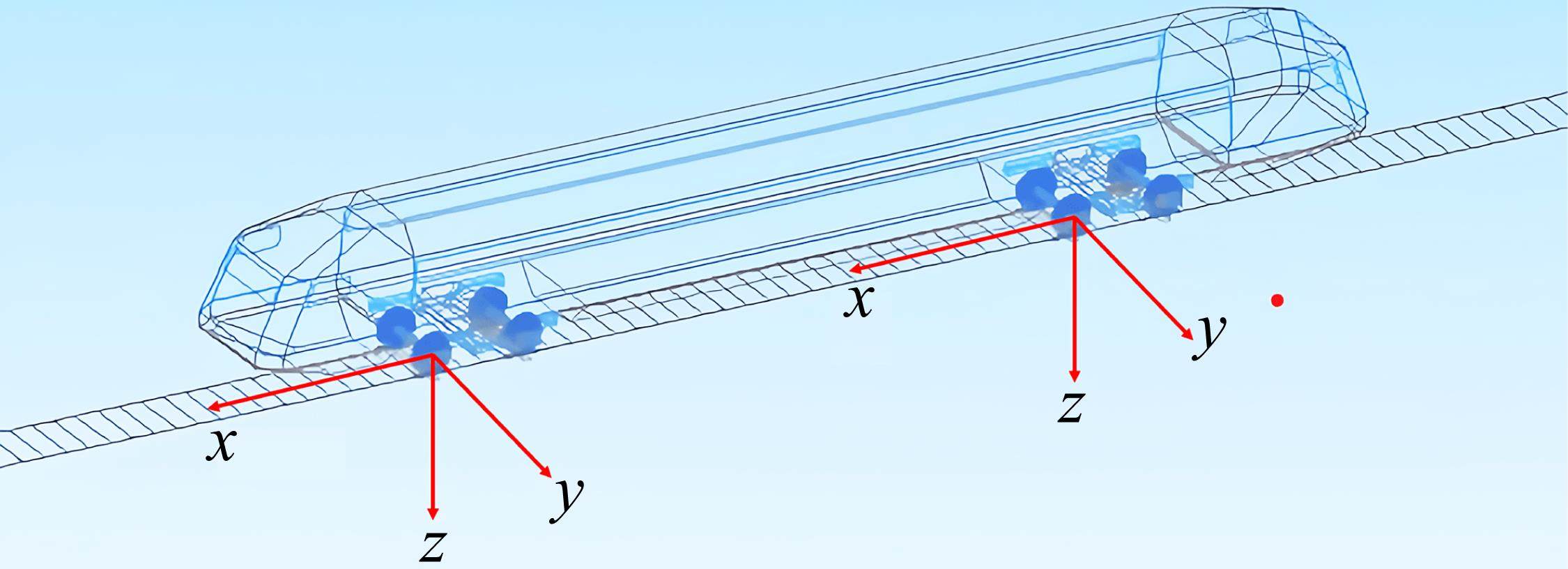
为使仿真数据真实有效,模型在280 km/h的速度下,通过脱轨系数以及轮重减载率分析了模型的有效性,模型验证如图3所示。根据我国《高速动车组整车试验规范》[21]规定,当速度大于200 km/h时,脱轨系数以及轮重减载率应小于等于0.8。由图中可以看出,车辆通过曲线线路的最大脱轨系数为0.167,最大轮重减载率为0.37,远小于所规定的数量限制,由此可得该模型符合高速列车动力学要求。
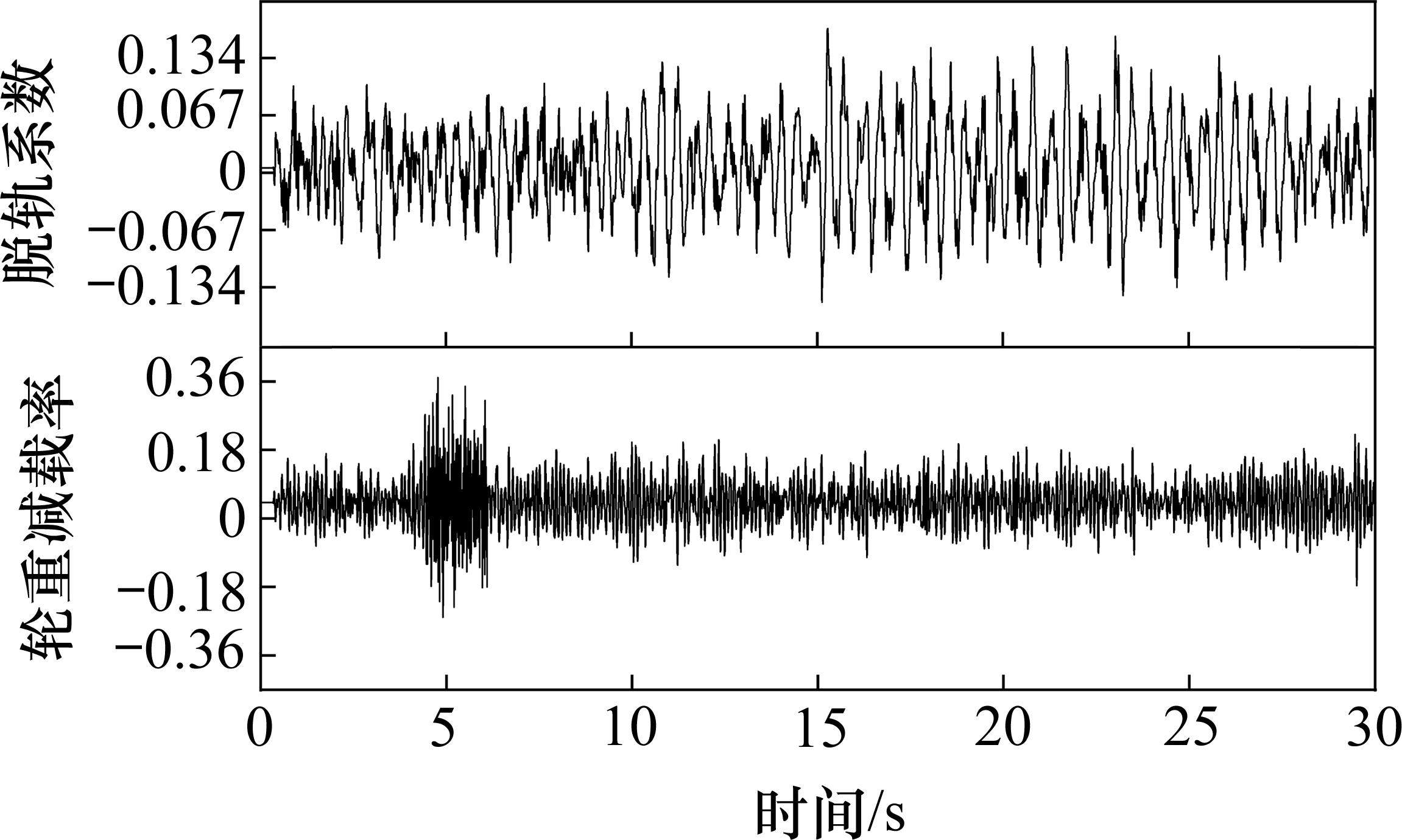
图4为前转向架构架左侧的横向加速度的6种故障部分时域和频谱信号图。由图4仿真数据可得,6种故障信号的时域图分布比较相似,且由频谱图可以看出,故障频率几乎都在20 Hz以下,几乎无法区分。
3.2 振动信号的RIME-VMD分解及重构
通过VMD对信号进行分解时,首先需设置分解层数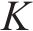
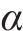
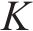
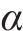
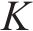
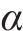

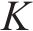
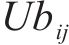
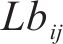
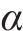
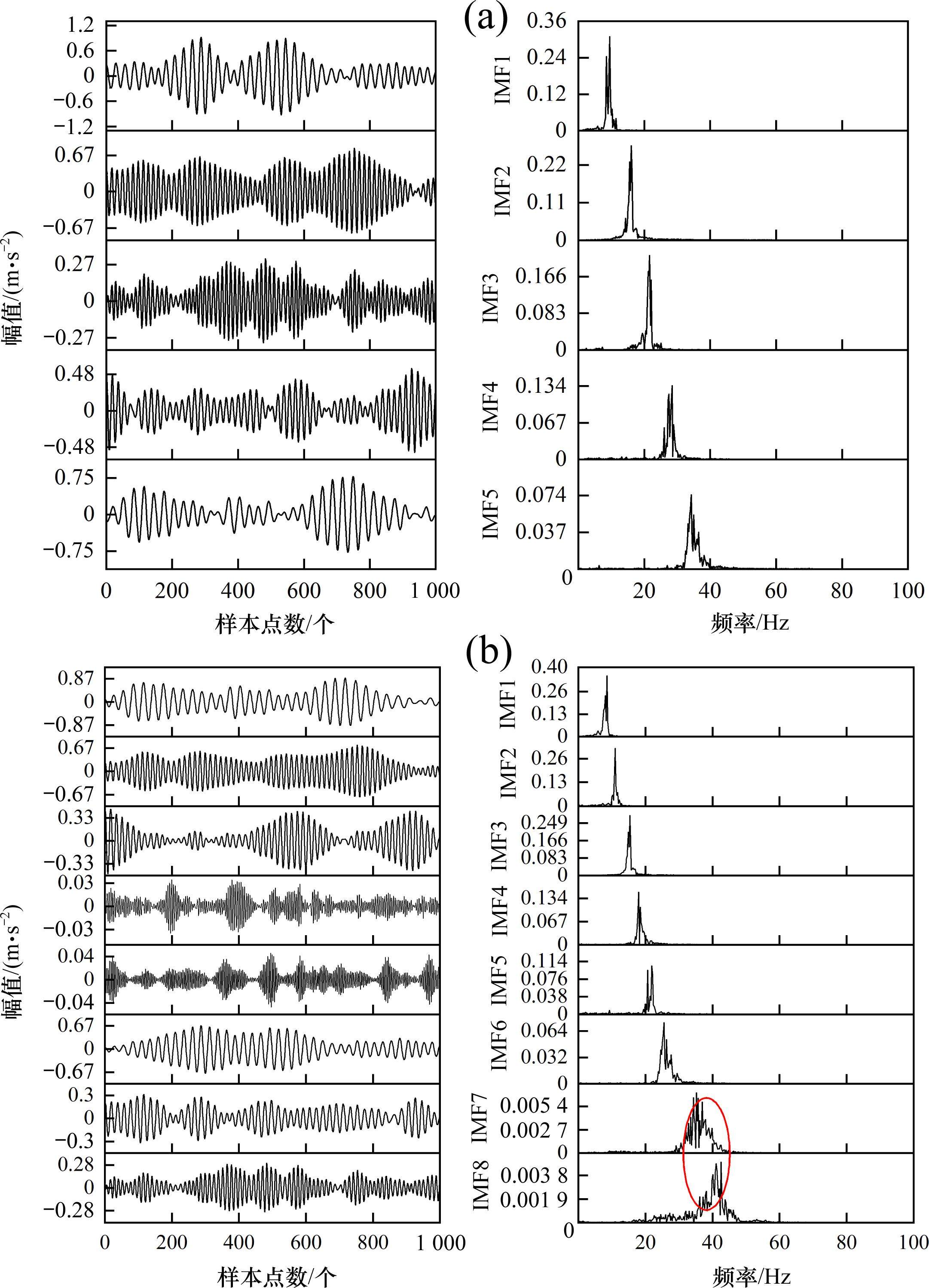
由图5(a)可以看出,RIME-VMD分解后的任意2个模态分量互不重叠,没有产生过分解现象,同时同一模态分量中也不存在不同尺度的信息,分解后的故障频率主要集中在20 Hz以下,没有产生分解不充分的现象。GWO-VMD分解结果如图5(b)所示,虽然IMF1~IMF6分解充分,但是IMF7和IMF8出现了过分解现象,说明通过GWO算法在寻优时产生了局部最优的现象。图6为原始VMD分解结果,图6(a)中,当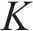
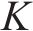
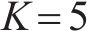
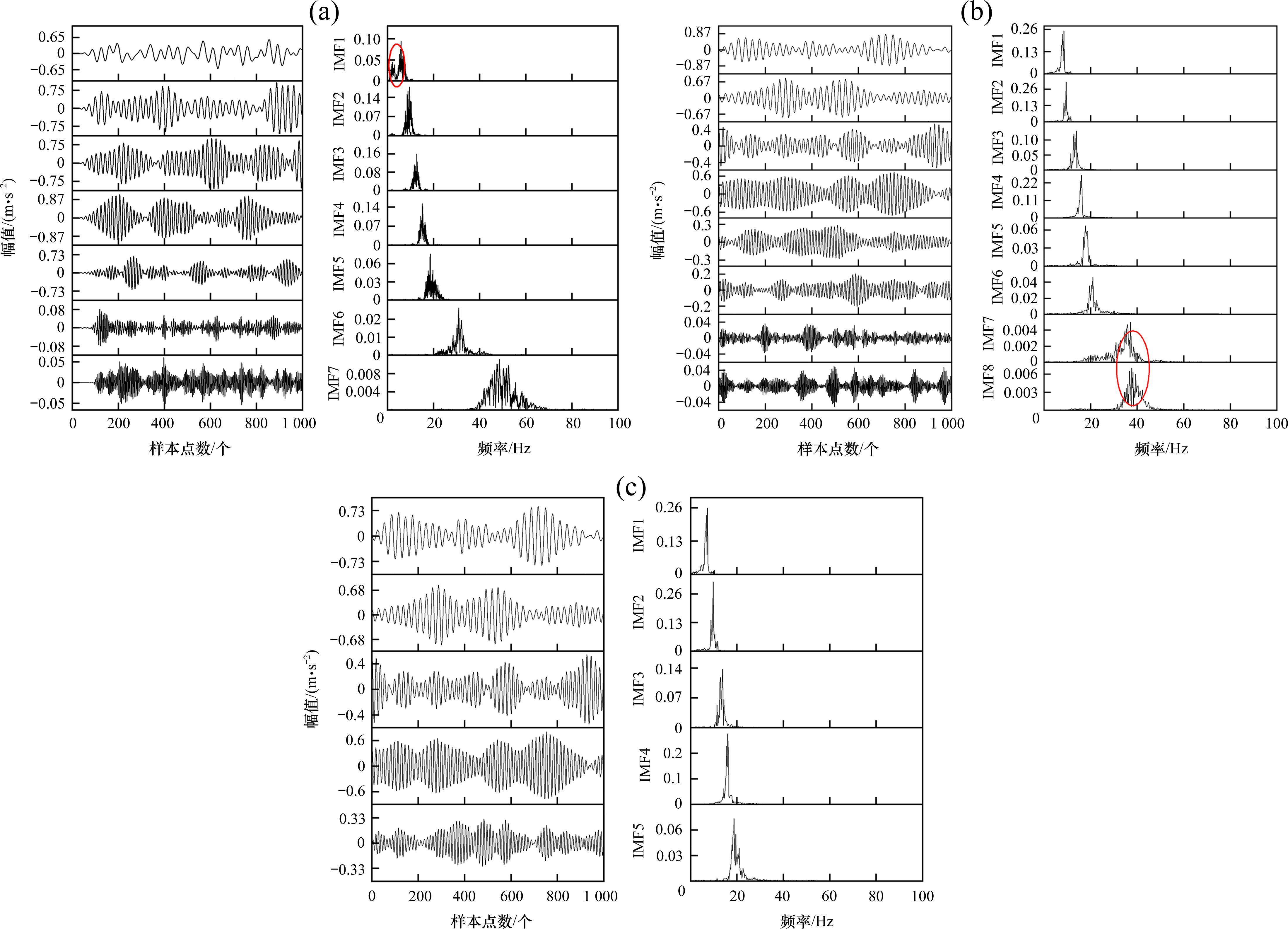
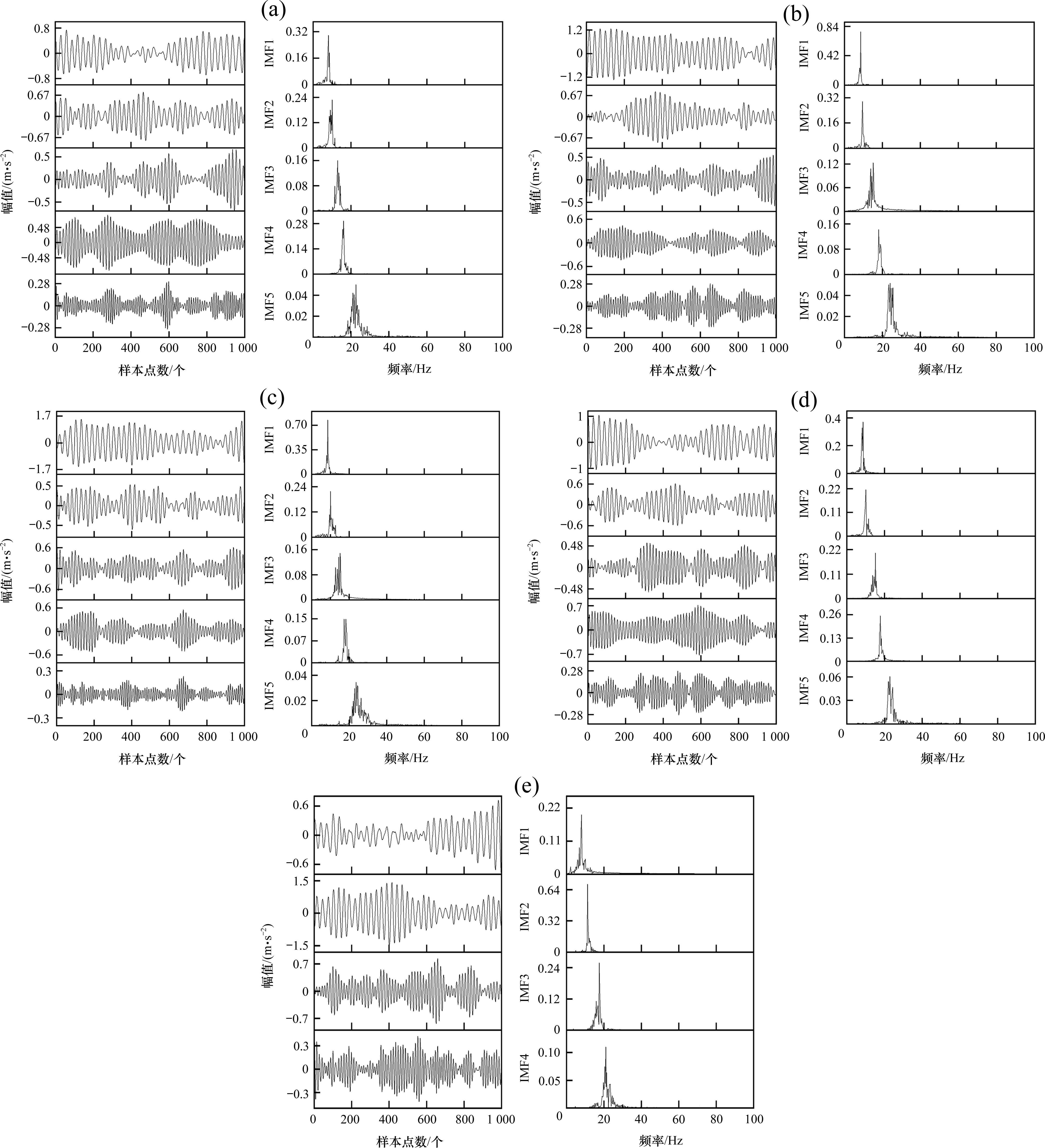
为模拟真实环境中的复杂情况,在仿真过程中引入了轨道激励谱。图7为RIME-VMD分解后的其他5种故障信号的结果,以最小包络熵作为适应度函数可以更好地捕捉和保留信号的本质特性,特别是对于非平稳信号,最主要的是有助于RIME优化算法避免陷入局部最优,从而更好地找到全局最优解,由6种故障信号的分解效果来看,表现出了更强的鲁棒性。
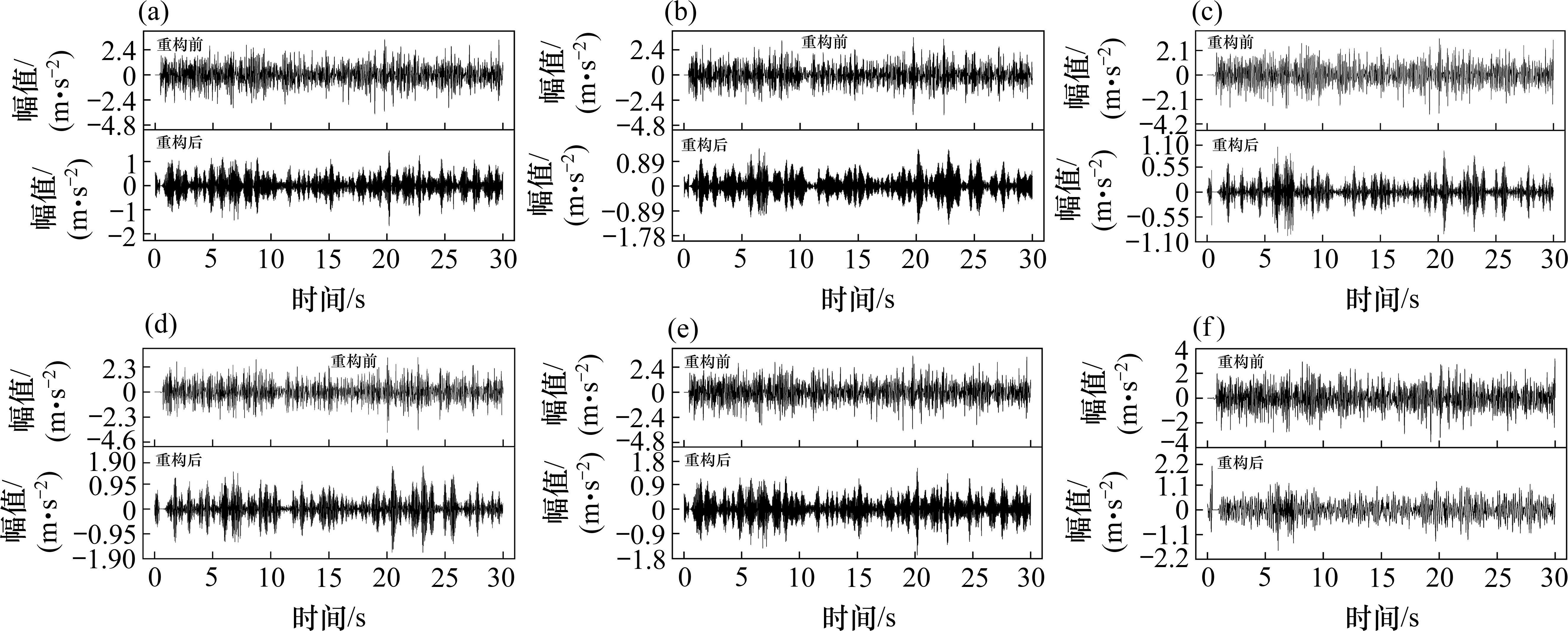
为使其在降噪的同时确保信号不失真,在重构信号的过程中选择不同尺度上峭度值较大的前4阶IMFs分量,并且在这4个IMFs分量中选取相关性系数较高的前3阶IMFs来重构信号。表2列出了6种故障信号经过RIME-VMD全拆后的各IMFs的峭度值和相关性系数,选取进行重构的IMFs分量为表中加粗的IMF。图8展示了6种故障的原始信号和重构后的信号。从图中可以明显看出,当在信号重构时,同时考虑不同尺度的峭度值和原始信号的相关性,可以有效地实现去噪,显著提高了信号的质量和清晰度。
| IMF1 | IMF2 | IMF3 | IMF4 | IMF5 | ||
|---|---|---|---|---|---|---|
| 故障1 | 峭度值 | 2.99 | 3.93 | 3.15 | 37.42 | 66.42 |
| 相关性系数 | 0.651 | 0.562 | 0.253 | 0.403 | 0.584 | |
| 故障2 | 峭度值 | 3.25 | 3.07 | 2.79 | 42.96 | 65.02 |
| 相关性系数 | 0.61 | 0.61 | 0.43 | 0.6 | 0.18 | |
| 故障3 | 峭度值 | 3.55 | 2.84 | 3.18 | 34.67 | 58.59 |
| 相关性系数 | 0.83 | 0.46 | 0.34 | 0.31 | 0.19 | |
| 故障4 | 峭度值 | 3.22 | 2.71 | 4.55 | 36.07 | 64.29 |
| 相关性系数 | 0.85 | 0.45 | 0.4 | 0.33 | 0.13 | |
| 故障5 | 峭度值 | 3.01 | 2.95 | 2.98 | 34.77 | 58.58 |
| 相关性系数 | 0.69 | 0.48 | 0.46 | 0.57 | 0.39 | |
| 故障6 | 峭度值 | 2.891 | 2.94 | 3.65 | 41.59 | — |
| 相关性系数 | 0.56 | 0.84 | 0.43 | 0.28 | — |
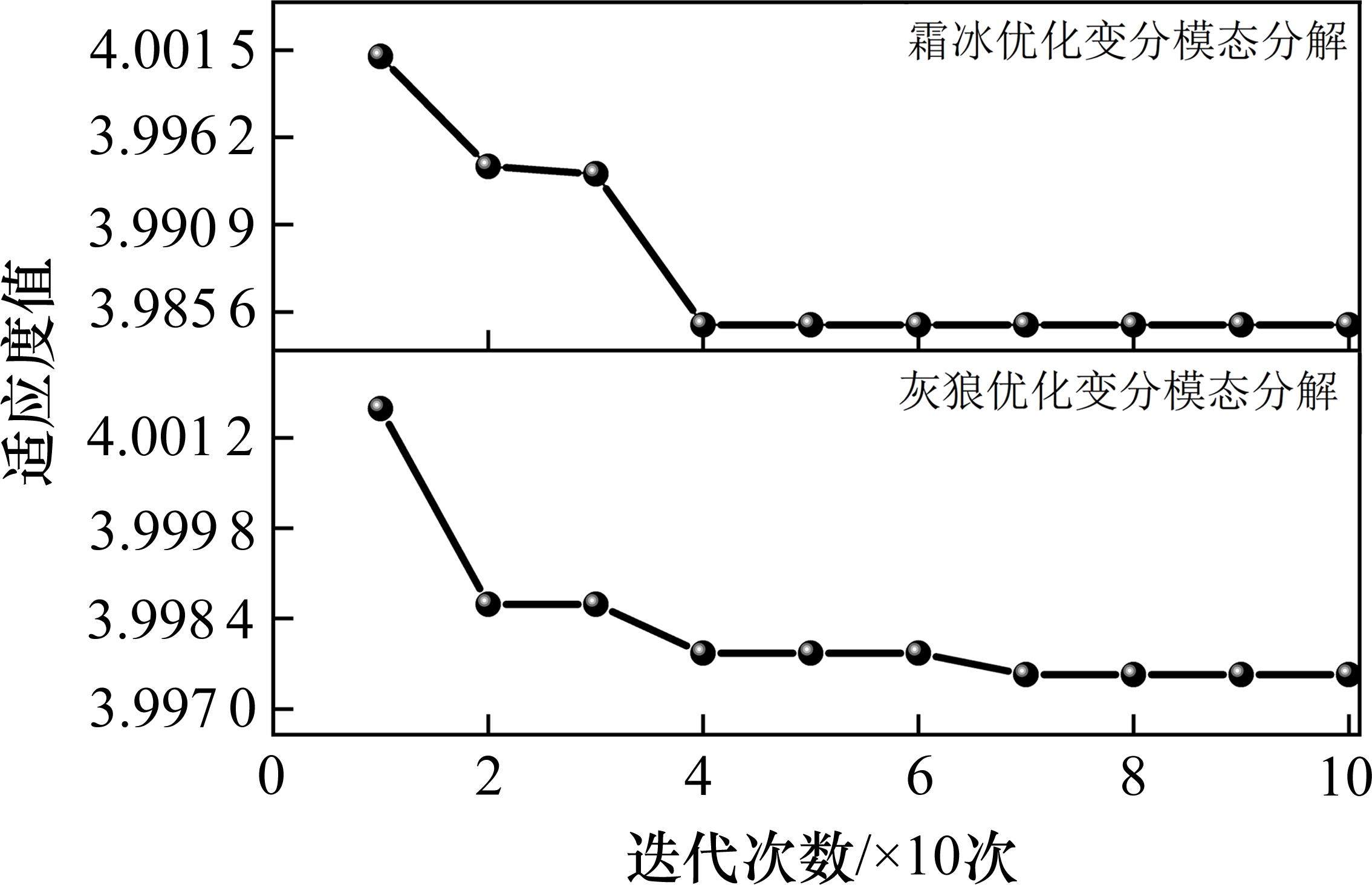
为了说明RIME-VMD的高效,图9为RIME-VMD方法和GWO-VMD方法在分解6种故障信号时的平均优化迭代曲线图,RIME-VMD和GWO-VMD每个方法在寻优的过程中总共迭代10轮,每轮迭代10次。由图9可以看出,RIME-VMD用最少的迭代次数可以寻得全局最优的参数组合。表3为不同方法分解6种故障信号时,所需的平均时间。通过平均分解时间也可以看出,RIME-VMD相比于GWO-VMD的高效性;虽然原始VMD分解效率最快,但是在参数的选择上人工试错成本较高,不利于高速列车故障诊断的需求。
| 方法 | RIME-VMD | GWO-VMD | VMD |
|---|---|---|---|
| 时间/s | 63.25 | 316.7 | 36.2 |
3.3 特征提取与支持向量机故障识别
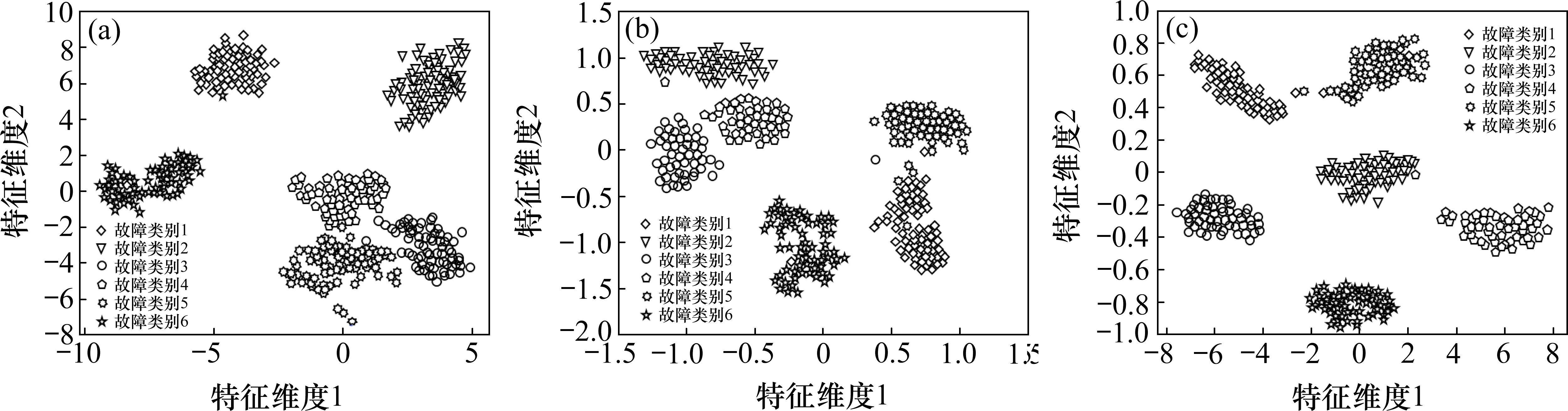
通过RIME-VMD对6种故障信号的分解及重构后,再计算出重构信号的不同尺度上的奇异熵、样本熵、排列熵分别作为故障特征向量,为了去除特征之间的冗余信息,提高故障诊断的效率与准确率,通过t-SNE的非线性降维算法,计算出高维数据中点之间的相似性,组成一个相似性矩阵,并通过相似性将高维数据映射到低维中,而不相似的特征在低维空间中会远离。图10为t-SNE降维后的特征可视化图。通过t-SNE将高维特征映射到低维的过程中,保持高维空间中点之间的相对距离和概率分布,在低维空间中尽可能地重现这些关系,降维后不同特征维度上的正负值并不代表特征的正负值,而当特征分布在某一维度的正半轴时,说明该特征在该维度上对这一故障有较高的重要性。由图10可以看出降维后各个故障之间的特征分离程度较高,无明显交叉重叠部分。
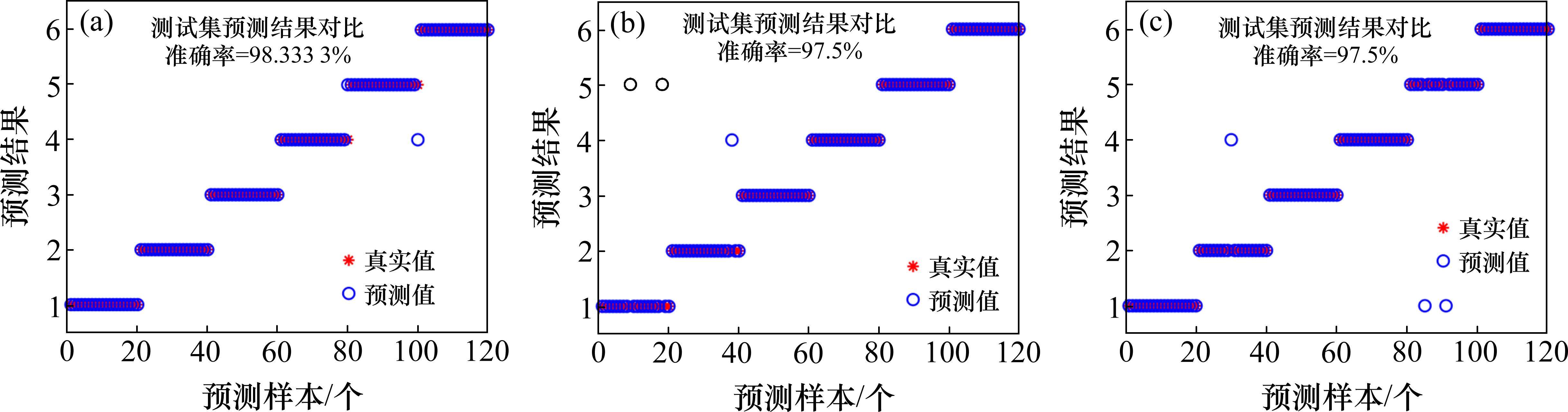
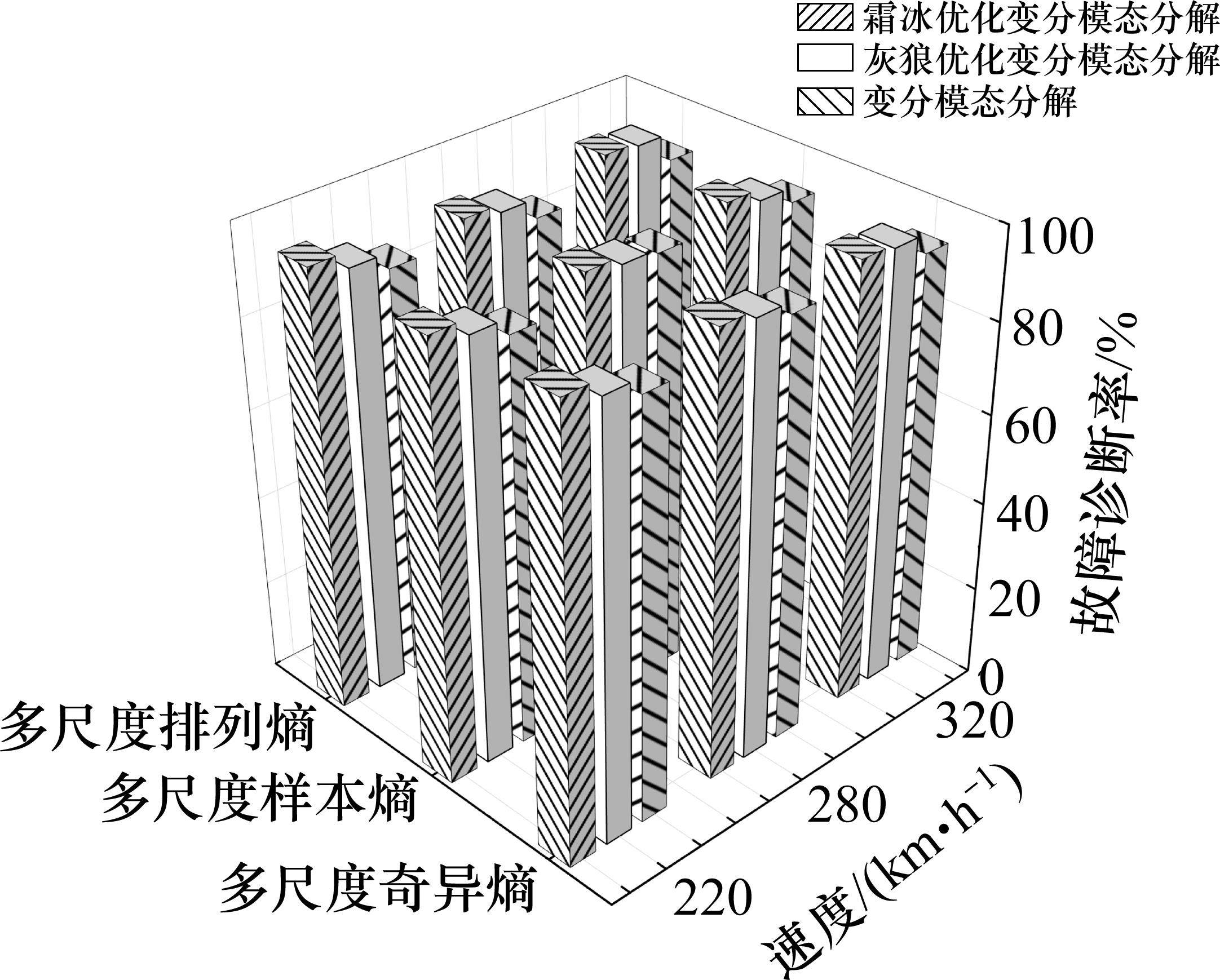
每个故障取70个数据点作为一个样本,6种故障总共包含600个样本集,随机选取480个样本作为训练集,120个样本作为测试集。将6种故障的样本集与训练集输入到支持向量机中进行分类,分类后的准确率如图11所示。以多尺度奇异熵作为特征,通过图11(a)分类后的结果看出,120个测试样本,这2个误判结果分别是故障4和故障5,这也可以从降维后的特征可视化的图10(a)中看出,故障4和故障5这2个特征有少许交集。为了证明该方法的优越性,以同样的方式,分别提取了6种故障在220 km/h下的多尺度样本熵和多尺度排列熵作为特征值进行了故障识别,识别的准确率如图11(b)和图11(c)所示。以多尺度样本熵和多尺度排列熵作为特征值时,故障1和故障5出现了误判的情况,且从降维后特征可视化图10(b)和图10(c)中可以看出,除了其他几种故障特征,故障1和故障5之间的特征存在较少交集,故障识别率分别达到了97.5%。为了验证该方法的鲁棒性,分别在280 km/h、320 km/h速度下进行了仿真,并与GWO-VMD和原始VMD的方法进行了故障诊断识别率的对比,对比结果如图12所示。通过故障诊断的准确率可见,RIME-VMD通过霜冰优化算法的全局搜索能力以及正向贪婪机制,避免在不同工况下VMD分解时参数陷入局部最优,增强了VMD分解的鲁棒性,准确分解出横向减振器各故障信号包含的故障子频率,有效提取了故障特征,提高了故障诊断的准确率,证明了该方法的有效性和优越性。
4 结论
1) 针对VMD在高速列车横向减振器故障诊断中参数自适应不足的问题,根据RIME算法高效的搜索能力以及正向的贪婪机制,利用最小包络熵作为适应度函数,可以在不同工况下获得全局最优参数组合,提高了VMD分解的鲁棒性。
2) 相较于GWO-VMD方法,RIME-VMD通过根据当前迭代次数计算粒子的附着系数和归一化适应度值,自适应地调整粒子移动和更新的策略,减少了迭代次数,并且在保证可靠性的前提下提高了分解效率和准确率。虽然原始VMD的方法分解效率较快,但是人为预设参数的成本较高,不利于高速列车横向减振器故障诊断的需求。
3) 利用峭度值和相关系数双重指标来选择分解后的模态分量进行信号重构,通过对比发现重构后信号的质量和清晰度显著提高。此外,通过多尺度的奇异熵、样本熵以及排列熵和t-SNE降维技术,有效地提取和融合了故障特征,增强了故障识别的可靠性。通过故障识别率的对比,验证了该方法的优越性。
秦永峰,李刚,齐金平等.基于RIME-VMD的高速列车横向减振器故障诊断[J].铁道科学与工程学报,2025,22(03):942-953.
QIN Yongfeng,LI Gang,QI Jinping,et al.Fault diagnosis of transverse damper for high-speed trains based on RIME-VMD[J].Journal of Railway Science and Engineering,2025,22(03):942-953.

