随着我国铁路这一重大基础设施的规划与发展,高速铁路更趋于智能化与电气化,由此带来的运营维护压力也随之增大,传统的微机监测方法以及人工巡线检测方法已经难以满足现场中的实时性要求。为满足“十四五”铁路科技创新规划中提出的“构建人防、物防、技防‘三位一体’的安全保障体系”发展要求,我国大力发展了高速轨道检测车技术,检测车在区段中运行过程中能够快速高效准确地采集各设备的相关数据,为轨旁设备的故障诊断与状态检测提供了先决条件[1]。同时,补偿电容作为保证无绝缘轨道电路(Jointless Track Circuit,JTC)中列车控制信号能够正常稳定地进行长距离传输的重要装置,在保证列车安全高效地运行上起着较为重要的作用,但由于列车行驶振动、引接线老化、环境变化等因素,补偿电容易发生故障从而危及行车安全以及影响运营效率。因此在运营速度不断增高,运行时速不断加快的背景下,利用检测车对均匀分布在轨道上的补偿电容进行故障识别与状态监测,对保障列车可以安全高效地运行具有较为重要的意义。已有针对补偿电容的故障诊断与容值估计研究的报道。CÔME等[2]利用基于混合约束半监督独立因子分析的方法对铁路补偿电容进行了故障分析与诊断。张帅等[3]利用变分模态分解(Variational Mode Decomposition, VMD)对JTC的分路电流进行分解并以能量值为特征进行补偿电容的特征提取,但没有说明VMD的参数该如何选取,也没有利用真实数据进行方法验证,缺乏实际数据验证。崔一博等[4]利用感应电压曲线与股票曲线的变化相似性,提出一种基于股票分析和灰关联的补偿电容故障诊断方法,获得较为准确的效果。洪玲等[5]利用小波包分解的方法对列车的分路电流数据进行分解,并按照断线、正常与容值下降故障3种情况进行特征提取,实现了补偿电容的诊断与容值估计,取得了良好的效果,但在数据来源方面与现实有些差别。王少迪等[6]根据轨道检测车的工作原理对轨道检测车采集补偿电容脉冲数据的过程进行建模分析并对补偿电容实现了容值估计,最终利用实际数据进行了验证,获得了较为准确的结果。武晓春等[7]根据不同轨旁设备故障对感应电压信号的影响,提取了各个设备故障情况下的感应电压幅频特征,利用t分布随机邻域嵌入方法进行多特征融合再输入到深度残差网络中进行训练,实现了包括补偿电容在内的轨旁设备故障检测。罗依梦等[8]利用Dempster-Shafer证据融合理论,对轨道检测车采集到的补偿电容脉冲数据与感应电压数据进行了融合,实现了对补偿电容的故障诊断,此种方法与利用单一的数据相比提高了补偿电容的诊断准确率,并在实际数据中得到了验证,但由于缺少理论分析,此方法的适用性有待提高。尽管上述对补偿电容的故障诊断与状态监测研究逐步深入,逐渐贴合实际,但仍存在以下不足亟待提高与完善:1) 现有的对补偿电容进行工作状态分析的模型大多为基于传输线理论的列车分路电流模型,缺少信号从钢轨到轨道电路信息采集模块这一电磁过程的建模分析,尚未建立采集感应电压数据的电磁模型;2) 对于利用信号分解方法对补偿电容进行容值估计,未能应用人工智能对其进行有效的改进与优化;3) 针对采集到的感应电压数据,缺少一个较为准确地判断补偿电容工作状态的方法。本文面向轨道检测车这一技术背景下感应电压曲线的变化特点,综合考虑信号传输过程与电磁感应过程,建立检测车采集感应电压这一过程的联合仿真模型并获得仿真数据。在此基础上,设计一种较为适宜的适应度函数,并引入改进的蜣螂优化算法(Improved Dung Beetle Optimizer, IDBO)实现了对VMD参数的寻优;最终利用寻优结果对仿真数据进行VMD分解后提取特征,通过建立每一个补偿电容作用区域内的特征值与其自身容值之间的映射关系实现对补偿电容的容值估计,为现场补偿电容运营维护提供较为可靠的参考。
1 轨道检测车数据采集过程的模型建立及验证
为准确模拟出现场中轨道检测车采集感应电压这一过程,建立基于传输线理论的四端网络模型与基于电磁场理论的有限元模型2种模型的联合仿真模型[9]。基于传输线理论的四端网络模型主要计算从发送端发出的信号经过钢轨与补偿电容组合而成的四端网络后到达当前列车位置的信号幅值大小。基于电磁场理论的有限元模型主要计算出STM线圈处的磁场强度,进而计算得到仿真感应电压大小。
首先,对于传输线理论的等效四端网络模型,JTC的各个设备通常表示为2×2的矩阵形式,如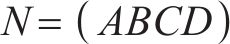
设备 名称 | 矩阵 名称 | A | B | C | D | 备注 |
|---|---|---|---|---|---|---|
| 空心线圈 | 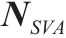 | 1 | 0 | 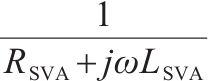 | 1 | 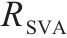 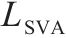 |
| 发送端匹配变压器 | 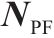 | 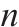 | 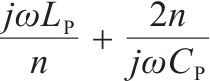 | 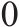 | 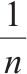 | 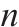 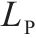 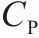 |
| 接收端匹配变压器 | 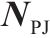 | 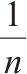 | 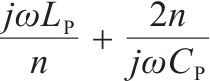 | 0 | 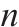 | 同上 |
| 调谐单元BA1 | 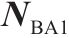 | 1 | 0 | 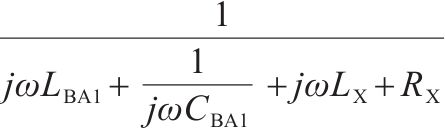 | 1 | 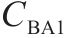 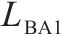 |
| 调谐单元BA2 | 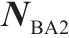 | 1 | 0 | 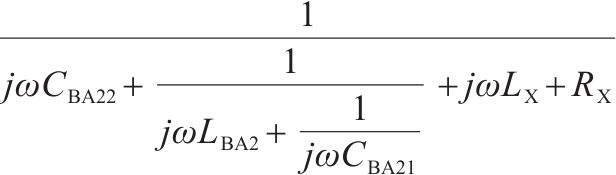 | 1 | 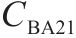 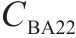 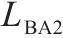 |
| 补偿电容 | 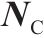 | 1 | 0 | 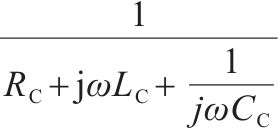 | 1 | 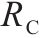 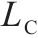 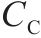 |
| 钢轨 | 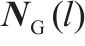 | 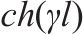 | 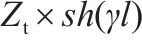 | 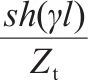 | 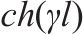 | 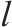 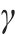 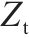 |
根据原理,在ZPW-2000A型轨道电路中,发送端发出的信号可以表示为:

式(1)中: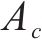
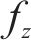
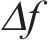
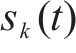
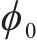
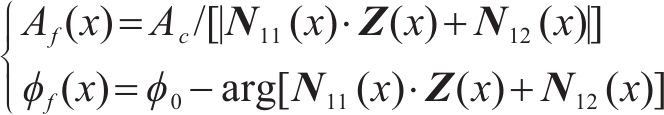
式(2)中: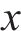
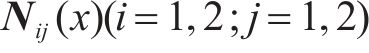
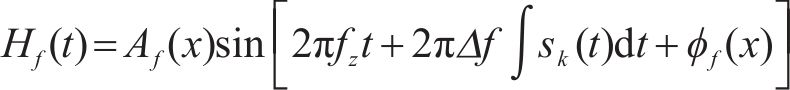
由于列车车载STM采集信号方式为离散采集,设STM的采样频率为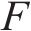
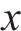
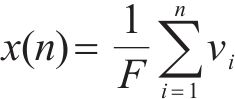
由式(4)可知,采样时间为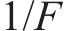
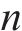
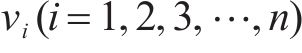
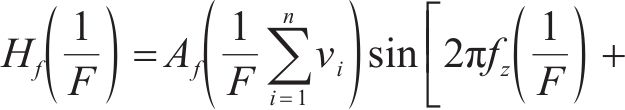
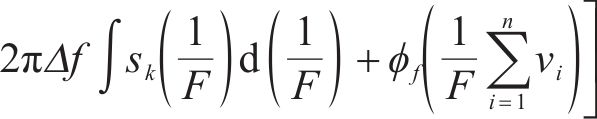
随后,根据三维涡流场下的麦克斯韦方程组恒等式,基于ANSYS Maxwell 3D软件建立轮对与钢轨之间的电磁有限元模型,主要步骤包括材料选取与建立,设置边界条件,按式(5)添加激励源,设置求解域等,ZPW-2000A型轨道电路结构图与仿真得到的水平磁感应强度分布图如图1所示[11-12]。
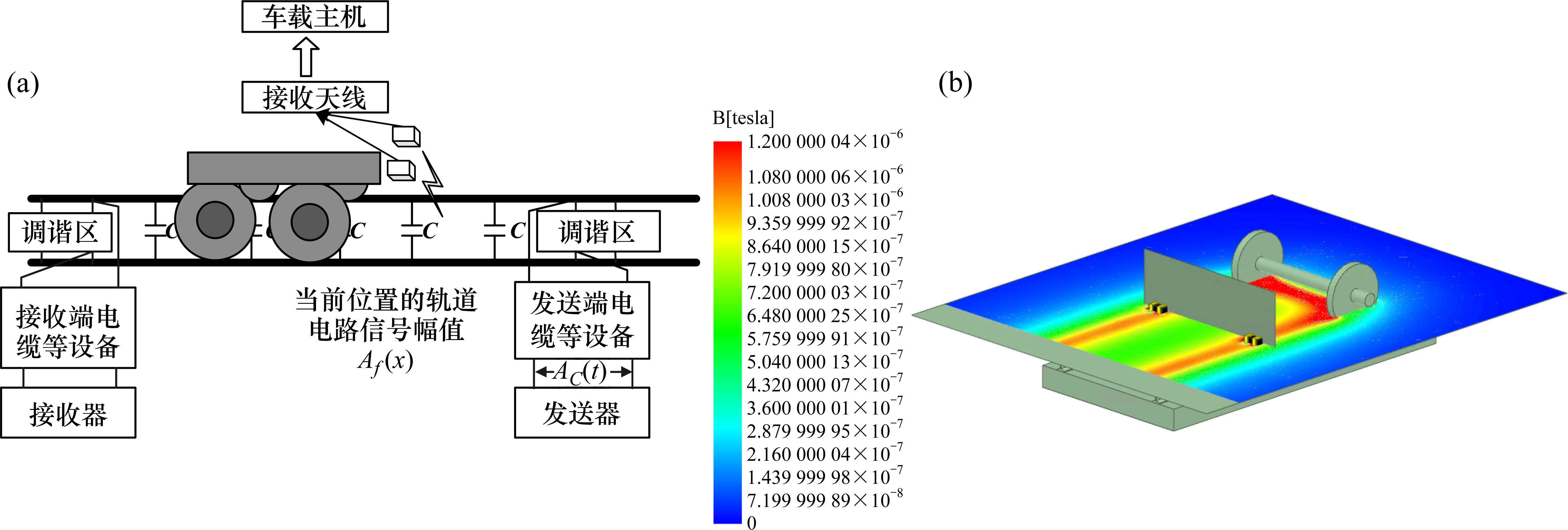
根据图1(b)可知,在轨道检测车的STM采集感应电压过程中,磁场主要集中在钢轨周围、轮对及STM线圈周围,其中磁场强度在列车轮对处达到最大,这一点与轨道检测车采集感应电压的原理一致。为了进一步验证模型的准确性,根据式(2)与式(3)遍历计算整个区段的分路信号幅值,并将其依次代入有限元模型中计算磁场强度,从而得到感应电压的仿真数据。随后,将仿真数据与轨道检测车在现场采集的同类型区段的真实数据进行对比,结果如图2所示。
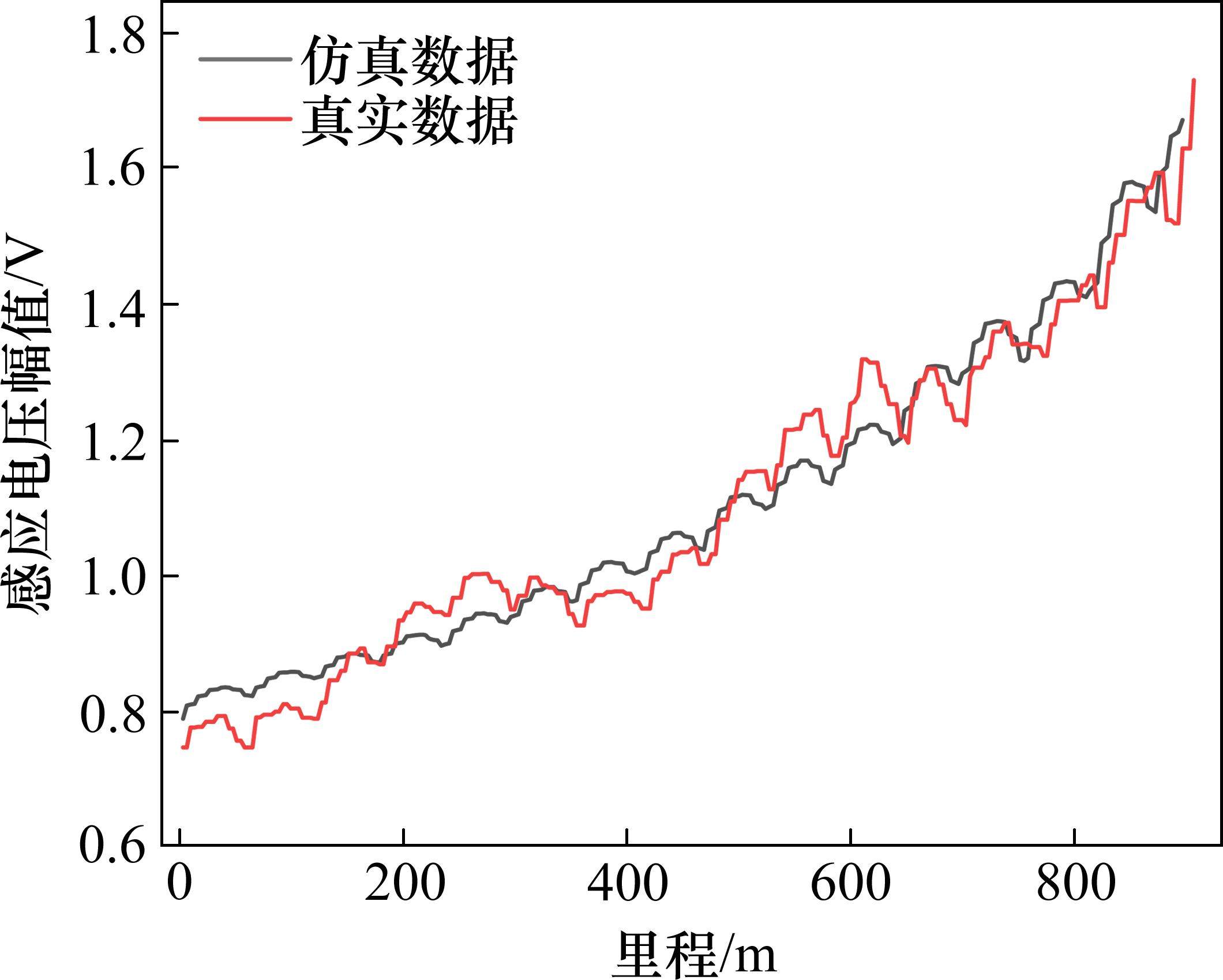
图2中,仿真数据与真实数据之间从发送端到接收端的变化趋势大致相同,但在各个补偿电容作用区域时有所不同,其主要原因就是实际中补偿电容的安装间距与标准规定的间距略有区别,钢轨与道床的阻抗受温度湿度等环境影响以至于与标准阻抗之间产生了一定误差。总体而言,真实感应电压数据与仿真数据的相关性在95%以上,且仿真轨道电路的出入口以及补偿电容处的感应电压与真实数据的差值百分比均在5%以下。由此可见,本仿真模型可以较为准确地仿真出检测车采集到的感应电压数据,可作为后续补偿电容容值估计的理论依据。
2 变分模态分解的参数优化
当补偿电容发生故障时,STM线圈采集到的感应电压曲线会发生变化,本文利用VMD分解非线性且不平稳的感应电压信号,以实现原始信号中各个内涵模态分量(Intrinsic Mode Functions, IMF)的有效分离。对于给定的信号,VMD首先通过求解变分约束问题进行信号分解,并约束每个分量的带宽和最小,以保证给每个分量分配各自的中心频率与有限带宽[13]。但在VMD分解原始信号之前需要设定k值与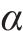
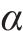
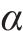
2.1 改进的蜣螂优化算法
蜣螂优化算法[14]是2022年东华大学薛建凯等提出的群智能优化算法,算法包括滚球、跳舞、繁殖、觅食、偷窃5种行为,其中前2种行为属于探索,后3种属于开发,其算法流程如图3所示。DBO算法在绝大多数基准函数上都拥有良好的寻优能力,但其在某些特定函数上存在着一定的局限性。因此本文在DBO基础上进行了改进。
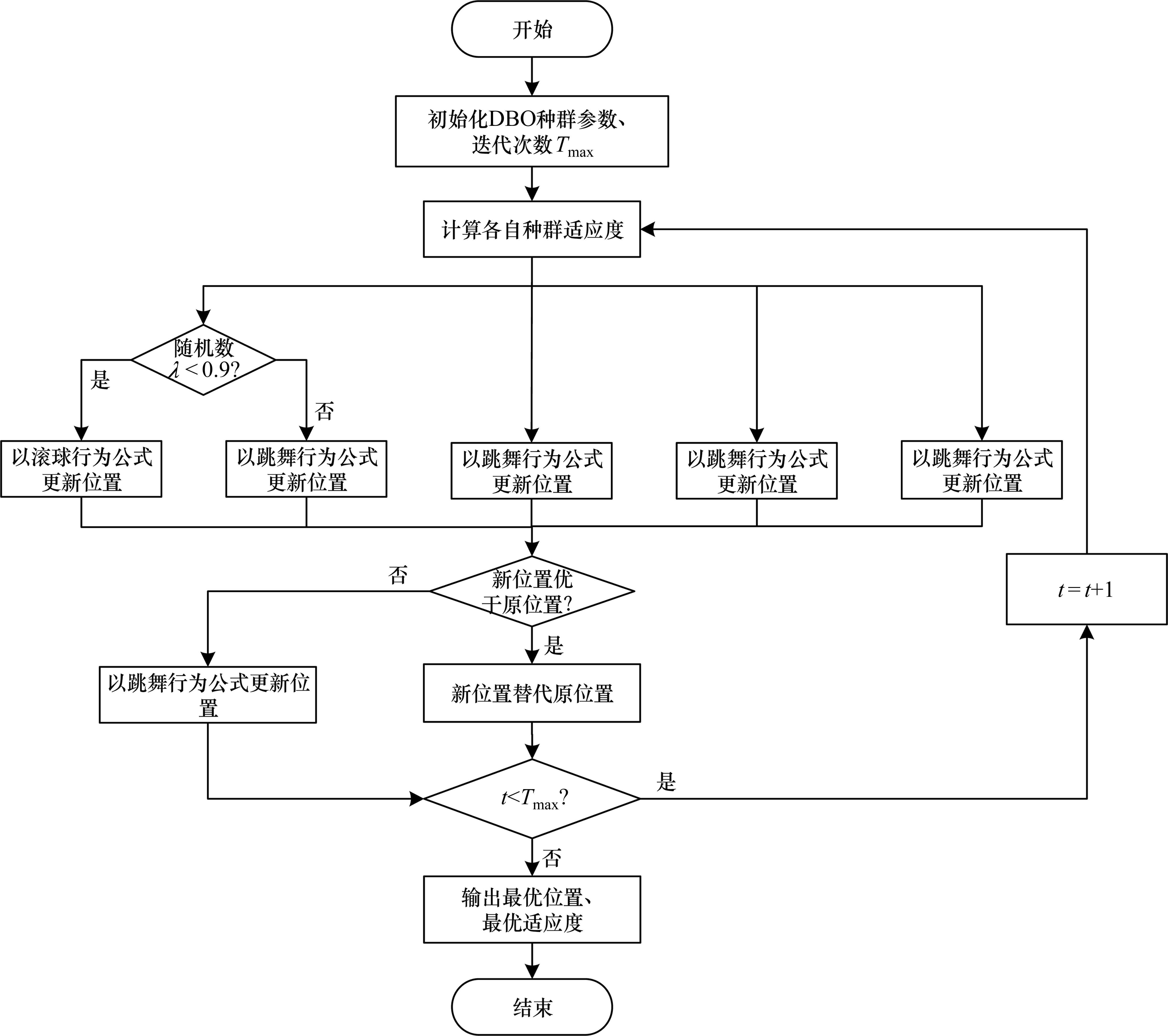
2.1.1 自适应的种群分配方式
本文提出一种自适应分配种群个数的方法,设标准DBO算法中负责探索的蜣螂个数为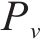
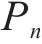
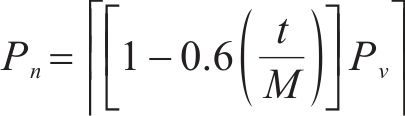
式(6)中:t为当前迭代次数;M为总迭代次数,随着迭代次数的增加,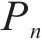
2.1.2 拥挤机制与轮盘赌策略
本文在跳舞阶段中加入了拥挤机制,即当2个跳舞行为的蜣螂距离过小时就会扰动其中一个蜣螂位置,以此来提高算法探索阶段的探索范围。此外,还在探索与开发之间的过渡阶段设置了轮盘赌策略,即向开发阶段传递一个当前最优值改为传递一组最有优势的几个值,并按照值的优劣分配概率区间,值越优则分配的概率区间越大,如式(7)所示:
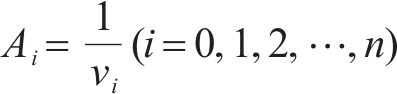
式(7)中: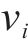
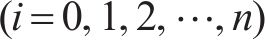
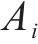
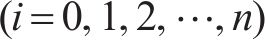
2.1.3 开发阶段控制参数调整
在标准DBO的开发阶段中,繁殖阶段与觅食阶段的蜣螂活动半径是线性递减的,而线性递减很难保持算法的探索与开发之间的平衡,为了在后期进行局部精细开发,加快收敛速度,本文对半径的变化进行了改进,如式(8)所示:
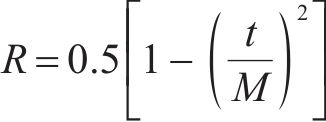
式(8)中:将半径R改为指数变化趋势,并添加系数0.5控制R开发阶段的初始区域大小。
2.2 适应度函数的选取
利用优化算法来优化VMD的参数,关键就是需要一个适宜的适应度函数,考虑到防止过分解产生虚假分量和模态混叠现象以及分解不完全的情况,本文提出一种名为“相关性中心频率比”的指标作为适应度函数:
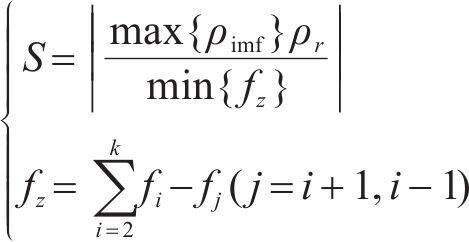
式(9)中: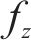
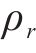
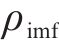
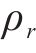
2.3 基于IDBO算法的VMD参数优化
在VMD分解之前,首先利用改进后的DBO优化VMD的2个参数,并将其与现今几种主流优化算法包括灰狼算法[15](Grey Wolf Optimizer, GWO),麻雀算法[16](Sparrow Search Algorithm, SSA),遗传算法[17](Genetic Algorithm, GA),鲸鱼算法[18](Whale optimizer algorithm, WOA)进行了对比,VMD的参数范围为k∈[2,7]与α∈[500,6 500],优化算法的参数均采用原文中的推荐参数。
寻优过程与结果如图4与表2所示,DBO算法在第163次达到收敛,而IDBO算法在第105次就达到了收敛,且DBO陷入了局部最优,因此IDBO的收敛速度较之前的DBO有所改进,寻优能力也较之前有较大的提高。此外,虽然SSA、IDBO均达到了全局最优值,但SSA算法明显计算时长更长;而WOA与GWO虽然分别是收敛速度最快和计算速度最快的算法但两者最终均陷入了局部最优,故综上所述,IDBO与标准DBO乃至与其他4种算法相比,在此VMD参数优化问题上更具有优势,最终优化得到的VMD参数分别为α=5 000,k=5。
| 算法 | 计算时间/min | 到达收敛的迭代次数/次 | 适应度函数 最小值 |
|---|---|---|---|
| GA | 25 | 417 | 0.430 726 487 |
| SSA | 47 | 169 | 0.430 404 489 |
| WOA | 44 | 101 | 0.430 554 962 |
| GWO | 4 | 273 | 0.433 459 289 |
| DBO | 15 | 163 | 0.430 502 259 |
| IDBO | 12 | 105 | 0.430 404 489 |
3 仿真数据的容值估计
3.1 对仿真数据进行VMD分解
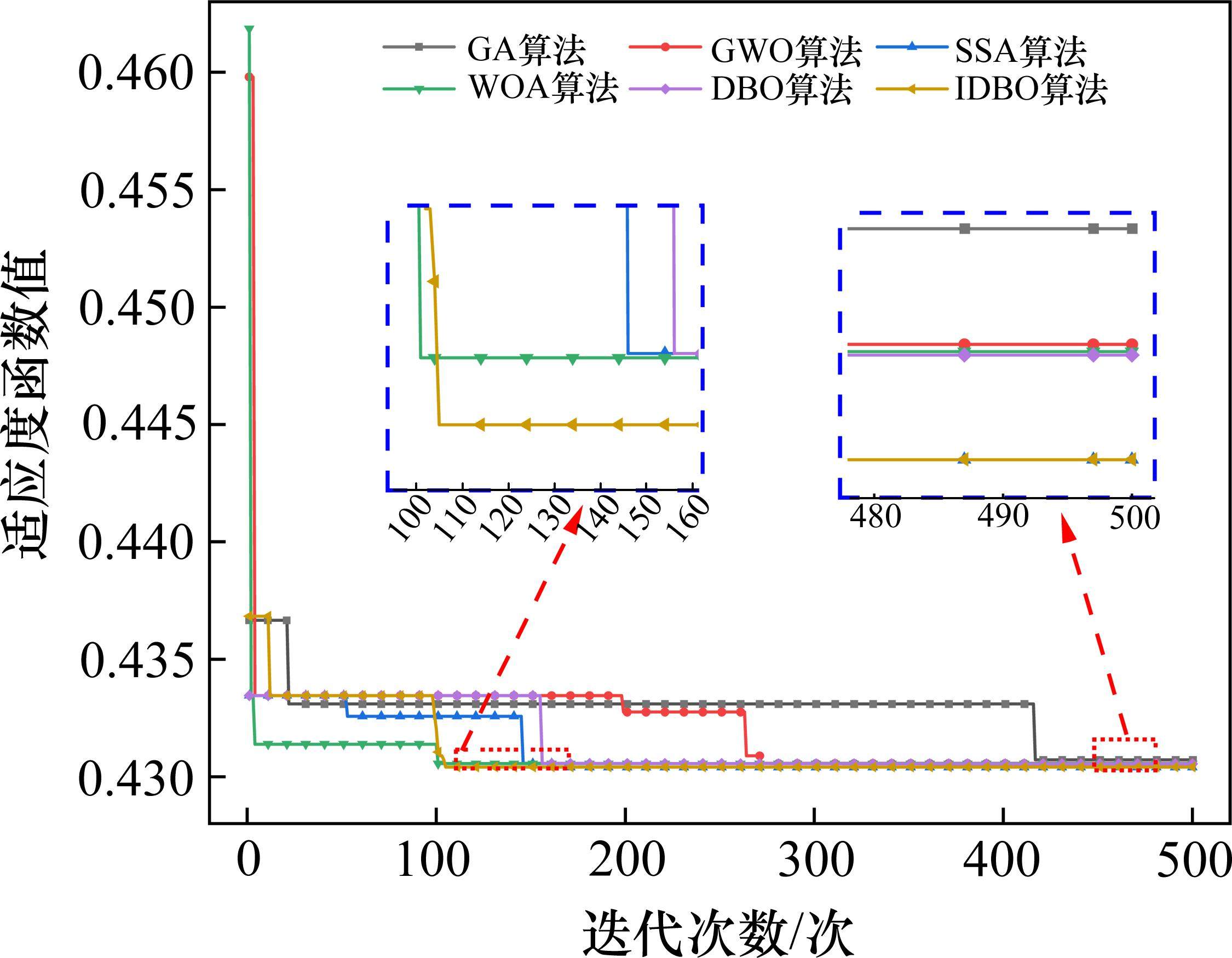
为了对补偿电容的容值进行估计,根据搭建的模型,设置仿真区段长度为1 280 m,区段的电容个数为16,区段载频为2 600 Hz,正常工作的电容容值为40 μF,设置C8发生了容值下降故障,其他电容容值均为正常[19]。对于C8故障电容,将其容值设置为0、20、40共3种,不同容值大小对应的感应电压原始信号图像如图5所示。
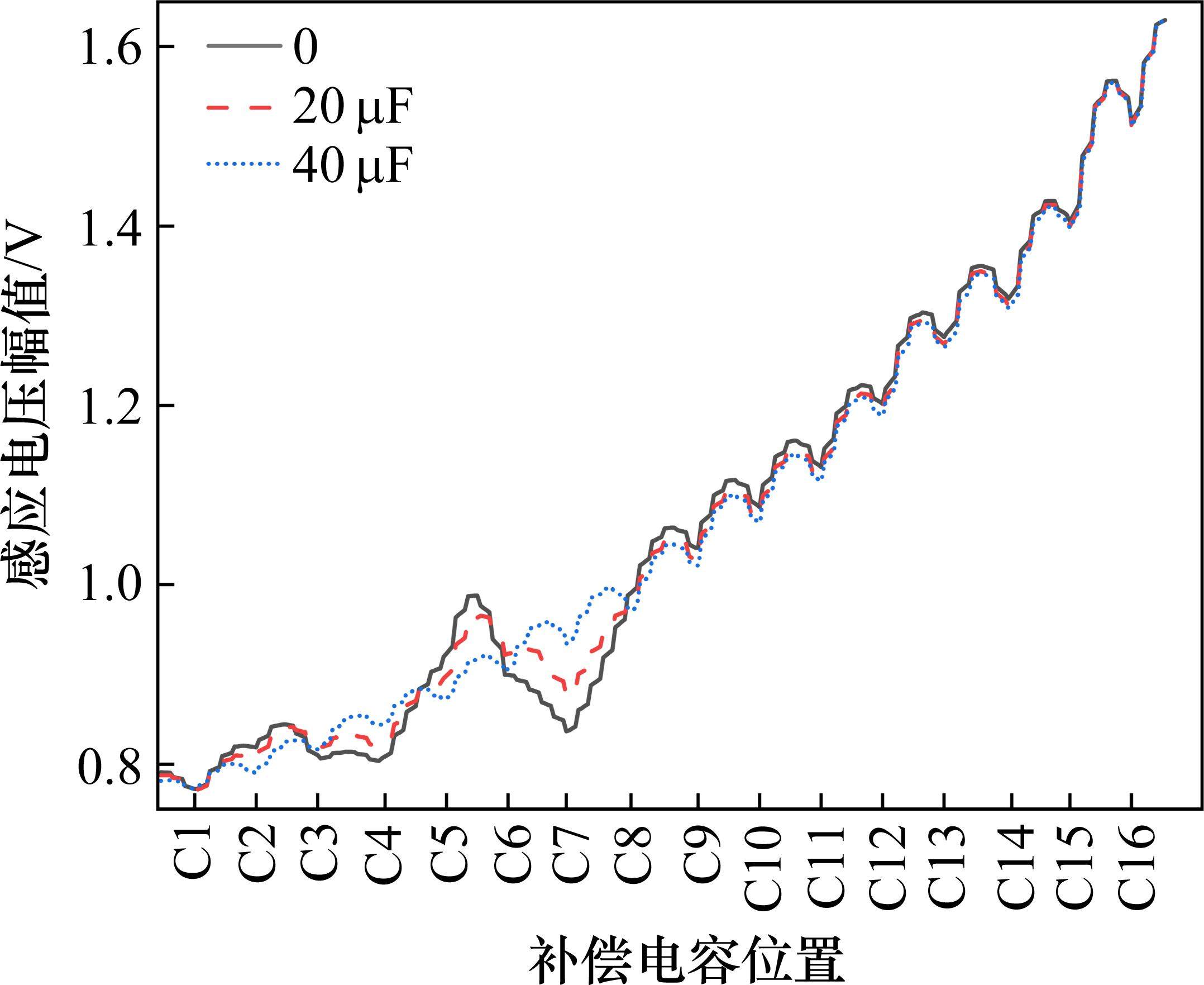
由图5可知,在C8之前的C9~C16并没有因为C8容值下降而发生变化,C8后面的电容也没有因C9的原因改变变化趋势,依旧是先增大后减小的趋势,因此可以得出区段中某一补偿电容发生容值下降故障时,其对其他补偿电容作用区域的感应电压影响较小,故障传递性较小。以优化后得到的2个参数对3种C8容值下降的仿真数据分别进行VMD分解,得到如图6的结果。
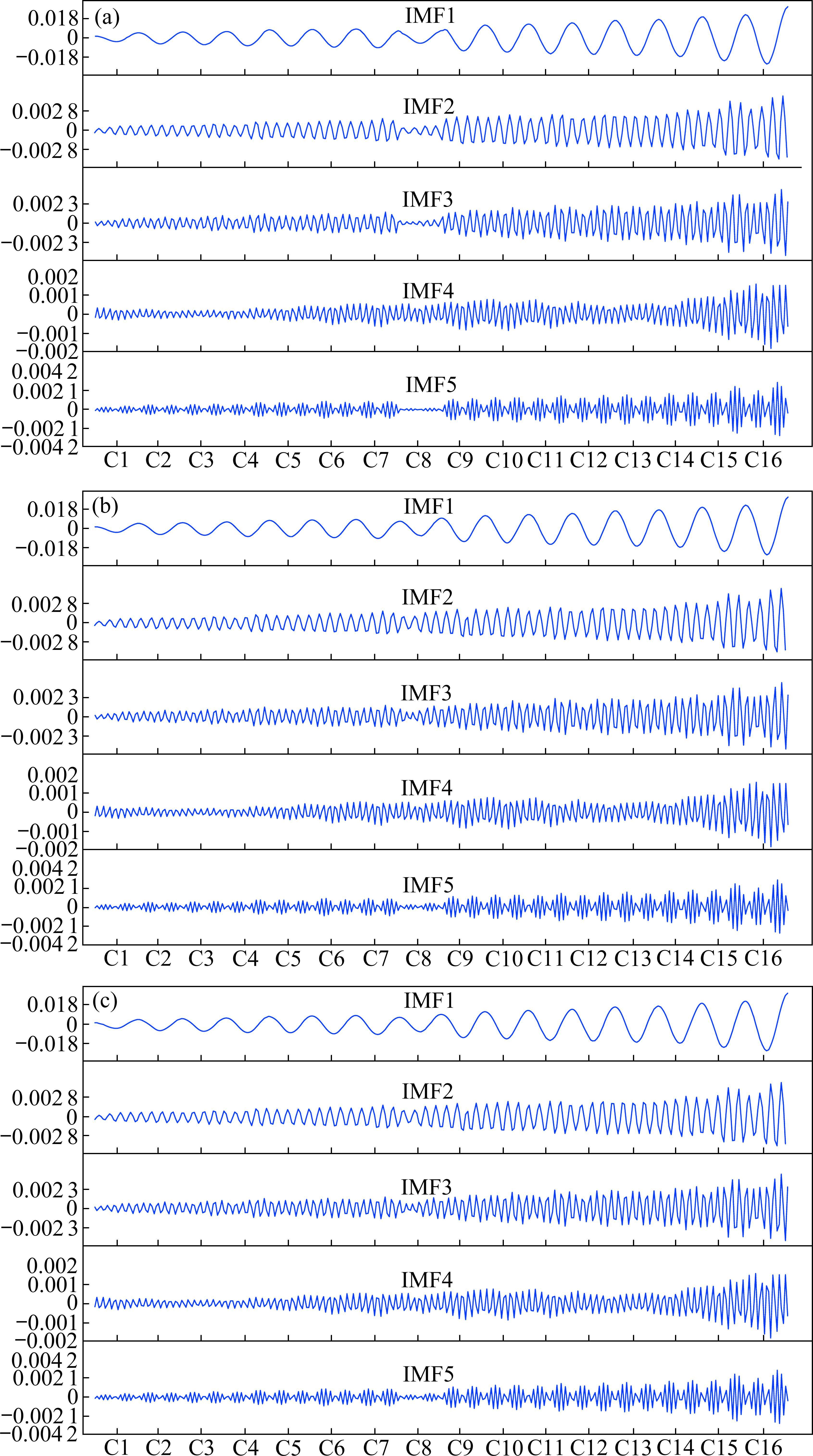
由图6所示,IMF1表示原始信号的主要趋势,IMF2与IMF3表示原始信号在较小时间段内的周期性小波动,IMF4与IMF5表示原始信号高频段的变化,由此可见,经过VMD分解可以将原始信号分解为不同部分。容值下降故障在现场中就会导致信号的高频段发生变化,且据观察,IMF5的信号波动大多集中于各个补偿电容的作用范围内,故本文选用IMF5来对补偿电容的容值下降过程进行分析。
据观察可知,在3种不同容值下降情况下的C8作用范围内IMF5结果与其他补偿电容作用范围内的区别较为明显,故本文提出一种按照每个补偿电容作用区域来分割区段进而去单独估计补偿电容容值的方法。由于仿真数据干扰较少,针对仿真数据分割补偿电容作用区域的方法可以对正常曲线求极小值并以各个极小值之间的中点为分割线。对于真实数据可以按照补偿电容设置标准,根据补偿电容理论间隔设置分割线[19]。
随后在VMD分解得到每个补偿电容作用区域内的IMF5分量的基础上,按照上述方法分割成16个补偿电容作用区域并分别提取能量特征,求分段能量步骤如下。
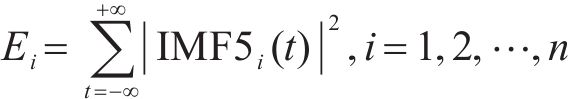
式(10)中: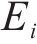
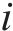
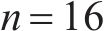
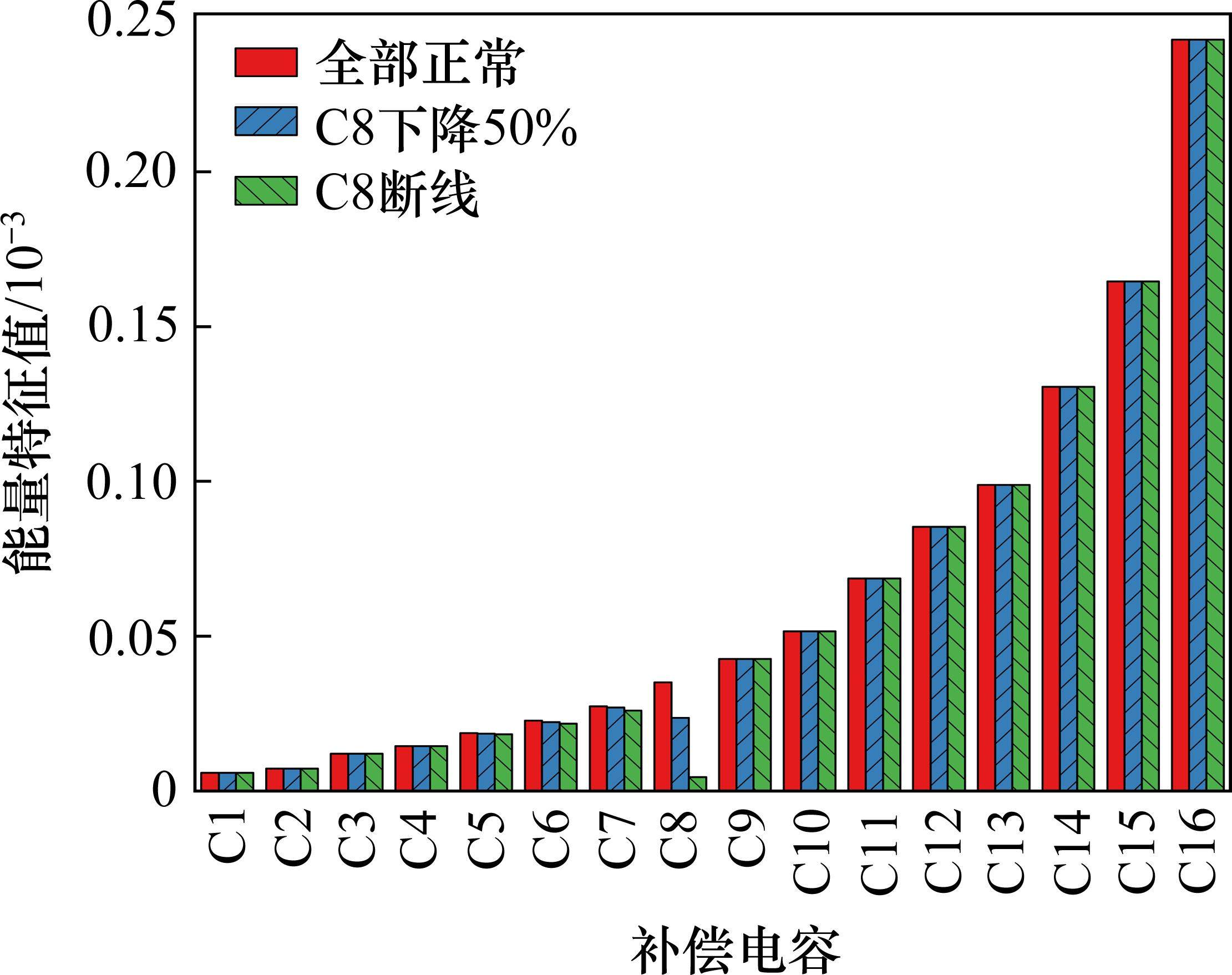
图7表示C8断线、容值下降50%与正常时所有补偿电容作用区域内的IMF5能量特征值大小。3种情况下的C8作用范围能量特征值有较大差异,而在C8之后的各个补偿电容作用区域内均有不同程度的能量特征值下降,但下降幅度较小,在允许的误差范围内。因此可以以每个补偿电容作用区域内的信号变化情况单独表征对应的补偿电容工作状态。
3.2 容值估计
为了探究补偿电容作用区域的能量特征值与容值之间的关系,本文将C8电容值在[0, 40]区间内以等间隔步长采样1 000个点。通过对原始信号进行VMD分解,计算C8作用范围内的能量特征值,并生成能量特征值与C8容值大小的关系曲线。同理,设置其他15个补偿电容发生容值下降故障,并求得能量特征值与容值关系曲线,如图8所示。
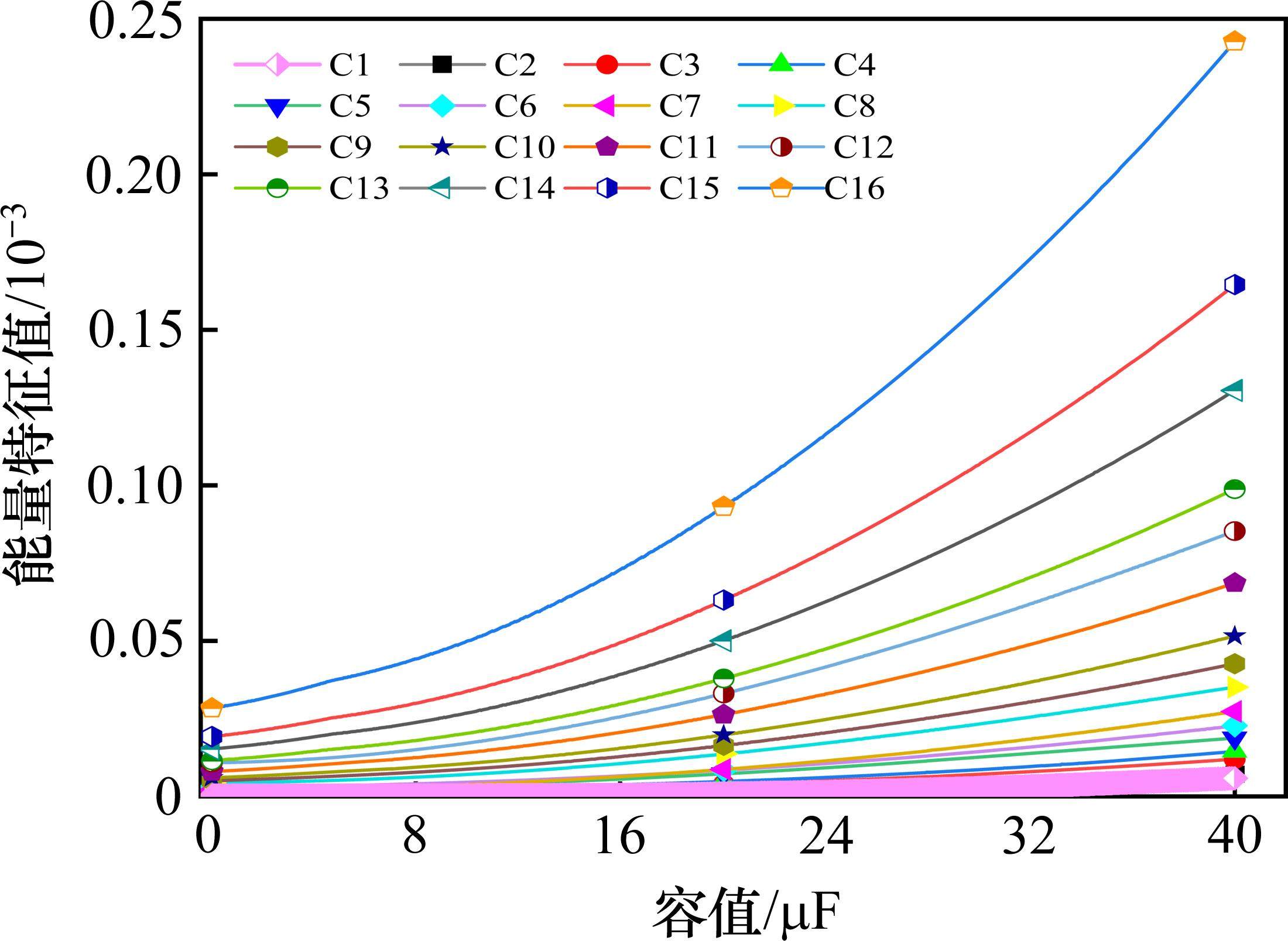
如图8所示,区段内补偿电容的能量特征值与其容值大小呈现类似正比的关系,通过感应电压数据进行容值估计与故障识别,进而精确判断两者的关系,分别将16个电容能量曲线进行线性拟合,指数拟合与多项式拟合,结果如表3所示。
| 拟合方式 | 函数形式 | R-square拟合优度 |
|---|---|---|
| 指数 | 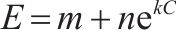 | 0.802 3 |
| 线性 | 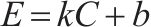 | 0.965 9 |
| 多项式 | 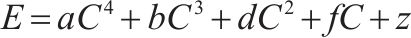 | 0.999 2 |
如表3中结果可知,多项式拟合的结果最优,所以得到能量值与容值的关系表达式,其中a、b、d、f、z均为多项式拟合的参数:
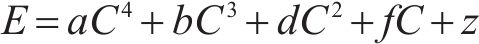
综上,在已知补偿电容数量与其在区段中位置的情况下,即可利用式(12)对感应电压数据进行区段中每一个补偿电容的容值估计与故障识别。
4 现场数据检验
京广高速中某一段轨道电路经过工作人员实际勘测后,得知C10电容容值下降至10 μF,其他电容容值均在正常范围内无故障。同时检测车运行并采集到的归一化感应电压曲线如图9所示。利用图9中的真实数据曲线对本文方法进行验证,对于区段中单一的补偿电容故障,首先利用区段长度进行补偿电容的区段分割,然后从靠近发送端的电容开始对每个电容依次求取VMD分解后的小区段能量特征值,均代入相应的容值能量关系拟合曲线中,直到有电容求出来的容值超出了5%这一正常范围内则可以判断该电容发生了容值下降故障[20]。
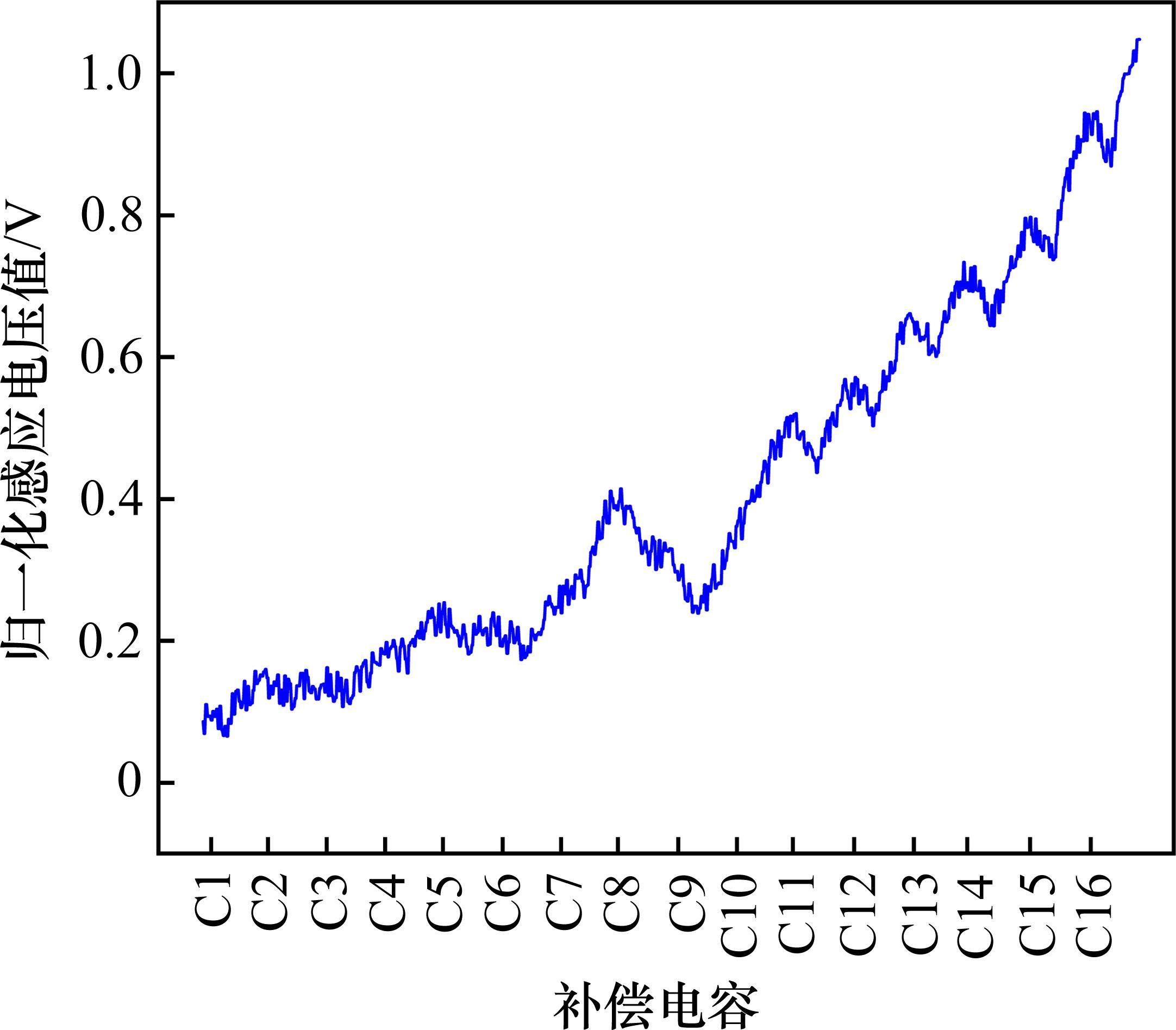
实际计算后,发现C10的特征值为0.01,所对应的容值是10.9 μF,说明C10发生了容值下降故障,需要及时更换。同时容值估计出的容值与人工现场测量的绝对误差仅为0.9 μF,也没有出现误判其他电容的情况,故说明本文提出算法可以有效地识别到区段中故障电容,并可以估计其容值的大小。
随后为了验证本文提出方法的普遍性与有效性,选取轨道检测车检测并经过人工现场勘察的30个发生单一补偿电容容值下降故障的区段,共480个电容,其中包括30个故障电容。利用此数据标明序号后对本文方法进行验证。结果如图10所示。
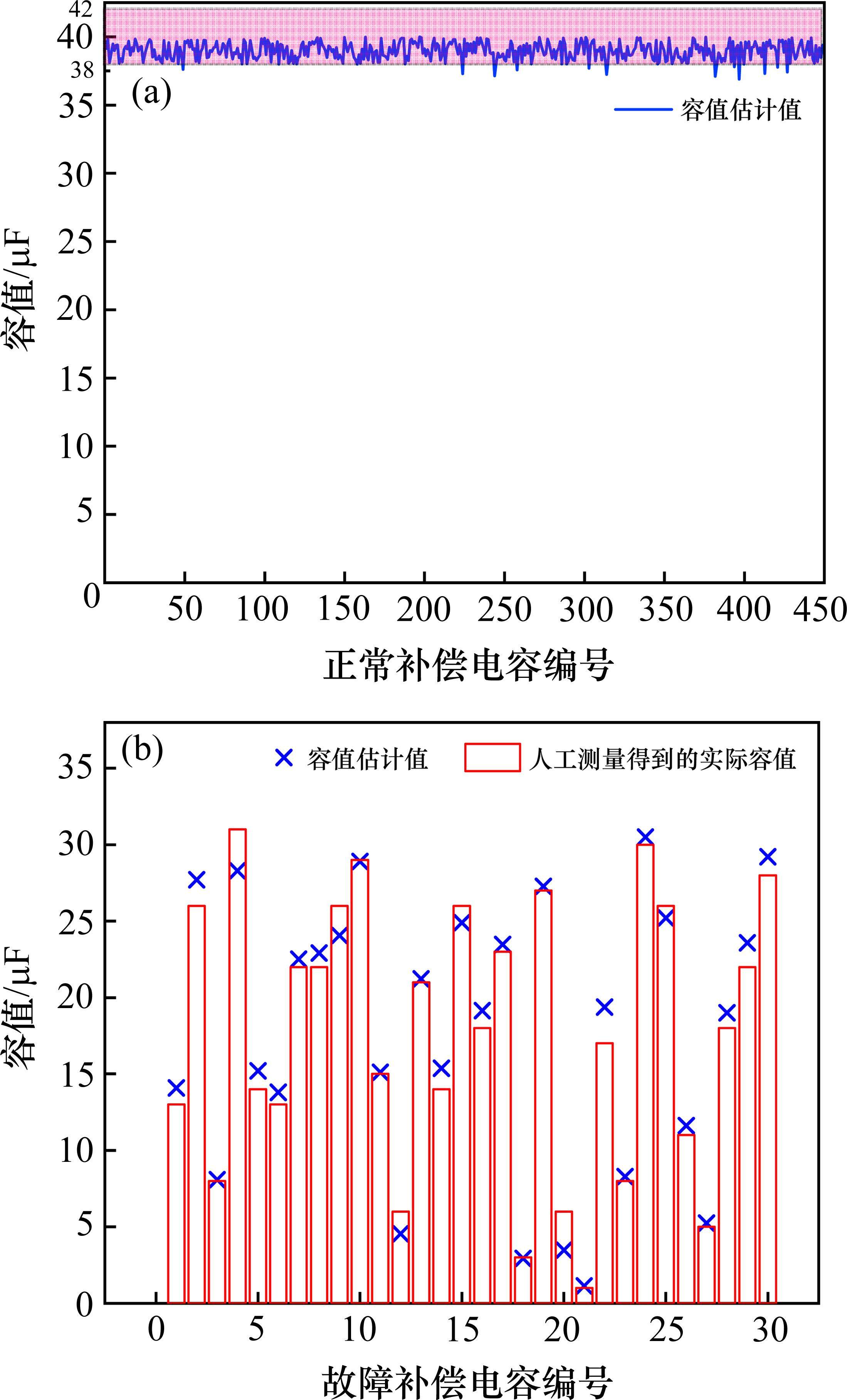
本文提出的容值估计方法在估计现场正常的电容数据时,绝大多数没有超过国铁集团规定的上下5%的范围;且对于故障的电容数据,本文算法也完成了区段中补偿电容的精确识别,即可以精准识别出具体是哪个补偿电容发生了容值下降,其中有16个补偿电容容值下降超过一半,需要及时更换。此外,在估计故障电容容值时,估计值的最大误差仅为2.7 μF,识别故障准确率为96.6%。此外,在估计故障电容容值时,造成误差的原因有可能是检测车获得的数据与人工检测获得的数据有一定的时间误差,检测车数据普遍比人工检测提前一段时间。因此本文算法在面对区段中单一补偿电容的容值下降情况时有一定的实际意义,可以为现场补偿电容的故障识别提供参考。
5 结论
1) 为满足“十四五”规划中提出的安全发展要求,以补偿电容为研究对象,基于传输线理论与电磁场理论建立了等效四端网络与有限元联合仿真模型。成功模拟了检测车这一技术环境下的感应电压采集过程,并获得了较为准确的仿真数据。
2) 利用轮盘赌与拥挤机制改进了DBO优化算法,相比于标准DBO优化算法更具有鲁棒性,适用范围更加广泛,寻优能力更强,收敛速度更快。
3) 提出一种较为适宜的“相关性中心频率比”适应度函数,利用此适应度函数经IDBO优化后得到的VMD参数可以很好地对仿真数据进行分解,提取能量特征后建立了区段中每个补偿电容能量特征与容值的回归模型,并以此给出了容值估计公式。利用同等类型的真实区段数据进行验证后结果表明,本文方法可以在补偿电容故障的区段中精确估计容值并识别出故障电容,误差可以保持在2.7 μF以下,故障电容识别准确率达到96.6%,为现场中的补偿电容的状态监测与故障识别提供了一种较为可靠的方法参考。
王世林,王钟锐,陈光武等.基于参数优化的JTC补偿电容容值估计与故障识别[J].铁道科学与工程学报,2025,22(02):909-920.
WANG Shilin,WANG Zhongrui,CHEN Guangwu,et al.Fault detection and compensation capacitor capacity estimation in JTC based on parameter-optimized variational mode decomposition[J].Journal of Railway Science and Engineering,2025,22(02):909-920.

