在土木工程领域,有限元技术在静力学分析、动力学响应预测以及构件设计优化等方面得到了广泛应用。采用有限元技术精细模拟结构的材料属性、结构响应以及施工条件,对建筑结构的性能进行全面评估,可极大地提高工程设计的可靠性和效率。然而,在实际工程中,结构连接的简化、材料参数的不确定性以及施工中的偏差等均对初始有限元模型的准确度产生影响,特别是对于复杂结构,如混塔式风力机塔筒,初始有限元模型无法准确捕捉到结构的真实特性[1-2],因此,为了提高模型的准确度,确保设计的可靠性和结构的安全性,必须对初始有限元模型进行修正。
根据待修正参数的处理方式,有限元修正方法可分为确定性和不确定性2种。确定性方法将待修正参数视为精确数值,忽略了参数本身的不确定性;而不确定性方法考虑参数的概率特性,更全面地反映不确定性因素,克服了确定性方法的局限性。基于贝叶斯理论的修正方法是一种较为普遍的不确定性模型修正手段[3-4]。BECK等[5]将贝叶斯理论应用于土木工程模型修正,简化后验概率密度函数为正态分布,为模型修正提供了理论依据;CHEUNG等[6]提出了Markov Chain Monte Carlo(MCMC)算法,并通过双自由度系统模型验证了其有效性;易伟建等[7]采用MH-MCMC算法成功识别四层实验室结构损伤,证实了贝叶斯方法的应用价值。这些方法为混塔式风力机塔筒有限元模型的修正提供了有效的途径。
调整和优化模型的参数是提高模型准确度的关键。MH算法被广泛用于后验概率密度函数的估算[8],该算法通过构造马尔可夫链,生成随机样本,并采用逐步迭代的方式逐渐逼近目标概率分布。然而,MH算法在循环计算过程中可能会遇到“停滞”问题[9],这可能导致所生成的样本集无法真实反映修正参数的概率密度分布。此外,MH算法在每一步迭代中都需要调用复杂的有限元模型进行计算,使修正过程的耗时显著增加。
针对上述问题,本文提出了一种基于代理模型与自适应调整方差的混塔式风力机塔筒有限元模型修正方法。该方法通过动态调整MH算法中的建议分布方差优化样本点在解空间中的布局,进而提升模型修正的精确度。同时,引入了Kriging代理模型,在迭代过程中替代有限元模型,从而有效提高计算效率,并结合混塔式风力机塔筒工程案例对其进行了分析与验证。
1 模型建立及误差分析
1.1 模型概况
以位于吉林省白城市通榆县的一处实际混塔式风力机(如图1(a)所示)为研究对象,建立了该混塔式风力机塔筒的有限元分析模型(如图1(b)所示)。塔筒结构参数见表1。为确保模拟的准确性,选择六面体实体单元C3D8R模拟混凝土、螺栓和螺母;钢筋与预应力钢筋采用三维桁架单元T3D2进行模拟,钢塔截面选用壳单元S4R进行模拟,并将机舱和叶片的质量视为施加在钢塔顶部的荷载。

| 混塔式风电机 | 叶轮、轮毂和机舱质量/t | 底座材料 | 混凝土塔段 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 额定功率/MW | 叶片数/个 | 叶片直径/m | 轮毂高 度/m | 额定转速/(r·min-1) | 高度/m | 数量/节 | 顶部直径/m | 底部直径/m | 材料 | ||
| 5 | 3 | 193 | 160 | 8 | 250 | C45 | 112.05 | 31 | 4.74 | 8.25 | C65 |
| 过渡段 | 钢塔段 | 预应力索 | 螺栓和螺母 | ||||||||
| 高度/m | 材料 | 高度/m | 顶部直 径/m | 底部直径/m | 结构阻尼比 | 材料 | 数量/个 | 截面面积/mm2 | 材料 | 螺纹规格 | 性能 等级 |
| 1.53 | Q355 | 43.8 | 3.38 | 4.49 | 2% | Q355 | 36 | 140 | 钢绞线 | M56 | 10.9 |
1.2 模型误差分析
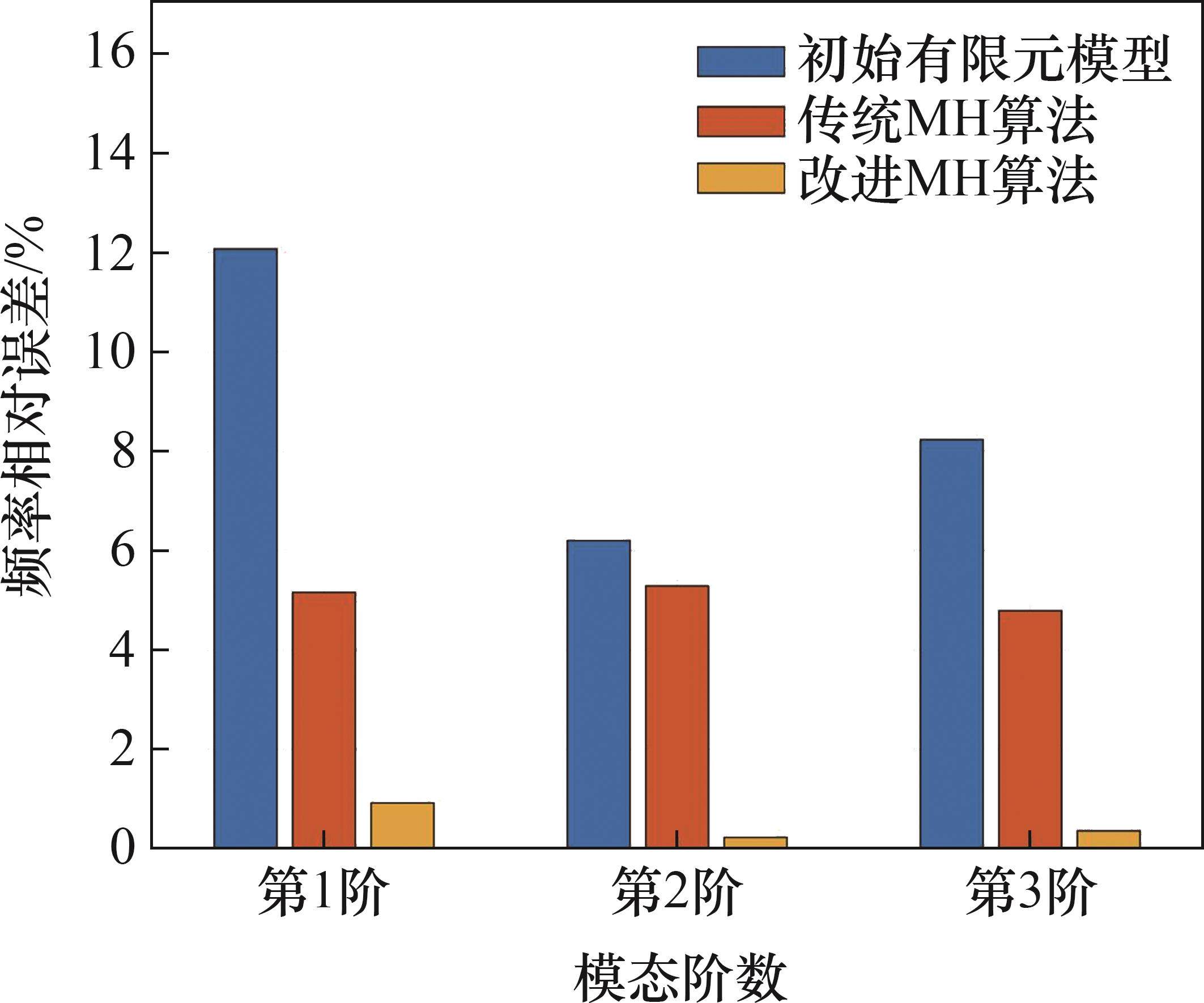
混塔式风力机塔筒的初始有限元模型与实际模型的前三阶频率的相对误差分别为12.07%、6.20%和8.23%,两者之间存在显著差异。为了确保模型的精确性和可靠性,必须对初始有限元模型进行修正。
2 有限元模型修正理论
2.1 贝叶斯理论
贝叶斯理论在模型修正领域得到了广泛应用,特别是在描述随机变量的条件概率和边缘概率密度方面发挥着至关重要的作用[10-12]。对于待修正参数的后验概率密度函数,可以用贝叶斯公式进行表述:
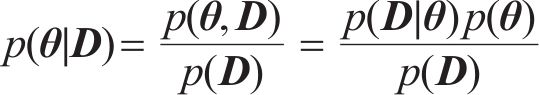
式中: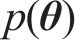
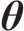
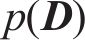

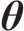
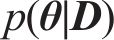
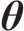
张建新[13]指出,当均值和方差不明确时,若已知参数的取值范围,则先验分布会呈现出均匀分布的特征。因此,可以将先验概率密度函数视作常数,式(1)可表述为
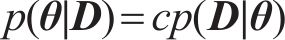
式中: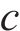
2.2 灵敏度分析
在修正塔筒模型前,要对模型的各个参数进行灵敏度分析[14-15],从而筛选并调整关键参数以优化模型。塔筒模型参数的灵敏度表达式为
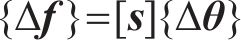
式中: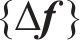

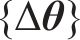
由式(3)可知,结构中j行、l列的参数的第i阶灵敏度矩阵可以写成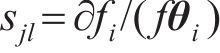
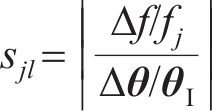
式中: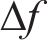
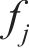
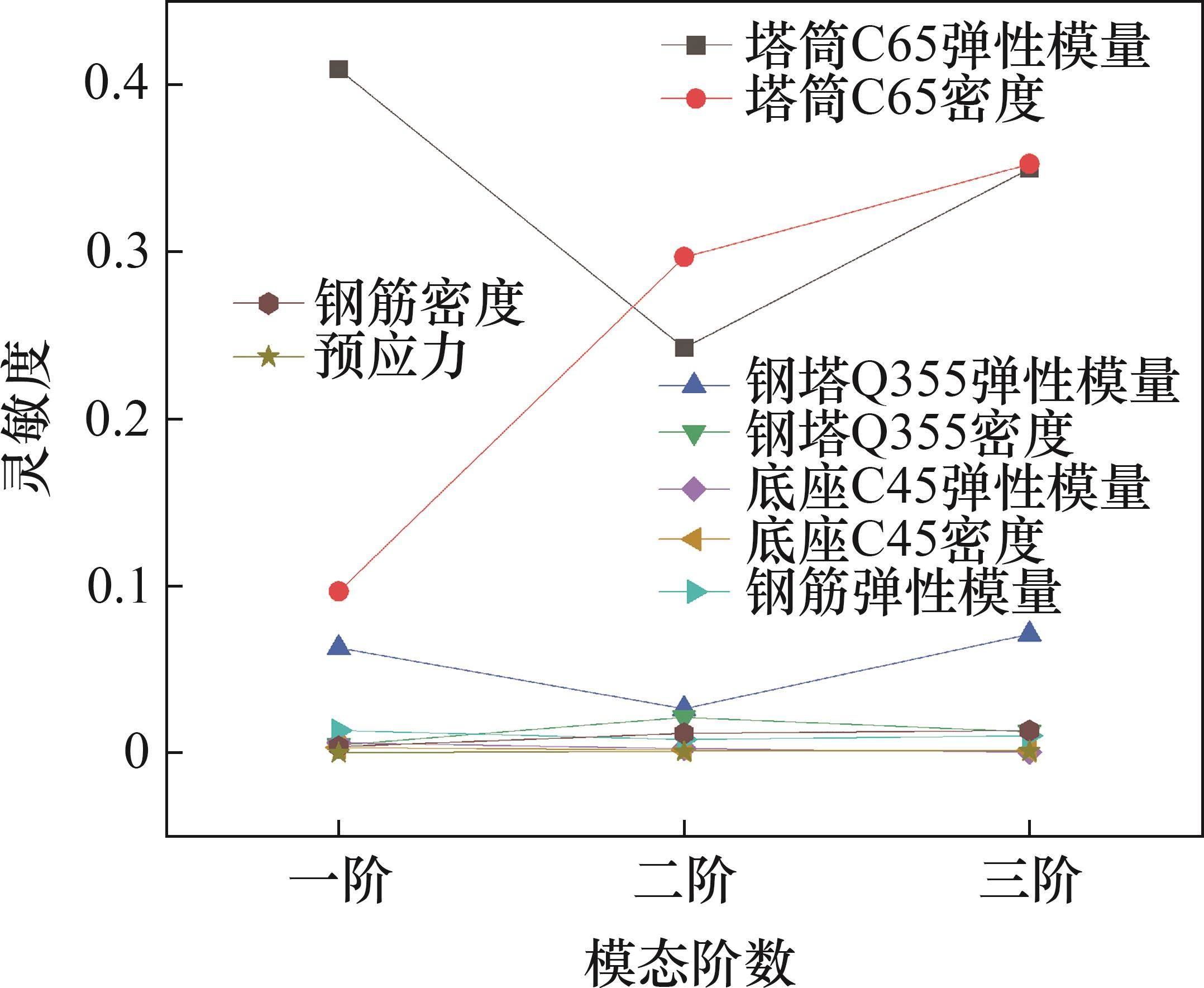
计算9个塔筒参数的灵敏度,结果如图2所示。从图2可见:塔筒C65混凝土的弹性模量和密度对整体结构频率的影响最为显著。因此,确定C65混凝土的弹性模量和密度作为修正参数。根据统计学原理,假设C65混凝土弹性模量和密度的先验分布均服从高斯分布。为了更清晰地反映参数调整前后的变动情况,采用修正前后参数的比值来描述待修正参数的变化情况。
2.3 构建目标函数
在混塔式风力机塔筒模型修正过程中,首先要构建待修正参数的目标函数[16],该步骤的核心在于推导出相应的似然函数。鉴于结构模态参数的独立性,前几阶模态的条件概率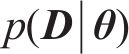
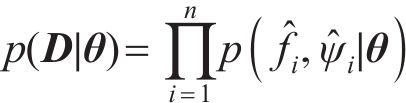
式中: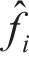
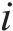
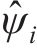
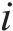
模态置信度准则[17]能够精准反映塔筒整体振型之间的关联性。模态振型的相对误差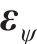
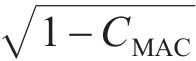
对于第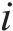
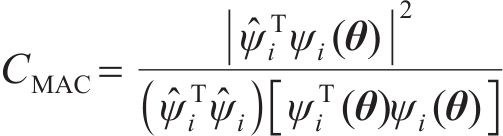
式中: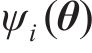
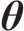
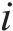
各模态频率间的相对误差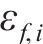
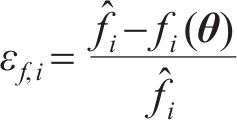
式中: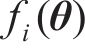
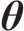
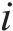
若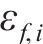
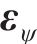
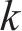
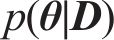
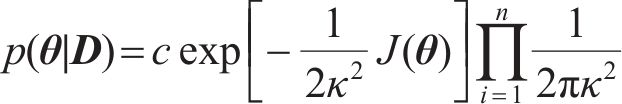
其中,
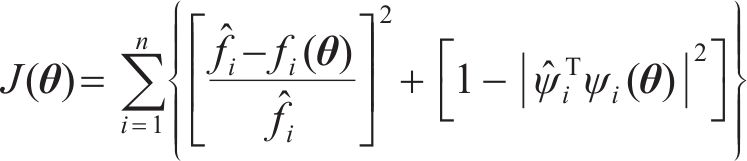
LAM等[20]指出,为确保修正结果的精确性,应对后验概率密度函数中的方差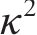
3 基于代理模型的自适应模型修正算法
在传统MH算法中,建议分布的方差不变,导致模型修正过程中出现接受率过低或过高的问题[21]。为解决此问题,本文提出一种自适应调整建议分布方差的方法,通过不断优化建议分布的方差来提升模型修正精度,即当实际接受率高于目标接受率时,增大建议分布的方差,反之,则减小方差;同时,采用代理模型替代有限元模型进行计算,以提高模型修正效率。
3.1 自适应MH抽样算法
由于后验概率分布具有高维度和非标准性的特点,通常采用MCMC算法作为求解策略,其核心在于通过抽样生成一系列在后验分布上表现稳定的样本点,利用这些样本点来准确估算待修正参数。MCMC算法中的MH抽样方法[22]通过构造后验分布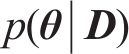
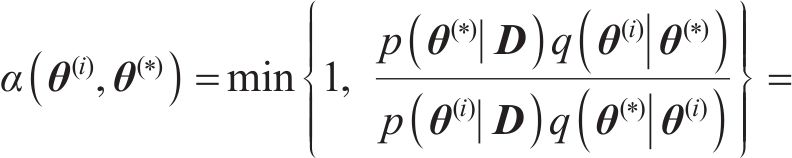
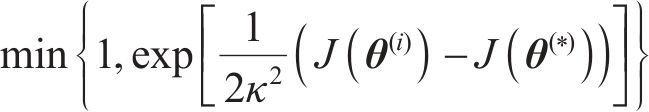
式中: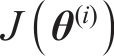
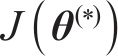
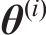
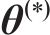
3.2 Kriging代理模型
通过采样代理模型[23]来替代重复的有限元计算可以显著提高计算效率。目前主要的代理模型为响应面代理模型[24]、支持向量机代理模型[25]、人工神经网络代理模型[26]、径向基函数代理模型[27]以及Kriging代理模型[28-29]。本文基于文献对各类代理模型的精度、计算效率及鲁棒性等进行综合评估,选用Kriging模型作为模型修正的代理模型。具体步骤如下:首先,采用MATLAB软件中的Dace工具箱对选取的样本点及其响应进行训练,以构建Kriging模型;然后,将训练好的代理模型融入自适应MH修正算法中。
3.3 拉丁超立方(LHS)采样
在训练代理模型前,需要通过抽样来选择样本点,以保证样本数量最小化,并最大化获取设计空间的信息量[30-31]。拉丁超立方采样(LHS)方法将设计空间划分为多个相同概率的子区间,并在每个子区间内采样,在满足预期精度的同时大幅度减小所需的采样点数量,从而有效缩短构建代理模型的时间。
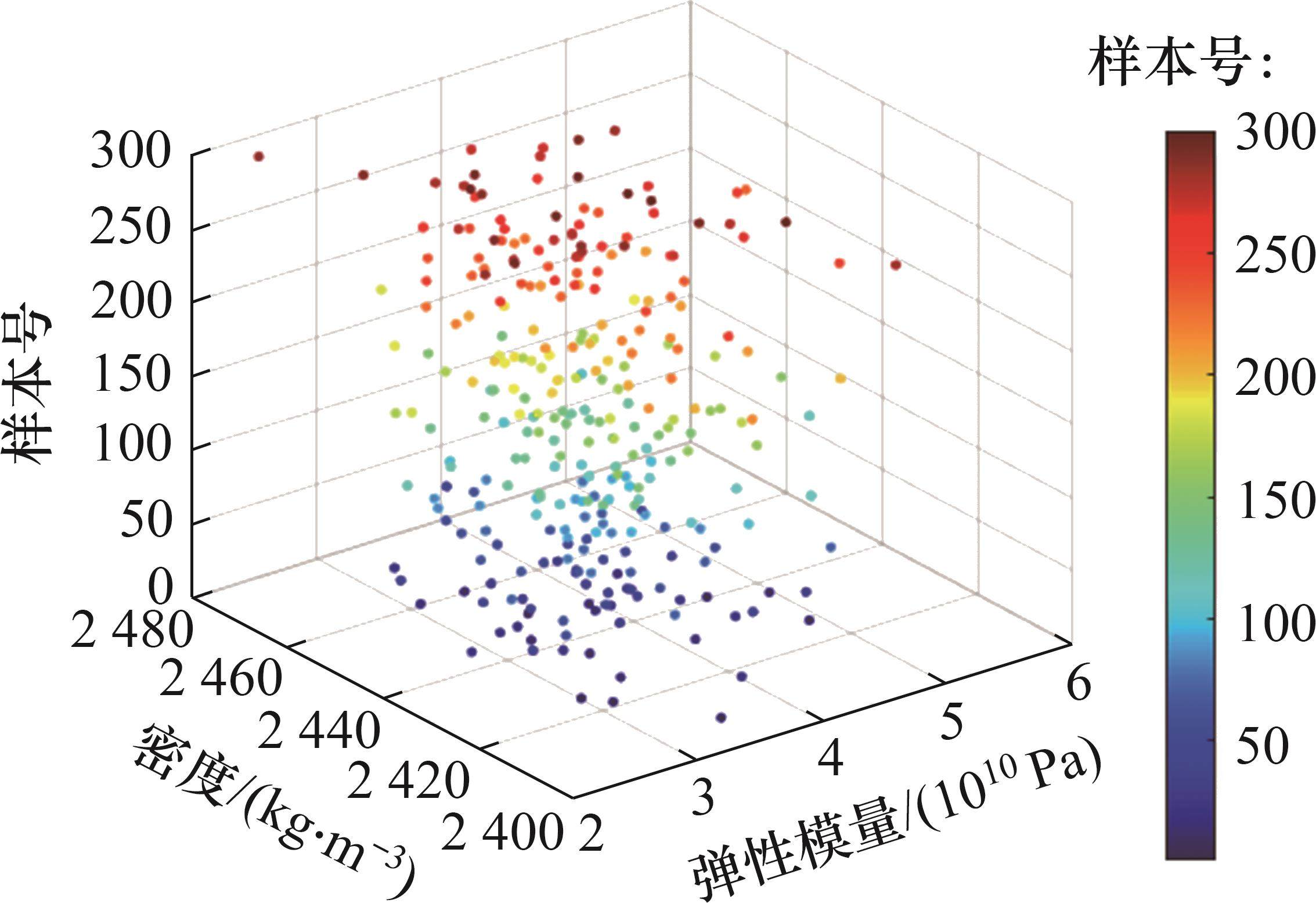
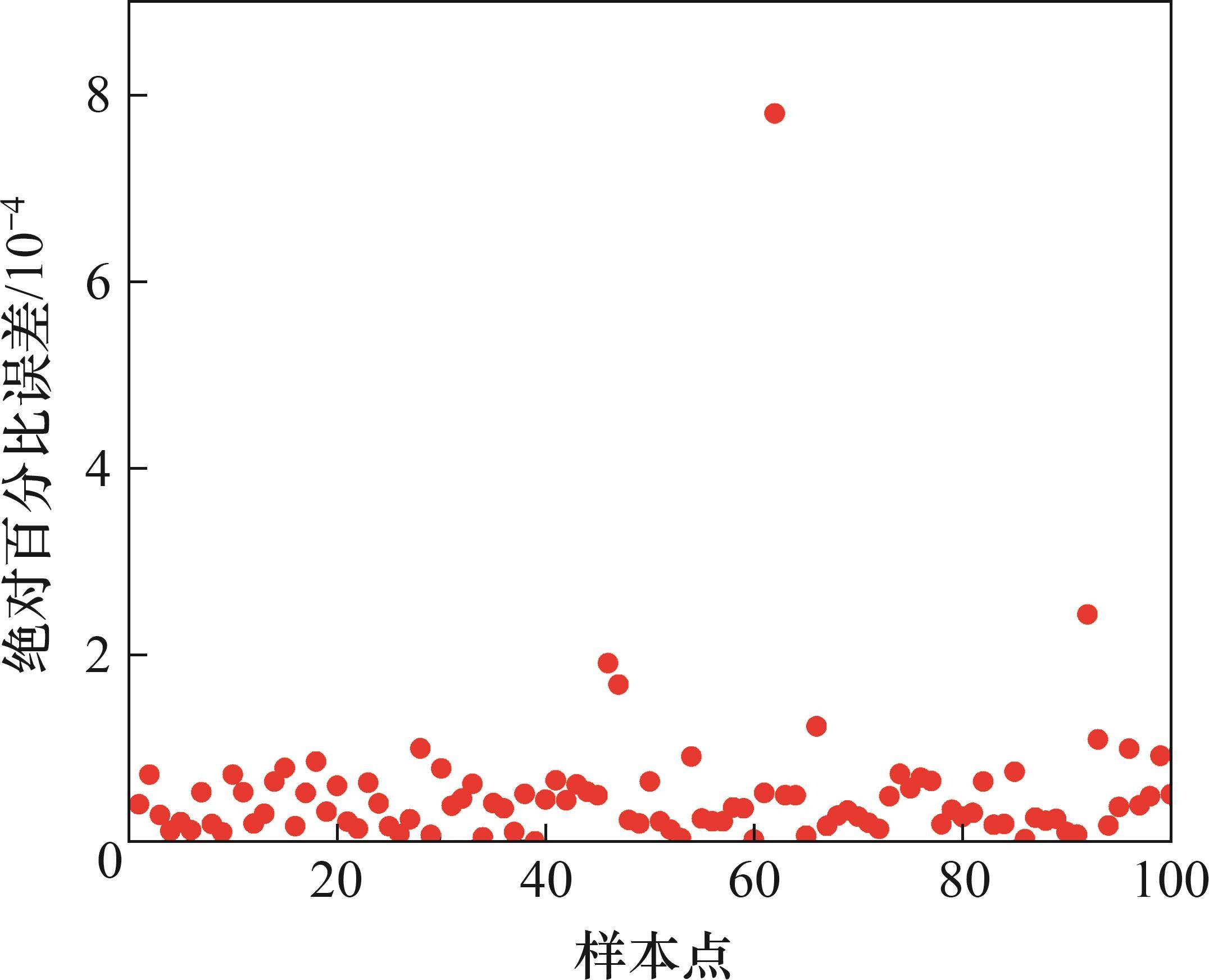
采用LHS抽样方法抽取300组样本点(如图3所示),并在有限元模型中计算这些样本点的模态参数。随后,对代理模型进行训练,选用其中的200组样本及其模态参数作为训练样本,并构建了Kriging模型,剩余的100组样本作为检验样本。样本点的绝对百分比误差如图4所示。从图4可见:样本的绝对百分比误差均低于0.000 8。经过训练得到的Kriging模型误差极小,精度极高。因此,该Kriging模型可以有效替代塔筒有限元模型模态参数的计算。
3.4 基于Python的Matlab-Abaqus交互访问
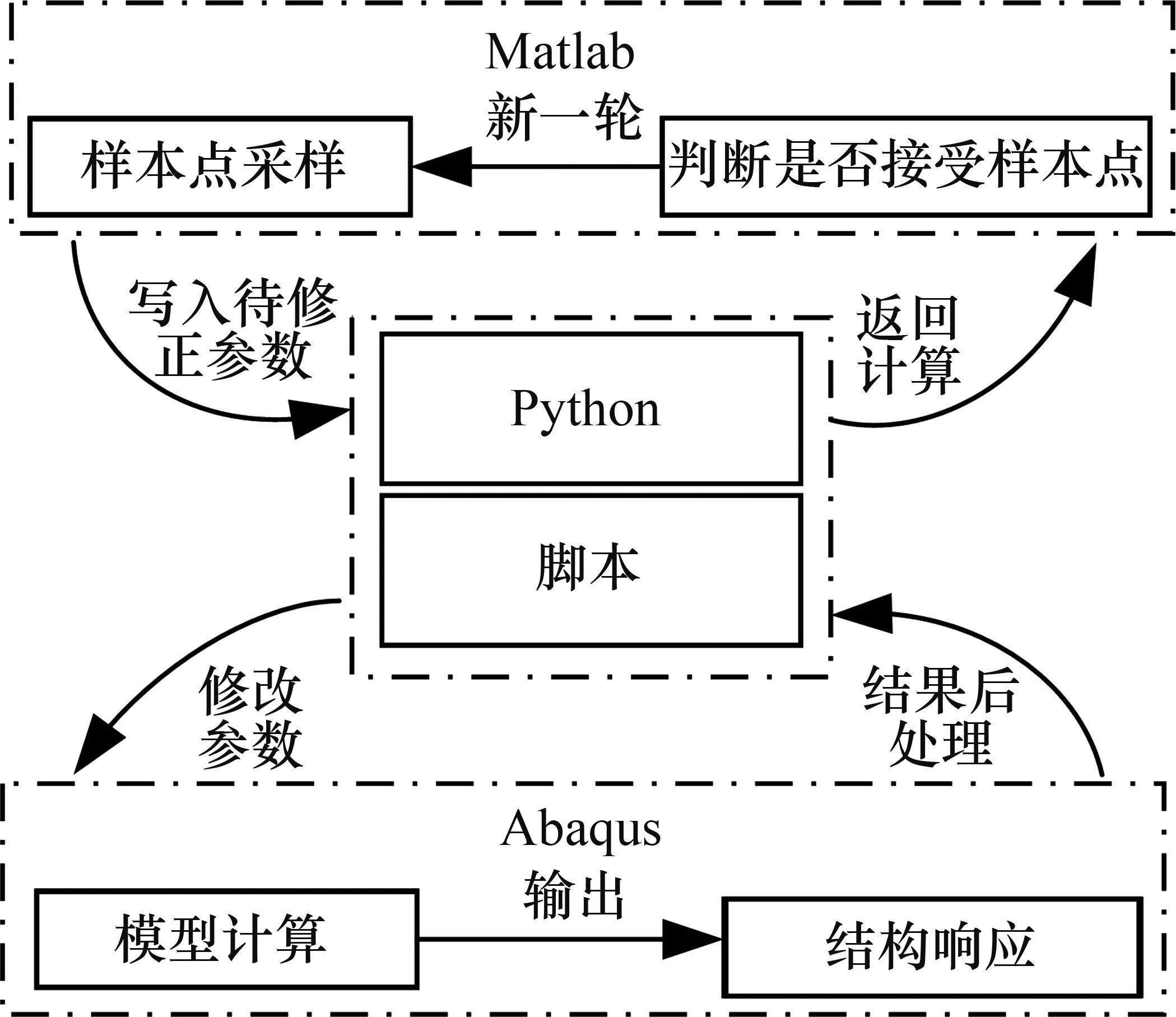
将抽取的样本点批量导入塔筒有限元模型中,以获取每组样本点对应的模态参数。本文开发了Python脚本用于调用Matlab中的待修正参数,可同时向Abaqus提交3组样本点,实现了模型参数的自动调整,并将样本点对应的结构响应导入Matlab中,简化了模型修正流程,将计算时间降低了1/3以上。交互访问过程的示意图如图5所示。
3.5 改进后有限元模型修正算法
采用Kriging模型及自适应调整方差的方法对传统MH抽样算法进行优化,模型修正算法流程如图6所示,其主要步骤如下。
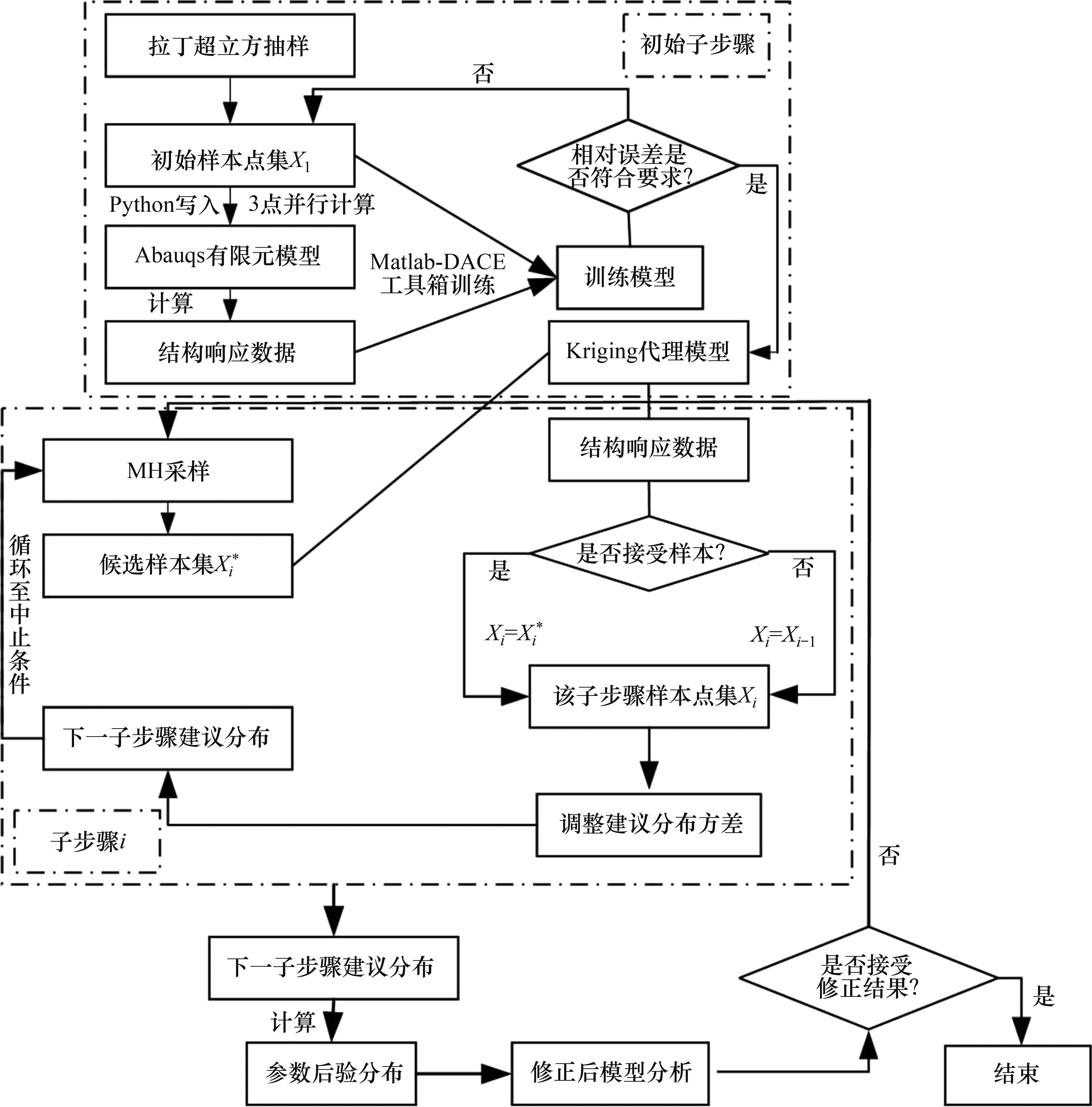
1) 采用LHS抽样方法,生成训练模型所需的样本点;随后,利用Python脚本将样本点输入有限元模型中进行计算,并将计算结果导出用于训练Kriging模型。
2) 利用Dace工具箱,采用Kriging模型对生成的样本点及其响应进行训练;训练完成后,采用绝对百分比误差来评估代理模型的精确度。
3) 应用优化后的Kriging模型进行计算,输出塔筒的模态参数,显著缩短了模型修正时间。
4) 在MH抽样过程中,将建议分布的方差设置为可变参数,使其能够基于每次迭代过程中的接受率进行自适应调整,以提高抽样的效率和准确性。
4 混塔式风力机塔筒模型修正案例
为了验证改进后的MH算法的准确度,分别采用传统MH算法及改进后的MH算法对塔筒的有限元模型进行校正,2种方法的迭代终止条件均设定为完成3 000步迭代。在有限元计算过程中,单次迭代的计算时间约为20 min,因此,完成3 000次迭代需要约1 000 h。采用Kriging模型只需训练300个样本点,相当于只执行300次有限元计算,并且可以同时处理3组样本点,因此,Kriging模型的计算时间仅为传统算法的1/30,计算效率显著提高。
传统MH算法与改进后的MH算法所生成的马尔可夫链如图7所示。从图7可见:传统MH算法在抽样过程中多次出现“停滞”问题,尤其是在 1 500~2 700步出现了长时间停滞,进而影响计算精度;而改进后的MH算法在抽样过程中几乎没有出现“停滞”现象,展示了其优越的遍历性能。
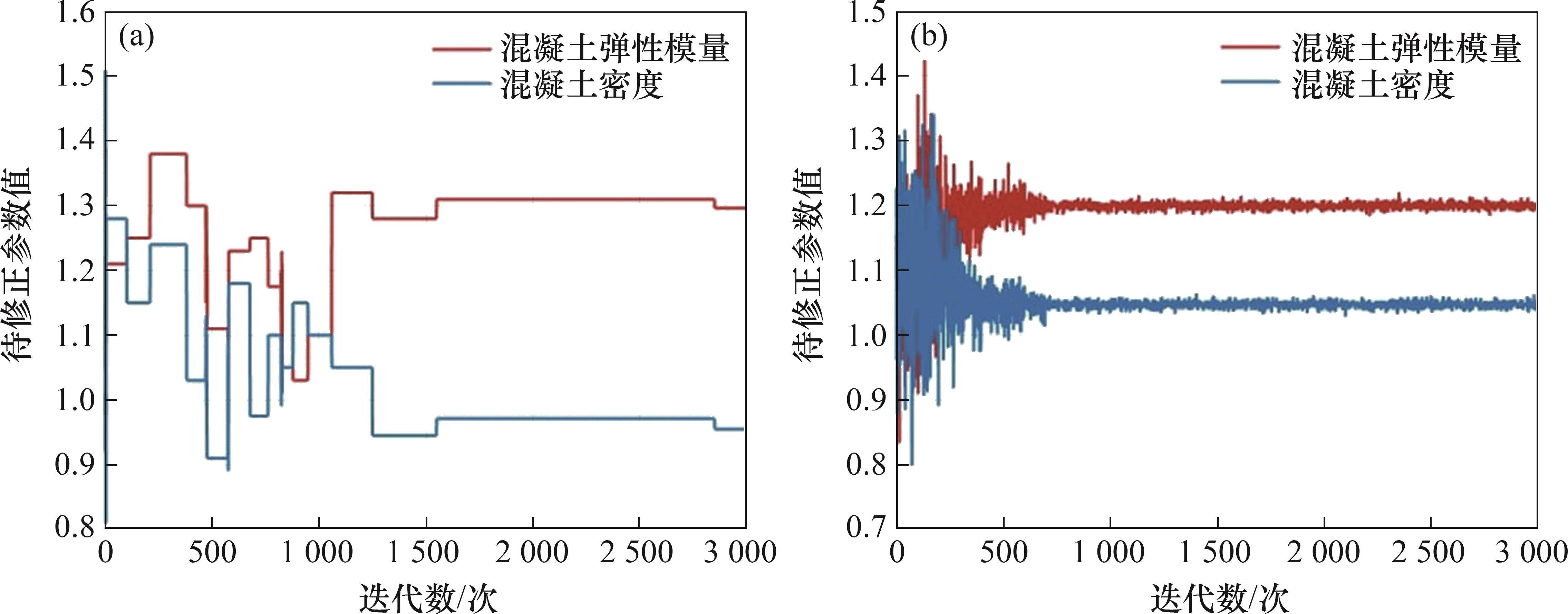
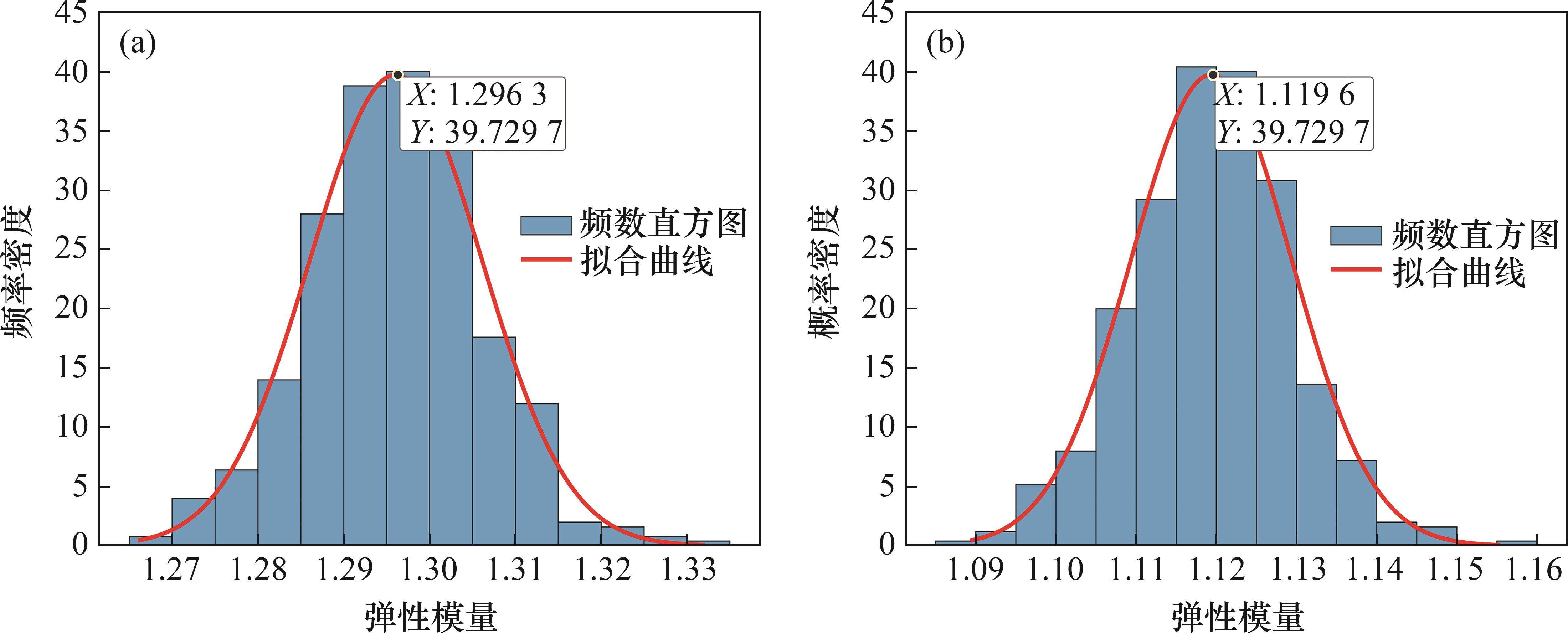
根据生成的马尔科夫链,分别提取待修正参数混凝土弹性模量的第2 500步至第3 000步的抽样样本绘制直方图,结果如图8所示。根据模态频率误差公式计算通过不同方法获取的后验均值,并进行对比分析,结果如图9所示。表2所示为不同算法获得的待修正参数比值。
| 修正参数 | 传统MH算法 | 改进MH算法 |
|---|---|---|
| 混凝土弹性模量 | 1.296 3 | 1.199 6 |
| 混凝土密度 | 0.954 7 | 1.046 8 |
从图8可见:修正后的参数后验分布近似呈现出高斯分布的特性,且选择高斯分布最大值作为修正结果。
从表2可见:修正后混凝土弹性模量提升了20%~30%。目前规范中采用的混凝土弹性模量简化计算公式可能过于保守,混凝土构件的实际弹性模量往往大于公式计算的结果。同时,修正前后混凝土密度变化较小,表明混凝土密度对混塔式风力机频率的影响较小。因此,在实际工程中需要重点修正的参数为混凝土的弹性模量。
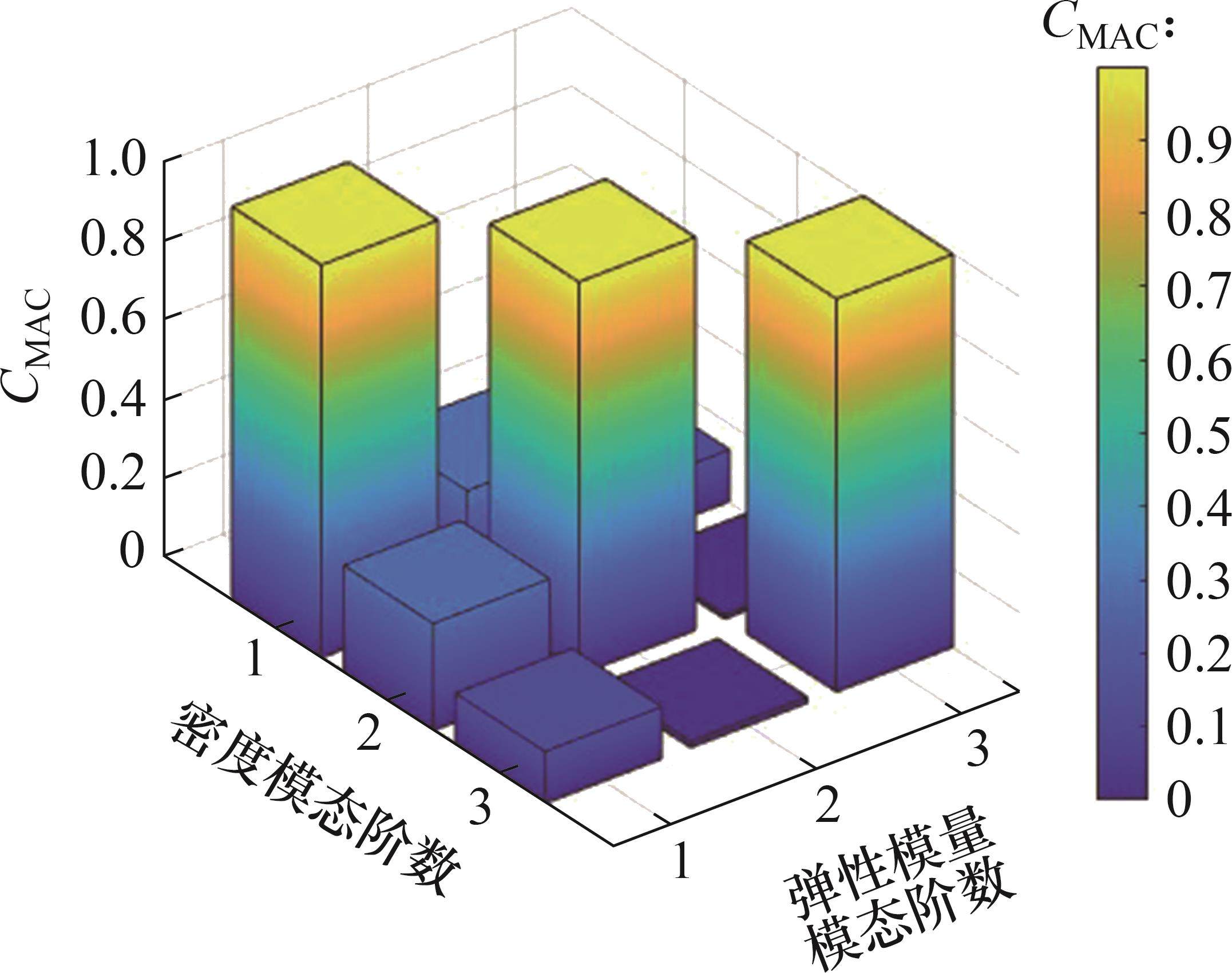
以后验均值修正的参数构建一个与实际塔筒结构更为吻合的有限元模型。从图9可见:在前三阶频率模态中,修正模型的频率相对误差小于未修正模型的相对误差;在第一阶频率模态中,未修正模型的相对误差大于15%,而采用传统MH算法和改进MH算法修正后的模型频率相对误差分别约为5%和1%,这表明2种修正方法均显著提高了模型的准确性,尤其是改进的MH算法效果更佳;在第二阶频率模态中,采用传统MH算法修正后,频率相对误差变化较小,而改进MH算法将误差大幅减至约0.2%,表明改进MH算法在减小频率误差方面具有明显优势。综上可知,相较于传统MH算法,改进的MH算法在显著提高了模型频率的准确性。修正后模型的模态置信度CMAC如图10所示。从图10可见,模型修正前后,前三阶振型的CMAC均接近1,这表明调整C65混凝土的弹性模量和密度虽然改变了混凝土塔段的整体刚度,但对归一化后振型的影响较小。
5 结论
1) 针对采用传统MH算法存在的“停滞”问题以及抽样效率低的问题,提出一种结合自适应调整MH抽样中建议分布方差的Kriging代理模型的方法修正混塔式风力机模型参数。该方法通过持续优化MH算法的建议分布,使生成的样本点逐步逼近真实的概率密度分布。
2) Kriging代理模型极大地提升了修正效率。
3) 在混塔式风力机塔筒模型修正过程中,调整混凝土的弹性模量和密度对归一化后的结构振型影响并不显著。
4) 后续研究应针对高维待修正参数进行有限元模型修正,评估该算法的精度,并研究更多的频率模态对模型修正准确性的影响,以提高模型修正方法的全面性和可靠性。
唐伟伟, 徐军, 王丹, 等. 混塔式风力机塔筒有限元模型修正研究[J]. 中南大学学报(自然科学版), 2025, 56(2): 651-659.
TANG Weiwei, XU Jun, WANG Dan, et al. Finite element model updating of steel-concrete wind turbine tower[J]. Journal of Central South University(Science and Technology), 2025, 56(2): 651-659.

