金属增材制造技术[1-8]通过激光、电子束等高能热束逐层堆积材料,可实现脱离模具制造三维实体零件,在工程领域获得了广泛关注。其中基于同轴送粉的激光立体成形(Laser solid forming, LSF)技术[9-11]具有快速自由成形、材料利用率高的优点,成为金属零部件增材制造工艺的常用加工方法。但目前通过LSF打印出高质量、高性能的零部件仍是一项挑战,这是由于不匹配的工艺参数组合会导致出现多种缺陷(裂纹、气孔、基体变形等)。采用试错的方法进行工艺参数选择时存在速度慢、成本高的缺点。结合数值方法进行工艺优化将带来显著的效益,而通过仿真技术实现工艺优化过程也存在两方面的问题,一方面,数值方法能否准确模拟成型过程中产生的缺陷至关重要;另一方面,优化过程中产生的大量仿真计算开销也亟待解决。
增材制造过程比较复杂,涉及传质、传热、相变、晶粒生长等现象的强热流固耦合问题。目前,依据所关注的物理现象和求解问题的尺度不同,数值模拟模型可分为三类:粉末尺度高保真“热-流”耦合模型、基于粉末连续体假设的“热-流”耦合模型和基于连续体假设的热传导模型[12-13]。其中粉末尺度的数值模拟相较于其他方法能从更加细微的角度获得加工中孔隙的分布和形貌,且能较好平衡计算量精度的问题,具有较高的工程应用潜力。国内外学者使用多种计算方法对粉末尺度下的增材制造数值模拟展开研究。YAN等[14]、WANG等[15]结合离散元法(Discrete element method, DEM)模拟与有限体积法(Finite volume method, FVM)模拟金属粉末熔化凝固过程,在多层多道环境下模拟出孔隙的易产生位置。KHAIRALLAH等[16]采用任意拉格朗日-欧拉法(Arbitrary lagrange-euler, ALE)研究了316L不锈钢金属粉末熔化凝固成形过程,揭示了熔池流动、材料飞溅、孔洞形成、粉床剥蚀等现象的物理机理。上述基于网格的计算方法,在计算中需要对变形网格进行规整化,可能带来较大的数值扩散误差。由于不需要高阶插值与网格离散,无网格方法为直接求解热流固耦合问题提供了可能。增材过程中颗粒间的相互作用影响了残余应力、温度分布和缺陷各向异性微观组织的形成,而目前很少有数值研究集中在单个颗粒和颗粒-颗粒界面长度尺度上发生的物理现象。最优运输无网格方法(Optimal transportation meshfree, OTM)是由LI等[17-23]提出的一种基于最优运输理论和局部最大熵插值函数的无网格方法,可以在统一的拉格朗日框架下求解“热-流-固”强耦合模型,结合介观粉末尺度模型与考虑相变的材料模型,可以从粉末尺度直接模拟增材制造过程中带能量耗散的粉末多体动态接触、粉末液化、热力耦合、相变与多相混合等仿真难点问题,准确模拟材料成型过程。
增材制造仿真模型网格规模大多在百万量级且过程涉及热力耦合、相变等复杂现象,导致计算速度缓慢,严重延缓优化周期。基于数据学习的模型[24-28]通过对设计空间中样本点的分析,寻找设计变量和输出性能之间的影响规律,用以代替复杂耗时的数值过程。通过仿真获得样本点训练代理模型,近似构建工艺-性能的关系代替耗时的仿真计算,可有效降低优化过程中大量的仿真时间消耗。
本文探讨采用OTM法结合粉末尺度仿真模型直接整体模拟TC4同轴送粉激光立体成型工艺过程,重点关注打印过程中的孔隙缺陷,并结合代理模型与优化方法建立工艺参数优化策略。
1 粉末尺度工艺过程直接数值模拟
金属增材制造过程是多物理场的复杂强热流固耦合问题,高精度的数值模拟是后续开展工艺参数优化设计的关键。建立粉末尺度仿真模型并采用可以真实反映粉末颗粒与基材强热流固耦合过程的OTM方法,可直接模拟粉末尺度下的成型工艺过程并对结果进行分析。
1.1 OTM计算框架
OTM法是一种基于变分原理,结合最优输运理论(Optimal transportation theory)对时间的离散、物质点(Material point)对空间的离散以及局部最大熵无网格插值函数(Local max-entropy interpolation, LME)的数值求解方法。空间离散与单个时间步长原理如图1所示(空心点表示节点,实心点表示物质点)。整个计算域被离散为节点和物质点,节点上储存位移、速度、加速度和温度,物质点储存应力和应变等信息;计算过程中采用物质点充当积分点,可以有效避免计算结果在拉伸载荷下的不稳定性。
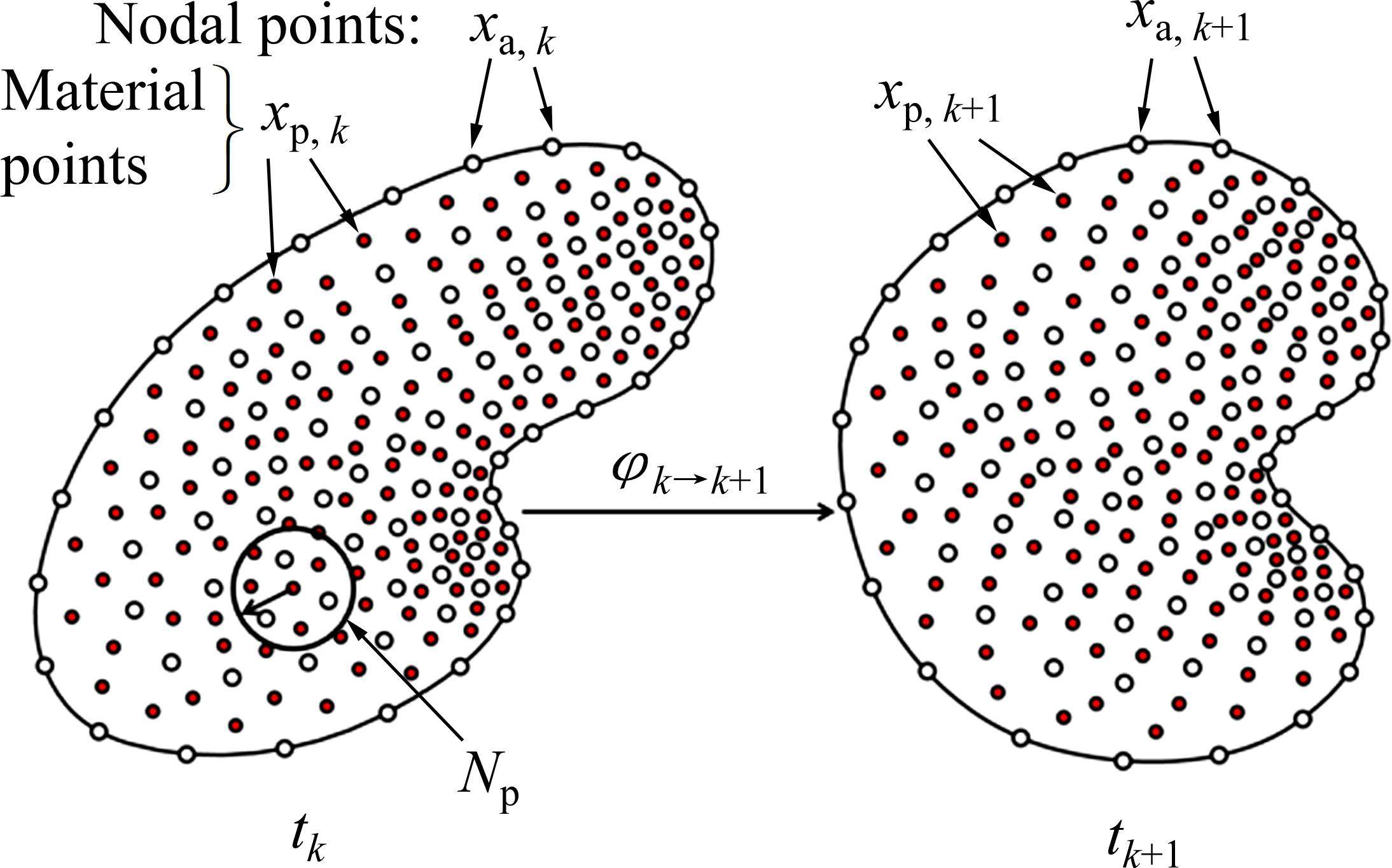
OTM中采用局部最大熵无网格插值函数作为物理场的形函数,解决了传统无网格法难以准确施加位移边界条件的问题,提高了数值解的高效稳定性;采用最优运输理论对时间离散,保证了哈密顿作用量的时间离散形式满足动量守恒条件,且收敛性能得到严格的数学证明[27];采用基于能量释放率的物质点失效方式,能够较好模拟材料的损伤情况,该方式已被证明可收敛到Griffith断裂准则[29]。OTM整体耦合求解方法采用拉格朗日坐标系统一描述固体域与流体域,克服了流固耦合中最困难的统一坐标系问题。同时,流体域与固体域两相界面的平衡与协调将自动满足,无需求解和插值界面信息,这极大地提高了耦合系统求解的精确性与收敛性。动态接触面的检测以及接触力的计算可通过动态调整物质点与节点的连接关系自动进行,没有产生额外的计算成本。使用OTM方法可直接模拟LSF工艺过程中粉末多物态的转化以及熔池内部熔凝过程,精确预测打印的成型结果。
1.2 粉末级工艺数值模型
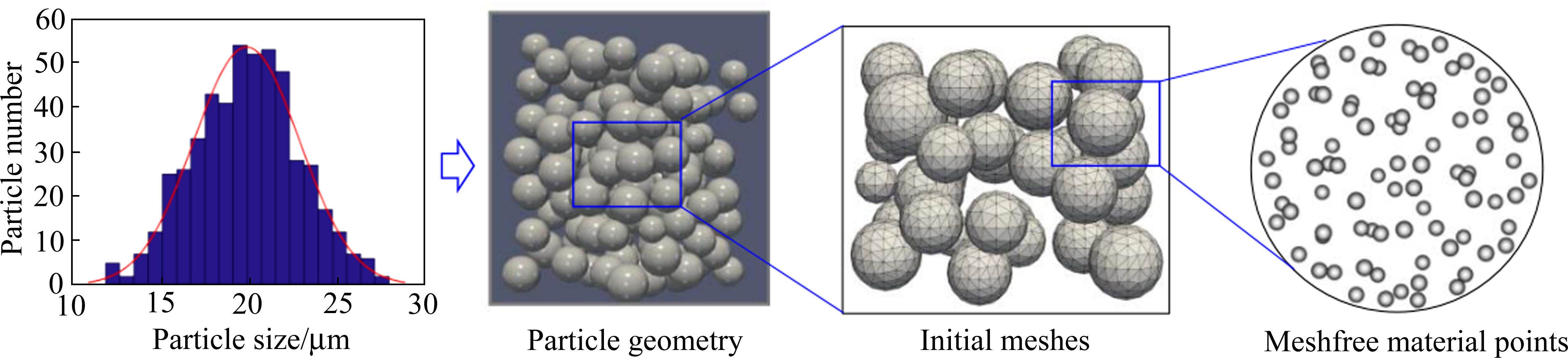
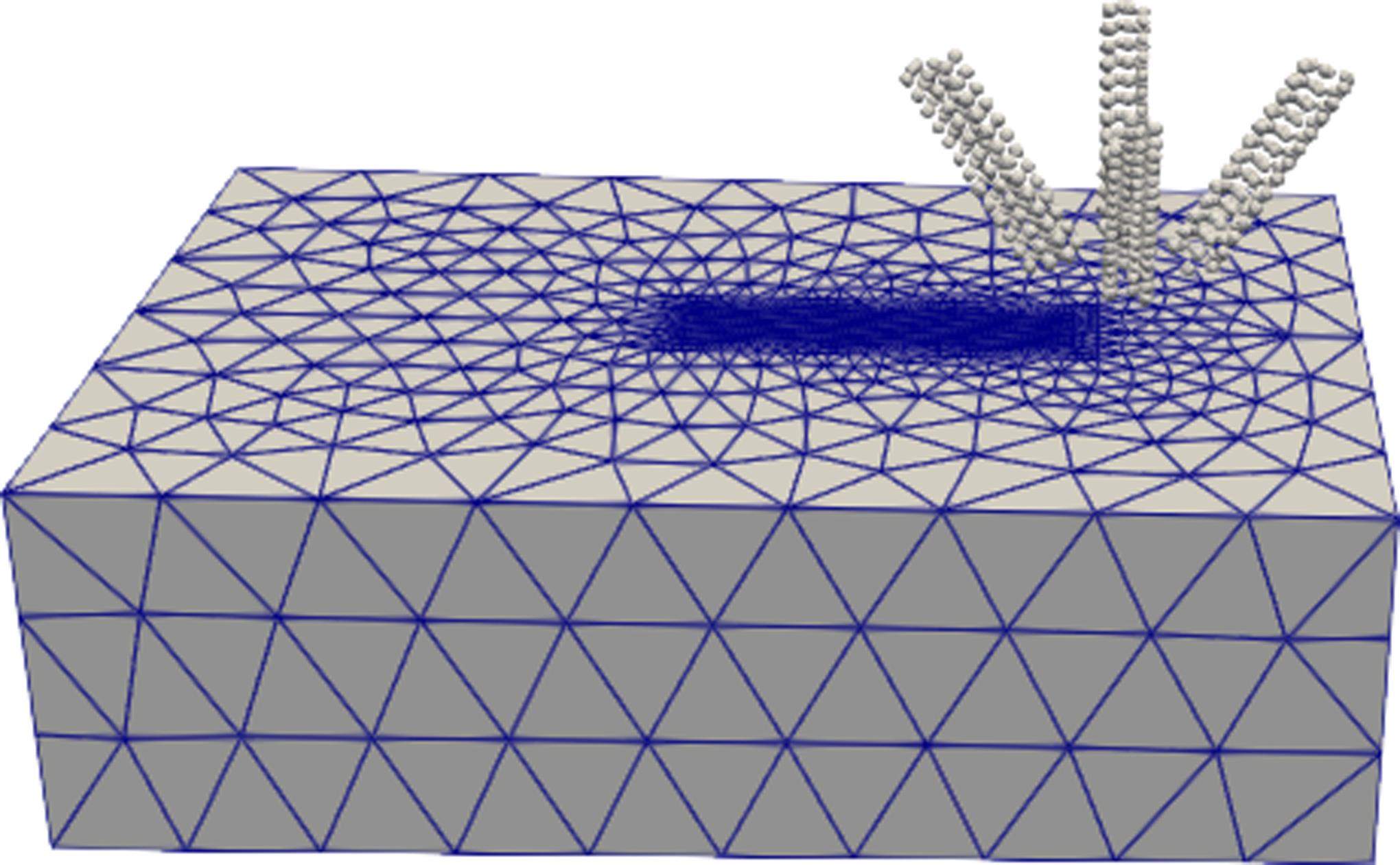
在同轴送粉工艺中,粉末束与激光束同步移动,喷射的粉末与基材在激光区域受热熔融后快速冷却到室温。送粉工艺介观尺度数值模型建立流程如下:通过统计确定粉末颗粒尺寸分布(见图2)与粉末束信息,生成粉末颗粒几何模型(见图2);对基材进行建模,完成粉末尺度仿真模型(见图3)。模型具体参数为:基材尺寸5 000 mm

1.3 激光热源模型
增材制造工艺涉及复杂的热传导、高加热/冷却速率下的对流和辐射,热输入与热损失的准确描述直接影响着温度场和应力变形场的计算结果和准确度。热源是引起残余应力、相变和物理形变的根源,激光热源、热对流与热辐射等热边界条件的准确施加是增材制造工艺仿真的关键[30-31]。在实际过程中,激光以光斑的形式照射到粉末和基体表面,粉末和基体通过表面吸收激光能量。在计算过程中,将激光热源建模为粉末上与时间相关的热流边界。由于OTM的拉格朗日描述特性,热流边界可以直接施加在与热源射线发生作用的粉末节点上;利用Ray tracing射线追踪法搜索确定粉末束和基材表面上受热通量辐射的节点,这些节点在计算过程中将被施加热通量。光斑上的热量分布不均匀,中心多而边缘少,仿真中采用提出的超高斯分布热流密度近似物理激光束。热流密度表达式为:
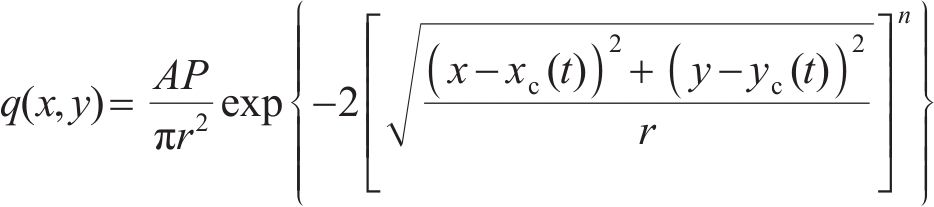
式中:t为时间;x、y为空间坐标;q为热流密度;A为材料表面吸收率;P为激光功率;r为激光半径。激光束的中心由时间相关的坐标函数xc(t)和 yc(t)控制;n为激光阶数,热通量分布形状可通过改变阶数n来选择,当n>2时即为超高斯热通量。
考虑蒸发引起的能量损失,将蒸发潜热看作是粉体/基材与环境的对流热通量:
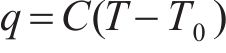
式中:C为组合对流换热系数;T为热力学温度;T0为环境温度。熔池表面节点的辐射散热被建模为遵循Stefan-Boltzmann定律的黑体辐射:
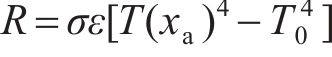
式中:R为辐射热流;σ为Stefan-Boltzmann常数;ε为物体发射率。通过整合颗粒系统中的热通量、热传导、热对流和熔池表面的热辐射进行求解,从而预测整个作用域的温度变化,并进一步决定局部材料状态。
1.4 材料参数
增材制造过程涉及多相混合与转换,OTM本构模型采用了包括固相、液相和气相的全域本构模型,其中材料点的局部状态由温度T决定。当局部温度低于熔点时,物质点处于固相;当温度超过熔点或沸点时,材料点转变为液相或气相。
材料在固相状态时,本构关系为:
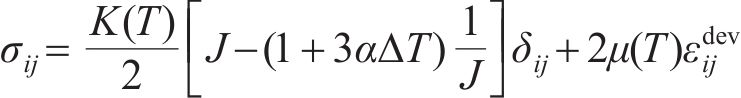
式中:K(T)为温度相关的体积模量;J为局部材料的Jacobian;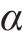

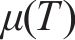
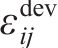
材料在液相状态时,本构关系采用Murnaghan-Tait状态方程:
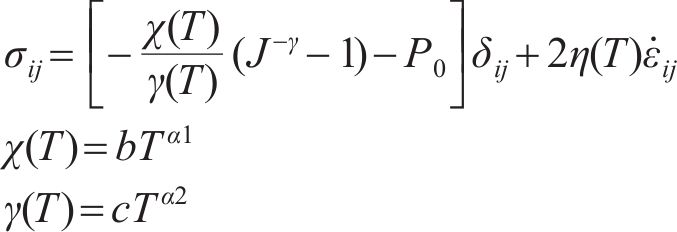
式中:T为温度;b、c、α1、α2为公式系数;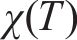
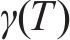
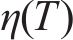
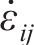
材料在气相状态时,本构关系采用理想气体状态方程:
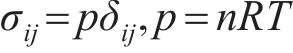
TC4材料参数见表1。
Density/ (kg·m-3) | Elastic modulus/GPa | Poisson’s ratio | Heat capacity of solid/ (J∙kg-1∙K-1) | Heat capacity of fluid/ (J∙kg-1∙K-1) | Thermal conductivity of solid/ (W∙m-1∙K-1) | Thermal conductivity of fluid/ (W∙m-1∙K-1) | Melting point/℃ |
|---|---|---|---|---|---|---|---|
| 4 400 | 110 | 0.34 | 612 | 900 | 10 | 28 | 1 640 |
Boiling point/℃ | Latent heat of fusion/ (kJ∙kg-1) | Heat of vaporization/ (kJ∙kg-1) | b | c | 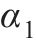 | 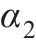 | |
| 3 260 | 286 | 9 700 | 2×1010 | 47.65 | -1 | -0.354 |
1.5 粉末尺度工艺过程模拟与缺陷分析
选取试验方案[32]中的工艺参数(见表2)建立激光金属增材过程仿真模型,采用OTM方法进行整体耦合求解。
| Laser power/W | Scanning speed/(mm∙s-1) | Feeding rate/(g∙s-1) | Powder diameter/μm |
|---|---|---|---|
| 200 | 8.5 | 2.75 | 45-150 |
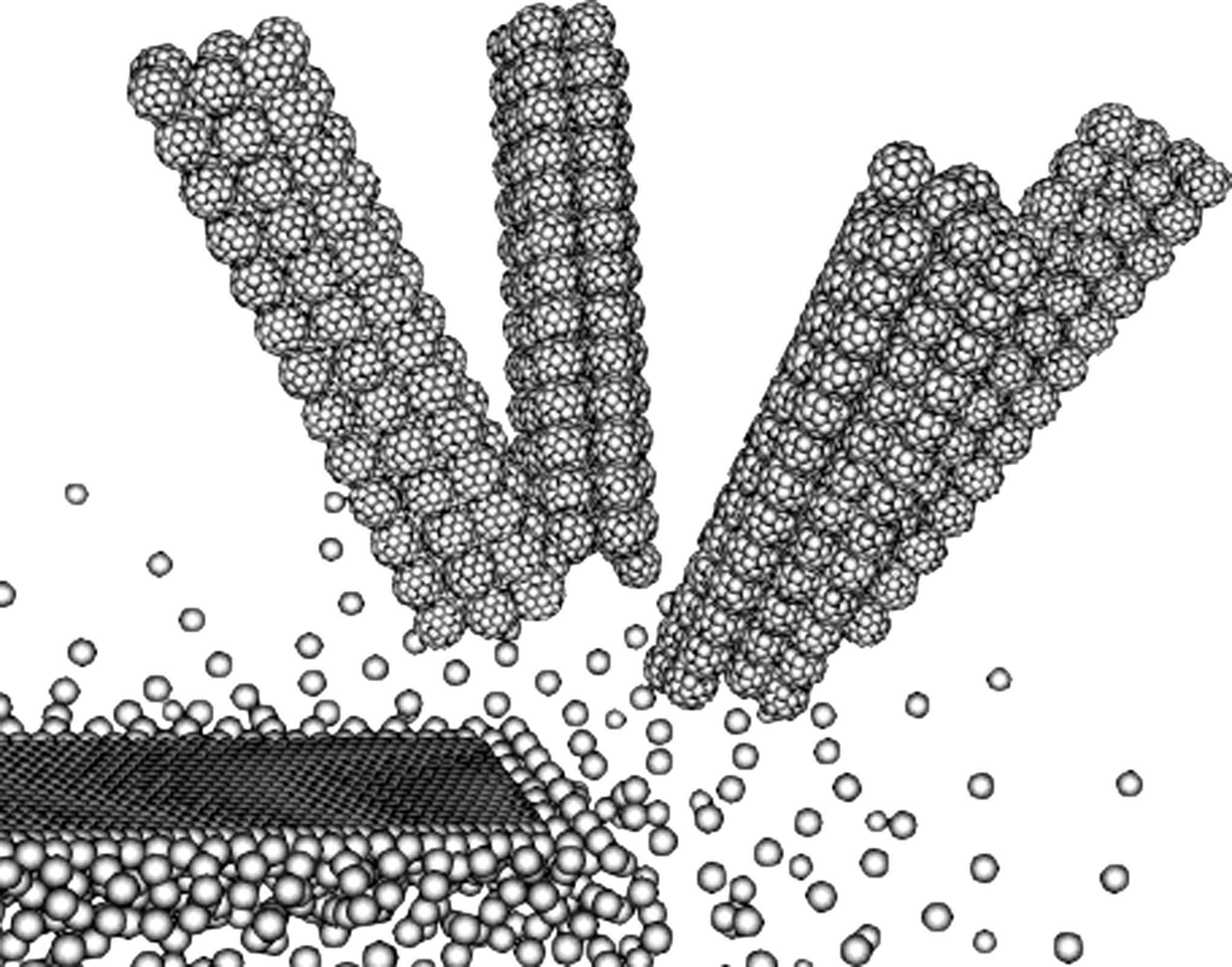
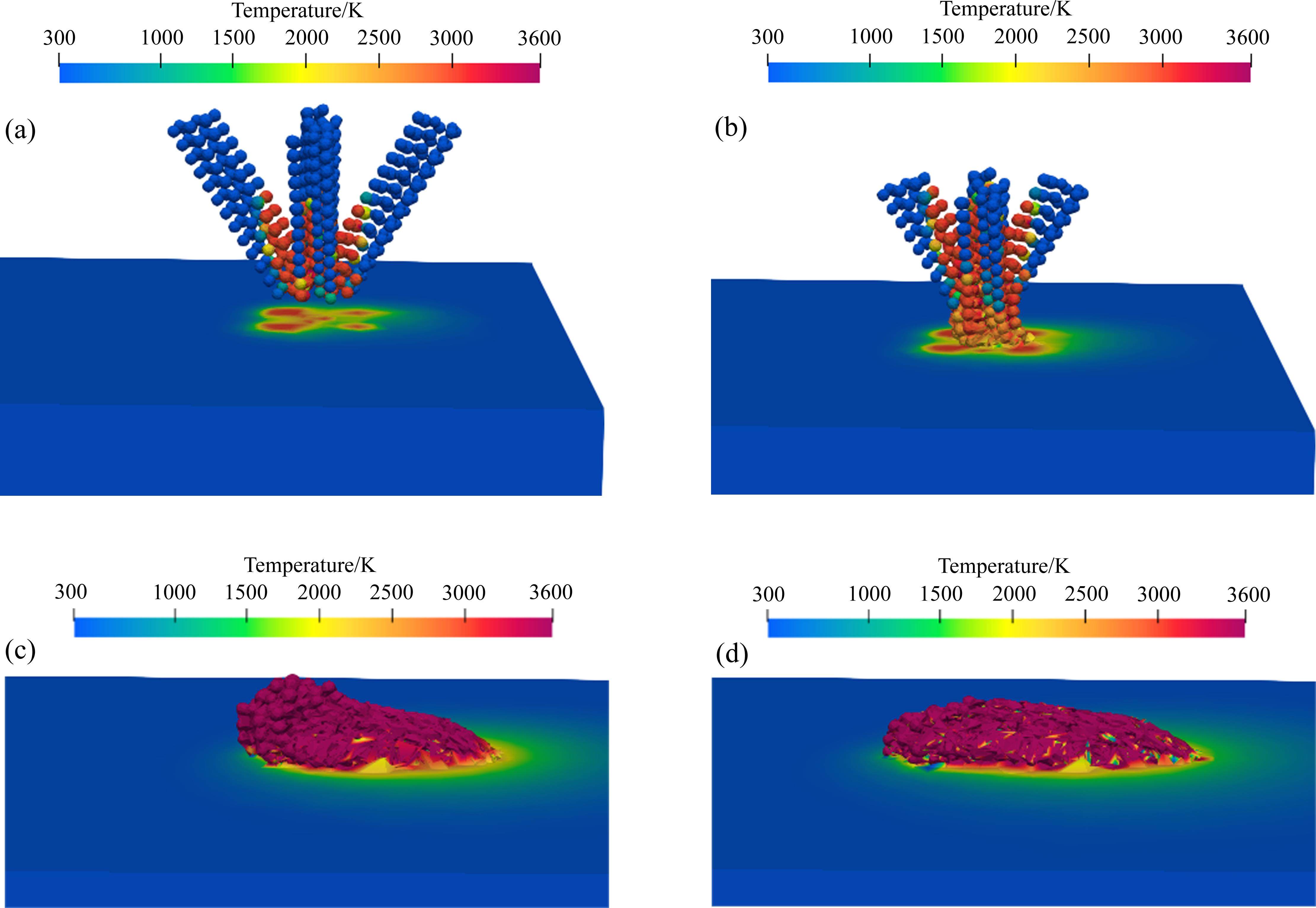
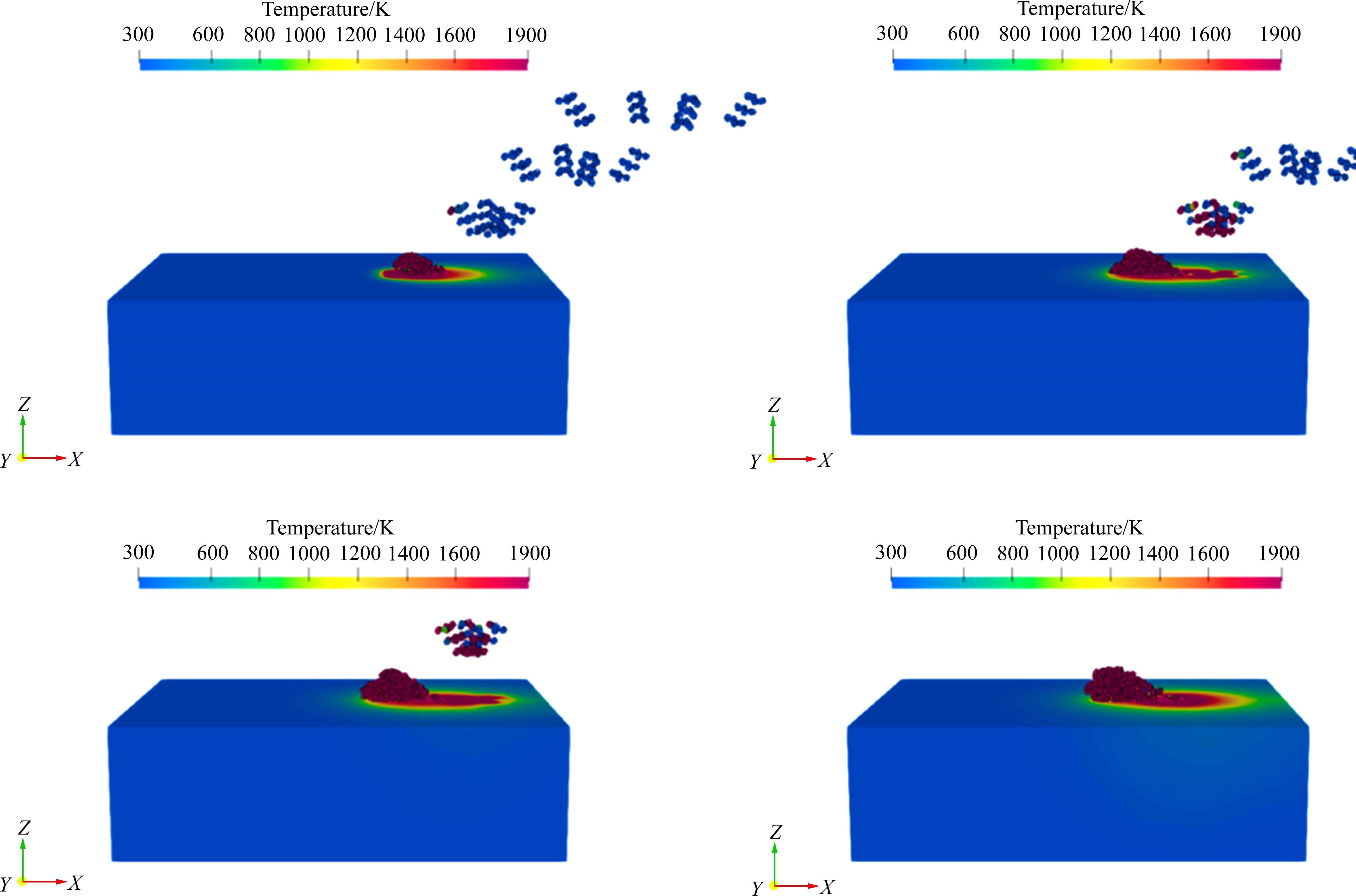
从模拟过程(见图5)可观察到,4束粉末颗粒束在空中逐渐向中心汇聚;在激光照射下,部分粉末颗粒受热开始熔化坠落。同时,基材吸收部分激光热量在表面开始形成微小熔池,与坠落粉末融合成熔覆层;随着激光热源的前进,形成的熔覆层离开激光热源区,开始散热并逐渐凝固,形成较为完整的形貌,工艺过程贴近实际情况。
为定量说明仿真结果的准确性并进一步探究工艺参数与孔隙率之间的影响关系,采用基于图像识别的孔隙率分析方法计算仿真结果的孔隙率。其计算流程为:通过对凝固的熔覆部分进行提取(见图6(a)),进行逐层等距切片得到切片横截面(见图6(b)),对横截面进行像素处理、查找,识别其中的内孔(见图6(c)),通过计算多个切片的内孔面积与熔覆层总面积可得到不同工艺参数结果下的孔隙率。
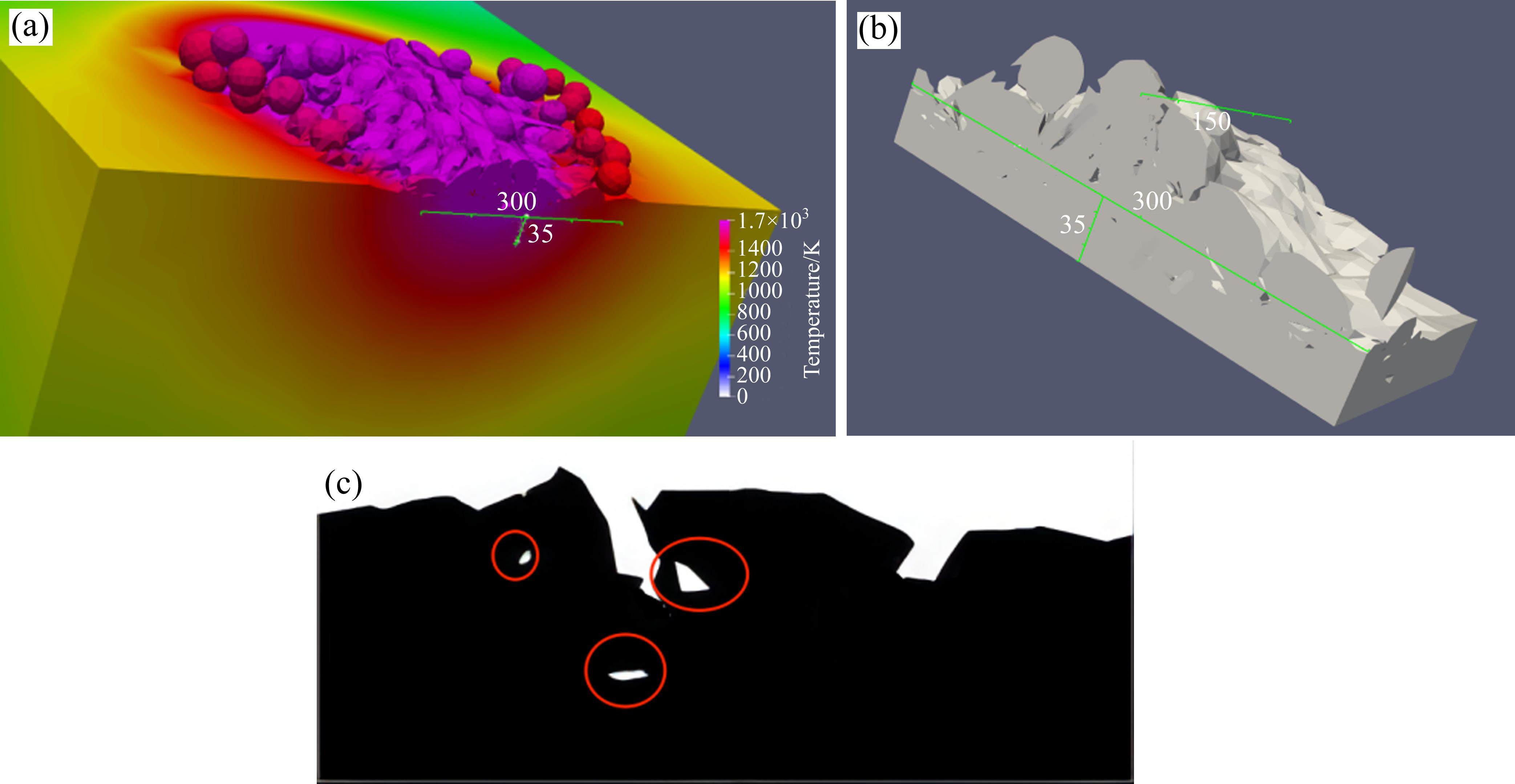
基于图像识别的孔隙率计算公式:
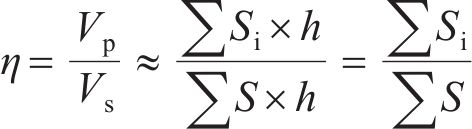
式中:Vp为孔体积;Vs为实体体积;

分析式(7)可知,整体孔隙率由若干个切片孔隙推算得到,每个切片可认为是对其附近孔隙情况的代表;当切片数量足够多时,计算结果将足够逼近真实结果。该方法计算原理与试验的孔隙计算原理相符,速度快且方便对大量计算模型进行批处理操作。
OTM方法与试验结果[32]对比见表 3,试验设备由一个最大功率750 W的激光器和一个4喷嘴同轴给粉系统组成,打印过程在充满氩气的条件下进行,试验工艺参数见表2。仿真结果可观察到部分粉末还未完全熔凝,是产生孔隙的主要原因(见图6(a)和(b)),与文献试验结果的孔隙率产生原因吻合,且计算孔隙率误差为6%,表明结合粉末尺度仿真模型的OTM数值模拟方法可较好地模拟出孔隙的形成与分布。
| Method | Porosity/% | Porosity type | Δ1)/% |
|---|---|---|---|
| Lecture[32] | 0.25 | Lack of fusion | - |
| OTM | 0.235 | Lack of fusion | 6% |
为进一步验证模拟结果的准确性,设计了一组多层打印的增材打印方案,即在同一工艺参数下进行多层打印,观测每层打印后的形貌。采用的工艺参数如表4所示,共打印了4个试件。4个试件的工艺过程分别为单道扫描1、2、3、4次,每层打印长度为20 mm,打印方案示意图如图7所示。测量打印后冷却至室温时的各熔覆层宽度、高度。采用的打印设备型号为铂力特公司BLT-C1000,其喷嘴数量为4个,采用6000 W光纤激光器,最终打印结果见图8。
| Laser power/W | Scanning speed/(mm∙min -1) | Feeding rate/(g∙min-1) | Hatch spacing/mm | Powder diameter/μm |
|---|---|---|---|---|
| 3000 | 600 | 10 | 0.5 | 53-180 |
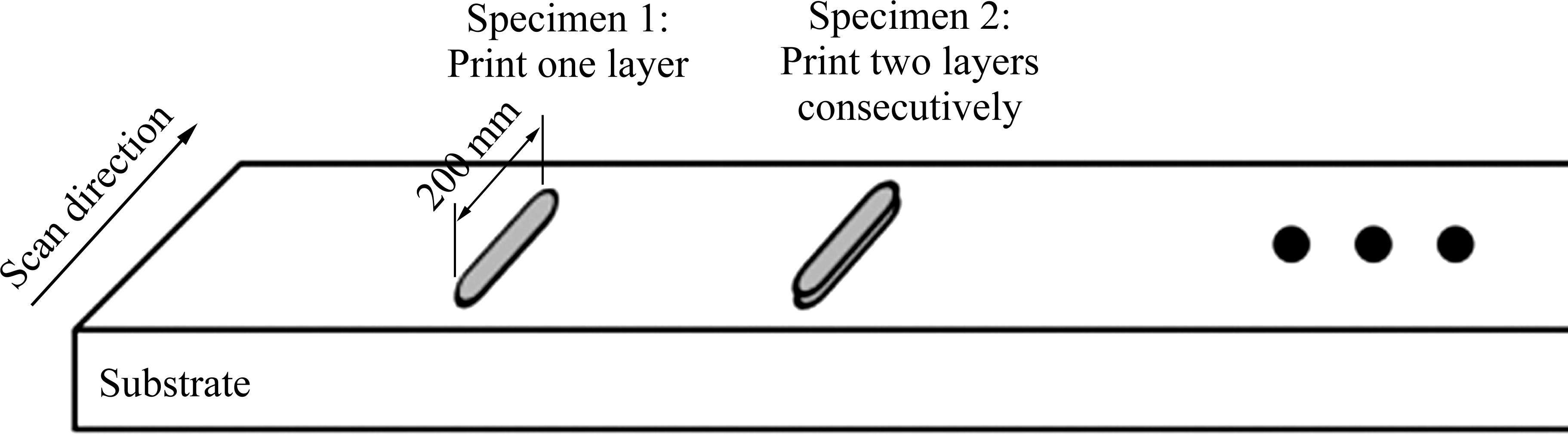
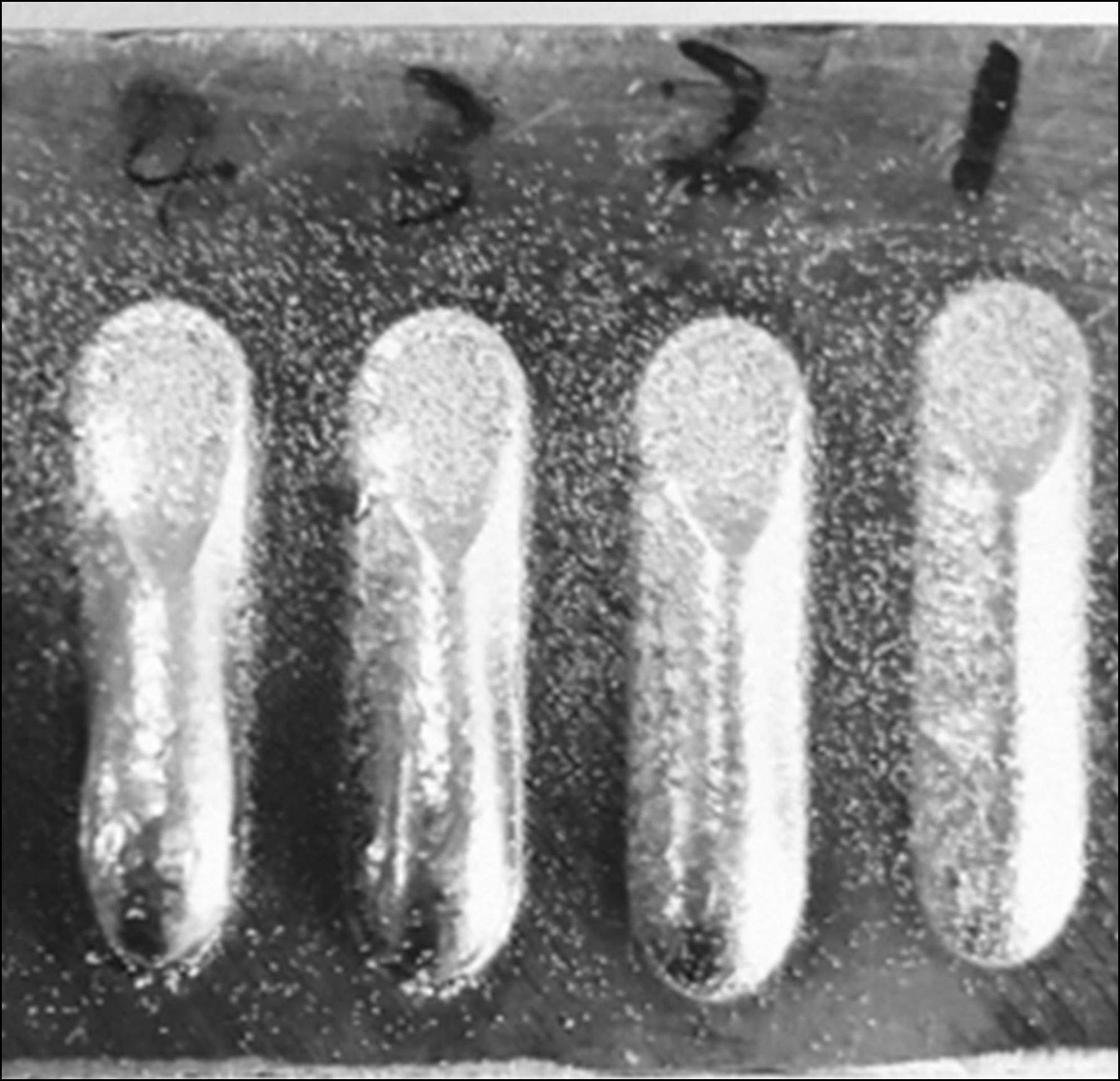
根据设计方案进行数值模拟,模拟了4层的粉末熔覆过程。根据实验方案中的粉末尺寸以及工艺参数,将粉末直接建模成微米级的颗粒集合体,建立了LSF多层打印过程,采用OTM方法进行求解。从模拟结果可以观察到(见图9),随着4束粉末颗粒在空中逐渐汇聚进入激光照射范围,部分粉末颗粒受热熔形成粉末坠落。同时,激光部分热量被基材吸收,在基材表面形成浅浅的熔池,粉斑脱落后与基材熔池融合形成熔覆层;随着基材的运动,熔覆层逐渐移出激光照射区域,由于基材内部的热传导基于熔覆层与环境的对流换热共同作用,移出激光区的熔覆层散热开始凝固堆积,熔覆层高度逐层增加。
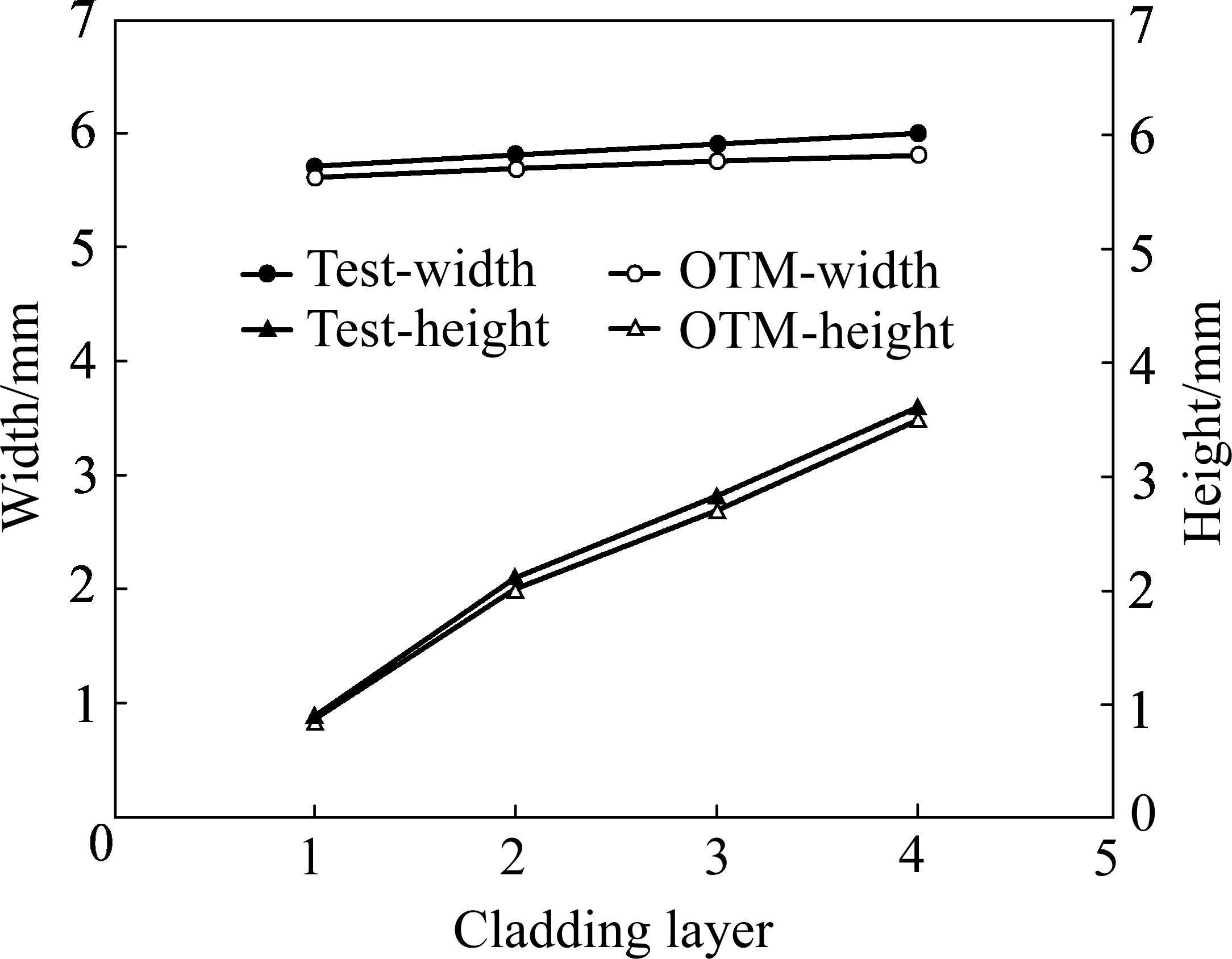
为定量说明模拟结果的准确性,分别测量了试验与模拟熔覆层的最大高度与最大宽度,如图10所示。可以看出,随着打印层数的增加,熔覆层高度基本呈现线性递增的趋势,而宽度变化较小,基本保持不变。OTM过程仿真结果与试验结果吻合良好,宽度和高度的最大相对误差在5%以内。
2 工艺参数优化设计
增材制造仿真模型网格规模大多在百万量级,且计算过程涉及多相转变、物理场耦合等复杂物理过程,导致数值仿真计算速度缓慢。通过构建高精度代理模型探究工艺参数与孔隙率之间的影响关系,代替数值仿真过程结合优化算法,实现了工艺参数的优化设计过程。
2.1 工艺参数-孔隙率影响关系建立
利用OTM方法求解得到的样本点数据开展了LSF工艺参数与孔隙率关系的代理模型构建。分四个步骤。
2.1.1 筛选关键输入变量
LSF工艺参数众多,由于激光功率、扫描速度、送粉速率为影响打印质量的主要输入参数,因此,选择这三个工艺参数作为输入变量。并采用正交设计进行采样,且误差分析点数量设为8,各输入参量的取值如表5所示。
| Process parameter | Range of value |
|---|---|
| Laser power/W | [150-250] |
| Scanning speed/(m∙s-1) | [0.008, 0.012] |
| Feeding rate/(g∙s-1) | [2.08, 3.48] |
2.1.2 获取训练样本点与误差分析点
采用正交试验设计方法,按照表5-6中的方案抽取对应数量的样本点和误差分析点,将样本点和误差分析点输入到OTM模拟框架,获得对应工艺下的孔隙率。
| Sample No. | Laser power/W | Scanning speed/(m∙s-1) | Feeding rate/(g∙s-1) | Porosity/% |
|---|---|---|---|---|
| 1 | 1(150) | 1(0.008) | 1(2.08) | 3.054 |
| 2 | 1 | 2(0.010) | 2(2.784) | 4.482 |
| 3 | 1 | 3(0.012) | 3(3.48) | 2.914 |
| 4 | 2(200) | 1 | 2 | 1.924 |
| 5 | 2 | 2 | 3 | 0.920 |
| 6 | 2 | 3 | 1 | 1.530 |
| 7 | 3(250) | 1 | 3 | 0.758 |
| 8 | 3 | 2 | 1 | 0.962 |
| 9 | 3 | 3 | 2 | 0.828 |
2.1.3 无量纲化处理
为消除量纲之间的影响以及不同参数间量级的不统一,采用归一化方法,对三个输入变量进行归一化处理,采用式(8)所示方法。
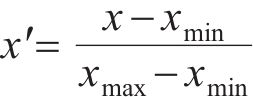
式中:x为当前样本点;xmin为样本点最小值;xmax为样本点最大值。
2.1.4 构建代理模型
对归一化的样本点进行代理模型构建,并利用误差分析点对构建的代理模型进行精度检测。用于拟合数据的模型为正交多项式(Orthogonal polynomial, OP)和径向基神经网络(Radial basis function network, RBF network)。
为验证各代理模型对工艺参数-孔隙关系之间关系预测结果的准确性。在设计范围内随机选取工艺参数组合进行仿真,将代理模型预测孔隙率结果与仿真结果进行对比,采用R2对各代理模型的拟合精度做出定量评估,定义:
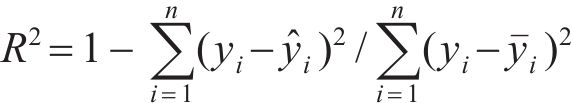
式中:n为样本点个数;i为样本点序号;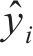
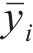
模型的精度对比结果见表7,径向基神经网络对孔隙率的预测高达98.5%,拟合精度明显高于正交多项式,说明对于高复杂度的关系多项式回归代理模型解决非线性强耦合问题的效果并不理想,而径向基神经网络由于激发函数引入的非线性以及多层网络的学习对非线性耦合问题有较好的拟合精度,可作为代替数值仿真过程的工具进行后续的工艺参数优化。
Comparison No. | Porosity/% | Surrogate model | |
|---|---|---|---|
| OP | RBF | ||
| R2 | - | 0.238 | 0.985 |
| 1 | 0.0269 | 0.0312 | 0.0295 |
| 2 | 0.0277 | 0.0173 | 0.0273 |
| 3 | 0.0180 | 0.00634 | 0.01524 |
| 4 | 0.0115 | 0.00263 | 0.00991 |
| … | … | … | … |
2.2 LSF工艺参数-孔隙率影响规律
采用构建的LSF工艺参数-孔隙率的RBF模型,研究三个主要工艺参数对LSF制备的熔覆层孔隙率的影响。探究结果见图11,图中P为激光功率(W),v为扫描速度(m/s),f为送粉速率(g/s)。
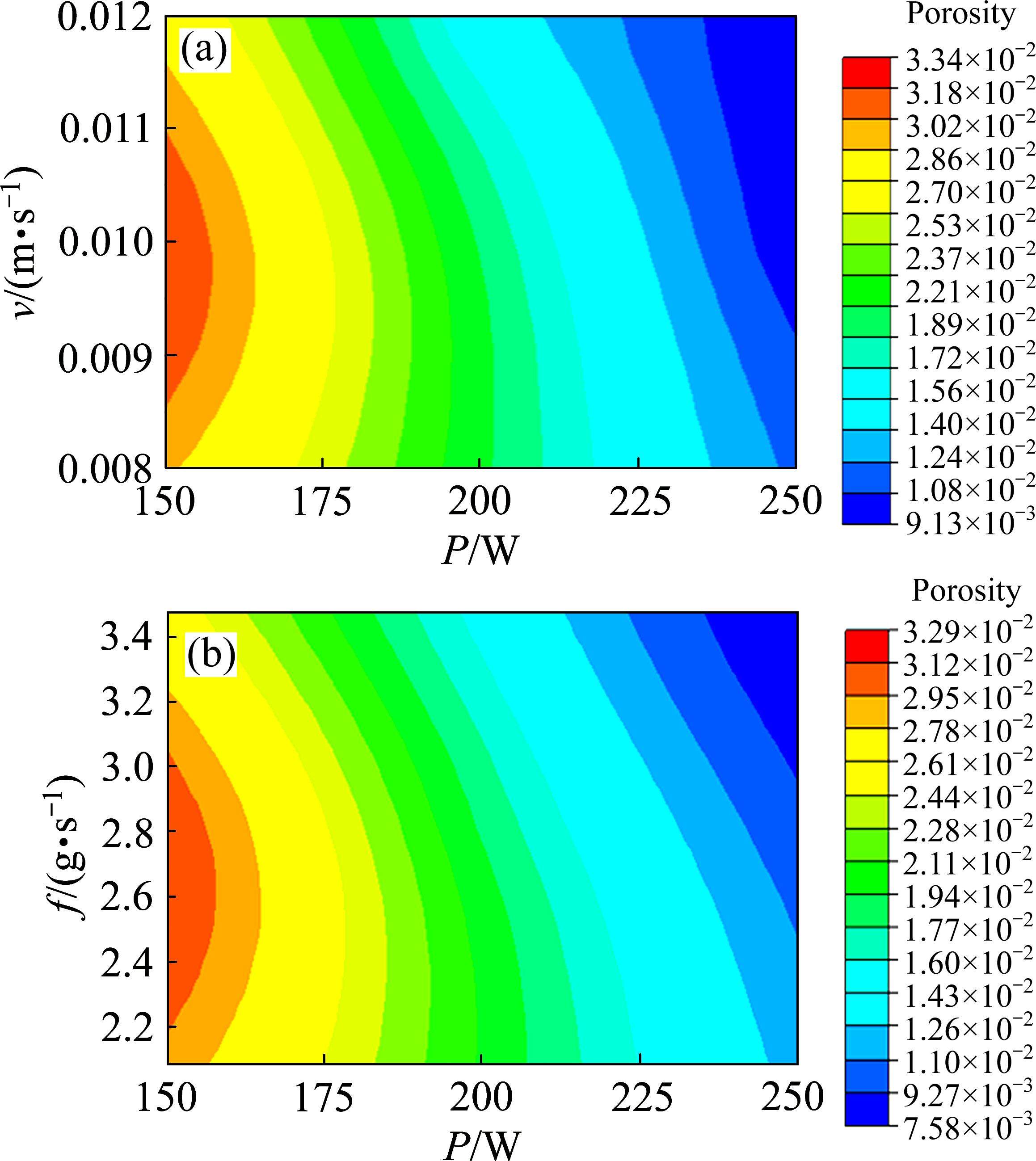
由图11可以看出,在图中所示工艺参数范围内,随着激光功率的升高,熔覆层孔隙率均呈现降低的趋势。分析认为,这可能是激光功率较低时,熔覆层粉末未完全熔覆,存在冶金不良的问题。随着激光功率的升高,这种情况得到改善。进一步分析可以发现,适当提高扫描速度和送粉速率可以使孔隙率在较高功率下得到改善。分析认为,这可能是扫描速度较低时,粉末容易堆积,导致内部存在粉末未完全熔覆,而送粉速率较低时,有可能无法提供足够的粉末原材料满足正常打印的需要。
可见,以上三个主要工艺参数相互影响,必须搭配合适的取值才能获取材料的最优性能。
2.3 基于代理模型的工艺参数优化
基于径向基神经网络进行工艺参数优化过程,建立工艺参数优化数学模型:
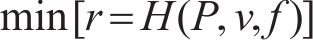
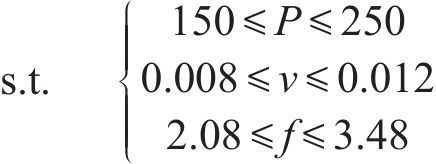
式中:r为孔隙率;P为激光功率(W);v为扫描速度(m/s);f为送粉率(g/s)。考虑到工艺参数-打印性能的高度非线性关系,选择处理全局问题效果较好的多岛遗传算法,表8所示为多岛遗传算法参数。
| Sub-population | Number of island | Number of generations | Rate of crossover | Rate of mutation | Rate of migration |
|---|---|---|---|---|---|
| 10 | 10 | 15 | 1 | 0.01 | 0.01 |
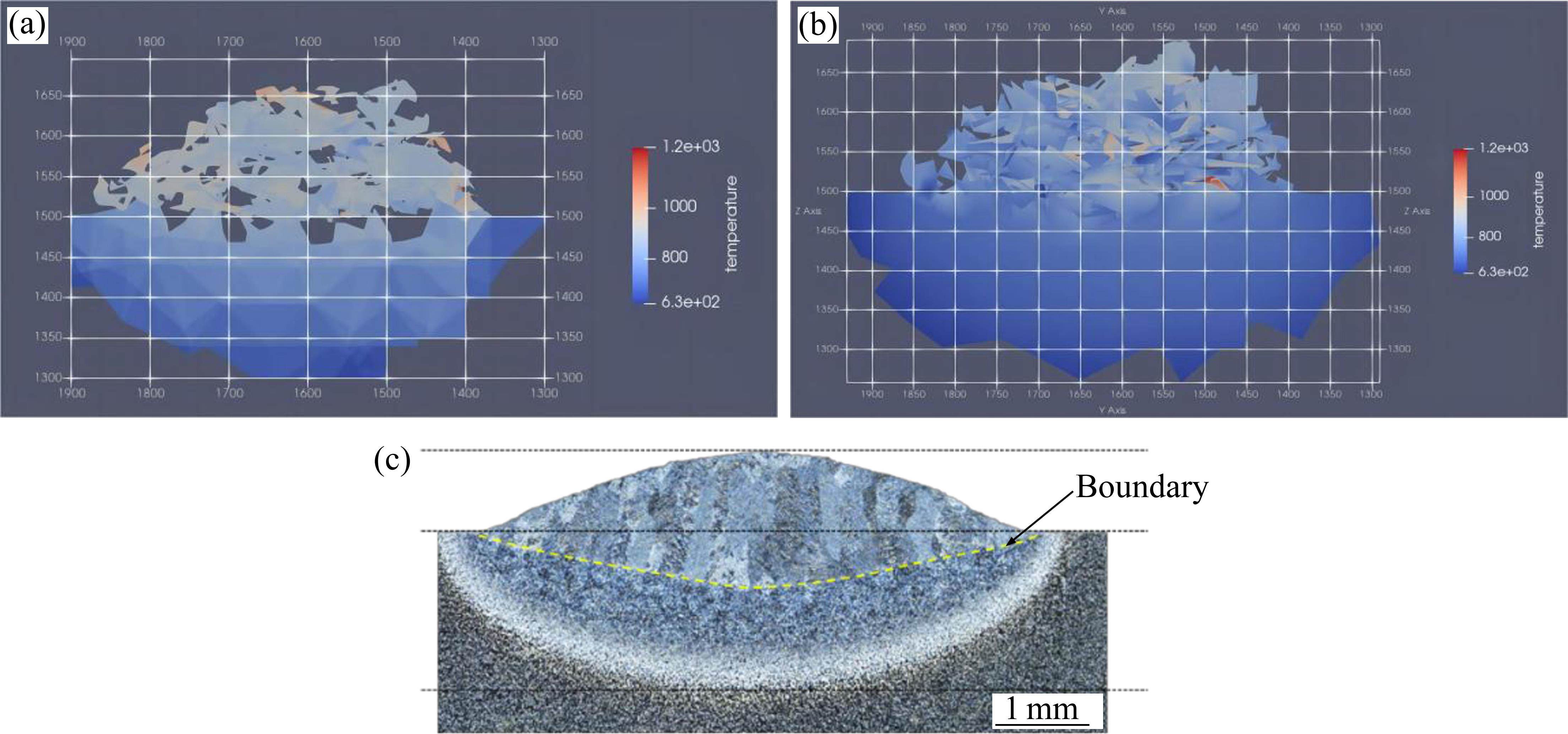
工艺参数优化过程如下:随机初始化种群,在设计空间中进行1500次迭代,收敛后得到优化后工艺参数(见表9)。代理模型预测孔隙率为0.573%,采用优化后工艺参数进行数值仿真得到孔隙率结果为0.586%;两者相比,后者比前者高了2.27%。工艺参数优化前后熔覆层结果的对比如图12所示。由图12可观察到,使用初始设计参数进行仿真得到的熔覆层中粉末与基材熔融不够充分,导致底部孔隙较多,且熔覆层形貌不完整(见图12(a))。采用优化后工艺参数仿真得到的熔覆层内部孔隙较少且无大孔隙,组织较为致密,熔覆层轮廓较完整(见图12(b))。采用优化后的工艺参数进行单层激光熔覆的试验,结果如图12(c)所示,试验设备为BLT-C1000。打印熔覆层较为致密,且轮廓形状与仿真结果基本相同;通过CT测得孔隙率为0.697%,仿真预测结果与试验结果的宽度和高度的相对误差分别为3.33%和4.76%。考虑到试验环境的不确定性,试验结果与仿真结果的误差在可接受范围内。
| Laser power/W | Scanning speed/ (m∙s-1) | Feeding rate/ (g∙s-1) | Predicted porosity/% | Simulated porosity/% | Δ/% |
|---|---|---|---|---|---|
| 249.49 | 0.01 | 3.44 | 0.573 | 0.586 | 2.27 |
3 结论
1) OTM方法基于变分原理,在统一的拉格朗日框架下求解物质运动方程,可以有效解决增材制造中涉及粉末多体动态接触、粉末软化、热力耦合、相变与多相混合的仿真难点。
2) 与试验结果对比,结合粉末尺度仿真模型的OTM方法可较好地模拟增材制造过程,并预测孔隙的分布与形貌,可作为研究增材制造工艺参数与打印结果关系的有效仿真手段。
3) 增材制造中工艺参数-性能之间呈现高度非线性关系,采用径向基神经网络代理模型可在较少样本点条件下达到较高的拟合精度。
4) 通过结合代理模型技术与优化方法实现了增材制造过程工艺参数的优化设计,优化后的打印结果外貌完整细密、孔隙率低且与预测结果相差较小,证明可通过将数值模拟与优化方法结合的策略进行金属增材制造的工艺参数优化。
孟庆泽, 樊江, 袁庆浩. 基于粉末级成型模拟的金属增材制造工艺优化[J]. 中国有色金属学报, 2025, 35(1): 196-208. DOI: 10.11817/j.ysxb.1004.0609.2024-45058
MENG Qingze, FAN Jiang, YUAN Qinghao. Process optimization of metal additive manufacturing based on powder scale simulation[J]. The Chinese Journal of Nonferrous Metals, 2025, 35(1): 196-208. DOI: 10.11817/j.ysxb.1004.0609.2024-45058

