我国高速铁路多采用“以桥代路”的全封闭式建设理念,高速铁路桥梁常长达几千米甚至几十千米,高速铁路桥上行车成为常态。我国地处世界两大地震带——环太平洋地震带和欧亚地震带交汇处,地震分布范围广、活动频繁,为地震最活跃的国家之一[1],致使高速列车震时和震后桥上行车难以避免。因此,开展高速铁路桥梁抗震设计与行车安全研究具有重要意义。传统基于有限元的强震动力响应预测分析方法耗时长而精度差[2, 3],难以进行车桥耦合地震响应的准确预测与行车安全的快速评估。近年来,随着人工智能、代理模型相关理论的快速发展,许多学者将有限元理论和代理模型相结合,一定程度上解决了以往计算效率低下的问题,为结构抗震减震理论与技术研究提供了新思路和新途径。但代理模型种类繁多,适用性差异大,常用的如多项式响应面(RSM)、支持向量机(SVM)、径向基函数(RBF)、多项式混沌展开(PCE)等代理模型通常仅适用于模拟线性或弱非线性动力行为,难以准确模拟复杂非线性系统的动力行为。而神经网络代理模型具有强大的非线性拟合能力,已被运用于桥梁抗震[4-11]等领域。例如,张博耀[4]利用LSTM神经网络建立了地震动-索塔响应模型与地震动-箱梁响应模型,以Kullback-Leibler散度为损伤指标来判断桥梁的健康状态。廖聿宸等[5]提出了一种基于层叠式残差长短时记忆神经网络(ResLSTM)的数据驱动建模方法,实现桥梁非线性地震响应预测。张学兵等[6]提出了CNN-LSTM混合神经网络对高铁简支梁桥地震响应进行预测,并与振动台试验进行对比,验证了所提模型的准确性。然而,以上研究所提代理模型只关注了地震对桥梁的影响,没有考虑车桥耦合的影响,模型的超参数需要不断调试才能获得较优的组合,建模效率较低。LI等[7]对比了前馈神经网络(FNN)、卷积神经网络(CNN)和长短期记忆神经网络(LSTM)模型对车桥耦合振动时程响应的预测效果,提出了贝叶斯深度学习代理模型用于预测分析随机车桥耦合系统的桥梁动力响应。王晓辉等[8]构建了WOA-BP移动荷载参数识别代理模型,高效准确地识别了桥梁结构上的移动荷载参数。何旭辉等[9]基于SSA-BP神经网络模型研究了轨道及桥梁结构参数随机性对竖向车-轨-桥耦合系统动力响应的影响。毛建锋等[10]基于PSO-LSTM神经网络模型提出了重载车桥系统随机振动响应预测方法,高效准确地预测了桥梁响应。石小双等[11]基于GWO-CNN-LSTM模型构建了车体振动加速度与轨道高低不平顺值的关系,验证了该模型用于轨道高低不平顺值反演的有效性。然而,以上研究所提代理模型没有考虑地震对车桥系统的影响,基于代理模型开展地震作用下车桥系统的响应预测研究仍较少。综上,同时考虑地震激励与车辆激励,基于代理模型开展车桥耦合系统非线性响应预测相关的研究尚需进一步发展。基于此,本文以地震作用下车桥耦合系统为研究对象,考虑桥梁结构非线性与车速影响,采用灰狼优化算法(GWO)优化传统LSTM,分单输入单输出(SISO)与多输入多输出(MIMO)分别构建GWO-LSTM代理模型,开展车桥非线性系统地震响应预测研究。基于R2、MAE、MSE、MAPE、RMSE等多类评价指标,对比LSTM、GWO-LSTM这2种神经网络的预测效果。针对部分工况,进一步融合多策略提出MSGWO-LSTM代理模型,强化与提升代理模型的预测精度。本文旨在探讨MSGWO-LSTM代理模型在高速铁路非线性响应预测中的适应性,限于篇幅,只考虑了竖向车桥耦合系统。
1 地震下高速铁路系统非线性模拟
地震作用下高速铁路系统轨道-桥梁结构可能进入塑性阶段,导致动力响应显著增大。传统基于商用有限元软件,如ANSYS、UM、SIMPACK等,或者基于自编程序的车桥动力分析很难考虑结构的复杂非线性行为。为此,本文将轮轨耦合关系通过理论推导封装为轮轨耦合单元,并二次开发集成到OpenSees软件[12-13]。本文所提轮轨耦合单元类似于通用的梁柱单元,该单元将所有节点的速度、加速度等量存储在单元内部,其能够自动存储上一时刻的数据并将其运用到下一时刻的计算中,从而保证了运动状态的传递。用轮轨耦合单元将列车模型与桥梁-轨道模型耦联,从而拓展出OpenSees车桥耦合振动分析功能。上述处理的好处在于可直接使用OpenSees的地震非线性分析功能开展地震车桥耦合振动分析。
所开发的轮轨耦合单元的准确性与可靠性已经在文献[12-13]中进行了阐述,为了论文的完整性,此处摘录部分结果如下。整个验证模型为经典的独轮车过简支梁模型,不考虑车辆及简支梁阻尼的影响。将本文模拟结果与Biggs解析解[14]以及YANG等[15]的经典数值解进行对比,见图1。由图1可知,三者的计算结果吻合良好,说明了所提方法的准确可靠性。故后续本文采用OpenSees进行高速铁路车桥耦合动力分析。
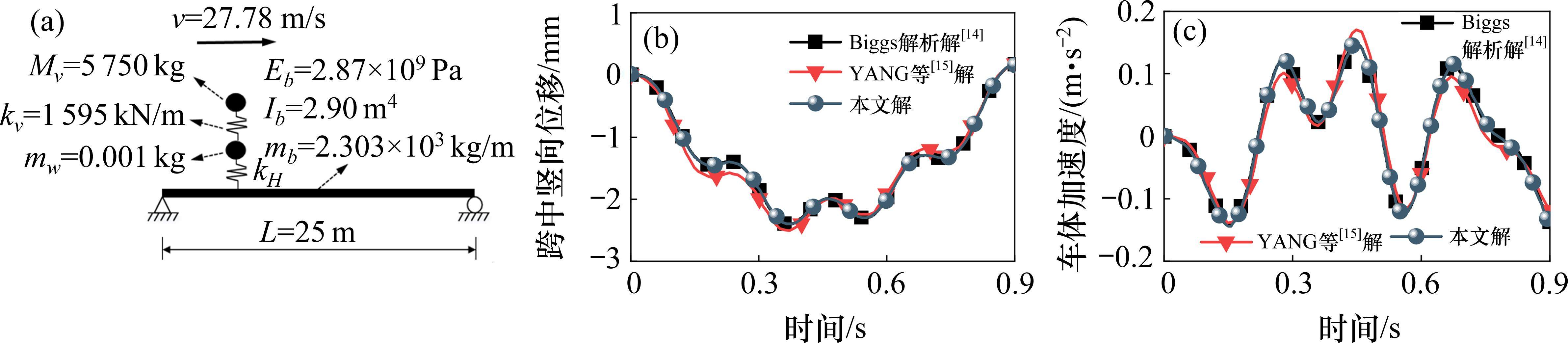
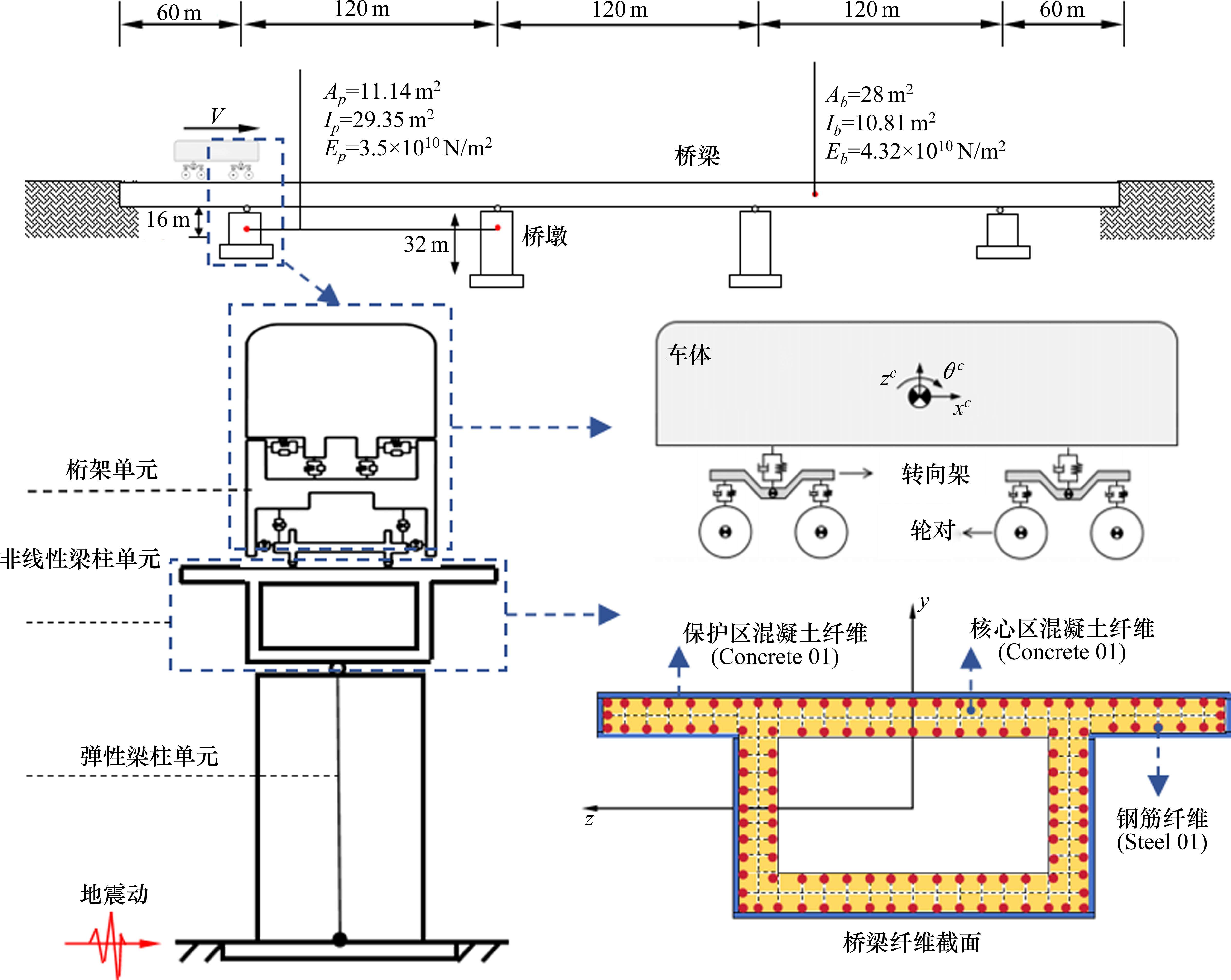
如图2所示,采用四轴多刚体车辆模型,单节车辆共10个自由度。在OpenSees中建模,车体和转向架均考虑为刚体,采用elasticBeamColumn(弹性梁柱单元)模拟;一、二系悬挂弹簧和阻尼采用Truss单元模拟。桥梁模型为5跨(60+120×3+60) m连续梁,全长480 m,桥墩采用elasticBeamColumn模拟,各墩高沿顺桥向依次为16、32、32和16 m。梁体采用单箱单室等高度直腹板箱形截面。值得注意的是,考虑到地震下桥梁结构可能进入非线性,故选用nonlinearBeamColumn(非线性梁柱单元)模拟主梁,采用Fiber Section(纤维截面)模拟箱梁截面。纤维截面保护区采用C40混凝土,核心区为C50混凝土,钢筋为HRB400。地震参数根据《建筑抗震设计规范》(GB 50011—2010)[16]取值,假设桥址处为II类场地,设计地震分组1组,8度设防,忽略桩土相互作用。考虑EI Centro竖向地震激励,采用一致激励输入法。列车速度考虑50、100、150 km/h这3个级别。分别记录桥梁跨中竖向位移、车体竖向加速度、轮轨力等数据构成响应数据库。具体参数取值可参考文献[12-13]。
2 代理模型构建
在传统LSTM代理模型基础上,引入Dropout层以防止模型训练过拟合,引入灰狼优化算法(GWO)进行超参数自动选优,从而构建并训练了GWO-LSTM代理模型。对比分析后发现GWO-LSTM在部分车速工况下响应预测精度超出限值,因此在第4节提出了融合多策略的MSGWO-LSTM代理模型,进一步提升模型的预测精度。下面简单介绍LSTM、GWO-LSTM神经网络模型的相关理论。
2.1 LSTM神经网络
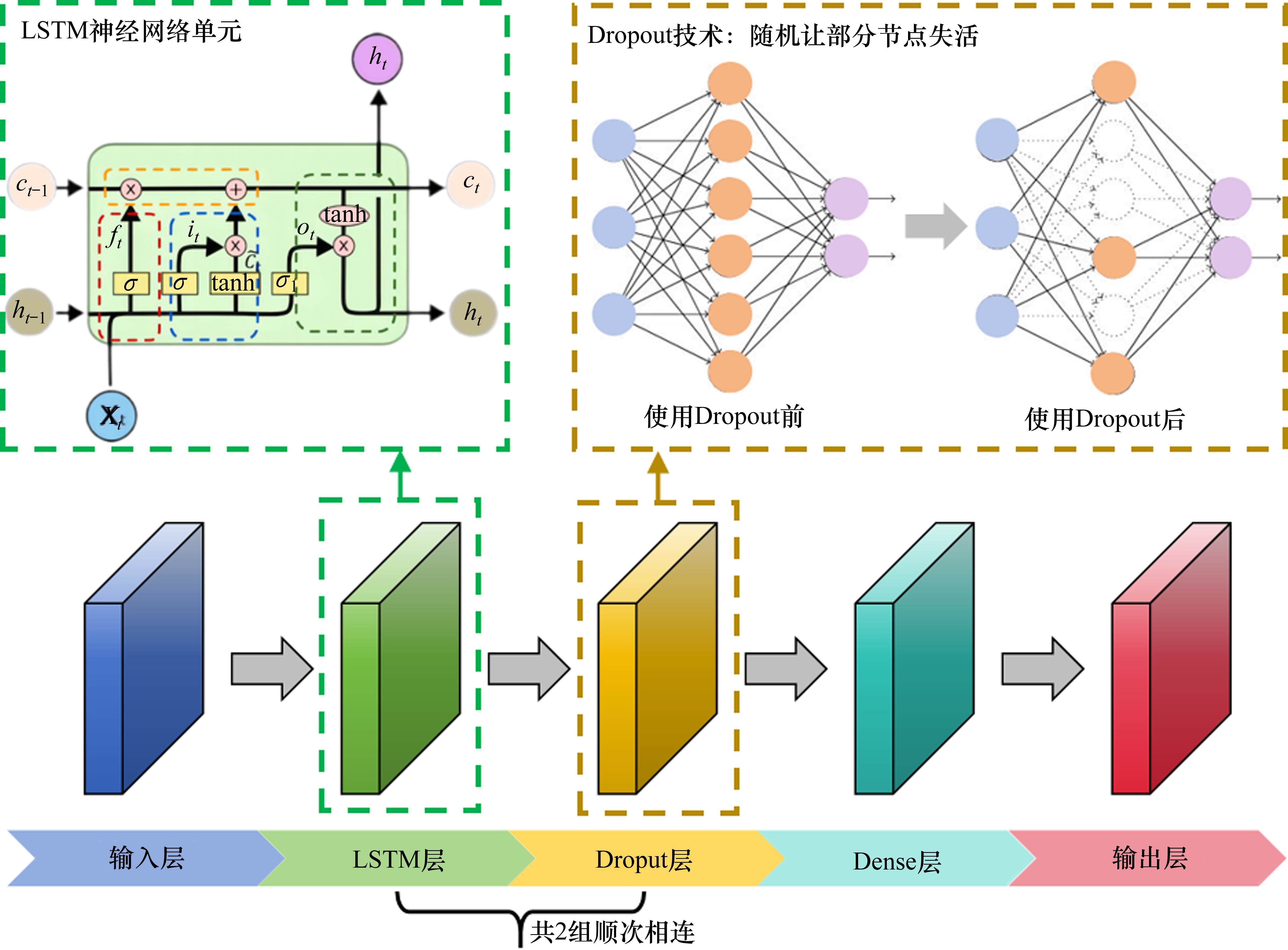
LSTM,即长短期记忆网络,具备大部分RNN(循环神经网络)模型的特性,同时能有效捕捉长序列之间的语义关联,缓解梯度消失或爆炸现象。LSTM网络架构采用门控机制(输入门、遗忘门和输出门)与记忆细胞来学习如何取舍过去的信息和提取当前的输入信息[17]。Dropout[18]技术是一种在训练神经网络时随机让部分节点失活的方法,其能减轻模型的过拟合现象,因此,本文在LSTM模型架构中添加了Dropout层以防止模型训练过拟合。经过试算,确定使用2组LSTM、Dropout层顺次相连,节点失效概率设置为0.2,采用Adam优化算法[19]对网络进行训练,所组成的模型架构能良好平衡训练的稳定性与准确性。所建LSTM模型架构如图3所示。
2.2 GWO-LSTM神经网络
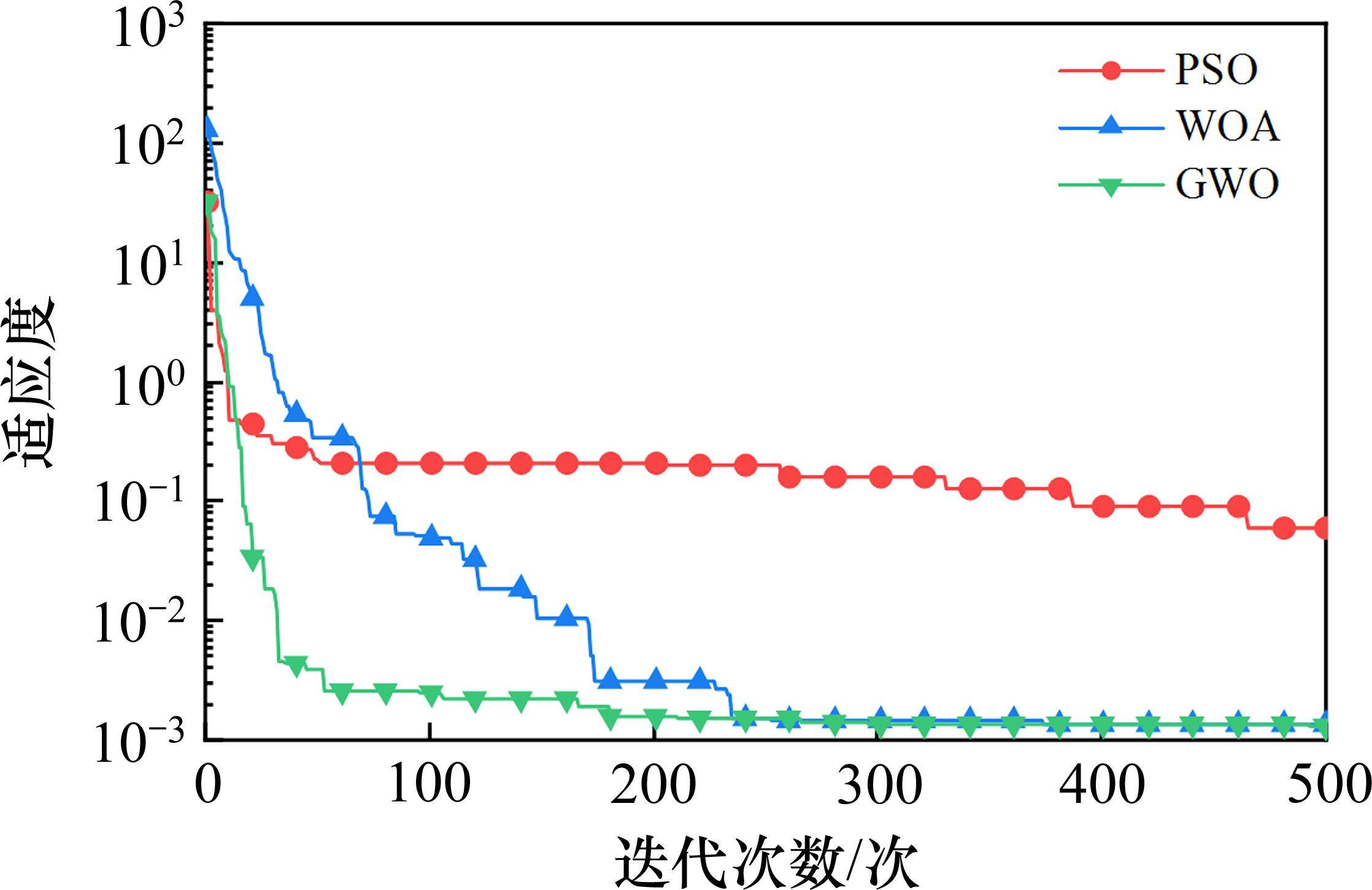
在构建LSTM神经网络时需要设置许多超参数,如初始学习率、隐藏层神经元个数、训练迭代次数等,超参数选取的合理性将对LSTM性能产生较大影响。但目前并无成熟的理论来选择具体的超参数,往往通过经验估计或不断试算来确定超参数大致范围,以使训练模型满足精度要求,从而使得建模效率低下。为提升LSTM神经网络性能,选出合适的优化算法,本文采用19个CEC测试函数[20]初步检验了灰狼优化算法(GWO)、鲸鱼优化算法(WOA)、粒子群优化算法(PSO)共3种常用算法的寻优性能。图4展示了其中一种测试函数的各算法迭代过程曲线。由图4可知,GWO的收敛速度最快、精度最高,证明其寻优性能在所选算法中最佳。综上,本文决定采用GWO对初始学习率、隐藏层1和隐藏层2的神经元个数、训练迭代次数、批处理数共5个超参数进行优化,构建了GWO-LSTM神经网络。
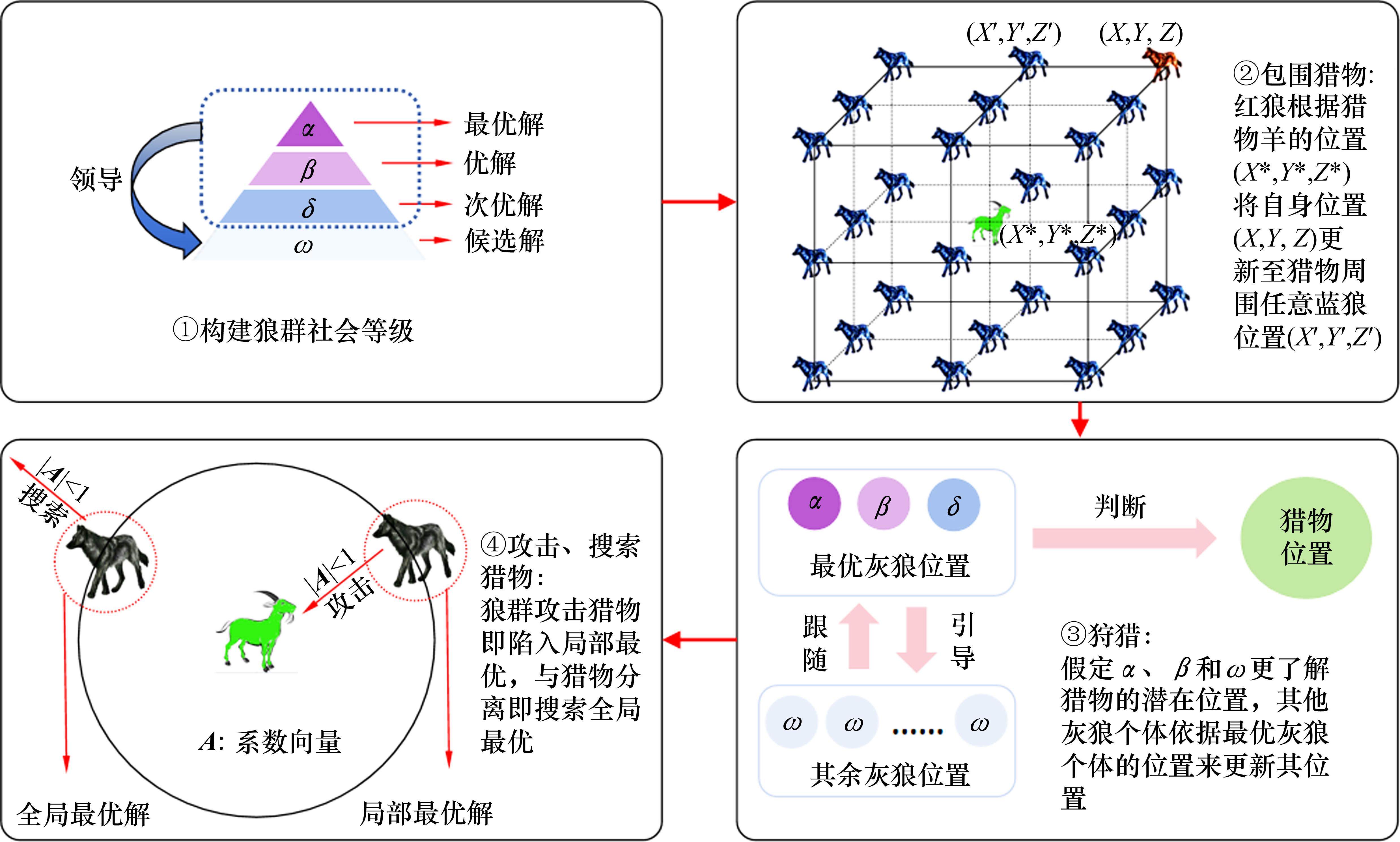
灰狼优化算法[20](GWO)是一种群体智能算法,其模拟自然界中灰狼种群等级机制和捕猎行为。通过不同类型的灰狼来模拟社会等级,通过狼群跟踪、包围、追捕、攻击猎物等过程来模拟狼的捕猎行为,实现优化搜索目的。GWO优化算法流程如图5。
本文将GWO与LSTM相结合,构建GWO-LSTM代理模型,其预测流程如图6所示,具体步骤如下。
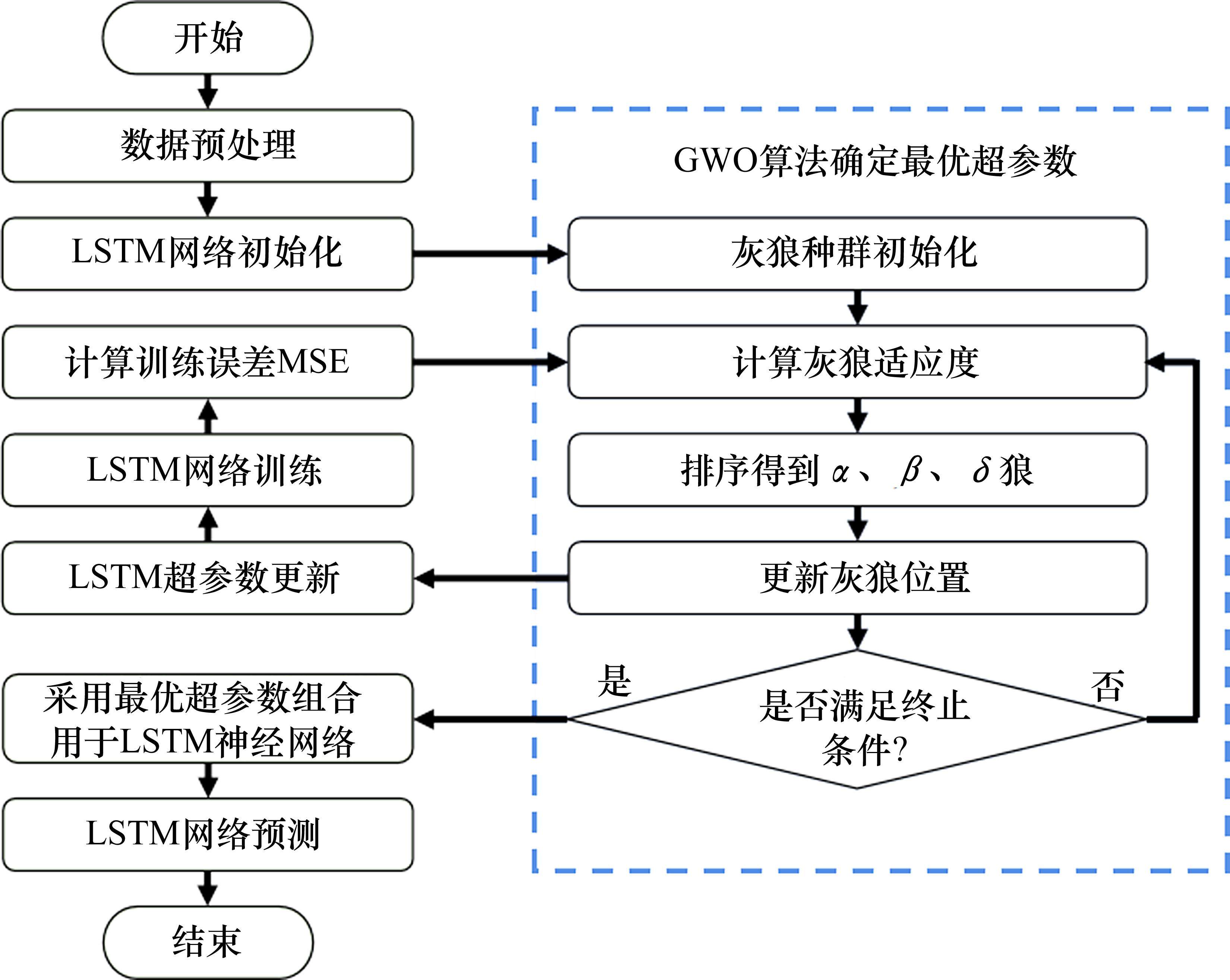
步骤1:从OpenSees软件获取地震响应数据池,并进行数据预处理。
步骤2:初始化灰狼种群,即确定5个需优化的超参数范围,前述5个超参数寻优范围依次为[0.001,0.01]、[20,800]、[20,500]、[100,800]、[8,256]。灰狼种群个数为10,算法最大迭代次数为30,采用训练误差MSE值作为适应度函数值。
步骤3:计算个体适应度值,更新灰狼位置,将更新的位置作为LSTM网络新的超参数,并训练网络,计算训练误差,寻找最优解。
步骤4:判断是否满足终止条件,若满足则输出最优解,否则返回步骤3。
步骤5:将输出的最优解作为最终的LSTM超参数组合,对LSTM再训练后进行预测和评估。
2.3 代理模型评价指标
为了综合评估LSTM、GWO-LSTM代理模型的预测效果,本文采用平均绝对误差(Mean Absolute Error, MAE)、平均绝对百分比误差(Mean Absolute Percentage Error, MAPE)、均方误差(Mean Squared Error, MSE)、均方根误差(Root Mean Squared Error, RMSE)、决定系数(Coefficient of Determination, R2)等多类指标作为判别依据。各类指标的计算公式见表1。
| 平均绝对误差MAE | 平均绝对百分比误差MAPE | 均方误差MSE | 均方根误差RMSE | 决定系数R2 |
|---|---|---|---|---|
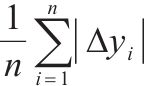 | 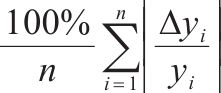 | 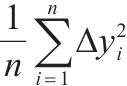 | 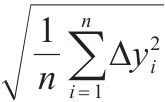 | 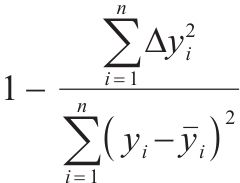 |
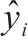
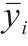
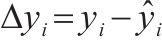
3 代理模型预测效果对比
以计算获得的桥梁跨中竖向位移、车体竖向加速度、轮轨力时程与地震加速度时程作为数据库,各工况均为一次采样获得一条时程,每条时程分别取连续的3 200个数据点,其中前70%的数据(2 240个)作为训练集数据点,后30%的数据(960个)作为测试集数据点,进行代理模型训练与预测。为加快代理模型的收敛速度,通过线性函数归一化法将所有训练集数据转换至(-1,1)之间,代理模型的预测效果均基于归一化数据来评估。为获得具有原始特征的时程数据,将预测的地震响应数据反归一化后与原始数据进行对比。此外,考虑代理模型的输入输出变量个数以及各变量之间是否影响,分单输入单输出(SISO)与多输入多输出(MIMO)这2类构建代理模型,分别对比桥梁结构线性与非线性2种工况下代理模型的预测效果。
3.1 单输入单输出(SISO)
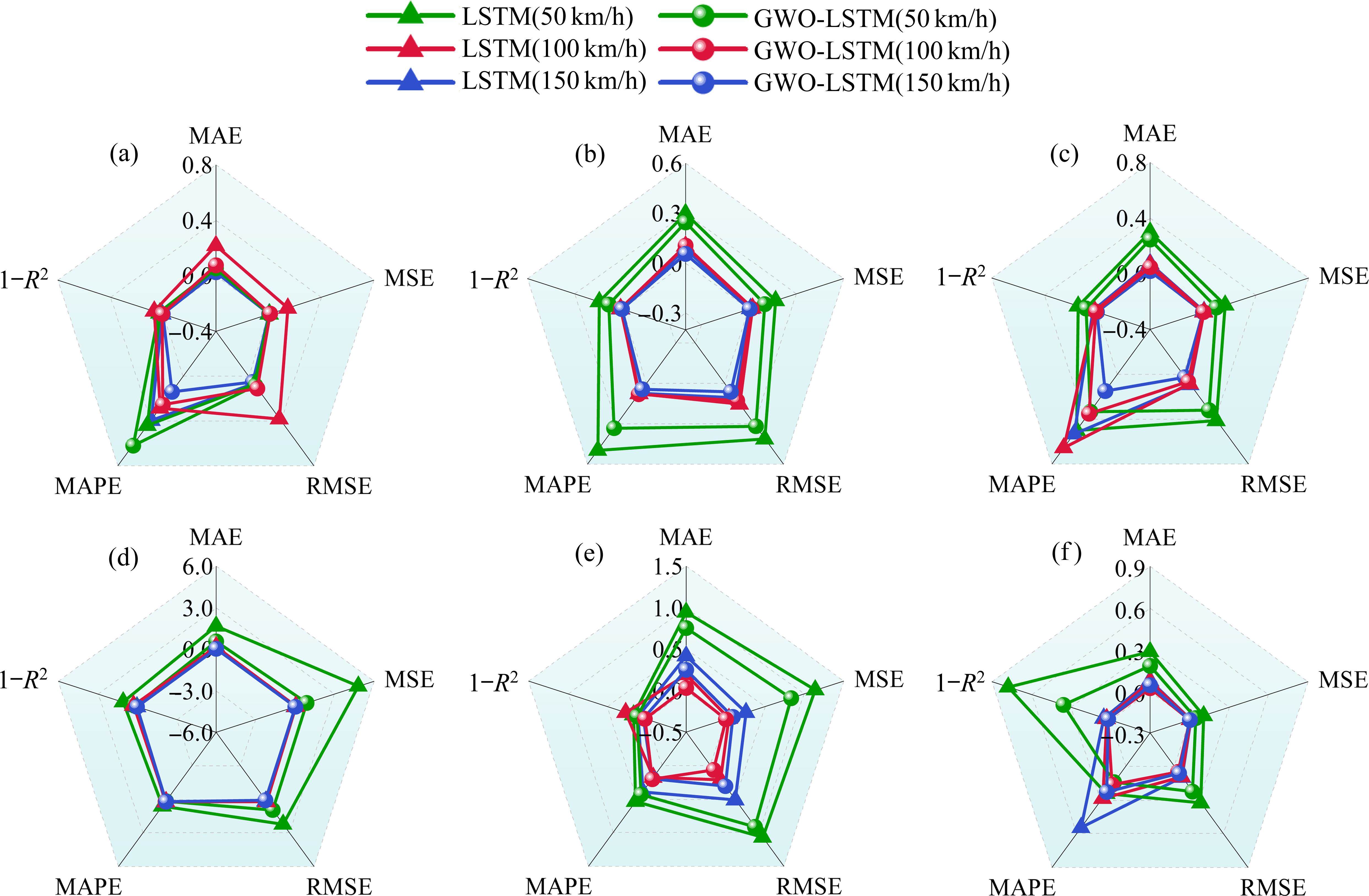
对SISO类代理模型,仅采用单一响应如桥梁跨中竖向位移响应作为输入,训练模型,以此预测桥梁跨中竖向位移,不考虑其他响应的影响。同理进行车体竖向加速度和轮轨力响应预测,针对每个响应需要训练一个模型,且各响应间互不影响。图7与图8分别为响应结果与响应精度对比,考虑不同的车速和结构是否非线性的影响,限于篇幅,此处仅展示了位移预测结果。图7中的横坐标指测试集时程数据点,后文的预测值与真实值对比图同理。基于可视化一致性的考虑,图8处选择1-R2在雷达图中展示,后文雷达图同理。

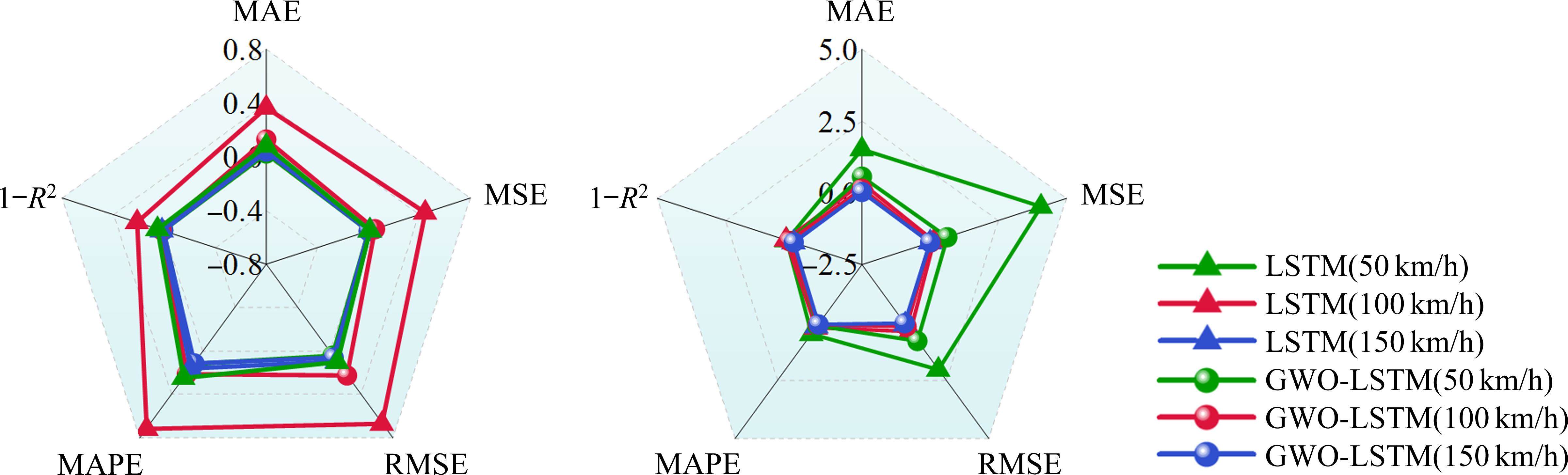
由图7和图8可知,随着车速的增加,桥梁结构线性与非线性下,传统LSTM模型的预测精度明显下降,而GWO-LSTM模型在各工况下R2稳定在0.95~0.99之间,其余评价指标接近0,仍能保持较高的预测精度。原因是GWO能在局部寻优与全局搜索之间实现平衡,避免模型陷入局部最优,所以相较于LSTM模型,GWO-LSTM模型的预测效果较好。
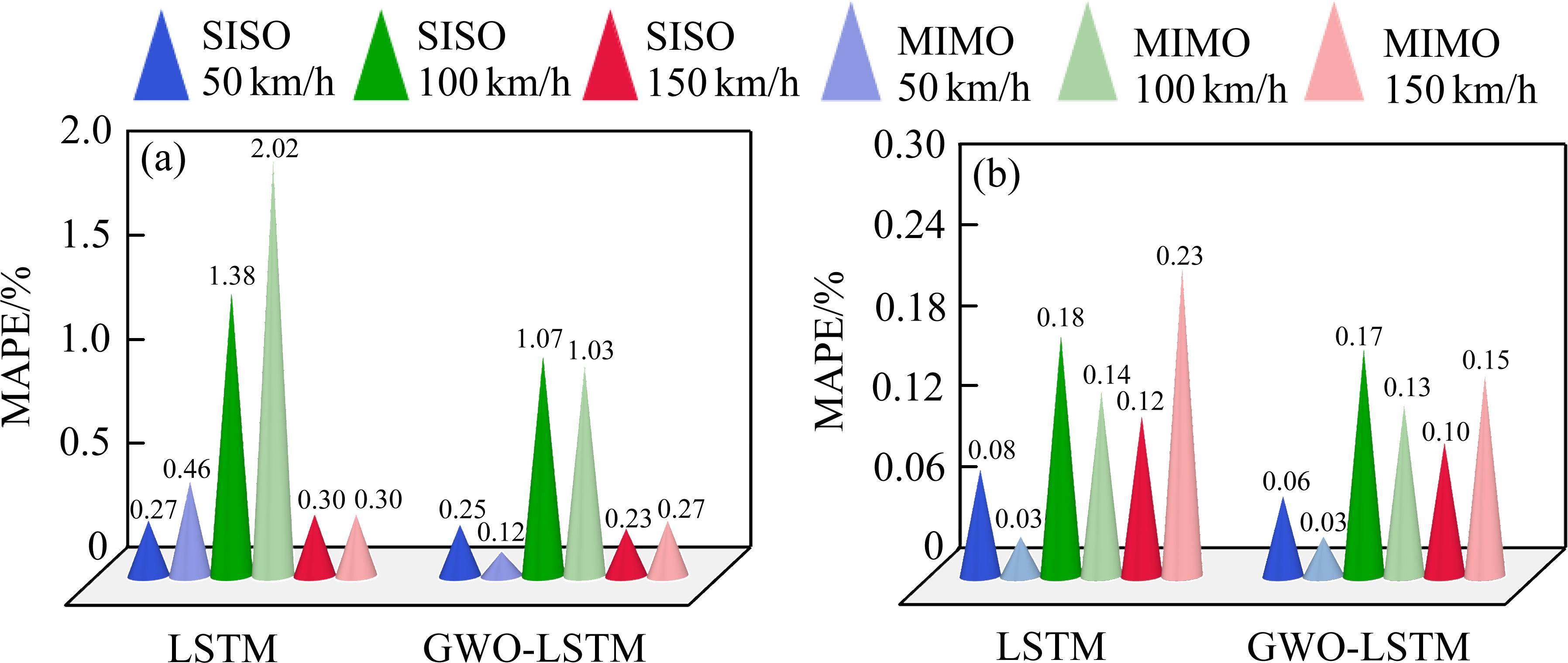
将各预测模型的MAPE指标汇总进一步分析,如表2所示,可知GWO-LSTM模型的MAPE均比LSTM模型小,例如在车速100 km/h工况下,LSTM代理模型的桥梁位移响应预测MAPE值超过了25%,而GWO-LSTM模型将该值控制在10%以内。整体来看,桥梁结构线性与非线性工况下,GWO-LSTM模型的MAPE均少于10%,大部分不超过5%,证明了该模型具有良好的预测精度。
| 评价指标 | 车速/(km∙h-1) | 网络类型 | 桥梁跨中竖向位移 | 车体竖向加速度 | 轮轨力 | |||
|---|---|---|---|---|---|---|---|---|
| 非线性 | 线性 | 非线性 | 线性 | 非线性 | 线性 | |||
| MAPE/% | 50 | LSTM | 3.70 | 4.89 | 2.96 | 0.86 | 0.27 | 0.08 |
| GWO-LSTM | 1.82 | 2.62 | 1.81 | 0.78 | 0.25 | 0.06 | ||
| 100 | LSTM | 26.02 | 50.45 | 7.87 | 7.44 | 1.38 | 0.18 | |
| GWO-LSTM | 6.85 | 8.89 | 0.06 | 5.21 | 1.07 | 0.17 | ||
| 150 | LSTM | 7.89 | 24.91 | 0.69 | 0.31 | 0.30 | 0.12 | |
| GWO-LSTM | 1.80 | 1.92 | 0.46 | 1.24 | 0.23 | 0.10 | ||
3.2 多输入多输出(MIMO)
对MIMO类代理模型,将桥梁跨中竖向位移、车体竖向加速度、1号轮轮轨力和地震动时程同步作为输入,训练代理模型,同时预测前3个变量的响应。此时,不需要训练3个代理模型,同时可以考虑各响应间的相互关联。图9和图10分别为响应结果和响应精度对比,同样考虑不同的车速和结构是否非线性,限于篇幅,此处也仅展示位移预测结果,其余2个变量的地震响应预测结果不再展示。
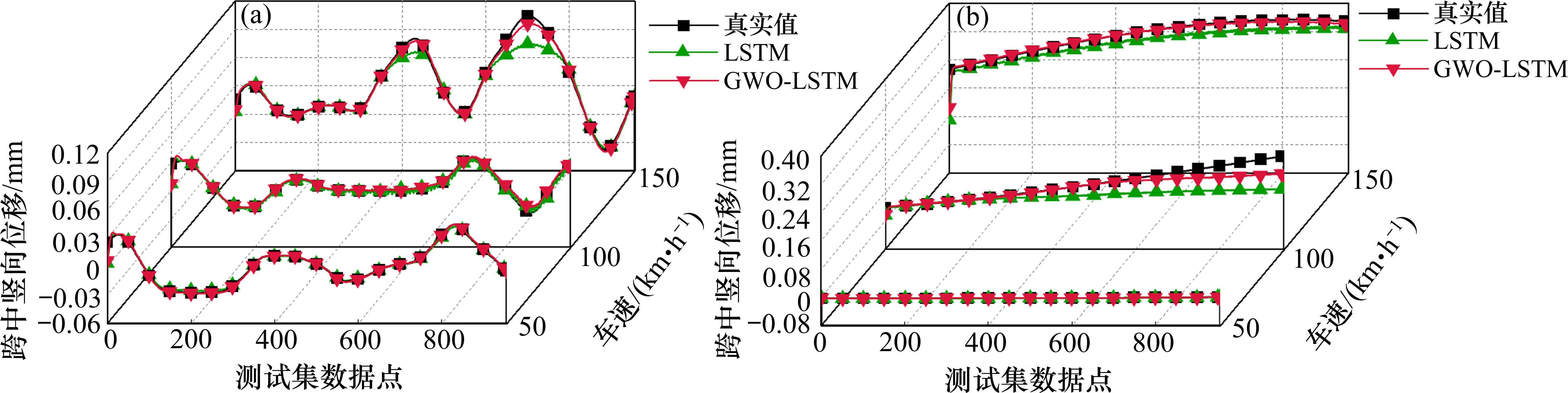
从图9可以看出,在桥梁结构非线性工况下,传统LSTM模型在峰值附近的预测结果与真实值相差较大,而GWO-LSTM模型的预测值与真实值在整个时程均较为吻合;在桥梁结构线性工况下,传统LSTM模型在部分工况下已无法预测,但GWO-LSTM模型仍能保持较高的拟合水准。从图10可知,相较于LSTM模型,GWO-LSTM模型的R2更接近1,其余指标更接近0,说明GWO-LSTM模型在同时预测桥梁位移、车体加速度、1号轮轮轨力时,仍具有比LSTM模型更高的预测精度。
将各工况下预测模型的MAPE指标汇总进一步分析,如表3所示。由表3可知,MIMO模式下,LSTM模型对桥梁跨中竖向位移的预测效果较差,且MAPE均大于GWO-LSTM模型。除50 km/h和100 km/h车速下的桥梁跨中位移响应外,GWO-LSTM模型的MAPE值都少于3%,且部分MAPE值不超过1%。综合来看,GWO-LSTM模型能够准确地同时预测3种变量的地震响应,利用MIMO类代理模型进行车桥耦合地震响应预测具有较高的可信度。
| 评价指标 | 车速/(km∙h-1) | 网络类型 | 桥梁跨中竖向位移 | 车体竖向加速度 | 轮轨力 | |||
|---|---|---|---|---|---|---|---|---|
| 非线性 | 线性 | 非线性 | 线性 | 非线性 | 线性 | |||
| MAPE/% | 50 | LSTM | 29.74 | 14.45 | 0.08 | 1.62 | 0.46 | 0.03 |
| GWO-LSTM | 9.56 | 1.57 | 0.51 | 0.64 | 0.12 | 0.03 | ||
| 100 | LSTM | 32.76 | 34.30 | 1.14 | 21.54 | 2.02 | 0.14 | |
| GWO-LSTM | 16.71 | 10.42 | 0.33 | 4.96 | 1.03 | 0.13 | ||
| 150 | LSTM | 5.97 | 7.43 | 0.30 | 1.65 | 0.30 | 0.23 | |
| GWO-LSTM | 2.92 | 1.94 | 0.41 | 0.42 | 0.27 | 0.15 | ||
此外,对比表2和表3可以发现,不管是SISO还是MIMO类代理模型,桥梁位移响应预测精度明显较车体加速度和轮轨力预测精度差,预测更难。
3.3 SISO与MIMO预测效果对比
上述分析按是否考虑各变量之间的相互影响,分SISO与MIMO分别构建代理模型。此处以轮轨力变量为例,对比SISO与MIMO的预测效果。当预测轮轨力时,2类输入输出方式下各代理模型预测的MAPE如图11所示。由图11可知,对于传统LSTM代理模型,SISO相较于MIMO训练模型的MAPE值,平均相差了49%;而GWO-LSTM代理模型的MAPE值平均相差为33%,说明当预测轮轨力时,GWO-LSTM模型比LSTM模型具有更好的稳定性。整体而言,采用MIMO模式训练的GWO-LSTM代理模型在高速铁路非线性地震响应预测中有更好的适应性。
综合上述分析表明,无论是SISO和MIMO哪种输入方式,以及是否考虑桥梁结构的非线性,在绝大多数情况下,GWO-LSTM代理模型均能保持较高的预测精度,明显优于LSTM代理模型。但部分工况下,GWO-LSTM代理模型预测精度超限,针对该问题,接下来进一步进行改进。
4 融合多策略改进灰狼优化算法
GWO在求解全局优化问题时,存在早熟收敛、易停滞在局部最优解的问题[21]。从前文预测结果可知,虽然GWO-LSTM整体预测效果较好,但小部分预测指标MAPE大于10%,超出预测精度限值。为解决此类问题,提出融合多策略灰狼优化算法(Multi Strategy Grey Wolf Optimizer,MSGWO),进一步提升代理模型的预测性能。
4.1 多策略理论
4.1.1 策略1:改进Tent混沌初始化
GWO的初始化影响其搜索性能,而当个体在搜索域中分布不均匀时,其可能会远离全局最优解,从而降低GWO收敛速度。基于Tent混沌映射方法[22],引入随机变量,可有效改善搜索性能。引入随机变量后的Tent混沌映射表达式如下:
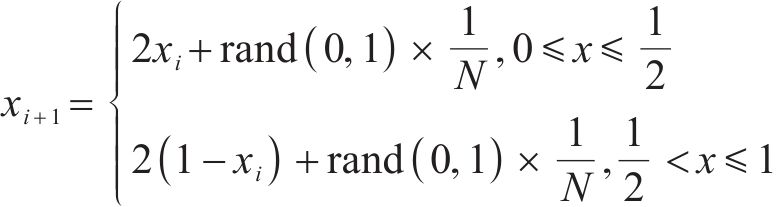
式中:xi为灰狼位置;N为序列内灰狼个数;rand(0,1)/N为随机变量,该随机变量保持了Tent混沌映射的随机性、遍历性与规律性。
4.1.2 策略2:自适应狩猎权重系数
GWO通过模拟狼群社会层次结构展开狩猎。但在原始的算法中,头狼的权重系数相同,与真实狼群等级制度矛盾。利用引力搜索算法[23]中的质量更新方法,可自适应地实现离猎物越近时头狼权重越高,进而实现α狼主导狼群活动,β、
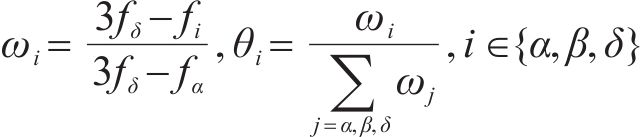
式中:ɷi为粒子(灰狼)惯性质量;θi为各头狼对应权重;fi为各狼的适应度值。
4.1.3 策略3:改进头狼位置更新机制
在原始GWO算法中灰狼更新位置的机制相同,没有考虑头狼的领导地位,不符合狼群的实际情况。当狼群被头狼吸引到一起时,种群多样性迅速下降,此时算法将早熟收敛。因此,本文对α、β、δ狼分别采用了不同的位置更新策略,其中α狼采用Levy分布策略[24],β狼采用鲸鱼优化算法[25]中的螺旋更新机制,而δ狼则跟随α、β狼更新位置。3种狼位置更新公式如下。
α狼:
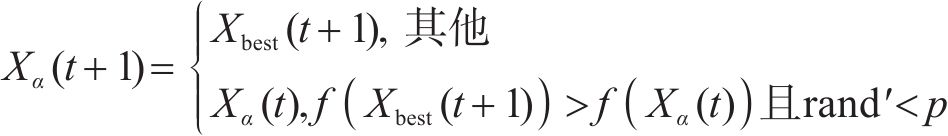
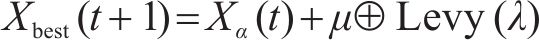
β狼:
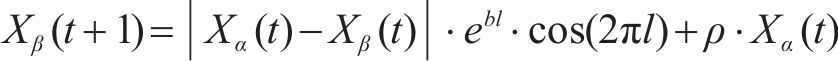
δ狼:
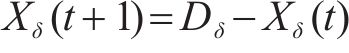
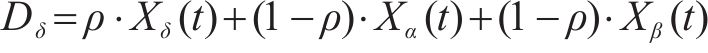
式中:X为狼的位置;f为个体适应度函数;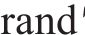
4.1.4 策略4:改进收敛因子
在原始GWO算法中收敛因子a呈线性变化,难以模拟灰狼在自然界中的复杂狩猎行为。采用正弦变化的收敛因子a改进线性搜索过程,可实现在迭代初期增大狼群勘探范围,在迭代后期减小勘探范围,以此加快收敛速度。改进的正弦a表达式如下:
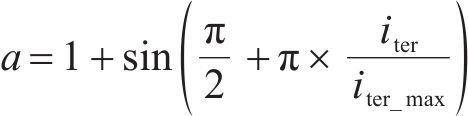
式中: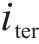
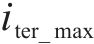
融合上述4类改进策略,构建了MSGWO-LSTM新的代理模型。接下来对新模型进行预测效果分析。
4.2 MSGWO-LSTM模型预测表现
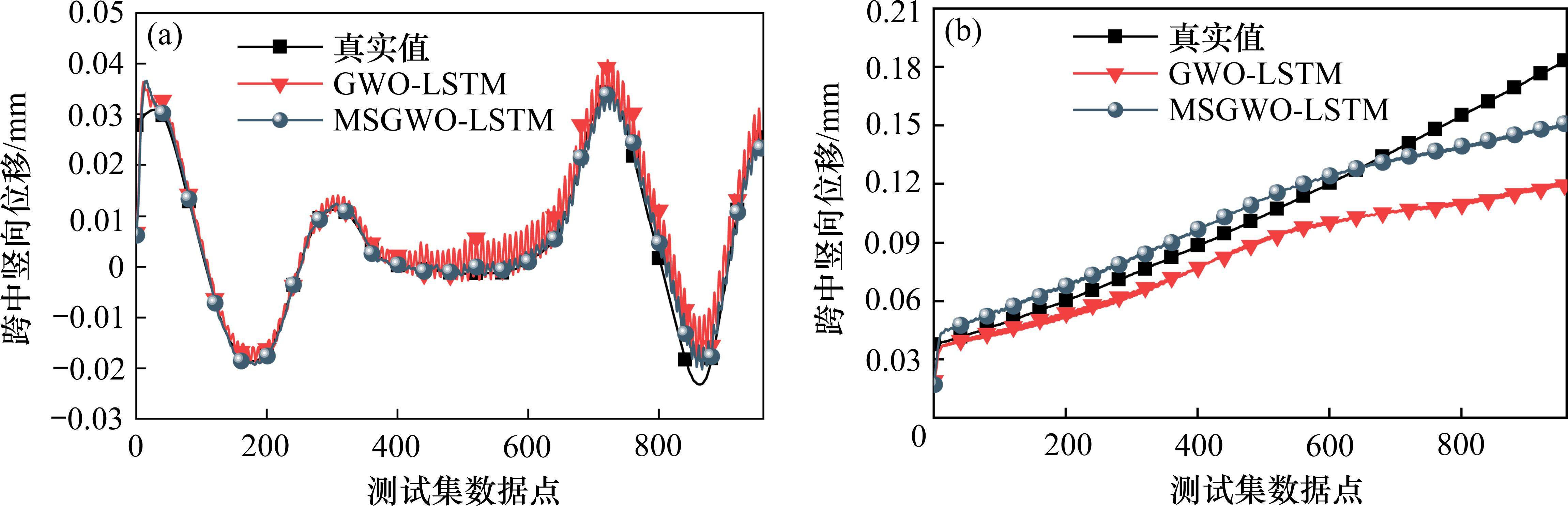
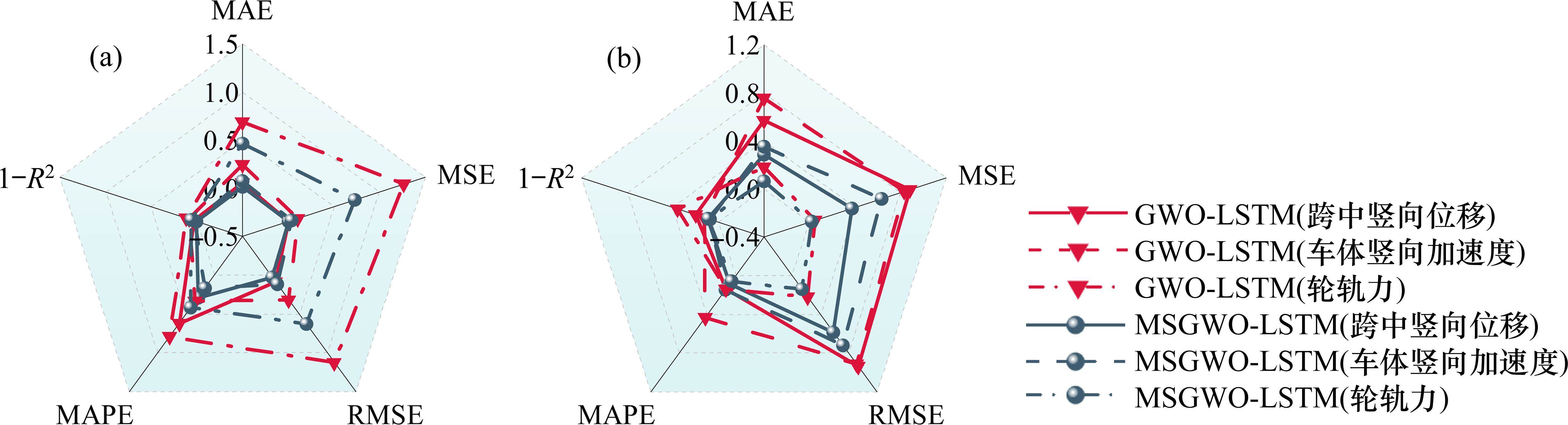
针对前文GWO-LSTM代理模型预测桥梁跨中竖向位移的MAPE大于10%的工况,利用MSGWO-LSTM代理模型重新进行预测,算法参数设置与2.2节步骤2处设置保持一致。在车速v=100 km/h、MIMO工况下,2个模型的桥梁位移响应预测结果时程对比如图12所示。为进一步证明新模型的优越性,利用新模型对该工况下的前述3种变量的地震响应进行预测,新旧模型的响应预测评价指标对比如图13所示。从图12可知,相较于原模型,改进的MSGWO-LSTM模型的预测值与真实值更吻合,其预测表现更稳定。从图13可知,同时预测3种变量的地震响应时,在桥梁结构线性与非线性工况下,MSGWO-LSTM模型的R2相比GWO-LSTM模型更接近1,其余评价指标更小,说明采用融合多策略改进灰狼优化算法确实提升了模型的预测精度。
将各工况下预测模型的MAPE指标汇总列于表4。根据表4可知,相比于原代理模型,MSGWO-LSTM代理模型将桥梁跨中竖向位移预测的MAPE降低至5%左右,满足精度要求。其中考虑桥梁结构非线性时,预测指标MAPE由16.71%降为4.06%,降低了75.7%;在桥梁结构线性工况下,预测指标MAPE由10.42%降为5.82%,只降低了44.1%。对比线性与非线性工况,发现GWO-LSTM模型预测效果由10.42%增至16.71%,而MSGWO-LSTM模型预测效果由5.82%降低为4.06%,说明MSGWO-LSTM模型非线性预测表现更佳。此外,MSGWO-LSTM模型对于车体竖向加速度、轮轨力2类预测对象的预测效果均有一定提升,其中车体竖向加速度的预测指标MAPE分别降低了15.2%、3.4%,轮轨力的预测指标MAPE分别降低了17.5%、23.1%。说明融合多策略改进GWO算法后,突破了灰狼优化算法的局限性,显著提升了模型的预测性能,MSGWO-LSTM代理模型具有更好的预测效果。
| 评价指标 | 车速/(km∙h-1) | 网络类型 | 桥梁跨中竖向位移 | 车体竖向加速度 | 轮轨力 | |||
|---|---|---|---|---|---|---|---|---|
| 非线性 | 线性 | 非线性 | 线性 | 非线性 | 线性 | |||
| MAPE/% | 100 | GWO-LSTM | 16.71 | 10.42 | 0.33 | 4.96 | 1.03 | 0.13 |
| MSGWO-LSTM | 4.06 | 5.82 | 0.28 | 4.79 | 0.85 | 0.10 | ||
5 结论
1) 在SISO模式下,无论是否考虑桥梁结构非线性,GWO-LSTM代理模型预测指标R2稳定在0.95~0.99之间,其余评价指标均接近0,且MAPE指标控制在1%左右,GWO-LSTM预测表现明显优于传统LSTM代理模型。在MIMO模式下,GWO-LSTM预测性能较SISO略有下降,出现了个别工况MAPE>10%的问题,其综合预测表现仍优于LSTM代理模型。
2) 相比GWO-LSTM,融合多策略改进的MSGWO-LSTM代理模型预测响应的R2更接近1,其余评价指标更小,说明融合策略可进一步提升模型的预测精度与泛化性能。
3) 整体上看,所构建的MSGWO-LSTM代理模型在非线性、MIMO模式下具有更好的预测准确性和泛化性,可准确预测地震下车桥系统非线性响应。研究成果可为高速铁路车桥系统地震响应预测及行车安全评估等研究提供一定参考价值。
Adam: a method for stochastic optimization
[EB/OL]. (刘汉云,王子逸,韩艳等.基于MSGWO-LSTM的车桥非线性系统地震响应预测研究[J].铁道科学与工程学报,2025,22(02):734-747.
LIU Hanyun,WANG Ziyi,HAN Yan,et al.Research on earthquake response prediction of nonlinear vehicle bridge systems based on MSGWO-LSTM[J].Journal of Railway Science and Engineering,2025,22(02):734-747.

