突变风是指风速在极短的时间内突然增大的加速气流,其发生概率小、破坏性强,对结构的安全起决定性的作用。突变风的存在非常普遍,自然界中诸如下击暴流、龙卷风和台风等,而当车-桥系统跨越山区峡谷地带复杂风场[1]、隧道出入口[2]、大型桥塔[3]以及风屏障[4, 5]等区域也会出现突变风现象。随着我国越来越多大跨度桥梁的建设,突变风环境下桥梁自身的稳定性以及列车行车安全性越来越受到关注。矩形、圆形钝体断面作为桥梁、建筑结构及构件简化形式,目前有关突变风的研究多以这2类断面为研究对象,研究内容主要是以加速气流为特点的突变风作用下的三分力非定常特性[6-8]。SARPKAYA等[9]通过水洞试验发现二维圆柱体和一些非对称柱体在加速流体作用的初始阶段均会出现三分力系数非定常现象,且阻力系数影响明显,存在过增现象。MATSUMOTO等[10]通过百叶窗模拟的突变风风洞试验也发现二维圆柱和矩形柱体的阻力系数“过增”现象。TAKEUCHI等[11]通过主动控制装置发现加速气流下椭圆截面的非定常气动力也会出现明显的过增现象,阻力过增可达2~3倍,升力则有7~10倍,而且在CFD的模拟中出现了同样的结果,不过数值远小于试验结果。还有一些研究发现加速气流对三分力系数几乎无影响,并不会出现过增现象。YANG等[6, 8]通过百叶窗模拟的突变风下矩形棱柱截面测压实验,发现在整个Re范围下阻力系数和升力系数几乎都不受影响,甚至是变小。而刘庆宽等[12]通过电压控制的方法模拟加速气流作用下的圆柱,发现三分力系数无非定常现象。赵杨等[13]在二维圆柱和方柱中也得出加速气流对阻力系数与侧力系数2个系数影响不大的结论。目前有关突变风的研究直接以列车和桥梁作为研究对象的较少,研究手段主要是通过改装现有常规风洞生成具有加速特点的突变气流进而研究其作用下的列车和桥梁气动力非定常特性。针对列车,松本胜[14]通过百叶窗模拟突变风研究了突变风荷载对火车的影响,发现当平均风速随时间呈阶跃状变化时,在达到平稳升力之前,一旦反向,其绝对值就会比平稳升力大很多。寇丽君[15]发现突变风下列车气动力和气动力矩数值变化明显,进而TAKEUCHI等[16]以列车车厢作为试验对象发现突变风荷载的冲击效应和风的上升时间与目标风速相关,突变气流对其阻力和升力的放大系数在1.5~2.0范围内。针对桥梁,马赛东[17]通过多风扇主动控制风洞探究了突风对流线箱梁、开槽箱梁等桥梁节段模型的气动特性的影响,发现在突风作用下风压系数会出现过增现象,但是阻力系数和升力系数无明显的过增现象,而加速度与风攻角是影响风压系数、静气动力系数和斯托罗哈数的重要因素。同样,赵诗宇[18]在闭口流线箱梁中也发现风压过增现象。然而,DONG等[19]通过多风扇主动控制风洞研究强阵风下闭口钝体箱梁的气动力变化规律,发现短时间阵风下的阻力、升力和升力力矩系数均明显大于均匀流动条件下的系数,进而于淼[20]基于整体位移响应总结了突变气流对该桥产生的荷载与内力变化规律。由此可知,上述关于突变风对列车、桥梁结构气动力作用的研究多为风洞试验且仅针对单车或单桥结构。一方面,风洞试验生成的突变风加速度无法恒定,不能准确探究不同加速度作用的差异;另一方面,目前针对突变风作用下车-桥系统的气动非定常特性尚无研究,而李文舒等[21]通过采用错列布置的二维圆柱和矩形钝体结构为抽象模型发现横风中高速列车-桥梁系统存在复杂气动干扰效应。因此,本文的研究手段基于ANSYS fluent的数值模拟,其中,突变风的模拟通过MATLAB生成具有恒定加速度的特征的突变风速时程,并以C语言编译方式在fluent UDF接口定义为入口速度条件。此外,为了充分全面认识风-车-桥的耦合作用,本文的研究对象是车-桥系统模型,即以和谐号钝体列车和流线型箱梁作为车-桥系统整体进行研究。
1 车-桥系统模型及数值模拟
1.1 车-桥系统模型
该箱梁横断面为扁平闭口六边形,全宽B=34 m,桥轴线处梁高D=3.5 m,该列车为和谐号标准列车,全宽b=3.365 m,高d=3.4 m。CFD计算不考虑桥面栏杆和其他附属设施,主要考虑到目前有关突变风的研究主要以二维圆形、矩形钝体截面为研究对象,本文尝试研究一个钝体列车和一个流线型箱梁组成的车-桥系统简化模型在突变风作用下的气动特性,暂时不考虑桥梁栏杆、轨道等设施因素的影响。如图1所示,其中模型内部十字圈圆心即扭心点。
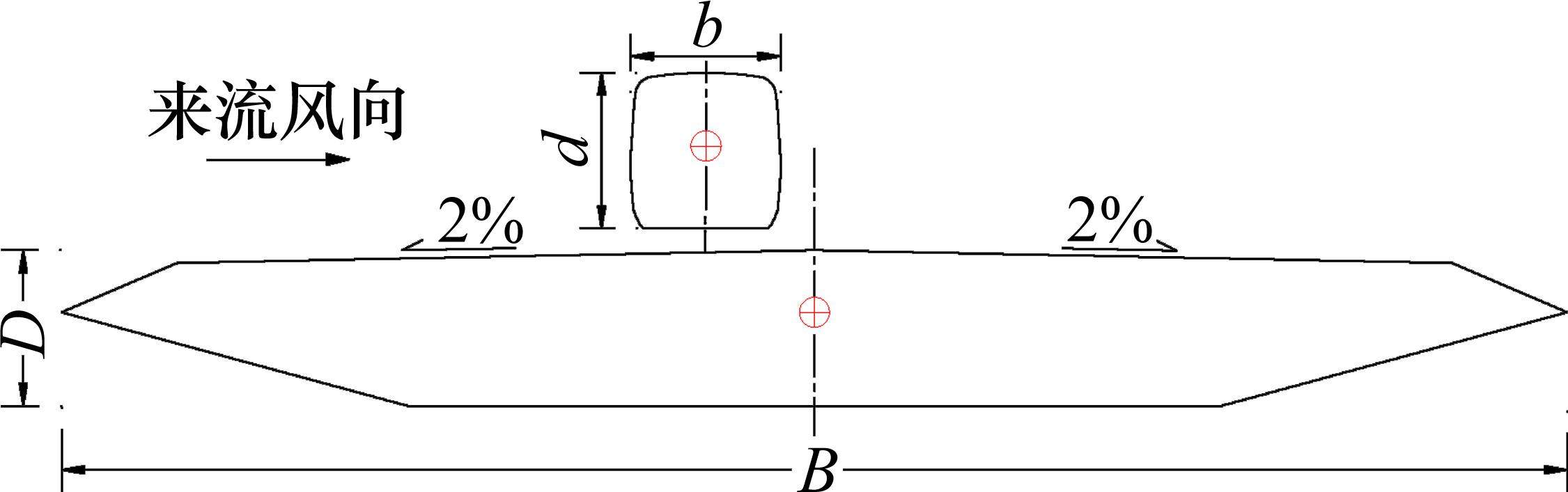
1.2 计算模型及参数设置
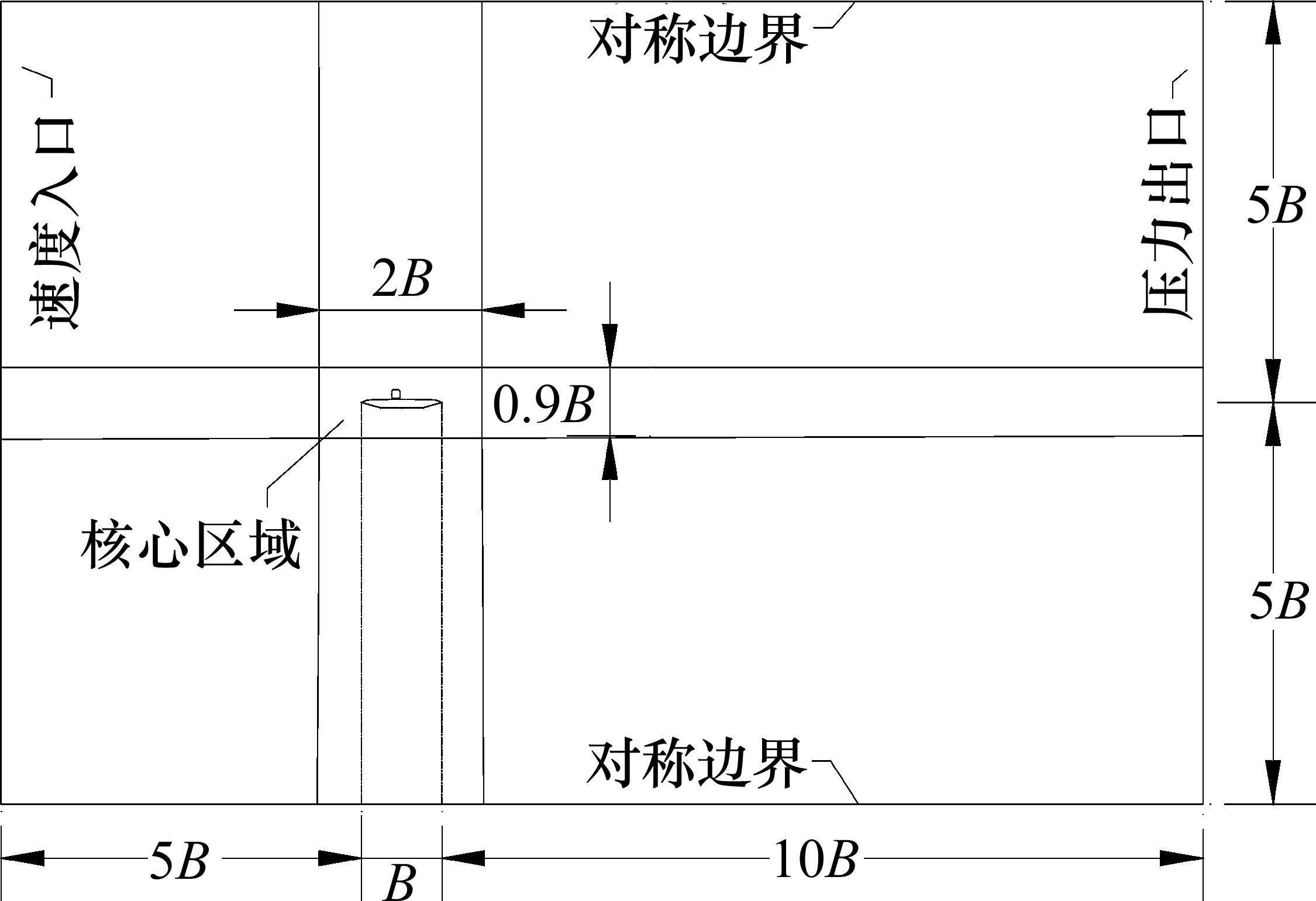
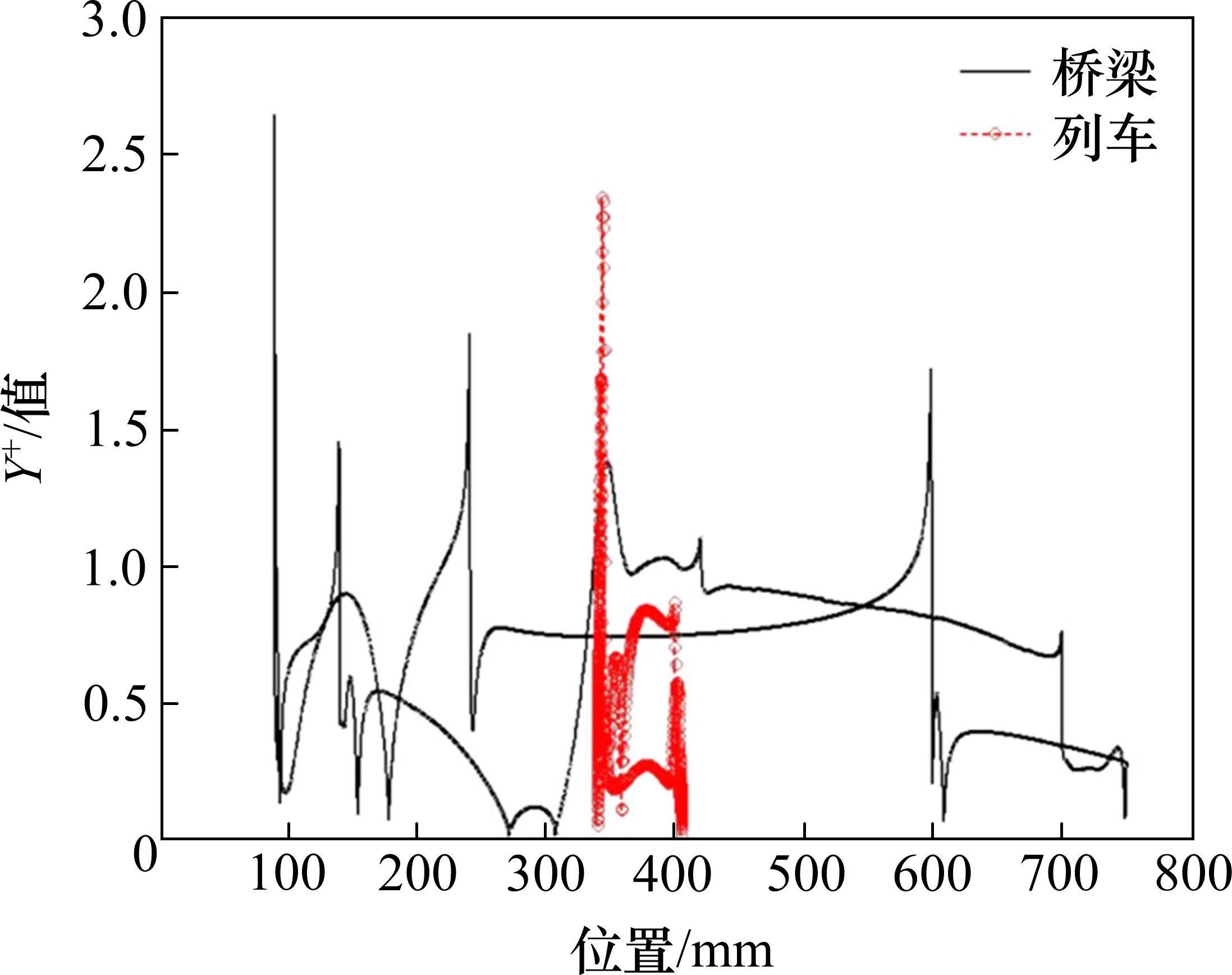
基于CFD Fluent开展瞬态数值分析。CFD模拟采用1∶50的模型缩尺比,计算域的入口、上侧和下侧边界到箱梁模型断面中心的距离均为5B,对应的模型堵塞度为2%,满足堵塞度不大于3%的要求。下游出口到箱梁的距离为10B,目的是减小下游边界对模型区流动的影响。此外,从箱梁截面扭心所在中线按上下取0.45B,左右取1.0B设置车-桥系统计算核心矩形区域。车-桥系统模型计算域划分示意图如图2所示,车-桥系统模型计算域网格布置见图3。采用计算域分区划分网格以控制网格的正交性和相邻网格边长比不大于1.2,其中二维主梁和列车表面第1层网格高度为0.000 045 m,即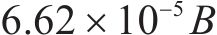
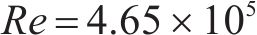

1.3 突变风模型及工况设置
据现场实测可知,诸如热带气旋、龙卷风和下击暴流等突变风均表现出类似的特征,即平均风速有一个阶跃,风速的上升或下降持续的时间较短,而脉动风速是一个0均值随机过程。根据现有的突变风模型,比如中国帽式阵风、IEC阵风、TSI阵风等,提炼出加速度和初速度2个关键参数。由于现有研究证明脉动风速项对三分力系数的影响较小[8, 13],故在本文中突变风的数值模拟不含脉动项,突变风模型可见式(1)。
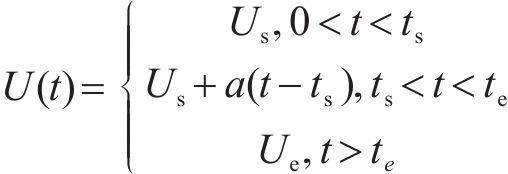
式中: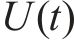
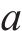
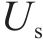
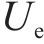
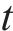
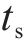
根据已有的风洞试验研究[8],计算工况以有无初速度分为A、B这2类,每类工况按4 m/s2的加速度梯度分为3组,另设置对照组均匀流工况C。工况具体设置如表1。
| 工况 | 初速度Us/(m∙s-1) | 末速度Ue/(m∙s-1) | 加速度a/(m∙s-2) | 加速起始时间ts/s | 加速终止时间te/s |
|---|---|---|---|---|---|
| A1 | 0 | 7 | 7 | 0 | 1 |
| A2 | 0 | 11 | 11 | 0 | 1 |
| A3 | 0 | 15 | 15 | 0 | 1 |
| B1 | 4 | 11 | 7 | 2 | 3 |
| B2 | 4 | 15 | 11 | 2 | 3 |
| B3 | 4 | 19 | 15 | 2 | 3 |
| C | 10 | 10 | — | — | — |
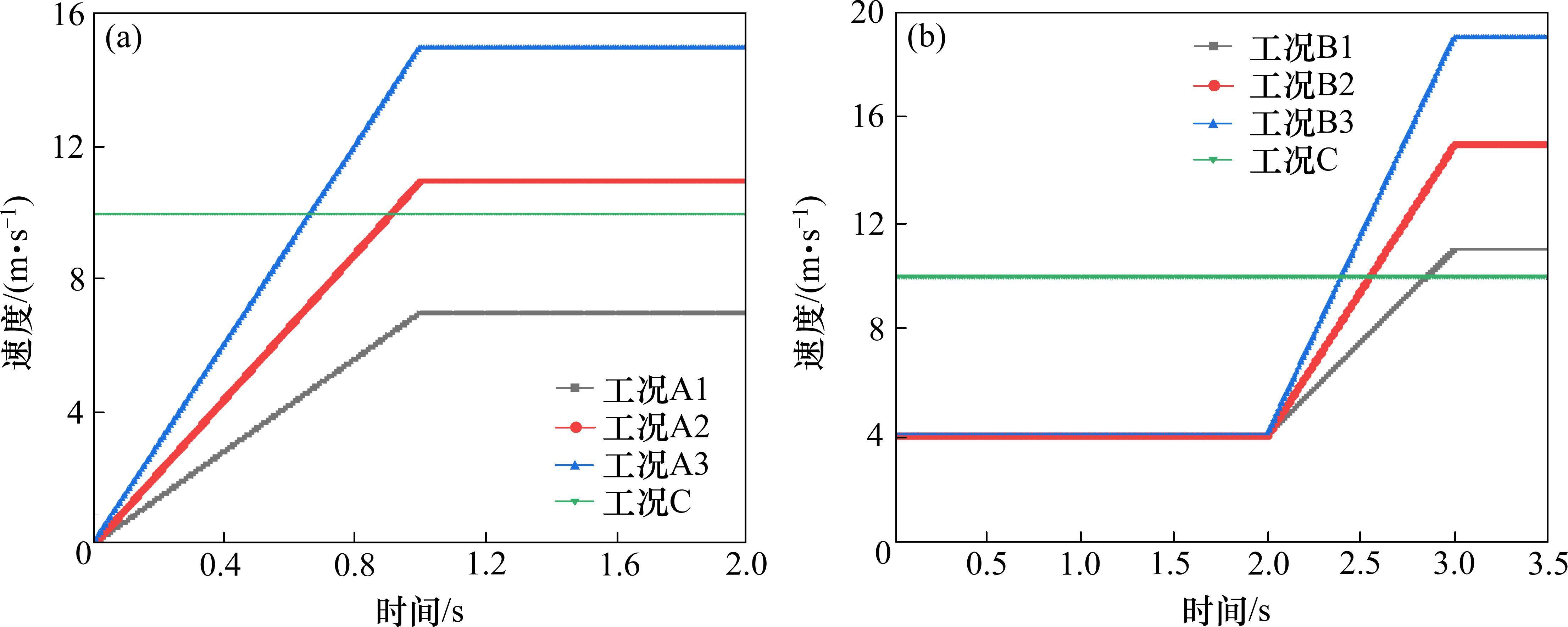
根据工况表在fluent UDF接口设置生成如图5所示的突变风工况A、B及均匀流工况C风速时程。
1.4 气动力系数及其时变性定义
选取4个时变气动系数用于车、桥及车-桥系统整体的突变风下非定常气动特性研究,即时变压力系数CP(t)、时变阻力系数CD(t)、时变升力系数CL(t)、时变扭矩系数CM(t),定义如下:
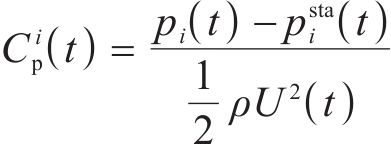
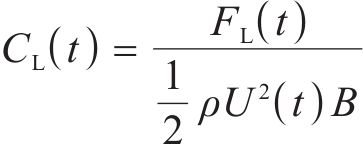
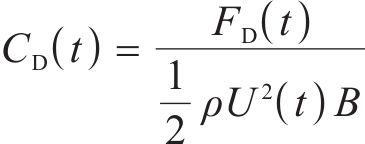
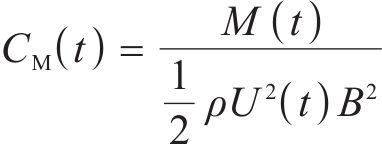
其中,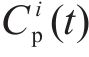
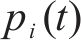
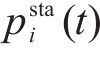
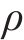
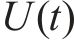
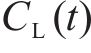
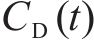
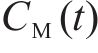
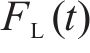
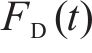
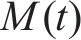
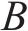
2 模型验证
2.1 车-桥系统模型风洞验证
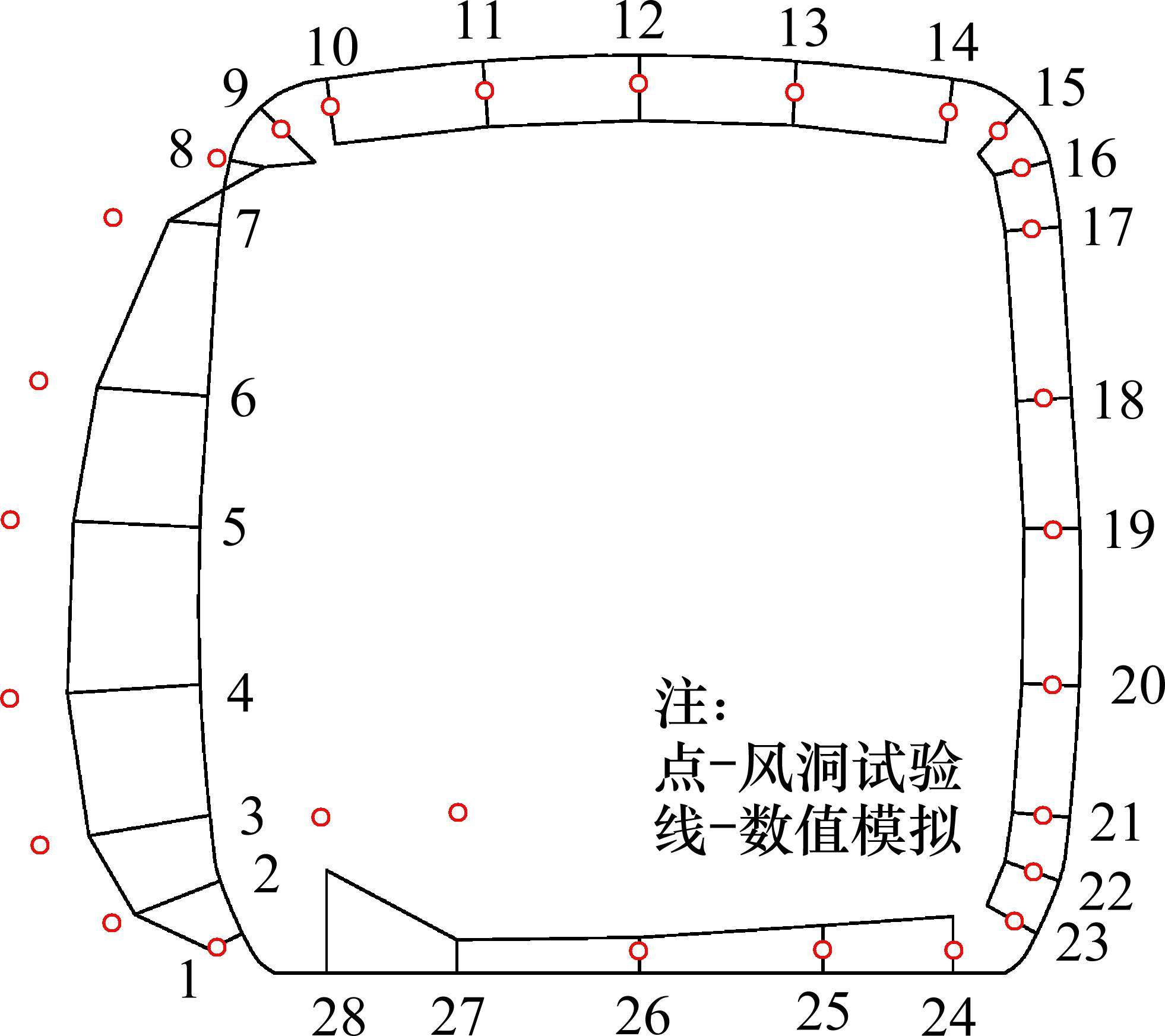
为了验证车-桥系统网格模型的准确性,在中南大学边界层风洞(CSU-1)进行了0°攻角10 m/s均匀流下车-桥系统列车测压试验,如图6所示,进而积分得到列车三分力系数。三分力系数作为评价静风荷载的一组无量纲参数,其中,列车阻力系数数值明显大于升力系数和扭矩系数,所以横风作用下列车安全的关注点一般为阻力系数值。考虑到阻力系数值远大于升力系数和扭矩系数,不同于阻力系数采用相对误差衡量,对于升力系数和扭矩系数值采用绝对误差衡量。通过数值模拟与风洞试验得到车-桥系统下列车断面三分力系数数值,见表2。可见数值模拟结果普遍小于风洞试验,而2种方式得到的阻力系数基本相符。

| 三分力系数 | 风洞试验-A | 数值模拟-B | 误差(相对/绝对) |
|---|---|---|---|
| 升力系数 | -0.248 9 | 0.109 6 | 35.85 |
| 阻力系数 | 1.212 2 | 1.072 7 | -11.50 |
| 扭矩系数 | -0.141 5 | -0.079 7 | -22.12 |
此外,通过比较数值模拟与风洞试验得到的列车断面压力系数分布,如图7所示。可见2种方式得到压力分布趋势大体一致,证明了车-桥系统网格模型的可靠性。
2.2 车-桥系统模型网格密度验证
为了进一步验证车-桥系统模型网格密度的合理性,通过对车-桥系统网格模型进行三分力系数网格密度无关性检验,结果如表3~表5所示,可得出本文在兼顾效率和准确性下采用的网格密度是合理的。
| 组别 | 网格总数/万 | 列车升力系数 | 相对误差/% | 箱梁升力系数 | 相对误差/% |
|---|---|---|---|---|---|
| 稀疏-X1 | 33(0.35T) | 0.111 9 | 2.111 6 | -0.691 0 | -1.868 1 |
| 本文-X0 | 93(T) | 0.109 6 | 0.000 0 | -0.704 2 | 0.000 0 |
| 密集-X2 | 150(1.6T) | 0.106 8 | -2.565 8 | -0.706 1 | 0.270 4 |
| 组别 | 网格总数/万 | 列车阻力系数 | 相对误差/% | 箱梁阻力系数 | 相对误差/% |
|---|---|---|---|---|---|
| 稀疏-X1 | 33(0.35T) | 1.073 6 | 0.075 7 | 0.017 1 | 0.035 0 |
| 本文-X0 | 93(T) | 1.072 7 | 0.000 0 | 0.016 8 | 0.000 0 |
| 密集-X2 | 150(1.6T) | 1.075 4 | 0.243 7 | 0.016 8 | 0.000 0 |
| 组别 | 网格总数/万 | 列车扭矩系数 | 相对误差/% | 箱梁扭矩系数 | 相对误差/% |
|---|---|---|---|---|---|
| 稀疏-X1 | 33(0.35T) | -0.075 0 | -5.870 0 | -0.161 4 | -0.938 7 |
| 本文-X0 | 93(T) | -0.079 7 | 0.000 0 | -0.162 9 | 0.000 0 |
| 密集-X2 | 150(1.6T) | -0.082 4 | 3.362 9 | -0.163 2 | 0.194 8 |
2.3 雷诺数效应
根据陈政清[22]编著的《桥梁风工程》,“在圆柱或方柱绕流中,当Re数很低时,由于黏性影响,阻力系数变得非常大,直至Re>104后,曲线才基本水平。这一性质对于大跨度桥梁近乎流线型的主梁断面的三分力系数测量具有重要指导意义。”
本文雷诺数通过式(6)计算:
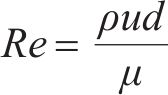
式中: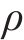
由此获得最小雷诺数数值Remin为1.86×105,该值大于104,故在本文雷诺数范围内三分力系数保持恒定,不会出现三分力系数随风速变化而不一致的雷诺数效应。而且后文中车-桥系统各工况阻力系数在不同风速工况平稳后数值相等的结果,也印证了这一结论。
3 结果与讨论
3.1 基于突变风时程的车-桥系统三分力规律分析
通过ANSYS fluent计算得到突变风工况A、B及均匀流工况C作用下车-桥系统模型三分力时程曲线,如图8~图10所示。可见突变风工况A、B与均匀流工况C在最终风速平稳后车、桥的三分力大小与最终速度大小成正比,说明计算结果的可靠性。
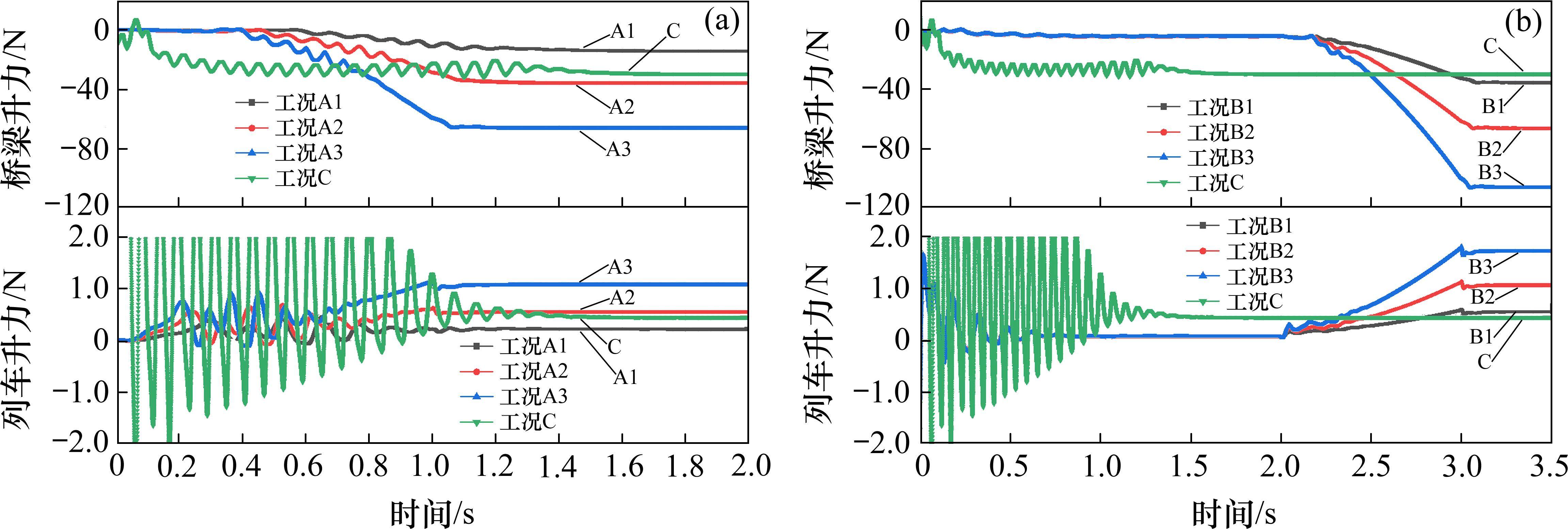
3.1.1 升力
根据图8可知,各工况下流线型箱梁的升力数值大于钝体列车,其中箱梁受到向下的升力作用,列车则受到向上的作用。此外,两者达到平稳时间无太大差异。如图8(a)所示,针对无初速的A类工况下车-桥系统,加速初段,A类工况间升力差别不明显,直到加速中段后,在一定范围内,随着加速度增大,升力绝对值增长速率变快,基本符合线性变化。如图8(b)所示,针对有初速的B类工况,从加速初段起,在一定范围内,随着加速度增大,升力绝对值增长速率同样变快,基本符合线性变化。
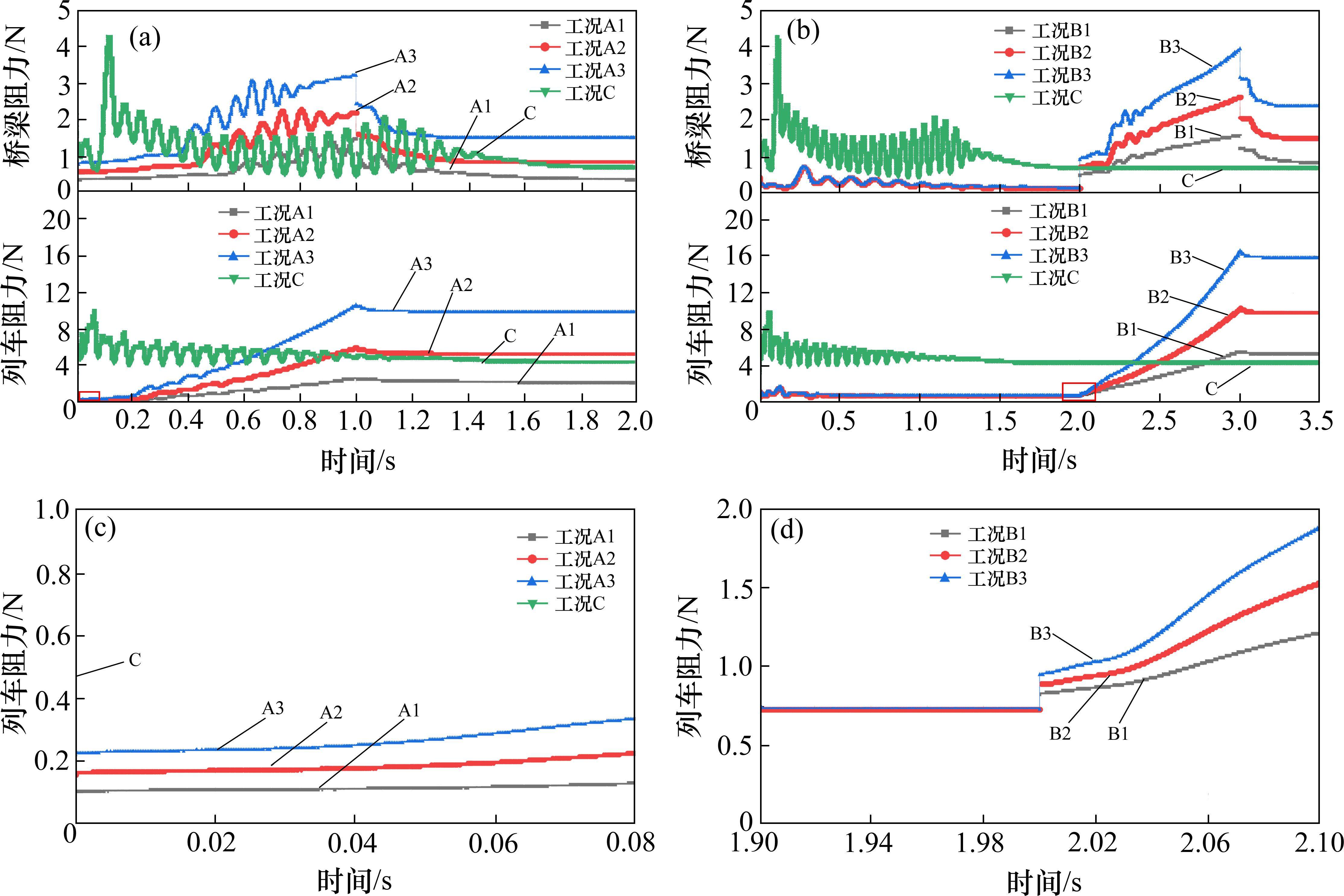
3.1.2 阻力
根据图9(a)和图9(b)可知,各工况下钝体列车的阻力数值大于流线型箱梁,两者均受到向右的阻力作用,而达到平稳时间无太大差异。此外,针对各类工况,加速起始瞬间,车-桥系统阻力数值有跃升,其中箱梁跃升现象更明显,列车阻力局部放大图可见图9(c)和图9(d);加速过程中,在一定范围内,随着加速度增大,流线型箱梁和钝体列车阻力绝对值增长速率变快,基本符合线性变化;加速终止瞬间,车-桥系统阻力数值有跃跌,其中箱梁跃跌现象更明显。对比图9(a)和图9(b)可知,有初速使得车-桥系统阻力绝对值增长速率变大。
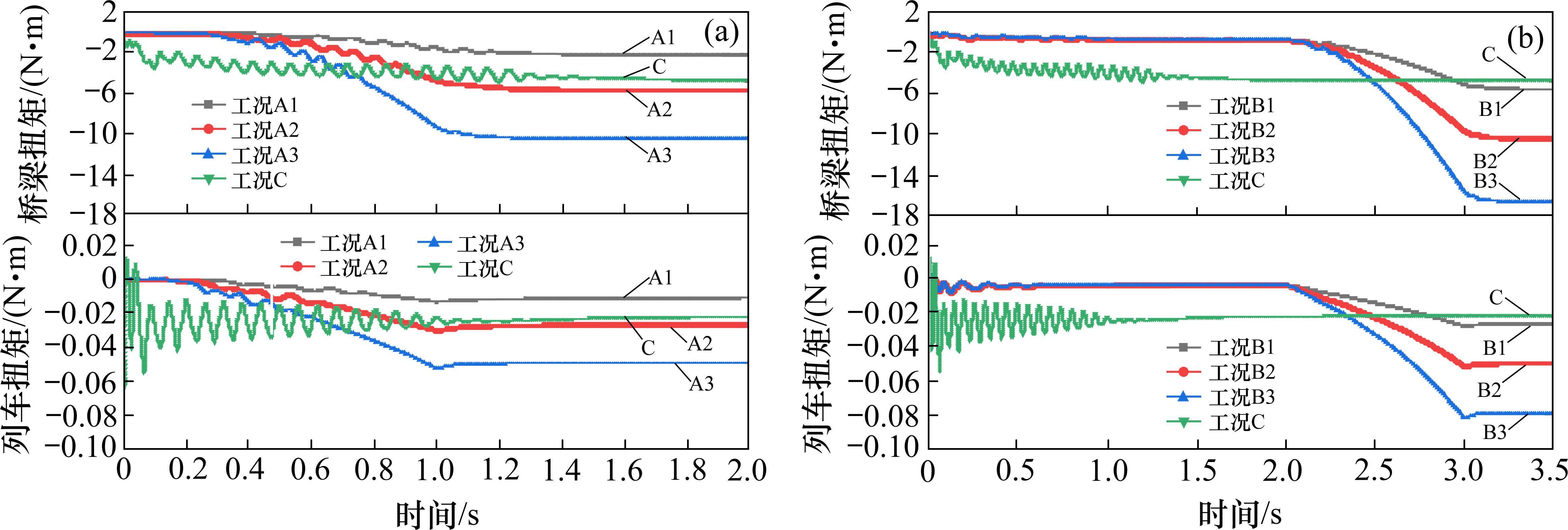
3.1.3 扭矩
根据图10可知,各工况下流线型箱梁的扭矩数值大于钝体列车,两者均受到顺时针的扭矩作用,而两者达到平稳时间无太大差异。如图10(a)所示,针对无初速的A类工况下车-桥系统,加速初段,A类工况间扭矩差别不明显,直到加速中段后,在一定范围内,随着加速度增大,扭矩绝对值增长速率变快,基本符合线性变化。如图10(b)所示,针对有初速的B类工况,从加速初段起,在一定范围内,随着加速度增大,扭矩绝对值增长速率同样变快,基本符合线性变化。
3.1.4 超冲系数
根据3.1.1~3.1.3节的分析,阻力在气流加速段出现了超冲现象,即在加速过程中,阻力数值超出该工况下最终风速的平稳数值的现象。为了衡量这一超冲现象,定义超冲系数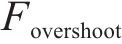
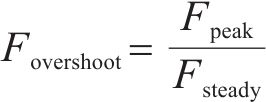
式中: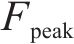
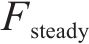
超冲系数在一定程度上表征了惯性力与准定常力的比值,在此列出阻力的超冲数值,如表6所示。可见对于钝体列车,超冲系数值维持在1.0~1.1,加速度造成的阻力超冲现象并不明显;而对于流线型箱梁,超冲系数值最大可达4.1,加速度造成的阻力超冲现象显著,在各种突变风工况下,在一定范围内,加速度越大,阻力超冲系数越小。此外,因为初速度的存在,B类工况的超冲系数值比之A类工况有所减小。
| 工况 | 流线型箱梁 | 钝体 列车 | 工况 | 流线型箱梁 | 钝体 列车 |
|---|---|---|---|---|---|
| A1 | 4.1 | 1.2 | B1 | 3.2 | 1.1 |
| A2 | 2.6 | 1.1 | B2 | 1.8 | 1.1 |
| A3 | 2.1 | 1.1 | B3 | 1.7 | 1.0 |
3.2 基于突变风时程的车-桥系统阻力系数规律分析
通过处理上节提到的三分力时程可以获得突变风工况A、B及均匀流工况C作用下车-桥系统模型三分力系数时程,3个气动力系数均出现显著的非定常特性,在加速初段,升力系数CL(t)、阻力系数CD(t)和扭矩系数CM(t)波动幅度大,加速后段逐步平稳,回到均匀流相应水平。由于篇幅限制,本文只展示阻力系数时程规律分析结果,如图11所示。由图11可见,突变风工况A、工况B与均匀流工况C在最终风速平稳后车、桥的阻力系数基本相互符合,印证了本文计算的可靠性,并提示突变风作用下的结构气动力非定常特性是短期效应。为了衡量这一效应,引入非定常效应(非定常效应,即从加速时刻起到平稳时刻止,三分力系数时程曲线与平稳时三分力系数值横轴围成区域的面积叠加。其中,均匀流工况C以0时刻为起点,A类工况根据本文图幅以0.2 s时刻为起点,B类工况以2.0 s时刻为起点,见图11中的“起始线”点虚线)。此外,需要说明的是,针对无初始速度的A类工况,加速初始阶段的阻力系数不具实际意义,故在下文不作分析。
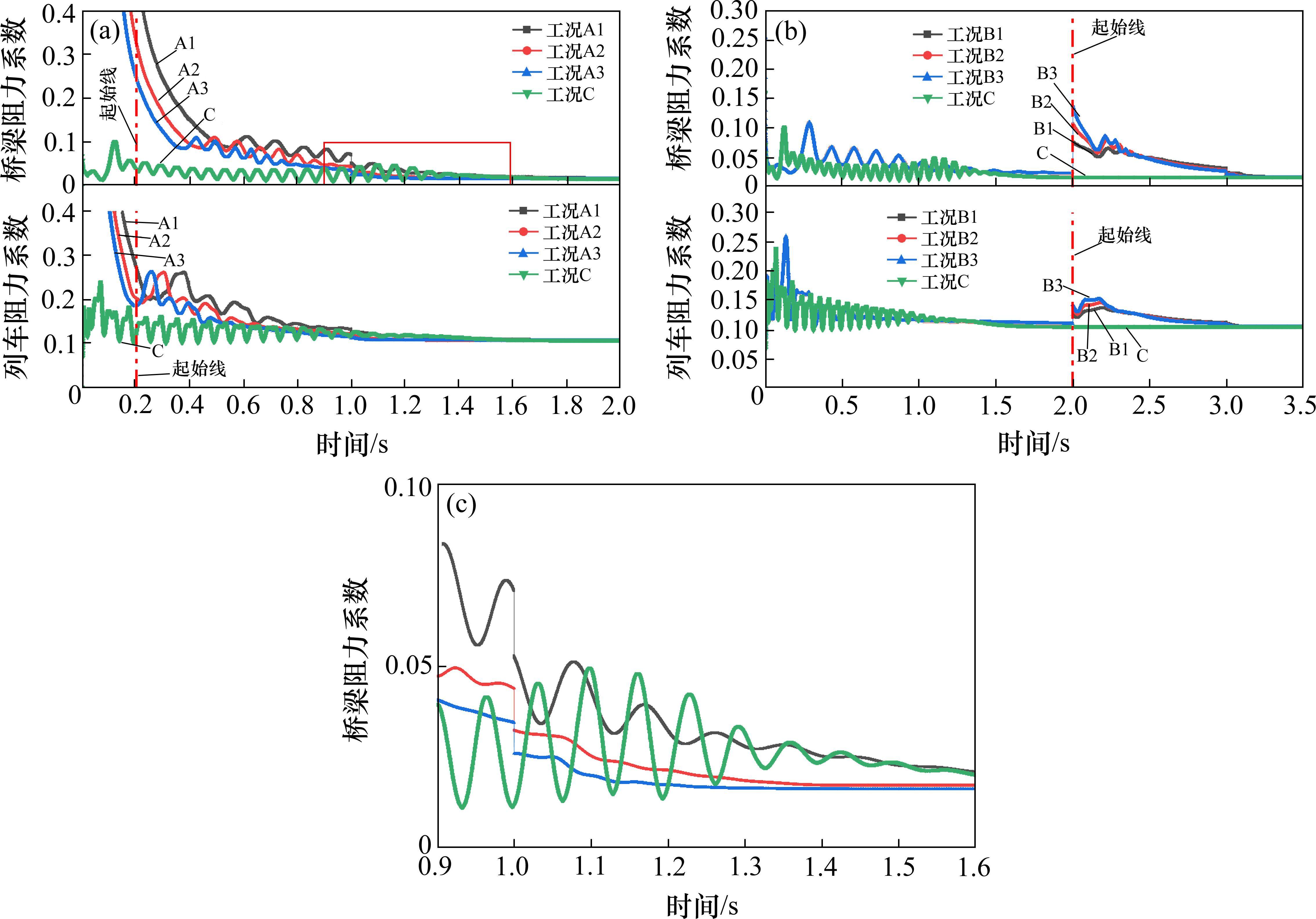
根据图11可知,各工况下钝体列车的阻力系数与流线型箱梁基本同时达到平稳,波动幅度差异不明显,而列车平稳后数值更大。如图11(a)所示,针对无初速的A类工况,与均匀流工况C相比,由于加速度的存在,A类工况阻力系数具有更大幅度的波动性,体现为更大的非定常效应,此外,在一定范围内,随着加速度增大,阻力系数达到平稳的时刻会提前,波动幅值差异不明显,所以非定常效应逐渐减小。如图11(b)所示,针对有初速的B类工况,与均匀流工况C相比,由于加速度的存在,B类工况阻力系数同样具有更大幅度的波动性,不过波动幅度小于A类,此外,在一定范围内,随着加速度增大,阻力系数达到平稳的时刻无明显差异,而波动幅值逐渐增大,所以非定常效应逐渐增大。
无初速工况三分力系数非定常效应呈现随着加速度的增大而减小的现象,可能与平稳耗时有关。根据均匀流工况结果可知,风速越大,平稳耗时越短。这可能表明,当速度足够大时,三分力系数达到平稳的时间将实现同步。
4 结论
1) 在各突变风工况中,车-桥系统中流线型箱梁比钝体列车受到的升力和扭矩大,而钝体列车比流线型箱梁受到的阻力更大。
2) 车-桥系统在加速初始和结束时刻会出现阻力跃升和跃跌,原因可能在于加速度的有无,因为阻力的产生是模型断面前后表面的压强差的面积分,由此当开始加速和终止加速时,阻力作用在前后表面的差异是显著的,表现为阻力突变。而升力、扭矩与上下表面的压强差有关,当加速开始和终止时,风对上下表面的压强影响基本是同步的,则不会出现明显的突变。其中流线型箱梁在加速过程中出现阻力超冲现象,超冲系数值最大可达4.1,而钝体列车超冲系数值维持在1.0~1.1之间,基本无阻力超冲现象。此外,比之无初速工况,有初速会降低阻力超冲系数值。
3) 3个气动力系数均出现显著的非定常特性,在加速初段,升力系数CL(t)、阻力系数CD(t)和扭矩系数CM(t)波动幅度大,加速后段逐步平稳,回到均匀流相应水平。
4) 具有初速度的工况车-桥系统三分力绝对值增长速率更快,而不具有初速度的工况车-桥系统三分力系数非定常效应则更为明显,说明初速度的存在会减弱三分力系数非定常效应。
5) 在不同加速度的工况之间,非定常效应也存在差异性,对于有初速的突变风工况,在一定范围内,车-桥系统三分力系数非定常效应随着加速度的增大而增大,然而,对于无初速的工况则随着加速度的增大而减小,这可能是平稳耗时导致的。
Investigation on the unsteady aerodynamic force on a 3: 2 rectangular section under accelerating airflow
[C]//肖洋,何旭辉.突变风下车-桥系统三分力系数演化规律的CFD分析[J].铁道科学与工程学报,2025,22(02):723-733.
XIAO Yang,HE Xuhui.CFD analysis of the evolution rule of the three-component force coefficient of the vehicle-bridge system under abrupt wind action[J].Journal of Railway Science and Engineering,2025,22(02):723-733.

