轴向磁通电机具有体积小、质量小、效率和可靠性高等优点,广泛应用于航空航天、风力发电和电动汽车等重要领域[1-3]。与传统径向磁通电机相比,轴向磁通电机扁平形状的定转子使得散热更加容易,并且在相同功率需求下体积更小,适用于结构紧凑的应用场景[4-5],但传统轴向磁通电机只能单自由度输出动力,且需要机械变速箱来匹配高速电机与低速负载等[6]。多端口磁性行星齿轮永磁电机既继承了轴向磁通电机的优点,又融合了行星磁齿轮的驱动特点,可以实现不同端口之间的能量转换,实现直接驱动和多自由度功率输出,适用于航空航天、电动汽车和新型军事装备等领域,对轴向磁通电机新拓扑结构的发展具有重要意义。
近年来,为解决传统轴向磁通电机单自由度输出动力的问题,国内外学者基于轴向磁通电机结构,提出改变其定转子数量来设计不同拓扑结构的轴向磁通电机[7-12]。LIU等[9]设计了一种新型空间盘式行星电机,该电机综合了盘式电机和永磁行星齿轮的优点,可以实现多端口不同方向的动力输出,提高了动力传动系统的紧凑性,但由于该电机定子结构的特点,使得定子和盘式转子之间形成不均匀气隙,降低了电机的电磁特性。ZHU等[7]设计了一种新型多端口磁性行星齿轮永磁电机,实现了动力和扭矩在不同电气或机械端口之间的灵活组合和分配。基于以上研究,本文设计了一种新型多端口盘式永磁电机(multi-port disk permanent magnet motor, MDPMM)。MDPMM环形弧线定子周向端部影响区域的漏磁和磁场分布较为复杂,研究其电磁特性时主要采用有限元仿真来降低分析难度[10],但有限元仿真耗时较长,在电机设计前期需要频繁调整电机结构参数,因此,该方法并不利于电机的前期设计。等效磁网络法[13-14]融合了有限元法和磁路法的优点,在电机设计初期能够快速、准确地解析MDPMM受环形弧线定子端部影响区域的磁场分布,为后期优化该电机结构参数以提高电磁特性和动力学特性奠定基础。于慎波等[15]采用三维等效磁网络法将轴向磁通电机的三维等效磁网络模型简化为二维等效磁网络模型,以简化磁路计算。GHODS等[16]以游标直线电机为模型,采用等效磁网络法降低了模型计算的复杂性,提高了计算的准确性。
在多自由度电机的基础上,本文结合多端口磁性行星齿轮永磁电机和轴向永磁电机,提出一种新型多端口盘式永磁电机,该电机具有多自由度功率输出、结构紧凑等优点。首先,介绍了该电机的工作原理及驱动特点;其次,采用等效磁网络法和等效磁化强度法对该电机环形弧线定子区域的漏磁系数和磁场分布进行求解;最后,将有限元与解析计算结果进行对比,验证等效磁网络模型与空载气隙磁密解析模型的有效性。
1 结构原理
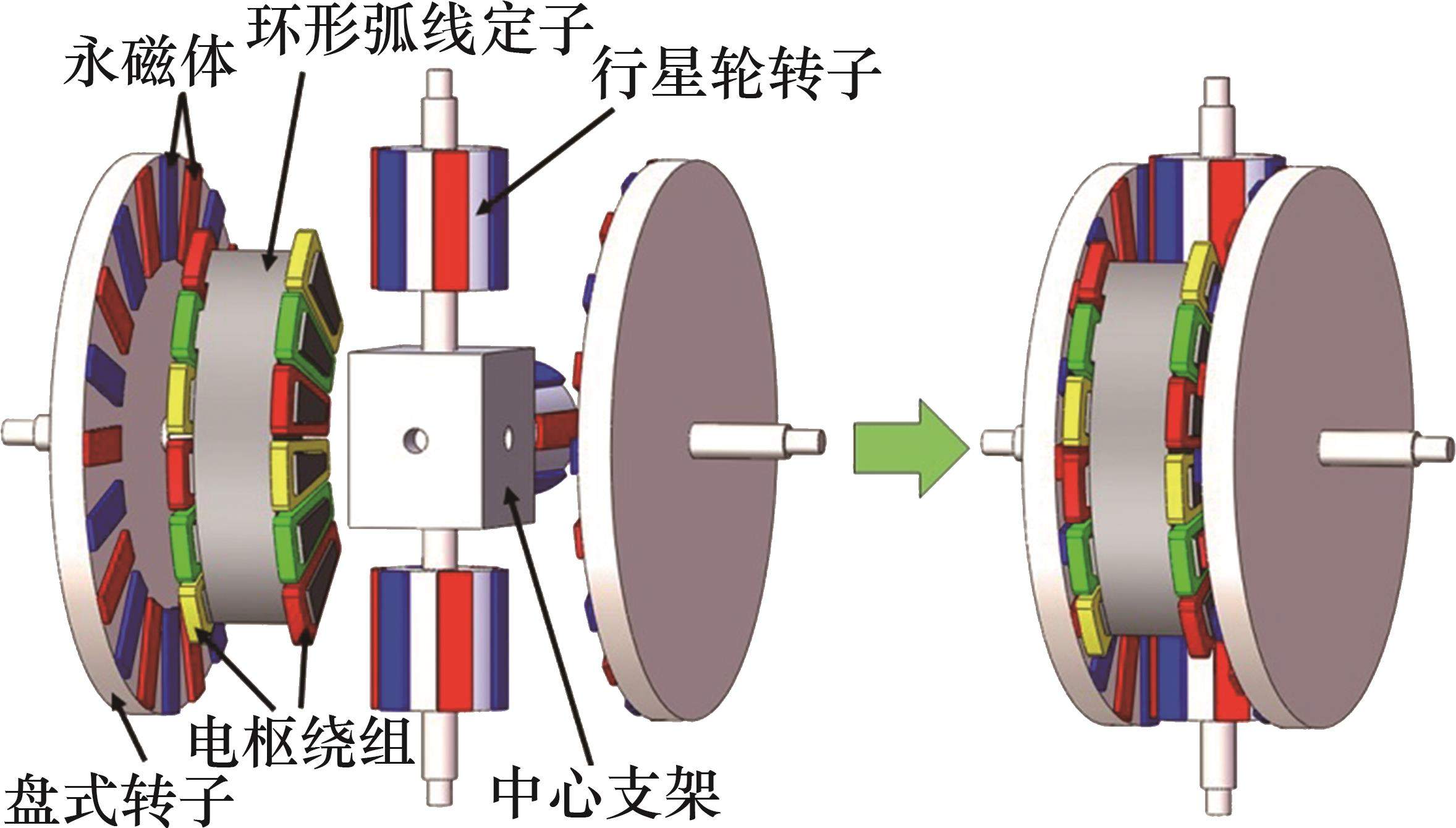
新型多端口盘式永磁电机结构如图1所示,它主要由环形弧线定子、左右盘式转子和行星轮转子组成。在环形弧线定子上开有电枢槽用以嵌放绕组,电枢绕组通入三相交流电产生旋转磁场驱动盘式转子转动,实现盘式转子的动力输出;行星轮转子在两盘式转子间周向放置,由转子轴固定在支架上,盘式转子与行星轮转子上贴有NS极相间的永磁体,盘式转子在环形弧线定子电枢绕组产生的旋转磁场驱动下,通过其表贴的永磁体和行星轮转子表贴的永磁体产生磁力耦合来驱动行星轮转子旋转,实现行星轮转子的动力输出。由于盘式转子和行星轮转子通过其表贴的永磁体相互磁力耦合传递动力,因此,盘式转子与行星轮转子的驱动关系符合磁齿轮传动的减速关系。可以看出,MDPMM在实现盘式永磁电机和复合驱动系统一体化的同时,也实现了多自由度的动力输出,适用于要求结构紧凑和多自由度动力输出的领域。
2 等效磁网络模型
MDPMM磁路主要由盘式转子与环形弧线定子间的磁路以及盘式转子与行星轮转子间的磁路两部分组成。由于环形弧线定子周向存在端部,盘式转子磁极与环形弧线定子端部齿之间出现磁场分布不均匀的现象,且两端部存在气隙磁阻异常的磁通路,因此,本文主要对MDPMM环形弧线定子的磁网络模型进行分析研究。
2.1 磁路分析
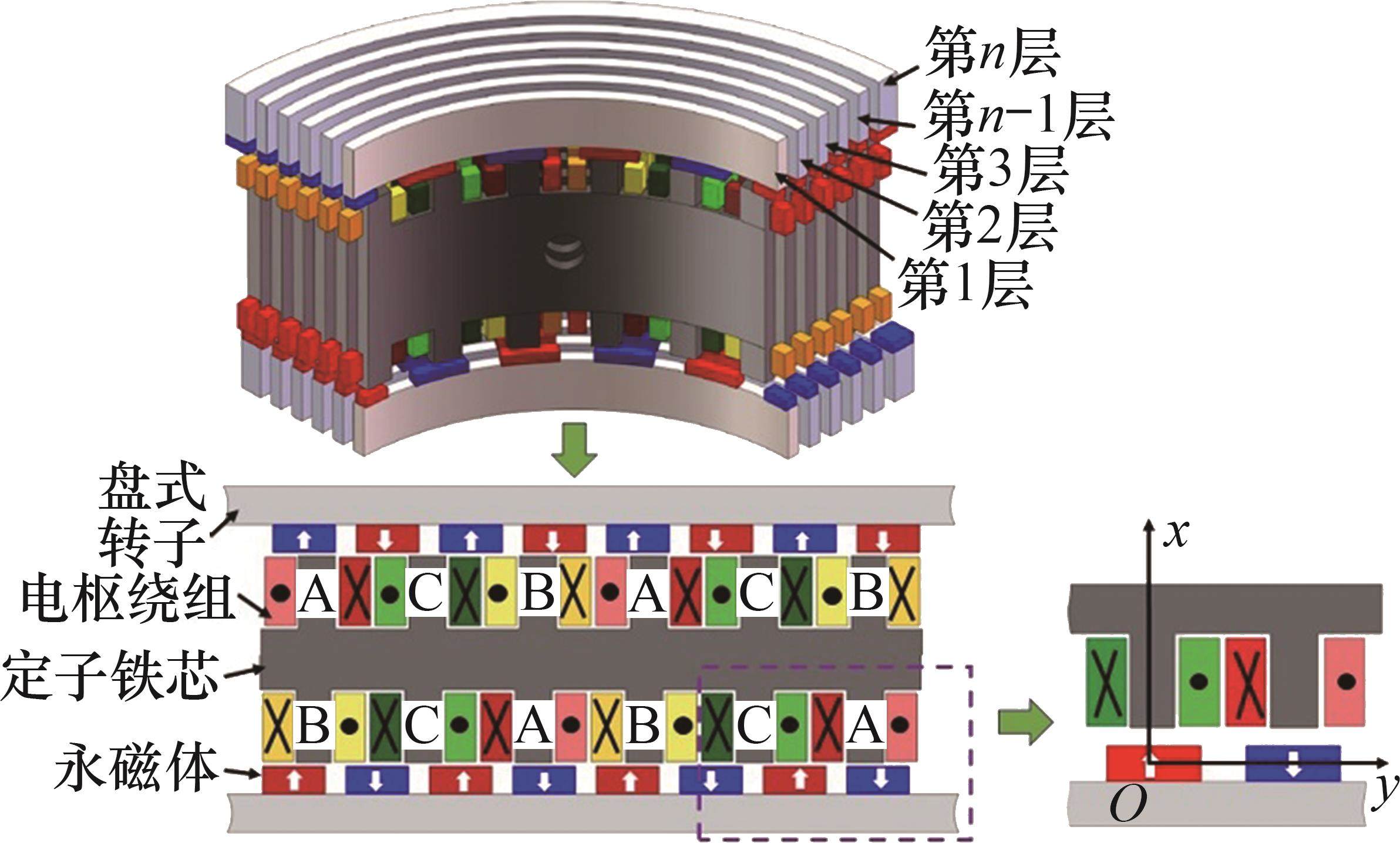
在MDPMM中,环形弧线定子和盘式转子结构上具有对称性,对磁路进行分析时,取环形弧线定子下端部与下盘式转子的1对磁极区域进行分析,以便对其静态行为进行描述。首先,将环形弧线定子区域的三维模型沿径向等分成n层,取任意层展开成二维模型,再取其端部一个极距区域放在直角坐标系下对磁路进行分析,如图2所示。
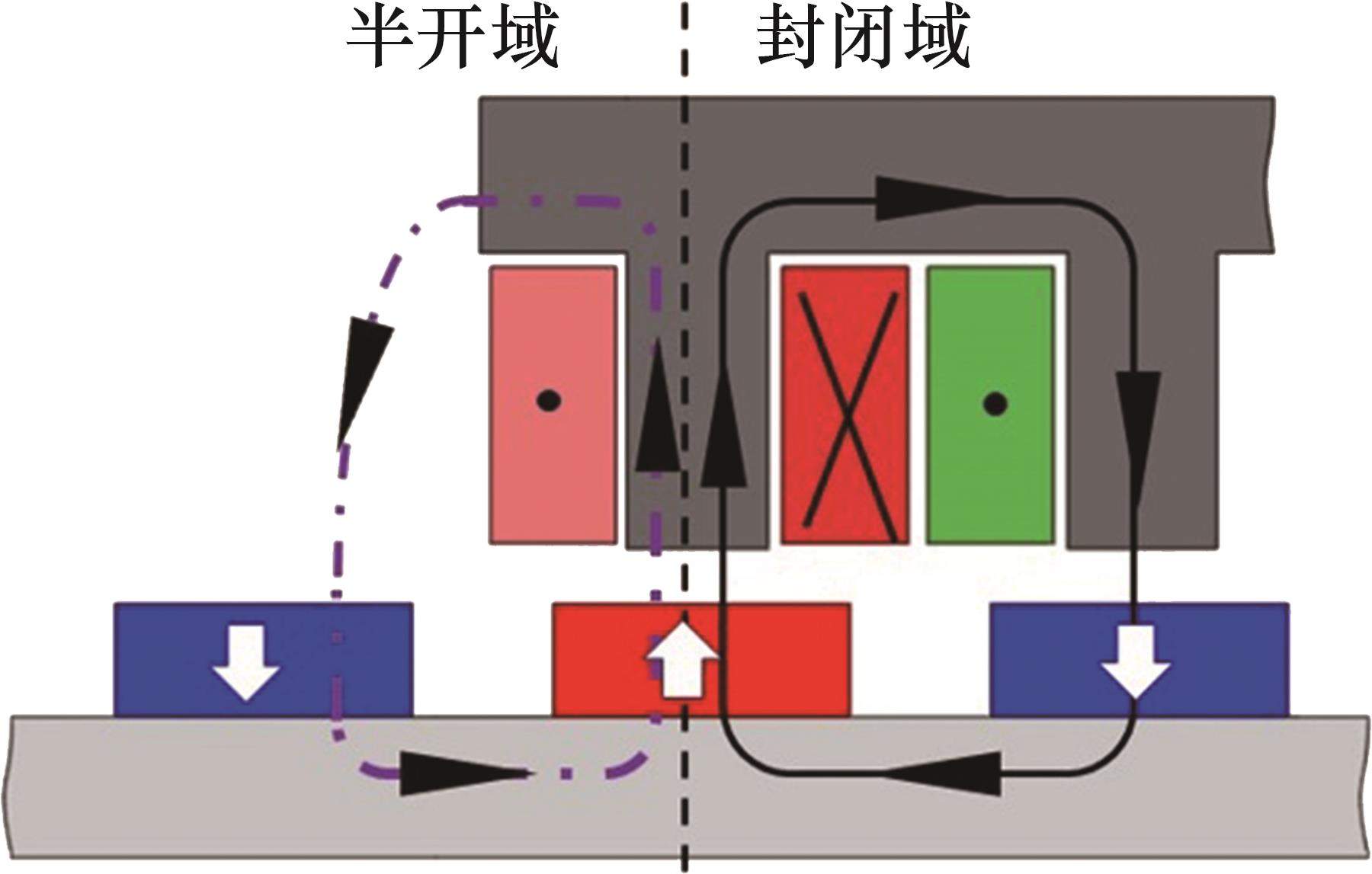
等效模型静态磁路模型如图3所示。端部区域磁路包含半开域和封闭域两部分磁路,且端部具有特有的气隙磁路。在盘式转子磁齿极面与环形弧线定子端部齿中心线对齐时,磁极产生的一部分磁通经过下气隙、电枢铁芯、端部气隙后流入盘式转子另一磁极,再穿过盘式转子轭部形成闭合回路;另一部分磁通经过下气隙、电枢铁芯、下气隙后流入盘式转子另一磁极,再穿过盘式转子轭部形成闭合回路。在对应磁网络模型中,各部分以相应的磁阻来表示,其磁阻可分为气隙磁阻、环形弧线定子极和定子轭磁阻、盘式转子磁极和转子轭磁阻。
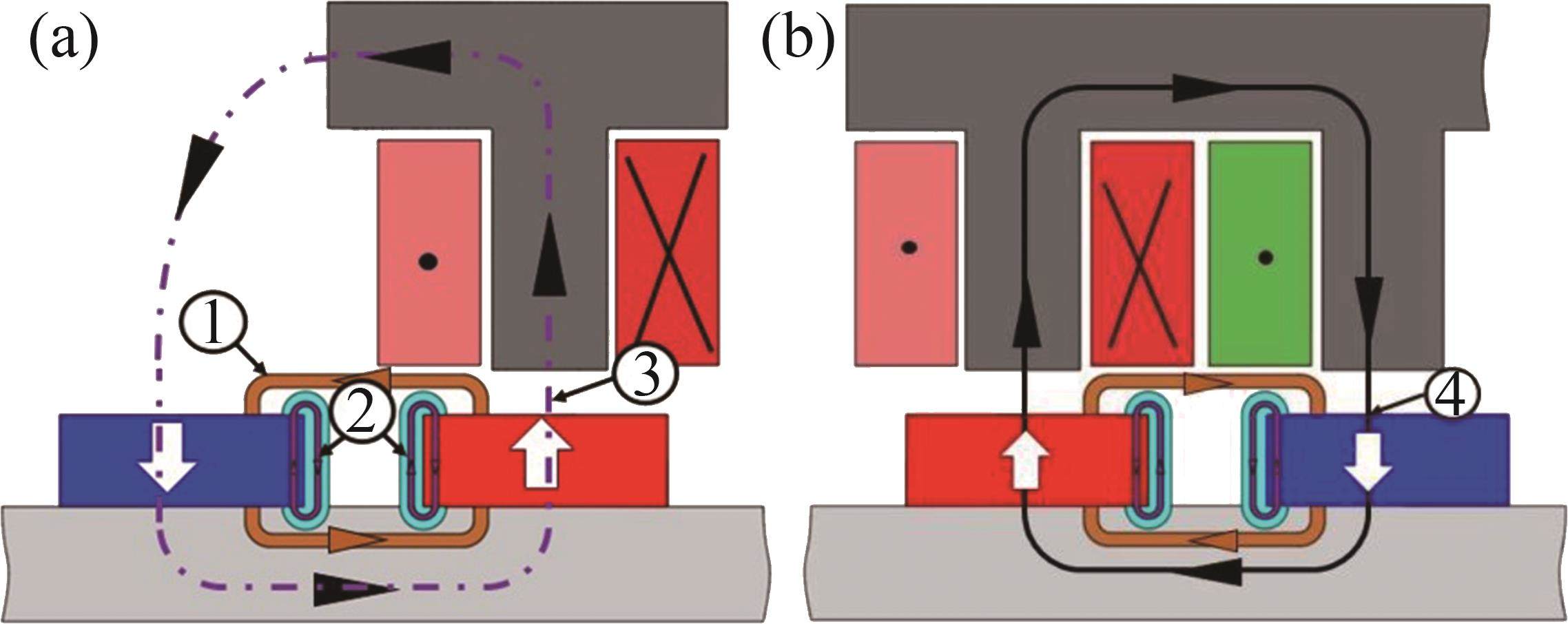
为了分析盘式转子转动过程的动态行为,建立MDPMM环形弧线定子端部区域对应的两个特殊位置磁路模型,其中一个为盘式转子的一个磁齿极面与环形弧线定子端部齿中心线对齐位置;另一个为盘式转子的一对磁齿极面与环形弧线定子端部两齿中心线对齐位置,如图4所示。为了提高等效磁网络法的计算精度,考虑盘式转子磁齿之间、磁齿边缘及磁齿周向漏磁,图4中回路①表示相邻磁齿间漏磁磁路,回路②表示磁齿边缘漏磁磁路,回路③表示受环形弧线定子端部影响的主磁路,回路④表示未受环形弧线定子端部影响的主磁路。
2.2 等效磁网络模型
建立考虑环形弧线定子端部效应的等效磁网络模型,如图5所示。在该磁路中,永磁体由虚拟内禀磁通Φri和磁阻Rm组成;盘式转子磁齿边缘、相邻磁齿之间、磁齿周向的漏磁阻分别为Rmr、Rmm、Rma;Φm为永磁体总磁通;Rg为气隙磁阻;Re为端部永磁体外区域的气隙磁阻;Rmσ为永磁体端部漏磁磁阻。
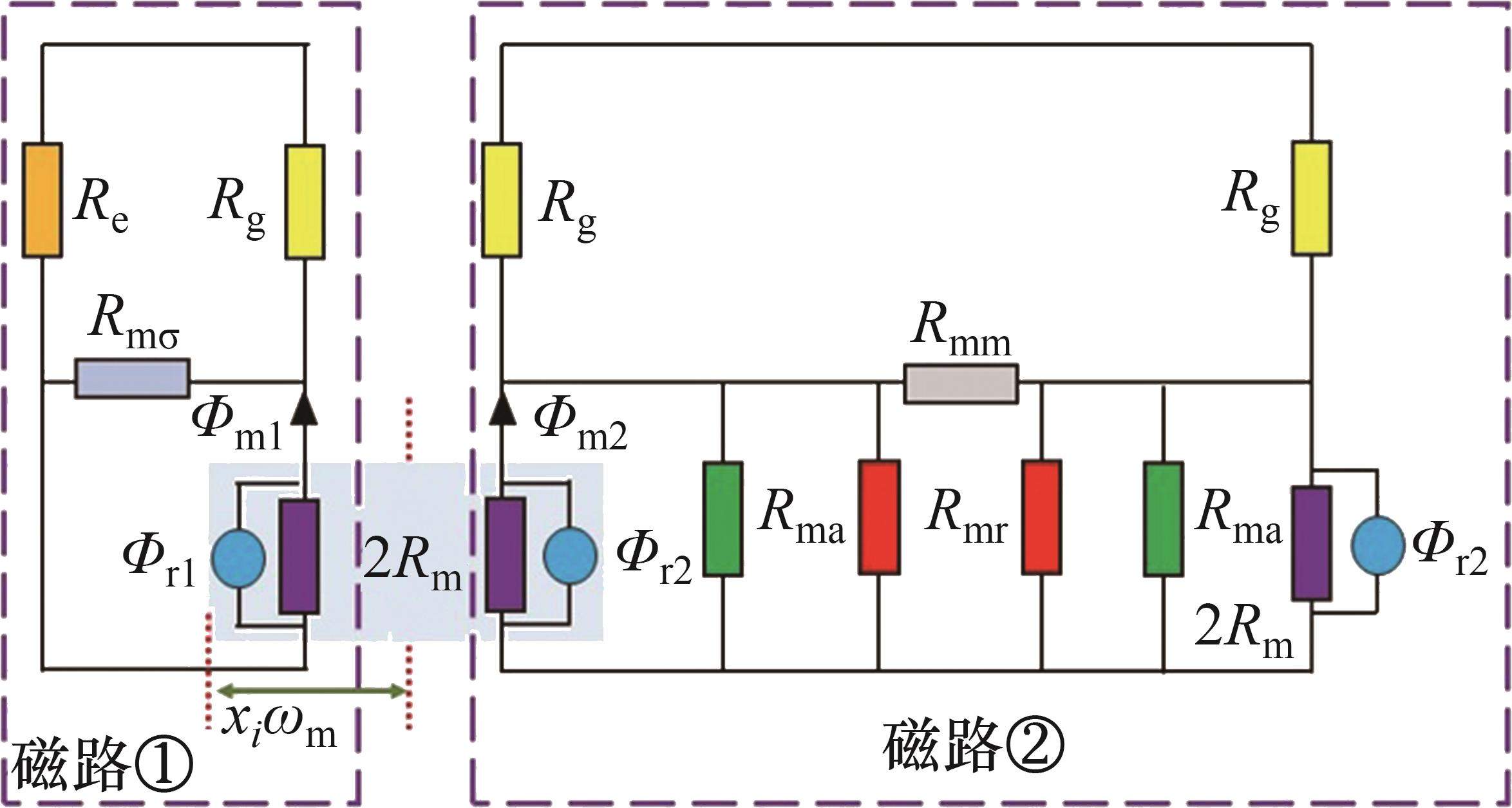
对于考虑端部效应的环形弧线定子端部区域等效磁网络模型,当盘式转子任意磁极与环形弧线定子端部齿耦合时,该磁极磁通将分为磁路①磁通和磁路②磁通。本文引入磁通分布系数xi(0≤ xi≤1)来衡量该磁极磁通不均匀分配状态,如图5所示。本文以磁齿极面中心线与环形弧线定子端部齿中心线对齐位置来分别研究磁路①磁通和磁路②磁通。
2.3 等效磁网络模型参数计算
对受环形弧线定子端部截面影响的磁路①简化等效后,得到等效磁网络模型,如图6所示。在该磁路中,端部磁场为半开域磁场,通过端部磁路的气隙磁通量Φg1和端部永磁体外区域的气隙磁阻Re分别为:
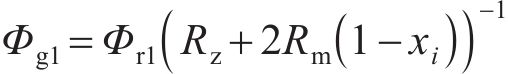
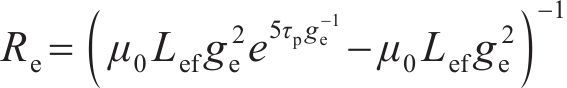
式中: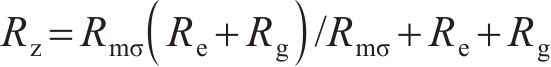
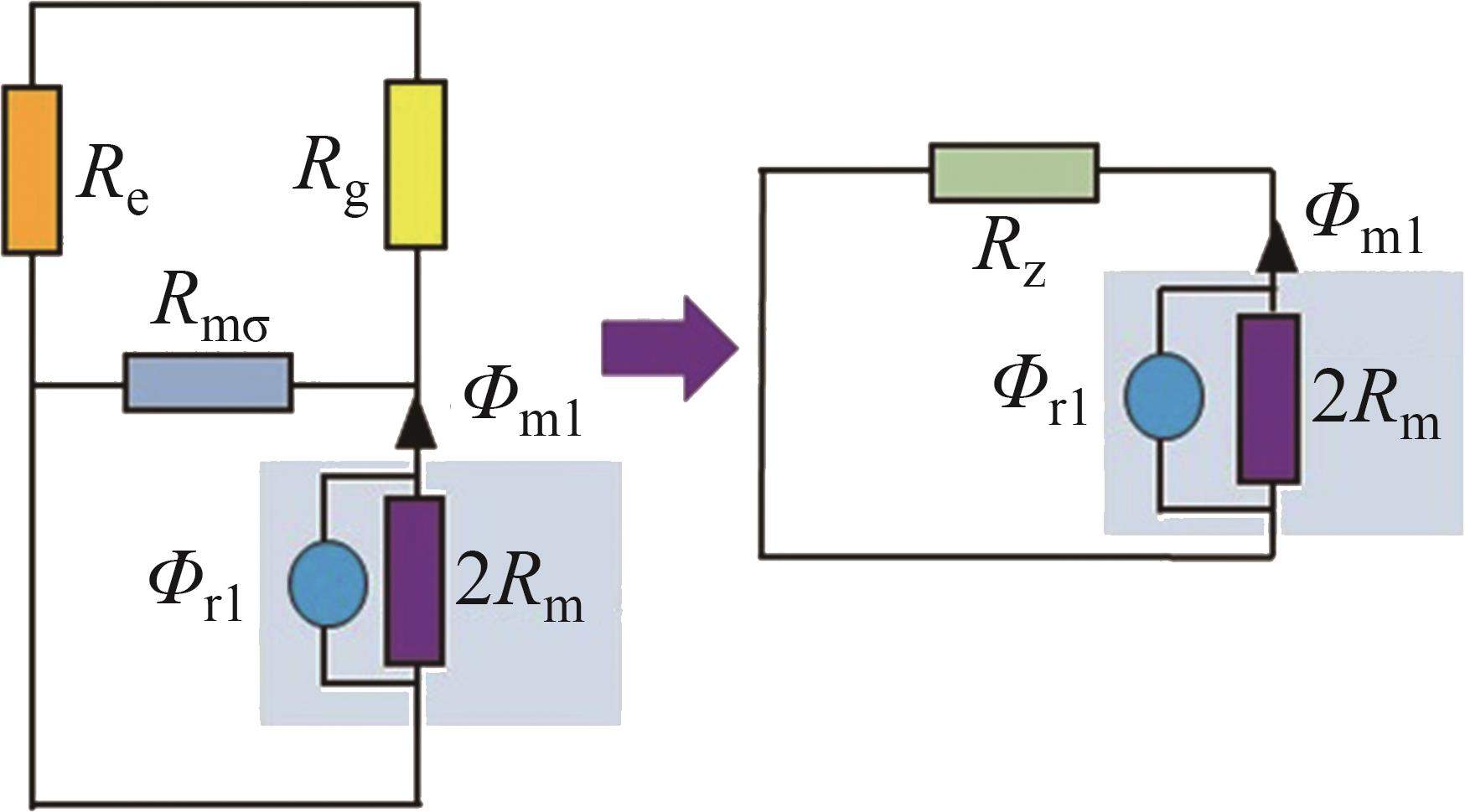
端部漏磁主要为相邻磁齿间漏磁,将漏磁路径等效为圆周长的1/4,沿该路径积分得
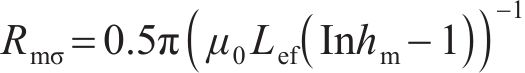
式中:hm为永磁体厚度。
因此,受环形弧线定子端部截面影响区域的平均气隙磁通密度为
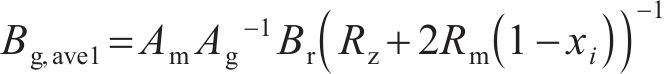
式中:Am永磁体轴向面积;Ag为气隙面积;Br为永磁体剩余磁化强度。
对未受环形弧线定子端部截面影响的磁路②简化等效后,得到等效磁网络模型,如图7所示。计算每极气隙主磁通Φg2和每极总磁通Φm2为:
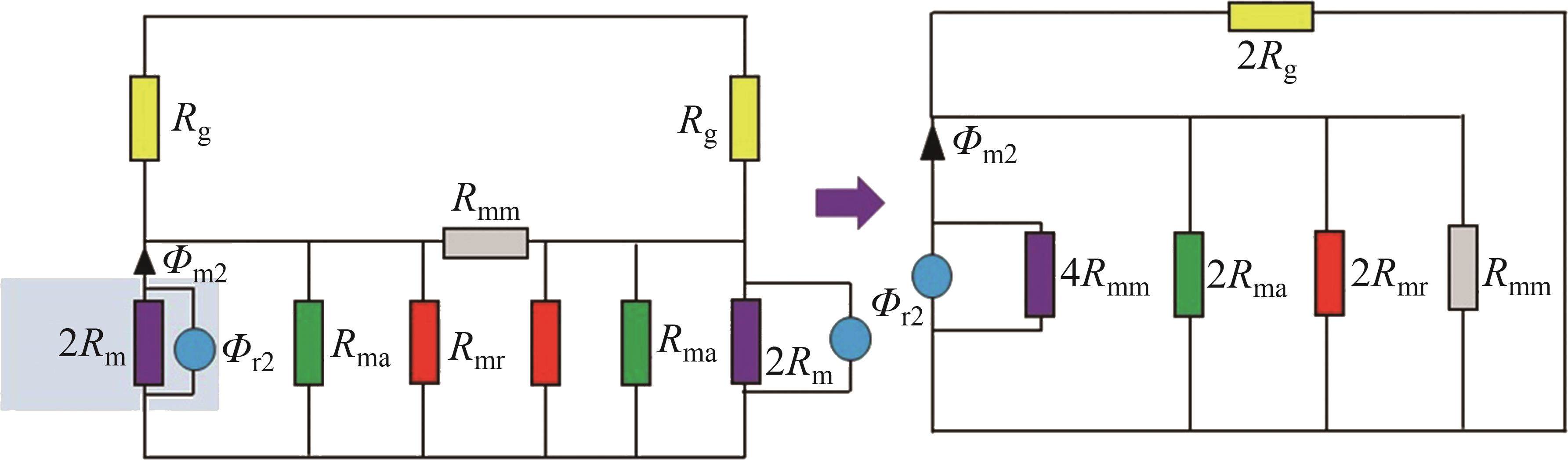
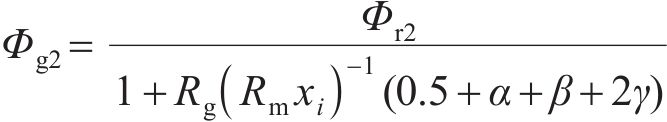
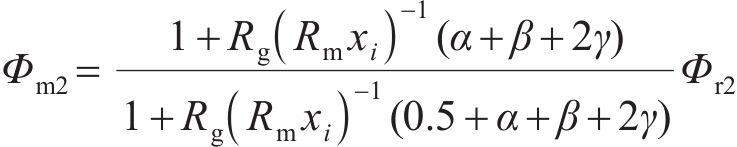
式中: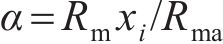
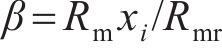
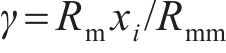
因此,未受环形弧线定子端部截面影响区域的平均气隙磁通密度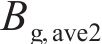
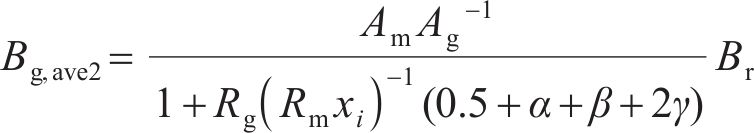
3 磁阻及空载漏磁系数计算
3.1 转子永磁体漏磁部分的计算
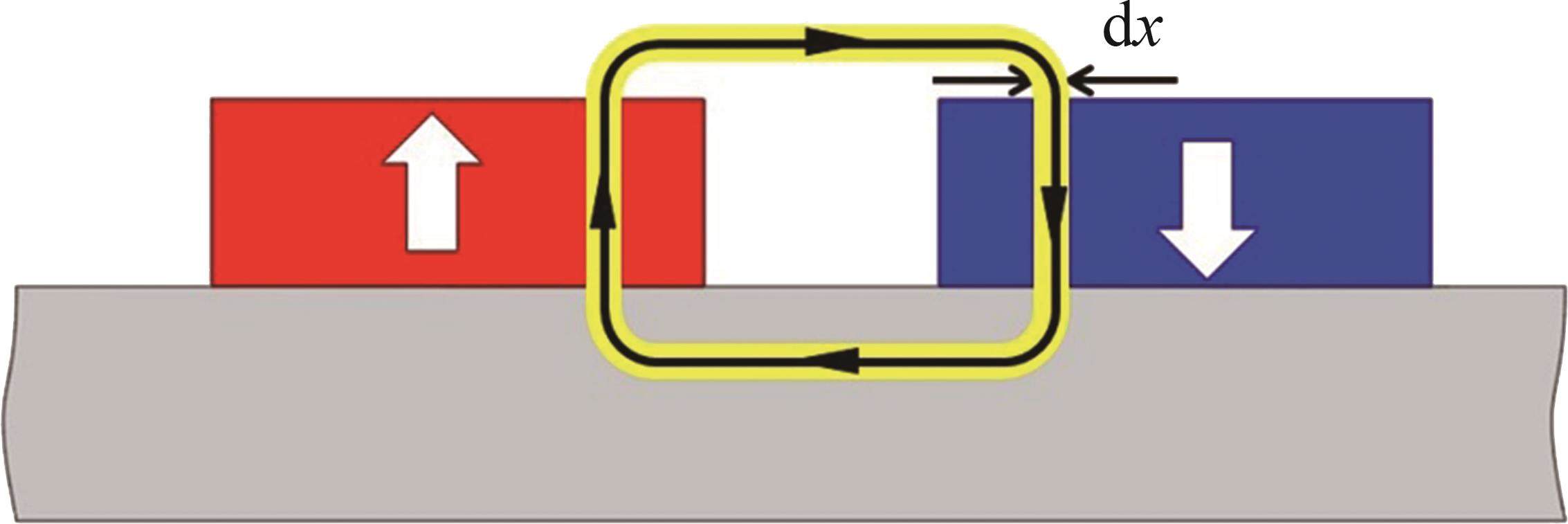
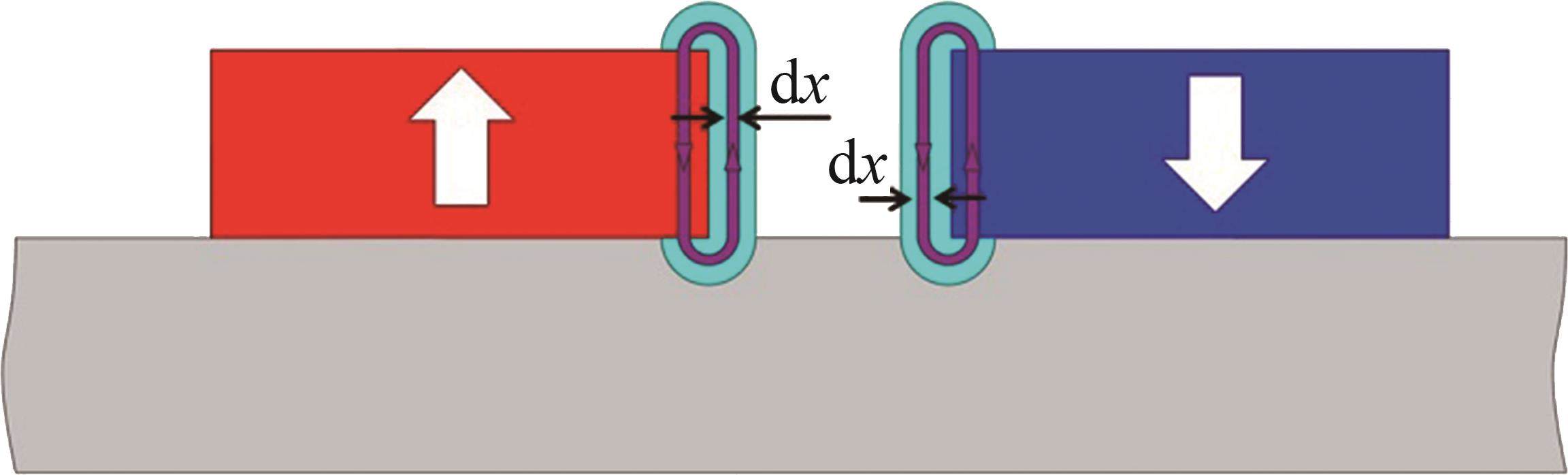
对MDPMM盘式转子永磁体漏磁进行分析,得出盘式转子永磁体和气隙之间的漏磁路径在气隙中由4条直线和4条弧段组成,如图8所示。相邻永磁体漏磁路径在气隙中由2条直线和2条弧段组成,如图9所示。采用圆弧直线磁导率法计算其漏磁阻分别为:
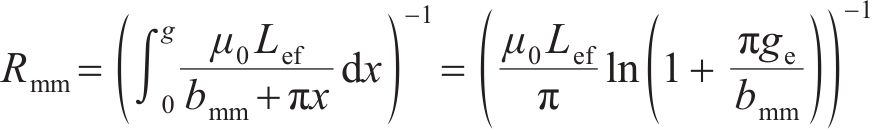
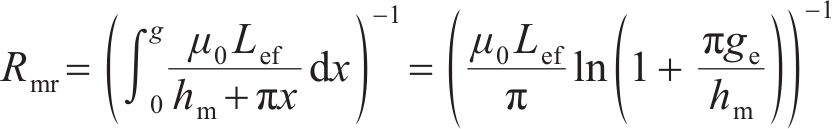
式中:bmm为相邻两永磁体之间的距离。
3.2 其他磁阻计算
在MDPMM等效磁网络模型中考虑了盘式转子永磁体周向漏磁,其永磁体周向漏磁模型如图10所示。周向漏磁阻Rma、永磁体内磁阻Rm和气隙磁阻Rg计算公式如下:
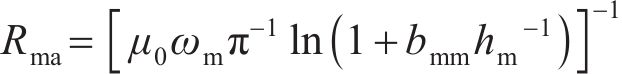
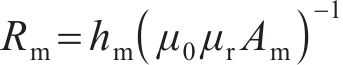
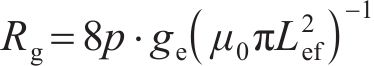
式中:μr为永磁体相对磁导率;p为极对数;ωm为永磁体宽度。
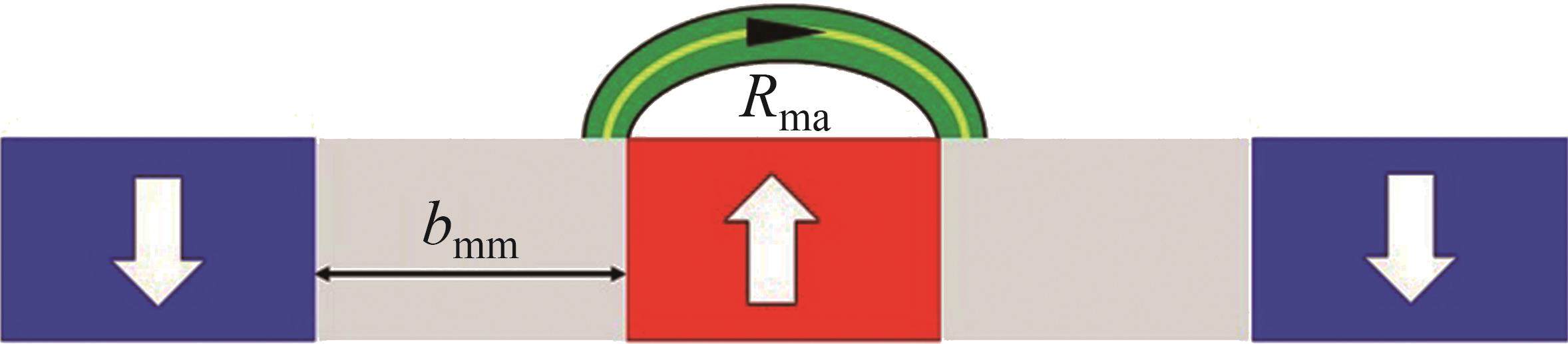
在该模型中,由于存在开槽效应,盘式转子转动过程中磁通流过的气隙路径在不断变化,引入卡氏系数kc[17],则等效气隙为
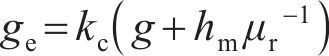
式中:g为气隙长度。
3.3 空载漏磁系数计算
在MDPMM等效磁网络模型中,受环形弧线定子端部截面影响和未受环形弧线定子端部截面影响的磁路漏磁状态并不一致,需要单独等效计算。2种不同等效磁网络模型的空载漏磁系数分别为:
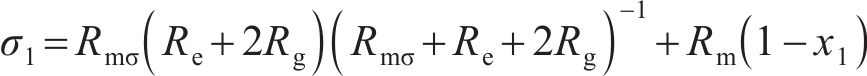
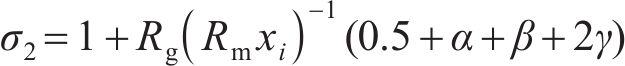
式中:σ1为端部漏磁;σ2为极间漏磁。
4 空载气隙磁密解析
4.1 电机磁场分区域模型
MDPMM环形弧线定子及对应下盘式转子区域模型,如图11所示。
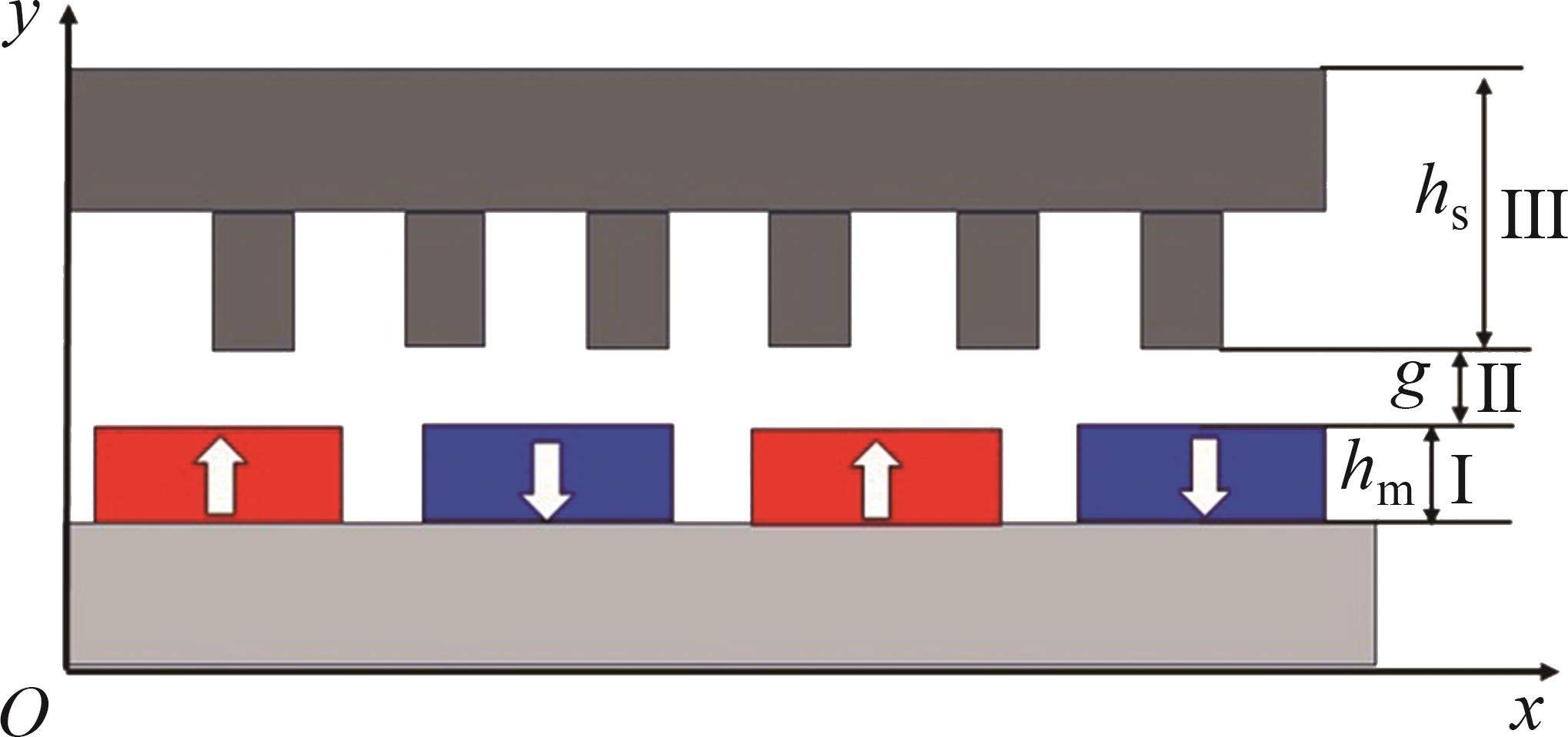
为简化该区域磁场计算,忽略电机径向磁场变化,并假设永磁体磁导率与空气磁导率相等、定转子铁芯磁路不饱和。基于上述假设,该区域模型可分为永磁体区域I、气隙区域II和环形弧线定子齿槽区域III。
4.2 磁场解析
永磁体励磁通过等效磁化强度法[18]分析,其磁化强度矢量M(x)用傅里叶级数展开表示为:
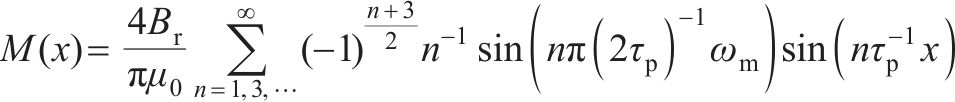
根据麦克斯韦微分方程可得电机分区域模型中各区域的数学模型。
永磁体区域:
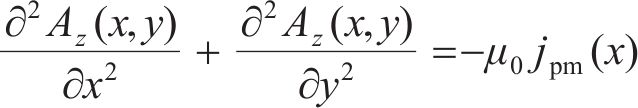
气隙区域:
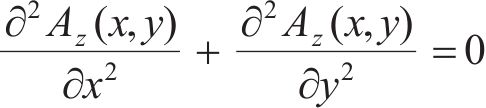
式中:jpm(x)为永磁体的等效电流密度。
在空载状态时,由拉普拉斯方程解析得出气隙区域II的磁场解析式如下:
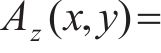
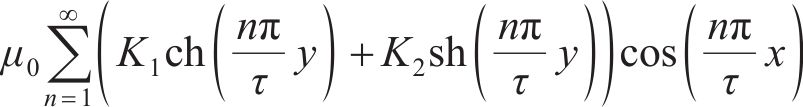
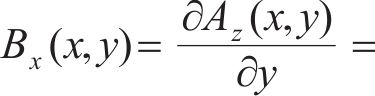
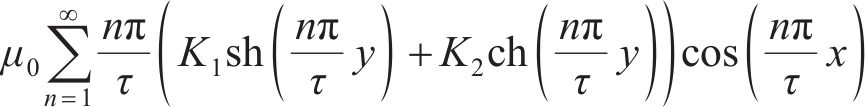
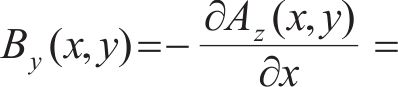
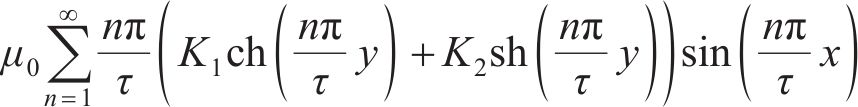
式中:τ为磁场谐波法解析的半波波长;K1、K2分别由边界条件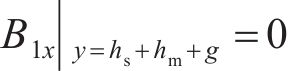
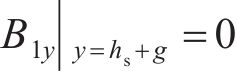
4.3 齿槽对气隙磁场的影响
在MDPMM中,环形弧线定子开槽使气隙磁密的谐波分量增加,为了分析齿槽对气隙磁场的影响,建立环形弧线定子铁芯单槽物理模型,采用许-克变换[18]分析定子齿槽结构对气隙磁场的影响。为了便于分析,假设定子齿槽无限深、盘式转子铁芯表面光滑、定转子铁芯磁导率无穷大。由于永磁体和空气磁化特性是线性变化的,即定子齿槽内任一位置的磁通密度与定转子之间的磁位差呈正比关系,定义该比例系数λ,即B(x, y)=λΦm,则气隙与任意单个齿槽内(x,y)位置处的气隙磁导函数为
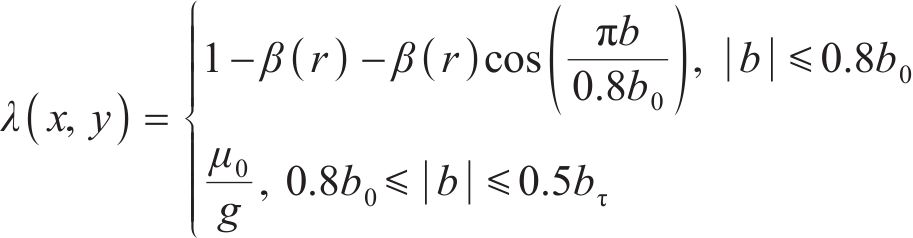
式中:b为距槽中心线的空间位置角;bτ为槽距角;b0为槽口空间角;β(r)=(Bmax-Bmin)/(2Bmax),由许-克变换确定。
对环形弧线定子单槽物理模型经许-克变换可得等效气隙和槽内任一点的磁通密度β(r)为
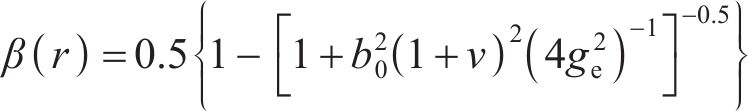
在电机气隙半径r处的相对磁导函数为
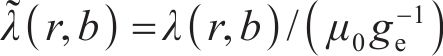
忽略槽之间的影响,则MDPMM环形弧线定子及对应下盘式转子区域气隙磁导分布为周期函数。在极坐标下,取A相绕组轴线为坐标轴,将式(24)进行傅里叶分解得到MDPMM环形弧线定子区域等效气隙在半径r处的相对磁导分布函数为
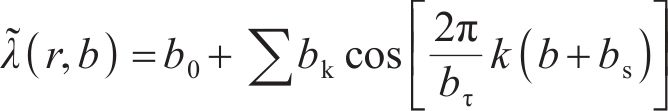
其中:bs为b相绕组轴线与定子槽中心线之间的空间夹角;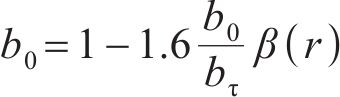
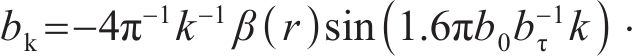
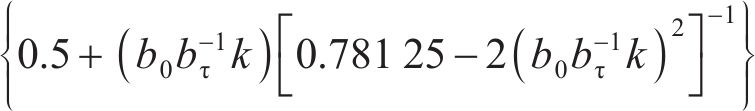
则考虑齿槽效应MDPMM永磁体产生的气隙磁场分布为
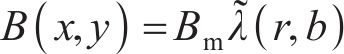
5 有限元验证
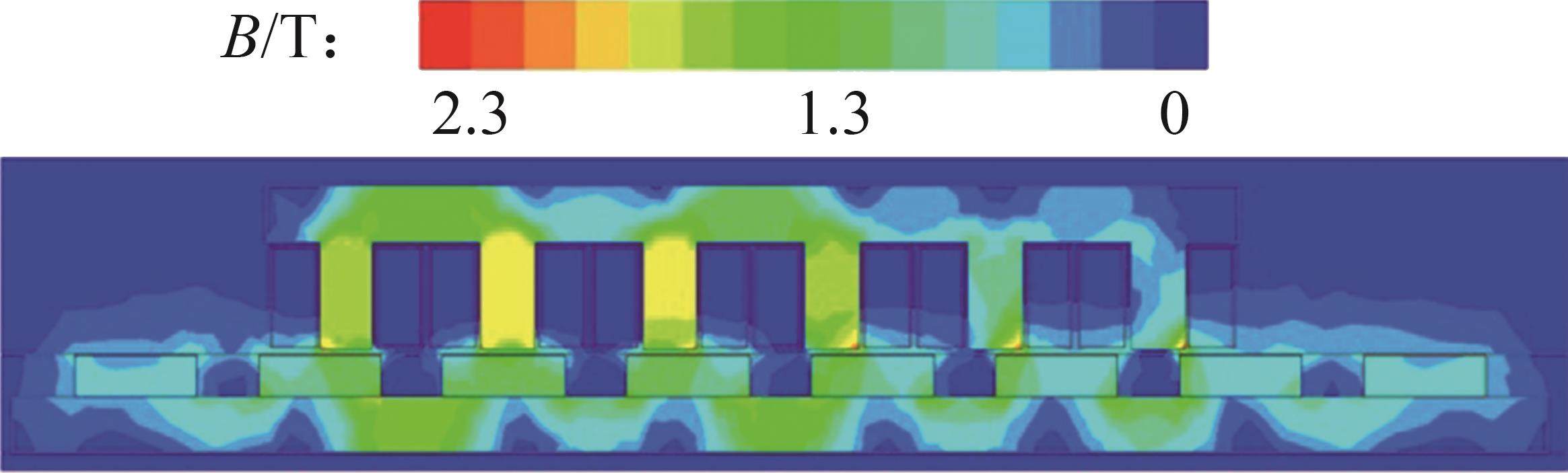
为了验证MDPMM的气隙漏磁与空载气隙磁密解析模型的正确性,根据表1中电机主要结构参数建立部分环形弧线定子及盘式转子的二维模型进行有限元仿真分析,并将仿真结果与解析计算结果进行对比,其MDPMM环形弧线定子对应盘式转子区域的二维空载磁通密度分布云图如图12所示。
| 参数 | 值 | 参数 | 值 |
|---|---|---|---|
| 盘式转子半径r1/mm | 80 | 行星轮转子半径r2/mm | 16 |
| 盘式转子极对数 | 11 | 行星轮极对数 | 4 |
| 磁齿长度Lef/mm | 60 | 气隙长度δ1/mm | 0.5 |
| 磁齿厚度hm/mm | 4 | 极距τp/mm | 12 |
| 环形弧线定子槽数/个 | 6 | 槽距τt/mm | 10 |
5.1 气隙漏磁系数和平均气隙磁密的验证
用等效磁网络法分别对受环形弧线定子端部截面影响和未受环形弧线定子端部截面影响的磁路气隙漏磁系数和平均气隙磁密进行计算可知,2种磁路的气隙漏磁系数计算值分别为1.263、1.167,有限元仿真值分别为1.375、1.222,计算值和仿真值的相对误差分别为8.15%、4.50%;2种磁路的平均气隙磁密计算值分别为0.481、0.492,有限元仿真值分别为0.497、0.503,计算值和仿真值的相对误差分别为3.22%、2.19%。在计算时忽略铁芯磁饱和的影响,使得等效磁网络法计算结果偏低。此外,MDPMM环形弧线定子周向尺寸还会影响端部永磁体的极间漏磁,且气隙漏磁系数与气隙长度、永磁体尺寸和性能等因素有关。这些因素是MDPMM周向端部效应的典型表征因素,对MDPMM后续的电磁参数和输出特性的优化分析具有重要意义。
5.2 空载气隙磁密验证
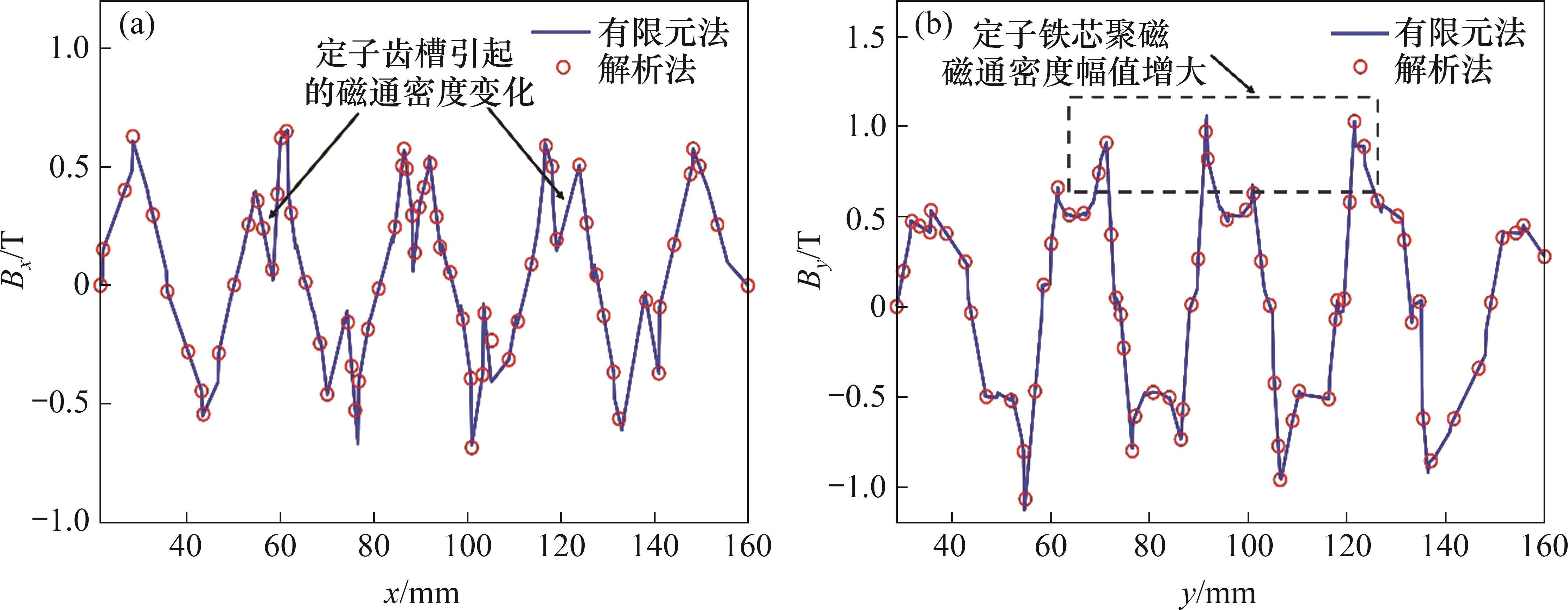
利用解析法和有限元法计算MDPMM环形弧线定子对应盘式转子气隙区域中心线处x和y方向气隙磁通密度,结果见图13。从图13可以看出:齿槽效应引起气隙磁通密度发生变化;在受环形弧线定子端部截面影响和未受环形弧线定子端部截面影响的磁路区域中,y方向气隙磁通密度分量的最大值分别为1.06 T和0.65 T,气隙磁通密度幅值增加了38.7%,表明MDPMM环形弧线定子端部效应的显著性。环形弧线定子铁芯具有较高的磁导率,远高于空气的磁导率,因此,在未受端部影响的区域,盘式转子和环形弧线定子之间的磁力线更加集中,磁路长度变短,磁导率增加,气隙磁通密度得到提升,实现了聚磁效果。而在环形弧线定子端部区域,由于形成了半开域磁场,端部气隙突然增大,使得受环形弧线定子端部影响的磁路状态发生变化,通过环形弧线定子端部的漏磁量增加,这将影响该电机的空载气隙磁场分布,进而使得电机电磁特性发生改变。有限元分析结果表明:在不影响电机性能的情况下,增加MDPMM环形弧线定子的周向尺寸可以提高盘式转子和环形弧线定子之间的聚磁效果。此外,MDPMM采用环形弧线定子能够使得盘式转子在相同永磁体用量的情况下,有效提高该区域的气隙磁通密度。
6 结论
1) 引入磁通分布系数建立受环形弧线定子端部影响的等效磁网络模型,并计算各等效磁阻,解析计算受环形弧线定子端部截面影响和未受环形弧线定子端部截面影响磁路的气隙漏磁系数和平均气隙磁密,2种磁路的气隙漏磁系数计算值分别为1.263、1.167,有限元仿真值分别为1.375、1.222,计算值和仿真值的相对误差分别为8.15%、4.50%;2种磁路的平均气隙磁密计算值分别为0.481、0.492,有限元仿真值分别为0.497、0.503,计算值和仿真值的相对误差分别为3.22%、2.19%。
2) 建立了该电机环形弧线定子对应盘式转子区域的分区域解析模型,采用等效磁化强度法计算齿槽效应的空载气隙磁场磁通密度,并利用有限元仿真结果进行验证,解析结果与仿真结果基本吻合,能够满足工程计算精度的要求,在提高计算效率的同时,为MDPMM的优化设计提供依据。
基于优化过调制方法的永磁同步电机动态电流轨迹追踪策略
[J/OL]. 中国电机工程学报, 2024: 1-12. [樊溢国, 刘欣. 新型多端口盘式永磁电机气隙漏磁及空载气隙磁密[J]. 中南大学学报(自然科学版), 2025, 56(2): 536-544.
FAN Yiguo, LIU Xin. Air gap leakage and open circuit air gap flux density of new multiport disk permanent magnet motor[J]. Journal of Central South University(Science and Technology), 2025, 56(2): 536-544.

