当前,我国交通基础设施建设的重点正在向中西部转移,一批战略性铁路通道建设正在进行[1-2]。我国中西部地区山区较多,桥梁在线路中的占比非常高。然而,我国中西部地区位于欧亚地震带上,受印度板块的强烈挤压,地震断裂带十分活跃,这些铁路桥梁的地震安全备受关注[3-4]。铁路桥梁下部结构设计因受刚度控制,常采用较为粗壮的实体墩,难以形成塑性铰延性体系,支座系统是结构地震下的首要薄弱部位[5-6]。减隔震结构抗震体系是通过特定的减隔震措施来适应强震作用下的结构变形需要,进而通过延长周期或提高耗能来减缓地震作用,保护结构主体免受地震破坏。因此,采用减隔震设计一般要求主体结构基本保持弹性工作,仅减隔震装置发生可控制的变形或损伤,并且应易于震后修复或更换。由此,结构的震后功能可以得到最大程度的保障或最快速度地恢复,因此也是一种理想的韧性结构[7]。尽管我国现行铁路工程抗震设计规范未包含有关桥梁减隔震设计的相关内容,但出于建设项目的实际需要,减隔震技术已实际应用于我国的重要铁路桥梁抗震设计中。由于铁路桥梁下部结构设计受刚度控制,难以采用橡胶类减隔震支座产品,多选用摩擦摆支座,必要时辅以软钢阻尼器以增加耗能能力[8-11]。摩擦摆支座和软钢阻尼器均属于位移依赖型的阻尼器,具有显著的非线性行为。准确模拟其力学行为,并分析采用该阻尼装置的桥梁结构在特定的震动作用下的响应,需要开展非线性时程分析[12-14]。事实上,迄今为止绝大多数的结构减隔震行为研究都是采用非线性时程分析方法。然而,这种时域分析方法不仅费时费力,也只能通过选用少量的模拟地震波进行分析,由此导致的评估结果偏差难以确定。与此同时,针对位移型减隔震系统的基于等效线性化原理的频域分析方法也得到了广泛应用,如美国AASHTO规范、我国的现行公路抗震设计规范、城市桥梁抗震设计规范等均引入了该方法[15-17]。然而,该方法的相关计算公式为隐式过程,在实际计算中需要多次迭代,计算效率低下。本文针对铁路桥梁减隔震设计中广泛使用的摩擦摆支座与钢阻尼器组合减震体系,结合铁路桥梁的结构特点和等效线性化计算原理,提出具有很高模拟精度的显式计算方法。通过大量抽样分析,检验了该方法的计算误差。进一步基于典型高速铁路桥梁,进行了广泛系统的减隔震设计参数抽样,并开展了大量的非线性时程分析,验证了铁路桥梁位移型减隔震体系基于等效线性化方法进行计算的可行性,进一步讨论了时域计算方法与谱分析方法的优缺点。
1 等效线性化显式分析方法
1.1 等效线性化基本原理与计算方法
等效线性化的基本思想是将位移依赖型阻尼隔震体系的滞回耗能等效为速度依赖型的黏滞耗能,用割线刚度对应的等效线性系统近似表征实际的非线性结构系统,进而将必须依赖非线性时域分析方法的求解过程转变为可采用等效线性系统频域分析的求解[18-19]。
如图1所示,依据等效线性化的基本原理,典型双线性依赖型阻尼隔震系统的主梁地震位移为[15]
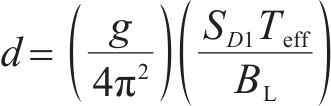
式中: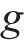
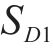
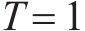
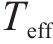
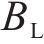
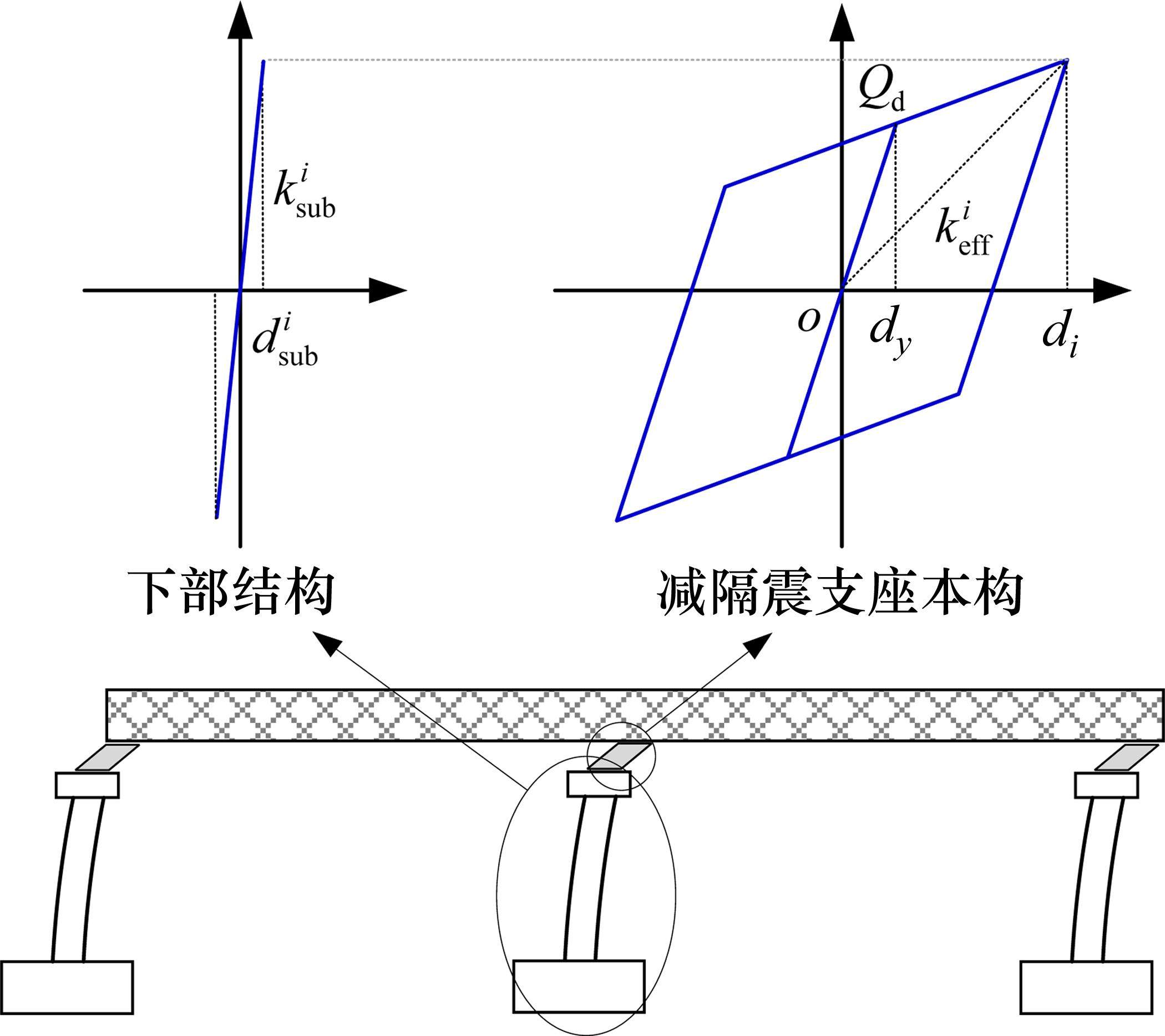
等效线性结构周期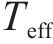
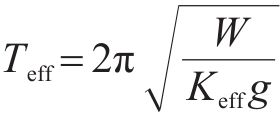
式中: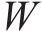
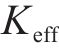
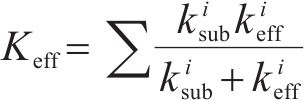
式中: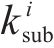
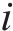
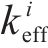
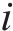
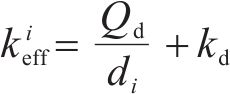
式中: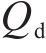
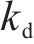
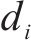
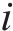
反应谱阻尼调整系数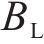
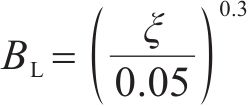
式中: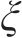
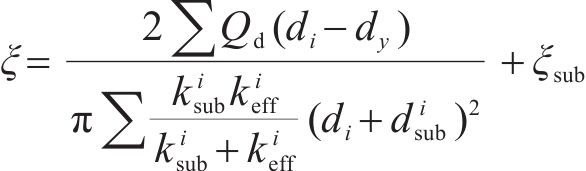
式中: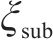
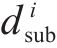
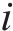
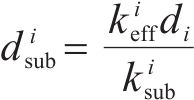
根据图1,主梁、各支座与墩的位移响应,应满足:
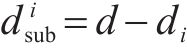
式(1)~式(8)是个隐式过程,需要进行迭代计算。首先,假定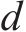
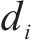
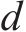
需要指出的是,式(1)~式(8)主要参照AASHTO规范,我国公路桥梁抗震设计规范和城市桥梁设计规范也引入了该方法,基本求解过程非常相似,但在反应谱调整的处理上略有差异,后两者采用了阻尼调整系数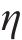
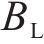
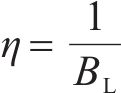
其中,在公路桥梁抗震设计规范中:
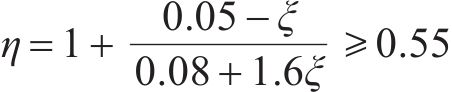
在城市桥梁抗震设计规范中:
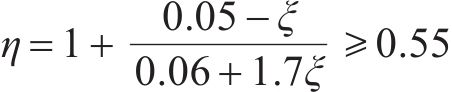
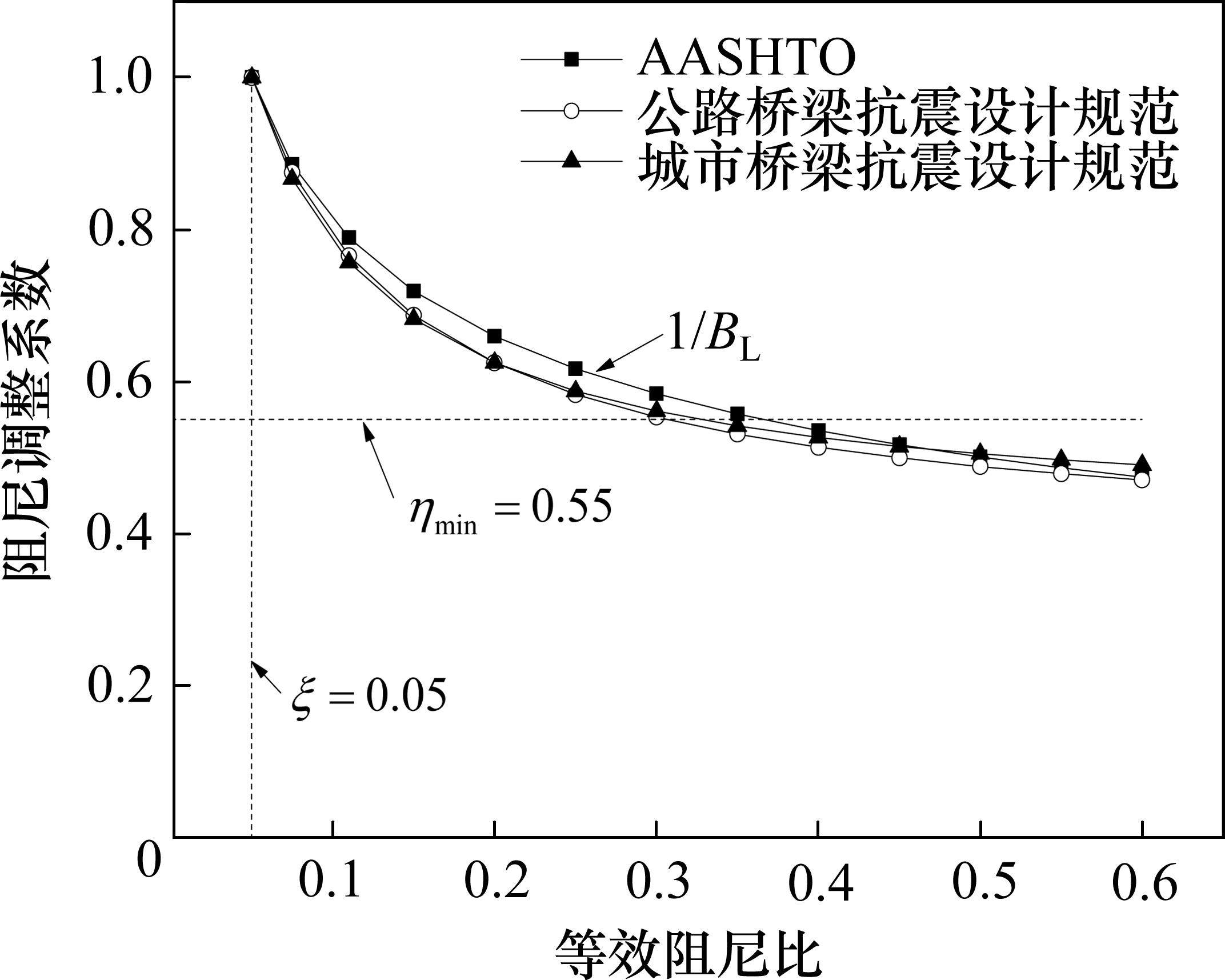
3种阻尼调整系数计算的比较如图2所示,可见三者总体基本相当,但当等效阻尼比小于0.35,我国公路桥梁抗震设计规范和城市桥梁抗震设计规范的结果非常接近,但均低于AASHTO规范的结果,当等效阻尼比大于0.35,我国公路桥梁抗震设计规范和城市桥梁抗震设计规范因为下限值0.55的规定而明显高于AASHTO规范。
1.2 铁路桥梁减隔震显式分析方法
1.2.1 基本公式
如前所述,铁路桥梁多采用较为粗壮的实体墩,因此下部结构整体的刚度较大,一般远超减隔震系统的等效刚度,即
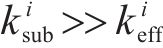
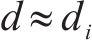
铁路标准梁为简支结构,结构体系较为简单,不同墩位间的耦合效应相对较小[20]。并且铁路桥梁的减隔震设计多采用摩擦摆支座辅以钢阻尼器的方案,这也是我国高烈度地区铁路桥梁实际采用的方案,支座和钢阻尼器组合体系等效刚度可简化为
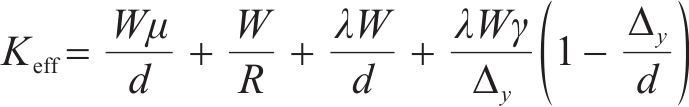
代入式(1),同时我国规范体系常用的阻尼调整系数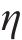
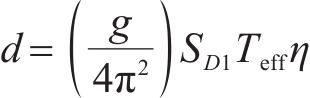
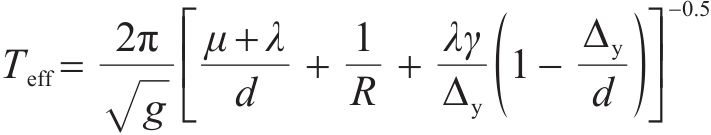
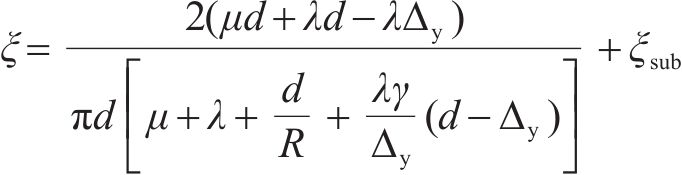
式中: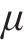
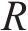

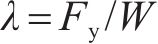
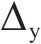
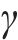
无论是式(1)~式(8),还是式(15)~式(17),均是基于等效线性化的计算原理,也均是一个隐式的求解过程。其根本原因在于式(1)或式(15)中与地震设计谱相关的变量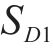
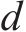
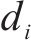
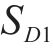
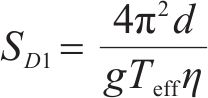
这表明对于每一个减隔震设计方案,存在一个以支座位移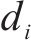
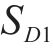
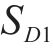
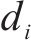
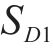
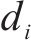
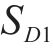
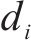
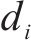
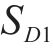
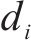
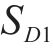
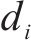
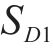
图3所示为4组采用不同摩擦摆支座与钢阻尼器参数的组合减震体系的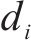
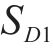
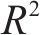
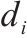
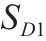
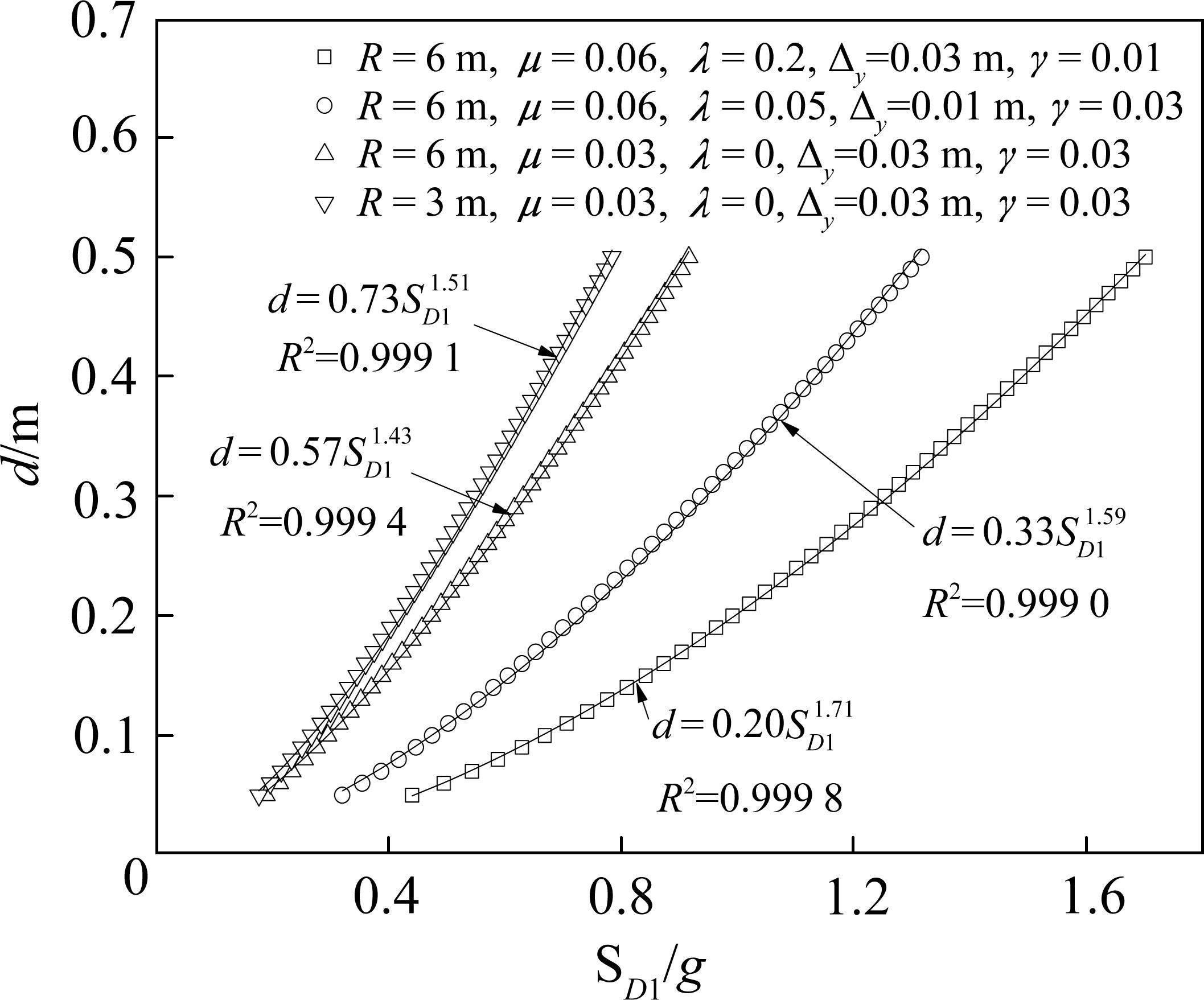
为在更广泛的范围内检验幂函数对摩擦摆支座与钢阻尼器组合减震体系的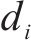
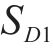
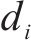
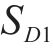
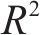

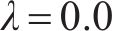
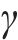
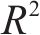
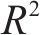
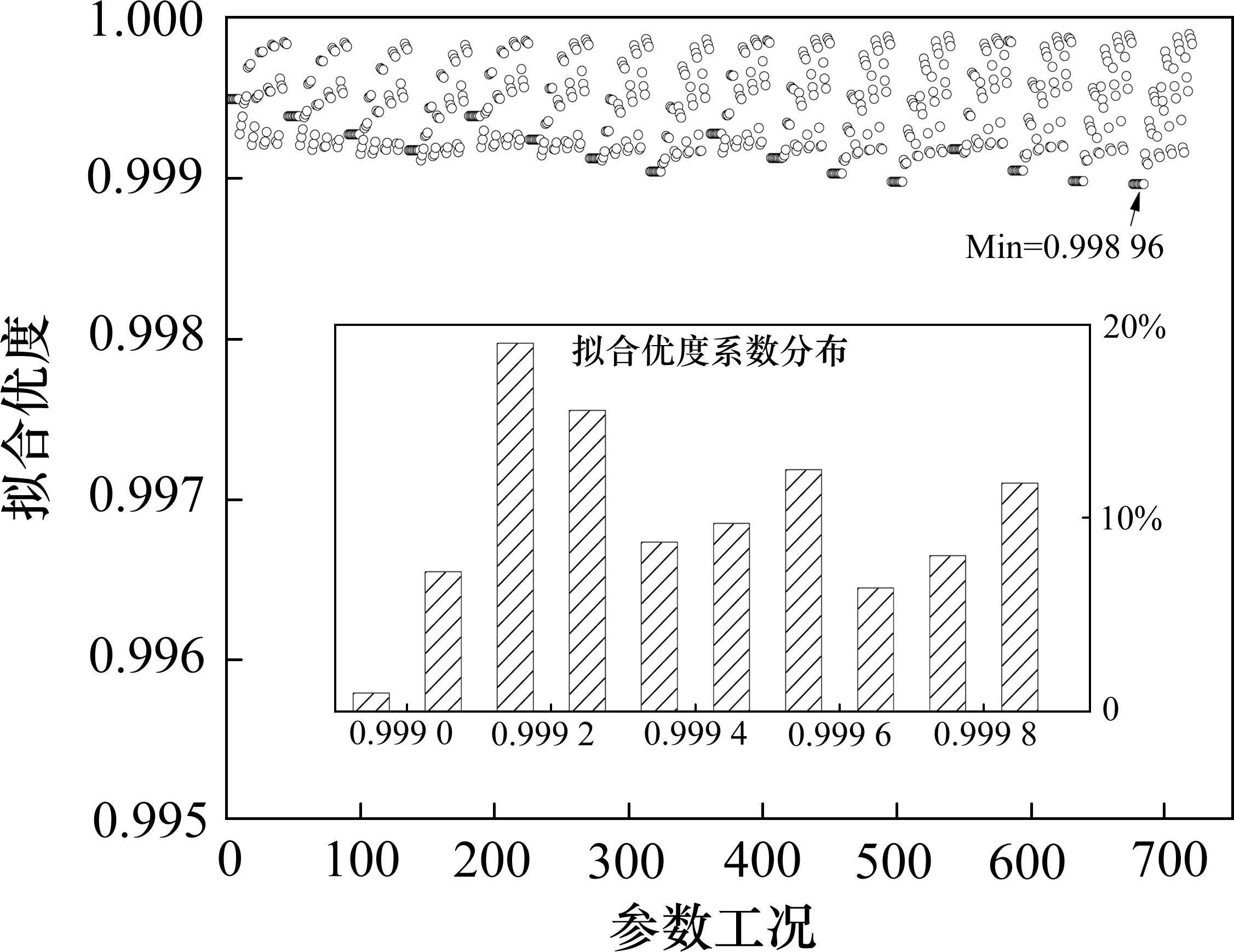
由此,可以合理推断我国铁路桥梁常用的摩擦摆支座与钢阻尼器组合减震体系,基于等效线性化计算方法的隐式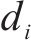
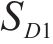
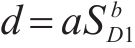
式中: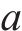
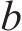
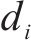
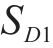
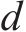
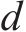
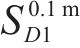
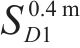
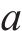
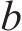
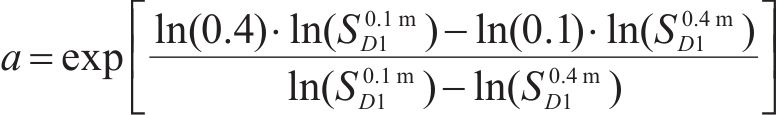
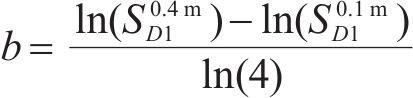
1.2.2 案例分析
某铁路简支梁桥单跨主梁恒载16 000 kN,罕遇地震峰值加速度为0.45g,特征周期为0.65 s,摩擦摆支座等效半径3 m,摩擦因数0.05,固定墩和活动墩各设一个钢阻尼器,总屈服力800 kN,阻尼器屈服位移0.02 m,屈后/屈前刚度比0.02,求地震下的支座位移响应。
选用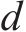
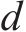
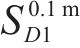
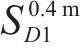
输入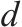 | 式(16)求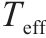 | 式(17)求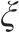 | 式(10)求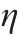 | 式(18)求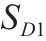 |
|---|---|---|---|---|
| 0.1 m | 1.713 s | 0.467 | 0.456 | 0.277 |
| 0.4 m | 2.527 s | 0.296 | 0.556 | 0.454 |
将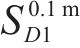
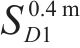
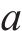
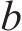
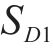
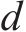
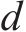
1.2.3 误差分析
为进一步检验这种显式计算方法的计算误差,基于拉丁超立方抽样方法,对摩擦摆支座等效回转半径
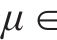
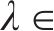
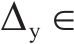
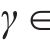
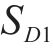
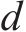
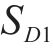
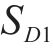
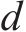
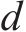
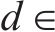
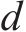
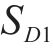
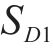
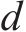
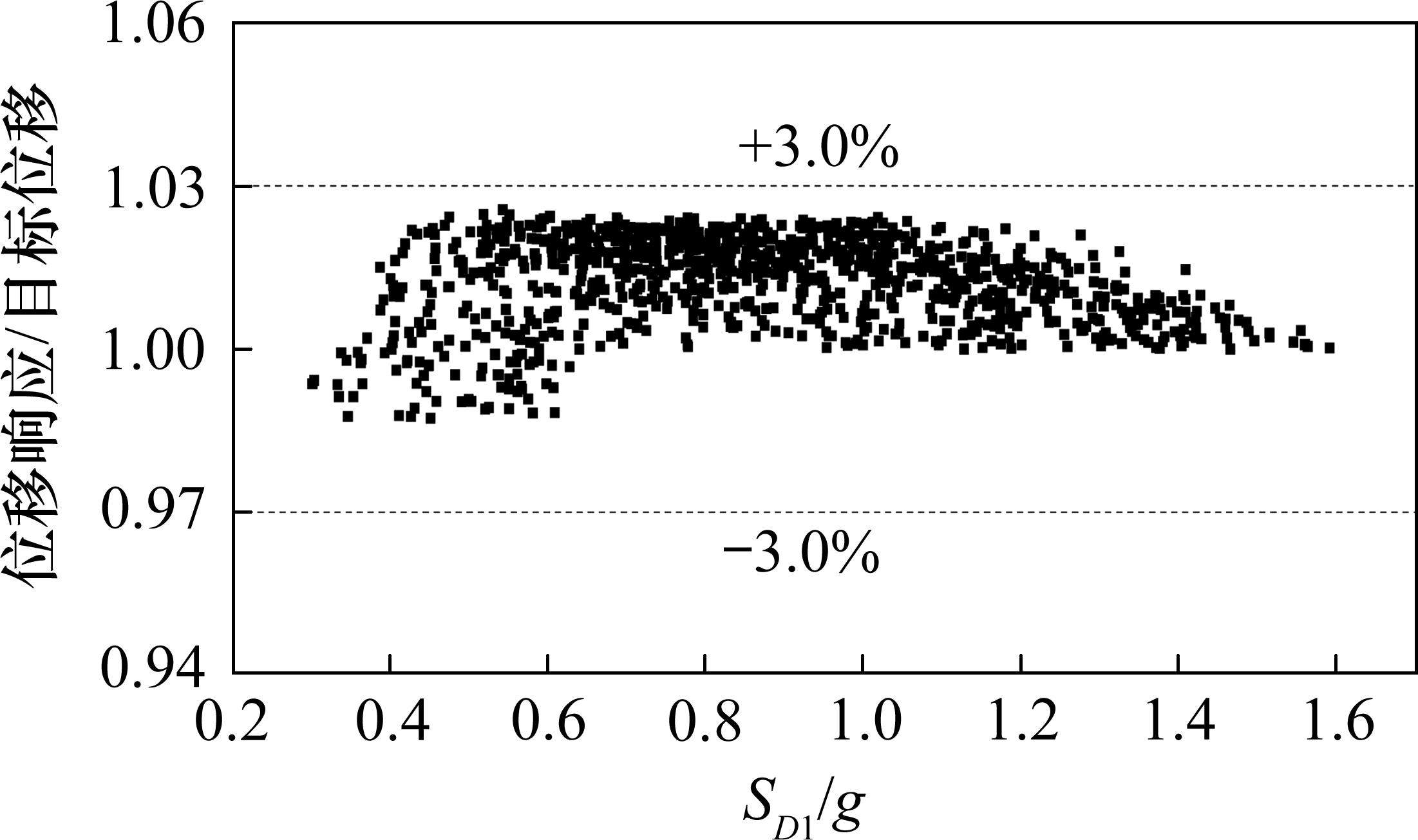
2 典型减隔震高铁桥梁响应参数分析
2.1 桥梁结构与建模
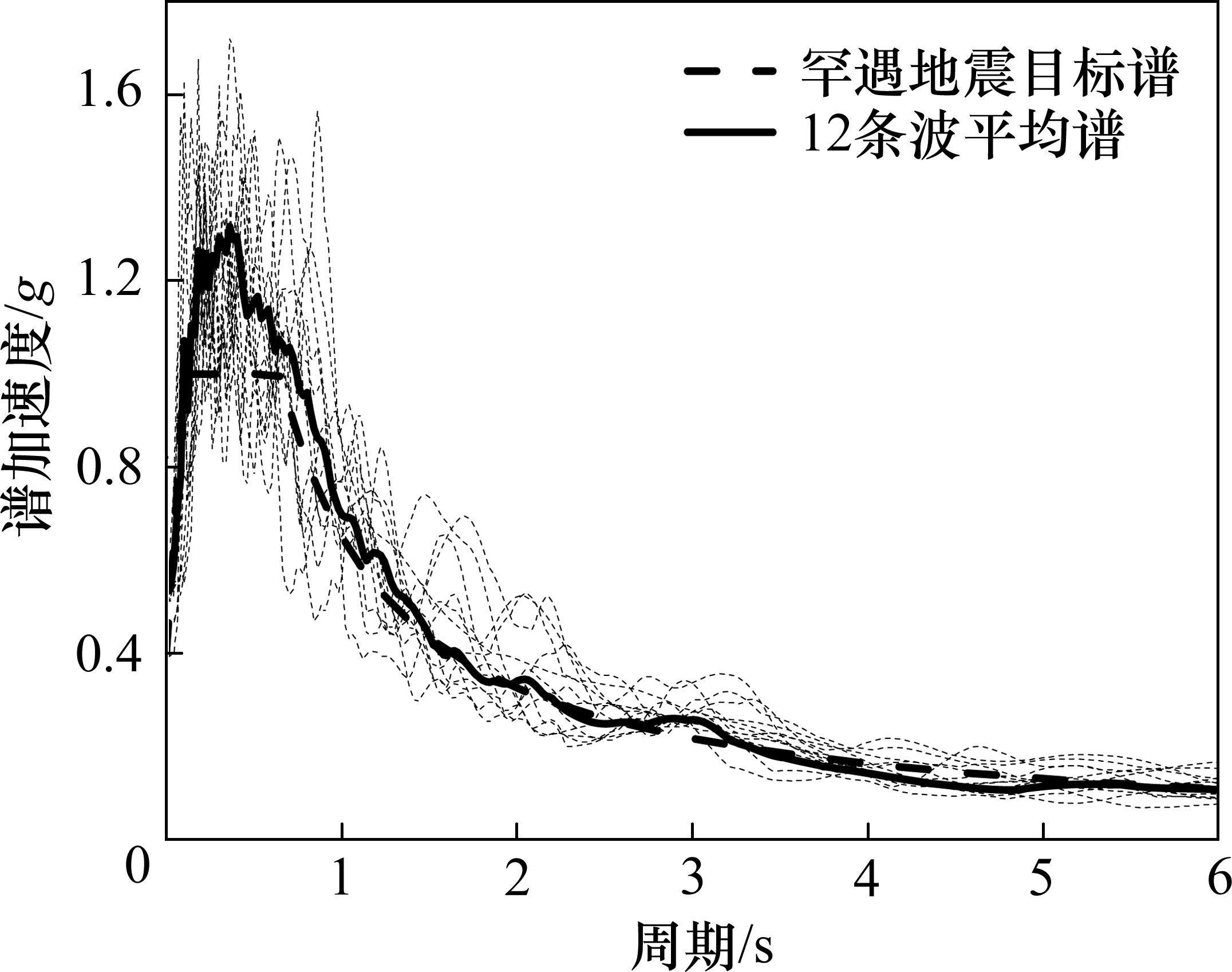
某时速350 km高速铁路双线简支梁桥,横断面如图6(a)所示。主梁为箱形断面,单跨跨度31.5 m,单跨主梁梁重8 220 kN,二期恒载4 160 kN。桥墩为圆端型实心桥墩,墩高12 m,钻孔灌注桩群桩基础,桩径1.25 m,桩长48 m,桩数10,梅花形布置。根据桥址场地地震安评结果,罕遇地震峰值加速度为0.4g,特征周期为0.65 s,水平地震动反应谱如图7所示。
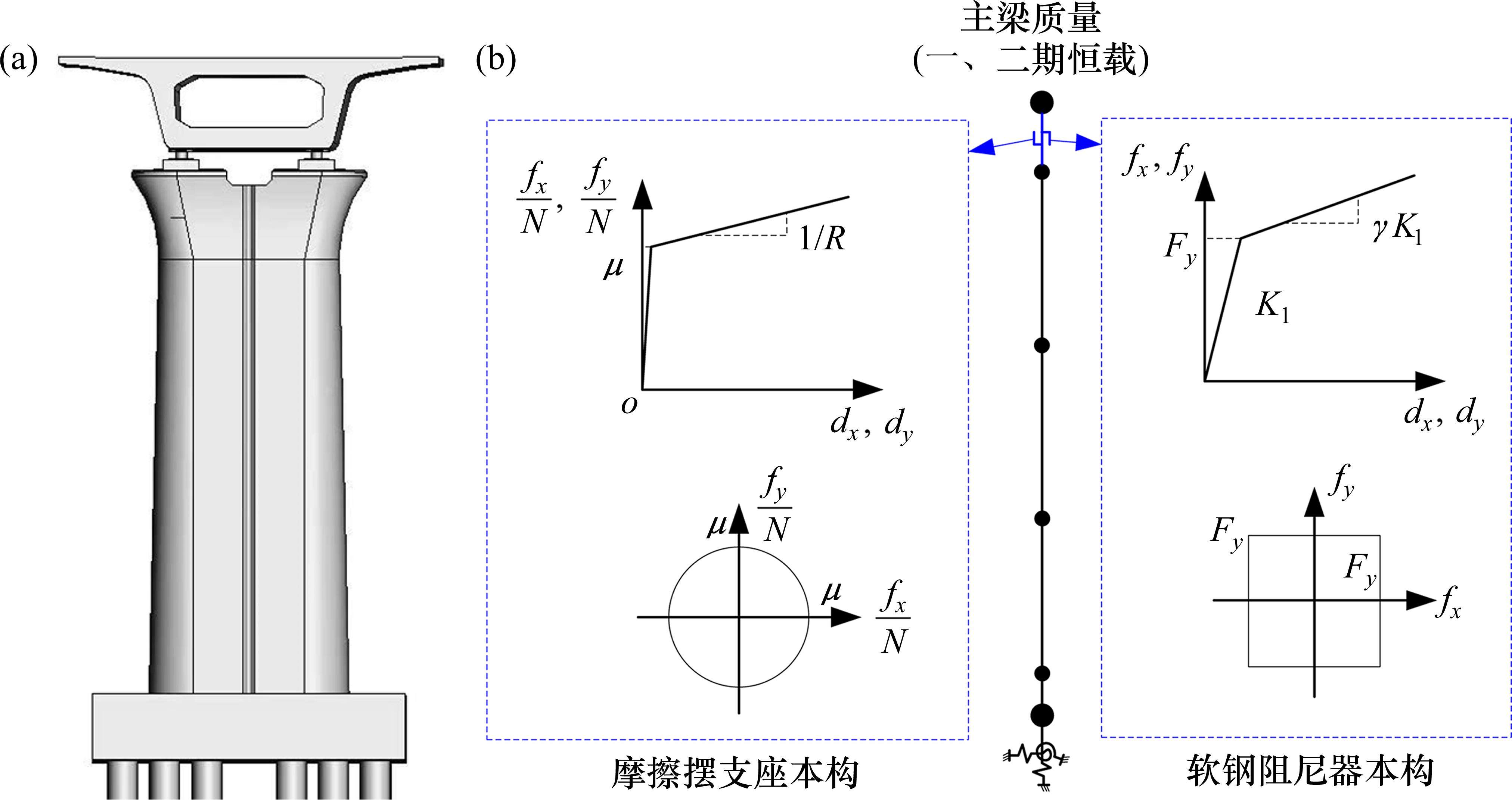
考虑桥梁规则性,基于OpenSees平台按单墩-质量体系建立结构有限元分析模型,其中上部结构模拟为质点,质量包括一跨主梁的一、二期恒载,桥墩和桩均按弹性梁柱单元模拟,承台模拟为质点,桩-土相互作用弹簧采用m法进行计算。摩擦摆支座采用singleFPBearing单元模拟,软钢阻尼器采用双线性本构模拟[10-11],如此则摩擦摆支座和软钢阻尼器的滞回耗能可由相应的非线性单元直接考虑,此外结构的阻尼比按0.05考虑,采用瑞利阻尼。结构有限元模型见图6(b)所示。
2.2 参数抽样与分析
考虑结构地震作用强度较高,拟采用摩擦摆支座+软钢阻尼器组合减震体系。为对组合减隔震体系进行充分的参数分析,以与建议的显式计算方法相比较,针对不同的摩擦摆支座设计参数与钢阻尼器设计参数以及地震动峰值加速度进行了100次抽样,其中摩擦摆支座等效回转半径取3、4、5和6 m这4种,摩擦因数取0.03、0.04、0.05、0.06这4种,钢阻尼器屈服力与梁恒载总重之比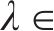
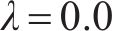
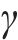

为针对减震体系开展非线性时程分析,在太平洋地震工程研究中心的强震记录库中选取与反应谱相协调的强震记录共12条,基本信息如表2所示。12条强震记录所对应的反应谱及其平均谱绘于图7中,可以看出,平均谱与设计谱具有非常好的匹配关系,特别是在减隔震体系常见的1~3 s区间[8-14]。
| 地震名 | 年份 | 站点 | 震级 | PGA/g |
|---|---|---|---|---|
| Imperial Valley-02 | 1940 | El Centro Array #9 | 6.95 | 0.215 |
| Imperial Valley-06 | 1979 | Delta | 6.53 | 0.238 |
| Chi-Chi, Taiwan | 1999 | TCU085 | 7.62 | 0.054 |
| Chi-Chi, Taiwan | 1999 | TCU053 | 7.62 | 0.223 |
| Chi-Chi, Taiwan | 1999 | TCU060 | 7.62 | 0.201 |
| Chi-Chi, Taiwan | 1999 | WSF | 7.62 | 0.073 |
| Chi-Chi, Taiwan | 1999 | CHY057 | 7.62 | 0.039 |
| Chi-Chi, Taiwan | 1999 | CHY057 | 7.62 | 0.056 |
| Chi-Chi, Taiwan | 1999 | TCU122 | 7.62 | 0.261 |
| Westmorland | 1981 | Parachute Test Site | 5.90 | 0.155 |
| Chi-Chi, Taiwan | 1999 | CHY102 | 7.62 | 0.050 |
| Kocaeli, Turkey | 1999 | Zeytinburnu | 7.51 | 0.108 |
针对每一次抽样,通过修改模型中的摩擦摆支座单元和模拟软钢阻尼器的双线性本构单元的基本参数进行结构模型重建,并根据PGA的抽样调整12条地震波的输入强度。通过非线性时程分析,计算所有抽样工况下的结构地震响应。与此同时,基于1.2节中所建立的显式计算方法,计算各抽样工况下的减隔震体系支座响应。
2.3 结果分析
2.3.1 非线性时程分析与等效线性化方法
图8(a)所示为上述100个抽样工况分别基于非线性时程分析和显式计算方法对支座相对位移的分析结果对比。其中,全部地震波分析结果列出了100个抽样工况对应12条地震波共计1 200个分析工况的结果;地震波平均结果是每一个抽样工况12条地震波结果的平均值。从图8(a)中可以看出,对应同一减隔震设计方案参数和地震动作用强度,12条地震波下的支座位移分析结果离散性比较明显,但其平均结果与显式方法的分析结果具有很好的线性相关性,与理想的线性相关性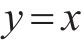
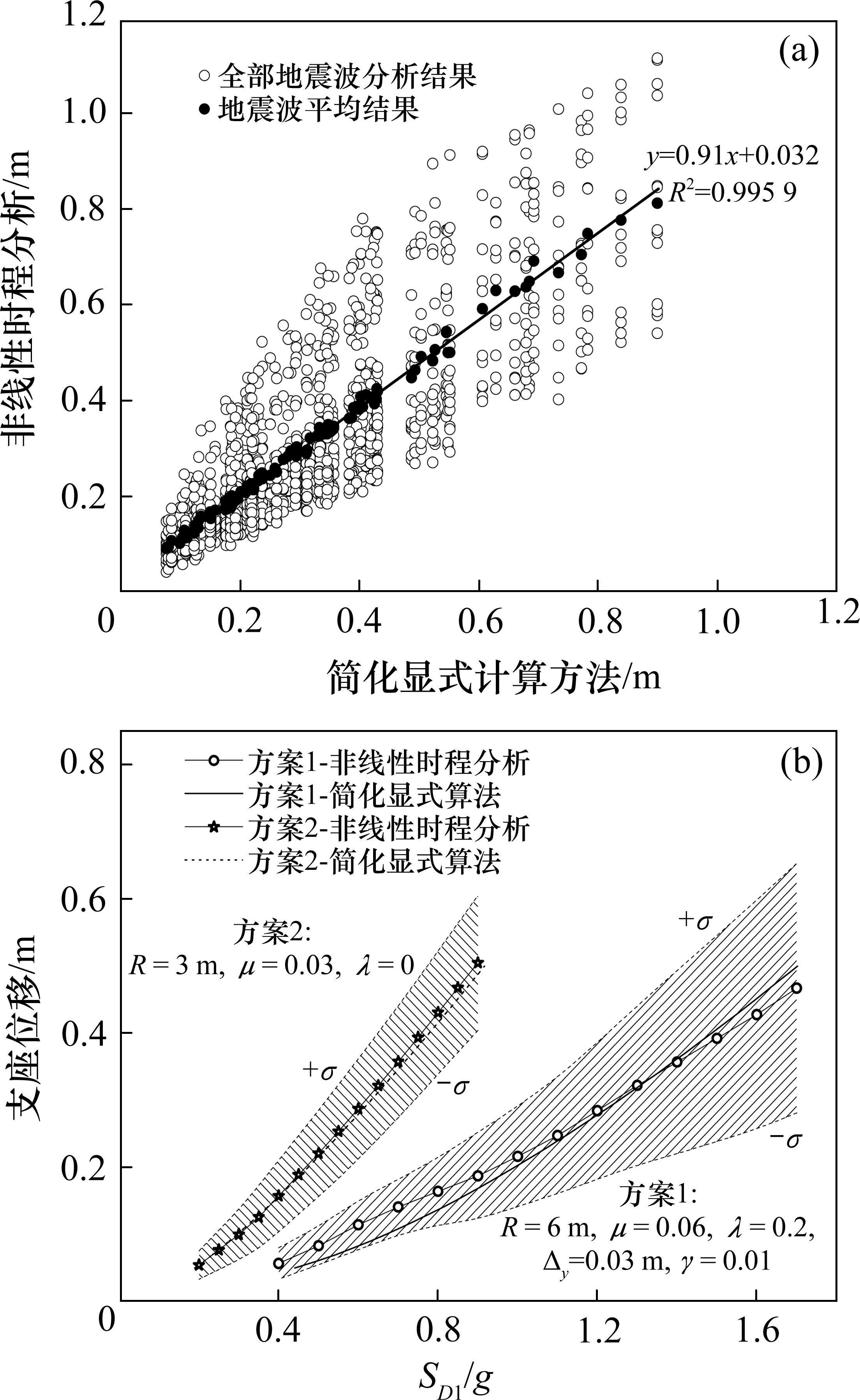
为进一步比较2种分析方法的差异,选取2种典型减隔震参数设计方案,基于上述12条地震波并考虑不同的地震动作用强度PGA,分别采用非线性时程方法和显式计算方法分析减隔震体系的支座相对位移,结果如图8(b)所示,其中非线性时程分析结果取12条波的平均值,并给出正、负1倍标准差的范围。方案1中支座摩擦因数取常用的上限值0.06,软钢阻尼器屈服力达到主梁重量的20%,代表较高的阻尼耗能设计方案;方案2中无钢阻尼器,且支座摩擦因数取偏低值0.03,代表较低的阻尼耗能设计方案[8-14]。可以看出,2种方案的非线性时程分析结果和显式方法的计算结果基本一致,其中方案2偏差很小,方案1则由于采用了更高的支座摩擦因数和更大的钢阻尼器屈服强度,结构的非线性程度更强,相比之下偏差略为显著,但均未超出12条波的平均值±1倍标准差的范围。这表明,等效线性化计算方法与非线性时程分析方法具有较好的一致性。
需要指出的是,尽管非线性时程分析方法能够较好地模拟减隔震结构在特定地震波作用下的非线性行为,但结构未来将遭遇的地震波无法预知,只能根据潜在的震源机制、发震概率、传播与衰减特性、场地覆盖层的滤波与放大效应等预估其频谱特性,进而在此基础上寻找与之相协调的强震记录或生成人工地震波[21]。但即使对应同一目标谱,与之相协调的不同地震波仍可能会导致离散性较大的结果,因此客观上需要选取较多的地震波进行分析以确保结果的合理性。但非线性时程分析费时费力,在实际设计中要求进行大量工况的非线性时程计算并不现实。AASHTO规范要求采用非线性时程方法应不少于3条地震波,采用3条时应取其最大值,采用7条及以上时可取平均值[15]。但根据图8(b)中的分析结果,即使采用了12条地震波,标准差与平均值的比值仍可达0.2~0.4。由此可见,当采用非线性时程方法进行计算时,其分析结果受具体的地震波选用影响较大。
2.3.2 阻尼调整系数
如前所述,关于阻尼调整系数,AASHTO规范、我国公路桥梁抗震设计规范和城市桥梁抗震设计规范给出了不同的计算表达式,其中我国公路桥梁抗震设计规范和城市桥梁抗震设计规范还给出了0.55的下限值规定[16-17]。
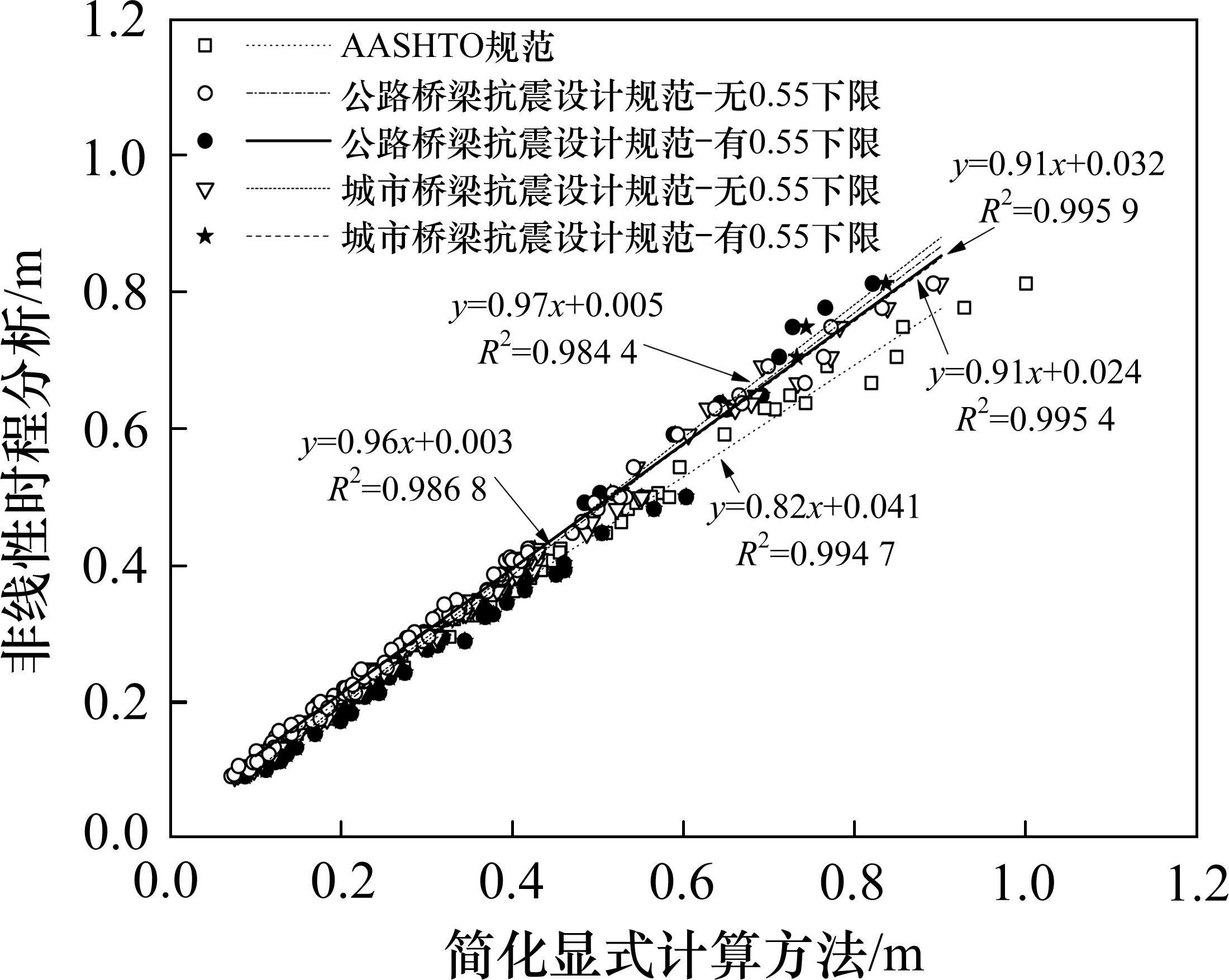
图9所示为2.3.1节中100个抽样工况基于不同阻尼调整系数的显式计算方法的预测结果与每工况基于12条地震波非线性时程分析结果的平均值的对比。可以看出,AASHTO规范建议的调整系数会导致相对偏高的估计结果,幅度约为20%,我国公路桥梁抗震设计规范和城市桥梁抗震设计规范建议的调整系数计算方法则结果非常相近,但当考虑阻尼调整系数的下限值0.55时,会导致显式计算方法计算误差在一定程度上增大,相比之下,基于公路桥梁抗震设计规范,即式(10)的符合性较好,所有100个抽样工况拟合优度最高,且显式方法的分析结果总体偏高约10%,略偏安全。
3 分析与讨论
2008年汶川地震以后,我国相继颁布了《公路桥梁抗震设计细则》《城市桥梁抗震设计规范》和《公路工程抗震设计规范》,整个公路与市政桥梁的抗震设计规范体系发生了很大的变化,其中最为显著的即为将减隔震体系正式引入到规范中[22]。由此,极大地推进了我国公路与市政桥梁减隔震技术的发展与应用。2020年,《公路桥梁抗震设计规范》颁布,2023年,《城市桥梁抗震设计标准》(报批稿)也已完成,2本规范进一步完善了减隔震设计的相关规定。目前,我国在中、西部高烈度地震区的铁路建设需求显著增加,对相关减隔震技术存在很大的现实需求,然而现行《铁路工程抗震设计规范》未包含相关内容,目前已在修订中[23]。
由于减隔震体系具有显著的非线性行为,究竟是应采用非线性时域分析还是等效的谱分析方法存在很大的争议,笔者在参与编写《城市桥梁抗震设计规范》中也深感困惑。对于一条确定的地震波,非线性时程分析方法无疑是最合适的,但设计中采用的地震波和结构实际经历的地震波是不可能一致的。更重要的是,非线性时域的分析结果受具体的地震波影响很大,离散性也很大,尽管我国现行公路和市政桥梁抗震设计规范参照AASHTO规范对时域分析的地震波数量给出了相应的规定,但在减隔震的设计实践中,不乏存在对所选择的地震波进行调整的状况,使得设计结果存在一定的不确定性,给工程安全保障和规范管理带来一定的隐患。基于等效线性化的谱分析方法在国内外桥梁减隔震设计规范中的应用非常广泛,一般是与时域分析方法并列可选的,除非遇到特殊的减隔震设计情况[15, 24-25]。
当前,我国铁路桥梁抗震设计规范亟待引入减隔震设计的相关内容,如何选择合理的分析方法是个不可忽视的问题。考虑到铁路桥梁的结构标准化程度高,减隔震设计方案的可选择空间上也存在明显的限制条件[26-27],建议对于减隔震机制比较明确的常规减隔震体系,可优先采用等效线性化的谱分析解析方法,既可显著提高分析效率,同时也能保证其可靠性,毕竟非线性时程分析中的地震波也是基于设计谱进行选择的,设计谱本身就代表平均地震动的意义[28-29];或者综合考虑两者算法,如控制2种分析方法的结果偏差不能超过20%,用具有唯一性的等效线性化谱分析方法的结果作为设计依据,用非线性时域分析的结果作为校验。
4 结论
1) 铁路桥梁典型组合减震体系的支座位移响应可以很好地表征为1 s周期反应谱值的幂函数关系,由此建立的显式计算方法在常用的设计参数界限范围内,误差均少于3%。
2) 基于等效线性化原理的解析方法与非线性时域分析的平均结果之间具有较好的一致性,但非线性时程方法的分析结果受具体地震波的影响较大,即使对应同一目标谱,与之相协调的不同地震波仍会产生较大的离散性。
3) 建议在设计实践中优先选择等效线性化解析方法或者综合考虑2种算法的结果,建议阻尼调整系数采用我国公路抗震设计规范的建议公式。
苏伟,李晓波,王雨权等.铁路桥梁典型减隔震设计显式计算方法[J].铁道科学与工程学报,2025,22(02):712-722.
SU Wei,LI Xiaobo,WANG Yuquan,et al.Explicit analytical method for typical isolated system of railway bridges[J].Journal of Railway Science and Engineering,2025,22(02):712-722.

