随着高速铁路的迅速发展,列车在强侧风作用下的安全事故时有发生,造成重大的经济损失和人员伤亡,列车行车安全引起了越来越多的关注[1-2]。风屏障作为一种简单、有效的防风措施,可为列车提供较为安全的运行风环境,在国内外得到广泛应用[3-5],如兰新线在铁路沿线设置风屏障以保障列车行车安全。风屏障对车-桥系统气动特性的影响不仅与风屏障自身有关,而且与其下部结构形式密切相关[6-7]。国内外学者采用数值模拟、风洞试验等方式对风屏障开展了研究。LI等[8]通过风洞试验和有限元分析研究不同透风率风屏障对桥上四车道列车抗风性能的影响,研究结果表明车桥系统的最大动力响应主要取决于风屏障对列车气动力的影响,设置透风率为10%的风屏障可使桥梁跨中最大横向位移减少10 mm,轮重减载率减小到0.1。董国朝等[9]通过风洞试验与数值模拟研究风屏障对主梁及高速列车气动力特性的影响,并通过数据包络法选出了风屏障参数的最佳取值,其为风屏障高度3.5 m、透风率为20%。REN等[10]研究了兰新线上不同参数风屏障的防风效果,研究结果表明高度为4 m、透风率为20%的风屏障防风效果最佳,雷诺数效应可忽略不计。ZHANG等[11]通过风洞试验研究不同类型主梁在不同风屏障下的局部风场特性,风屏障高度与透风率对风剖面和功率谱影响较大,开口形式对局部风场特性影响较小。邱晓为等[12]通过风洞试验研究风屏障对简支箱梁桥上风场分布的影响,研究结果表明风屏障能有效降低桥面风场的平均风速,但会增大桥面风场湍流强度。郭向荣等[13]通过风洞试验和有限元分析研究新型导风栏杆参数对风-车-桥耦合振动的影响,研究结果表明安装导风栏杆后桥梁跨中横向位移增大,但桥梁振动幅度增量有所减小。蒋硕等[14]通过风洞试验研究导风屏障对主梁桥面风场特性的影响,研究结果表明导风屏障对风场特性的影响主要受遮挡作用与导风作用共同控制,增大其下部尺寸可以使得内流向风速降低。邹思敏等[15]通过数值模拟研究风屏障对静态、动态列车气动特性的影响,研究结果表明合成风攻角法可以较好地反映在无风屏障时列车的气动特性,但存在风屏障时该方法不再适用,静态模型无法揭示列车和桥梁的瞬态效应。徐昕宇等[16]通过建立风-车-桥有限元模型研究突风效应对列车走行性的影响,突风效应对列车加速度影响显著,但对轮轴横向力和轮重减载率的影响有限。然而,国内外学者对风屏障的研究大多数针对单幅车-桥系统,对同层双幅桥-列车系统的风屏障研究较少。由于同层双幅桥之间存在气动干扰效应[17-19],风屏障防风效果可能受到影响。为此,有必要研究风屏障对公铁同层双幅桥-列车气动特性的影响。本文以某大跨公铁同层双幅斜拉桥为背景,通过风洞试验研究风屏障对不同来流方向时铁路主梁、公路主梁、列车气动特性的影响,为同类型双幅桥梁风屏障设计提供参考和依据。
1 工程概况
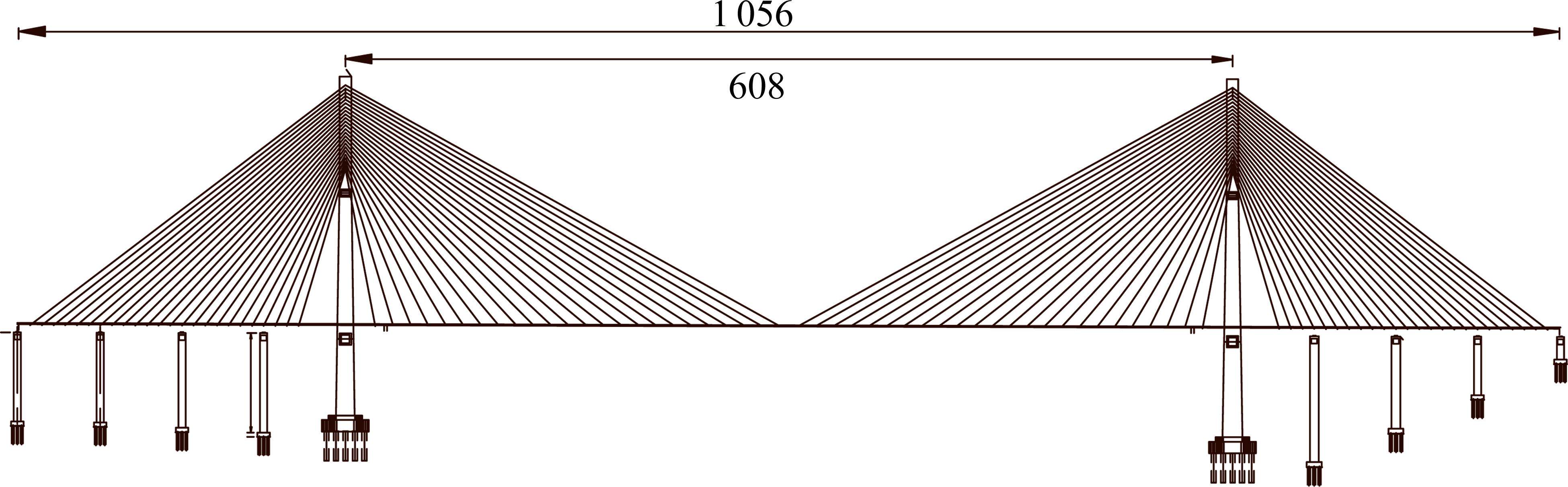
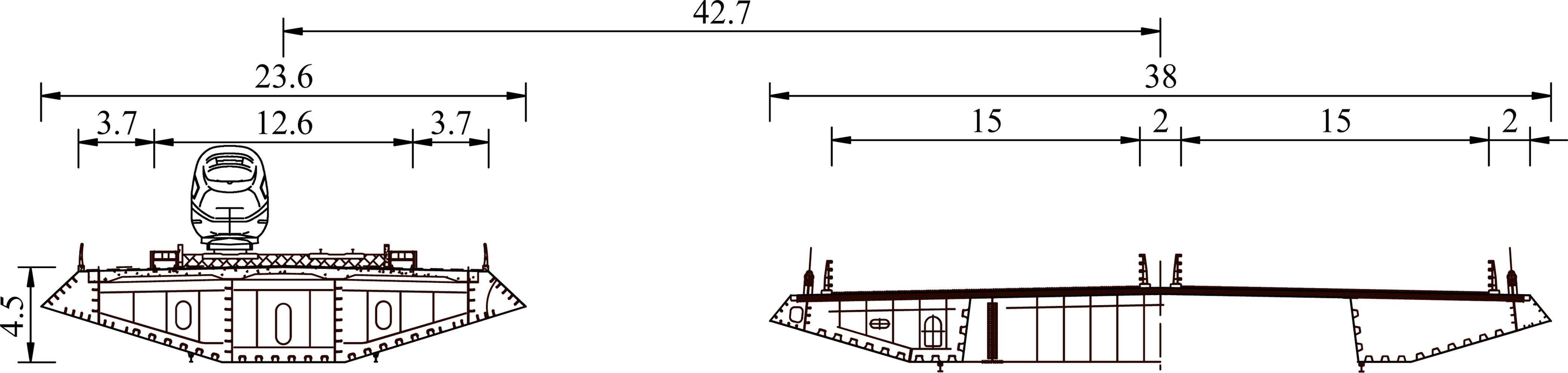
某新建大跨双幅公铁同层斜拉桥位于川渝地区,该桥公铁合建部分铁路为双线高速铁路,主梁宽为23.6 m,高为4.5 m,是典型流线型箱梁,斜拉索采用双索面形式;公铁合建部分公路为双向六车道高速公路,设计速度100 km/h,主梁宽为38 m,高为3.5 m,是PK型箱梁,桥梁布置如图1所示。铁路主梁与公路主梁平行布置,在结构上相互独立,铁路主梁和公路主梁中心间距为42.7 m,双幅主梁断面如图2所示。
2 试验概况
2.1 试验模型与设备
本试验在中南大学风洞实验室CSU-Ⅲ风洞内完成,该风洞的试验段尺寸为0.8 m×1.4 m×2 m,风速范围为0~25 m/s。节段模型缩尺比为1∶100,列车模型长为0.75 m、宽为0.034 m、高为0.035 m,铁路主梁模型长为0.75 m、宽为0.236 m、高为0.045 m,公路主梁模型长为0.75 m、宽为0.38 m、高为0.035 m,为避免端部效应,模型两端各增加一块端板以消除端部效应。铁路与公路模型的主结构由钢板和PVC板构成,主梁则由钢管制作,确保了模型的整体刚性。列车模型则选用高质量木料制成,并在其内部配备加劲梁,以确保模型的强度和刚性达到设计要求;附属设施如栏杆、检修轨道等均由PVC板雕刻而成,节段模型示意图如图3所示。

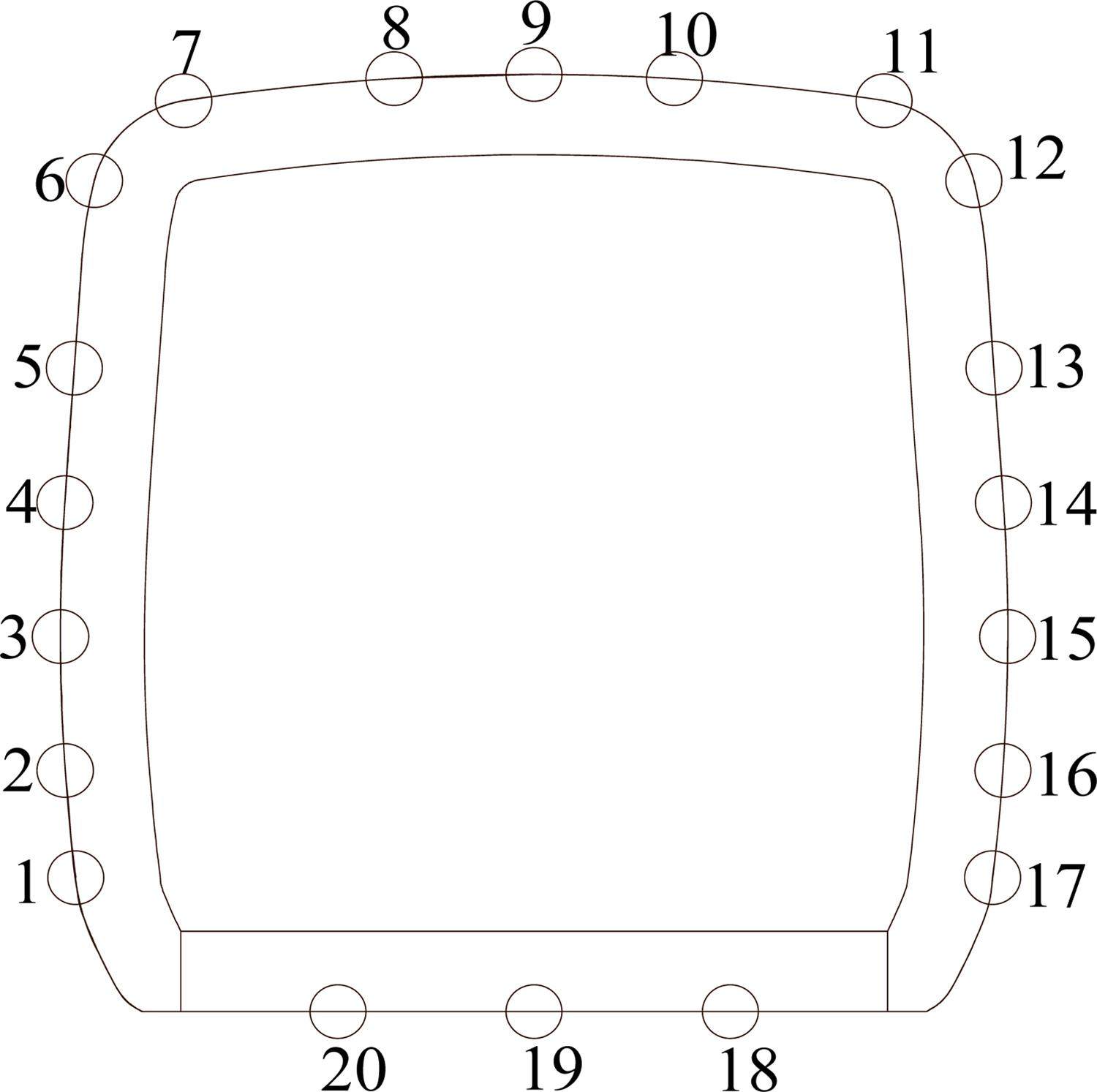
铁路主梁、公路主梁的气动力由动态测力天平获得,列车模型表面风压由电子式压力扫描阀系统测得,列车气动力由对列车表面风压进行积分获得。列车表面共布置20个测点,试验模型测压孔布置如图4所示。试验在0°攻角、风速为16 m/s条件下展开。
2.2 试验工况
为研究风屏障对公铁同层双幅桥-列车气动特性的影响,选取高为3 m、透风率为30%的直立式风屏障进行了如表1所示工况的风洞试验,分别为无风屏障、有风屏障时的双幅桥-列车,包含2种不同来流方向:1) β=0°时,公路主梁位于下游;2) β=180°时,公路主梁位于上游。
| 工况编号 | 来流方向 | 示意图 |
|---|---|---|
| Case 1 | β=0° | |
| Case 2 | ||
| Case 3 | β=180° | |
| Case 4 |
2.3 数据处理
对各测压点测试的风压时程Pi进行无量纲处理,每一点的风压可以用压力系数Cpi进行描述:
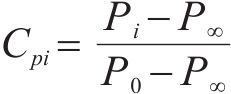
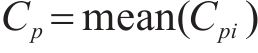
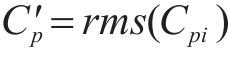
式中:Pi为试验测点处测得的风压,以指向试验模型表面的压力为正;P∞为参考静压,该静压是通过皮托管侧孔测量;P0为无穷远处参考点的总压;Cp为主梁表面测点平均风压系数。
列车与主梁气动力系数表达式为:
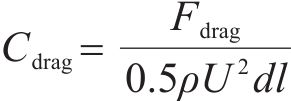
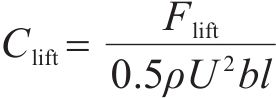
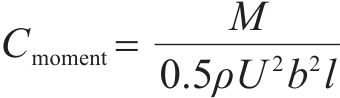
式中:d、b、l分别为列车或主梁的高度、宽度、长度;ρ为空气密度;U为平均风速;Ch、Cv、Cm分别为主梁的阻力系数、升力系数、扭矩系数;Fh、Fv、M分别为主梁的阻力、升力、扭矩,通过动态测力天平测得;CH、CV、CM分别为列车模型的阻力系数、升力系数、扭矩系数;FH、FV、M分别为列车模型的阻力、升力、扭矩,通过对模型测压截面的平均风压积分得到,具体计算公式可见文献[20]。
3 结果与讨论
3.1 铁路主梁气动力系数
图5给出了不同工况下铁路主梁平均气动力系数结果。由图5可知,在β=0°时,相对于无风屏障,有风屏障时铁路主梁平均阻力系数增加了0.39,出现这种现象的原因可能是因为风屏障导致主梁迎风面增加造成的[21];铁路主梁平均升力系数、平均扭矩系数数值变化较小且方向发生变化,变为相反方向。在β=180°时,相对于无风屏障,有风屏障时铁路主梁平均阻力系数增加了0.31,但2种工况下铁路主梁平均阻力系数较β=0°都有所减小,这可能是由于上游公路主梁的遮挡作用造成的;铁路主梁平均升力系数数值有所增加且方向发生变化;铁路主梁平均扭矩系数变化较小。
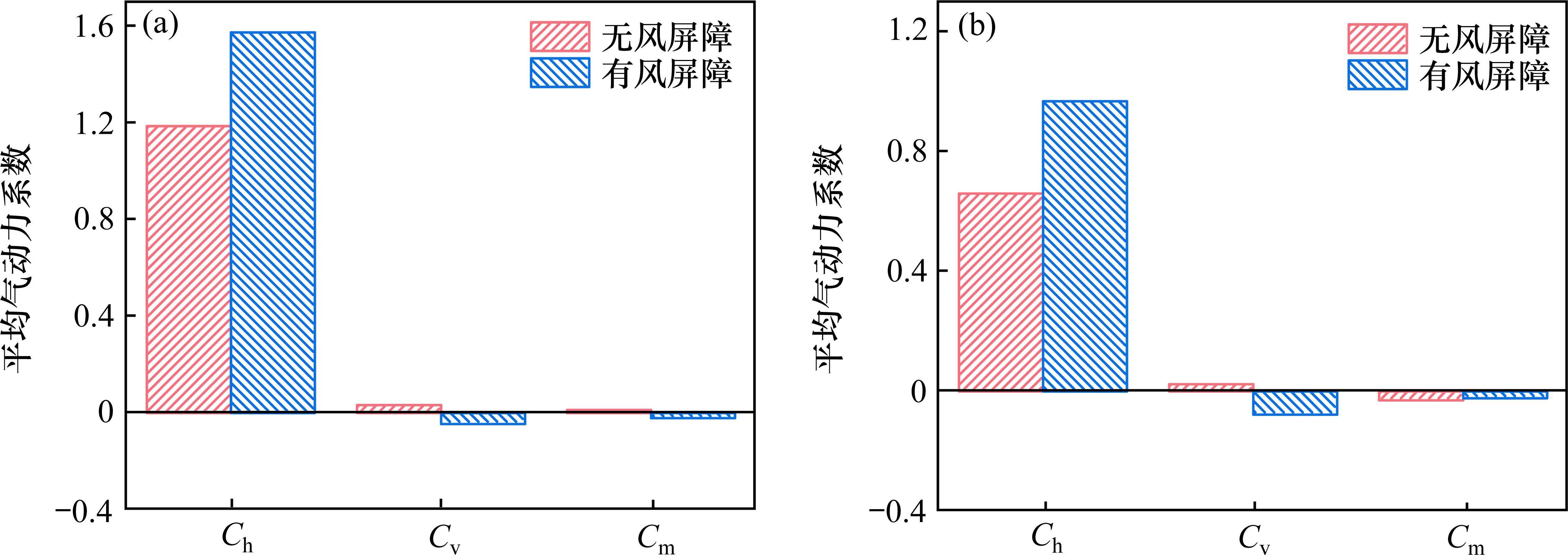
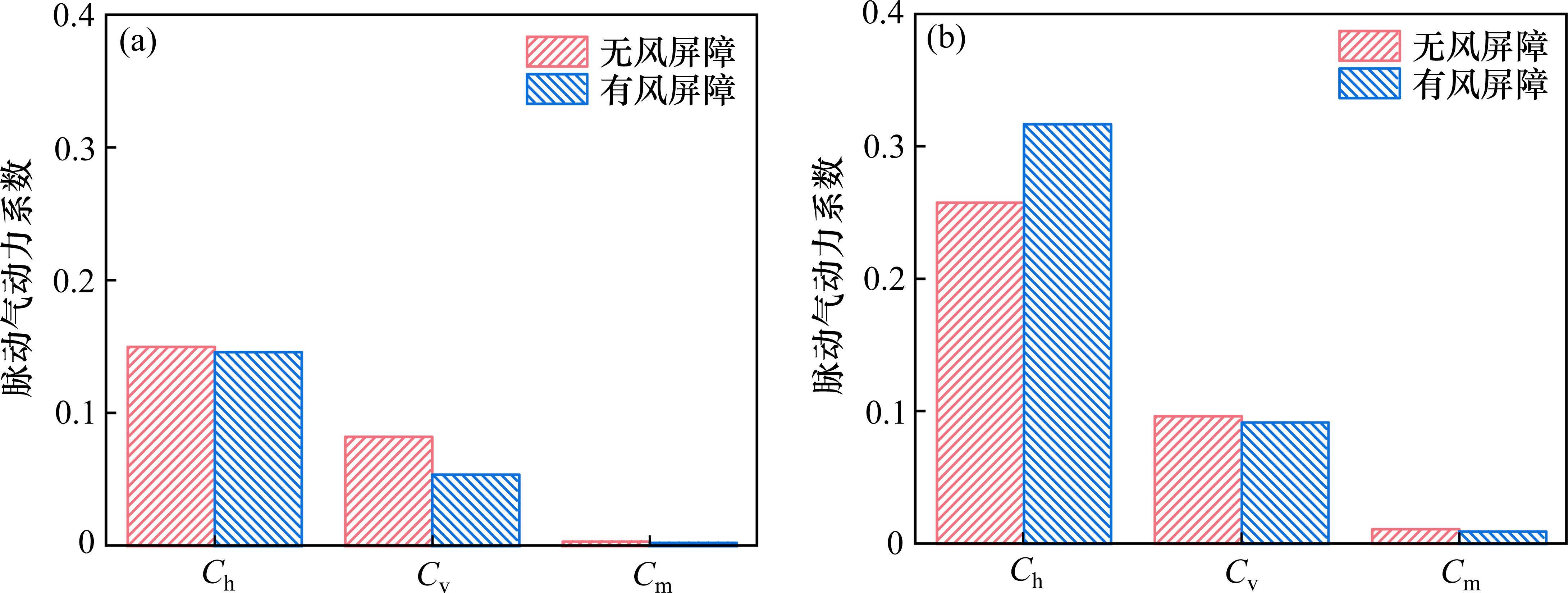
图6给出了不同工况下铁路主梁脉动气动力系数结果。由图6可知,在β=0°时,相对于无风屏障,有风屏障时铁路主梁脉动阻力系数、脉动扭矩系数变化较小,脉动升力系数减小了0.03。在β=180°时,相对于无风屏障,有风屏障时铁路主梁脉动升力系数、脉动扭矩系数变化较小,脉动阻力系数增大了0.06。
3.2 公路主梁气动力系数
图7给出了不同工况下公路主梁平均气动力系数结果。由图7可知,在β=0°时,相对于无风屏障,有风屏障时公路主梁平均阻力系数减小了0.12,且2种工况下公路主梁平均阻力系数较β=180°时均有所减小,出现这种现象的原因可能是上游铁路主梁的遮挡作用造成的;有风屏障时公路主梁平均升力系数数值基本保持不变但方向发生变化,变为相反方向;公路主梁平均扭矩系数变化较小。在β=180°时,相较于无风屏障,设置风屏障后公路主梁平均阻力系数减小了0.22;同时,风屏障的存在使得公路主梁的平均升力系数变化幅度不大,且其方向保持不变;此外,公路主梁的平均扭矩系数在风屏障作用下也仅显示出轻微的变化。
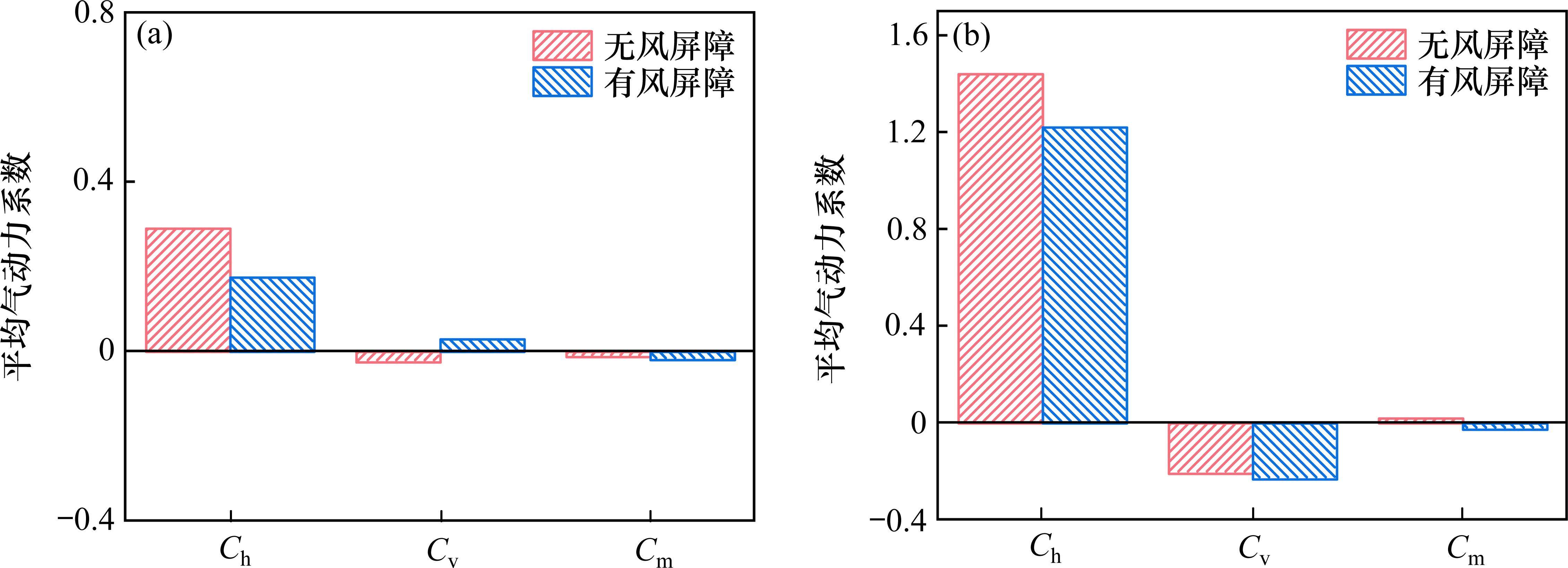
图8给出了不同工况下公路主梁脉动气动力系数结果。由图8可知,在β=0°时,相对于无风屏障,有风屏障时公路主梁脉动阻力系数、脉动升力系数、脉动扭矩系数变化较小。在β=180°时,相对于无风屏障,有风屏障时公路主梁脉动阻力系数增加了0.05,公路主梁脉动升力系数减小了0.02,公路主梁脉动扭矩系数变化较小。
3.3 列车气动力系数
图9给出了不同工况下列车平均气动力系数结果。由图9可知,在β=0°时,相对于无风屏障,有风屏障时列车平均阻力系数显著降低,出现这种现象的原因是由于风屏障的遮挡作用造成的;有风屏障时列车平均升力系数数值减小了0.12且方向发生变化,变为相反方向,这可能是风屏障的存在使得列车处于主梁前缘绕流形成的低速区域中造成的;列车平均扭矩系数变化较小。在β=180°时,相对于无风屏障,有风屏障时列车平均阻力系数减小了0.27,但降低的幅度远小于β=0°时;有风屏障时列车平均升力系数、平均扭矩系数数值均有所减小但方向未发生变化。
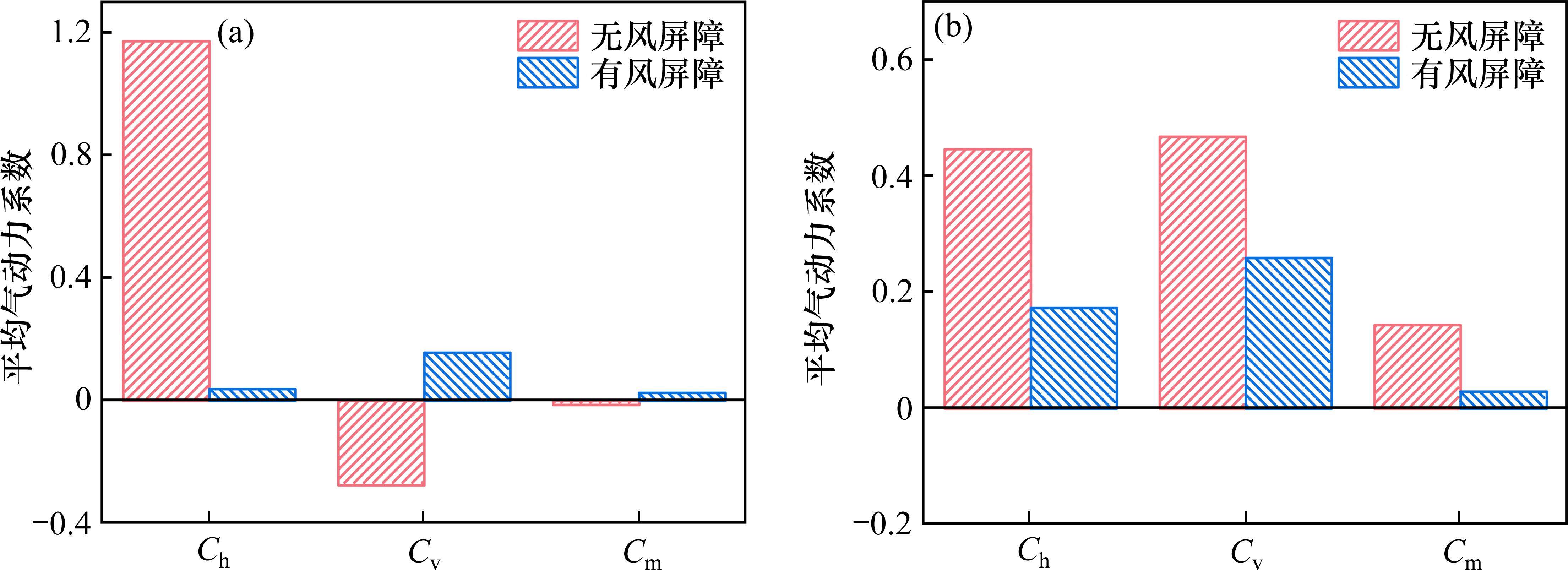
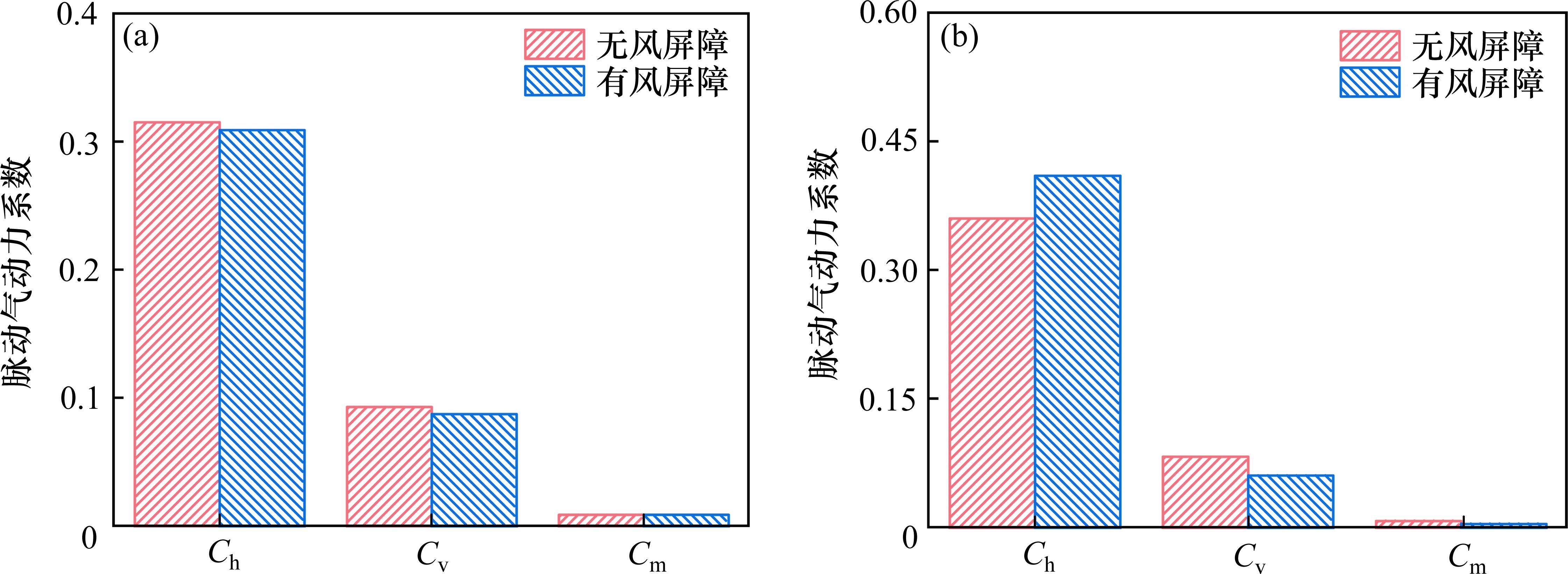
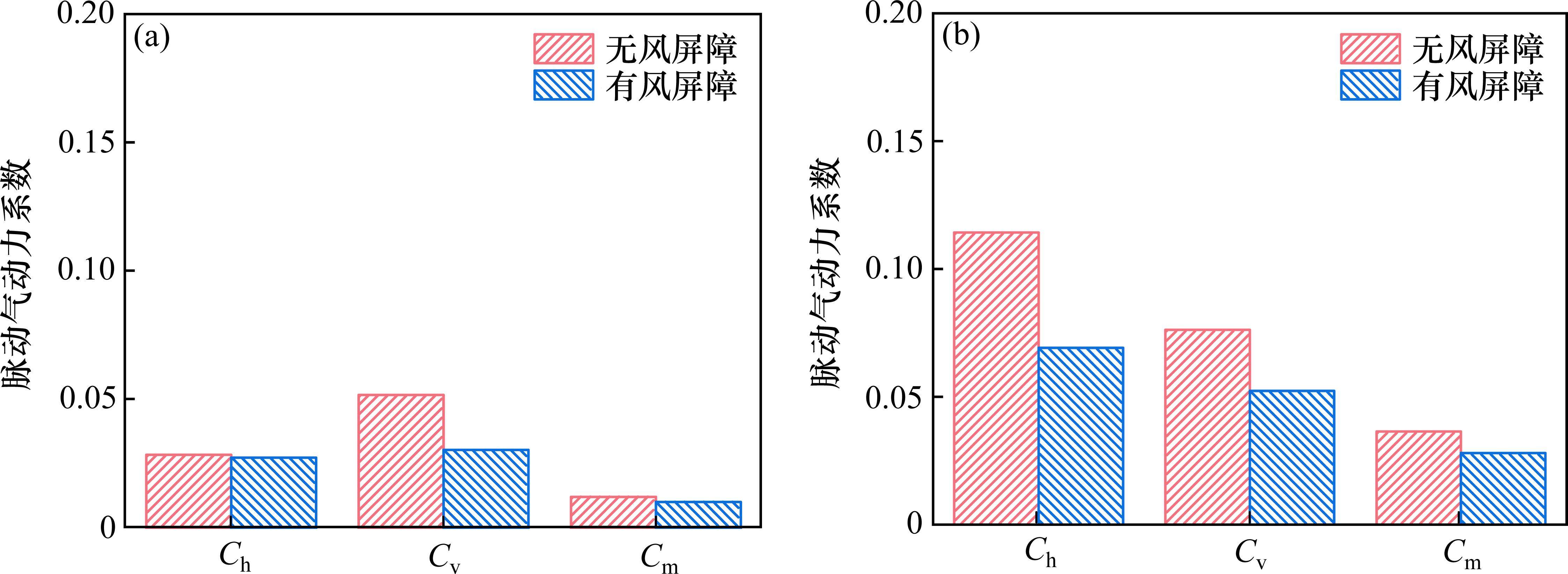
图10给出了不同工况下列车脉动气动力系数结果。由图10可知,在β=0°时,相对于无风屏障,有风屏障时列车脉动阻力系数、脉动扭矩系数变化较小,脉动升力系数减小了0.02。在β=180°时,相对于无风屏障,列车脉动阻力系数减小了0.04,脉动升力系数减小了0.02,脉动扭矩系数减小了0.01。
3.4 列车表面平均风压特性
对比各工况下列车平均风压系数结果,根据列车表面平均风压分布情况能推断气流在列车表面分离和再附情况,并对气动力系数结果进行一定程度的解释。图11为不同工况下列车表面的平均风压系数分布情况。其中,列车断面被设定为风压的基准点(零风压点),断面内侧区域表现为正压值,而外侧区域则呈现负压值。
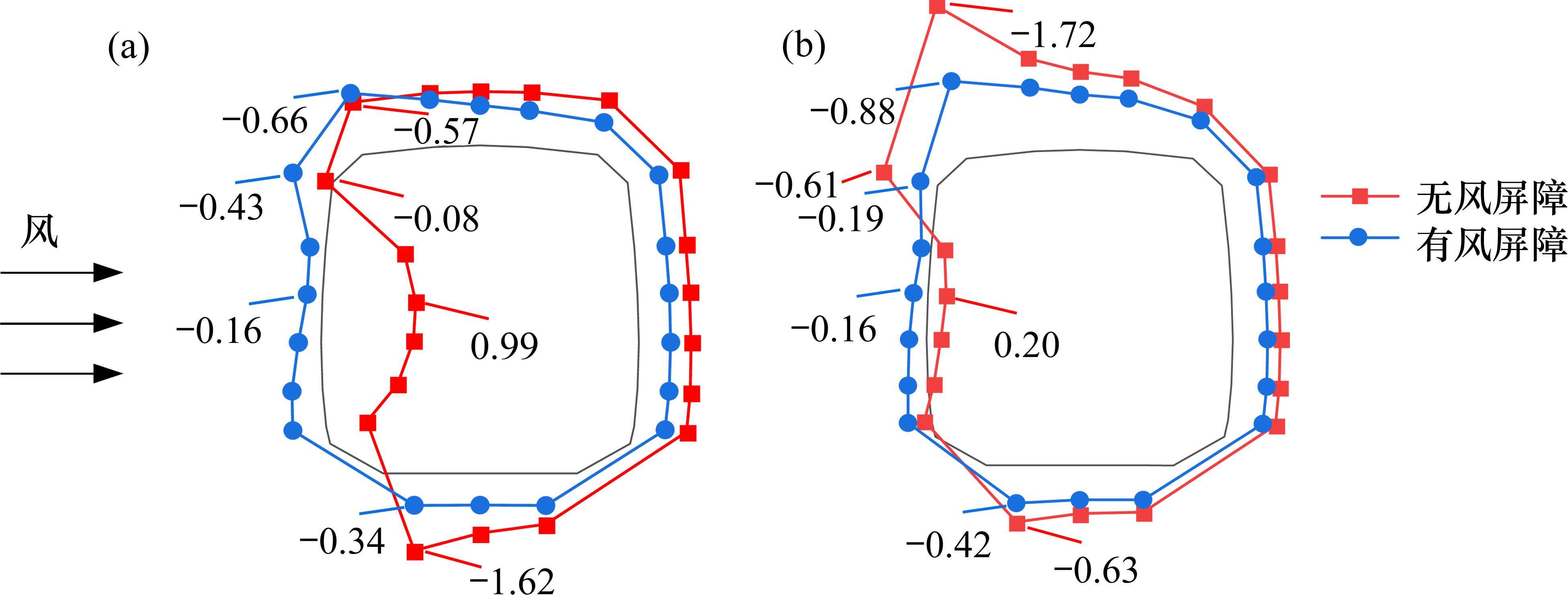
图11(a)所示为β=0°时列车的平均风压分布情况。从图中可以看出,2种工况下列车表面平均风压系数在迎风面与顶部交界处均发生突变,剪切层中流动分离所引起的强夹带和吸力使得该处负压急剧增加。有风屏障时列车表面平均风压系数极值出现在迎风面与顶面交界处,为-0.66;无风屏障时列车表面平均风压系数极值出现在列车迎风面底部,为-1.62。正因为无风屏障时列车底面平均风压系数小于顶面平均风压系数,而有风屏障时列车顶面平均系数小于底面平均风压系数,这导致了有、无风屏障时列车升力系数方向发生变化,风屏障的存在是造成这种差异的主要原因。在这2种工况下,列车背风面受漩涡脱落影响均为负压且较为接近,无风屏障时列车迎风面均为正压,而有风屏障时列车迎风面均为负压,因此,无风屏障时列车迎风面与背风面的压差较大,这也解释了无风屏障时列车阻力系数显著大于有风屏障时的原因。
图11(b)所示为β=180°时列车的平均风压分布情况。可以看出,2种工况下列车表面平均风压系数在迎风面与顶面交界处均发生突变。无风屏障时列车表面平均风压系数极值出现在迎风面与顶面交界处为-1.72,有风屏障时列车表面平均风压系数极值也出现在该处为-0.88。有、无风屏障时列车顶面平均风压系数均小于底面且无风屏障时列车顶面与底面压差较大,这解释了2种工况下列车升力系数均为正值且无风屏障时列车升力系数比有风屏障略大的原因。在这2种工况下,列车背风面受漩涡脱落影响均为负压且较为接近,无风屏障时列车迎风面均为正压,而有风屏障时列车迎风面均为负压,但2种工况列车下迎风面压差相较于β=0°时更小,这解释了无风屏障时列车阻力系数大于有风屏障时且变化幅度小于β=0°的原因,上游公路的气动干扰可能是造成这种差异的原因。
3.5 列车表面脉动风压特性
对比各工况下列车脉动风压系数结果,列车表面脉动风压系数可以进一步解释列车表面的气流流动情况,图12所示为各工况下列车表面的脉动风压系数。
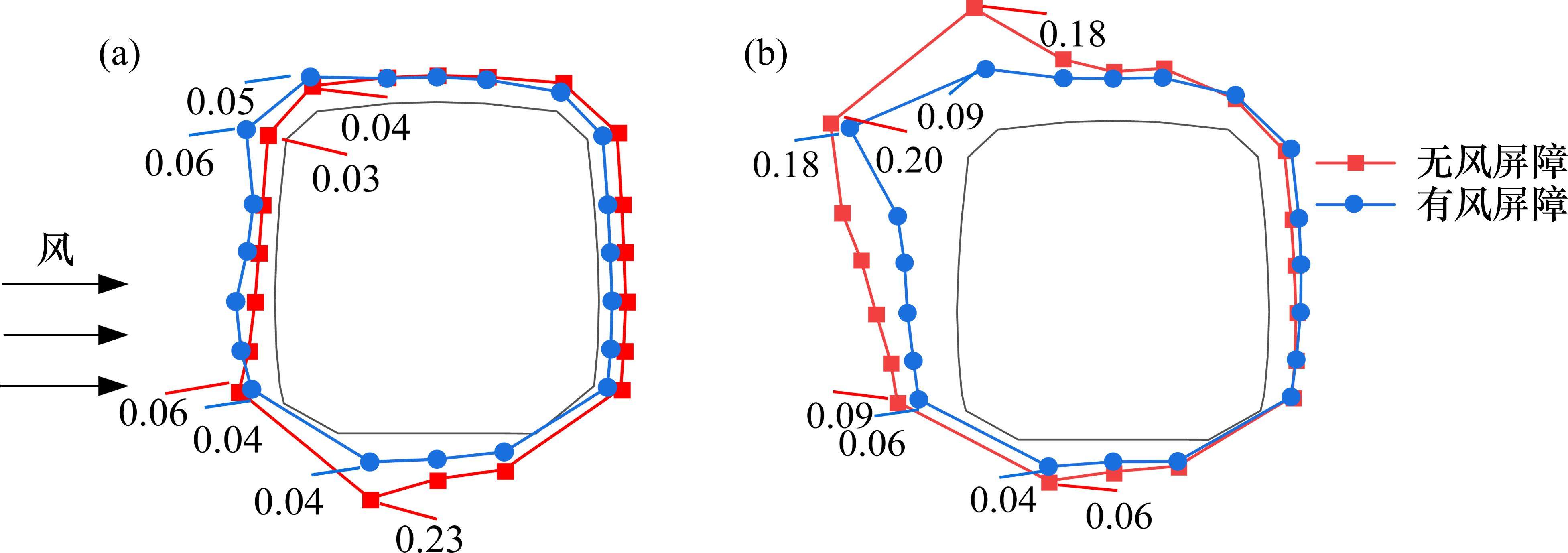
图12(a)所示为β=0°时列车的脉动风压分布。可以看出,在无风屏障条件下,列车顶面脉动风压系数较小;列车背风面脉动风压系数较小,该区域处于尾流脱落区,脉动性较弱;列车表面脉动风压系数极值出现在底部圆弧过渡段,为0.23,气流在此处波动较大,因此该区域内气流脉动性较强。在有风屏障条件下,受风屏障遮挡作用,列车表面脉动风压系数均较小,表明有风屏障时列车表面气流脉动性较弱。
图12(b)所示为β=180°时列车的脉动风压分布。可以看出,在无风屏障条件下,列车底面脉动风压系数较小;列车背风面脉动风压系数较小,该区域处于尾流脱落区,脉动性较弱;列车表面脉动风压系数极值出现在顶部圆弧过渡段区域,为0.20,气流在此处波动较大,因此该区域内气流脉动性较强。在有风屏障条件下,受风屏障遮挡作用,列车表面脉动风压系数整体有所减小,但在列车顶部圆弧过渡段区域列车脉动风压系数减少幅度较小,表明当β=180°时风屏障对列车顶部圆弧过渡段区域内气流脉动性削弱作用有限,出现这种现象可能是上游公路主梁的气动干扰效应造成的。
4 结论
1) 不同风向角下风屏障对铁路主梁平均气动力系数的影响基本相似。β=0°时风屏障主要影响铁路主梁脉动升力系数,而β=180°时风屏障主要影响铁路主梁脉动阻力系数。
2) 无论β=0°或β=180°,由于风屏障的存在,公路主梁平均阻力系数整体有所减小;β=0°时风屏障对公路主梁脉动气动力系数影响较小,而β=180°时风屏障主要影响铁路主梁脉动阻力系数和脉动升力系数。
3) β=0°时风屏障对列车平均阻力系数的影响大于β=180°时风屏障的影响;而β=180°时风屏障对列车脉动阻力系数的影响大于β=0°时风屏障的影响。
4) β=0°时,风屏障对列车平均风压系数分布的影响主要体现在迎风面与底面;β=180°时,风屏障对列车平均风压系数分布的影响主要体现在迎风面与顶面。
5) β=0°时,风屏障能有效降低列车底部圆弧过渡段区域内气流脉动性;β=180°时,风屏障对列车顶部圆弧过渡段区域内气流脉动性削弱作用有限,说明风屏障在不同风向角下对列车表面风压脉动性的影响存在差异。
6) 不同风向角下风屏障对公铁同层双幅桥-列车气动特性的影响存在明显差异,故在同类型双幅桥梁-列车系统风屏障设计中需综合考虑不同风向角下的气动特性差异。
邹云峰,刘政华,何旭辉等.风屏障对公铁同层双幅桥-列车气动特性的影响[J].铁道科学与工程学报,2025,22(03):1144-1153.
ZOU Yunfeng,LIU Zhenghua,HE Xuhui,et al.Effect of wind barrier on aerodynamic characteristics of twin parallel decks for rail-cum-road bridge and train[J].Journal of Railway Science and Engineering,2025,22(03):1144-1153.

