2015年以前,我国在中小跨径桥梁工业化建设中,大多采用混凝土板梁和T梁进行预制装配,但其自重较大,且易出现裂缝和下挠问题。近年来推广应用的平腹板叠合梁桥(简称“FSRC叠合梁桥”)通过剪力连接件将工字钢梁与桥面板连接,因其重量小、充分发挥材料特性等优点,该结构在中小跨径桥梁领域中得到广泛应用[1-3]。与混凝土腹板相比,FSRC叠合梁桥的钢腹板更为纤薄,在受到偏载作用时,容易发生失稳破坏[4-6]。为了提高FSRC叠合梁桥的横向刚度和稳定性,目前通常采用增设竖向加劲肋和增加主梁数量的方法。然而,采用这种方法可能会导致腹板上剪力分布不均匀,从而降低剪力的传递效率并导致腹板局部应力集中。另外,负弯矩区钢梁受压而桥面板受拉的受力特征造成混凝土板极易开裂,降低桥梁结构使用寿命[7-10]。波纹腹板由于其波折状的结构特征,大幅度地增加了钢梁的稳定性,采用波纹腹板代替平腹板,可使得加劲肋等钢构件数量大幅度减少,从而减少焊接量,提高经济性和施工效率[11-13]。波纹腹板叠合梁桥(简称“CSRC叠合梁桥”)具有结构特征上的巨大优势,但由于波纹腹板的纵向刚度较弱,其与FSRC叠合梁桥在力学性能方面的差异还需进一步研究。国内外已有学者将波纹腹板叠合梁与采用其他腹板形式的叠合梁进行对比。顾建成等[14]通过对比波纹腹板-混凝土组合T梁桥与平腹板-混凝土组合T梁桥全桥实体仿真模型在车辆偏载情况下的力学性能,发现波纹腹板-混凝土组合T梁桥在抗裂、抗扭及稳定性方面均有一定的优势。刘华琛[15]对比叠合梁腹板形状(波纹腹板和平腹板)对整体抗扭性能造成的影响,发现波纹腹板抗扭性能略弱。JUNG等[16]等对钢桁腹与波纹腹板叠合梁的力学性能进行了试验研究,与钢桁腹叠合梁相比,波纹腹板叠合梁有较高的刚度和抗剪性能。MOON等[17]对波纹腹板叠合梁在均匀弯曲作用下的横向扭转屈曲进行了理论分析和有限元分析,与平腹板叠合梁相比,其翘曲常数较大,且弹性侧扭屈曲强度随着波折角度的增大而增加(最大增加10%)。综上可知,以上针对采用波纹腹板、平腹板和桁架3种腹板形式的叠合梁的抗扭、抗剪以及稳定性等受力性能分别进行对比,并取得较好的研究进展。然而,关于波纹腹板和平腹板叠合梁桥的抗扭性能的评价不一致。同时,抗弯承载力一直是钢混叠合桥梁领域的研究重点。现有研究往往因为这2种腹板形式的差异而侧重于抗扭和抗剪性能,却缺乏对抗弯性能的充分研究。此外,立足新发展阶段,落实绿色低碳发展理念,大力推广钢结构而不是大量使用钢材,在保证结构安全的前提下,用最少的钢材,建造结构性能最优异的钢混组合桥梁,把用钢量控制在合理、适用的范围内,从源头上降低碳排放。FSRC叠合梁桥和CSRC叠合梁桥由于腹板形式等构造不同,用钢量也有显著的差异性。为更直观且全面地比较腹板形式分别为波纹腹板和平腹板的叠合梁桥受力性能的差异,避免由于前提条件的差异而导致结论不一的情况,本文以某三跨连续双主梁CSRC叠合梁桥为背景,在保持梁高和用钢量一致的前提下,分别对应此2种腹板形式设计2根试验梁进行加载,并采用有限元软件分别建立CSRC叠合梁桥与FSRC叠合梁桥的全桥模型,对两者的纵向弯曲、扭转以及稳定性等方面进行全面对比。
1 试验概况
1.1 工程背景
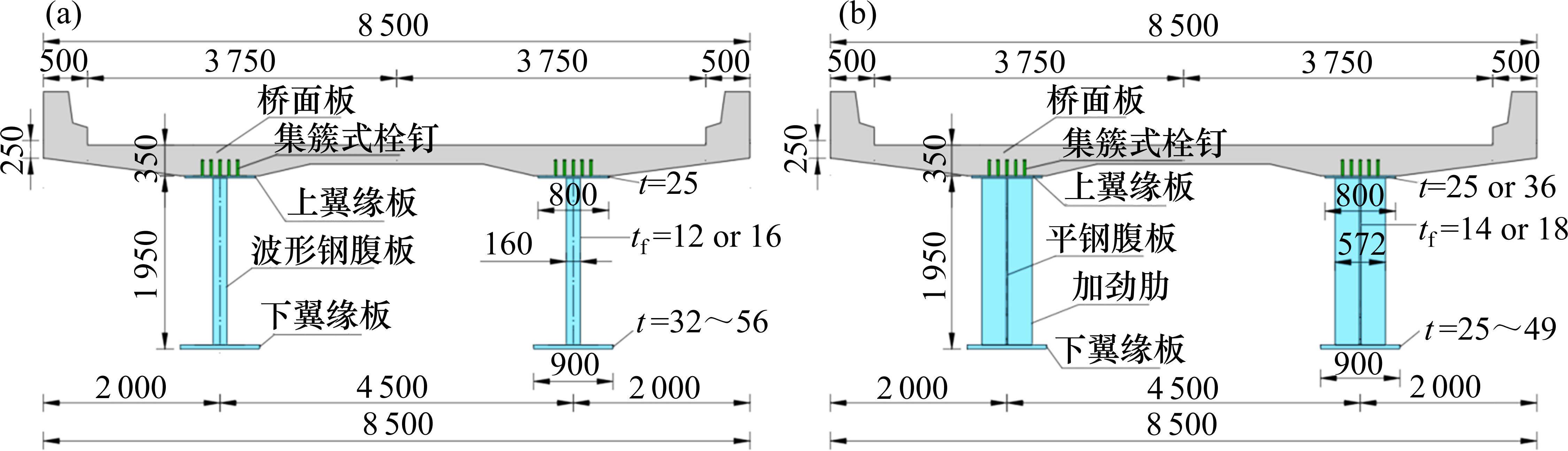
山东九龙东枢纽天桥为25 m+45 m+25 m三跨连续双主梁CSRC叠合梁桥,其钢梁尺寸参数如下表1所示,桥面板以预制为主,采用C50混凝土,墩顶局部区域采用现浇UHPC桥面板,布置双车道,宽8.5 m;波纹腹板采用1 000型,钢梁采用Q355钢,采用栓钉与桥面板连接,如图1(a)所示。本文参照此桥钢梁设计参数,以梁高与用钢量一致为原则,设计了FSRC叠合梁桥,钢梁尺寸如表2所示。参照现行同等跨径布置的CSRC叠合梁桥与FSRC叠合梁桥通用图册,由于平腹板与波纹腹板相比,横向稳定性较差,因此平腹板厚度往往要比波纹腹板较厚,且多处焊接加劲肋,加劲肋间距约2.5 m。与CSRC叠合梁桥相比,FSRC叠合梁桥腹板受力,为保证两者用钢量一致,其下翼缘较薄,桥面板及配筋等其他参数与CSRC叠合梁桥一致。
| 梁段位置 | 钢梁尺寸/mm | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 腹板 | 顶板 | 底板 | 腹板高厚比h/tf | 宽厚比b/t | |||||
| 高/mm | 厚/mm | 宽/mm | 厚/mm | 宽/mm | 厚/mm | 顶板 | 底板 | ||
| 边跨跨中 | 1 893 | 12 | 800 | 25 | 900 | 32 | 157.8 | 19.2 | 16.6 |
| 中跨跨中 | 1 889 | 12 | 800 | 25 | 900 | 36 | 157.8 | 19.2 | 14.7 |
| 支点 | 1 858 | 16 | 800 | 36 | 900 | 56 | 118.3 | 13.3 | 9.5 |
梁段 位置 | 钢梁尺寸 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 腹板 | 顶板 | 底板 | 腹板高厚比h/tf | 宽厚比b/t | |||||
| 高/mm | 厚/mm | 宽/mm | 厚/mm | 宽/mm | 厚/mm | 顶板 | 底板 | ||
| 边跨跨中 | 1 900 | 14 | 800 | 25 | 900 | 25 | 135.2 | 16.0 | 21.2 |
| 中跨跨中 | 1 896 | 14 | 800 | 25 | 900 | 29 | 135.2 | 16.0 | 18.3 |
| 支点 | 1 865 | 18 | 800 | 36 | 900 | 49 | 105.2 | 11.1 | 10.8 |
1.2 试验梁设计与制作
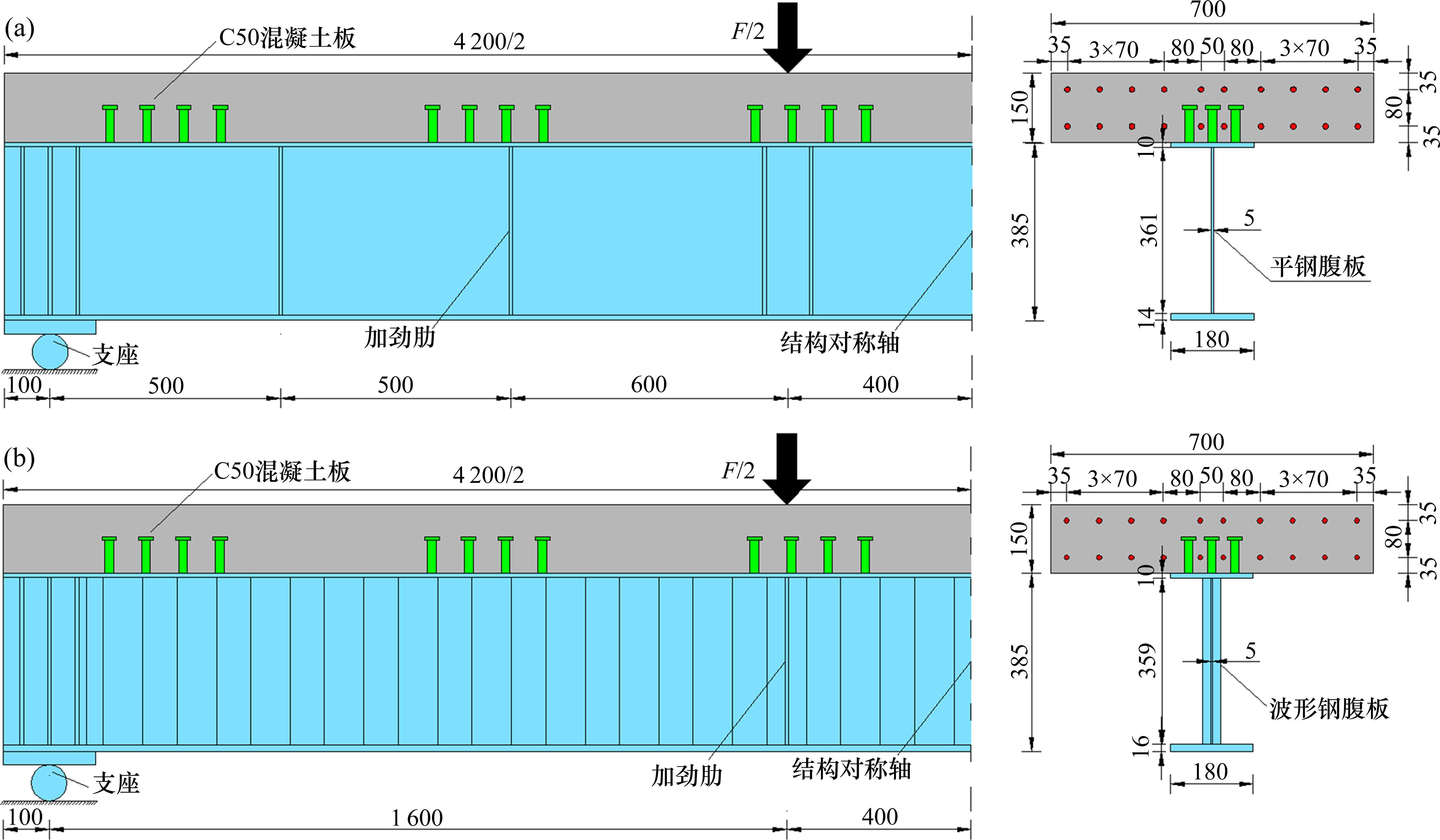
参照上述2组实桥尺寸,按照刚度等效和中性轴相对位置不变的要求,并考虑构件的可制作性,以1∶5的比例进行缩尺设计。波纹腹板叠合梁(简称CSRC试验梁)和平腹板叠合梁(简称FSRC试验梁)缩尺模型的整体尺寸一致且用钢量相同。如图2所示,试验梁长为4 200 mm,桥面板宽700 mm,厚度为150 mm,钢梁高385 mm,钢梁均在支座及加载位置处布置加劲肋,FSRC试验梁还需间隔500 mm布置加劲肋以增强截面稳定性。桥面板与钢梁之间通过6组集簇式栓钉连接,每组间隔700 mm,栓钉采用ML15AL,规格为Φ19×80 mm。其中,每组栓钉横向间距为50 mm,纵向间距为80 mm。2根试验梁桥面板相同,板内设有2层HRB400钢筋,直径为12 mm,上翼缘厚度均为10 mm,由于实桥腹板厚度经缩尺后差别较小,故试验梁腹板厚度均为5 mm。不同之处在于2根试验梁钢梁下翼缘厚度分别为14 mm和16 mm,参照实桥尺寸,FSRC试验梁的加劲肋和腹板增厚的用钢量与CSRC试验梁下翼缘加厚以及腹板波折形式增加的用钢量相同,从而保证两者用钢量一致。
| 桥型 | 上翼缘板/kg | 波纹腹板/kg | 下翼缘板/kg | 横梁/kg | 加劲肋/kg | 总用钢量/kg |
|---|---|---|---|---|---|---|
| CSRC | 35 206 | 43 660 | 57 175 | 20 683 | 4 163 | 160 887 |
| FSRC | 35 206 | 44 425 | 47 595 | 20 683 | 14 071 | 161 980 |
试验梁材料与实桥一致,实测C50混凝土立方体抗压强度fcu为60.8 MPa;钢材屈服强度fy为385 MPa,极限强度fu为551 MPa;HRB400钢筋屈服强度为448 MPa,极限强度为614 MPa;栓钉极限强度为420 MPa。
1.3 试验梁加载及测试
试验采用千斤顶进行2点加载,加载间距为800 mm,如图3(a)所示。梁体四分点截面腹板布置应变花,跨中纯弯段布置纵向应变片,如图3(b)所示。以每30 kN为一个加载等级,持荷5 min,采集传感器数据。按荷载控制逐级加载至加载力不再上升后,改为位移控制,每2 mm为一级,直至试件完全破坏。

2 试验结果与分析
2.1 试验过程及破坏特征
对于FSRC试验梁,荷载加至710 kN时,钢梁下翼缘达到屈服强度,荷载继续增至751 kN时,跨中桥面板底面开裂,挠度增加幅度变大。当荷载达到1 004 kN时,跨中桥面板底面裂缝延伸至侧面,且随后梁体四分点剪跨区段腹板发生变形,与腹板高度方向呈一定角度,桥面板侧面出现斜裂缝。荷载增至1 112 kN时,剪跨区桥面板侧面斜裂缝随着荷载的增加延伸至加载端处,贯穿整个桥面板侧面高度,并使得桥面板顶面一定范围内呈三角形剥离,与此同时试验梁发生一声巨响,荷载急剧下降,加载结束。跨中桥面板底面出现多条贯通的横向裂缝,剪跨区范围内出现多条从四分点区域起斜向开裂的裂缝,且有一条主裂缝延伸开裂至桥面板加载端侧面顶部,为典型的剪切破坏,试验梁破坏情况如图4所示。

对于CSRC试验梁,当荷载增至660 kN时,钢梁下翼缘屈服,随后荷载加至690 kN时,跨中桥面板底面开裂,梁体变形明显增大。当荷载增至1 020 kN时,跨中桥面板底面横向裂缝延伸至侧面。当荷载达到1 116 kN时,加载端内侧桥面板顶部出现裂缝,且侧面边缘混凝土呈现扇形压溃,随后下降,加载结束。梁体跨中桥面板底面出现多条贯通的横向裂缝,为典型的弯曲破坏。虽然具有手风琴效应,波纹腹板底部受力变形,但底部一定范围内依旧受纵向应力影响较大,试验梁破坏情况如图5(b)所示。

2组试验梁都在跨中桥面板的侧面和底面多处产生弯曲裂缝,与FSRC试验梁腹板发生剪切变形且桥面板剪切破坏相比,CSRC试验梁波纹腹板并未发生局部屈曲,桥面板顶面混凝土压溃,呈带状贯通顶面。由于波纹腹板剪切屈曲强度较大,从而减小由于腹板变形而引起叠合梁发生剪切脆性破坏的风险。
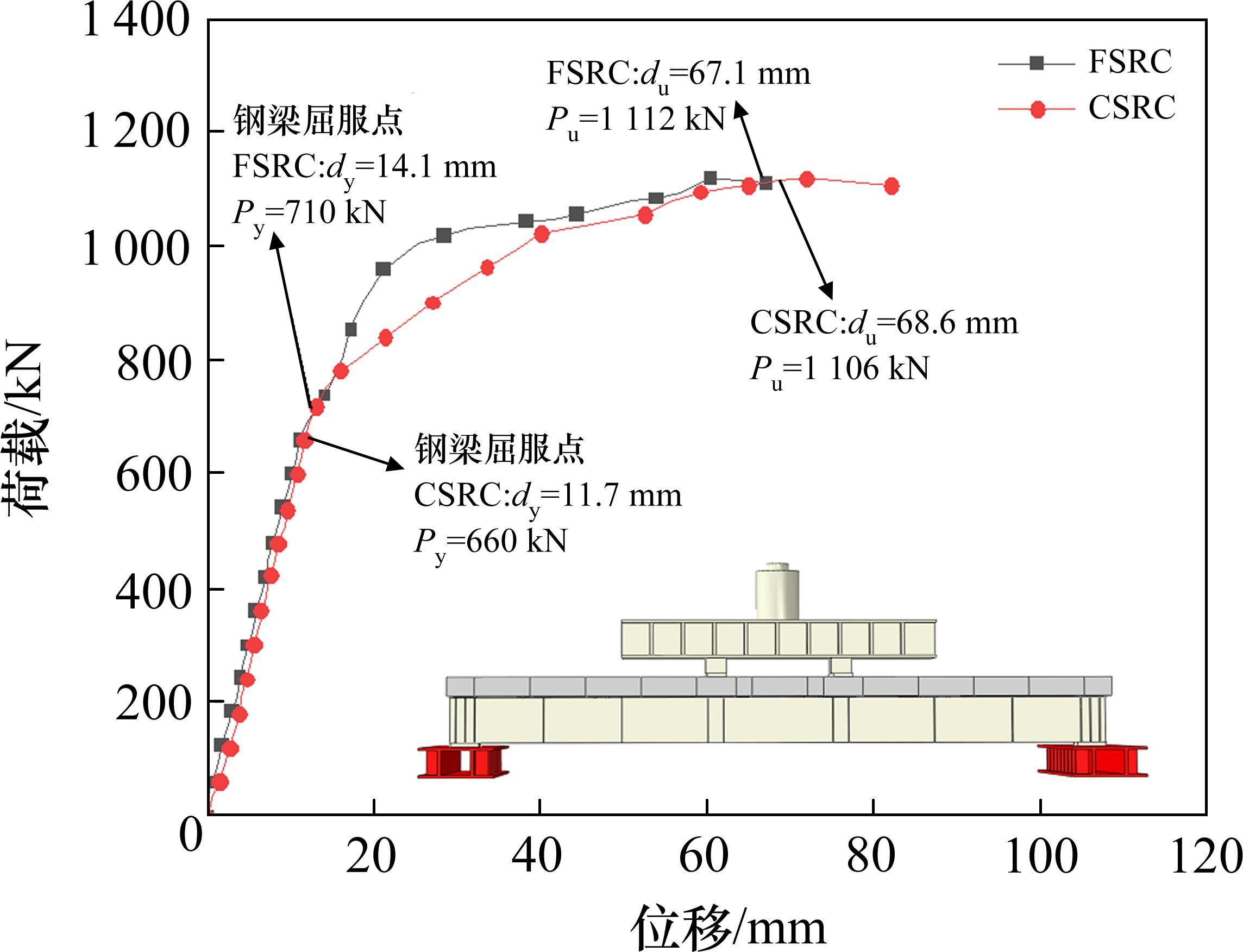
2.2 荷载-位移曲线
图6为2组试验梁荷载-位移曲线,其中,Py表示钢梁屈服荷载,Pu表示试验梁极限荷载,δy和δu分别为屈服荷载和极限荷载对应的挠度,2组曲线变化趋势基本相同。在弹性阶段,2组试验梁的荷载-位移曲线均近似为直线,且刚度几乎相同,FSRC试验梁的屈服荷载Py为710 kN(0.64Pu),对应挠度δy为14.1 mm,CSRC试验梁的屈服荷载Py为660 kN(0.60Pu),对应挠度δy为11.7 mm。在弹塑性阶段,钢梁达到屈服强度导致试验梁刚度呈现出非线性关系,由于波纹腹板纵向刚度较小,CSRC试验梁挠度发展速度明显大于FSRC试验梁。在破坏阶段,FSRC试验梁的极限承载力Pu为1 112 kN,对应挠度δu为67.1 mm,钢梁大部分截面受拉屈服,CSRC试验梁的极限承载力Pu为1 106 kN,对应挠度δu为82.2 mm,由于FSRC试验梁发生剪切破坏,平腹板发生压曲失稳,CSRC试验梁与FSRC试验梁的承载力几乎相同。
2.3 跨中截面纵向应变
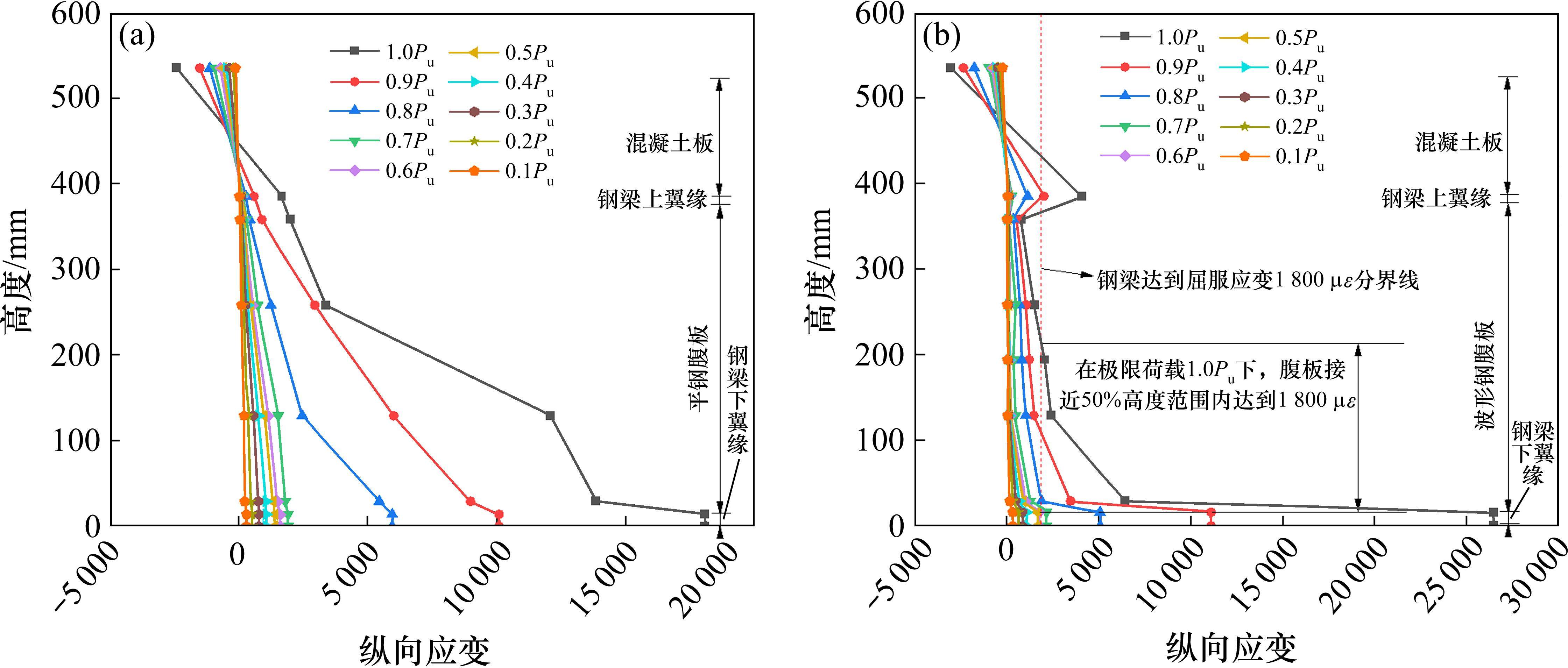
如图7所示,2组试验梁在弹性阶段(0.6Pu之前)时,FSRC试验梁截面纵向应变符合平截面假定,CSRC试验梁桥面板与钢梁上下翼缘应变符合平截面假定,波纹腹板受手风琴效应影响,腹板靠近钢梁上翼缘一侧应变几乎没有,靠近钢梁底部的应变较大,但也远小于屈服应变(钢材屈服应变约为1 800 με),因此在弹性阶段波纹腹板的抗弯贡献可忽略不计。在塑性阶段,FSRC试验梁由于腹板逐渐发生剪切变形,极限荷载下腹板局部应力偏大,而CSRC试验梁腹板顶部应变仍然较小未达到屈服应变,但腹板底部接近50%高度范围内的纵向应变均达到屈服应变,因此在计算塑性阶段波纹腹板叠合梁的极限承载力时,波纹腹板的抗弯承载力不可忽略。加载后期,2组试验梁钢梁下翼缘均达到10 000 με以上,钢梁应变强化效应显著。
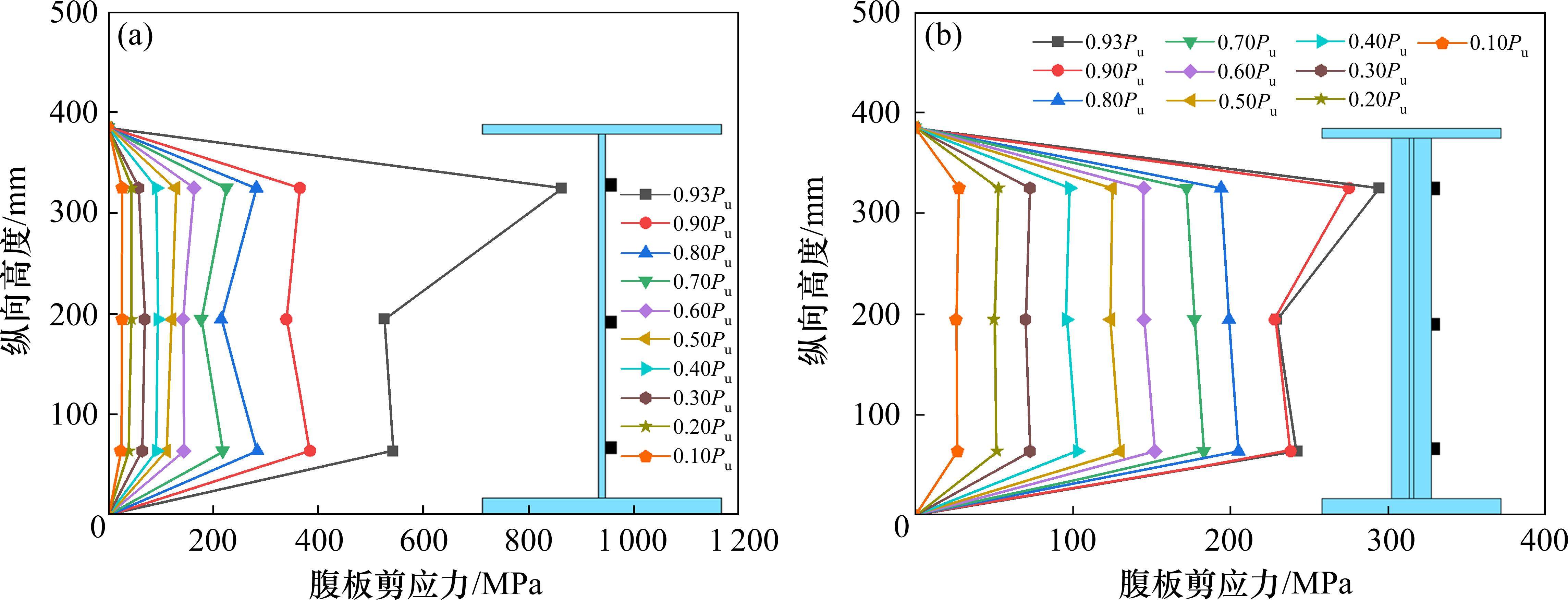
2.4 腹板剪应力
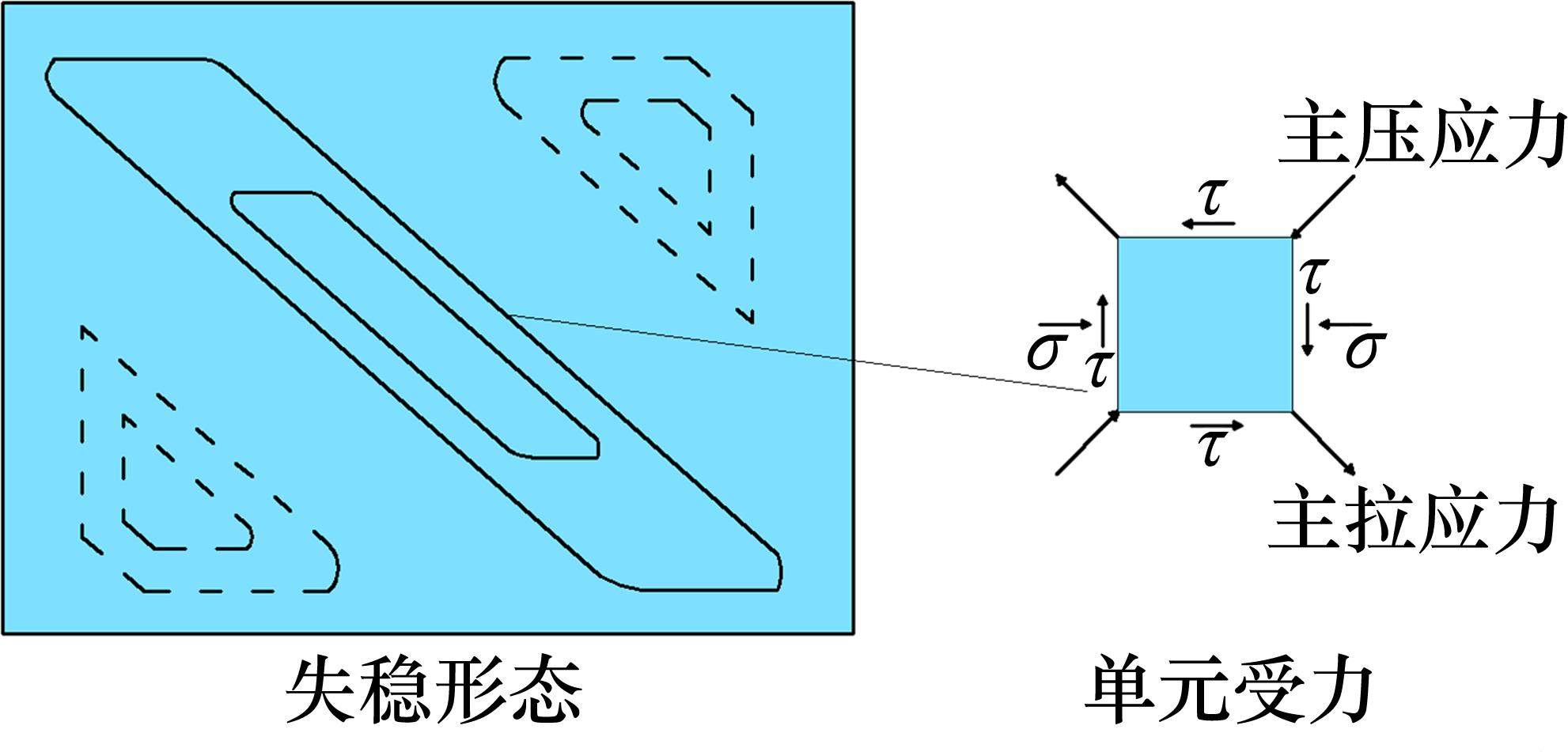
如图8所示,在弹性阶段(0.6Pu之前),2组试验梁剪应力均小于Q355钢材剪切屈服强度222 MPa,且分布均匀。当荷载增至0.9Pu时,2组试验梁腹板剪应力均达到剪切屈服强度,随着荷载的继续增加,FSRC试验梁腹板剪应力分布变得不均匀,在极限荷载在试验梁发生剪切破坏,而与之相比,CSRC试验梁剪应力仍分布均匀,发生弯曲破坏。如图4(a)所示,FSRC试验梁剪跨区腹板剪切变形与腹板高度成一定角度,腹板受到纵向应力和剪应力影响,由此产生的主压应力使得腹板发生斜向失稳变形,如图9所示。因此,波纹腹板叠合梁相较于平腹板叠合梁有着更优异的屈曲稳定性。
3 有限元模型
为避免缩尺效应的影响,真实地反映实桥的受力性能,并进一步对比2组桥型的力学特性,采用有限元软件ABAQUS建立2组试验梁模型以及2组叠合梁全桥模型,以进行扩展分析。桥面板和栓钉均采用实体单元C3D8R模拟,钢梁采用壳单元S4R模拟,钢筋采用桁架单元T3D2模拟。桥面板混凝土和实桥负弯矩区UHPC在单轴受压和受拉状态下的本构关系曲线遵循规范[18-19]中规定的理论公式,其中混凝土和UHPC极限压应变分别为3 300 με和4 080 με,弹性模量分别为3.45×104和4.52×104,UHPC初裂强度为6.6 MPa。钢材和栓钉采用双线性随动强化材料模型,采用上述试验材性参数,弹性模量为2.06×105 MPa,屈服应变εy为1 800 με,考虑钢材强化效应,塑性阶段钢材刚度取初始刚度1/100,极限应变为15εy(27 000 με)[20]。钢筋和栓钉均采用内置约束置于桥面板中,栓钉底面与钢梁上翼缘表面设置绑定约束,桥面板底面与钢梁表面采用法向硬接触,切向罚摩擦,摩擦因数取0.3[3]。试验梁边界条件按简支梁约束条件设置,采用跨中2点对称位移加载方式,全桥模型边界条件按连续梁约束条件设置。
如图10(a)和图10(b)所示,有限元缩尺模型与试验梁的荷载-位移曲线在初始刚度、承载力和总体趋势方面高度吻合,有限元分析所得的极限承载力与试验结果之间的差异仅为5.9%,误差相对较小。
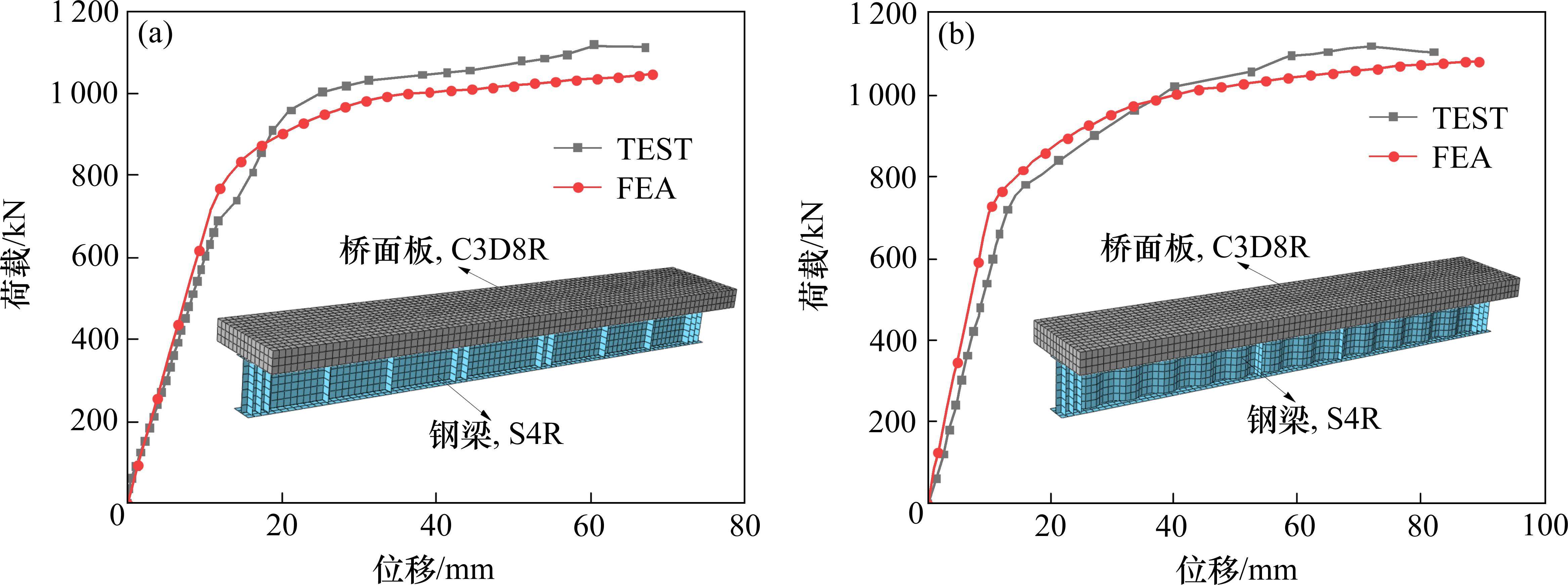
因此,本文建立的非线性有限元模型能准确地模拟试验梁的受力情况,保证以此建模方法建立的全桥模型的真实性,CSRC叠合梁桥和FSRC叠合梁桥有限元全桥模型如图11所示。

4 实桥力学性能对比分析
4.1 承载力对比
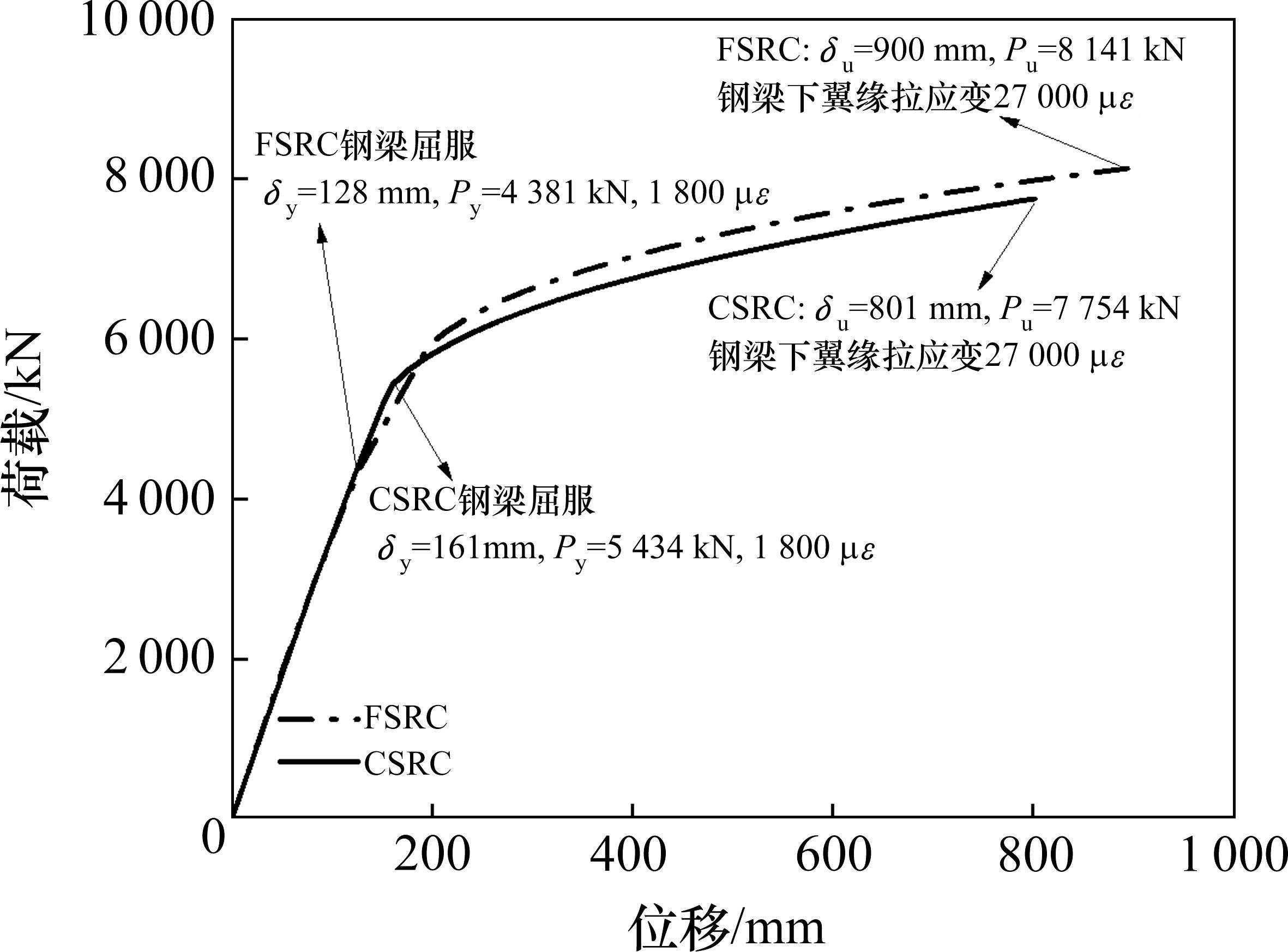
为比较此2组叠合梁桥的承载能力,对中跨进行位移加载,图12为2组有限元模型加载过程中的荷载-位移曲线,两者发展趋势相似。在弹性阶段,2组模型荷载-滑移曲线都近似为直线,基本重合,CSRC叠合梁桥屈服荷载Py为5 434 kN,对应屈服挠度δy为161 mm,FSRC叠合梁桥屈服荷载Py为4 381 kN,对应挠度δy为128 mm。在弹塑性阶段,钢梁下翼缘达到屈服强度导致叠合梁刚度呈现出非线性关系,由于波纹腹板手风琴效应,CSRC叠合梁桥挠度发展速度略大于FSRC叠合梁桥。在破坏阶段,桥面板局部压溃,叠合梁挠度增加较快,钢梁大部分截面受拉屈服,当荷载达到8 141 kN时,FSRC叠合梁桥钢梁下翼缘达到极限拉应变27 000 με(15εy),此时对应极限挠度δu为900 mm,而CSRC叠合梁桥极限荷载Pu为7 754 kN,对应极限挠度δu为801 mm,此时钢梁下翼缘达到极限拉应变,其极限承载力略小于FSRC叠合梁桥,但相差仅4.7%。因此,在同等用钢量的情况下,CSRC叠合梁桥与FSRC叠合梁桥弹性刚度几乎相同,塑性刚度和极限承载力略小。
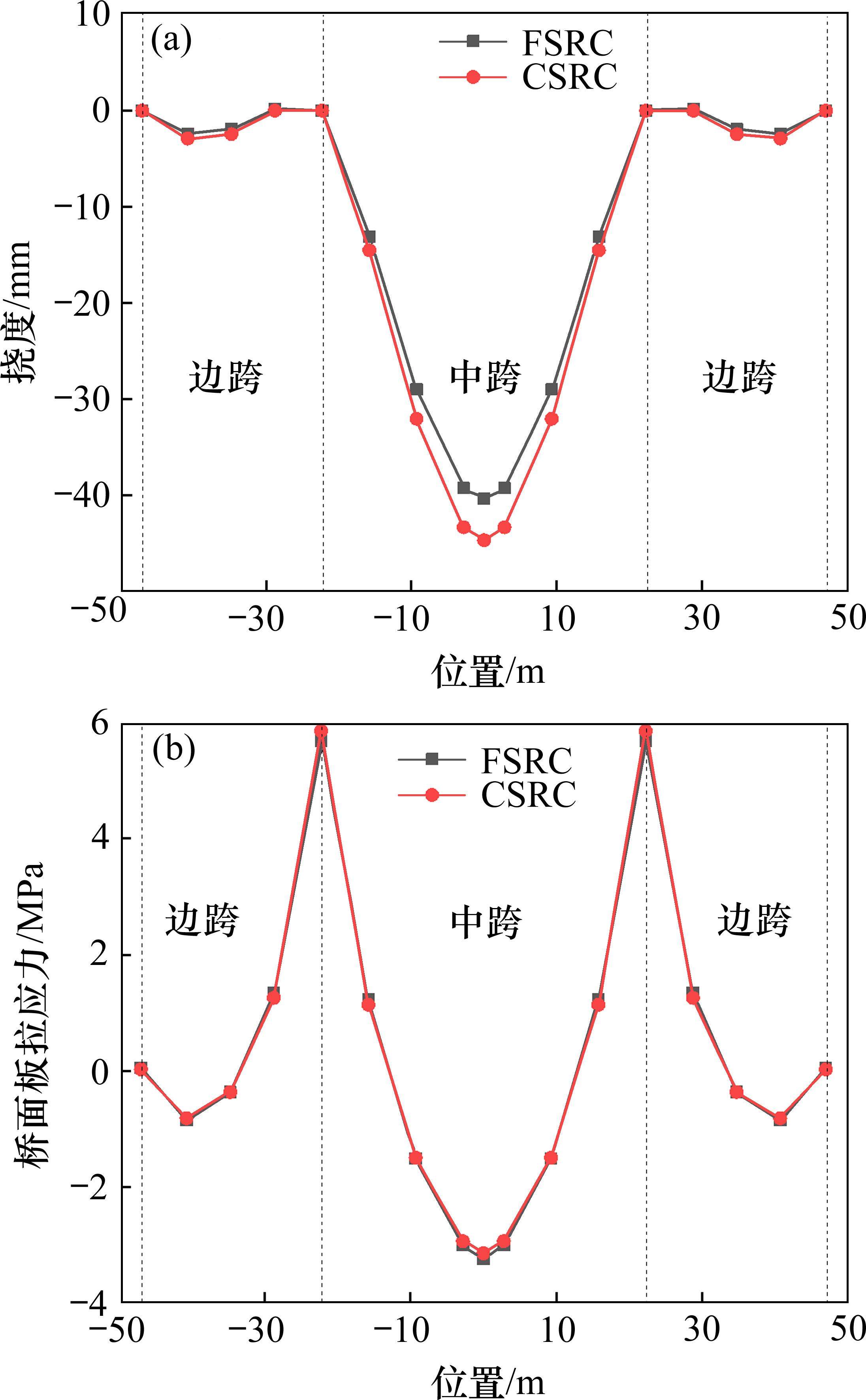
4.2 纵向弯曲
按相关规范[21]中的相关规定对结构进行正常使用极限状态下挠度与抗裂性计算,荷载取1.0恒荷载+0.7车辆荷载,如图13(a)、图13(b)所示,分别比较2组全桥模型的挠度和桥面板拉应力。由图13(a)可知,与FSRC叠合梁桥相比,CSRC叠合梁桥主梁挠度略大将近9.6%,这是因为与平腹板相比,波纹腹板的纵向刚度较小,但两者挠度相差较小且都符合规范[21]要求的连续梁的竖向挠度小于计算跨径的1/600。由图13(b)可知,CSRC叠合梁桥在挠度略大于FSRC叠合梁桥的情况下,其负弯矩区UHPC桥面板上缘平均拉应力反而与FSRC叠合梁桥的桥面板上缘平均拉应力几乎相同。经分析,负弯矩桥面板拉应力主要是由于钢梁受力,栓钉连接件限制桥面板和钢梁之间的纵向滑动而在桥面板中产生拉应力,当负弯矩钢梁下翼缘受压时,波形钢腹板由于纵向刚度弱,具有一定纵向伸缩空间,从而减小钢梁通过连接件传递至桥面板内的拉应力,降低桥面板开裂的风险。
4.3 刚性扭转
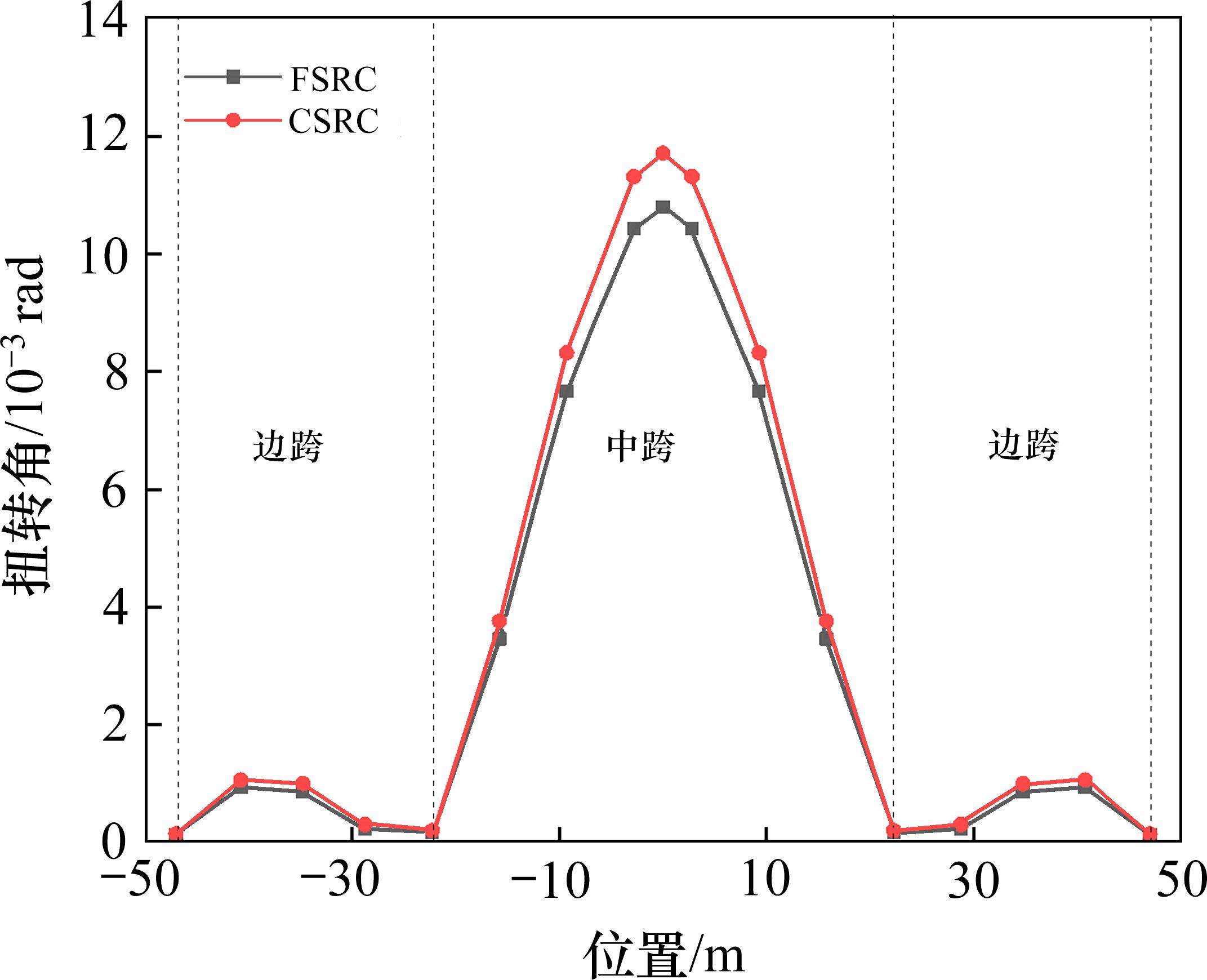
4.3.1 扭转角
如图14所示,考虑最不利荷载工况,比较2种腹板形式叠合梁桥的扭转角。由图15可知,CSRC叠合梁桥的刚性扭转角沿顺桥分布规律与FSRC叠合梁桥一致,跨中最大转角约为FSRC叠合梁桥的1.08倍。虽然波纹腹板在自由扭转时,由于波纹腹板的波峰波谷给结构上下翼缘板提供了额外的面外刚度,对翼缘板产生了面外支撑,使得波纹腹板自由扭转时的抗扭刚度大于平腹板,但是在弯扭作用下,连续梁桥发生约束扭转,波纹腹板纵向刚度较弱,对混凝土桥面板的约束比平腹板弱,因此扭转角较大,并且这两组叠合梁腹板厚度并不相同,平腹板厚度大于波纹腹板,导致CSRC叠合梁桥的扭转角略大于FSRC叠合梁桥,相差约为8%。
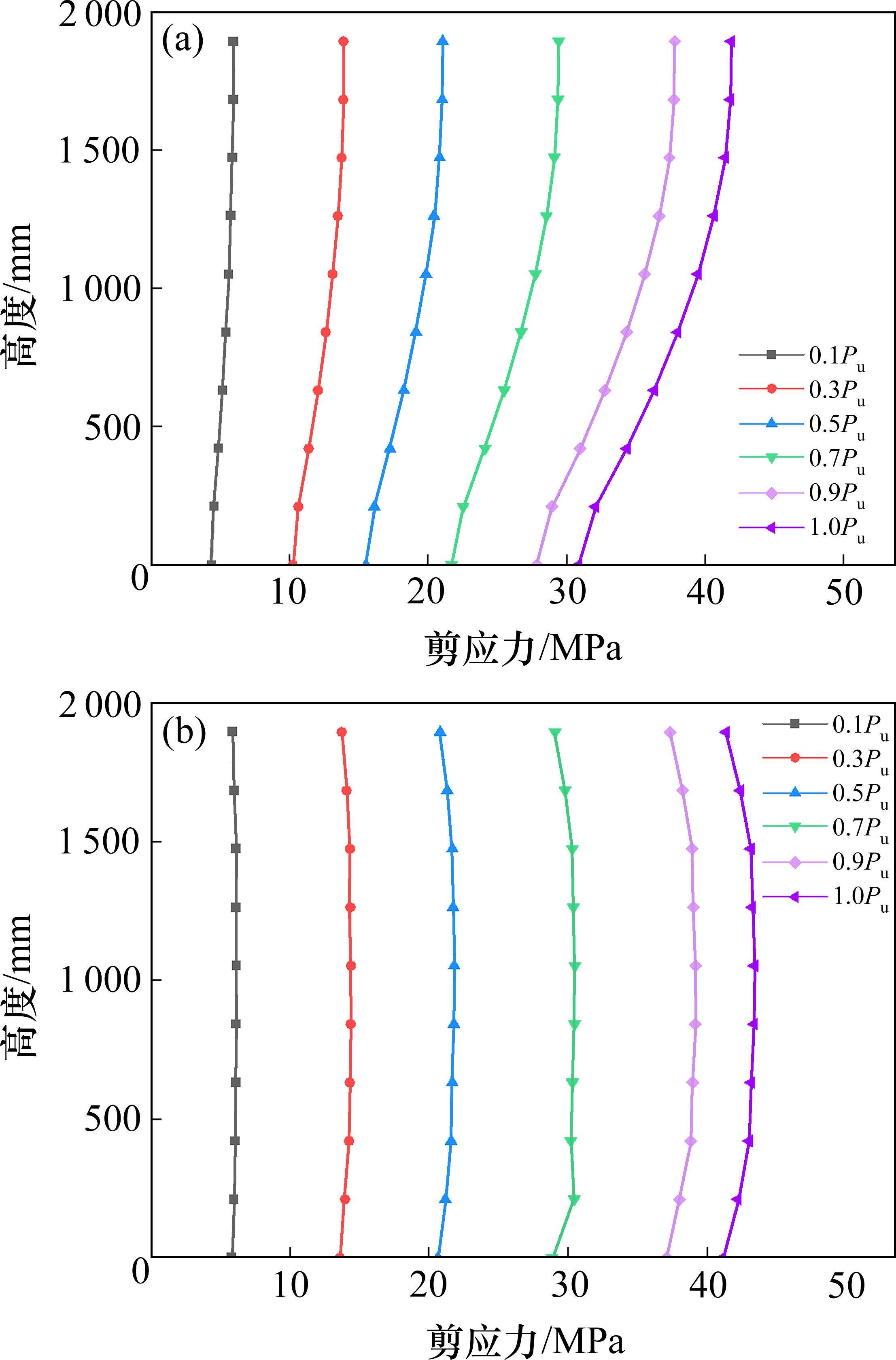
4.3.2 腹板附加剪应力
将偏载分解为正载和附加扭矩共同作用,车辆偏载作用下的剪应力包括弯曲剪应力和附加剪应力。由于正载相同,其作用在2组叠合梁桥上产生的弯曲剪应力相差不大,为对比腹板形式对剪应力产生的影响,从而比较剪跨区由附加扭矩产生的附加剪应力大小及分布。由图16(a)、图16(b)所示,即使波纹腹板厚度较薄,其和平腹板的最大剪应力几乎相同。然而,平腹板随着荷载的增加,剪应力分布逐渐不均匀,而波纹腹板即使在极限荷载下,腹板剪应力仍均匀分布,波纹腹板的波折形式提高了其抗剪能力。
4.4 屈曲稳定性
除桥梁自重外,基于影响线分布,分别考虑边跨跨中、中墩墩顶和中跨跨中最不利工况,从而布置车辆荷载并进行屈曲稳定性分析[16]。计算表明,2组叠合梁屈曲稳定性均满足规范要求(考虑材料非线性影响的屈曲稳定系数大于2.0)[22]。CSRC叠合梁桥失稳形式为中墩墩顶加劲肋发生局部压曲,而FSRC叠合梁桥失稳形式均为腹板发生局部屈曲失稳,如表4所示,前者的前五阶屈曲因子为后者的5.0倍以上。与FSRC叠合梁桥相比,CSRC叠合梁桥的稳定性更强,且全桥除支点以外几乎没有加劲肋,可大幅度减少加劲肋的数量,从而降低钢材和焊材的消耗,在提高经济性的同时还能够避免由于加劲肋焊缝引起的焊接缺陷问题。
| 工况 | 屈曲模态 | CSRC叠合梁桥 | FSRC叠合梁桥 |
|---|---|---|---|
| 边跨跨中最不利加载 | 1阶 | 19.552 | 2.995 |
| 2阶 | 20.350 | 3.286 | |
| 3阶 | 21.534 | 3.304 | |
| 4阶 | 22.463 | 3.400 | |
| 5阶 | 22.486 | 3.435 5 | |
| 中墩墩顶最不利加载 | 1阶 | 14.410 | 2.294 |
| 2阶 | 14.428 | 2.305 | |
| 3阶 | 15.412 | 2.633 | |
| 4阶 | 15.770 | 2.661 | |
| 5阶 | 16.186 | 3.016 | |
| 中跨跨中最不利加载 | 1阶 | 14.324 | 2.453 |
| 2阶 | 14.342 | 2.908 | |
| 3阶 | 14.344 | 2.910 | |
| 4阶 | 14.360 | 2.967 | |
| 5阶 | 15.301 | 3.070 |
5 结论
1) 平腹板叠合梁腹板易发生剪切屈曲变形,导致剪切脆性破坏,而波纹腹板叠合梁发生弯曲延性破坏。弹性阶段波纹钢腹板纵向应变几乎为0,其抗弯贡献可忽略不计,但极限抗弯状态下,波纹腹板纵向应变沿高度呈线性分布,靠近受拉翼缘侧腹板50%高度范围内已进入钢材受拉强化阶段,波纹腹板抗弯贡献不可忽略不计。如何合理地考虑波纹腹板抗弯承载力和钢材强化效应有待进一步研究探索。
2) 虽然波纹腹板纵向刚度弱,但在梁高和用钢量一致的前提下,与平腹板叠合梁相比,波纹腹板叠合梁不仅构造简化,其初始刚度、极限抗弯承载力和抗扭刚度均相差不大,并且偏载作用下波纹钢腹板叠合梁附加剪应力分布更均匀,并且波纹腹板的手风琴效应可释放负弯矩区混凝土板拉应力,可有效提升叠合梁桥负弯矩区的抗裂性能。
3) 波纹钢腹板叠合梁桥屈曲稳定系数为平钢板叠合梁桥的5.0倍以上,可有效减少腹板加劲肋焊接量,提高抗疲劳性能。
王术剑,查上,邓文琴等.波纹腹板与平腹板叠合梁桥力学性能对比分析[J].铁道科学与工程学报,2025,22(03):1132-1143.
WANG Shujian,ZHA Shang,DENG Wenqin,et al.Comparative analysis of mechanical properties of composite girder bridges with corrugated steel web and flat steel web[J].Journal of Railway Science and Engineering,2025,22(03):1132-1143.

