预制桩在软土地基沉桩施工的过程中,其贯入作用将挤压桩周的土体,在桩周土体中引起极高的超静孔隙水压力[1-3],使得桩周土体中的应力场发生较大变化,土体有效应力降低,桩基无法快速发挥其承载力,影响地基的正常固结,还可能会导致桩周土体隆起、邻桩上浮、偏位或折断、桩基承载力降低等对施工产生不利的影响[4],但随着时间的推移,土中的超静孔隙水压力会逐渐消散,土体开始固结,有效应力增加,桩的承载力逐渐增加[5-7]。因此,求解超静孔隙水压力的消散速度是预测地基固结和预制桩长期承载力的关键。
RANDOLPH[8]基于平面应变理论和剑桥模型,对孔压的一维方程进行求解,得到了超静孔压沿径向方向消散的解析解。GUO等[9-13]进一步将原本的一维超静孔压消散方程扩展到二维,并在初始条件中加入土体深度产生的影响,可以同时考虑土体径向和竖向的孔压消散过程。赵明华等[14-16]探索了沉桩时挤土效应产生的超静孔压的分布形式,提出了多种沉桩完成后初始时刻桩周土体径向孔压分布函数。在土体物理力学性质对固结过程的影响方面,曹权等[17-19]从三维强度特性、弹塑性特征、土体应力历史、应变软化及变固结系数等方面对沉桩后土体超静孔压的消散规律进行了研究。
影响超静孔压消散的一个重要因素是土体的渗透系数,在桩贯入过程中会破坏桩周土体内部的孔隙和毛细通道,在一定范围内形成扰动区,致使扰动区内土体的渗透系数降低[20-21],减缓超静孔压的消散速度。在受扰动地基的固结理论方面,TRAN等[22]在扰动区和非扰动区各自设置渗透系数,以连续流量条件将两区的渗流联系起来,分别求解了两区内的超静孔压解析解。BASU等[23]基于六边形的排水管地基模型,在扰动区和非扰动区之间加入了一个过渡区,获得了受扰动地基的二维固结解析解。但在实际中,打桩扰动区的径向渗透系数不是定值,越靠近桩身的土体受挤压越严重,径向渗透系数越小。卢萌盟等[24-25]推导了桩土共同承受附加应力的前提条件下径向渗透系数受扰动变化的复合地基二维固结解。张玉国等[26]推导了真空预压竖井地基因施工扰动导致的径向渗透系数变化的超静孔压消散解析解,分析了3种不同变化模式的固结速率。郭彪等[27]在考虑竖向渗流的情况下,对径向渗透系数变化的砂井地基固结进行求解。ZHANG等[28]在研究散体材料柱复合地基固结问题时也考虑了地基土径向渗透系数的变化,并推导了孔压的解析解。这些研究的优点是考虑了径向渗透系数在扰动区的连续变化,从而得到一个更贴近实际工程情况的解析解,但模型都是将地基土或扰动区土体视为一个完整土体进行求解。需要指出的是,上述理论模型虽然具备模拟径向渗透系数变化的能力,但是难以考虑挤土效应带来的土体压缩模量和密度变化,因而难以对沉降和结构-土的相互作用进行预测。
基于此,本文提出径向多圈层桩周土体固结模型,将扰动区土层从桩壁到未扰动区沿径向方向分为若干圈层,每层可独立设置径向渗透系数,并对压缩模量、密度等土体物理力学参数进行独立设置。根据模型推导桩周土体超静孔隙水压力消散的解析解,随后将模型退化为无扰动的情况对结果进行验证,分析扰动区半径、扰动渗透系数比和扰动渗透系数对超静孔压消散的影响。
1 数学模型
1.1 固结模型
图1所示为受打桩扰动后的桩周土体固结模型,其中,r0、rd、R、re分别为预制桩半径、打桩后产生的扰动区半径(即n-1层土体外半径rn-1)、塑性区半径以及地基固结过程中超静孔隙水压力的影响区半径(即n层土体外半径rn),其中,rn一般为塑性区半径R的5~10倍,本文取5R。为了模拟扰动区渗透系数变化的特点,将扰动区内的土体从桩土界面到扰动区边界划分为若干圈层,每一个圈层从桩顶位置俯视都为一个空心圆柱体。设 r为水平距离,ri为第i圈层土体的外半径,u0为打桩刚完成时在塑性区范围内(r0<r<R)产生的初始超静孔隙水压力。在塑性区以外(r>R)的土体中,初始超静孔隙水压力u0为0。

为便于推导,对模型进行以下假定:
1) 桩周土体为饱和土,渗流服从Darcy定律,固结过程只考虑径向渗流。
2) 扰动只影响桩周土体的水平渗透系数,土体受到的扰动仅发生在打桩过程中,在随后固结过程中土体的渗透系数不发生改变。
3) 扰动区内的土体分为若干层后,同一层内部的土体径向渗透系数为定值,不随水平距离r发生改变。
1.2 径向渗透系数分布模型
图2所示为扰动区土体径向渗透系数的分布模式,其中,kd为土体受扰动后径向渗透系数的最小值,kh为未扰动区土体径向渗透系数,并定义kh/kd表征渗透系数的扰动强度。
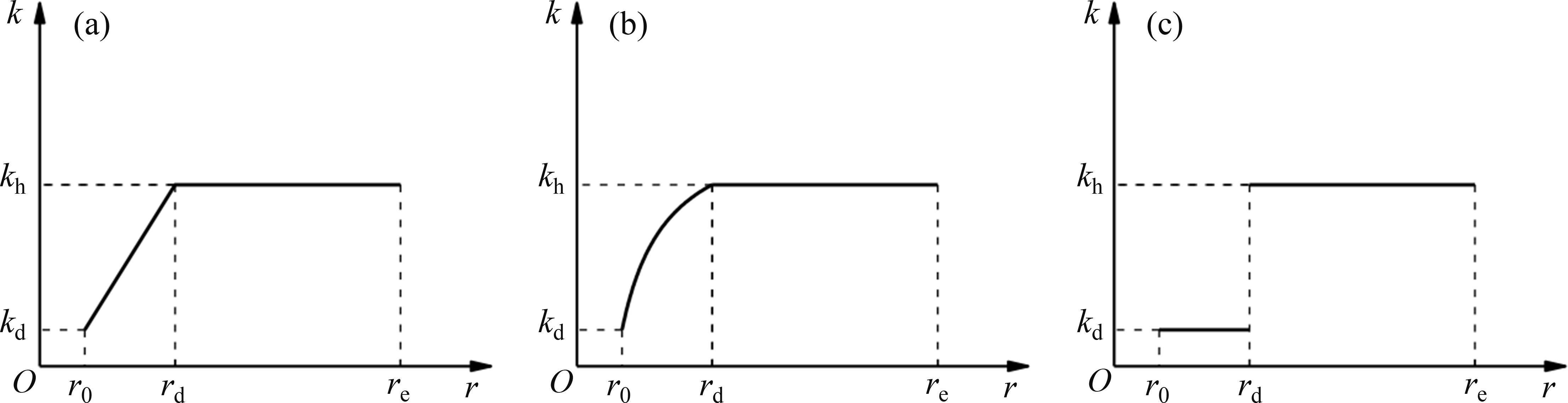
模式1,土体径向渗透系数k在扰动区内线性增长,表达式为

模式2,扰动区内土体径向渗透系数以双曲形式增长,表达式为
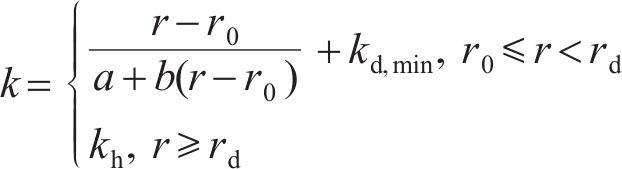
模式3,将土体分为2部分,径向渗透系数在扰动区和非扰动区界面rd处发生突变,两区内部的渗透系数均保持不变。

2 超静孔压求解
2.1 控制方程
根据RANDOLPH等[29]对桩周土体径向固结的解析解,超静孔隙水压力在径向方向的消散与土体的径向固结系数C相关。在多圈层的地基模型中,由于径向固结系数,因此,每个圈层都需要一个独立的控制方程,将非扰动区整体当作一个圈层,第i圈层的超静孔隙水压力ui可以表示为:
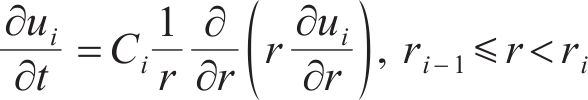
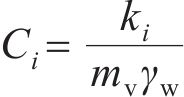
式中:t为固结开始后经过的时间;Ci为第i圈层土体的径向固结系数;ki为第i圈层土体的径向渗透系数;mv为土体体积压缩系数;γw为水的重度。
2.2 初始孔压和边界条件
大量试验研究结果[30-32]表明,打桩产生的初始超静孔压在塑性区沿径向方向向外逐渐减小,到弹性区处为0,根据RANDOLPH[8]结合平面应变理论对试验结果的分析,初始超静孔压的表达式为
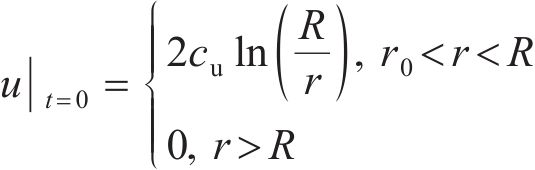
塑性区半径R与预制桩半径r0的关系为
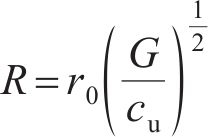
其中:cu和G分别为土体的不排水固结强度和剪切模量,本文剪切模量G取50cu。
桩土界面为不透水界面,固结过程中在影响区外产生的超静孔隙水压力为0,即影响区边界为自由排水界面,因此,边界条件为
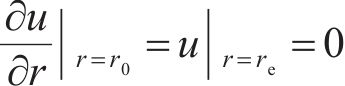
各个圈层之间的渗流满足连续流量条件,因此,在扰动区与非扰动区之间的界面也应满足连续流量条件:
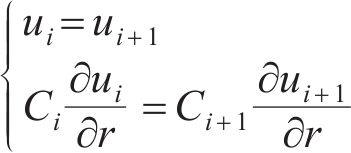
2.3 方程求解
对第i圈层的孔压方程(4)进行分离变量,令
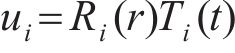
代入方程(4)得

式中:
由式(11)可以得到2个微分方程,通解分别为

其中:Bi、Di、μi均为常数;J0和Y0分别为0阶第一类和第二类贝塞尔函数。
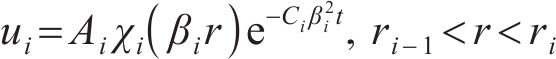
其中:
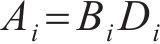
设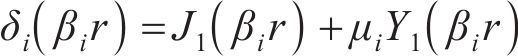
接下来利用定解条件解出通解中的待定系数βi、μi以及Ai。
将第1圈层和非扰动区圈层(第n圈层)的通解代入边界条件式(8)中得
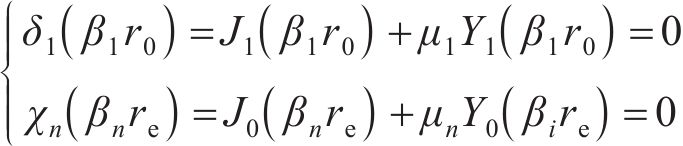
对式(14)进行整理得到
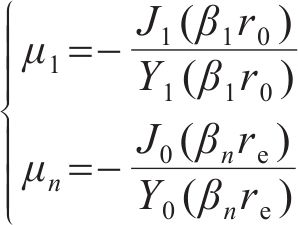

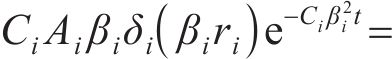
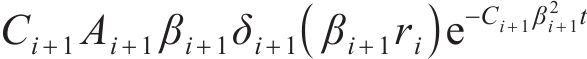

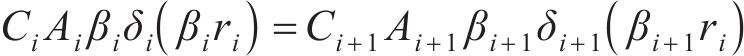
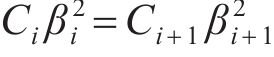
由式(20)推广至所有连续流量界面,将所有的特征值βi转化为关于β1的函数:
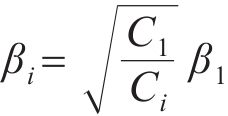
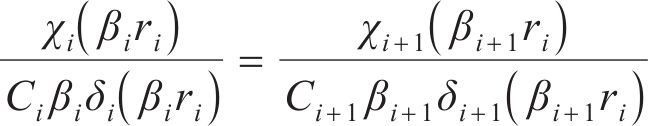
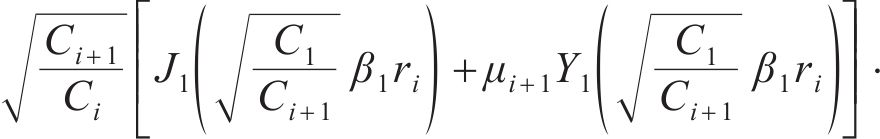

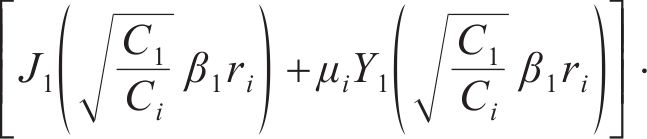
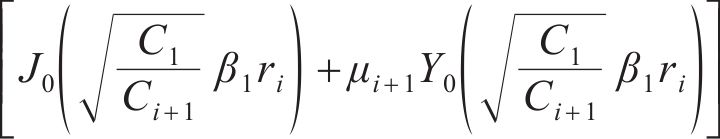
将式(23)改写为μi+1关于μi的表达式:
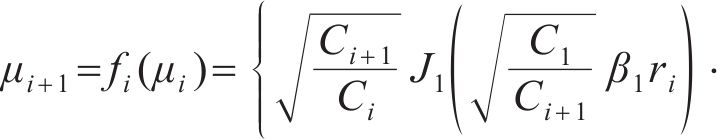
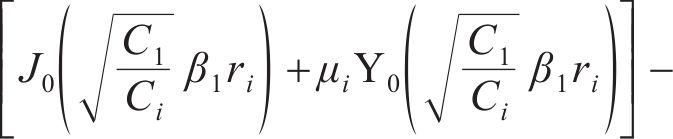
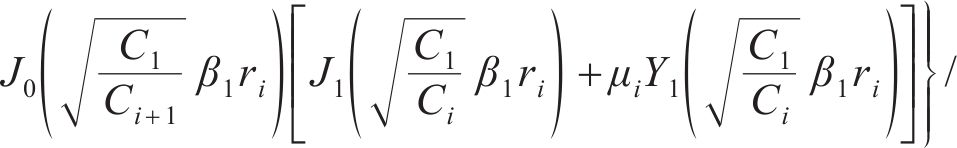
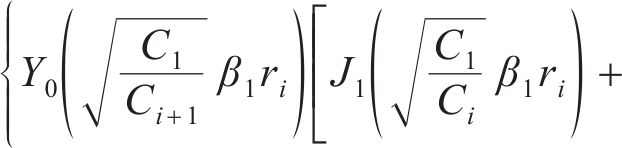
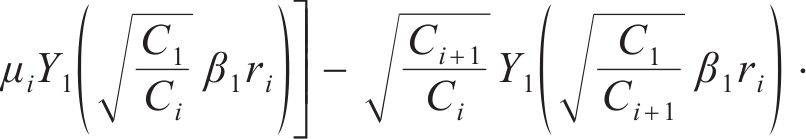
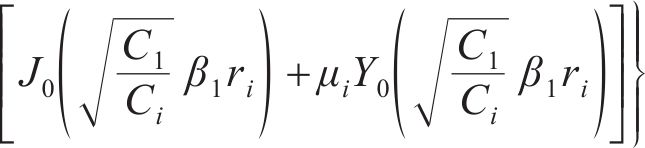
再结合式(15)可以得到关于特征值β1的超越方程,β1可以通过求解该超越方程得到,同时通过 式(21)计算得到其他的特征值βi。由于贝塞尔函数具有周期性,式中βi和μi有无穷多个解,因此,第i圈层超静孔隙水压力径向消散表达式为
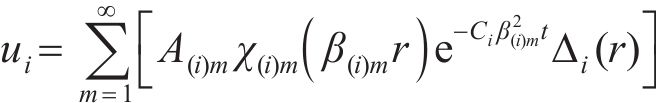
其中,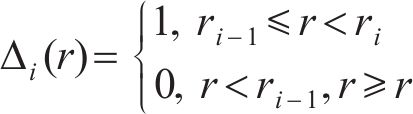
根据叠加原理,整个固结影响区的孔压表达式为:
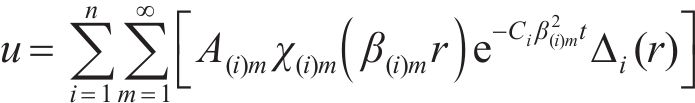
为求解常数A(i)m,由式(18)变形可得
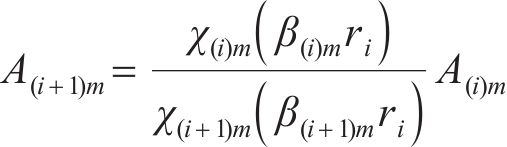
经过递推可以得到A(i)m关于A(1)m的表达式为:

将初始条件(6)代入式(26),等式两边同乘
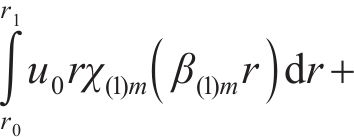
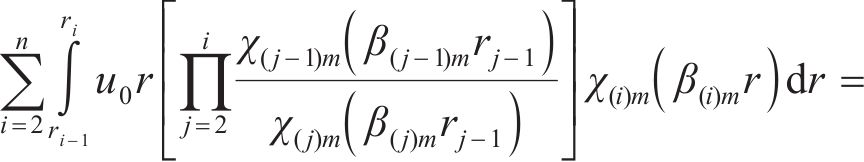

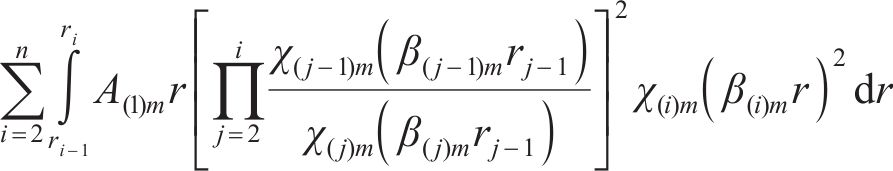
通过积分计算,最终A(1)m可以写为
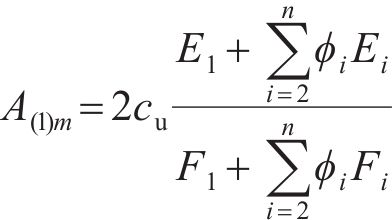
其中:

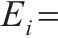
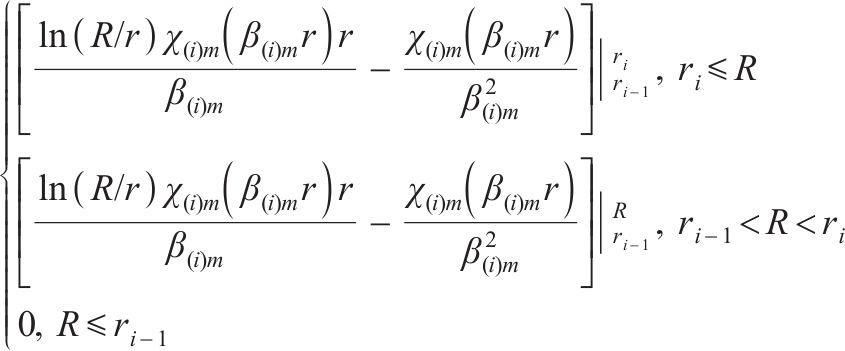
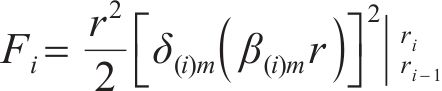
利用式(28)可以求得其他待定系数A(i)m。至此,通解式(13)中所有的待定系数皆由定解条件解出,再将其代入式(25)或式(26)即可得完整的超静孔压。
3 退化验证
使用量纲一化参数进行验证和对比分析。将超静孔压以不排水固结强度作为参照标准(u/cu),水平距离以预制桩半径为参照标准(r/r0),定义时间因子为
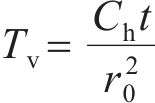
当扰动区土体径向渗透系数的最小值kd与非扰动区土体径向渗透系数kh一致时,该解退化为不考虑扰动效应时的超静孔压解,并与RANDOLPH等[29]的解进行对比。
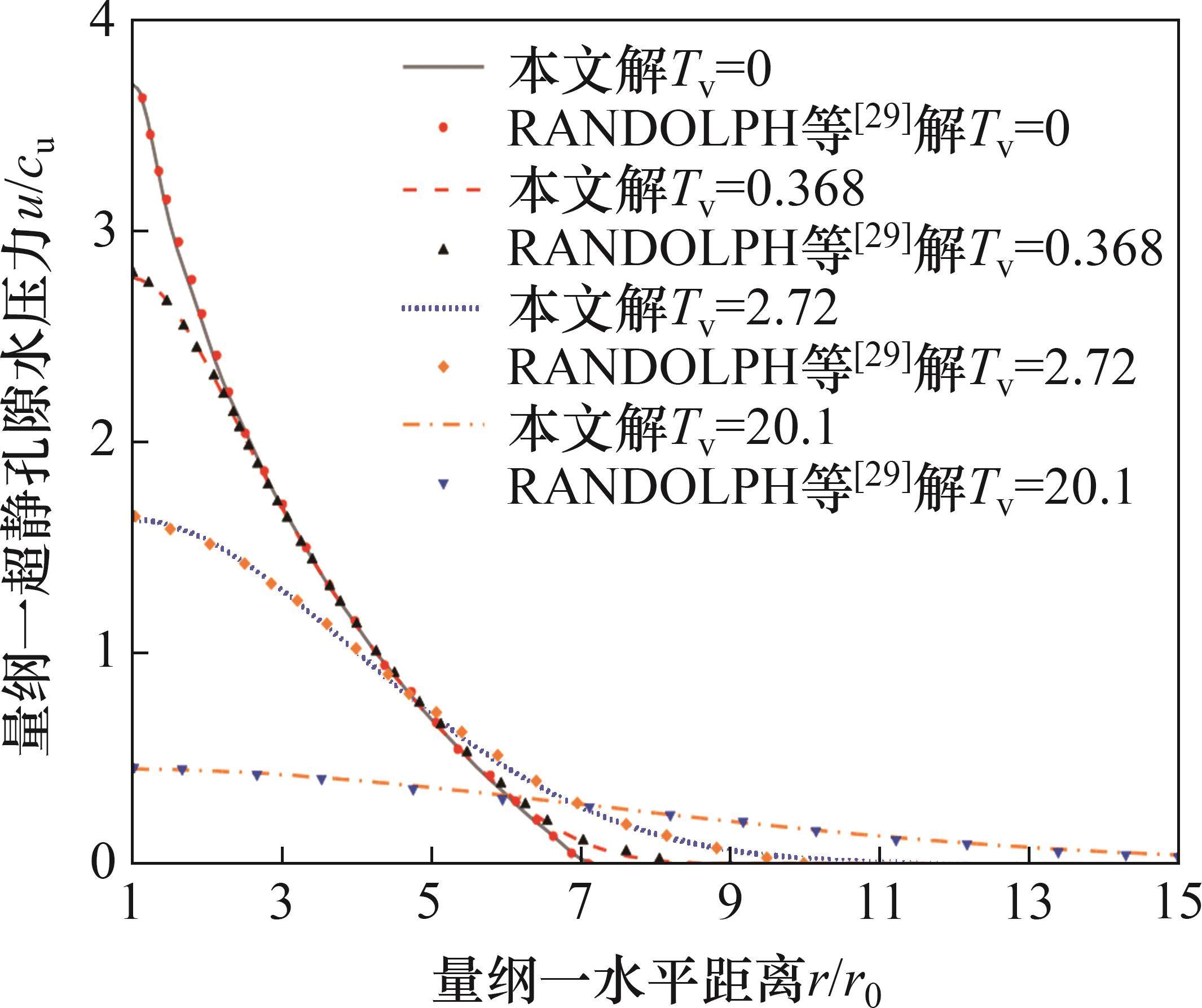
图3所示为不同时刻超静孔压沿径向方向的分布。从图3可以看出,本文解退化为不考虑扰动效应时与RANDOLPH等[29]的解基本重合,可以证明本文径向多圈层固结模型及其解的正确性。超静孔隙水压力主要在水平距离为15r0以内分布,在此范围以外,对超静孔隙水压力影响较小。因此,在两桩中心距小于15r0且桩数较多时,应考虑群桩效应。
4 参数分析
为探究受打桩扰动后桩周土排水固结的一般规律,将从扰动区半径与预制桩半径之比(rd/r0)、渗透系数扰动强度(kh/kd)和扰动区径向渗透系数分布模式分析不同程度的打桩扰动对超静孔隙水压力消散产生的影响。其中,扰动区半径和渗透系数扰动强度的增大都意味着预制桩的贯入挤土效应更加显著。
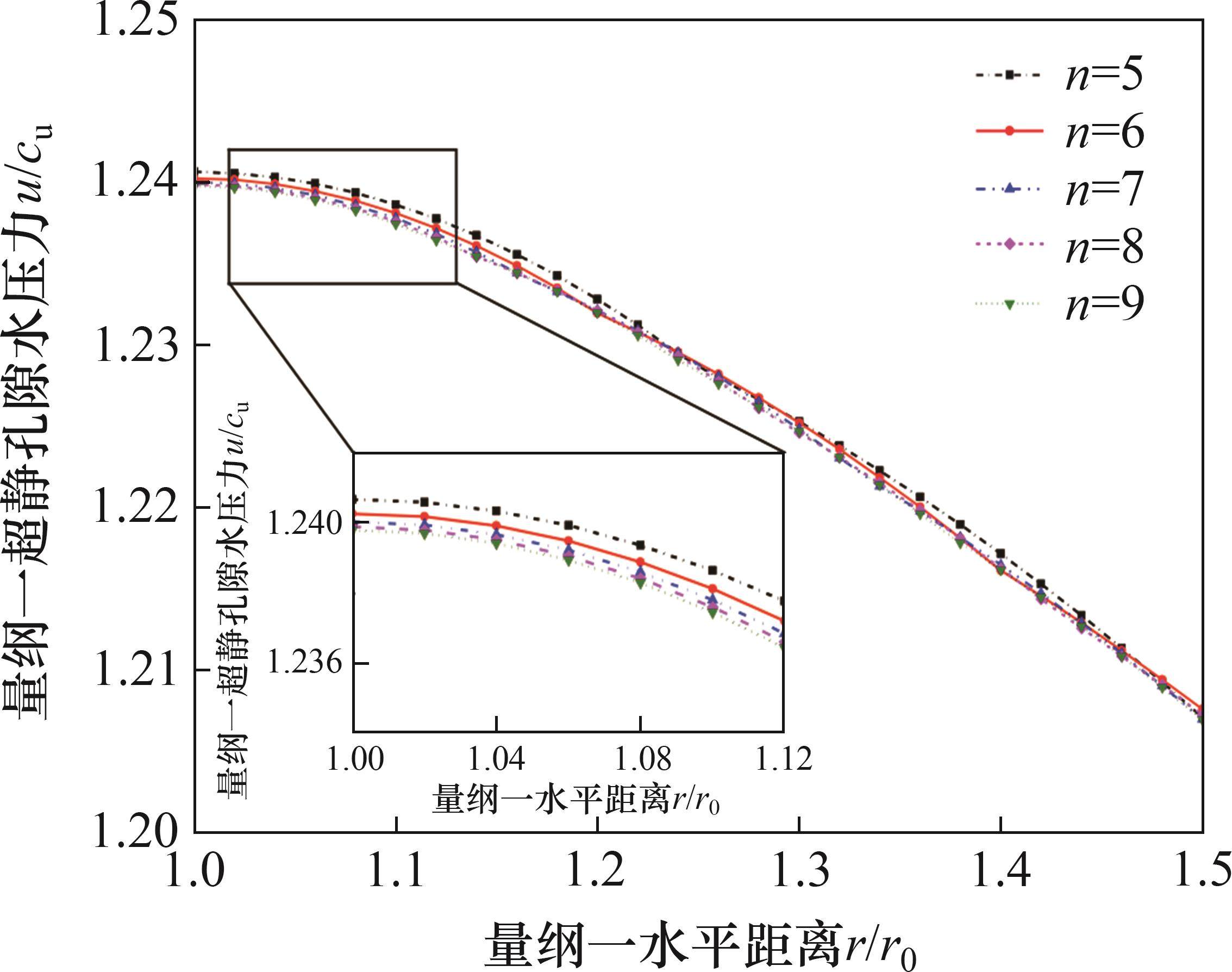
由于径向渗透系数在同一圈层中取值固定,扰动区所划分的圈层数量越多,对渗透系数径向变化的刻画越准确,因此,扰动区的分层数会对孔压的计算结果产生一定影响,但在划分数量达到某一阈值后影响变得忽略不计。扰动区分层数n对超静孔压的影响如图4所示。从图4可以看出:在扰动区分层数为8时,曲线已经与分层数为9的曲线基本重合,可以认为此时扰动区的分层数已对计算结果影响不大。因此,本文采取扰动区分8层进行敏感参数分析。
4.1 扰动区半径影响
图5所示为在时间因子Tv=10、扰动区径向渗透系数比(kh/kd)为4、渗透系数分布采用模式1时,打桩引起的扰动区半径与预制桩半径之比(rd/r0)对超静孔压沿径向分布的影响。由图5可知,当扰动区半径增大时,同一水平距离的超静孔压会随之增大;对比各曲线r0处超静孔压,即最大超静孔压的变化可以发现每次增加同样大的扰动区半径后,最大超静孔压每次的增幅会越来越大,表明扰动区半径较小时对孔压影响十分有限,而相较于较小的扰动区,在更大的扰动区基础上扰动区半径发生的变化会对超静孔压的消散速率产生更加显著的影响,这与打桩时桩径越大对桩周土体扰动效应越显著的原理相符。同时,各条曲线均在相应的扰动区半径处与不考虑扰动的曲线相交,并在扰动区之外基本重合,说明超静孔压在扰动区之外的消散速度受到扰动区半径的影响很小。
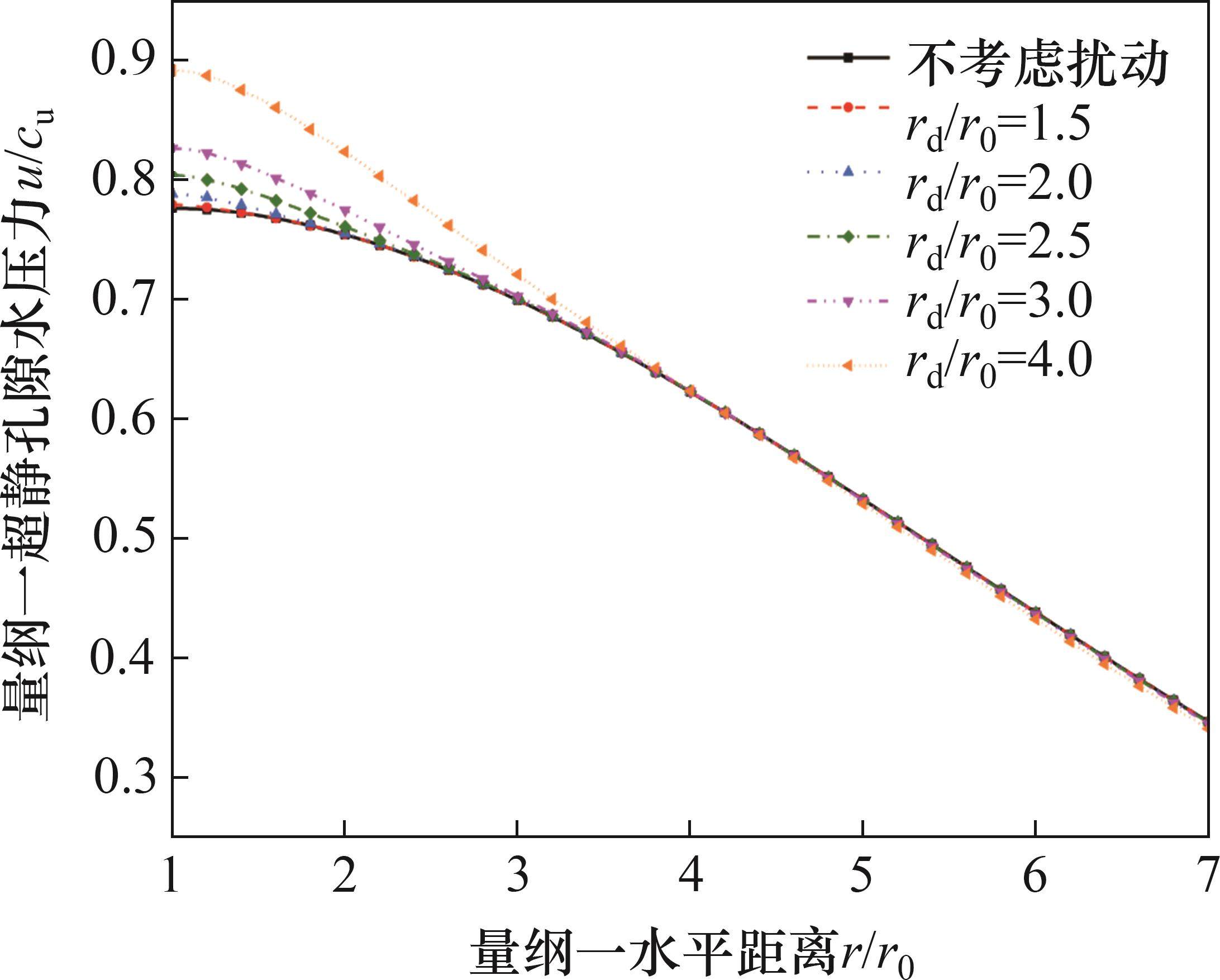
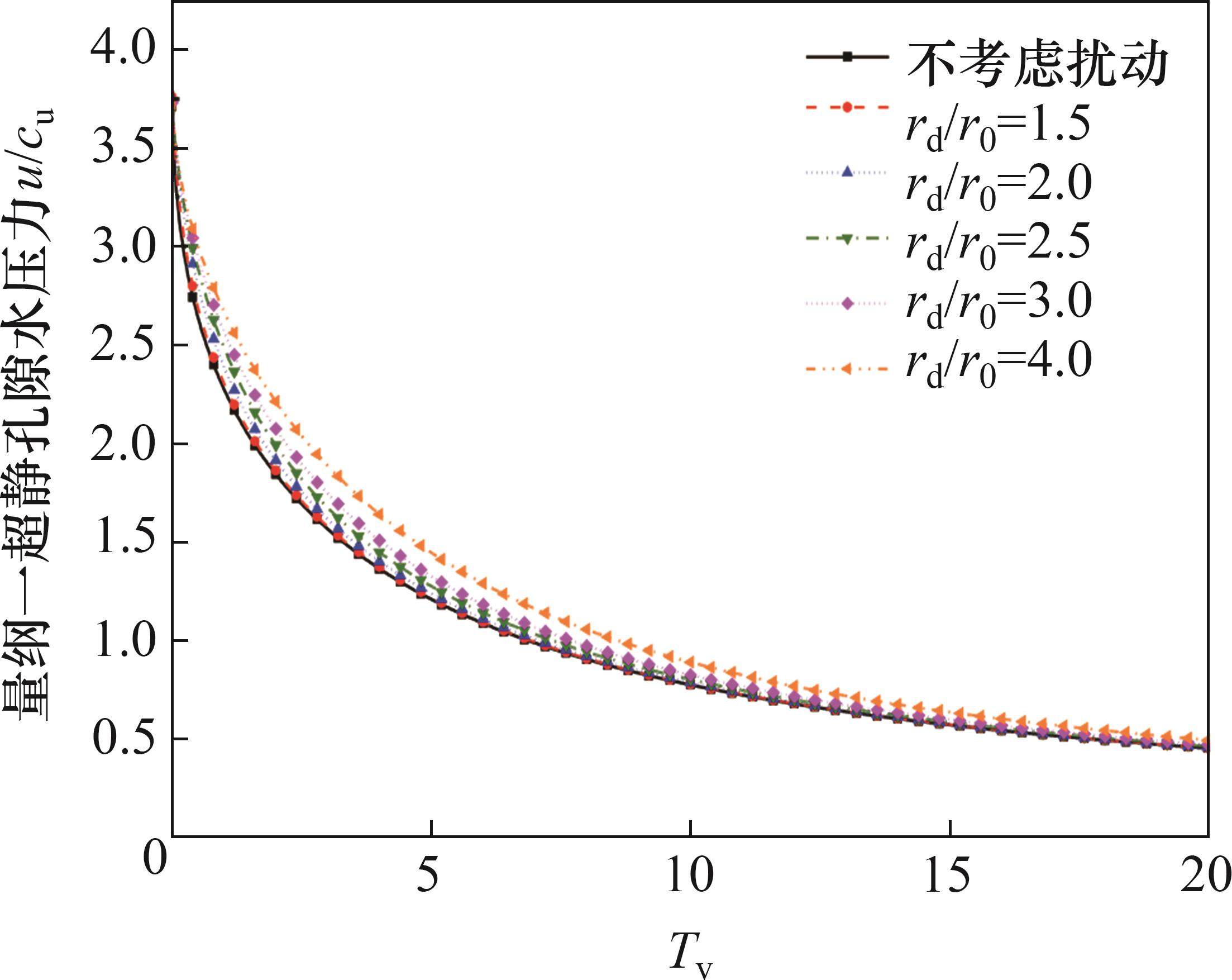
图6所示为相同条件下扰动区半径对最大超静孔压随时间变化规律的影响。从图6可以看出,在排水固结开始后,在同一时刻,扰动区半径越大,桩壁处的最大超静孔压越大,表明扰动区半径增大会使桩周扰动区土体的超静孔压的消散速率降低,固结速度减缓;当固结进行到一定程度后,在同一时刻,最大超静孔压之间的差距在逐渐缩小,在Tv=20时,扰动区半径为4r0,与无扰动情况的最大超静孔压差距很小。由此可以得出,扰动区半径的增大对超静孔压的消散有不利影响,但主要发生在固结过程的前期,在固结后期对超静孔压的消散速率影响十分有限。
4.2 渗透系数扰动强度的影响
图7所示为时间因子Tv=10、扰动区半径比rd=2r0、渗透系数分布采用模式1时,渗透系数扰动强度(kh/kd)对超静孔隙水压力沿径向分布的影响。从图7可以看出:在同样的水平位置,渗透系数扰动强度越大,超静孔隙水压力也越大;对比各曲线最大超静空隙水压力可发现,与扰动区半径对超静孔压的影响不同的是,渗透系数扰动强度增加同样大小时,最大超静孔压每次的增幅会越来越小,说明渗透系数扰动强度增大到一定程度后,并不会无限地减缓超静孔压消散速度;同样,各曲线都在2r0的扰动区边界处接近并在扰动区之外基本重合,扰动径向渗透系数对扰动区之外的超静孔压消散速度影响也十分小。
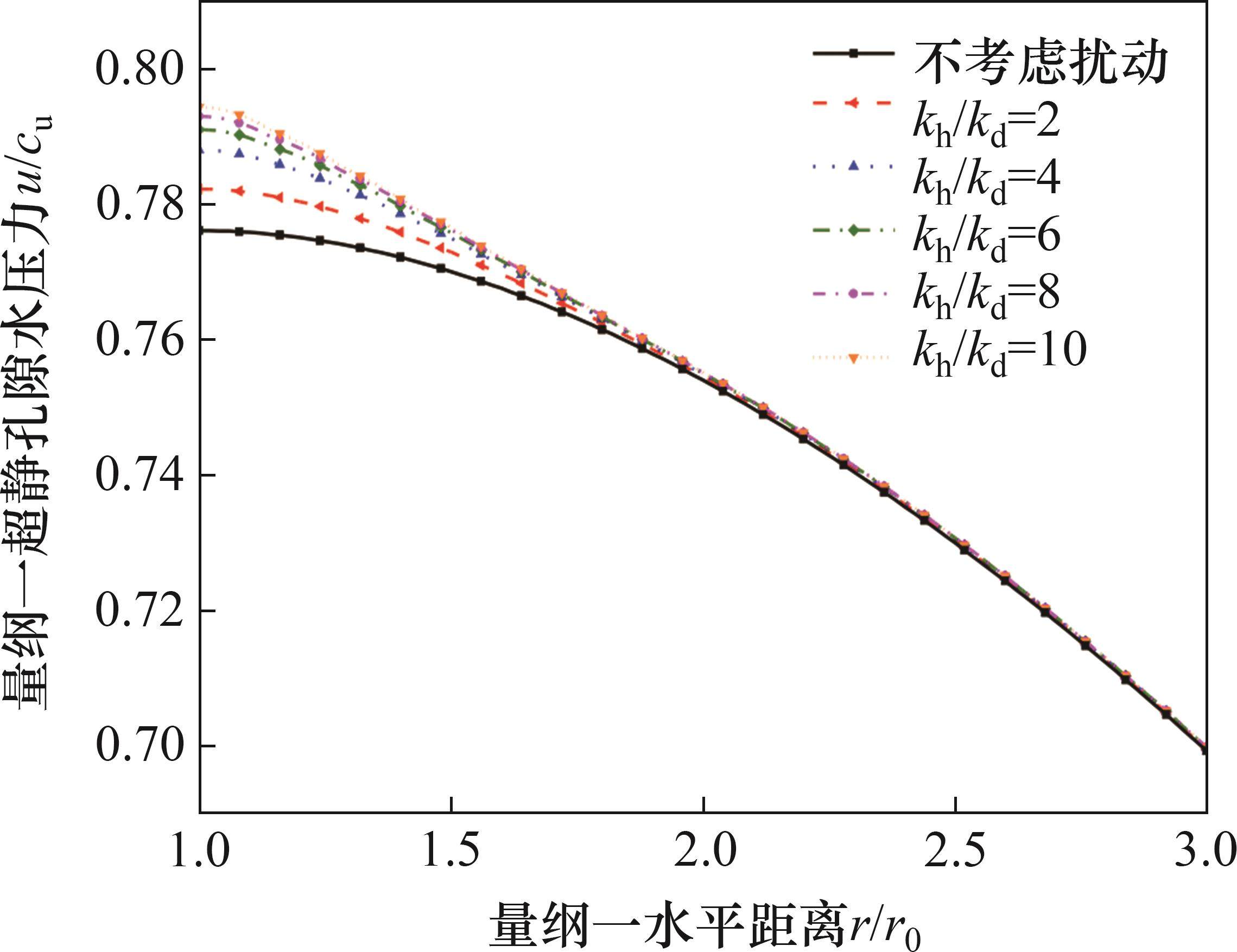
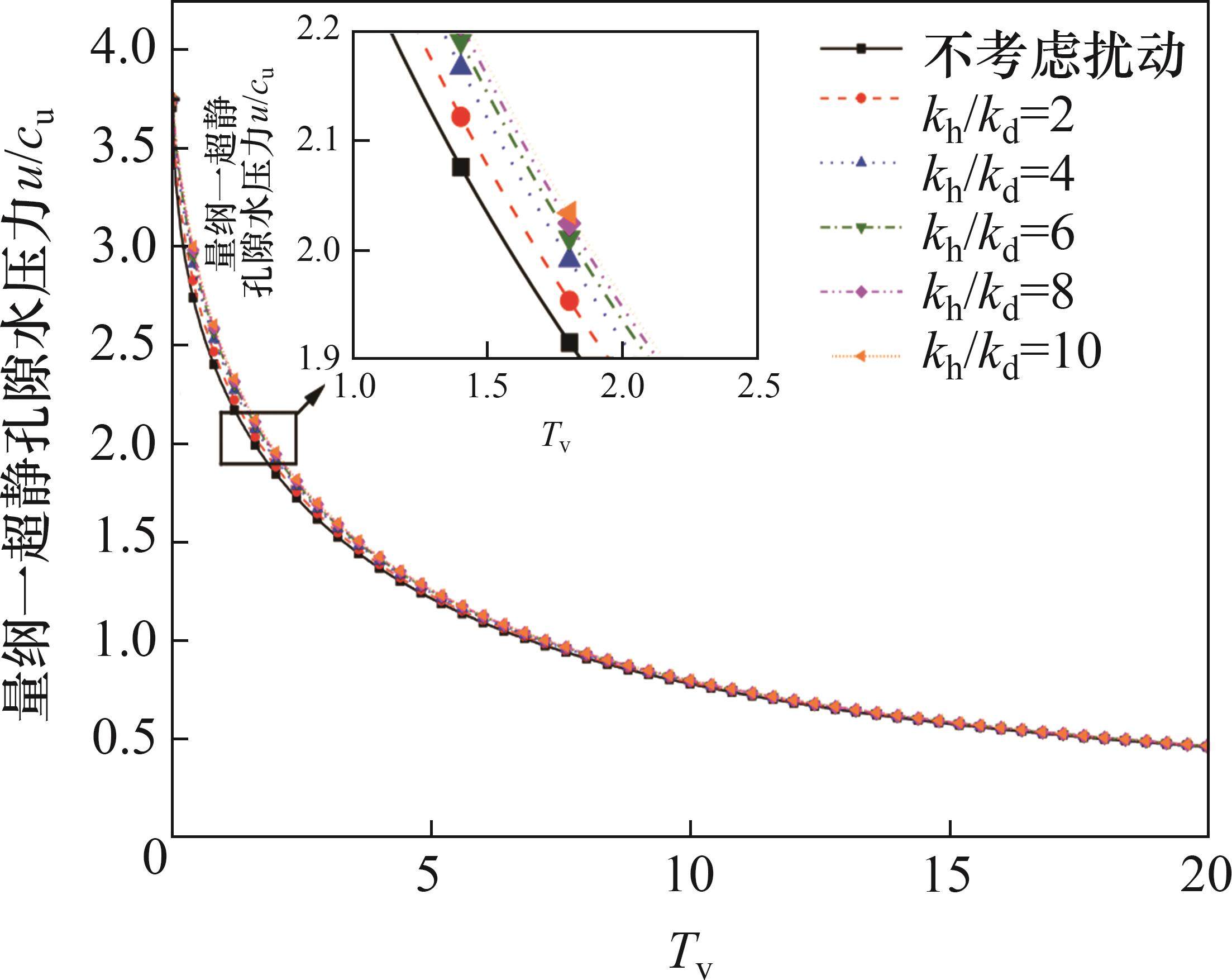
图8所示为相同条件下渗透系数扰动强度对最大超静孔压随时间变化规律的影响。对比图6和图8可知:增大渗透系数扰动强度对超静孔压消散速率的影响要远小于增大扰动区半径所带来的影响,原因是超静孔压主要分布在桩附近的扰动区,且该处孔隙水的水力梯度大,虽然扰动区渗透系数扰动强度增大,但在扰动区半径较小的情况下,扰动区排水路径短,孔隙水可以很快流向非扰动区,孔压消散速度仍然较快。而增大扰动区半径则会使扰动区的排水路径变长,将水里梯度较小的区域包含在内,土体的孔压无法在短时间内快速消散。
4.3 扰动区渗透系数分布模式影响
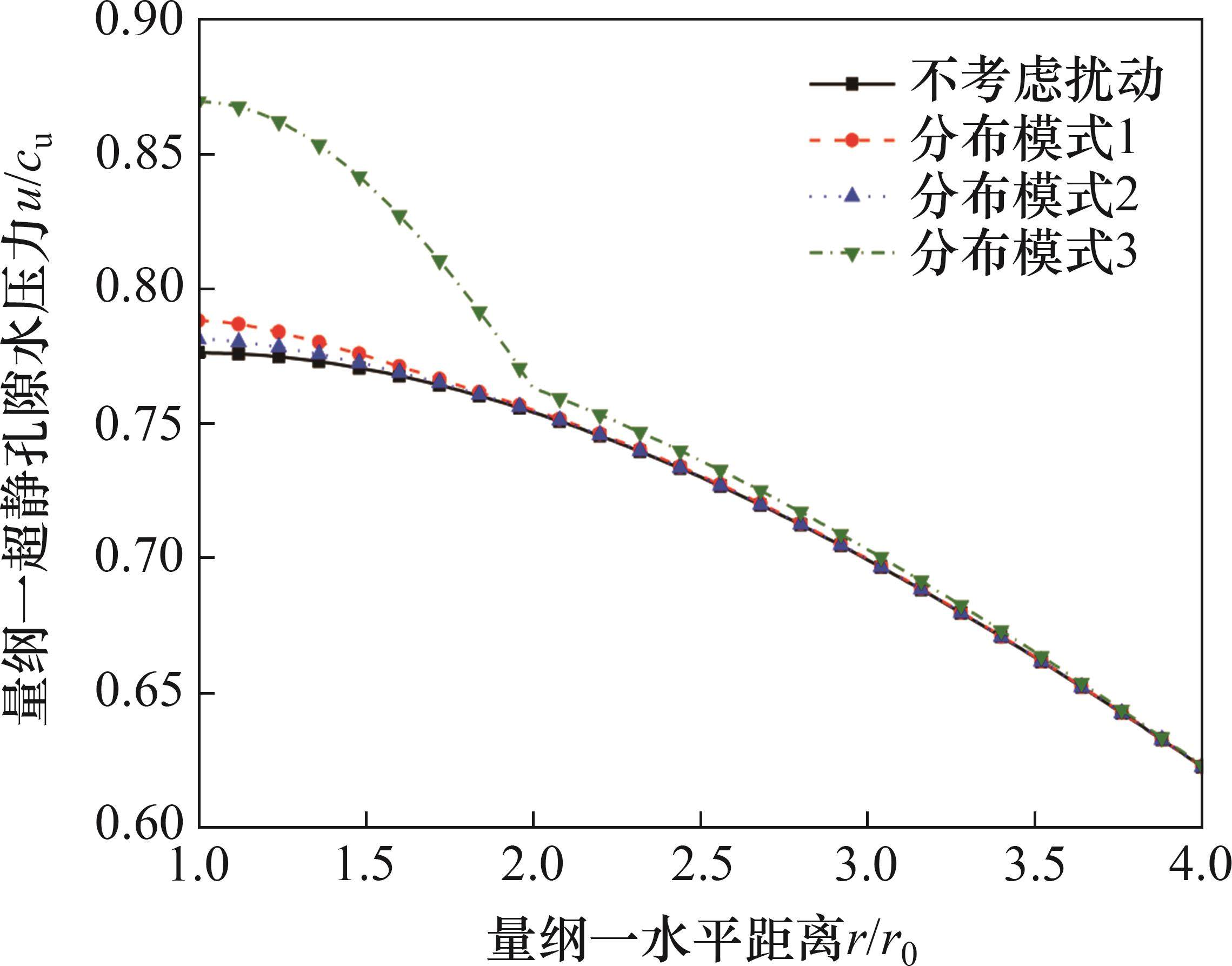
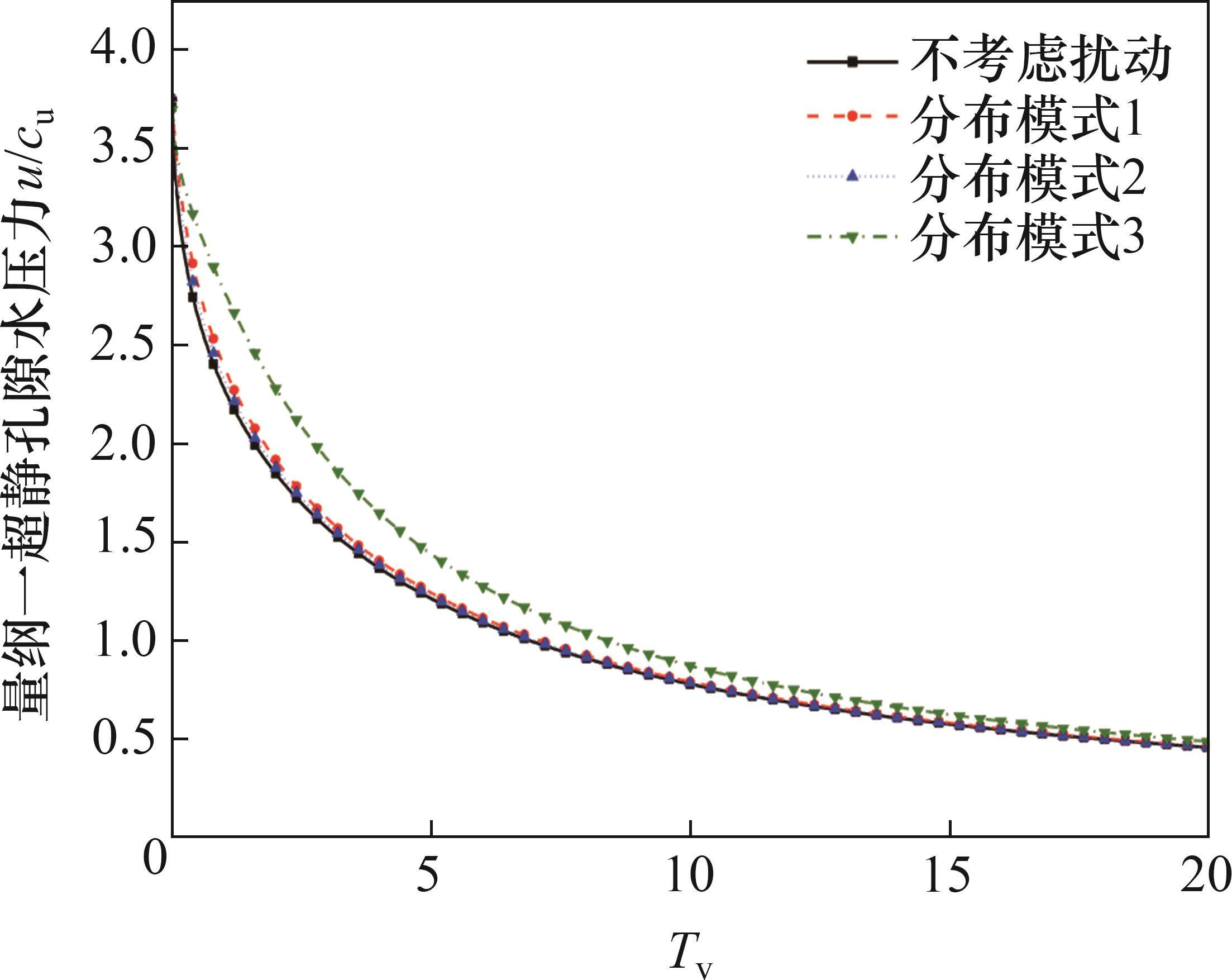
图9和图10所示为不同的扰动区水平渗透系数分布模式对超静孔压消散速率的影响。由图9和图10可知:只是简单地将扰动区划分为一个完整圈层的简化方法(即在扰动区边界发生水平渗透系数突变的分布模式3)大大高估了扰动效应对超静孔压消散速率的减缓作用,在扰动区形成了一个孔压很高的区域,对非扰动区的孔压产生了较大的影响。此外,对比更加符合真实情况的另外2种分布模式可以发现,水平渗透系数线性增长的分布模式1对超静孔压消散的影响要比分布模式2的稍大,这是因为2种分布模式的水平渗透系数仅在桩壁的r0处和扰动区半径的rd处相等,在扰动区其他地方,分布模式1的水平渗透系数均要高于分布模式2的水平渗透系数。
5 结论
1) 打桩引起的扰动效应会减缓桩周地基超静孔隙水压力消散速率,从而减缓地基土的固结速度。减缓作用主要发生在固结前期的扰动区土体中。
2) 扰动区土体超静孔压的消散速率随着扰动区半径与预制桩半径之比(rd/r0)的增大而减小,且扰动区半径越大,减小幅度越大。
3 )增大渗透系数扰动强度(kh/kd)会使超静孔压消散的速率减小,但远小于增大扰动区半径所带来的减小幅度,且在增大到一定程度后不再减缓超静孔压消散速度。
4) 将扰动区内的渗透系数看作一个固定值会严重高估扰动效应对超静孔压消散速率的减缓作用,计算时建议采用更符合实际情况的分布模式1和分布模式2。
5) 超静孔隙水压力主要在水平距离为15r0以内分布,在此范围外对超静孔隙水压力的影响较小。因此,当两桩中心距小于15r0且桩数较多时,应考虑群桩效应。
席睿辰, 张云鹏, 梅国雄, 等. 考虑打桩扰动效应的预制桩桩周土体固结解析解[J]. 中南大学学报(自然科学版), 2024, 55(12): 4604-4614.
XI Ruichen, ZHANG Yunpeng, MEI Guoxiong, et al. Analytical solution for consolidation of soil surrounding a prefabricated pile considering disturbance effect caused by pile driving[J]. Journal of Central South University(Science and Technology), 2024, 55(12): 4604-4614.

