为保障高速列车运营的安全性、平稳性和舒适性,我国《高速铁路设计规范》[1]严格规定路基工后沉降不宜超过15 mm,差异沉降不应大于5 mm。高铁动载是引发地基变形的重要诱因,导致轨道不平顺度增大,造成地基动力响应成倍增加,进而加剧地基变形[2]。为有效管控高速铁路地基变形病害和沿线环境振动问题,增强高铁韧性,保障运营安全,亟待开展高铁动载下软土地基振动与变形特性的相关研究。针对上述问题,部分学者通过土工模型试验,研究了列车动荷载下地基土体动应力传递分布特性和变形机理。现有试验主要包括循环动三轴试验和大型足尺模型试验,前者主要探究循环动载下土体的应力-应变机理,分析塑性应变随加载次数的变化规律[3-5];后者则是从宏观层面研究总结累积变形随加载次数的变化规律,并给出相应计算公式[6-8]。模型试验能够较为真实、直观地反映路基的动应力分布和变形发展规律,但受试验条件、模型比尺等因素限制,难以全面剖析地基的真实变形特性。
针对循环荷载下路基的累积变形预测,既有研究[9-12]提出多种经验模型并用于工程实践。然而,经验模型高度依赖试验数据,同一参数难以适用于其他地基,且计算精度和普适性较差。开展理论或数值计算方法研究是解决高铁荷载下地基变形问题的有效路径。管凌霄等[13]基于状态演化模型,研究了累积变形有限差分计算方法。王威等[14]研究了基于Burgers模型的路基长期变形计算方法。PUNETHA等[15]采用岩土流变模型研究了一种考虑主应力轴旋转的计算方法,发现主应力轴旋转对累积变形影响显著。吕玺琳等[16-17]建立了ABAQUS三维有限元模型,研究了桩土复合路基的累积变形。综合力学理论的严密逻辑和经验模型法的高效计算,力学-经验法在高速铁路长期变形预测中得到了越来越广泛的应用。该方法是通过理论方法或数值模型得到地基土体的动应力分布,再结合累积应变经验模型得出高铁地基长期变形的计算方法,其中部分学者侧重于通过试验研究拟合并提出新的经验模型[18-19],另有一些学者着重于动应力计算方法研究,并基于他人经验模型进行变形计算[20-22]。徐长节等[23]通过研究发现列车动荷载是引发铁路地基变形的重要因素。
综上,现有研究多聚焦于长期荷载作用下高铁地基的累积变形预测,而很少涉及高铁动载下地基变形的理论计算方法、真实高铁动载引起的地基变形机理等。研发精度高、效率高的地基变形计算模型并揭示地基变形规律是研究的重点。为此,本文作者基于高铁弹塑性地基2.5维有限元动力计算方法[24],研究高铁动载下软土地基变形分布规律,分析地基塑性变形规律及车速的影响,相关研究成果可为高铁地基变形管控提供依据。
1 软土地基弹塑性2.5维有限元模型
1.1 地基-轨道系统2.5维有限元控制方程
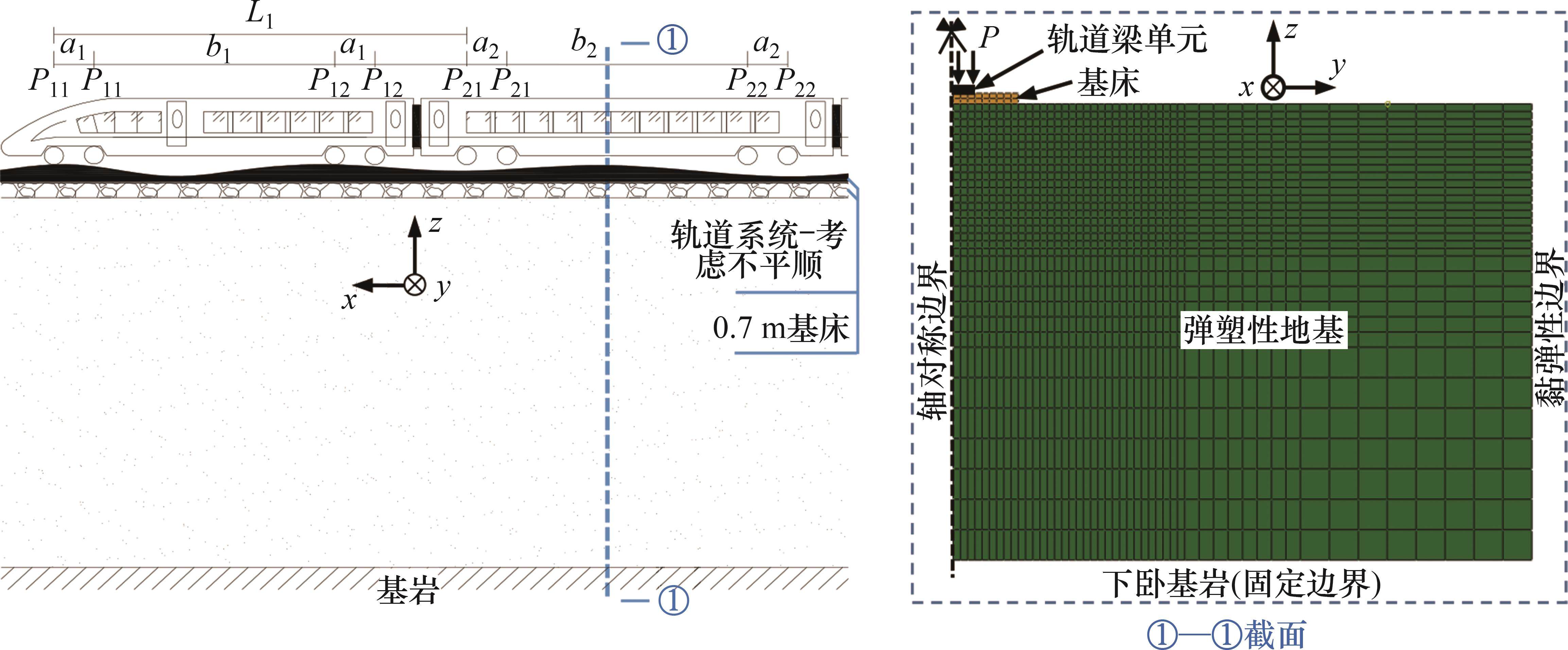
本文采用2.5维降维求解方法,假设轨道和地基土体的几何形状与材料性质沿高铁运行方向保持不变,对列车运行方向和时间进行双重Fourier变换,将时间-空间域四维动力问题转换到频域-波数域内的二维问题进行解答。考虑Cartesian坐标系,以列车运行方向为x向,水平垂直列车运行方向为y向,竖向为z向,弹塑性地基-轨道系统耦合计算模型如图1所示。本文定义的对时间t和x向的双重Fourier变换如下:
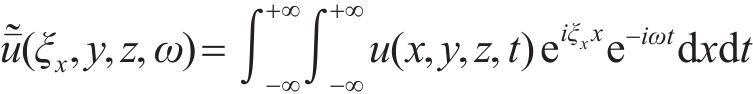
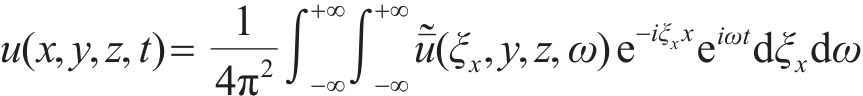
式中:上标“~”和“-”分别表示波数域和频域;u表示振动位移;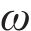
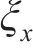
1.1.1 地基土体动力控制方程
将高铁动荷载下地基振动变形问题视为材料非线性问题,采用切线刚度法求解。当屈服准则判定土体屈服后,通过更新整体刚度矩阵和体荷载来模拟弹塑性土体的变形,实现每一迭代步内都是弹性求解。
频域-波数域内土体的运动和本构方程为
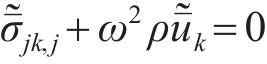
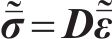
式中: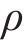
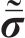
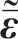
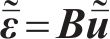

联合式(3)、(4),并采用Gerklin虚功原理可得土体2.5维有限元控制方程,其矩阵形式为
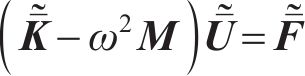
式中:
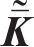
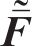
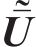
1.1.2 轨道系统模型
无砟轨道由钢轨、轨道板、扣件等部件组成。列车荷载作用下轨道系统以竖向振动为主,整个轨道系统变形可近似为整体变形,采用欧拉梁模型模拟,频域-波数域内的2.5维动力方程为:
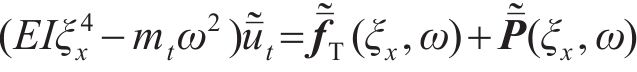
式中:
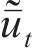
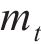
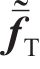

采用位移协调条件耦合式(5)和式(6)可得地基-轨道系统2.5维有限元控制方程。
为消除有限元模型截断边界处反射波对计算结果的影响,采用黏弹性人工边界模拟半无限空间。作用于边界节点上的弹簧-阻尼荷载表达式参见文献[24]。
1.2 地基土弹塑性本构积分算法
采用摩尔-库仑屈服准则描述地基土体的塑性变形。摩尔-库仑准则在π平面上存在6个棱角奇异点,造成数值计算收敛缓慢。为使棱角拐点处平缓连续,采用贾善坡等[25]改进的摩尔-库仑屈服函数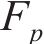
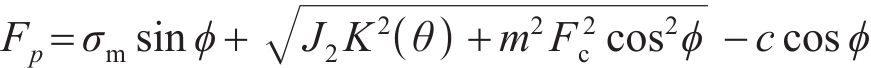
式中:Fc、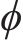
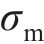
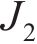
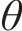
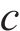
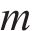
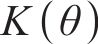
后向欧拉积分算法包括弹性试探和塑性修正,当应力超出屈服面时(Fp>0),进行塑性修正,将其逐渐迭代到屈服面上。
根据塑性理论的正交流动法则,塑性应变率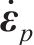
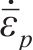
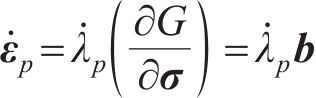
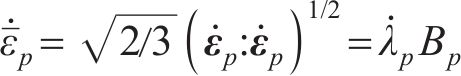
式中: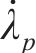
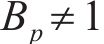
依据各向同性硬化法则,黏聚力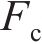
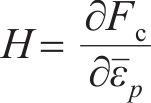
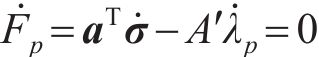
式中:a为屈服函数关于应力的一阶偏导数;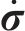
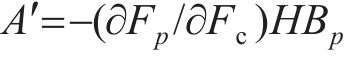
当弹性试探应力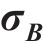
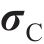
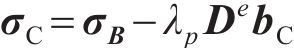
后向欧拉积分算法是将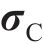

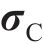
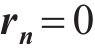
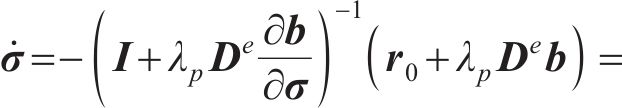
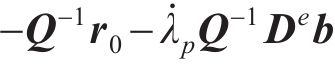
式中:I为单位矩阵;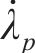
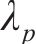
将屈服函数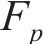
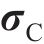
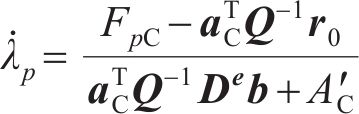
式中: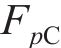
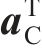
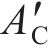
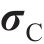
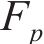
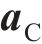
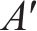
将式(14)代入式(9)和(13)可求得应力变化率和等效塑性应变率。
为保证计算程序的收敛性,采用一直切线模量算法更新方程的迭代过程。略去式(12)中下标C即得标准隐式后向欧拉算法表达式:
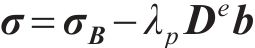
对式(15)求微分可得:
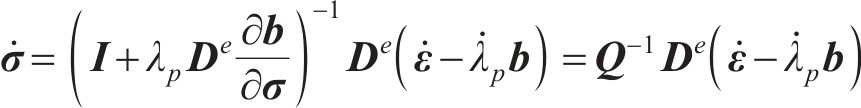
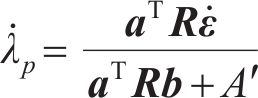
式中: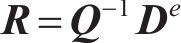
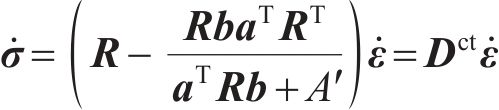
式中: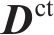
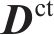
1.3 初始应力法生成体荷载
在每一荷载增量步中,位移增量
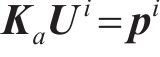
式中:Ka为总刚度矩阵;i为指迭代次数;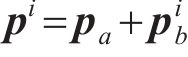
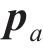
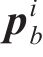
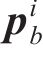
在每一次迭代中,引起应力重分布的体荷载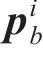
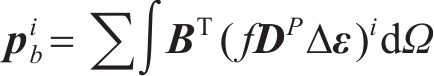
式中: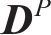
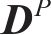
1.4 高铁动荷载数学模型
列车动荷载主要由两部分组成,一部分基于轮轴移动,另一部分由轨道不平顺引起的轮轨相互作用。每节列车由1个车厢、2个转向架和4个轮对组成(如图1所示),则列车移动荷载可表示为:
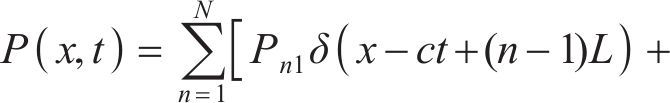
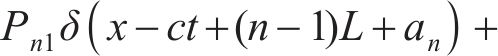
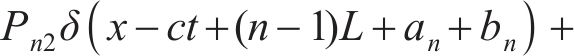

式中:c为车速;N为车体总数;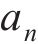
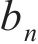

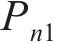
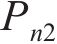
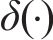
准静态列车荷载视轨道平滑,仅考虑轴重的移动效应,式(21)中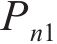
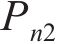
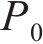
修正列车荷载考虑轨道不平顺,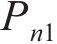
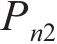
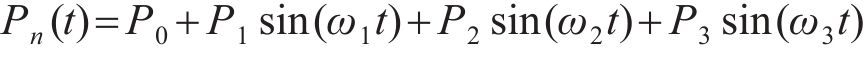
式中: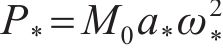

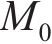
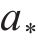
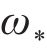
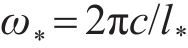
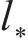
频域-波数域内列车荷载表达式为:
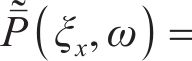
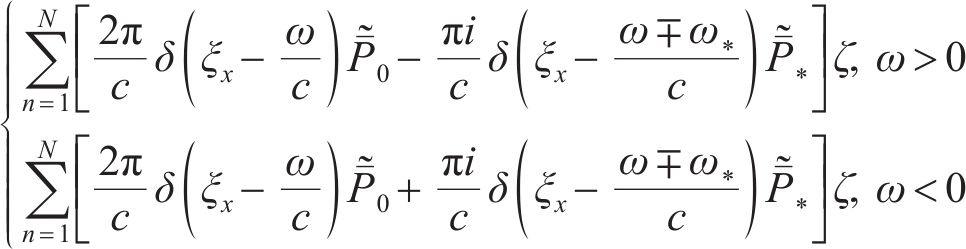
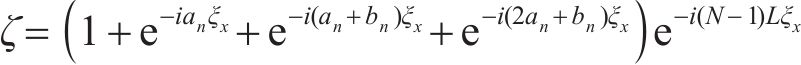
基于上述理论建立的2.5维有限元弹塑性地 基-轨道系统耦合计算模型的准确性和可靠性已在文献[24]中得到验证。
2 计算模型和参数
本文依托Visio studio2015平台,编制FORTRAN程序计算分析。选取单线路基建立模型,如图1所示,考虑土体弹塑性,将地基简化为均质土体,选取上海第②层典型软土(粉质黏土),厚30.0 m。选取低路堤路线段以考虑最大可能变形,并将路堤基床视为弹性体。依据上海光源工程勘测[27]和《高速铁路设计规范》[1],土体及基床参数见表1。轨道系统采用Euler梁模拟,相关参数见表2[28]。
| 路基 | 宽/m | 厚/m | 弹性模量/MPa | 泊松比 | 密度/(kg·m-3) |
|---|---|---|---|---|---|
| 道床 | 8.0 | 0.7 | 150.0 | 0.3 | 1 900 |
| 粉质黏土 | — | 30.0 | 44.7 | 0.4 | 1 830 |
| 路基 | 动阻 尼比 | 黏聚力/kPa | 内摩擦角/(°) | 瑞利波速/(m·s-1) | |
| 道床 | 0.038 | — | — | — | |
| 粉质黏土 | 0.030 | 10.5 | 14.7 | 93.4 |
| 宽度/m | 单位长度质量Mt/(kg·m-1) | 弯曲刚度EI/(MN·m-2) | 动阻尼比 |
|---|---|---|---|
| 3.0 | 540 | 13.254 | 0.1 |
以轨道中心线所在垂面为对称面,取半结构进行建模计算分析,选取任意垂直轨道截面进行有限元离散。计算模型宽为40.0 m、深为30.0 m,单元网格尺寸沿与轨道中心最小间距为0.2 m、最大间距为2.0 m。在模型左侧对称截面设置轴对称边界,右侧截断边界设为黏弹性边界以吸收边界处的反射波,下卧基岩层设为固定边界。高铁荷载采用CRH380AL动车组列车,考虑8节车厢,列车特征参数见表3[28]。
| 车厢质量/kg | 转向架质量/kg | 轮对质量/kg | 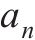 | 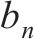 | 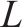 |
|---|---|---|---|---|---|
| 38 884 | 3 060 | 1 517 | 2.5 | 15.0 | 25.0 |
依据我国《建筑振动荷载标准》[29]修正列车荷载中的轨道高低不平顺计算参数如表4所示。
| 参数 | 低频 | 中频 | 高频 |
|---|---|---|---|
| 波长/m | 10.0 | 2.0 | 0.50 |
| 矢高/mm | 3.5 | 0.4 | 0.08 |
3 软土地基变形分析
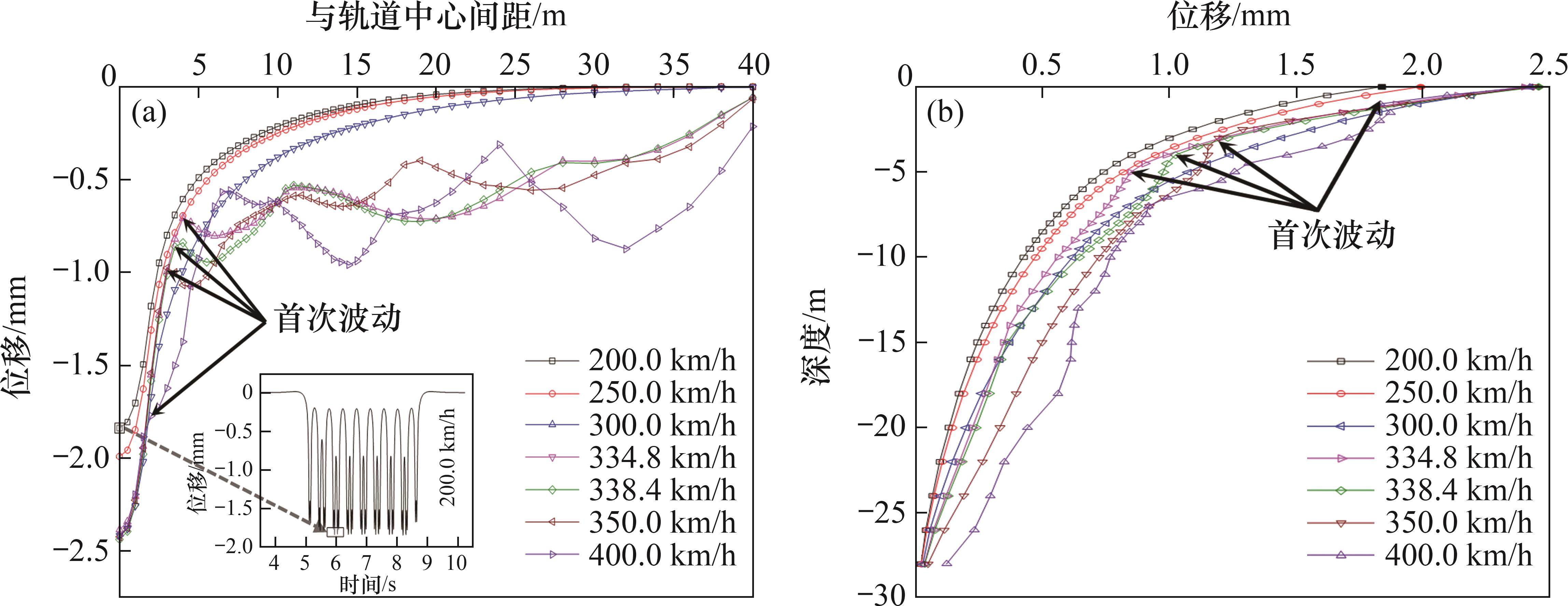
高铁动载分别采用准静态列车荷载以及考虑轨道不平顺的修正列车荷载。依据现行的高速铁路设计速度,取列车近城镇速度(200.0 km/h)、正常运行速度(250.0、300.0、350.0 km/h)以及超高速(400.0 km/h)计算时间。当车速接近地基土的瑞利波速93.4 m/s(临界速度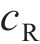
3.1 准静态列车荷载下地基变形特性
准静态列车荷载主要体现移动轴重作用。图2所示为各车速条件下距轨道中心10.0 m(y向)×10 m(z向)范围内地基土体竖向最大振动位移(时程峰值)云图,图中相邻等值线间的振动位移差为0.2 mm。由图2可知:最大振动位移出现在轨道下方的地表处,随振动波沿地表和深度方向的传播逐渐减小,且沿地表的衰减速率大于深度方向的衰减速度(沿地表的等值线分布密度大于沿深度方向的分布密度);当车速低于临界速度时,振动波呈无干涉的圆弧状向周围传播。随着车速的提高,振动位移增大,位移等值线变密,表明沿地表和深度的衰减速率有所增大,这是因为提高车速会增大响应频率,频率越高,与轨道中心间距衰减越快;当车速接近临界速度时,振动响应最为强烈,位移峰值最大。此时,在距轨道中心4.0 m以外、深度2.0 m以内的区域,等值线不再呈圆弧形而呈现内凹形,表明此范围内发生了振动波的叠加干涉,致使局部的振动位移发生变化;随车速继续提高,振动位移有所减小,且振动波的叠加干涉区域逐渐向轨道中心靠近;当车速为400.0 km/h时,叠加干涉范围进一步向深度方向延伸,位移等值线呈不规则的波浪状,说明振动波的叠加干涉程度更为强烈。
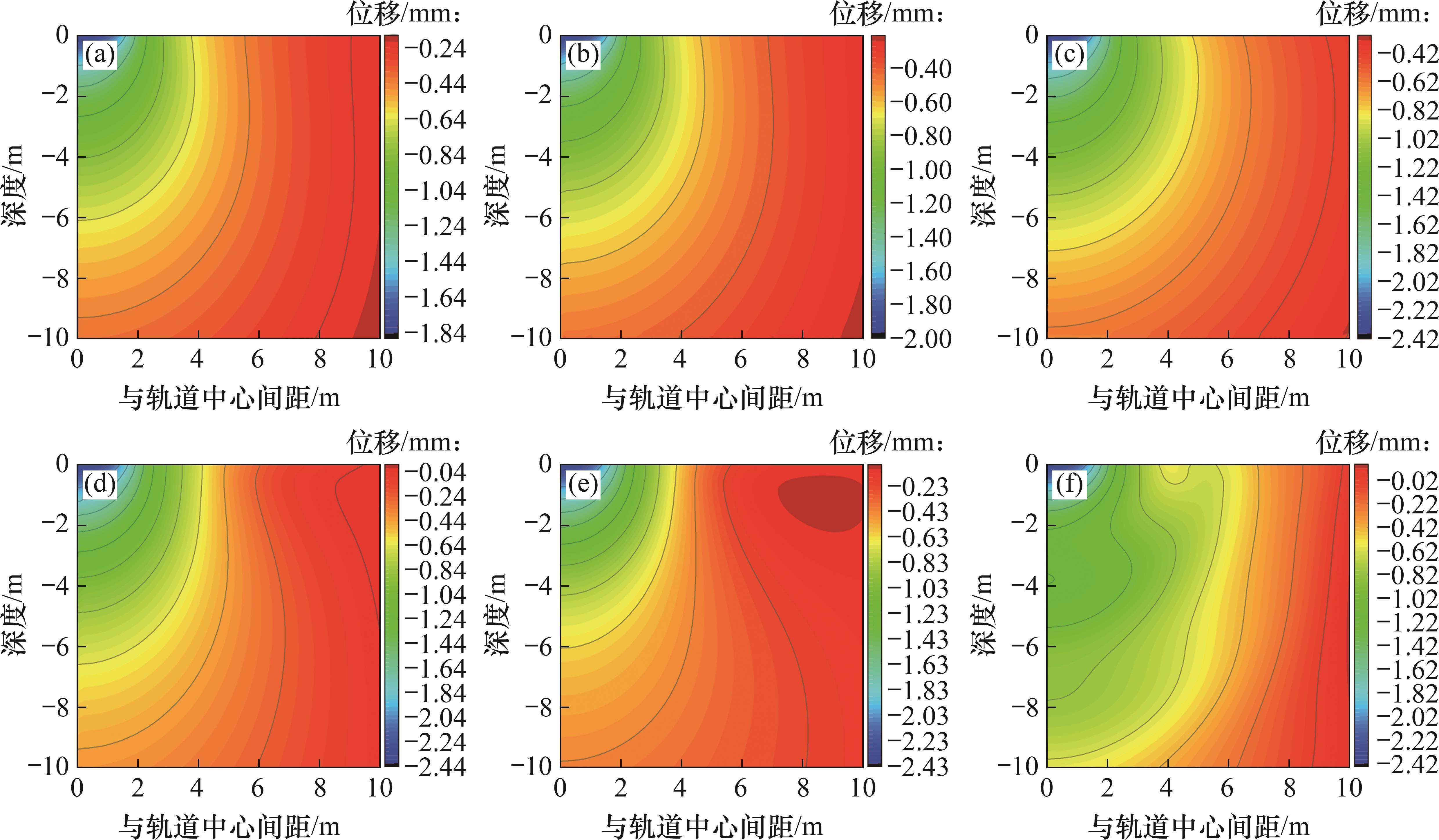
图3所示为不同车速条件下沿地表及轨道中心线下深度方向的最大竖向位移衰减曲线。由图3(a)可见:在轨道中心处,车速达到临界速度时土体的振动位移最大;当车速低于临界速度时,振动位移沿地表的衰减曲线较为光滑;当车速接近或高于临界速度时,在距轨道一定距离处的振动位移衰减曲线出现明显波动,且波动区域会随车速提高逐渐向轨道中心靠近;在波动现象出现之前,振动位移沿地表的衰减速率随车速逐渐提高;衰减曲线的波动性随车速提高而增强,且距轨道中心越远,波动的波长越长。这是由于高频短波沿地表衰减较快,随与轨道中心距离增大,振动显著频段波长逐渐增大。由图3(b)可知:当车速低于临界速度时,轨道中心下方沿深度方向的振动位移衰减曲线较为平滑;当车速接近或高于临界速度时,衰减曲线在一定深度处同样出现了波动现象,且随车速提高波动开始出现的位置深度逐渐变小。不同于地表处,当车速介于334.8~350.0 km/h时,首次波动出现后,沿深度方向的衰减曲线不再具有波动性;当车速为400.0 km/h时,在图3中所示的范围内,沿深度方向的衰减曲线始终具有波动性。此外,图3中衰减曲线的波动规律与图2中波的叠加干涉区域的位置和规律一致。
振动位移峰值沿地表和深度衰减曲线的波动性源于波的叠加与干涉。图4所示为单轮对移动荷载下振动波的传播与干涉示意图。其中,标记Tn (n=1,2,3,4)的曲线为Tn时刻地基中振动波波面。轮对荷载P由0点以速度c向右移动,在Tn时刻,荷载由0点移动到PTn位置;当车速低于临界速度(图4(c))时,振动波在传播过程不会相遇,没有发生波的干涉;当车速达到临界速度(图4(b))时,轮对荷载时刻作用于波阵面上,荷载作用点即为振动波唯一的相遇点,此处发生波的干涉,波的叠加干涉导致振动放大,此时,马赫角β=90°;当车速超过临界速度(图4(a))时,振动波在传播过程中相遇并发生叠加干涉;当两波相遇时,若相位差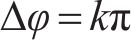
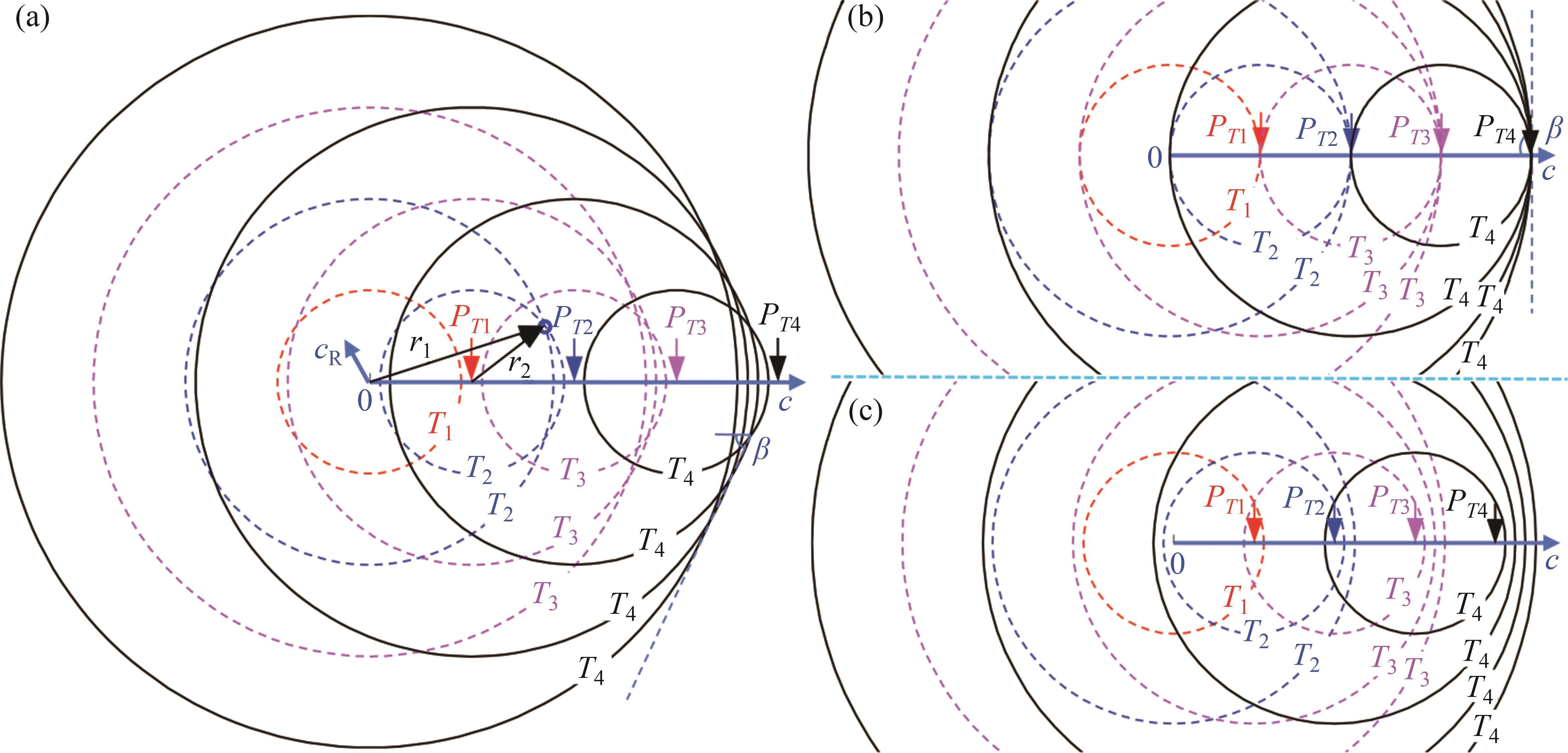
瑞利波只存在于距地表一定深度范围内,因此,当车速介于334.8~350.0 km/h时,沿深度方向的最大竖向位移衰减曲线在首次波动后便不再波动(图3(b));当车速400.0 km/h时,沿深度方向的最大竖向位移衰减曲线始终具有波动性,这是由于当车速超过地基土体的剪切波速时,在较深的土体中发生了剪切波的叠加干涉。
图5所示为不同车速条件下距轨道中心10.0 m×10.0 m范围内地基土体的塑性变形云图。由图5可知:地基土塑性变形主要集中在距轨道中心水平距离4.0 m以内、深度2.0 m以内的区域,且同时存在下沉(负向)和隆起(正向)的塑性变形区;隆起塑性变形是列车运行时地基土体受挤压所致,主要分布在深度0.3 m以内的地表附近,其中,深度0.5~1.5 m范围为主要的下沉塑性变形区;当车速较低时,塑性变形主要位于距轨道中心2.0~3.0 m范围内;随着车速提高,下沉塑性变形区逐渐向轨道下方和右下方扩展,而隆起塑性变形区基本保持不变。对比图2和图5可知:在各车速条件下,地基的塑性变形相较于总振动位移小1~4个数量级;当车速较低时,塑性变形极小;当车速接近临界速度时,塑性变形急剧增大。塑性变形远小于振动位移,这从侧面印证了列车荷载下地基振动为小应变问题。
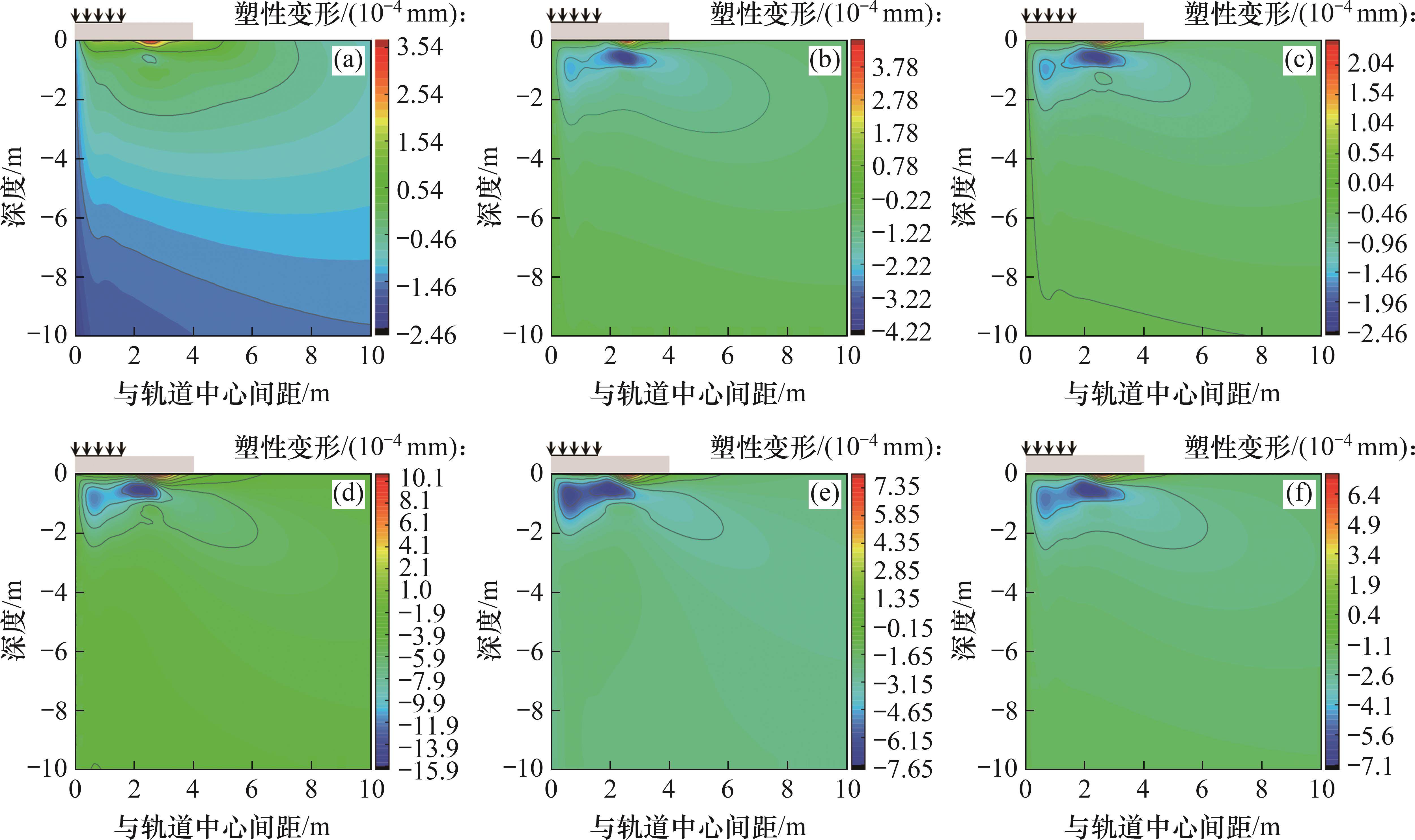
图6所示为地表塑性变形沿地表变化曲线及轨道中心处塑性变形时程曲线。从图6可见:在不同车速条件下,轨道中心处塑性变形时程曲线在列车通过时呈阶梯形下降,表明塑性变形随时间逐渐累积增大;当车速为200.0 km/h和250.0 km/h时,塑性变形时程曲线几乎为直线,塑性变形几乎为0;当车速接近临界速度时,塑性变形显著高于其他车速的塑性变形。由塑性变形沿地表的变化曲线可知,距轨道中心2~4 m范围内的地表塑性变形为正值,是挤压隆起区,此区域位于路堤下方,这可能由此导致的路堤不均匀沉降;当车速接近临界速度时,地表各处塑性变形最大,表明地基塑性变形主要由地基的类共振条件控制。此外,由于本文计算模型假定土体为连续体,忽略了土颗粒之间的离散性,距轨道较远处的塑性变形计算结果偏大。
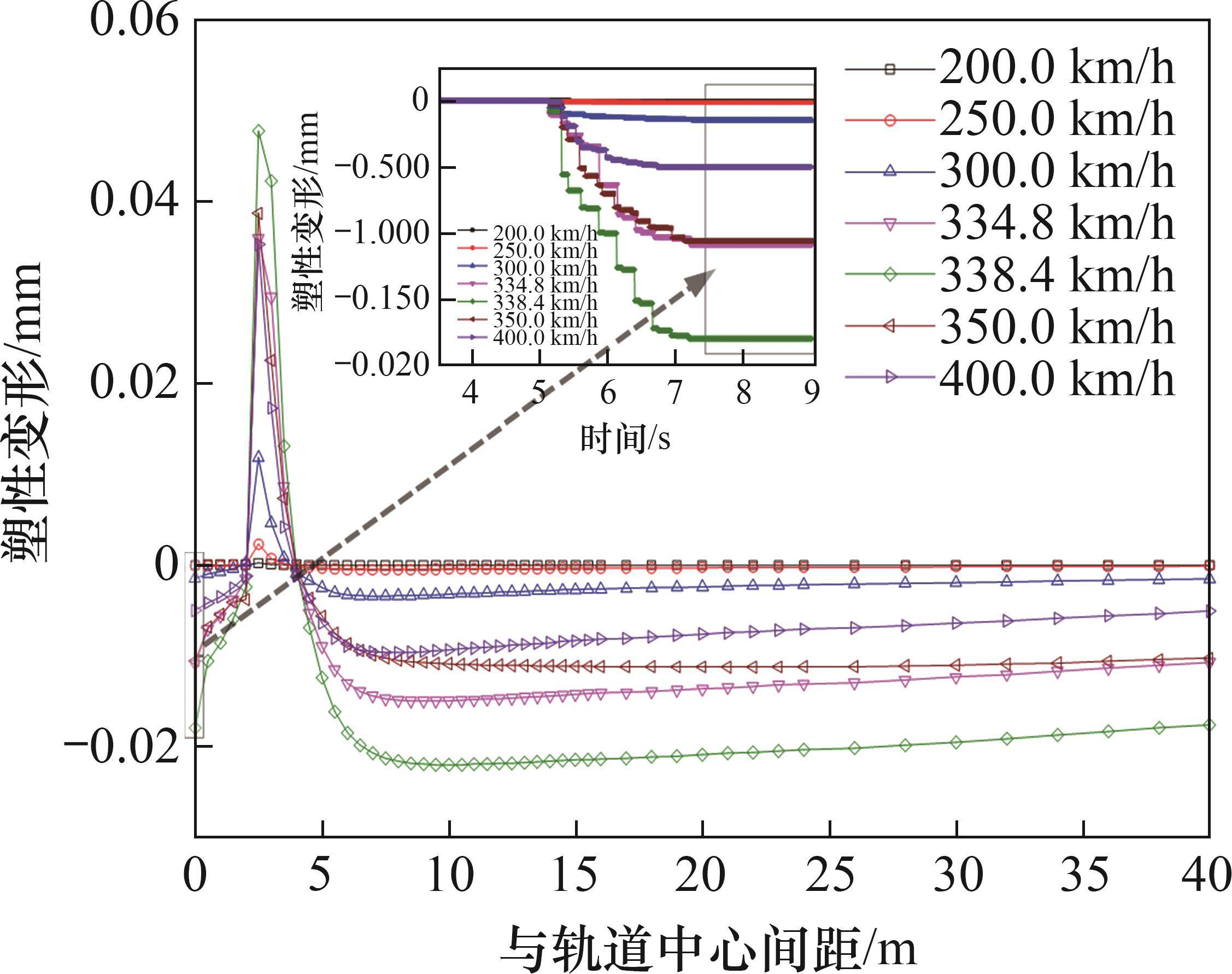
3.2 修正列车荷载下地基变形特性
考虑轨道不平顺对地基振动变形的影响,分析修正列车荷载下地基土体的变形特性。在车速200.0~400.0 km/h范围内,表4中3种几何不平顺的荷载激励频率分别为低频5.6~11.1 Hz、中频27.8~55.6 Hz、高频111.1~222.2 Hz。
图7所示为修正列车荷载下距轨道中心10.0 m(y向)×10 m(z向)范围内地基土体竖向最大振动位移(时程峰值)云图,图中相邻等值线间的振动位 移差为0.2 mm。对比图2和图7可知:当车速为200.0 km/h时,位移云图无明显变化,此时,轨道不平顺对地基振动位移影响可忽略;当车速为250.0 km/h和300.0 km/h时,振动位移明显增大,等值线变密,表明位移沿地表和深度的衰减速率增大,这是由于轨道不平顺引发的较高频率振动对地基振动位移影响较大;当车速接近或高于临界速度时,在波的叠加干涉区域,振动位移等值线的波动性更大,波的叠加干涉更为强烈。这是由于考虑轨道不平顺条件下,轮轨相互作用产生多频段激励力,使列车荷载的激励频率更多,所引发地基振动波的主频也更多,故振动波在传播过程中发生叠加干涉的层次也更多。这也造成了车速300.0 km/h时,距轨道中心4 m以外地表附近处的位移等值线出现略微波动。
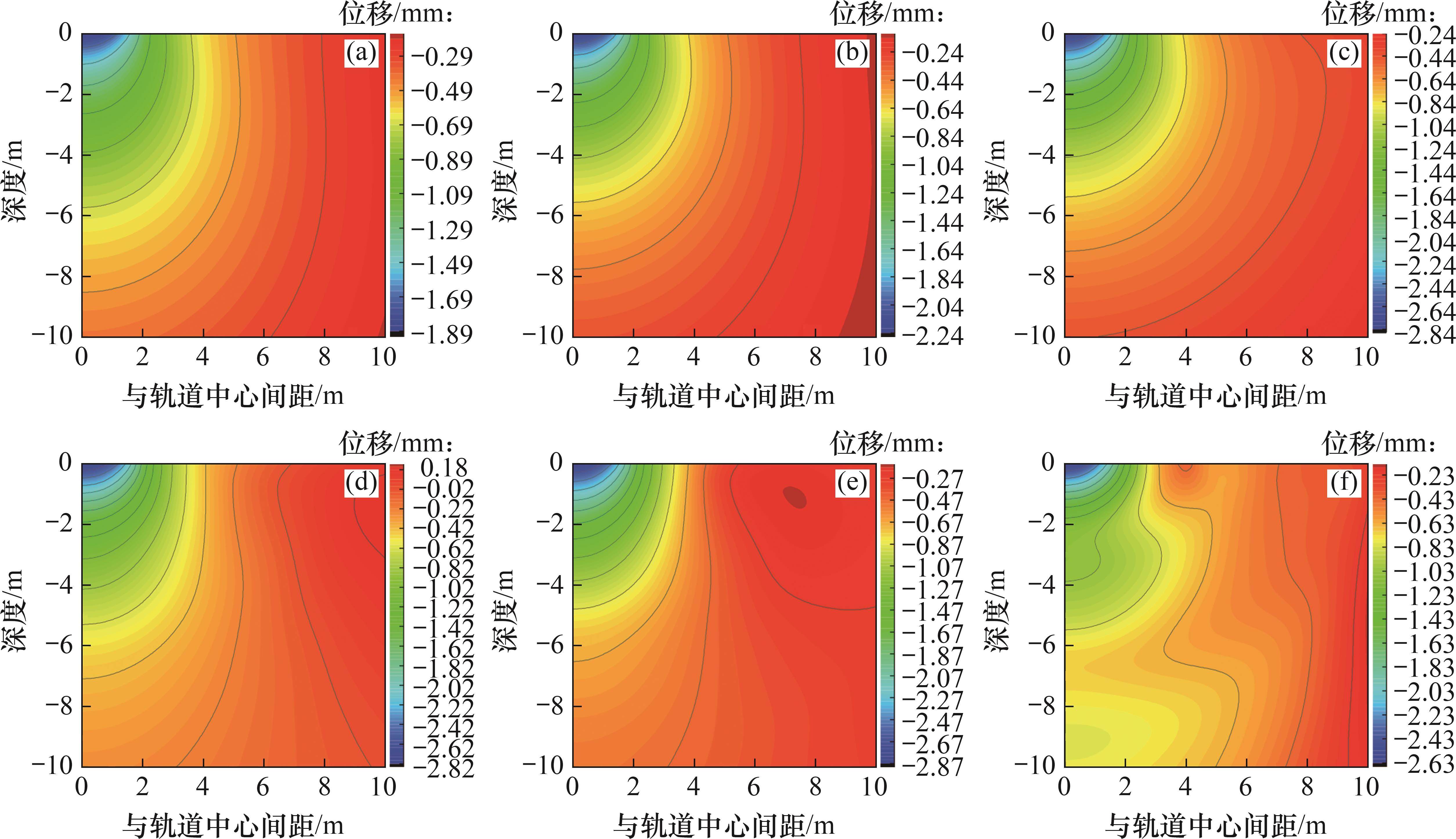
图8所示为修正列车荷载下竖向位移峰值沿地表和深度的变化曲线。从图8可见:与准静态列车荷载相比,当车速为200.0 km/h时,两类荷载引起的位移峰值相差较小,即轨道不平顺对振动位移的影响较小;当车速分别为250.0、300.0、338.4、350.0和400.0 km/h时,修正列车荷载引起的位移峰值较准静态荷载明显增大,轨道中心处位移增幅分别为0.24、0.42、0.38、0.45和0.21 mm,轨道不平顺的动力作用明显。因此,当车速高于250.0 km/h时,需考虑轨道不平顺对振动位移的影响。在典型轨道不平顺条件下,当车速分别为300.0 km/h和350.0 km/h时,轨道不平顺的动力作用最为显著,引起的振动位移大于车速接近临界速度时的振动位移。这是由于高铁运行时,轮对与轨道不平顺相互作用引发特定频段的振动波,与列车轮轴移动引发的振动波产生叠加效应,当车速致使两类振动波叠加产生较大合振幅时,振动响应较大。当车速为300.0 km/h和350.0 km/h时,振动波叠加效应比临界速度下的振动叠加效应更强,因此,振动位移较大。表明修正列车荷载下地基振动位移由类共振条件和轨道不平顺激励力共同控制。
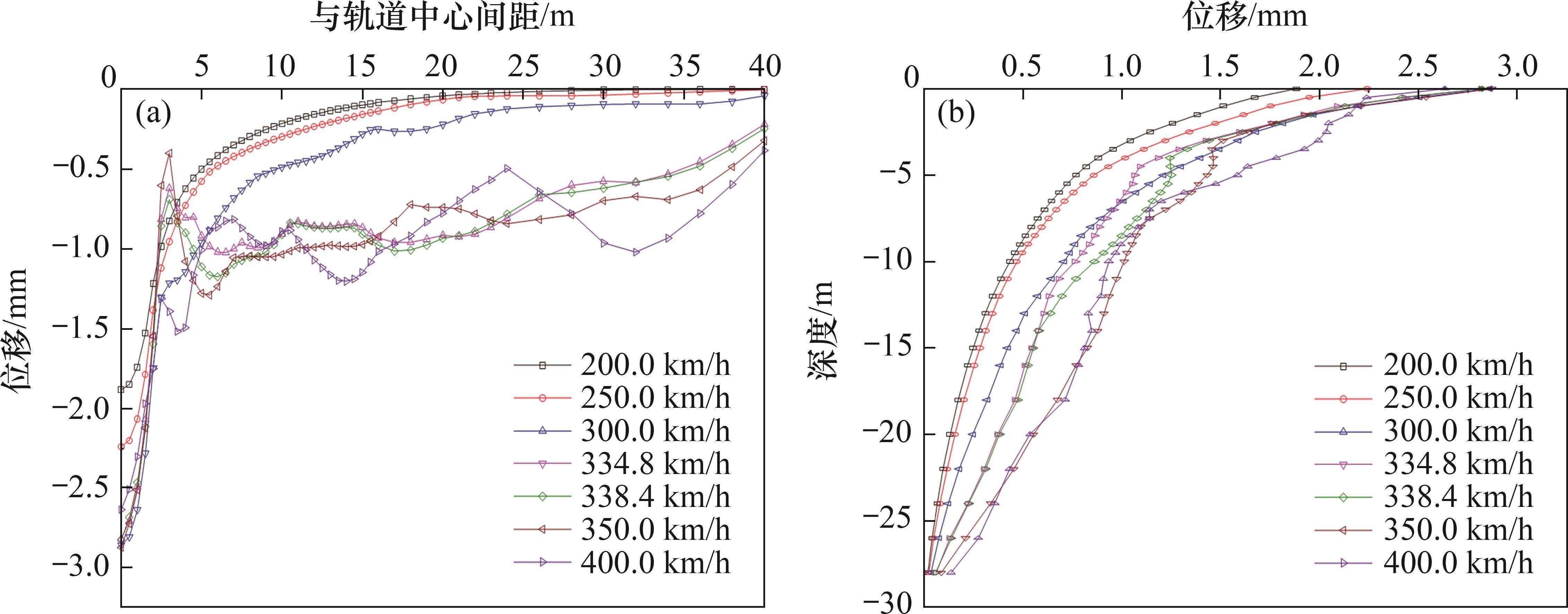
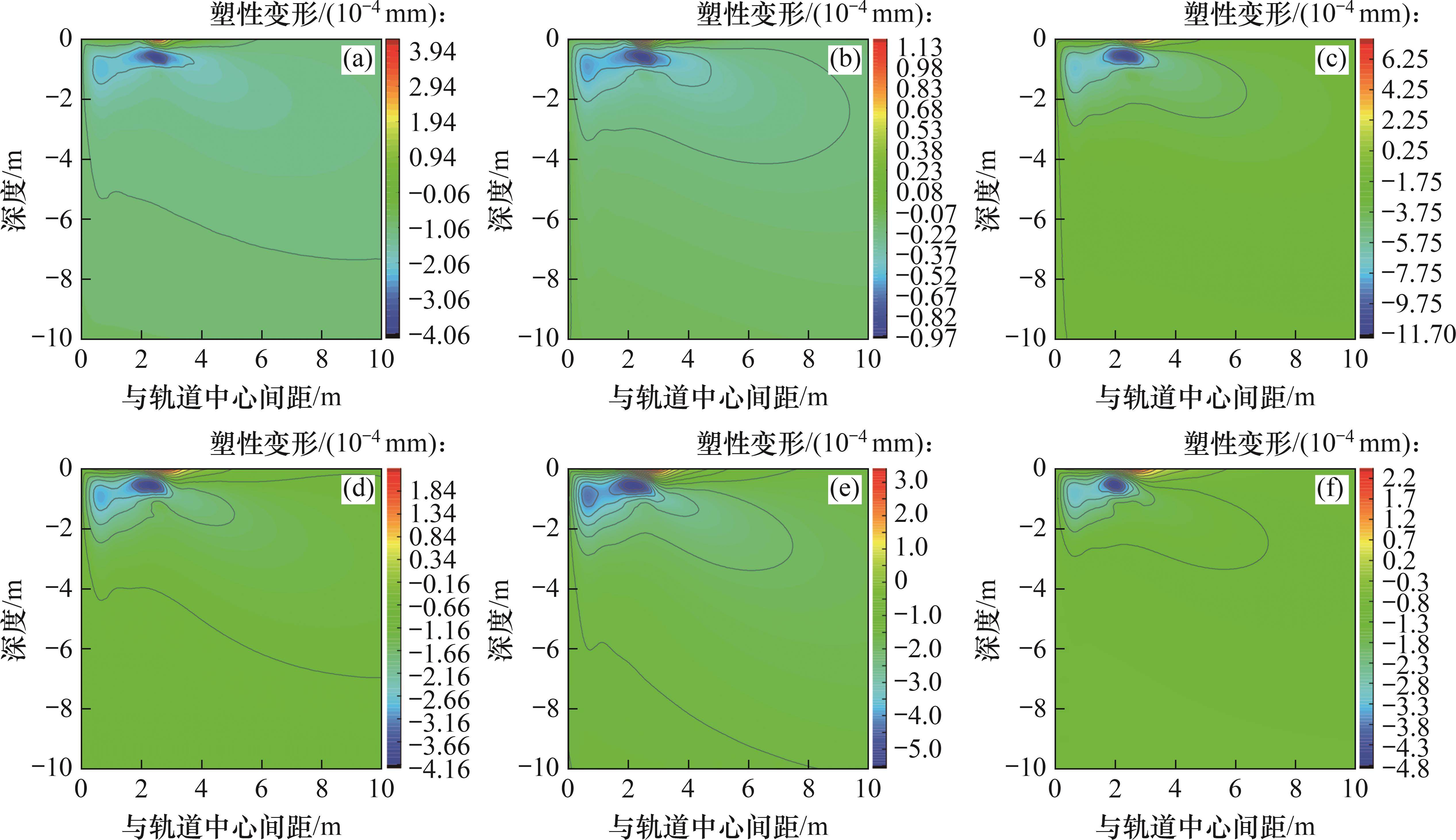
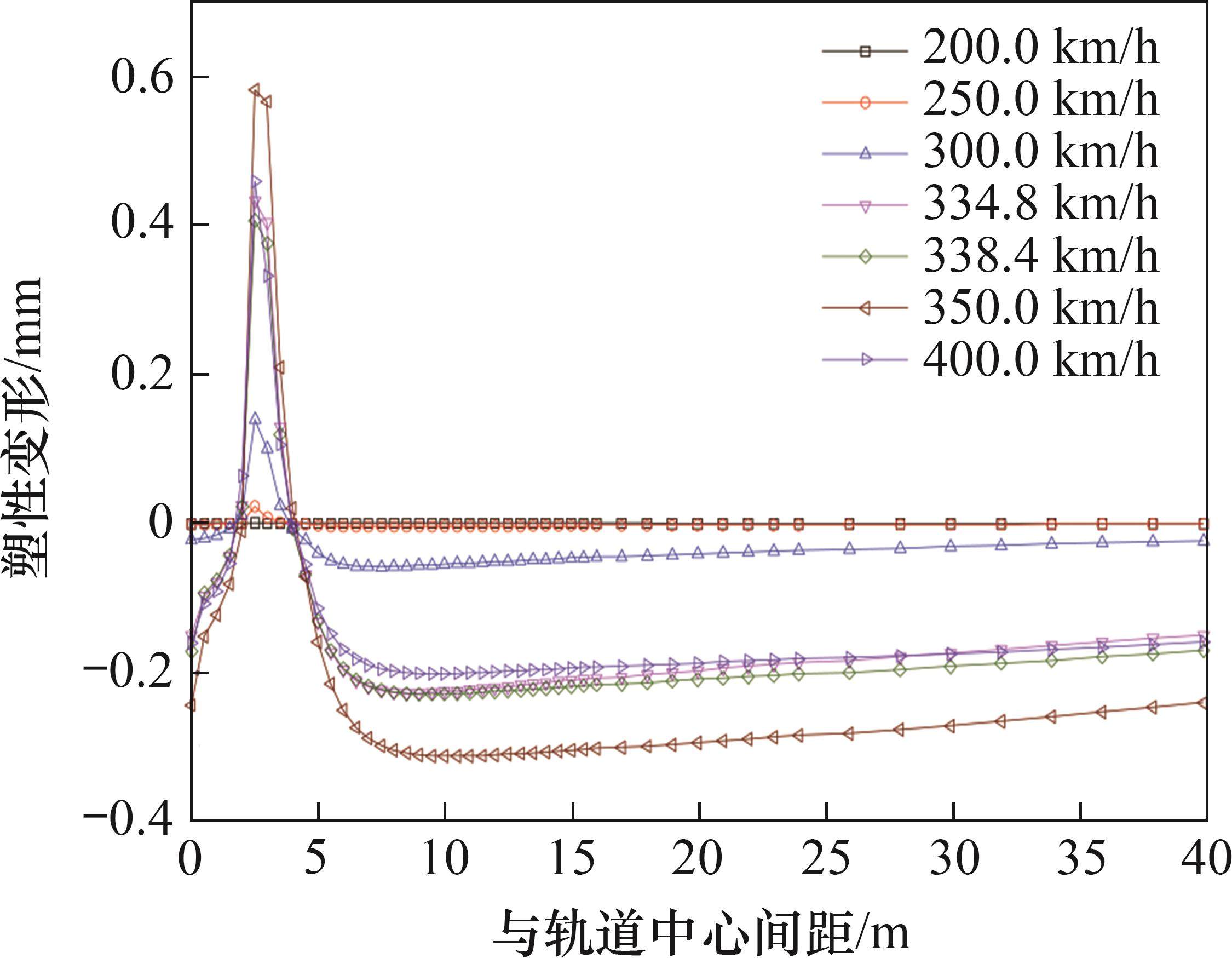
图9和图10所示分别为修正列车荷载下的土体塑性变形云图与地表最大塑性变形变化曲线。与准静态列车荷载(图5)相比时,修正列车荷载下塑性变形区的分布特征类似,但修正列车荷载下的塑性变形更大,分布范围更广。在各车速下,修正列车荷载引起的下沉最大塑性变形比准静态列车荷载大1~6倍,表明轨道不平顺激励力与移动轮轴力产生的振动波叠加效应对塑性变形影响显著,在对高铁荷载下地基塑性变形进行预测时,应考虑轨道不平顺的影响。此外,当车速为350 km/h时,地基土体的塑性变形最大,表明修正列车荷载作用下塑性变形不仅取决于土体类共振条件,而且受轨道不平顺的显著影响。
4 结论
1) 轨道下方地表处的振动位移最大,且振动沿地表的衰减速率大于深度方向的衰减速度。同时,振动位移的幅值及其沿地表和深度方向的衰减速率均随车速提高而增大。
2) 当车速高于临界速度时,准静态列车荷载会引发地基中振动波的叠加干涉,且随车速增大而逐渐增强。在修正列车荷载(考虑轨道不平顺)作用下,地基振动波的叠加干涉更为强烈,且振动位移显著增大。
3) 地基土体的塑性变形主要集中在距轨道中心水平距离4.0 m、深度2.0 m以内的区域,且同时存在下沉和隆起的塑性变形区,应注意由此引起的不均匀沉降。随车速提高,隆起塑性变形区基本不变,而下沉塑性变形区逐渐向下方和右下方扩展。
4) 在准静态列车荷载下,地基振动位移和塑性变形主要受类共振条件控制。在修正列车荷载下,地基振动位移和塑性变形与准静态荷载时相比显著增大,表明塑性变形受轨道不平顺激励力与移动轮轴力产生的振动波叠加效应影响显著,此时,振动位移和塑性变形均受类共振条件与轨道不平顺激励力共同控制。
纪颖波, 张继严, 毕俊伟, 等. 高铁荷载下软土地基振动与塑性变形特性[J]. 中南大学学报(自然科学版), 2024, 55(12): 4615-4627.
JI Yingbo, ZHANG Jiyan, BI Junwei, et al. Vibrations and plastic deformations of soft ground induced by high-speed trains[J]. Journal of Central South University(Science and Technology), 2024, 55(12): 4615-4627.

