高速铁路隧道属于不利于流场和声场扩散的半封闭空间,由于缺乏必要的声学设计,列车在隧道内行驶时车内外及隧道洞口噪声均显著增大。TAN等[1-2]的仿真研究发现隧道内列车气动噪声源大于明线段,张良涛等[3-4]对车内噪声的测试结果表明列车行驶在隧道内时车内噪声比隧道外明线段增大4~7 dB(A),李志强等[5-6]对车外噪声的测试结果表明隧道洞口附近列车通过噪声比明线段增大2~3 dB(A)。根据POISSON等[7-9]对国内外高速铁路车外辐射噪声研究结果,在300 km/h以上时车外噪声源强已达到90 dB(A)以上,高速列车对隧道洞口附近环境噪声影响将进一步加剧。近年来,随着噪声源识别技术及气动仿真技术提升,李晏良等[10-11]开展了高速列车车外噪声源识别,ZHU等[12-14]开展了关键气动部位的噪声源特性仿真分析,研究成果深化了对高速铁路噪声源分布、机理特性及传播规律的认识。伍向阳等[15-17]在噪声源特性识别研究基础上建立了相对完善的350 km/h及以下速度级明线段多等效声源噪声预测理论,但对隧道区段的噪声计算理论研究鲜见报道。师利明等[18-20]对公路隧道噪声开展试验和理论研究,并从隧道混响声控制的角度提出了隧道噪声控制措施,但公路车流量大,其车辆噪声源可近似等效为无限长线声源,而高速铁路车流量相对较小,动车组长度有限,无限长线声源的混响声理论应用于高铁隧道具有明显局限性。为探究高铁隧道洞口噪声影响规律,本文在多等效声源的直达声预测方法基础上,从统计声学基础理论出发,建立适用于高速铁路噪声源特征的隧道洞口混响声理论模型,研究了隧道洞口直达声与混响声的理论解析方法。针对350 km/h高速铁路隧道洞口,建立了基于几何声学的仿真分析模型并开展现场测试,利用实测数据对理论及仿真模型进行可靠性验证。
1 高速铁路隧道洞口噪声理论研究
高速铁路隧道洞口噪声由列车运行产生的直达声和隧道混响声2个部分组成,下面分别基于高速铁路多等效声源噪声预测方法和统计声学方法建立相应的理论计算方法。
1.1 基于多等效声源的直达声理论
高速铁路噪声源分布相对复杂,基于多等效声源的噪声传播理论已成为高速铁路噪声预测计算的主流模型。伍向阳[15]通过将高速动车组噪声源划分为下部区域、车体区域和受电弓区域3部分,并将下部区域噪声源等效为有限长不相干偶极子线声源、车体区域噪声源等效为有限长不相干单极子线声源、受电弓区域噪声源等效为偶极子点声源,建立了以列车通过时段等效声级作为预测参数的三等效声源噪声理论模型,经验证远场噪声预测误差小于1 dB(A)。目前该方法已经纳入我国《环境影响评价技术导则 声环境》(HJ 2.4―2021)[21]标准中。本文借鉴其不同区域噪声源机理特性及等效方法,对噪声源进行离散,通过叠加计算接收点处各子声源的声能量和,建立了满足直达声时变分析需求的数学理论模型。
假设动车组下部区域和车体区域噪声源沿车体长度方向分布,按照车体长度L将声功率均分为N等份,每份长度Δx=L/N。当动车组车头与接收点纵向距离为x0时,噪声源与接收点相对位置关系见图1。
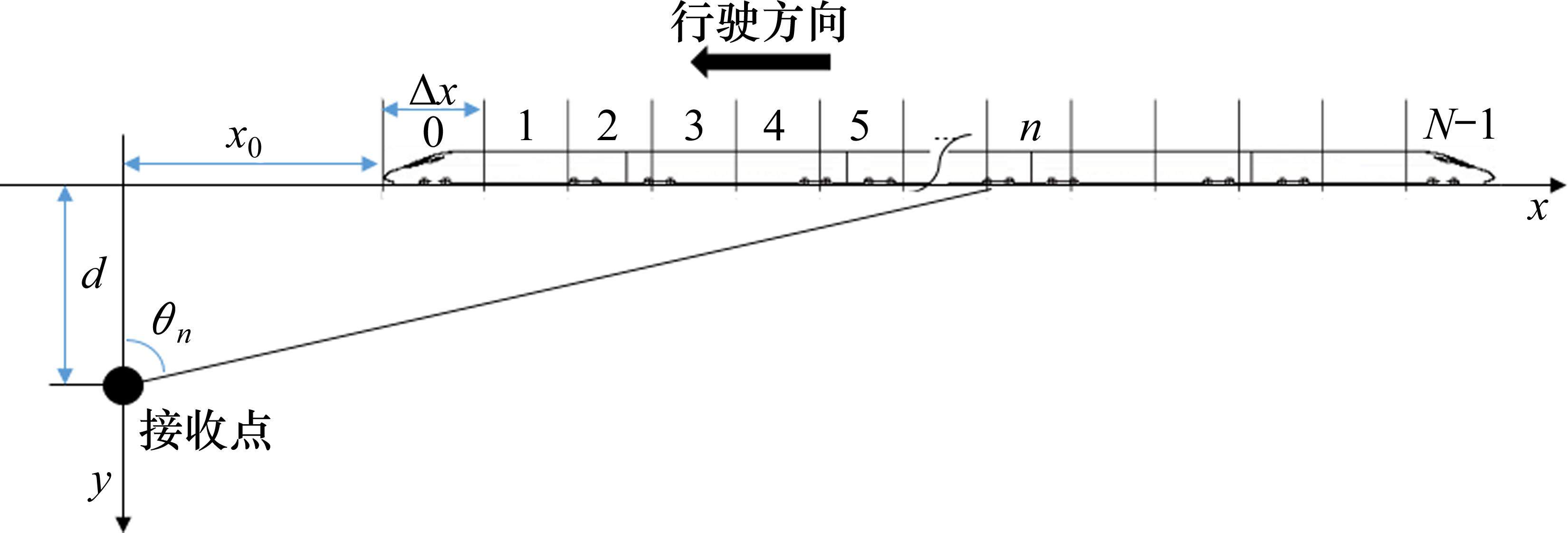
根据下部区域偶极子点声源指向性特征,得到下部区域贡献声压Prail(x0)为:
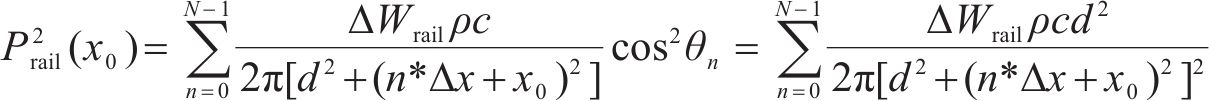
根据车体区域单极子点声源指向性特征,得到车体区域贡献声压Pbody(x0)为:
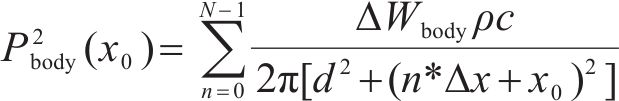
根据受电弓区域偶极子气动点声源指向性特征,得到受电弓区域贡献声压Psdg(x0)为:
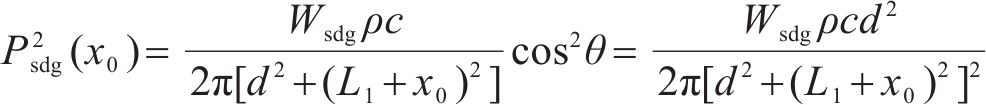
式中:ΔWrail为下部区域Δx长度的声功率,W;ΔWbody为车体区域Δx长度的声功率,W;Wsdg为受电弓区域声功率,W;d为接收点与线路的距离,m;L1为受电弓至车头的距离,m;θn为下部区域或车体区域第n等份声源至接收点连线与垂直线路方向的夹角;θ为受电弓至接收点连线与垂直线路方向的夹角。
对三等效声源贡献量进行能量求和,得到动车组车头与接收点纵向距离为x0时的直达声总声压Pzd为:
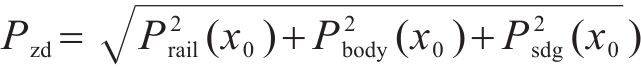
1.2 基于统计声学的隧道混响声理论
高速铁路隧道可近似为截面接近圆形的长空间结构,在隧道内部吸声特性主要与隧道壁及轨道板等的吸声性能有关,在隧道洞口处噪声辐射至外部自由空间,其吸声系数可等效为1,因此隧道洞口附近与深入隧道内部处的单位长度空间吸声量有明显差异。此外,动车组全部位于隧道内和部分驶出隧道时噪声源特性及对隧道噪声的影响也存在显著不同:首先是受隧道内有限空间流场影响,根据TAN等[1-2]的仿真成果,动车组位于隧道内时气动噪声源大于明线段,其次是已驶出隧道的噪声源将不再对隧道内混响声产生明显贡献。因此需分别针对动车组全部位于隧道内时和部分驶出隧道时2种工况进行混响特性理论分析。
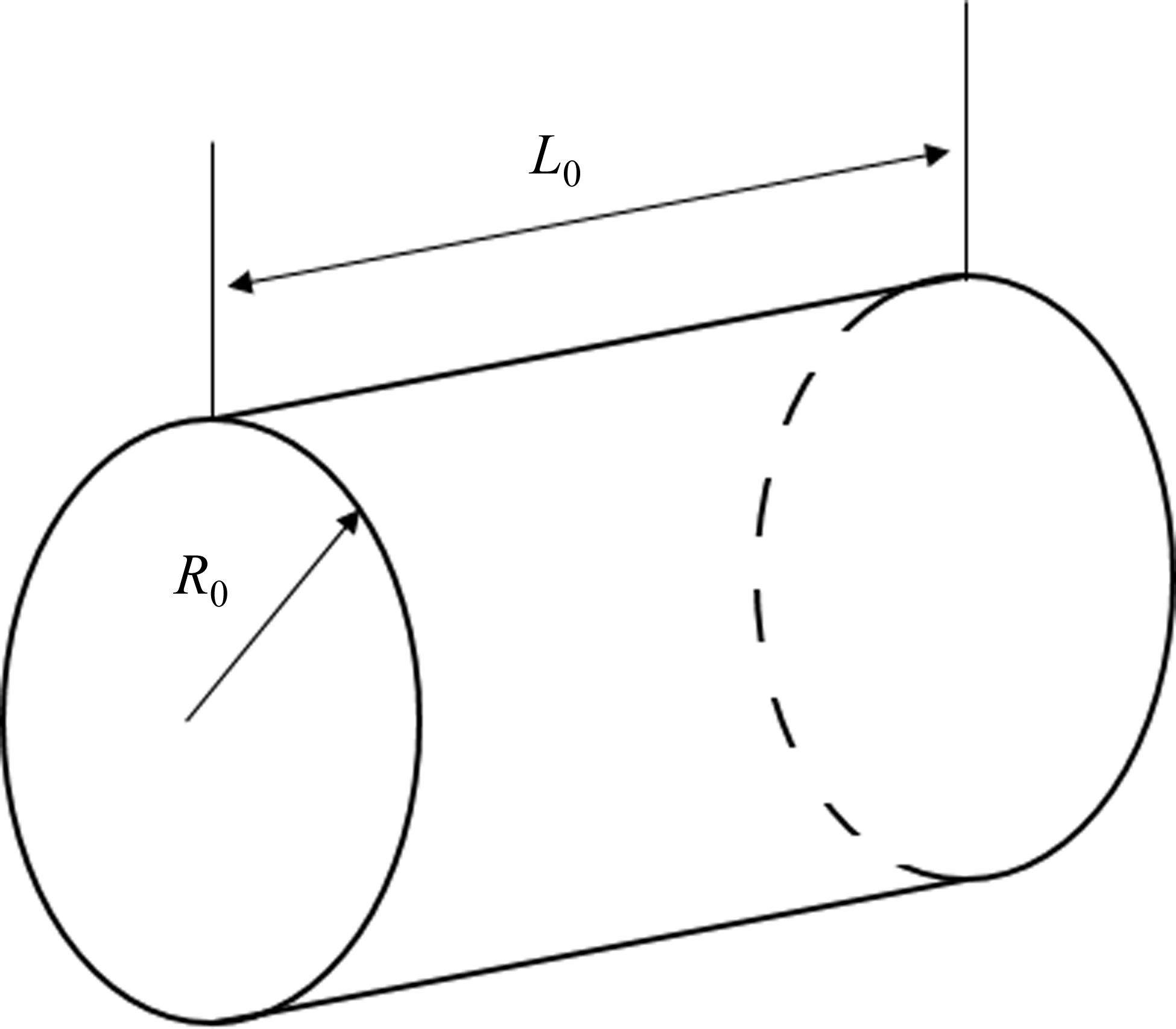
根据统计声学理论分析典型声学参数的计算方法。当动车组全部位于隧道内时,假定隧道壁及轨道等水泥结构边界的降噪系数(250、500、1 000和2 000 Hz的平均吸声系数)均为a,对于图2所示长度为L0、截面等效为半径R0的圆形隧道,其平均吸声系数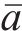
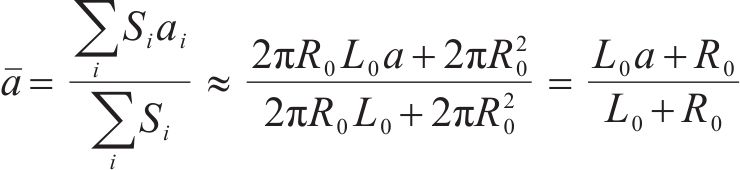
式中:L0为隧道长度,m;R0为隧道半径,m;a为隧道内水泥边界吸声系数,无量纲。
在某一时刻长度为L的动车组车头行驶至距离隧道洞口为x的位置处,根据混响时间的赛宾公式,由隧道洞口至动车组中间位置处的空间范围内混响时间RT可近似为:
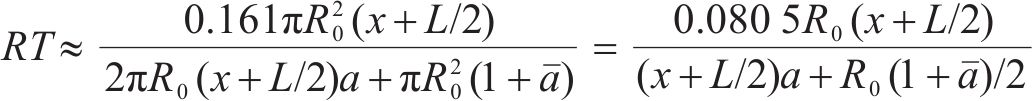
式中:RT为洞口至动车组中间位置的空间范围内的混响时间,s;L为动车组长度,m;x为车头至隧道洞口距离,m。
根据350 km/h高速动车组噪声源空间分布及占比情况,基于统计声学的高速铁路噪声源可近似为有限长运动线声源,本文将其等效为总声功率Win、单位长度声功率Win1的有限长线声源。隧道内直达声与混响声的叠加可表示为声能密度的叠加,在动车组所在区域内隧道单位长度声能密度EZ可表示为:
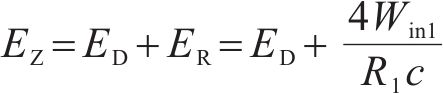
其中:EZ为总声能密度,J/m3;ED为直达声声能密度,J/m3;ER为混响声能密度,J/m3;c为声速,m/s;R1为隧道单位长度房间常数,m2,计算公式为:
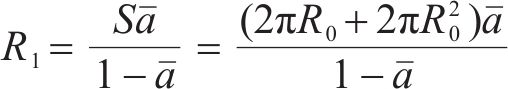
其中:S为单位长度隧道内表面积,m2。动车组所在区域的混响声将扩散至隧道洞口并向外辐射,在不考虑混响声随时间衰减和空气吸收衰减情况下,混响声能均匀扩散至隧道洞口处时的声能密度为:
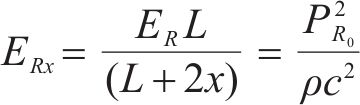
其中:ERx为混响声能由动车组所在区域扩散至隧道洞口时的声能密度,J/m3;ρ为空气密度,kg/m3;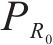
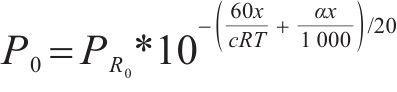
假设声能量自隧道洞口扩散衰减,将隧道洞口处混响声源近似为半径为R0的圆形平面声源,距离圆心为r的远场处近似按球面波扩散,混响声压PRr可表示为:
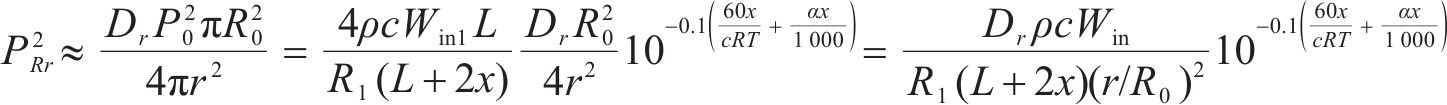
式中:Dr为隧道洞口混响声辐射指向性指数,无量纲;r为隧道洞口中心与接收点的距离,m。
当动车组部分驶出隧道时,混响特性需考虑洞口自由扩散边界条件影响。假设某时刻动车组已驶出隧道的长度为x,则隧道内混响噪声来源于位于隧道内的L-x长度噪声源。隧道口处吸声系数等效为1,车尾处界面的吸声系数仍近似为隧道内部平均吸声系数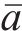
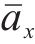
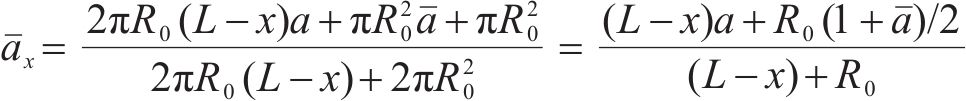
此时式(8)的房间常数R1计算时替换为上述随时间变化的平均吸声系数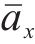
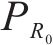
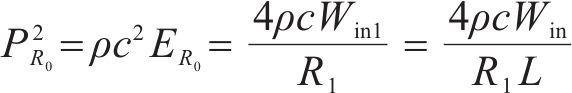
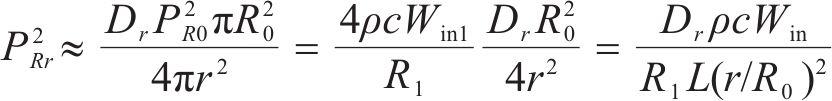
在分别获得隧道洞口直达声Pzd和混响声PRr后,即可通过能量求和的方式获得两者叠加的声压Pz:
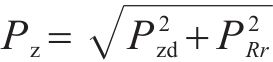
2 隧道洞口噪声仿真研究
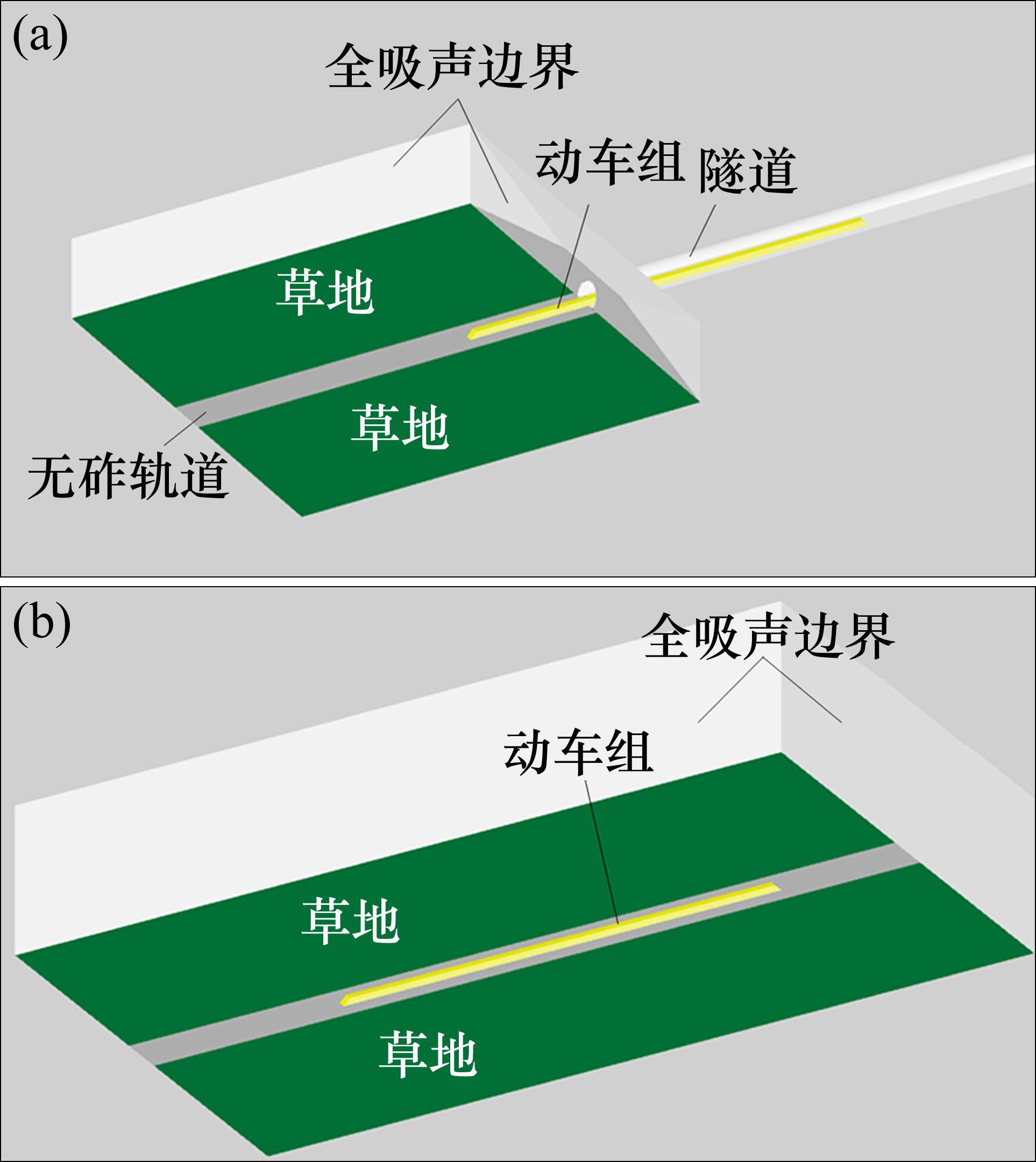
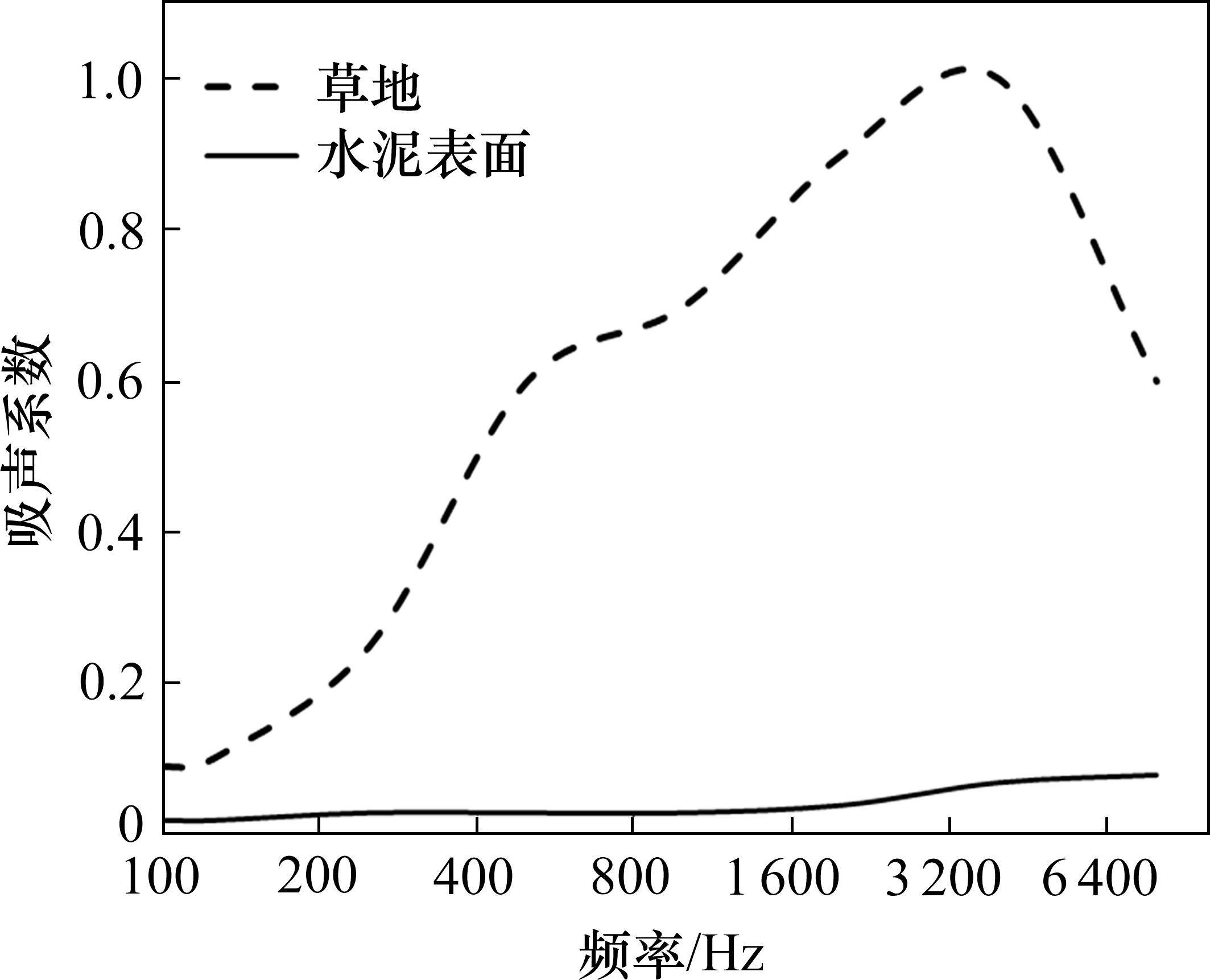
基于几何声学的噪声仿真软件,建立350 km/h高速铁路隧道洞口噪声仿真三维模型,计算动车组行驶至不同位置时对隧道洞口噪声的影响。隧道模型如图3(a)所示,其线路为无砟轨道路基形式,线路及隧道壁等均为水泥材质,隧道外线路两侧为草地,所用软件的材料参数数据库中提供了典型草地及水泥表面的吸声系数,见图4,可在仿真模型中直接调用。动车组设为长200 m、宽3 m、高4 m的长六面体,车体表面均设为吸声系数为0的全反射边界。为模拟隧道外噪声自由传播条件,三维模型中其余边界面均设置为吸声系数为1的全吸声边界。为对比分析隧道与明线段噪声影响差异,同时建立路基段噪声的对比仿真模型,其线路形式及线路两侧边界条件与隧道外环境一致,如图3(b)所示。隧道模型在洞口外35 m、距离线路25 m的轨上3.5 m处设置一噪声接收点,用于提取动车组行驶至不同位置时的声压级并与实测结果比较;明线模型在距离车头前方50 m至车尾后方50 m、距离线路25 m的轨上3.5 m处布设一系列接收点,通过接收点与动车组相对位置变化模拟动车组驶过不同位置时的噪声时域变化。
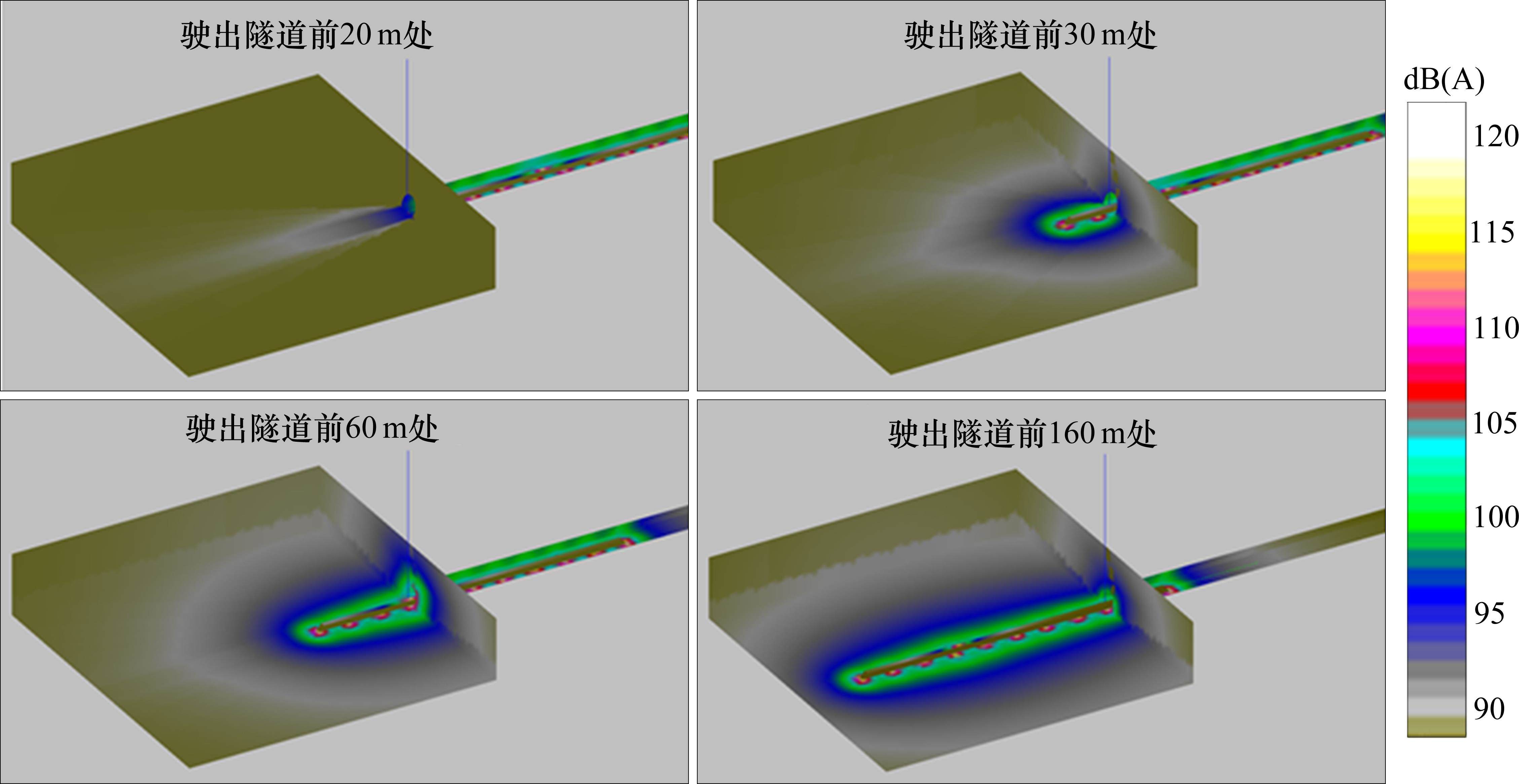
根据文献[10]中350 km/h动车组车外噪声源识别试验获得的各区域声功率分布,将下部区域及车体区域声功率按照动车组长度平均至车长范围内,根据TAN等[1-2]对高速动车组及隧道的1/8缩尺模型在隧道内、外气动噪声的仿真结果,隧道内整车气动噪声源声功率约为明线上的3.2倍,故将动车组位于隧道内部分的气动噪声源加大5 dB(A),其中对明线段下部区域的气动噪声源按照30%进行计算。分别计算动车组驶出隧道前距离隧道洞口50、20和0 m与驶出隧道30、60、90、120、160和200 m以及完全驶出隧道后的噪声分布。部分计算工况的噪声分布如图5所示。
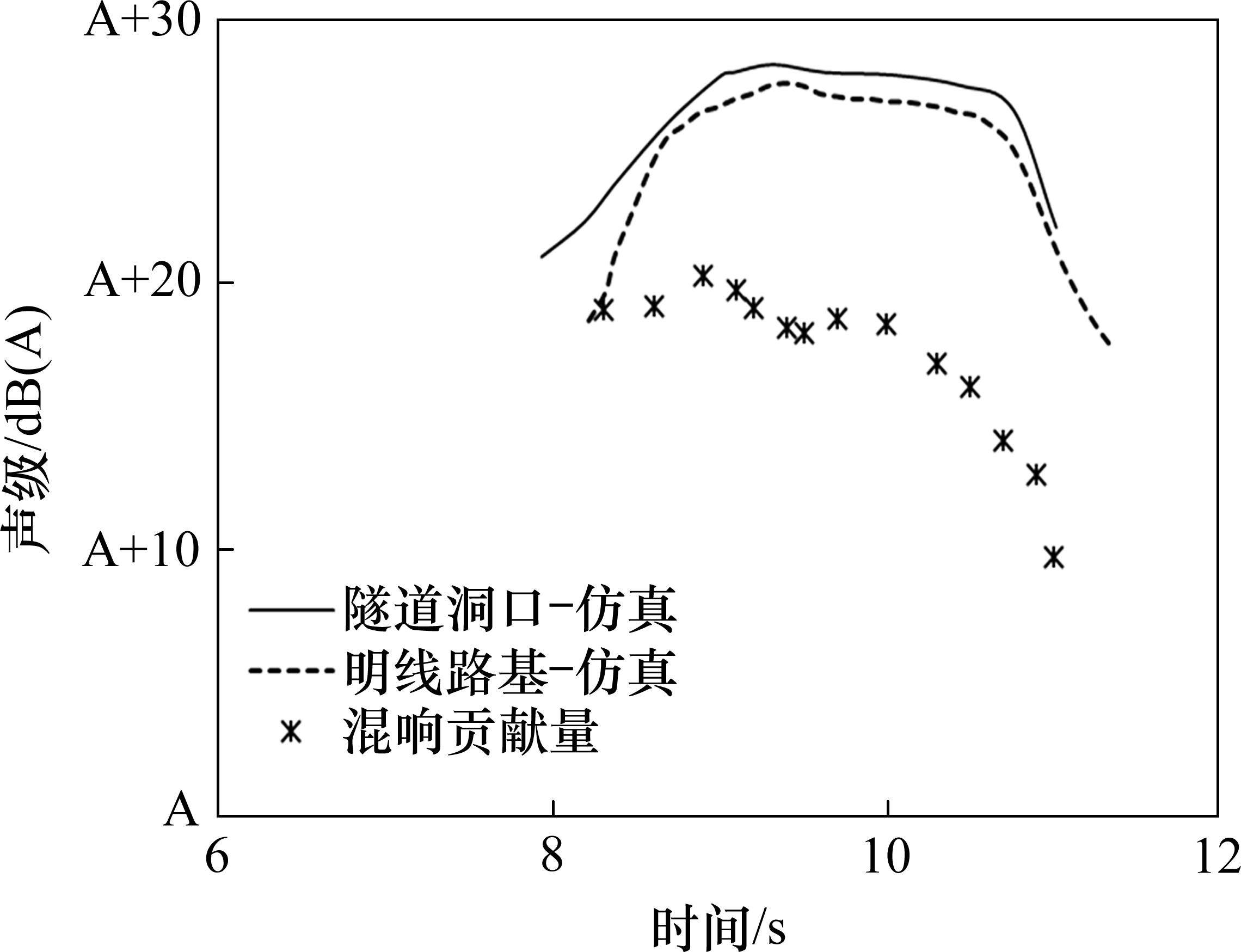
为分析隧道洞口噪声与明线段噪声差异,提取不同计算模型中位于隧道洞口外35 m、距离外侧轨道中心线25 m、高于轨面3.5 m的接收点处的噪声值。通过将位置参数按照速度转化为时间参数,得到动车组驶出隧道时的噪声时域曲线。将隧道洞口与明线段仿真计算结果进行能量差分析,近似得到隧道混响声对洞口总噪声的贡献量(其中也包括了隧道引起气动噪声源增大的影响)。仿真分析结果如图6所示,其中,根据混响声贡献量随时间变化特征可知,动车组驶出隧道过程中混响声先增大后减小,且在动车组大部分车体驶出隧道后混响声快速减小。
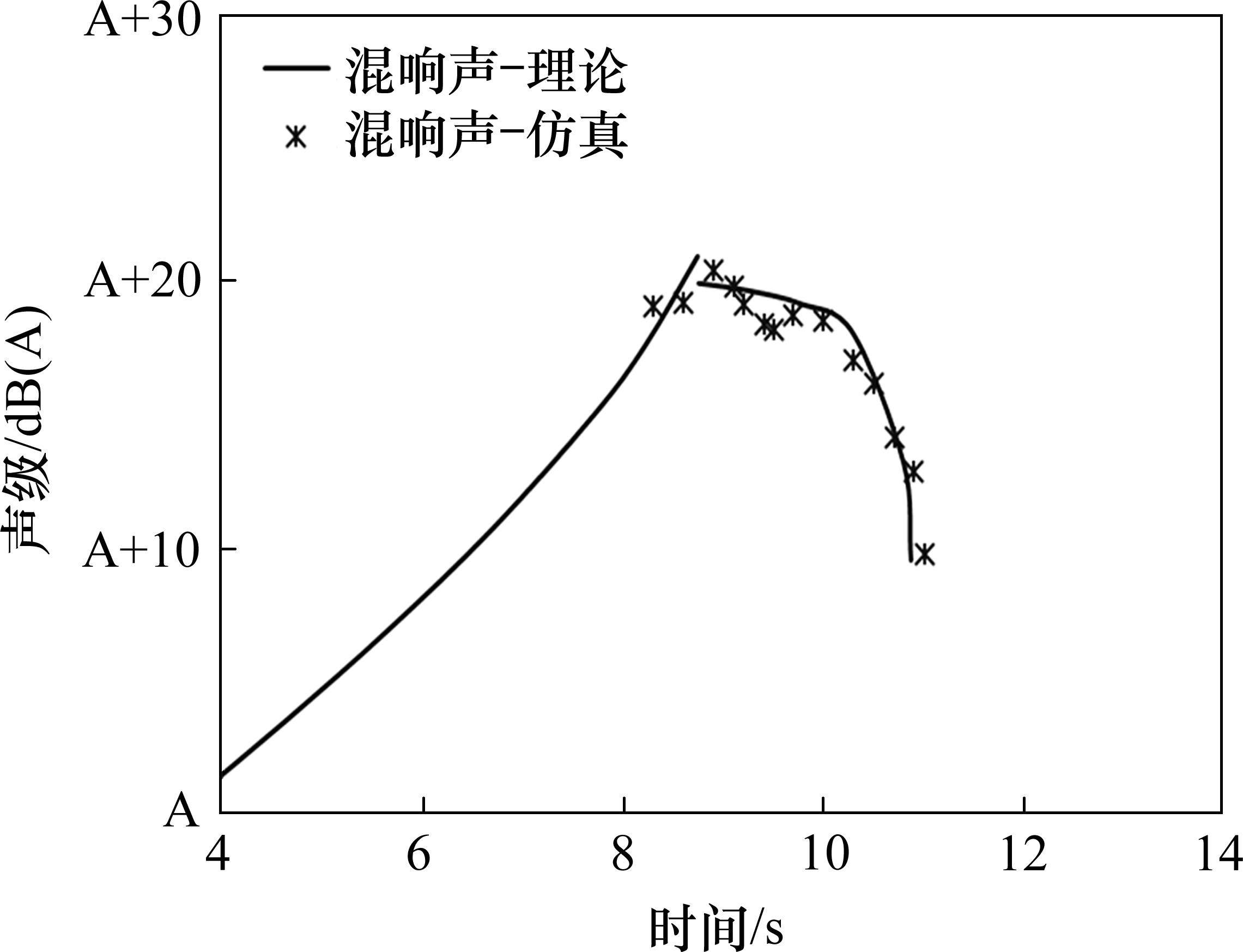
基于上述混响声仿真计算结果,对混响声理论模型的可靠性进行验证。在隧道洞口混响声的理论公式中,水泥结构表面降噪系数设为0.06,与仿真模型中隧道水泥壁面降噪系数一致。认为隧道外近似为自由声场环境,忽略隧道外环境引起的混响声指向性特征,将Dr设为1。利用式(11)和式(14),分别计算得到动车组驶出隧道前和驶出隧道过程中混响声对隧道洞口外噪声接收点处的贡献量,并与仿真得到的结果进行对比,如图7所示,理论计算结果与仿真计算结果在混响声级大小及随时间的变化趋势上均具有较高的一致性。
3 试验验证
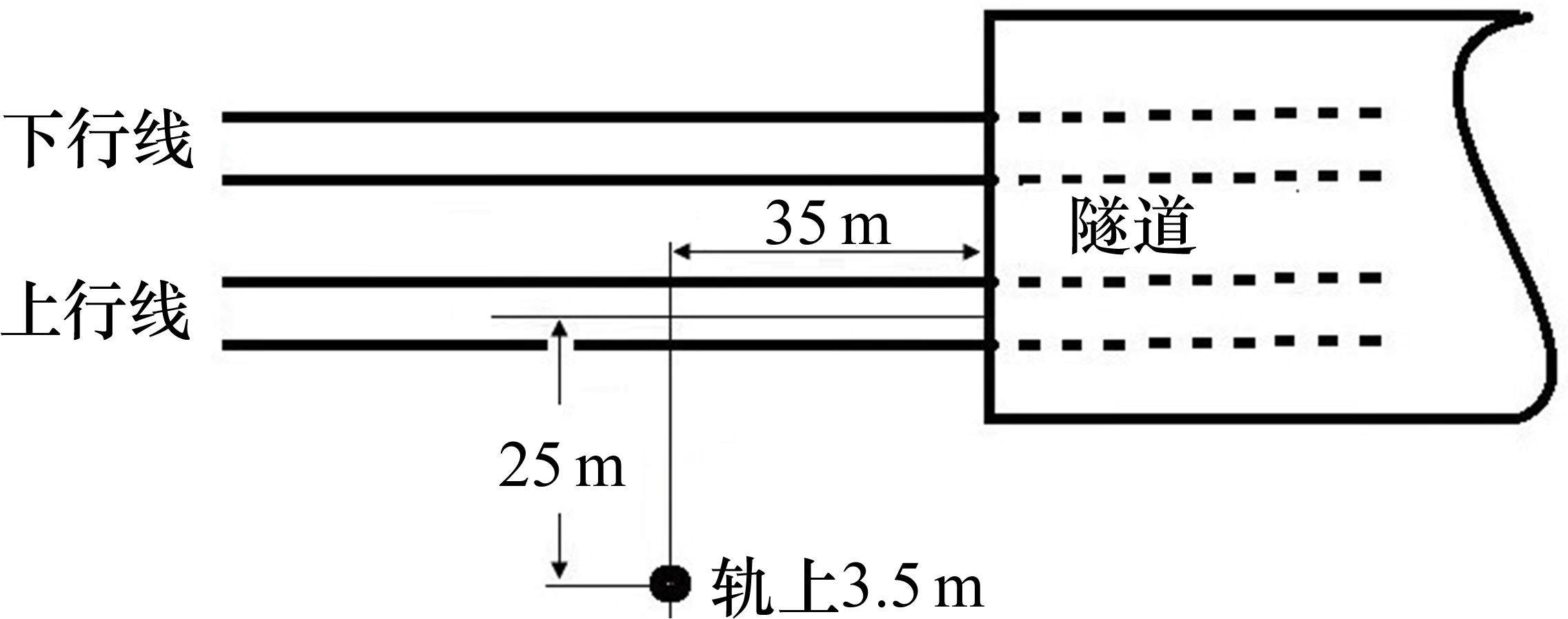
为验证上述理论及仿真分析模型的计算结果可靠性,在我国某设计时速350 km高速铁路隧道洞口开展噪声试验,隧道长度约为7.5 km,隧道内壁半径约为6.5 m,洞口外300 m范围为路基无砟轨道,线路两侧为相对平坦的草地。试验动车组为CRH380A型车,试验速度350 km/h。测点示意图及现场试验环境照片分别见图8和图9,测试传声器布设于上行线一侧隧道洞口外35 m、距离外侧轨道中心线25 m、高于轨面3.5 m处,方向水平指向铁路。测试使用B&K3050数据采集模块和B&K4189噪声传感器,通过拾取动车组驶出隧道的噪声时域信号后按照每0.1 s间隔进行等效声级计算,获得测点处动车组驶出隧道过程的噪声时程曲线。

3.1 理论计算结果与实测数据对比
利用文献[10]的噪声源识别结果,分别对隧道混响声与直达声开展理论计算,并对混响声与直达声的能量叠加后得到总噪声,理论计算的时程曲线与实测结果的对比见图10。
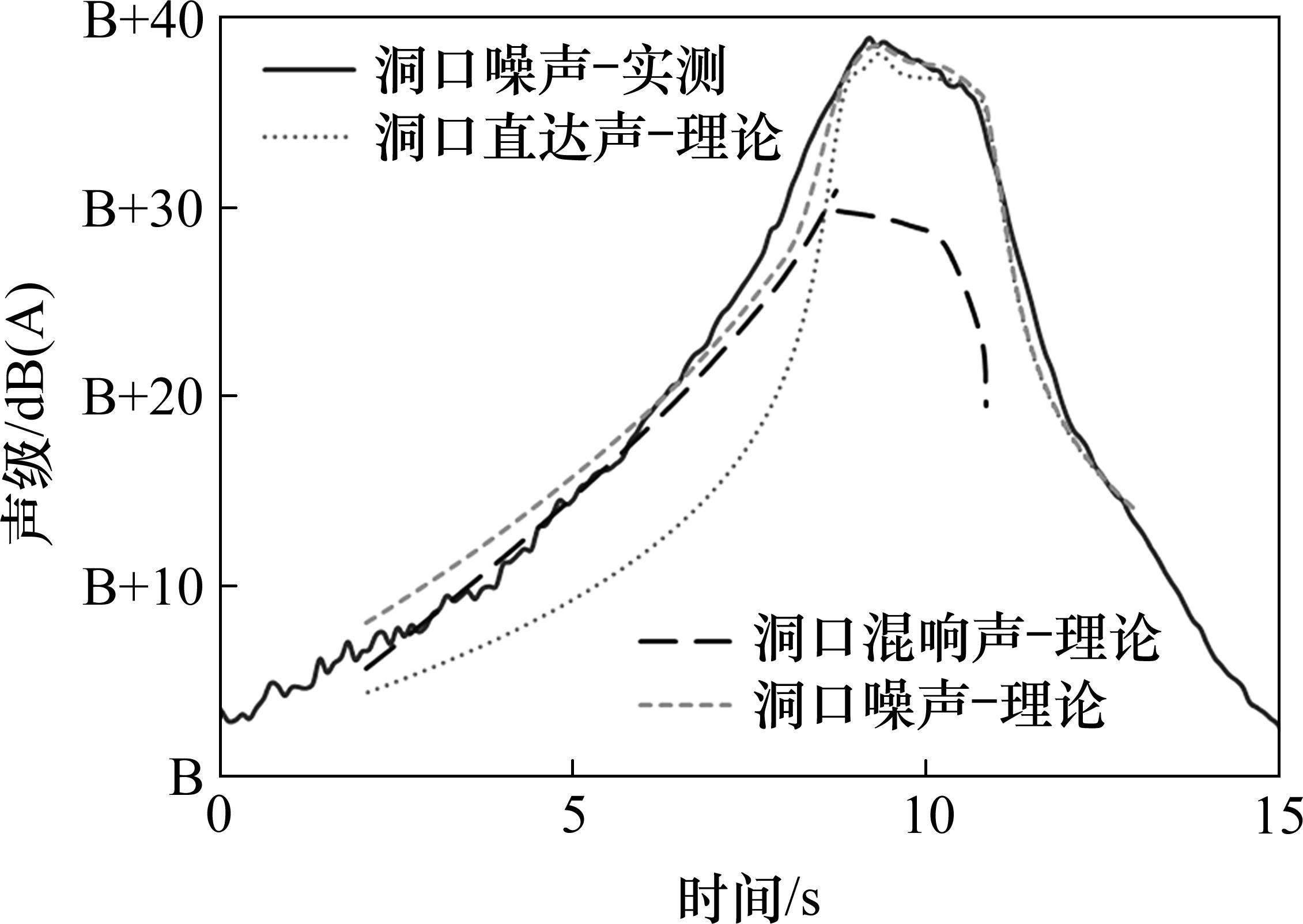
根据理论计算得到的直达声、混响声及总噪声的声级曲线可知,动车组在隧道内行驶时,隧道外测点直达声与混响声均随时间增大,且在一定时段内混响声明显大于直达声,是动车组驶出隧道前洞口噪声大于明线段的主要因素;随着动车组抵近隧道洞口,直达声快速增大并超过混响声;在动车组驶出隧道过程中,测点处混响声随时间呈降低趋势并在大部分车体驶出隧道后迅速减小,该时段直达声高于混响声约7~8 dB(A),受混响声影响隧道洞口总噪声比直达声增大1 dB(A)左右。总体上,动车组驶出隧道洞口过程中噪声时程变化特征的理论计算结果与实测结果基本一致。从列车通过暴露声级(TEL)角度,理论计算结果与实测结果差异为0.8 dB(A),从车头车尾通过测点时段等效声级LA,eq角度,理论计算结果与实测结果差异为0.4 dB(A),2项评价指标差异均小于1 dB(A)。试验验证结果表明本文所提出的隧道洞口噪声理论计算模型是准确可靠的。
3.2 仿真计算结果与实测数据对比
对图6中明线路基段和隧道洞口的仿真结果与实测结果进行对比,如图11所示。隧道洞口仿真结果与实测结果吻合度较高,但在动车组驶出隧道洞口的时段存在一定差异,主要表现在2个方面:1) 动车组车头行驶至隧道洞口时实测声级水平最高,并明显大于仿真结果;2) 动车组大部分车体驶出隧道后实测噪声明显小于仿真结果。本文分析认为上述差异主要由2方面因素造成:首先是噪声源的设置与实际噪声源分布不同。根据李晏良等[10-11]噪声源识别试验获得的噪声源强分布云图,受气动效应影响,除受电弓区域外,头车鼻锥至排障器以及第1转向架区域是沿车体方向源强显著较大的位置,而仿真模型将轮轨及车体区域的声功率按长度进行平均,未考虑声源分布不均衡的影响;其次是仿真结果为动车组驶至不同位置时的噪声稳态计算结果,与实际工况下噪声瞬态变化特征有所不同。当动车组后半段驶出隧道洞口时,仅隧道内小部分车体的噪声源会产生混响声,且该部分混响声会因动车组的快速移动以及在洞口处的扩散而减小,因此仿真计算得到的稳态混响声会大于实际混响声,图11中实测隧道洞口噪声曲线与仿真的路基明线段噪声曲线在t=10 s后(动车组大部分车体已驶出隧道)的时段具有较高的一致性,也从侧面反映了动车组后半段驶出隧道时混响声仿真结果偏大的问题。
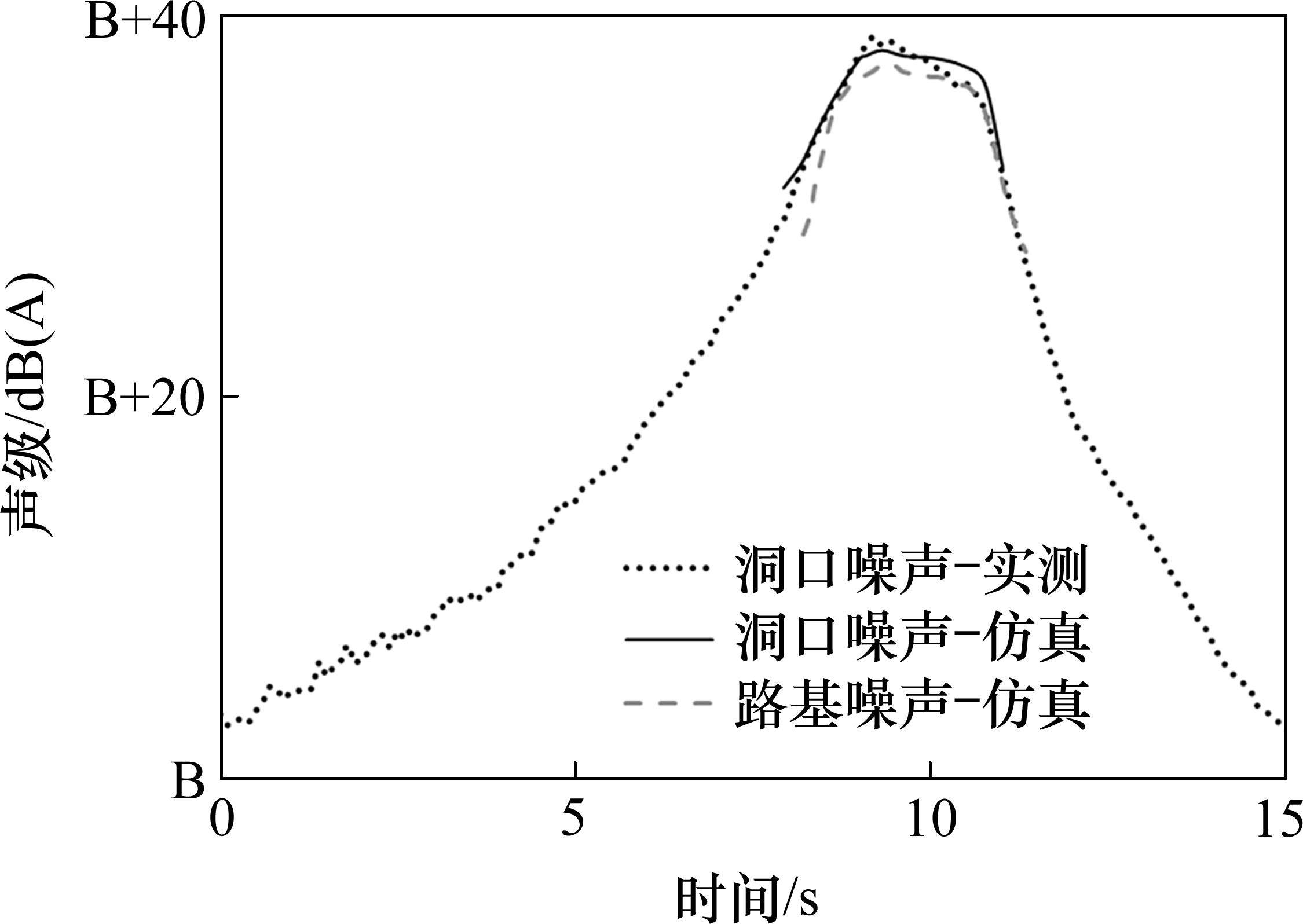
虽然动车组驶出隧道过程中仿真与实测结果时域曲线有一定差异,但从声能量统计平均的角度,对于列车通过暴露声级(TEL)、车头车尾通过测点时段等效声级(LA,eq)2项指标,仿真结果偏大均不超过0.5 dB(A),对于声能量等效平均的参数,隧道洞口仿真计算的准确度也满足工程应用需求。
4 结论
1) 建立基于统计声学的高速铁路隧道洞口混响声理论模型,结合高速铁路多等效声源直达声预测方法,提出了高速铁路隧道洞口噪声理论计算模型,实现对直达声和混响声贡献量的解析,得到直达声和混响声对隧道洞口总噪声影响的时变特征,经现场试验验证,理论与实测隧道洞口噪声时变特征基本一致,TEL及LA,eq计算误差在1 dB(A)以内,该理论分析模型为隧道洞口噪声的快速预测计算提供了一种新方法。
2) 建立基于几何声学的隧道洞口噪声仿真模型,研究动车组行驶至不同位置时对隧道洞口噪声影响,与现场试验结果的对比显示,受声源分布特征的影响,在动车组前半段驶出隧道时噪声仿真结果偏小;在动车组后半段驶出隧道过程中,基于稳态仿真的混响声结果偏大导致总噪声仿真结果偏大。经现场试验验证,TEL及LA,eq仿真计算结果比实测结果大0.5 dB(A)以内。
3) 理论与仿真结果均表明,动车组驶出隧道前,隧道洞口混响声贡献量呈增大趋势,动车组驶出隧道过程中混响声贡献量呈减小趋势,并当大部分车体驶出隧道后混响声快速降低。在动车组驶出隧道前,隧道洞口附近噪声以混响声为主,在动车组驶出隧道过程中,以已驶出隧道的声源产生的直达声为主。
4) 本文隧道洞口噪声理论计算模型和几何声学仿真模型计算误差均满足隧道洞口声环境分析和预测需求;虽然理论模型计算误差略大于仿真模型,但计算效率更高,且能够快速解析直达声和混响声的影响参数及变化规律,对于分析隧道洞口噪声变化机制、针对不同噪声研究相应控制措施具有重要指导意义。
李志强,王晨歌,郑撼等.高速铁路隧道洞口噪声理论计算方法研究[J].铁道科学与工程学报,2025,22(03):921-929.
LI Zhiqiang,WANG Chen’ge,ZHENG Han,et al.Theoretical calculation method of noise around portal of high-speed railway tunnel[J].Journal of Railway Science and Engineering,2025,22(03):921-929.

