高速道岔作为轨道系统三大薄弱环节之一,其设备状态与动车组行车安全和乘客乘坐体验直接相关,因此在线路日常运营中需要对道岔区段状态进行长期跟踪监测。道岔结构复杂,养护维修难度较高,工务部门检养修工作量主要集中在道岔位置。目前对高速道岔的状态检查主要依赖人工静态检查。这种方式检测效率较低且对人工经验依赖较高。除人工静态检查手段外,依托高速综合检测列车的动态检测手段在铁路基础设施状态监测中发挥着愈发重要的作用。挖掘海量动态检测数据特征,对认识掌握高速动车组振动规律、开展基于车辆动态响应的轨道状态辅助评价等都具有十分重要的意义[1-2]。高速动车组通过道岔区段时,轮对需要完成从基本轨到尖轨位置的运动过渡,其运动轨迹将在尖轨与基本轨之间切换,相较于区间线路,高速道岔具有更为复杂的结构设计[3]。随着服役时间的增加,尖轨降低值[4-6]、轨道几何状态[7-8]、道岔区轨面短波不平顺[9]、因钢轨磨耗带来的道岔区作用廓形改变[10-11]等问题逐渐凸显,使得高速动车组过岔时运动稳定性降低,横向平稳性不良问题发生概率随之增高[12],严重时还将出现脱轨倾覆[13]。动车组过岔时的运动性能与道岔当前状态直接相关[14-17]。道岔当前状态反映出道岔服役过程中的状态变化,其也与道岔理论设计初始状态息息相关。通过速度、轨下结构、道岔类型、辙叉号等因素均会影响道岔设计参数,使得不同类型道岔初始状态间存在差异,最终表现为动车组在通过不同类型道岔时可能具有不同的车辆动态响应特征[18-22]。根据现有研究成果不难得出以下结论:动车组通过道岔区段时,受多种复杂因素耦合作用,车体处横向振动将呈现出不同表现形式。这需要设计多个合理有效的观测指标从不同角度科学、合理地定量描述车体横向加速度数据特征,实现对典型工况进行有效剥离;结合现场实际情况,分析其形成原因,探索动态响应数据与轨道系统的映射关系,以期实现基于车辆动态数据的基础设施状态“检养修”闭环。目前《高速铁路线路维修管理标准》中对车体横向加速度峰值进行了规定,用以评估动车组通过道岔区段的车体横向振动最大幅值特征。除最大幅值外,动车组通过道岔时车体振动能量、振动序列混乱度、振动频率等也是表征道岔通过性能的重要信息。由于目前相关研究尚属空白,因此亟须开展相关研究,以认识、挖掘、掌握车体横向振动特征与规律。鉴于此,本文提出了车体横向加速度均方根值和车体横向加速度排列熵值2个指标量化道岔区段动车组车体横向振动能量和振动序列混乱度特征。在明确道岔区段车体横向加速度数据选取规则基础上,以高速综合检测列车采集到的车体横向加速度为研究对象,探讨了高速动车组通过当前铺设量最大的1/18高速道岔时车体横向振动规律。由于含有局部毛刺成分的异常车体横向加速度数据的排列熵计算结果存在异常干扰了对振动规律的认识,提出了基于小尺度滑动标准差和有效零点数的异常数据识别方法以及基于自适应噪声的完整集合经验模态分解(Complete Ensemble Empirical Mode Decomposition with Adaptive Noise, CEEMDAN)的异常数据修正方法。
1 车体横向振动量化指标
1.1 道岔区车体横向加速度数据选择规则
1/18高速道岔设计长度为69 m,在提取道岔区段车体横向加速度数据时,为保证能够完整提取并保留动车组通过道岔前后的部分振动特征,这里将车体横向加速度的提取长度设置为80+69+80,共计229 m。具体含义为道岔前80 m,道岔全长69 m,道岔后80 m。这主要是考虑到动车组通过道岔时车体可能会出现1 Hz以内的横向振动,为了能够对其进行较为完整的有效捕捉,将岔前岔后距离选择为80 m。
目前高速综合检测列车在车体底板位置装配加速度传感器,通过空间采样方式采集动车组运行过程中车体横向加速度数据,采样频率为4 m-1,即1 m采集4个点。根据上述数据选择规则,1/18高速道岔对应的车体横向加速度序列A={ax},x=0.25×1,0.25×2,…,0.25×N。式中N为916。道岔区数据的自动提取参照文献[5]和[23]进行。
1.2 车体横向加速度量化指标
通过计算车体横向加速度的均方根(Root Mean Square, RMS)和排列熵(Permutation Entropy, PE)用以描述动车组通过道岔区段时车体处横向振动的振动能量特征和振动序列混乱程度特征。
1) 车体横向加速度均方根值计算公式如下。
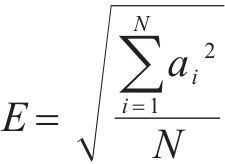
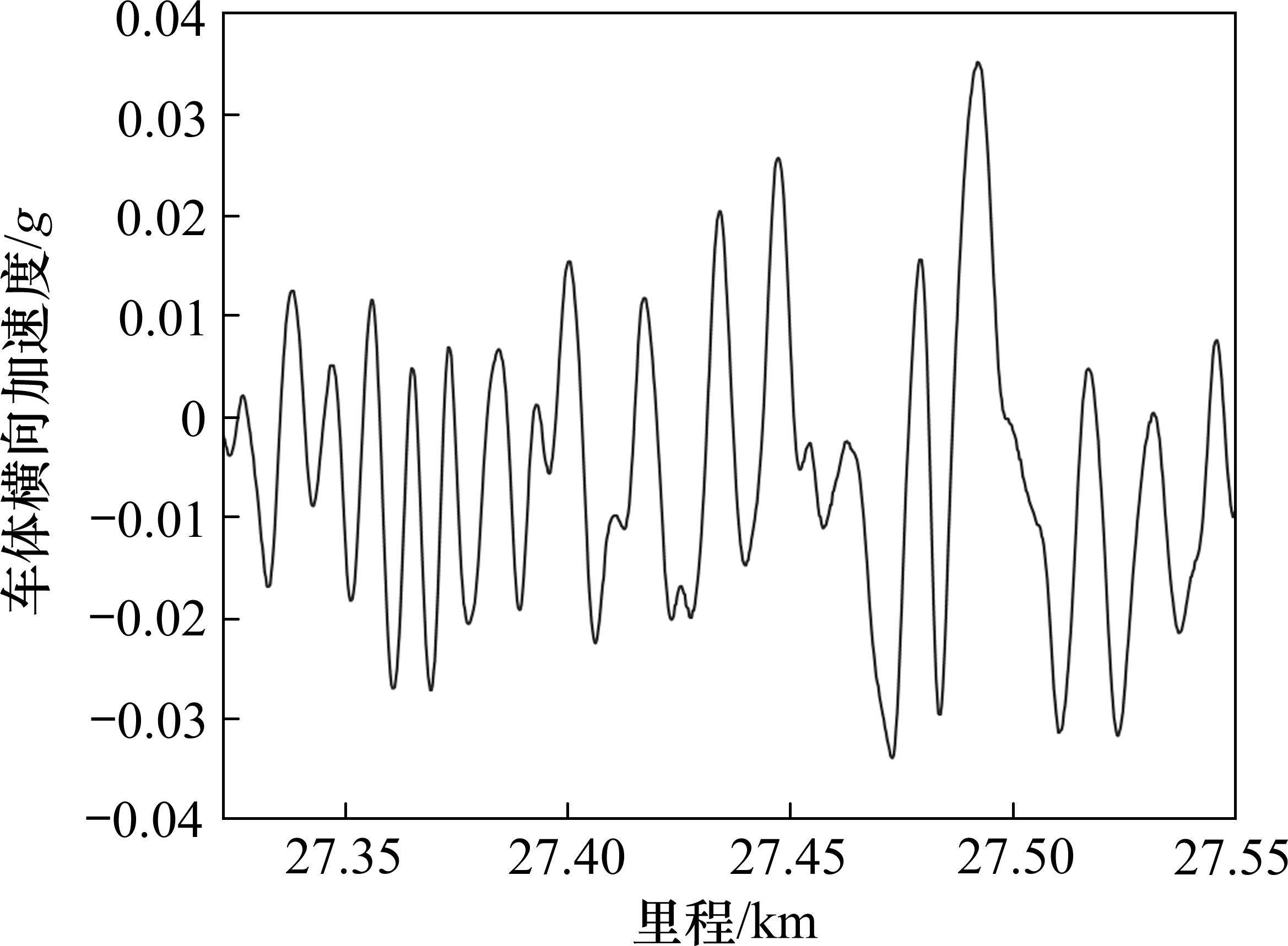
式中:N为道岔区段车体横向加速度序列采样点数;ai为第i个车体横向加速度数据。
2) 车体横向加速度排列熵计算过程如下。
① 计算状态向量Ai。给定相空间维度m,追溯车体横向加速度在道岔区第i个采样点处的系统轨迹,该轨迹即为第i个采样点位置状态向量Ai:
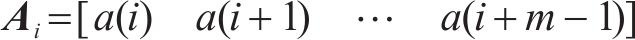
② 相空间重构。给定时间延迟
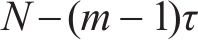
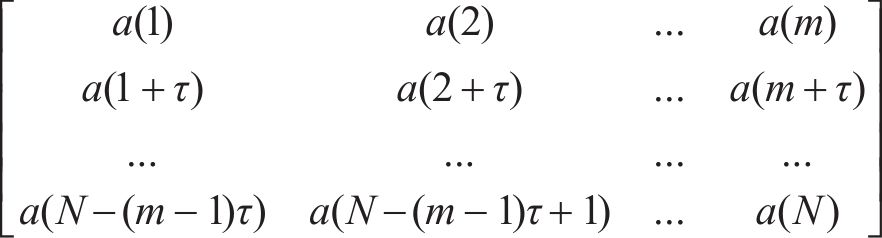
③ 计算排列向量
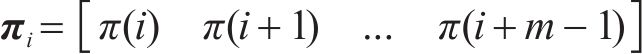
④ 计算不同形式排列向量出现频率。排列向量的表达形式由相空间维度m直接决定,最多存在m!种表达,不同采样点位置对应的排列向量
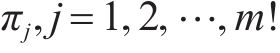
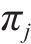

式中:N为道岔区段车体横向加速度序列采样点总个数;m为相空间维度;
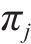
⑤ 计算道岔区段车体横向加速度排列熵。计算公式如下:
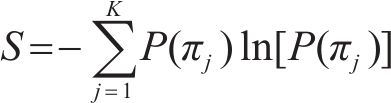
式中:K为不同表达形式排列向量总数;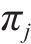
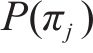
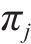
不同表达形式的排列向量出现的概率满足如下关系:
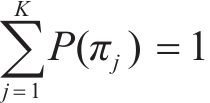
2 异常车体横向加速度数据识别与修正
2.1 异常车体横向加速度数据特征
根据公式(6),排列熵由各排列向量出现频率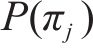
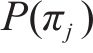
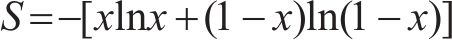
对公式(8)求导,可得:
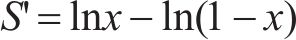
当x=1/2时,S’=0,S有且仅有一个极大值点,即:

当K超过2时,排列熵最大值很难通过公式直接推导,因此这里通过数值模拟方式进行。根据K值和公式(6),随机生成10 000条数据记录,表1为排列熵最大值及其对应P值的数值计算结果。
| K | 最大排列熵值 | 对应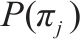 |
|---|---|---|
| 3 | 1.098 6 | 均为1/3 |
| 4 | 1.386 3 | 均为1/4 |
| 5 | 1.609 4 | 均为1/5 |
| 6 | 1.791 8 | 均为1/6 |
| 8 | 2.079 4 | 均为1/8 |
| 10 | 2.302 6 | 均为1/10 |
| 15 | 2.708 1 | 均为1/15 |
通过上述分析可知,当各排列向量等概率出现时,排列熵值取为最大,即:
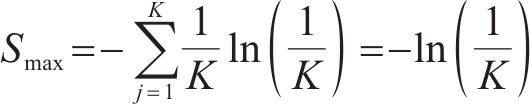
式中:K为表达形式不同的排列向量总数量。
在计算道岔区段车体横向加速度排列熵时,取相空间维度m为3,此时排列向量总数K为6。根据表1,此时最大排列熵值为1.791 8。计算发现,部分道岔车体横向加速度排列熵值明显大于其他道岔且数值接近理论最大熵值。图1为其中一处道岔车体横向加速度原始波形。
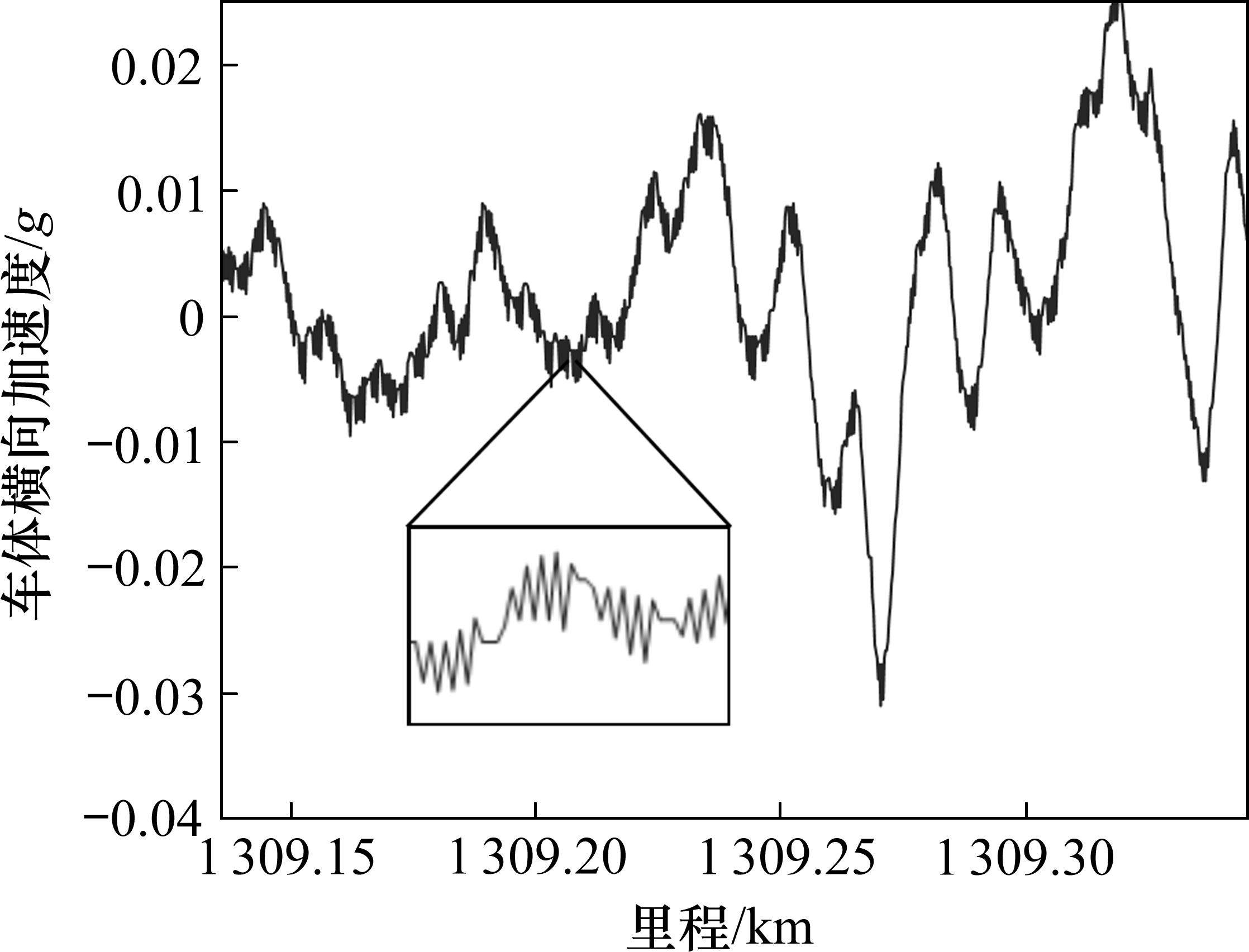
从图1可知,动车组通过该道岔区段时车体横向加速度幅值分布在0~0.03g范围内。但车体横向加速度波形叠加了明显的毛刺成分(图中方框标出),这说明此时采集到的车体横向加速度除了包含动车组通过当前道岔时车体横向振动信息外,还存在毛刺干扰项。由于干扰项的存在,依照公式(4)得到的排列向量结果异常,继而使公式(5)计算得出的各排列向量出现频率结果异常,最终导致道岔区车体横向加速度排列熵值失真。因此在研究动车组通过高速道岔时车体横向振动特性时必须对该类异常数据进行识别与修正。
2.2 基于小尺度滑动标准差和有效零点数的异常数据识别
异常车体横向加速度可看作在正常车体横向加速度基础上叠加了局部毛刺信号,即:
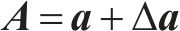
式中:A为异常车体横向加速度序列;a为正常车体横向加速度序列;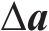
对上述异常车体横向加速度数据的识别可转化为识别车体横向加速度序列是否含有局部毛刺成分。根据观察可知,这种局部毛刺成分具有如下特征:
1) 相较于正常车体横向加速度幅值,该局部毛刺成分幅值较小;
2) 由于该成分的存在,车体横向加速度数据在较小尺度范围内数据波动明显。
基于上述数据特征,提出小尺度滑动标准差σ指标对局部毛刺成分进行识别,具体计算公式如下:
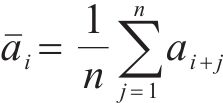
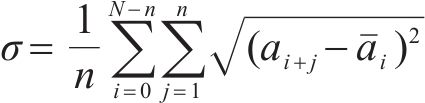
式中:n为小尺度分辨率;i为移动次数;j为小尺度内的当前参与计算的采样点序号;ai+j为第i次移动后小尺度内的第j个车体横向加速度幅值;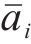
分别计算50组含有局部毛刺的异常车体横向加速度和250组正常车体横向加速度的小尺度滑动标准差,发现将小尺度滑动标准差阈值取为0.05g时可对二者进行有效区分。
对实测道岔区车体横向加速度数据计算小尺度滑动标准差值并以0.05g为阈值进行验证,结果显示取小尺度滑动标准差0.05g为阈值时能够有效识别出含有局部毛刺成分的异常数据。在异常数据外,识别结果中还存在一类数量较少的未含有局部毛刺干扰的数据,典型示例如图2所示。
从图2可以看到,动车组通过该道岔区段时车体横向加速度幅值分布在0~0.04g范围内。相较图1,该车体横向加速度极值点个数多。根据频率计算公式(15)可知,动车组通过该组道岔时车体横向振动频率较高。该类数据的小尺度滑动标准差超过0.05g的原因为:动车组通过该组道岔时车体处的横向振动频率较高,车体横向加速度零点个数较多且零点位置附近数据幅值波动较大使得小尺度标准差值较大。
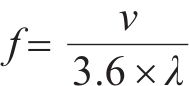
式中:v为运行速度,km/h;λ为波长,m。
为减少计算误差,定义该零点与前一零点之间所包含的车体横向加速度幅值最大值超过0.005g时,该零点为有效零点。计算小尺度滑动标准差筛选得到的异常数据和这类数据的有效零点数,结果如图3所示。
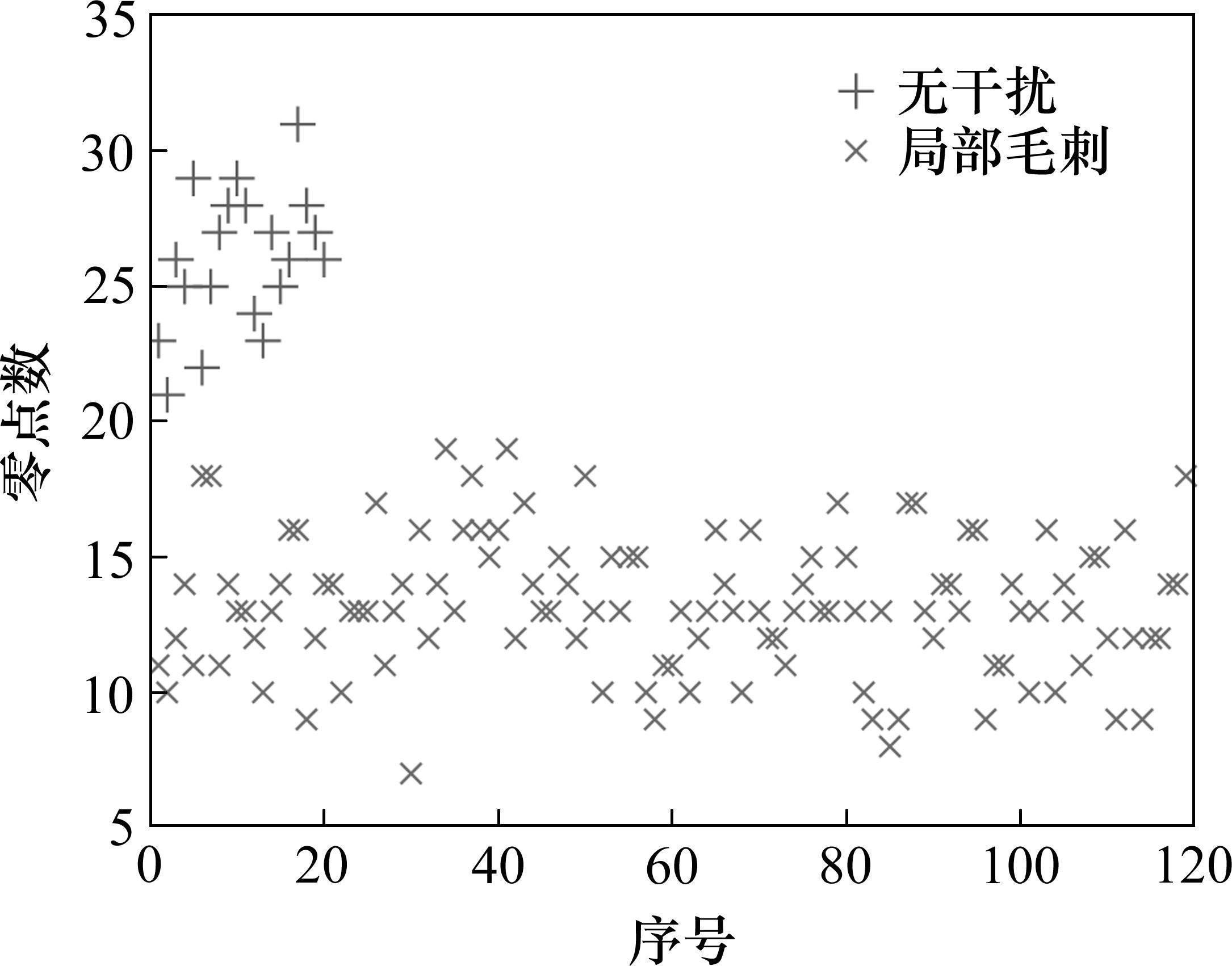
从图3可以看到,无干扰的车体横向加速度零点个数均超过20,主要分布在25~30范围内。存在局部毛刺干扰的车体横向加速度零点个数均小于20,主要分布在10~15范围内。
根据上述分析,可利用有效零点数对小尺度滑动标准差识别结果进行二次判断且判定阈值可选择为20。识别含有局部高频毛刺干扰的异常车体横向加速度数据的具体步骤如下。
1) 计算车体横向加速度小尺度滑动标准差σ;
2) 当小尺度滑动标准差σ大于0.05g时,计算车体横向加速度有效零点数;
3) 若有效零点数小于20,则判断当前车体横向加速度为含有局部毛刺成分的异常数据。
2.3 基于CEEMDAN的异常数据修正
根据公式(12)可知,修正该类异常车体横向加速度数据的关键在于剔除信号中所含有的局部毛刺成分。考虑到异常成分与正常信号在频率上存在较大差异,因此选择能对非稳态信号按频率成分进行自适应分解的CEEMDAN[24]。它在经验模态分解[25](Empirical Mode Decomposition, EMD)基础上进行。相较于同样基于EMD的集合经验模态分解[26](Ensemble Empirical Mode Decomposition, EEMD),CEEMDAN解决了其重建之后白噪声无法完全抵消,加和之后噪声过大的问题,具有更高的分解精度和计算效率。
对车体横向加速度A(x)进行CEEMDAN的步骤如下。
1) 设定添加噪声总次数为N。
2) 构造用于求解第1个本征模态函数(Intrinsic Mode Function, IMF)的第i个新信号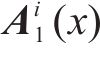
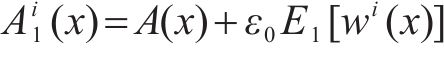
式中:A(x)为原始车体横向加速度序列;wi(x)为第i次添加的服从标准正态分布的白噪声序列;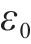
3) 对新生成的每个新信号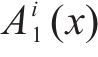
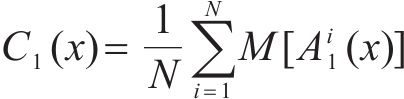
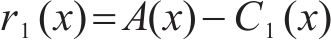
式中:M(∙)为通过EMD算法产生的局部平均值函数;N为添加噪声总次数;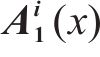
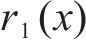
4) 依照公式(19)构造用于求解第m个IMF的第i个新信号Ami(x),最终得到N个新信号。
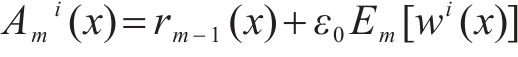
式中: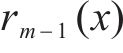
5) 对新生成的每个信号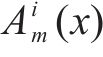
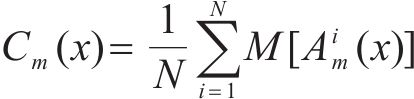
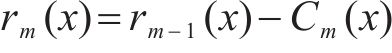
式中:Ami(x)为用于求解第m个IMF时新生成的第i个信号;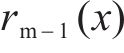
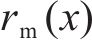
6) 原始车体横向加速度最终被自动分解为K个IMF和一个残余项。
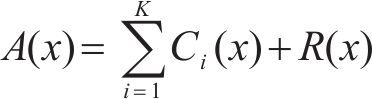
式中: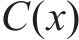
进行CEEMDAN前须预先设置添加噪声总次数为N和信噪比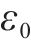
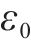
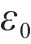
基于CEEMDAN的异常车体横向加速度数据修正步骤如下。
1) 对异常车体横向加速度做CEEMDAN,得到K个IMF和一个残余项;
2) 对K个IMF分别计算功率谱密度并将功率谱密度最大值对应频率记为振动主频Fi;
3) 判断第i个IMF振动主频Fi是否小于20 Hz。若小于20 Hz,记为有效信号;
4) 叠加有效信号,得到修正后的车体横向加速度。
对图1所示异常车体横向加速度信号进行修正,所得结果如图4所示,图4(a)为修正前原始信号,图4(b)为利用提出的方法进行修正得到的结果。
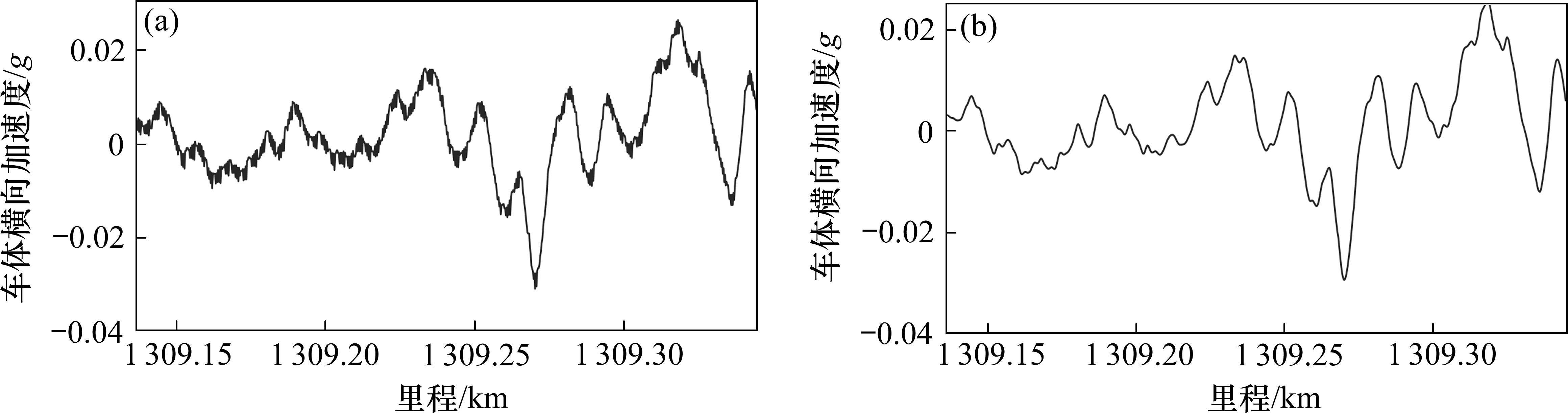
从图4可以看出,经过所提出的方法修正后的车体横向加速度信号中既保留了原始信号中的有效成分并有效剔除了带来干扰的局部毛刺成分。
利用所提出的识别方法对高速综合检测列车以直向且速度超过100 km/h通过道岔时的28 000组数据进行分析,共计得到96组异常数据,异常率为0.34%。对96组含有局部毛刺成分的异常车体横向加速度进行修正后计算排列熵值并与修正前的排列熵值进行对比,修正前后对比情况如图5所示。
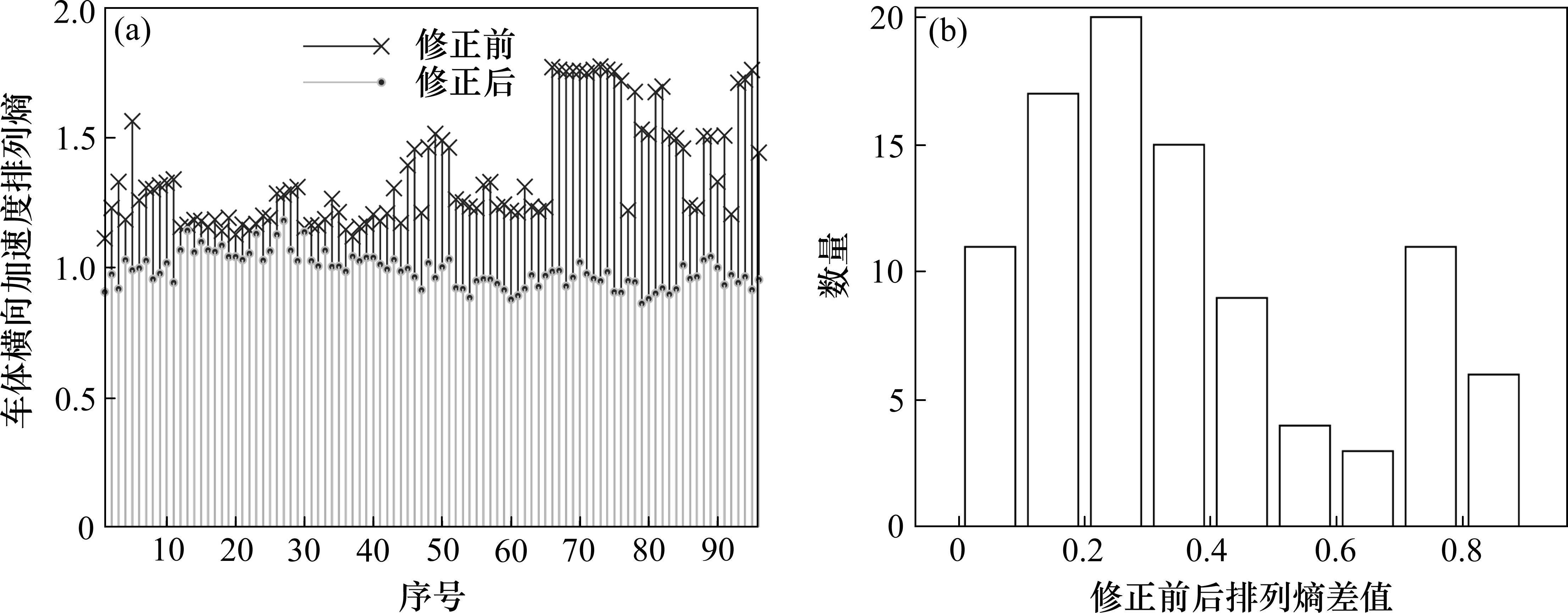
根据图5(a),修正前异常车体横向加速度排列熵值较大,均超过1.20,部分区段超过1.75,接近理论最大排列熵值。修正后车体横向加速度排列熵值均小于1.18,其中55处道岔修正后排列熵值小于1.0,修正后每组道岔对应车体横向加速度排列熵值均有所下降。根据图5(b),修正后车体横向加速度排列熵值下降明显,部分异常数据修正后排列熵值降低超过0.8;68处道岔修正后排列熵值降低超过0.2,降幅超过15%。这表明,局部毛刺成分明显干扰了排列熵的计算结果,对其进行识别与修正是必要的。
3 车体横向振动特征分析
按照轨下结构、通过速度、道岔类型对1/18高速道岔进行分类后,对全路铺设数量最多的5类1/18高速道岔[6]分别计算动车组通过时车体横向加速度均方根值和排列熵值并计算相应累积分布,结果如图6所示。其中参与分析的250(不含)~350 km/h管理标准道岔的通过速度不低于250 km/h,200~250 km/h管理标准道岔的通过速度不低于180 km/h。
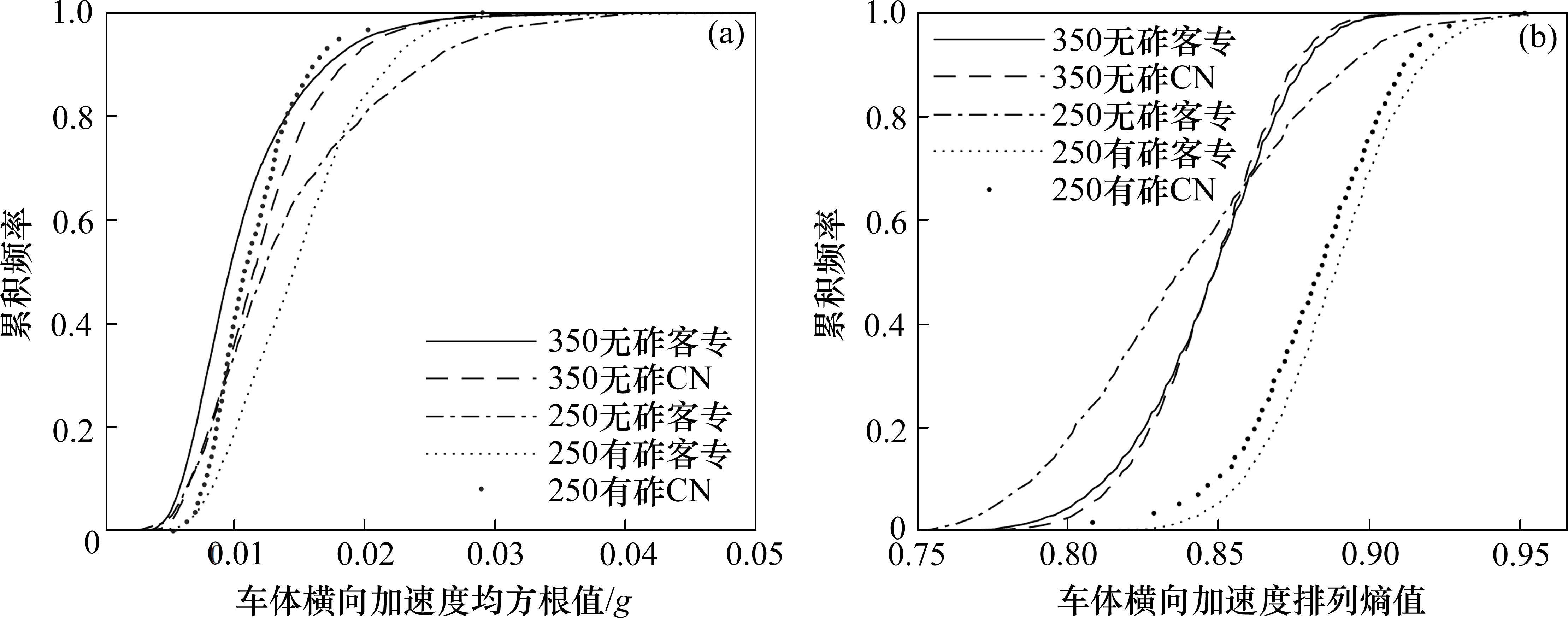
从图6(a)可以看到,动车组在通过各类型各组1/18高速道岔时车体横向加速度均方根值均小于0.05g且累积分布曲线均呈现平滑上升特征。从图6(b)可以看到,动车组在通过各类型1/18高速道岔时车体横向加速度排列熵值均分布在0.75~1.00范围内。此外各类型道岔对应的排列熵累积分布曲线均呈现S型特征,说明各类型道岔车体横向加速度排列熵值遵循较为明显的正态分布。
对各类型1/18高速道岔不同累积频率对应均方根值、排列熵值进行统计,结果如表2、表3所示。
| 道岔类型 | 350无砟客专道岔 | 350无砟CN道岔 | 250无砟客专道岔 | 250有砟客专道岔 | 250有砟CN道岔 |
|---|---|---|---|---|---|
| 累积概率0.2 | 0.007 0 | 0.008 1 | 0.008 2 | 0.010 1 | 0.008 6 |
| 累积概率0.5 | 0.009 6 | 0.011 5 | 0.012 2 | 0.014 5 | 0.010 8 |
| 累积概率0.95 | 0.019 9 | 0.021 1 | 0.028 4 | 0.024 1 | 0.018 1 |
| 道岔类型 | 350无砟客专道岔 | 350无砟CN道岔 | 250无砟客专道岔 | 250有砟客专道岔 | 250有砟CN道岔 |
|---|---|---|---|---|---|
| 累积概率0.1 | 0.812 3 | 0.816 4 | 0.788 1 | 0.858 0 | 0.849 0 |
| 累积概率0.95 | 0.885 8 | 0.882 0 | 0.905 8 | 0.926 7 | 0.918 7 |
从表2可以看到,各类型道岔在不同累积概率下车体横向加速度均方根值相对大小存在差异。对引起动车组车体最小横向振动能量的20%道岔而言:同等通过速度下,无砟道岔引起的车体横向振动能量小于有砟道岔;对无砟道岔,通过速度更高的高管理速度道岔引起的车体横向振动能量小于通过速度较低的低管理速度道岔;对250(不含)~350 km/h管理标准无砟道岔,客专型道岔引起的车体横向振动能量小于CN型道岔。对引起动车组车体最大横向振动能量的5%道岔而言:同等通过速度下,有砟道岔引起的车体横向振动能量小于无砟道岔;对无砟道岔,通过速度更高的高管理速度道岔引起的车体横向振动能量小于通过速度较低的低管理速度道岔;对250(不含)~350 km/h管理标准无砟道岔,客专型道岔引起的车体横向振动能量小于CN型道岔。其中有砟道岔优于无砟道岔主要原因是参与统计的无砟道岔数量相对较少,数据离散程度较大。不同类型道岔累积分布曲线的累积概率增长幅度差异明显,这反映出同一类型道岔时所对应的车体横向加速度均方根值数据内部的离散程度不同。这主要与每组道岔运用过程中的状态变化有关。上述分析说明道岔类型是引起动车组车体横向振动能量差异的因素之一。而当前道岔的服役时间、通过总重等因素是更为关键的影响因素。
结合图6(b)和表3可知,在不同的累积概率下,200~250 km/h管理标准有砟各类型道岔车体横向加速度排列熵值均大于200~250 km/h管理标准无砟道岔,也明显大于250(不含)~350 km/h管理标准无砟各类型道岔。这说明有砟道岔引起的车体加速度振动序列混乱程度大于无砟道岔。对累积分布曲线的累积概率增长幅度进行分析,250(不含)~350 km/h管理标准无砟客专型道岔、250(不含)~350 km/h管理标准无砟CN型道岔、200~250 km/h管理标准有砟客专型道岔、200~250 km/h管理标准有砟CN型道岔4类道岔增长幅度较为接近,200~250 km/h管理标准无砟客专型道岔明显较小。这说明200~250 km/h管理标准无砟客专型道岔对应的车体横向加速度排列熵值离散程度较大。上述分析说明不同道岔类型引起的动车组车体横向加速度序列混乱程度存在明显差异。
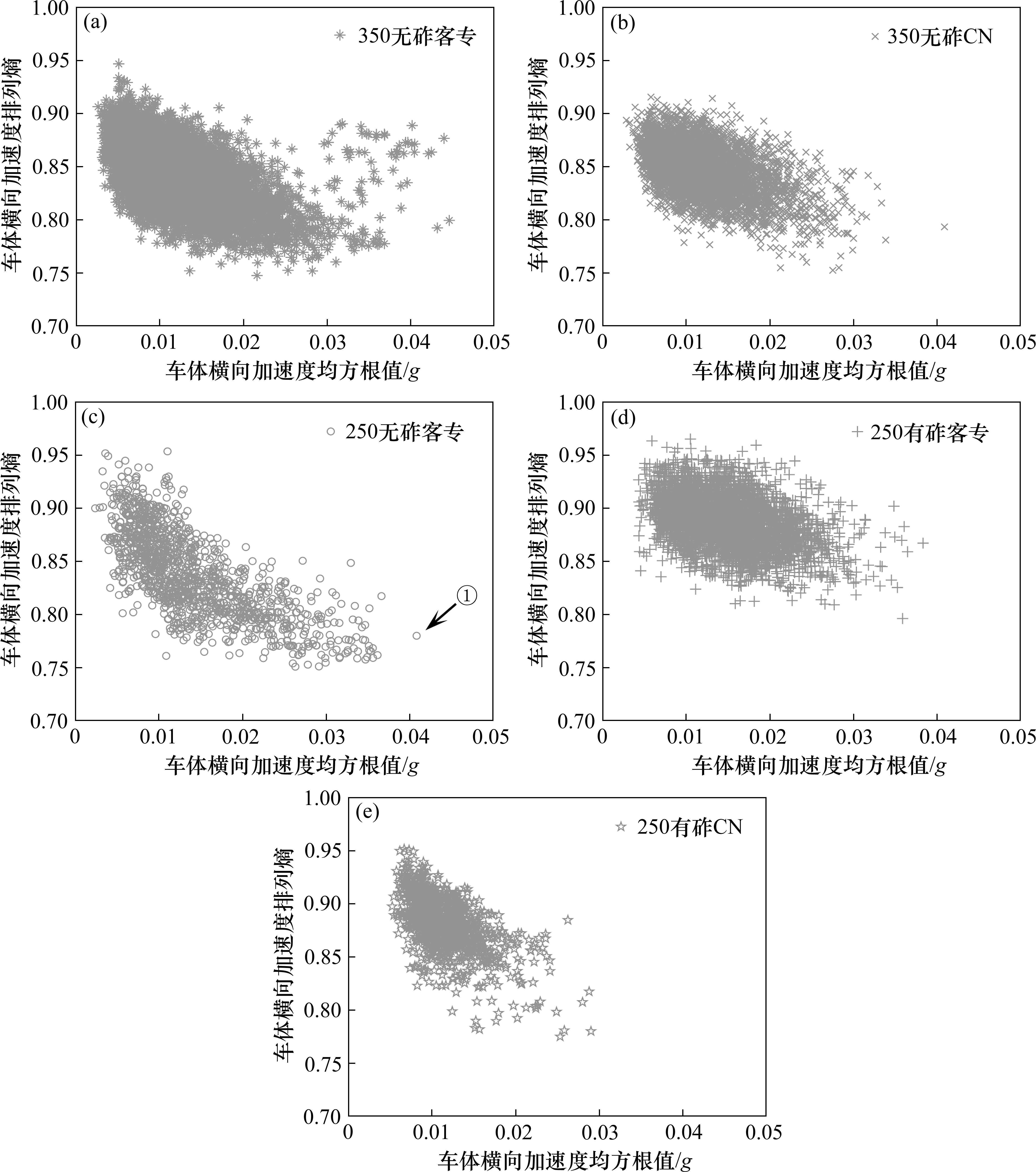
绘制各主型1/18高速道岔车体横向加速度均方根值与排列熵散点图,结果如图7所示。各集中分布区域对应的数值如表4所示。
| 道岔类型 | 350无砟客专道岔 | 350无砟CN道岔 | 250无砟客专道岔 | 250有砟客专道岔 | 250有砟CN道岔 |
|---|---|---|---|---|---|
| 均方根 /g | <0.030 | <0.022 | <0.025 | <0.027 | <0.017 |
| 排列熵 | 0.78~0.91 | 0.80~0.90 | 0.78~0.90 | 0.82~0.95 | 0.85~0.93 |
从图7可以看到,5种主型1/18高速道岔车体横向加速度均方根-排列熵散点图中各点分布较为集中,集中分布区域面积大小存在差异。表4给出了集中分布区域的车体横向加速度均方根值和排列熵值范围。此外,对同一类型不同道岔而言其车体横向加速度均方根值与排列熵值间存在一定的负相关关系,即均方根值越大时排列熵较大概率对应较小数值。这种负相关对应关系在200~250 km/h管理标准无砟客专型道岔中体现最为明显。
这里以高均方根值低排列熵值(车体横向加速度均方根值为0.040 8g,排列熵为0.78)的200~250 km/h管理标准无砟客专型1/18高速道岔(图7(c)中①)为例,图8为车体横向加速度原始波形。
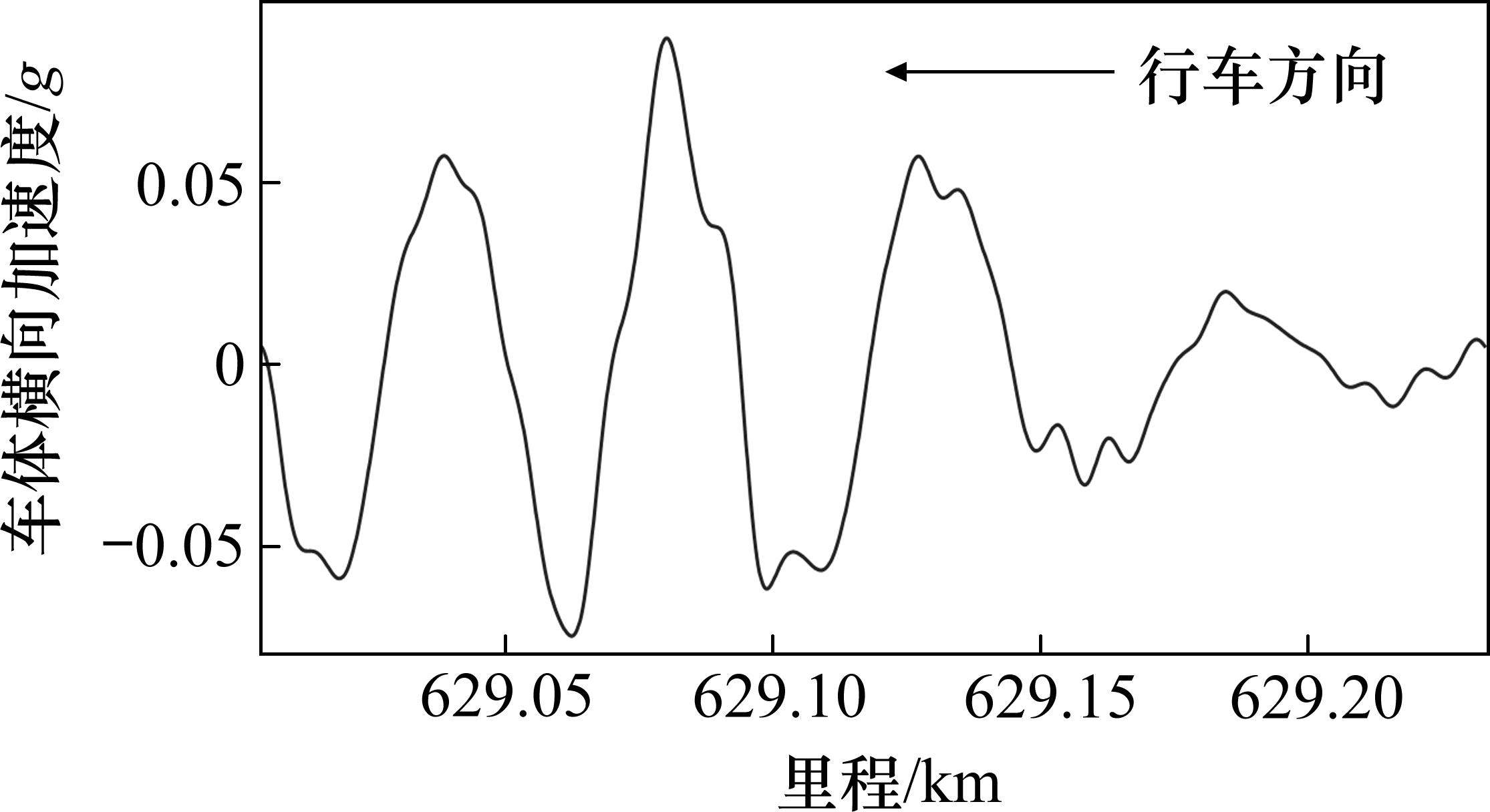
根据图8可知,高均方根低排列熵对应的车体横向加速度波形具有明显谐波特征且车体横向加速度最大幅值超过0.06g;根据公式(15)计算可知此时振动频率约为1.65 Hz。该数据特征与动车组发生低频周期性晃动时的数据特征一致[12]。由此可知,动车组在通过该组道岔时出现了较为明显的低频周期性晃动问题。
4 结论
1) 车体横向加速度含有局部毛刺成分时将会严重影响车体横向加速度排列熵计算结果的准确性。提出的小尺度滑动标准差与有效零点数的2个指标能够有效识别出上述异常数据;应用基于CEEMDAN的数据修正方法可以有效剔除数据中的局部毛刺干扰,保证排列熵值计算结果有效性。
2) 动车组通过主型1/18高速道岔时车体横向加速度均方根值均小于0.05g,车体横向加速度排列熵值分布范围为0.75~1.00。
3) 不同道岔类型引起的动车组车体横向加速度序列混乱程度存在明显差异,有砟道岔引起的车体加速度振动序列混乱程度大于无砟道岔。
4) 不同类型道岔车体横向加速度均方根值与排列熵值均呈现集中分布特征,集中分布区域面积略有差异。其中高均方根值低排列熵值与低频周期性晃动工况对应程度高。
解婉茹,刘金朝,赵钢等.道岔区高速动车组车体横向振动特性分析[J].铁道科学与工程学报,2025,22(01):1-12.
XIE Wanru,LIU Jinzhao,ZHAO Gang,et al.Analysis of the carbody’s lateral vibration characteristic of high-speed emus in turnout area[J].Journal of Railway Science and Engineering,2025,22(01):1-12.

