高速综合检测列车在车体地板位置安装了车体垂向振动加速度采集传感器和车体横向振动加速度采集传感器[1],目的在于实时采集高速综合检测列车通过不同速度等级、不同轨下结构类型、不同轨道区段时的车体振动信息,用以辅助评价线路轨道状态[2-10]。其原理是将车辆系统视为受迫振动系统,将线路轨道状态视为系统输入,将车体动态响应视为系统输出,通过系统输出来反映系统输入剧烈程度,以达到辅助评价线路状态的目的。因此,当所用于辅助评价线路轨道状态的车体垂向、横向振动加速度被当作车辆系统的一种输出形式以反映轨道状态时,若要有效反映轨道状态,就必须保证这部分输出的输入来源为轨道系统(轨道几何状态、轨面短波状态、钢轨作用廓形等)。高速综合检测列车与在役客运动车组同时被编入当前路网运行图中,在高速综合检测列车执行任务期间,会出现与临线动车组相向而行的情形,也就是常说的“会车”。国内外多名学者从不同角度、运用不同分析手段对不同外部状态下的动车组会车特性进行了分析[11-20],结果表明:高速列车交会时,由于气动性能改变,动车组车体横向振动加剧。这与目前高速综合检测列车会车状态下的车体横向加速度数据特性一致:会车发生时,车体横向振动加速度幅值明显增加,大多超过0.06g(高速线路轨道动态质量容许偏差I级管理值),部分位置车体横向加速度幅值甚至超过0.09g(高速线路轨道动态质量容许偏差II级管理值)。动车组会车引起的车体横向加速度幅值增大是真实存在的,但产生原因非线路状态不佳,而是气动效应影响。目前在利用车体横向加速度辅助评价线路状态时,检测人员通过手动方式对这部分超限记录进行删除,以避免误报。但车体横向加速度数据在检测过程中自动存储,会车信息不会体现在原始波形图中。因此在利用车体横向加速度数据分析轨道系统与车辆系统间相互作用关系时,需要对会车区段进行标注。但目前对动车组会车状态下车体横向加速度数据的特征分析还尚属空白。基于此,以高速综合检测列车采集到的车体横向加速度数据为研究对象,通过大量会车数据分析,在挖掘车体横向加速度数据特征、掌握高速动车组会车横向振动特性的基础上,提出一种基于车体横向加速度的动车组会车识别方法。
1 会车状态下车体横向振动特性分析
1.1 波形特征
某CRH380A型高速综合检测列车在250(不含)~350 km/h管理标准线路上以300 km/h速度执行检测任务时,与临线动车组发生会车,会车开始里程为K40+820,会车结束里程为K40+940。临线动车组型号也为CRH380A,列车长度203 m。会车及其前后车体横向加速度原始波形如图1所示,图中虚线框标注位置为会车区段。根据统计分析目前车体横向加速度I级超限常出现在道岔区段。图2、图3分别展示了道岔区段单点型、连续型的车体横向加速度I级超限原始波形。
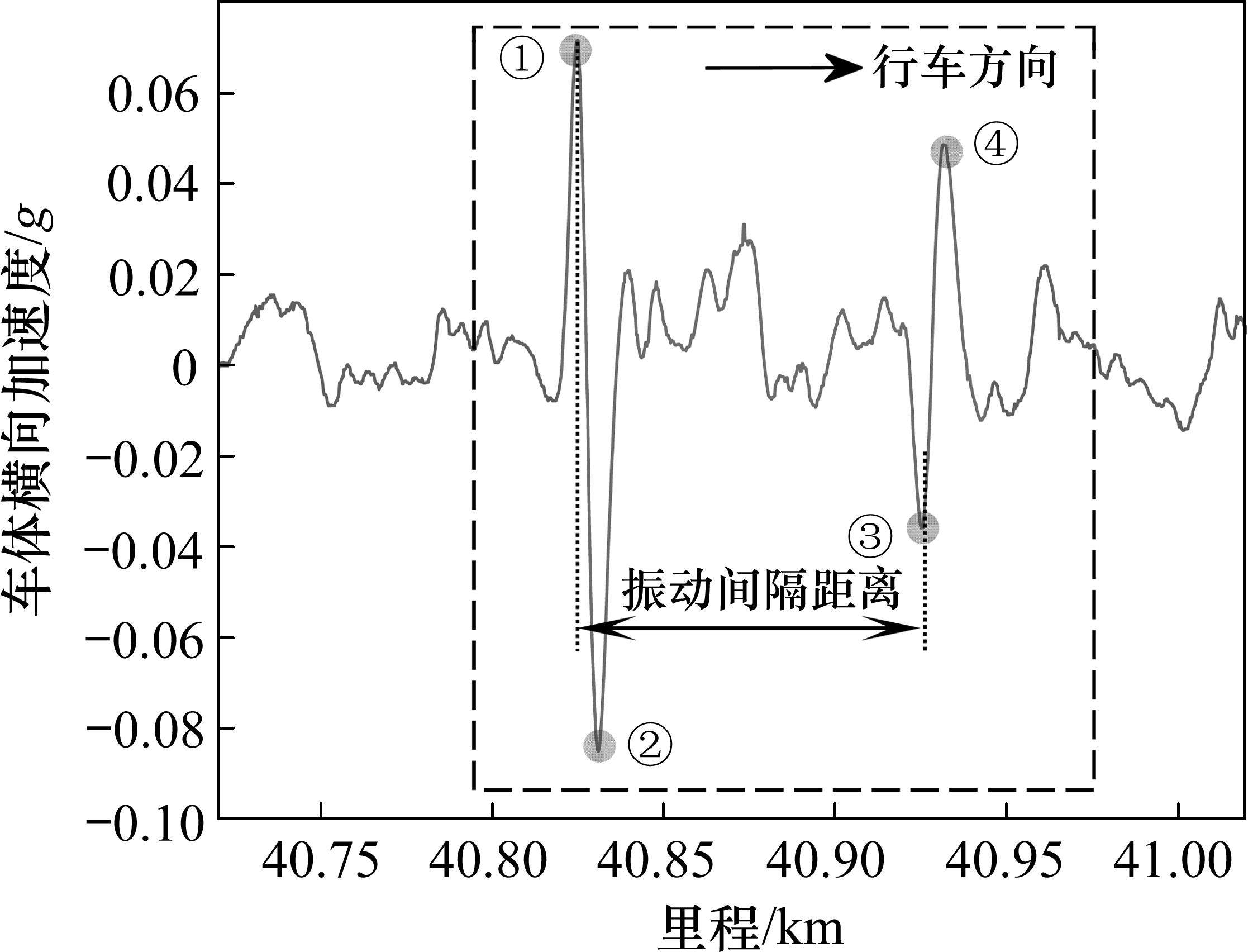
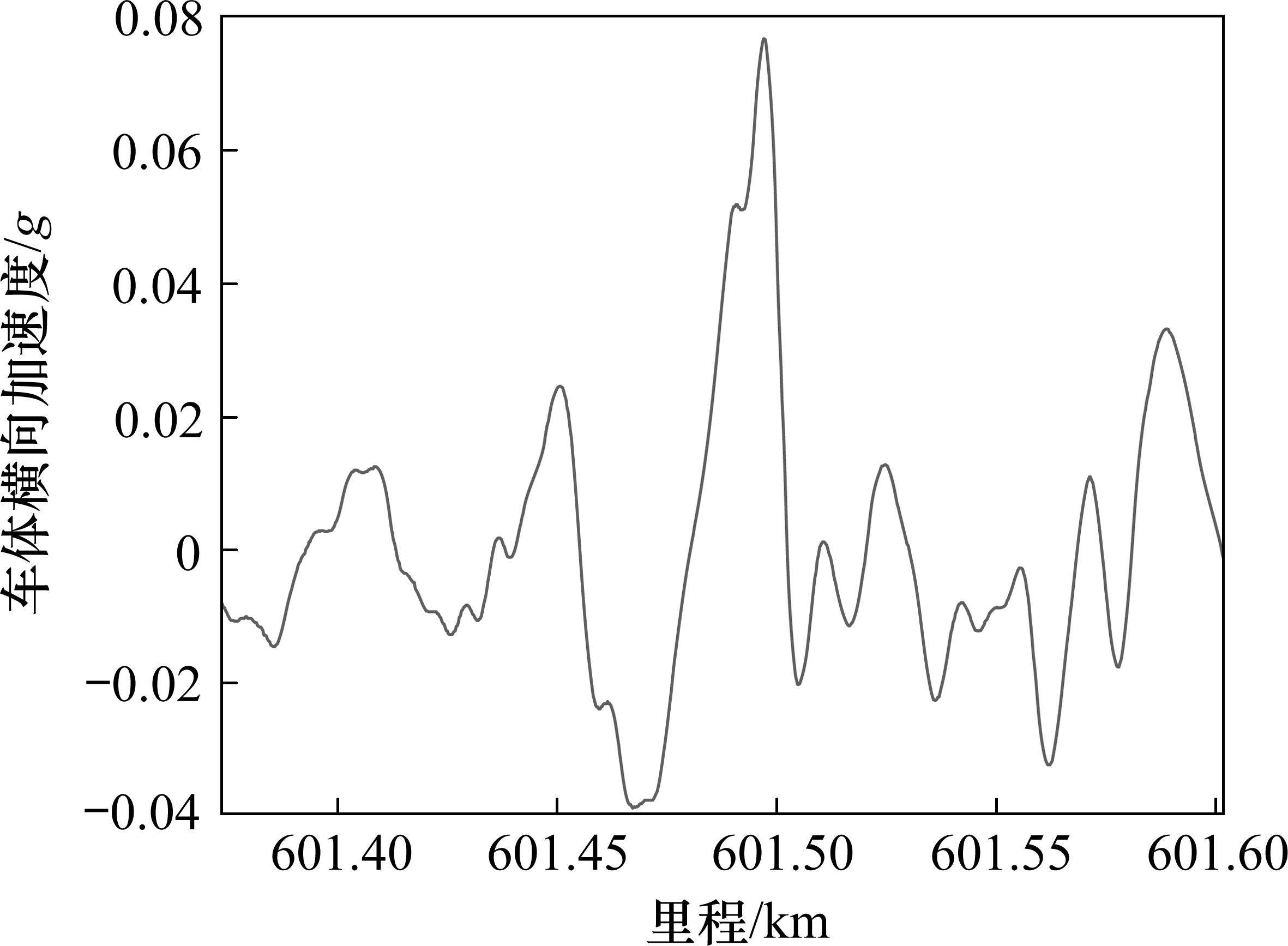
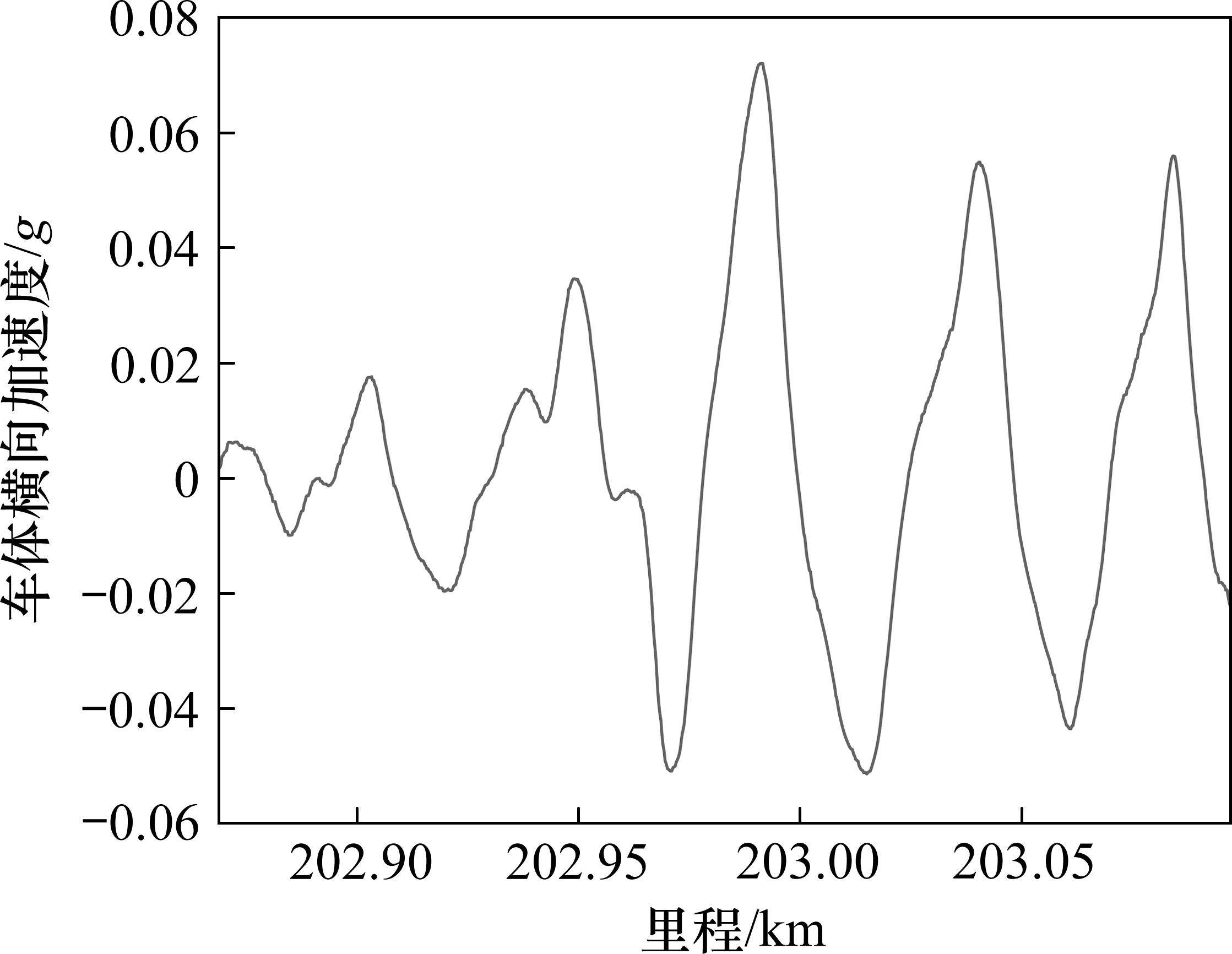
从图1可以看到,发生会车前,动车组横向振动平稳,车体横向加速度幅值范围为0~0.02g,最大位置远小于高速铁路维修管理I级日常保持标准0.06g,这说明动车组车体处横向振动平稳。动车组行驶至K40+820位置时与临线动车组发生会车,此时车体横向加速度幅值迅速增加,达到0.072g(图中①),超过《修规》I级限值(0.06g)。此后动车组车体继续振动,车体横向加速度幅值进一步增大,达到0.085g(图中②),接近II级限值(0.09g)。该次振动中,后峰值点车体横向加速度幅值约为前峰值点的1.18倍。此后动车组迅速恢复平稳。随后第2次横向振动发生,此时距离第1次横向振动发生约为100 m,约为临线动车组列车长度的一半。车体横向加速度幅值迅速增大,达到0.036g(图中③),此后动车组车体继续振动,车体横向加速度幅值进一步增大,达到0.049g(图中④),该次横向振动车体横向加速度幅值并未达到I级超限标准。后峰值点车体横向加速度幅值约为前峰值点的1.36倍。此外还可以看到,动车组车体的2次横向振动方向相反。对比图1与图2、图3可知,虽然动车组会车、经过部分道岔区段时,车体横向加速度幅值均会超过0.06g,但动车组在会车状态下车体横向加速度除幅值外,其他特征明显区别于通过道岔:车体横向加速度存在2个明显谐波振动且振动迅速收敛,即在一定长度范围内共存在4个明显峰值点。
从上述分析中不难发现,会车发生时动车组车体横向振动突然加剧,车体横向加速度幅值急剧增加,达到超过现行修规对车体横向加速度的规定。在线路实际检测中将作为“异常值”被手动剔除。
1.2 统计特征
区别于线路状态不佳引起的车体横向加速度大值偏差,动车组发生会车时,存在4个车体横向加速度峰值点(图1中的①②③④),且各个峰值点间具有比较明确的数量关系。这里对会车状态下各峰值点数据特征进行分析,峰值序号依据峰值点出现时间进行排列。
以该CRH380A型高速综合检测列车运行速度大于150 km/h通过250(不含)~350 km/h管理标准线路时采集到的车体横向加速度数据为研究对象,共得到462处非道岔区的车体横向加速度最大幅值超过0.06g的会车记录,会车发生时动车组的运行速度、运行线路、区段属性(桥梁、隧道、路基)、临线参与会车动车组车型均存在差异。
运行过程中所采集到的车体横向振动加速度的符号代表了动车组车体的振动方向。从图1可以看到,当前会车状态下,第1、第4峰值点符号相同,第2、第3峰值点符号相同。根据振动波形可知,4个峰值点的符号关系可以简化成2类:第1、第4峰值点符号相同或第1、第3峰值点符号相同。表1给出了这462处会车记录中第1峰值点与第3、第4峰值点车体横向加速度的符号对应关系。
| 类型 | 数量 | 占比/% |
|---|---|---|
| 第1、第4峰值点相同 | 462 | 100 |
| 第1、第3峰值点相同 | 0 | 0 |
根据表1可知,不同会车状态下均有第1峰值点与第4峰值点符号相同。这说明会车过程中高速动车组产生的2次横向大幅振动的振动方向相反。
提取462处会车各自第1、第2、第3、第4峰值点处对应的车体横向加速度幅值并绘制相应的累积分布曲线,结果如图4所示。
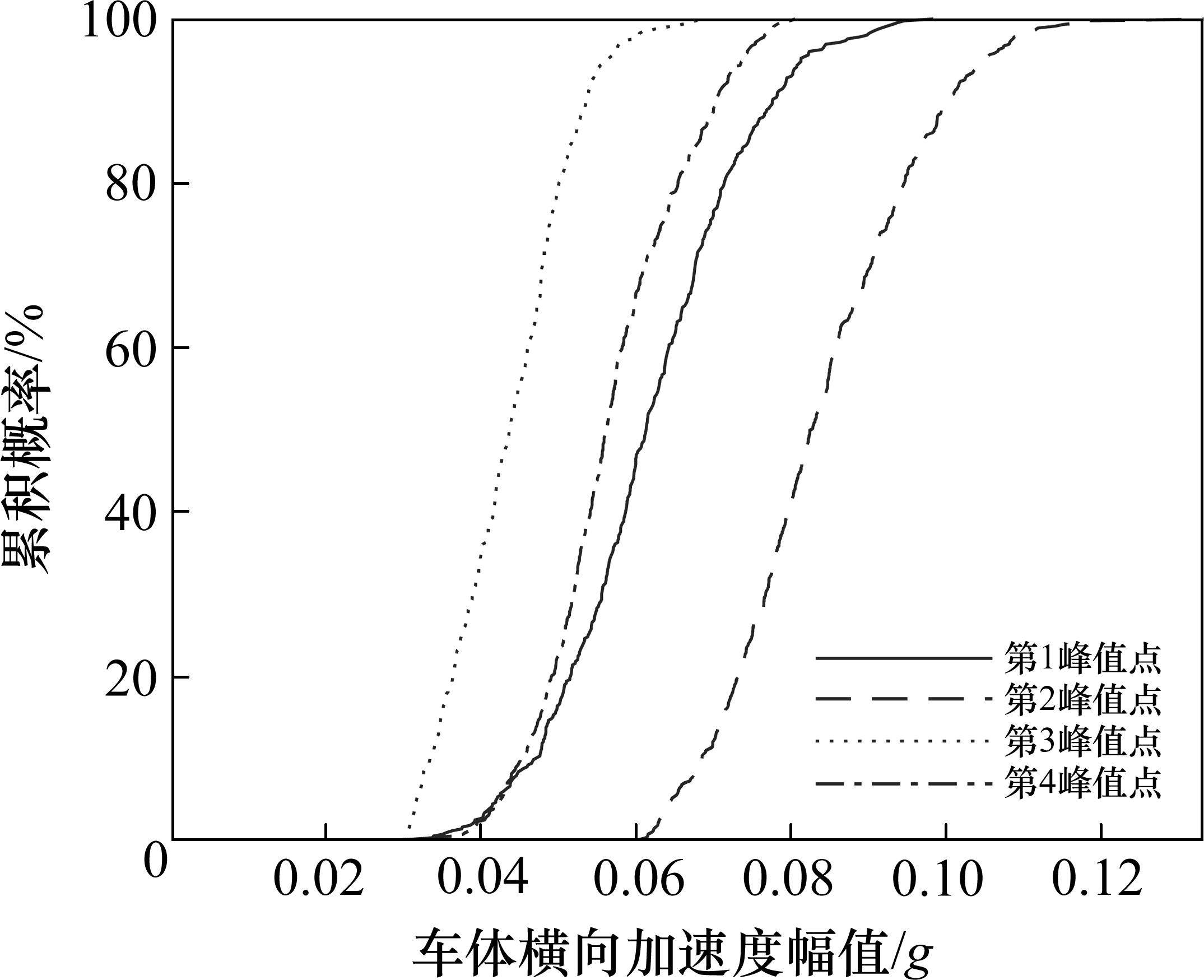
从图4可以看到,对同次振动而言,第2峰值点车体横向加速度幅值明显大于第1峰值点;第4峰值点车体横向加速度幅值明显大于第3峰值点。对比前后2次振动,第2峰值点车体横向加速度幅值明显大于第4峰值点,第1峰值点车体横向加速度与第4峰值点相当。这说明会车刚发生时的车体处横向振动剧烈程度明显大于会车即将结束时的横向振动。
为更好认识同次横向振动时不同峰值点间车体横向加速度幅值间的数量关系,这里计算同次振动后峰值点车体横向加速度幅值与前峰值点的比值。计算公式如下:
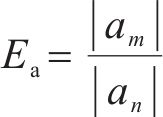
式中:|am|为后峰值点对应车体横向加速度幅值绝对值;|an|为前峰值点对应车体横向加速度幅值绝对值。
计算462次会车2次横向振动的2个峰值点车体横向加速度幅值比值,结果如图5所示。
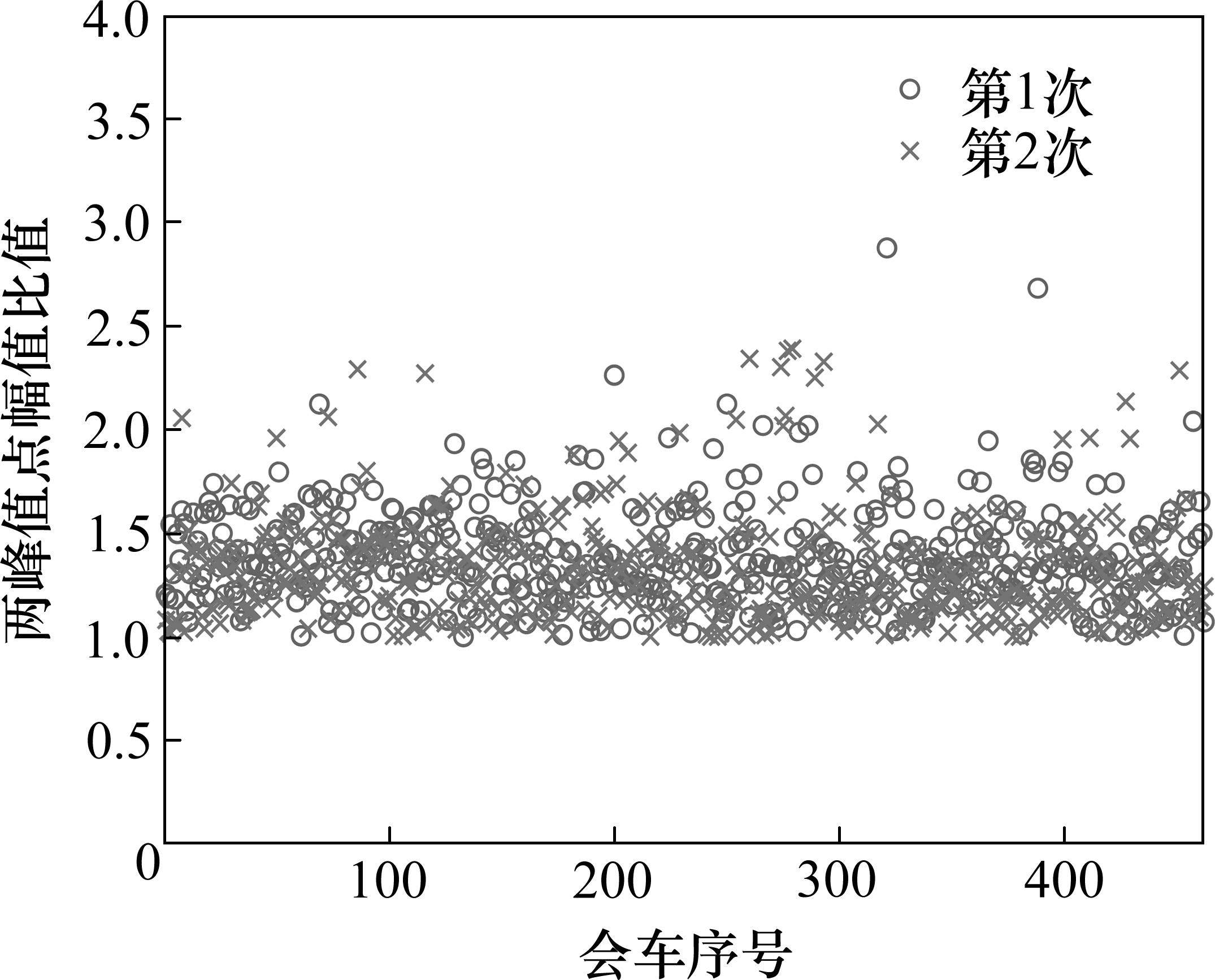
从图5可以看到,该动车组在与不同动车组在不同线路上发生的不同会车中,第2峰值点与第1峰值点幅值之比大都分布在1.0~2.0范围内,个别位置超过2.5;第4峰值点与第3峰值点幅值之比大都分布在1.0~2.0范围内,均小于2.5。
分别绘制第2峰值与第1峰值幅值比值、第4峰值与第3峰值幅值比值分布情况,结果如图6所示。其中1.0~1.1是前闭后开区间,即[1.0,1.1)。
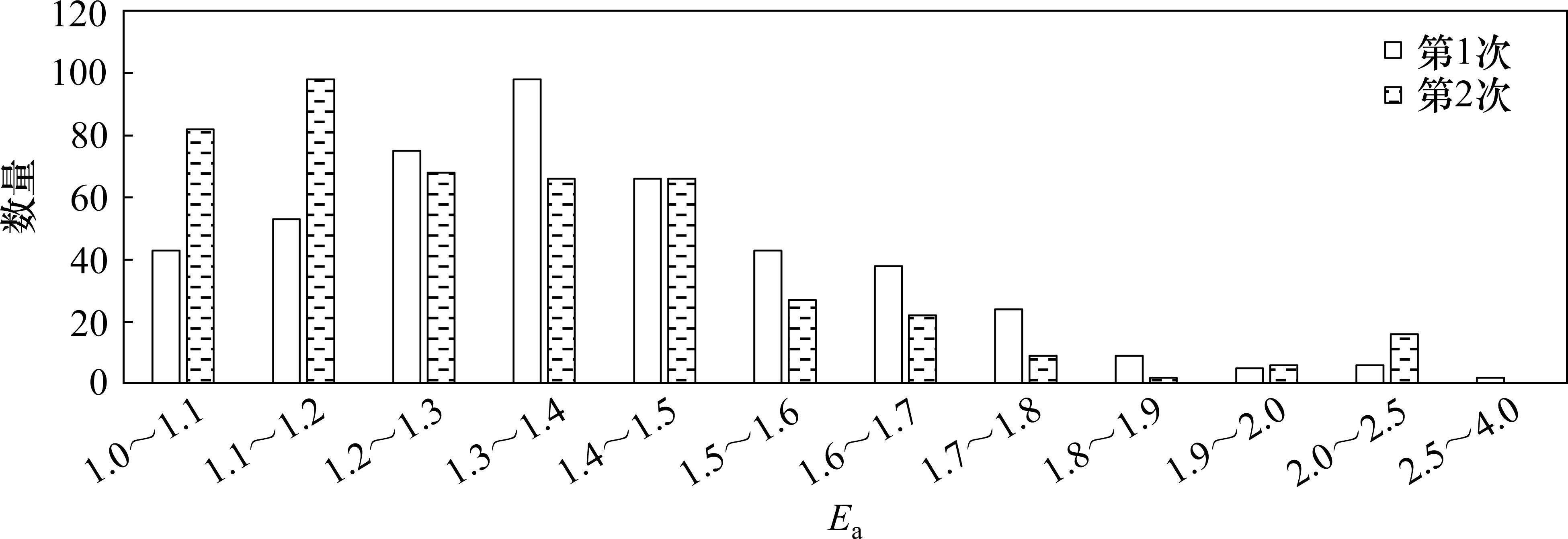
从图6可以看到,在1.0~2.0范围内,第2峰值与第1峰值比值主要分布在1.0~1.8范围内,且呈现出以1.3~1.4为中轴的近似对称分布;第4峰值与第3峰值比值主要分布在1.0~1.5范围内,1.1~1.2数量最多,1.0~1.1次之,1.2~1.3、1.3~1.4、1.4~1.5数量相当。
从图1可以看到,2次振动谐波特性明显,这里对2次振动的半波长进行统计,结果如图7所示。图中5~6 m为前闭后开区间,即[5,6)。
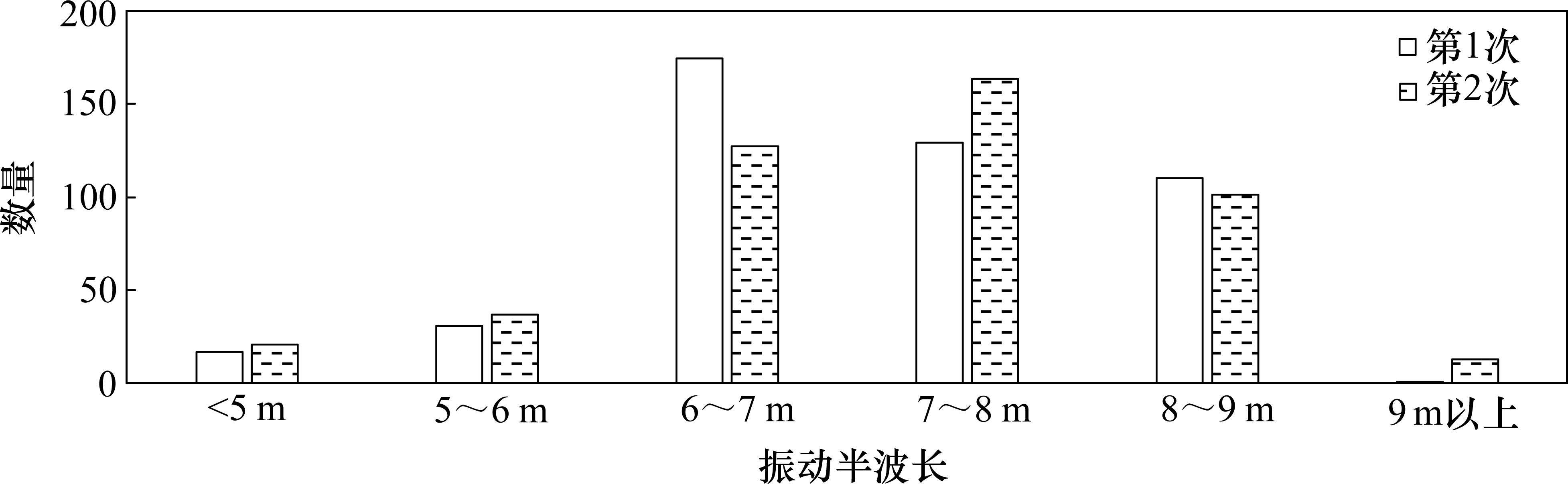
从图7可以看到,会车状态下2次横向振动的半波长均主要分布在6~9 m范围内。结合图6和图7,可得2次横向振动性质相同,主要是受气动效应影响。
对计算462次会车2次横向振动的间隔距离(见图1)进行统计,结果如图8所示。
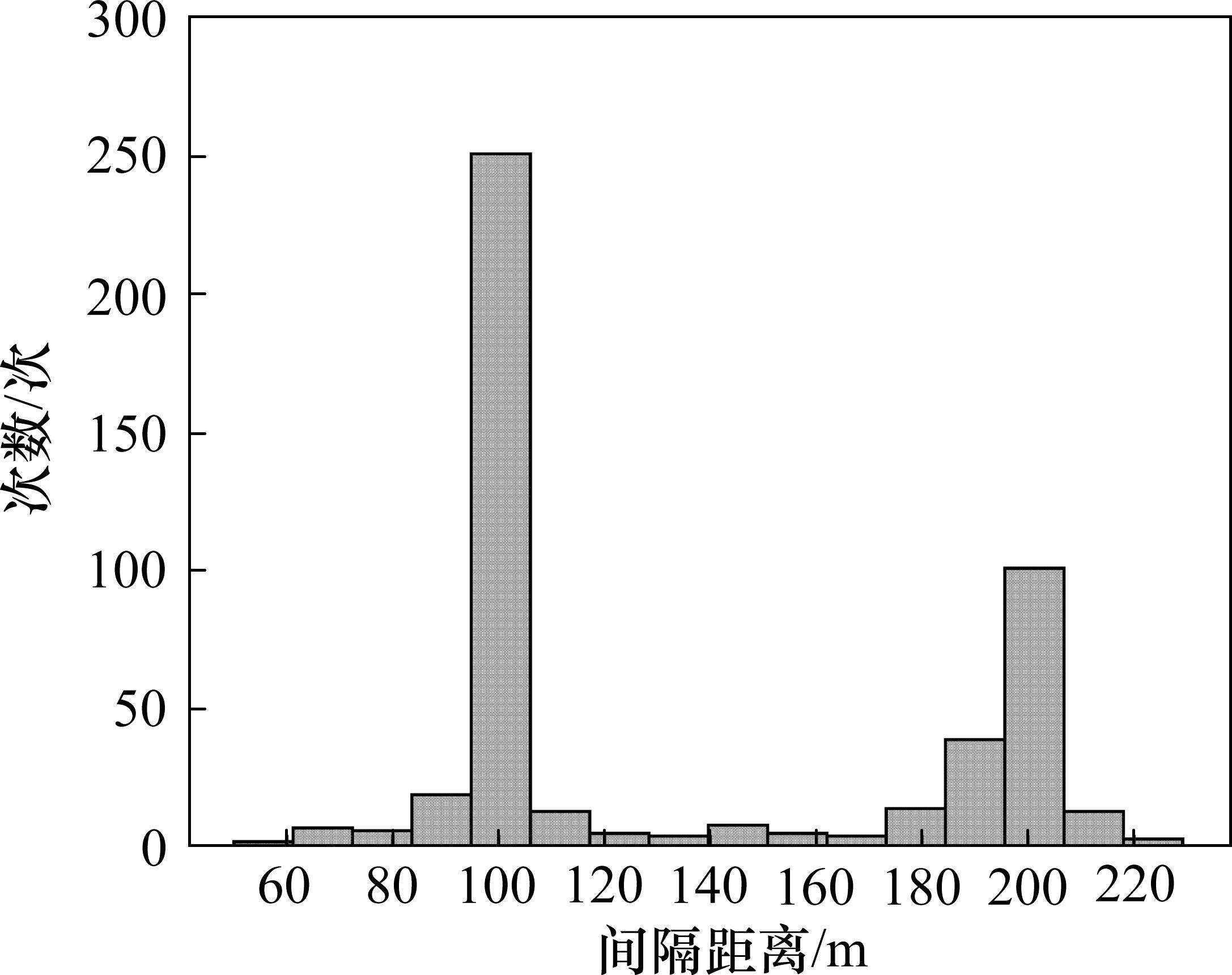
从图8不难看出,2次横向振动的间隔距离大致可分为2类:约100 m和约200 m。从数量关系上,2次横向振动间隔距离为100 m的情形更为常见。
表2给出了现行在役常见动车组列车长度。结合表2和图8不难得出,高速动车组在运行过程中与临线动车组发生会车时,将会发生2次较为剧烈的横向振动。第1次发生在动车组车头与临线动车组头车车头接近时,此时可看作会车起点;第2次发生在动车组车头与临线动车组尾车车头接近时,此时可看作会车终点。
| 型号 | 长度/m | 型号 | 长度/m | |
|---|---|---|---|---|
| CRH2A | 201.40 | CR400AF-A | 414.15 | |
| CRH5A | 211.50 | CR400AF-B | 439.8 | |
| CRH380A | 203.00 | CR400BF-A | 414.26 | |
| CRH380B | 202.95 | CR400BF-B | 439.91 | |
| CR400AF | 208.95 | — | — | |
| CR400BF | 209.06 | — | — |
2 基于车体横向加速度的会车识别方法
通过上述分析可以提炼归纳出会车状态下的车体横向加速度存在以下数据特征。
1) 会车状态下车体横向振动加剧反映为车体横向加速度幅值急剧增大,会车阶段车体横向加速度最大幅值超过现行维修管理标准中的车体横向加速度I级管理限值0.06g;
2) 会车状态下发生2次横向振动反映为车体横向加速度出现2次幅值明显的谐波波形且间隔距离可估。决定2次谐波间隔距离的主要因素为临线动车组长度,次要原因为2列列车运行速度差。运行速度差异不大时,临线动车组长度约为200 m时,间隔距离约为100 m;当临线动车组长度约为400 m时,间隔距离约为200 m。当运行速度差存在时,间隔距离将会有所延长或缩短,具体数值可计算。
3) 会车状态下发生的2次横向振动均会迅速收敛且2次振动方向相反,反映为会车区段共存在4个车体横向加速度幅值明显区别于其他位置的峰值点,且第1峰值点与第4幅值点车体横向加速度符号相反。
4) 会车状态下发生的2次横向振动,在同次振动内都存在后峰值点幅值大于前峰值点,反映为第2峰值点车体横向加速度幅值大于第1峰值点,第4峰值点车体横向加速度幅值大于第3峰值点。
5) 会车状态下发生的2次横向振动时间较短,反映为2次振动半波长均分布在6~9 m范围内。
根据上述数据特点,基于车体横向加速度的会车识别方法核心思想为判断一段车体横向加速度数据是否满足下列条件:
1) 车体横向加速度幅值较大,第2峰值点车体横向加速度幅值超过0.06g;
2) 100 m或200 m范围内,车体横向加速度数据共存在4个明显峰值点;
3) 第4峰值点车体横向加速度与第1峰值点车体横向加速度异号;
4) 第2峰值点对应车体横向加速度幅值大于第1峰值点;
5) 第1、第2峰值点,第3、第4峰值点间间隔距离应符合相应要求。
基于车体横向加速度的会车识别方法即是对上述要求的具体实现。
图9给出了运行速度超过150 km/h时通过非道岔区的基于车体横向加速度的会车识别方法的实现流程。
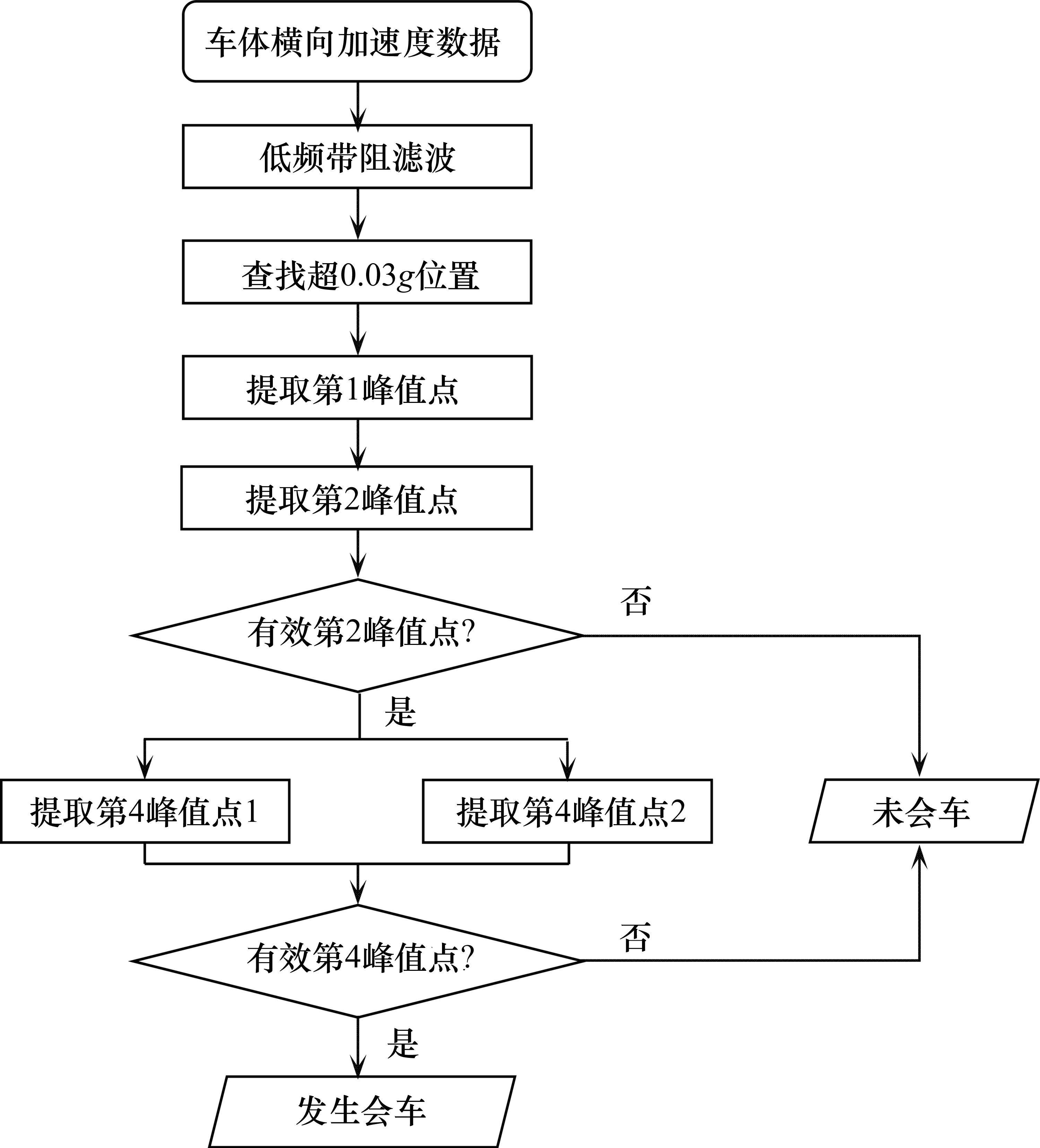
其具体步骤如下。
1) 对车体横向加速度进行0~0.1 Hz低频带阻滤波,滤除低频趋势项。
滤波具体实现采用傅里叶变换和傅里叶逆变换联合的方式,具体过程如下:
记采集到的车体横向加速度信号为{a(n),n=1,2,…,N},其中N表示采样点数。对该信号进行离散傅里叶变换:
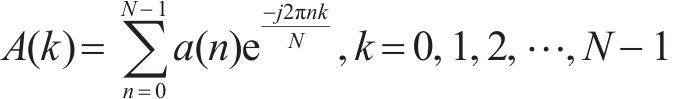
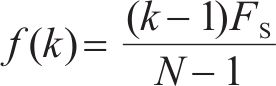
式中:n为当前数据点序号;k为频率索引,表示频域中的各个频率分量;Fs为采样频率,Hz;A(k)为傅里叶变换结果;f(k)为对应频率。
根据所确定滤波范围[Fl, Fh],确定出频率f(k)在[Fl, Fh]之外的整数。
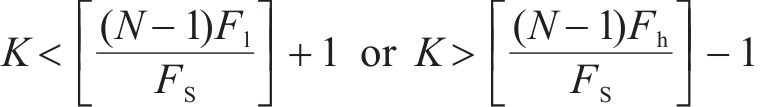
式中:[ ]为取整;Fl为下限截止频率,这里为0.1;Fh为上限截止频率,这里为采样频率;
令相应项的傅里叶系数为0。按照下式进行傅里叶逆变换得到低频带阻滤波后的车体横向加速度信号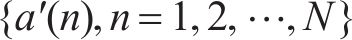
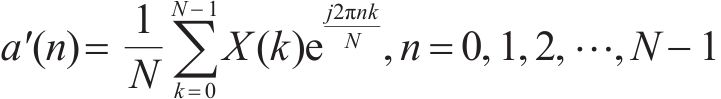
2) 获取第1峰值点对应位置序列{L1(i),i=1,2,…,M}。
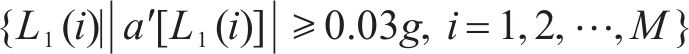
式中:L1(i)为第i个第1峰值点对应位置信息;|a′[L1(i)]|为第i个第1峰值点对应车体横向加速度幅值;g为重力加速度;M为第1峰值点序列总长度。
3) 获取可能第2峰值点对应车体横向加速度幅值序列{A2(i), i=1,2,…,M}和对应位置序列{L2(i), i=1,2,…,M}。
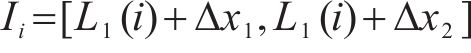
式中: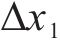
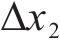
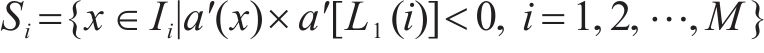
式中:Si是在区间Ii内与第1峰值点符号相反的所有车体横向加速度的集合。

式中:L2(i)为第i个可能第2峰值点对应位置信息;A2(i)为第i个可能第2峰值点对应车体横向加速度幅值。
4) 根据第2峰值点对应车体横向加速度幅值序列获取有效第2峰值点对应位置序列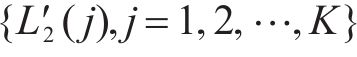
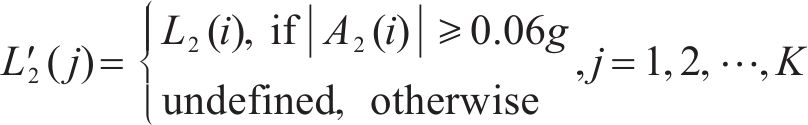
式中:g为重力加速度;K为有效第2峰值点序列包含数据个数。
5) 依据有效第2峰值点对应位置序列得到新的第1峰值点序列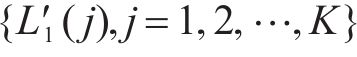
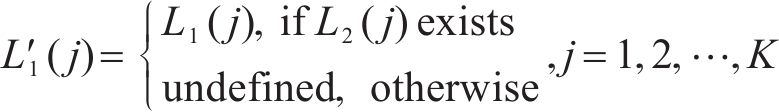
6) 根据表3信息,获取第1、第2类可能第4峰值点对应车体横向加速度幅值序列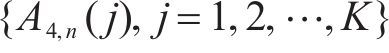
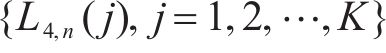
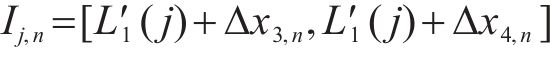
式中: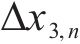
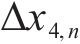
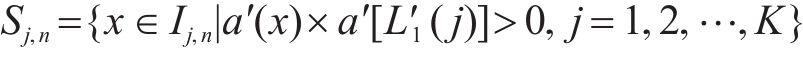
式中:Sj是在区间Ij内与第1峰值点符号相同的所有车体横向加速度的集合。
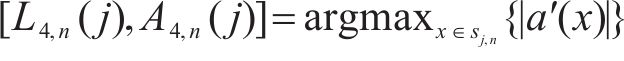
式中:L4,n(j)为第n类第j个可能第4峰值点对应位置信息;A4,n(j)为第n类第j个可能第4峰值点对应车体横向加速度幅值。
| 类别 | 动车组长度/m | 第4峰值点可能分布范围/m |
|---|---|---|
| 第1类 | 约200 | 距第1峰值点50~150 |
| 第2类 | 约400 | 距第1峰值点100~300 |
7) 根据第4峰值点对应车体横向加速度幅值序列获取有效第4峰值点对应位置序列{L4(m),m=1,2,…,Y}。
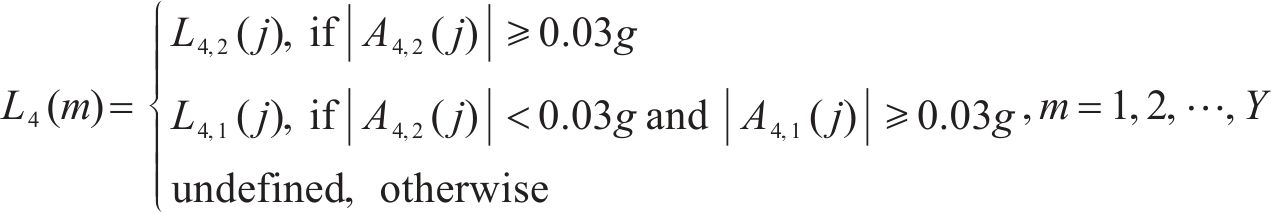
8) 依据有效第4峰值点对应位置序列得到有效第1峰值点序列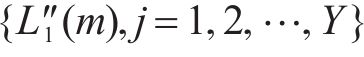
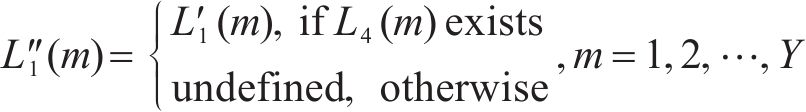
9) 得到会车区段区间集合。
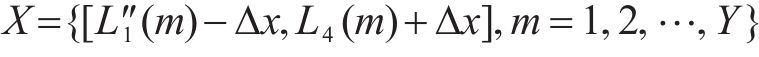
式中: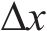
3 实例验证
通过抽样方式选择该检测车本年度在运行速度大于150 km/h时通过250(不含)~350 km/h管理标准线路的10条检测数据进行分析,分析不包含道岔。该方法识别出的会车数量与误识数量如表4所示。
| 序号 | 检测里程/km | 会车识别数 | 误报数 |
|---|---|---|---|
| 总计 | 3 368 | 95 | 0 |
| 1 | 117 | 0 | 0 |
| 2 | 337 | 17 | 0 |
| 3 | 332 | 0 | 0 |
| 4 | 44 | 3 | 0 |
| 5 | 337 | 17 | 0 |
| 6 | 332 | 1 | 0 |
| 7 | 374 | 2 | 0 |
| 8 | 1212 | 36 | 0 |
| 9 | 18 | 8 | 0 |
| 10 | 265 | 11 | 0 |
根据表4可知,本文所提出的会车识别方法对共计3 368 km的车体横向加速度数据进行分析,共计查找到会车区段95处。其中95处发生会车,0处误报,识别成功率为100%。
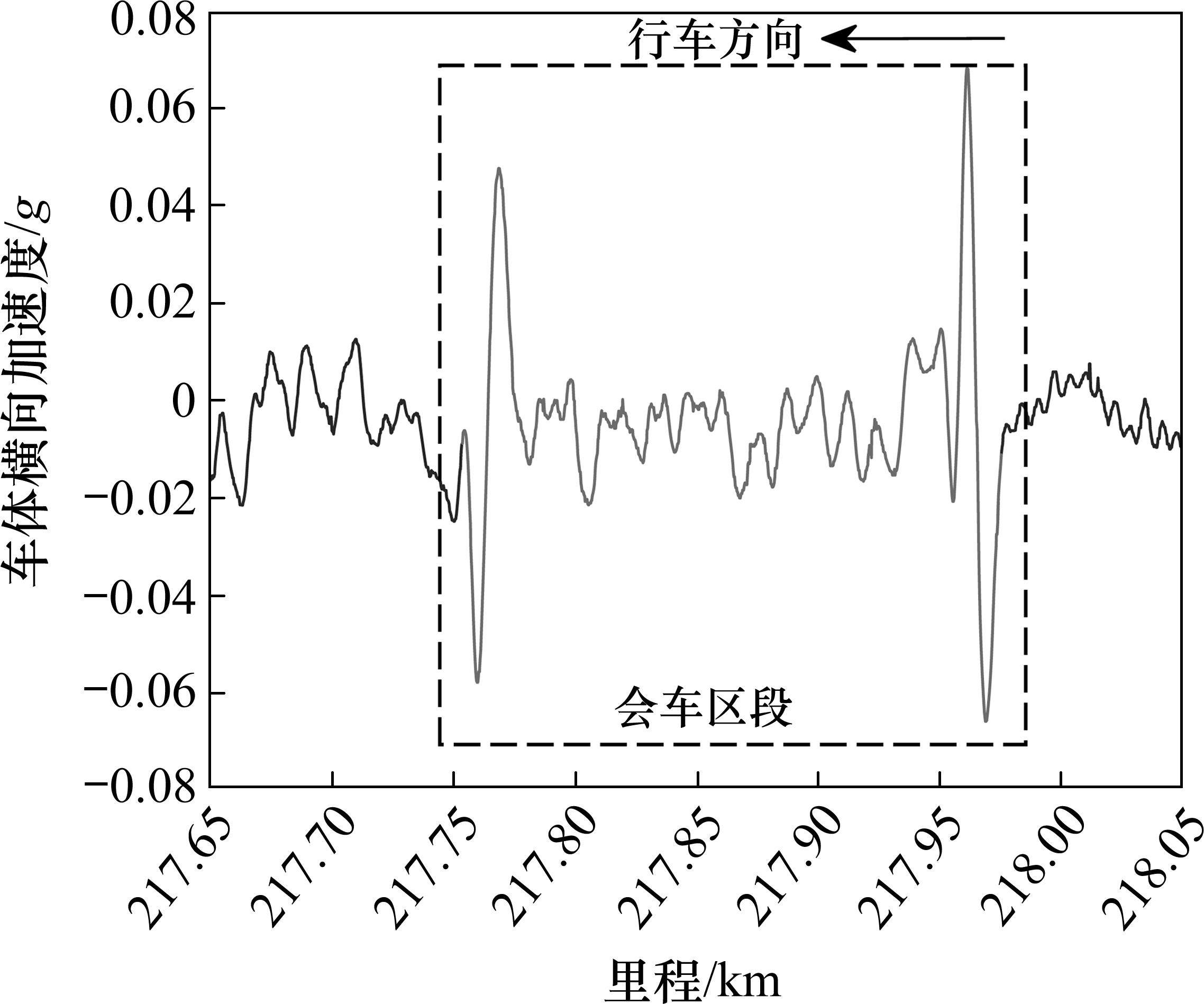
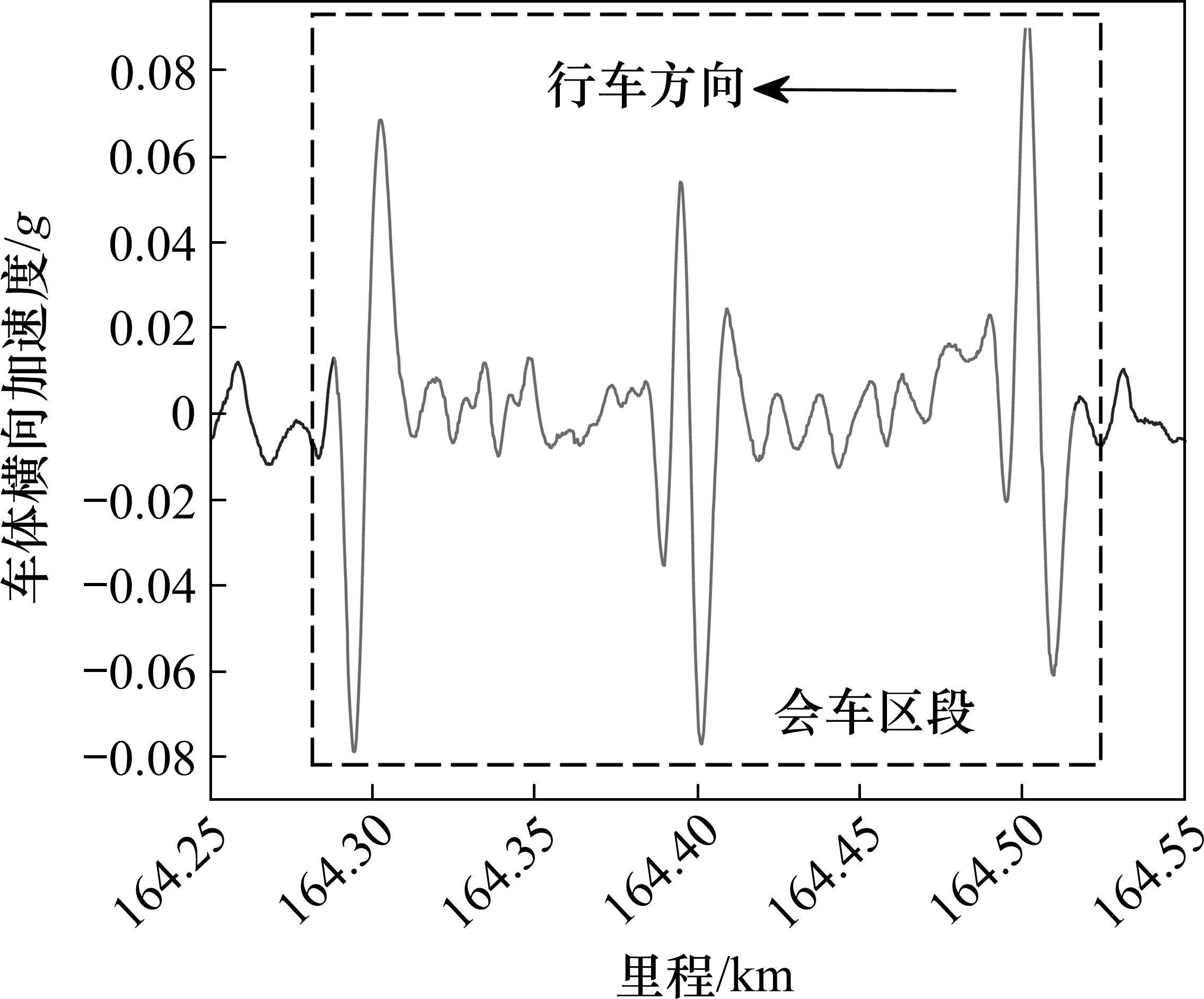
图10、图11是应用所提出的方法对检测车通过表4中的线路5时采集到的车体横向加速度分析识别得到的其中2个会车区段K217+750~K217+980与K164+280~K164+530。通过与检测人员确认该检测车10月在该线路执行检测任务时,行驶至这2个区段时与临线动车组发生会车。根据识别结果,动车组第1次会车时临线动车组为16编组动车组,第2次会车时临线动车组为2列8编组动车组重联。
4 结论
1) 会车发生时,车体横向振动加剧,车体横向加速度幅值明显增大但收敛迅速,在波形上表现为存在4个明显峰值点。
2) 会车发生时,动车组产生2次明显且方向相反的横向振动,车体横向加速度波形表现为存在2个明显谐波。第1次横向振动幅度明显大于第2次横向振动。
3) 根据目前在役动车组列车长度,会车引起的2次横向振动间隔距离主要分为100 m和200 m这2类。同次振动的半波长集中分布在6~9 m范围内。
4) 利用所提出的会车识别方法对运行速度超过150 km/h的非道岔区实测车体横向加速度进行分析,会车识别率为100%。还可以根据会车波形识别临线动车组是否为重联动车组。
解婉茹,高彦嵩,杨飞等.高速动车组会车横向振动特性及识别方法研究[J].铁道科学与工程学报,2025,22(02):523-532.
XIE Wanru,GAO Yansong,YANG Fei,et al.research on transverse vibration characteristics and recognition methods of high-speed trains passing each other[J].Journal of Railway Science and Engineering,2025,22(02):523-532.

