弓网系统由受电弓与接触网两大主体构成,是轨道列车系统的重要组成部分,起到为列车提供牵引电能并反馈制动回路的重要作用[1]。随着列车运行速度的不断提升,弓网系统的动力学性能亟需达到更高标准,以确保高速状态下的列车能保持平稳、安全地运行[2-3]。当列车以较高速度行驶时,受电弓沿接触线的滑动会引起弓网耦合振动,从而影响弓网系统的接触性能与受流质量[4-6]。在承受接触线某一频率的振动激励后,随着激励幅度的不断增大,滑板与接触线间从良好接触状态转变为脱离接触状态。这种受电弓跟随接触线持续振动的动力学现象,一般用受电弓跟随性描述,并以脱离时的临界激励幅值作为其评价指标。列车速度越快,弓网振动越剧烈,对受电弓的跟随性也提出了更高的要求。因此,研究高速受电弓的跟随性具有重要的科学意义和工程应用价值。弓网的跟随性能与受电弓的结构参数密不可分[7],需采用受电弓等效模型研究特定结构参数对跟随性能的影响,如归算质量模型[8-10]、多刚体模型[11-13]、刚柔混合模型等[14-15]。为权衡计算精度与计算效率,目前国内外大多采用归算质量受电弓模型来模拟受电弓与接触网的耦合振动关系,进而探索弓网参数定量变化引起的跟随性变化[16-19],但是关于跟随性的理论推导和规律性总结研究存在不足。关金发等[20]推导受电弓二质量块等效模型的传递函数,并用于弓网动力学性能分析,但尚未研究传递函数与受电弓跟随性能之间的联系。本文首先推导受电弓三质量块等效模型的传递函数,借助传递函数建立反映受电弓跟随性能的数学理论模型;在此基础上,通过数学计算获取对应的跟随性曲线,并与数值仿真和地面试验结果对比以验证方法的合理性;最后通过仿真计算、理论推导及灵敏度分析得到三质量块等效参数对受电弓跟随性的影响规律。
1 跟随性数学模型及推导
1.1 基于传递函数的数学模型
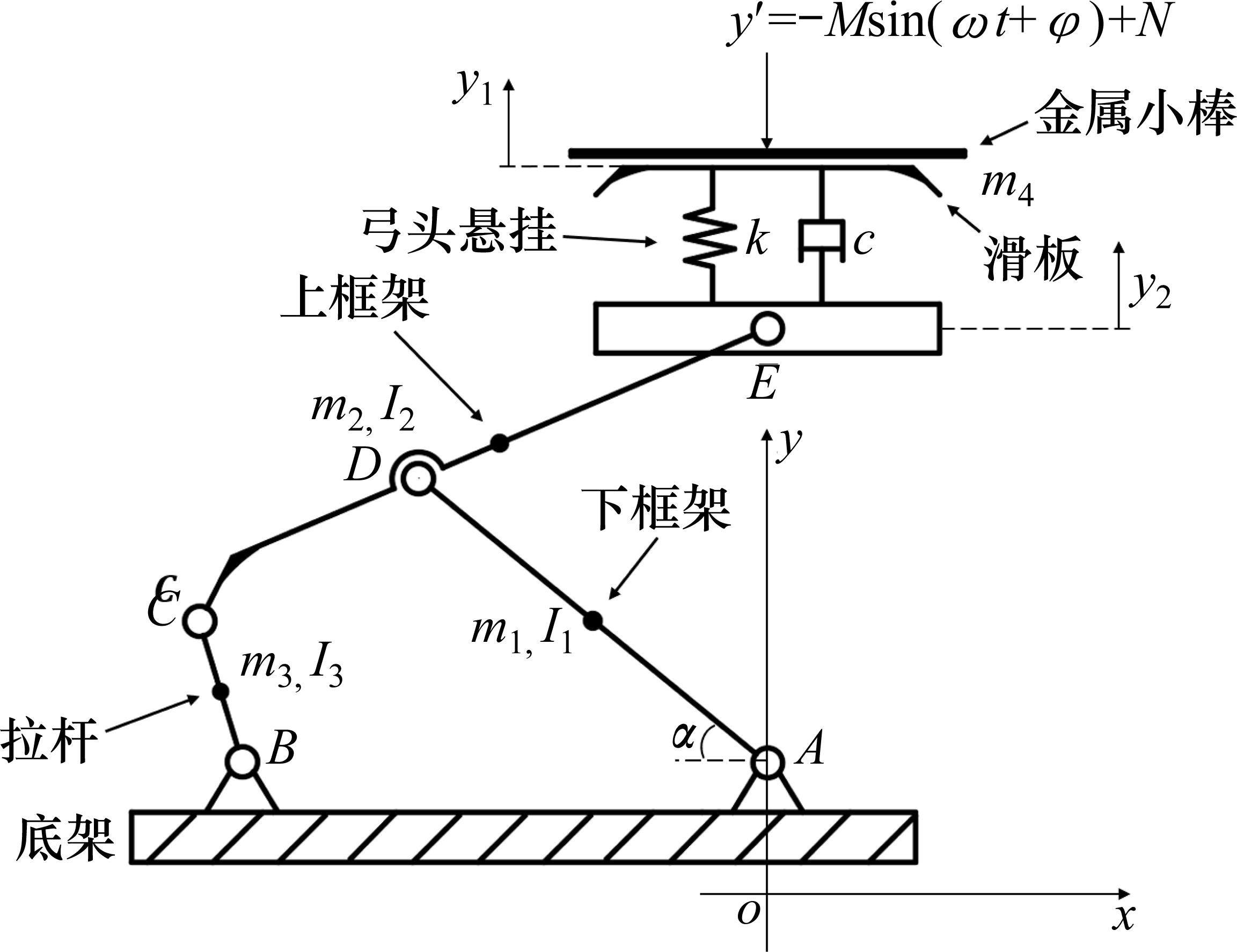
为研究受电弓的跟随性规律与弓头、框架参数之间的关系,结合EN-50318: 2018[21]标准,将受电弓简化为三质量块等效模型作为研究对象。等效模型见图1。
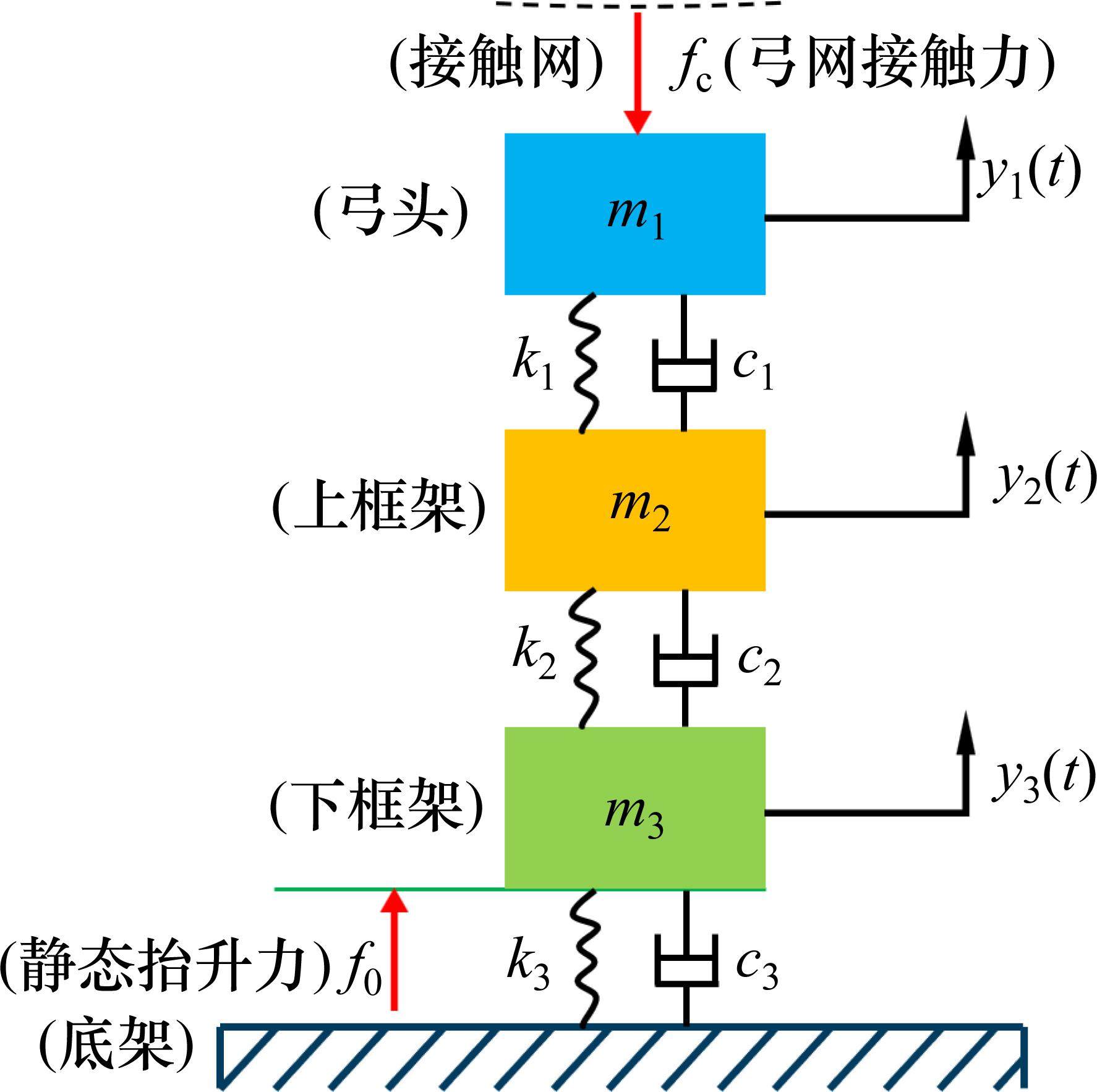
根据达朗贝尔原理可以得到该三质量块等效模型的运动微分方程:
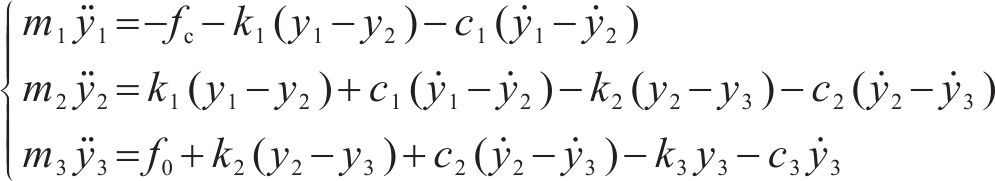
将式(1)进行拉普拉斯变换,有
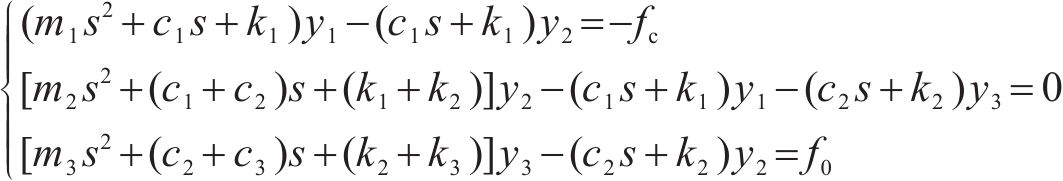
式中: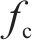
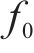
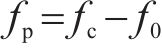
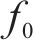
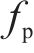
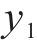
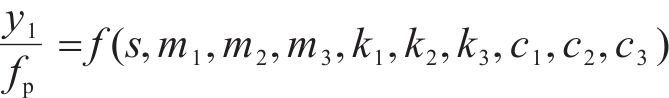
可令
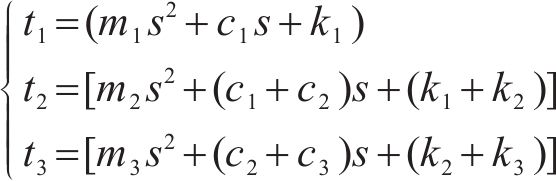
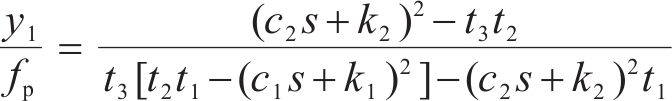
试验或仿真中测试跟随性时,通过读取弓网接触力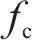
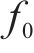
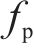
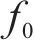
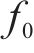
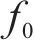
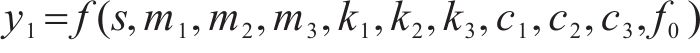
式中含有10个未知数,分别为三质量块的等效质量、刚度、阻尼系数以及激振频率,此时代入三质量块等效参数即可得出理论计算的连续跟随性曲线。表1为台架试验测得的高速受电弓三质量块等效参数。
| 模型 | 等效质 量/kg | 等效刚度/ (N∙m-1) | 等效阻尼/ (N∙s∙m-1) |
|---|---|---|---|
| 弓头 | 4.93 | 8 000.00 | 59.39 |
| 上框架 | 5.95 | 14 695.17 | 8.88 |
| 下框架 | 8.02 | 12.33 | 123.99 |
1.2 反共振频率与跟随性极值
现考虑跟随性极值下的频率并探讨其规律。对跟随性表达式中s求偏导,得到
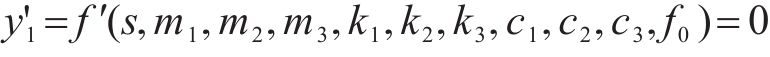
该式较为复杂,参数较多,且存在s的9次高阶项,难以精确计算出解析解。但是在给定三质量块等效参数及静态接触力时,该式仍可用于计算数值解以分析跟随性规律。
将三质量块系统的运动微分方程(1)以矩阵形式表达,可得
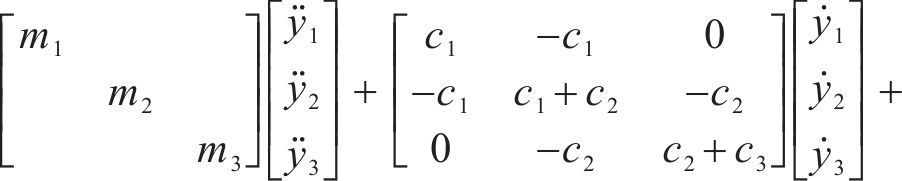
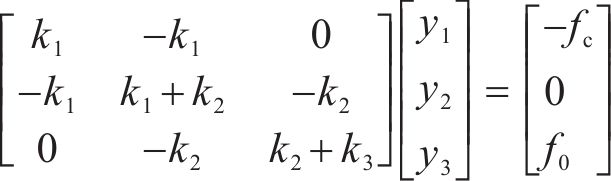
采用比例阻尼的简化方法,认为阻尼矩阵C与质量矩阵M和刚度矩阵K线性相关,即令:

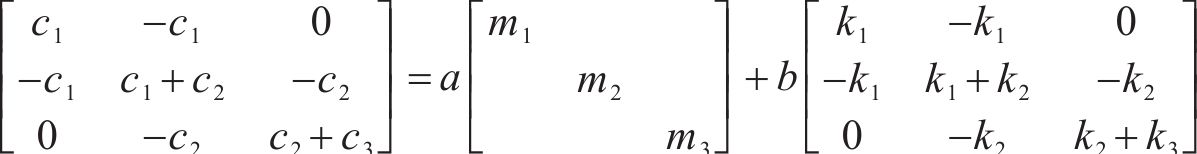
三质量块系统的无阻尼固有频率可以通过特征方程求解,即:
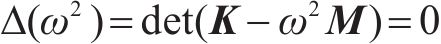
式中存在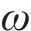
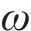
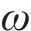
因为比例阻尼的特殊性,用u正则化后的阻尼矩阵C将成为对角矩阵,有:
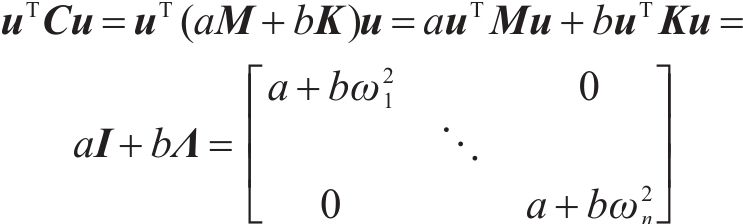
令
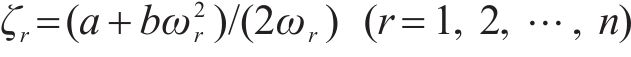
代入三质量块等效模型参数,可以计算出该等效模型的有阻尼2阶固有频率,即弓头与下框架的反向共振的频率约为6.4 Hz。
建立三质量块数值仿真模型,代入三质量块等效参数,得到三质量块等效模型的有阻尼2阶固有频率,即弓头与下框架的反向共振的频率约为6.41 Hz,说明理论推导的频率计算方法比较准确。
2 模型验证
2.1 跟随性台架试验
跟随性台架试验采用FCS全数字电液伺服控制系统,控制液压作动器模拟接触线振动,辅以位移传感器和力传感器测量作动器振动位移及接触压力数据。试验过程中,调节受电弓气泵压力以调节平均接触力,使试验过程在平均接触力为80 N下进行。考虑高速受电弓的振动实际情况,结合标准GB/T 21561.1—2018及GB/T 21561.2—2018,初步选取加载频率0~20 Hz。加载频率小于1.5 Hz时,跟随性幅值一般较大,暂不对其做研究;加载频率大于12 Hz时,跟随性幅值一般较小,且受条件限制,台架试验仪器精度较差。由此选取加载频率范围为1.5~12 Hz,每次增加0.5 Hz,施加各频率下正弦扫幅激励。随着激振振幅的增大,接触压力波动幅度也在增大,在接触压力为0的时刻,受电弓出现离线现象。记录此时的频率和幅值,以确定受电弓在不同频率作用下跟随接触线的能力。力传感器、位移传感器安装位置与弓头接触关系如图2所示,整个台架试验系统的数据传输流程如图3所示。

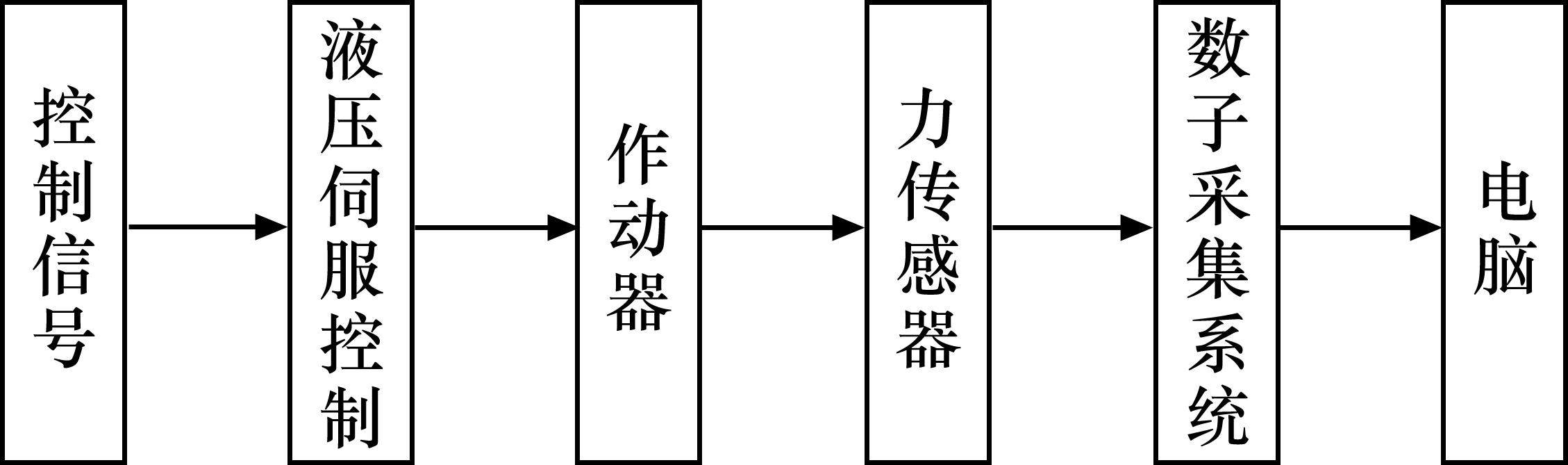
扫幅信号的反馈值通过液压缸内置的位移传感器记录。位移传感器记录的原始数据为电压值,位移信号与电压信号以一定的关系对应,因此在试验开始前,需要对拉线传感器进行标定。
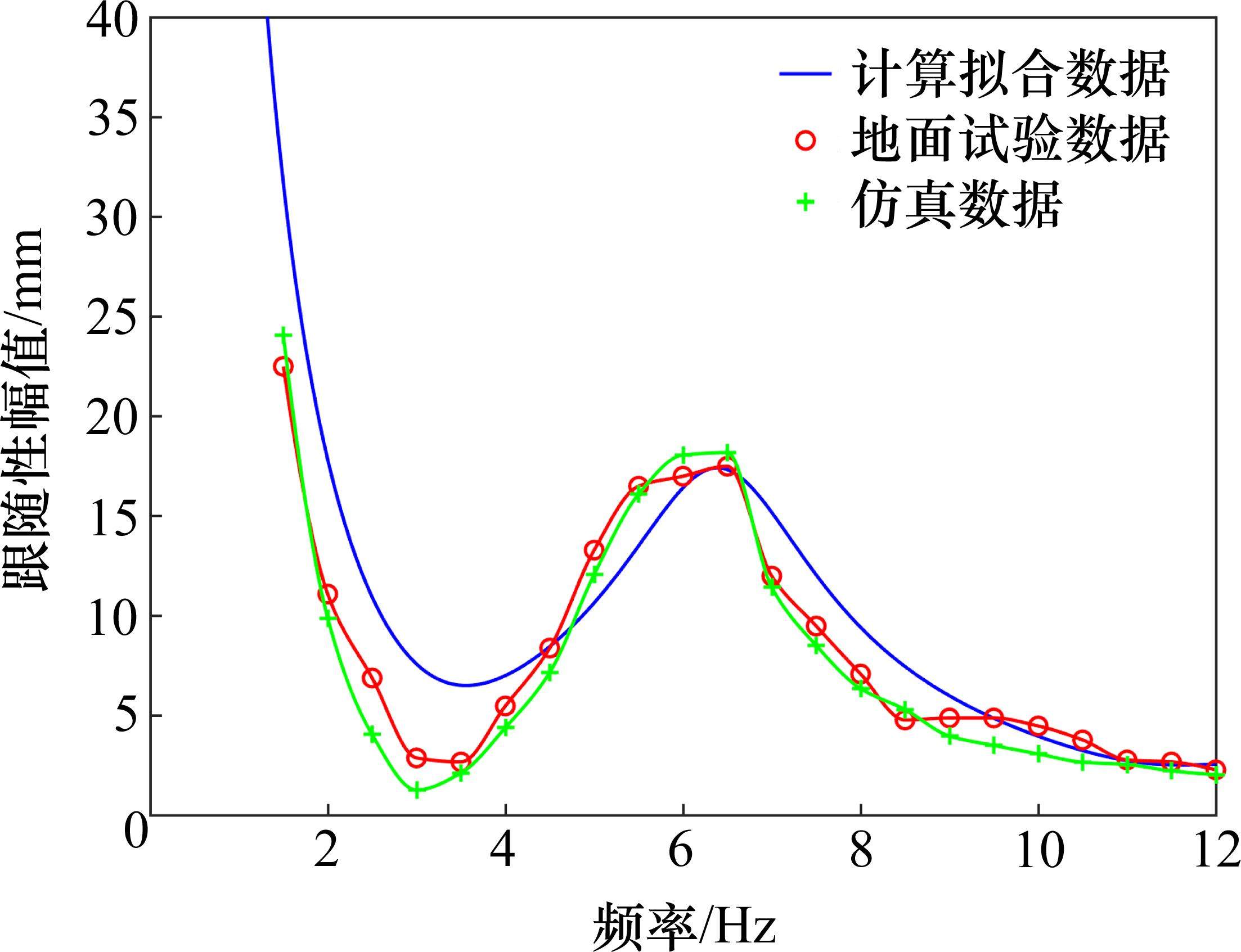
在作动器加载频率不变的前提下,分别对作动器位移传感器数据和作动器与滑板之间的力传感器数据进行时域分析,做出作动器的位移曲线和滑板的力曲线。在力曲线中找出第1次达到0的点,此时刻对应的位移,即为作动器分离时对应的幅值,也即受电弓跟随性幅值。读出1.5~12 Hz频率范围内的跟随性幅值并绘制成平滑曲线,结果见图5。
2.2 跟随性数值仿真
建立高速受电弓的多刚体动力学模型,由于试验不考虑风环境和弓纵向运动的影响,可用金属小棒代替接触网与受电弓进行接触和跟随性仿真测试,如图4所示。
利用步函数控制受电弓升弓高度,如式(14)前半式;利用扫幅函数控制小棒振动频率和振幅,如式(14)后半式,来模拟台架试验时作动器在不同频率下对弓头进行等频正弦扫幅激励的场景测试。
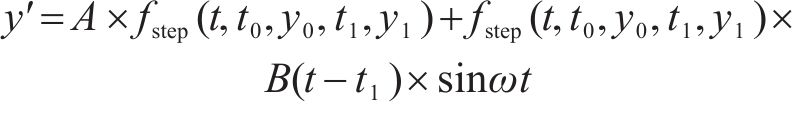
式中:A、B是确定升弓高度和扫幅强度后选定的常数;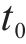
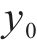
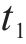
数值仿真设置加载频率范围与台架试验相同,取1.5~12 Hz,每次增加0.5 Hz,施加各频率下正弦扫幅激励。观察受电弓与金属小棒的接触力仿真结果,读取振荡接触力第1次达到0时对应的时间,将该时间代入对应频率下小棒扫幅激励函数表达式,即可得出在该频率下受电弓的跟随性幅值。观察并计算出规定频率范围内所有的跟随性幅值后绘制成平滑曲线,结果见图5。
2.3 结果比对与模型验证
结合仿真、试验与理论计算得到该型受电弓的跟随性曲线,如图5所示。可见基于传递函数计算和动力学模型数值仿真得到的跟随性曲线均与试验结果的趋势一致,关键极值点的频率与幅值无明显差异,有较好的匹配性,说明用该方法计算跟随性是较准确的、可行的,建立的数值仿真模型也是较成功的。数学模型的准确性为后续从理论公式计算上寻找跟随性规律提供了依据。
图5中显示试验、仿真、理论计算得到的跟随性幅值整体是随输入频率的增大而迅速减小的,说明随着施加激振频率的增大,受电弓的跟随性能在急剧下降。各条曲线中段出现一处极大值,频率均在6.4 Hz附近,与前文理论计算及数值仿真得到的2阶固有频率接近,说明跟随性极大值基本发生在弓头与下框架的反向共振频率下,此时弓头与下框架的反向共振运动从相位上提升了受电弓的跟随性能。
3 跟随性演变规律
基于上述较为精确的数学模型,得到跟随性极值的发生频率后,通过改变三质量块等效参数,得到不同的跟随性曲线,从而观察质量块参数对跟随性的影响规律。图6~图8中的带圈实线为试验数据拟合的跟随性曲线,普通实线为通过传递函数计算得到的跟随性曲线,其余不同线型的曲线为改变三质量块某一等效参数计算得到的跟随性曲线。
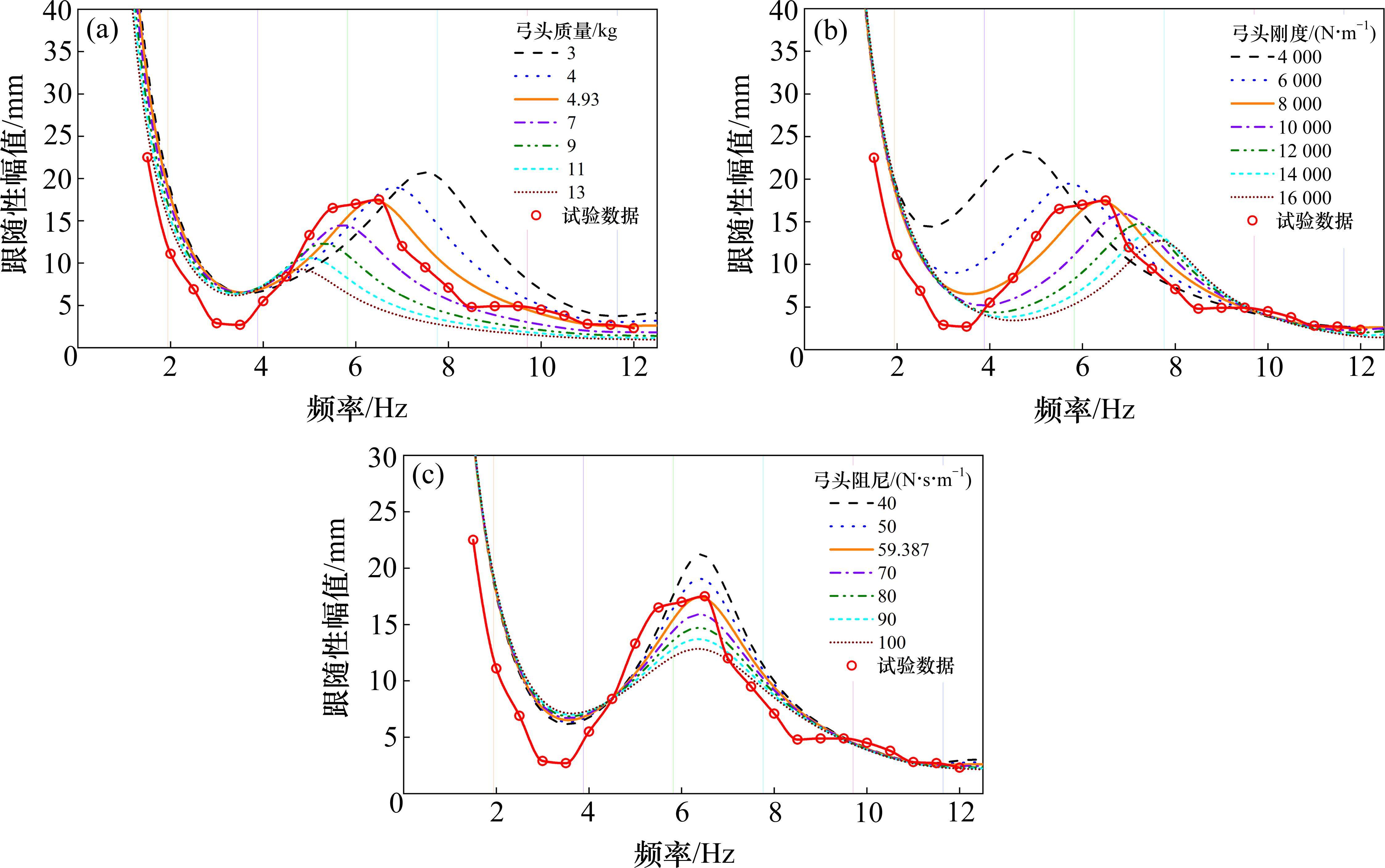
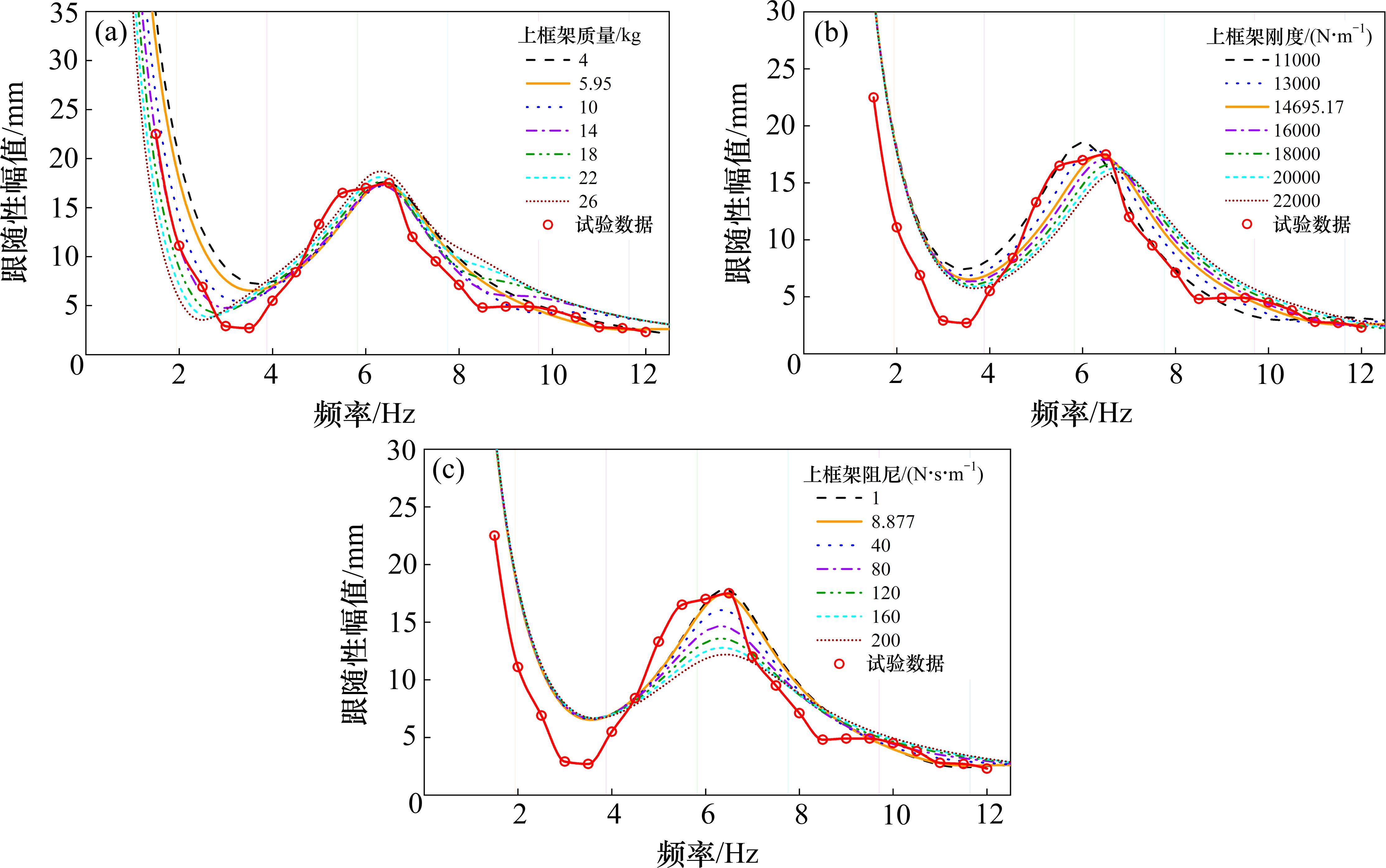
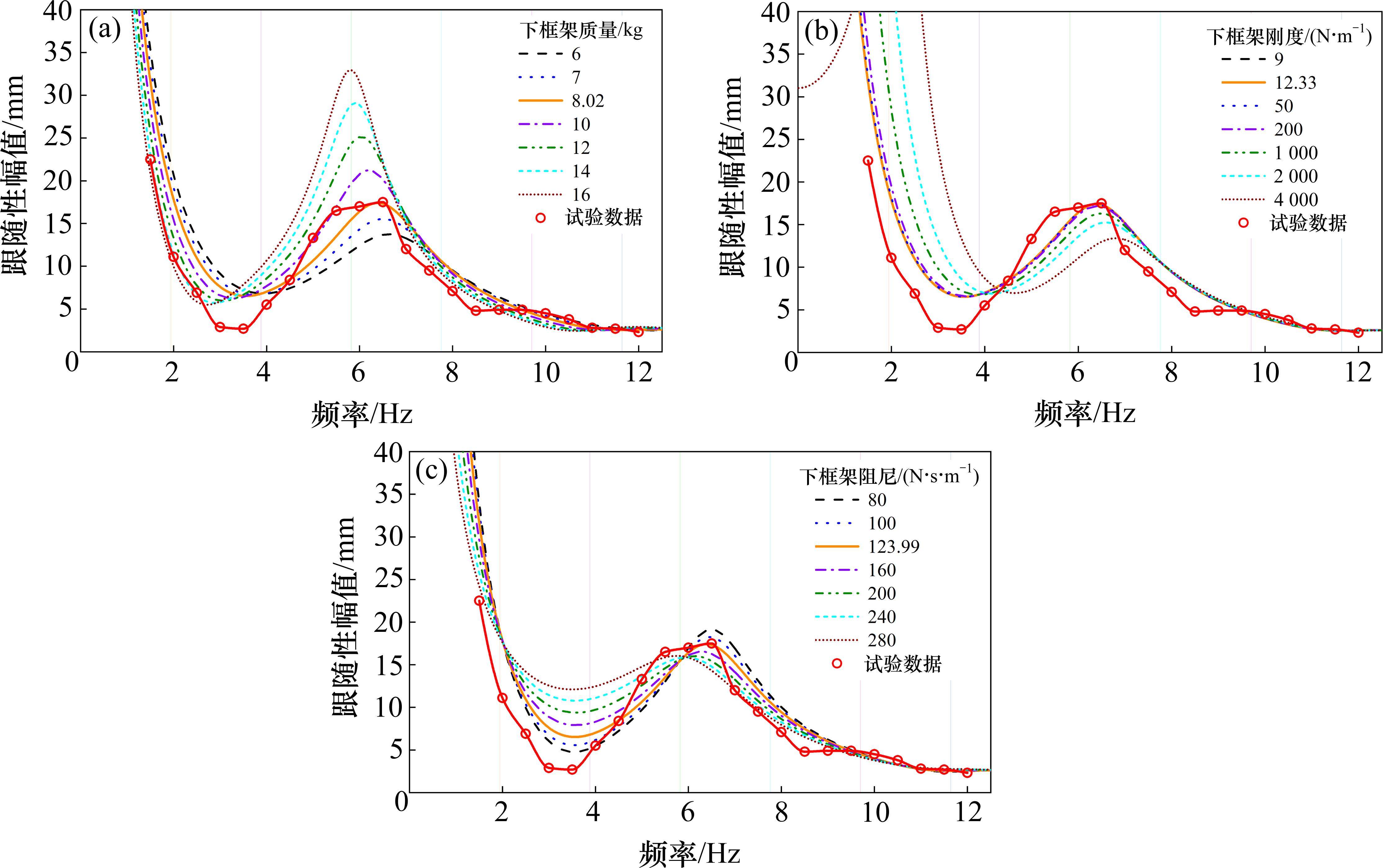
由三质量块等效参数变化的跟随性曲线图可以判断出:弓头与上框架的等效质量越小,跟随性越好,上框架的等效质量减小时极大值略微降低;下框架的等效质量越大,跟随性越好。弓头、框架的等效刚度越小,跟随性越好,跟随性极值频率变小;弓头与上框架的等效刚度变大时,跟随性极小值有降低趋势。弓头与上框架的等效阻尼越小,跟随性极大值越大,跟随性越好;下框架的等效阻尼越大,跟随性越好,但是跟随性极大值会略微降低;等效阻尼引起的跟随性极值频率变化不明显。
为辨别出各参数对受电弓跟随性的影响因子,对弓头、框架的等效质量、刚度、阻尼系数进行了灵敏度分析,结果见图9~图11。
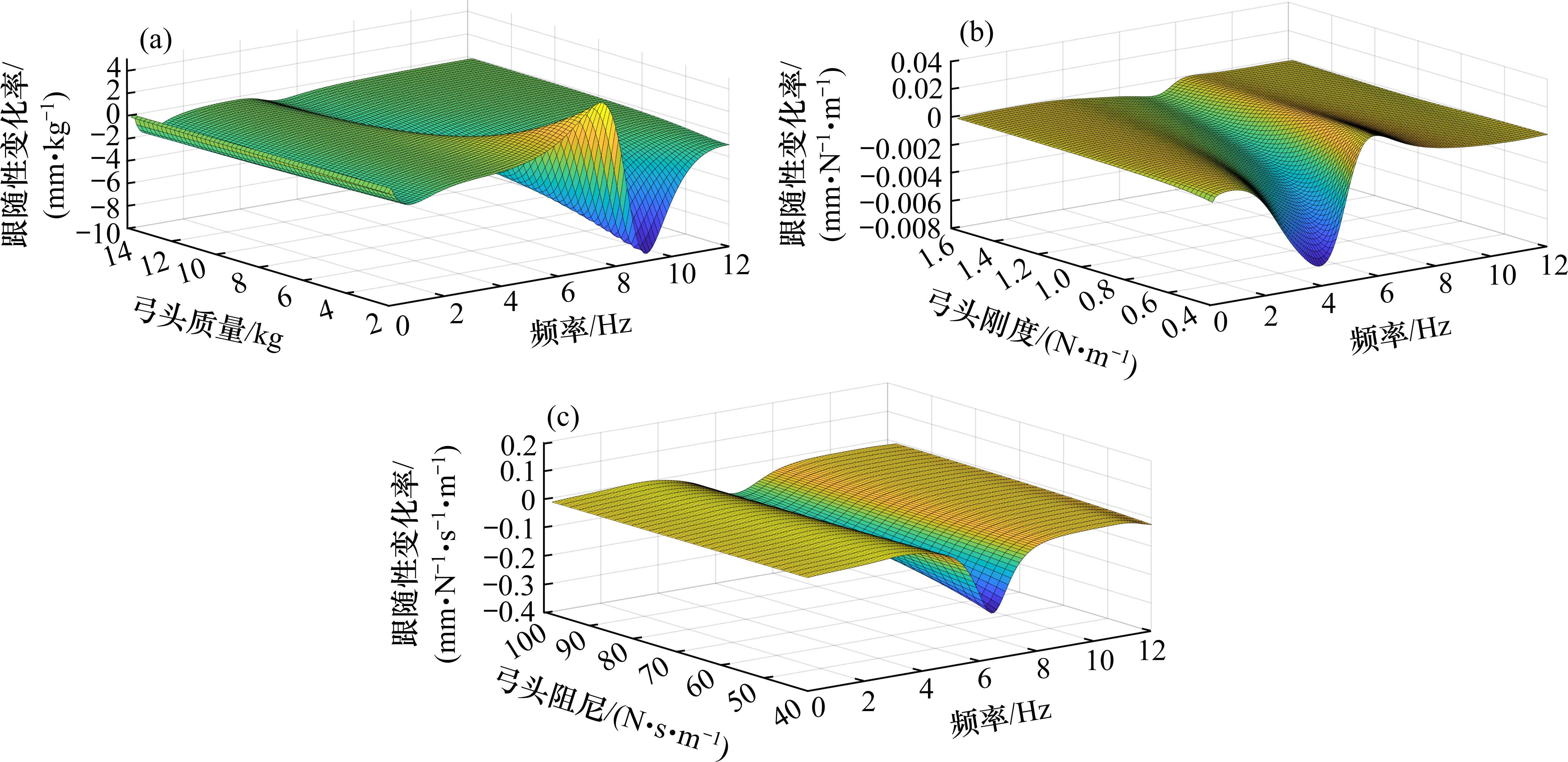
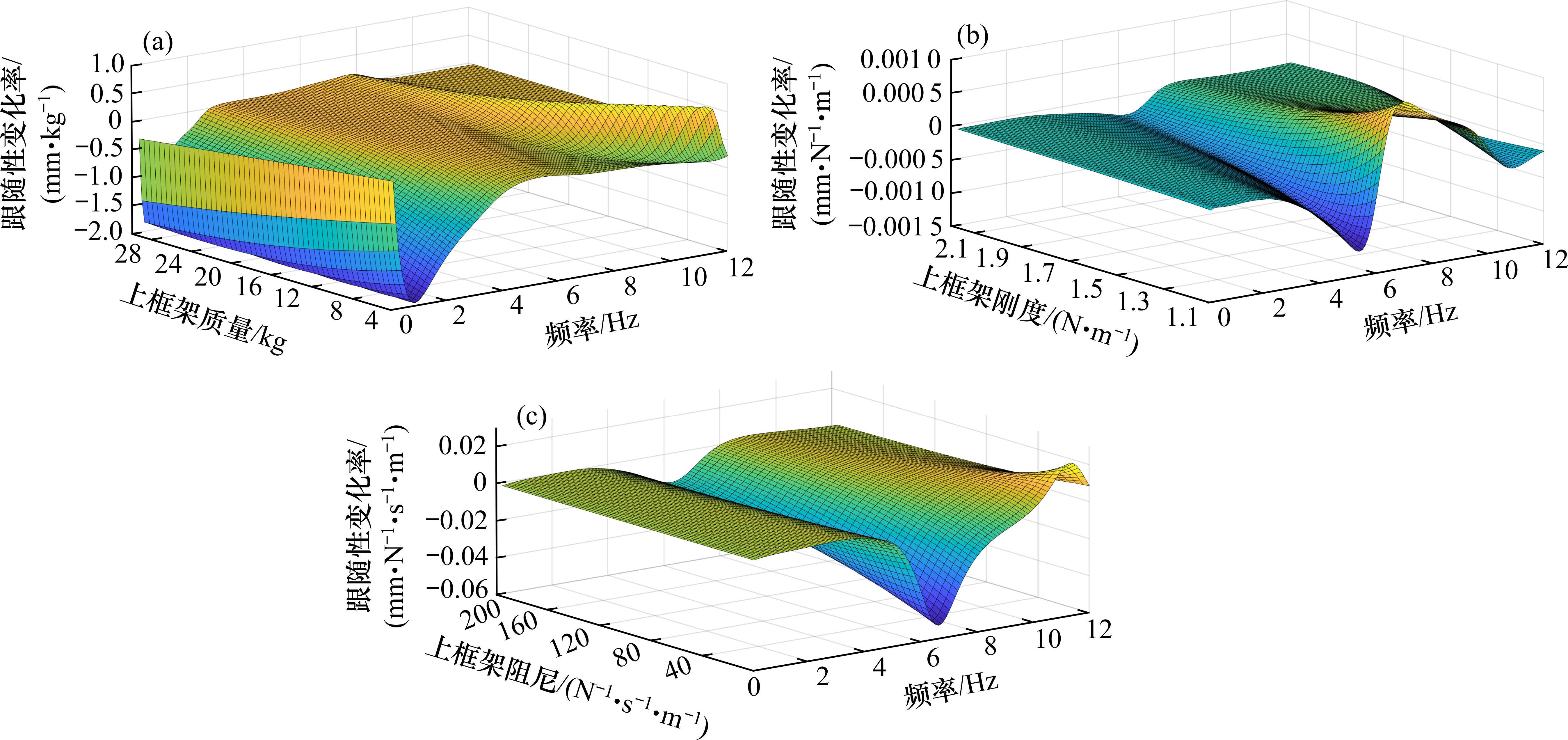
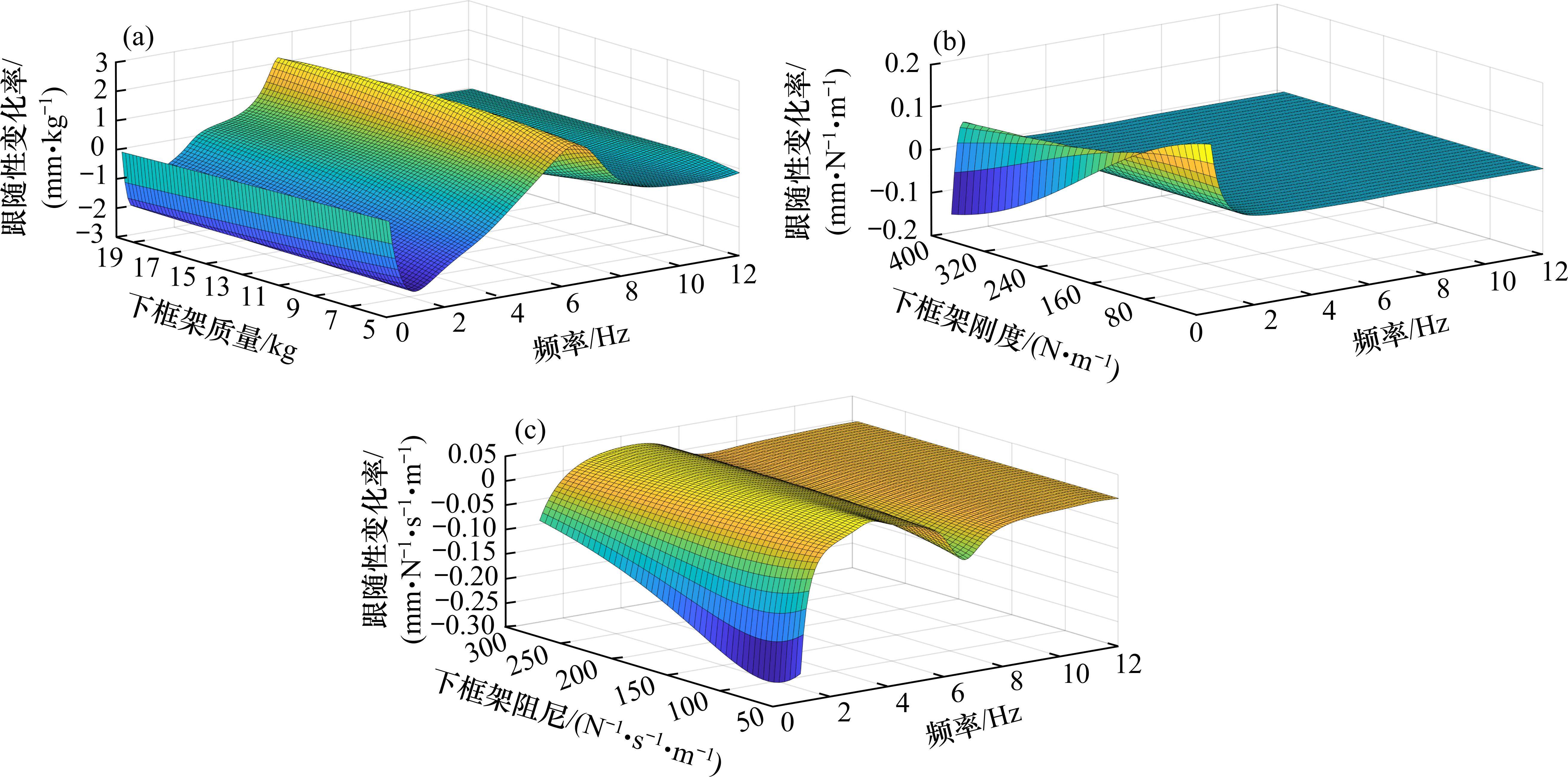
从灵敏度分析可以看出,弓头、框架的等效质量参数对跟随性影响较大,变化率数量级较大,范围为100~101;其次是等效阻尼系数,变化率数量级为10-2~10-1;最后是等效刚度,变化率数量级普遍低于10-3,其中下框架的等效刚度改变几乎不影响跟随性结果。
4 结论
1) 跟随性曲线的极大值发生频率与受电弓的反共振频率相关,反共振频率一般为受电弓的2阶固有频率。
2) 弓头与上框架的等效质量、刚度、阻尼以及下框架的等效刚度越小,跟随性越好;下框架的等效质量、阻尼越大,跟随性越好。当上框架的等效质量减小,下框架的等效阻尼增大时,跟随性极大值会略微降低。
3) 弓头、框架的等效质量增大时会引起跟随性极值频率变小,等效刚度增大则会引起跟随性极值频率变大。
4) 弓头、框架的等效质量对跟随性影响较大,其次是等效阻尼,最后是等效刚度,其中下框架的等效刚度改变几乎不影响跟随性结果。
理论、仿真与试验结果主要分析了1.5~12 Hz激振频率下的跟随性变化规律,对小于1.5 Hz及大于12 Hz的跟随性规律考虑存在局限。但建立的跟随性数学模型是比较准确的,结合受电弓等效参数变化对跟随性的影响规律,仍可以为后续从跟随性上优化弓网动态性能提供一定的理论参考。
刚性接触网-受电弓系统快速仿真方法
[J/OL]. 西南交通大学学报, 2023: 1-11. (孔令楠,周宁,程尧等.基于传递函数的高速受电弓跟随性研究[J].铁道科学与工程学报,2025,22(02):533-542.
KONG Lingnan,ZHOU Ning,CHENG Yao,et al.Research of the following-performance of high-speed pantograph based on transfer function[J].Journal of Railway Science and Engineering,2025,22(02):533-542.

