截至2023年底,我国铁路营业里程已突破15.8万km。随着铁路运营网络不断扩大,在大风区域开行列车已成为常态化现象。风速对列车的稳定性和安全性具有重要影响,强风会导致列车表面气压剧烈波动,引发列车横摆超限[1],增加发生安全事故的风险。近几年,世界各地有多起因强风而发生的出轨或翻车事故[2],因此,预测铁路区间风速对铁路安全运行至关重要。目前,国内外学者对风速预测进行了深入研究。常见的算法有极端梯度提升算法[3]、极限学习机(Extreme Learning Machines, ELM)[4]、支持向量回归[5]、最小二乘支持向量机(Least Squares Support Vector Machine, LSSVM)[6]、BP神经网络[7]等,均已被广泛应用于风速预测领域。传统的ELM只包含一个隐含层,当数据样本较多时,ELMELM难以充分提取训练样本的深层特征,针对这一问题TANG等[8]提出深度极限学习机(Deep Extreme Learning Machine, DELM)的概念,它结合自动编码器(Auto-Encoder, AE)的特征提取能力和ELM的快速训练能力,提取非线性数据特征时相较于常见的算法效果显著,而且具备深度学习技术的强大学习能力,但其参数的选择会直接影响到泛化性能,从而降低预测结果的稳定性。在预测模型的实际应用中,风速信号具有强烈的非线性特性,导致其预测精度不能满足实际需求。在对风速信号进行预处理时,通常采用信号分解法,以减少模型的预测困难。DING等[9]提出一种基于自适应噪声完备集合经验模态分解(Complete Ensemble Empirical Mode Decomposition with Adaptive Noise, CEEMDAN)的短期风速预测模型。KOSANA等[10]使用改进的自适应噪声完备集合经验模态分解(Improved Complete Ensemble Empirical Mode Decomposition with Adaptive Noise, ICEEMDAN)实现了一种混合预测框架,其中CEEMDAN和ICEEMDAN通过单次分解较好地解决了风速序列的非平稳性问题,但是很难处理波动性较高的风速信号。李颖智等[11]将CEEMDAN与排列熵相结合来判断每个分量的随机程度,再将随机程度较高的分量通过CEEMDAN进一步分解并预测,通过二次分解的方式有效提高预测精度,但二次分解计算量较大,训练效率低,并且会出现对数据变化敏感度不高等问题,造成风速序列分解不完全或过度分解等情况。除信号分解技术之外还可以利用优化算法提升模型泛化性能[12-14]。随着科学研究的不断发展,越来越多的群智能优化算法被提出。XUE等[15]提出一种新颖的群智能优化算法,即麻雀搜索算法(Sparrow Search Algorithm, SSA),该算法以其快速收敛和易实现等特点而闻名,并被广泛应用于各种优化问题的求解。但是SSA在实际应用中往往具有一定的局限性,从而使模型的预测效果出现浮动,导致预测精度不稳定。因此,需对SSA进一步改进以提升其在解决复杂工程问题时的稳定性。本文提出一种基于AMSD-WTSSA-DELM模型的铁路沿线短期风速预测方法。首先,针对原始风速序列的随机性极强,现存二次分解方法的分解不完全或过度分解导致其对数据变化不敏感等问题,提出自适应多步分解方法(Adaptive Multi-Step Decomposition, AMSD)。AMSD利用高度非线性的原始风速序列与分量的相关性,以及分量所包含的潜在模式、趋势和周期性等内在信息进行自适应多步分解,将非平稳的风速序列分解成若干平稳序列,从而降低预测难度。针对SSA算法易陷入局部最优、找到最优解困难和搜索依赖精英种群等缺陷,提出改进WTSSA算法,并通过8个包含单峰和多峰测试函数对该算法的性能进行综合验证。针对AMSD方法输出的分量,构建以WTSSA来优化权重参数和偏置的DELM模型,同时对随机选取3个分量的最优适应度曲线进行分析,验证WTSSA的实用性。汇总所有分量的预测数据,以合成最后的预测输出。最终,利用AMSD-WTSSA-DELM模型对实际铁路沿线风速数据进行预测分析,以验证本文方法的有效性和可靠性。
1 自适应多步分解(AMSD)
AMSD由ICEEMDAN、基于样本熵(Sample Entropy, SE)和皮尔逊相关系数(Pearson Correlation Coefficient, PCC)的自适应重构、分解方法和变分模态分解(Variational Mode Decomposition, VMD)等3个部分组成。1) 使用ICEEMDAN用序列进行初步分解;2) 基于SE和PCC的自适应重构和分解方法对符合已建立条件的分量进行重构,并筛选出需再次分解的分量;3) 使用VMD进一步分解。合并所有分解得到的分量,判断是否存在未充分分解的序列,如有,则重复步骤直到满足平稳性要求。
1.1 相关算法理论介绍
1.1.1 改进的自适应噪声完备集合经验模态分解(ICEEMDAN)
ICEEMDAN是一种具有自适应特点的时频分析算法[16],可将风速序列分解为一组频率递减的本征模态函数(Intrinsic Mode Function, IMF)。每个IMF展示原始风速数据在不同频率范围内的特征,相较于CEEMDAN和传统的经验模态分解以及集合经验模态分解,ICEEMDAN经过改进,解决了分解过程中可能出现的伪模态问题。此外,通过引入非高斯白噪声,改进的算法更有效地应对模态混叠问题,进一步减少了残留噪声的影响。所以AMSD利用ICEEMDAN在原始风速序列上的适应性高,去噪效果好和稳定性高等特点,用于初步分解,能有效降低序列非平稳性。
1.1.2 变分模态分解(VMD)
VMD[17]是通过构造带约束条件的变分问题,引入拉格朗日乘法算子和二次惩罚因子,将约束问题转换为非约束问题,最后采用交替方向乘子法求解。在保证所有IMF带宽之和最小的条件下,VMD将信号分解为K个IMF分量,有效提取不同频率成分,具有高分解精度和准确性,揭示信号内在结构和特征。在再次分解中使用VMD,能提高分解精度和准确性,并能进一步降低具有强非线性特征序列的非平稳性。
1.1.3 样本熵(SE)
SE[18]是衡量时间序列复杂度的算法,它不受数据长度影响,可用于分析各种时间序列数据的复杂性,揭示隐藏规律。本文在AMSD方法中使用样本熵来评估各分量的复杂度。一般而言,样本熵值越大序列复杂度越高;反之,值越小。
1.1.4 皮尔逊相关系数(PCC)
PCC[19]是一种用于衡量2个变量之间相关程度的方法,AMSD通过综合分析PCC和SE评估原始序列与分量的长期相关表现和分量所包含的潜在模式、趋势和周期性等内在信息。一般情况下,PCC的取值在(-1,1),相关程度可分为以下几种情况:当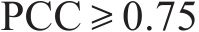
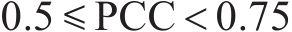
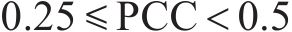
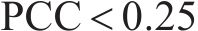
1.2 基于SE和PCC的自适应重构、分解方法
具体方法步骤如下。
步骤1:对原始数据X用ICEEMDAN分解得到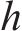
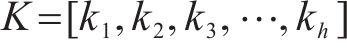
步骤2:因数据不同,若使用经验值作为静态阈值,则对数据变化不敏感,影响筛选结果。因此需要自适应更新阈值机制,更新公式如下所示:
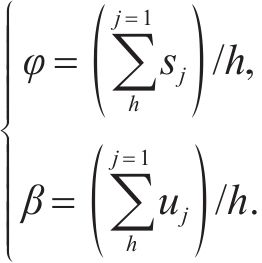
式中: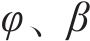
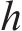
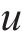
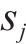
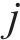
步骤3:模态分解出现过度分解的情况是不可避免的,文献[20]采用了自适应重构方法,有效解决了过度分解问题。考虑到AMSD在分解过程中应避免过度分解,利用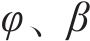
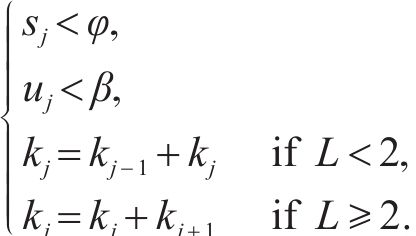
式中: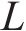
通过筛选得到样本熵值与相关系数较为异常的模态分量。选取第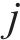
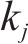
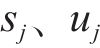
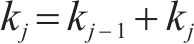
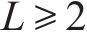
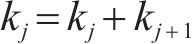
步骤4:现有二次分解方法在阈值选取上采用经验法,然而,这种方法对数据变化不敏感。为提高AMSD的适应性和数据变化敏感性,建立如下条件筛选需二次分解的分量,即:
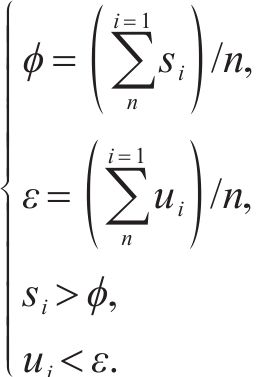
式中: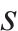
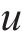

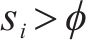
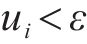
2 改进麻雀搜索算法(WTSSA)
2.1 改进策略
尽管SSA算法易实现且快速,但存在找到最优解困难、搜索依赖精英种群和易陷入局部最优等挑战。为提升优化能力,采取以下措施提升全局搜索和局部探索能力,加快收敛速度。SSA具体原理见文献[15]。
2.1.1 Chebyshev混沌映射
引入Chebyshev混沌映射对SSA算法进行改进,从而增加种群多样性,提高搜索空间覆盖率,加快收敛速度,提高算法的优化性能,公式如下:
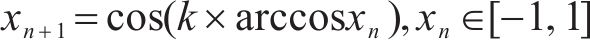
2.1.2 自适应权重策略
在SSA中引入了随迭代次数变化的惯性权重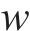
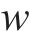
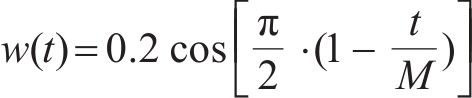
式中:M为最大迭代次数;t为当前迭代次数;权重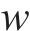
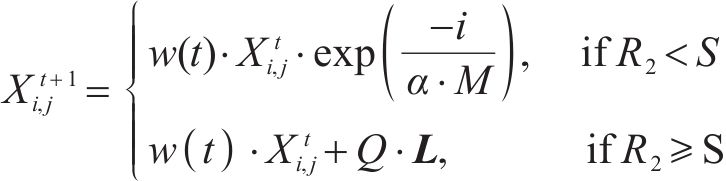
式中: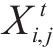
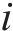
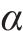
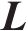
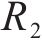
2.1.3 自适应t分布扰动策略
为改善SSA后期迭代中种群多样性下降、易陷入局部最优问题,引入自适应t分布策略对麻雀个体位置进行变异操作。t分布函数如下:
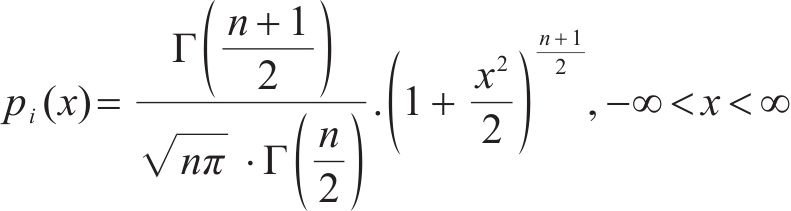
根据当前循环中发现者所确定的最佳位置,应用t分布扰动策略对跟随者的位置进行调整,相关公式如下:
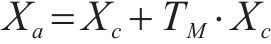
式中: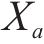
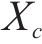
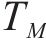
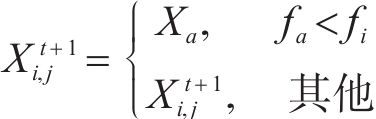
式中: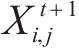
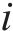
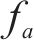
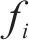
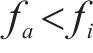
2.2 算法验证
为评估WTSSA算法的性能,分别在单峰(F1~F3)和多峰函数(F4~F6)下进行测试,并与原始SSA、PSO、GWO和DBO算法进行性能比较。测试函数参数设置如表1所示。实验结果与收敛曲线如表2和图1所示。
| 编号 | 函数名称 | 维度 | 搜索范围 | 最优值 |
|---|---|---|---|---|
| F1 | Sphere | 30 | [-100, 100] | 0 |
| F2 | Schwefel1.2 | 30 | [-100, 100] | 0 |
| F3 | Quartic | 30 | [-1.28, 1.28] | 0 |
| F4 | Generalized Rastrigin | 30 | [-5.12, 5.12] | 0 |
| F5 | Generalized Penalized 2 | 30 | [-50, 50] | 0 |
| F6 | Kowalik | 4 | [-5, 5] | 0.000 3 |
| 测试函数 | DBO | GWO | PSO | SSA | WTSSA | |
|---|---|---|---|---|---|---|
| F1 | 最优值 | 4.62×10-155 | 3.46×10-29 | 8.4 | 4.2×10-237 | 0 |
| 平均值 | 7.43×10-116 | 3.59×10-27 | 8.999 | 3.61×10-52 | 0 | |
| 标准差 | 1.36×10-116 | 2.32×10-27 | 21.414 | 6.59×10-53 | 0 | |
| F2 | 最优值 | 7.17×10-13 | 1.67×10-9 | 78.354 | 0 | 0 |
| 平均值 | 1.23×10-39 | 0.000 1 | 62.431 | 2.78×10-24 | 0 | |
| 标准差 | 2.26×10-40 | 3.94×10-5 | 168.7 | 5.08×10-25 | 0 | |
| F3 | 最优值 | 0.001 1 | 0.001 3 | 5.694 | 0.001 5 | 0.000 18 |
| 平均值 | 0.001 3 | 0.002 1 | 3.119 | 0.001 9 | 0.000 17 | |
| 标准差 | 0.000 9 | 0.001 8 | 1.044 | 0.001 3 | 0.000 11 | |
| F4 | 最优值 | 0 | 0 | 75.996 | 0 | 0 |
| 平均值 | 0.728 | 4.464 | 27.662 | 0 | 0 | |
| 标准差 | 0.132 | 3.209 | 128.544 | 0 | 0 | |
| F5 | 最优值 | 5.71×10-5 | 0.2 | 24.524 | 3.63×10-14 | 2.01×10-14 |
| 平均值 | 0.46 | 0.237 | 35.882 | 7.26×10-11 | 6.85×10-11 | |
| 标准差 | 0.686 | 0.71 | 61.646 | 3.40×10-11 | 3.08×10-11 | |
| F6 | 最优值 | 0.000 3 | 0.000 3 | 0.000 3 | 0.000 3 | 0.000 3 |
| 平均值 | 0.000 4 | 0.009 | 0.008 | 0.000 2 | 4.82×10-5 | |
| 标准差 | 0.000 7 | 0.007 | 0.005 | 0.000 3 | 0.000 3 | |
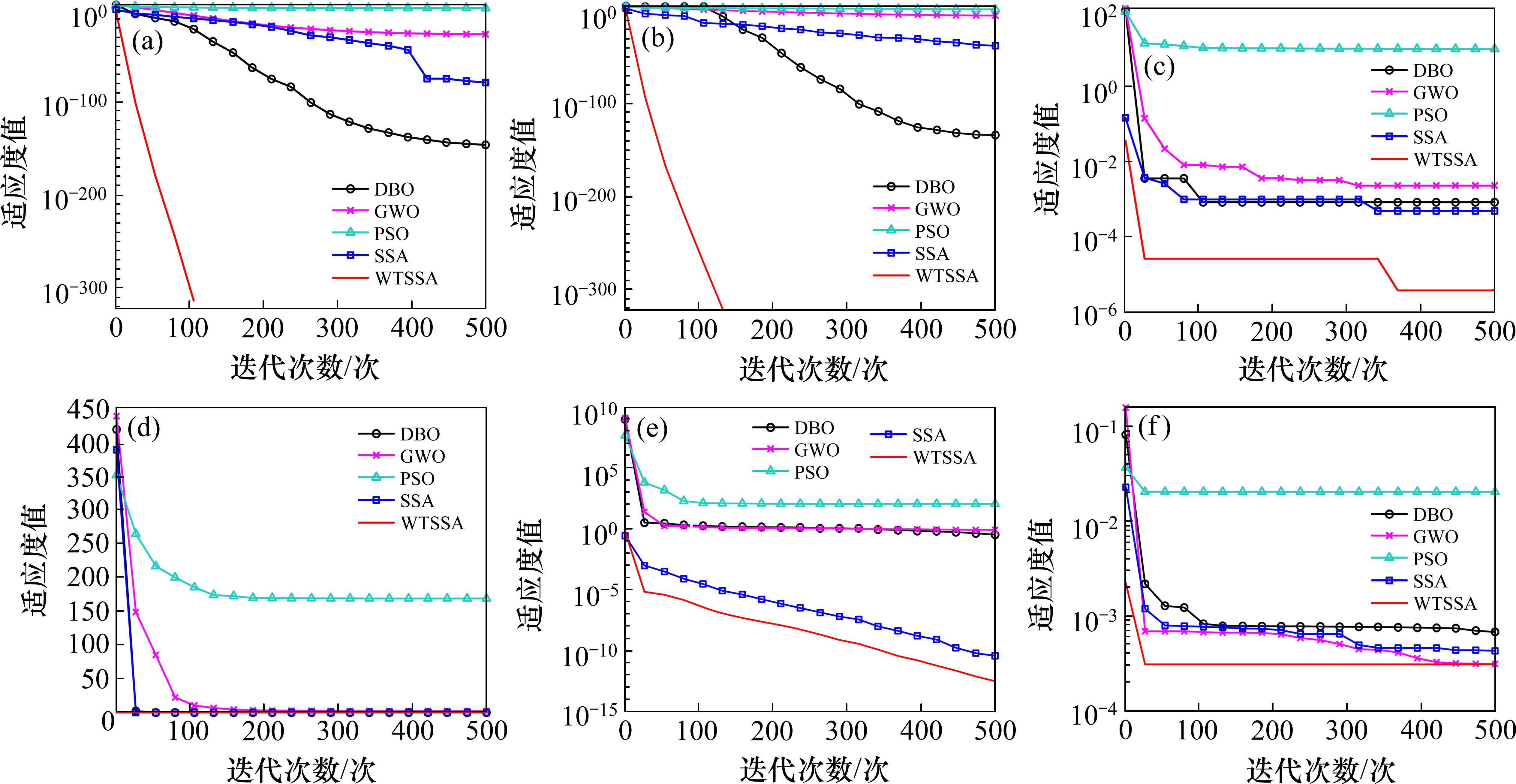
通过观察图1,发现WTSSA相较于DBO、GWO、PSO和SSA等算法,在单峰和多峰函数下,收敛速度更快、优化精度更高。在图1(d)所示的F4函数收敛曲线上,由于WTSSA收敛速度很快,一开始就找到最优解,所以图上显示为一条直线。综上所述,将自适应权重策略、自适应t分布和Chebyshev混沌映射有效融合到SSA算法中,能增强综合优化能力,克服传统SSA的缺陷,提升模型泛化性能,更好发挥模型拟合能力。
3 基于AMSD-WTSSA-DELM模型的预测方法
3.1 WTSSA-DELM预测模型
3.1.1 深度极限学习机(DELM)
DELM是一种深度学习网络,由多个极限学习机自编码器ELM-AE堆叠而成。在ELM模型的基础上,ELM-AE通过添加正则化项进行优化,自动编码器AE可以在无监督环境下进行训练,训练后将输入和输出连接一致。DELM通过减少重构误差,实现对原始输入的精确还原,其分层训练机制能有效捕捉数据的深层次特征,避免了对关键参数进行细致调整,从而提升模型的运算效率。详细原理可参考文献[8]。
3.1.2 基于WTSSA算法的DELM参数优化流程
由于在DELM中,输入层的权重和偏置值是随机生成的,影响模型预测的稳定性。因此为提高模型的泛化性能,需优化DELM的权重和偏置。流程如下。
步骤1:设置SSA的相关参数,包含种群数量n、最大迭代次数M等以及DELM的关键参数寻优范围。
步骤2:通过式(4)中的Chebyshev混沌序列初始化麻雀种群。
步骤3:分析麻雀个体的适应度值,同时标记当前种群的全局最佳和最差适应度值及其相应位置。
步骤4:根据适应度值对种群进行排序。
步骤5:选择适应度排名前pNum的个体作为发现者,其余为跟随者,利用加入自适应权重策略后的式(6)更新发现者的位置。
步骤6:剩余的麻雀作为加入者,更新跟随者的位置。
步骤7:利用式(8)来确定通过t分布扰动后的更新位置,并使用式(9)替换跟随者的位置。
步骤8:按照预警者的数量,随机选择一定比例的麻雀作为预警者,并对它们的位置进行更新。
步骤9:更新位置后,重新计算麻雀个体的适应度值,并更新每个个体的最佳位置以及整个种群的全局最优位置。
步骤10:检查迭代次数是否已经达到预设的M次,若已达到,则结束算法并输出最优解;若未达到,则返回步骤3继续执行。
3.2 AMSD-WTSSA-DELM预测模型实现流程
本文提出的风速预测方法实现流程如图2所示,具体过程如下。
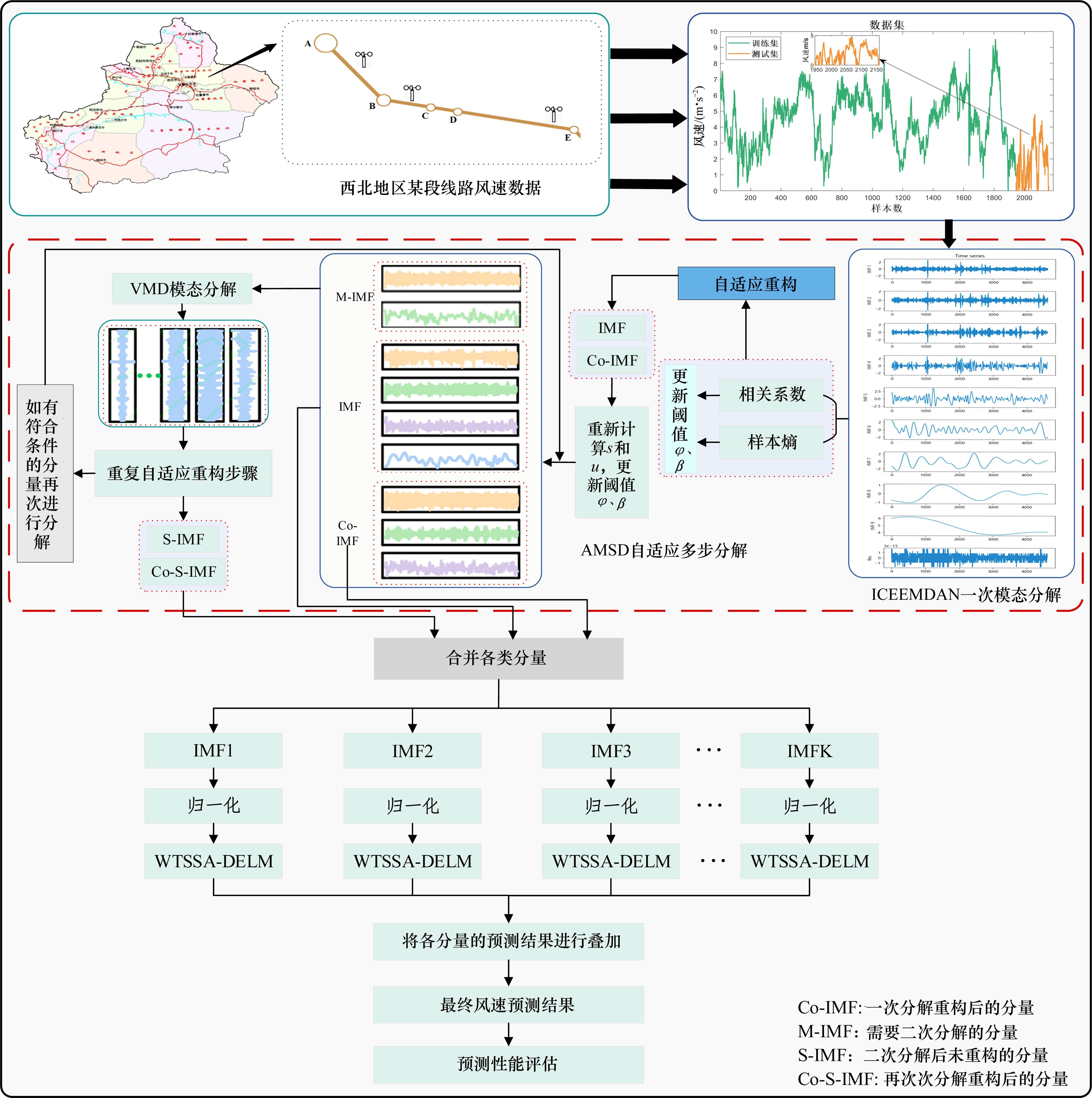
1) 对原始的风速序列使用多步分解方法AMSD,降低原始序列的非平稳性;同时,给出最后需要预测的分量,准备训练预测模型。
2) 进行归一化处理,确保所有模态分量的值均在0~1的范围内。
3) 为每个模态分量独立构建一个基于DELM的预测模型,并使用WTSSA优化DELM模型的权重和偏差参数。
4) 汇总所有分量的预测数据,以合成最终的预测输出。
5) 使用相关的评估指标衡量模型的预测性能。
3.3 模型评估指标
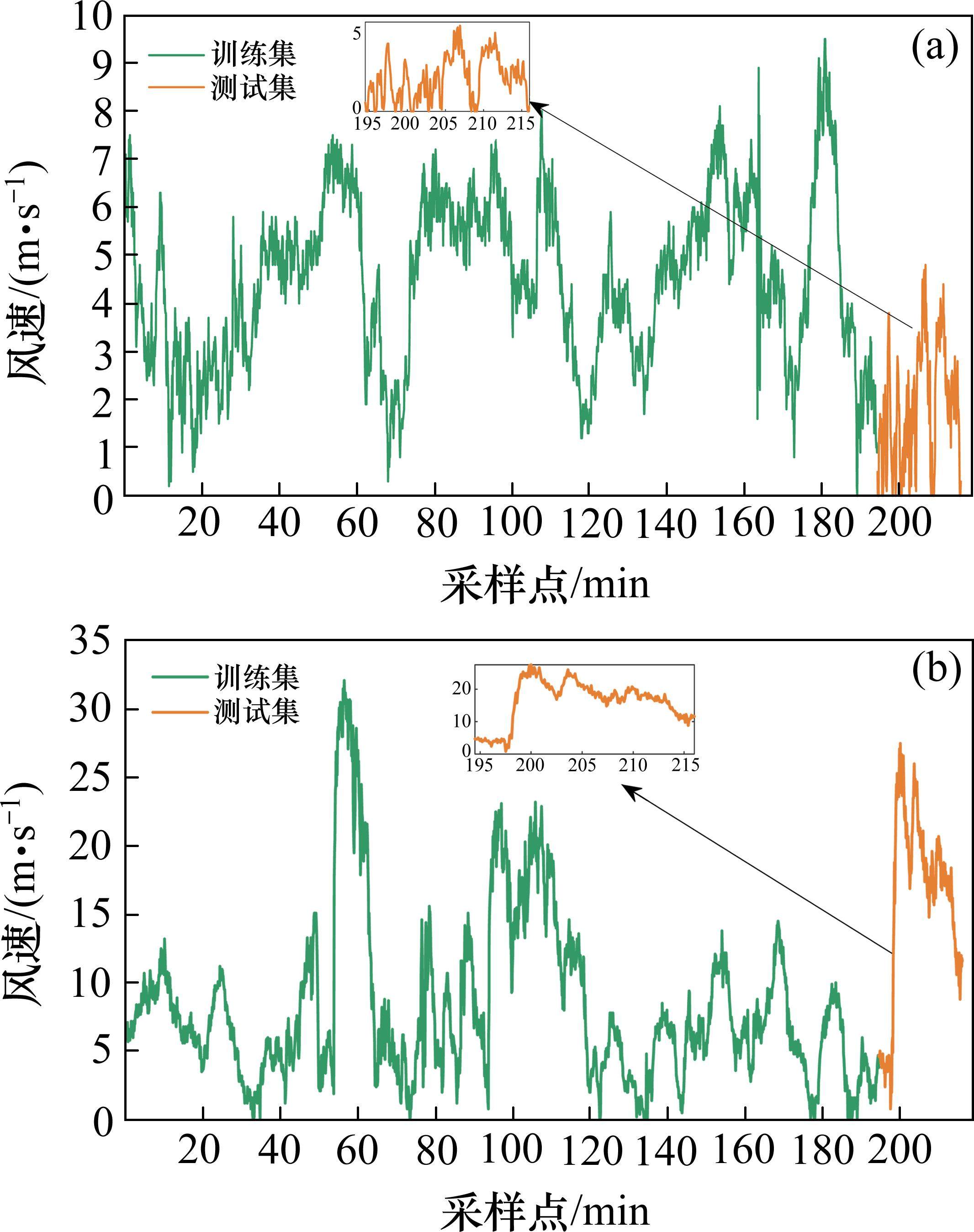
通过使用平均绝对误差(Emae)、决定系数(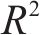
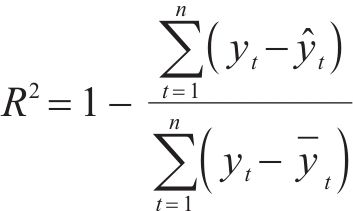
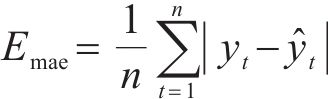
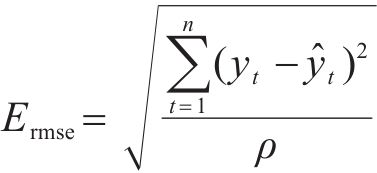
式中:Emae表示预测值与真实值之间的平均绝对误差;Ermse表示预测值和真实值的均方根误差;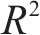
4 实例分析
4.1 数据描述
所使用的数据集是中国铁路某公司提供的2015年和2016年的西北地区某段线路上采集到的数据,数据采集频率为10 min。为充分体现本文模型的泛化能力和普适性,采用2016年1月1日至1月15日和2016年3月12日至3月26日的2组风速数据分别作为正常风速实验数据和大风风速实验数据。每组数据集共有2 160个数据点,其中90%作为训练集,剩下的10%作为测试集评估模型的预测能力。2组实验数据变化曲线如图3所示。
4.2 自适应多步分解(AMSD)
正常风速段实验数据为例,图3(a)所示的风速数据呈现出明显的非平稳性,为更好处理这一特性,采用AMSD方法。
1) 使用ICEEMDAN对原始风速数据进行分解,生成一系列子序列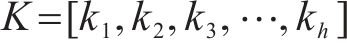
2) 对各IMF分量进行样本熵和相关性计算,计算结果如表3和表4所示。根据各模态分量的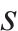
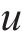

| 序列编号 | Original | IMF1 | IMF2 | IMF3 | IMF4 | IMF5 | IMF6 | IMF7 | IMF8 | IMF9 | res |
|---|---|---|---|---|---|---|---|---|---|---|---|
| s | 1.394 | 0.428 | 0.240 | 0.259 | 0.165 | 0.117 | 0.071 | 0.060 | 0.018 | 0.003 | 1.96×10-4 |
| u | — | 0.171 | 0.170 | 0.193 | 0.231 | 0.323 | 0.424 | 0.548 | 0.403 | 0.332 | 0.107 |
| 序列编号 | Original | IMF1 | IMF2 | IMF3 | IMF4 | IMF5 | IMF6 | IMF7 | IMF8 | Co-IMF |
|---|---|---|---|---|---|---|---|---|---|---|
| s_ | 1.394 | 0.428 | 0.240 | 0.259 | 0.165 | 0.117 | 0.071 | 0.060 | 0.018 | 0.003 |
| u_ | — | 0.171 | 0.170 | 0.193 | 0.231 | 0.323 | 0.424 | 0.548 | 0.403 | 0.332 |
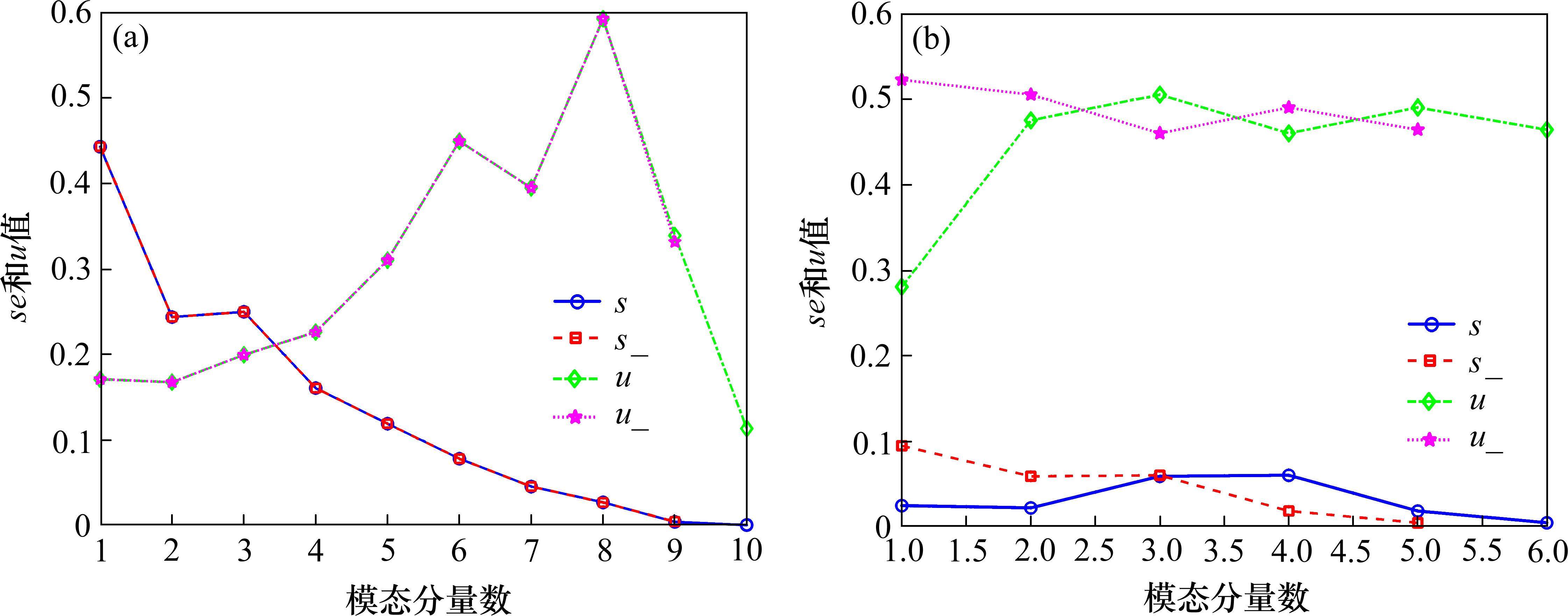
3) 自适应重构式(2)之后再次计算重构之后分量的s和u值,并在式(3)建立的条件上筛选出需要进行二次分解的分量。计算结果表明,IMF1、IMF2、IMF3和IMF4需要进行再次分解。
4) 由图5可知,IMF1、IMF2、IMF3和IMF4数据变化剧烈,频率相对较高,使用VMD将以上4个分量分别进行再次分解,降低整体数据的非线性。需再次分解的分量用M-IMF表示。
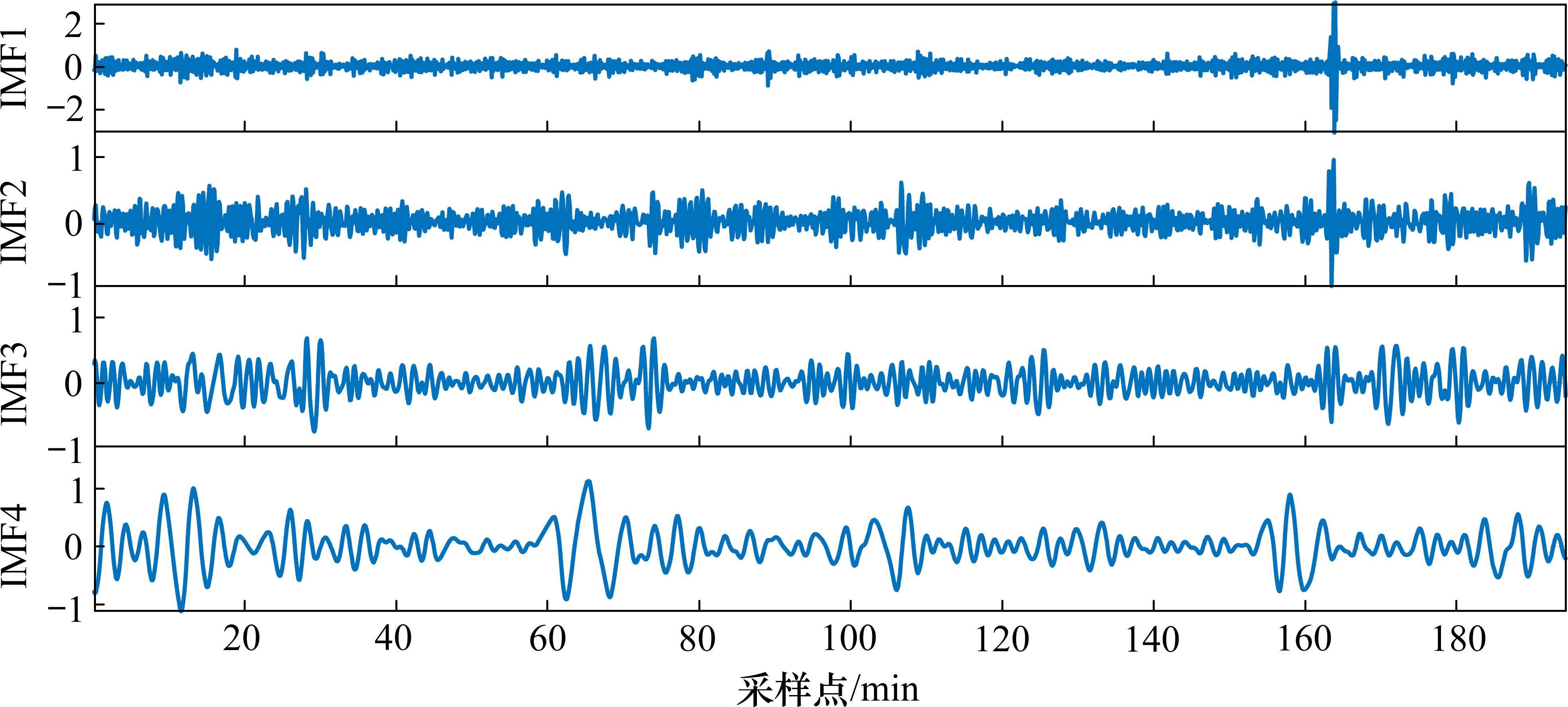
5) 再次分解后各分量的复杂度会大幅减少,序列会更加平稳。为避免过度分解问题进行自适应重构,以M-IMF1为例,其s和u值变化曲线如图4(b)所示。
通过观察样本熵和相关系数的变化,再次分解后各分量的复杂性和相关性比较均匀,分解终止并合并输出所有模态分量。实验结果表明,AMSD方法能够自适应地降低原始序列的非平稳性,并且其中的自适应重构方法能有效处理多步分解中产生的过分解问题。最后对AMSD方法产生的分量进行归一化处理,准备输入给预测模型进行训练和测试。
4.3 DELM预测模型参数优化
利用WTSSA对DELM模型的权重和偏置进行优化,并以模型测试误差的均方根误差(Ermse)作为适应度函数。在实验设置中,麻雀种群的规模被设定为30(n=30),同时将最大迭代次数限制在50(M=50),旨在保证预测性能的同时,减少模型训练所需的时间。
为验证WTSSA对DELM模型预测性能的影响,在AMSD方法产生的风速模态分量中随机选取3个分量为例,分别应用WTSSA和SSA这2种算法对DELM模型的权重和偏置参数进行优化,优化过程中的最优适应度变化趋势如图6所示。
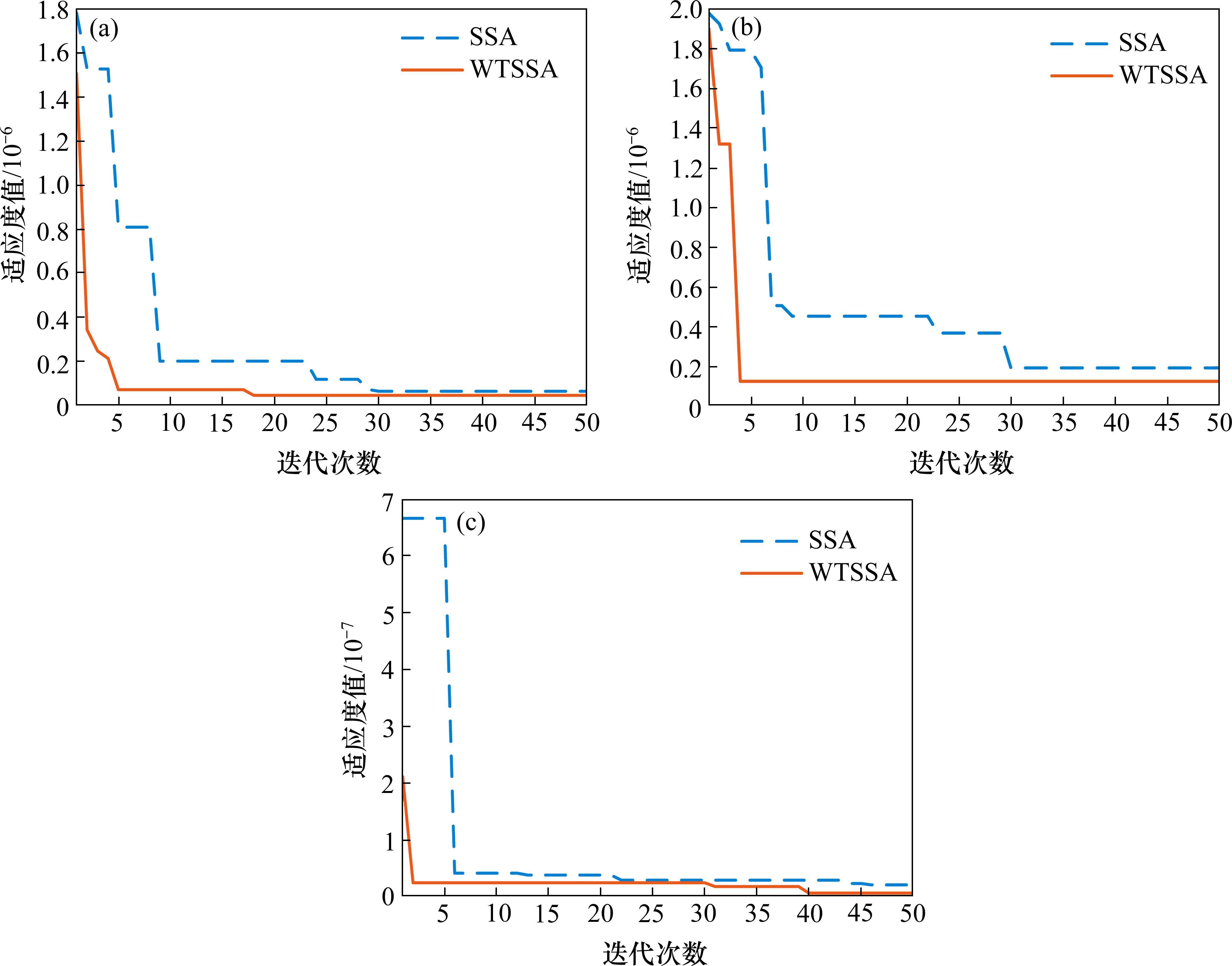
实验结果表明,相对于SSA算法,WTSSA算法在分量IMF4、IMF8和IMF15的寻优过程中,迭代次数分别提前12次、26次和5次,尽管WTSSA陷入局部最优,但其收敛曲线始终位于SSA下方,并且具有更快的收敛速度。表明WTSSA能够有效弥补SSA的不足,在实际参数优化中充分证明WTSSA在寻找最优解方面具有更优越的性能。
4.4 预测结果分析
4.4.1 正常风速预测结果分析
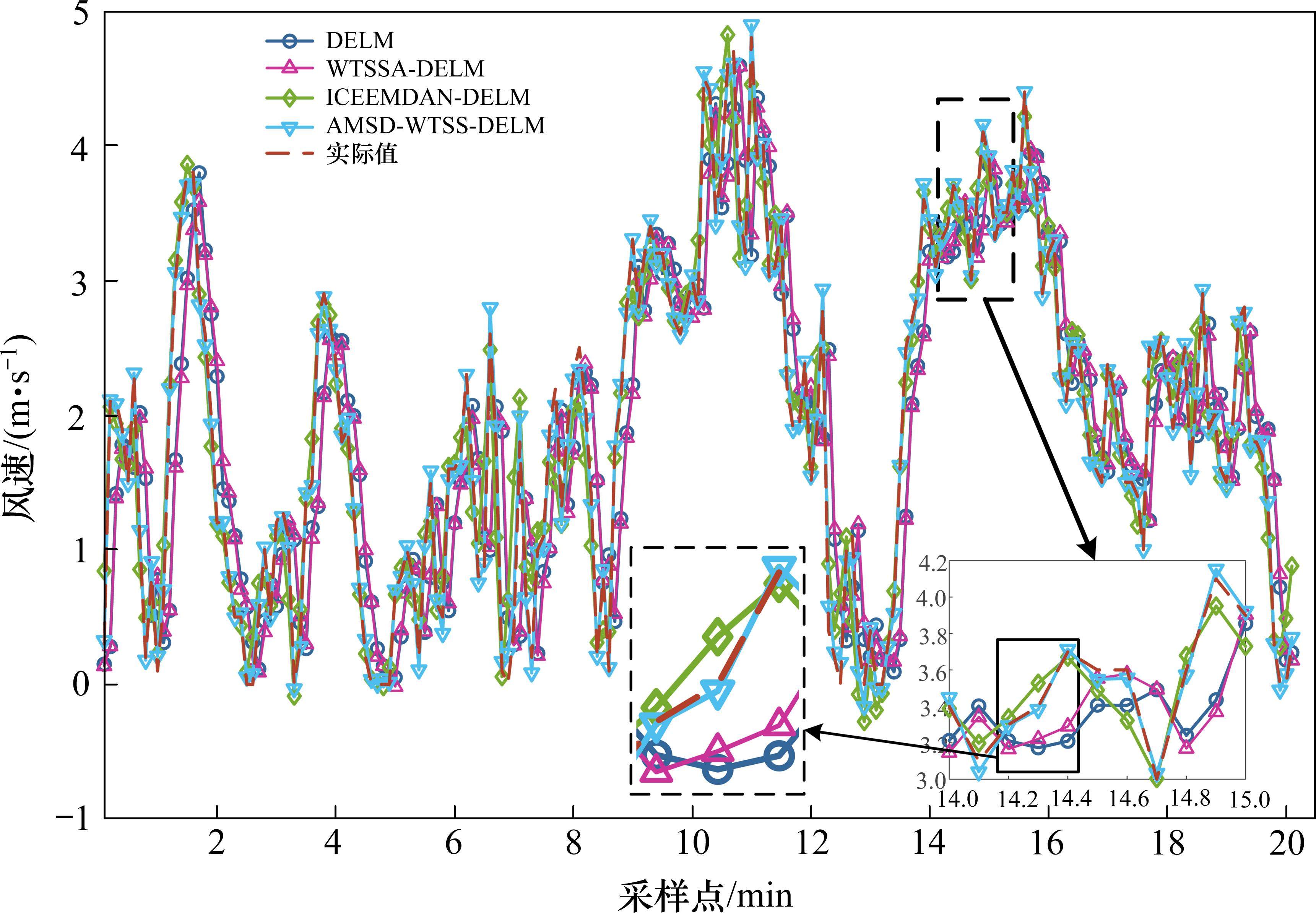
为全面验证所提出预测模型的性能,进行以下3组对比实验:1) 将DELM模型与其他几种预测方法进行对比。2) 对比SSA和WTSSA分别对DELM模型参数进行优化的效果。3) 单一模型和EMD改进分解算法之间的对比。最终分析本文提出的预测模型实验结果,可以依次证明相关方法的有效性和整体有效性。实验结果数据如表5所示,为方便分析,在图7中只展示每组实验精度最高的预测结果。
| 实验类型 | 算法类型 | Emae | Ermse | R2 |
|---|---|---|---|---|
| 单模型 | LSSVM | 0.703 3 | 0.878 2 | 0.499 6 |
| ELM | 0.583 7 | 0.731 4 | 0.647 9 | |
| BP | 0.535 0 | 0.679 9 | 0.695 8 | |
| DELM | 0.544 4 | 0.678 5 | 0.697 0 | |
| WTSSA | SSA-DELM | 0.497 3 | 0.634 0 | 0.721 6 |
| WTSSA-DELM | 0.492 4 | 0.626 2 | 0.753 7 | |
| 一次分解 | EMD-DELM | 0.324 7 | 0.538 6 | 0.890 6 |
| EEMD-DELM | 0.221 5 | 0.377 4 | 0.939 2 | |
| CEEMD-DELM | 0.264 7 | 0.554 8 | 0.918 3 | |
| CEEMDAN-DELM | 0.265 4 | 0.541 9 | 0.922 5 | |
| ICEEMDAN-DELM | 0.191 4 | 0.335 7 | 0.956 9 | |
| 本文方法 | AMSD-WTSSA-DELM | 0.052 7 | 0.120 4 | 0.996 7 |
如表5所示,与单一模型LSSVM、BP、ELM相比,DELM具有更好的表现,Ermse、Emae和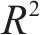
然而,从图7可以看出,由于正常风速实验数据的测试集风速序列的随机性、波动性等非线性特性比较强,其预测效果的提升并不明显,同时预测值的趋势存在时间上滞后和超前等问题,其简称为时迟问题,时迟问题对我国铁路大风预警规则而言影响很大。因此,采用群体智能优化算法和模态分解技术来提高预测的准确性是十分必要的。参数优化后的预测模型结合了群智能优化算法,能够更好地跟踪实际数据趋势。同时注意到SSA-DELM与DELM相比,R2提升3.53%,Ermse和Emae分别降低6.56%和2.46%,证明群智能优化算法可以有效提升预测模型的泛化性能,使模型更加稳定。因原始SSA的缺陷,提出WTSSA算法,为证明该算法的有效性,将原始SSA替换为WTSSA,对比DELM的优化效果。WTSSA-DELM与DELM相比,Emae和Ermse分别降低9.55%、7.71%,R2提升8.13%。
第3组实验对比了EMD及其改进算法结合DELM进行预测,来证明ICEEMDAN的优越性。如表5所示,EMD-DELM、EEMD-DELM、CEEMD-DELM、CEEMDAN-DELM、ICEEMDAN-DELM与WTSSA-DELM相比,Emae分别降低34.06%、55.02%、46.24%、46.10%、61.13%;Ermse分别降低13.99%、39.73%、11.40%、13.46%、46.39%;R2分别提升了5.56%、11.32%、8.84%、9.34%、13.42%;由3种评估指标的对比结果可知,效果提升最为明显的是ICEEMDAN-DELM。ICEEMDAN分解算法在解决EMD算法的模态重叠和端点效应、EEMD算法的重构误差大、CEEMD算法对高频噪声处理能力有限等局限性,以及CEEMDAN的残余噪声和伪模态问题后,预测的准确性得到显著提高。而且从图7放大后的子图上可以看出,加入ICEEMDAN分解算法之后,进一步减小了时迟问题,说明分解算法不仅在预测精度上提供帮助,还对解决时迟问题有一定的效果,但可以看出其在一定程度上仍然存在时迟问题。
最后,为充分降低原始序列的复杂度,利用本文提出的AMSD方法进行多步分解。从表5中可以得出,与DELM相比,Emae、Ermse分别降低了90.32%、82.25%,R2提升了43.00%。从图7放大后的子图上可以看出,加入本文提出的AMSD方法之后,不仅在预测精度上得到了最佳的预测结果,充分克服了时迟问题,预测结果的趋势跟踪基本跟实际值保持一致。
4.4.2 大风风速预测结果分析
为进一步验证本文模型的普适性和泛化能力,选取一段大风速时段进行实验并预测风速,结果数据如表6所示,预测结果曲线如图8所示。如表6所示,同样DELM相比其他单一模型具有更好的表现,Ermse、Emae和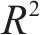
| 实验类型 | 算法类型 | Emae | Ermse | R2 |
|---|---|---|---|---|
| 单模型 | LSSVM | 1.133 2 | 1.484 9 | 0.939 7 |
| ELM | 1.042 2 | 1.419 6 | 0.944 8 | |
| BP | 1.090 5 | 1.397 2 | 0.946 6 | |
| DELM | 1.033 4 | 1.373 3 | 0.948 4 | |
| WTSSA | SSA-DELM | 1.035 0 | 1.354 8 | 0.949 8 |
| WTSSA-DELM | 0.975 6 | 1.296 1 | 0.964 9 | |
| 一次分解 | EMD-DELM | 0.568 2 | 0.958 3 | 0.986 5 |
| EEMD-DELM | 0.432 0 | 0.560 9 | 0.991 3 | |
| CEEMD-DELM | 0.474 0 | 0.607 0 | 0.989 9 | |
| CEEMDAN-DELM | 0.436 5 | 0.543 8 | 0.991 9 | |
| ICEEMDAN-DELM | 0.324 0 | 0.413 5 | 0.995 3 | |
| 本文方法 | AMSD-WTSSA-DELM | 0.149 4 | 0.355 9 | 0.999 0 |
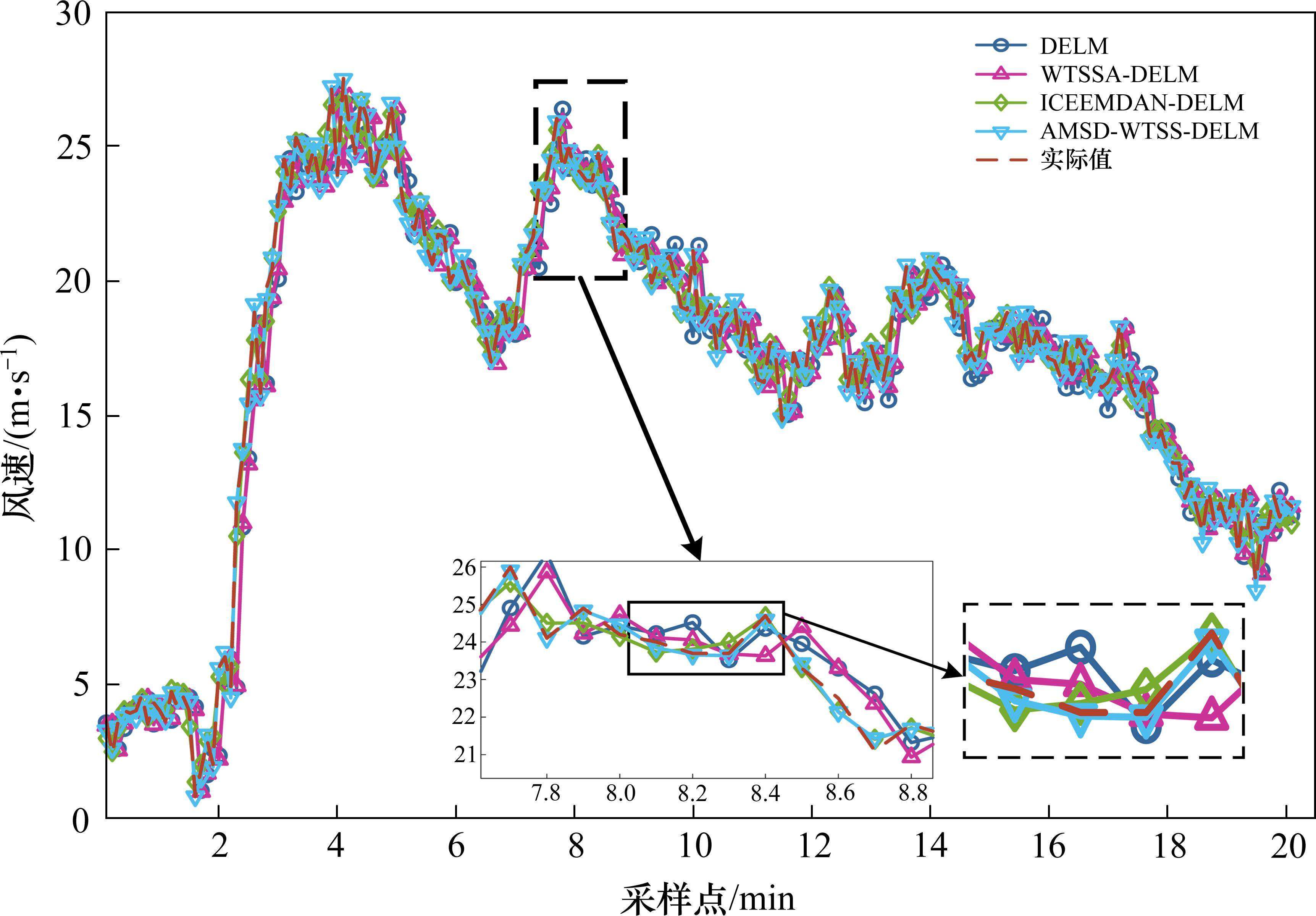
如表6所示,第3组实验中EMD-DELM、EEMD-DELM、CEEMD-DELM、CEEMDAN-DELM、ICEEMDAN-DELM与WTSSA-DELM相比,Emae分别降低41.76%、55.72%、51.41%、55.26%、66.79%;Ermse分别降低26.06%、56.72%、53.17%、58.04%、68.10%;R2分别提升2.24%、2.74%、2.59%、2.80%、3.15%。由3种评估指标的对比结果可知,其中提升效果最为明显的是ICEEMDAN-DELM。
从表6中可以得出,AMSD-WTSSA-DELM与DELM相比,Emae、Ermse分别降低85.54%、74.08%,R2提升5.34%。同时相较于2次实验的WTSSA-DELM模型和ICEEMDAN-DELM模型结果,可以看出,本模型R2更大,Ermse和Emae更小。通过2组数据上所得出的实验结果,可以看出,本模型使原始信号和预测结果之间的拟合程度控制在99%以上,且从图7和图8可以看出,组合预测模型AMSD-WTSSA-DELM相比于其他方法能够更好地跟踪实际数据趋势,在预测精度和时迟问题上得到明显的改进。
5 结论
1) 通过应用本文提出的AMSD方法将原始序列分解成多个相对稳定的子序列,从而降低了预测难度。与传统的二次分解相比,可以显著提高模型对不同模式风速数据的适应性。
2) 提出的WTSSA算法能够深入挖掘样本空间中的潜在区域,增强算法在全局和局部搜索中的优化能力,并提升麻雀种群内部的竞争力。有效地解决了SSA算法常见的易陷入局部最优解和低精度收敛问题,展现出更加卓越的优化性能。
3) 通过WTSSA算法对DELM模型的关键参数进行优化,不仅显著提高了模型的预测能力,还确保了预测结果的稳定性和精确性,相较SSA算法表现更佳。
4) 所提模型对风速数据具有更好的预测效果,2次实验中决定系数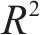
5) 通过2组实验数据分析,证明本方法在风速预测任务中能够准确预测短期风速,更为重要的是充分克服风速数据的非平稳性和波动性导致的机器学习预测的时迟问题,能够实时跟踪真实数据。模型泛化性能高,可为铁路系统和智能化管理提供有力技术支撑。
尼比江·艾力 ,张林鍹,李奕超等.基于AMSD-WTSSA-DELM模型的铁路沿线短期风速预测方法[J].铁道科学与工程学报,2025,22(02):543-556.
AILI Nibijiang,ZHANG Linxuan,LI Yichao,et al.Short-term wind speed prediction method along the railroad based on AMSD-WTSSA-DELM model[J].Journal of Railway Science and Engineering,2025,22(02):543-556.