轴承作为机械系统中的关键组成部分之一,其性能直接关系到整个机械设备的稳定性、效率和寿命[1]。亚健康是处于健康和故障之间的状态,识别出轴承的亚健康状态,就可以提前预警,预防机械故障的发生,近年来,已有大量关于轴承故障诊断的研究[2-4],但主要集中在故障发生后的定位问题,对于轴承的亚健康状态识别的研究相对匮乏。要识别轴承的亚健康状态,需要从轴承复杂振动信号中提取能反映其状态变化的信号特征。信号分解算法可用于挖掘原始信号中的特征信息[5],SUN等[6]利用经验模态分解(empirical mode decomposition, EMD)将振动信号分解为若干IMF分量,进而提取特征,但EMD无法解决分解信号时的模态混叠及端点效应问题。HAN等[7]利用局部均值分解(local mean decomposition, LMD)将振动信号分解为有限乘积函数来提取原始信号的特征信息,但LMD对噪声非常敏感,而轴承振动信号包含大量背景噪声,这会导致LMD的分解效果较差。VMD作为一种先进的信号处理技术,在轴承中得到了大量应用[8-10],它克服了模态混叠和端点效应的问题,并且能抑制噪声干扰,但是,传统的VMD算法在处理轴承信号时面临参数选择主观的问题。WANG等[11]以最小平均包络熵为适应度函数,利用麻雀搜索算法(sparrow search algorithm, SSA)自适应获取VMD的最优参数,但以单一指标作为适应度函数不能很好地表征信号状态特征,并且SSA易陷入局部最优。轴承振动信号包含轴承状态变化的重要信息,但它是非线性的[12],利用信号分解算法对振动信号进行预处理后仍会保留非线性特征,而熵能有效地描述非线性数据的动态特性,提供关于系统状态复杂性、不确定性及其时间演化的重要信息,基于熵的方法被广泛用于轴承故障诊断和机械设备健康监测中。TAN等[13-14]提出新的曼哈顿熵算法和敏感多尺度符号动态熵算法,能准确估计机械信号复杂度,提取出优异特征,区分轴承各种状态。RAJABI等[15]采用排列熵提取轴承信号特征。ZHUANG等[16]采用样本熵提取轴承信号特征。ROSTAGHI等[17]证明了散布熵(dispersion entropy, DE)在性能评估方面的有效性。TAN等[18]提出一种新的叠加改进复合多尺度散布熵算法,能准确提取轴承故障敏感特征,相比多尺度散布熵、多尺度样本熵等其他熵算法具有一定优势。与排列熵不同,DE能够充分考虑到幅值的差异,并且其计算效率高于样本熵。然而,DE仅仅量化了信号在单一尺度下的不规则性,会忽略隐藏在其他尺度下的一些有价值的信息。因此,SUN等[19]将DE进行粗粒化,得到多尺度散布熵(multiscale dispersion entropy, MDE)。但由于粗粒度过程的性质,随着尺度的增大,粗粒化序列会变得越短,这导致无法充分利用信号中的信息,并且DE和MDE只反映了原始信号的特征信息,对动态变化不是很敏感。针对上述问题,本文提出一种参数自适应VMD结合改进散布熵特征的轴承亚健康状态识别模型。本文的创新点如下:1) 在SSA算法中引入tent混沌映射、鱼鹰优化算法(osprey optimization algorithm, OOA)的位置更新策略和柯西变异策略,解决了SSA易陷入局部最优的问题,提高全局搜索能力,采用ISSA自适应获取VMD最优分解参数。2) 考虑包络熵和互信息各自的特点,建立它们的综合指标为最优参数VMD的适应度函数,解决了单一指标作为适应度函数不能很好地表征信号状态特征的问题。3) 利用时移多尺度分析[20]代替DE传统的粗粒化过程,解决了传统粗粒化导致特征提取不充分的问题,并引入分数阶微积分的计算,提出了时移多尺度分数阶散布熵(time-shifted multiscale fractional dispersion entropy, TSM-FrDE),它可以从不同分数阶来衡量时间序列的动态变化,对轴承信号的动态变化更敏感。
1 相关理论
1.1 SSA算法改进
SSA可以概括为一个搜索-跟踪-警示的抽象模型,它模拟了麻雀觅食过程中如何获得待优化问题的解,SSA数学模型如下。
1) 探索者位置更新:探索者主要用于确定觅食方向和区域,其位置更新如下:
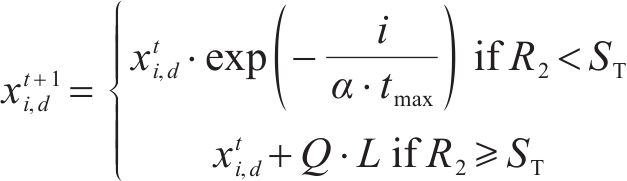
式中: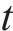
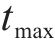
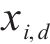
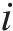
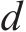
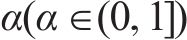
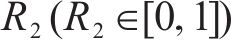
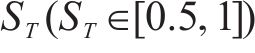
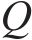
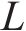
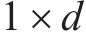
2) 跟随者位置更新:跟随者会因为觅食地点不好而改变它们的位置,或者为了获得食物而寻找能提供最好食物的探索者,其位置更新如下:
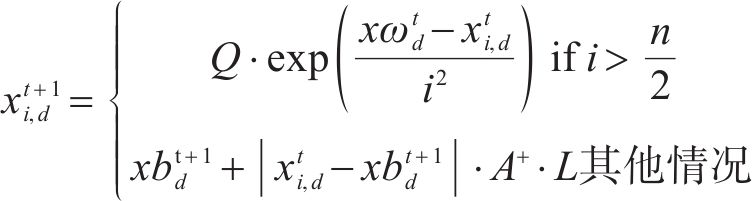
式中: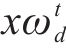
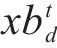
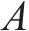
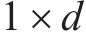
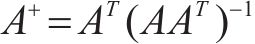
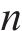
3) 侦察和警示行为:觅食时,一些麻雀负责保持警惕,其位置更新公式如下:
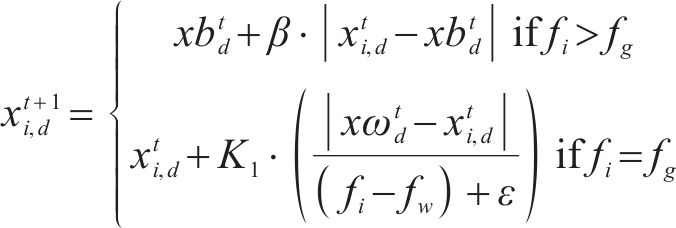
式中: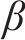

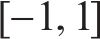
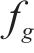
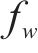
SSA算法存在的问题有:1) SSA使用随机方法生成种群,使得搜索空间分布不均匀,搜索效率较低;2) SSA探索者位置更新依赖于上一阶段的位置,导致全局勘探效率较低;3) SSA算法在迭代后期,跟随者会向适应度最好的麻雀个体靠拢,减弱了种群多样性,影响收敛速度。因此,SSA算法改进包括初始化改进、探索者位置更新改进和跟随者位置更新改进3方面。
1) 初始化改进:tent混沌映射具有良好的随机性和遍历性,利用该性质初始化种群,能提高全局搜索性能,其迭代过程如式(4)所示:
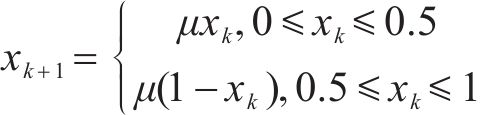
式中: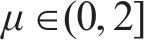
2) 探索者位置更新改进:OOA算法有着识别最佳区域和摆脱局部最优方面的探索能力,利用该性质改进麻雀探索者位置更新策略,可以提高探索者全局勘探效率,OOA算法的位置更新如式(5)所示:
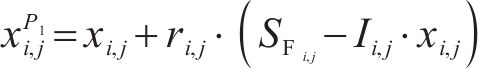
式中: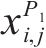
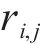
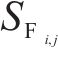
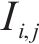
2) 跟随者位置更新改进:引入柯西变异对跟随者位置进行扰动,扩大搜索空间,提升算法跳出局部最优的能力,柯西变异策略如式(6)所示:
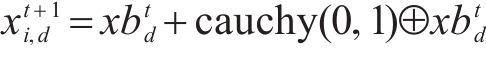
式中: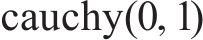
1.2 最优参数VMD
VMD是一种自适应信号分解方法,它采用非递归分解方式,按照预定的模态数K和惩罚因子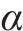
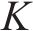
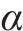
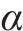
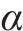
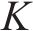
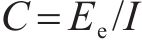
式中: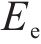

将C的最小值作为ISSA的适应度函数,表示为:
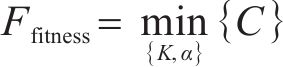
参数自适应VMD的具体步骤如下。
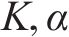
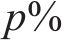
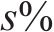
1.3 IMF分量选择与信号重构
经VMD分解的IMF分量可以看作2部分,一部分包含大量故障信息,另一部分为冗余成分,为了更好地表征轴承状态特征,需要去除冗余成分。PCC可用于衡量轴承信号和IMF之间的相关性,相关系数越大,则该IMF所包含原始信号的故障信息就越多,选择相关数大于0.3的IMF分量对信号进行重构,这样可以消除信号冗余成分,避免丢失敏感信号信息[21],PCC的计算公式如下:
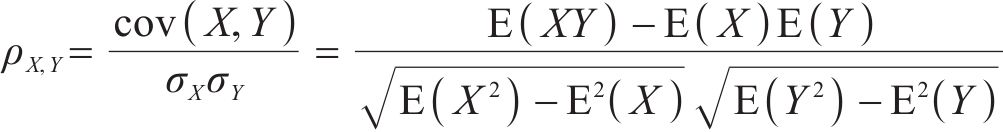
式中:
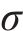
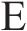
1.4 时移多尺度分数阶散布熵
DE是衡量非线性时间序列的强大工具,MDE是对DE的改进,但MDE存在对动态变化不敏感以及传统粗粒化导致特征提取不全面的问题,为此本文提出TSM-FrDE来提取轴承信号特征,其计算步骤如下。
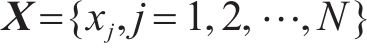
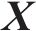
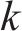
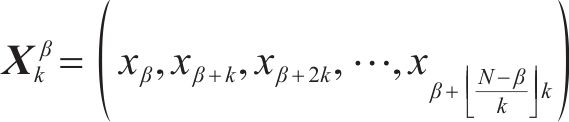
式中: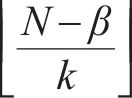
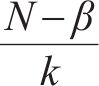
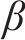
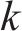

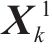
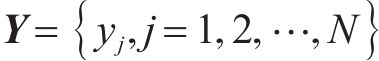
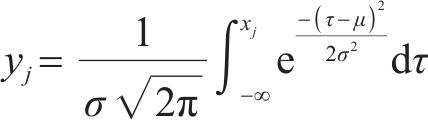
式中: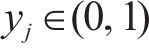
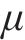
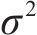
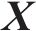
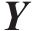
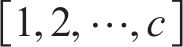
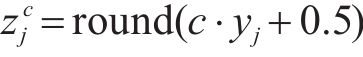
式中: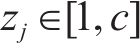
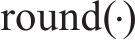
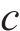
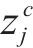
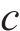
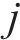
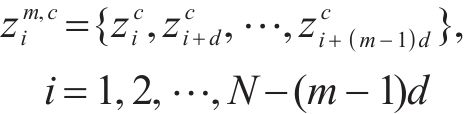
式中: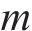
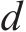

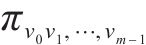
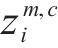
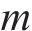
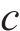
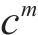
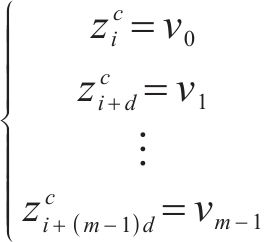
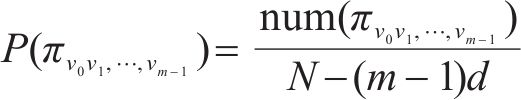
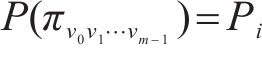
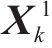
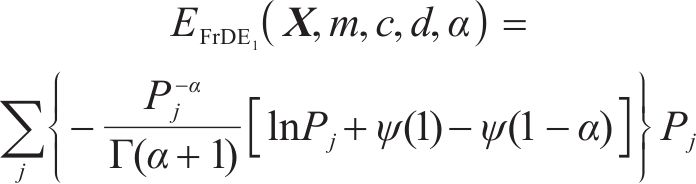
式中: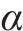

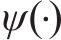
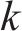
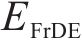
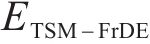
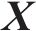
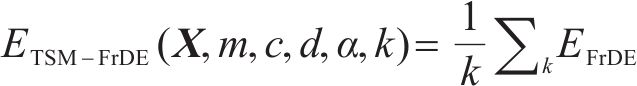
1.5 轴承亚健康状态识别
重构信号的TSM-FrDE特征能反映出轴承的全寿命周期状态变化规律,现在需一个指标来准确定位亚健康初始时刻,而欧式距离可以度量健康轴承信号特征和待测信号特征之间的绝对距离,切比雪夫不等式常用来划分轴承状态阈值,因此本文采用欧氏距离结合切比雪夫不等式作为亚健康状态识别模型,欧氏距离如式(18)所示,切比雪夫不等式如式(19)所示:
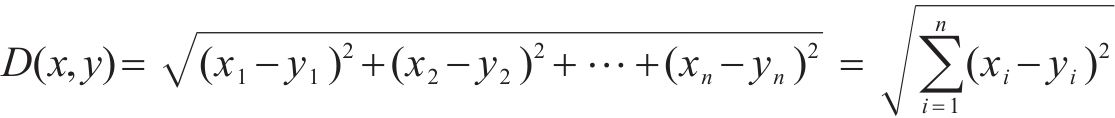
式中: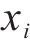
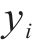
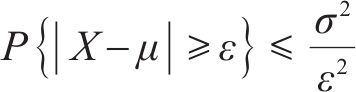
式中: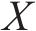
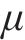
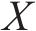
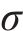
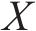
2 轴承亚健康状态识别流程
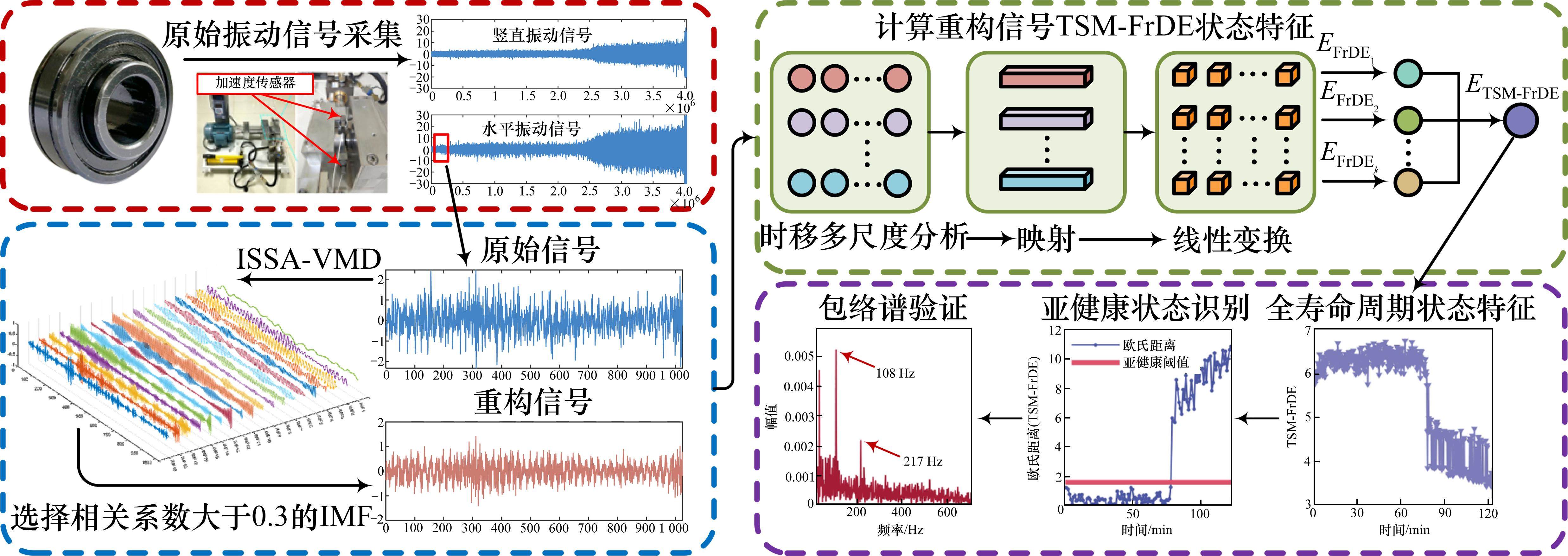
基于ISSA-VMD和TSM-FrDE的轴承亚健康状态识别流程如图1所示,具体步骤如下。
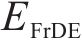
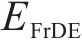
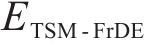
3 仿真验证
为了验证本文方法的有效性,建立不同仿真信号分别对ISSA算法和TSM-FrDE算法进行分析。
3.1 ISSA算法验证
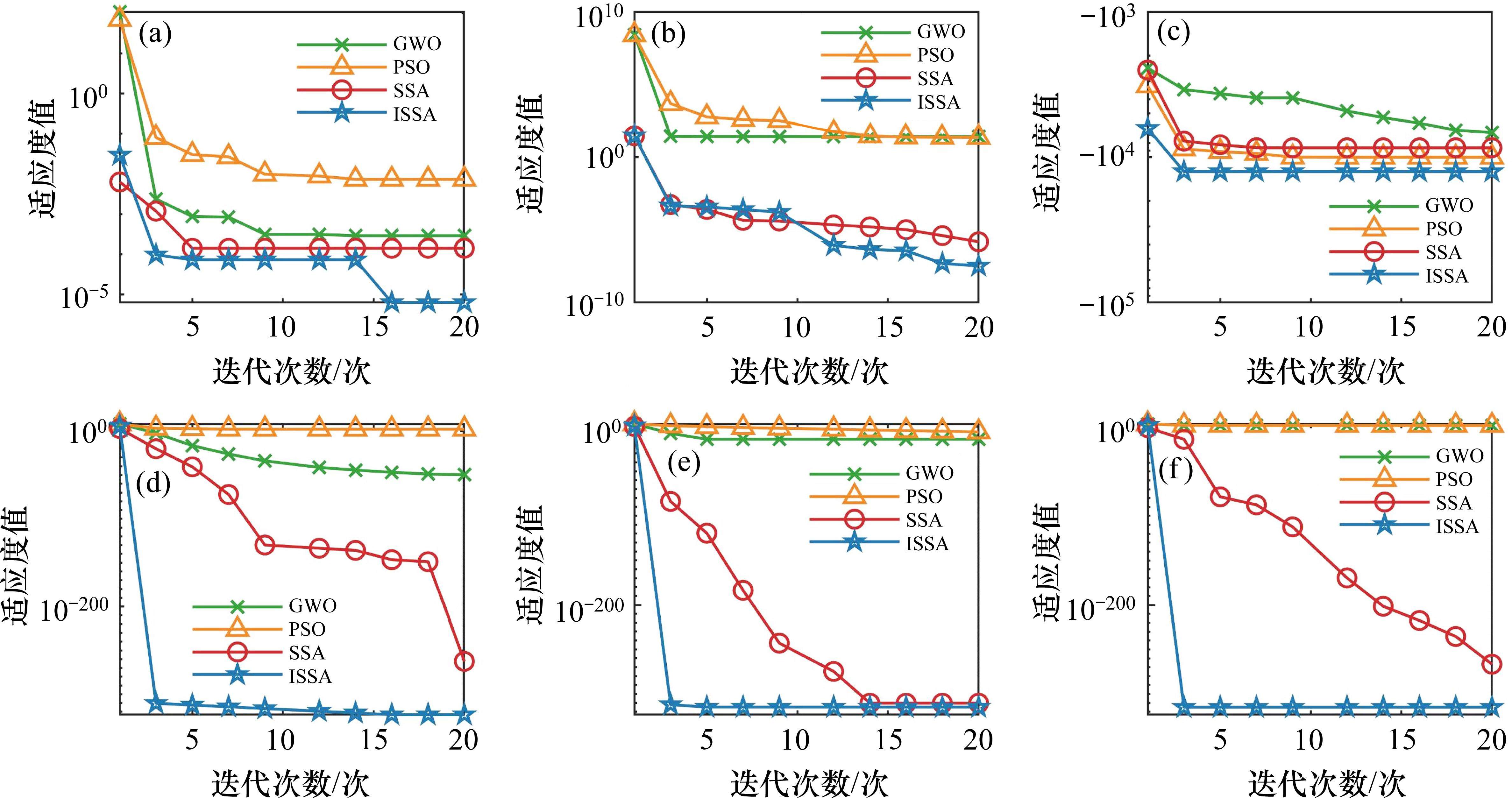
为了证明ISSA算法有效性,选取未改进SSA算法、灰狼优化算法(grey wolf optimizer, GWO)和粒子群优化算法(particle swarm optimization, PSO)进行对比分析。算法最大迭代次数设置为1 000次,每种算法粒子数设置为100,在智能优化算法标准测试函数CEC2005和CEC2021中各选取3个标准测试函数进行仿真分析。测试函数基本信息如表1所示。
| 测试函数集 | 序号 | 类型 | 函数 |
|---|---|---|---|
| CEC2005 |  | 单峰函数 | 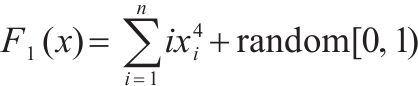 |
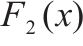 | 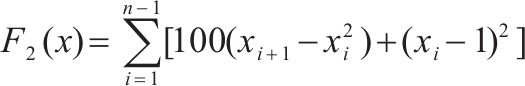 | ||
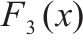 | 多峰函数 | 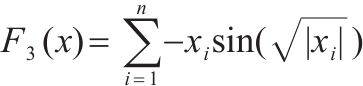 | |
| CEC2021 | 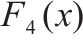 | 混合函数 | Hybrid Function 1 (N=3) |
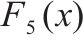 | 组合函数 | Composition Function 2 (N=4) | |
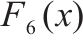 | Composition Function3 (N=5) |
采用优化算法求解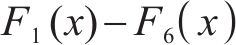
3.2 TSM-FrDE算法验证
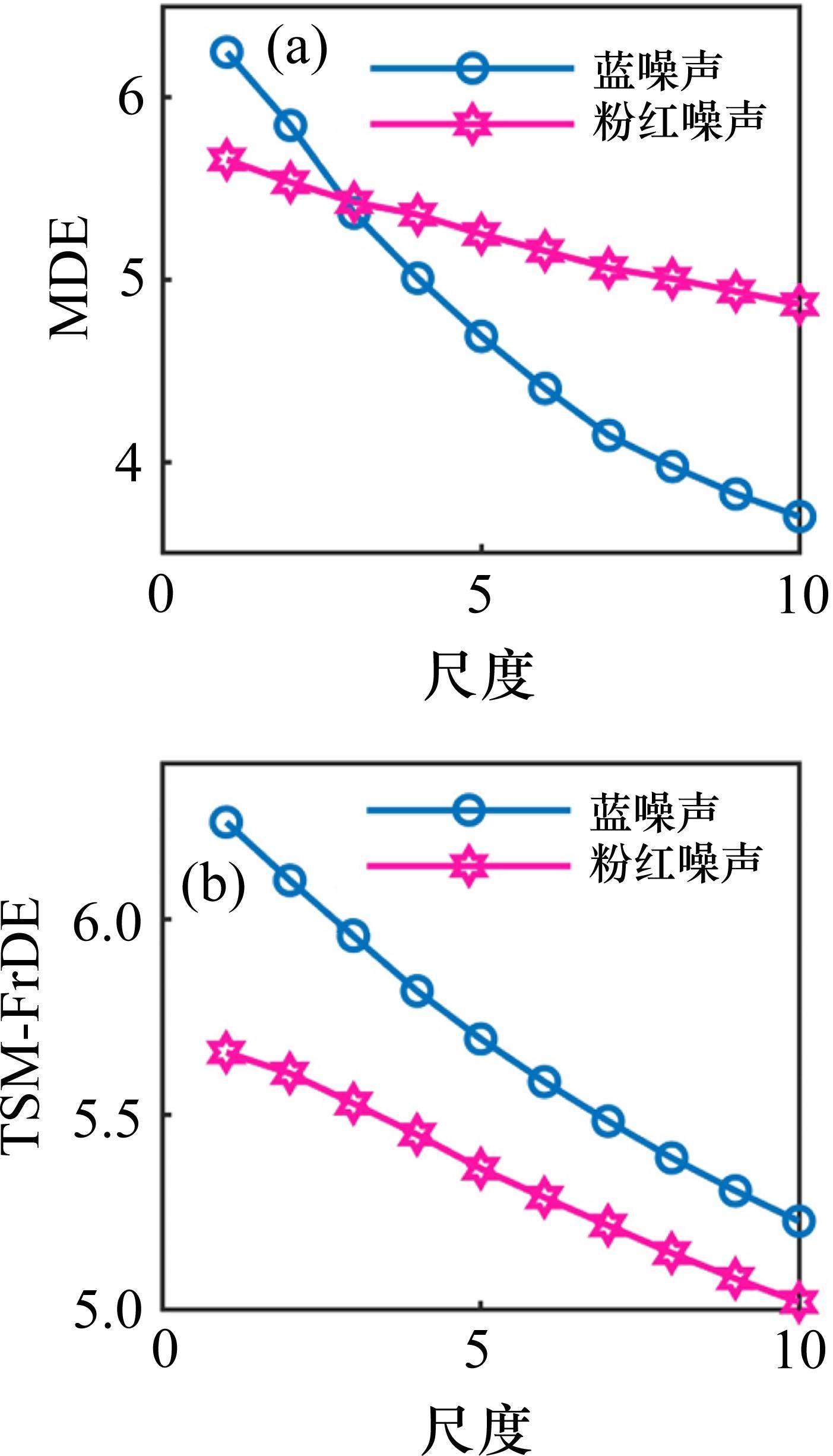
TSM-FrDE要表征轴承全寿命周期状态特征,其必须具备有效识别不同信号的能力,这里通过分析TSM-FrDE和MDE对于蓝噪声和粉红噪声的识别效果来评估它们对于不同信号的识别能力,从图3可以看出,在任意尺度下TSM-FrDE的值未出现混叠现象,说明TSM-FrDE区分不同信号的能力更强。
4 试验验证
4.1 数据来源
数据集1:采用XJTU-SY滚动轴承全寿命周期数据,该数据集包括转速2 100、2 250和2 400 r/min共3种工况,每种工况包括水平和垂直全寿命周期振动信号,试验采样频率为25.6 kHz,采样间隔为1 min,每次采样时长为1.28 s。本文选取工况1中的数据集Bearing1_1,最终失效位置为外圈,外圈故障特征频率理论值107.91 Hz。
数据集2:采用IMS的滚动轴承全寿命周期数据,包含3个数据集,每个数据集中包含了4个轴承的振动数据,采样频率为20 kHz,采样间隔为10 min,每次采样时长为1 s。本文选取数据集2中的轴承1,最终失效位置为外圈,外圈故障特征频率理论值236.4 Hz。
4.2 轴承亚健康状态识别可行性验证
本小节选取数据集1验证本文所提方法的可行性。
1) 基于ISSA-VMD-PCC的数据处理
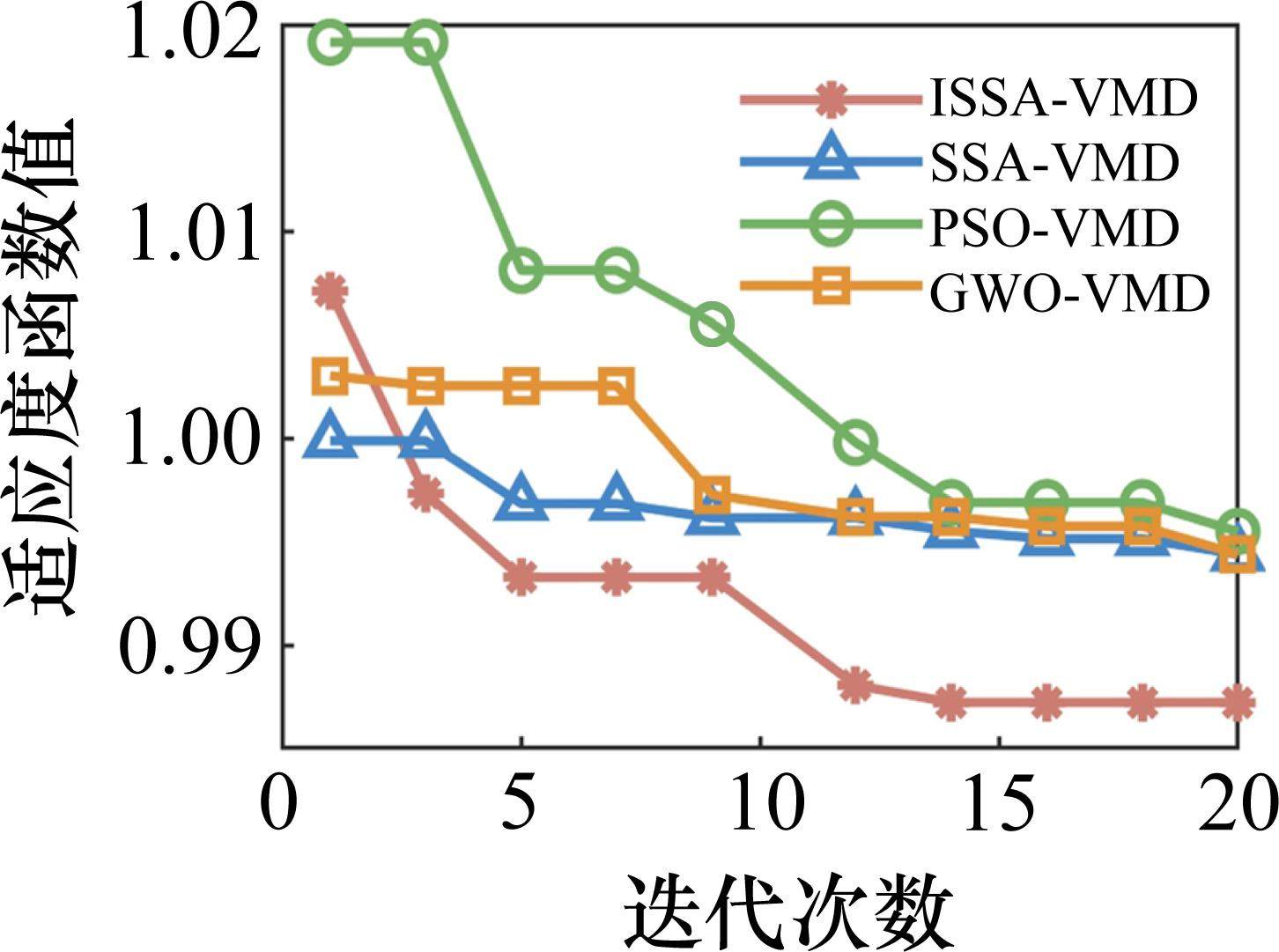
采用包络熵和互信息的复合指标为适应度函数,设置种群数量为30,迭代次数为20,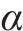
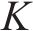
| 序号 | 数据样本点选取 | 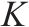 |  |
|---|---|---|---|
| 1 | 11 023:12 046 | 17 | 5 875 |
| 2 | 21 023:22 046 | 20 | 1 080 |
| 3 | 31 023:32 046 | 18 | 5 850 |
| 4 | 1 605 632:1 606 655 | 20 | 1 175 |
| 5 | 1 630 000:1 631 023 | 17 | 6 182 |
| 6 | 1 650 000:1 651 023 | 18 | 1 795 |
| 7 | 1 660 000:1 661 023 | 19 | 1 636 |
| 8 | 1 680 000:1 681 023 | 16 | 7 750 |
| 9 | 2 600 000:2 601 023 | 19 | 1 887 |
| 10 | 2 630 000:2 631 023 | 20 | 1 750 |
| 11 | 2 640 000:2 641 023 | 18 | 2 311 |
| 12 | 3 150 000:3 151 023 | 19 | 1 044 |
| 13 | 3 160 000:3 161 023 | 19 | 9 880 |
| 14 | 3 180 000:3 181 023 | 17 | 9 765 |
| 15 | 4 010 000:4 011 023 | 20 | 4 259 |
| 16 | 4 020 000:4 021 023 | 18 | 2 479 |
选取Bearing1_1的1 024个样本点,利用优化得到的
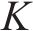
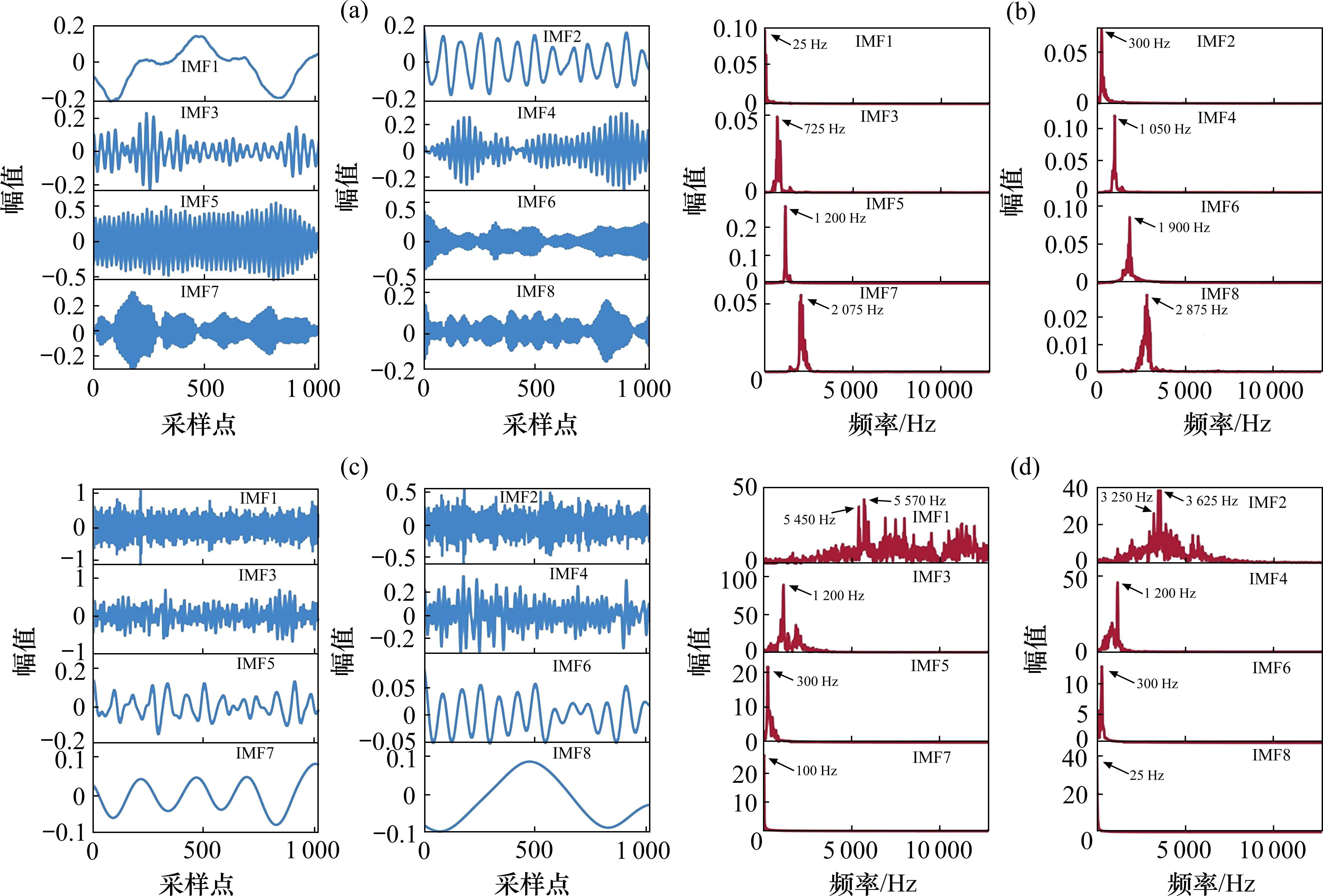
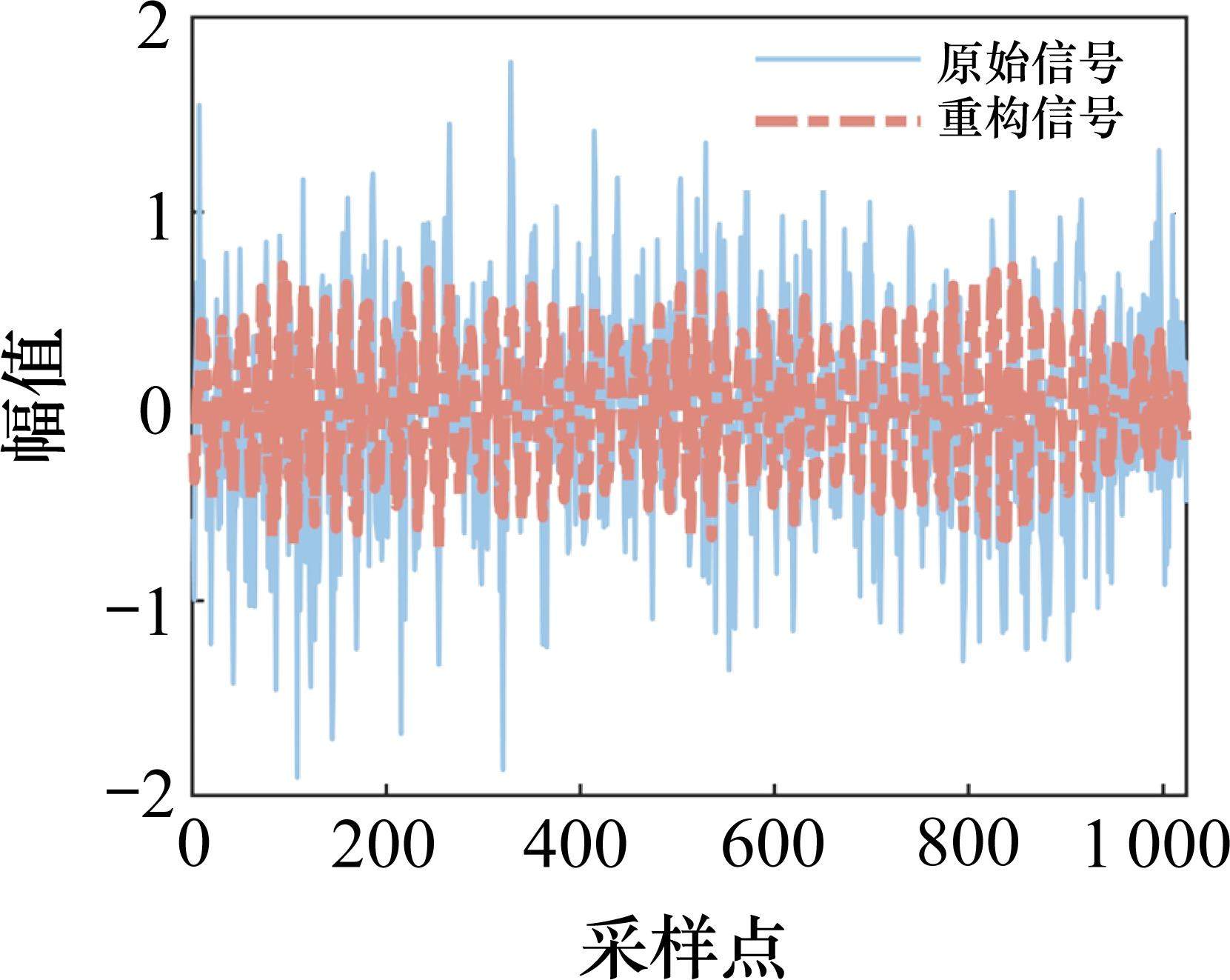
然后根据PCC,计算每个IMF与原始信号之间的相关系数,如表3所示,选择相关系数大于0.3的IMF分量重构信号,原始信号与重构信号如图6所示,可以看出重构信号去除了大部分的尖峰噪声信号,在保留原始信号大部分特征的同时波形更加平滑和连续,完成了对轴承信号的初步降噪。
IMF 分量 | 相关 系数 | IMF 分量 | 相关 系数 | IMF 分量 | 相关 系数 |
|---|---|---|---|---|---|
| IMF1 | 0.281 9 | IMF7 | 0.190 2 | IMF13 | 0.257 5 |
| IMF2 | 0.192 5 | IMF8 | 0.221 1 | IMF14 | 0.534 8 |
| IMF3 | 0.287 6 | IMF9 | 0.272 7 | IMF15 | 0.273 6 |
| IMF4 | 0.316 6 | IMF10 | 0.201 0 | IMF16 | 0.196 1 |
| IMF5 | 0.278 1 | IMF11 | 0.160 3 | IMF17 | 0.173 7 |
| IMF6 | 0.169 7 | IMF12 | 0.231 3 | IMF18 | 0.181 5 |
2) 基于TSM-FrDE的轴承全寿命周期状态特征提取
TSM-FrDE的计算涉及嵌入维数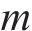
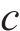
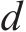
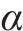
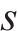
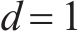
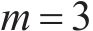
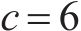
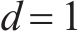
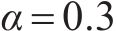
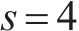
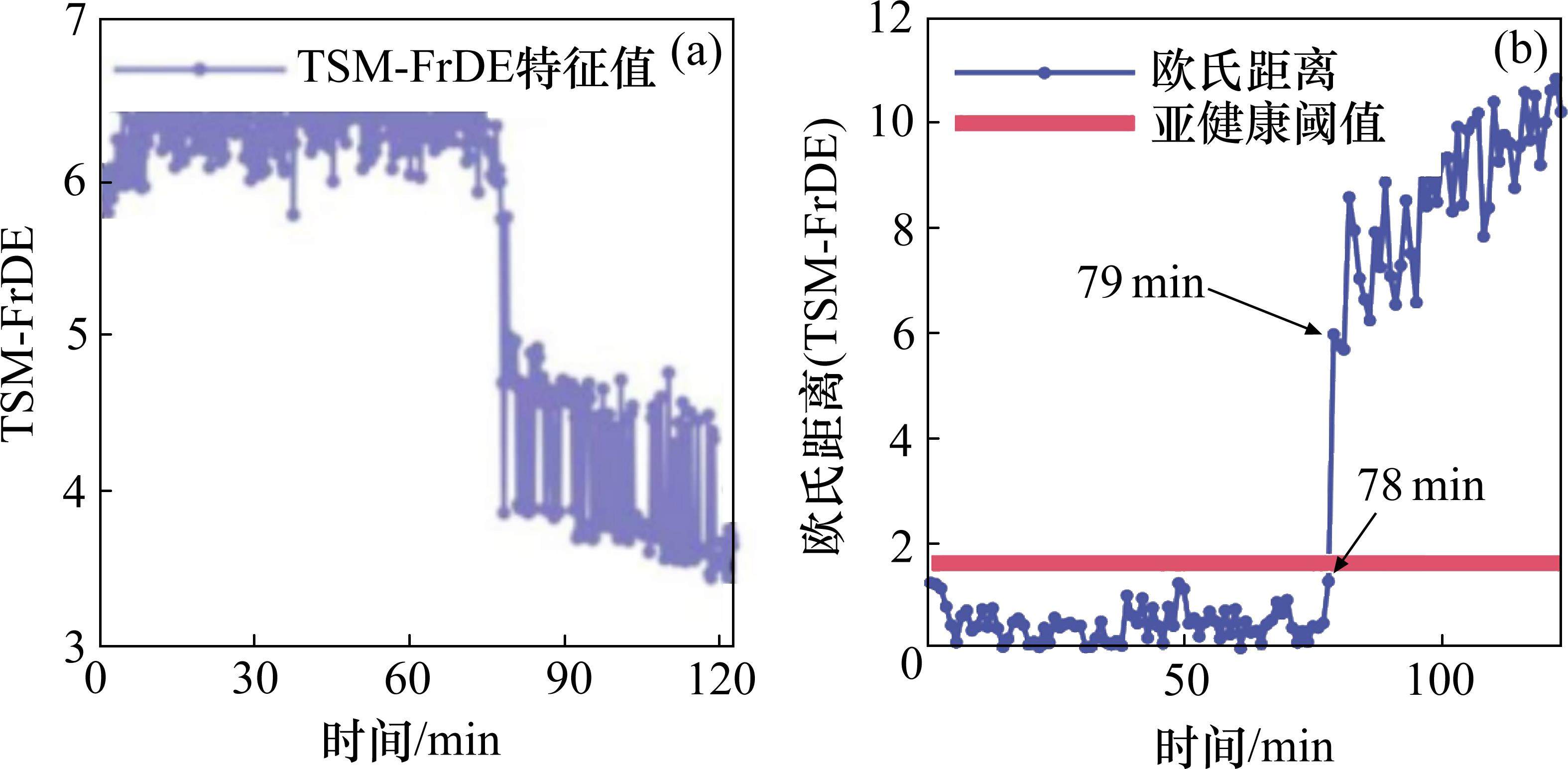
3) 基于欧式距离和切比雪夫不等式理论的轴承亚健康状态评估
因为从图7(a)得知轴承是在60~90 min之间进入亚健康状态,所以选取前40 min的数据为健康数据,将后续数据视为测试数据,计算健康数据和测试数据之间的欧式距离,并利用切比雪夫不等式原理设定亚健康阈值,如图7(b)所示,从图中可知,轴承运行到第78 min时仍处于健康状态,运行第79 min时性能发生退化,轴承进入亚健康状态。
4) 本文所提方法正确性验证
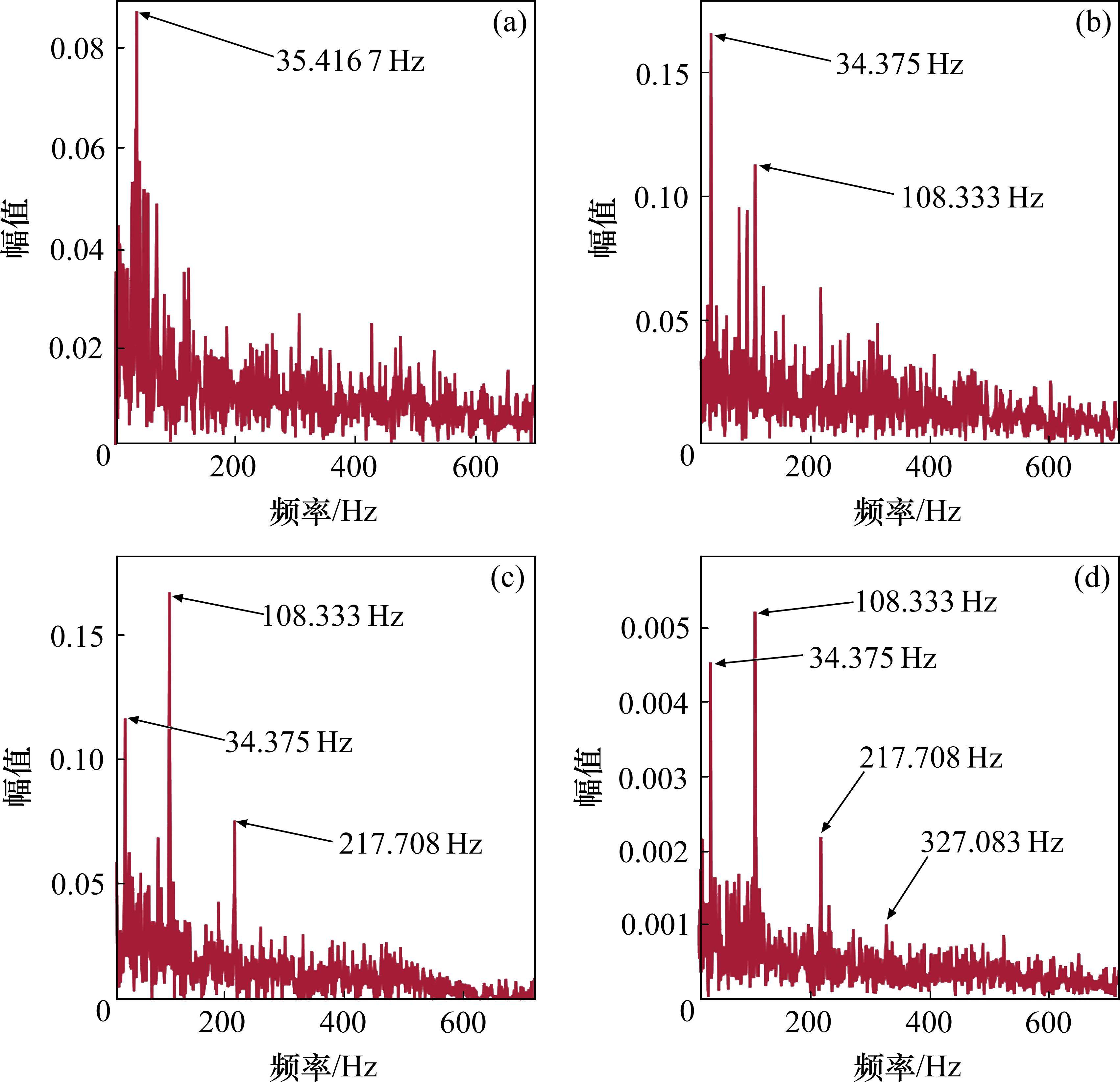
由以上分析判断出轴承在第79 min时进入亚健康状态,为了验证识别结果的正确性,利用ISSA-VMD-PCC方法对第50、78、79和80 min的信号进行降噪,然后进行包络谱分析,如图8所示。第50 min时,轴承还处于健康状态,此时只有1倍转频35.4 Hz,78 min时虽然出现108.3 Hz的频率,接近外圈故障特征频率理论值107.91 Hz,但是其频谱峰值较小,不能说明此时进入亚健康状态,在79 min和80 min时,出现108.3 Hz及其倍频的频率成分217.7 Hz和327.1 Hz,并且108.3 Hz的频谱峰值明显,说明在第79 min轴承性能发生退化,但此时还能继续正常运行,轴承进入亚健康状态,验证了本文所提方法的正确性。
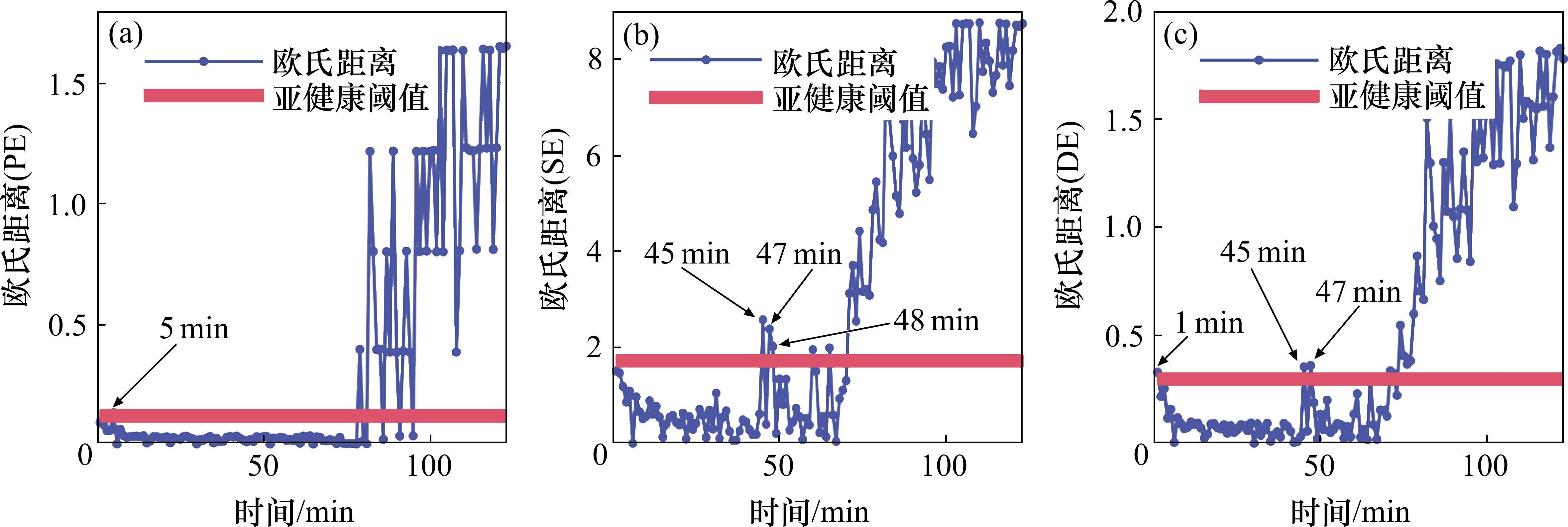
5) TSM-FrDE指标与其他状态特征对比
选用排列熵(permutation entropy, PE),样本熵(Sample entropy, SE)和未改进的DE作为对比,根据这3种特征指标,分别计算健康数据和测试数据之间的欧式距离,如图9所示。上面验证了轴承在第79 min进入亚健康状态,从图9可以看出以PE、SE和DE作为状态指标时存在虚警,并且在第78~79 min时欧氏距离变化的幅值不大,而本文提出的欧氏距离(TSM-FrDE)方法在第78~79 min时有明显的阶跃变化,且无虚警,经过图7和图9的对比说明本文所提方法对于轴承亚健康状态识别的灵敏度和准确率最高。
4.3 基于ISSA-VMD和TSM-FrDE方法的鲁棒性能验证
本小节选用数据集2验证本文所提方法鲁棒性。首先利用ISSA搜索到的VMD最优参数为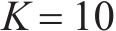
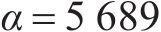
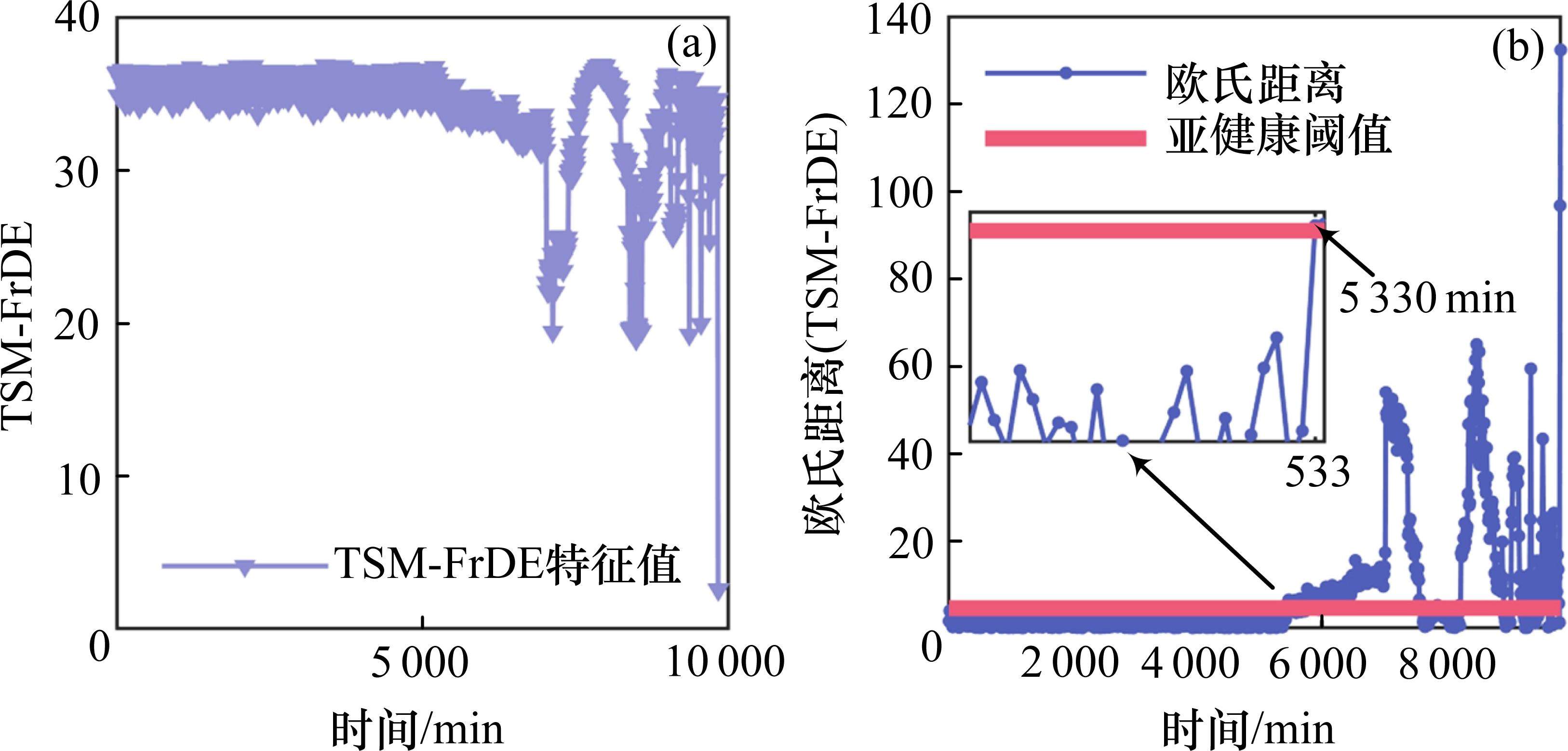
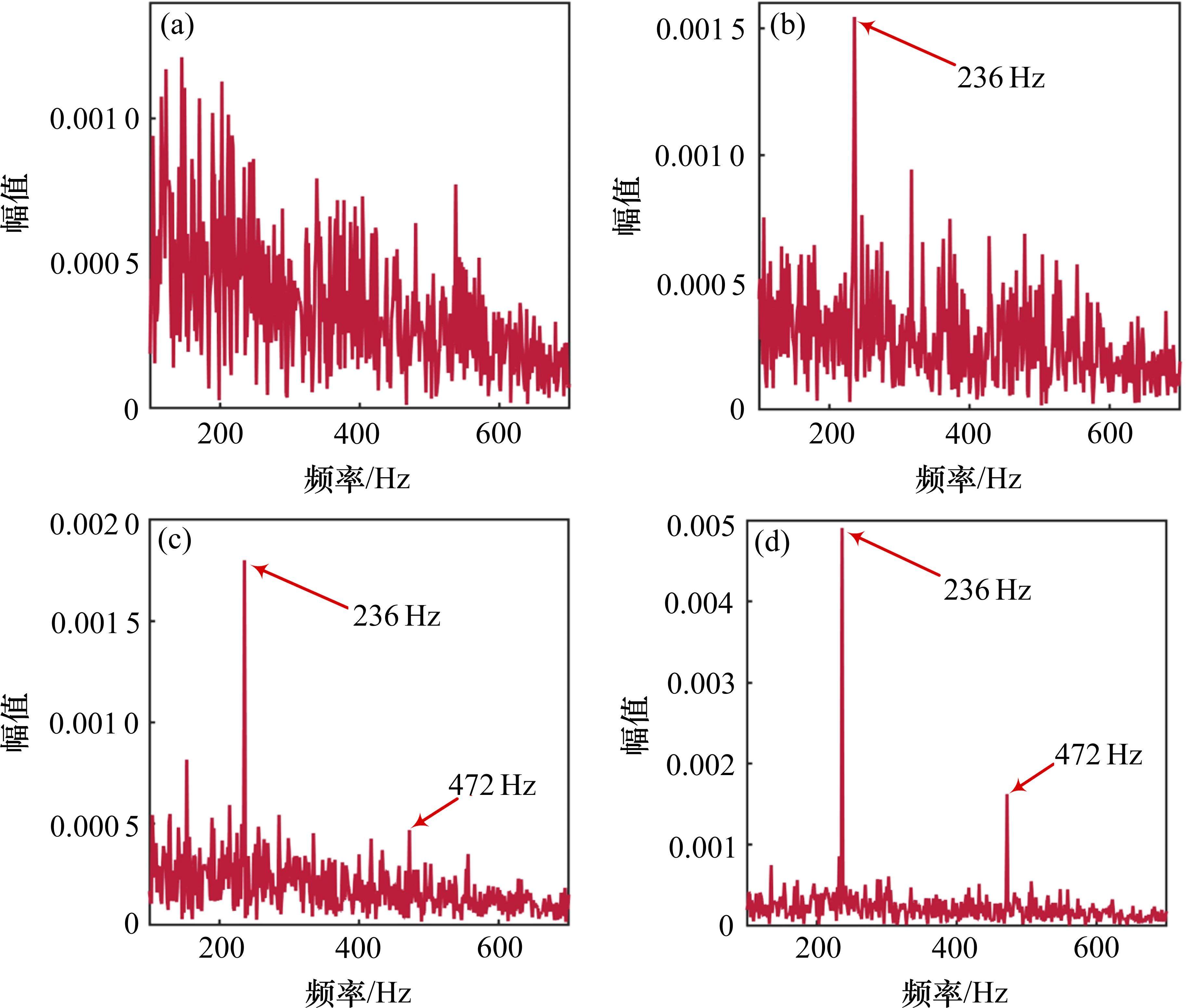
5 结论
1) 提出一种基于最优参数VMD和时移多尺度分数阶散布熵的轴承亚健康状态识别方法,解决了轴承亚健康状态特征微弱,亚健康状态难以识别的问题,当轴承进入亚健康状态时即可给出预警,防止设备发生重大故障,使得轴承的维修由故障发生后的被动维修变为主动的预测性维修。
2) 采用多策略对SSA优化算法进行改进,相比PSO、GWO和未改进SSA算法,ISSA在优化精度和速度方面更具优势。设计了包络熵和互信息的综合指标作为ISSA-VMD的适应度函数,相比单一指标能更全面表征轴承状态。将时移多尺度分析和分数阶微积分理论引入散布熵中,提高其表征轴承状态变化的能力,相比排列熵、样本熵和未改进散布熵,TSM-FrDE对于轴承变化更敏感,相比多尺度散布熵,TSM-FrDE具有更强的状态识别能力。
3) 选用XJTU-SY和IMS轴承数据集进行试验验证,结果表明:ISSA-VMD无模态混叠问题,具有更好的信号分解效果,ISSA-VMD-PCC能消除掉信号中的大部分噪声,TSM-FrDE能识别出轴承健康状态与亚健康状态之间的微弱变化,本文所提方法具有可行性和鲁棒性,能有效识别轴承亚健康状态。
但本文的方法也存在不足之处:1) TSM-FrDE的计算效率有待提高;2) 基于切比雪夫不等式原理设定亚健康阈值存在主观因素。因此,更高效率的轴承状态监测指标和亚健康阈值自适应确定的方法值得进一步研究。
魏文军,甘洁.基于最优参数VMD和改进散布熵的轴承亚健康状态识别[J].铁道科学与工程学报,2025,22(02):887-899.
WEI Wenjun,GAN Jie.Bearing sub-health state identification based on optimal parameter VMD and improved dispersion entropy[J].Journal of Railway Science and Engineering,2025,22(02):887-899.

