混凝土是应用最广泛的建筑材料,抗压强度是衡量其质量的重要指标。为了准确评估混凝土抗压强度,最直接的方法是将试件养护至所需龄期进行物理试验。然而,该过程费时费力、经济性差,且易受操作人员主观判断和操作影响[1]。因此,开展混凝土强度预测研究对工程建设意义重大。首先,这有利于混凝土配比高效、精准调整,缩短试验周期并减少材料消耗;其次,快速预测混凝土抗压强度,可准确掌握强度发展趋势,确保其质量和结构安全。在材料科学领域,机器学习算法已被成功应用于预测混凝土抗压强度,包括人工神经网络[2-3](artificial neural network, ANN)、支持向量机[4-6]及随机森林[7]等算法。为了提高模型的预测精度,相关研究[8-10]将元启发式优化算法与机器学习算法相结合构建混合模型,克服了传统试错法难以寻找模型最佳参数的难题,并有效地规避模型在预测期望输出时出现的局部最小值和过拟合问题。然而,目前大多数研究依然以混凝土原料用量作为输入变量[11],集中于寻找能适应数据集的最佳模型,而未充分探索并开发出针对该问题的新算法。因此,本文首次提出了一种全新的算法,即基于人工神经网络和极端梯度提升(extreme gradient boosting, XGBoost)的混合集成模型(hybrid ensemble model based on neural network and gradient boosting, HEMNG)。该算法结合了ANN和XGBoost的优势,采用5个可解释特征(能够直接解释或理解其含义的特征)作为输入进行强度建模。为验证HEMNG模型的优越性,除了与ANN和XGBoost进行比较外,将其与支持向量机、决策树、随机森林、极限学习机和轻量级梯度提升机模型进行对比分析。此外,还将模型迁移到全新数据,对实验室条件下的混凝土配合比的抗压强度进行预测,探讨HEMNG模型在实际情况中的适用性。并基于HEMNG模型,量化分析了输入特征对抗压强度的影响,以验证模型的合理性。
1 HEMNG原理
1.1 集成优势
集成方法通过构建并结合多个学习器来完成学习任务,可获得比单一学习器优越的泛化性能[12]。此外,还具有以下优势:1) 稳健性,由于不同模型在同一问题上不会同时产生相同的预测误差,集成方法能够弥补单个模型的缺陷,从而提高整体预测的准确性。2) 抑制过拟合,集成算法包含多个学习器,能有效减少模型对单一学习器的依赖,从而避免模型过拟合。
1.2 个体学习器选择
基于集成学习理论创建新算法时,选择适当的个体学习器(单一算法)是保证算法性能的关键[13]。既要根据问题类型、数据集大小和数据的维度选择,还需综合考虑其他学习器的特点。在回归问题中,线性回归模型计算效率高[14],对异常值敏感且不擅长解决非线性问题;决策树在处理简单非线性问题时表现良好,但容易出现过拟合[15];另外,进化算法(如基因表达式编程),适用于解决非线性问题,但局部搜索能力较差,需借助表达式[16]。而ANN能处理复杂的非线性问题,有效捕捉数据间的映射关系。XGBoost在处理结构化数据方面表现出色,具备强大的正则化能力。因此,将ANN和XGBoost作为集成算法的个体学习器是一个不错的选择。两者可以相互补充,既能有效捕捉数据输入与输出之间的复杂关系,又能避免模型的过拟合问题。
1.2.1 人工神经网络
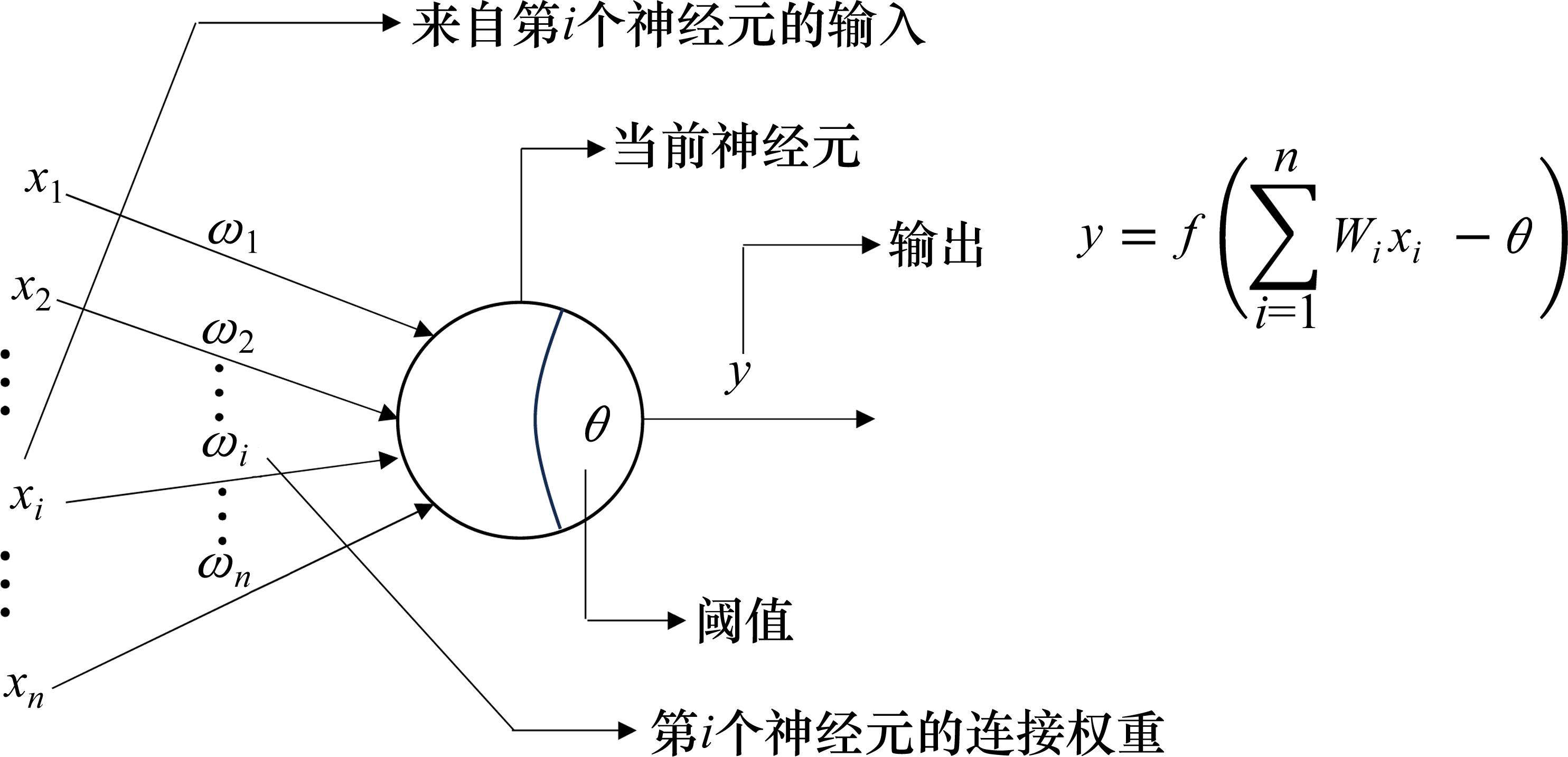
ANN是由神经元组成(如图1所示)的网络层次结构。神经元之间的连接权重会基于训练数据自动调整,以保证网络能够学习并捕捉输入数据中的复杂模式[17]。
1.2.2 极端梯度提升
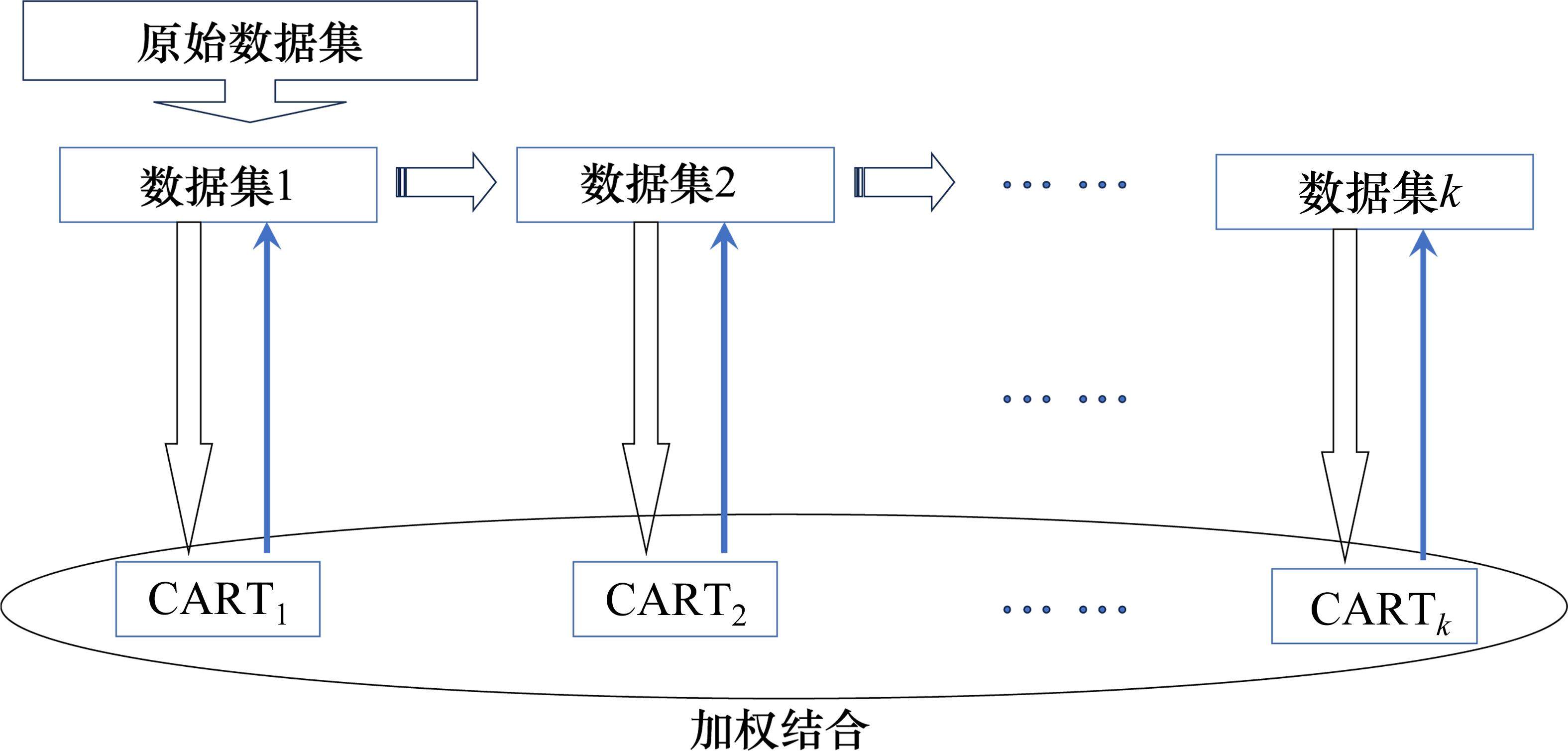
XGBoost采用分类回归树(classification and regression tree, CART)作为基础学习器。如图2所示,其核心在于计算每一轮迭代中损失函数的梯度,使其更专注于降低之前轮次中CART的残差[18-19],通过加权结合所有基础模型的输出,以提高模型的准确性。此外,为了抑制出现过拟合,XGBoost引入了正则化参数。
1.3 HEMNG算法
HEMNG是一种复杂的异质集成算法,而不仅仅是对2种学习器的预测结果取均值或加权结合。具体来说,HEMNG首先利用ANN进行初步训练,然后通过编程工具提取出ANN倒数第2层的输出,将其作为新的特征进行下一步学习。之所以选择ANN倒数第2层的输出,是因为不仅捕捉了底层输入的细节信息,还包含了高层次的特征信息,且比最后一层具有更低的过拟合倾向。随后,利用XGBoost作为最终算法,对这些新的特征进行进一步的学习和整合,使得HEMNG模型能够更好地把握数据之间的关系,从而提高整体性能。此外,通过调节正则化参数(alpha和lambda),可以控制HEMNG的复杂度,避免模型过拟合。
1.3.1 算法原理
HEMNG算法的原理是矩阵的运算,其中ANN的输出可表示为:
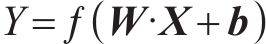
式中:X为输入矩阵,其维度为

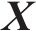
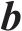
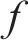
假设ANN有L层(包括输入和输出层),通过切片处理,ANN的倒数第2层的输出可以表示为:
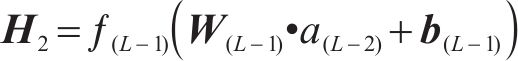
式中: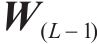
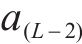
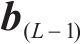
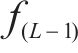

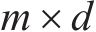
在HEMNG算法中,采用XGBoost算法完成对新特征的最终学习,对于每个样本,HEMNG的输出是所有CART预测输出的加权结合,可表示为:
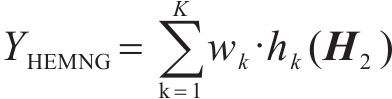
式中: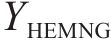
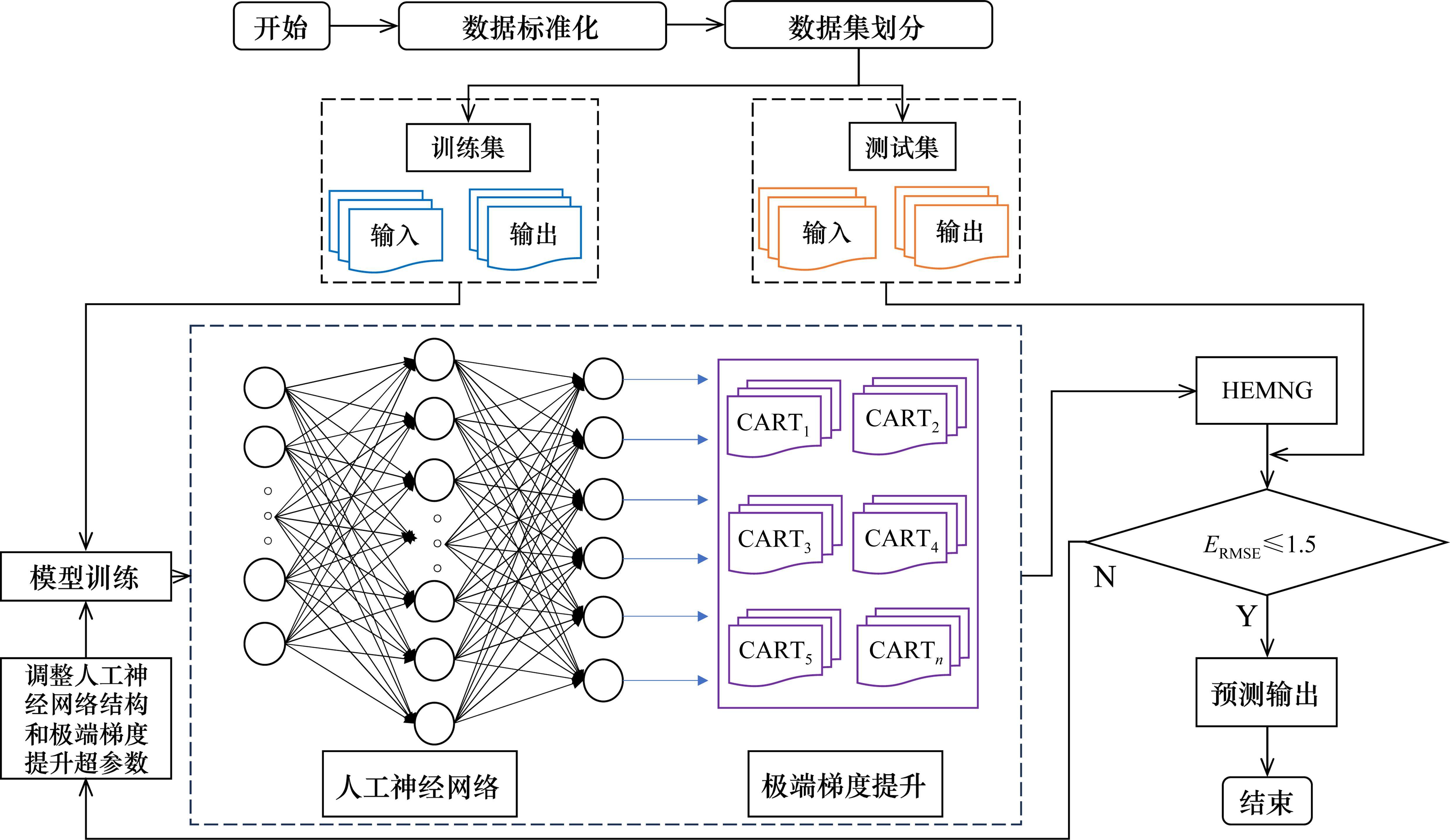
2 模型建立与计算
2.1 混凝土数据库
本文从混凝土检测中心获取了303组混凝土配合比数据,其中每个输入参数包括5个可解释特征,分别为水胶比、砂率、浆骨比、粉煤灰替代比例和混凝土龄期,输出参数为抗压强度。表1展示了数据中参数的极值、均值和标准差。数据集中的水胶比、砂率和浆骨比的范围在配合比中的分布广泛,涵盖了使用和未使用粉煤灰的情况,以及不同养护龄期下的混凝土配合比,保证了数据的多样性,有利于增强模型在应对未知数据时的鲁棒性。
| 特征 | 编号 | 特征类型 | 统计指标 | |||
|---|---|---|---|---|---|---|
| 最小值 | 最大值 | 均值 | 标准差 | |||
| 水胶比 | X1 | 输入 | 0.26 | 0.7 | 0.43 | 0.09 |
| 砂率 | X2 | 输入 | 0.3 | 0.68 | 0.45 | 0.05 |
| 浆骨比 | X3 | 输入 | 0.21 | 0.43 | 0.3 | 0.04 |
| 粉煤灰胶凝材料比值/% | X4 | 输入 | 0 | 51 | 19.2 | 12.3 |
| 龄期/d | X5 | 输入 | 1 | 90 | 24.3 | 19.74 |
| 抗压强度/MPa | ― | 输出 | 5.5 | 69.9 | 35.5 | 12.9 |
为了使模型能更好地捕捉数据间的非线性关系,对数据进行标准化处理,以消除不同特征之间的量纲和单位差异。这有助于加快模型学习速率和避免某些特征对模型的影响过大,从而提高模型的稳定性。标准化后,将数据集随机划分为训练集和测试集,其中242组(占总数据80%)的数据用于模型训练,另外61组数据则独立于训练集,用于评估模型性能。
2.2 模型性能评价指标
为了准确评估模型性能,使用2个度量指标,分别为:相关系数(R2)和均方根误差(ERMSE)。其公式如下:
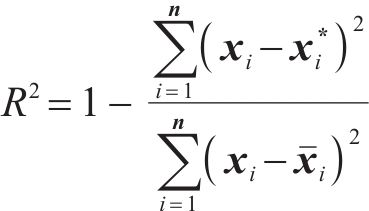
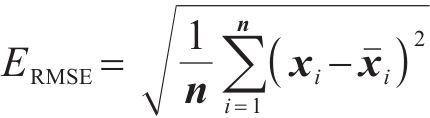
式中: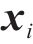
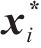
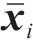
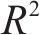
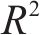
2.3 ANN模型
为确定ANN模型的最佳结构,采用试错法逐步增加隐含层数量和每层神经元个数。在仅有一层隐含层时,模型在训练集和测试集中表现均较差,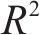
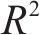
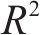
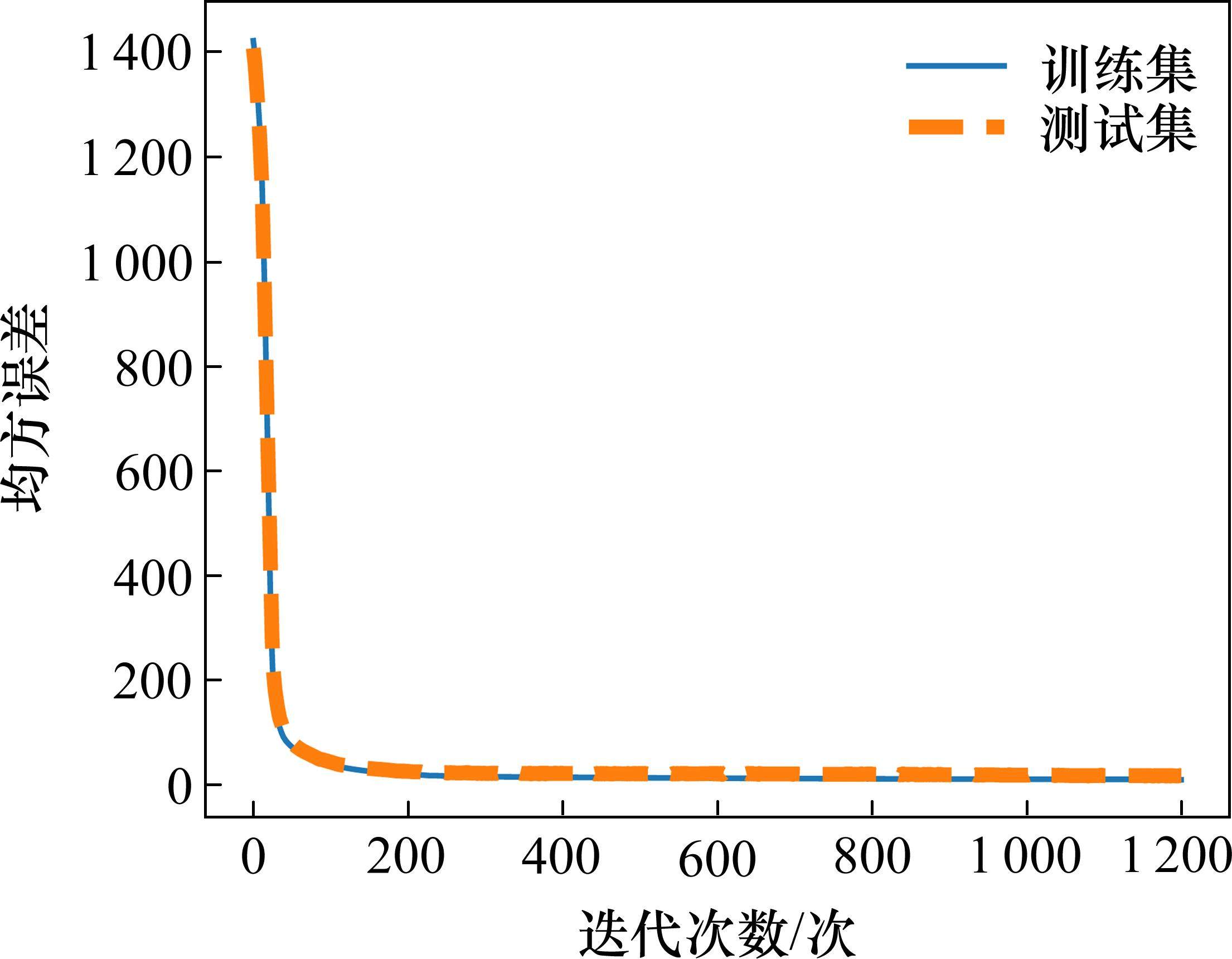
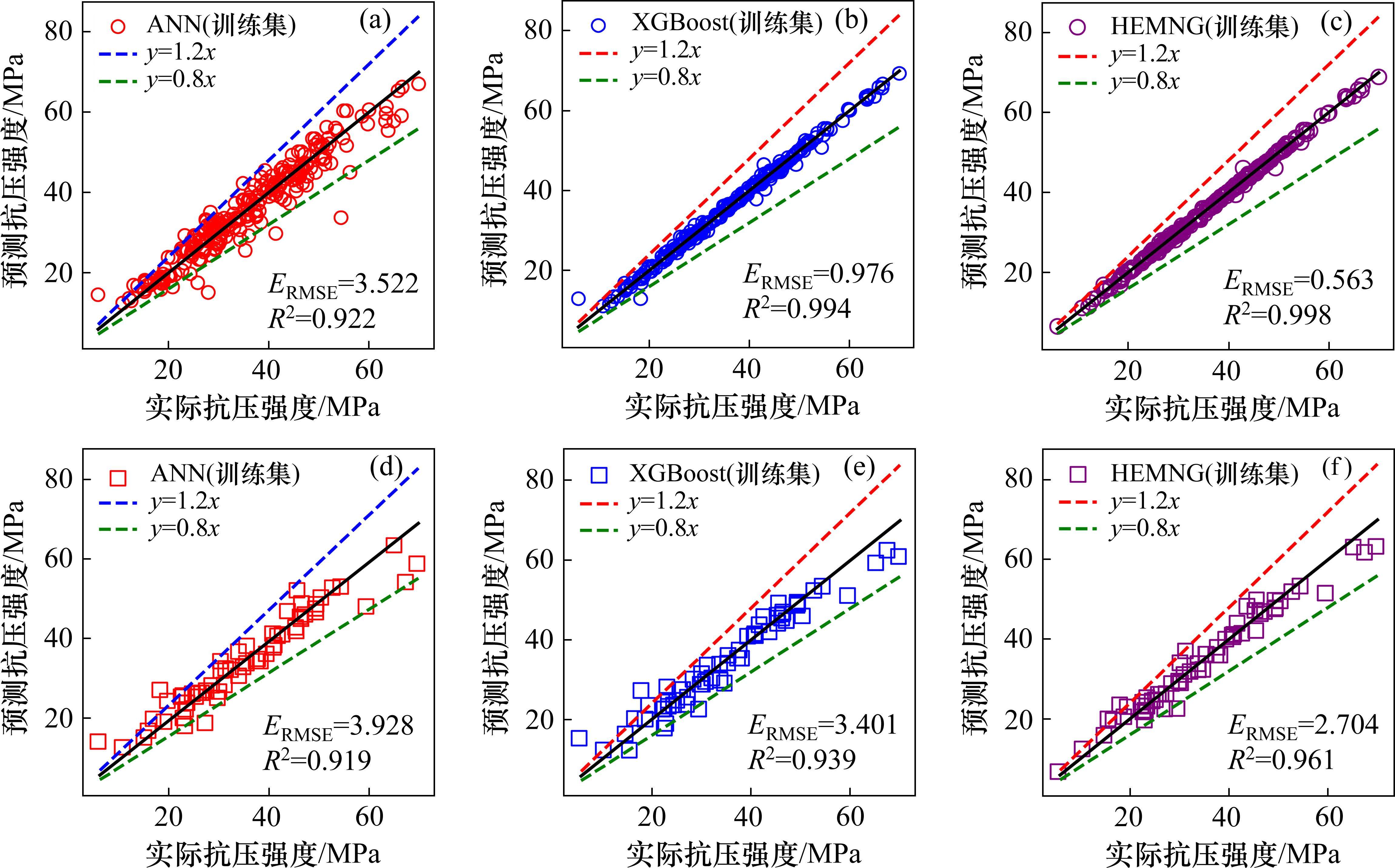
经过多次调整,发现ANN具有2层隐含层,且每层神经元个数分别为36和4时,模型性能最佳。学习曲线如图4所示,通过循环训练1 200次,模型在训练集和测试集中均方误差逐渐下降并趋于稳定,曲线平滑地收敛到最优解,未出现过拟合现象。ANN模型在训练和测试数据集上的实际值和预测值的对比如图5(a)和图5(b)所示,在训练阶段,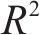
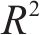
2.4 XGBoost模型
在XGBoost模型中,将超参数进行如下设置;最大深度为10、学习率为0.028、子节点权重的最小总和为2。为了控制模型复杂度以避免过拟合,将正则化参数alpha和lambda分别设置为1.2和4.9。如图5(c)和图5(d)所示,XGBoost模型在训练集中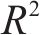
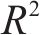
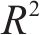
2.5 HEMNG模型
在对HEMNG进行训练时,截取性能最佳的ANN模型的倒数第2层输出作为新特征,并将 XGBoost的最佳参数用于训练最终模型。HEMNG模型在训练集展现出极高的拟合程度(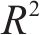
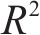
相比于单一的ANN和XGBoost模型,HEMNG模型结合了两者的优势,在训练集和测试集中表现出更高的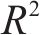
2.6 对不同输入数据类型的模型性能比较
为验证采用可解释特征作为输入的模型在预测混凝土抗压强度方面的优势,在相同数据集下,使用混凝土材料用量作为输入建立了相同结构的HEMNG模型。对比表2的数据,发现以材料用量的HEMNG模型在训练集和测试集中的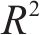
特征 类型 | 输入特 征数量 | 数据集 | 性能评价指标 | |
|---|---|---|---|---|
| R2 | ERMSE | |||
| 材料用量 | 7 | 训练集 | 0.990 | 1.259 |
| 测试集 | 0.889 | 4.572 | ||
| 可解释特征 | 5 | 训练集 | 0.998 | 0.563 |
| 测试集 | 0.961 | 2.704 | ||
2.7 与其他模型进行对比
为了更全面地评估HEMNG模型的性能,对比了HEMNG模型与几种常见模型(支持向量机、决策树、随机森林、极限学习机和轻量级梯度提升机)在训练集和测试集上的R2和ERMSE表现。由图7可知,HEMNG模型在训练集和测试集上的R2均高于其他模型,特别是在测试集上的表现更加突出,R2值为0.961,比性能次优的轻量级梯度提升机(R2为0.93)的准确度提高了3%,表明其拟合能力和泛化能力更强。此外,HEMNG模型在训练集和测试集上的ERMSE均低于其他模型,进一步突显了模型的高预测精度。因为在处理数据的方式上,ANN是基于神经网络的连续函数逼近,而XGBoost则是基于决策树的分段线性逼近,两者在捕捉数据模式和学习方式上相互补充,提升了HEMNG在处理复杂数据上的表现,同时增强了模型的稳健性和鲁棒性。
2.8 迁移验证
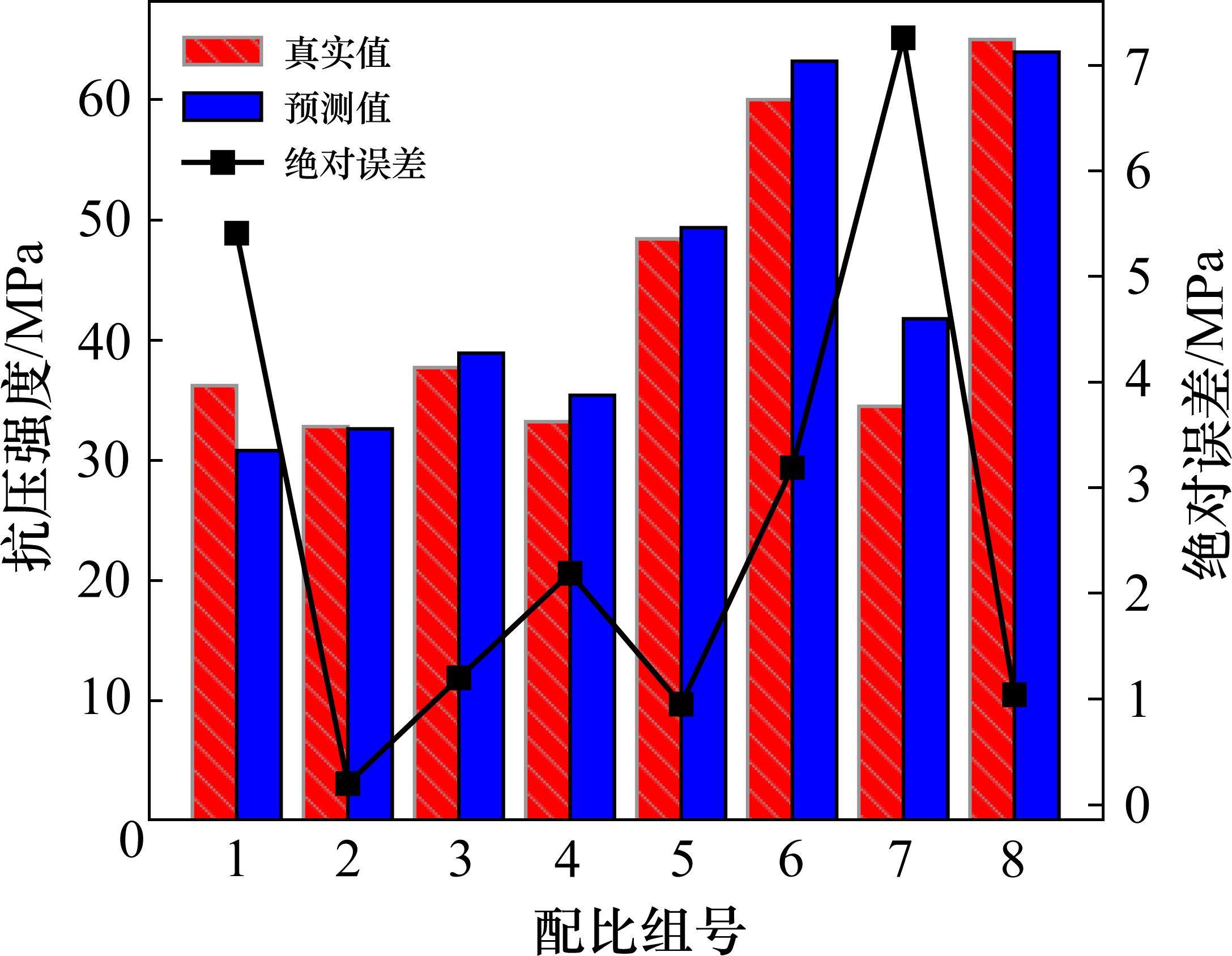
迁移验证是将HEMNG模型应用到全新的数据上,以评估其对未知数据的预测能力。本文利用8组全新的混凝土配比实验数据进行深入分析(见表3)。这些实验数据在训练数据集和测试集中均未出现,以防止任何可能引入模型的主观误差或偏差。从图8可以看出,HEMNG模型在应用于全新的数据时,其强度预测值与实际值较为吻合,显示出良好的预测准确性。特别值得一提的是,即使在完全未知数据上,模型的最大绝对误差仅为7 MPa。该模型可以快速预测给定设计配合比下的混凝土抗压强度,并在面对全新数据时保持较高的准确性。
| 配比组号 | 组成成分/(kg∙m-3) | 龄期/d | 抗压强度/MPa | |||||
|---|---|---|---|---|---|---|---|---|
| 水泥 | 水 | 粉煤灰 | 高性能减水剂 | 粗集料 | 细集料 | |||
| 1 | 200 | 150 | 120 | 6.08 | 805 | 1115 | 28 | 33.2 |
| 2 | 390 | 203 | 0 | 0.00 | 1 023 | 804 | 28 | 36.2 |
| 3 | 306 | 162 | 0 | 3.98 | 1005 | 927 | 28 | 32.8 |
| 4 | 377 | 162 | 0 | 4.91 | 968 | 893 | 28 | 37.7 |
| 5 | 310 | 145 | 85 | 8.30 | 910 | 960 | 28 | 48.4 |
| 6 | 425 | 140 | 65 | 10.78 | 970 | 820 | 28 | 60.0 |
| 7 | 356 | 158 | 65 | 8.63 | 900 | 927 | 28 | 44.1 |
| 8 | 460 | 140 | 60 | 11.44 | 969 | 791 | 28 | 65.0 |
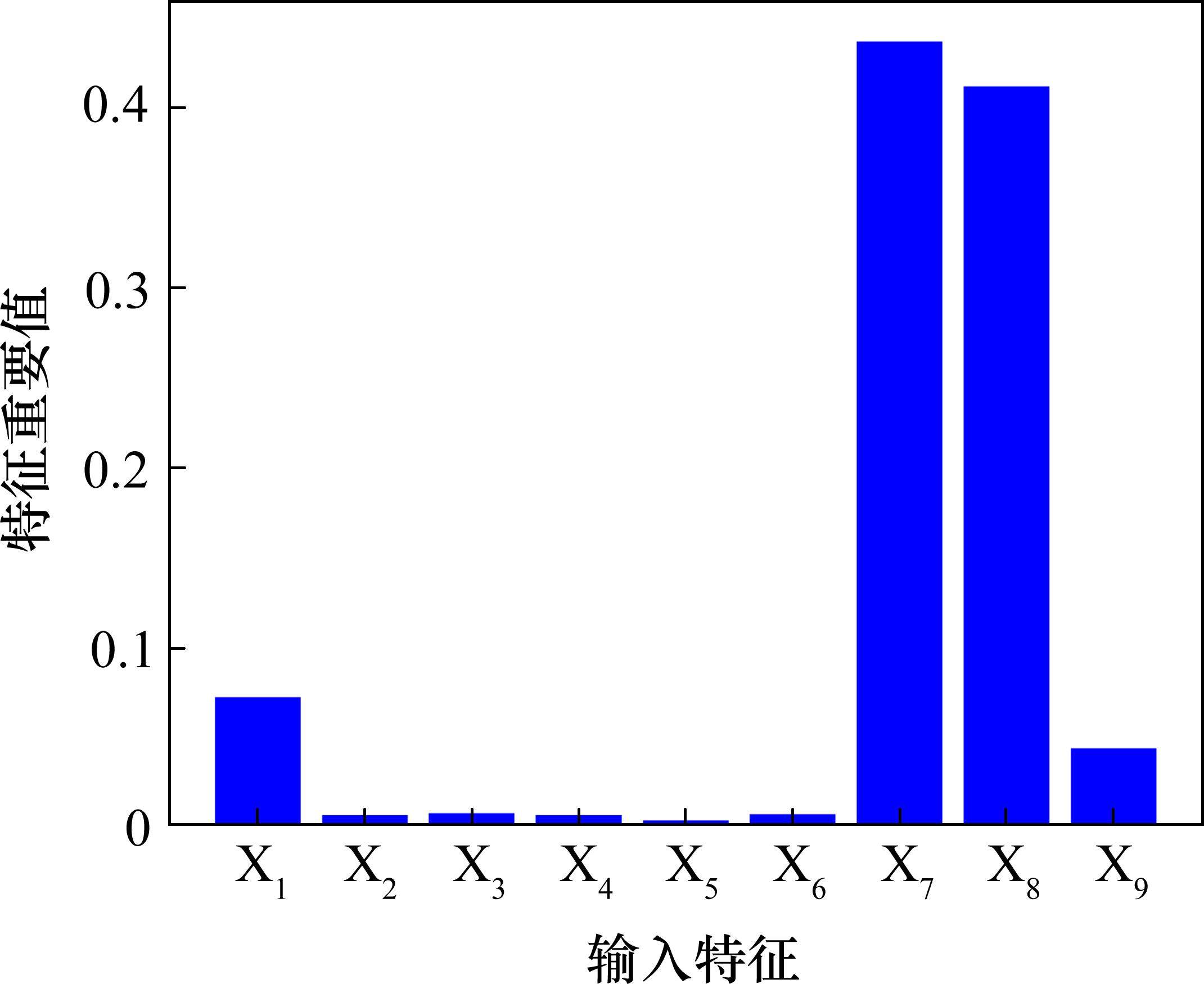
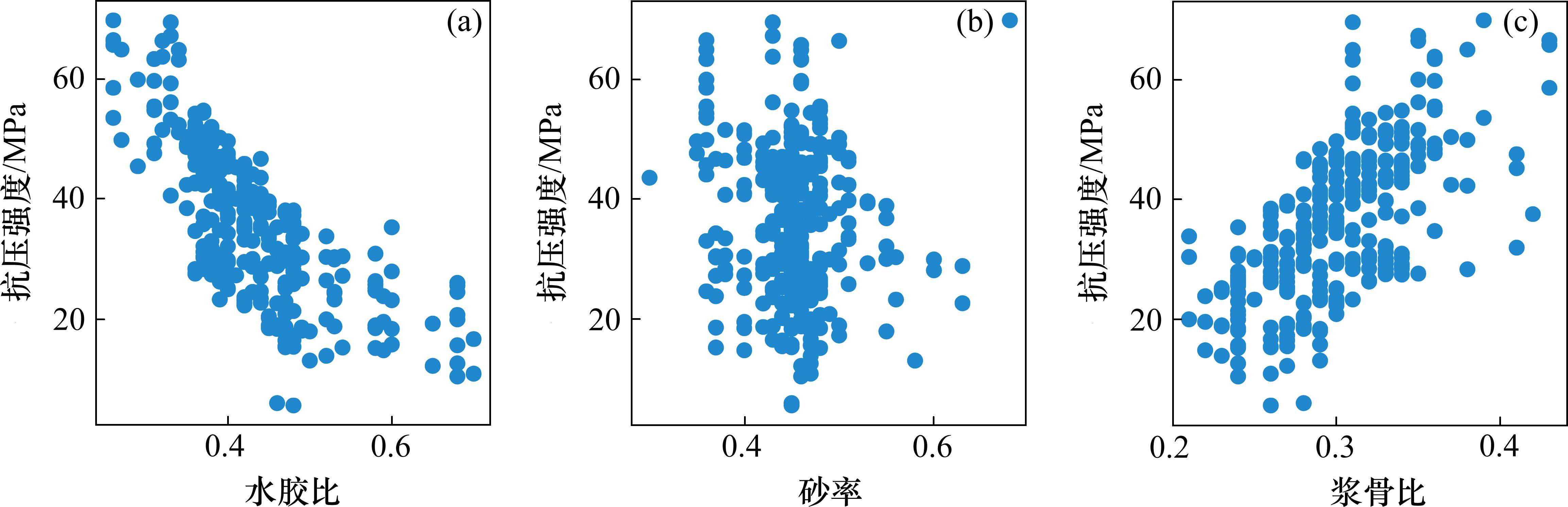
3 关键参数对抗压强度的影响
根据图6中的特征重要性分析结果,选取了对抗压强度影响最大的3个原始特征,即水胶比、砂率和浆骨比进行详细分析。如图9所示,从3个特征的数据分布可以看出,水胶比和浆骨比与混凝土抗压强度之间存在显著的相关性,而砂率则主要集中在0.45左右,没有呈现出明显的关联性。为了进一步探究这3个特征对抗压强度发展的影响,基于HEMNG模型进行敏感性研究分析。
3.1 单参数敏感性分析
为了量化水胶比、砂率和浆骨比对强度发展的影响,基于HEMNG模型分别改变水胶比、砂率和浆骨比3个特征的值来分析抗压强度的变化,在整个过程中,其他2个参数保持不变,具体结果如图10所示。
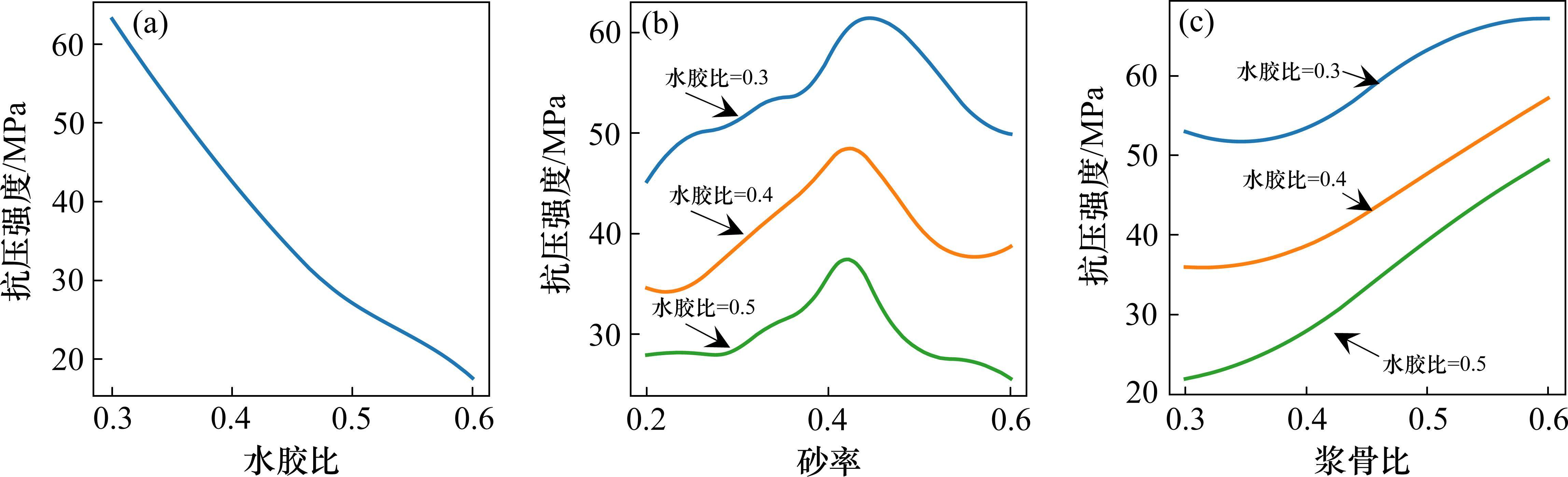
水胶比对抗压强度发展的影响如图10(a)所示,随着水胶比的增大,抗压强度明显降低。这与实验观察结果是一致的,在水胶比较高的情况下,虽然浆体的流动性增加,有利于填充和包裹骨料,但浆体中水分蒸发后会增加混凝土内部孔隙率,降低了混凝土的密实性。
在砂率方面,MOHAMMED等[20]探究了3种不同砂率(0.36、0.40、0.44)对抗压强度的影响。结果表明,无论采用何种骨料,增加砂率有助于提高混凝土抗压强度。但在其研究中,砂率的范围相对较小。因此,本文将砂率的范围扩展为0.3~0.5,进一步探究砂率对强度的影响。如图10(b)所示,随着砂率的增加,抗压强度逐渐提升,在达到峰值后下降。在整个过程中存在一个最佳砂率,使强度最大化。在达到强度最大值之前,砂的增加可填充骨料之间的空隙,提高混凝土密实性,从而提高抗压强度。然而,当砂率超过最佳点,砂粒表面积过大,部分沙粒无法完全被浆体所覆盖,导致孔隙增加,使抗压强度降低。
浆骨比对强度发展的影响如图10(c)所示。浆骨比对混凝土抗压强度的影响也是显著的,无论水灰比如何改变,提高浆骨比都能提升抗压强度。因为浆体在混凝土中起着黏结作用,浆体的增加会有更多的水化产物生成,同时提高了浆体与骨料之间的接触面积,使混凝土结构更紧密。值得注意的是,在水胶比为0.3,浆骨比增加到0.6时,强度增长趋势变平缓。表明水胶比并非越低、浆骨比越高就能够获得更高的混凝土抗压强度,这会导致混凝土的工作性能变差,浆体难以到达并填充骨料颗粒之间的空隙。
3.2 多参数敏感性分析
多参数分析基于HEMNG模型,通过水胶比、砂率和浆骨比的组合来预测分析混凝土抗压强度。在保证一个参数不变的情况下,改变另外2个参数进行预测分析。图11显示了混凝土抗压强度受这3个主要参数组合的影响。其中,箭头起始点代表高抗压强度,终点代表低抗压强度,在这个过程中,抗压强度由高到低变化。
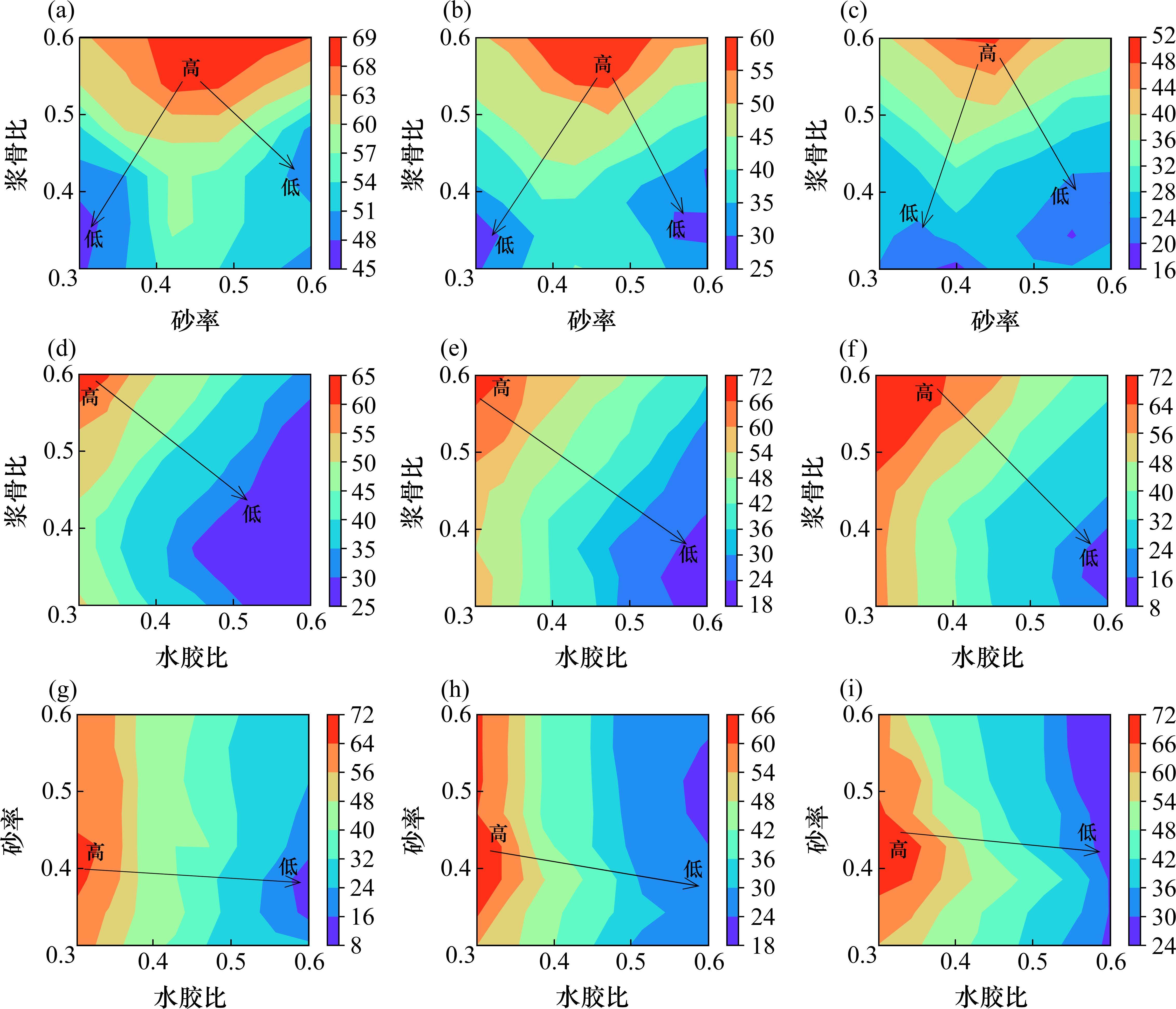
由图11(a)到图11(c)可知,在水胶比一定的情况下,随浆骨比的增大,最佳砂率呈现出先增大后减小的趋势。浆骨比在0.5~0.6时,无论水胶比如何改变,最佳砂率集中在0.45。图11(d)到图11(f)进一步证实了较高的浆骨比更有利于抗压强度的发展,在水胶比为0.3,浆骨比为0.6的情况下,保证了混凝土的高强度。当水胶比在0.3~0.4、浆骨比在0.5~0.6的情况下,砂率为0.5时更有利于强度的发展。由图11(g)到图11(i)可知,在浆骨比一定时,最佳砂率随水胶比的增大而减小。当水胶比从0.3增加到0.5,最佳砂率从0.45下降到0.35。基于抗压强度受各种因素影响的常识,可检验HEMNG模型的合理性。
4 结论
1) 提出的HEMNG模型使用5个可解释特征作为输入,抗压强度作为输出,可准确预测混凝土抗压强度。在测试阶段,R2和ERMSE分别为0.961和2.704。模型结合了ANN和XGBoost的优势,具有很好的泛化能力,在各性能指标上优于ANN、XGBoost和支持向量机等模型。
2) 实例验证显示,HEMNG模型的多数预测值与实际值相符,最大绝对误差仅为7 MPa,面对新数据时,也能保持较高的准确性。随着数据量的增加,模型在未知数据中的预测精度将进一步提高。
3) 基于HEMNG模型的敏感性分析表明:存在一个最佳砂率使抗压强度达到最大值;增大水胶比会降低混凝土抗压强度,最佳砂率会随着水胶比的增大而减小;随着浆骨比的增大,最佳砂率会表现出先增大后减小的趋势。模型所捕获的关系与影响混凝土抗压强度的理论一致,证明其预测的合理性。
周继发,曾晓辉,谢友均等.基于HEMNG模型的混凝土抗压强度预测[J].铁道科学与工程学报,2025,22(02):875-886.
ZHOU Jifa,ZENG Xiaohui,XIE Youjun,et al.Predicting concrete compressive strength based on HEMNG model[J].Journal of Railway Science and Engineering,2025,22(02):875-886.

