随着盾构技术在国内的快速发展,盾构隧道的数量井喷式增长,并朝大直径大埋深趋势发展,同时伴随高水压等复杂地质条件,这对盾构隧道的防水性能提出了更高的要求[1-3]。长期以来,许多国内外专家学者将提高管片接缝处密封垫的防水性能作为研究的重点,在管片接缝防水体系的建立、密封垫防水性能、密封垫断面结构优化、密封垫使用寿命预测以及密封垫老化性能等方面取得了一系列突破性进展。肖明清等[4]调研分析总结了国内盾构隧道管片接缝防水体系的各种布置形式,并指明了管片接缝防水体系未来的发展趋势。GONG等[5]从衬砌接缝的力学性能、密封垫的材料特性、密封垫防水性能的数值模拟发展、衬砌接缝的热力耦合分析4个方面对盾构隧道密封垫防水性能研究成果进行归纳总结,并指明了密封垫防水性能未来的研究方向。ZHANG等[6]以成都某地铁盾构隧道为例,研究了管片张角对密封垫防水性能的影响。薛光桥等[7]采用数值模拟的研究方法分析了“先压缩后错缝”加载模式下密封垫的防水能力。周文锋等[8]依托琼州海峡海底盾构隧道工程,通过建立流固耦合数值计算模型,分析了密封垫间接触应力分布规律及渗流规律。HEO等[9]为了消除施工过程中张开量和错台量等因素对密封垫防水性能的影响,开发了一种仅有一侧管片具有密封垫的防水体系,并通过防水试验证明了该系统的优越性。张稳军等[10]对比分析了2种截面形式的复合型密封垫在不同工况下的防水性能,得出了最优设计截面的复合型密封垫。肖明清等[11]从微观层面对双道密封垫的防水机理进行研究并建立了双道密封垫防水能力计算公式。李雪等[12]和DING等[13]基于自行研制的密封垫水密性试验装置,探究了单道密封垫与双道密封垫的最大设防压力以及失效模式。张稳军等[14]和张家奇等[15]基于阿累尼乌斯方程的“P-T-t”三元模型对密封垫长期防水能力进行了预测。李睿佳等[16]提出了一种更贴合工程实际的密封垫压缩老化试验方法,研究发现受压状态下的密封垫老化速度更快。总的来看,目前有关提升管片接缝防水性能的研究大多围绕密封垫展开,然而越来越多的研究指出沟槽断面形状尺寸也对管片接缝防水效果有影响。肖明清等[11]通过对管片接缝双道密封垫防水试验结果进行分析,认为沟槽形状与尺寸对密封垫防水能力具有一定影响。杨贵生等[17]以密封垫表面平均接触应力、闭合压缩力为评价指标,分析了沟槽侧边斜率、深度、宽度对密封垫防水性能的影响,给出了沟槽设计及优化的相关建议。贺创波等[18]探究了沟槽深度对橡胶密封垫变形形态和防水性能的影响,分析了沟槽深度为8 mm和10 mm这2种工况下密封垫压缩后的变形形态。本文以沟槽为研究对象,重点对沟槽断面形状尺寸进行优化,为管片接缝防水性能的研究开辟一种新思路。分析总结前人对于沟槽断面设计优化的思路,发现目前沟槽断面的设计优化多采用类比方法或依靠工程经验,这种方法设计效率较低,具有很大的局限性和盲目性。本文提出采用组合代理模型设计沟槽断面的方法,利用遗传算法对代理模型寻优,得到防水性能最佳的沟槽断面尺寸参数。基于代理模型的设计方法,在保证优化效果的前提下,显著提高了设计优化的效率,同时还为行业提供了一种可供参考的优化设计方案。
1 基本理论
1.1 密封垫间有效泄漏率计算
目前采用平均接触应力和有效接触应力指标计算有水压密封垫防水性能时,得到的结果与密封垫防水试验结果存在差异。肖明清等[19]提出基于有效泄漏率的密封垫防水性能评价方法,考虑了密封垫接触面凹凸不平和存在极细微渗漏孔洞的影响,将高于设计水压的泄漏率定义为有效泄漏率,认为泄漏率低的密封垫,其防水性能更好。密封垫防水试验结果与泄漏率模拟计算结果趋势基本一致,证明了以有效泄漏率作为密封垫防水性能的评价指标的合理性。本文根据肖明清等[19-20]推导出的密封垫间泄漏率计算公式来计算不同工况下密封垫间的有效泄漏率。
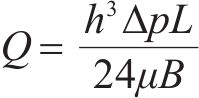
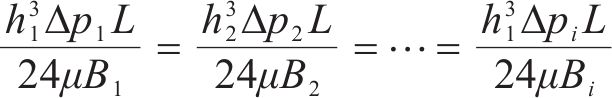
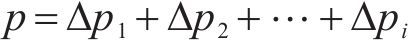
式中: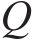
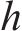
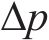
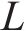
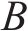
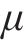
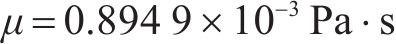
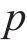
1.2 克里金模型
克里金(KRG)插值法是一种无偏估计方法,适合求解小样本高维非线性问题。对于给定的样本点:
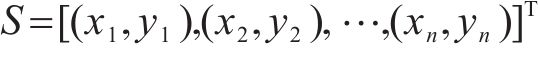
式中: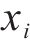
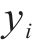
假设用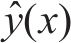
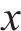
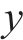
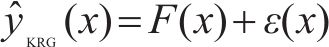
式中: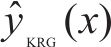
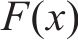
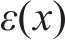
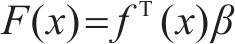
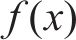
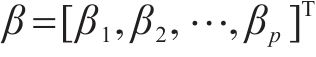
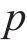
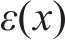
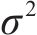
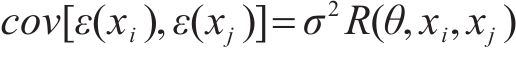
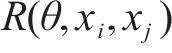
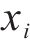
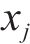
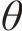
1.3 响应面模型
响应面分析法(RSM)的基本思想是通过近似构造一个具有明确表达式的多项式来拟合各因素与响应的函数关系,进而对问题进行预测和优化,可有效减少实验次数,并且考虑了因素之间的交互作用。本文采用2阶多项式拟合函数构造优化目标的响应面模型,对应的数学表达式为:
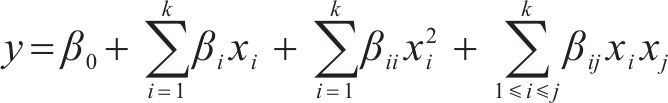
式中: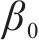
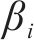
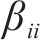
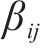
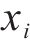
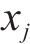
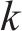
1.4 支持向量机回归模型
支持向量机回归模型(SVMR)是一种非参数回归方法,对小样本的非线性回归预测问题具有较好的建模性能,其基本思想是将不具有线性可分性的原始数据通过核函数映射到一个新的高维特征空间,使得原始数据可以在新的空间内建立线性回归模型。最优回归函数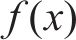
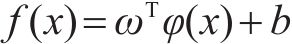
式中: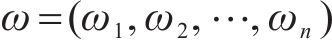
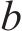
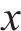
对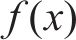
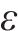
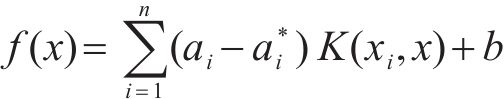
式中: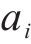
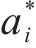
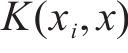
1.5 遗传算法
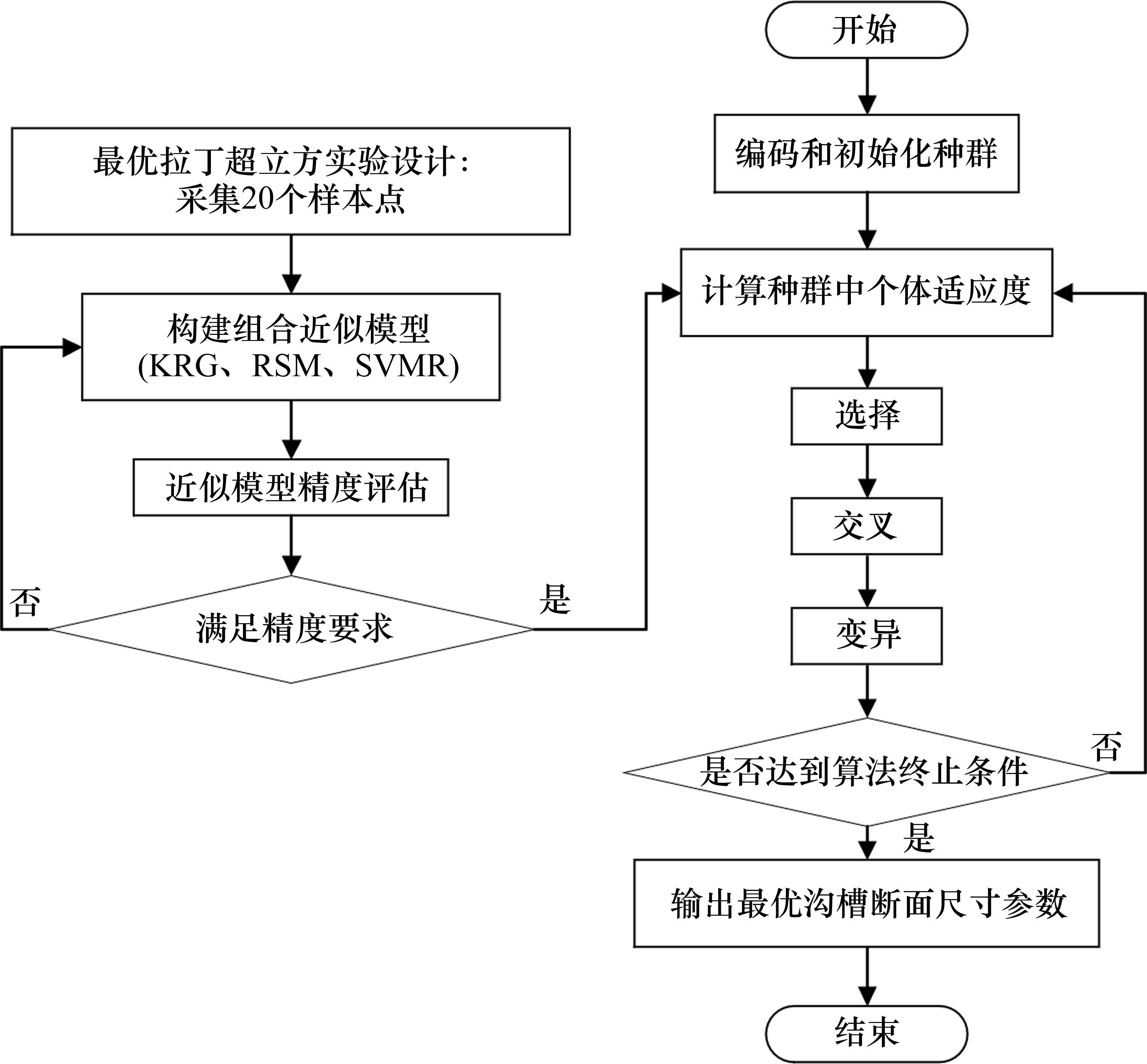
遗传算法(GA)是借鉴生物界自然进化规律演化而来的随机全局搜索和优化方法,能够自适应地控制搜索过程以求得最优解。本文采用最优拉丁超立方实验设计方法进行实验方案设计,构建基于克里金模型、响应面模型以及支持向量机回归模型的组合预测模型,将组合近似模型与遗传算法相结合,利用组合近似模型来计算种群中个体适应度,通过遗传算法得到最小适应度的个体,并对寻优结果进行数值模拟验证算法的有效性,运算流程图如图1所示。
2 数值模拟
2.1 几何模型
目前关于弹性密封垫防水失效机理的研究方法主要是数值模拟和室内试验。数值模拟通过构建足尺模型并赋予模型相应的材料属性、约束关系以及边界条件,能够得到模型任意时刻的变形形态和任意接触面应力的分布规律,具有低成本、高效率、可视化等特点。室内试验存在成本较高、费时费力等不足,但因其试验条件更接近工程实际,目前工程中仍以室内试验结果作为密封垫防水性能的判断依据。而本文对沟槽断面形状尺寸的优化研究中涉及沟槽断面数量较多,直接采用室内试验的研究方法成本较高、困难较大,而采用数值模拟方法可以对沟槽断面进行快速地优化改进和验证,通过数值模拟结果进行定性判定,为沟槽断面形状的优化提供参考依据。
选用南京和燕路长江隧道Ⅱ型密封垫和密封垫沟槽,断面结构分别如图2和图3所示,断面的相关参数如表1所示[21]。
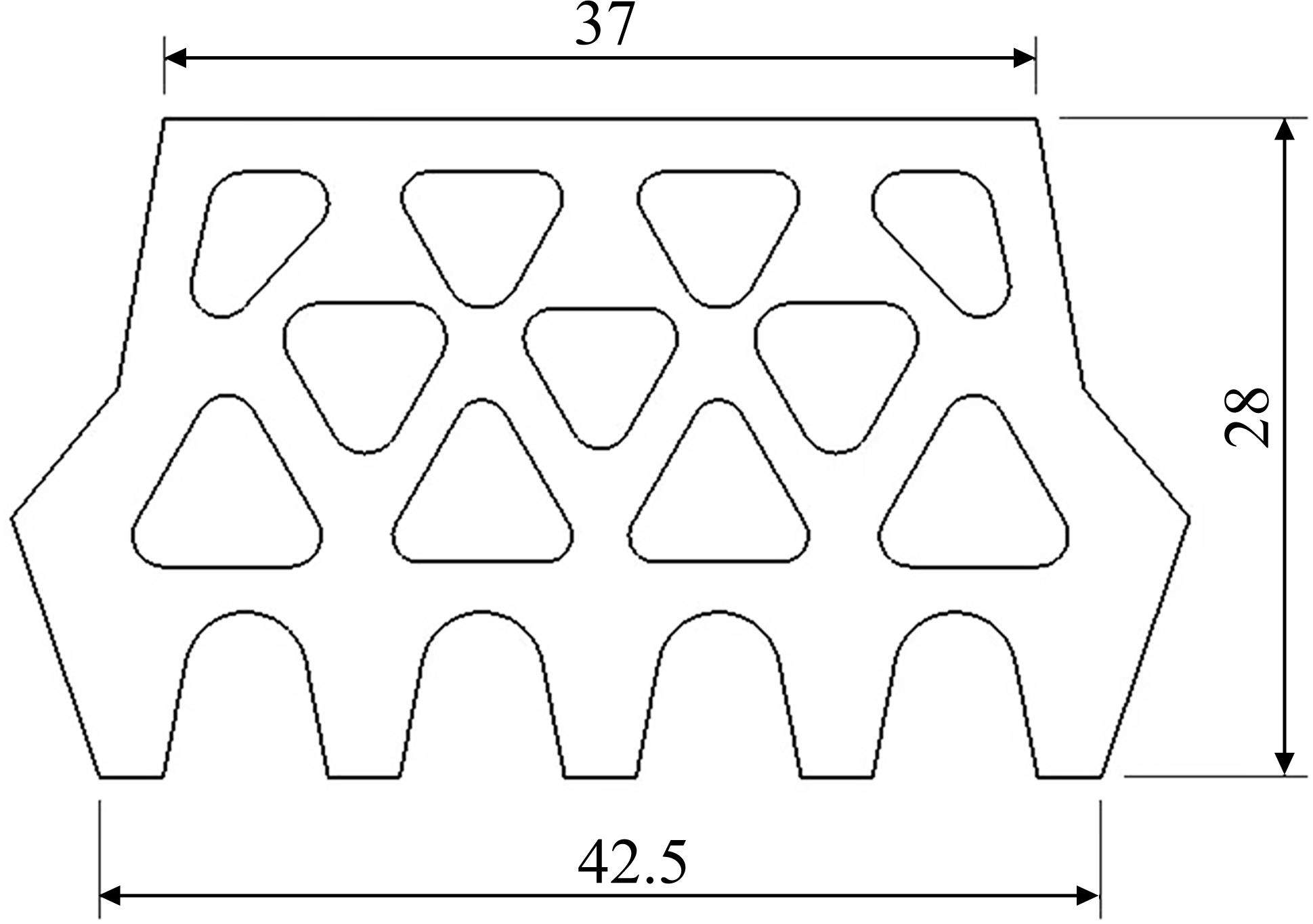
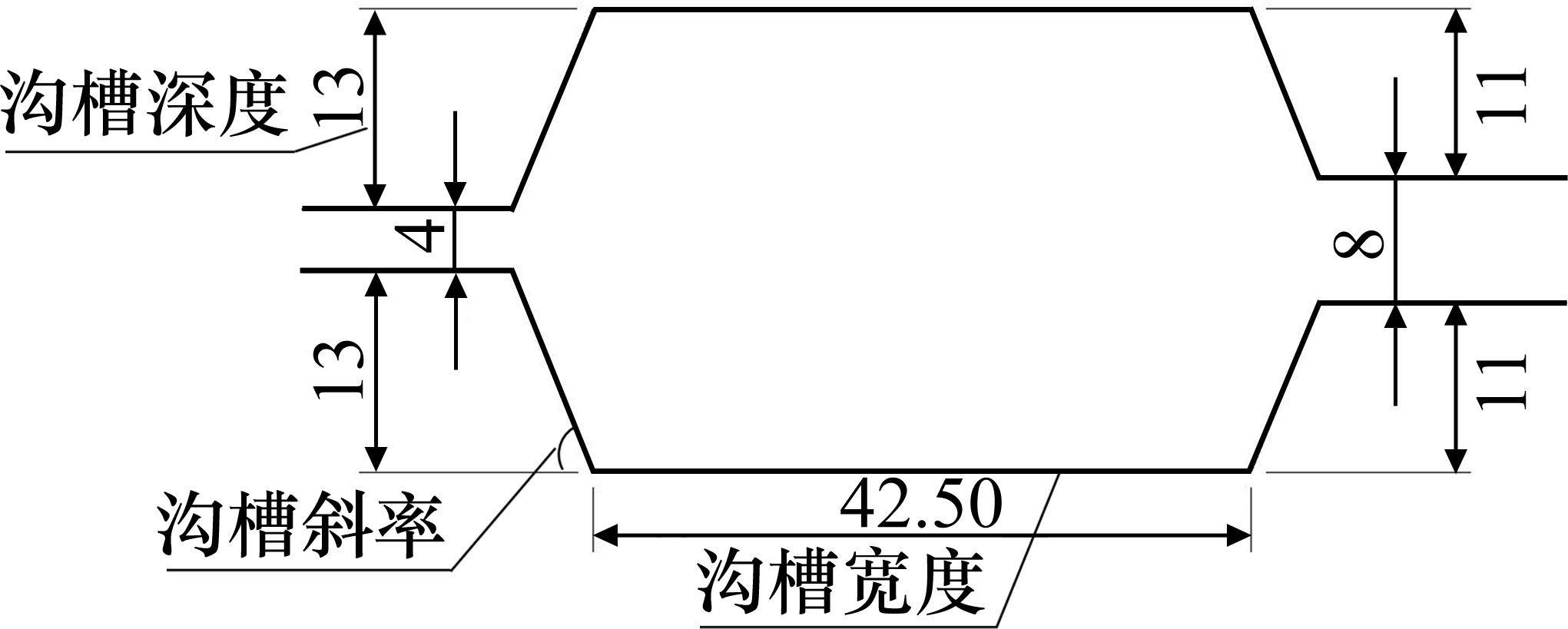
| 沟槽深度/mm | 单边沟槽面积/mm2 | 密封垫高度/mm | 密封垫面积(除孔)/mm2 | 沟槽与密封垫的面积比 |
|---|---|---|---|---|
| 15 | 753.3 | 28 | 703.2 | 1.071 |
2.2 材料本构模型和参数选取
根据图2和图3建立弹性密封垫和密封垫沟槽有限元模型,管片沟槽材料选用更贴合工程实际的C50混凝土,弹性模量34.5 GPa,泊松比为0.2,密度为2 420 kg/m3。由于混凝土沟槽的刚度远大于三元乙丙密封垫,在数值模拟时将沟槽设置为刚体。三元乙丙弹性密封垫为橡胶材料,在数值模拟中通常被视作具有各向同性不可压缩的超弹性材料。Mooney‐Rivlin 模型是一种经典的基于连续介质唯象理论的本构模型,对几乎所有橡胶材料的力学行为的模拟均具有较好的适用性,因此在进行数值模拟时选取Mooney-Rivlin超弹性本构模型。其应变能函数表达式为:
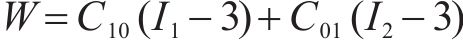
式中: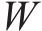
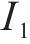
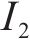
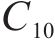
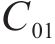
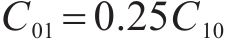
Mooney-Rivlin模型中的橡胶材料弹性模量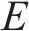
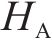
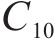
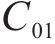
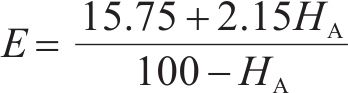
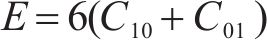
在本次数值模拟中,三元乙丙密封垫硬度为65 HA,C10和C01取值分别为0.592和0.148。
2.3 网格划分及接触设置
有限元模型采用多区域网格划分方法,如图4所示。有限元模型中设置密封垫与密封垫之间、密封垫与沟槽之间为面面接触,密封垫内部孔洞为自接触,接触面法向采用硬接触,切向采用罚函数接触。弹性密封垫间接触面的摩擦因数取0.5,沟槽与密封垫间的摩擦因数取0.3[22]。整个计算过程采用显式动力学方法进行。根据管片实际拼装情况,将下侧管片沟槽完全固定,对上侧管片沟槽施加向下的位移载荷模拟密封垫压缩过程。在上侧管片压缩16 mm,错台15 mm工况下,以面荷载方式施加0.8 MPa水压于密封垫的迎水面, 用以模拟外部水压对管片接缝密封垫的挤压作用。
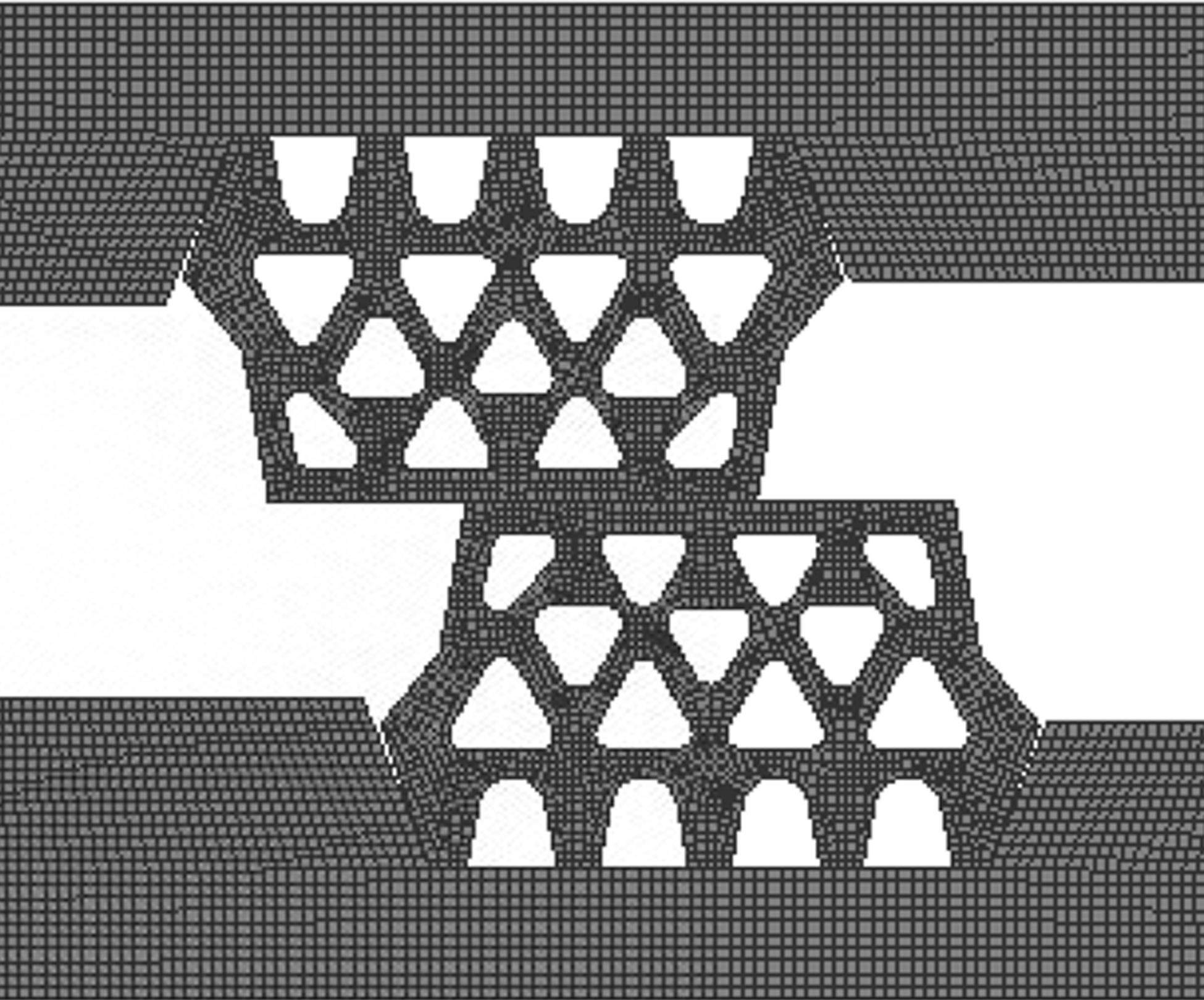
2.4 有限元模型验证
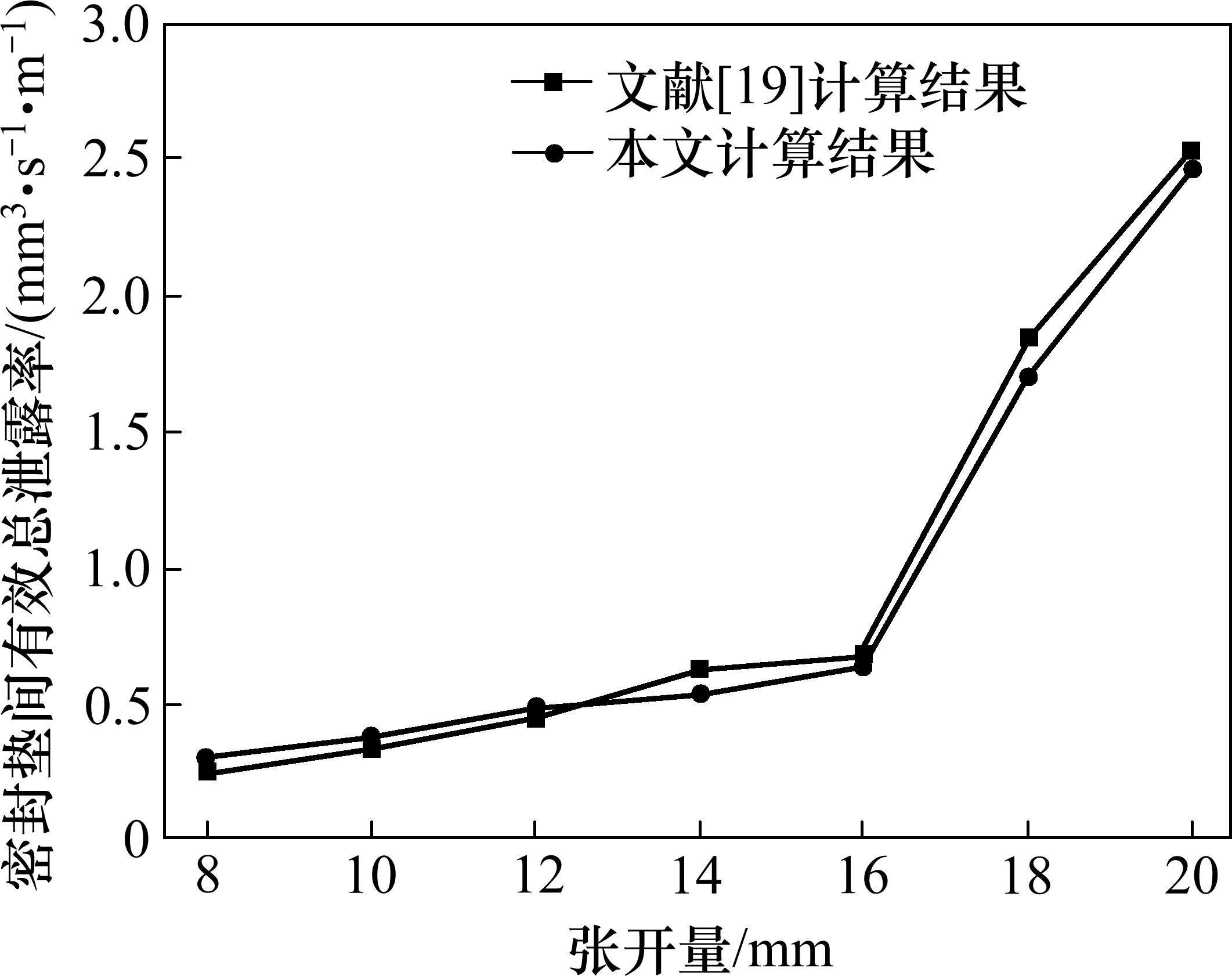
为了保证本文所建立的有限元模型的准确性,需要验证本文材料本构模型选择、参数设定、网格划分和接触设置等步骤是否正确。文献[19]通过开展室内试验给出了在错台量15 mm,外界水压0.8 MPa条件下,不同张开量所对应的密封垫间有效泄漏率数值,将本文模型在相同工况下模拟得到的结果与文献[19]试验结果进行对比,如图5所示,可以看出,两者有效总泄漏率均随着张开量的增大而增大,变化趋势相同,并且在同一的张开量下,两者所得有效总泄漏率数值相近,两者相差不超过10%。通过上述对比,在一定程度上验证了本文模型的合理性和准确性,为后续计算分析奠定了基础。
3 沟槽断面尺寸参数优化设计
3.1 沟槽尺寸参数范围确定
为确定合理的尺寸参数范围,提高组合模型的优化效果,首先通过单因素试验对沟槽尺寸参数范围进行讨论。初步选定沟槽斜率范围为55°~75°,深度范围为12.5~14 mm,宽度范围为42.5~46.5 mm。
图6(a)为沟槽斜率对密封垫间有效泄漏率的影响规律。可以看到,在不同沟槽宽度条件下,沟槽斜率对有效泄漏率的影响规律具有相似性。随着斜率的增大,密封垫间有效泄漏率呈增大趋势,尤其是斜率超过70°后,泄漏量明显增大。由此可见,通过调整沟槽斜率来对密封垫防水性能进行优化时,沟槽斜率范围可取55°~70°。
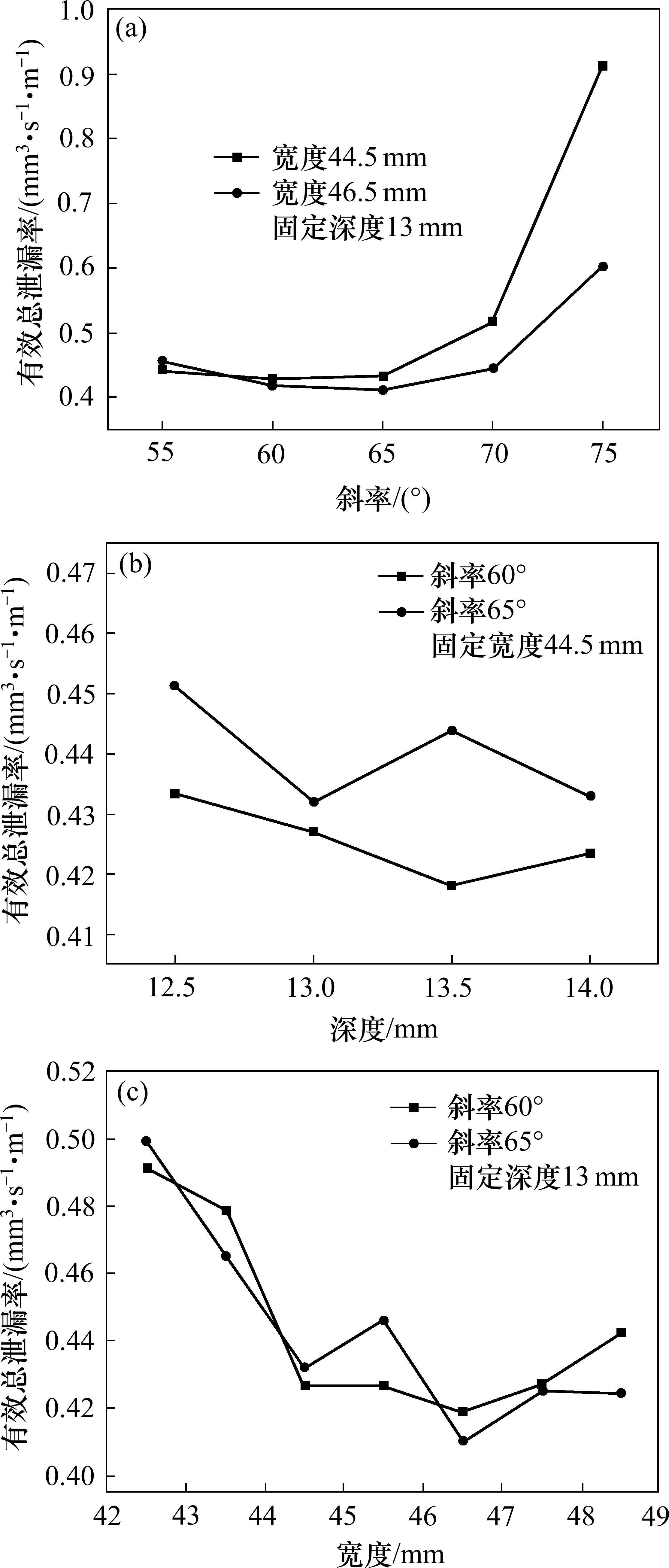
图6(b)展示了沟槽深度对密封垫间有效泄漏率的影响,可以看出深度范围从12.5 mm变化到14 mm时,不同沟槽斜率条件下泄漏率均变化不大,可知沟槽深度对泄漏率的影响较小,在后续优化时选取沟槽深度范围为12.5~13.5 mm。
沟槽宽度对密封垫间有效泄漏率的影响规律如图6(c)所示,随着沟槽宽度的增大,密封垫间有效泄漏率先急剧减小后又趋于平稳。沟槽宽度为42.5 mm时,有效泄漏率最大,宽度为46.5 mm时,有效泄漏率最小。沟槽宽度可取43.5~46.5 mm。
通过单因素实验确定沟槽尺寸参数的选取范围如表2所示。
| 斜率/(°) | 深度/mm | 宽度/mm | |||
|---|---|---|---|---|---|
| 最小值 | 最大值 | 最小值 | 最大值 | 最小值 | 最大值 |
| 55 | 70 | 12.5 | 13.5 | 43.5 | 46.5 |
3.2 最优拉丁超立方实验设计
原始的拉丁超立方实验设计方法在低维空间具有较好的均匀性,但在高维空间可能导致部分区域样本点发生聚集,失去采样的代表性和精度。本文采用的最优拉丁超立方实验设计方法在原始的拉丁超立方实验设计方法基础上,加入最大最小距离准则,计算所有采样点之间的欧氏距离,通过迭代优化,确保采样点之间的距离尽可能地大,以增加样本点之间的离散性和均匀性。
根据表2所列出的沟槽尺寸参数取值范围,采用最优拉丁超立方实验设计方法设计20组实验,对每组实验参数进行数值模拟,按照有效泄漏率的计算公式计算得到每组参数所对应的密封垫间有效泄漏率,为保证数值模拟结果的准确性,对每组实验参数进行多次模拟并求取平均值。结果如表3所示。
| 编号 | 斜率/ (°) | 深度/ mm | 宽度/ mm | 密封垫间有效泄漏率/(mm3∙s-1∙m-1) |
|---|---|---|---|---|
| 1 | 68.7 | 12.7 | 46.5 | 0.453 6 |
| 2 | 63.9 | 12.8 | 44.8 | 0.471 0 |
| 3 | 55.0 | 12.9 | 44.4 | 0.450 5 |
| 4 | 66.6 | 12.6 | 45.8 | 0.459 6 |
| 5 | 58.7 | 13.2 | 43.8 | 0.463 9 |
| 6 | 64.1 | 13.1 | 44.7 | 0.462 2 |
| 7 | 56.3 | 13.4 | 45.2 | 0.441 1 |
| 8 | 61.4 | 12.7 | 44.0 | 0.470 9 |
| 9 | 70.0 | 13.4 | 46.3 | 0.457 6 |
| 10 | 62.7 | 13.5 | 46.2 | 0.441 9 |
| 11 | 67.3 | 13.3 | 45.6 | 0.460 7 |
| 12 | 57.6 | 12.6 | 45.0 | 0.454 5 |
| 13 | 59.9 | 13.2 | 45.2 | 0.448 1 |
| 14 | 65.4 | 12.8 | 44.1 | 0.475 2 |
| 15 | 69.4 | 13.0 | 46.1 | 0.457 4 |
| 16 | 60.2 | 12.9 | 43.6 | 0.470 1 |
| 17 | 55.6 | 13.5 | 43.5 | 0.457 4 |
| 18 | 62.5 | 12.5 | 45.8 | 0.450 3 |
| 19 | 66.0 | 13.1 | 45.4 | 0.459 7 |
| 20 | 58.1 | 13.0 | 44.3 | 0.456 1 |
3.3 组合预测模型构建
本文采用克里金模型(KRG)、响应面模型(RSM)、支持向量机回归模型(SVMR)来构建组合预测模型,实现对密封垫间有效泄漏率的准确预测。通过给各单一模型赋予权重并相加,得到组合模型,采用均方误差作为组合模型精度的评价指标,使用留一法交叉验证测试模型的精度。为了得到最高精度的组合模型,应使模型的均方误差最小,该问题可用公式(13)表示。
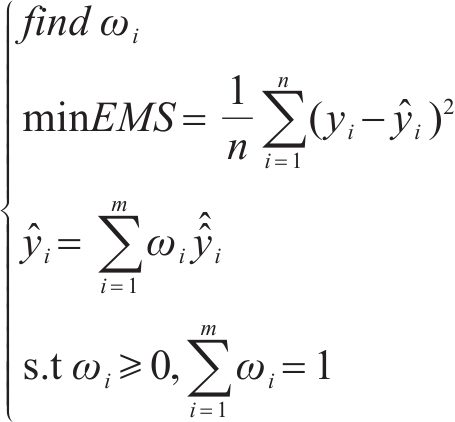
式中: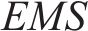
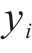
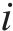
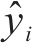
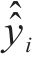
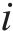
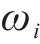
对问题13进行求解,求得组合模型中各子模型的权重系数如表4所示,子模型权重占比越大,表明该模型对问题的拟合程度越高,从表4可知支持向量机模型具有更高的拟合精度。
| 指标 | 权重系数 | ||
|---|---|---|---|
| KRG | RSM | SVMR | |
| 有效泄漏率 | 0.21 | 0.23 | 0.56 |
采用均方误差MSE、平均绝对百分比误差MAPE和相关系数R2这3种评价指标对比各单一预测模型和组合预测模型的预测效果,3种评价指标的数学表达式如下。
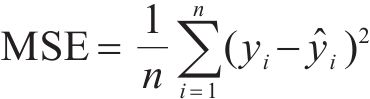
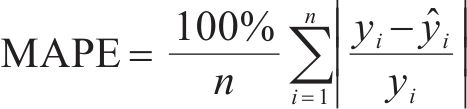
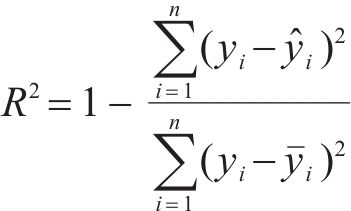
式中: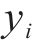
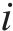
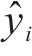
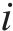
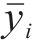
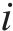
表5对比了各预测模型的精度,可以看出不同模型之间的精度存在一定差异。具体而言,各单一模型中,支持向量机模型效果最佳,其精度高于克里金模型和响应面模型。组合模型精度高于任意单一模型,预测效果最佳,MSE为3.47×10-6,MAPE为0.317,R2为0.955,这说明组合模型能够很好地组合各单一预测模型的优势,具有更高的预测精度。
| 评价指标 | KRG | RSM | SVMR | 组合模型 |
|---|---|---|---|---|
| MSE | 5.32×10-6 | 4.91×10-6 | 3.88×10-6 | 3.47×10-6 |
| MAPE | 0.411 | 0.402 | 0.351 | 0.317 |
| R2 | 0.931 | 0.936 | 0.943 | 0.955 |
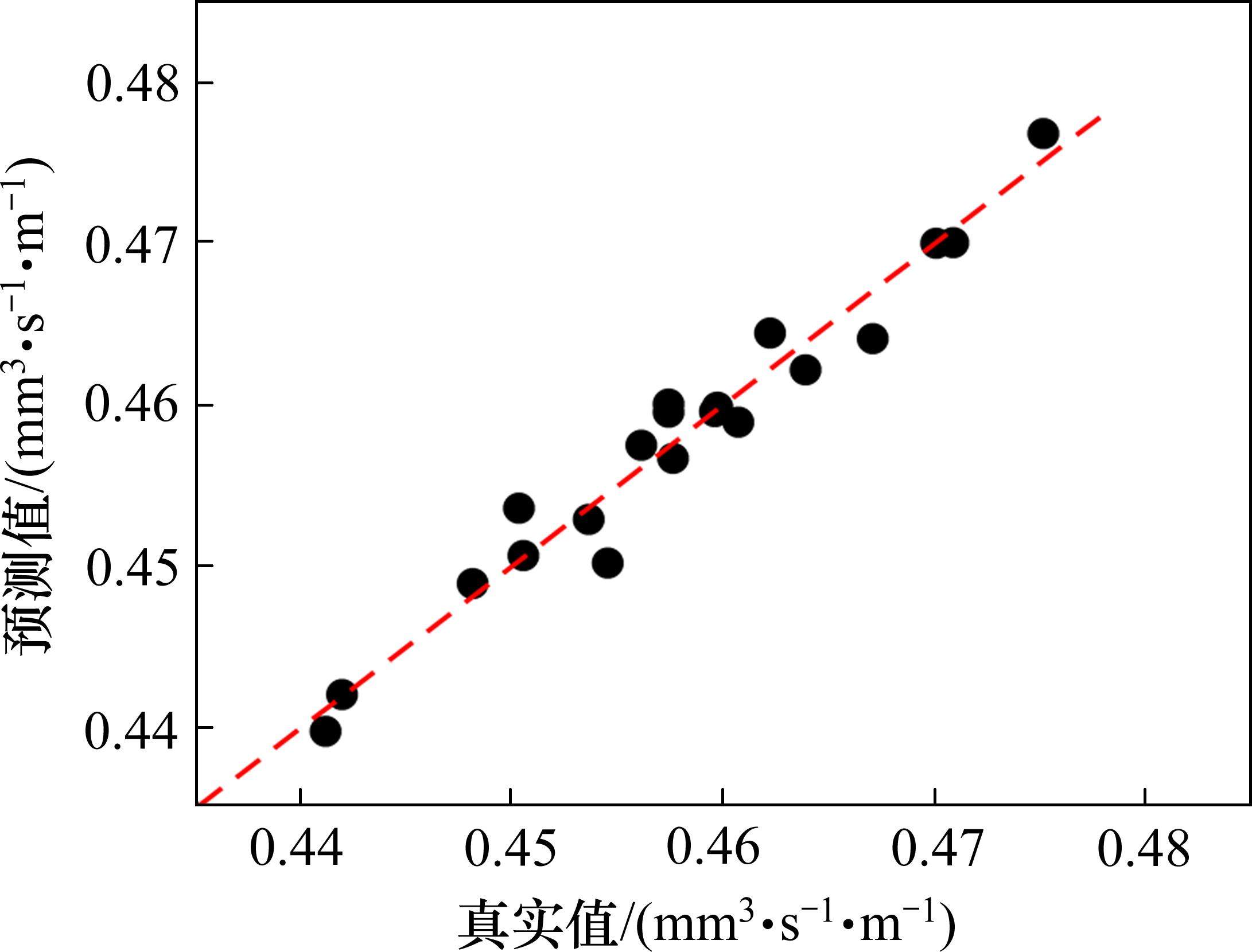
图7为组合模型预测值与真实值对比图,可以看出组合模型得到的有效泄漏率预测值与真实值具有较高的一致性,数据点较好地分布在拟合直线两侧,表明组合模型具有良好的预测精度,能够对有效泄漏率进行准确预测。
3.4 参数优化与验证
基于前文建立的组合模型,使用遗传算法对沟槽断面参数进行优化,以沟槽斜率、深度、宽度为优化变量,算法的适应度函数为密封垫间有效泄漏率。优化后的结果为沟槽斜率58.2°、深度12.7 mm、宽度46.5 mm,模型优化所得密封垫间有效泄漏率预测值为0.424 mm3/(s∙m),采用模型优化所得的沟槽尺寸参数进行多次数值模拟验证,数值模拟所得密封垫间有效泄漏率实际值为0.417 mm3/(s∙m),模型预测值与实际值相对误差为1.88%,说明本文建立的组合模型可较好地对有效泄漏率进行预测。优化前密封垫间有效泄漏率为0.505 mm3/(s∙m),优化后较优化前有效泄漏率降低了17.4%。此外本文还对比了优化前后密封垫间有效接触应力占比,优化前有效接触应力占比为36.75%,优化后为44.42%,优化后密封垫间有效接触应力占比有所提高,管片接缝处的防水性能得到改善。表6给出了沟槽优化前后各参数的具体数值。
| 斜率/(°) | 深度/mm | 宽度/mm | 密封垫间有效泄漏率/(mm3∙s-1∙m-1) | 密封垫间有效接触应力占比/% | |
|---|---|---|---|---|---|
| 优化前 | 68.2 | 13 | 42.5 | 0.505 | 36.75 |
| 优化后 | 58.2 | 12.7 | 46.5 | 0.417 | 44.42 |
4 结论与讨论
1) 由单因素实验可知,沟槽斜率、深度、宽度对密封垫防水性能有着重要影响,随着沟槽斜率的增大,密封垫间有效泄漏率呈增大趋势,沟槽深度的变化对密封垫间有效泄漏率的改变较小,密封垫间有效泄漏率随着沟槽宽度的增大先急剧减小后又趋于平稳。
2) 基于克里金模型、响应面模型以及支持向量机回归模型的组合预测模型能够充分结合各单一预测模型的优势,具有更好的预测效果。使用组合代理模型实现了由断面形状到有效泄漏率的快速计算,节约了数值模拟计算的成本,是提高密封垫沟槽断面优化效率的有效方法,将遗传算法与组合代理模型相结合能够快速高效地完成沟槽断面的优化设计。
3) 优化后管片接缝处的防水性能较优化前有明显提升。采用优化后的沟槽断面,密封垫间有效泄漏率为0.417 mm3/(s∙m),相较于优化前有效泄漏率降低17.4%,优化后密封垫间有效接触应力占比也有所提高,采用优化后的沟槽断面可提高管片接缝处的防水性能。
本文主要采用数值模拟方法开展了密封垫沟槽断面形状尺寸参数的优化研究,后续将根据本文的优化结果开展实验分析,进一步验证优化结果的可靠性。此外,本文关于管片沟槽优化的思路和方法可以为密封垫断面的优化提供参考和借鉴,未来的研究可以进一步拓展至密封垫断面参数的优化,以进一步提升管片接缝处的防水性能。
李怡函,肖明清,薛光桥等.基于组合模型的盾构管片沟槽断面尺寸优化研究[J].铁道科学与工程学报,2025,22(02):807-816.
LI Yihan,XIAO Mingqing,XUE Guangqiao,et al.Research on optimization of shield segment groove section size based on combined agent model[J].Journal of Railway Science and Engineering,2025,22(02):807-816.

