盾构法因其施工安全、掘进速度快、自动化程度高等优点被广泛应用于城市地下铁路和跨海越江隧道修建。盾构管片接缝作为隧道防水的薄弱环节,一旦发生渗漏,不仅会引发突水涌泥、隧道沉降变形等病害[1-2],而且补漏维修成本高昂,给盾构隧道的运营环境和结构安全带来巨大威胁[3-5]。弹性橡胶密封垫作为盾构隧道接缝防水的核心部件,依靠盾构千斤将弹性密封垫压紧闭合,产生接触应力来抵抗外部水压侵入。早期建设的盾构隧道通常采用单道密封垫防水模式,在一些小直径的城市地铁隧道得到了广泛应用[6-8],国内外学者对其防水性能开展了大量试验研究。GONG等[9-10]基于单道密封垫防水试验和数值模拟,研究了接缝张开量、错台量及密封垫硬度对密封垫防水性能的影响,提出了用平均接触应力指标描述密封垫防水能力的简化公式;ZHANG等[11]研发了一种可更换混凝土内衬的防水试验装置,实现了接缝张开、错台、转角的模拟,探究了3种变形状态下的渗漏模式;ZHANG等[12]采用足尺管片进行了接缝渗漏水试验,考虑了真实管片接缝工况对密封垫防水能力的影响。随着盾构隧道建设技术的进步和建设需求的提高,隧道的直径和设计水压进一步提升,传统的单道密封垫防水模式已不能满足工程需求。目前,对于大直径、高水压盾构隧道,普遍采用双道密封垫防水模式[13]。相较于单道密封垫体系和内道遇水膨胀橡胶体系,双道密封垫体系能够兼容更大的管片拼装误差[14],即便因粘接不良等施工缺陷导致外道密封垫失效,内道密封垫仍能有效抵抗外部水压,提高了盾构隧道的防水安全性。近年来,一些学者针对双道密封垫防水性能开展了试验研究。张子新等[15]和鲁志鹏等[16]分别依托上海苏州河深埋排蓄水隧道和江阴靖江长江隧道,开展了双道密封垫耐水压测试,对比分析了单、双道密封垫的防水效果;李雪等[17-18]通过双道防水试验,研究了张开、错台和转角工况下双道密封垫的防水能力阈值及防水失效模式;肖明清等[19-20]基于双道密封垫防水试验结果,给出了计算双道密封垫整体防水能力的经验公式;XIE等[21]基于双道防水试验研究,提出间隔布置双道密封垫以充分发挥双道密封垫防水能力。现有的试验研究大多聚焦于揭示不同工况下双道密封垫防水性能的变化规律,但对双道密封垫防水失效机理仍缺乏深入研究。如何解释双道密封垫模式的防水增强效应,对于盾构隧道防水设计至关重要。本文针对无间隙水压的常规工况和有间隙水压的特殊工况开展双道密封垫防水试验研究,结合微观渗流理论,分析双道密封垫的黏滞阻力效应和间隙水压反作用效应带来的防水增强效应,揭示双道密封垫的防水增强机理,为采用双道密封垫防水结构的大直径、高水压盾构隧道设计提供理论依据。
1 双道密封垫防水试验
1.1 试验材料
相较于外道密封垫,实际工程中的内道密封垫通常采用较小的截面尺寸,作为安全储备。为更加清晰地揭示双道密封垫的防水增强效应,避免内外道密封垫差异造成的影响,本试验内道和外道均采用相同形状尺寸的密封垫及沟槽,密封垫及沟槽的截面尺寸如图1所示,橡胶的主要参数满足《高分子防水材料 第4部分:盾构法隧道管片用橡胶密封垫》[22](GB 18173.4―2010)的相关规定。
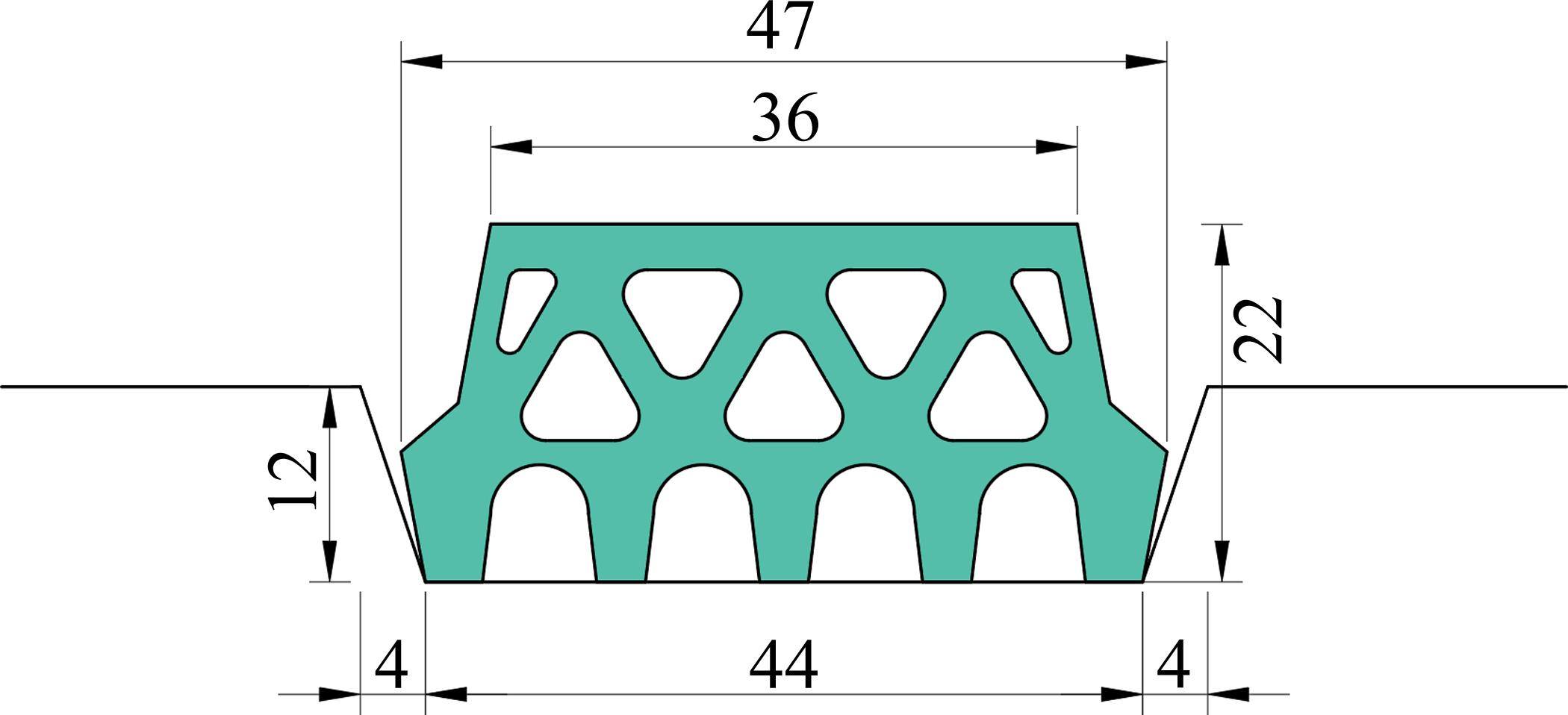
1.2 试验装置
试验装置如图2所示,试验装置包含上下沟槽板、反力梁、框架底座、千斤顶、水压表以及水压泵,可测试不同接缝张开量、错台量的盾构隧道接缝双道防水能力。试验装置剖面图如图3所示,试验时外部水压依次击穿内圈密封垫(模拟外道密封垫)和外圈密封垫(模拟内道密封垫)。注水孔所在的外道密封垫围成封闭空间定义为中心腔,内道与外道密封垫间的环形封闭空间定义为内水腔,内水腔水压表测得的水压定义为间隙水压。

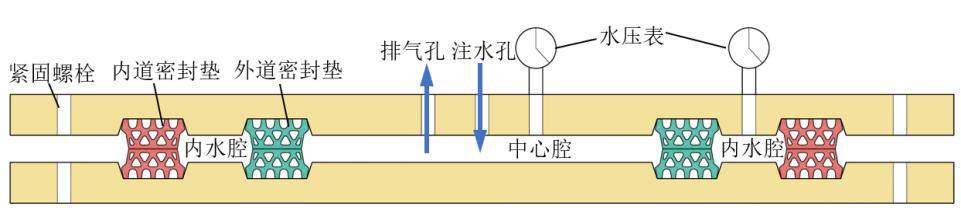
1.3 试验工况
在实际工程中,内外道密封垫间的空腔通常无水压作用,外水压自管片外侧依次击穿外道和内道密封垫,渗漏到隧道内部(以下称这种情况为常规工况)。在一些工程实例中,管片角部采用了加贴聚醚聚氨酯橡胶片的防窜流设计,使得内外道密封垫之间存在封闭的空腔,如图4(a)所示。因此,在一些特殊工况下,外道密封垫可能同时受到外水压和间隙水压作用:1) 如图4(b),由于施工质量问题导致的管片混凝土存在裂缝渗漏通道,在该通道的作用下外道密封垫未被击穿时内水腔中已存在积水;2) 如图4(c),出现高于百年设计水压的外部高水压,导致外道密封垫被击穿,在水压退去后内水腔仍余留积水。在这些特殊情形中,间隙水压对外道密封垫的反向挤压效果成了不可忽视的防水性能影响因素。本研究针对无间隙水压的常规工况和有间隙水压的特殊工况设置了2种不同的试验方法,分别探究有无间隙水压作用下的双道密封垫防水增强机理,试验工况如表1所示。
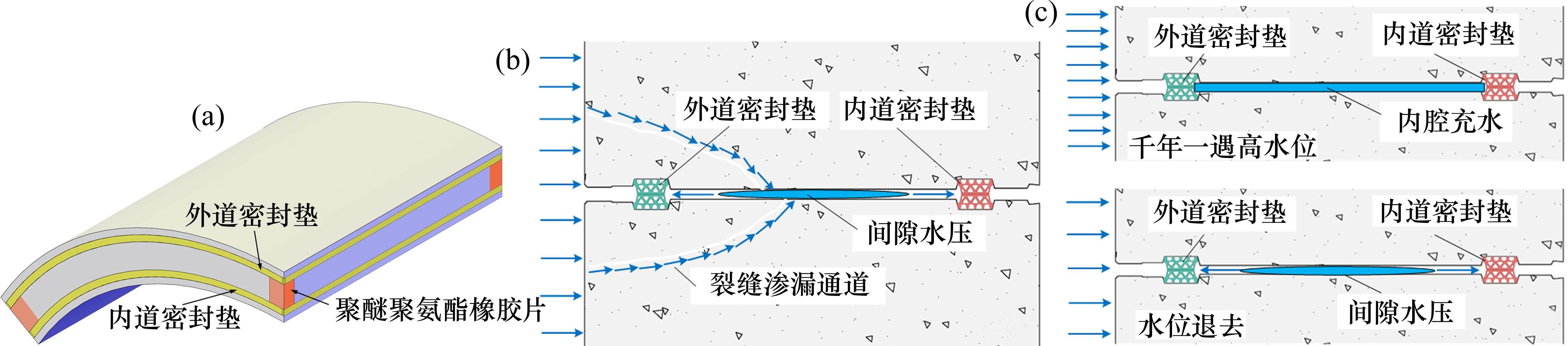
| 试验工况 | 常规工况 | 特殊工况 |
|---|---|---|
| 张开量设置 | 6 mm,8 mm,10 mm,12 mm,14 mm | 6 mm,8 mm,10 mm,12mm,14 mm |
| 错台量设置 | 0 mm,4 mm,8 mm,12 mm,15 mm,20 mm | 0 mm |
1.4 试验流程
试验流程如图5所示,实时记录试验全过程的水压表读数,得到各工况下的水压时程曲线。
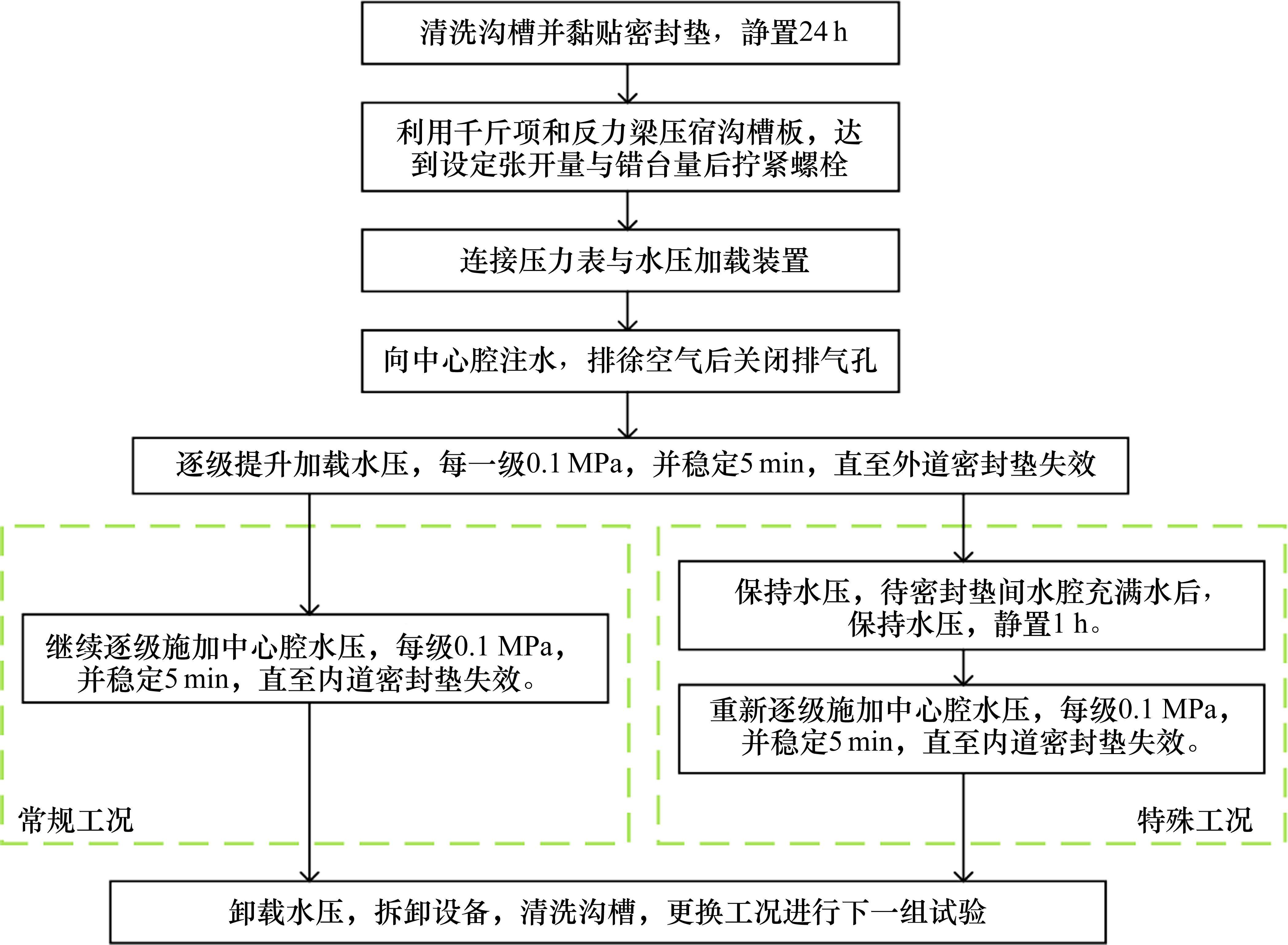
2 试验结果分析
2.1 常规工况测试结果
以张开8 mm,错台0 mm为例,常规工况下双道密封垫的水压时程曲线如图6所示。图中的1计时单位为水压加载稳定时间5 min,常规工况试验下双道密封垫防水可分为3个阶段:
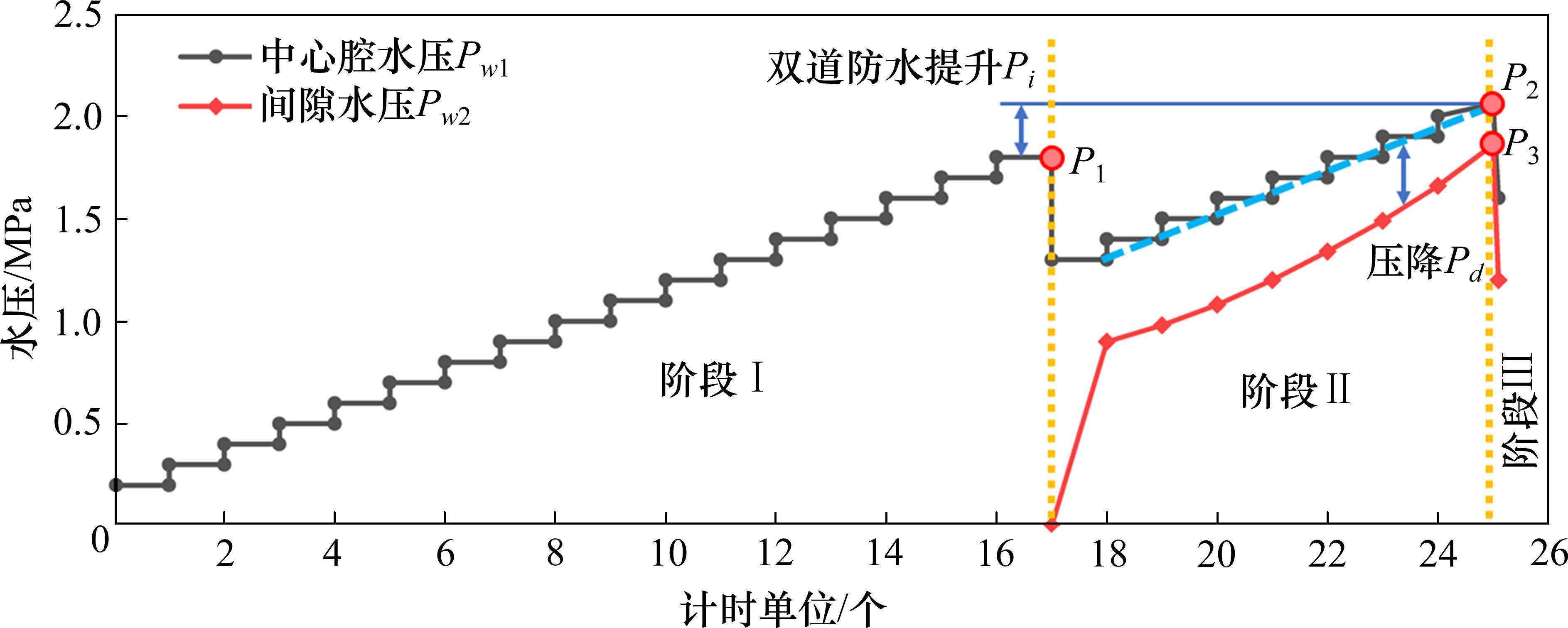
阶段I:中心腔持续提升加载水压,直至中心腔水压达到P1为1.80 MPa,外道密封垫失效;
阶段II:随着外道密封垫被击穿,间隙水压迅速增大,继续提升加载水压,中心腔水压Pw1和间隙水压Pw2同步上升,可以发现中心腔水压与间隙水压存在明显差值,记为压降Pd;
阶段III:逐级提升加载水压,直至内道密封垫渗漏,此时的中心腔水压P2为2.06 MPa,间隙水压P3为1.85 MPa,P2与P1的差值即为双道密封垫较单道密封垫的防水提升值Pi。
由于本试验内道和外道密封垫采用相同规格断面,理论上内外道的耐水压力是相同的。各组试验中击穿外道时的中心腔水压P1与击穿内道时间隙水压P3几乎相同,也证实了这一猜想。对比各工况试验数据可以发现,压力水从中心腔流入内水腔产生的压降Pd与双道密封垫的防水提升值Pi近似相等。因此可以认为,常规试验中双道密封垫防水相较于单道密封垫防水增强主要是因为水流从中心腔至内水腔产生了压力降低,使得渗漏时的双道密封垫体系能够承载更高的外部水压。
2.2 特殊工况测试结果
以张开8 mm,错台0 mm为例,特殊工况下双道密封垫的水压时程曲线如图7所示。特殊工况试验下双道密封垫防水可分为4个阶段:
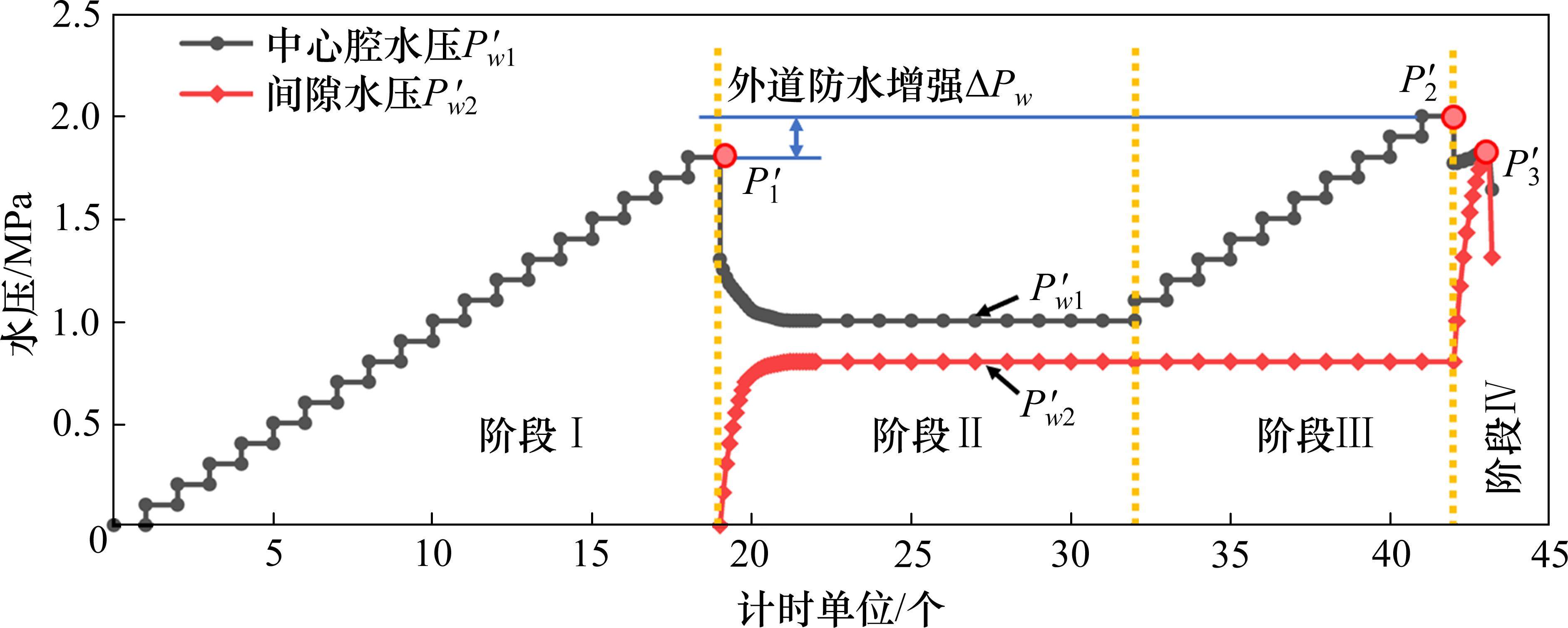
阶段I:中心腔持续提升加载水压,直至中心腔水压达到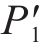
阶段II:随着外道密封垫被击穿,中心腔开始积水,间隙水压逐渐增大,此时中心腔不断向内水腔渗流而导致出现缓慢的压力降低。随着时间推进,最终中心腔与内水腔之间的压力达到稳定,此时外道密封垫已经恢复了部分防水能力。
阶段III:继续逐级加载中心腔水压,中心腔水压逐渐增大至P′2为2.01 MPa,外道密封垫第2次击穿渗漏,P′2与P′1的差值记为外道防水增强值∆Pw;
阶段IV:随着外道密封垫再次被击穿,间隙水压迅速上升,达到内道密封垫防水阈值后立刻发生渗漏,此时中心腔水压与间隙水压几乎相同,为1.82MPa,记作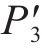
相比常规工况,在间隙水压的作用下,第2次渗漏时外道密封垫的防水能力得到了一定提升。但由于已经发生过一次渗漏,第2次渗漏发生时外道密封垫的渗漏路径充分扩张,几乎不存在常规工况下的压降效应。此时没有间隙水压作用的内道密封垫面临着高于自身防水阈值(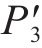
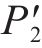
3 考虑黏滞阻力效应的防水增强机理分析
压力水从中心腔流入内水腔产生的压降Pd是常规工况下双道密封垫防水增强的主要影响因素。压降产生的原因是外部水压在击穿外道密封垫时,渗漏路径上黏滞阻力τ的作用,导致外部水压Pw1在击穿外道密封垫的过程中不断产生沿程压力损失,降低为Pw2,黏滞阻力作用下的压降效应机理如图8所示。
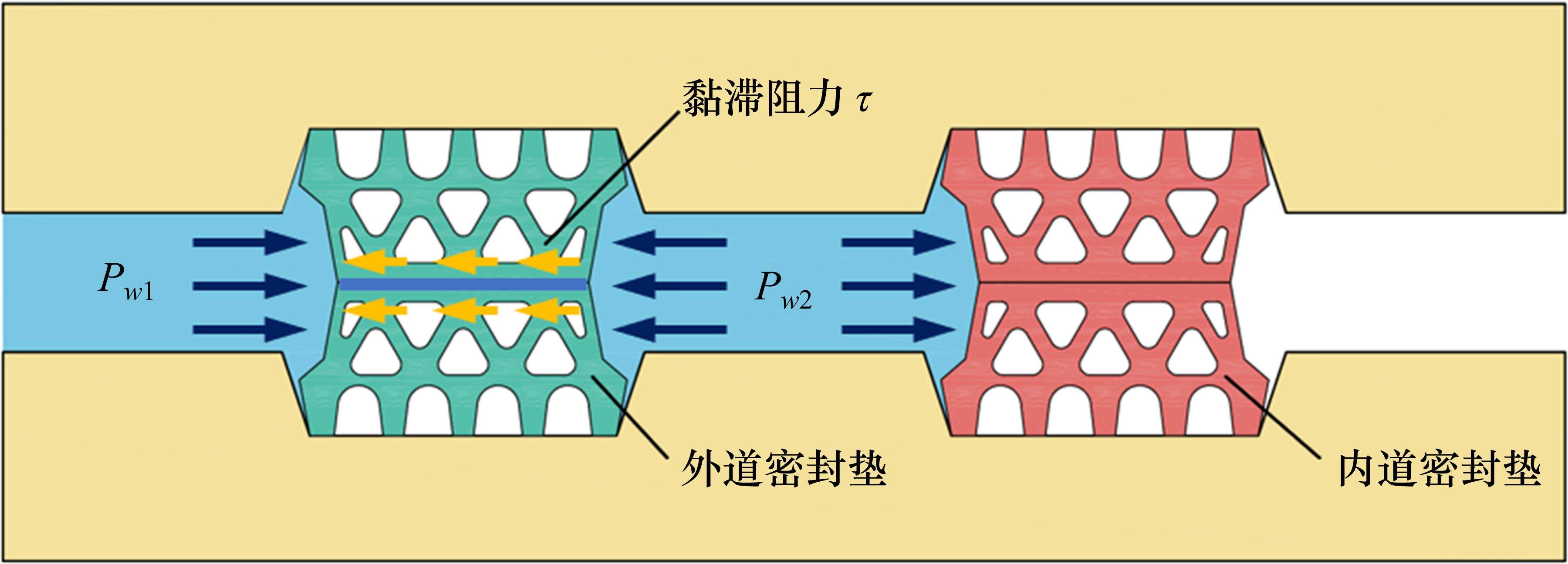
由于密封垫表面存在粗糙形貌特征,因此密封垫间的接触实质上是表面微凸体之间的接触,可将水流击穿密封垫后在上下密封垫间接触面形成稳定渗漏通道的过程近似等效为流体在多孔介质内部流动的过程。ERGUN[23]通过试验总结出了单位长度上流动压降和流体通过多孔介质时的流动速度的关系,并用“平均水力半径”和实验结合的方法得到半经验公式,如式(1)中,流体的压力损失分为2个部分,第1部分为黏滞能量损失,第2部分为动力学能量损失,当流体流速高时,主要的能量损失为动力学能量损失,当流速低时,黏滞能量损失起到主要作用。
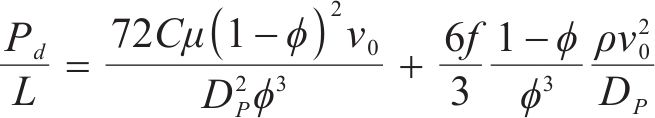
式中:Pd为压降值,Pa;L为渗漏路径长度,mm;μ为流体的动力黏滞系数,此处为水,取0.8×10-3 (Pa∙s);ϕ为孔隙率;DP为多孔介质平均粒子直径,mm;v0为流体流速,mm/s;C、f为C=25/16、6f=3.5是实验所得的经验常数,不含物理意义;ρ为流体的密度。
要利用式(1)进行压力损失分析,关键需要确定3个参数值,即流体流速v0、孔介质平均粒子直径DP和孔隙率ϕ,下面分别讨论3个参数的计算方法。
1) 流体流速v0的确定
渗漏通道中的流体的渗漏速度在试验中不方便测量,因此需要采用间接的方法进行测量。在外道密封垫即将发生渗漏的临界状态,在渗漏界面的最前端即将击穿点的速度为最小值且趋向于0,此时注水孔处水流速度的最大值为vmax,由水压泵出水口处的流量计得到。根据伯努利方程和牛顿内摩擦定律,渗漏通道中流体的平均流速v0与vmax关系如式(2)[24],通过试验测量并计算得到水流在密封垫接触面的平均渗漏速度,如表2所示。
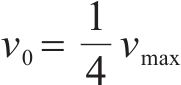
| 张开量/mm | 渗流速度/(mm∙s-1) |
|---|---|
| 6 | 2.5 |
| 8 | 2.1 |
| 10 | 1.7 |
| 12 | 1.6 |
| 14 | 1.5 |
2) 多孔介质平均粒子直径DP的确定
采用Bruker公司的Coutour-GT系列的三维光学表面轮廓仪对本研究所用的密封垫进行表面轮廓扫描,采样范围为1 270 μm×953 μm。扫描结果如图9(a)所示,结果表明,密封垫的表面轮廓形貌呈现出“条带状”的分布规律。沿宽度方向表现出较大的波动起伏,而沿长度方向的变化较小,因此,密封垫表面可以被等效为图9(b)所示的柱状模型。需要说明的是,密封垫间的接触实质上是三维的,沿着长度方向的形貌变化也会对渗流效应产生影响,为了简化计算,本文所采用的计算模型没有考虑沿密封垫长度方向的渗流。根据Hertz接触理论[25],将2个粗糙弹性体之间的接触等效为光滑弹性体和刚体之间的接触,且光滑弹性体简化成了连续半径为R的半圆柱体,如图9所示。半径R可由式(3)计算得到。
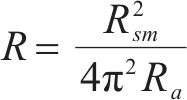
式中:Ra为轮廓算术平均差,nm;Rsm为轮廓平均宽度,μm。
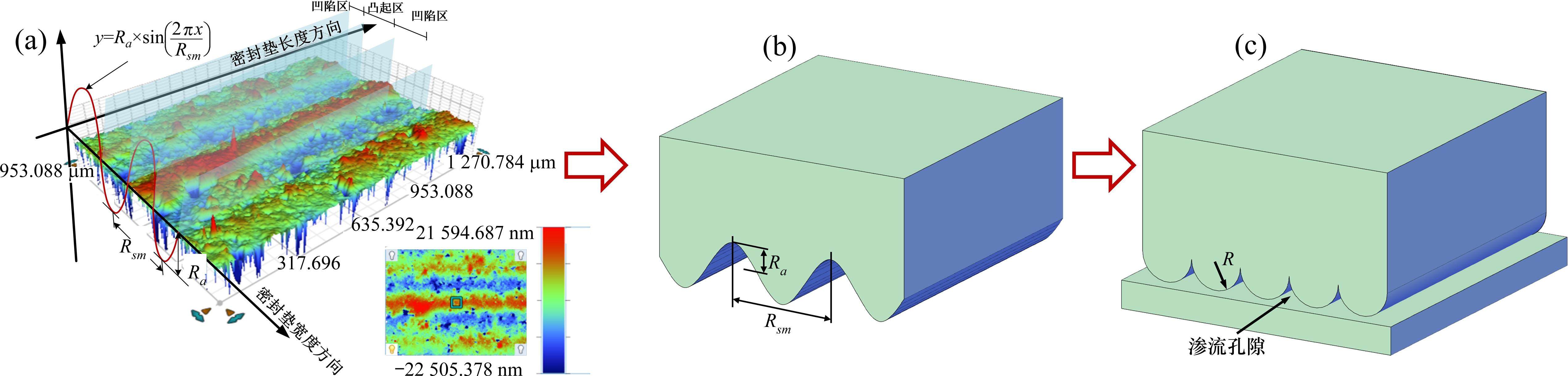
对密封垫表面6个采样点进行轮廓扫描,获取平均轮廓参数为:Ra=1 759.027 nm,Rsm=217.882 μm,计算得到半径R=0.683 6 mm,多孔介质的平均粒子直径DP=2R=1.367 mm。
3) 孔隙率ϕ的确定
孔隙率ϕ根据图9的简化模型可以求得,在无压缩状态且不考虑封闭孔隙下,得到孔隙率ϕ近似为(1-π/4),当接触面受压变形时孔隙得到填充,随着接触力增大孔隙率ϕ不断减小并趋近于0。不妨定义孔隙度影响系数α,使得:
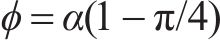
其中,α的取值范围为0~1,且α是与平均接触应力Pv有关的函数。对式(1)进行改写得到式(5)。
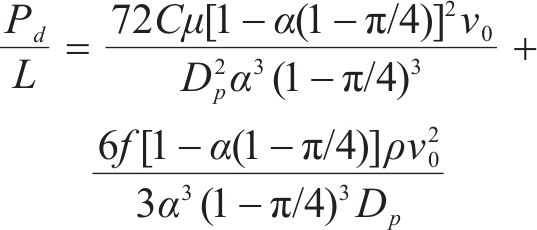
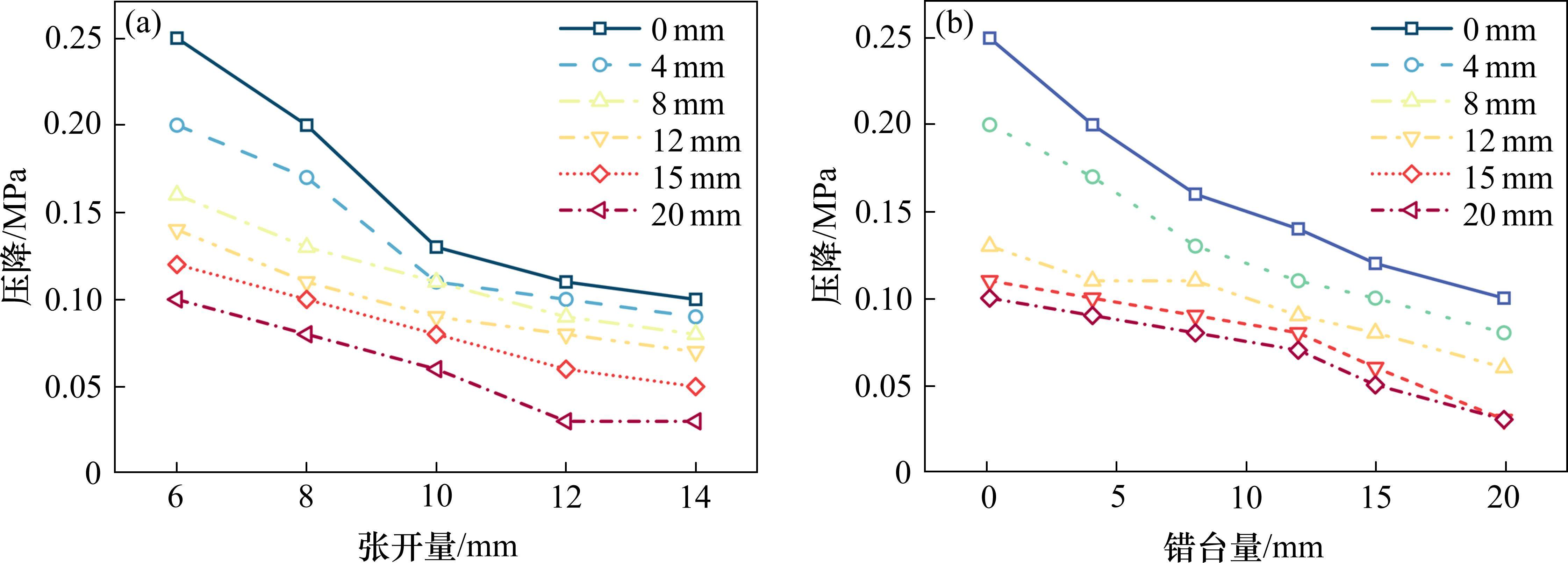
对常规工况下的防水试验数据进行整合,得到不同张开量与错台量下2个水腔中的压降数值,如图10所示。由图10(a)可知,对于固定的错台量,压降数值随着接缝张开量的减小而增大,这说明接触应力越大,孔隙率越小,黏滞阻力耗能效应越显著;对于固定的张开量,如图10(b),压降数值随着接缝错台量增大而减小,这是由于错台量增大,导致接触路径变短,降低了总体压力损失。由于压降与错台量近似线性负相关,可以认为相同张开量下单位距离压降数值相同。对各工况压降数值进行拟合,并对密封垫进行单轴压缩试验,得到不同张开量下单位距离压降数值和平均接触应力,如表3所示。
张开量/ mm | 单位距离压降 Pd/L/(Pa∙mm-1) | 平均接触应力 Pc/(N∙mm-2) |
|---|---|---|
| 6 | 7 340 | 2.453 |
| 8 | 5 970 | 1.633 |
| 10 | 4 386 | 1.203 |
| 12 | 3 617 | 0.896 |
| 14 | 3 029 | 0.733 |
将上述单位距离压降Pd/L、水流速度v0、多孔介质平均粒子直径DP代入式(5),可以计算得到不同张开量下的孔隙度影响系数α,用式(6)对α与平均接触应力Pc进行拟合,拟合结果如图11和式(7)所示。
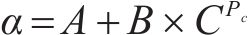
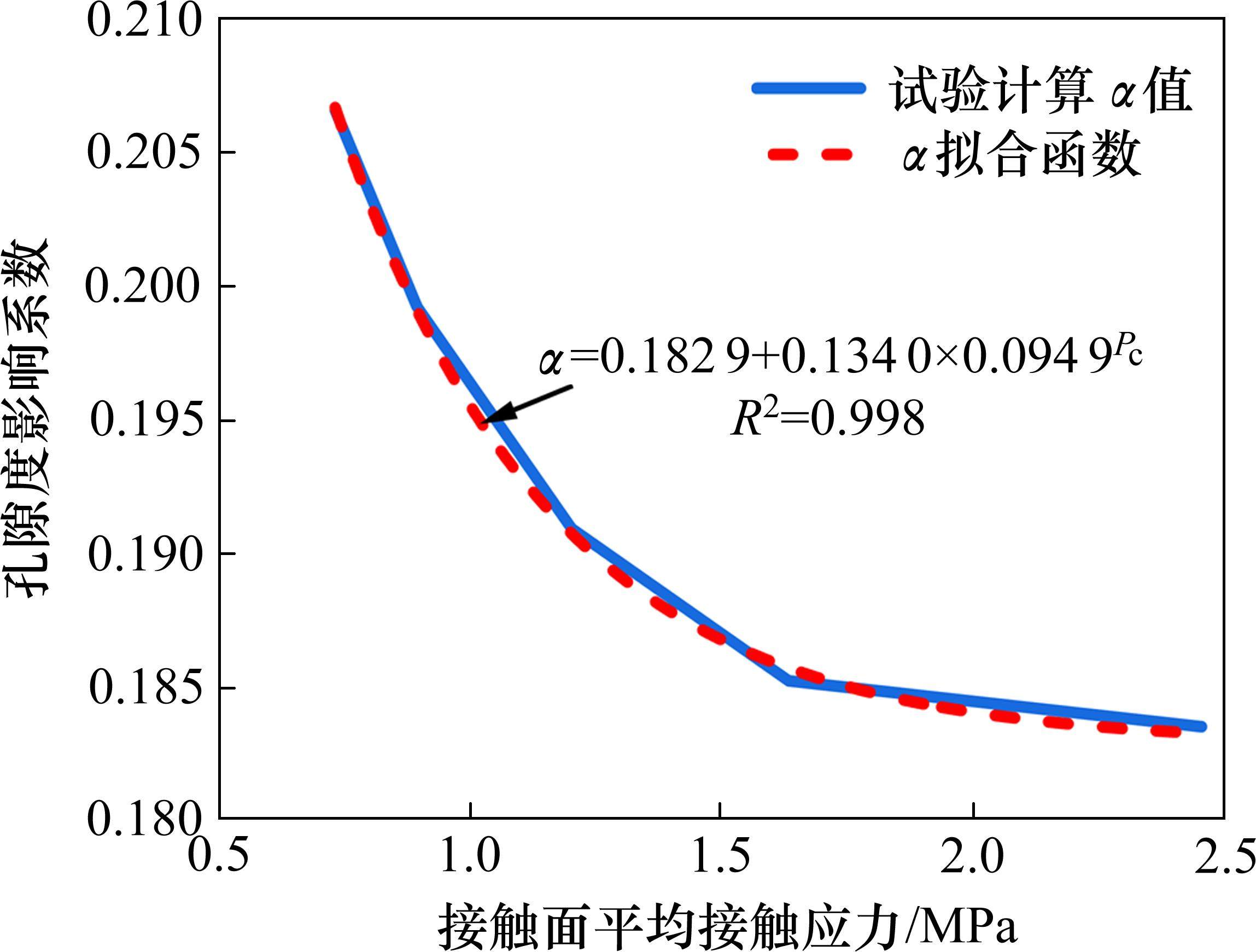
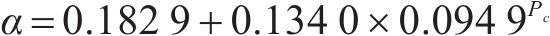
综上,通过测试最大水流速度、粗糙度参数和平均接触应力,代入式(2)、式(3)、式(7),可计算得到流体流速、平均粒子直径和孔隙率参数,代入式(5)即可实现不同工况下黏滞阻力压降效应的预测。
4 考虑间隙水压反作用效应的防水增强机理分析
内外道密封垫间的间隙水压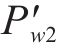
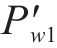
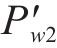
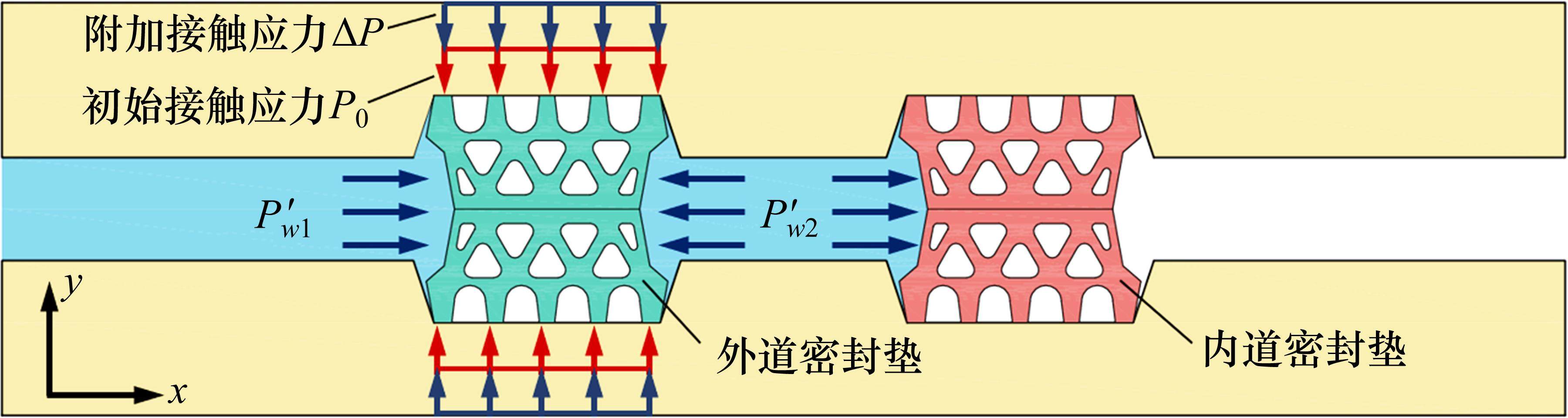
在双向限位的情况下,y轴和z轴方向上的应变为0。根据弹性理论可知,在x方向作用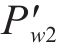
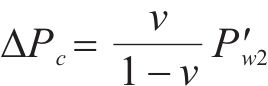
式中:ν为密封垫的等效泊松比。
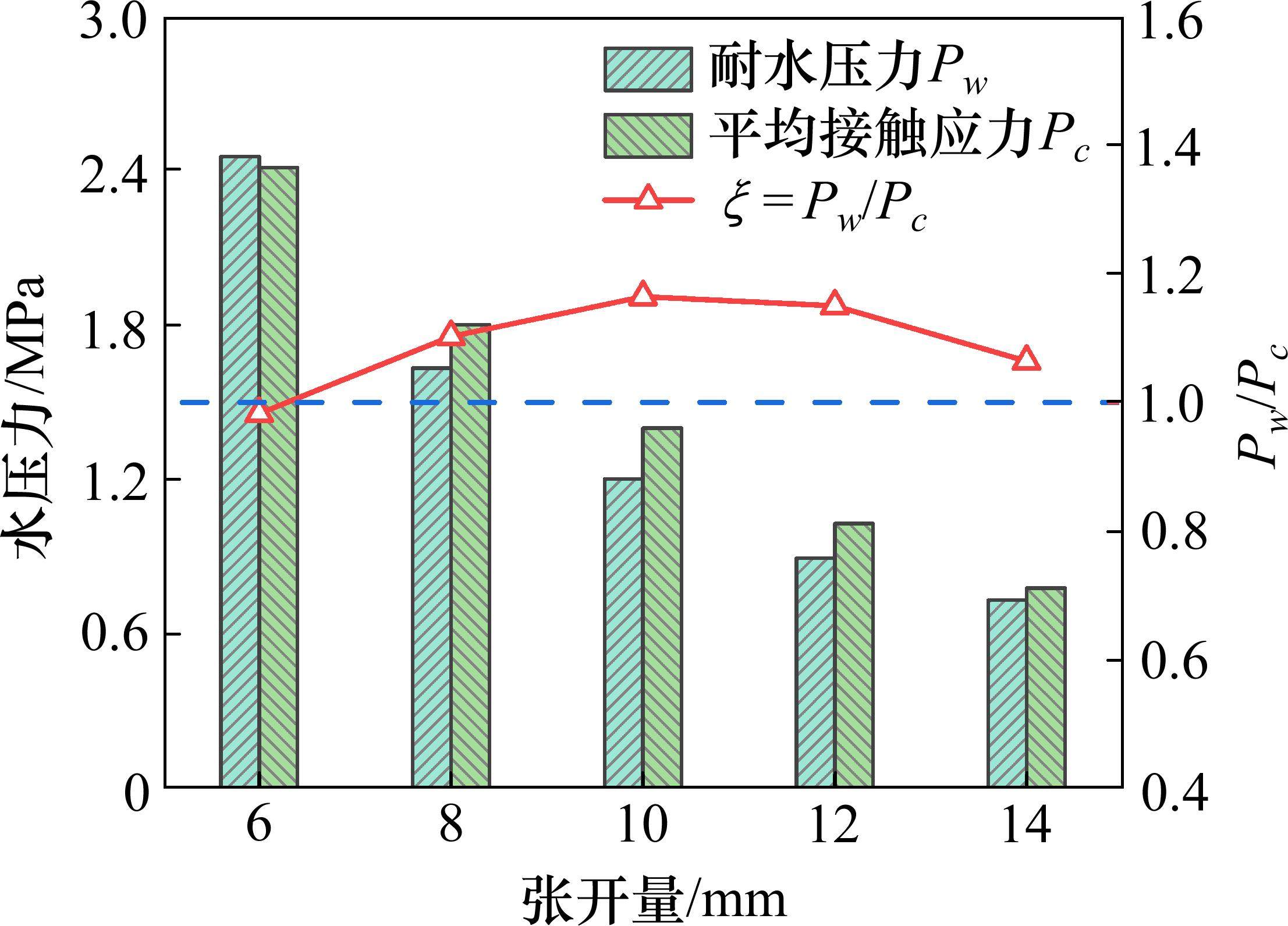
定义耐水压力Pw与平均接触应力Pc的比值为ξ,如式(9)。试验测得的不同接缝张开量下耐水压力与平均接触应力如图13所示。比值ξ变化范围为0.98~1.16,说明平均接触应力与耐水压力具有较高的相关性,借助式(9)能够利用平均接触应力近似得到耐水压力。
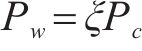
则对于相同的张开量,附加接触应力∆Pc带来的防水性能增强∆Pw可用式(10)表示:
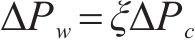
将式(10)代入式(8),可得防水增强值∆Pw与间隙水压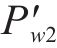
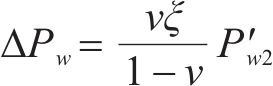
试验得到不同张开量下的间隙水压与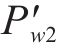
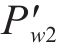
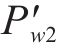
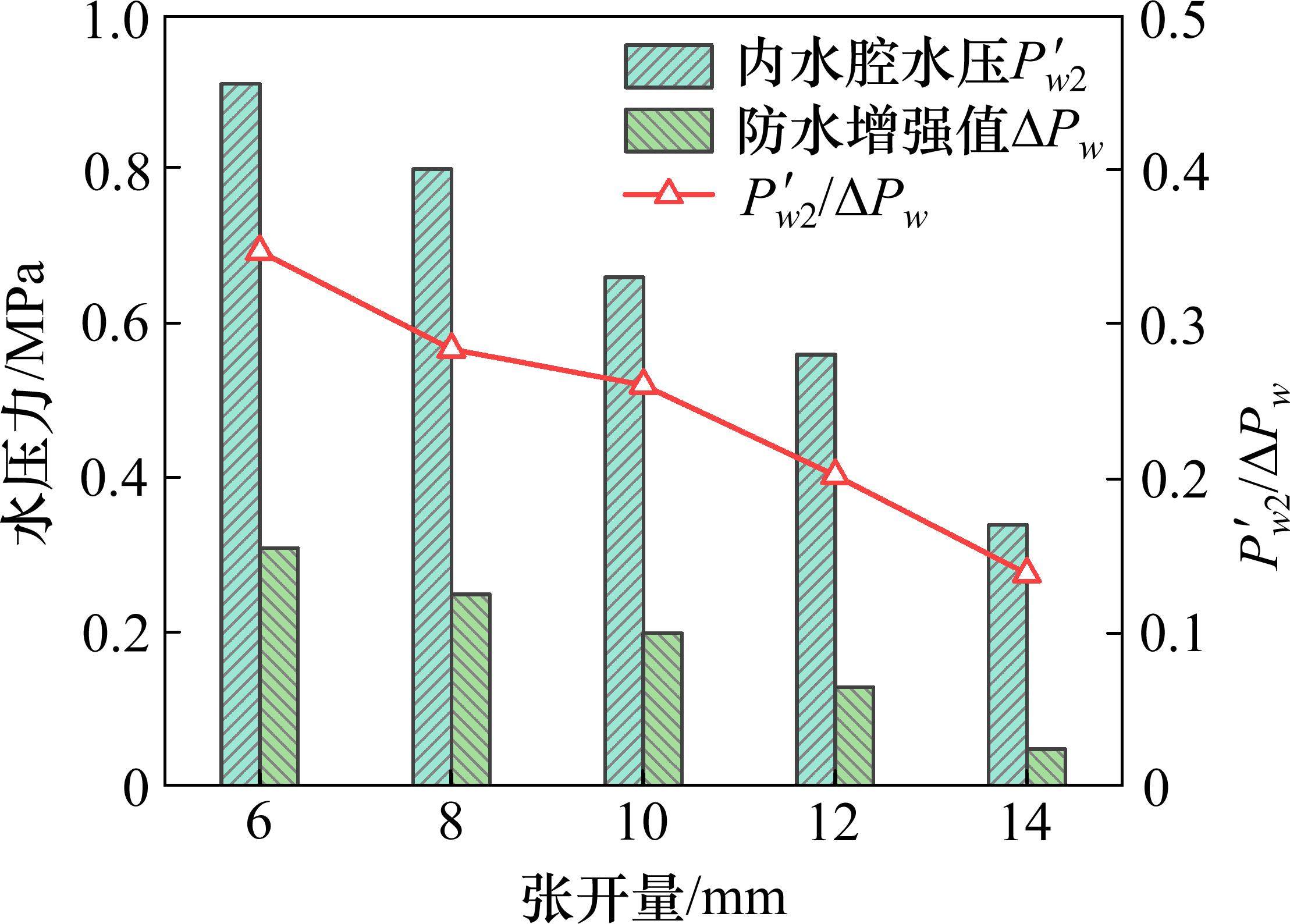
假定有效泊松比ν与压密率Ψ关系如式(12),定义压密率的计算公式如式(13):
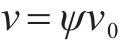
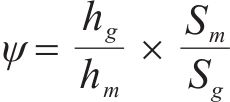
式中:hg为沟槽总深度,mm;hm为压缩后密封垫的高度,mm;Sm为密封垫的净面积,mm2;Sg为压缩后沟槽的净面积,mm2。
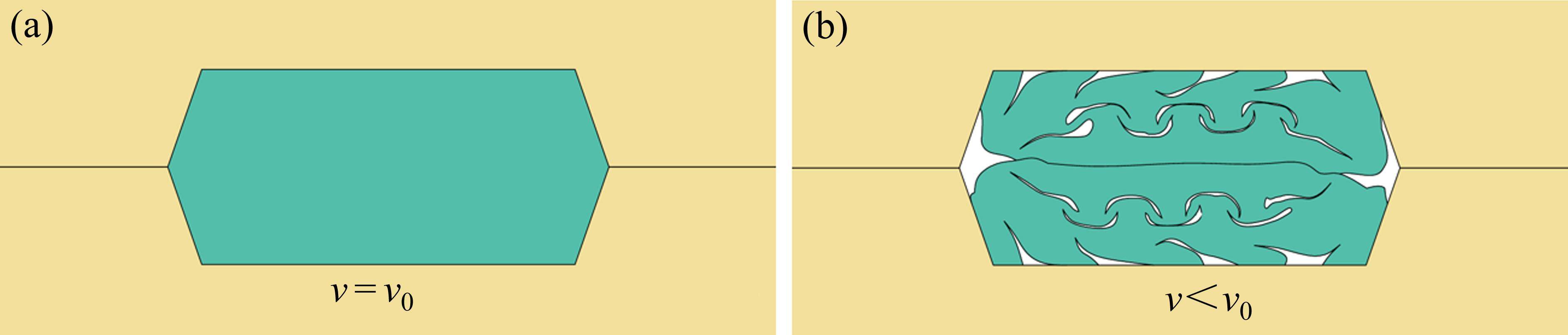
当弹性密封垫的净面积与沟槽的面积一致(Sm=Sg),且被完全压入沟槽(hg=hm),可认为弹性密封垫的孔洞全部被压密,视为实心的橡胶材料,如图15(a)所示。这时其有效泊松比ν应近似为材料的真实泊松比ν0,即0.5。然而,在真实情况下,0 mm接缝张开的密封垫的净面积仍小于沟槽面积,此时密封垫仍有部分空隙,理论上的等效泊松比ν小于真实泊松比,如图15(b)所示。因此,式(13)采用高度比和面积比的乘积定义压密率,综合评估密封垫的压密程度。
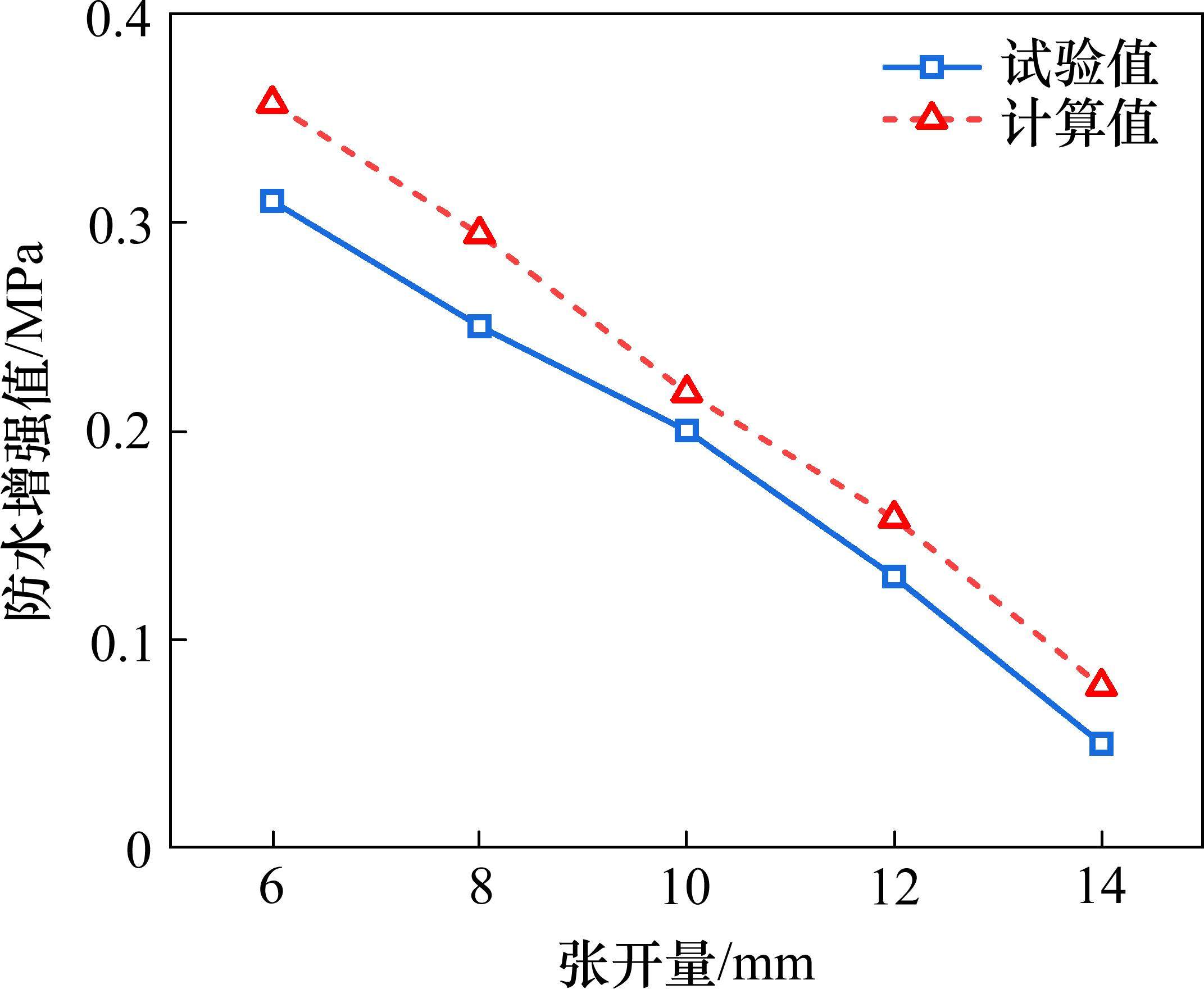
通过式(12)、式(13)计算得到等效泊松比,结果如表4所示。代入式(11)可以计算得到不同张开量下密封垫防水能力增强值,如图16所示。通过与试验值对比发现,计算得到的防水增强值比试验值略大,最大误差约为15.1%,能够较好地预测间隙水压作用下的防水增强效果。产生误差的原因可能是式(12)计算高估了材料的等效泊松比。如密封垫被充分压密时,孔洞虽然已经充分闭合,但仍存在不连续的接触面,进一步降低材料的等效泊松比。
| 张开量/mm | hg/hm | Sm/Sg | ν0 |
|---|---|---|---|
| 6 | 0.8 | 0.713 | 0.285 |
| 8 | 0.75 | 0.667 | 0.25 |
| 10 | 0.706 | 0.627 | 0.221 |
| 12 | 0.667 | 0.592 | 0.197 |
| 14 | 0.632 | 0.559 | 0.177 |
5 结论
1) 对于无间隙水压作用的常规工况,双道密封垫防水增强的主要原因是在黏滞阻力的作用下,外部水压击穿外道密封垫产生的压力降低,使得内道密封垫能够承载更大的外部水压。
2) 对于有间隙水压作用的特殊工况,双道密封垫防水增强的主要原因是在间隙水压的反作用下,外道密封垫产生附加接触应力抵抗外部水压,使得第二次渗漏时外道密封垫防水能力提升。
3) 接缝张开量越小,密封垫渗流孔隙率越小,黏滞阻力越大。接缝错台量越小,渗漏路径越长,压力损失越显著。引入孔隙度影响系数对Ergun公式进行修正,通过试验建立平均接触应力与孔隙率的转换关系,实现了黏滞阻力压降效应的计算。
4) 随着接缝张开量增大,密封垫的等效泊松比降低,间隙水压作用下的防水能力增强效应也相应减弱。引入压密率指标评价密封垫的等效泊松比,计算得到防水增强值与试验值最大误差约为15.1%。
龚琛杰,解超然,林赞权等.盾构隧道双道密封垫防水增强机理研究[J].铁道科学与工程学报,2025,22(01):272-283.
GONG Chenjie,XIE Chaoran,LIN Zanquan,et al.Waterproof enhancement mechanism of double gasket in shield tunnel[J].Journal of Railway Science and Engineering,2025,22(01):272-283.

