盾构法作为一种主要的隧道施工方法,因具有安全性高、施工效率高、对周边环境扰动小的特点,在地铁隧道建设中得到了广泛应用[1]。在盾构机推进过程中,需合理计算并设置开挖面支护力,以保证开挖面稳定,否则可能引起地面沉降或塌陷等事故[2]。因此,盾构开挖面的稳定性研究是盾构工程中的重要课题。众多学者采用理论分析、数值模拟、模型试验等手段,对此问题开展了深入研究[3-4]。这些手段中,理论分析模型因高效、准确的优势而广受青睐[5-6]。例如,雷明锋等[7]曾采用极限平衡法推导了迎坡条件下盾构开挖面的临界支护力;曹成勇等[8]基于极限分析理论推导了浅埋透水地层泥水盾构开挖面临界支护力;丁家浩等[9]建立了大断面矩形顶管隧道开挖面稳定性极限分析方法,为顶管法隧道顶推力的计算提供了理论支持。近年来,随着隧道工程的发展,遭遇的施工条件愈发复杂,对盾构隧道施工安全和变形控制的要求不断提高。土体和地下水环境作为施工中的关键因素,其固有的空间变异性对工程安全性具有显著影响。针对此问题,学界展开了诸多相关研究。PAN等[10]采用随机响应面法,开展了二维随机场下隧道稳定性概率分析;为研究地层参数三维空间变异性的影响,LI等[11]采用2个相关随机场组成的三维地质模型对圆形隧道工作面进行了概率稳定分析,模型中考虑了土体抗剪强度的空间变异性;HUO等[12]提出了一种高效的随机场模型,分析了旋转各向异性对隧道工作面破坏概率的影响,并将方法应用于多层土中。已有研究深入地分析了土体抗剪强度参数的空间变异性对隧道工作面稳定性的影响,为盾构隧道开挖面稳定性的概率分析和稳健性设计奠定了基础。但其仍存在一定局限,如对地下水影响的考虑不足,以及在开挖面破坏机制的精确性有待提高。本文通过随机场理论,考虑地层摩擦角、黏聚力和孔隙水压力系数空间变异性和自相关性的影响,采用K-L级数展开法生成相应的三维随机场。结合改进的空间离散三维螺旋破坏机制,建立适用于随机地层的盾构隧道开挖面极限支护力的计算模型。在此基础上,采用蒙特卡罗法分析各参数的变异性以及自相关距离对失效概率的影响。进一步,提出一种盾构隧道开挖面支护力稳健设计方法,并将其与工程实测结果进行了对比验证,为隧道工程可靠性设计提出了一种分析方法,可为盾构施工提供科学参考。
1 水土参数随机场的离散
地层物理力学参数和水力参数的空间变异性是其固有属性,可采用随机场理论量化表征这种变异性,并采用自相关函数表达参数之间的自相关性[13]。三维高斯型自相关函数可表示为:
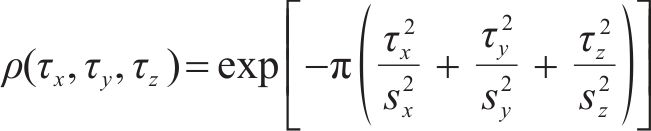
式中: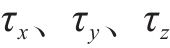
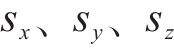
在随机场离散方法中,相较于其他方法,K-L级数展开法具有计算效率高、精度高的优点[13]。采用K-L级数法进行离散,获取地层各点坐标后,将其各参数离散成一组独立随机变量:
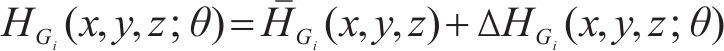
式中: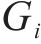
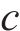
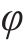
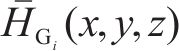
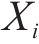
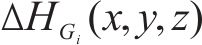
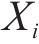
考虑到地层与水力参数的非负性,并参考已有研究[11],采用对数正态分布随机场表示地层参数,即:
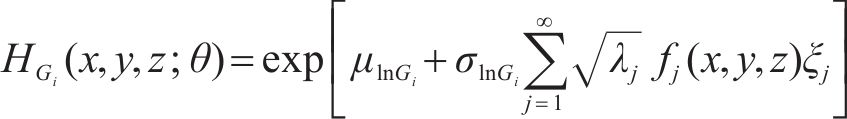
式中: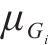
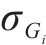
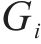
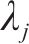
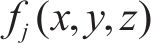
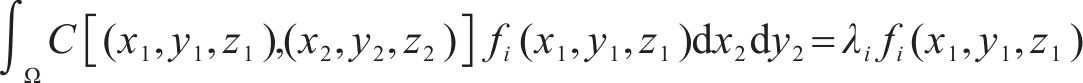
式中:协方差函数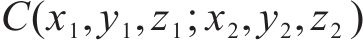
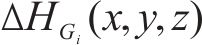
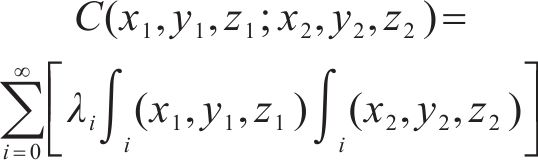
为便于表达数据的离散程度,定义变异系数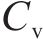
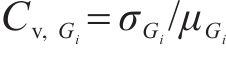
在保证计算精度的前提下,为提高计算效率,可选择截取K-L级数展开的前n项来分析。据此,式(3)可进一步表示为:
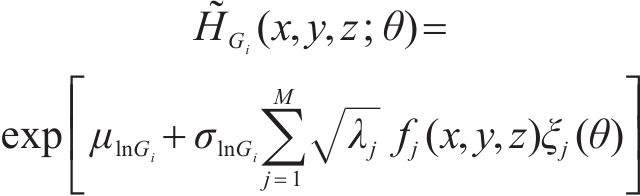
式中:截断项数M也是参数随机场所需离散的独立标准正态变量数目,可采用期望能比率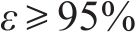
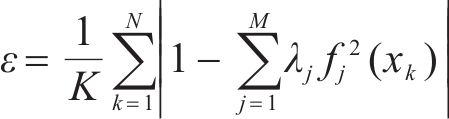
式中:K为随机场中离散点的数量;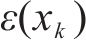
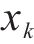
采用空间离散技术生成三维螺旋破坏机制时,为计算各离散点坐标,需获取各点的摩擦角和黏聚力,而生成地层参数的随机场又需要各点的坐标。为解决生成这些参数的随机场时所需的坐标点信息可能导致的逻辑死循环问题,采用LI等[14]提出的方法,将破坏机制可能涉及的地层离散为边长为0.5 m的立方体,于是只需获取各立方体中心的坐标,便可根据这些坐标生成地层和水力参数的随机场,并假定该随机场参数适用于整个立方体空间。参考相关文献[14]并经过试算,确定本文的离散范围如图1(a),图1(b)、1(c)、1(d)则展示了本文随机场离散效果,其中,摩擦角、黏聚力、孔隙水压力系数均值分别取为25°、10 kPa、0.3,变异系数均取为0.1,水平自相关距离为10 m,竖向自相关距离为2 m[13]。
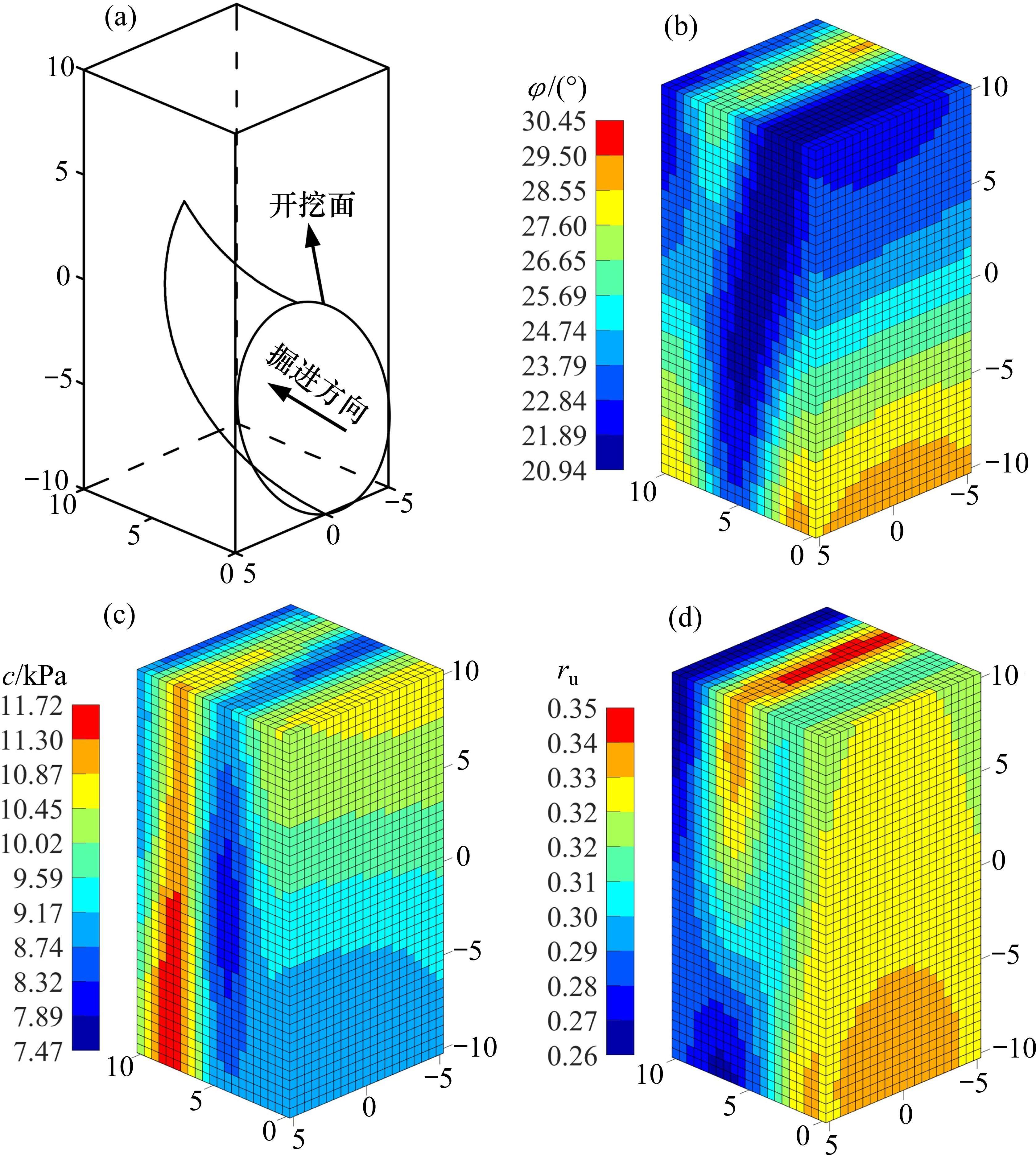
2 盾构隧道开挖面三维离散破坏机构生成
2.1 点对点生成的空间离散技术
MOLLON等[15]提出的空间离散技术可生成隧道开挖面三维失稳破坏机构,但其在局部坐标系中心的选取上仍存在一些问题。因此,本文通过空间离散技术生成破坏机构,并改进了局部坐标系中心的生成方法,其流程如图2。A、B、E分别为隧道开挖面的顶部、底部和中心点,F为破坏机构的顶点。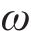
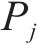
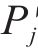
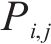
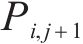
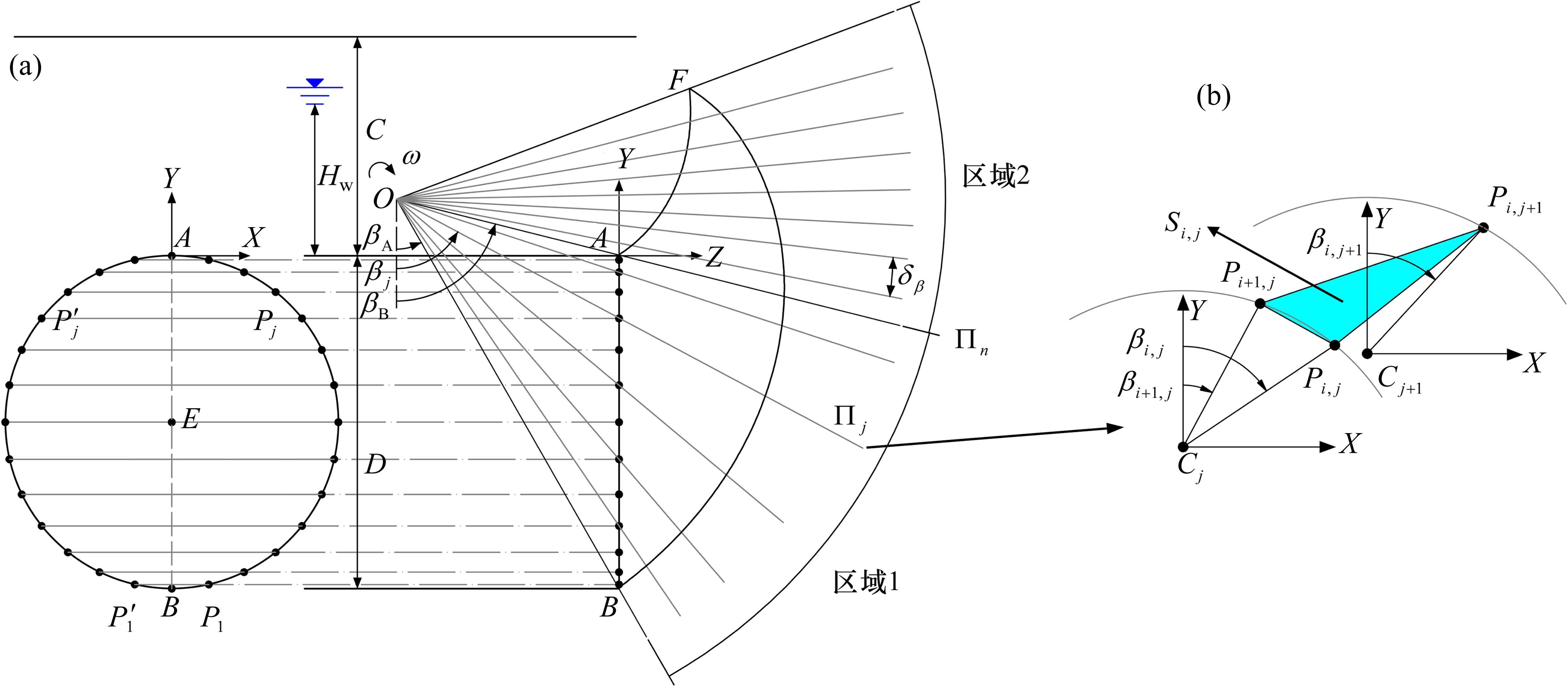
1) 微元三角形面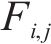
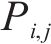
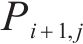
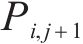

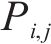
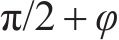
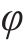
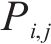

2) 点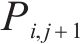
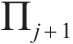
3) 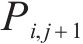
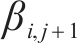
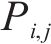
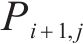
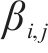
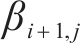
2.2 局部坐标系中心的确定
局部坐标系中心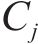
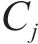
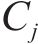
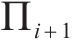
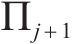
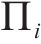
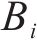
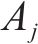
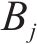
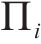
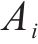
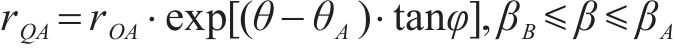
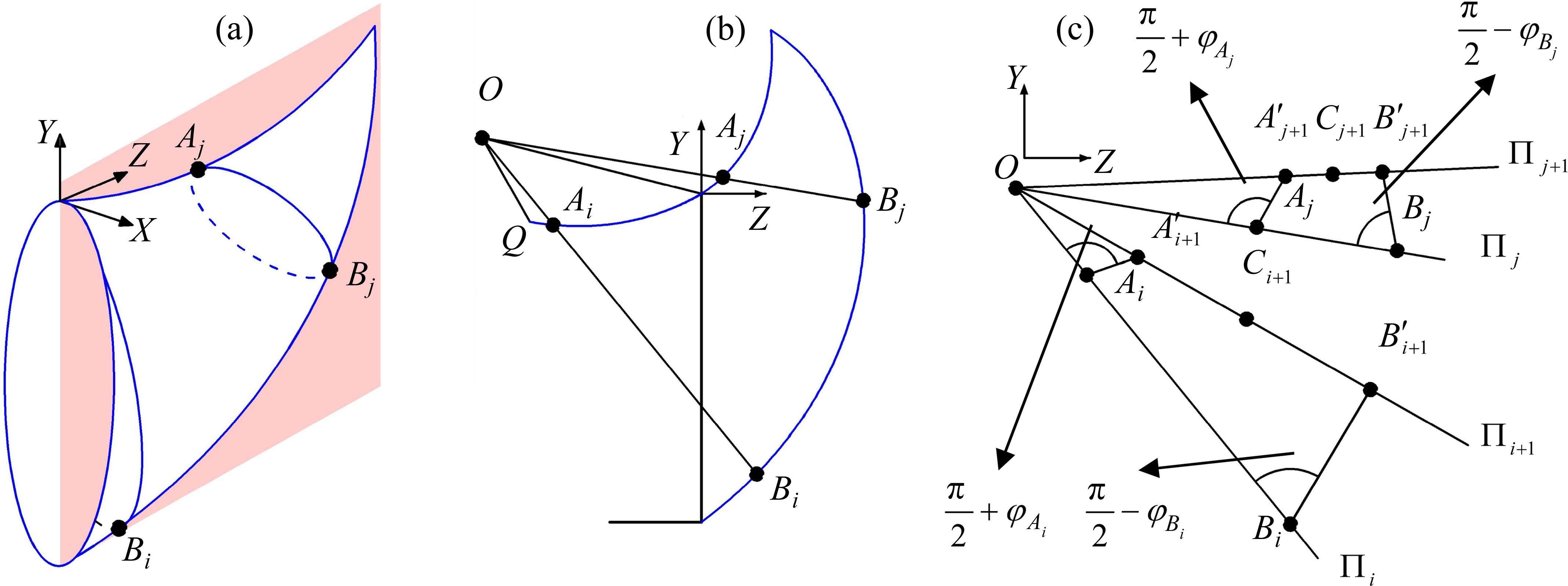
如图3(c)所示,获取各交点后,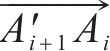
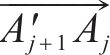
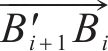
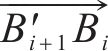
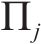
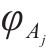
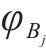
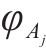
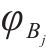
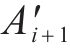
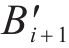
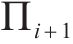
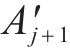
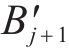
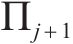
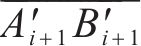
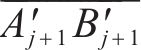
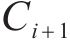
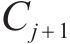
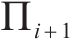
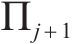
3 盾构隧道开挖面支护力极限分析法计算
3.1 功率计算
上覆土厚度大于隧道直径时,破坏机构不会与地表相交,而国内地铁隧道一般埋深大于直径[10-11]。因此,本研究考虑破坏机制不会延伸至地表。同时,假设在富水条件下,破坏机制完全位于水位下。根据上限定理,破坏机构所受外力包括开挖面支护力、土体重力和孔隙水压力,极限状态下外力做功功率与破坏机构表面土体剪切引起的能量耗散相等,即:
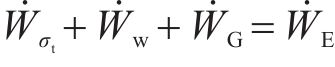
式中: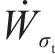
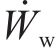
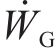
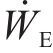
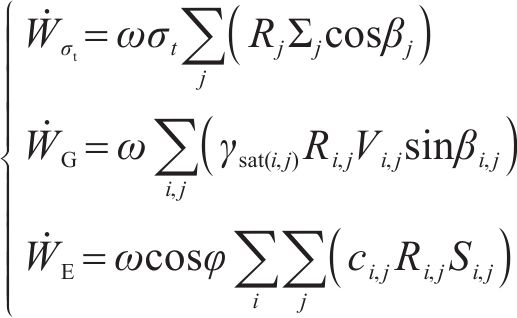
式中: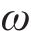
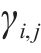
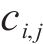
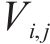
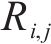
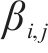
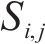
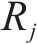
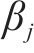
计算各单元体积重度时,每个单元体为三棱柱体,将其6个顶点的重度取均值以代表棱柱体的重度。对于能量耗散,各三角形单元体的黏聚力由其3个顶点黏聚力的均值获得。更具体的描述可在相关文献[14-15]中找到。
在考虑稳态渗流时,对于三维渗流问题,拉普拉斯方程难以求解,而针对大量的不确定性计算,若采用有限元软件进行渗流分析,计算量过大,计算速度受限,不利于工程应用。因此,采用BISHOP等[16]提出的孔隙水压力系数计算各点的孔隙水压力:
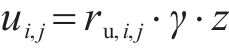
式中: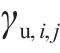
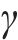
对于强透水地层(无黏性土),其在稳态渗流条件下渗流量非常大,将对工程安全产生严重不利影响,因此,本文进行强渗透地层开挖面支护力设计时,采用更保守的策略,不考虑渗流作用,采用静水压力计算其孔隙水压力:
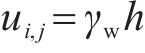
式中: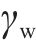
则地下水的作用可表示为速度间断面上孔隙水压力的功率之和:
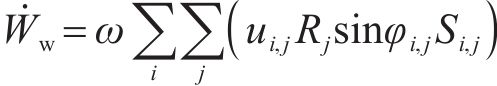
3.2 极限支护力求解
根据前文的功率计算,上限支护力可表示为:
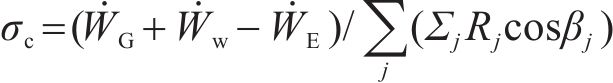
根据上限定理,由功率平衡计算的支护力只是无穷个上限解中的一个,而最优的上限解,即极限支护力受到旋转中心O的坐标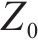
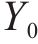
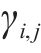
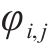
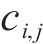
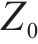
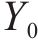
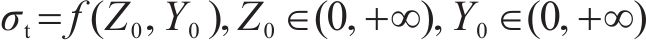
为求解多变量非线性方程,本文采用两阶段的求解策略。首先进行全局搜索,以确认最优结果所在局部范围。之后,通过Fminsearch函数(多变量无约束局域优化函数)进行局部寻优,以全局搜索的结果作为寻优初始值,防止结果落入局部最优。最终可计算得到考虑地层参数的空间变异性的开挖面极限支护力。
4 可靠性验证与参数分析
4.1 可靠性验证
为验证本文方法的可靠性,对确定性计算和不确定性计算进行了对比。定义实际采用的支护力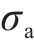
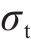
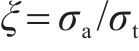
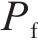
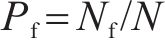
式中:
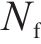
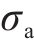
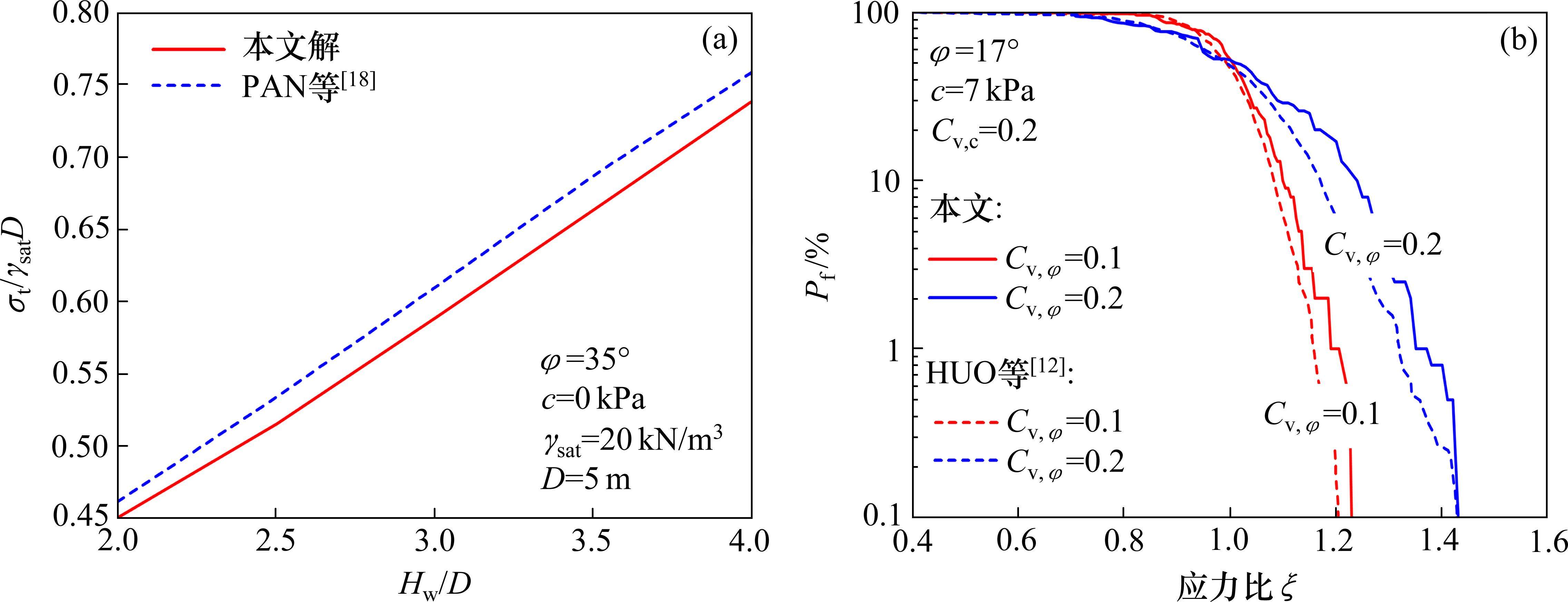
图4为本文结果与已有研究成果的对比图[12, 18]。由图4(a)可知,本文确定性分析的结果与PAN等[18]的研究成果基本一致,差别在4%以内,说明本文计算富水地层开挖面支护力的有效性,存在差别是由于本文改进了局部坐标系中心的生成方法。由图4(b)可知,在进行不确定性分析时,本文结果与HUO等[12]的结果表现出了相似的规律,存在一定差别,同样由于本文对局部坐标系中心生成方法的改进,以及不确定性计算的特性所致。综上所述,本文在确定性分析和不确定性分析中与已有研究均保持了良好一致性,可认为本文方法是有效的。
4.2 不确定性参数分析
针对盾构隧道开挖面稳定性问题,本文针对变异系数和自相关距离的影响进行不确定性参数分析。采用单层地层开展参数分析,其参数设置为: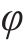
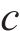
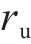
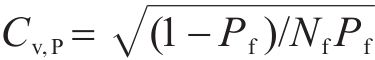
式中:Nf为当前的计算次数。
| 工况 | 随机参数 | 变异系数 | 水平自相关距离(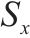 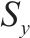 | 竖直自相关距离(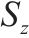 | ||
|---|---|---|---|---|---|---|
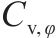 | 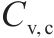 | 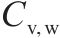 | ||||
| 1 | 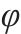 | 0.1 | — | — | 10 | 2 |
| 2 | 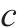 | — | 0.1 | — | 10 | 2 |
| 3 | 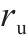 | — | — | 0.1 | 10 | 2 |
| 4 | 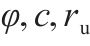 | 0.1 | 0.1 | 0.1 | 10 | 2 |
| 5 | 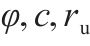 | 0.2 | 0.1 | 0.1 | 10 | 2 |
| 6 | 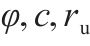 | 0.3 | 0.1 | 0.1 | 10 | 2 |
| 7 | 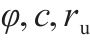 | 0.1 | 0.2 | 0.1 | 10 | 2 |
| 8 | 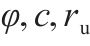 | 0.1 | 0.3 | 0.1 | 10 | 2 |
| 9 | 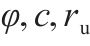 | 0.1 | 0.1 | 0.2 | 10 | 2 |
| 10 | 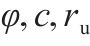 | 0.1 | 0.1 | 0.3 | 10 | 2 |
| 11 | 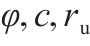 | 0.1 | 0.1 | 0.1 | 7.5 | 2 |
| 12 | 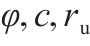 | 0.1 | 0.1 | 0.1 | 12.5 | 2 |
| 13 | 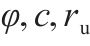 | 0.1 | 0.1 | 0.1 | 10 | 1 |
| 14 | 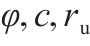 | 0.1 | 0.1 | 0.1 | 10 | 3 |
为研究计算次数对失效概率的变异系数和均值的影响,首先以工况1为例进行了400次计算,结果如图5。分析可知,进行100次计算之前,极限支护力的均值波动较大,随着计算次数的增加,波动逐渐减小,临界支护力的均值趋于稳定,失效概率的变异系数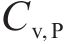
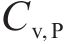
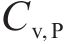
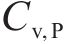
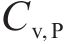
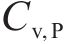
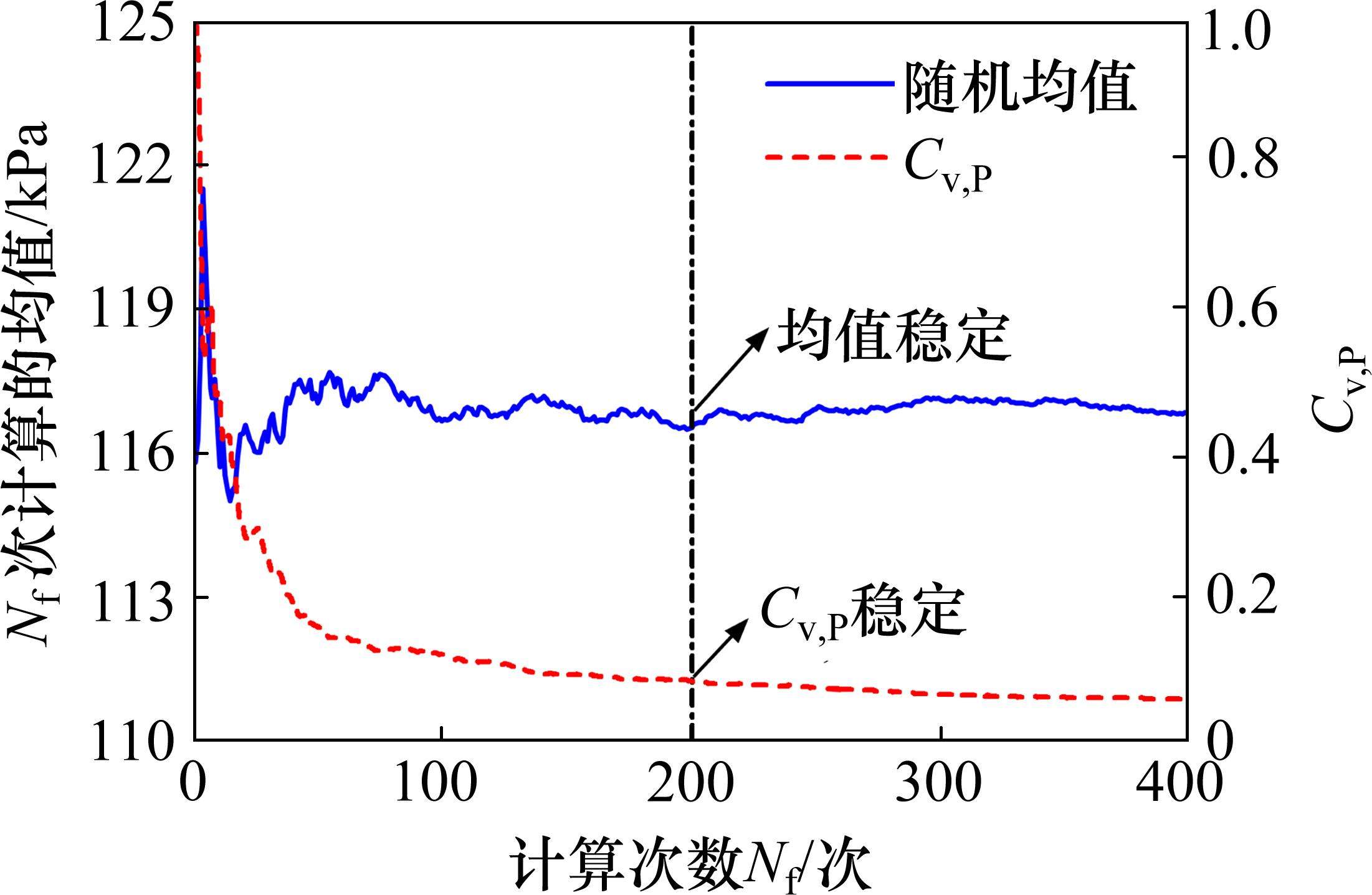
4.2.1 单参数不确定性的影响
定义不确定性计算结果的均值与确定性结果之比为均值比,其越接近1,表示随机模拟效果越好。图6展示了单参数变异性对极限支护力的影响,其中,直方图分格大小为0.015。由图可知,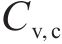
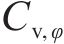
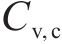
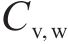
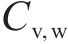
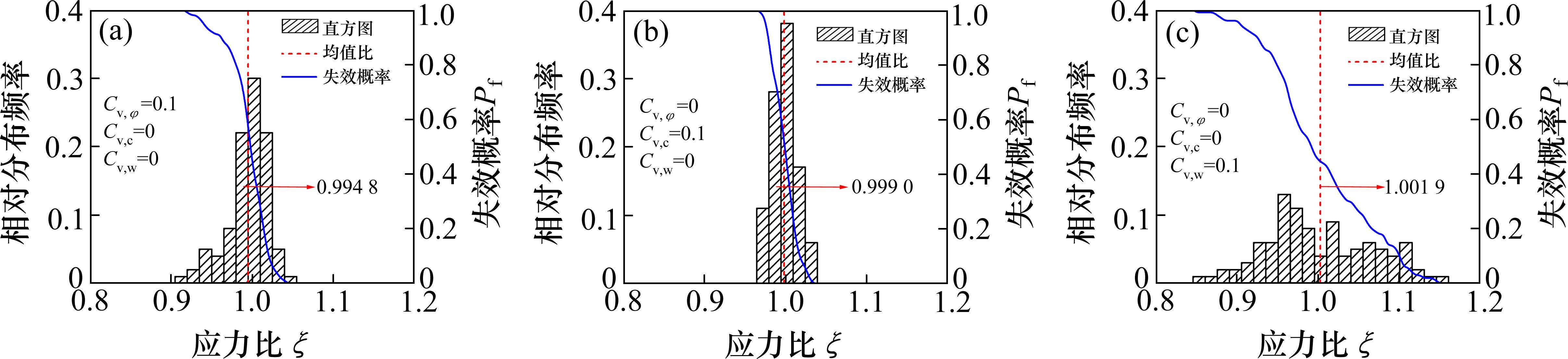
4.2.2 变异系数的影响
图7展示了多参数空间变异性影响下,各参数的变异系数对极限支护力的影响。分析可知,随着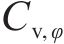
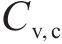
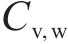
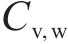
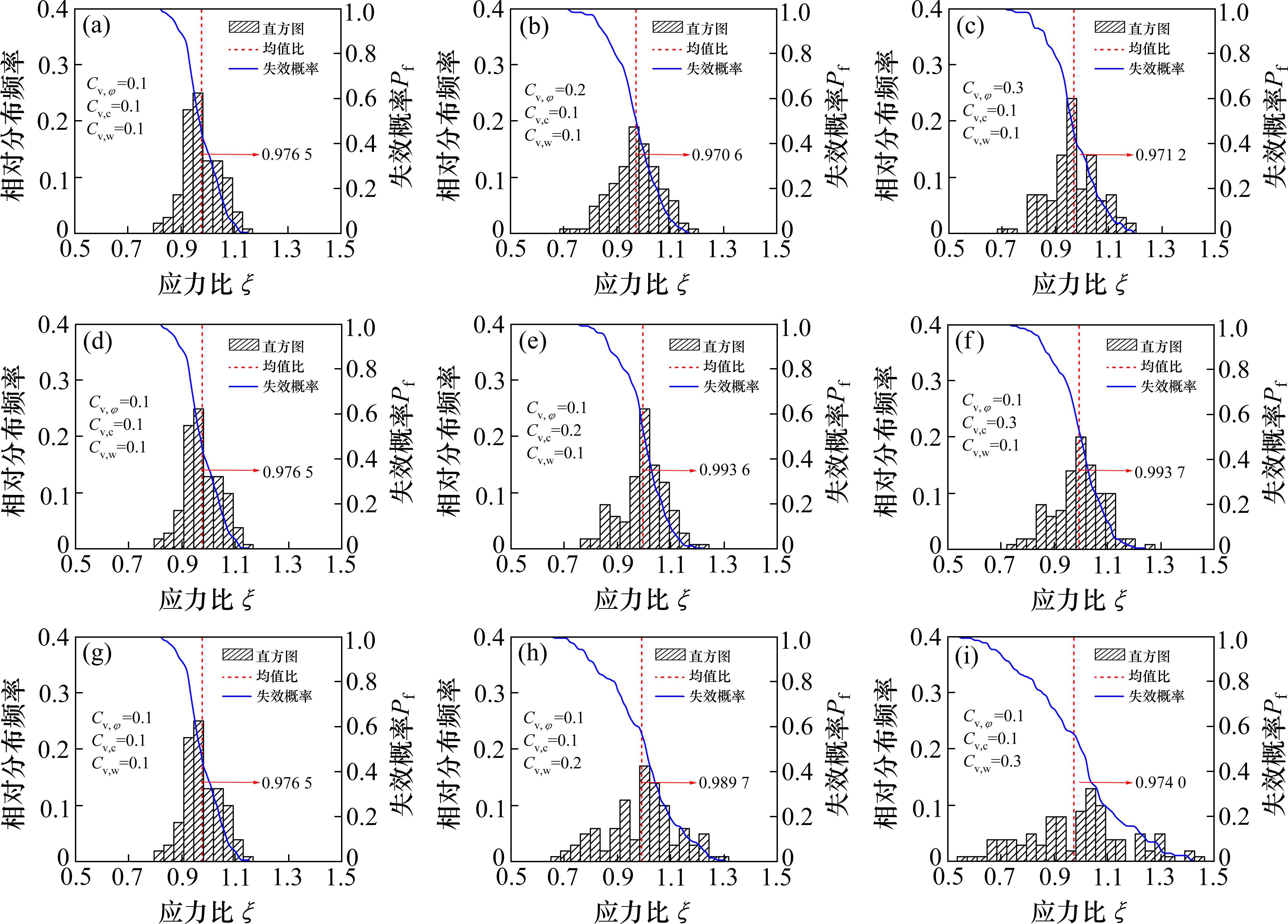
4.2.3 自相关距离的影响
图8展示了多参数空间变异性影响下,水平和竖向自相关距离对应力比分布直方图及失效概率曲线的影响。分析可知,随着自相关距离的增加,土体参数的关联性减小,变异性增大,应力比分布直方图更加分散,失效概率曲线则表现出更加陡峭的下降趋势,并在尾部表现出收敛性。这表明自相关距离的增大将增大应力比的变异性,但相较而言,自相关距离的影响小于变异系数的影响。
5 盾构隧道开挖面支护力稳健性设计方法及应用
5.1 支护力设计方法
基于前文分析可知,参数的变异性对盾构隧道开挖面稳定具有显著影响。因此,在进行开挖面支护力设计时,有必要考虑水土参数变异性的影响。但若对每一环管片的断面均进行失效概率分析,则其计算效率也难以接受。为此,本文提出了一种更为实用的盾构隧道开挖面支护力稳健性设计方法。设计流程如图9所示。设计步骤为:
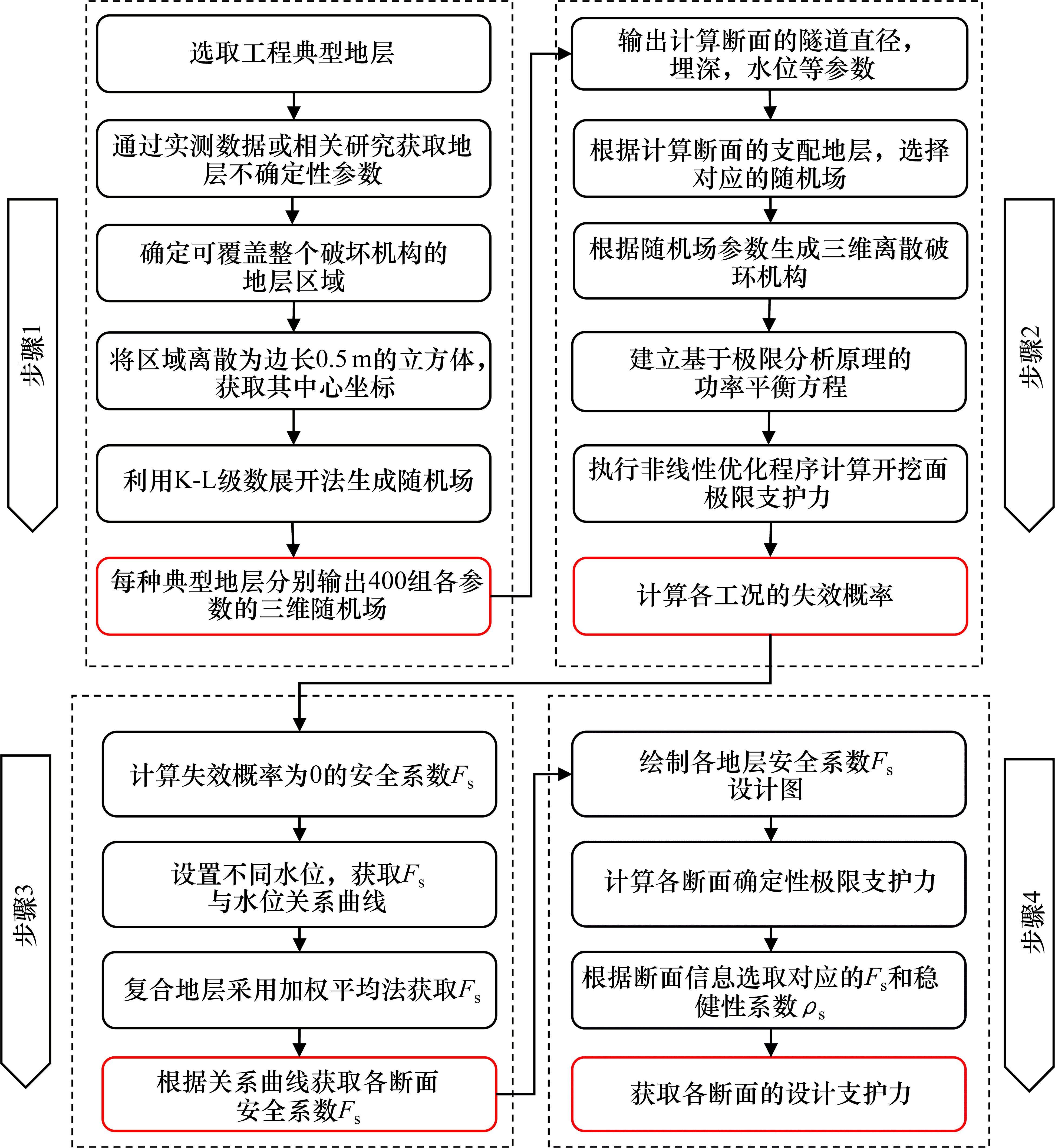
1) 生成水土参数随机场。首先,根据工程的纵断面图选取工程穿越的主要地层。通过实测或调研获取地层不确定性参数(摩擦角、黏聚力、孔隙水压力系数),在可覆盖破坏机构的范围内生成这些参数的三维随机场。
2) 不确定性计算。根据生成的随机场,对极限支护力进行不确定性计算,获取不同工况的失效概率。
3) 确定安全系数。将失效概率为0时最小的应力比定义为安全系数Fs。考虑到同一地层中,影响Fs的主要因素是水位高度,可通过绘制不同水位下的Fs曲线,快速确定各断面的设计安全系数的Fs。
4) 定义稳健性系数。为弥补上限分析无法计算地层变形的局限性,引入稳健性系数,考虑弹性模量的不同,为极限支护力增加设计冗余[19],其表达式为:
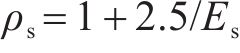
式中: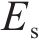
5) 计算设计支护力。获取各地层的Fs设计图后,通过对各地层开展确定性分析计算,将计算结果乘以稳健性系数和设计应力比,以获取设计支护力。对于复合地层,其设计支护力和稳健性系数可按各地层厚度占比取加权平均值,以反映不同地层对开挖面稳定性的影响。
5.2 工程案例分析
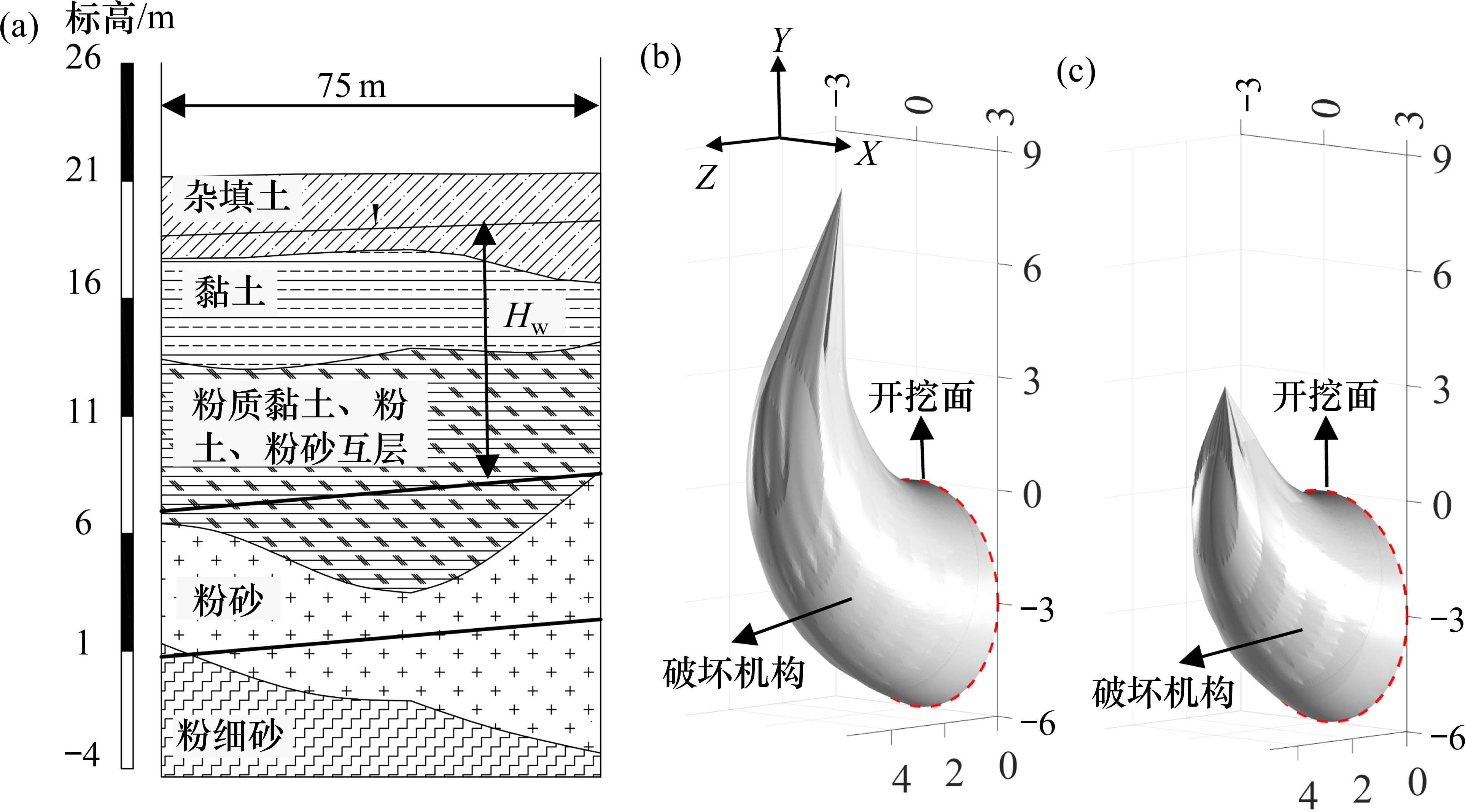
某地铁区间主要穿越粉质黏土、粉土、粉砂互层(地层1),粉砂(地层2)地层,选取其一段开展分析,纵断面图如图10(a)。图10(b)、10(c)分别展示了地层1、2中的典型破坏机构。其地层物理参数如表2,水土参数的变异系数参考相关文献选取[20],其中,由于对孔隙水压力系数变异性的研究较少,在饱和地层中,其主要受渗透系数影响[18],因此,采用土体渗透系数的变异系数对孔隙水压力系数的变异系数进行估计。
| 地层编号 | 岩土名称 | 湿重/ (kN∙m-3) | 摩擦角/(°) | 黏聚力/ kPa | 孔隙水压力系数 | 弹性模量/MPa | 自相关距离 | 变异系数 | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
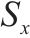 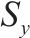 | 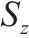 | 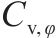 | 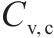 | 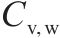 | |||||||
| 1 | 粉质黏土、粉土、粉砂互层 | 19.9 | 14 | 15 | 0.3 | 6.5 | 40 | 3 | 0.1 | 0.4 | 0.3 |
| 2 | 粉砂 | 19.7 | 27 | 0 | ― | 12.5 | 10 | 2 | 0.1 | — | — |
分别生成地层1、2的随机场进行分析,获取Fs与水位关系图如图11(a)。分析可知,地层1在分析中同时考虑了摩擦角、黏聚力及孔隙水压力系数的空间变异性,因此,其计算结果变异性较大,需要更高的设计安全系数以确保工程的稳定性和安全性。而地层2为强透水地层,采用静水压力计算孔隙水压力。因此,其设计安全系数相比地层1更小,但因为忽略了渗流,其设计结果更为保守。
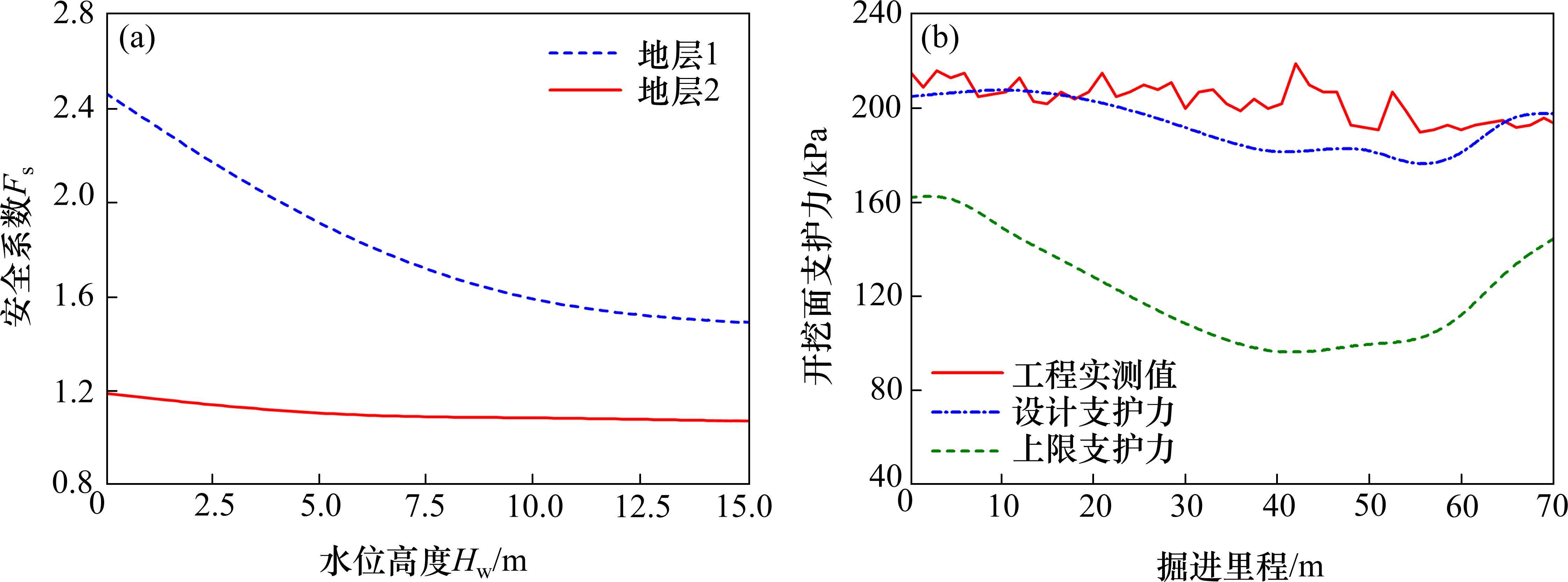
图11(b)展示了设计支护力与工程实际采用值的对比。相较于上限分析的结果,改进的稳健性设计支护力更接近于实测值。在粉砂地层中,本文采用较为保守的设计方法,忽略了强渗透土中开挖面渗流,设计结果与工程实测值非常接近。而在粉质黏土、粉土、粉砂互层地层,本文考虑了弱渗透土中开挖面的渗流,设计支护力略小于实际值。可知,实际工程设计中倾向于采取更保守的支护力设计策略,从而确保工程的安全。总体而言,本文的设计方法可为开挖面支护力设计提供参考与指导。
6 结论
1) 基于随机场理论,通过盾构隧道开挖面上限分析确定性计算确定随机场离散区域,并采用K-L级数展开法生成了服从对数正态分布的水土参数随机场,实现了水土参数空间变异性的模拟。
2) 基于空间离散技术,采用点对点逐点生成原理构建了盾构隧道开挖面三维不确定性失稳分析机构,进而基于上限分析定理建立了考虑水土参数空间变异性的盾构隧道开挖面极限支护力计算方法,并与已有研究成果进行了对比,结果表明,本文确定性计算结果与已有研究的结果差距不超过4%,不确定性结果与已有研究结果趋势基本一致,验证了计算方法的有效性。
3) 考虑水土参数变异系数和自相关距离的影响,设计14组工况,通过蒙特卡罗法进行了不确定性参数分析,结果表明,各参数变异系数及自相关距离的增大会导致不确定性计算的结果的离散程度增大,表现出更强的变异性。3个参数变异系数对极限支护力的变异性影响大小顺序为:孔隙水压力系数>黏聚力>摩擦角。各参数变异系数的影响相较于自相关距离的影响更明显。
4) 基于不确定性参数分析的结果,提出了一种便于工程应用的盾构隧道开挖面支护力稳健性设计方法,该方法可在考虑水土参数变异性影响的同时实现开挖面支护力的快速计算。结合工程案例对比发现,本文提出的支护力稳健性设计方法与实测结果吻合较好,适用于无黏性土和黏性土地层,可为盾构安全施工提供参考。
胡子威,雷明锋,张运波等.考虑水土参数变异性的盾构隧道开挖面支护力设计方法[J].铁道科学与工程学报,2025,22(01):259-271.
HU Ziwei,LEI Mingfeng,ZHANG Yunbo,et al.Design method for shield tunnel excavation face support force considering variability of water and soil parameter[J].Journal of Railway Science and Engineering,2025,22(01):259-271.

