地震引起边坡失稳是我国常见的工程灾害之一,对人类的生命财产及基础设施的安全运营造成了严重威胁。土钉具有易实施、经济等优点,在边坡工程中广泛应用[1]。因此,评估土钉支护边坡的地震稳定性及变形的工程价值重大。目前,地震作用下边坡动力响应分析主要有拟静力法、数值模拟和Newmark位移法。拟静力法将地震效应简化为恒定惯性力,与经典极限平衡法结合评估土钉参数对边坡地震稳定性的影响[2],或与极限分析法结合起来研究不同加筋模式下边坡临界高度和临界加筋强度[3-4]。尽管拟静力法简单有效,但难以充分反映地震的动力特征[5-8]。事实上,地震作用下土钉支护边坡的安全系数和位移是时变的,当震后位移累积到一定值时边坡才会发生破坏。因此,采用位移评价地震作用下土钉支护边坡稳定性更为合理。数值模拟可以有效分析地震作用下土钉支护边坡的应力和应变过程[9-12],被广泛用于研究边坡的渐进性失稳行为,但其涉及复杂的建模过程,且计算成本较高。相比之下,NEWMARK[13]以地震加速度时程曲线来表征地震的动力学性质,相较拟静力分析更为合理,又规避了应力应变分析的复杂性,可以计算边坡在地震作用下的位移,Newmark位移法已被众多学者广泛采用[14-17]。基于Newmark法,董建华等[14-17]研究了地震作用下二维土钉支护边坡的临界地震屈服加速度系数和永久位移,考虑边坡滑块下滑时边坡参数、土钉受力变化的影响,对边坡的震后位移计算方法进行改进。然而以上地震作用下土钉支护边坡的稳定性分析均假设边坡失稳为二维平面应变问题。事实上,在地震作用下,土钉支护边坡的破坏表现出显著的三维特征[18]。此外,二维分析模型忽略了土钉在水平方向的分布特征与其对边坡稳定性的影响效果。因此,开展地震作用下土钉支护边坡三维稳定性分析及震后位移计算是非常有必要的。基于极限分析上限法,结合边坡三维旋转破坏机制和Newmark位移法,对地震荷载诱发土钉支护边坡位移的影响规律开展研究。首先介绍边坡三维旋转破坏机制和土钉支护边坡的Newmark位移计算方法,然后将计算结果与振动台试验结果进行对比验证,最后开展土钉支护边坡临界地震加速度和Newmark位移系数的敏感性分析,探究土钉参数对边坡震后位移的影响。
1 土钉支护边坡震后位移计算模型
1.1 土钉支护边坡形式
土钉支护作为边坡抗震的一种有效手段,支护能力与土钉强度及分布特征息息相关。土钉的破坏形式主要为拉断破坏或拔出破坏[19],失效模型如图1所示。
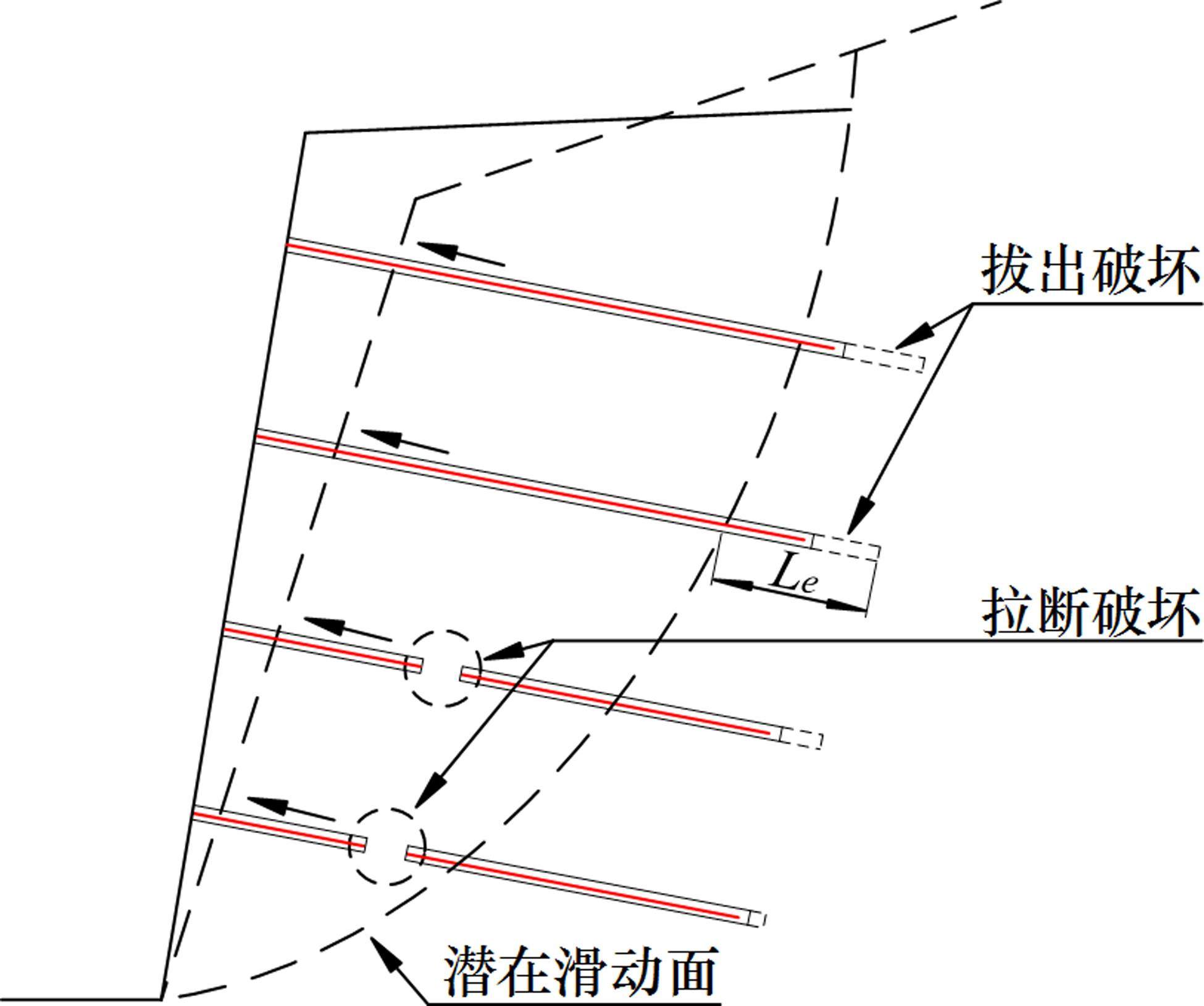
因此,开展土钉支护边坡稳定性极限分析时,需要考虑土钉的抗拉拔能力T,计算公式如下:
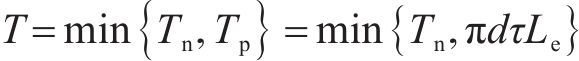
式中:Tn为土钉极限抗拉力;Tp为土钉抗拔力;d为土钉直径;τ为土钉与土的极限黏结强度;Le为土钉有效长度。
1.2 土钉支护边坡三维旋转破坏机制
如图2所示,边坡高度为H、宽度为B、底部倾角为β及顶部倾角为α。地震作用下土钉支护边坡的破坏模式采用MICHALOWSKI等[20]提出的三维旋转破坏机制,由顶角为2φ的曲锥体组成。在纵向对称平面中,其边界轨迹由2条对数螺旋线FAC及FA′C′定义,交点为F。2条对数螺旋线的旋转中心记为O,r0、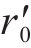
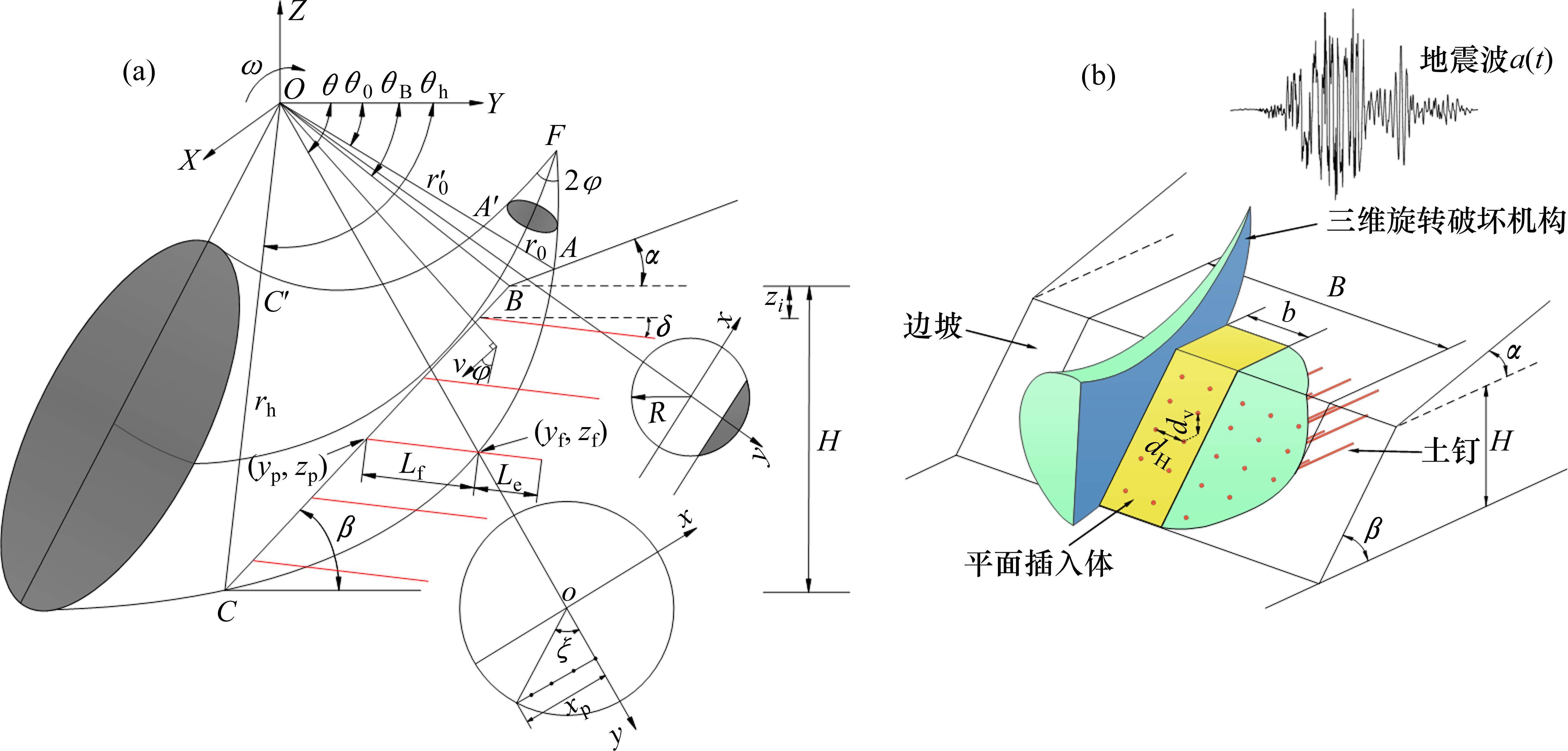
该三维破坏机制采用旋转速度场,整个破坏机制绕O点以恒定的角速度ω转动,内部任一点的速度大小v等于该点到旋转中心O点的距离乘以角速度ω。当边坡的宽度无限大时,为允许三维旋转破坏机制退化为平面应变破坏机制,MICHALOWSKI等[20]将三维旋转破坏机制沿纵向对称面剖开,并在其中插入宽度为b的平面块体,如图2(b)所示,其底部边界为对数螺旋线FAC。由于平面块体的插入,修正后的土钉支护边坡的三维旋转破坏机制由θ0、θh、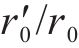
如图2(a)所示,以旋转中心O建立全局直角坐标系O-XYZ,以圆形横截面中心建立垂直纸面的局部直角坐标系o-xy。ξ为土钉在滑动面上的交点和oy轴的夹角,θ为土钉在滑动面上的交点与水平面的夹角,土钉与三维旋转破坏机制滑动面的交点由θ、ξ确定。由几何关系得到:
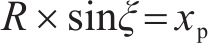
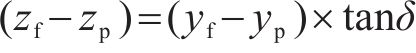
式中:xp、yp、zp分别为土钉在边坡坡面上的全局直角坐标系坐标,可由土钉的分布密度和分布特征确定,是已知量;xf、yf、zf分别为土钉与三维旋转破坏机制滑动面交点的全局直角坐标系坐标,是待求量。由几何关系可知xf=xp,yf与zf满足如下数学方程:
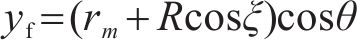
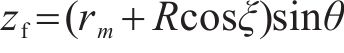
联立式(2)~式(5),可以得到xf、yf、zf及θ、ξ的值,以便计算土钉破坏时内能耗散。
1.3 功率和能耗计算
PAN等[21]提出边坡三维旋转破坏机制的离散方案,将该破坏机制的能耗计算由三维积分简化成累加计算,本文采用该方案计算地震作用下土钉支护边坡的外力做功和内能耗散。外力做功包括重力功率Wγ及地震荷载功率Ws,内能耗散包括滑动面土体的内能耗散Ds以及土钉内能耗散Dn。本节仅介绍Ws、Dn的计算,有关Wγ、Ds的计算参见文献[21]。
1.3.1 计算地震荷载的功率
地震发生过程中,尽管水平地震动与竖直地震动同时存在,然而2个方向的地震加速度较少同时达到峰值[22],竖直地震动对边坡永久位移的影响相对较小[3,23]。因此仅以水平地震动来表征地震动效应,即只考虑水平地震系数kh。地震力的功率Ws计算式如下:
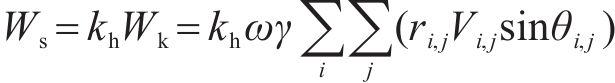
式中:γ为土体重度;ri,j为离散体与O点的距离;Vi,j为离散体体积,包括插入平面块体部分;θi,j为离散体重心和O点连线与水平面的夹角。
1.3.2 计算土钉的内能耗散
土钉总能量耗散等于各个土钉能量耗散dDn之和:
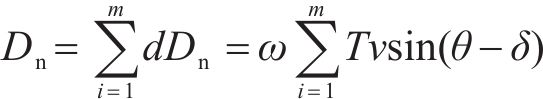
式中:m为破坏机制内部的土钉数量总和。
1.4 Newmark位移法
1.4.1 土钉加固边坡的屈服加速度ky
当土钉加固边坡处于临界状态,以水平地震加速度系数kh(t)表征的地震荷载效应参数恰好达到临界屈服加速度ky,即kh(t)=ky,旋转块体处于极限状态,得到临界屈服加速度ky为:
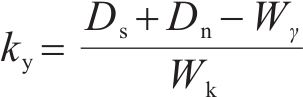
1.4.2 边坡旋转块体震后位移计算
当实际水平地震加速度kh(t)超过临界地震加速度ky时,边坡会发生位移。设t时刻旋转块体ABC绕点O的转动角加速度为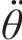
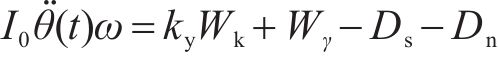
式中:I0为三维旋转破坏机制绕旋转轴OX的转动惯量。
对于kh(t)>ky的时段,得到三维旋转块体的转动角位移θ为:
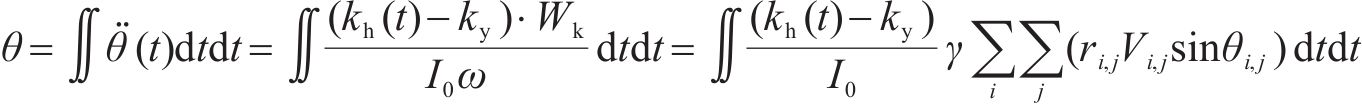
将旋转块体的转动角位移与到旋转中心O点的距离r相乘可得到该位置处的转动弧长,然后可利用几何关系求得其水平与竖向位移。土钉加固边坡坡脚处的水平位移为:
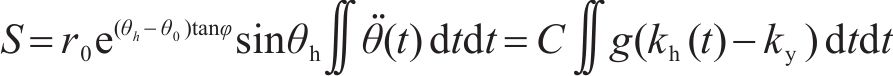
式中:C为位移系数,取决于边坡几何形状、土体抗剪强度参数及土钉参数情况,如式(12)所示;时间积分项仅取决于地震加速度曲线和土钉加固边坡的屈服加速度ky。
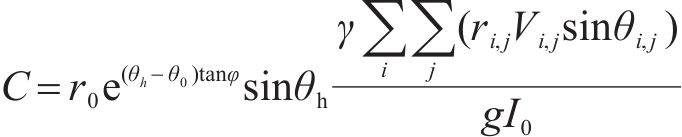
综合考虑土钉边坡支护中多个关键因素的影响,包括土钉极限抗拉拔力T、边坡高度H、土体重度γ、土钉纵横向间距dV和dH,提出无量纲系数Mt,定义如式(13)所示。Mt的分子与分母部分分别反映了土钉抗拉拔能力与分布密度。Mt表征边坡中土钉强度以及在空间布置上的三维特性,可以有效表征土钉支护边坡的效果,简化分析过程,方便工程应用和计算。
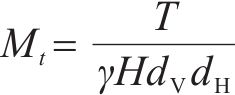
2 对比验证
与SAHOO等[18]的土钉支护边坡振动台缩尺模型试验结果进行对比,验证方法的合理性。边坡几何构造、土体参数及土钉参数取值与试验[18]保持一致,参数取值如表1所示[18]。所利用的地震波为1989年Loma Prieta地区Los Gatos测站观测所得。
| 模型参数简介 | ||
|---|---|---|
| 边坡几何特征 | H/m | 0.4 |
| β/(°) | 60 | |
| B/H | 2.25 | |
| 土体性质 | γ/(kN∙m-3) | 15.45 |
| c/kPa | 0.5 | |
| φ/(°) | 33 | |
| 土钉参数 | d/m | 0.01 |
| l/m | 0.3 | |
| δ/(°) | 0 | |
| Τ/kPa | 1.0 | |
| Tn/MPa | 222.4 | |
| dV/m | 0.13 | |
| dH/m | 0.225 | |
将所得到的土钉支护边坡三维旋转破坏机制的临界滑动面与SAHOO等[18]试验测得的破坏面进行对比,结果如图3所示。由图3(a)可知,模型试验测得的临界滑动面上半部分比本方法的预测范围大,下半部分比本方法预测范围小,但两者得到的破坏面形状和总面积具有较好的相似性。由图3(b)的俯视图可以看到,文献[18]的试验结果表明地震作用下土钉支护边坡破坏具有显著的三维效应,本文预测的破坏面在宽度方向略小于试验模型破坏范围,但是在破坏面形状与试验结果大致吻合。

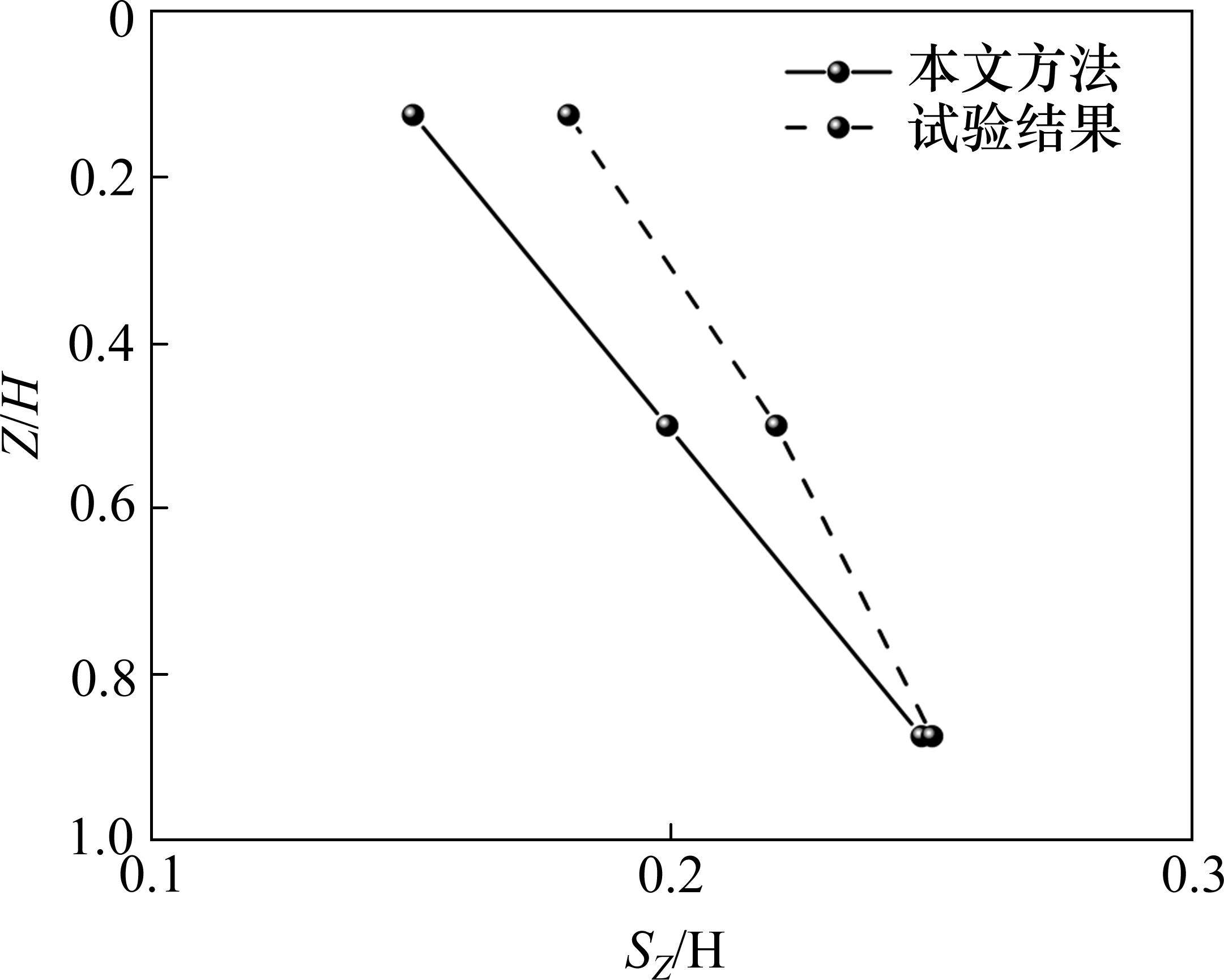
图4所示为SAHOO等[18]的试验结果与计算得到的归一化边坡坡面水平位移SZ/H随归一化边坡深度Z/H的变化曲线。可以看到,两者在深度方向上的变化趋势完全一致,随着边坡深度Z的增加,计算得到的震后位移与试验结果相差逐渐减小;在坡顶附近位置(Z/H=0.125),计算到的震后位移与试验结果相差较大,为16.5%;在边坡中间位置(Z/H=0.5),计算到的震后位移与试验结果相差9.4%;在边坡底部,本计算得到的震后位移与试验结果几乎一致,验证了方法的有效性。计算位移值与模型试验的测量值在坡顶位置的差距较大,可能是由于模型试验中容器是由有机玻璃板、钢角和钢筋制成的,边界是刚性的,容器壁的刚度会引起地震波的反射,使得边坡位移存在非真实强化的发展,这可能会导致试验模型所输出的位移信息比实际情况更大[18]。
3 参数敏感性分析
3.1 临界地震加速度ky
对于给定的无量纲系数Mt、B/H、c/γH、内摩擦角φ和边坡倾角β,计算相应的临界地震加速度ky。图5~图7给出了不同参数条件下,采用本文方法计算得到的土钉支护边坡的临界地震加速度ky,具体参数包括Mt=0.2、0.6、1.0,B/H=2、3、5,φ=20°、30°以及β=30°、45°、60°。
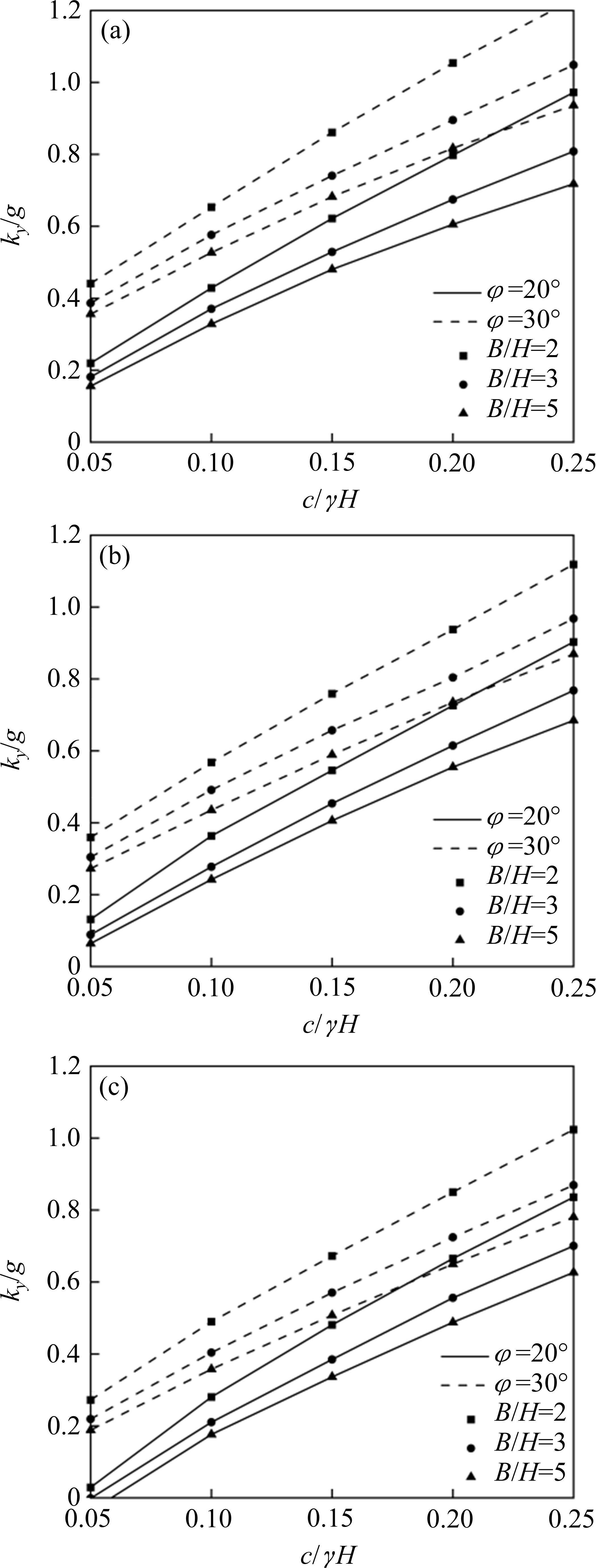
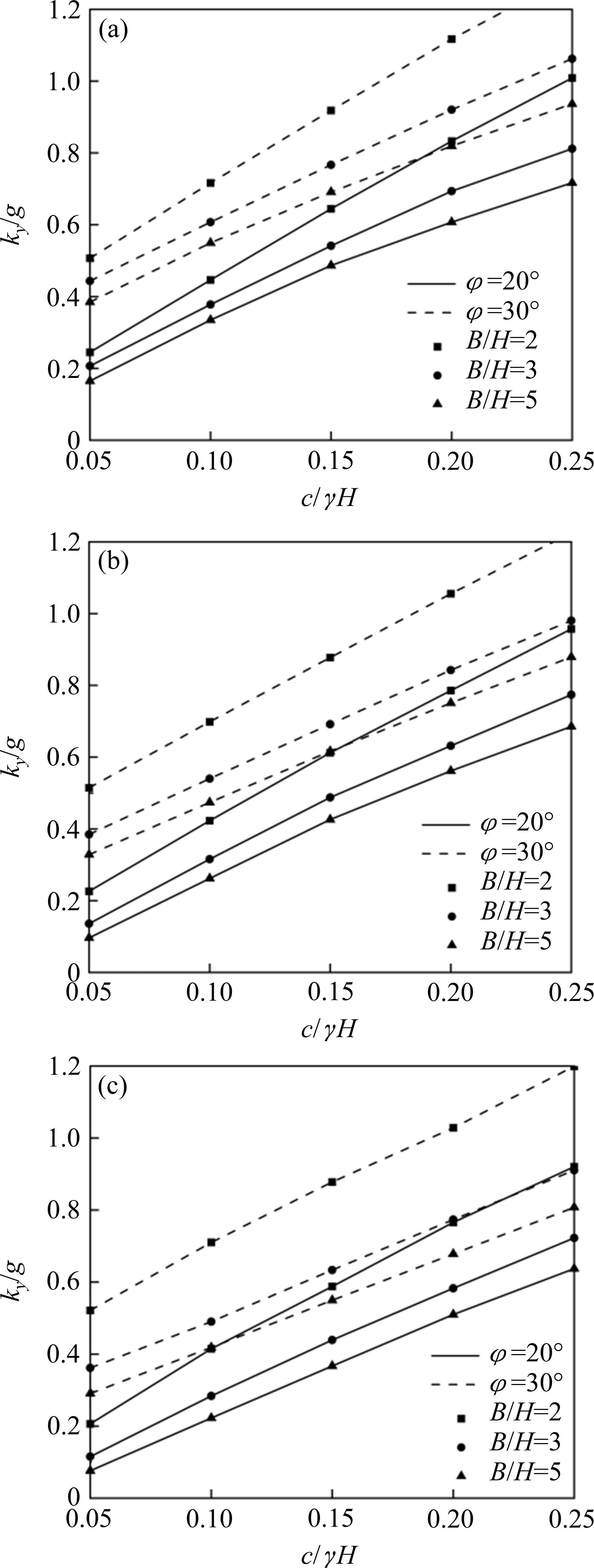
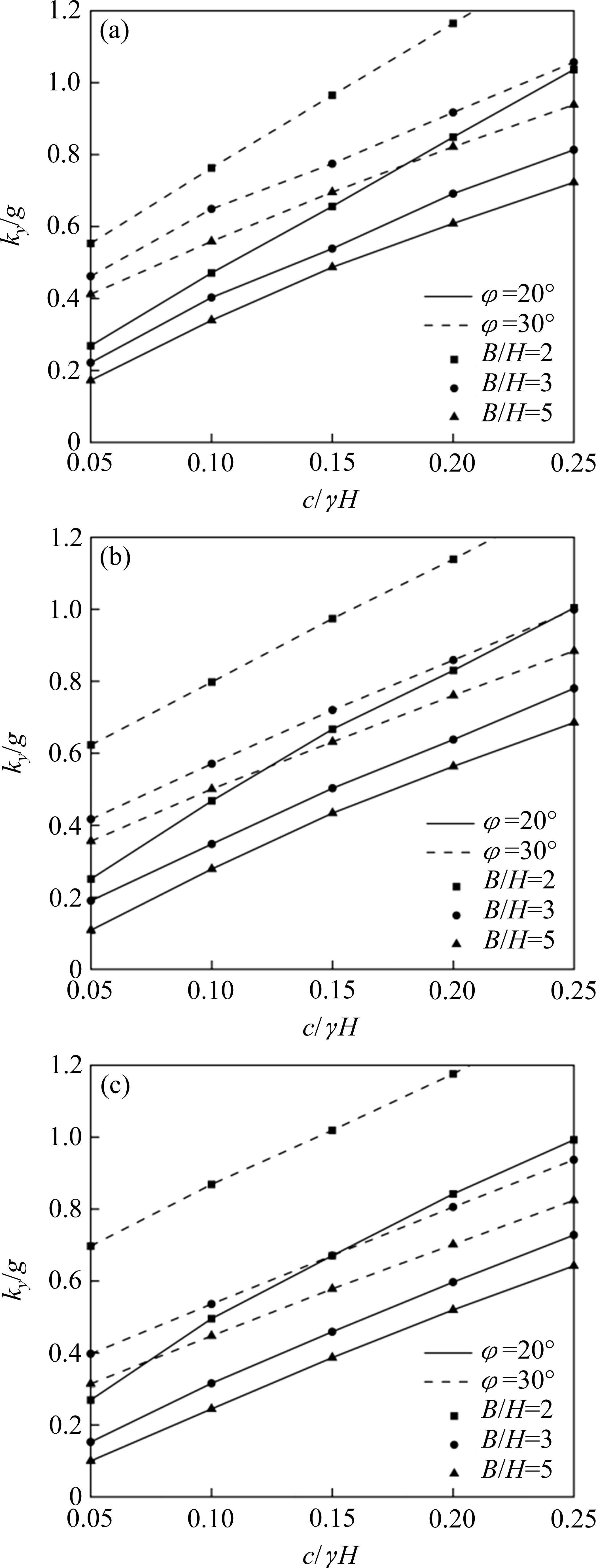
以B/H=2,c/γH=0.15,φ=20°,β=60°边坡为例,对ky进行敏感性分析,由图5~图7可知:
1) 土钉支护边坡中c/γH越大,临界水平地震加速度ky越大。如图5(c)所示,随着c/γH增大,对应的ky分别为0.03g,0.28g,0.48g,0.67g,0.84g。
2) 如图5(c)、图6(c)和图7(c)所示,Mt为0.2,0.6,1.0时,对应的ky分别为0.48g,0.59g,0.67g。土钉支护边坡中无量纲系数Mt越大,临界地震加速度ky越大,这表明采用土钉支护可有效提高边坡抗震稳定性。
3) 当土钉支护边坡的c/γH固定,临界地震加速度ky受无量纲系数Mt的影响并非均匀,且B/H越大,临界地震加速度ky受无量纲系数Mt的影响越小。当B/H=2,Mt从0.2以0.4的幅度增大到1.0,ky的增长率为22.9%和13.6%;当B/H=5,ky的增长率为9.1%和5.6%。随着无量纲系数Mt的增加,ky的增长幅度逐渐减弱,这说明土钉对地震诱发边坡变形的支护效果并不是线性增加的。
4) 无量纲系数Mt对临界地震加速度ky的影响程度与内摩擦角φ及边坡倾角β成正相关,即φ或β越大,无量纲系数Mt对临界地震加速度ky的影响越显著。如图5(a)和图7(a)所示,当β=30°时,Mt从0.2增大至1.0,ky增长率为5.6%;如图5(c)和图7(c)所示,当β=60°时,Mt从0.2增大至1.0,ky增长率为39.5%。同样,当φ=20°时ky增长率为39.5%,φ=30°时ky增长率为51.6%。
3.2 位移系数C
地震作用下土钉支护边坡位移计算如式(11)所示,由位移系数C与关于时间的二次积分项2个部分组成。本节讨论土钉支护边坡的无量纲系数Mt、B/H、c/γH、内摩擦角φ和边坡倾角β对位移系数C的影响规律。位移系数C变化受B/H、c/γH影响较小,在计算范围B/H=2~5,c/γH=0.05~0.25内,得到位移系数C平均值与计算值的最大偏差约为15%,但整个范围内的平均偏差仅约为5%。为反映Mt对位移系数C的影响,图8给出了B/H=2~5,c/γH=0.05~0.25,Mt=0.2、0.4、0.6、0.8时土钉支护边坡的位移系数C随着内摩擦角φ和边坡倾角β的变化曲线。
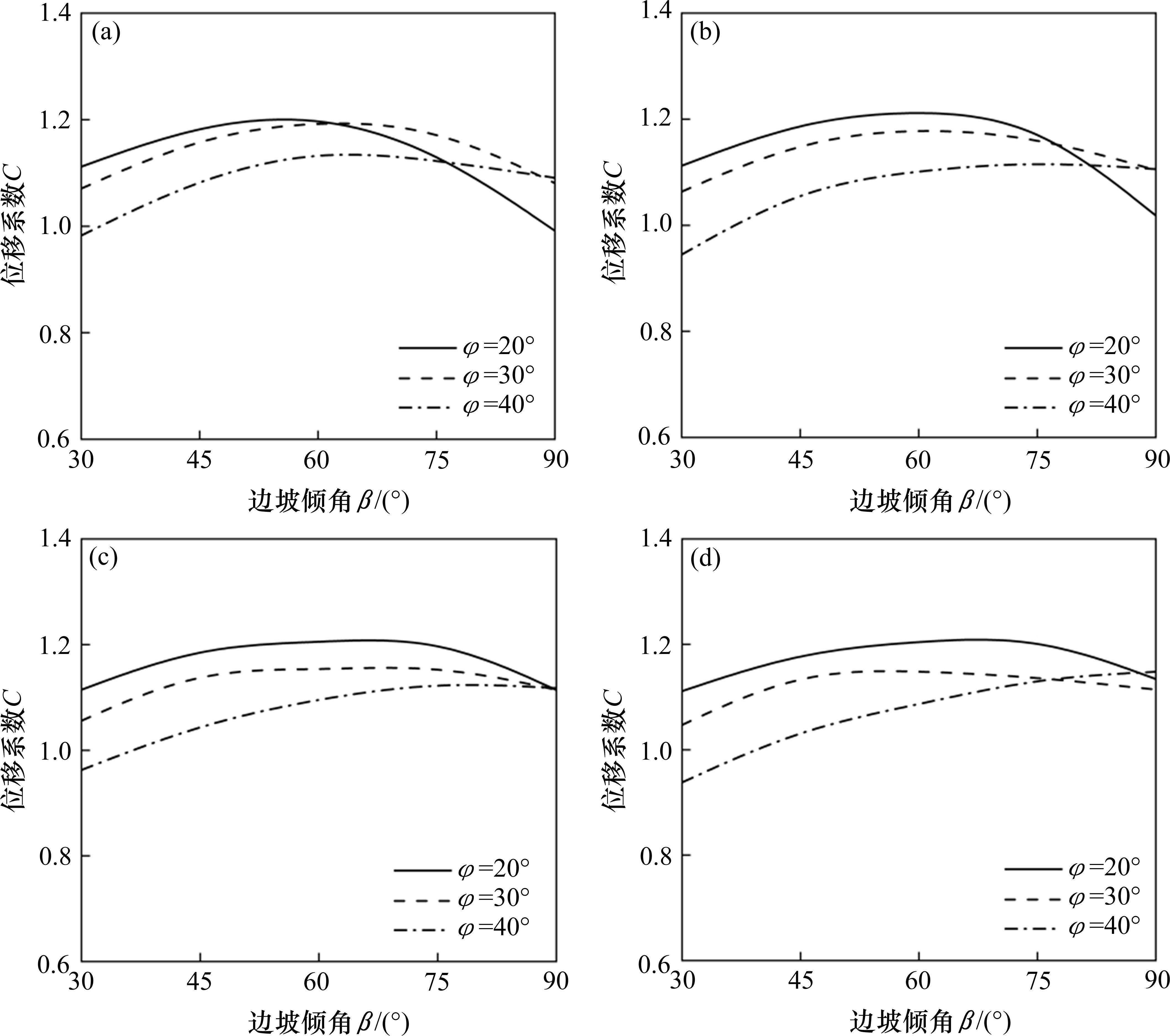
由图8可知,随着边坡倾角β的增大,位移系数C先增大后减小,且Mt越大,位移系数C取峰值时对应的边坡倾角β越大。以φ=20°为例,Mt=0.2、0.4、0.6时,C取峰值对应的边坡倾角β分别约为55°、60°、70°。当边坡倾角β较小时,内摩擦角φ越大,位移系数C越小。随着边坡倾角β的增大,内摩擦角φ的增大可能会导致位移系数C增大。以图8(a)为例,当β=30°时,φ=20°对应的位移系数C比φ=40°时大13.2%;而β=90°时,φ=20°对应的位移系数C比φ=40°时少9.1%。
3.3 地震积分位移
选取2个典型地震波,分别由1989年Loma Prieta地区Los Gatos测站及2008年汶川地震中卧龙台站观测所得。将地面峰值加速度(PGA)在地震时域内按比例缩放至km,得到一系列相同形式的水平地震加速度-时程曲线。通过式(11)进行二次积分,获得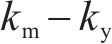
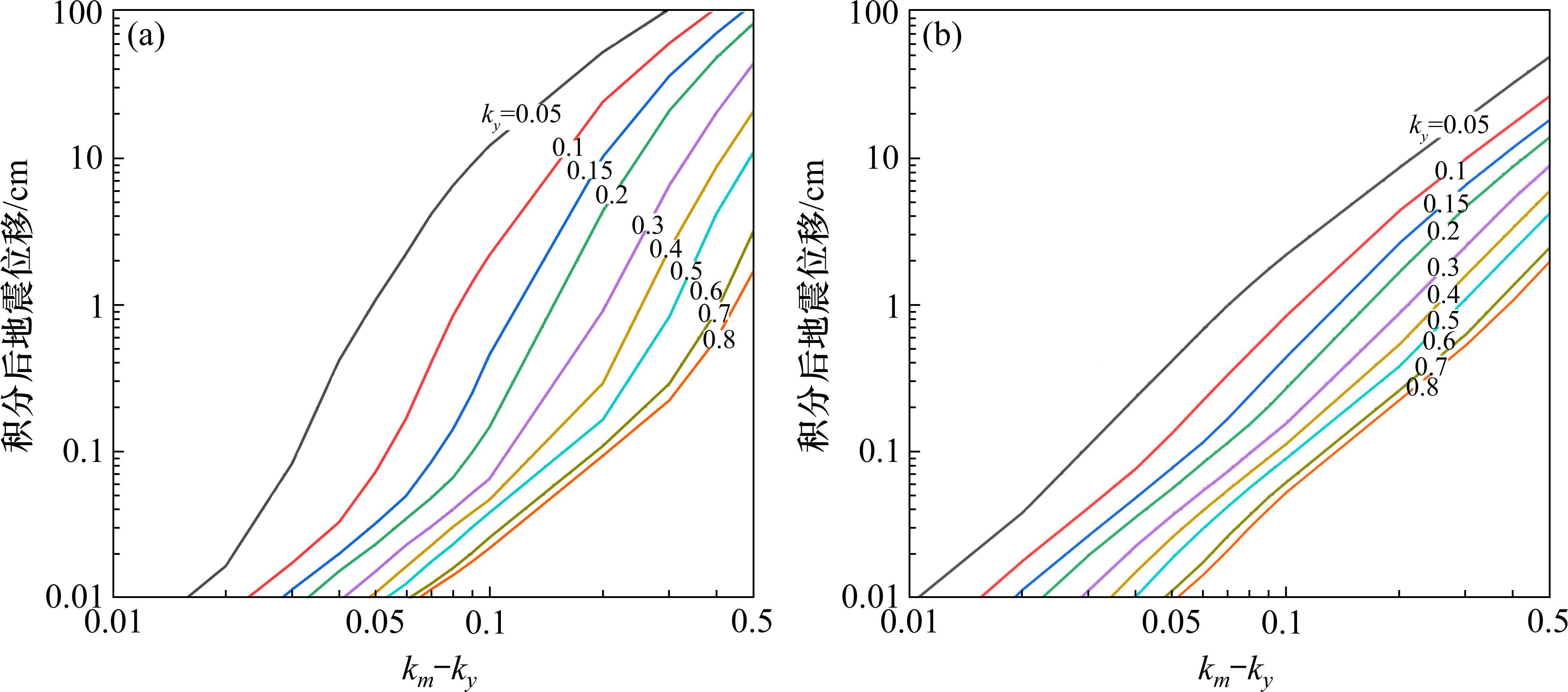
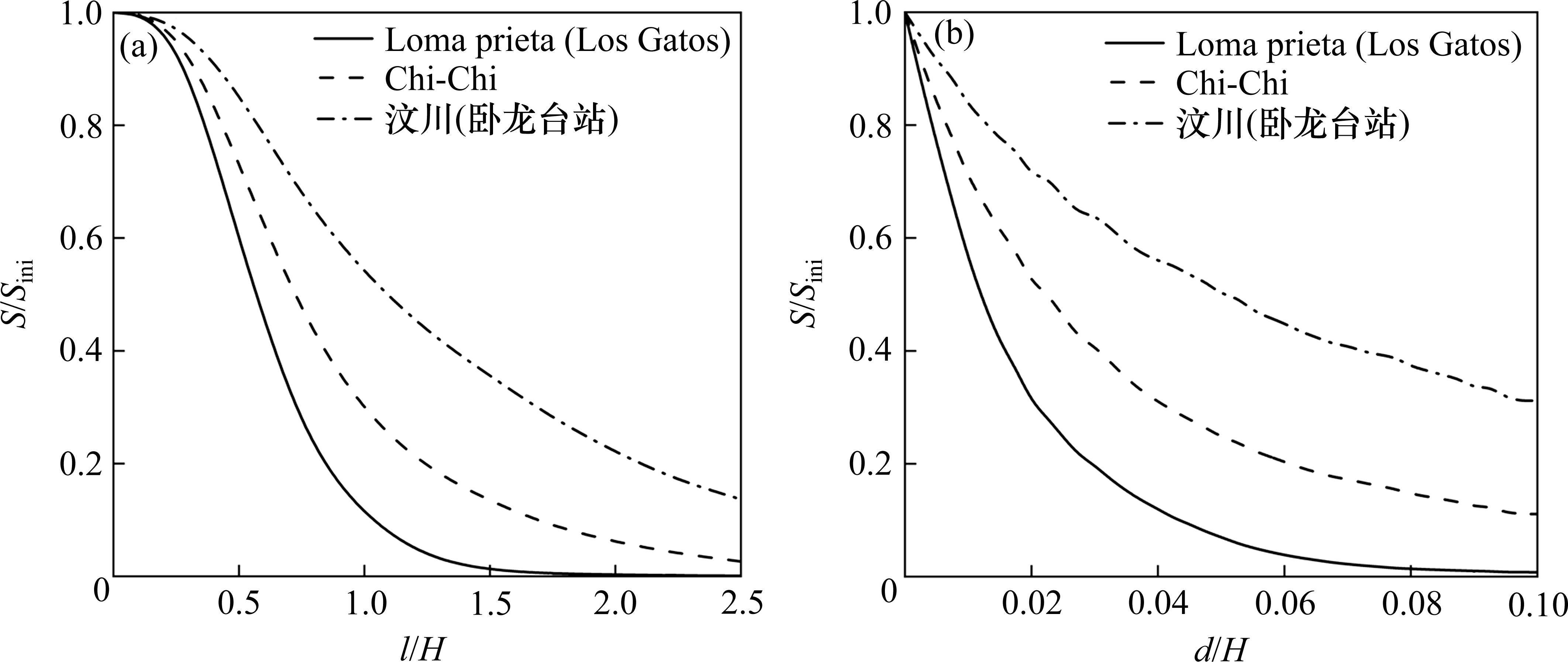
以表1中模型边坡参数为例,对无量纲系数Mt中土钉长度l、土钉直径d等参数进行敏感性分析,评估其对支护效果的影响,并确定最佳的支护方案。图10所示为不同地震荷载作用下边坡坡脚水平位移S与无土钉情况下边坡坡脚水平位移Sini之比随归一化的土钉长度l/H以及土钉直径d/H的变化曲线。由图10可知,考虑安全性与经济性,当l/H为1.0~1.5,d/H为0.04~0.06时,地震作用下边坡位移显著降低,具有良好的支护效应。
以某一边坡为例说明:β=60°,φ=20°,c=45 kN/m2,γ=20 kN/m3,H=15 m(c/γH=0.15),B/H=3,Mt=0.2。首先,通过图5(c)可以确定水平地震临界加速度系数ky=0.38g,查询图8(a)可确定位移系数C=1.22。然后,将地震波加速度时程曲线等比例缩放至PGA=0.8g,此时km-ky=0.42g,由图9(a)可以得到地震位移的时间积分项大小为12.20 cm。因此,可以计算得到该边坡在地震作用下的坡脚地震永久位移为1.22
4 结论
1) 基于极限分析上限理论,结合边坡三维旋转破坏机制和Newmark位移法,定义三维土钉支护边坡的无量纲系数Mt,建立地震荷载下土钉支护边坡的位移计算方法,探究了土钉长度、土钉直径对地震诱发边坡永久位移的影响规律。
2) 对同一边坡,土钉无量纲系数Mt为0.2、0.6、1.0时对应临界地震加速度ky分别为0.48g、0.59g、0.67g。土钉支护边坡中无量纲系数Mt越大,ky越大。但土钉对边坡稳定性的提升并非随着土钉长度和强度的提高而无限增长,当Mt从0.2增大到0.6及1.0,对应ky的增长率由22.9%降低到13.6%。
3) 随着边坡倾角β的增大,位移系数C先增大后减小,且Mt越大,位移系数C取峰值时对应的边坡倾角β越大。边坡倾角β小于75°时,内摩擦角φ增大会导致位移系数C减小。
4) 得到了位移系数C、临界地震加速度ky、2个典型地震下km-ky关于时间二次积分项的设计图表,基于边坡几何特征、边坡物理参数及Mt可预测土钉支护边坡的震后位移。
余家骥,黄旭东,陈志宇等.基于Newmark法的土钉支护边坡震后位移三维上限分析[J].铁道科学与工程学报,2025,22(01):161-171.
YU Jiaji,HUANG Xudong,CHEN Zhiyu,et al.Three-dimensional upper-bound analysis of seismic-induced displacements of soil nailed slopes[J].Journal of Railway Science and Engineering,2025,22(01):161-171.

