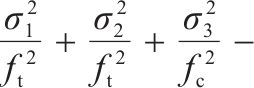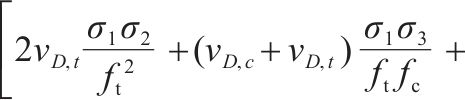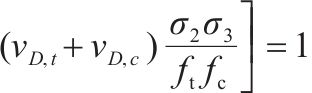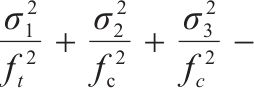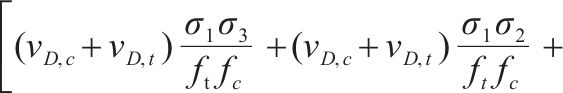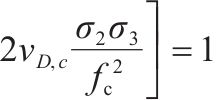目前,高级路面结构主要采用沥青路面,在交通荷载和环境温度作用下处于复杂三轴应力状态[1-2]。车辙是沥青路面的主要病害之一,沥青路面车辙可分为结构性车辙、磨损性车辙、压实性车辙和流动性车辙,其中流动性车辙是目前高速公路上车辙的主要类型,发生在路表[3]。不少学者对车辙产生的力学机理做了大量研究[4-6],普遍认为流动性车辙产生的主要原因是路面材料的高温软化流动,目前为止很少有强度理论可用来解释车辙现象。前期由于缺乏适用于沥青混合料的三轴试验设备,有关沥青混合料的强度研究主要集中在简单应力状态下的强度试验,如拉伸、压缩、弯曲和劈裂等试验[7-17]。传统的沥青路面设计主要采用最大拉应力和最大拉应变理论[18]。单一应力状态下的强度准则将高估三轴拉压复杂状态下沥青混合料的强度,而低估三轴受压强度[19]。近年来,众多学者开展了沥青混凝土的三轴强度特性研究[10, 20-25]。如XIA等[26]进行了不同加载速率下的直接拉伸、间接拉伸和无侧限压缩试验,建立了不同加载模式下沥青混合料的统一强度模型。QIAN等[27]将温度效应引入双剪统一强度模型,建立了考虑温度影响的统一沥青混合料强度模型。ZHANG等[28]提出了广义Drucker-Prager准则。HUANG等[19, 29-35]研发沥青混合料真三轴试验加载设备和方法,进行不同温度下沥青混合料的三向拉压和三向受压等不等应力状态三轴加载试验,提出系列八面体强度准则。目前这些准则主要通过拟合试验数据确定破坏包络曲线数学表达式,与相应试验数据相比计算精度较高,准则中的相关参数一般缺乏物理意义。丁发兴等[36]认为应力作用下脆性材料的纵向与横向遵循弹性应变和非弹性应变的分解,采用单元体相对耗能率求极值计算模型,提出描述材料非弹性体积膨胀引发失效的损伤比强度理论通用式和五经验系数损伤比表达式,并成功用于岩石和混凝土强度预测[36-41]。本文将损伤比强度理论继续应用于不同温度下的AC-13沥青混合料,主要工作如下:1) 应用损伤比强度理论,基于不同温度下AC-13沥青混合料的三轴强度试验规律,推荐五经验系数损伤比变量中的系数取值;2) 建议使用简化的围压三轴和二轴强度损伤比强度准则表达式的经验系数取值,并利用多种温度下AC-13沥青混合料围压三轴和二轴试验资料对简化准则进行验证;3) 利用沥青混合料损伤比强度准则解释车辙产生的力学机理,为预测荷载因素下流动性车辙的产生提供一种新思路。
1 损伤比强度理论
1.1 基本理论
1.1.1 基本假设
1) 应力作用时沥青混合料纵向总应变分解为非弹性应变与弹性应变,即
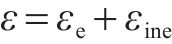
式中:ε、εe和εine分别为纵向总应变、弹性应变和非弹性应变。
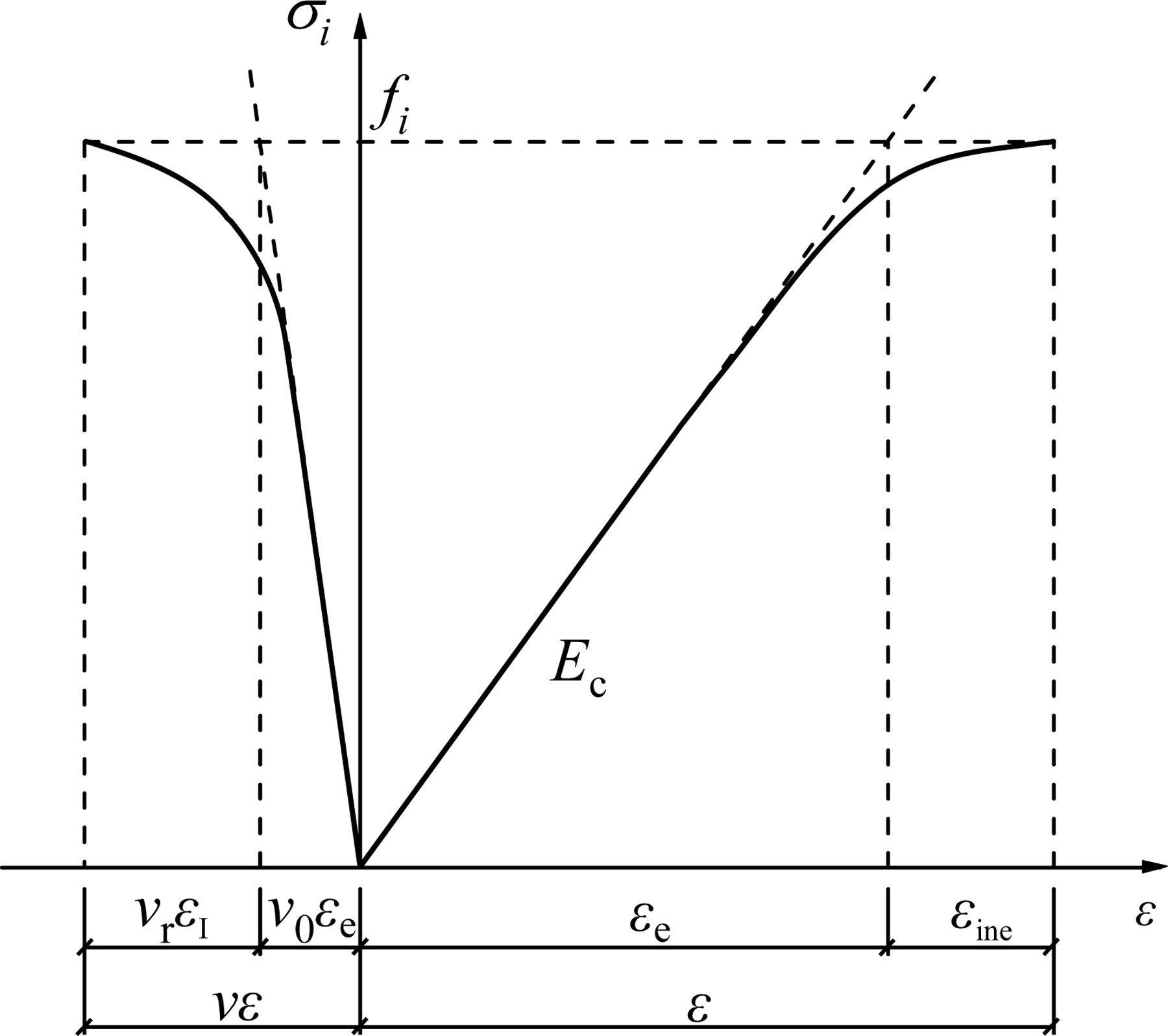
2) 沥青混合料横向总应变也分解为非弹性应变与弹性应变,且满足图1所表达的关系式:
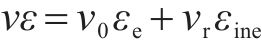
式中:v、v0和vr分别为横向变形系数、泊松比和损伤变形系数。
1.1.2 理论构建
丁发兴等[36]采用单元体相对耗能率求极值的计算模型,即单元体相对耗能率Ψ(t),将其表示为:
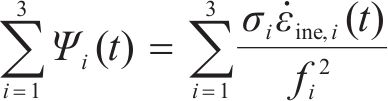
式中:Ψ(t)σi(i=1, 2, 3)为沥青混合料单元体名义主应力;fi(i=1, 2, 3)为沥青混合料单轴强度,当为压应力时fi=fc,为拉应力时fi=ft,fc和ft分别为单轴拉伸和压缩强度;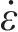
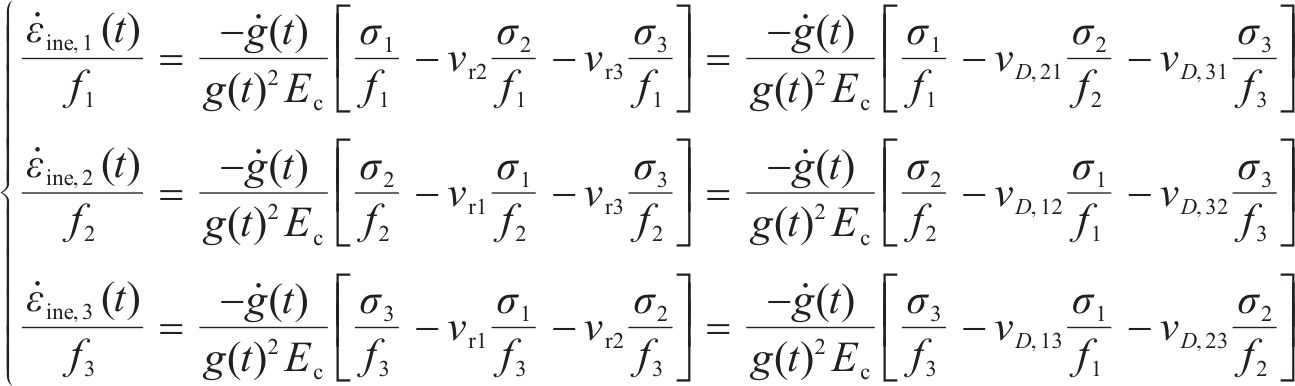
式中:g(t)为破坏过程t中割线模量与弹性模量之比;ġ(t)为g(t)对过程t的导数;vD,ij为i轴对j轴(i≠j)的损伤比,为:
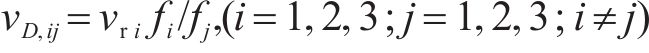
因强度理论是式(3)在破坏过程中满足的约束条件,根据材料单元体相对耗能率求极值的原理,经推导最终得到沥青混合料损伤比强度理论的通用表达式:
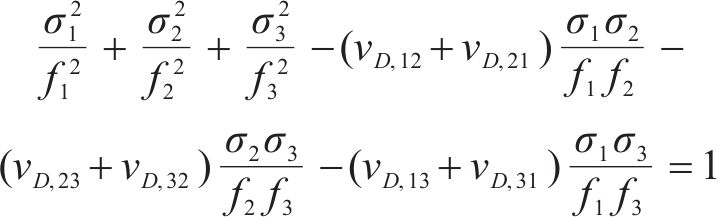
式中:损伤比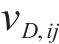
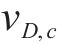
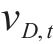
| 应力状态 | 主应力形式 |
|---|---|
| 三向拉伸 | 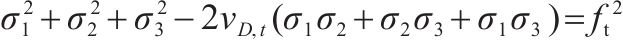 |
双向拉伸 一向压缩 |
|
一向拉伸 双向压缩 |
|
| 三向压缩 | 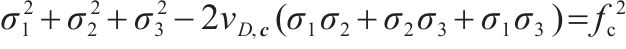 |
由于沥青混合料是各向同性脆性材料,其各主应力方向的损伤比取值相同且具有体积膨胀的失效规律,即某主应力方向为拉应力时,拉损伤比v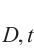
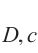
1.1.1 损伤比强度理论简化
针对围压三轴应力状态时,沥青混合料的损伤比强度理论可表示为:
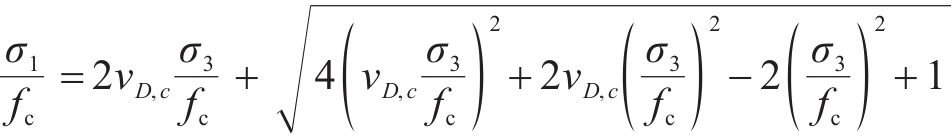
当沥青混合料处于围压三轴强度的弹塑性阶段时,此时压子午线上强度分布规律近似直线,围压三轴强度准则表达式[37]简化形式如下:
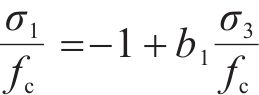
式中:b1称为侧压系数。
针对二轴应力状态,损伤比强度理论二轴形式的通用形式和简化形式见表2。表中c1~c4为经验系数,c1、c3和c4的取值与材料在单轴受拉损伤比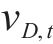
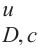
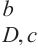
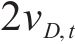
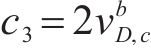
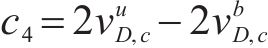
| 应力状态 | T/T | T/C | C/C |
|---|---|---|---|
| 通用形式 | 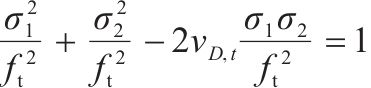 | 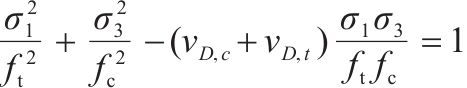 | 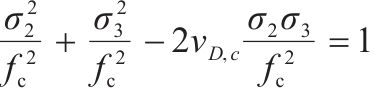 |
| 简化形式 | 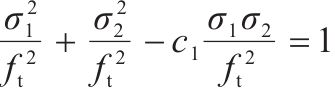 | 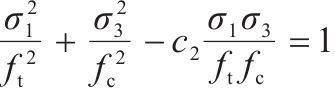 | 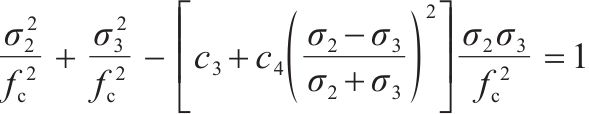 |
1.2 损伤比变量参数取值
三轴应力状态下沥青混合料的包络面特征与各向同性岩石基本一致,可采用其损伤比表达式[41],即:
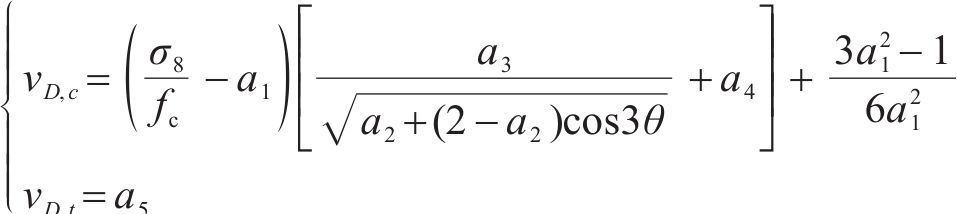
式中: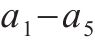
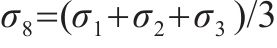
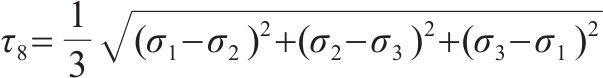
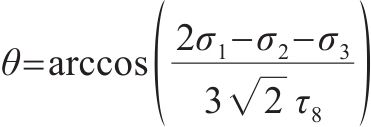
通过搜集多种温度下AC-13沥青混合料的三轴强度试验数据[19, 23, 31, 33],并将拉压子午线上八面体强度除以相应温度下的单轴抗压强度作无量纲处理,数据分布规律见图2。由图2可知,无量纲化后多种温度下AC-13沥青混合料的三轴强度分布规律基本一致。当然此规律仅针对本文中提到的AC-13沥青混合料试验数据,对于不同温度下AC-13或其他类型沥青混合料的强度规律还有待于深入研究。
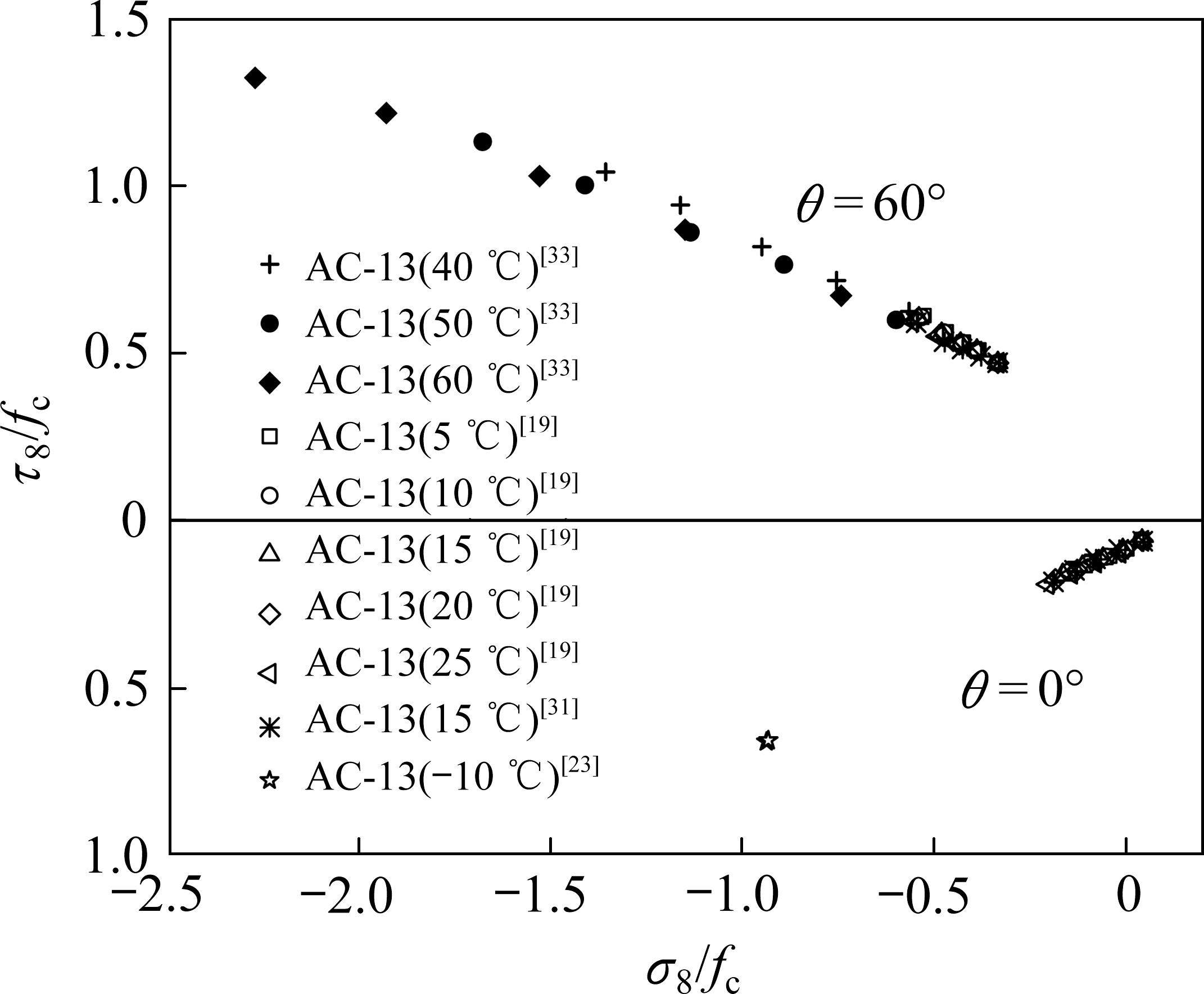
基于以上收集的沥青混合料试验数据,根据文献[41]提供的经验参数取值方法,损伤比变量式(9)中的5个经验系数取值建议分别为:ɑ1=-4, ɑ2=1.3, ɑ3=0.12, ɑ4=-0.004, ɑ5=0.1。由于缺乏沥青混合料的单轴拉伸纵、横向应力-应变曲线测试数据,受拉损伤比常量参数ɑ5取值暂参考轻骨料混凝土[36]。结合强度理论通用公式(式(6))和损伤比表达式(式(9)),可得到损伤比强度理论对应的沥青混合料三维破坏包络面,如图3所示,可见其包络面与轻骨料混凝土包络面[36]和岩石强度包络面[41]规律类似。
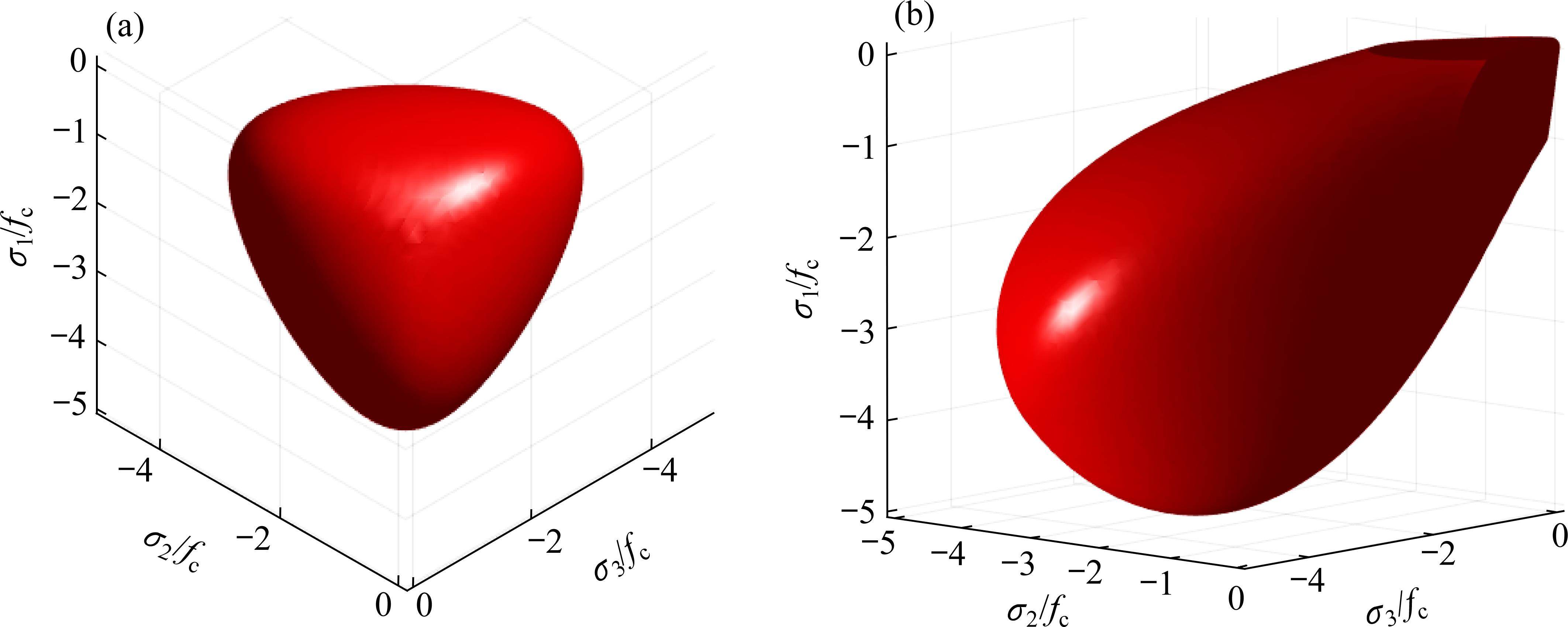
根据损伤比变量表达式,可获得典型应力状态下损伤比变量取值。本文建议的沥青混合料和文献[36]建议的轻骨料混凝土和普通混凝土的取值见表3。可见沥青混合料单轴受压损伤比取值介于轻骨料混凝土和普通混凝土之间,且双轴受压损伤比取值最大。当然单轴受压、双轴等压和三轴等压损伤比取值都为间接确定,仍需进一步的试验研究以直接确定。
| 材料 | 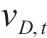 | 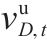 | 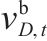 | 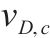 |
|---|---|---|---|---|
| 沥青混凝土 | 0.1 | 1.04 | 0.736 | 0.489 6 |
| 轻骨料混凝土 | 0.1 | 0.94 | 0.704 | 0.480 0 |
| 普通混凝土 | 0.15 | 1.09 | 0.694 | 0.499 8 |
2 强度准则验证与比较
2.1 真三轴强度准则
利用收集到的-10、5、10、15、20、25、40、50和60 ℃等温度下AC-13沥青混合料三轴强度数据[19, 23, 31, 33],与本文提出的强度理论预测值进行比较,本理论预测的破坏包络曲线变化规律与试验结果的比较见图4。从图中可看出:不同温度下AC-13沥青混合料无量纲化后的三轴强度变化规律无明显差别,且本理论预测的拉压子午线和偏平面与不同温度下AC-13沥青混合料三轴强度实测值变化规律都基本一致。
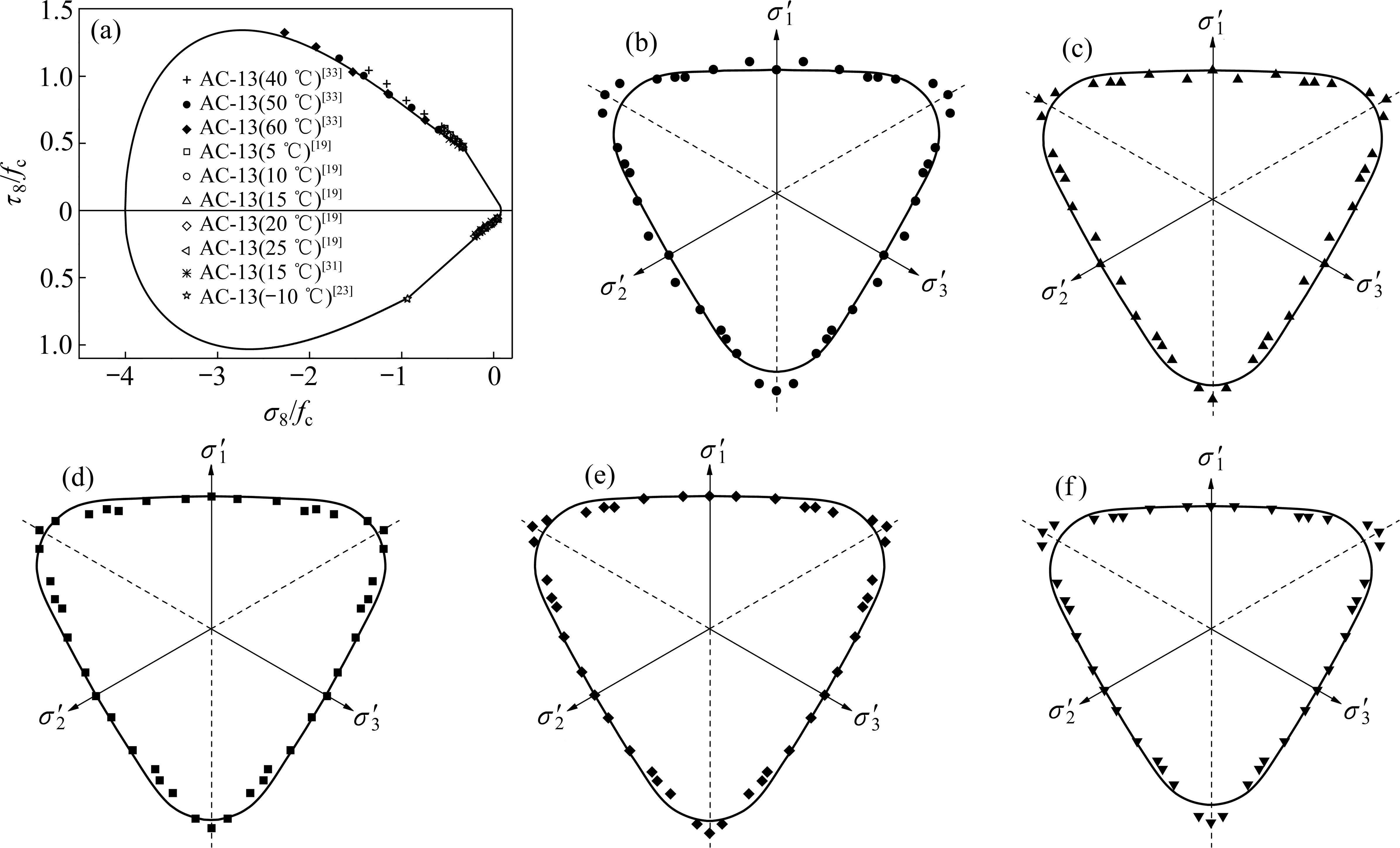
采用八面体剪应力值对本理论预测精度进行分析,比较结果见表4。可见当不同温度下的AC-13沥青混合料处于双轴受压一轴受拉状态时,本理论的预测精度相对较低,但整体上本理论对全部真三轴应力状态下的材料强度预测精度都较高。
| 应力状态 | 统计特征值 | 温度 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 5 ℃ | 10 ℃ | 15 ℃ | 20 ℃ | 25 ℃ | 40 ℃ | 50 ℃ | 60 ℃ | 5 ℃~60 ℃ | ||
| 三轴受压 | 均值 | 1.052 | 1.046 | 1.026 | 1.031 | 1.022 | 1.066 | 1.017 | 1.010 | 1.032 |
| 离散系数 | 0.033 | 0.029 | 0.025 | 0.020 | 0.014 | 0.029 | 0.013 | 0.013 | 0.029 | |
| 双轴受压一轴受拉 | 均值 | 0.957 | 0.943 | 0.918 | 0.940 | 0.948 | — | — | — | 0.937 |
| 离散系数 | 0.067 | 0.061 | 0.058 | 0.018 | 0.044 | — | — | — | 0.059 | |
| 双轴受拉一轴受压 | 均值 | 1.027 | 0.976 | 0.961 | 0.986 | 1.002 | — | — | — | 0.986 |
| 离散系数 | 0.053 | 0.053 | 0.050 | 0.045 | 0.058 | — | — | — | 0.057 | |
| 全部三轴应力 | 均值 | 1.014 | 0.987 | 0.968 | 0.985 | 0.992 | 1.066 | 1.017 | 1.010 | 0.993 |
| 离散系数 | 0.064 | 0.064 | 0.064 | 0.054 | 0.053 | 0.029 | 0.013 | 0.013 | 0.060 | |
2.2 围压三轴强度准则
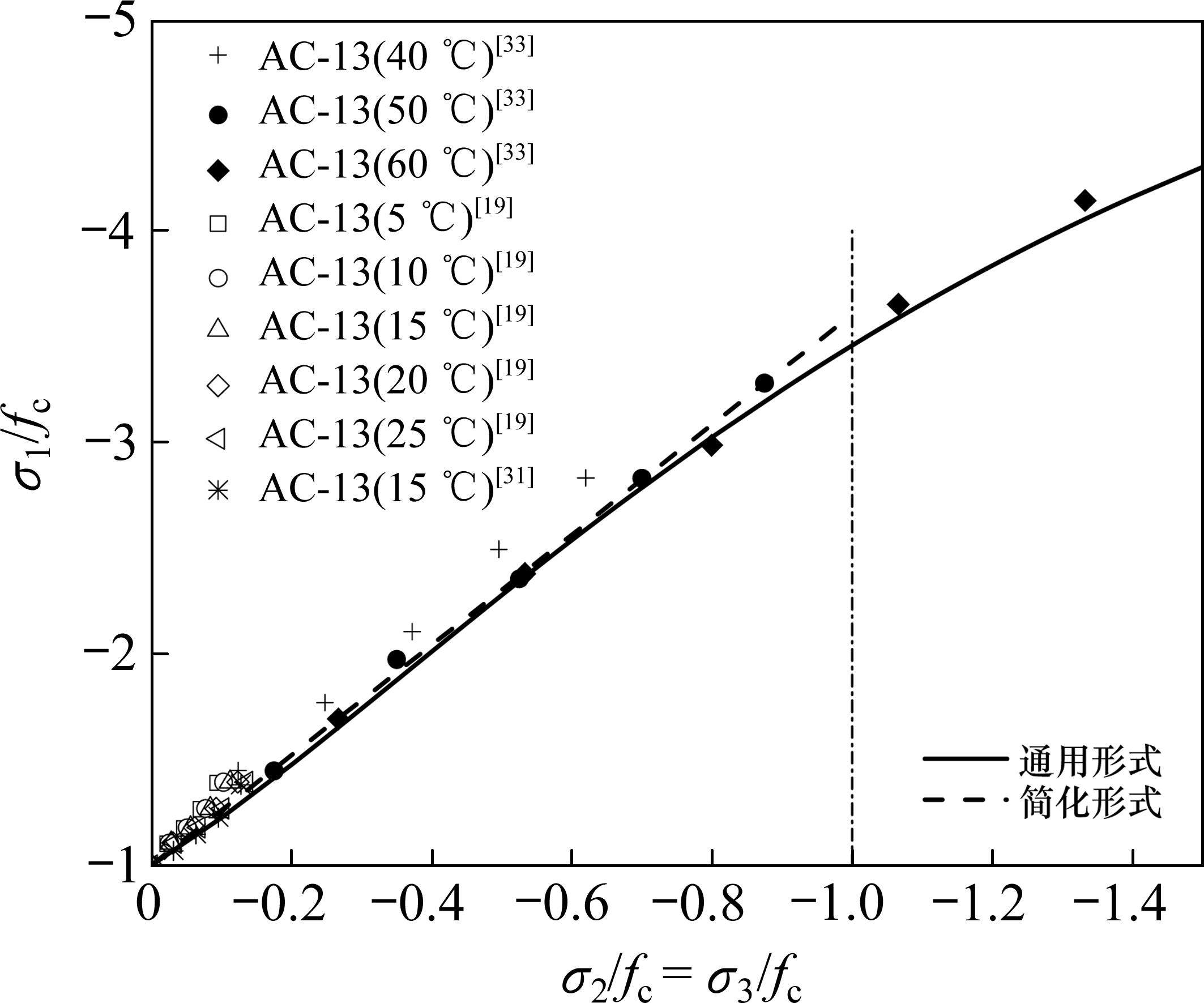
沥青混合料损伤比强度理论与围压三轴强度数据[19, 31, 33]的比较见图5(图中为“通用形式”),可见理论预测值与强度实测值符合良好。此外,当σ1/fc=σ2/fc >-1时,围压三轴强度的线性规律较明显。故针对-1≤σ1/fc=σ2/fc≤0应力范围,根据式(8)确定简化后的围压三轴损伤比强度理论的侧压系数为b1=2.6。对于轻骨料混凝土和普通混凝土,丁发兴等[37, 40]建议侧压系数分别为2.1和3.4,可见沥青混合料侧压系数在轻骨料混凝土和普通混凝土之间。简化后的围压强度理论所反映的直线见图5中的“简化形式”,其与“通用形式”基本一致。损伤比强度理论的“通用形式”和围压三轴时对应的“简化形式”预测结果与沥青混合料强度实测值(-1≤σ1/fc=σ2/fc≤0)比较的精度见表5,可见2类准则与各温度下AC-13沥青混合料相比计算精度都较高,整体“简化形式”准则的精度略高。
| 准则 | 统计特征值 | 温度 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 5 ℃ | 10 ℃ | 15 ℃ | 20 ℃ | 25 ℃ | 40 ℃ | 50 ℃ | 60 ℃ | 5 ℃~60 ℃ | ||
| 一般形式 | 均值 | 1.074 | 1.064 | 1.037 | 1.043 | 1.030 | 1.087 | 1.021 | 1.005 | 1.045 |
| 离散系数 | 0.040 | 0.040 | 0.035 | 0.027 | 0.019 | 0.038 | 0.168 | 0.013 | 0.040 | |
| 简化形式 | 均值 | 1.056 | 1.046 | 1.017 | 1.023 | 1.010 | 1.070 | 1.004 | 0.991 | 1.024 |
| 离散系数 | 0.037 | 0.031 | 0.028 | 0.017 | 0.011 | 0.030 | 0.013 | 0.013 | 0.035 | |
2.3 二轴强度准则
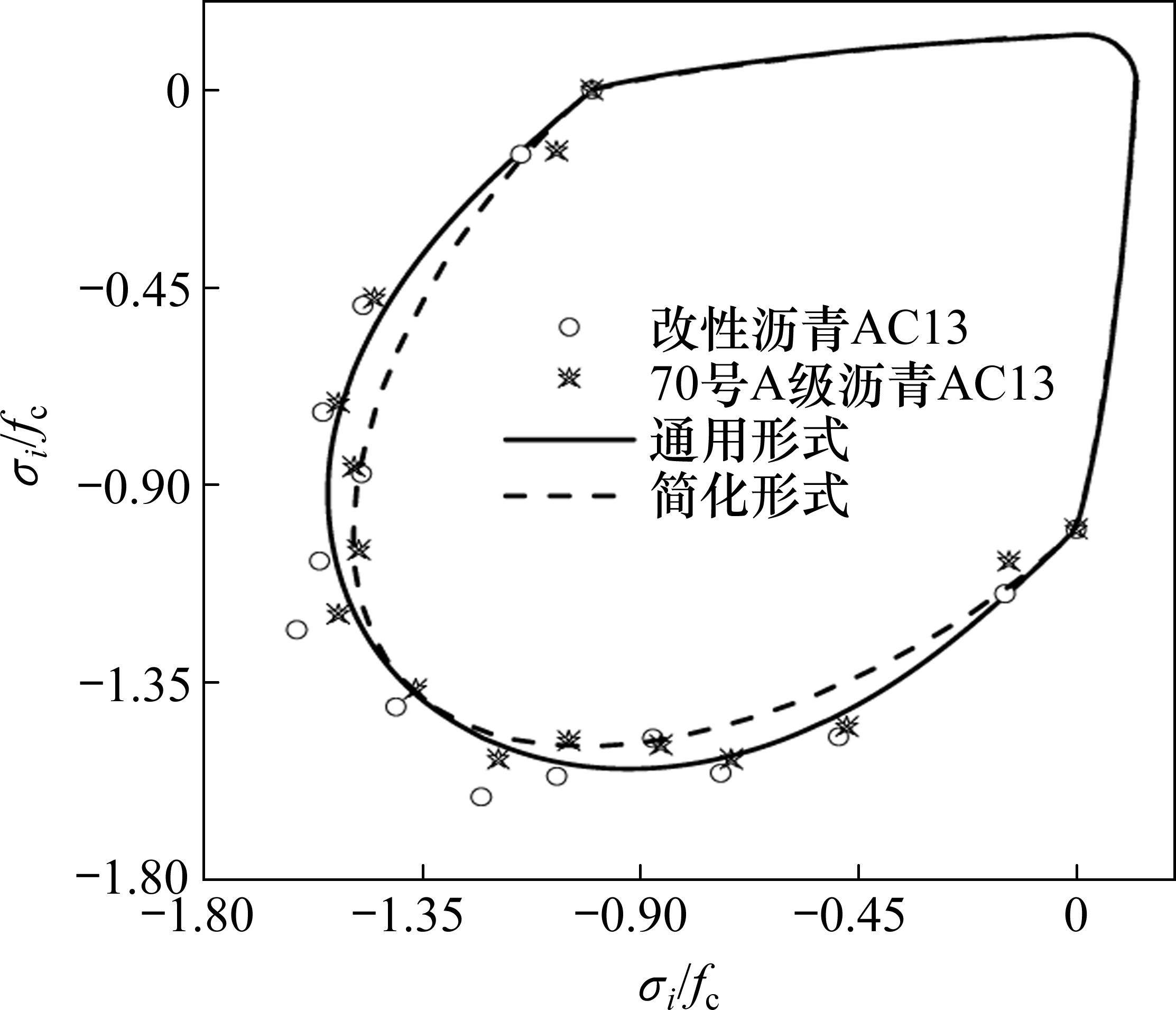
根据沥青混合料损伤比强度理论,可得AC-13沥青混合料二轴等压强度取值fcc=1.38fc。根据2.1.3节中简化二轴理论中经验系数c1~c4的取值方法,利用表3给出的典型应力状态下损伤比取值确定各经验系数c1~c4的取值为c1=0.2,c2=0.9,c3=1.472,c4=0.608。图6所示为沥青混合料损伤比强度理论“通用形式”和“简化形式”预测值与二轴强度实测结果[23]的比较,可见三者变化规律基本接近,其中通用形式与数据吻合更好,但简化形式更简单。
3 应用
根据沥青混合料损伤比强度理论,图7所示当子午线上八面体剪应力达到最大值时,沥青路面进入塑性流动破坏状态,也就是当沥青路面所受八面体正应力值σ8/fc小于-2.7,且八面体剪应力值位于破坏包络线以外时,此时沥青路面有可能产生车辙。
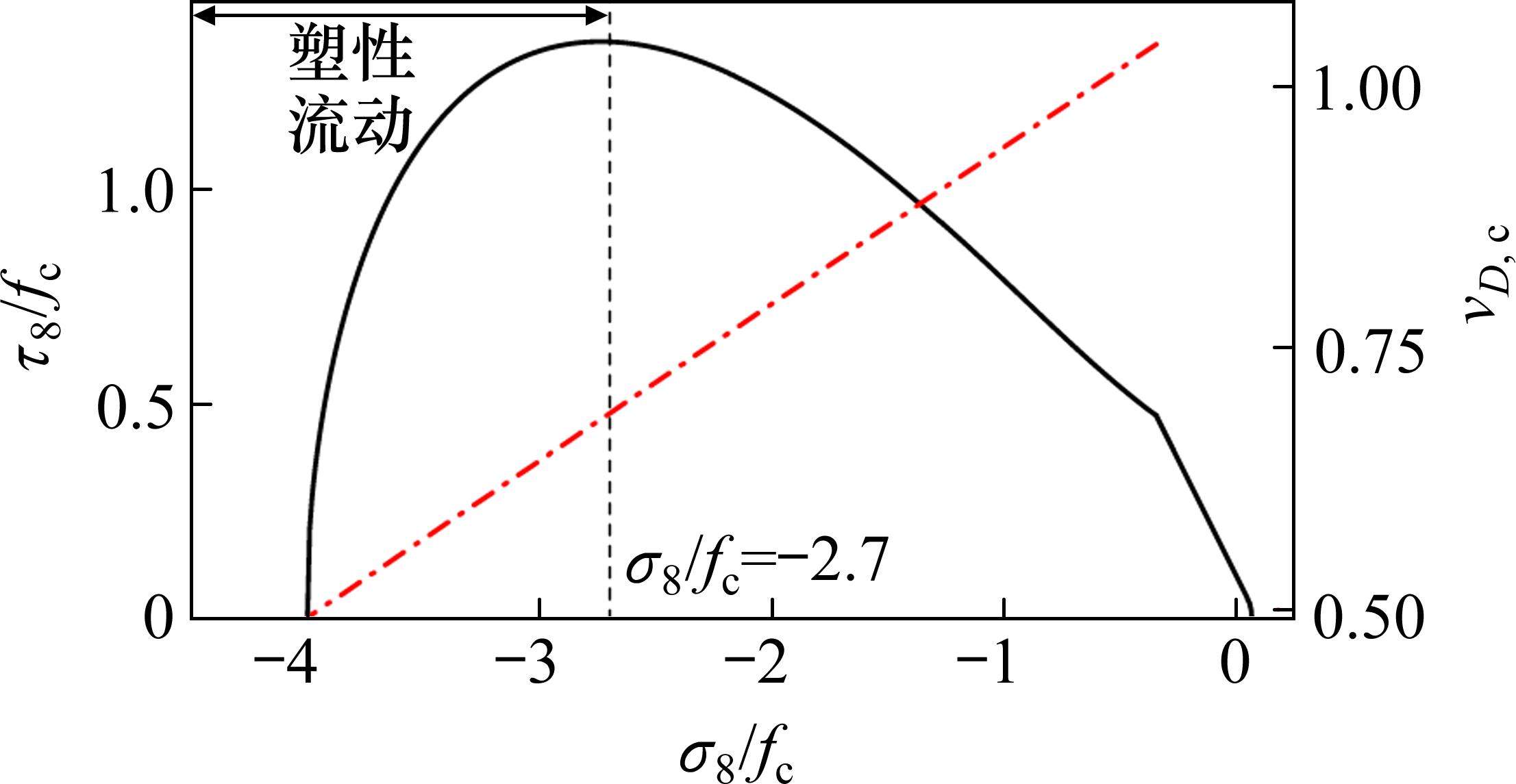
若以线弹性层状体系理论为基础计算结构层内部点的应力状态,可知车载作用下单圆荷载中心位置处道路表面的沥青所受3个主压应力大小几乎均等于轮胎对路面的压强,此时对应八面体剪应力值为0,沥青路面完全呈塑性流动状态。结合图7,对于单轴抗压强度仅为0.75 MPa的60 ℃环境温度下的AC-13沥青混合料[33],当路表单圆荷载中心位置的静水应力为-4fc时,即轮胎对路面作用的压强为3 MPa,对应八面体剪应力值为0,此时路面呈现流动性车辙。当考虑沥青路面结构的非线性行为时,可参照上述方法进一步提高预测车载作用下路面呈现车辙现象的准确性。若考虑疲劳荷载和外部环境作用对沥青路面强度的折减,则更易产生车辙。
4 结论
1) 推荐了沥青混合料损伤比变量五经验系数取值,形成沥青混合料损伤比强度理论,预测的不同温度下AC-13沥青混合料三轴强度变化规律与试验结果基本一致。
2) 推荐了围压三轴和二轴强度损伤比强度理论“简化形式”的经验系数取值,合理预测了不同温度下AC-13沥青混合料的围压三轴和二轴强度特性。
3) 沥青混合料损伤比强度理论揭示了大气高温时沥青路面单轴抗压强度降低,且车辆重载下沥青路面呈现塑性流动状态,导致路面出现车辙的现象。
吴霞,丁发兴,聂磊鑫.AC-13沥青混合料损伤比强度理论及车辙现象预测[J].铁道科学与工程学报,2025,22(01):172-180.
WU Xia,DING Faxing,NIE Leixin.Damage ratio strength theory and prediction of rutting phenomenon in AC-13 asphalt mixture[J].Journal of Railway Science and Engineering,2025,22(01):172-180.