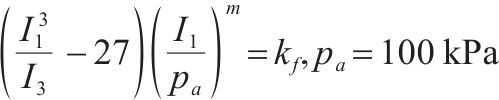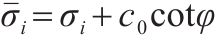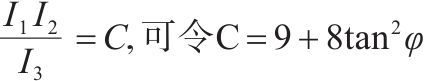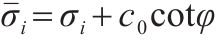土在自然界中广泛存在。黄土是在干旱气候条件下形成的特种土,为浅黄、灰黄或黄褐色,具有目视可见的大孔和垂直节理。我国西北的黄土高原是世界上规模最大的黄土高原,华北的黄土平原也是世界上规模最大的黄土平原,我国黄土总面积达63万km2,占全国土地面积的6%。水泥土主要包含水泥加固土和水泥稳定土两大类。水泥稳定土是指在经过粉碎的或原来松散的土中,掺入一定量的水泥和水,经拌和、压实和养生后得到的具有一定抗压强度的混合料,广泛应用于道路基层或底基层、浅基础持力层加固等方面。水泥加固土是指利用注浆法、深层搅拌法和高压旋喷法等将水泥浆液(或水泥粉)同土体原位拌和所形成的固结体,常用于软弱地基处理[1]。黄土和水泥土都属于黏聚摩擦材料。各类交通工程与建筑工程都与土密切相关,在基坑、边坡和隧道处的土体往往处于真三轴应力状态[2]。土的真三轴强度预测是工程界关注的焦点[3-5],众多学者针对岩土材料提出各种强度准则[6-11]。在经验型强度准则方面,Mohr-Coulomb单剪准则[12]是岩土材料应用最广泛的强度准则之一[13],但是其没有考虑中间主应力对材料强度的影响,不适用于真三轴强度预测。俞茂宏等建立了双剪强度理论[14],并将其应用于各类岩土类材料。MATSUOKA等[15]通过在主应力中增加“边界应力σ0”,将适用于砂土等无黏聚力颗粒材料的SMP准则改进为适用于黏聚摩擦材料的广义SMP准则。Lade-Duncan准则[16]是常用的无黏聚力土强度准则,随后LADE提出改进的非线性Lade强度准则[17],但依旧仅适用于无黏聚力土。参照广义SMP准则方法,也可通过增加“边界应力σ0”将Lade强度准则[17]推广至黏聚摩擦材料。在理论型强度准则方面,丁发兴等[18]提出材料单元体相对耗能率模型以反映混凝土和岩石等脆性材料表现出的抗压和抗拉强度差异很大的特性,提出了描述材料破坏的损伤比参数,构建了损伤比强度理论。2021年,丁发兴等[18]进一步提出考虑静水应力(也就是平均主应力)和Lode角影响的六经验系数损伤比表达式,并应用于各向同性岩石和多类混凝土的三轴强度预测[18-20]。随后吴霞等[21]将六经验系数损伤比表达式完善为五经验系数损伤比表达式,此时对应的拉压子午线与静水应力轴相交于同一点,展现了完整闭合的岩石强度包络面,此外该理论也适用于正交各向异性金属的二轴强度预测[22]。目前损伤比强度理论已经应用于多类混凝土和岩石等黏聚摩擦材料的三轴强度预测,并表现出较高的预测精度,由于黄土和水泥土也属于黏聚摩擦材料,为统一各种受力材料的强度理论,本文将损伤比强度理论进一步应用于原状黄土和水泥土,主要工作如下:1) 根据原状黄土和水泥土的真三轴强度规律,推荐损伤比变量中的5个经验系数取值,应用损伤比强度理论合理预测原状黄土和水泥土的三轴强度发展规律;2) 对原状黄土和水泥土损伤比强度理论与常用几类土强度准则进行比较分析,探讨其预测精度;3) 根据黄土损伤比强度理论预测自重下地表黄土的塑性流动深度。
1 损伤比强度理论
1.1 基本假设
在小变形条件下,应力作用下原状黄土和水泥土的纵向总应变和横向总应变都可分解为弹性应变与非弹性应变2部分,即
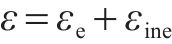
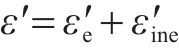
式中:ε为纵向总应变;εe为纵向弹性应变;εine为纵向非弹性应变;ε′为横向总应变;ε′e为横向弹性应变;ε′ine为横向非弹性应变。其中ε′、ε′e和ε′ine分别表示为
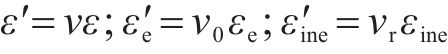
式中:v为横向变形系数;v0为泊松比;vr为损伤变形系数。图1所示为上述基本假设下的土体应变分解示意图。
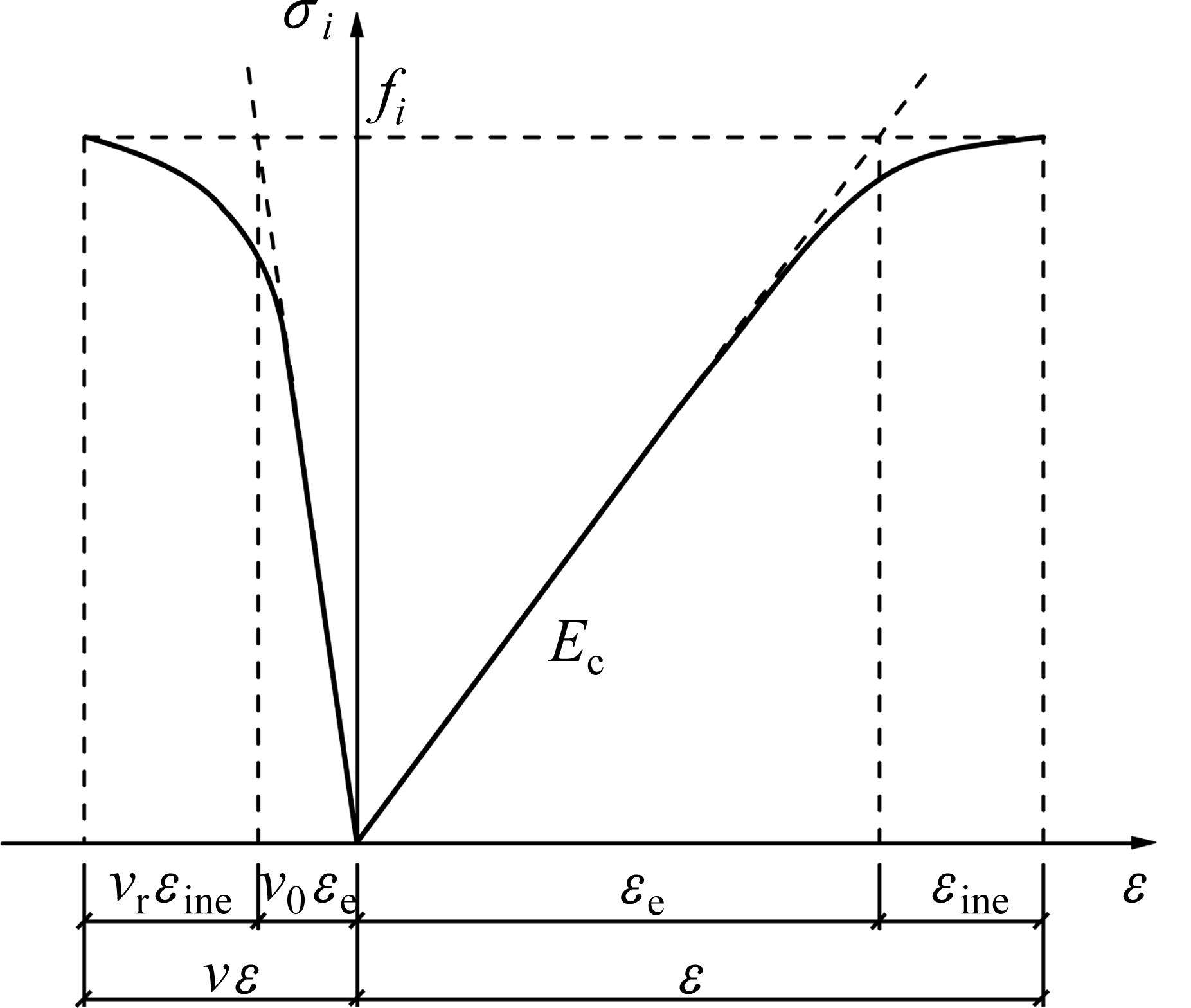
1.2 理论构建
将土体在荷载作用下引起的非弹性主应变视为破坏过程中主要耗能机制,丁发兴等[18]提出采用单元体相对耗能率的计算模型,该模型表示为
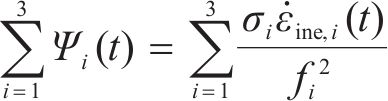
式中:Ψ(t)为t时刻单元体相对耗能率;σi(i=1, 2, 3)为破坏开始时单元体名义主应力;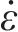
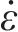
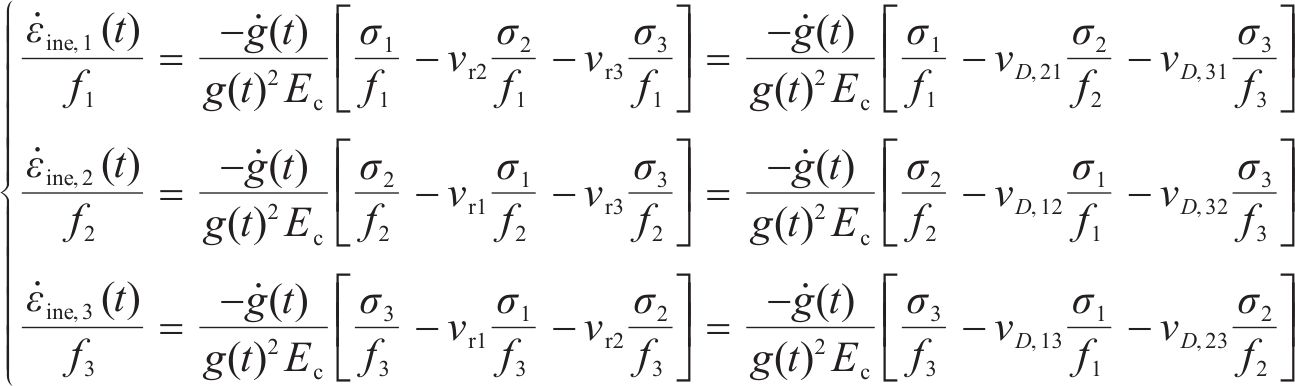
式中:g(t)为破坏过程t中原状黄土和水泥土割线模量与弹性模量之比,ġ(t)为g(t)对t的导数;vD,ij为i轴对j轴(i≠j)的损伤比参数,其值表示为
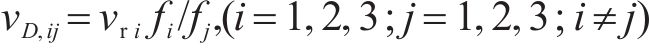
因强度理论是式(4)在破坏过程中必须满足的约束条件,经推导最终得到原状黄土和水泥土损伤比强度理论的通用表达式:
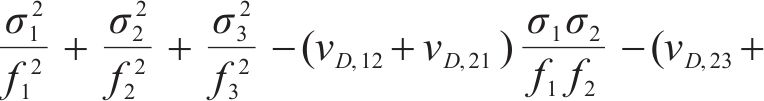
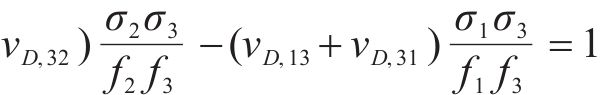
本文假定原状黄土和水泥土具有各向同性的特性,其损伤比也可直接简化表示为拉、压损伤比,其中v
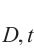
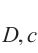
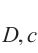
此外,对于原状黄土和水泥土,一般采用平均主应力p和广义剪应力q表示应力状态,主应力与平均主应力p和广义剪应力q的转换关系如下:
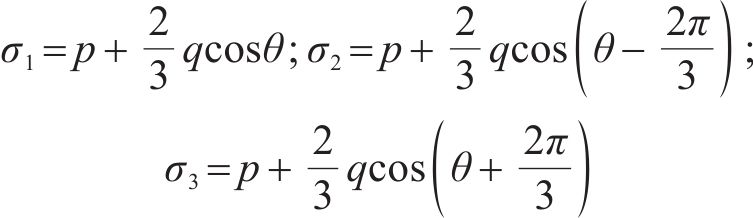
不同三轴应力状态下该类土体损伤比强度理论的广义应力和主应力形式见表1。岩土工程中常用的黏聚力c0和内摩擦角φ等强度参数可用单轴拉伸强度ft和单轴压缩强度fc表示[14],其关系式如下
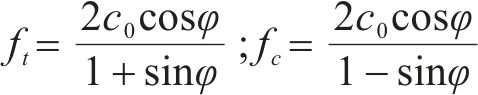
收集的原状黄土[11, 23]和水泥土[24-25]强度参数见表2,其中水泥土1和水泥土2[23]由水、水泥、砂和高岭土组成,水泥土3[25]由水、水泥和砂组成,更多详细介绍请查阅原文献。根据式(9)所示的关系式,可得到原状黄土和水泥土的单轴拉伸和压缩强度取值,见表2。
| 应力状态 | 主应力形式 | 广义应力形式 |
|---|---|---|
| 三轴受拉 | 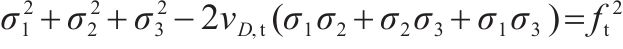 | 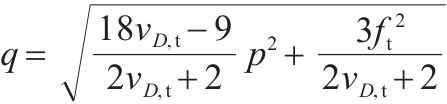 |
| 二轴受拉一轴受压 | 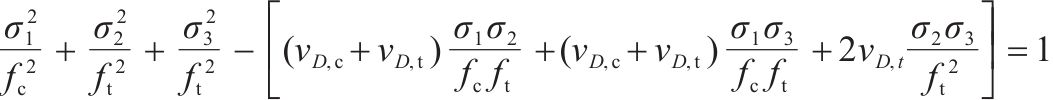 | 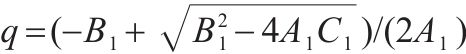 |
| 一轴受拉二轴受压 | 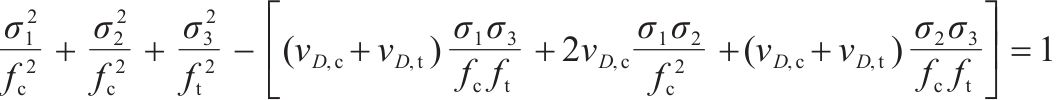 | 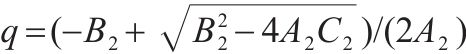 |
| 三轴受压 | 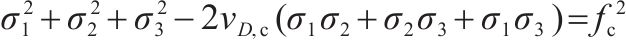 | 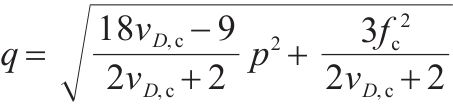 |
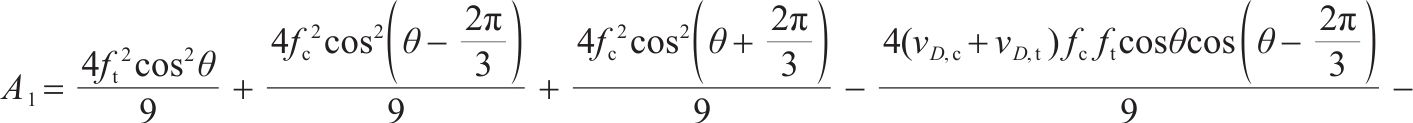
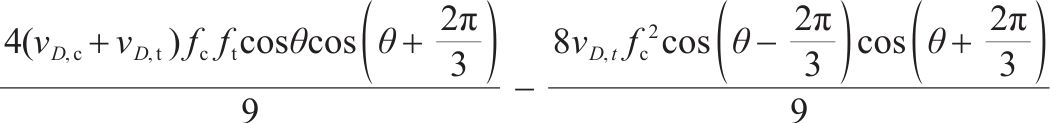
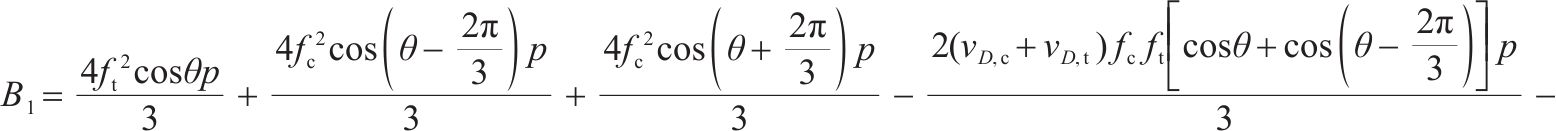
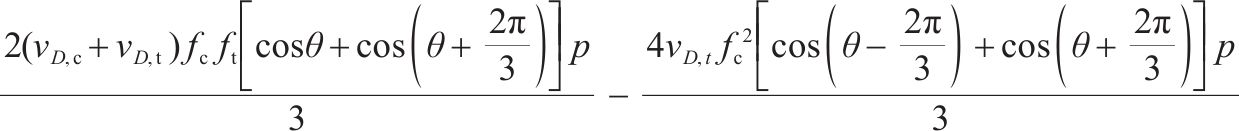
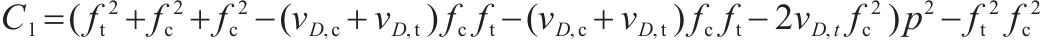
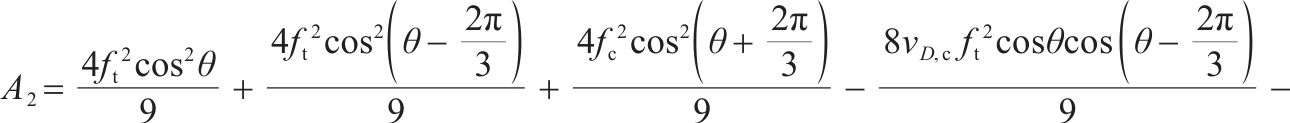
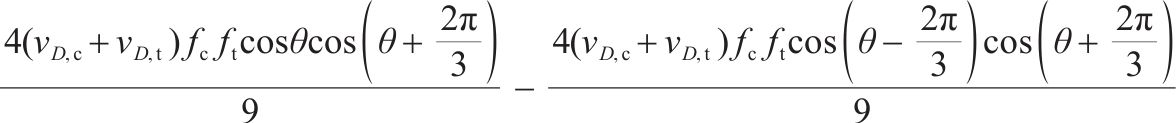
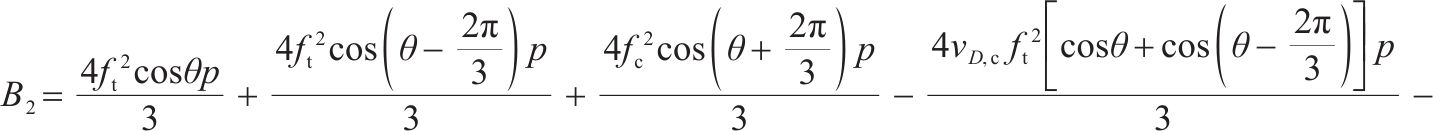
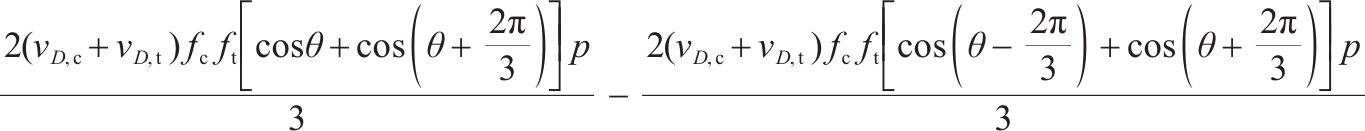
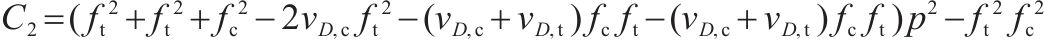
1.3 损伤比变量
参考岩石损伤比变量数学表达式[21],针对原状黄土和水泥土等黏聚摩擦材料的强度包络面特征,仍然采用相同的3个假设,即:1) 三轴受压应力状态下土体材料的偏平面光滑且外凸;2) 高平均主压应力下土体强度包络面的受压端因呈现塑性流动而闭合,并与平均主压应力轴相交于a1点;3) 相同Lode角时土体的受压损伤比取值随平均主压应力的增大而单调递减,且逐渐收敛至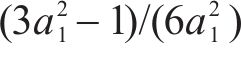
本文规定受压应力为正、受拉应力为负,以Lode角θ = 60°时(σ1=σ2≥σ3)为拉子午线,θ=0°时(σ1≥σ2=σ3)为压子午线。上述3个基本假设下,仍然采用与岩石相同的损伤比表达式[21]:
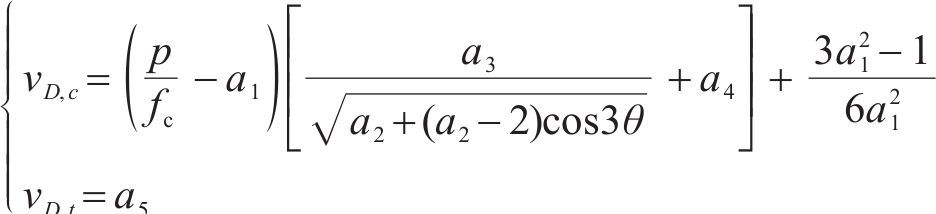
式中:a1-a5为经验系数;p=(σ1+σ2+σ3)/3;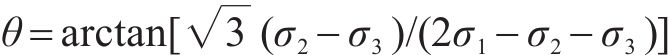
由式(1)可见:1) 受压损伤比参数用4个参数来反映随平均主应力和Lode角θ的影响,而拉损伤比仍为常数。2) 受压损伤比反映子午线与平均主应力轴压端相交于a1,且受压损伤比收敛于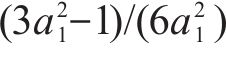
| 材料类型 | ɑ1 | ɑ2 | ɑ3 | ɑ4 | ɑ5 |
|---|---|---|---|---|---|
| 西安月登阁车站原状黄土 | 9.5 | 1.40 | -0.031 | 0.006 | 0.1 |
| 西安白鹿原原状黄土 | 16.0 | 1.50 | -0.035 | 0.003 | 0.1 |
| 水泥土 | 18.0 | 1.25 | -0.035 | 0.004 | 0.1 |
| 材料 | v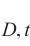  | v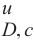 | v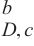 | v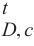 |
|---|---|---|---|---|
| 西安月登阁车站原状黄土 | 0.1 | 0.761 | 0.637 | 0.498 2 |
| 西安白鹿原原状黄土 | 0.1 | 1.000 | 0.823 | 0.499 3 |
| 水泥土 | 0.1 | 1.303 | 0.848 | 0.499 5 |
2 验证与比较
表3 所示五经验系数推荐值下各材料损伤比强度理论对应的三维强度包络数学曲面如图2 所示,可见在三轴受压区,原状黄土和水泥土强度包络数学曲面光滑且外凸。
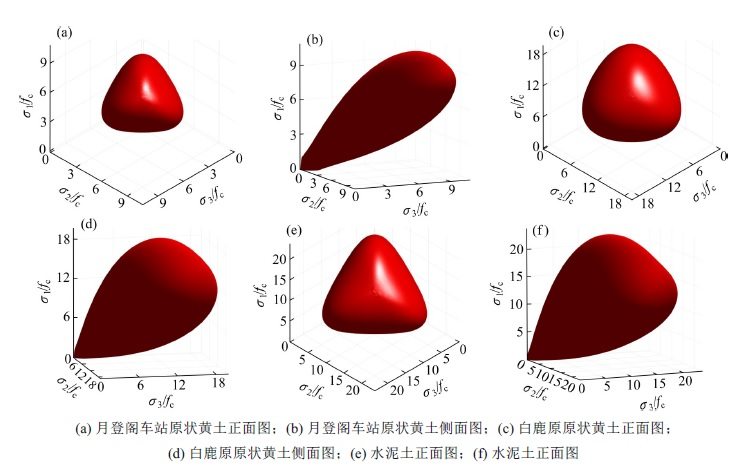
2.1 损伤比强度理论与数据比较
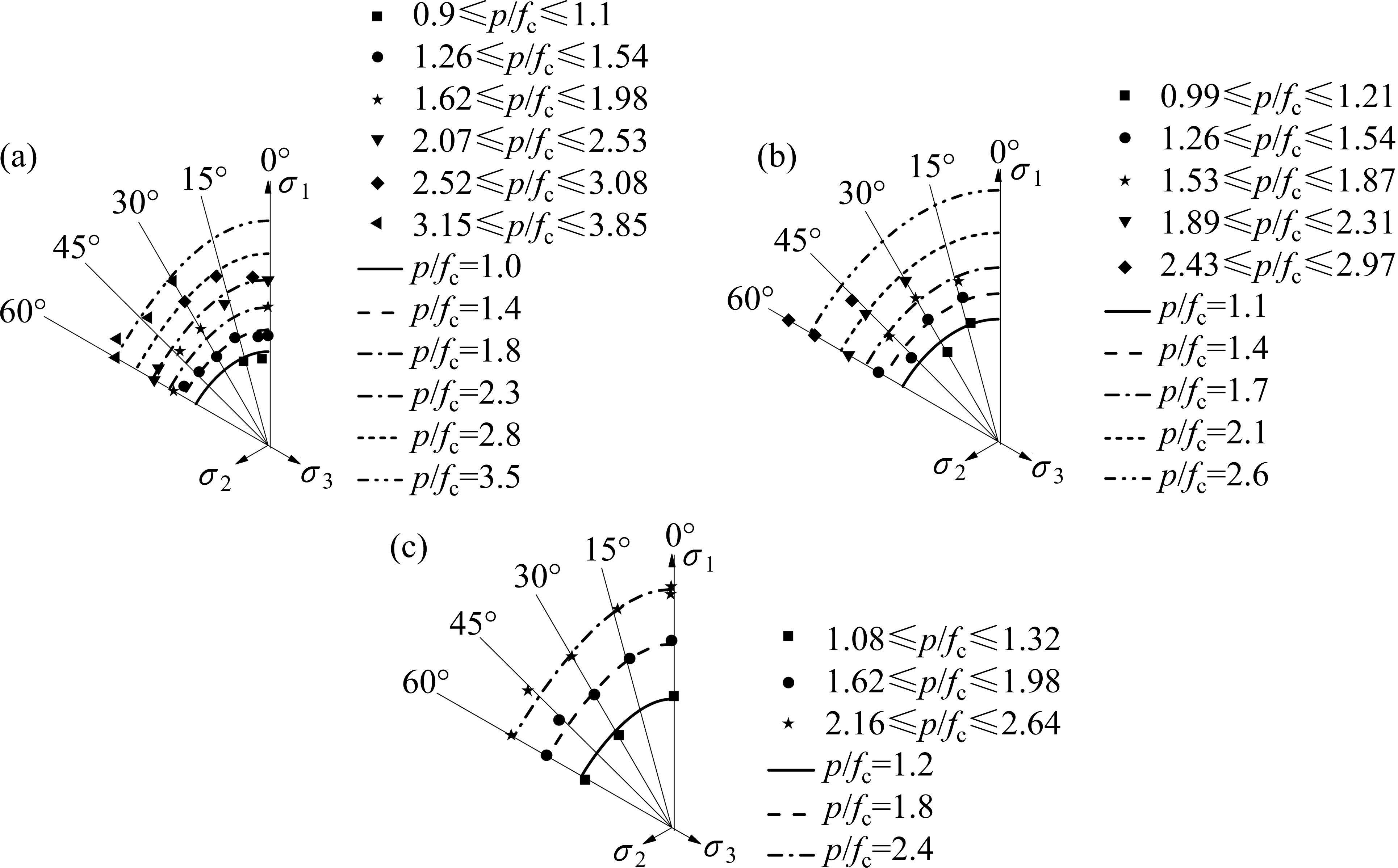
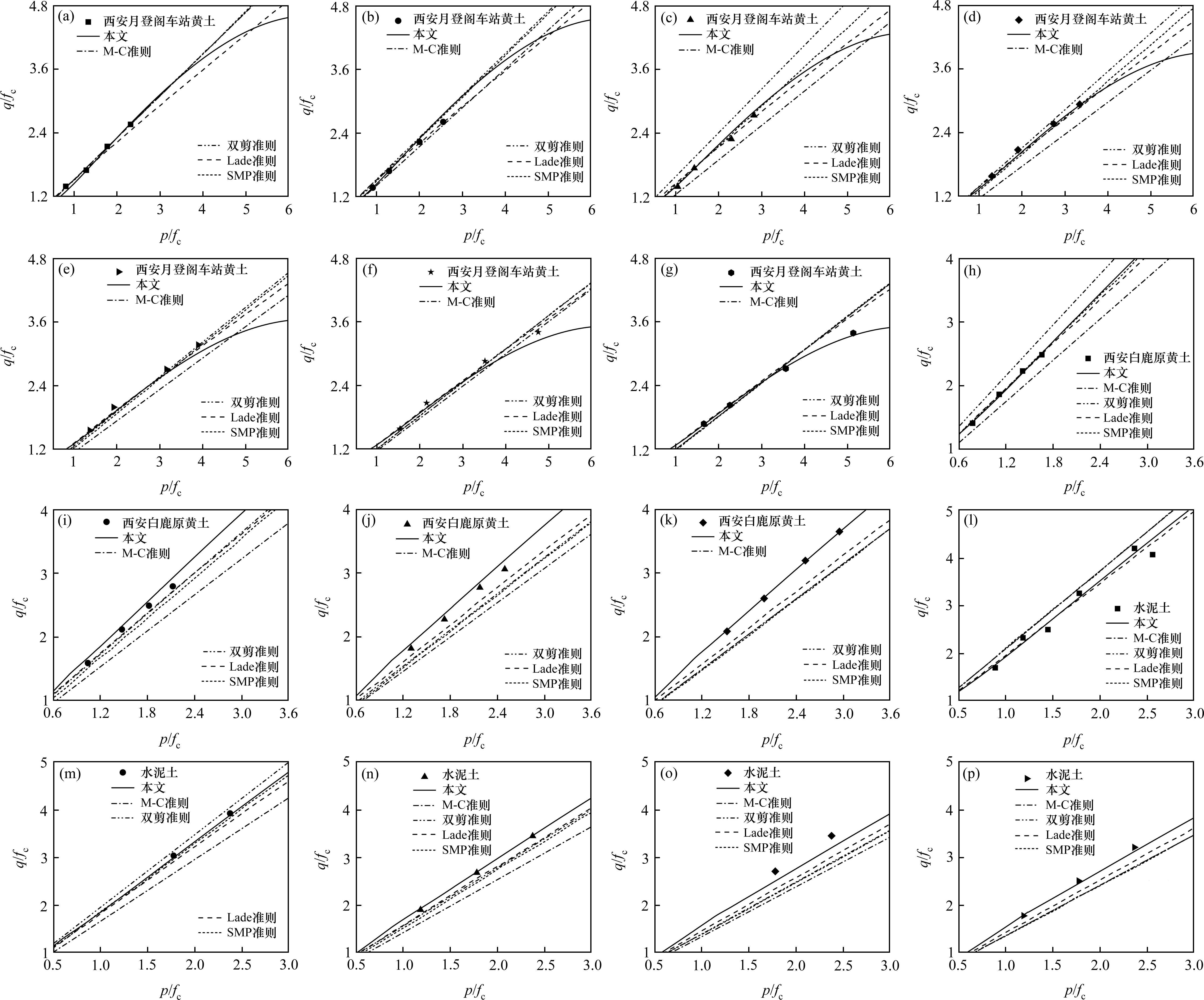
损伤比强度理论对应的拉压子午线、不同Lode角下的子午线和不同平均主应力下的偏平面强度变化规律与黄土[11, 23]和水泥土[24-25]试验数据比较见图3、图4和图5,由图3~5可知:
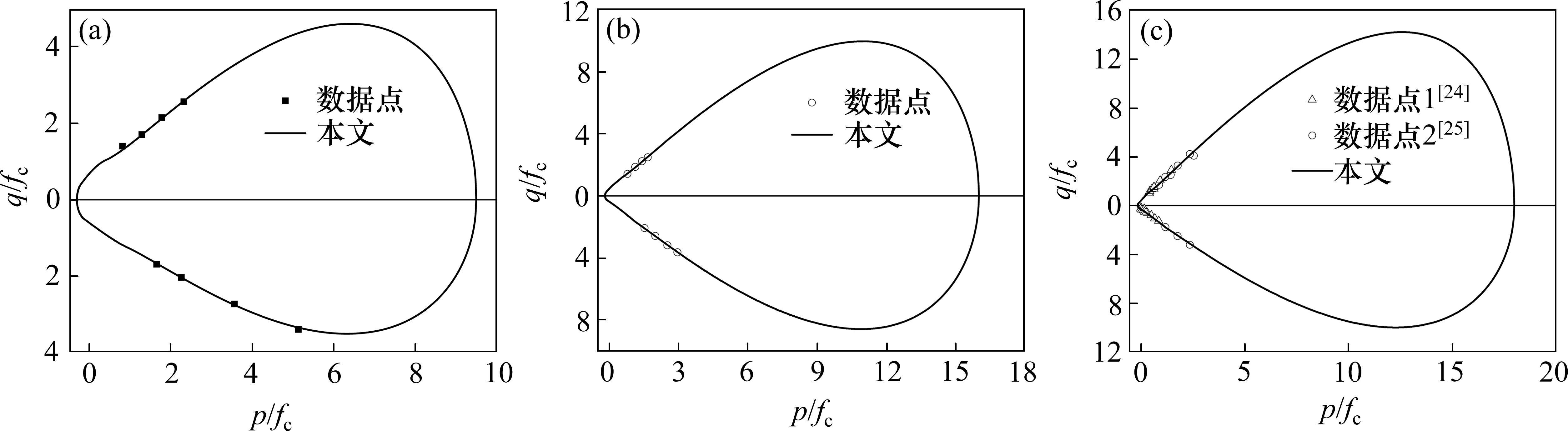
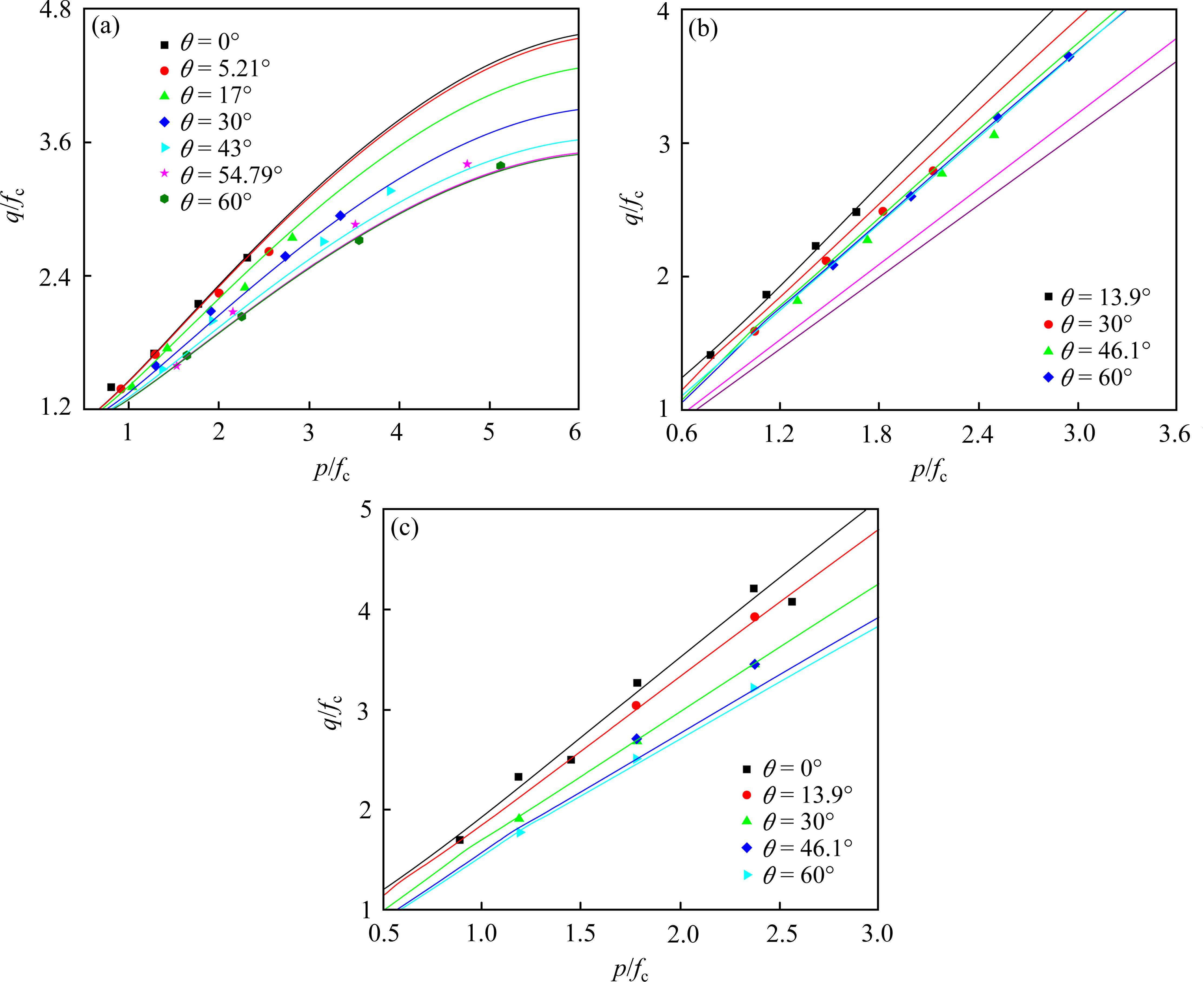
1) 损伤比强度理论所示的拉压子午线在低平均主压应力时与试验数据吻合良好,并在高平均主压应力时相交。
2) 损伤比强度理论预测的破坏包络曲线,如不同Lode角对应的子午线和不同平均主应力下的偏平面,都与原状黄土和水泥土强度实测值变化规律基本一致,能反映其真三轴强度特性。
对于三轴应力状态,采用广义剪应力值对准则进行比较,比较时采用试验值除以预测值,各类土计算精度比较结果见表5。可见对于各类黄土和水泥土,损伤比强度理论的预测精度良好,表明损伤比强度理论适用于黄土和水泥土等黏聚摩擦材料。
| 统计结果 | 西安月登阁车站原状黄土 | 西安白鹿原原状黄土 | 水泥土1 | 水泥土2 | 水泥土3 | 所有材料 |
|---|---|---|---|---|---|---|
| 均值 | 1.011 | 0.981 | 0.970 | 1.040 | 1.009 | 1.004 |
| 离散系数 | 0.031 | 0.022 | 0.130 | 0.064 | 0.041 | 0.060 |
2.2 各理论比较
利用土常用强度理论,如Mohr-Coulomb单剪准则[12]、双剪准则[14]、Lade准则[17]和广义SMP准则[15]与五经验系数下原状黄土和水泥土损伤比强度理论进行比较分析。各准则的表达式、参数数量及参数确定方法见表6。各强度准则所对应的子午线和偏平面变化规律与试验数据的比较如图6和图7所示,由图6~7可见:
| 分类 | 强度 准则 | 表达式 | 参数数量 | 参数确定 |
|---|---|---|---|---|
| 单剪 | M-C 准则 | 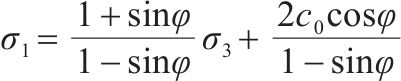 | 2 | 黏聚力c0,内摩擦角φ。 |
| 双剪 | 双剪 准则 | 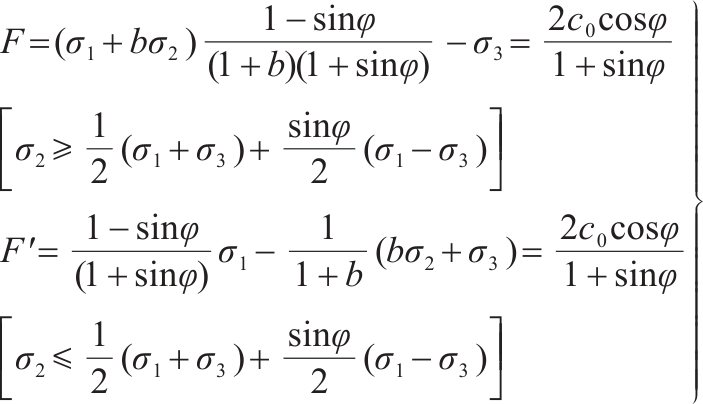 | 3 | 黏聚力c0,内摩擦角φ,b反映中间主切应力以及相应面上正应力对材料破坏程度,本文取1。 |
| 三剪 | Lade准则 |
考虑土的黏聚力,转换应力为:
| 4 | 黏聚力c0,内摩擦角φ,m和kf由最小二乘法确定:西安月登阁车站原状黄土:kf =100.913、m =0.187; 西安白鹿原原状黄土:kf =101.35、m=0.09; 水泥土:kf =101.5、m=0.049。 |
| 三剪 | 广义SMP 准则 |
考虑土的黏聚力,转换应力为:
| 2 | 黏聚力c0,内摩擦角φ。 |
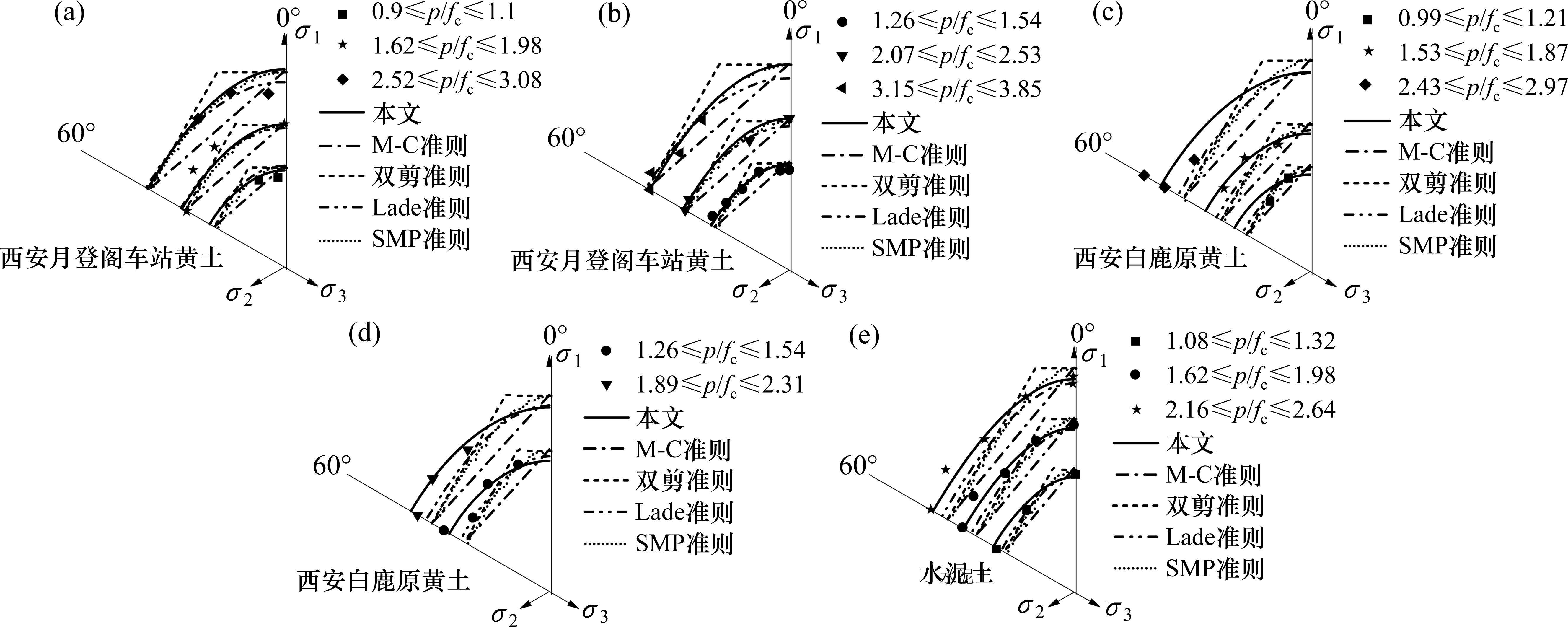
1) Mohr-Coulomb单剪准则没有考虑中间主应力影响,预测西安白鹿原原状黄土和水泥土真三轴强度时,理论结果明显偏于保守;双剪准则、Lade准则和广义SMP准则与西安月登阁车站原状黄土试验数据整体吻合良好,但由于准则参数较少,预测西安白鹿原原状黄土和水泥土的三轴强度时也偏于保守。
2) 仅损伤比强度理论所示的各子午线与平均主应力轴压端相交,预测的黄土和水泥土具有弹脆性、弹塑性和塑性流动3种状态,而其余准则的子午线压端都开口,预测的黄土和水泥土具有弹脆性和弹塑性2种状态,认为三轴等压下黄土不会发生破坏,因而它们难以反映三轴等压应力状态下土的塑性流动特征。
3) 整体上,建议的损伤比强度理论与西安月登阁车站原状黄土、西安白鹿原原状黄土和水泥土3类土都吻合较好。
各准则精度比较结果见表7,结果表明:Lade准则在预测西安月登阁车站原状黄土三轴强度时精度最高,而损伤比强度理论在预测西安白鹿原原状黄土和水泥土三轴强度时精度最高。
| 材料 | 本文 | MC准则 | 双剪准则 | Lade准则 | 广义SMP准则 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| 均值 | 离散系数 | 均值 | 离散系数 | 均值 | 离散系数 | 均值 | 离散系数 | 均值 | 离散系数 | |
| 西安月登阁车站原状黄土 | 1.011 | 0.031 | 1.069 | 0.069 | 0.978 | 0.058 | 1.000 | 0.034 | 1.027 | 0.123 |
| 西安白鹿原原状黄土 | 0.981 | 0.022 | 1.158 | 0.025 | 1.057 | 0.096 | 1.053 | 0.046 | 1.087 | 0.064 |
| 水泥土 | 1.009 | 0.041 | 1.082 | 0.114 | 1.033 | 0.104 | 1.049 | 0.058 | 1.045 | 0.102 |
3 应用
根据损伤比强度理论,当子午线上广义剪应力值达到最大时,材料开始进入塑性流动状态,即内部材料在三向压力下发生塑性流动,此时压缩变形很大。如图8所示,当西安月登阁车站原状黄土和西安白鹿原原状黄土所受平均主应力值p/fc分别大于6.4和10.0,且广义剪应力值位于破坏包络线以外时,开始进入塑性流动状态。在地表修建高铁、高速公路等工程时,摩擦桩本身可以做到稳定承载,但因更深处土体可能将处于塑性流动而压缩变形很大,导致基础持力层发生了破坏,从而地表出现不均匀沉降。
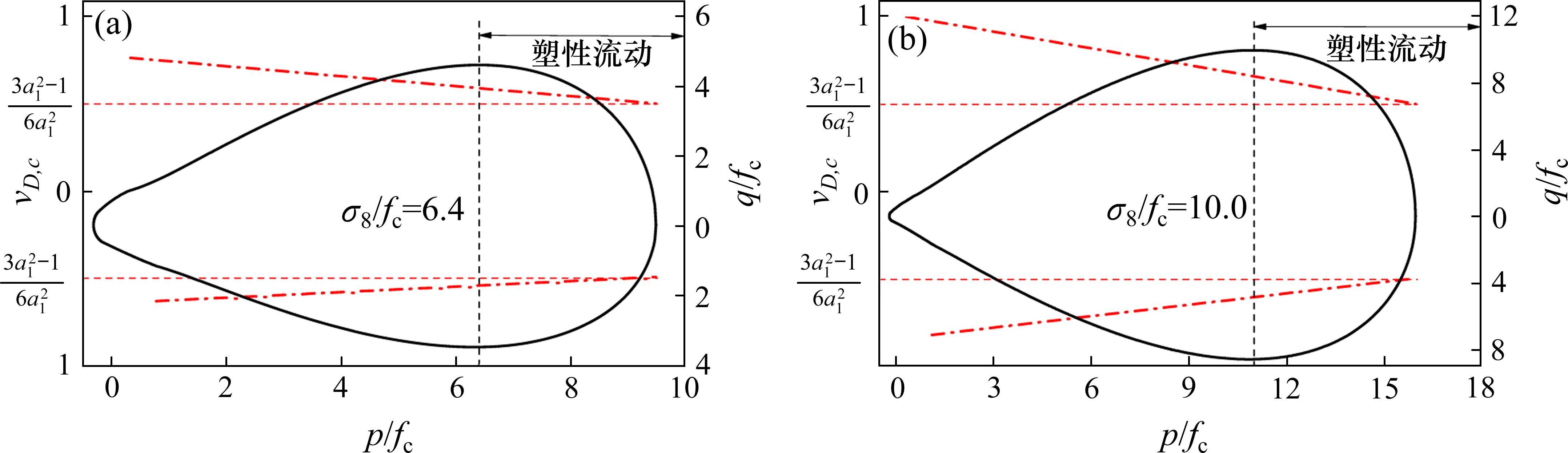
假设当地表黄土处于某一临界深度时,自重作用下黄土将处于塑性流动状态,此时对应的地表深度定义为塑性流动深度,该深度可由损伤比强度理论进行预测。假定地表深处的黄土处于三轴等压应力状态(σ1=σ2=σ3),若此时黄土处于塑性流动临界状态,则有p=σ1=σ2=σ3=a1fc,此处黄土所受自重应力为
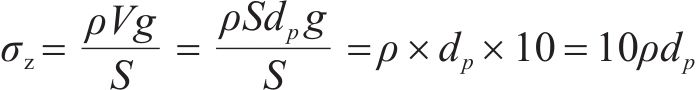
式中:dp为自重下黄土塑性流动深度,m;ρ为黄土天然密度,g/cm3。当仅考虑自重引起的应力时,有
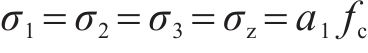
结合式(11)和式(12),可得重力作用下黄土处于塑性流动时的深度计算公式为
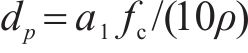
根据式(13),可得地表2类原状黄土的塑性流动深度见表8。由表8可知,西安月登阁车站原状黄土和西安白鹿原原状黄土的塑性流动深度分别为75 m和367 m。考虑到地表黄土类型较多,其实际密度和单轴抗压强度都存在一定的差异,各类黄土的实际塑性流动深度也略有差异,即便如此,损伤比强度理论预测结果仍具有一定的参考价值。
| 统计结果 | a1 | 单轴强度/kPa | 天然密度/(g∙cm-3) | 塑性流动 深度/m |
|---|---|---|---|---|
| 西安月登阁车站原状黄土 | 9.5 | 136 | 1.73 | 75 |
西安白鹿原 原状黄土 | 16.0 | 390 | 1.70 | 367 |
4 结论
1) 结合损伤比变量表达式,推荐了损伤比变量表达式中的五经验系数取值,相应损伤比强度准则所对应的原状黄土和水泥土三轴受压偏平面曲线光滑,三维包络面压端闭合,损伤比强度准则预测的原状黄土和水泥土三轴强度变化规律与试验结果基本一致。
2) 通过与原状黄土和水泥土常用的Mohr-Coulomb单剪准则、双剪准则、Lade准则和广义SMP强度准则比较分析,表明损伤比强度理论有较高的计算精度,且仅损伤比强度理论体现了拉压子午线与平均主压应力轴相交,预测的黄土和水泥土具有弹脆性、弹塑性和塑性流动3个状态。
3) 分析结果表明,原状黄土损伤比强度理论反映了该类土材料单轴受压压碎以及三向等压塑性流动的量化,且三向高压应力下该类土体将由弹塑性向塑性流动转变的特征,因而地表原状黄土由于重力作用而存在塑性流动深度。
On the existence of a unique class of yield and failure criteria comprising Tresca, von Mises, Drucker-Prager, Mohr-Coulomb, Galileo-Rankine, Matsuoka-Nakai and Lade-Duncan
[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2016, 472(2185): 20150713.吴霞,丁发兴,王宁.原状黄土和水泥土损伤比强度理论及地表黄土塑性流动深度预测[J].铁道科学与工程学报,2025,22(02):863-874.
WU Xia,DING Faxing,WANG Ning.Damage ratio strength theory of undisturbed loess and cemented soil and prediction of plastic flow depth of surface loess[J].Journal of Railway Science and Engineering,2025,22(02):863-874.