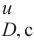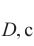岩石是一种脆性材料,单轴受压时具有体积膨胀的破坏规律。岩石三轴强度试验规律显示三轴受压时岩石随应力水平提升而塑性增强,表现为弹塑性特性,高围压时能产生明显的塑性变形[1]。GRAMBERG[2]根据岩石不同的变形和破坏形式,认为岩石等脆性材料在高温和(或)高围压条件下可表现出准塑性甚至完全塑性,破坏状态可发展为塑性流动。目前受试验机能力的限制,虽然实验上没有发现岩石强度子午线有靠近静水压力轴的趋向,破坏面压端仍呈开口的特性,但可以预见,岩石在高侧压应力和三轴等压应力状态下会出现塑性流动现象,此时子午线与静水压力轴有交点,破坏面为一个闭合的空间曲面。各类岩石工程都需要岩石强度理论的支持[3-5]。目前,根据试验规律而发展起来的各向同性岩石强度理论可分为主应力强度理论、剪应力强度理论和其他强度理论等3个理论体系,大多都是对各向同性岩石强度试验规律的唯象描述[6]。目前各向同性岩石强度准则的建立主要基于破坏面压端开口的假设,难以有效预测岩石强度发展规律,即难以预测岩石在高围压以及三轴等压状态下发生塑性流动,因此岩石的强度理论需要进一步发展。丁发兴等[7-9]提出了混凝土和各向同性岩石纵向与横向应变都服从弹性和非弹性应变分解假设,采用材料单元体相对耗能率求最小值的计算模型,发现了描述材料非弹性变形与破坏的损伤比参数变化规律,损伤比定义为脆性材料非弹性应变的相对横向变形效应,即强度和非弹性应变2个相对物理量的乘积,从而构建了混凝土与岩石损伤比强度理论,提出了压/拉损伤比变量计算方法并推荐了六经验系数取值。此外,损伤比强度理论还应用于轻骨料混凝土、钢纤维混凝土、正交各向异性金属的强度预测[10-11]。目前该理论还存在些许缺陷,即三轴高压应力状态时其包络面虽收敛但并非完全闭合,因此需进一步完善并用于岩石破坏机制分析与解释岩石力学规律。为此,本文主要工作如下:1) 根据岩石强度发展规律,提出新的五经验系数损伤比表达式,进一步完善各向同性岩石损伤比强度理论;2) 利用现有各类岩石多轴强度试验数据,推荐了损伤比参数中五经验系数的取值,并将损伤比强度准则与其他代表性准则进行比较;3) 应用该理论预测不同类型岩石所对应的塑性流动深度以及解释高地应力下隧道开挖导致硬岩岩爆的成因,最后提出地球“重力塑性耗能”观点,解释地球内在动力机制。
1 损伤比强度理论
1.1 基本假设
1) 小变形条件下,应力作用时各向同性岩石的纵向总应变分为弹性应变与非弹性应变2部分之和,即
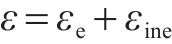
式中:ε为总应变,εe为弹性应变,εine为由损伤引起的非弹性应变。
2) 各向同性岩石的横向总应变ε′也分为横向弹性应变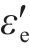
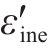
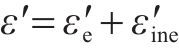
其中,ε′、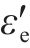
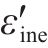
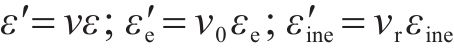
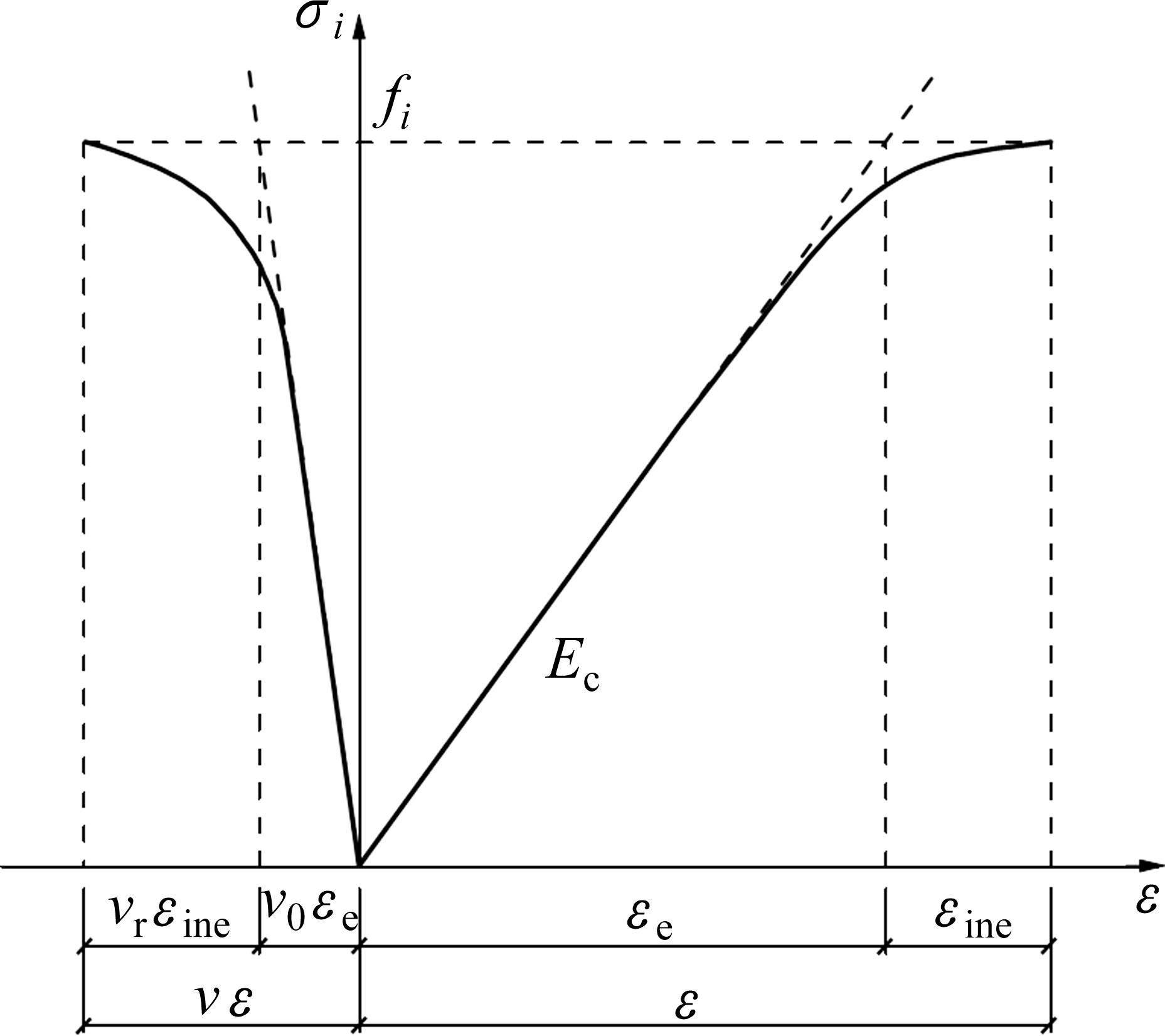
式中:v为应变全过程中的横向变形系数,v0为弹性应变部分的泊松比,vr为非弹性应变部分的损伤变形系数。2个基本假设的示意图如图1所示。
1.2 理论构建
将岩石因荷载因素产生的非弹性主应变εine,i(t)(i=1, 2, 3)视为破坏过程中唯一耗能机制,因岩石具有抗压强度和抗拉强度差异很大的特点,传统的材料单元体塑性耗能率计算模型难以有效反映这种差异带来的影响,丁发兴等[7]改用单元体相对耗能率计算模型,即破坏刚开始时刻代表着岩石单元体相对耗能率Ψ(t)表示为
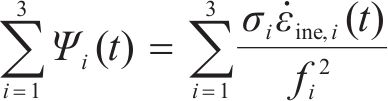
式中:fi(i=1, 2, 3)为单轴应力σi作用下岩石强度,(fi(i=1, 2, 3)为与σi对应的岩石单轴强度)当σi为压应力时fi=fc,σi为拉应力时fi=ft;σi(i=1, 2, 3)为破坏刚开始时岩石单元体名义主应力,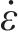
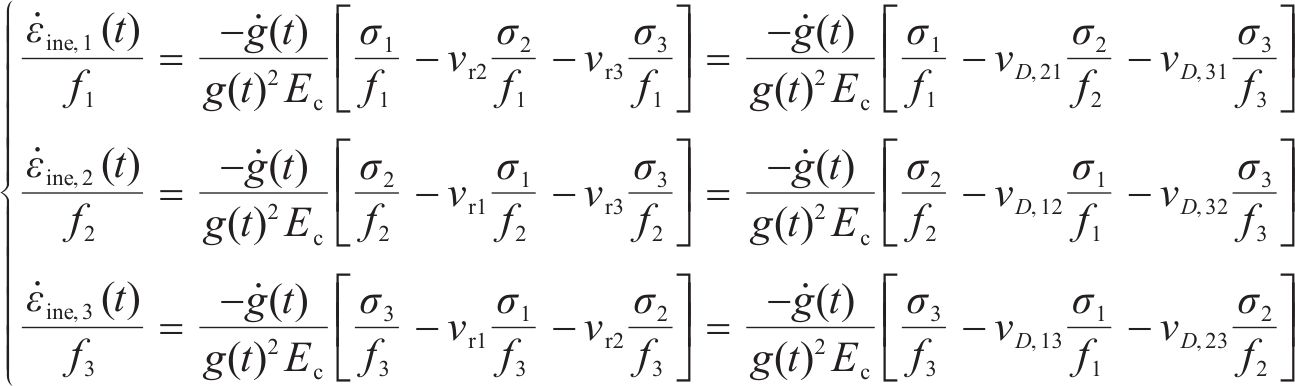
式中:g(t)为岩石割线模量与弹性模量的比值,是关于破坏过程t的函数;ġ(t)表示g(t)对t的导数;vD,ij为i轴对j轴(i≠j)的损伤比,定义为材料非弹性应变的相对横向变形效应,其值表示为
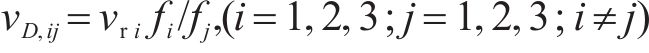
可见,损伤比参数是相对关系,是强度和非弹性应变2个相对物理量的乘积。当i轴和j轴同时处于受压或受拉应力状态时,损伤比vD即损伤变形系数vr,而对于其他应力条件,损伤比与损伤变形系数具有换算关系。
根据强度准则,式(4)在破坏过程中应满足约束条件,最终得到各向同性岩石损伤比强度准则的通用形式:
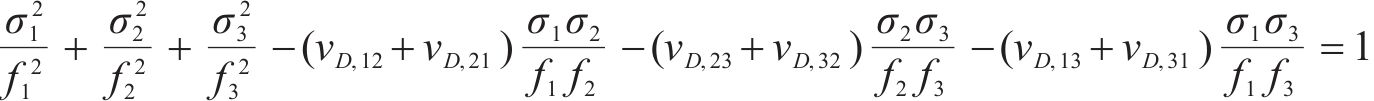
由于岩石各主应力方向的损伤比特性一致且具有体积膨胀的破坏规律,故岩石的损伤比可直接简化表示为拉损伤比和压损伤比,即某主应力方向为拉应力时损伤比为拉损伤比(用v
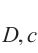
| 应力状态 | 主应力形式 |
|---|---|
| T/T/T | 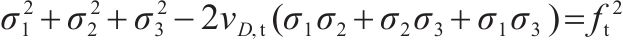 |
| T/T/C | 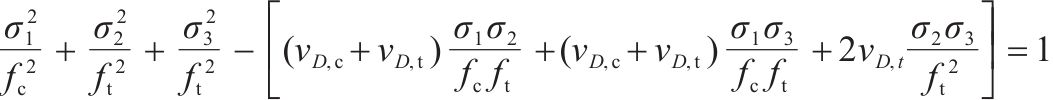 |
| T/C/C | 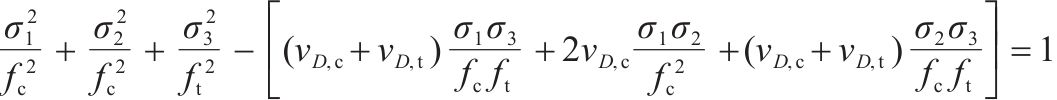 |
| C/C/C | 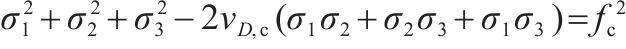 |
根据公式(7),当确定岩石的损伤比参数时,便能得到岩石的损伤比强度准则具体表达式,当损伤比v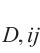
1.3 损伤比变量确定与验证
1.3.1 表达式
岩石处于三轴受压状态时,式(7)可改写为八面体应力形式:
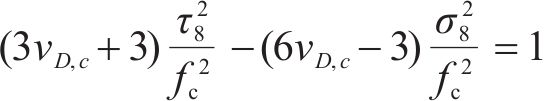
式中: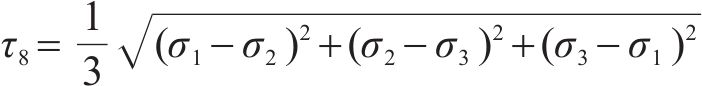
令拉压子午线与静水应力轴相交于一点a1,即当σ8/fc=a1时,τ8/fc=0。将其代入式(8),可得
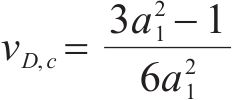
可见v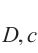
文献[7]定义拉应力为正,给出的六经验系数岩石损伤比变量表达式既考虑了Lode角θ的影响而反映偏平面外凸特性,也考虑了静水应力影响而实现子午线逐渐收敛特性,表达式如下:
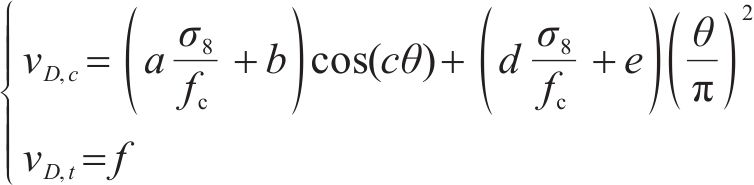
式中:a~f为经验系数,所有系数都是正数,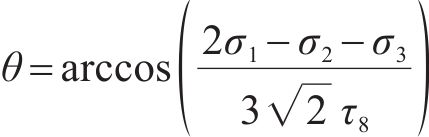
此外,式(10)表示的损伤比取值在高静水压应力条件下减小,即非弹性应变的相对横向变形效应减小,对应非弹性体积膨胀减小,从而岩石由脆性破坏向塑性破坏转变,反映了岩石在低围压下表现为脆性破坏而在高围压下表现为塑性破坏的规律与特征。然而,采用式(10)所示损伤比变量表达式的损伤比强度准则的理论拉压子午线与高静水应力轴不一定相交于同一点,故需对损伤比表达式进行优化。
针对三轴受压下岩石的强度包络面特征,为确定更合理的损伤比表达式,笔者提出以下3个假设:1) 破坏包络面压端因材料塑性流动破坏而闭合,子午线与静水应力轴相交于某一点;2) 相同Lode角下损伤比取值随着静水应力的增加而单调递减,并收敛至同一数值;3) 三轴受压应力状态下岩石强度包络面光滑且基本外凸。
定义压应力为正,此时拉子午线对应Lode角θ为60°,压子午线对应Lode角θ为0°。为满足上述基本假设要求,笔者提出以下五经验系数的岩石损伤比表达式,即:
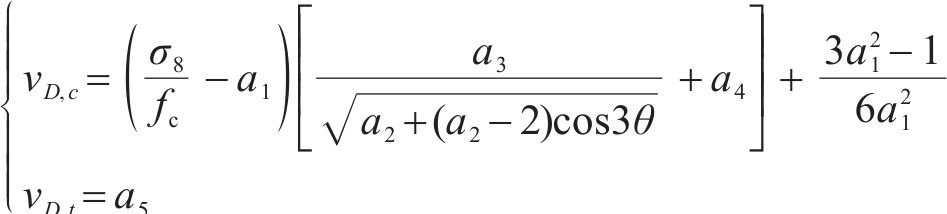
式中:a1~a5为经验系数。(σ8/fc-a1)项反映子午线与静水应力轴相交于a1,且σ8/fc=a1时,v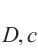
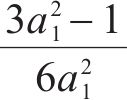
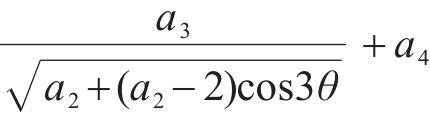
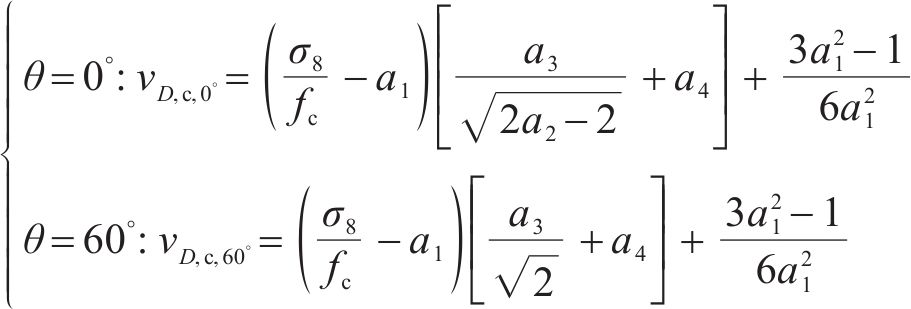
式(12)可表示为
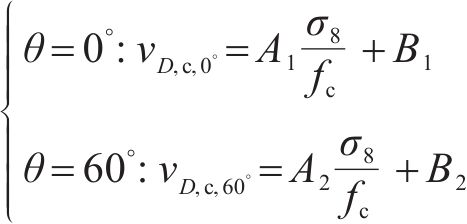
式中:当σ8/fc=a1时不同Lode角下的子午线相交于同一点,即有v
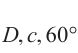
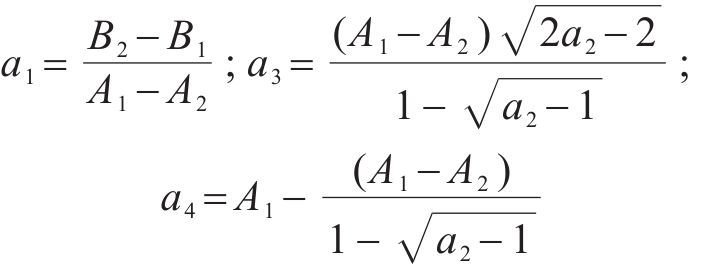
由式(12)~(14),参数a1~a4取值方法细节如下:1) 根据拉压子午线上的试验数据初步确定A1、B1、A2、B2取值,注意A1、B1、A2和B2取值需使拉压子午线与静水应力轴相交于同一点;2) 令双轴等压强度为fcc,将二轴等压应力状态(σ1=σ2=fcc, σ3=0,fi= fc)代入式(7)可求得fcc/fc取值,若fcc/fc取值不合理则返回步骤(1),然后在准则对应拉压子午线与试验数据吻合较好的基础上调整A1、B1、A2和B2取值;3) 将A1、B1、A2和B2取值代入式(14)得到a1取值;4) a2取值与偏平面是否外凸密切相关,1<a2<2,为简化计算,优先取a2=1.5,调整a2取值满足偏平面外凸特性;5) 将a2取值代入式(14)得到a3和a4取值。
图2所示为式(10)和式(11)损伤比表达式的损伤比强度准则在拉压子午线上变化规律的示意图,可见式(10)对应拉压子午线不能做到与静水应力轴交于相同点,而优化后的损伤比表达式(11)对应拉压子午线与静水应力轴拉端与压端都交于同一点。
1.3.2 经验系数确定
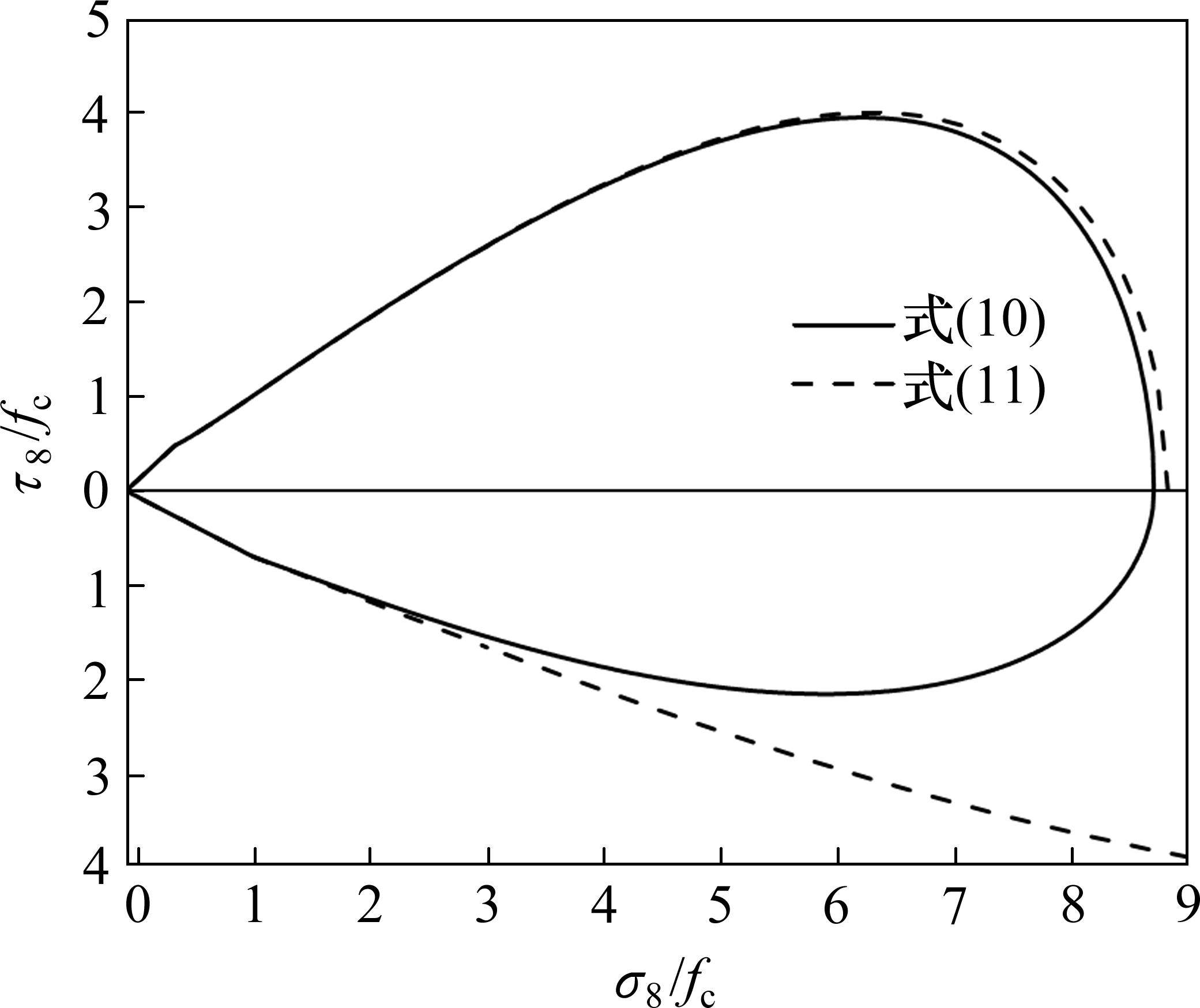
本文利用344组岩石多轴强度试验数据[12-21]确定准则中的经验系数取值,拉压子午线上岩石强度分布规律见图3。由图可知,当岩石单轴抗压强度分别小于和大于100 MPa时,岩石无量纲三轴强度分布规律基本一致,且在压子午线一侧,当岩石单轴抗压强度大于100 MPa时,岩石强度数据明显分布在外侧。故本文将收集到的数据大致分为“岩石Ⅰ类”(fc<100 MPa)和“岩石Ⅱ类”(fc>100 MPa) 2类。当然,此规律仅针对本文中所收集的岩石数据,对于更多的岩石类型强度规律还有待于进一步探索。根据“岩石Ⅰ类”和“岩石Ⅱ类”的强度数据,本文推荐损伤比表达式中各经验系数取值见表2。
| 材料类型 | ɑ1 | ɑ2 | ɑ3 | ɑ4 | ɑ5 |
|---|---|---|---|---|---|
| 岩石Ⅰ类 | 8.7 | 1.08 | -0.063 | 0.007 | 0.15 |
| 岩石Ⅱ类 | 10 | 1.05 | -0.062 | 0.006 | 0.15 |
根据损伤比变量表达式,可获得典型应力状态下损伤比变量取值见表3。此时的各向同性岩石损伤比强度理论反映了单轴受拉脆断(损伤比取值为0.15)、单轴受压压碎(“岩石Ⅰ类”损伤比取值为1.76;“岩石Ⅱ类”损伤比取值为2.34)、双轴受压压碎(“岩石Ⅰ类”损伤比取值为0.786;“岩石Ⅱ类”损伤比取值为0.833)以及三轴等压塑性流动的指标量化(“岩石Ⅰ类”损伤比取值为0.497 8;“岩石Ⅱ类”损伤比取值为0.498 3),且三轴高压下损伤比参数递减使得非弹性体积膨胀减小导致脆性岩石向塑性流动转变的特征。
| 材料 | v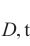 | v 受压) | v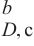 | v 塑性流动) |
|---|---|---|---|---|
| 岩石Ⅰ类 | 0.15 | 1.76 | 0.786 | 0.497 8 |
| 岩石Ⅱ类 | 0.15 | 2.34 | 0.833 | 0.498 3 |
1.3.3 典型验证
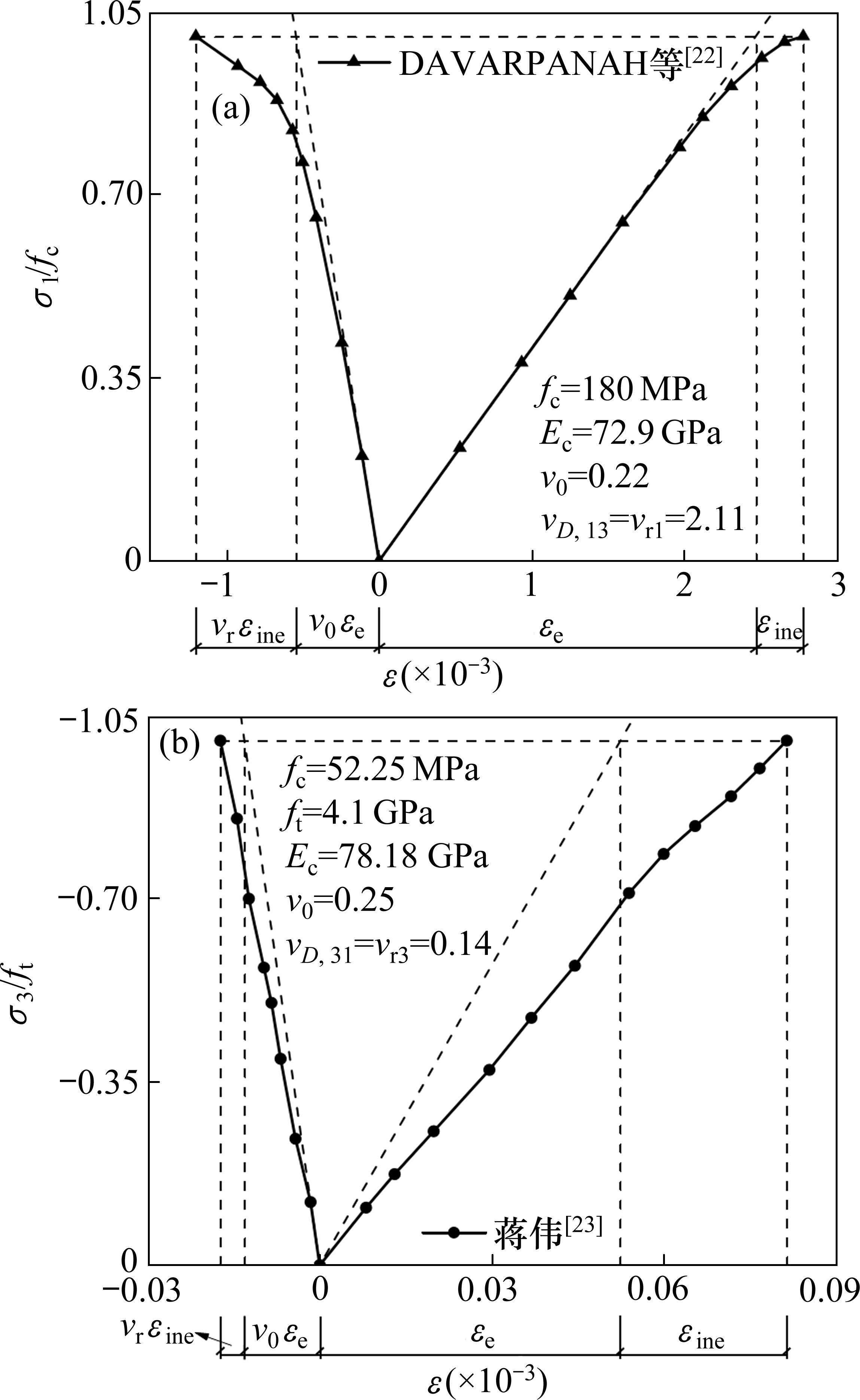
对于单轴应力状态下,利用图1所示的应变计算模型计算单轴应力-应变试验曲线得到损伤变形系数vr,再将损伤变形系数vr代入公式(6),计算出单轴受力损伤比试验值。如图4所示,由DAVARPANAH等[22]单轴受压试验结果计算所得单轴受压损伤比为2.11,而由损伤比变量表达式计算得到单轴受压损伤比v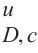
2 损伤比强度理论验证与比较
表2所示经验系数推荐值下“岩石Ⅰ类”和“岩石Ⅱ类”损伤比强度准则的三维破坏包络面形状类似,整体“岩石Ⅱ类”破坏包络面较大。已有试验数据范围内破坏包络面如图5所示,可见在三轴受压区,岩石三维破坏包络面光滑外凸,因岩石具有拉、压不等的损伤比参数特性,拉压交界处的岩石三维破坏包络面由于参数取值突变,因此此处仅具有连续和外凸的特征,并不光滑。
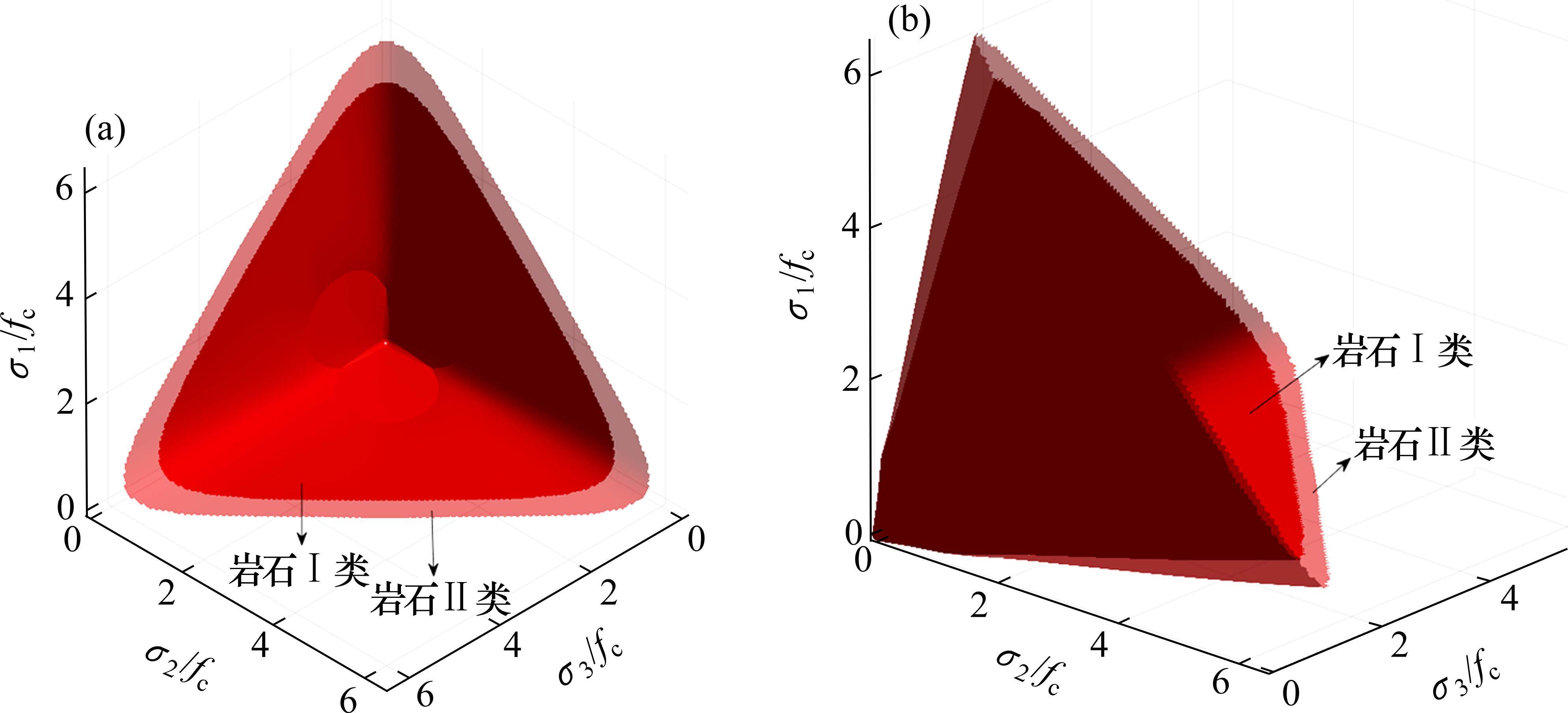
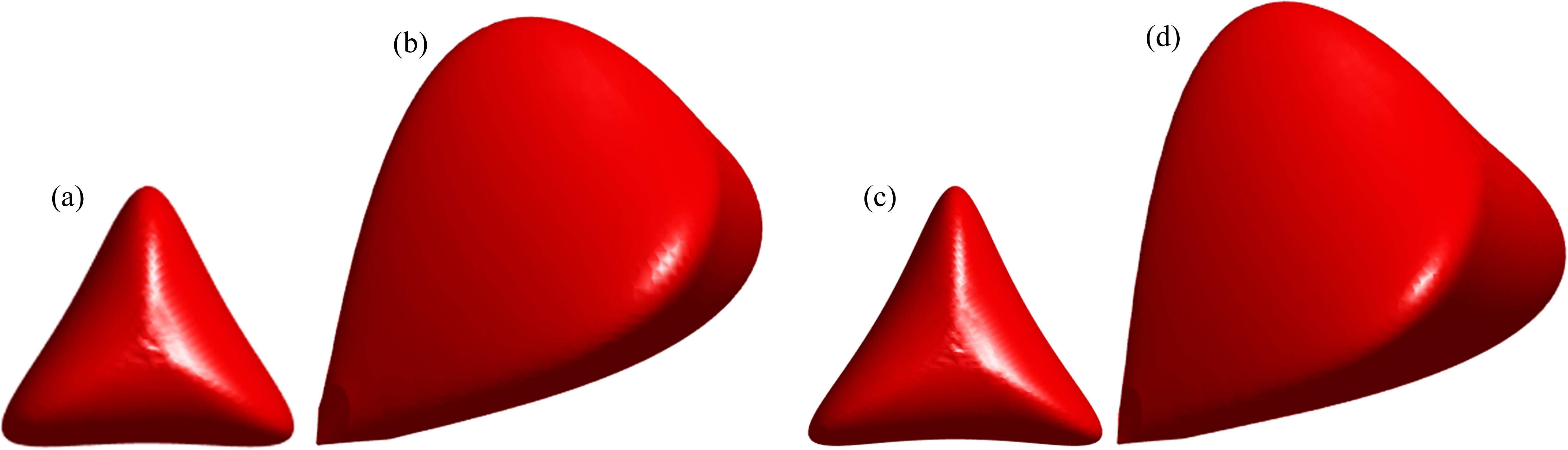
完整的岩石破坏包络面如图6所示,可见破坏包络面的拉端因拉伸脆性破坏而闭合,压端因塑性流动破坏而闭合。由于相同Lode角下损伤比参数随静水应力增加而线性递减的假设在高静水压力时略有偏差,此时岩石三维破坏包络面略呈现内凹特征。可见,损伤比参数随静水应力增加而线性递减假设可满足现有试验范围内包络面外凸的基本特征,虽然在高压下岩石不稳定特性或许会凸显,但DRUCKER等[24]指出不稳定材料可以产生内凹屈服面,因此将损伤比表达式进一步复杂化来体现高静水应力压端破坏包络面完全外凸特征,但意义并不显著。
2.1 强度理论验证
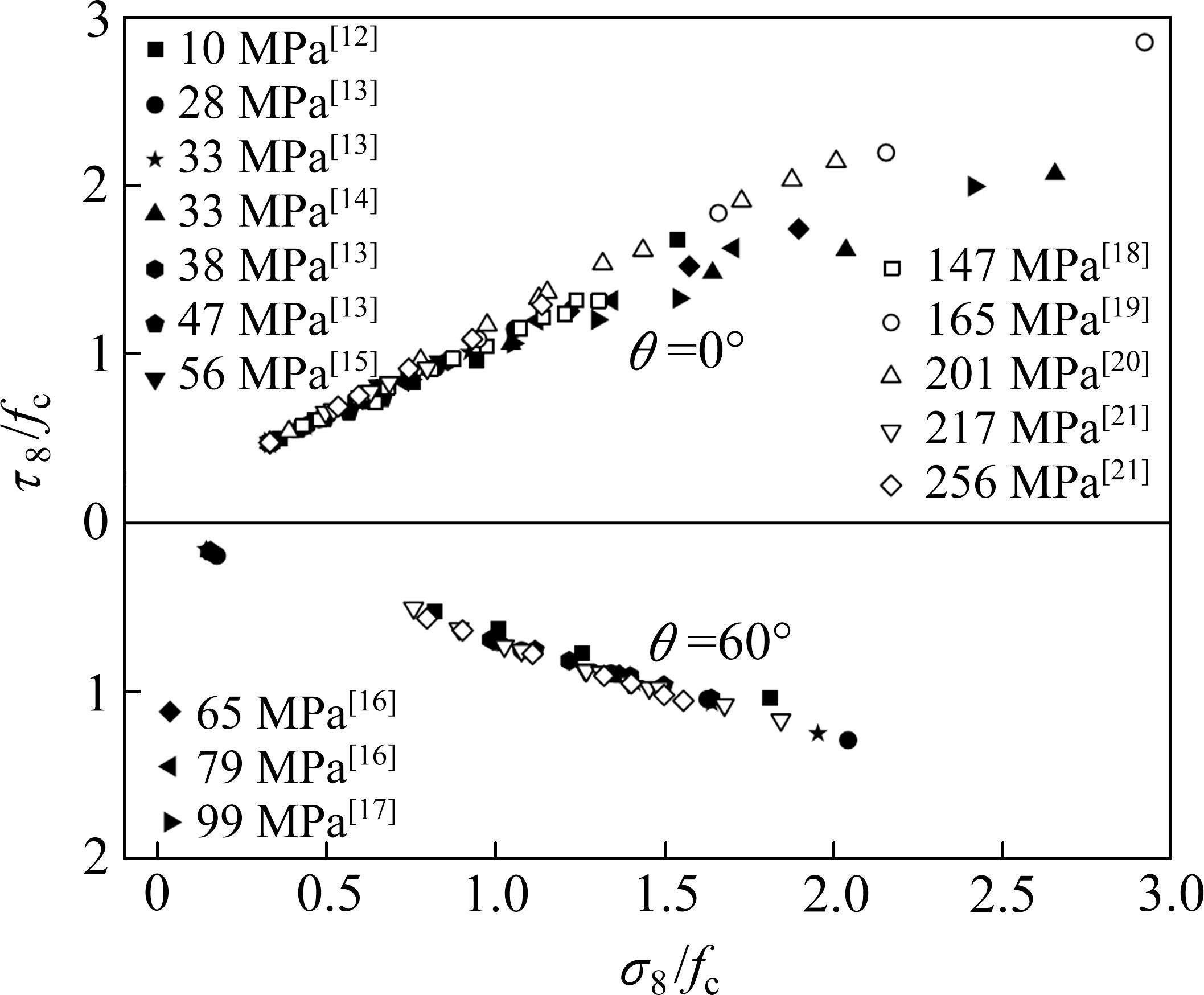
损伤比强度准则对应的拉压子午线和偏平面强度变化规律与“岩石Ⅰ类”试验数据[12-17]和“岩石Ⅱ类”试验数据[18-21]试验数据的比较如图7和图8所示,从图可看出:
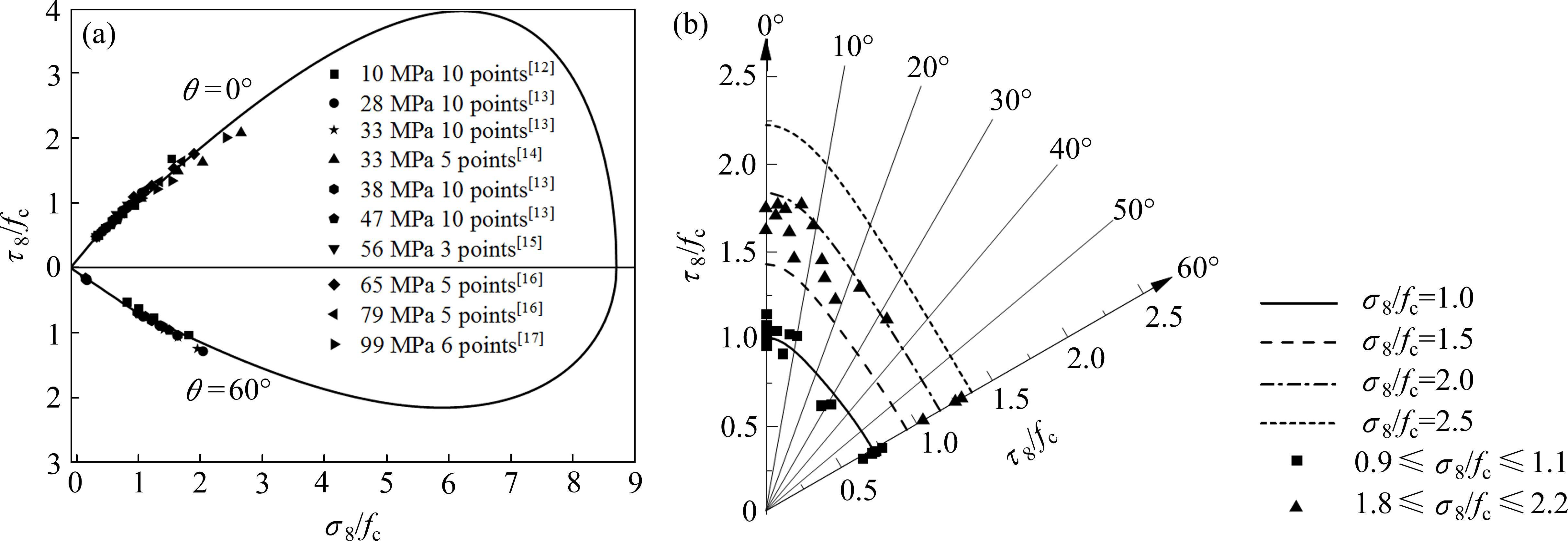
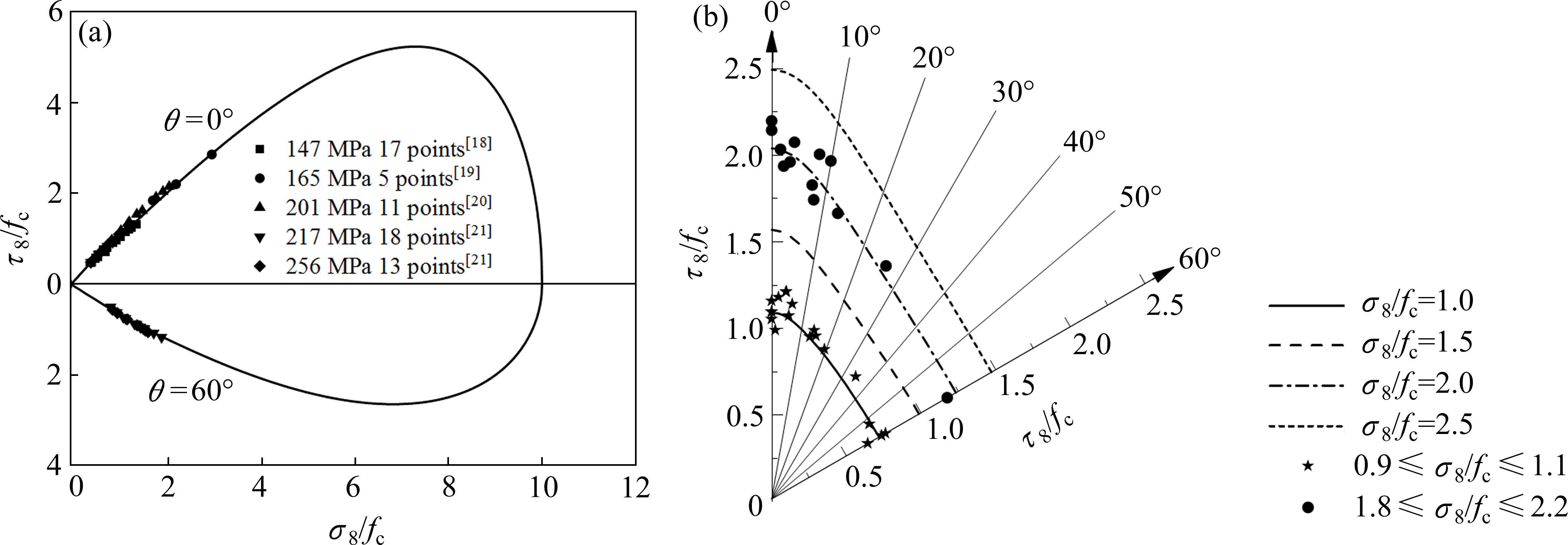
1) 随静水压力σ8的增大,岩石子午线上八面体剪应力τ8数值逐渐增加,但增长速率逐渐减小。当τ8值增加至最大值后子午线开始靠近静水压力轴直至与σ8轴相交,交点对应三轴等压应力状态,意味着岩石在三轴等压状态会发生塑性流动。
2) 在已有试验数据范围内,五经验系数岩石损伤比强度准则对应的三轴受压偏平面光滑外凸。
3) 五经验系数岩石损伤比强度准则的拉压子午线和偏平面强度预测值与“岩石Ⅰ类”和“岩石Ⅱ类”三轴强度实测值变化规律都较一致,反映了岩石的真三轴强度特性。
2.2 强度理论比较
本文对损伤比强度准则、单剪强度准则[25-26]、八面体强度准则[27-28]以及双剪强度准则[29]进行比较分析,准则中的参数取值方法参考文献[9]。各准则对应的拉压子午线规律与“岩石Ⅰ类”和“岩石Ⅱ类”试验数据的比较如图9所示,可见:
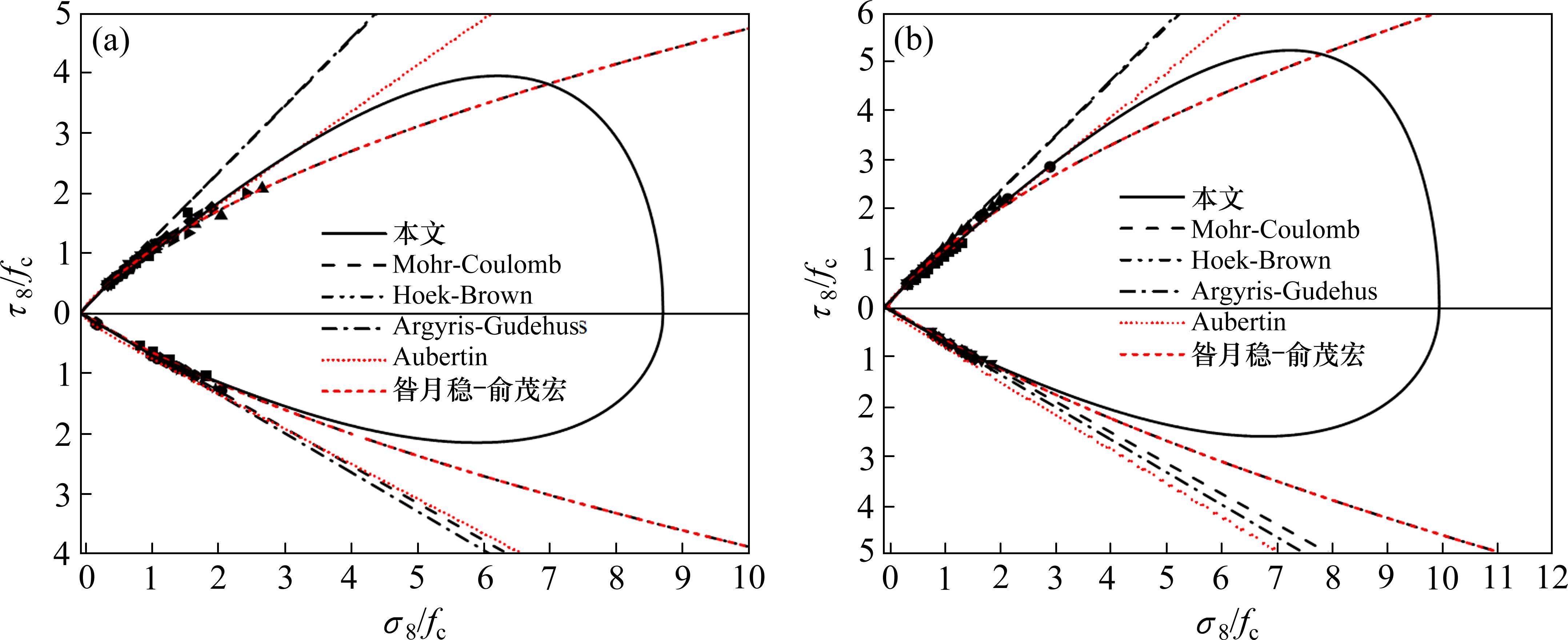
1) 损伤比强度准则,Hoek-Brown两参数单剪强度准则[26],以及昝月稳-俞茂宏三参数非线性双剪强度准则[29]的“岩石Ⅰ类”和“岩石Ⅱ类”拉压子午线规律与相应的试验数据分布规律较一致。
2) 除损伤比强度准则外,其余准则对应子午线压端开口,不与静水应力轴相交,难以预测岩石在高压及三向等压条件下塑性流动的破坏特征。
3) 基于理论推导的损伤比强度理论,因损伤比参数具有良好的物理意义,可以将实验结果与工程和科考结果有机结合,因而反映岩石强度发展规律,而经验型强度理论较难具备预测效果。
为直观描述各强度准则的精度,利用岩石八面体应力试验值与强度准则的八面体应力理论值的比值进行比较,比较结果见表4,可见2类岩石损伤比强度准则的计算精度都较高,与其他准则精度相当。
3 应用
3.1 塑性流动深度预测
随八面体正应力σ8的增大,子午线斜率减小对应岩石弹塑性逐渐增强;斜率减小为0时八面体剪应力τ8数值增加至最大值,之后子午线开始靠近静水压力轴,岩石逐渐处于塑性流动状态;σ8值减小至0时子午线与σ8轴相交,交点对应三轴等压应力状态。如图10所示,当岩石1类和岩石2类应力数据点位于破坏包络线以外,且分别在八面体正应力大于6.3fc和7.3fc时,岩石将处于塑性流动状态。对于地表岩石,其受压损伤比取值在2左右,表现为脆性,此时体积膨胀,但深部岩石随着重力引起的压应力增加而受压损伤比取值逐渐递减至0.5以下,此时体积基本不变,地球深部岩石呈现高压塑性。
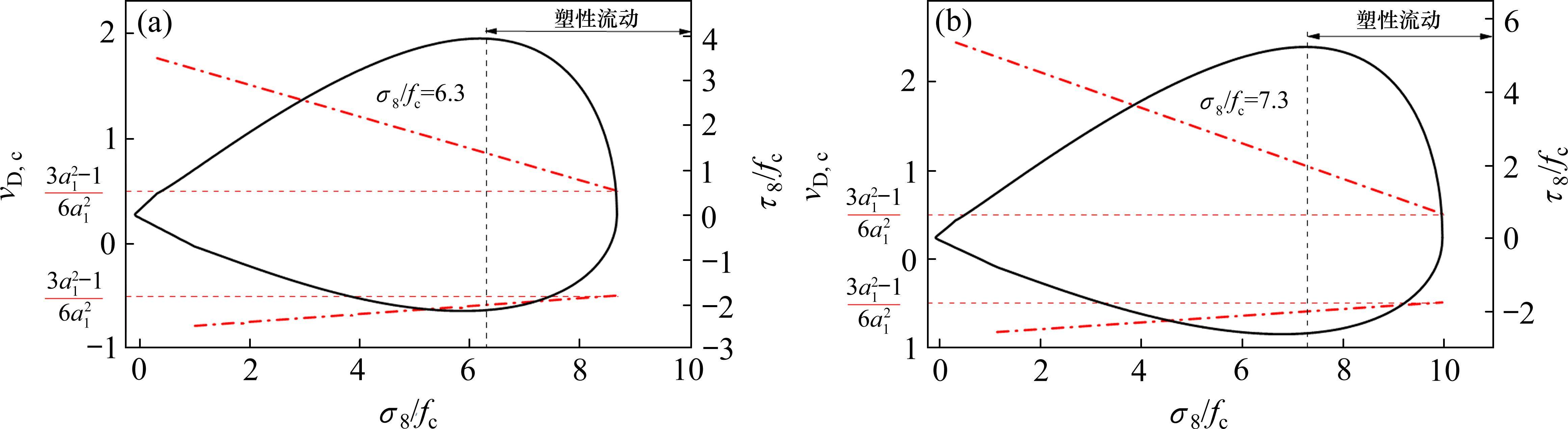
可见,损伤比强度理论将不同深度岩石的受力与变形状态由已有理论认知的“弹脆性和弹塑性”2个状态,推进至“弹脆性、弹塑性和塑性流动”3个状态,如图10所示。同时,损伤比强度理论揭示了岩石受压体积膨胀(对应压损伤比大于0.5)的破坏规律以及高压条件下体积膨胀减小(对应压损伤比线性递减)导致脆性岩石向塑性转变的机理,从而实现脆性破坏和塑性破坏的统一。
岩石拉压子午线规律和对应的压损伤比随静水应力的变化规律曲线见图10,图中损伤比为(3a12-1)/6a12时,拉压子午线和静水应力轴相交,对应σ1=σ2=σ3应力状态。地表深处的岩石处于三轴等压应力状态,仅考虑重力引起的应力时,根据拉压子午线和静水应力轴相交时对应的静水应力值,可计算出地表岩石处于塑性流动状态的最低深度。当地壳平均密度取2.6 g/cm3时,表5给出了不同岩石类型对应的塑性流动深度参考值。苏联于1970年开始在科拉半岛进行了钻井科考,当钻孔深度达到12 262 m后由于地层塑性和高温导致钻头被卡最终停止了钻探科考,如不考虑温度影响,此时地球深处对应的岩石单轴抗压强度约为38 MPa。此外,西部山地城市浅层地下空间的开发,也将面临重力作用软岩塑性流动问题,此时嵌岩桩基工程的钻孔往往成型困难。
| 岩石种类 | 单轴强度/MPa | 塑性流动深度/m |
|---|---|---|
| Fine siltstone[12] | 10 | 3 346 |
| Saraburi marble[13] | 28 | 9 369 |
| Phu Kradung siltstone[13] | 33 | 11 042 |
| Phra Wihan sandstone[13] | 38 | 12 715 |
| Phu Phan sandstone[13] | 47 | 15 727 |
| Coarse sandstone[14] | 33 | 11 042 |
| Red sandstone[15] | 56 | 18 738 |
| Sandstone[16] | 65 | 21 750 |
| Limestone[16] | 79 | 26 435 |
| Trachyte[17] | 99 | 33 127 |
| Apache Leap tuff[18] | 147 | 56 538 |
| KTB Amphibolite[19] | 165 | 63 462 |
| Westerly granite[20] | 201 | 77 308 |
| Dunham dolomite[21] | 217 | 83 462 |
| Westerly granite[21] | 256 | 98 462 |
3.2 岩爆成因解释
喜马拉雅等山脉深处高地应力隧道工程TBM(隧道掘进机)开挖时,因开挖卸载,周边岩体由三轴受压弹塑性应力状态,此时对应的损伤比取值相对较小,非弹性体积应变膨胀程度较小,卸载后周围岩体三轴压应力将逐渐降低,直至二轴受压应力状态,此时岩体应力卸载将导致非弹性体积应变增大而体积膨胀,也就是损伤比取值由小变大,岩体由弹塑性变弹脆性,因而最终诱发硬岩岩爆。
3.3 重力塑性耗能
在经典力学中,材料呈现塑性时被认为其处于耗能状态,耗能时将由机械能转变为热能。根据损伤比强度理论,地壳深部的岩石在重力下将处于弹塑性或塑性流动状态,此时岩石处于耗能状态导致温度上升,随着地下深度增加,压力和温度都在上升,以至于地球内部表现为高压与高温,物质密度增大。这种基于岩石损伤比强度理论下的地球重力塑性耗能规律的描述,笔者称之为“重力塑性耗能”。地球每年吸引轨道附近小行星(太空尘埃和陨石等),以及太阳光照射到地球上通过植物的光合作用吸收变成物质而略微增加质量,但也有利于地球“重力塑性耗能”。
地球“重力塑性耗能”对地球内部构造的解释如下:1) 地球表面的岩石圈是固态,包括弹脆性/弹塑性和塑性流动;2) 当地下深度超过某个临界状态时,温度的作用超过压力,由塑性固态物质逐渐过渡到部分熔融物质、液态-固态物质和液态物质,此处为地幔;3) 再之后是压力的作用超过温度,此处为地核,以铁为主的物质由液态逐渐过渡到液态-固态,由于地心的温度最高达6 000 ℃且压力达360 GPa,可以预测以铁、镍元素组为主的地球固态内核也是塑性体。
3.4 地球动力机制
大陆漂移学说是大陆移动的开创性理论,其认为地球上所有大陆在中生代以前曾经是统一的巨大陆块,称之为泛大陆或联合古陆,中生代开始分裂并漂移,逐渐达到现在的位置,目前大陆漂移理论已被板块构造学所取代。板块构造学说认为地球的岩石圈分为内部相对稳定的六大板块,这些板块在以每年1 cm到10 cm的速度在移动,板块相对移动而发生的彼此碰撞和张裂形成了地球表面的基本面貌。然而,“大陆漂移学说”和“板块构造学说”的动力机制至今一直没有阐释清楚。
当前科学界关于地球形成的主流观点为康德-拉普拉斯星云假说下的岩浆冷却,按该观点地球内部能量只有释放而没有补充。地球受自身重力作用之外,存在自转引起的向西漂移的潮汐力和指向赤道的离极力,还受月亮与太阳的引潮力影响,引潮力不仅引发地球表面海水潮汐变化,大陆的岩体也会产生相应的拉伸变形,科学家认为潮汐力、离极力和引潮力作用不足以让板块整体移动。
根据地球“重力塑性耗能”观点,重力作用下地球内部物质处于弹塑性或塑性流动状态产生能量且不断积累,重力下的地球内部是一个强大的能量体,当地球内部有能量释放且外部有月亮和太阳的引潮力共同作用时,将驱动地球板块逐渐发生移动。因此,笔者认为“大陆漂移”和“板块运动”是地球内部能量长期缓慢释放与潮汐力、离极力和引潮力共同作用的结果,其内部动力机制来源于地球的“重力塑性耗能”。
另外,根据地球“重力塑性耗能”观点,由于自身重力下地球内部是一个不断增大的高压与高温能量体,当地球内部能量积累到一定程度时,地球板块之间(如临界状态断裂带和火山口)在引潮力较大时发生地震和火山爆发等自然灾害,使得地球内部能量短期内得到快速释放。当能量释放到一定程度之后,由于地球深部岩石处于塑性流动状态而破坏部位将重新闭合,临界状态的断裂带和火山口恢复平静。可见,地球“重力塑性耗能”观点可为康德-拉普拉斯星云假说下的岩浆冷却提供能量补充。
4 结论
1) 根据深地岩石强度发展规律,提出了岩石受压破坏包络面基本特征的3个假设,建立了五经验系数损伤比表达式,构建了完善的岩石损伤比强度理论。
2) 根据现有岩石强度试验数据,推荐了损伤比表达式五经验系数取值,此时损伤比强度准则的计算精度与已有典型准则相当,岩石损伤比强度理论反映了单轴受拉脆断、单轴与双轴受压压碎以及三轴受压塑性流动的指标量化,且三轴高压下损伤比参数递减使得非弹性体积膨胀减小导致岩石将向塑性流动转变的特征,因此在试验范围之外,损伤比强度准则可进一步预测岩石呈现塑性流动的强度发展规律。
3) 根据岩石损伤比强度理论,指出重力作用下地壳固态岩石的受力与变形具有弹脆性、弹塑性和塑性流动等3个状态,且地壳深部岩石将呈现塑性流动,以及高地应力下硬岩隧道开挖,由于应力释放将引发高压岩体非弹性体积膨胀而导致硬岩岩爆的规律。
4) 根据岩石损伤比强度理论提出了地球“重力塑性耗能”,认为地球内部的地幔和地核物质处于液态或固态,是重力高压引发塑性耗能导致温度升高的结果,而“大陆漂移”和“板块运动”是地球“重力塑性耗能”引起地球内部能量增加而长期缓慢释放,以及与潮汐力、离极力和引潮力共同作用的结果,而火山爆发和地震等自然灾害时地球内部能量短期内快速释放的结果。地球“重力塑性耗能”观点可为康德-拉普拉斯星云假说下的岩浆冷却提供能量补充。
吴霞,丁发兴,吕飞等.各向同性岩石损伤比强度理论研究及应用[J].铁道科学与工程学报,2024,21(12):5186-5197.
WU Xia,DING Faxing,LÜ Fei,et al.Study and application of isotropic rock damage ratio strength theory[J].Journal of Railway Science and Engineering,2024,21(12):5186-5197.