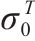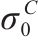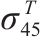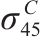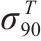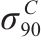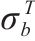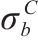屈服准则是判断金属材料是否产生塑性变形的依据,在金属塑性成型及有效利用材料方面具有非常重要的意义[1-3]。有关金属材料屈服准则的研究最早可以追溯到19世纪,1864年TRESCA提出了著名的最大剪应力屈服准则。半个世纪后的1913年,MISES从畸变能的角度出发,建立了一个考虑3个主应力的屈服准则,即后来应用最广泛的von Mises屈服准则。这2个著名的屈服准则都包含在HERSHEY[4]于1954年提出的屈服准则中。对各向异性材料,HILL[5]在von Mises准则的基础上,引入各向异性系数,建立了第1个正交各向异性屈服准则,即著名的Hill二次式屈服准则。随后,国内外学者提出了为数众多的各向异性屈服准则。2004年,俞茂宏等[6]对强度理论百年以来的发展进行了很好的梳理和总结,但主要针对的是各向同性材料的强度理论。最近,丁发兴等[7]对强度理论研究进展进行了归纳总结和展望,涉及的内容包括了各向同性和正交各向异性强度理论,宏观强度理论及微细观强度理论。由于Hill二次式屈服准则无法描述铝合金等存在的“异常”屈服行为,BARLAT等[8]提出了一个非二次式的Barlat 89屈服准则。BANABIC等[9]在Barlat 89屈服准则的基础上,通过增加材料参数,建立了预测精度更好的Banabic非二次式屈服准则。该准则能很好地预测铝合金和钢的塑性变形,在板料成型模拟中得到广泛应用[7]。近年来,丁发兴等[10-13]针对混凝土和各向同性岩石,提出了损伤比的概念,并建立了相应的强度理论,即损伤比强度理论。随后,吴霞等[14]将原来的六经验系数损伤比表达式,完善为五经验系数损伤比表达式,并通过经验系数作减法克服了原有模型的缺陷,展现了完整闭合的岩石强度包络面。2023年,吴霞等[15]在各向同性材料损伤比强度理论的基础上,建立了正交各向异性损伤比屈服理论。损伤比屈服理论基于一定的物理机制提出,且与很多材料的实验结果吻合良好,因此得到广泛关注。更多最新的有关材料屈服准则的研究,可见参考文献[16-20]。虽然Banabic非二次式屈服准则在板料成型领域得到广泛应用,但它是针对拉-压对称材料提出的,因此无法准确描述拉-压非对称材料的强度差效应(strength differential effect, SD效应)。为此,本文尝试采用将各向异性和拉-压非对称性解耦的方法,将Banabic非二次式屈服准则推广到拉-压非对称,从而拓宽这一经典理论的应用范围。鉴于损伤比屈服理论是基于一定的物理机制提出的,其参数物理意义明确且能反映SD效应,并与铝合金、镁合金等金属的实验结果吻合良好,得到了广泛关注。因此,本文尝试将推广的Banabic非二次式屈服准则应用到2种不同金属,并与损伤比屈服理论进行对比。一则通过与具有明确物理机制的理论的对比,验证本文建立的新准则的正确性;二则通过比较判断2种理论的优缺点和适用范围,为其工程应用提供一定的参考。
1 Banabic非二次式屈服准则向拉-压非对称的推广
1.1 Banabic非二次式屈服准则
为了更精确地预测铝合金等金属板料的塑性变形,BANABIC等[9]在Barlat 89屈服准则[8]的基础上增加3个材料参数,建立了一个新的非二次式屈服准则。BANABIC非二次式屈服准则针对板料建立,适用于平面应力状态,当x轴、y轴与材料各向异性主轴重合时,其表达式如下:
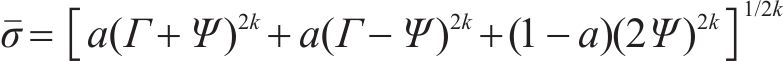
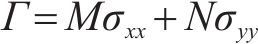
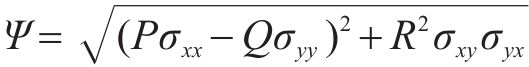
其中,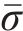
1.2 广义Banabic非二次式屈服准则的建立
由于Banabic非二次式屈服准则是针对拉-压对称材料建立的,无法描述材料的SD效应。鉴于Banabic非二次式屈服准则对铝合金等金属屈服行为的高预测精度及其在板料成型领域的广泛应用,本文尝试将其推广到拉-压非对称,以期拓展其应用范围。下面借鉴KHAN等[21]提出的各向异性和拉-压非对称性解耦的方法,将Banabic非二次式屈服准则推广到拉-压非对称。该方法的思路是将拉-压对称屈服函数乘以一个能表征材料SD效应的函数,即
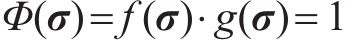
其中,σ是柯西应力张量;f(σ)描述各向异性屈服行为;g(σ)表征拉-压非对称性。g(σ)函数的选择应满足解耦塑性各向异性和拉-压非对称性的目的,即对于特定的拉伸和压缩应力状态,g(σ)应为不同的常数。
g(σ)可取一关于Lode参数的指数方程:
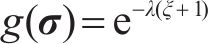
其中,e是自然对数的底数;λ是拉-压非对称系数;ξ是Lode参数,由下式给出:
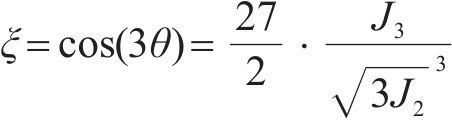
其中,θ是Lode角;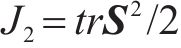
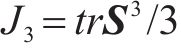
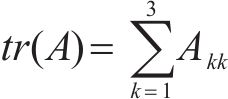
显然,对于单轴拉伸,ξ=1,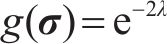
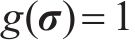
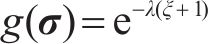
采用上述方法,Banabic非二次式屈服准则向拉-压非对称推广可由以下方程表达:
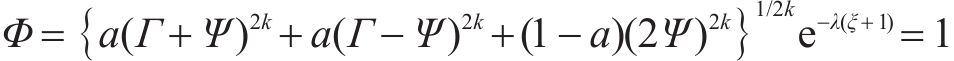
其中,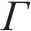
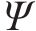
2 广义Banabic 非二次式屈服准则参数的标定方法
为了标定广义Banabic非二次式屈服准则中的材料参数,下面给出由所建立屈服准则导出的不同加载条件下的屈服应力和塑性应变比r值。
假设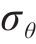
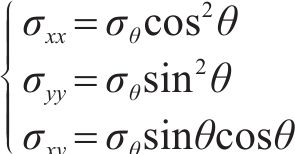
若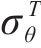
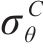
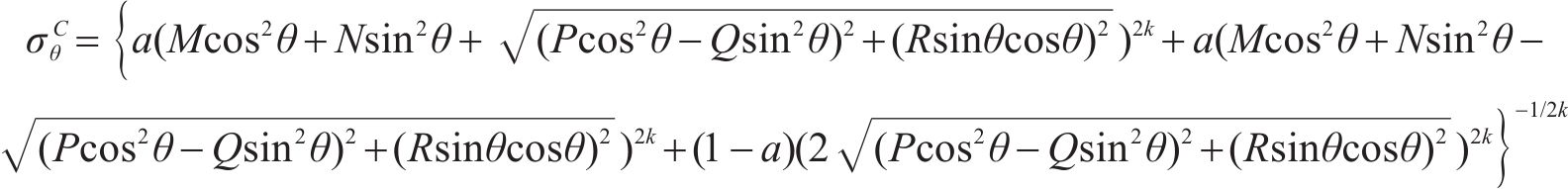
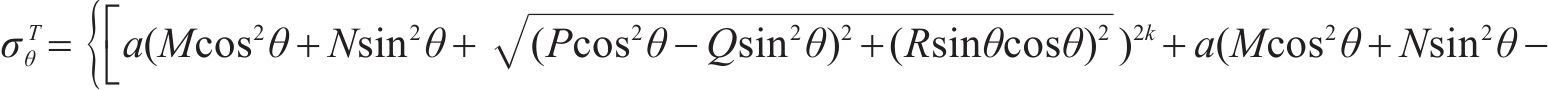
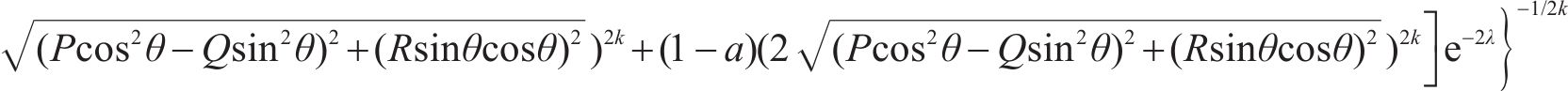
特别地有
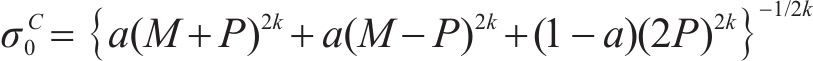
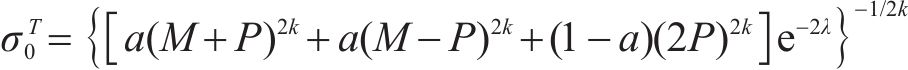
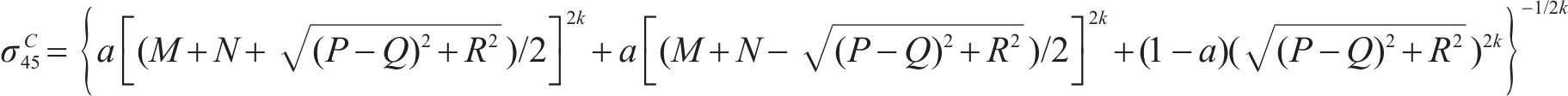
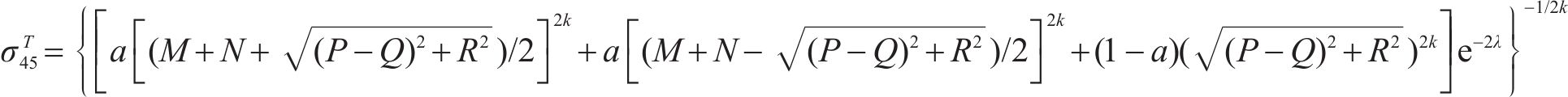
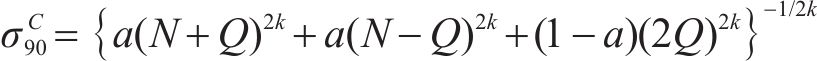
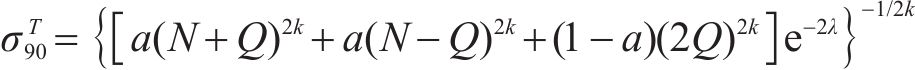
在等双轴压缩条件下,假设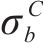
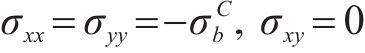
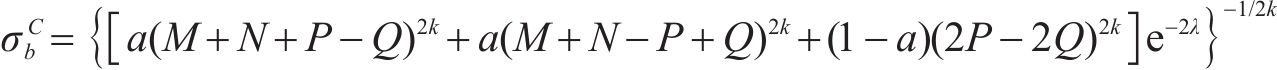
在等双轴拉伸条件下,当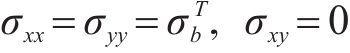
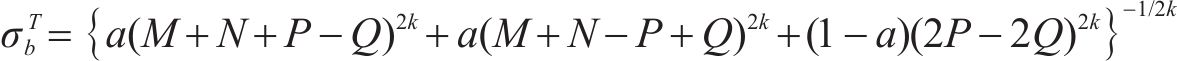
其中,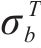
式(10)~(17)给出了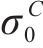
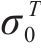
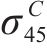
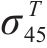
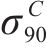
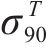
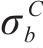
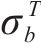
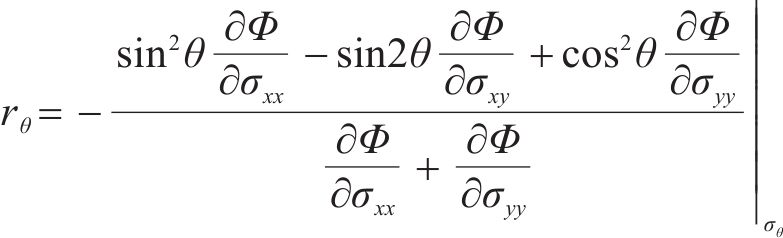
其中,θ为加载方向与材料x主轴方向之间的夹角。
特别地,有
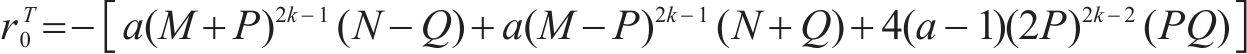
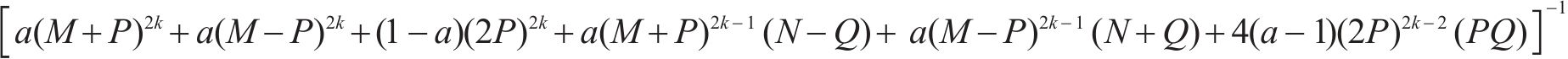
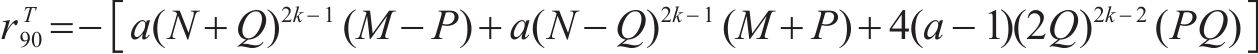
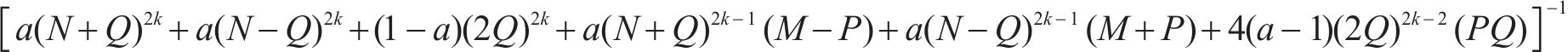
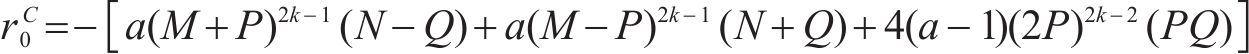
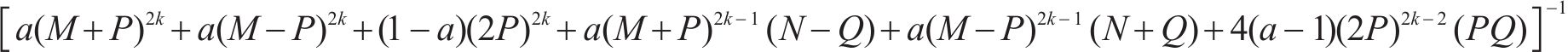
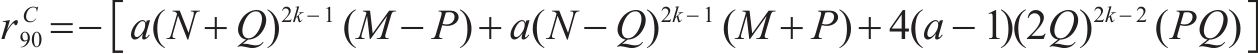
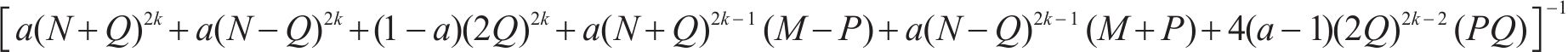
同样的,式(19)~(22)也给出了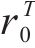
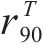
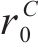
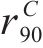
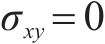
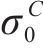
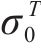
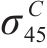
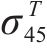
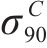
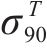
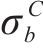
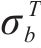
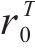
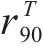
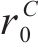
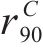
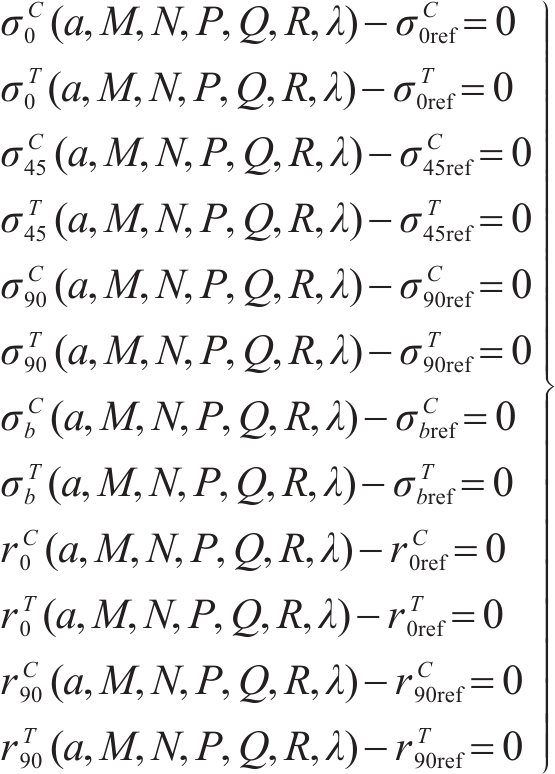
其中,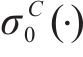
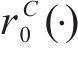
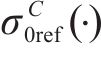
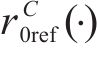
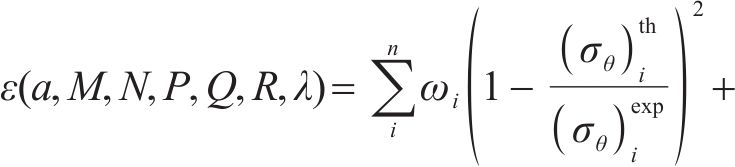
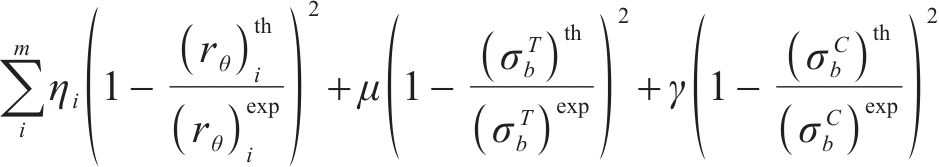
其中,n和m分别表示不同取向角θ下的屈服应力和r值的数量;上标表示该值是实验数据或理论预测值;wi,ηi,µ,γ是权重因子。下一步工作是优化a,M,N,P,Q,R,λ,从而得到误差函数的最小值。对于这一问题,有不同的数学处理方法,其中最速下降法是最方便的方法之一,本文采用这一方法。可以看出,本文在标定准则参数时,采用的实验数据个数超过了准则的参数个数,通过更多实验数据确定准则参数能更充分地体现出材料固有的规律,减少个别实验点由于实验误差等产生的影响。在下一节,本文将广义的Banabic非二次式屈服准则应用到2种不同的金属材料,并与损伤比屈服理论进行对比。
3 广义Banabic非二次式屈服准则与损伤比屈服理论的比较
为了评估广义Banabic非二次式各向异性屈服准则的预测能力,下面将其应用到AA5754-O铝合金的屈服以及Cu-Al-Be形状记忆合金的相变转换起始面预测中,并与损伤比屈服理论进行对比。关于AA5754-O铝合金的实验细节可参考文献[22],实验数据则由文献[23]给出。Cu-Al-Be形状记忆合金的实验细节可参考文献[24],实验数据由文献[25]给出。这2种金属材料的力学参数见表1,AA5754-O铝合金不同方向加载的塑性应变比r值见表2[23]。
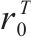 | 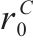 | 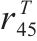 | 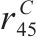 | 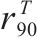 | 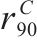 |
|---|---|---|---|---|---|
| 0.65 | 0.60 | 0.65 | 0.75 | 0.72 | 0.62 |
3.1 AA5754-O铝合金
下面用广义Banabic非二次式屈服准则预测AA5754-O铝合金的屈服行为,并与损伤比屈服理论进行对比。此处采用2种不同方案标定广义Banabic非二次式屈服准则的系数:1)包含双向等拉(压)实验数据;2)不包含双向等拉(压)实验数据。表3同时给出了由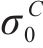
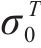
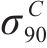
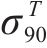
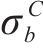
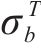
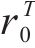
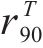
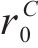
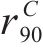
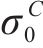
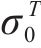
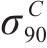
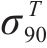
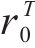
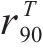
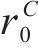
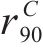
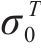
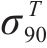
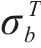
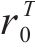
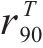
| AA5754-O | a | M | N | P | Q | λ |
|---|---|---|---|---|---|---|
| k=1 | 0.067 9 | 1.559 5 | 1.308 0 | 0.395 7 | 0.417 6 | -0.039 4 |
| k=3 | 0.742 7 | 0.504 1 | 0.396 4 | 0.488 7 | 0.547 8 | -0.125 8 |
| k=4 | 0.731 7 | 0.472 7 | 0.452 0 | 0.504 7 | 0.523 8 | -0.163 9 |
| k=3* | 0.571 1 | 0.531 8 | 0.493 6 | 0.481 7 | 0.507 1 | -0.078 6 |
| 材料 | 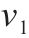 | 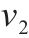 | 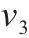 | 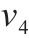 |
|---|---|---|---|---|
| AA5754-O | 1.136 | 0.943 | 1.040 | 1.040 |
| Cu-Al-Be | 1.383 | 0.383 | 0.883 | 0.883 |
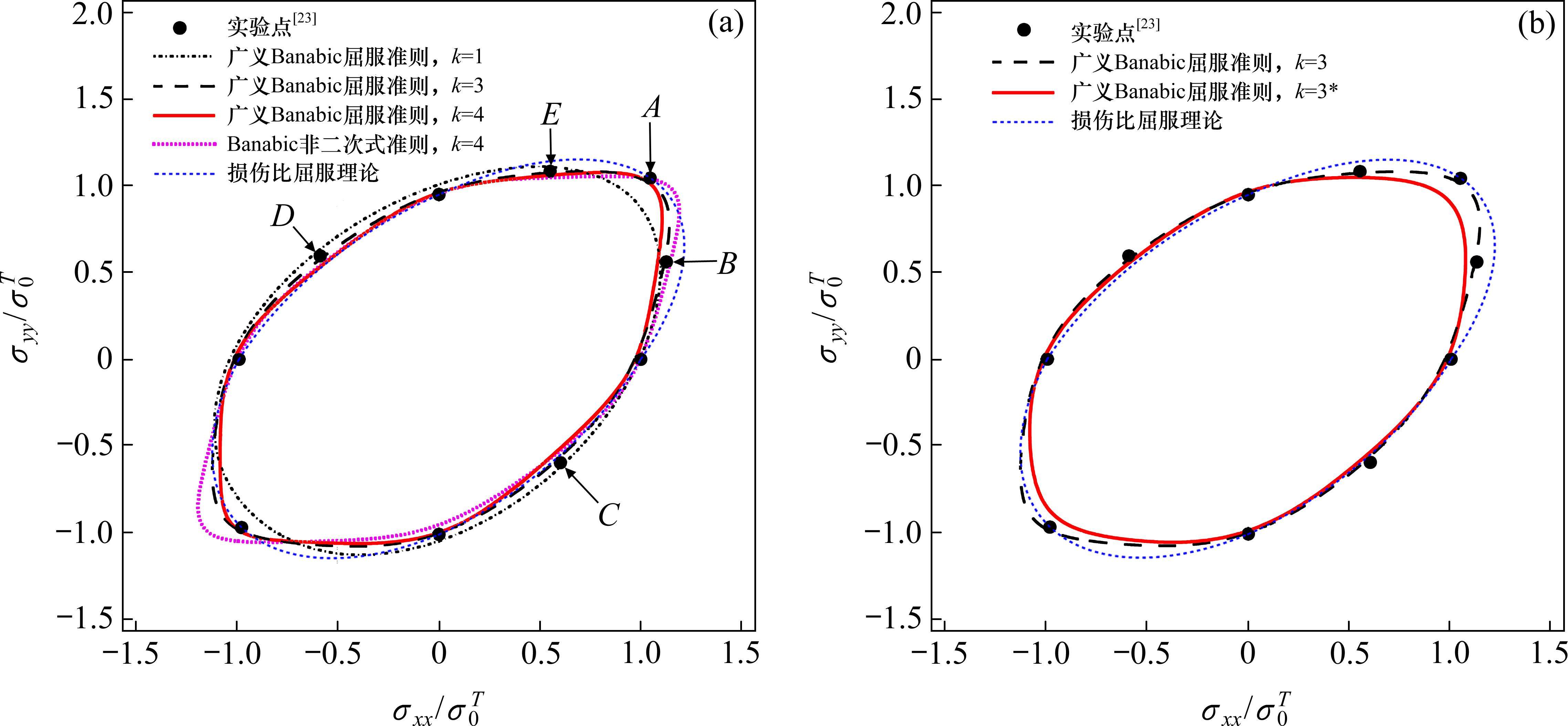
由图1(a)可以看出,Banabic非二次式准则理论屈服轨迹是拉-压对称的,在双轴拉伸区与实验结果吻合很好,但在双轴压缩区明显高估了材料的屈服应力。因此,基于拉-压对称假设建立的Banabic非二次式准则无法准确描述材料的SD效应。对比k取1,当k取3和4时,广义Banabic非二次式屈服准则与实验结果吻合更好。在纯剪切状态(C,D点),k取4时略微低估了其屈服应力,k取3时则与实验数据完全吻合。需要特别指出的是,广义Banabic非二次式屈服准则能精确模拟AA5754-O铝合金在双向等拉(压)区附近的大曲率屈服轨迹,损伤比屈服理论则明显高估了该区间的屈服应力(见B、E点)。因此,对于AA5754-O铝合金这种FCC晶体,Banabic非二次式屈服准则建议k取4,但广义Banabic非二次式屈服准则k取3时在纯剪状态与实验结果符合更好。由图1(b)可知,对于k取3,只用单轴加载实验数据及塑性应变比r值标定准则系数时,广义Banabic非二次式屈服准则除了在双向等拉(压)点附近低估了材料的屈服应力,其他区域与实验结果吻合很好。需要指出的是,损伤比屈服理论参数的标定必须采用双向加载实验数据。因此,在缺乏双向加载实验数据的情况下,广义Banabic非二次式屈服准则可以利用简单实验获得的数据标定参数,更便于工程应用。
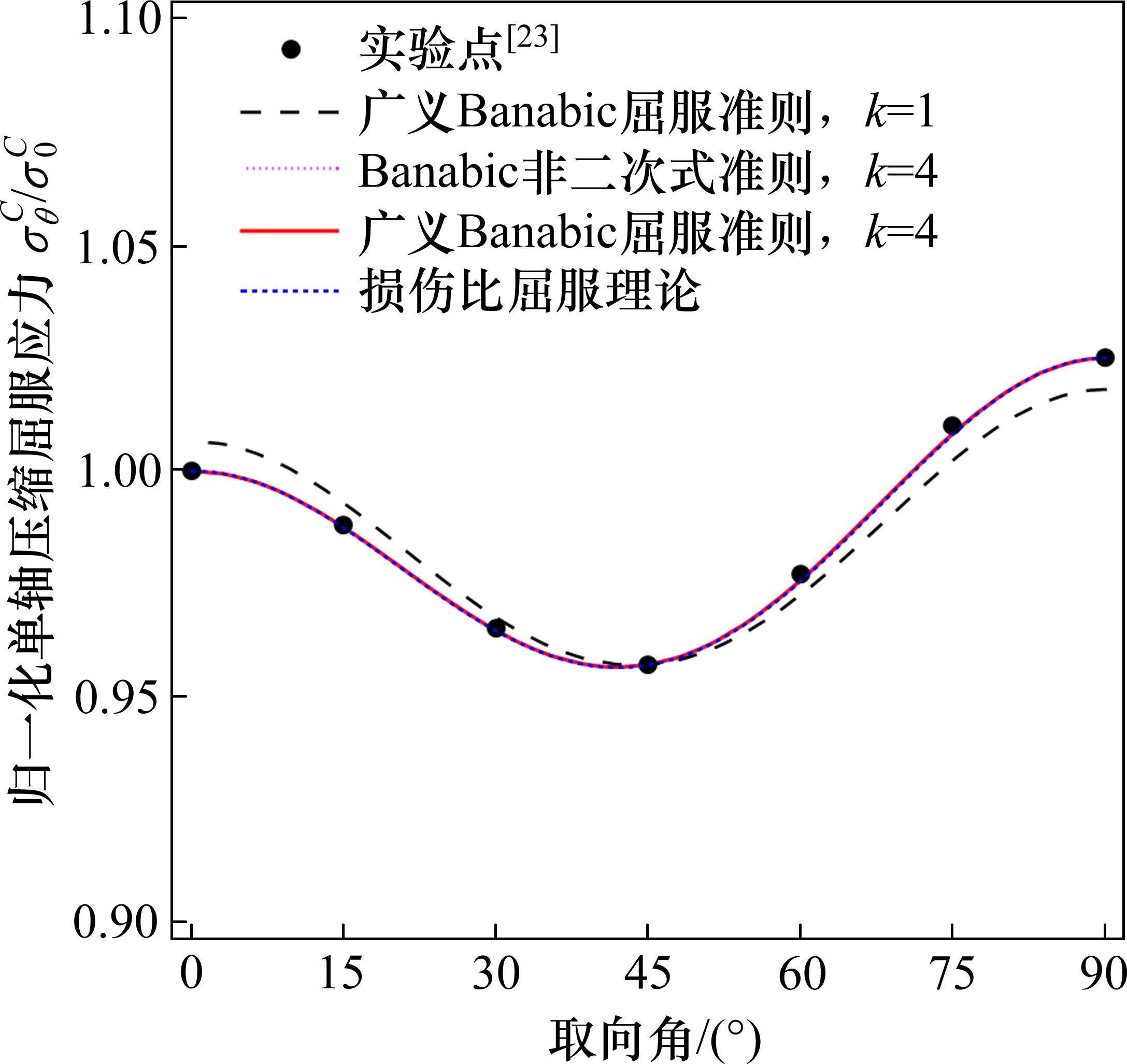
图2所示为广义Banabic非二次式屈服准则对AA5754-O铝合金单轴压缩屈服应力的预测与损伤比屈服理论的对比(应力均除以0°方向压缩屈服应力进行了归一化处理)。广义Banabic非二次式屈服准则的系数由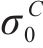
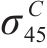
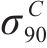
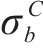
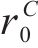
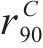
| AA5754-O | a | M | N | P | Q | R |
|---|---|---|---|---|---|---|
| k=1 | 0.527 9 | 0.508 3 | 0.562 2 | 0.492 5 | 0.463 0 | -1.035 1 |
| k=4 | 0.304 8 | 0.600 9 | 0.593 1 | 0.474 3 | 0.460 3 | 1.010 5 |
由图2可知,当k取4时,广义Banabic非二次式屈服准则对AA5754-O铝合金的单轴压缩屈服应力预测结果与损伤比屈服理论完全一致,二者与实验结果几乎完全吻合。由于损伤比屈服理论是基于明确的物理机理提出的,因此这一结果也在一定程度上佐证了其理论的正确性。当k取1时,广义Banabic非二次式屈服准则理论预测值与实验结果差别较大。当k取1时,Banabic非二次式屈服准则退化为Hill二次式准则,本文建立的准则相当于Hill二次式准则向拉-压非对称的推广。因此,二次式屈服准则无法精确描述铝合金的屈服行为,这是研究者们建立非二次式屈服准则的一个重要原因。
为了定量比较各屈服准则之间的预测能力,下面给出一个理论预测与实验结果相对误差的计算公式:
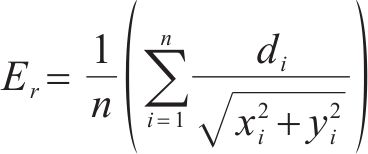
其中,(xi, yi)是实验数据坐标;n为实验点个数。参数di定义如下:
Ⅰ.单轴应力状态下,di为实验值与理论预测差值的绝对值。
Ⅱ.在双轴应力状态下,di为实验点与理论预测点的法向距离。
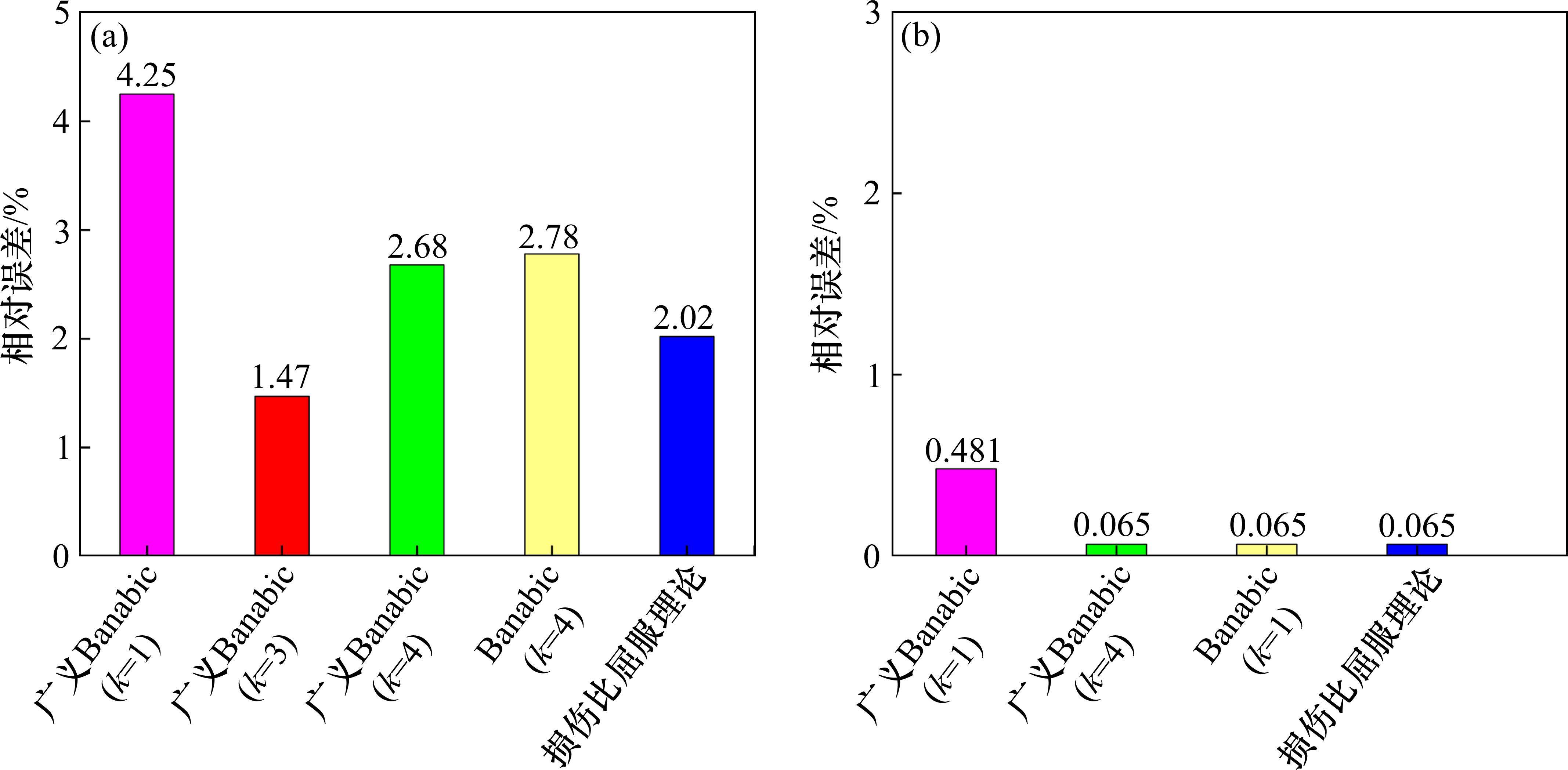
图3所示为不同屈服准则对AA5754-O铝合金屈服应力理论预测值与实验结果的相对误差柱状图。可以看出,双轴应力状态下,本文建立的广义Banabic非二次式屈服准则在k=3时预测精度最高(相对误差仅为1.47%),损伤比屈服理论也达到了很高的预测精度,误差仅为2.02%。在预测AA5754-O铝合金单轴屈服应力时,广义Banabic非二次式屈服准则(k=4)和损伤比屈服理论都达到了很高的预测精度,相对误差均为0.065%。需要指出的是,由于AA5754-O铝合金的拉-压非对称性并不显著,Banabic非二次式屈服准则在预测其屈服应力时误差也不大,双轴加载条件下也仅为2.78%。
3.2 Cu-Al-Be形状记忆合金
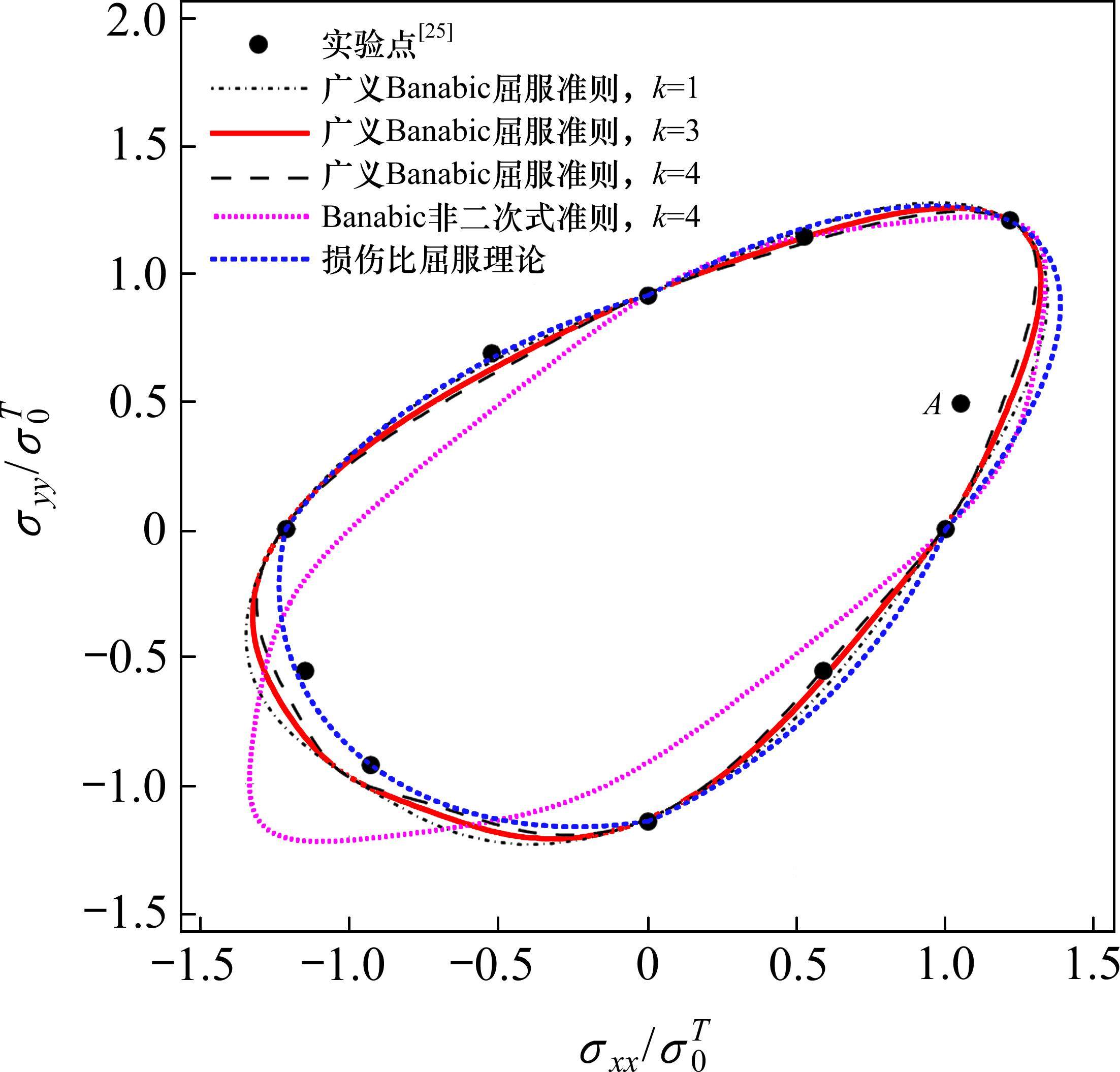
形状记忆合金(Shape Memory Alloys,SMA)在物理、力学性能方面通常具有拉-压非对称性。BOUVET等[24]对Cu-Al-Be形状记忆合金在多轴比例和非比例载荷下的行为进行了广泛的实验研究,获得了其由应力导致的相变转换(奥氏体到马氏体)条件。图4所示为Cu-Al-Be形状记忆合金相变转换起始“屈服面”实验结果,以及3种屈服准则的理论预测结果对比(由于实验点A疑是实验错误导致,对于该实验数据不作讨论)。可以看出,Cu-Al-Be形状记忆合金的相变转起始面具有明显的不对称形状,压缩“屈服”应力比拉伸“屈服”应力大20%左右。严格来说,形状记忆合金的相变转变起始面与金属的屈服面是有区别的。然而,由于两者都是应力空间中的域边界,因此用类似的模型来描述它们是合理的,例如LAYDI等[25]采用屈服准则来模拟形状记忆合金的相变转换起始面。在此,本文也采用屈服准则来预测形状记忆合金的相变转换“屈服”面。表6列出了由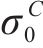
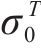
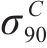
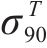
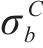
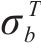
| Cu-Al-Be | a | M | N | P | Q | λ |
|---|---|---|---|---|---|---|
| k=1 | 0.492 5 | 0.383 4 | 0.446 5 | 0.417 2 | 0.436 4 | -0.208 4 |
| k=3 | 0.498 8 | 0.379 9 | 0.443 7 | 0.418 0 | 0.437 3 | -0.625 4 |
| k=4 | 0.499 7 | 0.379 3 | 0.443 6 | 0.418 0 | 0.437 4 | -0.832 7 |
由图4可以看出,Banabic非二次式准则理论屈服轨迹是拉-压对称的,在双轴拉伸区与实验结果吻合很好,但在双轴压缩区明显高估了材料的屈服应力。因此,基于拉-压对称假设建立的Banabic非二次式准则无法准确描述Cu-Al-Be形状记忆合金的SD效应。相比于k取1和3,当k取4时,广义Banabic非二次式屈服准则与实验结果更吻合,能较好地预测Cu-Al-Be的相变转换应力,但在双向等压区高估了其“屈服”应力。损伤比屈服理论预测精度高于广义Banabic非二次式屈服准则,能精确描述Cu-Al-Be形状记忆合金起始相变转换“屈服”面,但其理论“屈服面”在(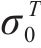
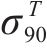
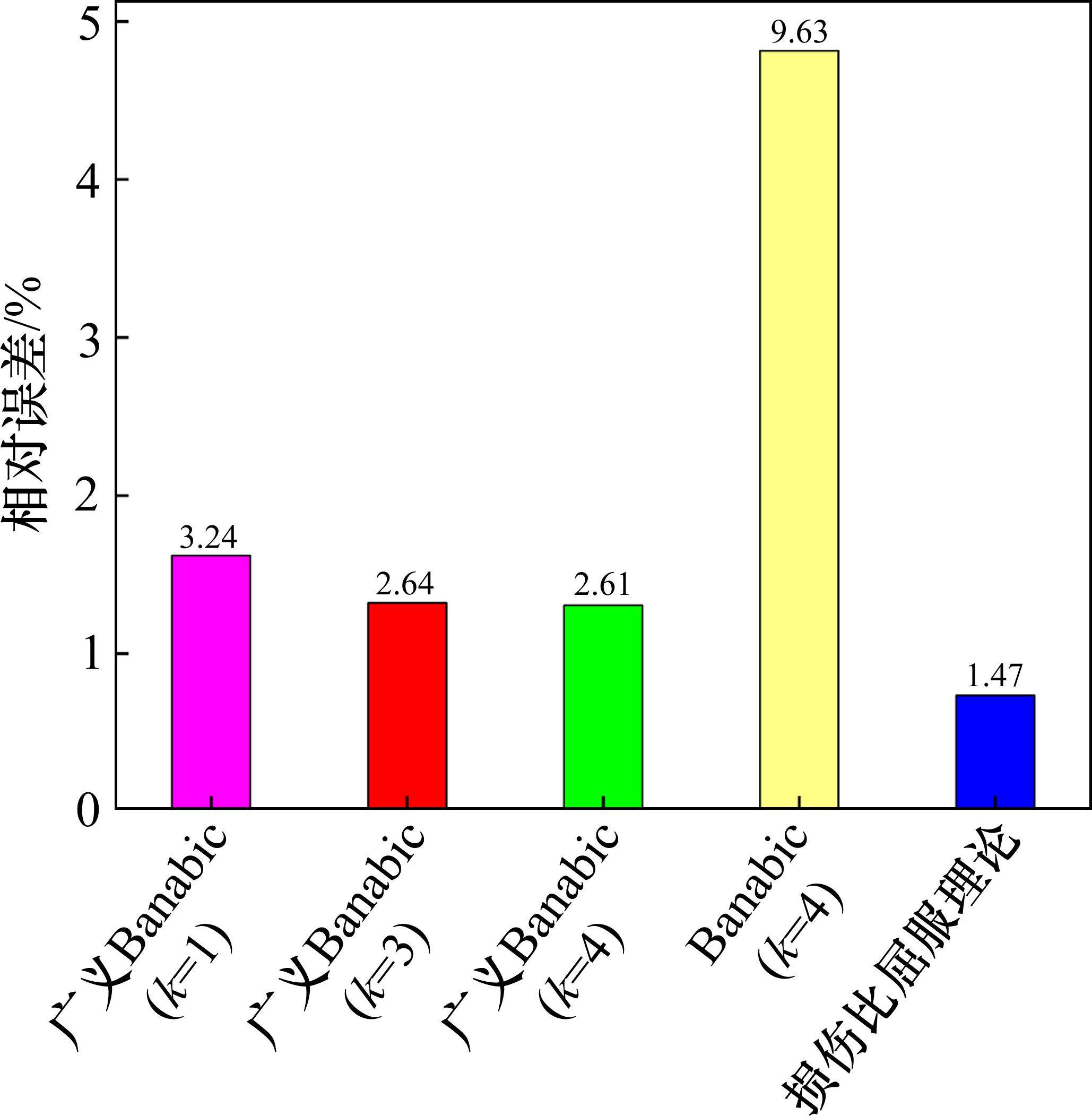
图5为双轴应力状态下不同屈服准则对Cu-Al-Be形状记忆合金“屈服”应力理论预测值与实验数据的相对误差柱状图。可以看出,损伤比屈服理论的预测精度最高,广义Banabic非二次式屈服准则在k取3和4时也达到了很高的预测精度,相对误差均低于3%。基于拉-压对称的Banabic非二次式屈服准则在描述Cu-Al-Be形状记忆合金这种具有显著SD效应的材料时会产生显著误差。
4 结论
1) 广义Banabic非二次式屈服准则和损伤比屈服理论都能精确预测AA5754-O铝合金压缩屈服应力随取向角的变化规律,二者的理论预测结果完全一致。
2) 在双向应力状态下,广义Banabic非二次式屈服准则能很好地模拟AA5754-O铝合金在双向等拉(压)区附近的大曲率屈服轨迹,损伤比屈服理论则高估了其屈服应力。
3) 对Cu-Al-Be形状记忆合金起始相变转换“屈服”面的预测,损伤比屈服理论预测精度高于广义Banabic非二次式屈服准则,但其理论预测屈服面出现了明显的内凹现象,这可能与Cu-Al-Be形状记忆合金损伤比系数较小有关。损伤比屈服理论应用到损伤比系数较小的金属时是否存在屈服面内凹的问题,有待进一步探讨。
4) 损伤比屈服理论和广义Banabic非二次式屈服准则各有千秋,前者具有明确的物理意义,后者在缺乏双向加载实验数据的情况下更便于工程应用。
余官平,陈雷,张健.广义Banabic准则与损伤比理论对金属屈服行为预测的比较[J].铁道科学与工程学报,2025,22(01):357-367.
YU Guanping,CHEN Lei,ZHANG Jian.Comparison of generalized Banabic criterion and damage ratio yield theory for prediction of metal’s yielding behavior[J].Journal of Railway Science and Engineering,2025,22(01):357-367.