随着高速列车的发展,载重的增长和运行速度的提高,轨道承受的负载及列车能耗也随之增大,列车和线路的运维成本与日俱增,车辆在运行过程中产生的振动、冲击、阻力、噪声等问题也日益凸显。动能与速度的平方及质量成正比,轻量化能抑制随高速化而增大的制动吸收能。如速度从220 km/h提高到270 km/h,动能增加1.5倍左右,但是,如果质量降低30%,则动能仅增加5%,可以明显降低牵引能耗[1]。降低高速列车轴重,可以降低车辆的制造成本,节省牵引动能,提高牵引、制动性能、运行速度及曲线通过速度,减少车辆对线路的冲击及减轻线路维护工作量,从而提高系统可靠性,降低列车全生命周期维护成本。现阶段高速列车制造中,轻量化车体材料已经得到广泛应用,轴重从17 t减轻到13 t,牵引变流器是列车的动力保证,也存在轻量化设计的需求。牵引变流器包括四象限整流器、中间直流环节和牵引逆变器[2-3]。中间直流环节主要包括LC二次谐振支路和支撑电容,占据了牵引变流器重量的40%左右。LC谐振回路的主要功能是吸收2倍于电网频率的脉动成分,从而消除脉动成分对电网及逆变器的影响[4-5]。然而,传统的LC谐振采用电感、电容串联,存在体积大、质量重的问题,并且由于无源器件老化存在参数偏移,会影响谐振回路的吸收效果[6, 7],因此取消LC谐振电路,有利于牵引变流器的轻量化,节约牵引能量,更灵活地调整谐振频率。随着功率器件与变流控制技术的发展,有源功率解耦(active power decoupling, APD)技术使用功率半导体器件,配合小容量储能元件,通过主动控制的方式弥补二次纹波脉动。相关研究者提出了各种有源功率解耦拓扑,如Buck拓扑[8-9]、Boost拓扑[10-11]、Buck-Boost拓扑[12-13]、H桥拓扑[14]、分裂电容拓扑[15]等方法,这些拓扑与整流器互相独立。对于高速列车来说,需要有源功率解耦拓扑能应用于大功率低开关频率的场景,同时器件数量尽可能较少,以满足轻量化研究的目的[16]。Boost拓扑器件应力高,电流跟踪性能差,不适用于大功率环境;Buck-Boost拓扑输入输出电流不连续,电感吸收纹波能量效率较低;H桥拓扑有源器件数量多,重量大,难以实现轻量化目标;分裂电容解耦电感取值过大;Buck拓扑应用场合广,主要通过电容存储纹波能量,可以有效减少解耦单元的体积和重量。本文选择Buck斩波有源功率解耦拓扑进行深入研究。沈来来等[17]采用的Buck拓扑,加强了对电容电压的控制反馈,有助于减小辅助电容,但拓扑中电容与其中一个开关管串接,这种非桥臂式结构不利于系统模块化。NGUYEN等[18]采用比例谐振控制器控制电源电流,采用比例积分控制器控制直流环节电压,建立电压-电流双闭环控制,实际响应速率较低,不适用于轨道交通低开关频率场景。MUTOVKIN等[19]使用直流母线电流作为辅助电感的电流指令值,采用比例谐振控制直流侧的二次脉动功率使其转移至辅助电路中,但实际中支撑电容大多是分布式配置,采集直流母线电流可行性不高,并且需要增设电流传感器,增加成本。对于高速列车大功率低开关频率的场景,常用的双闭环、状态反馈等控制器受限于低带宽,无法获得高质量的稳态波形,从而难以有效抑制低频谐波,经有源功率解耦后,依然会对电机有不良影响。而重复控制与传统控制方法不同,其在获取控制对象数学模型的基础上,嵌入了指令频率信号与指令信号整数倍频率的信号[20-21],可以实现被控量与理想值偏差的调节,从而控制每个采样点的跟踪,实现低带宽条件下高精度的指令跟踪[22-23],在高速列车大功率低开关频率的场景中能充分发挥其优越性。本文以标准动车组CR400AF为研究对象,针对牵引变流器直流环节Buck斩波有源功率解耦拓扑,提出了基于重复控制的功率解耦策略,实现了牵引变流器的轻量化。
1 Buck斩波有源功率解耦拓扑工作原理与参数设计
在理想情况下,整流器网侧的功率没有损耗,完全被直流侧利用,在瞬时状态下,直流侧瞬时功率应等于交流侧瞬时功率:
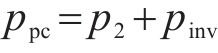
式中:

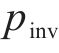
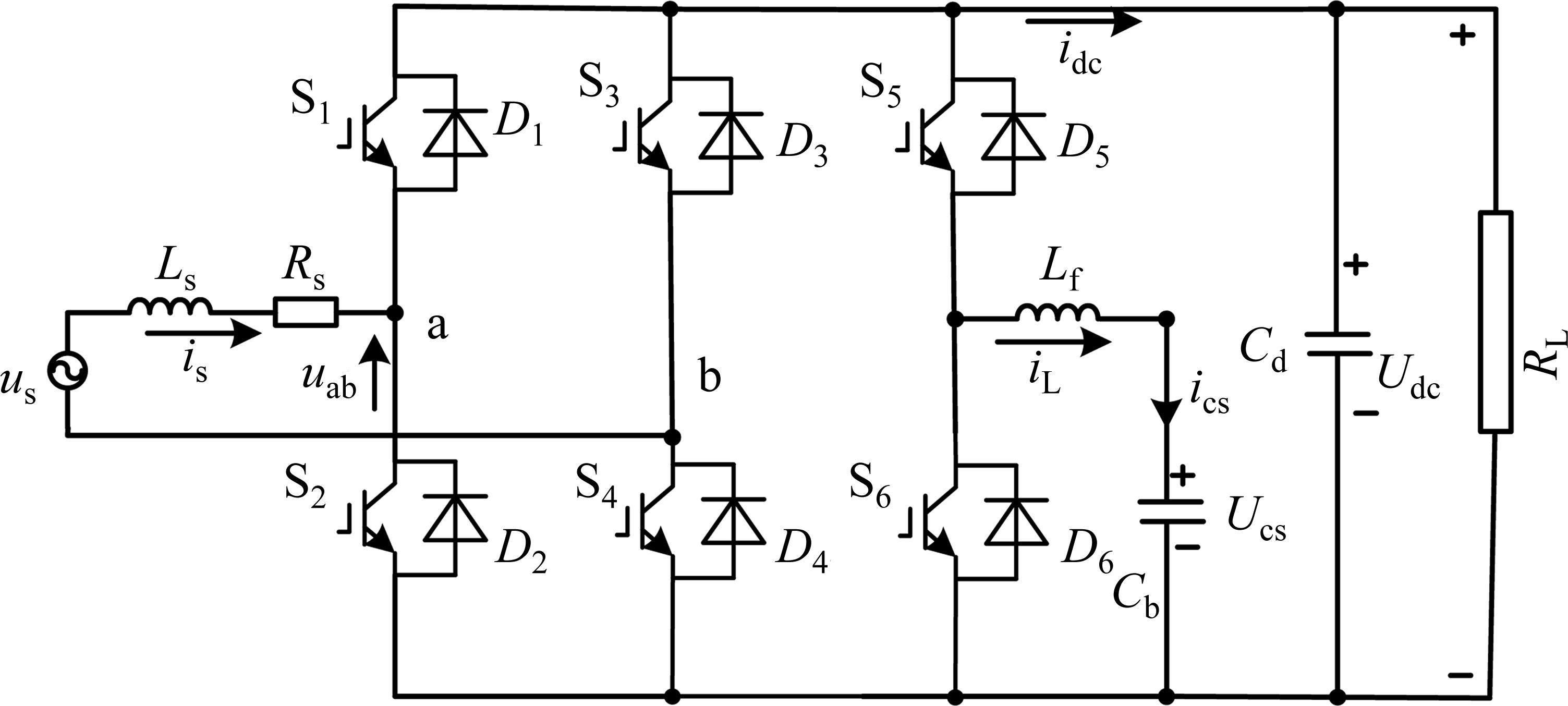
对比Buck斩波有源功率解耦的电感和电阻,电容在二次脉动频率时的阻抗相对较小,如果忽略电容此时的阻抗,则二次脉动全部被电容吸收。
Buck斩波有源功率解耦中的储能电容在不同工况下的不同状态下吸收或释放的功率补偿二次谐波功率,假设储能电容电流为:
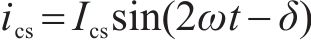
当电容电流为正弦波时,储能电容电压除包含正弦分量外还应叠加一个直流分量:
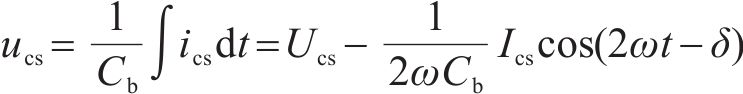
对应求出解耦电路产生的功率由电容功率和电感功率组成,如式(3)所示,由此可得解耦电路包括2倍频功率和4倍频功率。
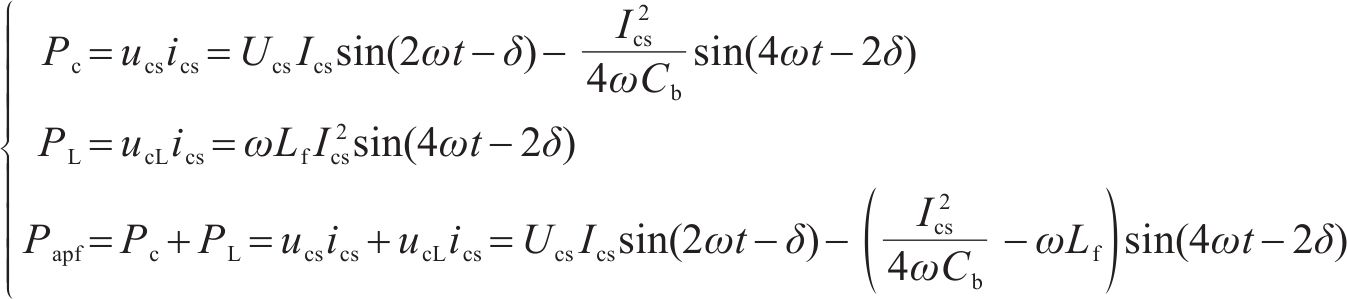
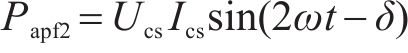
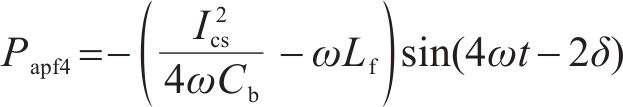
从式(6)可以看出,Buck斩波有源功率解耦可以将二次脉动功率弥补,但同时也会额外带来4倍于电网频率的脉动功率,进而导致直流母线电压中的4次谐波脉动。如果要消除新引入的干扰,就必须使用更大的电容和电感形成谐振回路。然而,电容和电感的增大与轻量化目标不符。因此,从高速列车应用角度来看,参数设计应达到2个目标:尽可能使储能电容最小化,以及降低4次脉动的输出功率。
为了抑制直流母线电压的二次纹波,有源功率解耦拓扑中的储能元件需要完全补偿二次纹波产生的脉动功率,结合式(3)与式(4),可得:
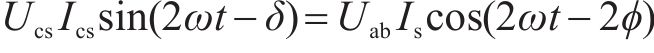
Buck斩波有源功率解耦工作在降压模式,因此桥臂电压不超过直流母线电压:
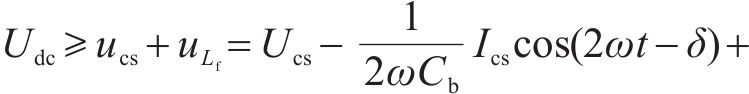
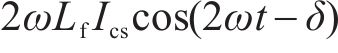
令占空比

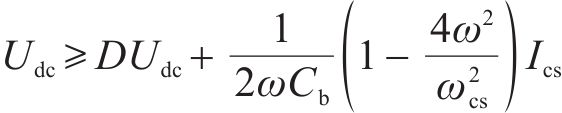
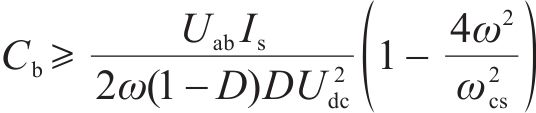
解耦电容应有较高的功率密度,即取值应尽量小:
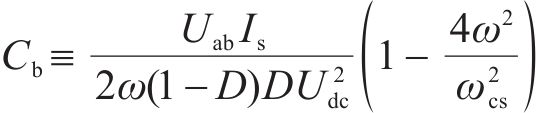
4次脉动功率最大幅值为:
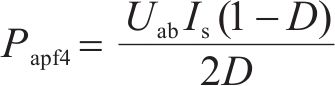
为保证一定的控制带宽和较小的电容量,Buck斩波的谐振频率应尽量取大。由于LC电路与Buck斩波开关谐波会产生共振,为了避免这种可能,谐振频率一般取为开关频率的1/10~1/5。谐振频率较高时,电感和电容取值较小,因此Buck斩波的谐振频率取开关频率的1/5。
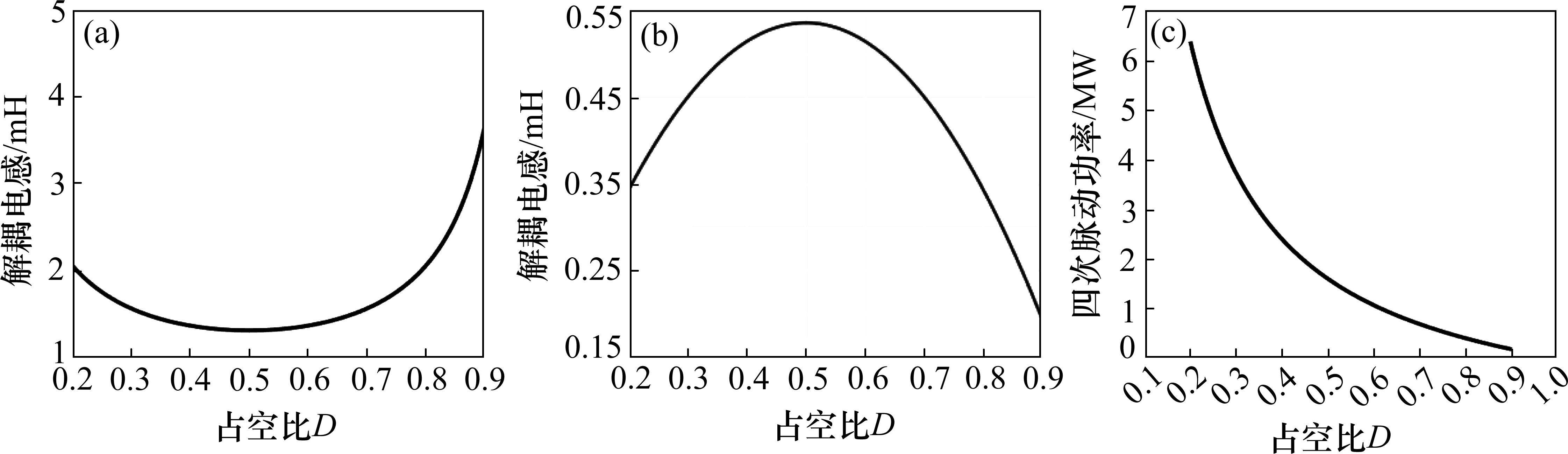
根据CR400AF相关参数,图2给出了Buck斩波有源功率解耦拓扑中解耦电容、解耦电感、4次脉动功率与占空比的关系。随着占空比的增大,4次脉动功率会对应减小。储能电容先减小后增大,D=0.5时,取得最小值。解耦电感先增大后减小,在D=0.5时,取得最大值。在考虑D取值时,如果取0.5,虽然电容值最小,但4次脉动功率和电感取值都较大,不满足前文提出的解耦电容尽可能小、输出的4次脉动功率少这2个目标。当D取大于0.5时,电容虽然会增大,但4次脉动功率和电感大小显著下降。综合以上因素,需要对电感电流、电容以及4次功率进行综合寻优。
2 基于粒子群优化算法的解耦参数最优设计
粒子群优化(particle swarm optimization, PSO)算法源于对鸟类捕食行为的研究,即鸟类会寻找离它们目前正在吃的食物最近的区域。PSO算法在可行解空间中初始化一群粒子,每个粒子代表极值优化问题的潜在最优解。每次粒子更新其位置时,都会计算并传递适应度值将新粒子的适应度值与个体极值和组极值的适应度进行比较,以更新个体极值pbest和群体极值gbest。
迭代过程中,第d-1步所在的位置+第d-1步的速度×运动的时间=第d步所在的位置。在每次迭代过程中,粒子通过个体极值和群体极值更新自身的速度和位置,即:
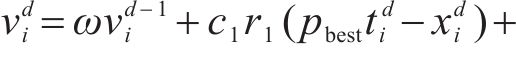
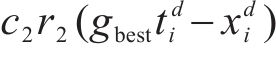
式中:


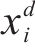
在设计Buck斩波有源功率解耦择优参数时,应使解耦电容容值,解耦电感感值和4次脉动幅值尽量接近群体最优值,据此建立如下多目标优化函数:
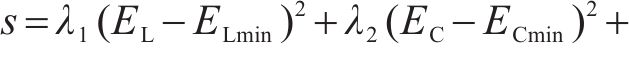
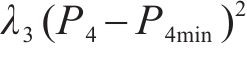
式中:




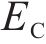



Buck斩波有源功率解耦参数选型的PSO算法的运行包括初始化参数、计算各个体适应度、迭代等步骤,具体流程见图3。
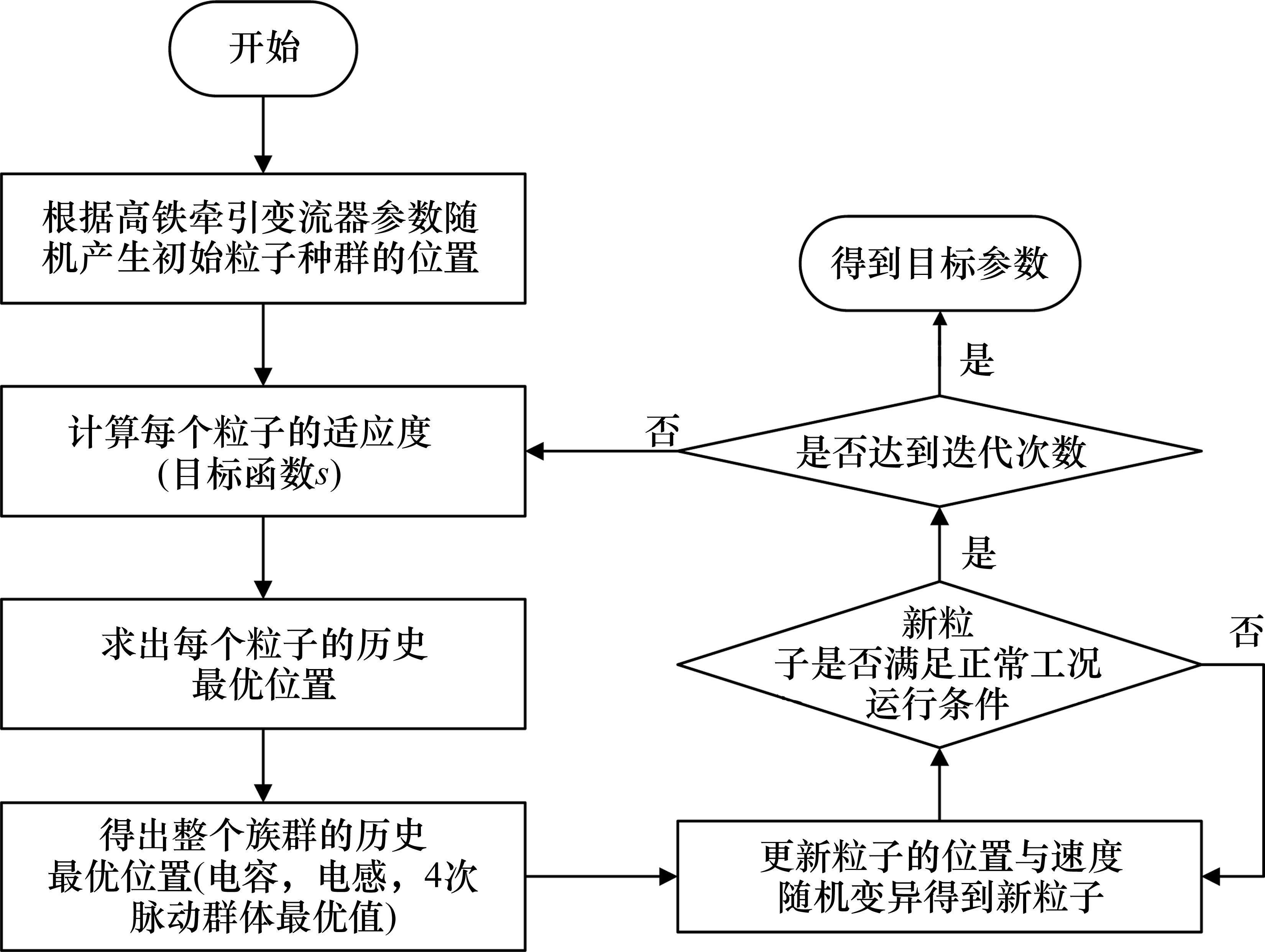
结合CR400AF高速列车实际中间直流电压、开关频率、支撑电容大小等条件,可以得到本次PSO算法求解的初始条件,本次选用的多目标权重为1、1、0.5,设置粒子数量为100,变量个数为3,迭代次数为200次来寻找最优解。运用MATLAB软件完成PSO算法,得到解耦电感、解耦电容、电压目标值的设计参数,如表1所示。
| 项目名称 | 参数 | 项目名称 | 参数 |
|---|---|---|---|
| 中间直流电压Udc/V | 3 600 | 解耦电感Lf/mH | 0.3 |
| 开关频率/Hz | 1 | 解耦电容Cb/mF | 2.0 |
| 解耦电容电压目标值Vav-ref/V | 3 250 | 支撑电容Cd/mF | 5 |
3 Buck斩波有源功率解耦控制策略
从前面的分析可知,解耦电容的电压按照脉动频率变化即可吸收二次脉动能量,因此以解耦电容电压为控制目标,控制系统框图如图4,包括二次脉动电流提取、直流分量跟踪、交流分量跟踪以及调制4个部分。
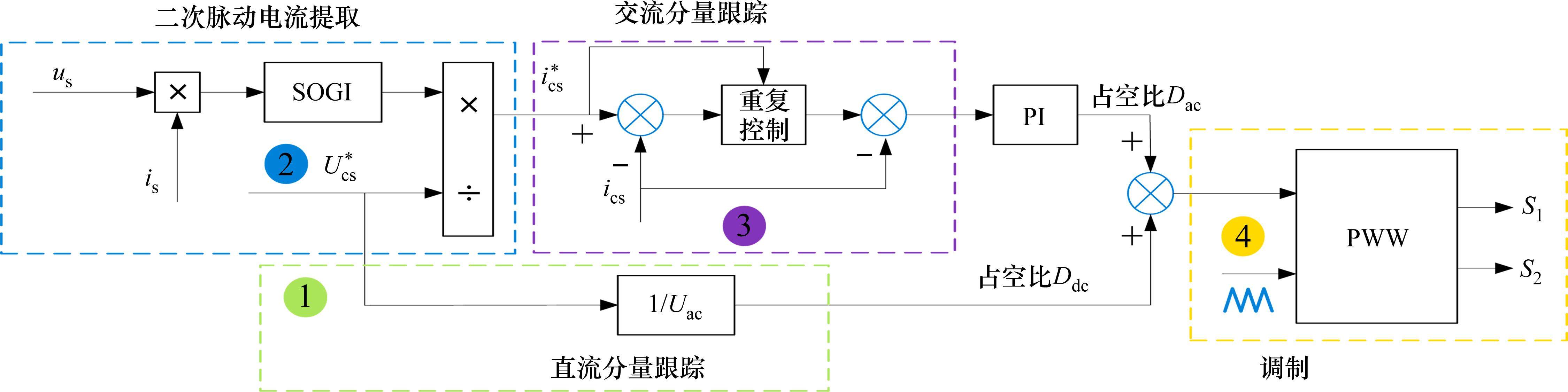
解耦电容电压包括直流部分和交流部分,电容电压给定值与直流环节电压Udc的比值等于直流分量跟踪的占空比给定。为了控制解耦电容电压的交流部分,通过控制解耦电路中的电流实现。首先通过二阶广义积分器(second order generalized integrator, SOGI)提取网侧二次脉动功率作为参考值,与电容电压目标值相除,得到电容二次脉动电流的参考值,再通过重复控制跟踪指令电流的变化与实际电容电流比较,经过PI调节后,得到电容交流电压分量控制的占空比,最后通过脉宽调制(pulse width modulation, PWM)得到2个绝缘栅双极型晶体管(insulated gate bipolar transistor, IGBT)的控制信号。
重复控制基于内模原理,本质上也是变增益控制的一种。内模原理的基本思想是把外部参考信号的数学模型置于控制器中,误差信号经过控制器的作用后,使对应谐振频率的开环增益达到无穷大,因此,重复控制对周期性信号有极高的控制精度,能够有效抑制谐波扰动,从而可以在低带宽条件下实现高精度的指令跟踪。为了实现对参考输入信号的无静差跟踪和谐波扰动的抑制,控制器中应包含基波及各次谐波的数学模型。
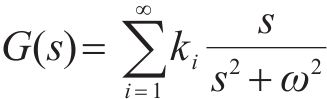
在实际重复控制的应用时,需要对理论模型进行改进,得到有补偿的改进重复控制模型。基于本文Buck有源功率解耦,得到改进后的控制框图如图5所示。其中,
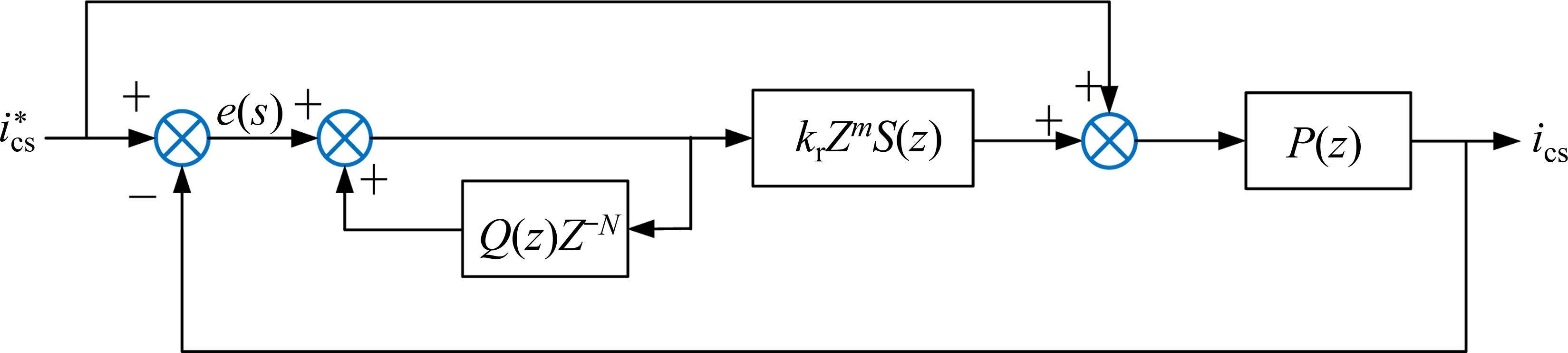
P(z)被控对象的数学模型为:
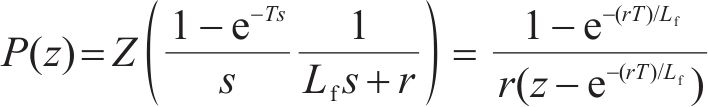
式中:T为采样频率;r为体现实际装置电感、电容的ESR,以及死区影响的虚拟电阻;Lf为辅助电感。
重复控制增益kr控制了输出信号的幅值大小。kr的取值越大,重复控制的控制作用越大,但会影响系统稳定性。补偿环节主要解决P(z)参数变化或系统建模不精确导致的系统不稳定问题。S(z)为低通滤波器,可以进一步对高频信号进行衰减,针对Buck斩波有源功率解耦的实际解耦电容,解耦电感的谐振频率,选取滤波器的截止频率。
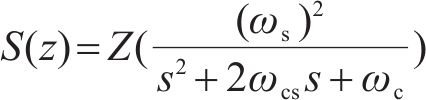
式中:ωc为谐振频率。
zm为线性相位超前补偿环节,用来补偿由P(z)和低通滤波器S(z)导致的相位滞后,实际应用中需满足krzmS(z)P(z)=1;zmS(z)可以改善被控对象P(z)的频率特性,进而使系统具备最优的稳定裕度和控制精度。
目前内模系数Q(z)主要有2种设计方法,一种是小于1的常数,另一种采用低通滤波器。前一种牺牲系统的稳态误差控制精度提高系统的稳定性,后一种在低频段维持信号的无静差跟踪特性,同时在高频段快速衰减高频信号。一般选用后一种方法作为Q(z),Q(z)的选取原则是使Q(z)在低频段满足Q(z)趋近于1,在高频段满足Q(z)趋近于0。通常选取:
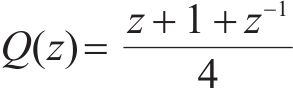
综上,结合实际条件,取kr=1.02,zm=z5,z-N=z-40,
4 仿真与实验验证
4.1 仿真结果分析
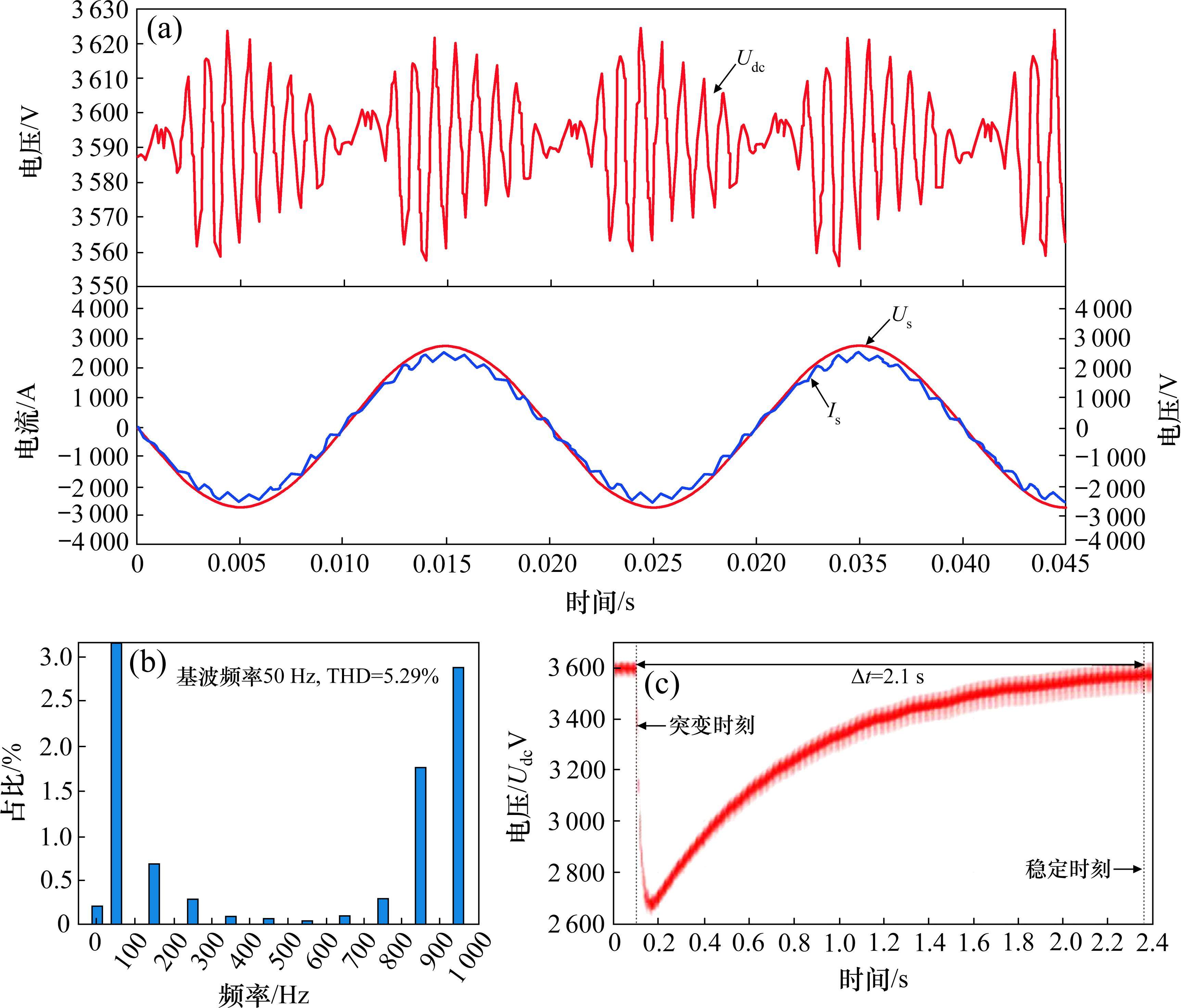
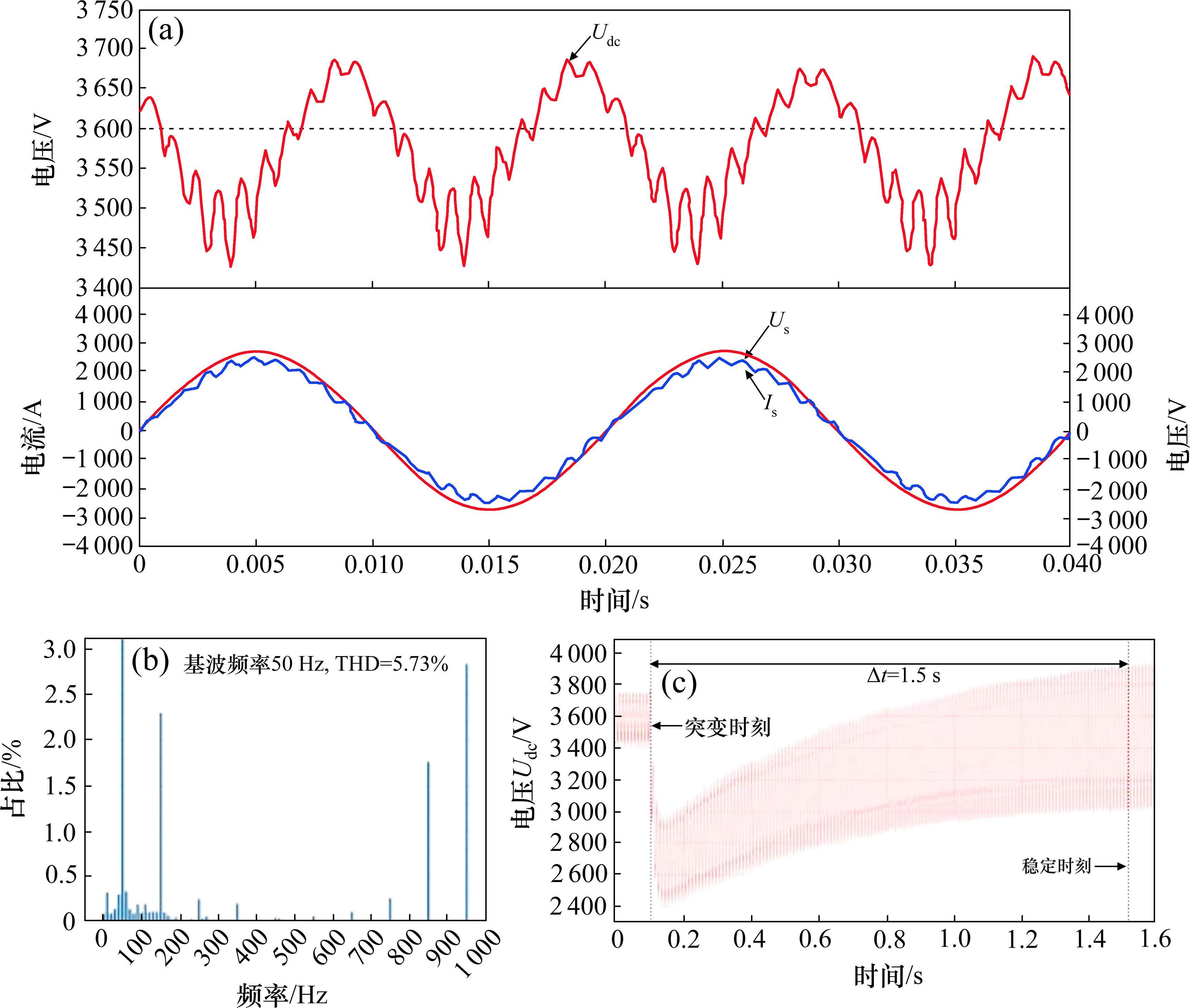
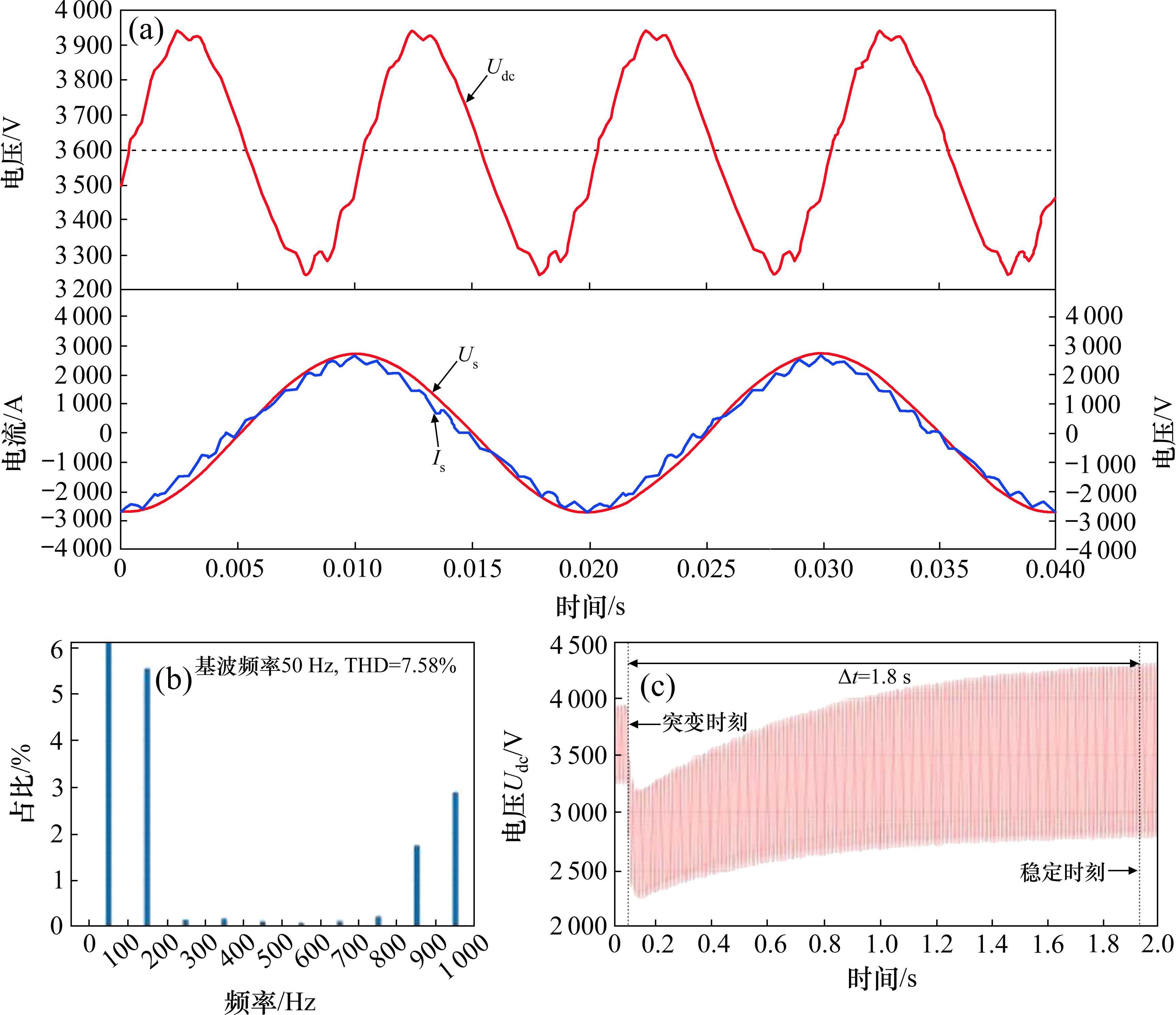
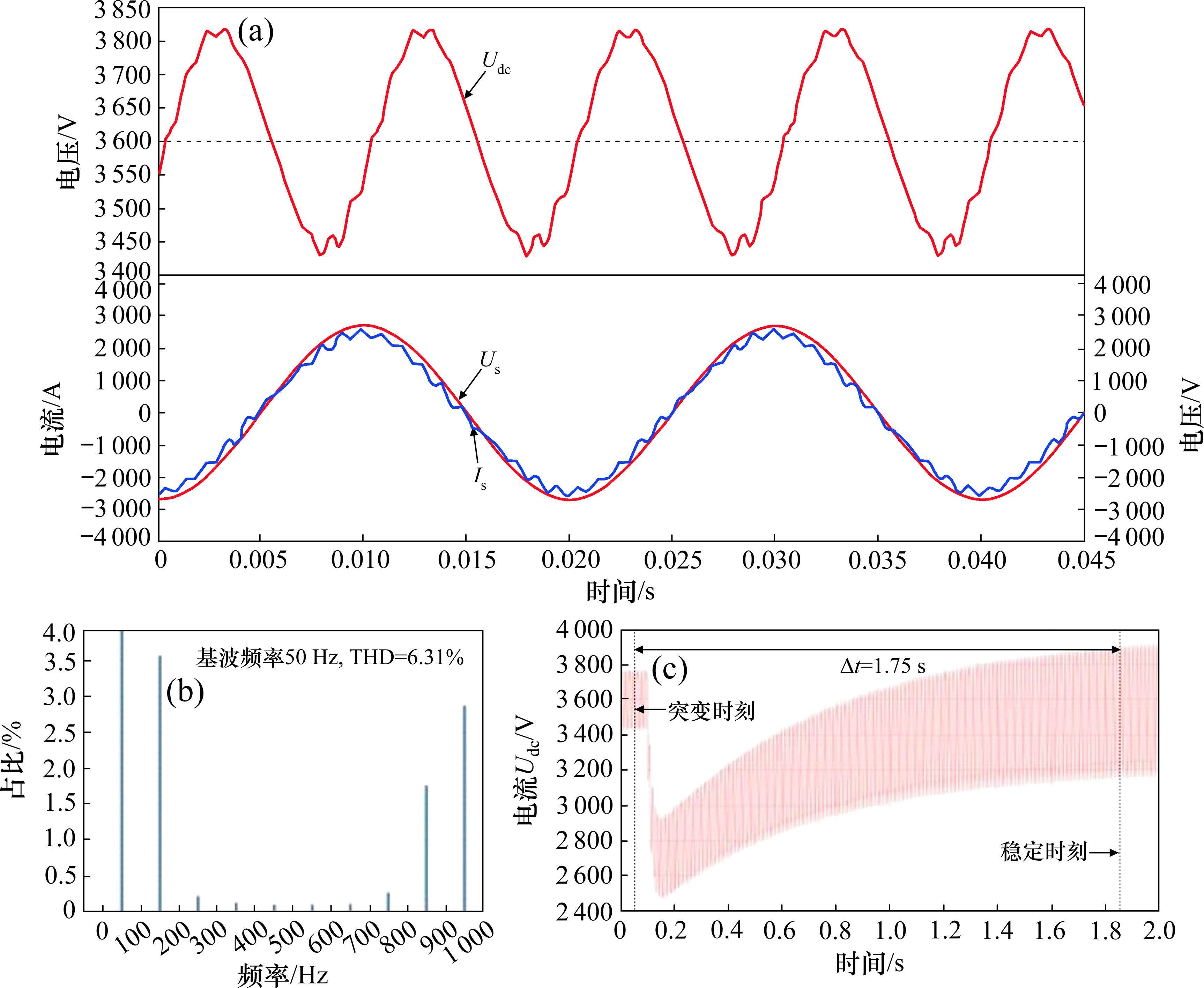
以CR400AF为例,建立具有Buck斩波有源功率解耦拓扑的牵引变流器仿真模型,有源功率解耦无源器件参数采用表1所示的PSO算法寻优结果。对其运行情况进行仿真,对比了4种拓扑的控制性能,4种拓扑的稳态工作波形如图6~图9,结果如表2所示。
| 拓扑 | 直流电压纹波/V | 网侧电流THD/% | 负载变化50%响应时间/s |
|---|---|---|---|
| LC滤波 | 35 | 5.29 | 2.10 |
| 无二次脉动抑制 | 350 | 7.95 | 1.80 |
| 10 mF支撑电容 | 160 | 6.73 | 1.75 |
| Buck拓扑 | 125 | 5.73 | 1.40 |
在没有抑制二次脉动拓扑时,即无LC谐振和Buck拓扑的情况下,直流电压的波动幅度很大;而投入Buck拓扑后,直流电压纹波降低到125 V,稳定了直流电压输出。但Buck斩波有源功率解耦的效果不及LC滤波,LC滤波的二次纹波大小仅为35 V左右。而对比网侧总谐波失真(total harmonic distortion, THD),LC与Buck斩波有源功率解耦方法都得到了较好的结果,分别为5.31%和5.68%。在负载突变50%时,Buck斩波有源功率解耦方法的响应时间最短,比LC滤波与无LC有更好的动态性能。
Buck斩波有源功率解耦工作后不仅可以有效滤除二次脉动,稳定直流电压输出,使网侧电流波形更加接近于正弦波,并且能在低带宽条件下实现高精度的指令跟踪,提高动态性能。由理论分析可以得知Buck斩波有源功率解耦投入后,引入了4倍频谐波,但含量相对很低,对牵引系统造成的不良影响基本可以忽略不计。
CR400AF标准动车组采用模块式变流器,辅助变流器使用2个变流模块单元,包含4个IGBT桥臂,仅使用了其中3个桥臂,剩余1个冗余桥臂,Buck斩波有源功率解耦拓扑和控制方案,可以使用现有辅助变流器中的冗余桥臂,对比LC谐振回路不需要额外增加功率器件与散热装置。对3种方案进行对比,如表3所示。在重量方面,Buck斩波有源功率解耦拓扑相比LC谐振回路减少28.3%,相比增大支撑电容减少5%。在成本方面,Buck斩波有源功率解耦拓扑电感电流有效值相比LC谐振回路没有增加,电容耐压有所下降,电感电容大小均减小。在工程应用选型时,决定电感、电容成本的关键因素是感值容值与电流电压等级,Buck斩波有源功率解耦拓扑电感、电容成本会相应降低,但考虑到拓扑改动,二者成本相当。在直流电压纹波方面,Buck斩波有源功率解耦拓扑相比LC谐振回路增大约90 V,相比增大支撑电容减少35 V,约为3.47%,符合少于5%的规定。同时,对比负载变化50%响应时间,Buck斩波有源功率解耦用时最少,比LC谐振回路减少34.8%,说明动态性能得到了提升。
| LC谐振回路 | 增加支撑电容 | Buck有源功率解耦 | |
|---|---|---|---|
| 电感值/mH | 5 | — | 0.3 |
| 电容值/mF | 5 | 10 | 2 |
| 电感电流有效值/A | 700 | — | 700 |
| 电容电压/V | 3 600 | 3 600 | 3 250 |
| 直流环节重量(约)/kg | 530 | 400 | 380 |
| 直流纹波峰值(约)/V | 35 | 160 | 125 |
4.2 实验结果分析
为了验证所提出算法的有效性,搭建了小功率的实验样机,如图10所示。利用现场可编程门阵列(field programmable gate array, FPGA)板卡进行模拟采样和PWM脉冲的输出,在中央处理器(central processing unit, CPU)板卡运行控制算法并输出占空比计算值。实验采用的参数如表4所示。

| 项目名称 | 参数 | 项目名称 | 参数 |
|---|---|---|---|
| 支撑电容Cd/mF | 0.42 | LC谐振电容/mF | 3 |
| 斩波开关频率/kHz | 10 | 解耦电感Lf/mH | 2 |
| LC谐振电感/mH | 0.84 | 解耦电容Cb/mF | 0.42 |
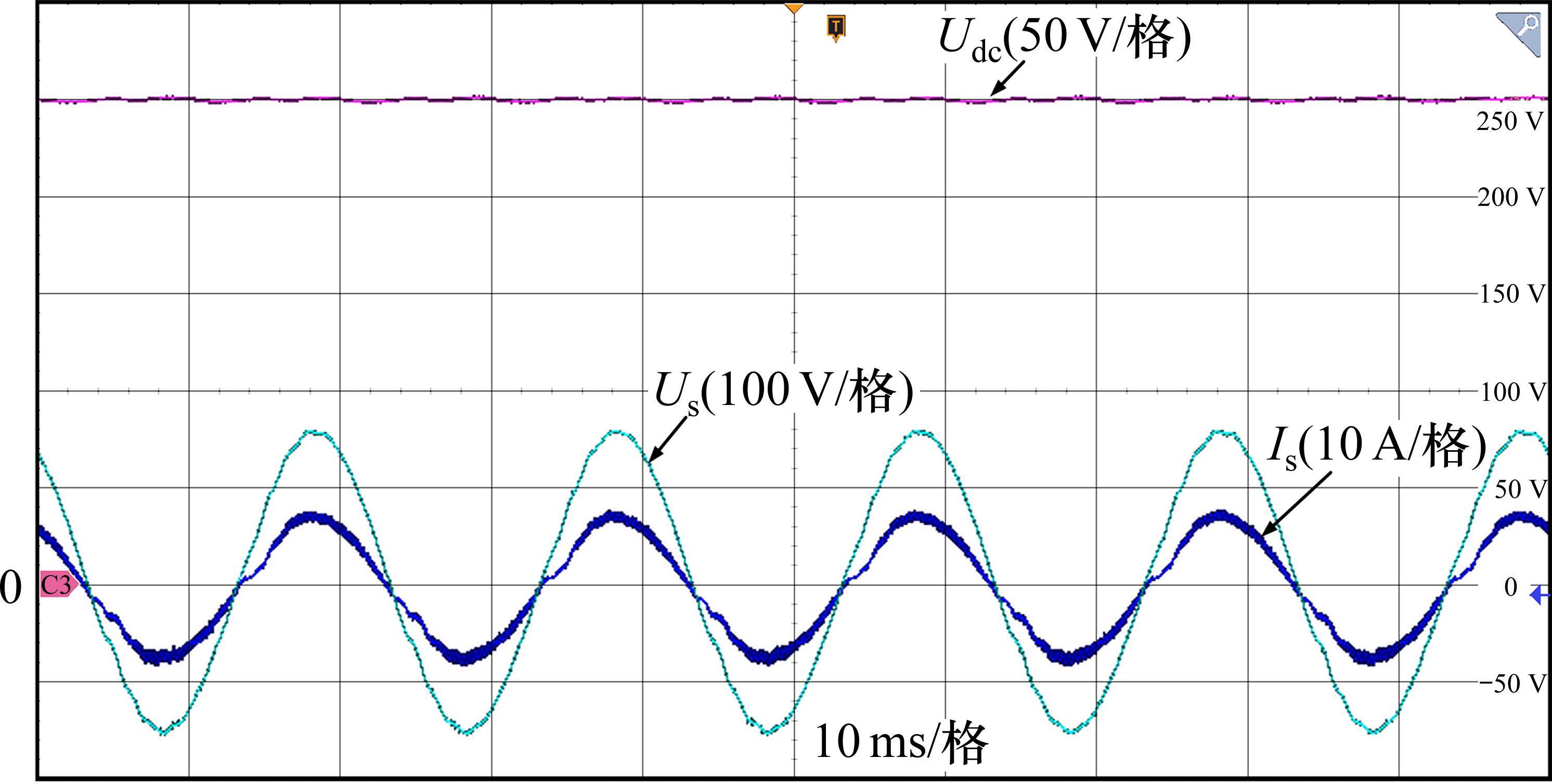
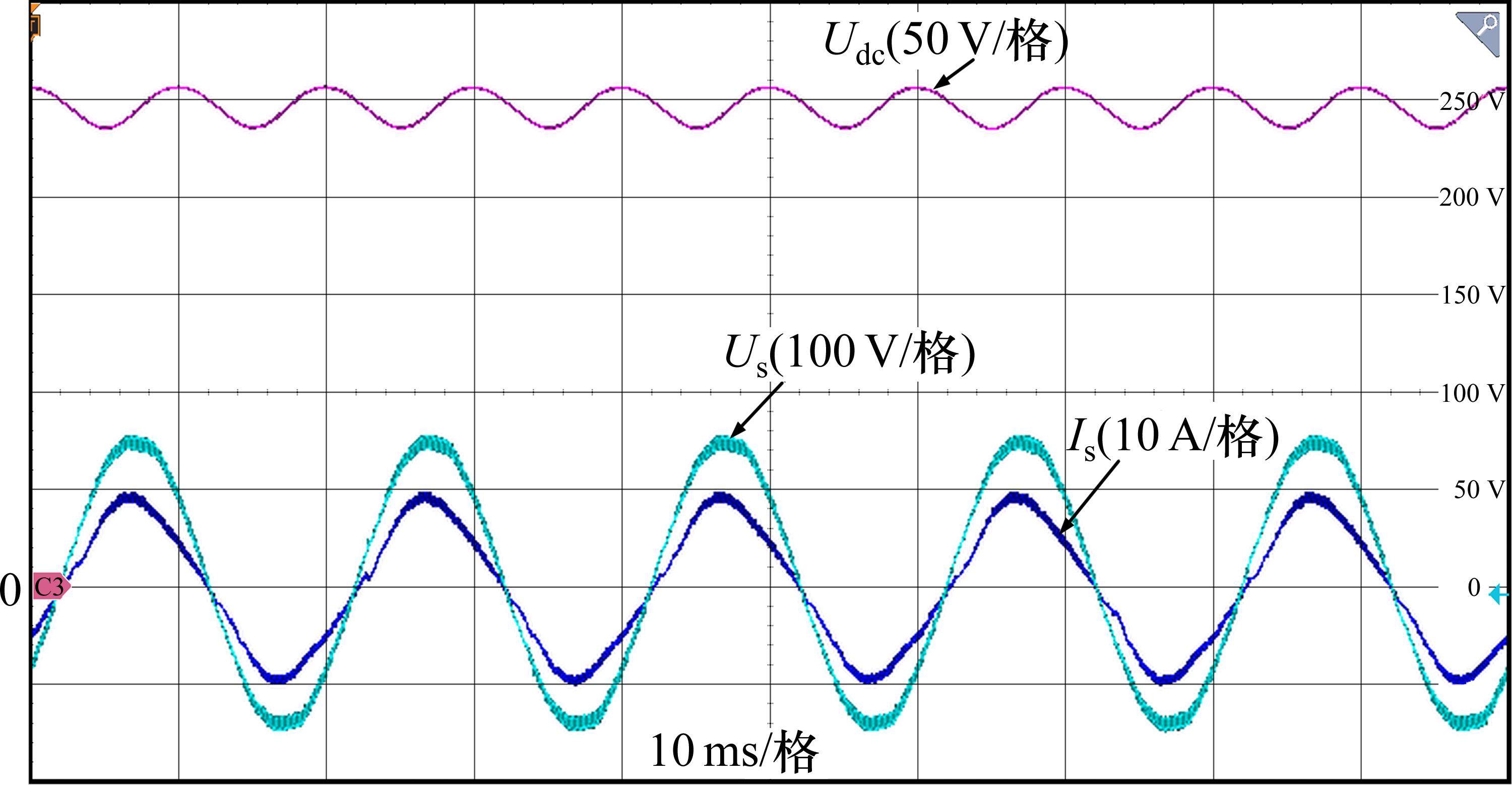
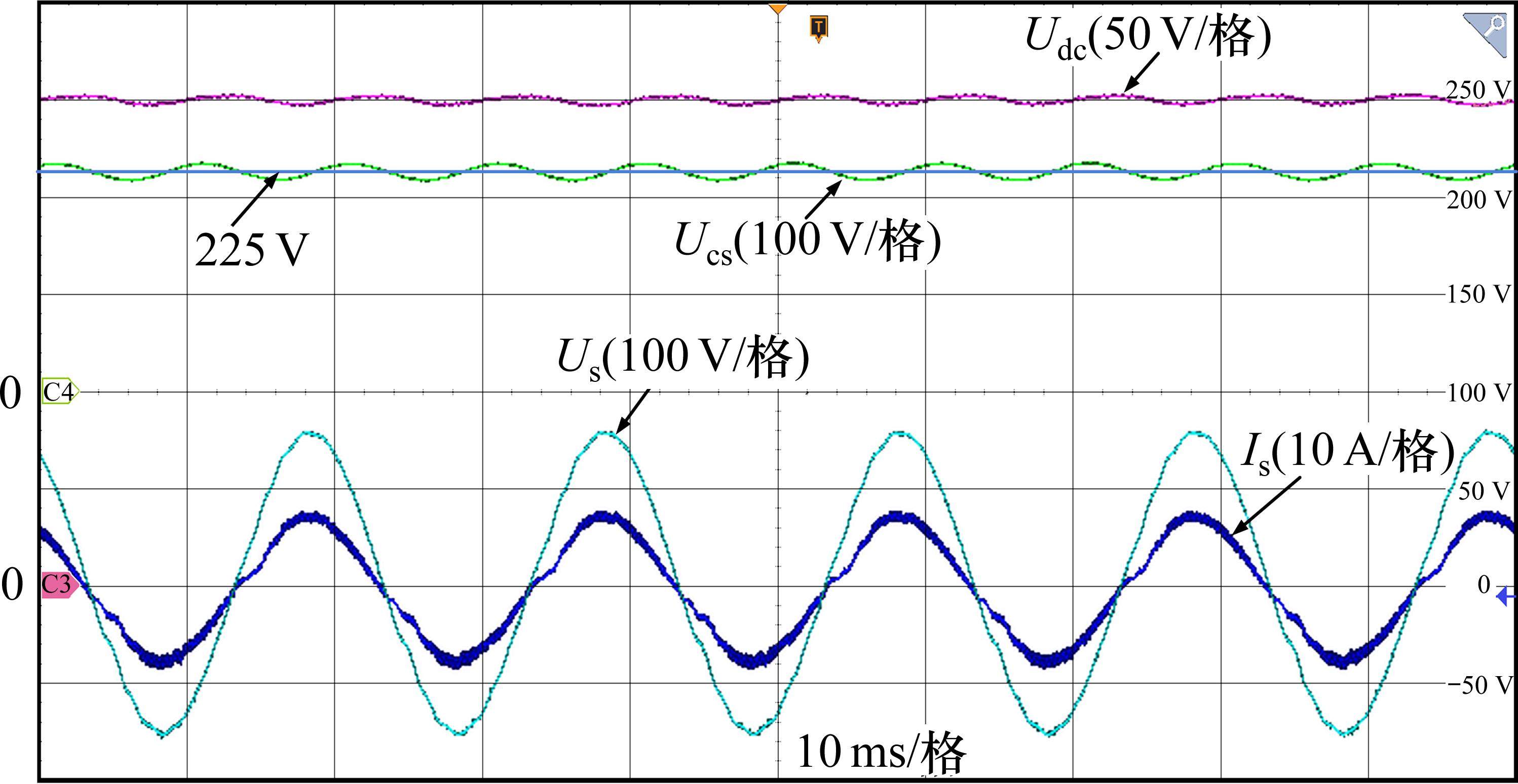
实验对比了直流侧电压为250 V,负载电阻120 Ω时,有LC、无LC和Buck斩波有源功率解耦3种拓扑的性能,3种拓扑的稳态工作波形如图11~图13,具体指标对比如表5所示。
| 拓扑 | 直流电压峰峰值波动/V | 网侧电流THD/% |
|---|---|---|
| 有LC滤波 | 3 | 7.80 |
| 无LC滤波 | 40 | 14.36 |
| Buck斩波有源功率解耦 | 5 | 8.36 |
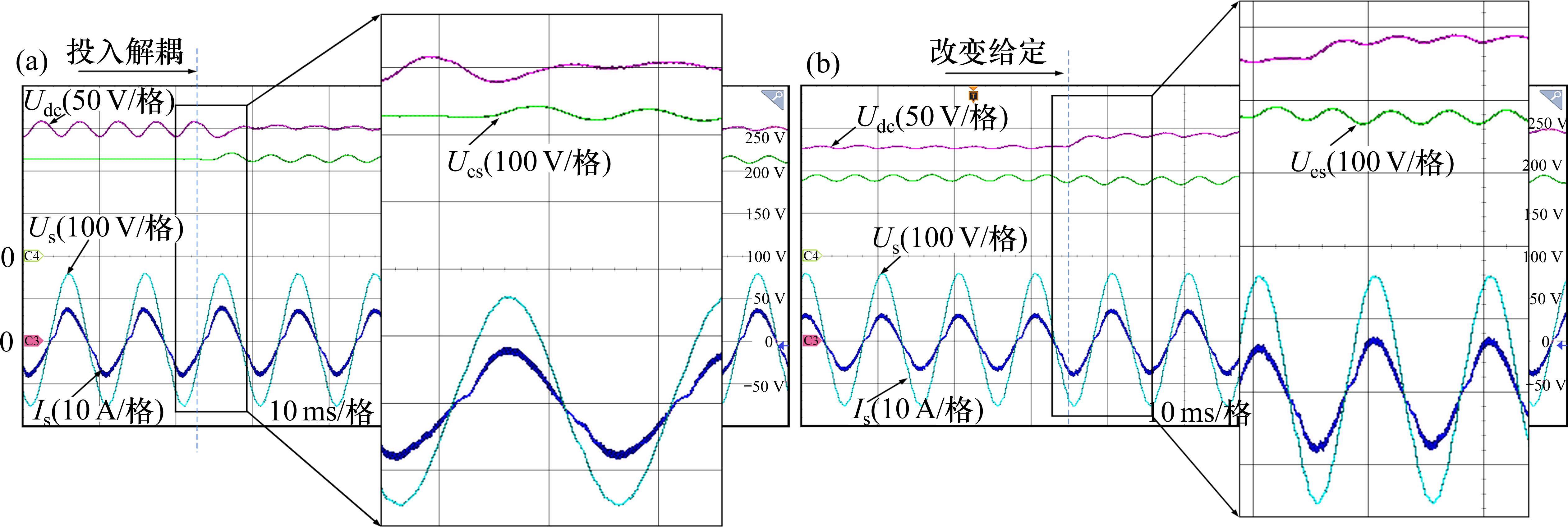
实验变流器输出具有LC谐振环节时,直流电压稳定,纹波电压峰峰值为3 V,网侧谐波电流也较低。当取消二次脉动时,中间直流电压脉动较大,峰峰值电压约为40 V,脉动幅值达到±8%,网侧谐波也增大1倍左右,无法满足系统控制需求。采用Buck斩波有源功率解耦拓扑以及重复控制算法后,直流电压纹波峰峰值降低到5 V,提高了直流电压的稳定性,网侧电流谐波、直流电压纹波抑制效果与LC滤波均较为接近。同时,对加入Buck斩波有源功率解耦的动态性能进行实验分析,如图14所示。图14(a)中,前段部分封锁Buck斩波控制信号,使之不参与作用,输出效果与无LC滤波效果相同,电压纹波和谐波含量均较高,投入Buck解耦拓扑后,系统稳定过渡到Buck解耦控制的效果,纹波电压和谐波电流都得到了有效抑制,拥有较好的动态性能。图14(b)展示了在不同直流电压给定情况下,Buck解耦电路同样可以快速跟随给定变化,控制性能没有发生大的变化,动态性能较好,在直流电压给定较低时,纹波更小。
5 结论
1) 通过PSO算法设计基于CR400AF变流器的拓扑参数,可以使解耦电容容值、解耦电感感值和4次脉动幅值尽量接近群体最优值,得到最优拓扑设计参数。
2) 基于重复控制的功率解耦策略,可以补偿系统在高频段的相位衰减,拥有更好的相角裕度,提升了系统动态性能,改善了稳定性,使之在低带宽条件下更好地跟踪二次脉动指令电流,从而得到更精确的交流分量占空比。
3) Buck斩波有源功率解耦可以有效滤除二次脉动,减小直流电压纹波,降低网侧电流谐波,为高速列车牵引变流器轻量化设计提供重要参考依据。
丁颢,曾一鸣,李卓鑫等.牵引变流器直流环节有源功率解耦控制策略研究[J].铁道科学与工程学报,2025,22(01):344-356.
DING Hao,ZENG Yiming,LI Zhuoxin,et al.Decoupling control strategy of active power in DC link of traction converter[J].Journal of Railway Science and Engineering,2025,22(01):344-356.

