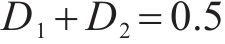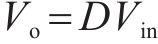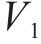与传统两电平Buck变换器相比,三电平的纹波频率更高、纹波幅值更小,滤波电感尺寸更小,更有利于直流变换器向高功率密度、高效、轻量小型化发展,作为恒流或恒压充电的充电装置被广泛应用于轨道交通储能系统中[1-2]。三电平Buck变换器通常采用2只开关管以占空比相等且相差180°的PWM驱动信号导通,使得飞跨电容电压保持为输入电压的一半,中点电位保持平衡[3]。但在实际工况中,由于驱动电路参数、印制板不完全一致导致开关管有所延迟[4]、电流谐波和负载阻抗的影响[5],使飞跨电容电压处于不均压状态,输出端的三电平波形不对称,影响输出电流、电压的纹波大小,严重时会造成开关管的损坏。随着SiC MOSFET等高频器件的发展与成熟,引入高频器件可以进一步提高输出电流纹波频率,减小变换器的体积和重量,但这种高频特性对中点电位的平衡要求更高[6]。张泽等[7-8]通过改进变换器拓扑结构提高了中点电位的自平衡能力。除此之外,调节开关管占空比也可以实现飞跨电容均压、保证中点电位平衡,但这种控制方式要考虑飞跨电容电压与输出电压的耦合关系。冯颖盈等[9-10]使用线性解耦方法将多电平Buck变换器解耦为多个单输入单输出系统,设计了输出电压和飞跨电容电压的闭环比例积分控制器,实验结果证明了解耦的正确性,其结构简单但响应速度慢、抗扰性较差。吴家荣等[11]提出了基于微分几何理论的解耦控制方法,推导了解耦子系统的状态反馈控制律并设计了控制器,增强了系统的抗干扰性。但其为电压单闭环控制,无法实现最大电流限制和恒流输出,与双闭环结构相比响应速度较慢。传统双闭环PI控制[12]实现简单,但其参数固定、动态响应较慢、对负载突变等不确定扰动调节能力较弱。随着微处理器不断发展,模型预测控制(model predictive control, MPC)具有动态响应速度快、可约束系统变量、适用于多目标控制系统等优势,已被应用于电力驱动、高压直流系统等电力电子领域中[13-14]。杨茹楠等[15]将有限集模型预测控制(finite control set MPC)应用于三电平Boost直流变换器电压的控制中,实现了直流母线电压和分压电容均压的多目标优化控制,但其开关频率不固定,导致输出电流纹波增大,滤波电感选取困难,且控制器在线计算量大。李敬泰[16]将连续集模型预测控制(continuous control set MPC)应用于飞跨电容型三电平Buck-Boost变换器飞跨电容电压和输出电流控制中,并验证了控制算法的有效性,但未实现输出电压的控制。自抗扰控制(active disturbance rejection control, ADRC)因其具有不依赖于控制系统的精确模型,能对系统总扰动实时估计并补偿,具有较强的鲁棒性和抗干扰性等优势也被广泛应用于电力电子系统控制中。李浩东等[17-18]针对双向DC-DC变换器设计了电压外环ADRC、电流内环PI控制算法,仿真实验表明自抗扰控制器有效减小了负载电流和母线电压的影响,提升了系统鲁棒性。基于上述研究,本文对飞跨电容型三电平Buck变换器不同工作模态的飞跨电容电压与输出电压进行解耦,提出了基于解耦的连续集模型预测控制,同时控制输出电流与飞跨电容电压2个目标,控制过程中无需调节权重系数。为了抑制由负载突变或系统未建模动态等干扰对输出电压的影响,在电流控制的基础上引入电压外环自抗扰控制,提高系统的抗扰动性。最后通过仿真验证了所提控制策略的可行性与有效性。
1 解耦及控制策略的提出
1.1 变换器工作原理及控制目标
飞跨电容型三电平直流变换器拓扑结构如图1所示,E为输入电源,大小表示为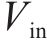
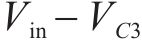
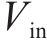
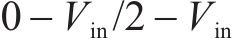
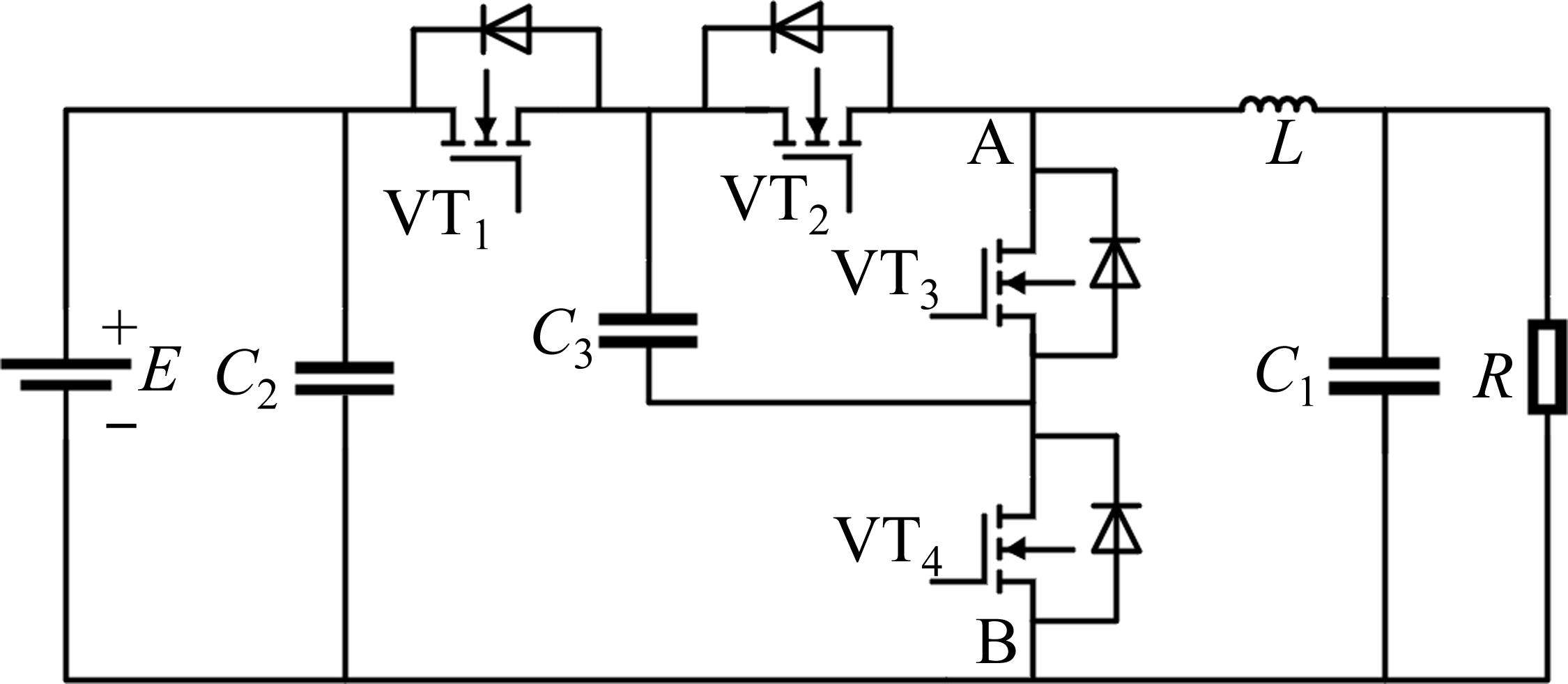
三电平直流变换器按照输出电流特性分为连续导通模式(continuous conduction mode, CCM)和不连续导通模式(Discontinuous Conduction Mode,DCM)。与CCM相比,DCM多了一段电感电流为0A的保持阶段,此时滤波电容放电,维持负载电阻两端电压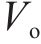

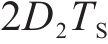

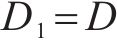
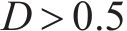
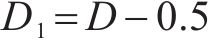

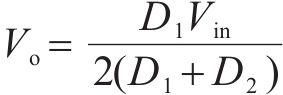
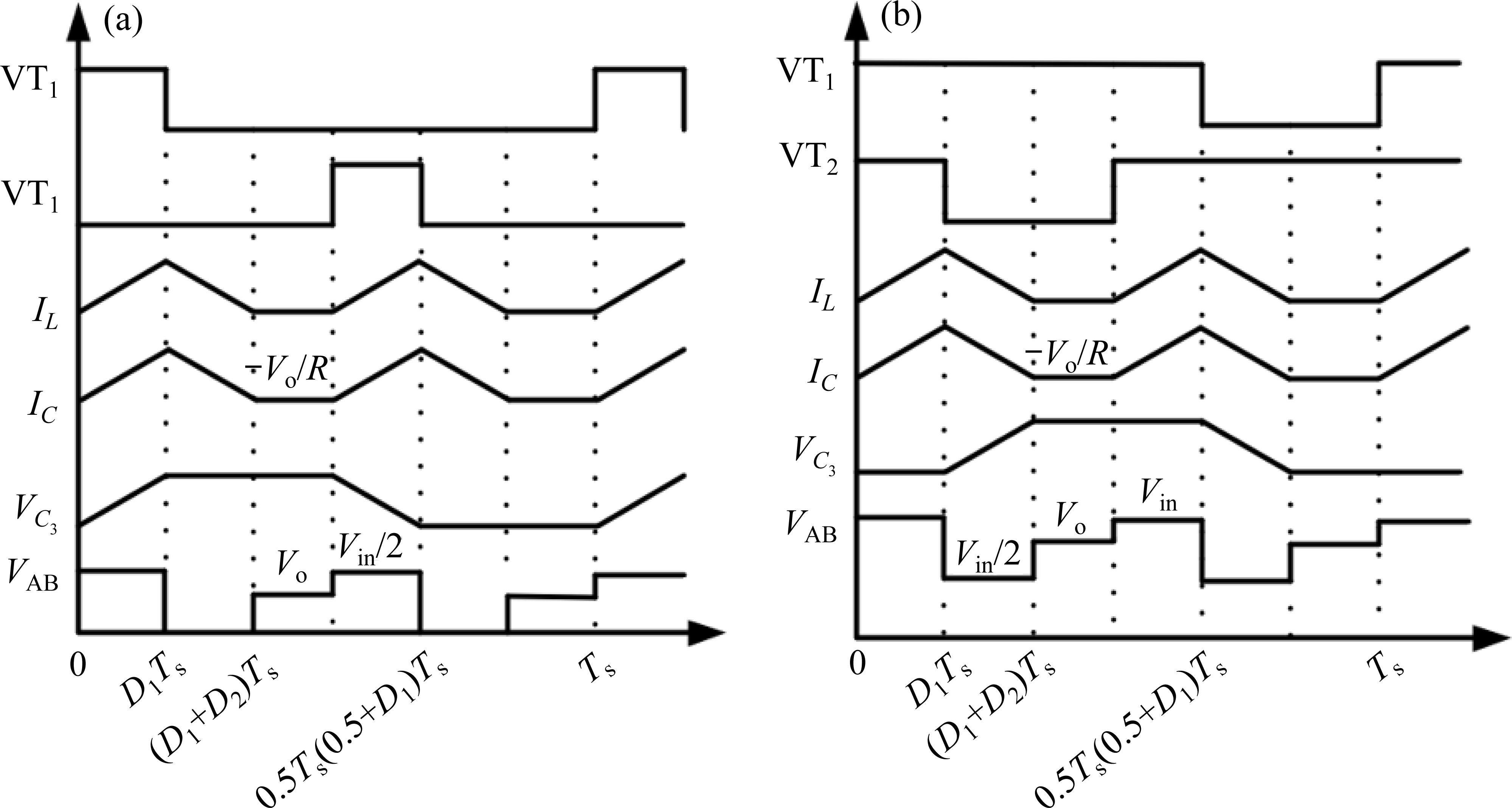
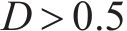
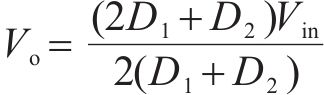
对于这种三电平Buck变换器拓扑结构主要有2个控制目标,第一为飞跨电容电压VC3控制为输入电压的一半,保持变换器三电平输出,第二为保持恒定电流对外充电。对于某些特定工况,变换器控制目标是恒压对外充电,因此需要在电流控制基础上引入电压外环控制,实现电压电流双闭环控制,提高变换器的响应速度,限制变换器最大电流。
1.2 飞跨电容电压与输出电压解耦及控制策略的提出
飞跨电容电压在一个周期内进行充放电,当开关管VT1、VT2的占空比和开关特性不一致时将导致飞跨电容电压产生偏移,使变换器无法正常工作,输出不对称的三电平,此时开关管管压不等于输入电压的一半,偏离严重时会损坏开关管,需要对其进行主动均压控制。由图2可知飞跨电容的充放电与VT1、VT2占空比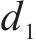
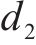
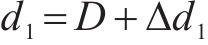
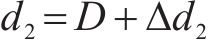
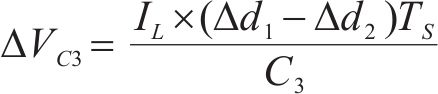
式中:IL为电流平均值。当飞跨电容偏离均压状态时,调节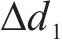
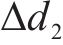
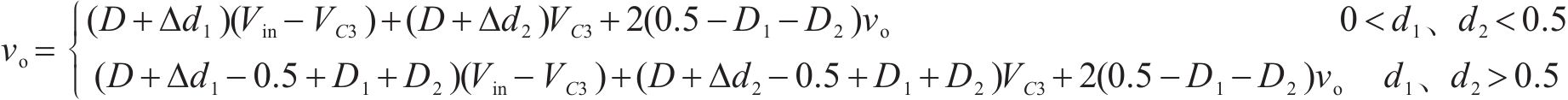
当飞跨电容型三电平Buck变换器工作在稳定状态时,飞跨电容电压始终保持在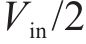
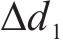

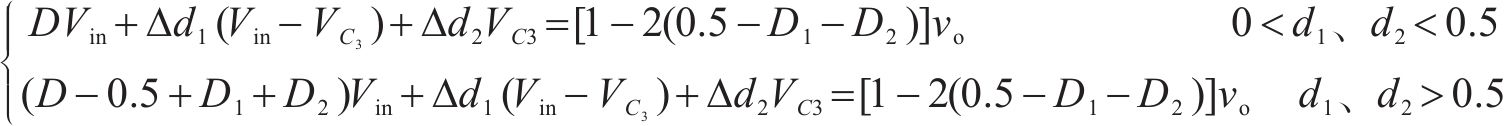
将式(1)和式(2)代入式(5)可得到DCM模式下输出电压与飞跨电容电压解耦的结果,如式(6)所示。
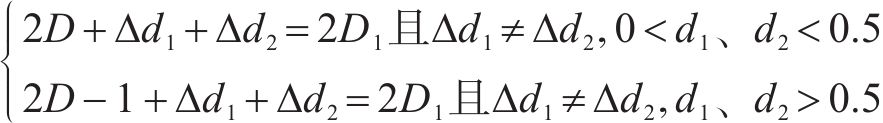
当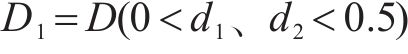
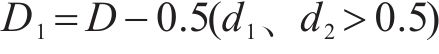
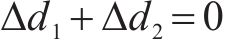
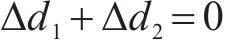
在经典PID控制中,微分环节根据偏差的微分信号对未来的信号进行预测并提前进行调节,但容易将噪声引入到控制系统中。而MPC对下一状态量的估计并不是直接对状态变量进行微分,而是根据模型预测方程求取,避免了噪声信号的引入,同时MPC可以实现飞跨电容电压和输出电流2个控制目标,响应速度较快,因此本文采用基于连续集模型预测控制的电流内环控制。为抑制负载突变或系统参数变化等内外部干扰的影响,保证变换器在最大电流范围内安全可靠地工作,设计外环自抗扰控制器以观测并补偿系统总扰动。电压外环输出控制量为电流内环电流参考值,完成电压控制到电流控制的转换,其结构如图3所示。
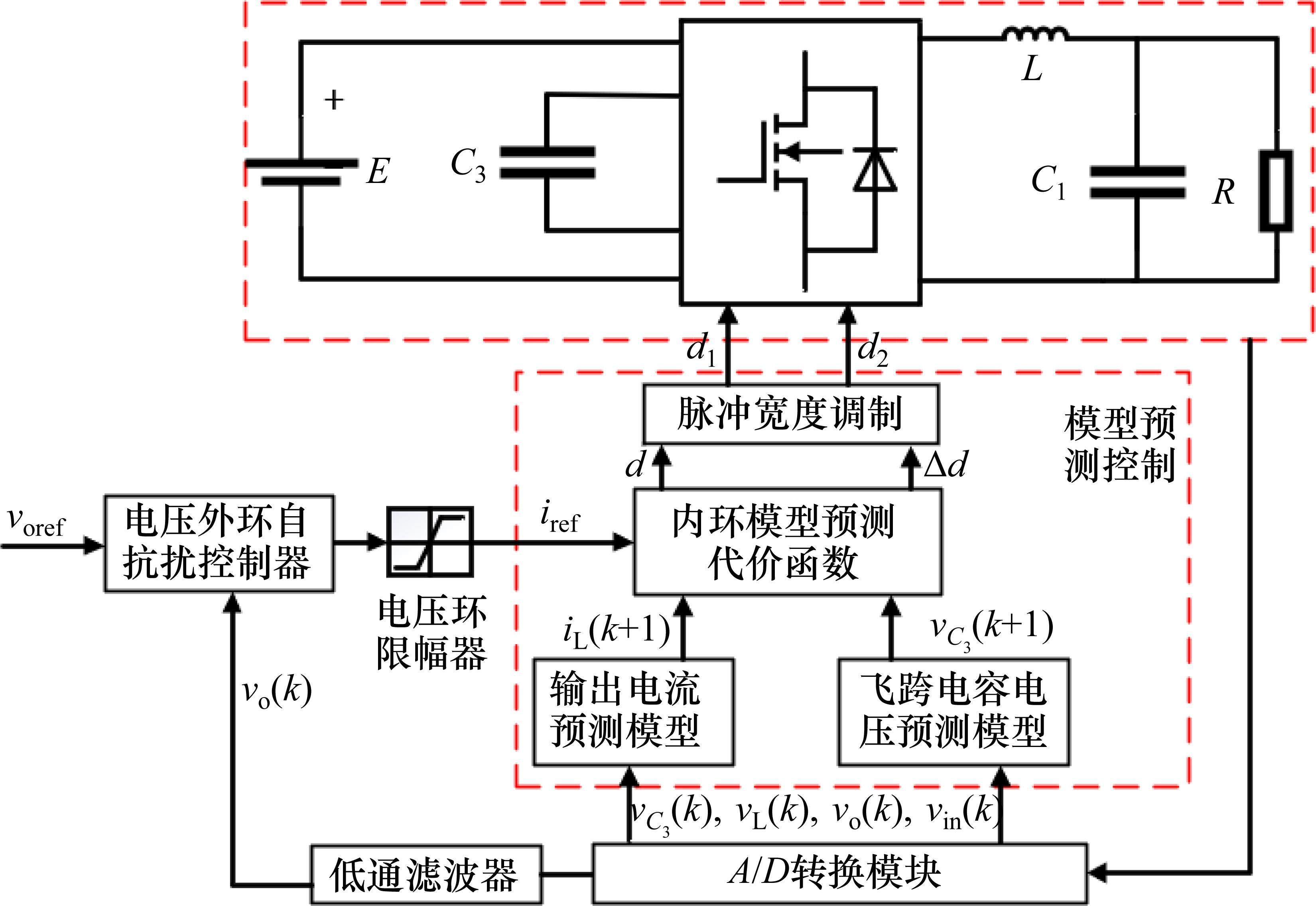
2 基于连续集模型预测的电流内环控制
对于恒流对外充电工况,本文建立了模型预测控制器实现输出电流和飞跨电容电压2个控制目标,利用过去时刻的状态量预测下一时刻的输出电流和飞跨电容电压,构建评价2个控制目标接近参考值接近程度的代价函数,当代价函数取极小值时得到下一时刻的最优控制规律。
2.1 飞跨电容电压与输出电流预测模型的建立
当

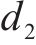
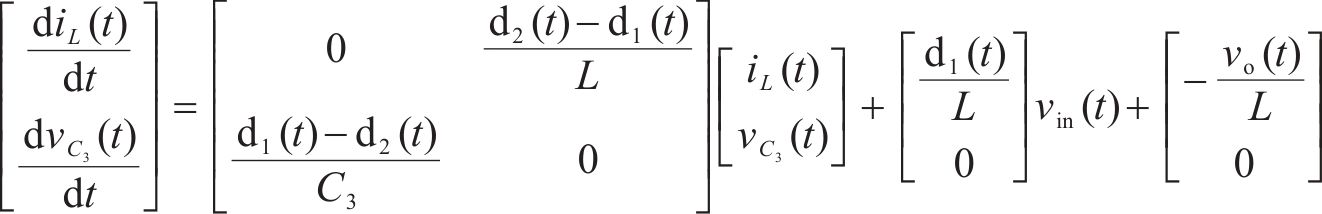
当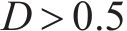
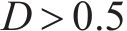
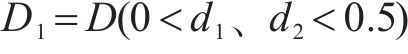
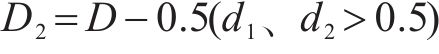
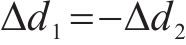
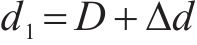
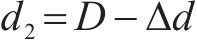
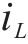

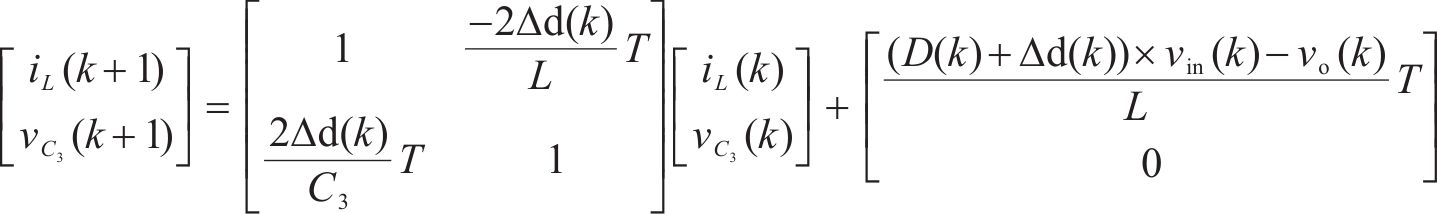
根据模型预测控制算法的原理,令预测得到的状态变量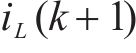
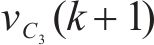
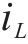

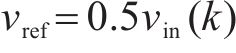
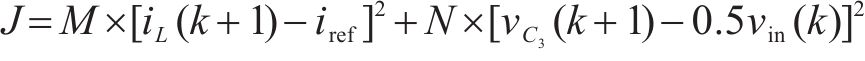
其中,M、N为电流和飞跨电容电压的权重系数,通过求J最小值获得最优控制律以达到最优控制效果。
2.2 代价函数寻优
为缓解减轻处理器的计算压力,减小计算时间,本文对控制量D、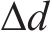
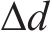
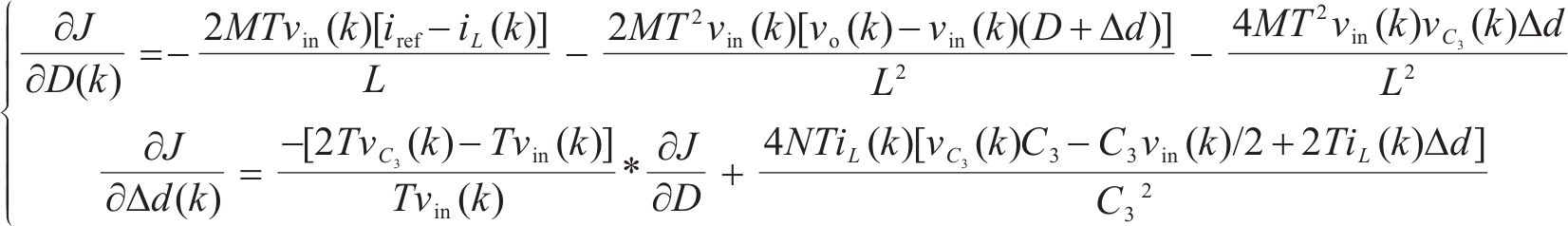
令各阶偏导数等于0,可以得到代价函数取最小值时的控制量D、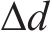
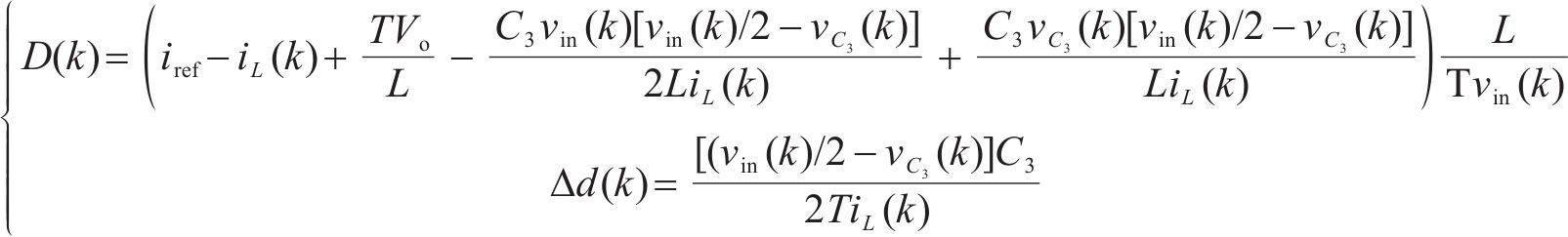
为了判断当D、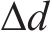
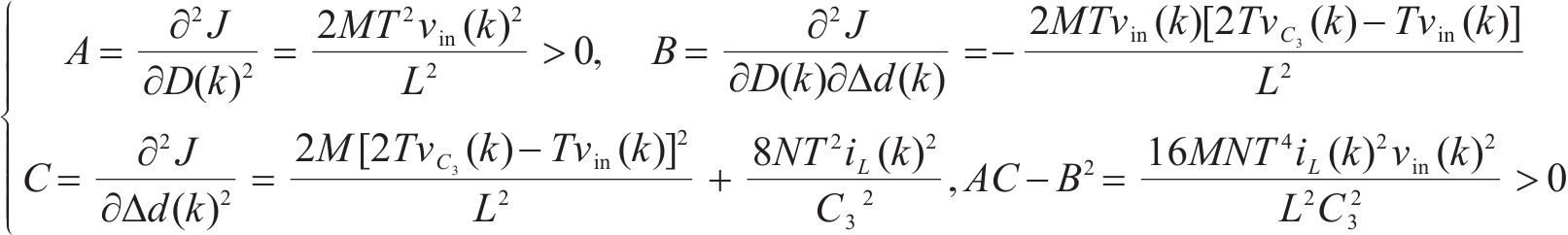
由式(12)可知,2阶偏导数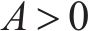
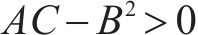
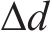
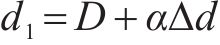
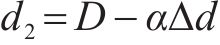
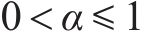
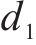
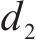
由于MOSFET开关管的导通和关断持续时间均应大于150 ns[19],即对于开关频率为50 kHz的变换器,开关管的占空比可能出现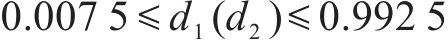
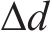
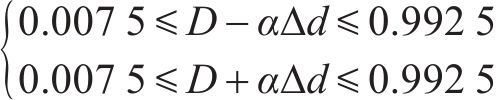
当式(11)求得的控制量D、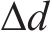
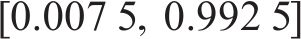
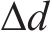
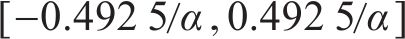
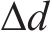
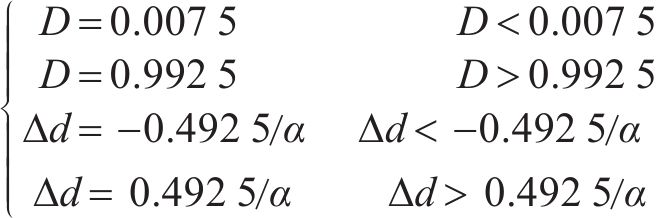
此时模型预测控制算法避免了一个周期内VT1、VT2始终保持开通或关断的情况,实现了工作模态的切换,保证了三电平输出。
2.3 飞跨电容电压与输出电流内环控制稳定性分析
飞跨电容电压控制环以输入电压的一半为控制目标,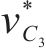
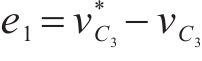
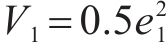
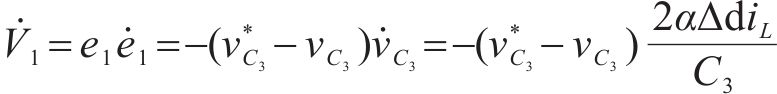
将式(11)中控制量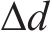
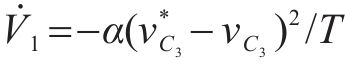
式中: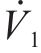
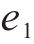
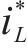
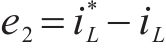
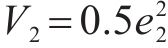
由上式可知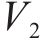
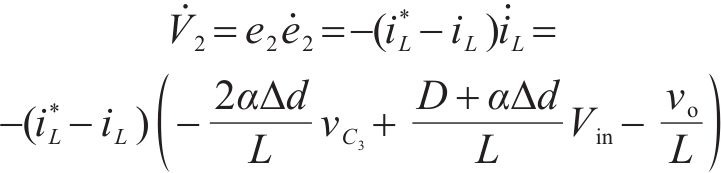
将式(11)中控制量D、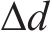
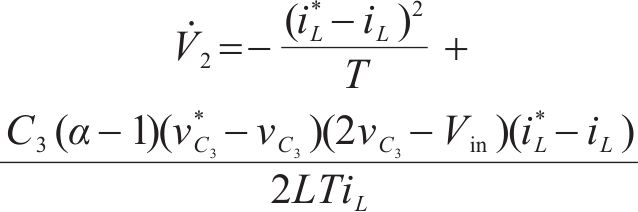
上文已证明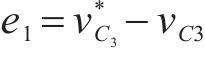
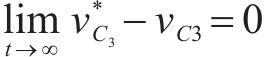
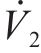
3 基于自抗扰算法的电压外环控制器设计
对于恒压对外充电工况,变换器的控制目标是保持输出电压恒定,因此需要在内部电流控制的基础上引入电压控制,电压外环控制器通过调节电流内环参考值实现输出电压的控制。本文引入ADRC对电压外环控制器进行设计,实时估计并补偿负载突变、电路参数变化或系统建模误差的不利影响。根据其电路原理并考虑系统受到内外扰动的情况,在微分方程中引入不确定扰动d,得到被控对象为
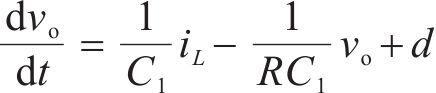
取状态空间变量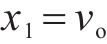
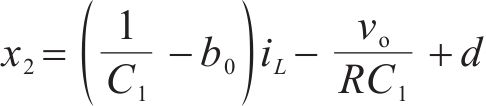
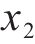
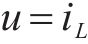
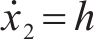
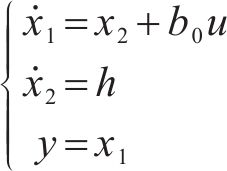
由上可采用简单的1阶线性ADRC,包括了微分跟踪器、扩张状态观测器和误差反馈控制律3部分。为降低控制器复杂度,本文省去跟踪微分器,设计如图4所示的电压外环闭环框图,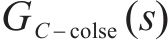
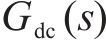
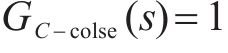
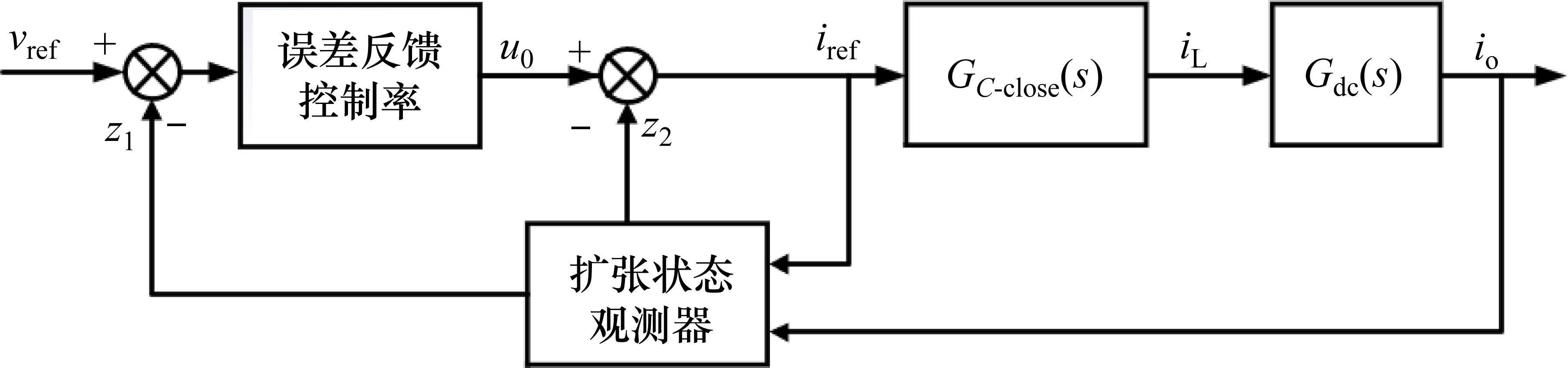
根据系统(22)设计如下所示的扩张状态观测器:
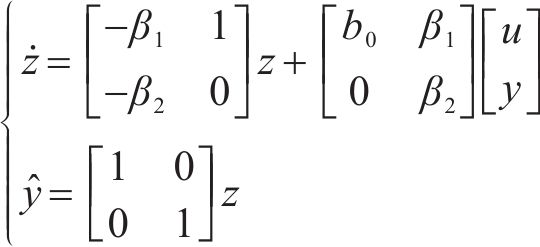
式中: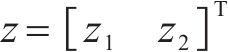
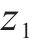
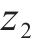
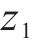
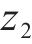
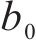
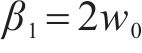
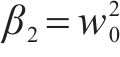
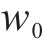
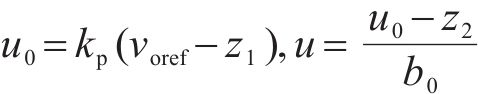
式中:kp为比例系数。由Lyapunov稳定性可得存在常数c,当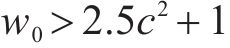
综上,自抗扰控制器需要整定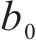
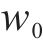
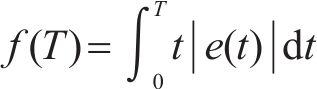
式中:T为仿真时间;e(t)为输出电压与参考值的误差。为避免PSO得到的解为局部最优解,其权重系数采用如下式所示的函数[21],迭代初期取较大值,保证粒子进行全局搜索,后期取较小值保证其收敛性:
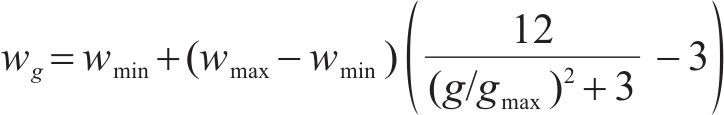
式中: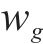
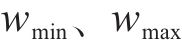
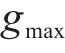
4 仿真及半实物实验验证
4.1 恒流及恒压输出工况仿真实验
为验证所提双闭环控制策略(MPC+ADRC)的有效性,在Matlab/Simulink搭建飞跨电容型三电平直流变换器模型,变换器参数如表1所示,分别利用所提控制策略和PI控制进行恒流输出和恒压输出仿真实验。
| 变换器参数 | 参数值 |
|---|---|
| 输入电源电压Vin/V | DC1 500 |
| 飞跨电容C3/uF | 600 |
| 滤波电感L/mH | 1 |
| 滤波电容C1/uF | 1 000 |
| 负载电阻R/Ω | 10 |
| 开关频率fs/kHz | 50 |
| 输入支撑电容C2/uF | 29 |
在电流单环控制中,传统PI控制方法是使用2个PI控制器分别对飞跨电容电压和输出电流进行控制,按照文献[13]的频域参数整定方法得到表2中的控制器参数。在电压电流双闭环控制中,电流内环控制器参数与单环控制相同,电压外环控制器参数由粒子群算法寻优得到,其参数值如表2所示。
| PI双闭环控制 | MPC+ADRC | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 电流环 | 飞跨电容电压环 | 电压环 | MPC | ADRC | |||||
| kp1 | ki1 | kp2 | ki2 | kp3 | ki3 | 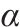 | kp | 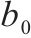 | 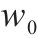 |
| 0.02 | 6.5 | 0.5 | 0.1 | 0.8 | 39 | 0.1 | 1 386 | 3 343 | 707 |
4.1.1 输出电流阶跃响应
当参考电流iref为100 A,飞跨电容初始电压设为750 V,在模型预测控制和PI控制下进行仿真,得到如图5所示的仿真结果。在PI控制中,随着输出电压上升,输出电流先下降至94.5 A后上升至100 A,稳态时间约为30 ms左右,而MPC的输出电流始终稳定在100 A,稳态时间为1 ms,具有较好的控制效果。
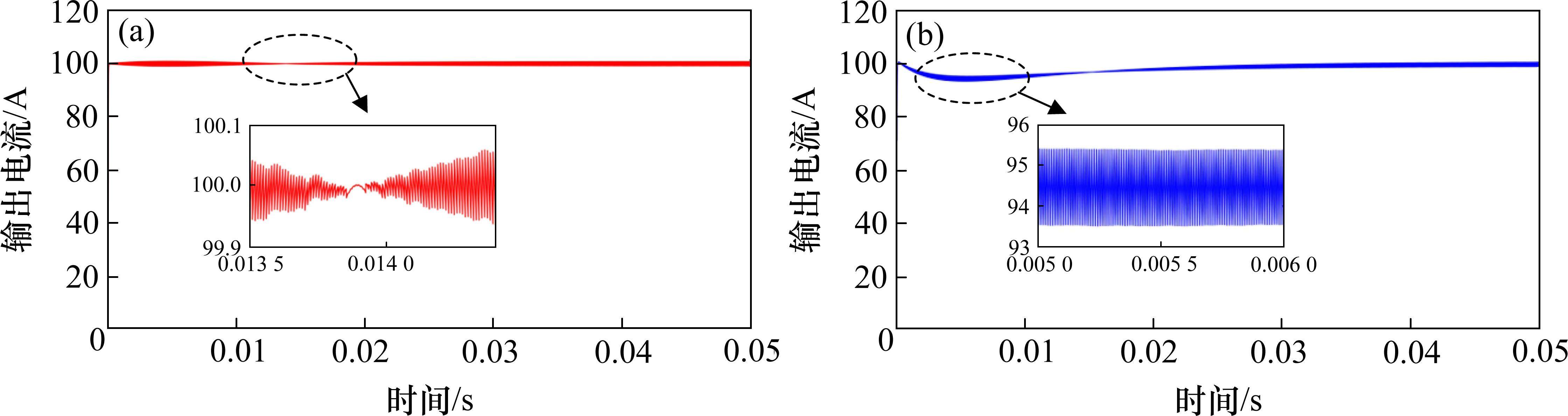
4.1.2 恒压输出工况仿真实验
1) 输出电压阶跃仿真
利用所提双闭环控制和PI双闭环控制进行输出电压阶跃响应仿真实验,控制器参数如表2所示,将变换器最大峰值电流设置为300 A,电压参考值设为950 V,其余电路参数与电流内环设置相同,其结果如图6所示。仿真波形表明所提双闭环控制响应时间为8 ms,比PI双闭环控制提高了10 ms,具有较快的响应速度,这是由于输出电流被限制在300 A,在输出电压的影响下输出电流有所下降,同4.1.1中现象相同。
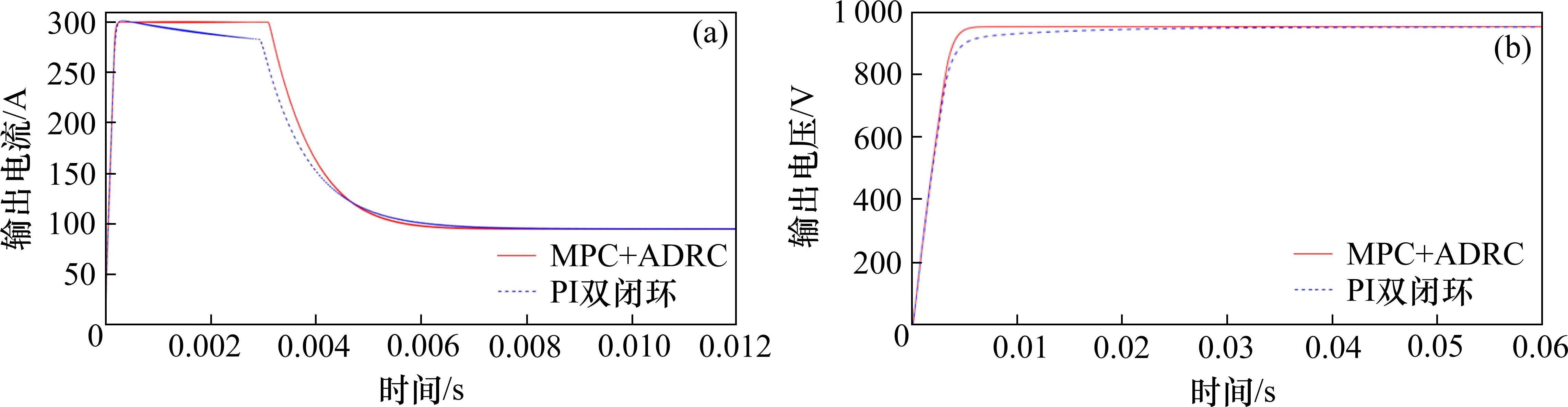
2) 输入电压阶跃变化仿真
当输入电压发生突变时分别对所提双闭环控制和PI双闭环控制进行验证,其中输入电压在0.35 s时从1 500 V变为1 400 V,0.5 s时从1 400 V变为1 500 V,输出电压参考值为950 V,其余参数与上文相同,仿真结果如图7所示。结果表明2种控制方法均能将飞跨电容保持在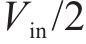
3) 负载电阻突变仿真
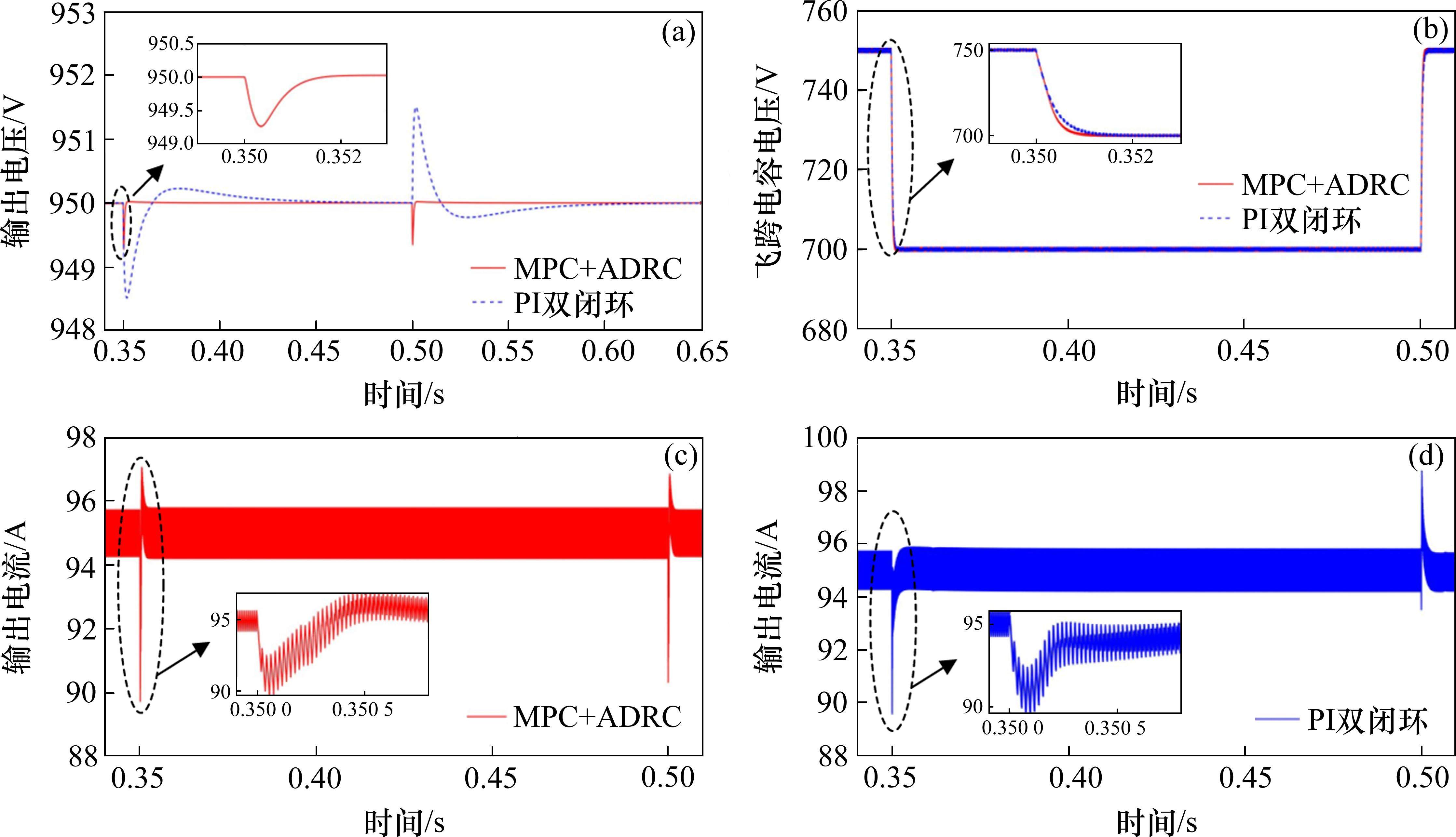
当负载电阻发生突变时对本文所提双闭环控制器进行验证,其中负载电阻在0.2 s时从5 Ω变为10 Ω,0.45 s时从10 Ω变为5 Ω,输出电压参考值为950 V,其余参数与上文相同,仿真结果如图8所示。
仿真结果表明所提双闭环控制策略经过60 ms的调节后输出电压均到达稳定状态,波动量为53.6 V左右,飞跨电容电压始终保持在输入电压的一半。而PI双闭环控制稳态时间约为130 ms,输出电压波动量为72 V左右。所提控制策略对负载突变引起的干扰具有更好的补偿效果和抗干扰性,系统的鲁棒性更强。
4.2 半实物仿真实验
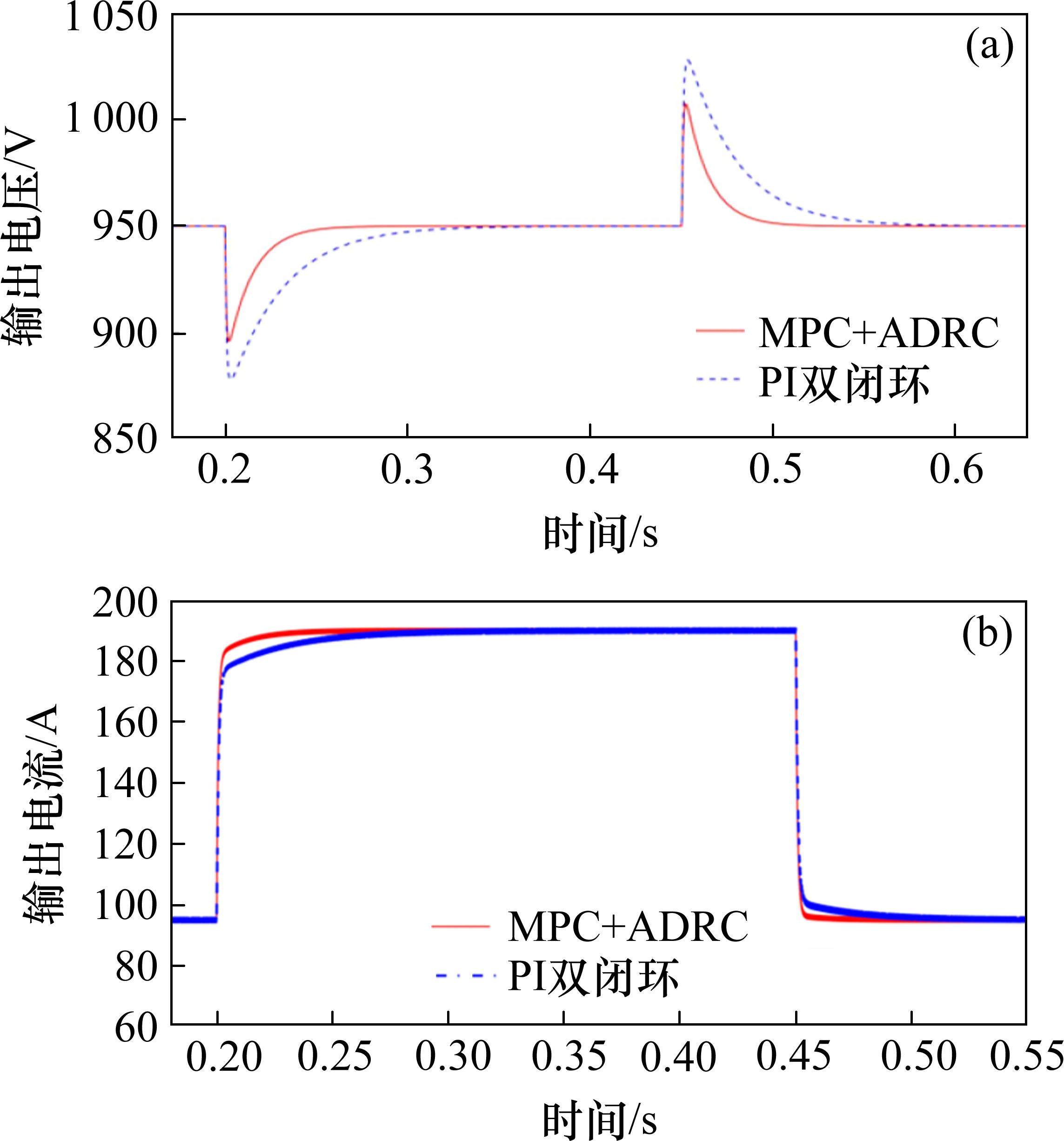
为进一步验证所提控制策略在工程中的有效性,本文基于dSPACE搭建了如图9所示的硬件在环半实物仿真实验平台,利用dSPACE硬件实时系统对变换器拓扑进行实时数字模型模拟,控制器采用TMS320F28335,两者通过硬线及连接器实现信号交互,半实物系统器件参数和控制参数与表1、表2中相同。
图10为输出电流阶跃响应实验结果,PI控制调节时间较长,而MPC始终稳定在目标值,响应速度快。对于输出电压阶跃响应实验,图11表明所提控制算法较PI双闭环具有更快的响应速度且无超调。
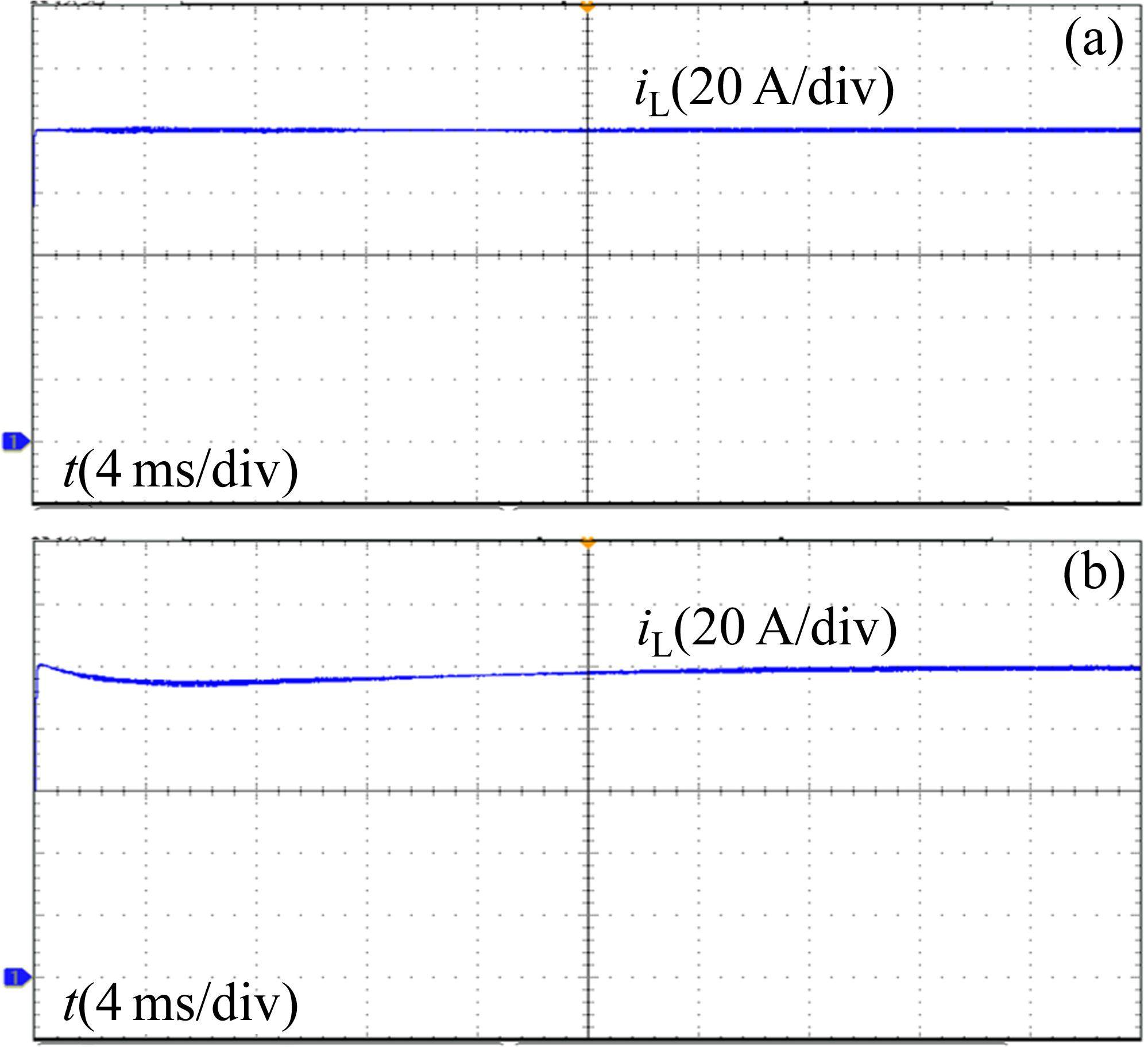
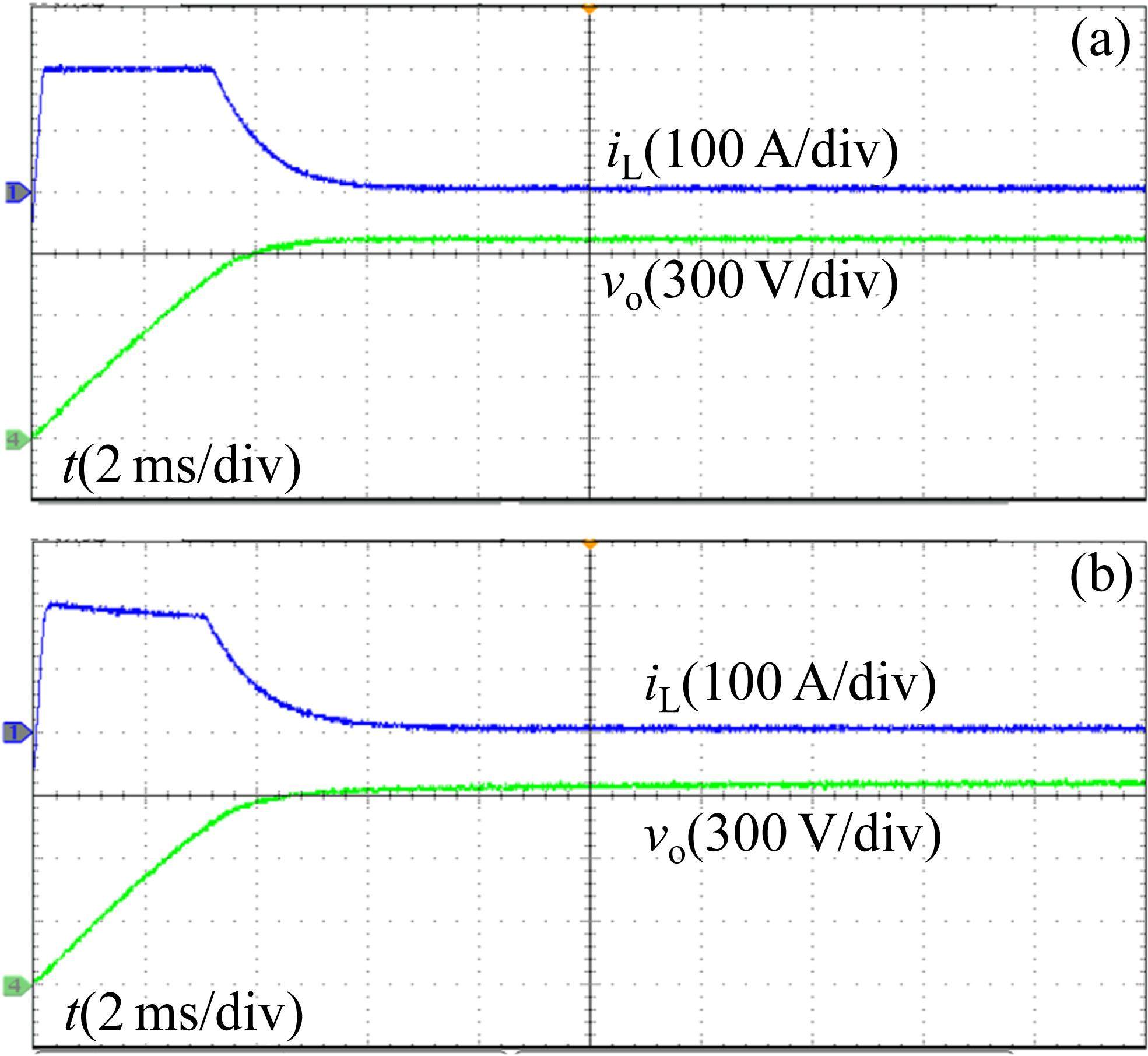
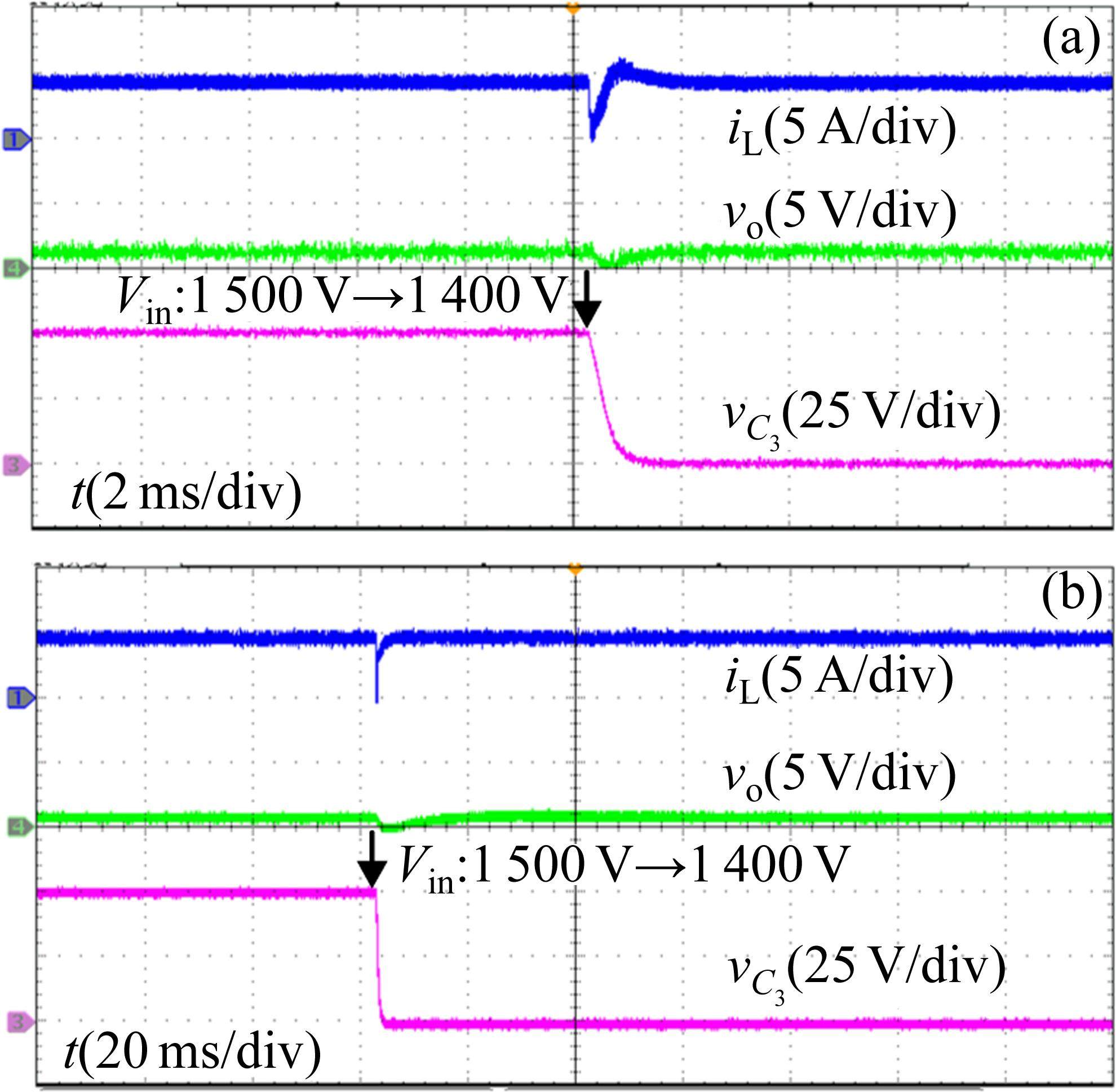
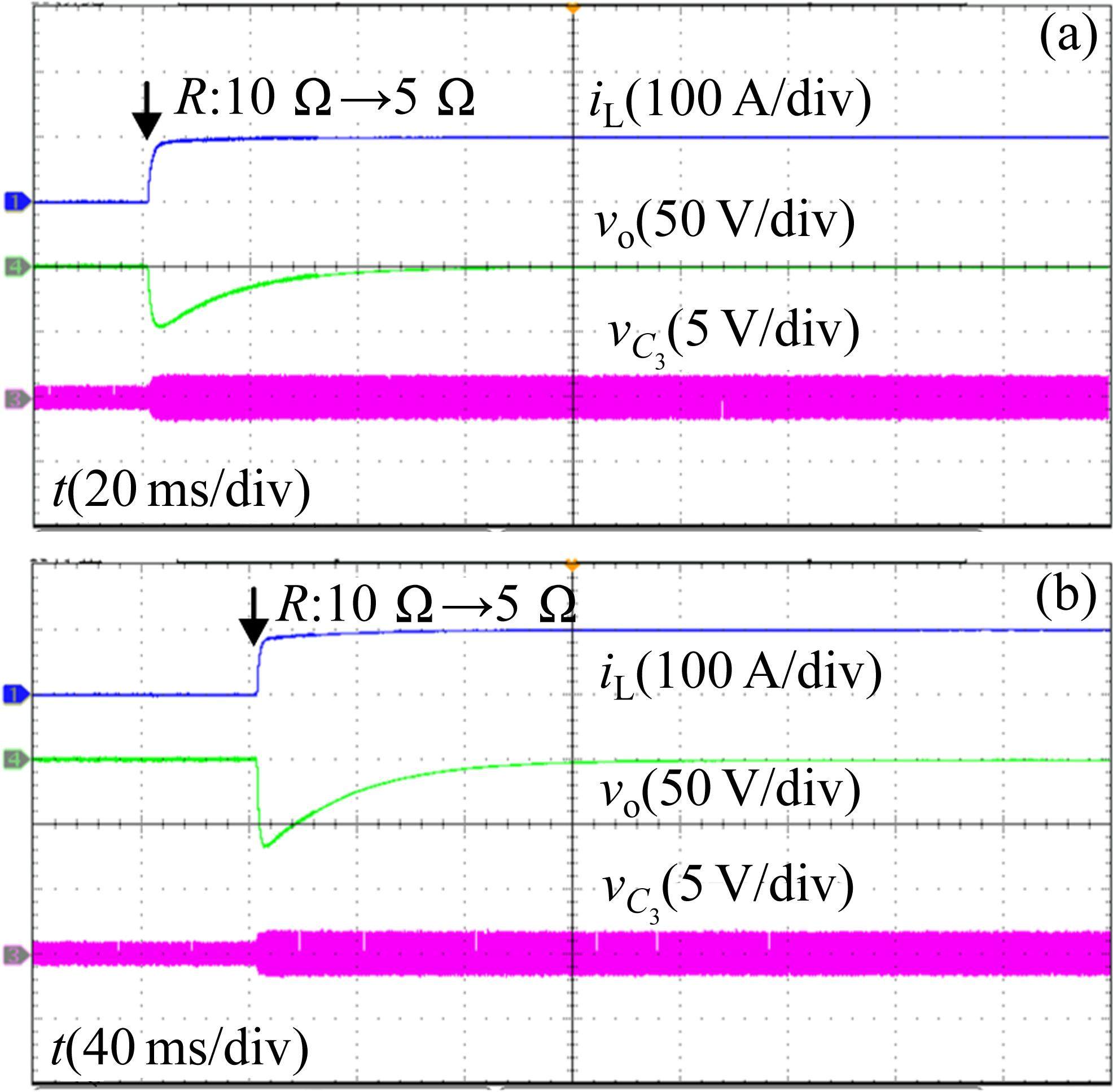
图12为输入电压从1 500 V突变为1 400 V在MPC+ADRC双闭环控制和PI双闭环控制下的实验结果,飞跨电容均能调节至均压状态,输出电压均产生小波动,所提控制策略较PI双闭环控制调整时间更快,鲁棒性更强。当负载电阻由10 Ω变为5 Ω时,图13表明MPC+ADRC双闭环控制下的电压波动量更小且调节时间更短,且飞跨电容始终处于均压状态,系统具有更强的抗干扰能力。实验与仿真结果基本吻合。
5 结论
1) 本文对变换器不连续导通模式下的输出电压与飞跨电容电压解耦,提出了基于解耦的连续集模型预测控制方法,该方法设计了离线控制律的计算方法,减少了计算时间,通过引入飞跨电容电压调节速率因子降低了飞跨电容电压调节对输出电流的影响;同时在内部电流的控制基础上设计了电压外环自抗扰控制器,实时估计并补偿负载突变对输出电压的影响,实现了电压电流双闭环控制。
2) 仿真和半实物实验表明对于电流控制,模型预测控制能在1 ms内达到参考电流值并保持稳定,而PI控制器调节30 ms后稳定在电流参考值。对于电压控制,本文所提出的双闭环控制的响应时间为8 ms,比PI双闭环控制提高了44%,在输入电压和负载电阻发生突变时能将飞跨电容电压稳定在输入电压的一半,对于输出电压的控制具有更快的响应速度和更小的超调量,系统具有更强的抗干扰能力和鲁棒性。
韩锟,马晓慧,李蔚.飞跨电容型三电平Buck变换器双闭环控制研究[J].铁道科学与工程学报,2025,22(02):829-840.
HAN Kun,MA Xiaohui,LI Wei.Research on double closed loop control of flying-capacitor three-level Buck converter[J].Journal of Railway Science and Engineering,2025,22(02):829-840.