冬季的降雪、冻雨天气,导致铁路道岔尖轨、可动心轨以及转辙机外锁闭装置等出现积雪、冻结现象造成转换受阻,影响我国铁路交通运输的正常运营。电加热道岔融雪设备是铁路信号系统的重要设备之一,已经在我国高铁线路上广泛安装使用,但近年来随着极端天气的概率升高,降雪区出现南移现象,多数南方地区冬季也要进行道岔除雪工作[1]。为推广道岔融雪装置应用,提升铁路运营安全水平,2024年国家铁路局对《铁路信号设计规范》《高速铁路设计规范》《城际铁路设计规范》等3项行业标准有关道岔融雪装置的设置范围和控制功能进行了局部修订[2-3],推动符合条件的地区进行道岔融雪装置的安装,保障冬季铁路运输的安全,提高运输效率。通过对电加热道岔融雪系统加热元件的传热过程和传热特性的分析研究,可以为系统的优化设计包括电加热元件的安装位置、分时加热时机、加热时长、多路功率配置等参数的选择提供理论依据。对传热过程的深入研究,可以更好地预测和改善由于温度不均匀、启动不及时等问题导致的道岔结冰、积雪等安全隐患,确保道岔在恶劣天气条件下的安全运行。很多学者都在对道岔融雪技术进行研究和探索。李凯等[4]对国内的融雪装置进行调查分析,针对积雪融化不充分的问题,提出了对青藏铁路道岔融雪电加热元件的安装改进方案,并进行了可行性分析。李兰兰等[5]通过对配以电加热道岔融雪系统的道岔结构进行传热分析,分析了不同融雪位置和不同环境条件对最小加热功率的影响。SZYCHTA等[6-8]根据目前的加热元件进行改进,设计了一种感应式加热器,进行了物理建模和现场试验,将理论与现场数据进行对比分析,并通过实验评估了电阻加热和感应加热的效率。MATEUSZ等[9-11]提出了一种道岔融雪加热元件无接触安装方式,通过ANSYS进行了有限元分析,对比了电加热元件常规安装方式和无接触安装方式的温度动态分布和融雪效果。LOTFI等[12]调查了全球寒区的气温,分析了各地区因为冬季雨雪天气产生的铁路事故,从实际出发提出了基础设施,机车车辆和运营3个部分的研究问题及其缓解方法。邱战国等[13-16]针对道岔融雪系统能耗高的问题,分析不同的加热方式,并通过仿真提高道岔融雪设备的能量利用效率。苏蕊等[17-20]基于国内外市场及自身技术发展,探讨了道岔融雪系统智能化方案,提高自动化程度和人机交互,降低能耗。综上,经过国内学者们对电加热道岔融雪系统安装方式研究和对道岔结构传热分析,我国道岔融雪技术已经有了较好的发展,国外学者通过对创新方式进行建模与现场实验对比分析以提高效率。本文立足于我国目前的道岔融雪系统,在前人的基础上利用MATLAB和COMSOL分析软件对道岔融雪进行传热分析,构建出更精准的传热模型,依据现场条件进行严谨的对比实验,才能进行后续针对性的优化和改进。
1 电加热道岔融雪传热过程分析
1.1 道岔几何模型构建及电加热元件安装
车站电加热道岔融雪系统由车站控制终端、电气控制柜、环境检测装置、电加热元件及安装卡具、隔离变压器、接线盒、连接线缆和信息通道等组成。
本文的研究对象是60 kg/m钢轨12号道岔尖轨部分,现场目前使用的是3 720 mm的1 300 W直把手直型电加热元件,所以在建模过程中尖轨部分取4 m。由于滑床板和轨枕之间设置传热系数较低的橡胶板,因此模型中忽略了轨枕及扣件,滑床台焊接在滑床板上侧位置,用于支撑尖轨,并保证其正常地左右滑动。道岔尖轨部分截面如图1所示。
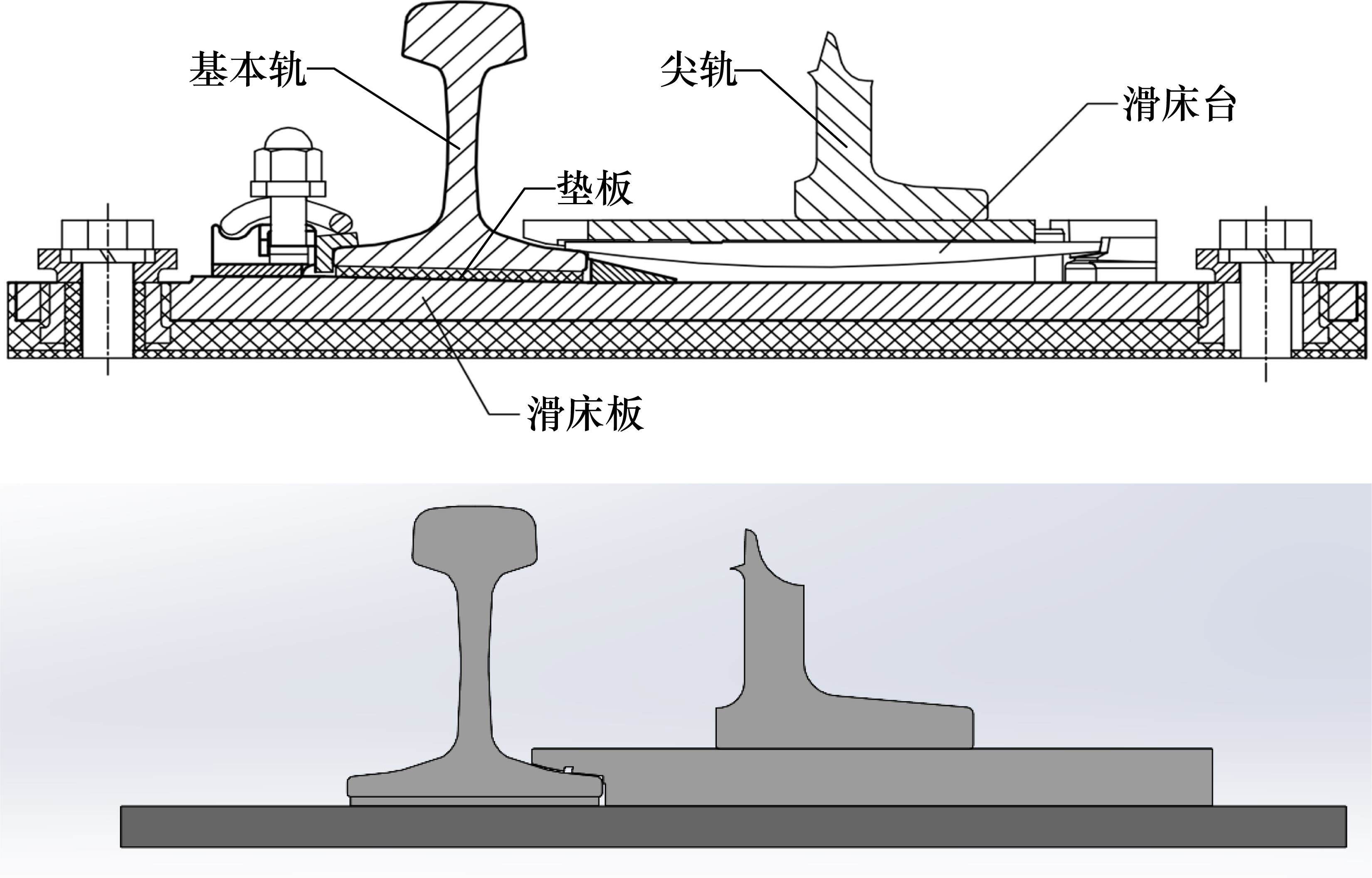
电加热元件可以安装在基本轨的轨腰和轨坡,心轨的轨腰,滑床板等位置。本次主要以现场常用的电加热元件为基础,构建轨腰加热的几何模型,如图2所示。

1.2 传热过程分析
电加热元件依靠通电后产生热量加热钢轨和融化积雪;钢轨的导热性较好,在被电加热元件加热后,会对周围的积雪和空气进行持续的热交换;积雪吸收电加热元件和钢轨的热量导致温度升高,同时要考虑其相变过程;空气也会对传热过程产生影响。热能传递的3种基本方式有热传导,热辐射与热对流,这3种方式的热量计算均可用公式进行表示[21]。传导热量qc的计算公式如式(1):
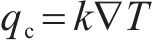
其中,qc为单位时间内单位面积的传导热量,W/m2;k为材料导热系数,W/(m∙K);∇T为温度梯度。
热辐射的计算基于斯特藩-玻尔兹曼定律,如式(2):
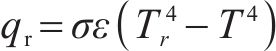
其中,qr为单位时间内单位面积的辐射换热量,W/m2;ε为材料表面辐射率系数;σ为斯特藩-玻尔兹曼常数;Tr为材料表面温度,K。
计算对流换热是基于牛顿冷却公式,如式(3):
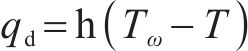
其中,qd为单位时间内单位面积的对流换热量,W/m2;h为换热系数,W/(m2∙K);Tω为流体温度,K。
由电加热元件、钢轨、积雪和空气构成的传热物理场中的主要传热形式如图3所示。
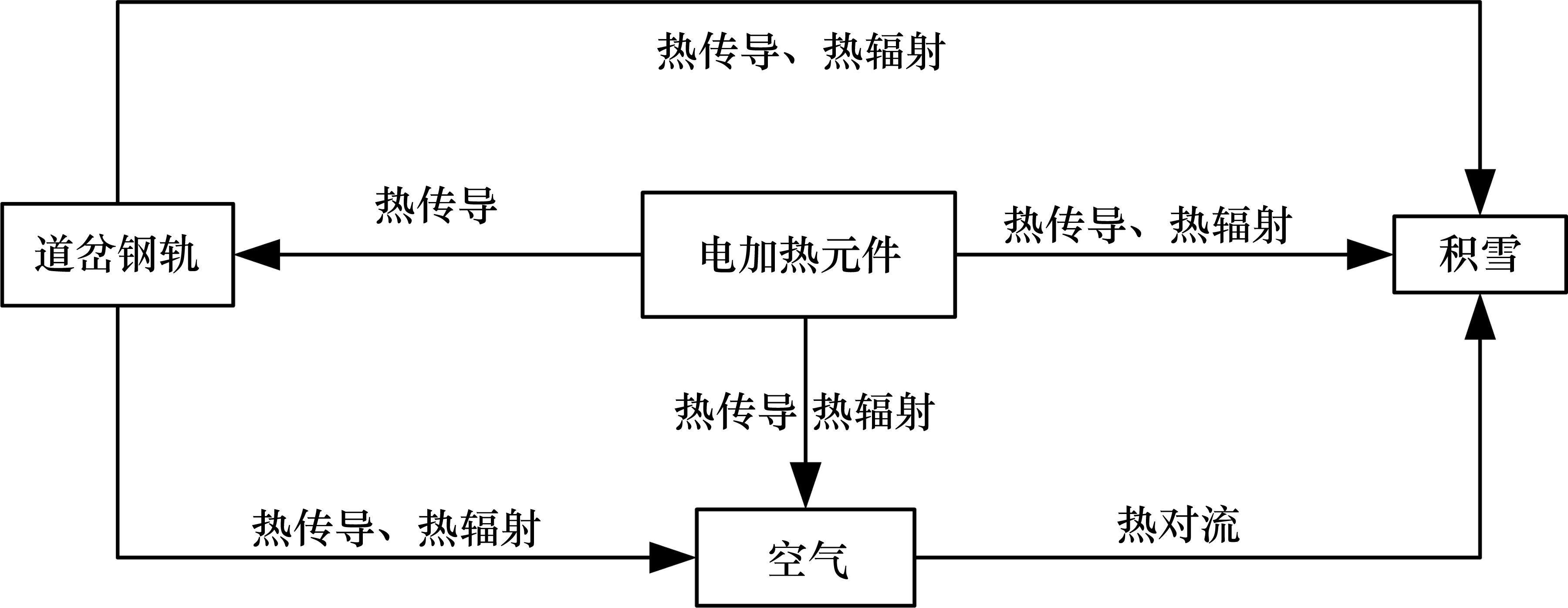
2 电加热道岔融雪模型构建
2.1 数学模型构建
道岔融雪可分为2种情况,在下雪前或刚下雪时加热元件已开始预热的实时融雪(以下简称一般情况),以及短时强降雪造成有积雪时才开始加热的滞后融雪(以下简称极端情况)。
在实时融雪情况下,电加热元件和钢轨的温度在雪落下时就能够将雪迅速融化。此时,电加热元件通电升温,钢轨受到电加热元件的热传导过程。可以得到钢轨的能量平衡方程[22],如式(4):
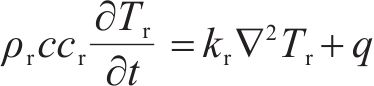
其中,ρr是钢轨的密度,kg/m3;cr是钢轨的比热容,J/(kg∙K);Tr是钢轨的温度,K;t是时间,s;kr是钢轨的热导率,W/(m∙K);q是热源和空气的影响,W/m2。
q包含热源的传导热以及加热条和钢轨散失到空气中的热量,如式(5):
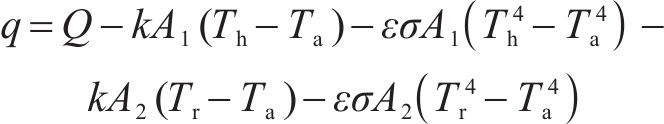
其中,Q是热源项,W/m2;A1和A2是传热接触面积,m2;Th是电加热元件的温度,K;Ta是空气的温度,K。
电加热元件所在的回路为纯电阻电路,其温度Th的计算如式(6):
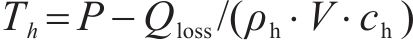
其中,P是加热条的热功率,W;Qloss是电加热元件散失到空气中的热量,W/m2;ρh是电加热元件的密度,kg/m3;V是电加热元件的体积,m3;ch是电加热元件的比热容,J/(kg∙K)。
使用有限差分法(Finite Difference Method)解决偏微分方程的数值近似解。时间上使用前向差分格式对时间偏导数进行离散化,如式(7):
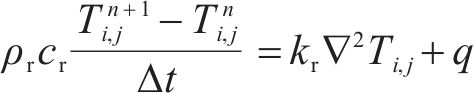
其中,T表示时间步n时刻在空间网格(i,j)处的温度;Δt表示时间步长。
空间上使用中心差分格式对∇2T项进行离散化:
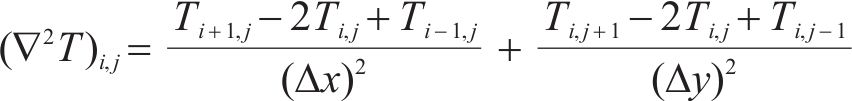
其中,Δx和Δy分别表示空间网格的横向和纵向步长。
根据以上离散化处理后,钢轨的能量平衡方程可以表示为:
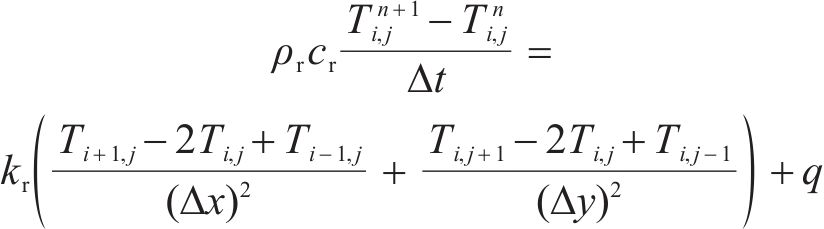
由于钢轨在长度方向具有均匀性,可以将问题简化为考虑二维截面内的温度分布。在这种简化模型中,钢轨下方与橡胶垫板接触,可定义为热绝缘边界,即底部不与橡胶垫板进行热交换。其余边界与周围空气接触,边界条件设定为与环境空气温度相等。这种简化不仅有效减小了计算量,同时也保留了沿长度方向的均匀性特征,使得模型更易于处理并符合实际情况。设定初始条件和环境条件,进行空间步和时间步的迭代更新钢轨温度,可得到钢轨温度随时间的变化。
钢轨温度计算流程如图4所示。
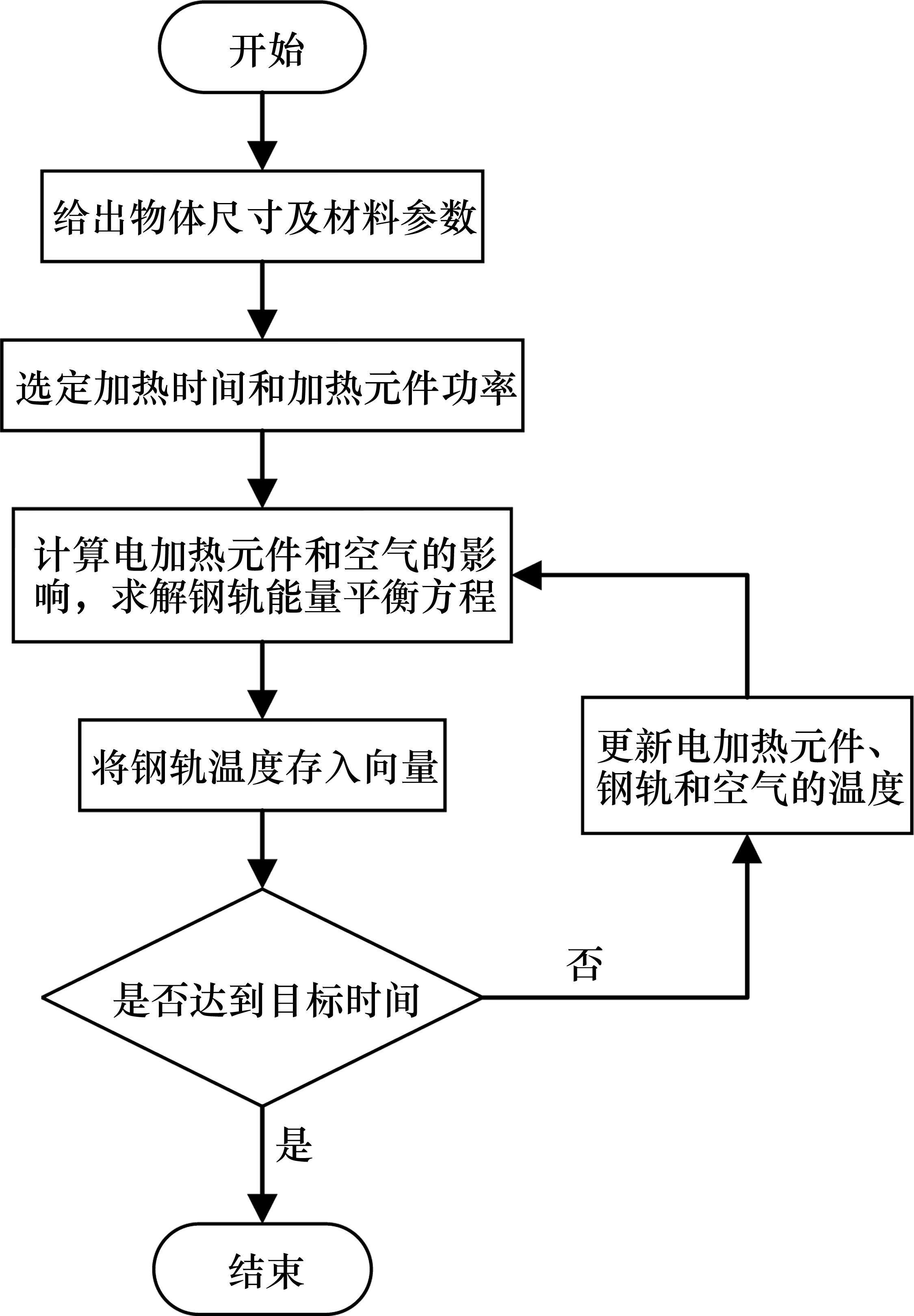
在极端情况下,短时强降雪导致滑床板上产生积雪时加热元件才开始进行工作,此时需要考虑积雪吸收热量并融化的过程。
对于钢轨来说,增加了对积雪的影响,其他过程与实时融雪类似。对于积雪来说,钢轨,加热元件和空气均对其产生影响,且加热过程中含有热传导,热辐射和热对流3种传热形式。
积雪是相变材料,需要考虑积雪融化产生相变带来的影响。根据传热过程分析,可以得到积雪的能量平衡方程:
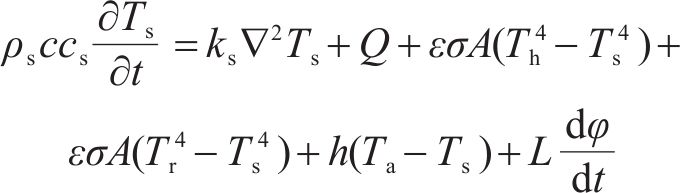
其中,ρs是积雪的密度;cs是积雪的比热容;Ts是积雪的温度;t是时间;ks是积雪的热传导系数;Q是热源项;ε是积雪的辐射率;σ是斯特藩-玻尔兹曼常数;ℎ是对流传热系数;Ta是空气的温度;L是相变潜热;φ是相变参数。
使用有限差分法将其离散化,得到的能量平衡方程为:
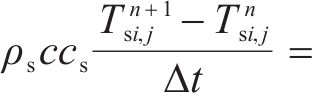
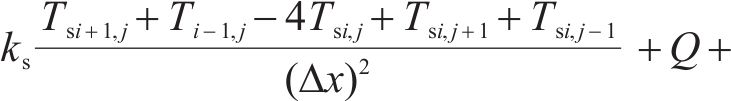
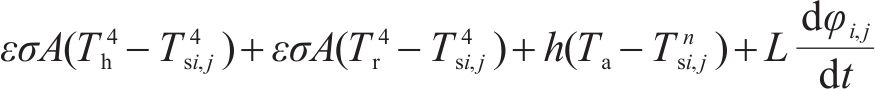
模型计算所用材料的参数如表1所示。
| 材料 | 密度ρ/ (kg∙m-3) | 比热容c/ (J∙kg-1∙K-1) | 导热系数k/ (W∙m-1∙K-1) |
|---|---|---|---|
| 钢轨 | 7 850 | 475 | 44.5 |
| 电加热元件 | 7 800 | 470 | 70 |
| 雪 | 150 | 2 100 | 0.2 |
| 空气 | 1.225 | 1 005 | — |
2.2 几何模型构建
使用Solidworks将画好的基本轨,尖轨,滑床台及滑床板等零件添加到同一个三维空间中形成集合体。
对一般情况和极端情况分别进行几何建模。一般情况下,电加热元件有预热过程,雪落下即迅速融化,基本不会产生积雪;极端情况下,需要对积雪进行建模,考虑积雪的影响,如图5所示。
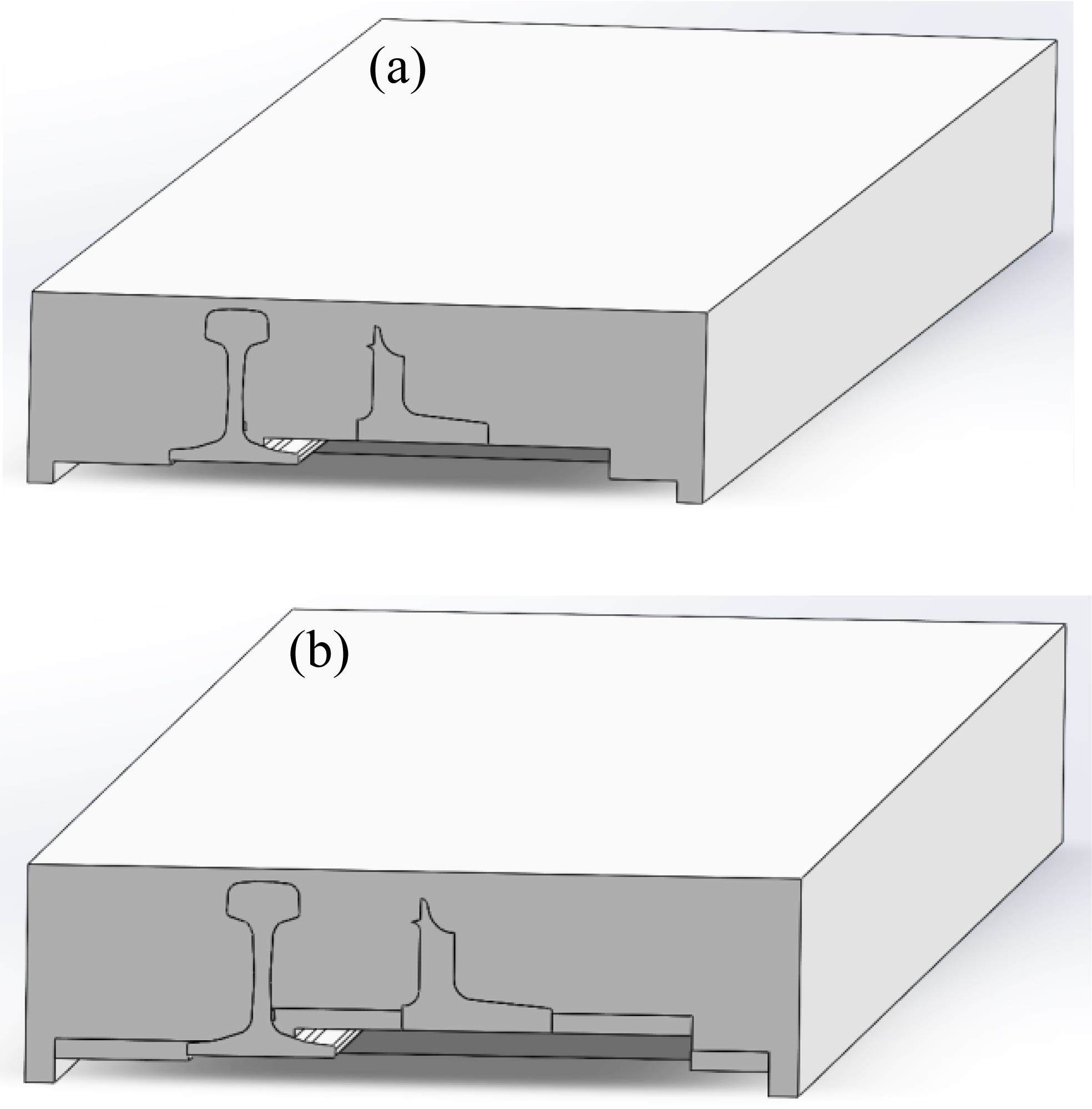
根据GB/T 2585—2021《铁路用热轧钢轨》要求,基本轨、尖轨采用在线热处理的钢轨制造,并且道岔区所使用的钢轨材质应与区间线路所铺设的钢轨材质保持一致,应采用U71Mn或U75V[23]。部分道岔材质如表2所示。
| 结构 | 材质 |
|---|---|
| 钢轨 | U75V钢 |
| 滑床台 | Q235钢 |
| 滑床板 | Q235钢 |
| 电加热元件 | 铬镍合金 |
| 垫板 | 橡胶 |
在仿真前要对几何模型进行网格分割,将一个复杂的结构分割成许多小的有限元素,通过对这些元素进行求解和组合,可以得到整个结构的结果。根据模型的几何形状、物理特性和所需精度来选择适当的网格划分大小。本次采用较细致的划分,一般情况的几何模型被划分为474 478个四面体单元,91 457个三角形单元,20 849个边单元,376个顶点单元;极端情况的几何模型被划分为503 116个四面体单元,111 055个三角形单元,23 395个边单元,402个顶点单元。划分后的网格图像如图6所示(忽略空气域)。

对模型进行网格无关性验证,网格划分数量分为40,20和5 W,分别进行模拟,得到的结果如图7所示。
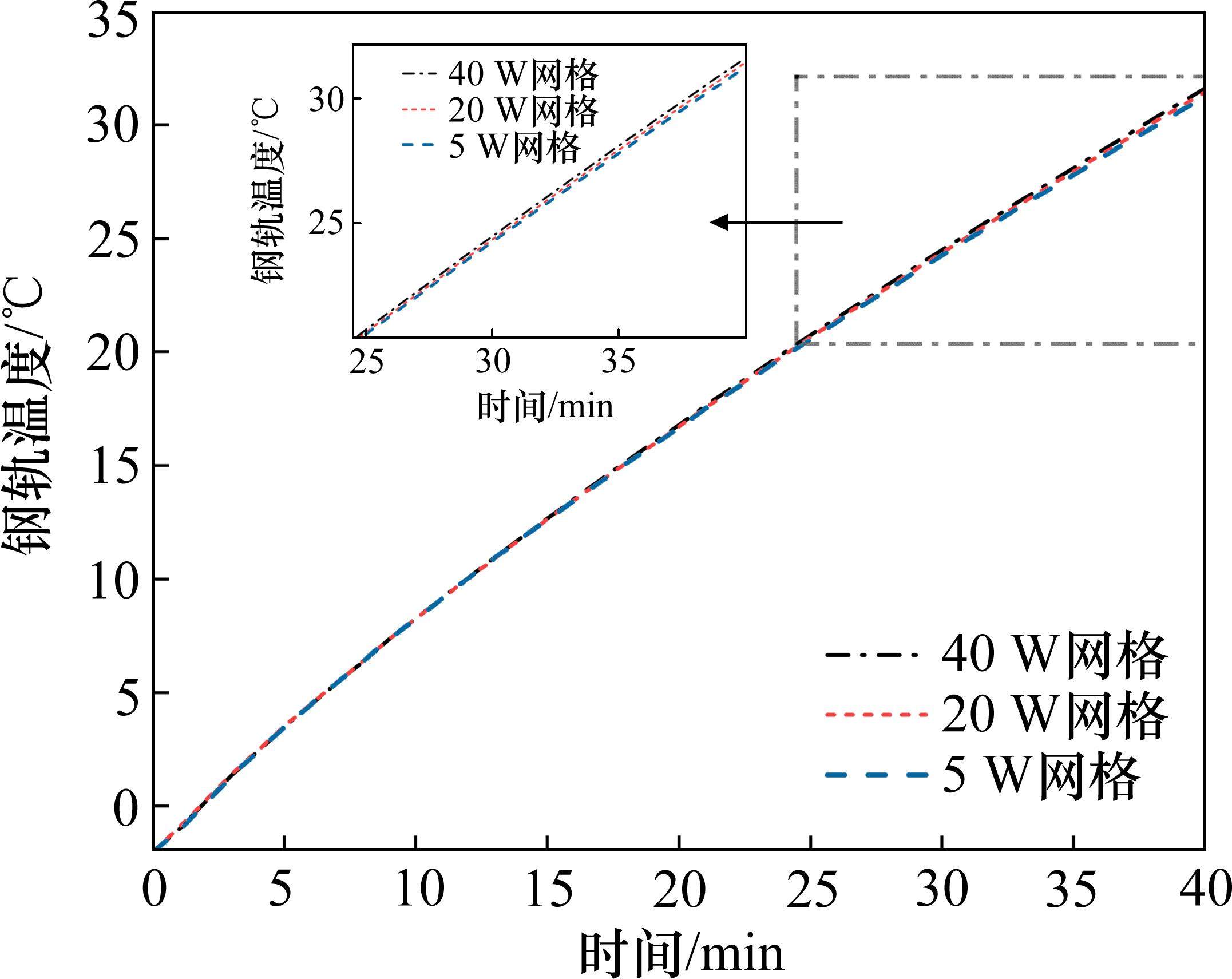
从图7可以看出,3条不同网格数量的轨温变化曲线基本一致,网格划分对结果的影响很小。
现场钢轨温度主要靠轨温传感器进行测量,轨温传感器通过专用卡具固定安装在基本轨底部,采集温度并向系统回传,传感器位置如图8所示。

3 实验验证及结果分析
3.1 实验验证
为了对模型的准确性进行验证,对2023年12月15日兰西动车所道岔融雪系统的轨温数据进行采集,现场实测部分数据如表3及表4所示。
| 钢轨温度/℃ | 加热时长/min | 钢轨温度/℃ | 加热时长/min | 钢轨温度/℃ | 加热时长/min | 钢轨温度/℃ | 加热时长/min | 钢轨温度/℃ | 加热时长/min | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1号道岔 | -1.6 | 2 | 7.3 | 10 | 15.7 | 17 | 22.0 | 25 | 27.0 | 33 |
| 3号道岔 | -1.5 | 2 | 7.1 | 10 | 15.3 | 17 | 22.0 | 25 | 26.6 | 32 |
| 5号道岔 | -1.3 | 2 | 7.1 | 9 | 15.4 | 17 | 21.9 | 25 | 26.7 | 31 |
| 7号道岔 | -1.5 | 2 | 6.3 | 9 | 14.7 | 17 | 21.6 | 25 | 26.7 | 32 |
| 9号道岔 | -0.7 | 2 | 7.9 | 10 | 15.5 | 18 | 21.3 | 25 | 25.0 | 32 |
| 11号道岔 | -1.0 | 2 | 7.6 | 10 | 14.7 | 17 | 20.8 | 25 | 25.5 | 32 |
| 13号道岔 | -1.4 | 3 | 5.8 | 10 | 13.3 | 17 | 19.8 | 25 | 24.5 | 33 |
| 钢轨温度/℃ | 加热时长/min | 钢轨温度/℃ | 加热时长/min | 钢轨温度/℃ | 加热时长/min | 钢轨温度/℃ | 加热时长/min | 钢轨温度/℃ | 加热时长/min | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1号道岔 | 10.5 | 3 | 17.7 | 10 | 24.1 | 18 | 28.6 | 25 | 28.5 | 33 |
| 3号道岔 | 11.6 | 4 | 19.3 | 12 | 25.3 | 19 | 32.6 | 27 | 25.7 | 34 |
| 5号道岔 | 10.7 | 3 | 17.9 | 10 | 24.3 | 18 | 28.8 | 25 | 27.1 | 30 |
| 7号道岔 | 9.8 | 1 | 16.6 | 8 | 22.6 | 16 | 27.5 | 23 | 31.9 | 31 |
| 9号道岔 | 13.8 | 6 | 21.0 | 14 | 26.6 | 21 | 28.9 | 29 | 23.5 | 37 |
| 11号道岔 | 12.7 | 5 | 20.3 | 12 | 25.8 | 19 | 32.2 | 27 | 24.7 | 35 |
| 13号道岔 | 14.1 | 6 | 20.9 | 13 | 25.8 | 20 | 32.3 | 28 | 24.2 | 36 |
| 15号道岔 | 10.1 | 2 | 17.1 | 9 | 23.2 | 24 | 28.3 | 24 | 27.0 | 32 |
对以上实测数据进行分析筛选,首先去除个别加热时间过长或过短的数据,再结合前后轨温变化去除不在加热时间内的数据,需要注意的是,由于停止加热时电加热元件温度比钢轨温度高,所以在停止加热后钢轨温度仍有小幅上升,还需去除这部分数据。经过对现场数据进行分析,在加热元件开始工作时,轨温为-2 ℃左右,由于系统刚启动,将轨温加热到30 ℃左右基本需要30~45 min;钢轨加热到30 ℃时停止加热,冷却后再次启动时轨温为10 ℃左右,加热到目标温度基本需要20~35 min。所有道岔均是在同一站场,钢轨温度均是在同一天取得的数据,所以各道岔环境条件可认定为一致,将有效的数据值放入后续的实验结果中用于模型验证。
根据这2种情况结合现场环境设定初始条件,将空气域的边界定为开放边界,钢轨下方是橡胶垫板,底部设定为热绝缘,初始条件及环境条件如表5所示。
加热 情况 | 钢轨初始温度/℃ | 环境温度/℃ | 加热时长/min | 风速/ (m∙s-1) | 相对湿度 |
|---|---|---|---|---|---|
首次 加热 | -2 | -3 | 40 | 0.3 | 0.5 |
| 冷却后再加热 | 10 | -3 | 30 | 0.3 | 0.5 |
进行仿真模拟,经过电加热元件加热之后,温度分布及钢轨温度如图9及图10所示。
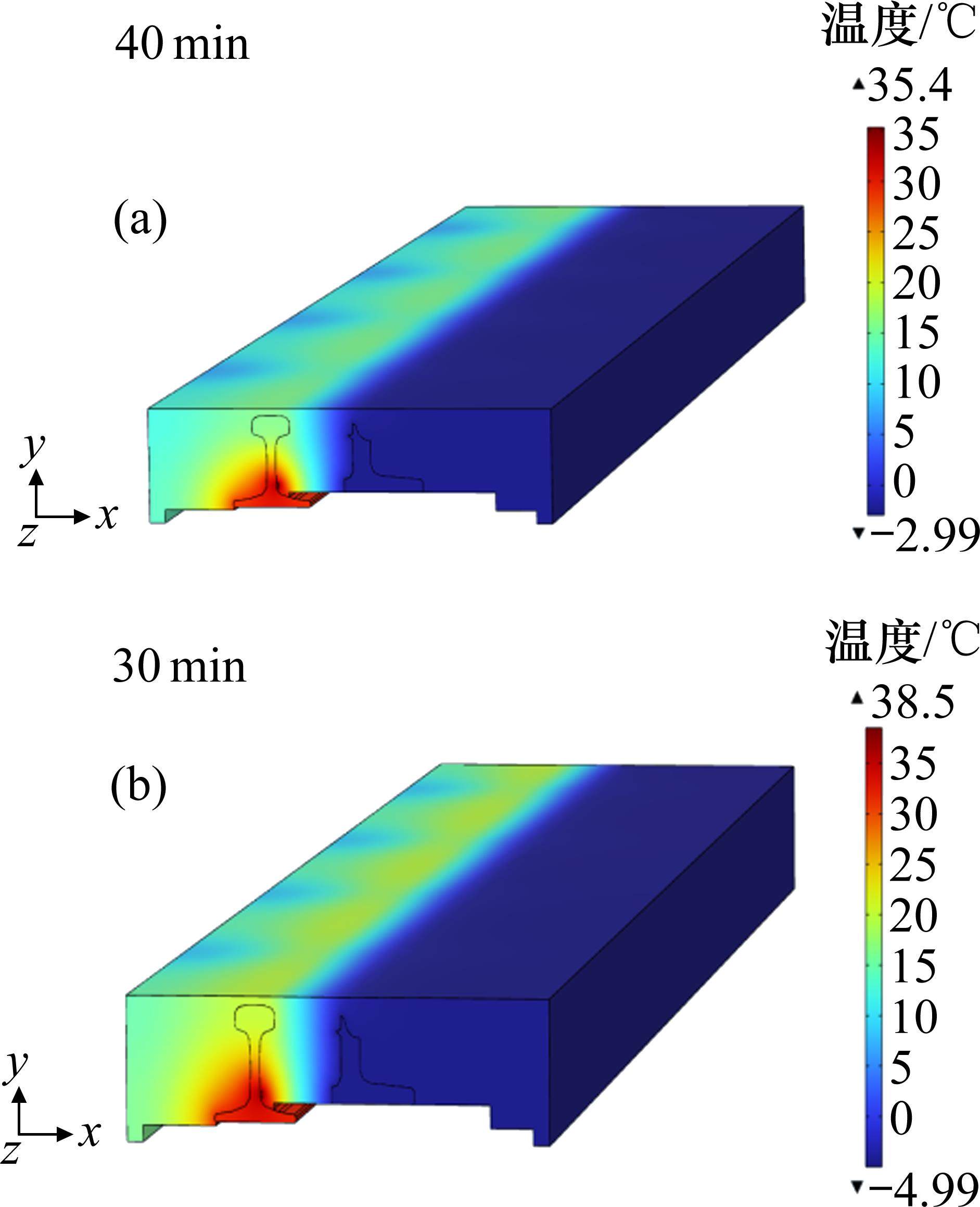
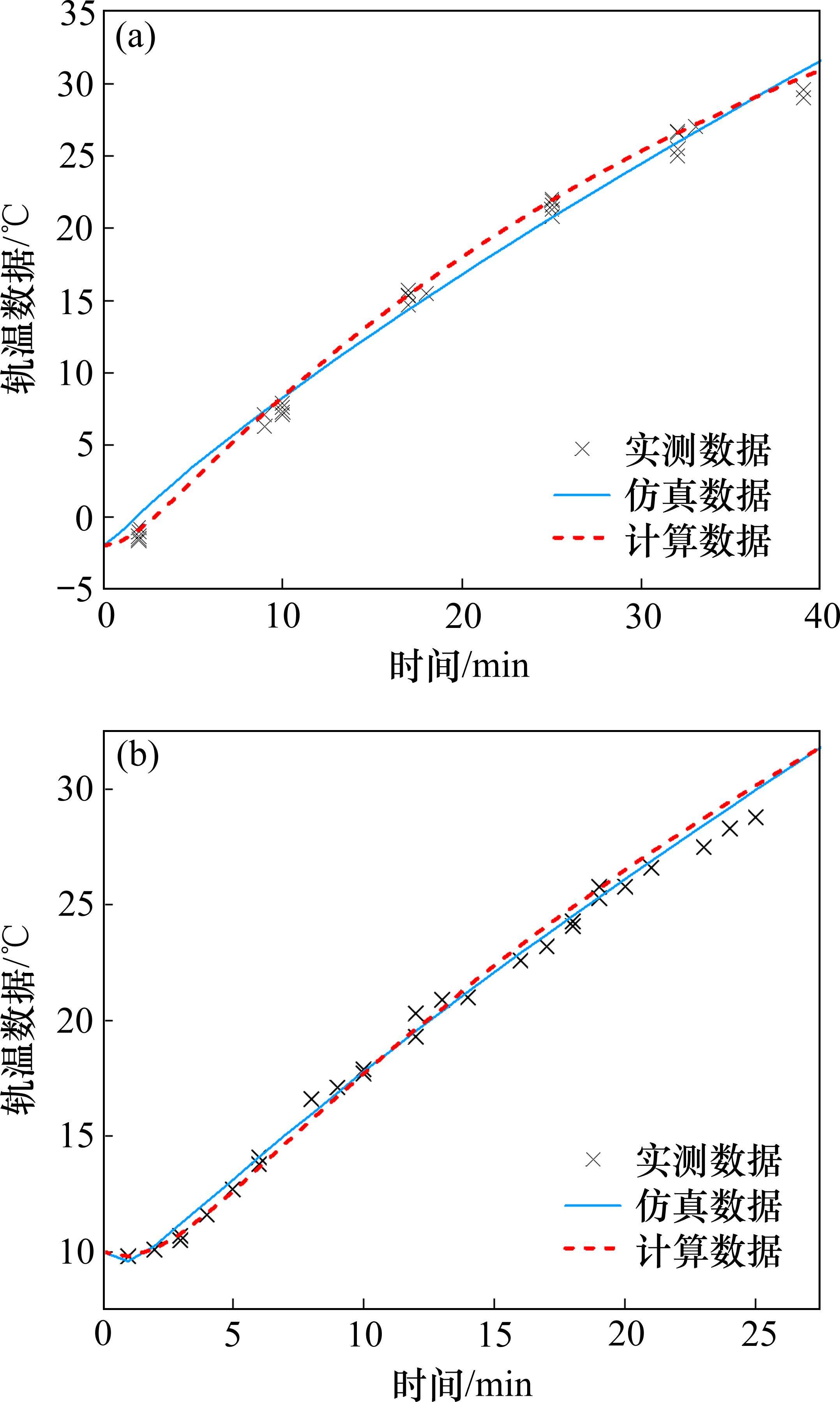
在首次加热过程中,多组道岔加热元件会同时开启,每7~8 min向系统传输一次轨温数据,数据采集点在这个阶段比较集中;在后续的加热过程中,由于人工操作的短时加热和故障报警的干预,各组道岔电加热元件的启停时间会变得不一致,导致数据采集点比较分散。实测数据与仿真数据和计算数据之间相差不超过±2 ℃,相对误差保持在7%以内,验证了模型的准确性。对产生误差的原因进行分析。
1) 在加热过程中,空气是流动的,然而模型无法准确模拟空气动态变化对钢轨的影响,这可能导致空气对钢轨的影响产生误差。
2) 每组道岔的电加热元件回路电流存在波动现象,导致电加热元件不会全程按照额定功率运行。因此,加热过程中的波动电流可能会引起误差。
3.2 结果分析
从图9及图10中的数据可以看出,首次加热在38 min左右加热到目标温度,冷却后再次加热时,由于冬季空气温度低,电加热元件刚开始加热,导致钢轨温度出现小幅度的下降,在26 min左右加热到目标温度。2次加热过程中,钢轨温度的上升幅度基本平稳。
对短时强降雪的极端情况进行模拟分析,环境条件为-5 ℃,积雪厚度为20 mm,其余条件与一般情况相同,加入与极端情况环境条件相同但无积雪的对照组,在积雪域设置探针,可得到积雪的相变程度,相变程度的范围为0~1,为1时积雪完全融化,结果如图11所示。
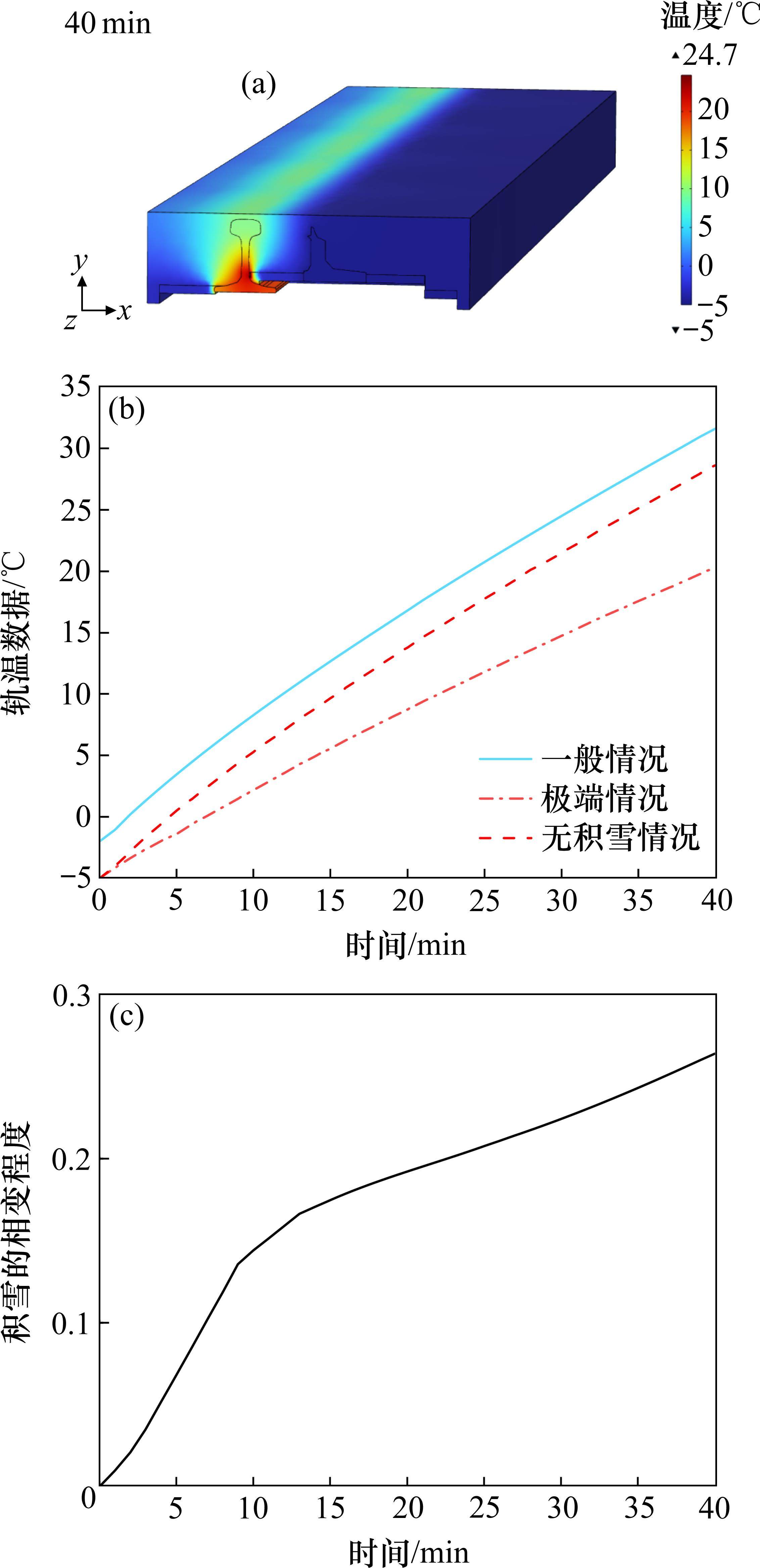
由图11可以看出,热量主要集中在加热条和钢轨下部,只有靠近电加热元件和钢轨的小部分积雪融化;初始温度不同时,温度有所降低,温度升高速率变化不大,在相同初始温度条件下,有无积雪对温度变化影响较大;积雪的融化程度在0~10 min有剧烈的变化,是因为靠近钢轨和加热元件的积雪受热迅速融化,而远离钢轨和电加热元件的积雪吸收不到足够的热量,使10~30 min融化程度变得平缓,30 min以后随着钢轨和电加热元件温度继续升高,相变程度的变化又有增加的趋势。40 min后相变程度小于0.3,极端情况下融雪效果不佳。
4 结论
1) 通过分析传热过程,建立数学模型,基于MATLAB和COMSOL分析软件研究物理场中的传热特性,讨论了一般情况下首次加热和再次加热的轨温变化,实测数据与仿真数据和计算数据之间相差不超过±2 ℃,相对误差保持在7%以内,验证了模型的准确性,为后续优化道岔融雪系统提供理论基础。
2) 经过对热传递公式及能量平衡方程的分析,热量传递效率与电加热元件本身材料的属性,电加热元件的安装方式及接触面积有关;对现场实测数据筛选分析的过程中,发现存在小部分加热时间过长或过短,需要对再次加热的情况进行深入分析,寻找其影响因素,便于对电加热元件进行研究和改进。
3) 物理模拟在气温-5 ℃,积雪厚度为20 mm的极端情况下轨温变化及积雪的相变程度,积雪厚度是影响温度变化的主要因素,此外还需考虑环境的初始温度,此时加热30 min后轨温为20 ℃,积雪融化程度小于0.3,表明现有道岔融雪面对极端情况仍有压力,需要根据不同地区的积雪量和环境温度为基础对电加热元件设置不同的方案。
关于发布铁道行业标准的公告(工程建设标准2024年第1批)
[EB/OL]. https://www.nra.gov.cn/xxgk/gkml/ztjg/bzgf/bzgg/202402/t20240201_344631.shtml.贺清,李宗霖,黄勇等.道岔融雪系统电加热元件传热模型构建及分析[J].铁道科学与工程学报,2025,22(02):841-851.
HE Qing,LI Zonglin,HUANG Yong,et al.Construction and analysis of heat transfer model for electric heating elements in switch snow melting system[J].Journal of Railway Science and Engineering,2025,22(02):841-851.

