近年来,我国地下空间开发迅速增长,尤其是城市隧道建设蓬勃发展[1-3]。盾构法由于建造速度快和对周边环境影响较小等优势,被广泛应用于隧道工程的建设[4]。环境复杂化是盾构技术重要发展趋势,新建隧道通常会不可避免下穿既有隧道,可能诱发既有隧道的沉降变形,甚至造成管片破损、螺栓屈服、接头渗漏水等病害[5-6]。因此需对下穿施工引起的既有盾构隧道变形进行预测和评估,以及时采取对应的加固控制措施。针对新建隧道下穿施工引发既有盾构隧道的纵向变形问题,研究主要采用有限元模拟[7-9]、模型实验[10-11]、现场实测[12]、理论解析[13]等手段。其中,理论分析以计算简便和力学概念清晰等优势,成为预测变形和指导施工的有效手段。盾构隧道的纵向变形本质上为复杂的三维力学问题,理论分析中,学者们通常采用等效连续化的思想,将这一复杂多维力学问题简化为弹性地基上的一维梁模型。张治国等[14-15]应用两阶段分析法,将既有盾构隧道简化为Winkler地基上的Euler-Bernoulli梁,建立了新建隧道下穿施工诱发既有盾构隧道变形计算模型。梁荣柱等[16-17]基于有限差分法,将既有盾构分别简化为Euler-Bernoulli梁和考虑剪切效应的Timoshenko梁,研究了盾构下穿引起上覆隧道纵向变形、张开角和错台量。传统Winkler地基模型只考虑了隧道的沉降对地基反力的影响,未涉及土体的连续性和剪切变形。为了提高计算精度,双参数地基模型被引入力学模型的构建。吕金剑等[18]考虑了土层的剪切系数影响,提出了小净距双线隧道下穿施工诱发运营盾构隧道纵向变形预测方法。目前理论研究多为确定性分析,往往忽略地层沿隧道轴线上的空间变异特性,其计算结果通常只能反映既有隧道的平均力学响应,难以全面预测其沉降变形。可描述土层空间变异特性的随机场理论已成功应用到地表沉降[19]、基坑开挖[20]、边坡稳定[21]等研究领域,而对于新建隧道下穿既有隧道工程研究的应用相对较少。此外,冯国辉等[22]研究新建隧道下穿既有管线考虑了侧向力的影响,获取了更精确的既有管线变形响应。类似地,新建隧道下穿既有隧道时,侧向土体对既有隧道也具有相似的约束效应。新建隧道盾构过程引起的土体附加应力,会作用在既有隧道和既有隧道的地基上,两者变形的差异会导致侧向土体与既有隧道存在相互作用。目前研究并未全面考虑土体侧向力、土层空间变异性和土体剪切传递作用对隧道变形的综合影响,限制了计算精度。针对此前研究的不足,本文考虑土体侧向力的约束效应,结合随机场和双参数弹性地基梁理论,构建新建隧道下穿既有盾构隧道的有限元力学模型,并通过2个典型算例验证合理性。之后依托工程实例对下穿前既有隧道的变形进行预测,并提出相对应的控制加固措施。
1 盾构下穿上覆既有隧道力学模型构建
为简化求解过程,作以下基本假定:
1) 将既有盾构简化为双参数弹性地基上的具有相同均质特性的连续梁,采用折减后的等效抗弯刚度来表征接缝的削弱作用。
2) 侧向土体对既有隧道的影响通过侧向力来表征,侧向土体作用力通过土体剪切层附加在隧道两侧。
3) 新建隧道下穿施工对上方地层的扰动采用Loganathan公式模拟。
1.1 既有隧道受力分析
基于Loganathan公式[23],隧道开挖对邻近土体自由位移场S(x,z)可表示为:
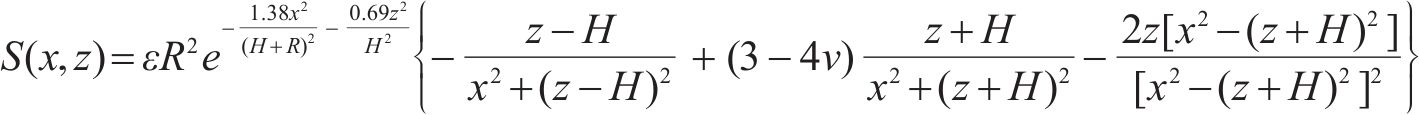
式中: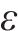
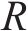
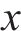

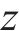
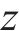
上述的Loganathan公式仅针对于新建隧道与既有隧道垂直的工况,若开挖隧道与既有隧道的夹角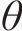
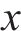
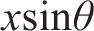
隧道开挖引起土体的位移,进一步转化为作用在既有隧道的附加荷载,如图1(a)所示,可表示为:
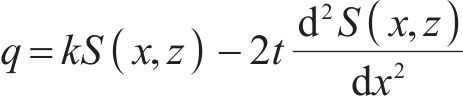
式中: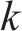

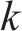

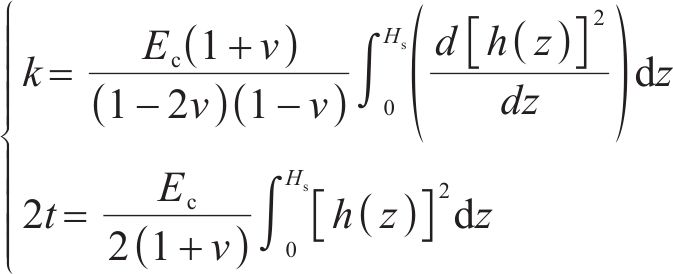
式中: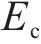
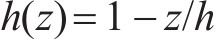
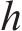
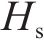
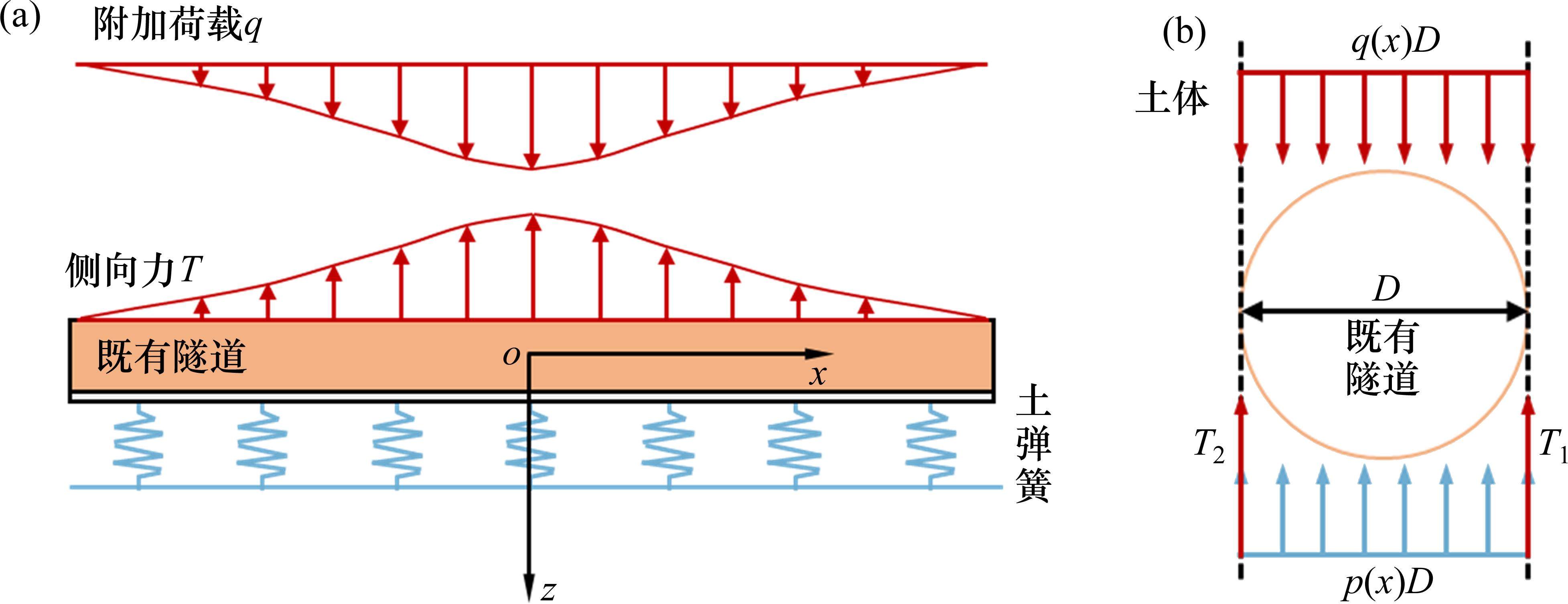
此外,借鉴冯国辉等[22]研究新建隧道下穿既有管线的成果,新建隧道下穿产生的附加应力,会同时作用于既有隧道和既有隧道的地基上,两者的差异变形导致存在相互约束作用,侧向土体对既有隧道的影响通过侧向力来表征,侧向土体作用力通过土体剪切层附加在管线两侧,如图1(b)所示,侧向力的大小与隧道的变形程度密切相关,在进行变形预测时,考虑侧向力的影响有利于进行更精确的分析。侧向力表达形式如下所示:
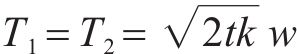
1.2 基于有限元法的求解分析
对于盾构下穿引起既有隧道的变形研究,传统对于力学模型的求解方法大多基于一般解析法或者有限差分方法对力学模型进行求解。一般解析法的最终解析解形式极为复杂,不利于引入过多的模型参数。而有限差分方法求解过程较为复杂,需要引入额外的节点作为边界条件进行求解。本文拟采用力学概念清晰且计算简便的有限元方法。目前的有限元方法在盾构隧道纵向力学行为分析方面的应用尚不多见,HUANG等[24]引入单参数弹性地基梁有限元模型研究了隧道纵向变形。考虑土弹簧剪切效应的双参数地基梁虽然形式上更为复杂,但求解流程与单参数模型类似。将整体的弹性地基梁进行离散,离散后的双参数弹性地基梁单元如图2所示。
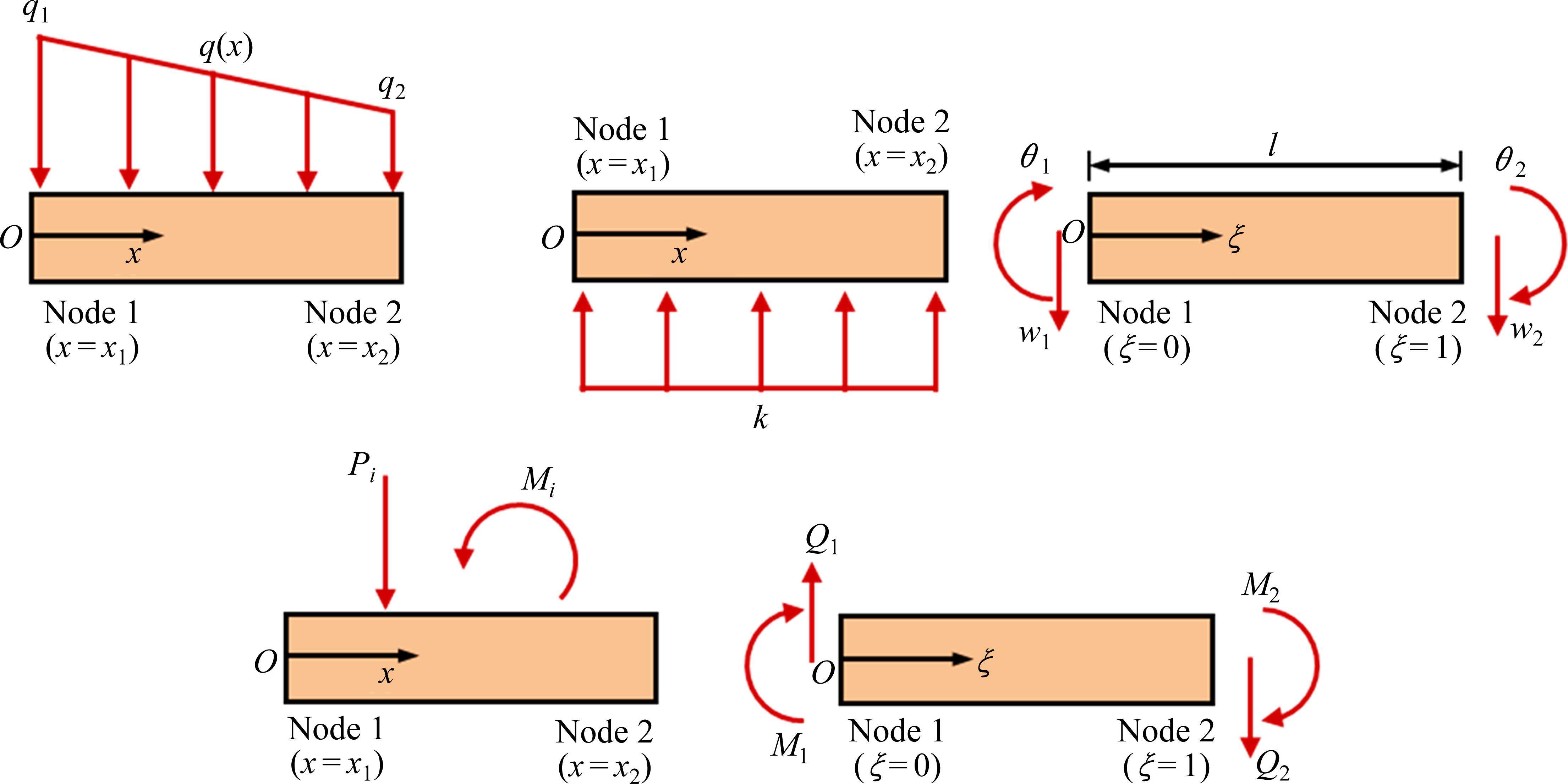
既有隧道受的外荷载主要为新建隧道开挖引起的附加荷载和土体侧向力,从式(1)可以发现附加荷载以及侧向力等荷载在较大尺度范围内为一非线性分布的形式。但为了方便研究,本文假设在每个单元内,荷载呈线性分布,因此其中一个梁单元内,外荷载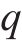
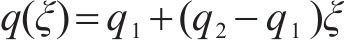
式中: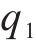
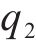
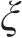
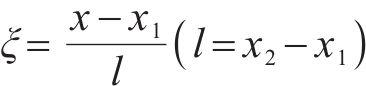
式中: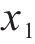
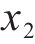
一个单元范围内,任意处梁的挠度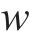
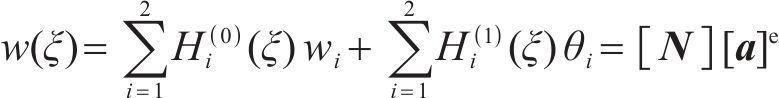
式中: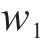
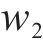
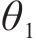
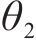
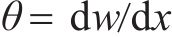
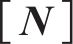
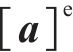
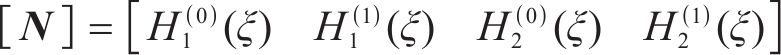
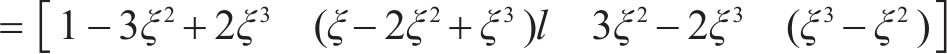
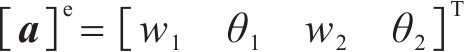
梁的总势能由变形能和荷载势能组成,变形能为弯曲应变能,荷载势能包括外荷载势能,梁的总势能可表示为:
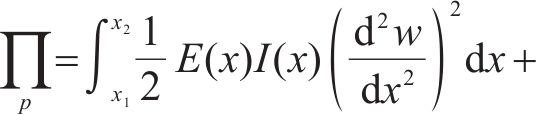
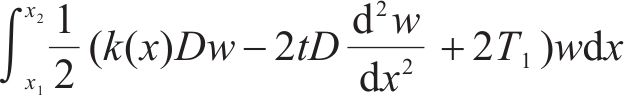
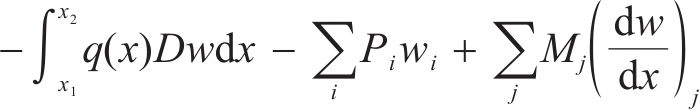
根据最小势能原理,弹性地基梁真实的位移场应使得系统的总势能取得极小值,所以有:
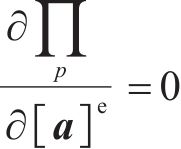
引入节点位移向量和形函数,则式(11)可表示为:
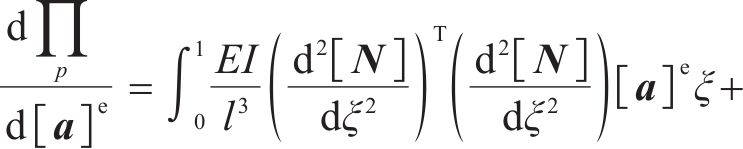
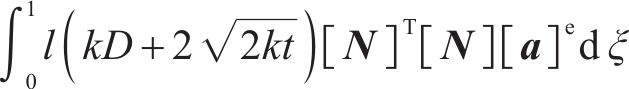
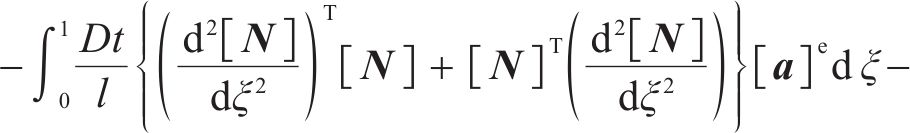
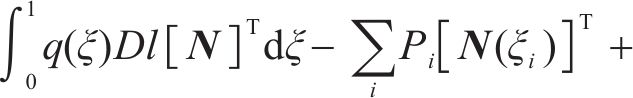
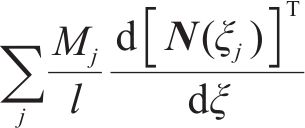
进一步可获得单元刚度、单元节点位移及单元荷载矩阵的关系,如下所示:
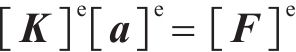
式中: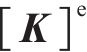
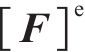
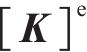
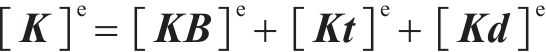
其中,



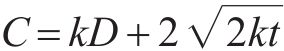
荷载矩阵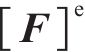
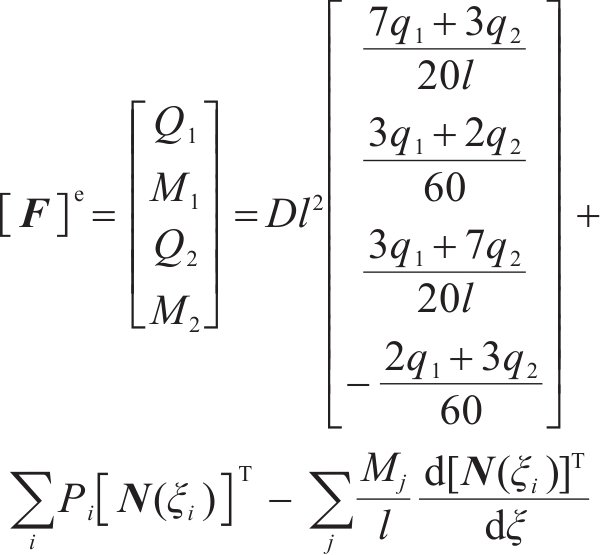
基于求解出的刚度矩阵、荷载矩阵,将不同单元的弹性模量、剪切系数及外荷载代入对应的单元刚度矩阵和荷载矩阵中,再整合为整体刚度和荷载矩阵,结合两端的边界条件即可求解。
1.3 力学模型参数获取
1.3.1 地基参数
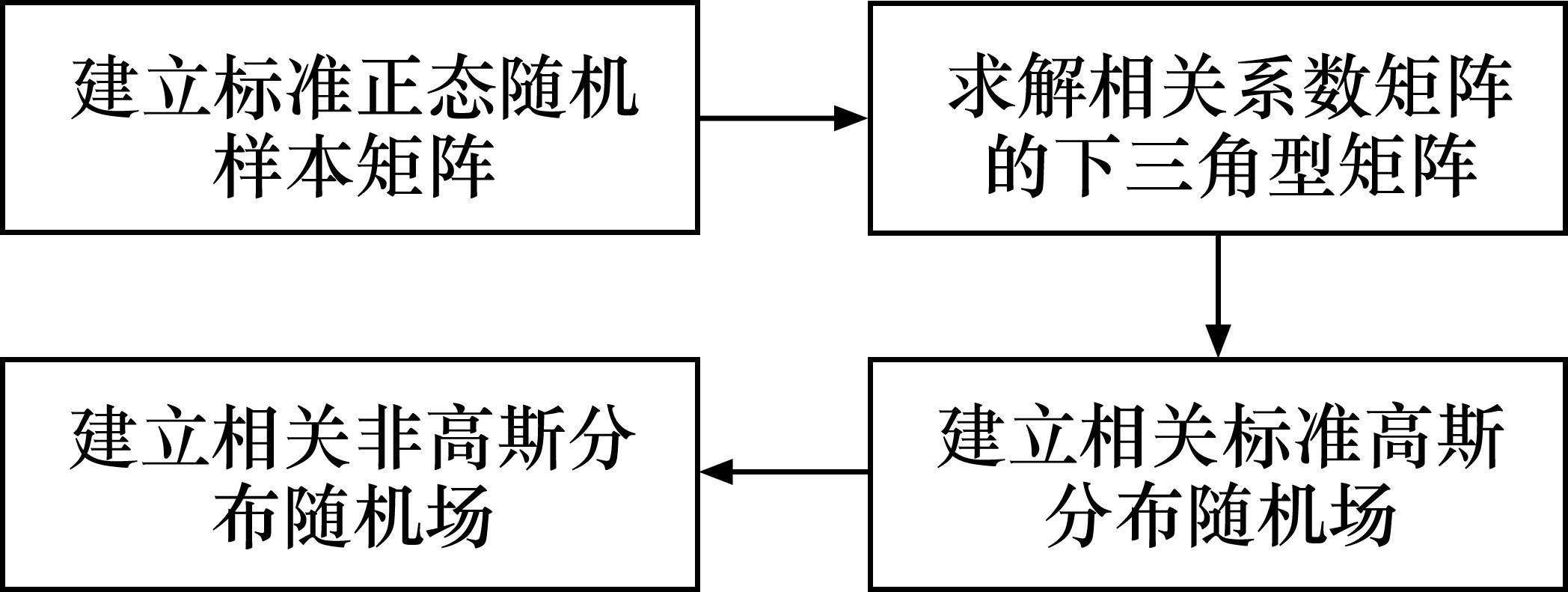
力学模型的参数主要包括地基参数和梁的等效抗弯刚度。通过引入随机场理论,量化了地基参数在纵向空间上的变异性。本文采用中心点法[25-26]生成弹性模型的随机场模型,简要步骤如图3所示,基于弹性模量、弹性刚度、剪切层刚度的关系,可构建后两者的随机场模型。
1.3.2 等效抗弯刚度
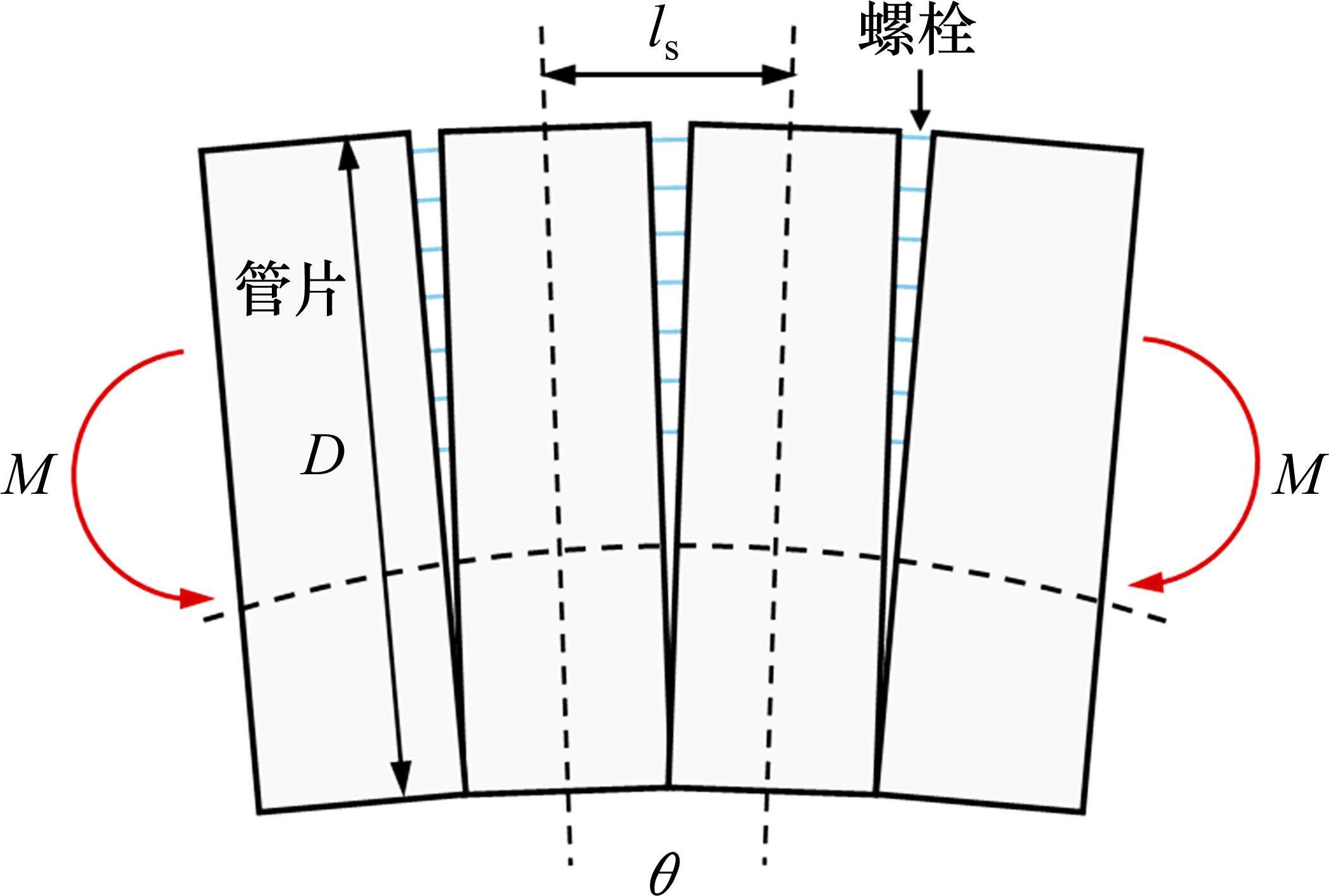
此外,盾构隧道是由管片和螺栓组成的非连续结构,将两者进行一体等效时,其等效抗弯刚度有所折减[27],采用日本学者志波由纪夫提出的力学分析模型,具体的隧道变形模式如图4所示,则隧道的等效抗弯刚度可表示为:
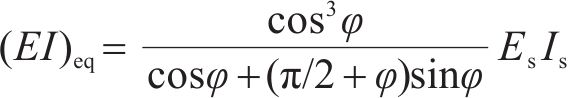
式中: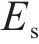
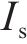
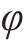
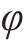
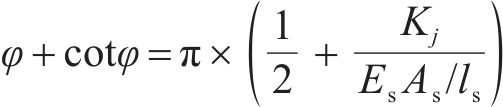
式中: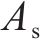
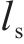
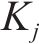
2 模型验证与分析
2.1 算例1(考虑侧向力)
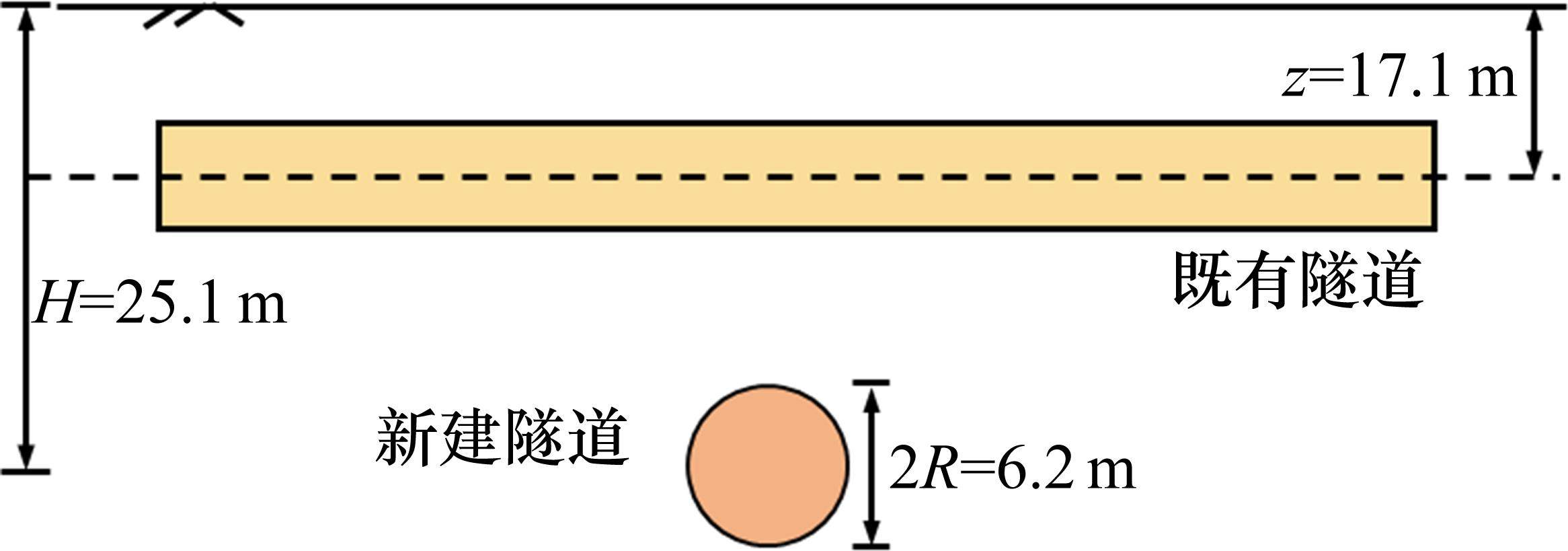
选择上海市轨道交通11号线上行线下穿既有地铁1号线工程作为算例[15]进行分析,下穿的剖面简化模型如图5所示。新建隧道和既有隧道的夹角为75°,其隧道的埋深分别为25.1 m和17.1 m,其间的竖向净距为1.8 m。此外,新建隧道与既有隧道均处于砂质粉土中,其土体模型取值为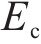
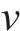

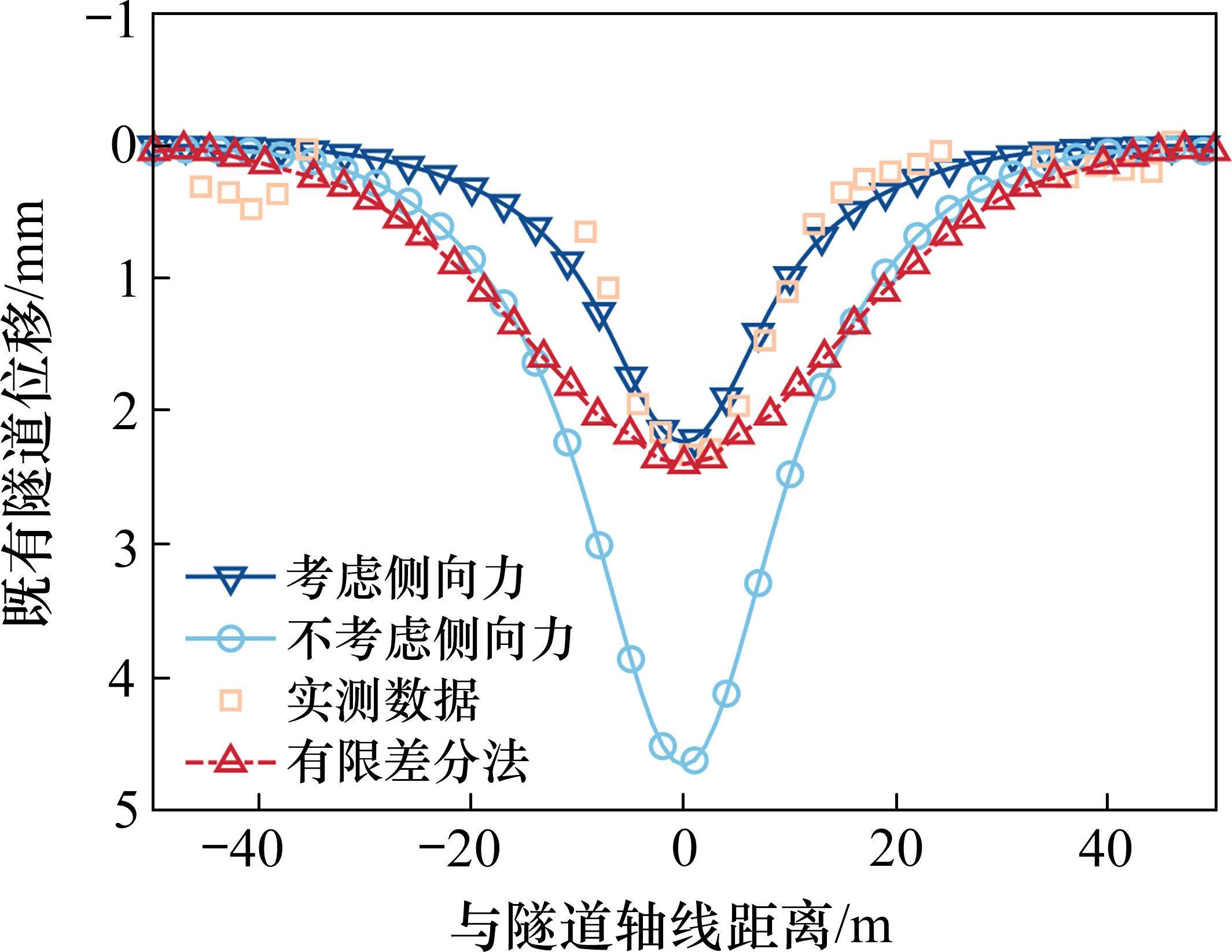
本文构建的力学模型计算结果与现场实测数据对比如图4所示。可见,本文力学模型计算结果与现场实测数据基本吻合,最大变形处误差为4%,左侧有一定的误差,分析原因可能与地层的不均匀性相关,以盾构隧道为中轴线的左右侧变形监测数据不对称也可说明这一点。此外还对比了不考虑侧向力和有限差分法的计算结果。可以发现,不考虑侧向力的误差较大,最大沉降变形达4.6 mm,误差达100%。有限差分法和本文提出的力学模型的计算误差较小,但对现场实测数据的拟合效果不如本文模型。
2.2 算例2(考虑地层随机场)
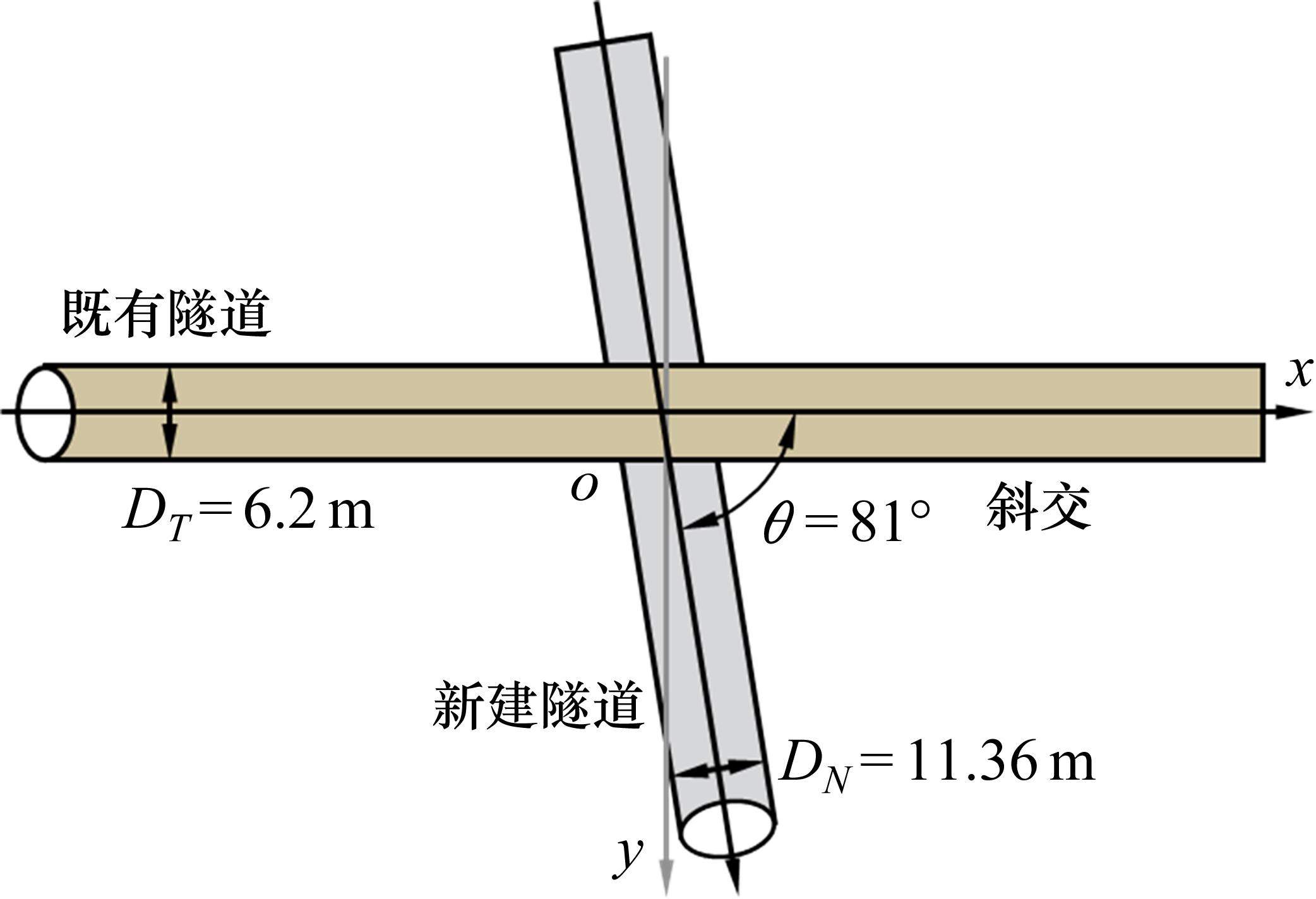
文献[28]依托杭州某新建地铁斜交下穿既有地铁隧道工程进行分析。隧道下穿平面示意图如图7所示,既有隧道的外径为6.2 m,新建隧道的外径为11.36 m,2个隧道的轴线埋深分别为13.5 m和23.78 m。此外,既有隧道处于淤泥、淤泥泥质黏土和淤泥质粉质黏土层中,而新建隧道的周边覆土主要为淤泥质粉质地层。
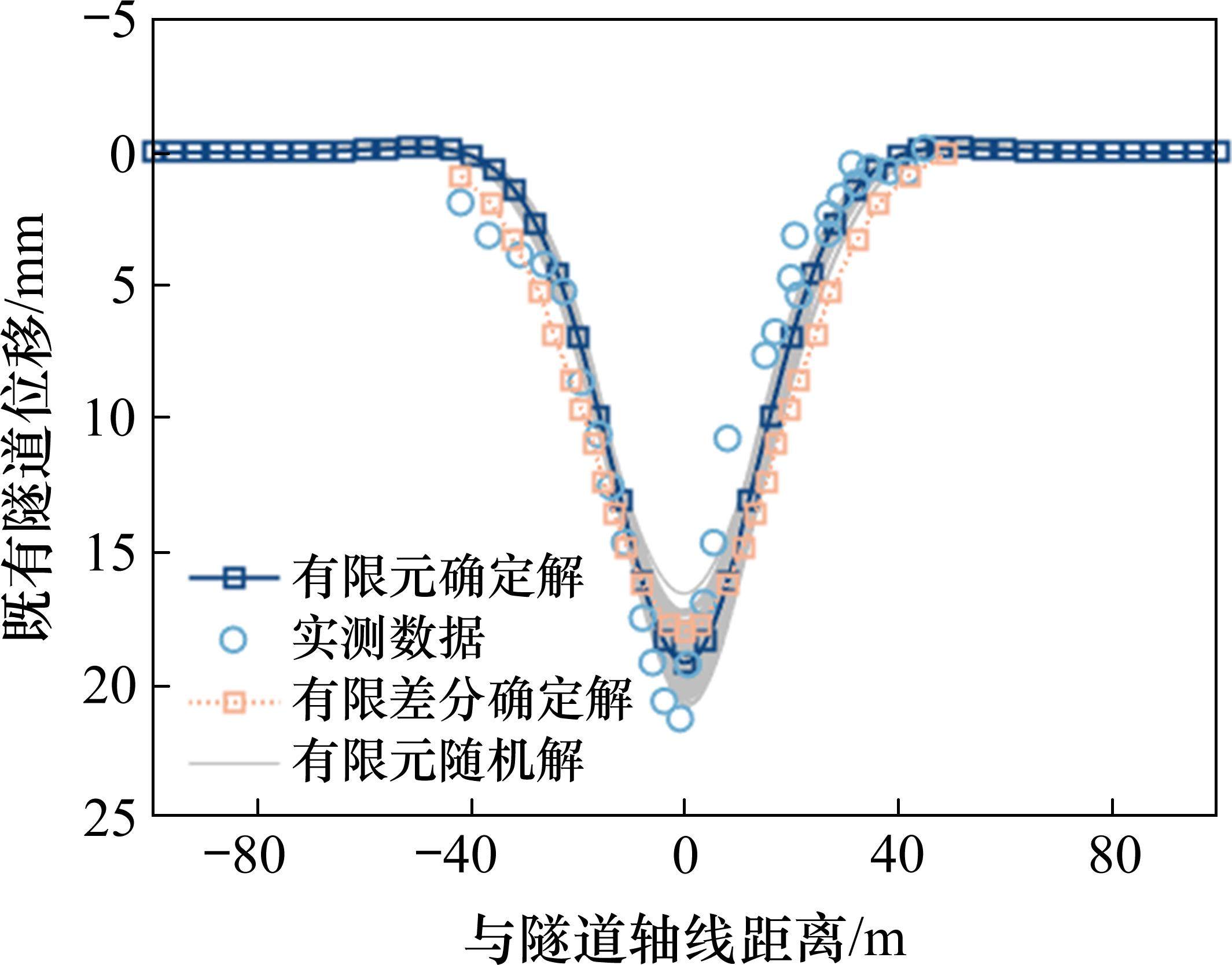
取新建隧道相交处轴线两侧各100 m,既有隧道计算长度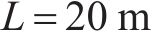
3 工程应用
3.1 工程概况
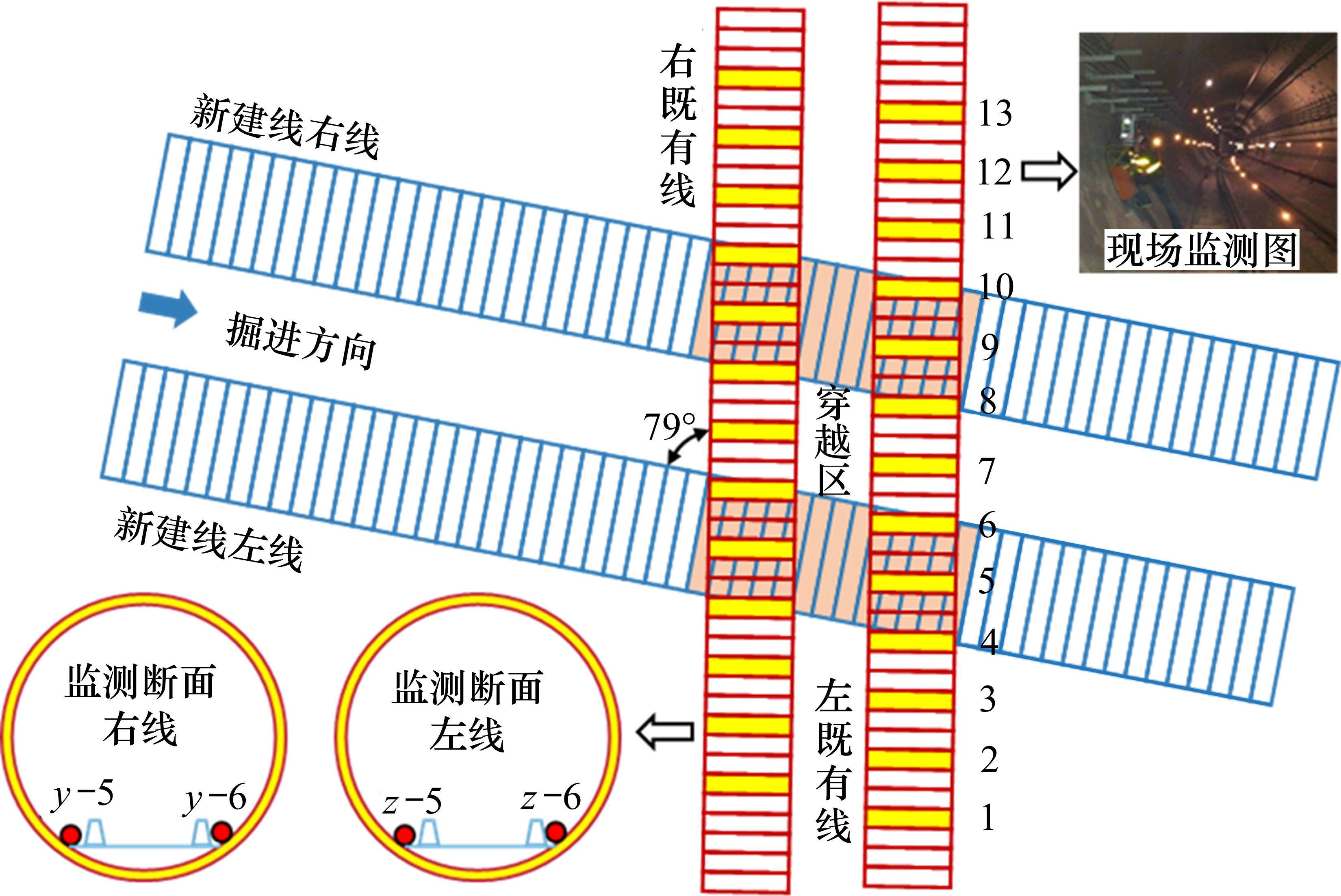
某新建地铁下穿既有运营地铁线,盾构下穿长度为20.8 m。两隧道净距约5.5 m,夹角约为79°,新建线和既有线的隧顶埋深分别为26.5 m和15.1 m;既有线处于砂质黏性土地层中,管片外径6 m,环宽1.5 m,管片厚度为0.3 m,横断面的螺栓个数为10个,其直径为0.03 m。新建线盾构机刀盘开挖直径8.84 m,管片外径8.5 m,环宽1.6 m。新建线路的左线和右线将依次下穿既有线路的右线和左线,具体下穿的平面关系如图9所示。
3.2 基于理论模型的沉降变形预测
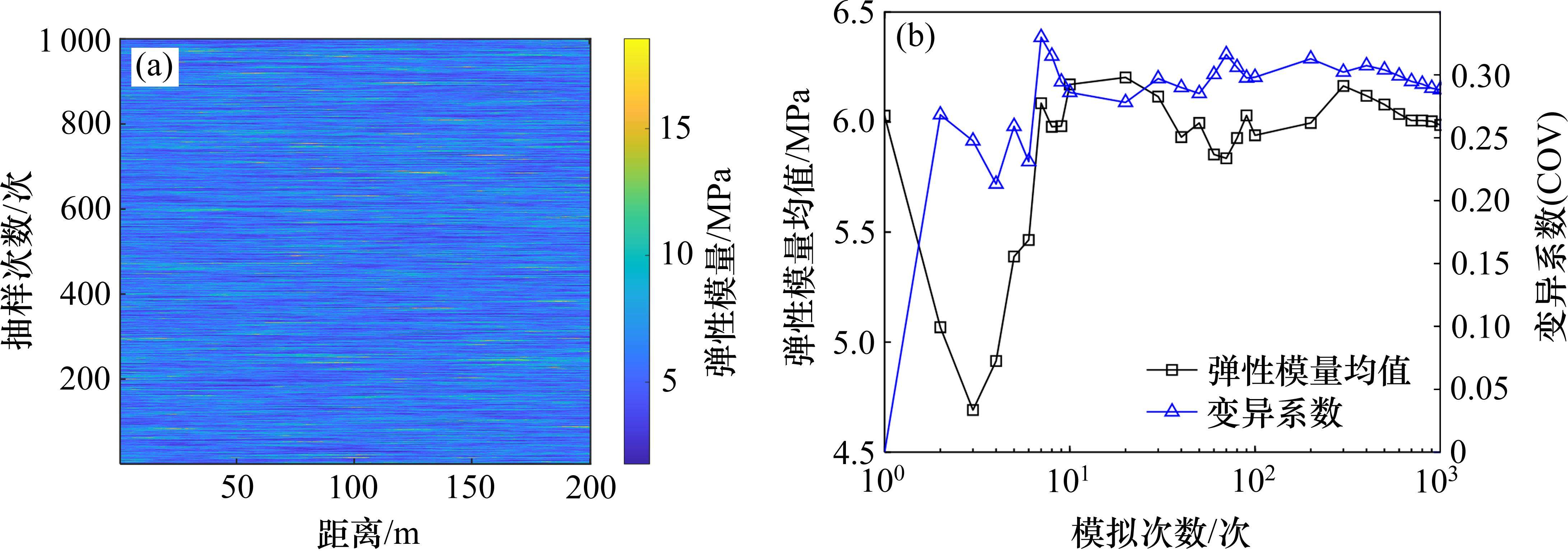
基于本文提出的力学模型对新建隧道下穿施工影响下,既有线的沉降变形进行预测分析。进行不确定性分析时,需考虑地层的基床变异性。根据工程的工程地质勘察报告,弹性模量的均值取值为6 MPa。参考蒋水华[26]的研究,变异系数取值为0.28。采用Matlab软件生成随机场模型,其中进行了1 000次抽样,将每次抽样的结果呈现,具体如图10(a)所示。图10(a)中的不同颜色表示弹性模量不同,不同抽样次数或者纵向不同位置处地基土的弹性模量的分布呈现明显的变异特性。此外,根据弹性模量与地基弹性刚度、剪切层刚度的关系可以进一步得到后两者的随机场。为验证随机场模型的准确性和合理性,选取土层某位置处的随机场变量参数进行分析。其中随机场的抽样次数为1 000次,土层随机场的均值、变异系数与抽样次数的变化关系如图10(b)。可以看出随模拟次数增加,弹性模量的均值及变异系数前期有所波动,但逐渐稳定,最后都收敛于预设的给定值,这表明本文构建的随机场模型具备一定的合理性。
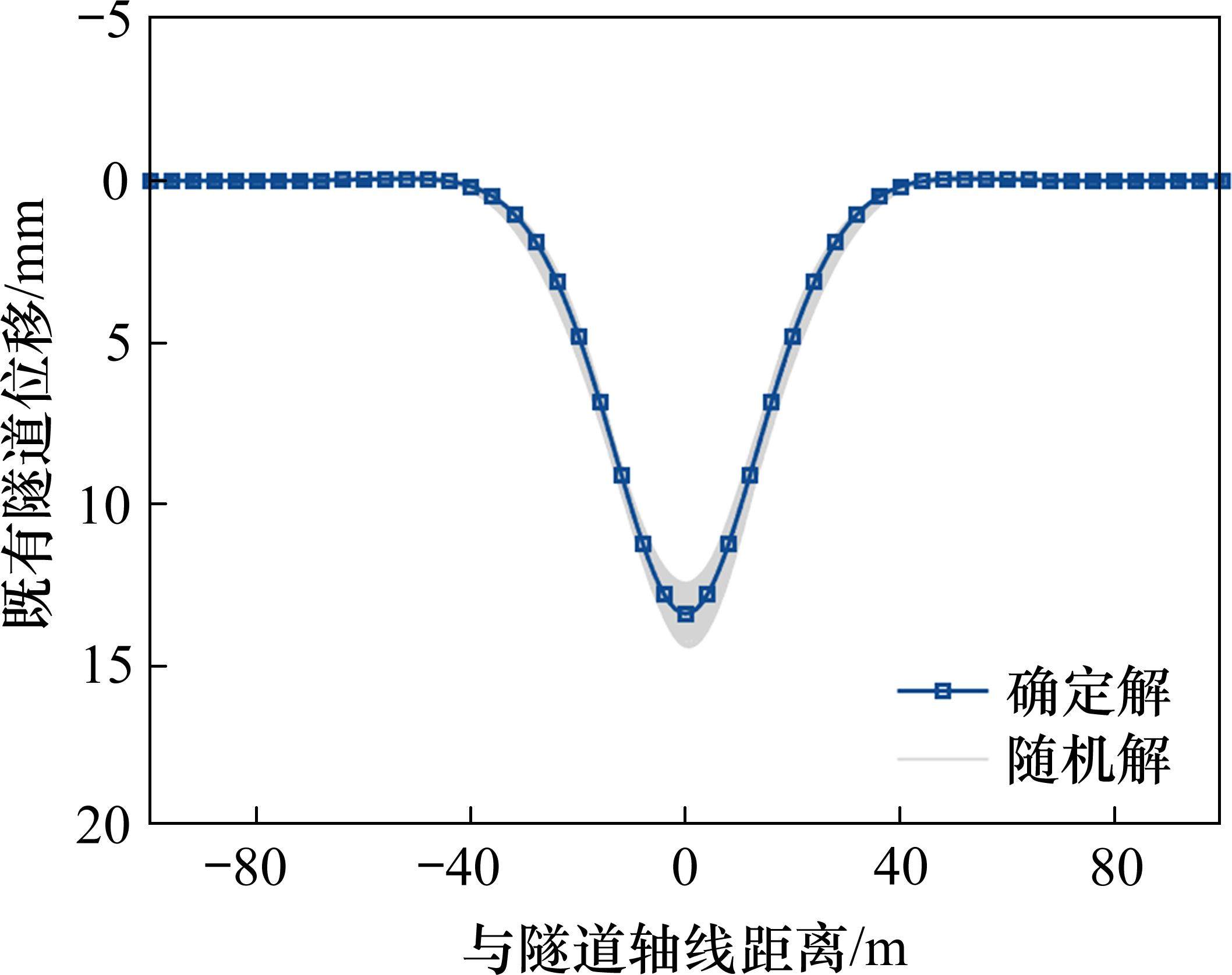
地层损失率取0.7%,将生成的地层压缩系数和地基剪切系数随机代入力学模型中,可以得到既有隧道的沉降变形如图11。文中对比了确定性分析和不确定性分析的既有隧道变形,可以发现,确定性分析情况下的既有隧道最大变形量为13.9 mm,根据广东省《城市轨道交通既有线结构技术保护规范》,城市轨道交通既有结构安全控制值的隧道竖向位移为15 mm,处于较安全的状态。但在不确定分析情况下,既有隧道的沉降变形区间为13.3~15.4 mm,最大值略大于控制值,隧道可能处于不安全的状态,因此需要对新建线与既有线交叉重叠区域进行加固处理。
3.3 定向立体注浆加固控制技术
基于理论计算结果和现场实际,为了使新建线下穿施工对既有线隧道的扰动降至最低,本文针对性提出了3种控制措施,分别为地中水平定向钻孔注浆、洞内径向孔超前注浆以及洞内纵向超前水平注浆,如图10所示。
1) 地中水平定向钻孔注浆。考虑到地面狭小的施工空间,新建线隧道左线下穿既有线时,采用水平定向钻孔注浆预加固技术措施,如图12(a)所示。在地面施工“L型”钻孔(造斜段+水平段)至设计位置,通过钻孔成孔后,全孔下入钢阀管,并进行定点、定量控制注浆,实现钢阀管管棚支护+预注浆加固+跟踪注浆综合加固作用,通过水平钻孔将浆液注入新建线与既有线交叉重叠区域的岩土层中,待浆液硬化将岩土胶结成一个整体,起到止水和固结松散地层作用,提高其自稳强度和抗扰动能力,降低下穿风险。
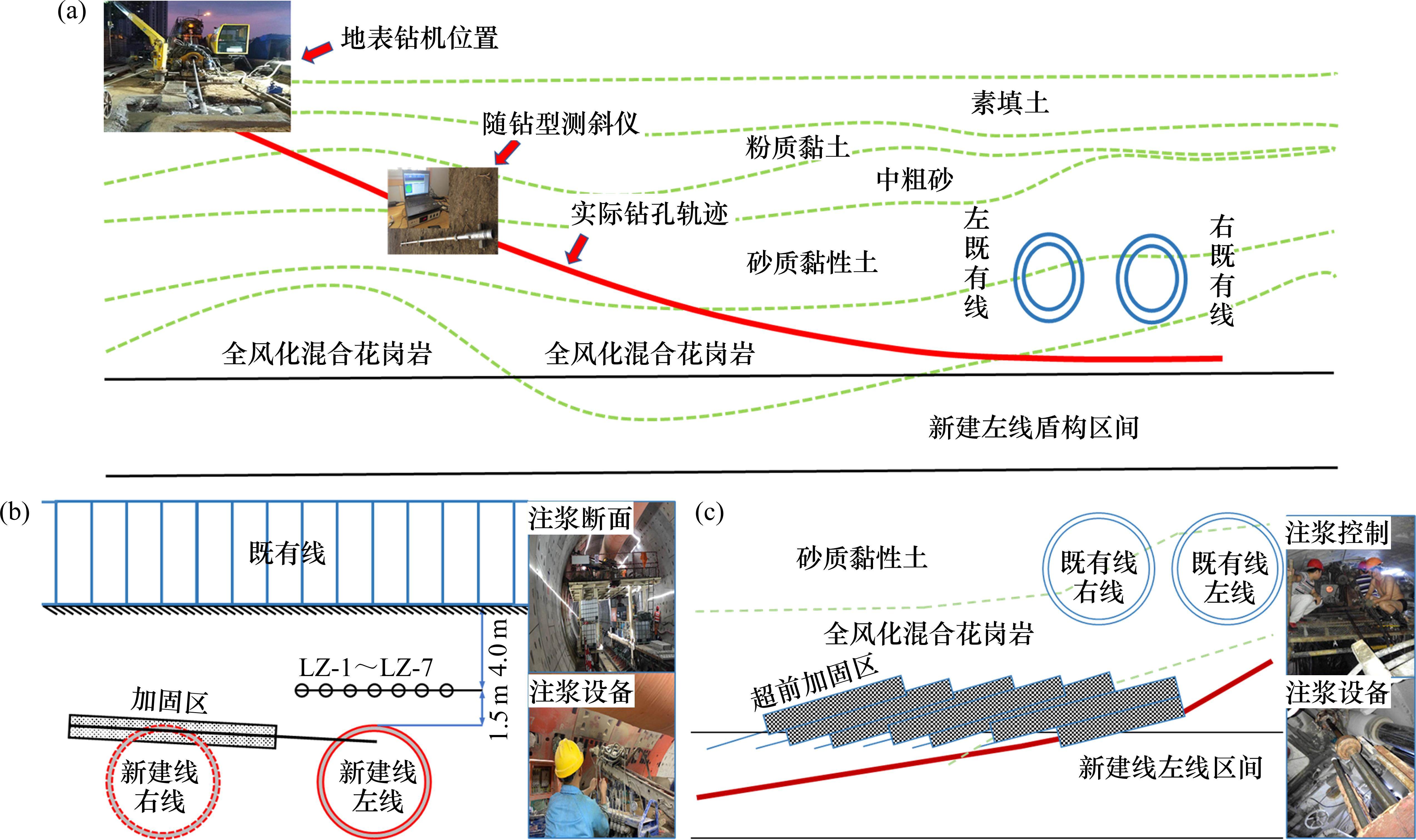
2) 洞内径向孔超前注浆。待新建线左线通过后,从左线隧道洞内往右线上方钻孔注浆,如图12(b)所示。在既有线左线隧道对应位置,左侧拱角处设计为钢管片,钢管片预留钢阀管孔口,设计8环环宽为1.6 m的钢管片,每环管片布设2个钢阀管孔和2个WSS注浆孔,钢阀管从钢管片预留孔钻入,穿过新建线右线隧道拱顶上方注浆加固,钢阀管留在地层中起到管棚支撑作用。钢阀管定向注浆是一种超前支护技术,起到临时超前支护作用,提高地层的自稳能力,防止土层坍塌和地表下沉。
3) 洞内纵向超前水平注浆。在实施了地中水平定向钻孔注浆及洞内径向孔超前注浆2种加固措施以后,在新建隧道下穿既有线区域下方,增加了洞内盾构纵向超前注浆加固的辅助措施,如图12(c)所示。在下穿段每推进3~6环施工一个循环,利用盾体上部4个孔进行超前注浆,采用水泥+水玻璃类双液浆,设计外插角度为8度,孔间距为1.2 m。每循环注浆加固刀盘前方5.7~11.7 m,加固的水平宽度约4.8 m。
3.4 基于现场实测的加固效果评价
为对新建线下穿既有线的施工扰动及立体加固效果进行评估,采用自动化监测手段动态采集既有线断面监测点数据并进行分析。现场监测点的布设综合考虑了隧道下穿对运营期既有线的扰动程度,在下穿位置左既有线和右既有线每隔3环各布设了13个监测断面,监测断面布点情况如图9所示。
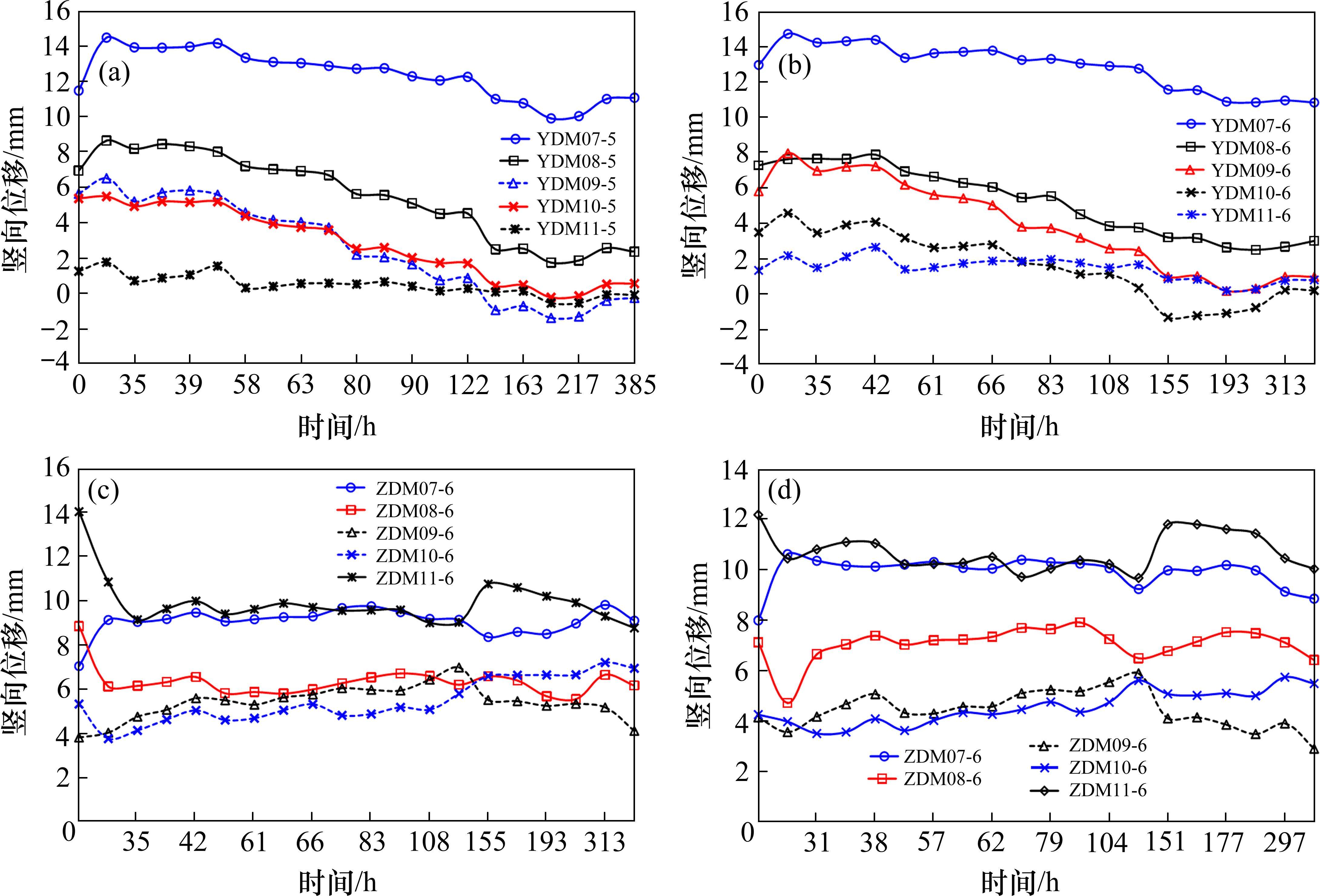
监测结果如图13所示,其中图13(a)、图13(b)、图13(c)、图13(d)分别对应右线和左线5号点和6号点的变形时程曲线。可以看出,新建隧道穿越既有线右线过程中,关于轴线对称的5号点、6号点的时程变化规律相似,皆表现为穿越前随着新建隧道掘进靠近既有隧道而使得既有线呈现略微隆起,隆起幅度为1~2 mm,而后开始出现沉降,各个断面的沉降情况有所不同。此外,左右线的沉降最大值基本皆出现在同一时间段,但是由于进行了注浆加固,既有隧道的最大累计沉降值(6 mm)远低于控制值,处于安全的范围内。既有线左线与右线的变形规律相似,先是出现隆起,而后出现沉降。但相比于右线,左线的最终沉降值较小,大部分监测点的最大沉降累积变形约为1~2 mm,最大的沉降变形出现在断面11的5号点,约为5 mm,也远低于沉降控制值,说明了加固措施的有效性,加固增强了地层的自稳性,使得新建隧道施工对既有隧道扰动较小。
4 结论
1) 综合考虑了新建隧道下穿施工过程中既有隧道周围土层的侧向力和土层的空间变异性对既有隧道沉降的影响。研究将土层侧向力视为与变形程度相关、抵抗沉降变形的力,并采用随机场理论来描述土层的空间变异性。在此基础上,结合双参数弹性地基梁理论及最小势能原理,构建了不确定性的有限元力学分析模型。
2) 选取2个算例对模型进行验证分析,考虑地层侧向力时,本文提出的方法求解得到的既有隧道变形更加接近实测数据;考虑地层空间变异性时,相比确定性方法更能准确反映地层变形的不安全状态。有限差分法和本项目力学模型的计算误差较小,但对现场实测数据的拟合效果不如有限元法。实际工程中应该考虑这两者的综合影响。
3) 将力学模型用于实际下穿工程的变形预测,确定性分析情况下的既有隧道最大变形量为13.9 mm,小于城市轨道交通既有结构安全控制值的隧道竖向位移为15 mm,处于较安全的状态。但不确定分析情况下的既有隧道的沉降变形区间为13.3~15.4 mm,最大值略大于控制值,隧道仍可能处于不安全的状态,因此需要对新建线与既有线交叉重叠区域进行加固处理。
4) 为了使新建线下穿施工对既有线隧道的扰动降至最低,针对性提出了“地中水平定向钻孔注浆+洞内近接区域横纵向交叉注浆”的软土地层定向立体注浆加固技术,并基于现场实测数据对加固效果进行了评价,加固后的新建隧道施工对既有隧道扰动较小,最大沉降约为6 mm。
阚绍德,黄旭民,梁禹.考虑土层侧向力和变异性的隧道下穿引起既有隧道纵向沉降分析与控制[J].铁道科学与工程学报,2025,22(04):1723-1734.
KAN Shaode,HUANG Xumin,LIANG Yu.Analysis and control of longitudinal settlement of existing tunnels induced by tunnel underpass considering the lateral earth pressure and spatial soil variability[J].Journal of Railway Science and Engineering,2025,22(04):1723-1734.

