近十年来,我国交通设施发展迅猛。为保证地形地貌复杂地区交通(铁路、公路)线路的平顺性和车辆运营的平稳性,桥梁所占比例越来越高[1],比如高速铁路中桥梁线路平均占比达55%[2]。同时,城市高架桥建设规模日益增大,也会形成大量桥梁桩基础。基础安全是桥梁安全的关键环节[3],因此,开展大直径桥梁基桩的安全可靠性研究具有重要的现实工程意义。目前常采用确定性分析方法来评价基桩安全[4],即对基桩周边岩土体的设计计算参数(如黏聚力c、内摩擦角φ、土体重度γ等)赋予均值,然后按此均值计算基桩的安全系数,用安全系数衡量基桩安全程度,同时作为安全储备的度量。但工程往往存在不确定性[5-7],例如岩土(尤其是物理、力学性变化较大的软岩)参数的不确定性、实际载荷大小与分布的不确定性等,这些不确定性导致由常规的确定性分析方法计算得到的结果常常与实际情况有很大偏差。因此,考虑设计计算参数的不确定性(即随机性),采用基于概率理论的可靠性分析计算方法来评价桥梁基桩的可靠性及安全性,不仅客观、科学,而且更具工程实际意义[8]。在桩基工程设计中,不仅基桩承载力要满足极限状态下设计要求,而且基桩沉降也应小于其在正常使用状态下所规定的限值[9-10]。对于对沉降有严格要求的高等级公路以及铁路(尤其是高速铁路)桥梁桩基,目前桩基沉降计算方法主要有有限元与有限差分等分析方法[11]和荷载传递法[12]等,然而由于地基土的复杂性导致土体物理参数存在不确定性,使用传统基桩沉降计算方法无法考虑地基土的不确定性,计算结果与实际桩基沉降会存在一定的差距,这将给基桩安全带来潜在风险,因此开展基于沉降控制的基桩可靠性研究就显得尤为重要[13]。基桩沉降的影响因素远比承载力的影响因素复杂,这导致基桩沉降的理论计算方法远没有基桩承载力的理论计算方法成熟和完善[14],其计算结果也往往与实际工程情况不符,尤其是场地条件复杂的桩基工程。虽然采用有限元数值分析方法可较好地解决桩基工程的沉降计算问题,但将其直接用于计算桩基的失效概率及可靠性指标,势必会导致数值计算工作量巨大。代理模型法是工程中常用的高效的近似计算方法。对于计算量较大的工程问题,可以使用代理模型替代原模型加速计算过程[15]。随着人工智能(artificial intelligence, AI)方法的快速发展,以数据驱动方法来建立更高质量的预测模型已逐渐成为趋势,也有诸多学者采用人工智能的方法应用于基桩沉降方面并取得诸多成果[16-17],这为代理模型的构建提供了新的途径[18]。因此,本文拟通过数值模拟计算和人工智能(AI)方法构建沉降代理模型来研究风化泥质软岩中桥梁基桩的可靠性。首先,采用正交试验设计原理设计基桩沉降数值模拟计算方案;再建立三维有限元数值模型,模拟基桩在不同参数取值和荷载下的沉降值;其次,基于数值模拟计算结果,采用人工智能方法(比如BP神经网络、ANFIS模糊神经网络和随机森林)构建基桩沉降代理模型,并比选出最佳沉降代理模型;最后,基于最佳沉降代理模型,采用蒙特卡洛法对桥梁基桩的沉降进行可靠性分析研究。
1 桥梁基桩沉降数值模拟计算
本节先在分析确定桥梁基桩沉降的影响因素及其取值范围的基础上,基于正交试验设计原理,设计出桥梁基桩沉降数值模拟计算方案;再采用有限元数值分析法,按设定的计算方案模拟计算得到桥梁基桩在不同情况下的沉降。下面以某实际的在建工程为例,通过模拟计算获得不同岩土参数和荷载条件下的桥梁基桩沉降数据,为后续建立沉降代理模型提供数据集。
1.1 数值模拟计算方案
桥梁基桩的沉降是由多因素导致的[19],但若在设计数值模拟计算方案时考虑因素过多,则计算工作量将急剧增加。为平衡模拟计算工作量和计算效果,通常只择取主要的因素作为影响变量,而其他因素则取规定值。因此,本文根据工程场地条件和文献调研结果,选取岩土的重度γ、弹性模量E、内摩擦角φ、黏聚力c以及桩-土界面摩擦因数ratio和桩顶压强p(即桩顶单位面积所受竖向荷载值)6个影响因素参与数值模拟计算方案的设计。同时,为了让各影响因素取值范围足够宽,能够包含该地段大部分的岩土体参数范围,结合工程实际情况,本文取γ=16~21 kN/m3、E=5~100 MPa、φ=5°~35°、c=5~80 kPa、p=1 000~20 000 kPa、ratio=1/3~2/3[20]。
鉴于正交试验设计方法设计的模拟计算方案具有均衡分散性和综合可比性,而且正交表能保证各个因素之间相互独立,能以较少的模拟计算次数获得较全面而真实的反映自变量与因变量之间关系的计算结果[21],从而确定出最优的因素组合方案,从而节约试验时间和成本。因此本文采用正交试验设计法设计基桩沉降数值模拟计算方案。
一般来说,数值模拟计算得到的沉降数据点越多,后文构建沉降代理模型的精度就越高。兼顾建模精度和计算工作量,本文对上述6个影响因素均取9个水平如表1所示,采用正交表L81(96)(其中L为正交表代号,81为试验次数,9为水平数,6为因素数)来设计基桩沉降数值模拟计算方案。
| 编号 | 岩土重度 γ/(kN∙m-3) | 岩土弹性模 量E/MPa | 岩土内摩擦 角φ/(°) | 岩土黏聚 力c/kPa | 桩顶压强 p/kPa | 摩擦因数 ratio |
|---|---|---|---|---|---|---|
| 1 | 16 | 5 | 5 | 5 | 1 000 | 0.33 |
| 2 | 16.63 | 16.88 | 8.75 | 14.48 | 3 375 | 0.37 |
| 3 | 17.25 | 28.75 | 12.5 | 23.95 | 5 750 | 0.425 |
| 4 | 17.88 | 40.63 | 16.25 | 33.43 | 8 125 | 0.46 |
| 5 | 18.5 | 52.5 | 20 | 42.9 | 10 500 | 0.50 |
| 6 | 19.13 | 64.38 | 23.75 | 52.38 | 12 875 | 0.54 |
| 7 | 19.75 | 76.25 | 27.5 | 61.85 | 15 250 | 0.58 |
| 8 | 20.38 | 88.13 | 31.25 | 71.33 | 17 625 | 0.62 |
| 9 | 21 | 100 | 35 | 80 | 20 000 | 0.67 |
1.2 数值建模过程
本部分以1.1节所述工程的桥梁大直径基桩为例,基于ABAQUS有限元分析方法建立桥梁基桩沉降数值模型,并通过ABAQUS二次开发平台,将python编制的脚本编入ABAQUS,实现了ABAQUS前处理自动化建模,以及后处理自动提取桩顶沉降,提高了建模和提取数据的效率,其中前处理是根据6因素9水平的正交表(表2),批量生成桥梁基桩模型的inp文件并导入ABAQUS计算,后处理则是批量提取计算得到的ODB文件基桩的沉降值。
模拟计算 方案编号 | 岩土重度 γ/(kN∙m-3) | 岩土弹性模量E/MPa | 岩土内摩擦角φ/(°) | 岩土黏聚 力c/kPa | 桩顶压强 p/kPa | 桩-土摩 擦因数 | 基桩沉降 s/cm |
|---|---|---|---|---|---|---|---|
| 1 | 16.63 | 5 | 35.00 | 42.50 | 8 125 | 0.58 | 2.07 |
| 2 | 18.50 | 88.125 | 5.00 | 51.88 | 3 375 | 0.58 | 1.33 |
| 3 | 16.00 | 100 | 12.50 | 51.88 | 12 875 | 0.46 | 3.52 |
| 4 | 17.25 | 40.625 | 5.00 | 61.25 | 17 625 | 0.67 | 2.01 |
| 5 | 20.38 | 5 | 8.75 | 23.75 | 10 500 | 0.67 | 2.77 |
| 6 | 19.75 | 52.5 | 16.25 | 51.88 | 20 000 | 0.67 | 1.58 |
| 7 | 17.875 | 88.125 | 20 | 14.375 | 17 625 | 0.33 | 12.20 |
| 8 | 16.625 | 28.75 | 16.25 | 70.625 | 15 250 | 0.54 | 6.47 |
| … | … | … | … | … | … | … | … |
| 76 | 16 | 16.875 | 23.75 | 61.25 | 15 250 | 0.5 | 8.01 |
| 77 | 18.50 | 40.625 | 12.50 | 70.63 | 8 125 | 0.33 | 1.54 |
| 78 | 18.50 | 52.5 | 20.00 | 42.50 | 1 000 | 0.50 | 0.933 |
| 79 | 17.25 | 28.75 | 12.50 | 23.75 | 1 000 | 0.42 | 0.658 |
| 80 | 17.25 | 76.25 | 35.00 | 70.63 | 20 000 | 0.37 | 0.483 |
| 81 | 19.75 | 76.25 | 27.50 | 61.25 | 1 000 | 0.58 | 1.23 |
为了减少模型的边界效应对基桩沉降造成的影响,取模型区域的长、宽和高分别为40,40和30 m。同时取位于模型正中心的大直径灌注桩直径和桩长分别为1.2 m和 20 m。基桩采用弹性本构模型,弹性模量取值为25 GPa,泊松比取值为0.15,重度取值为24 kN/m3。地层岩土体本构模型选择Mohr-Coulomb强度准则,泊松比取值为0.3,其他计算参数则根据表2模拟计算方案设定值取用。
根据模型的几何对称性,在利用ABAQUS建模时取模型的1/4进行分析计算(图1)。模型的约束条件为:底部同时约束水平和竖直位移,侧面仅约束水平位移。基桩和土体单元均采用三维节点线性六面体单元(C3D8)进行网格离散。
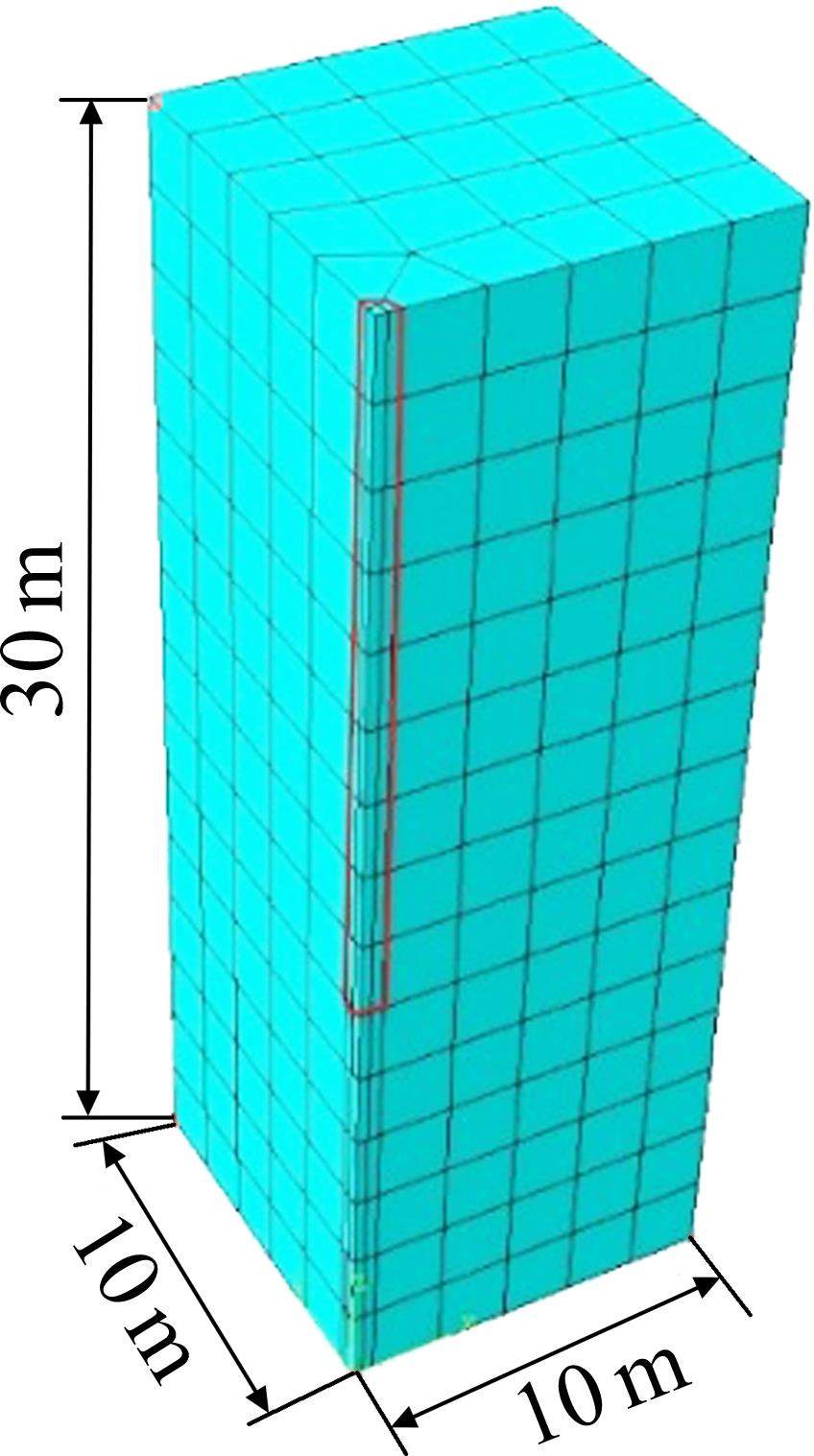
根据正交表L81(96)设计的81个模拟计算方案(表2),将各方案中设定的各因素水平值输入上述计算模型进行模拟计算,可得81个桥梁基桩沉降模拟计算方案的计算结果,表2为部分计算结果。
2 基于人工智能(AI)的沉降代理模型构建
本节基于上述数值模拟计算结果,分别采用BP神经网络、ANFIS模糊神经网络和随机森林法建立桥梁基桩沉降代理模型,并对各模型的性能进行对比分析。性能评价指标选用可决系数R2、平均绝对误差δMAE、平均相对误差δMAPE和均方误差δMSE。
2.1 BP神经网络沉降代理模型
BP神经网络是一种非线性拟合模型,广泛用于解决岩土工程领域预测回归问题[22]。它可以通过输入大量的样本进行自我学习,分析隐含在样本之间的关系,建立相应的数学模型。BP神经网络通常由输入层、隐含层、输出层3层组成。假设在输入层有m个节点,输出层有n个节点,在隐含层有n个节点数,内部层与层之间由训练得出的函数表达式为:
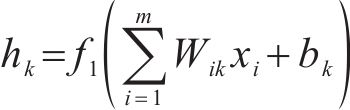
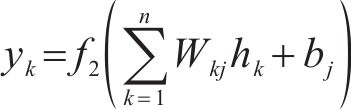
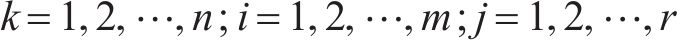
式中:hk为含层的输出值;yk为输出层的输出值;xi为输入层的输入变量;Wik为输入层与隐含层之间的权值;bk代表输出层的阈值;f1(x)和f2(x)分别为隐含层和输出层的线性激励函数和非线性激励函数。
由式(1)和式(2)可以得到输入变量x与输出量y的函数表达式:
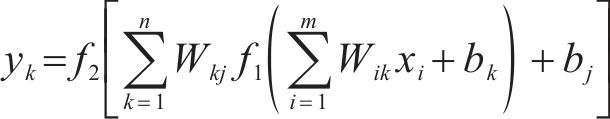
式中: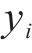
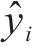
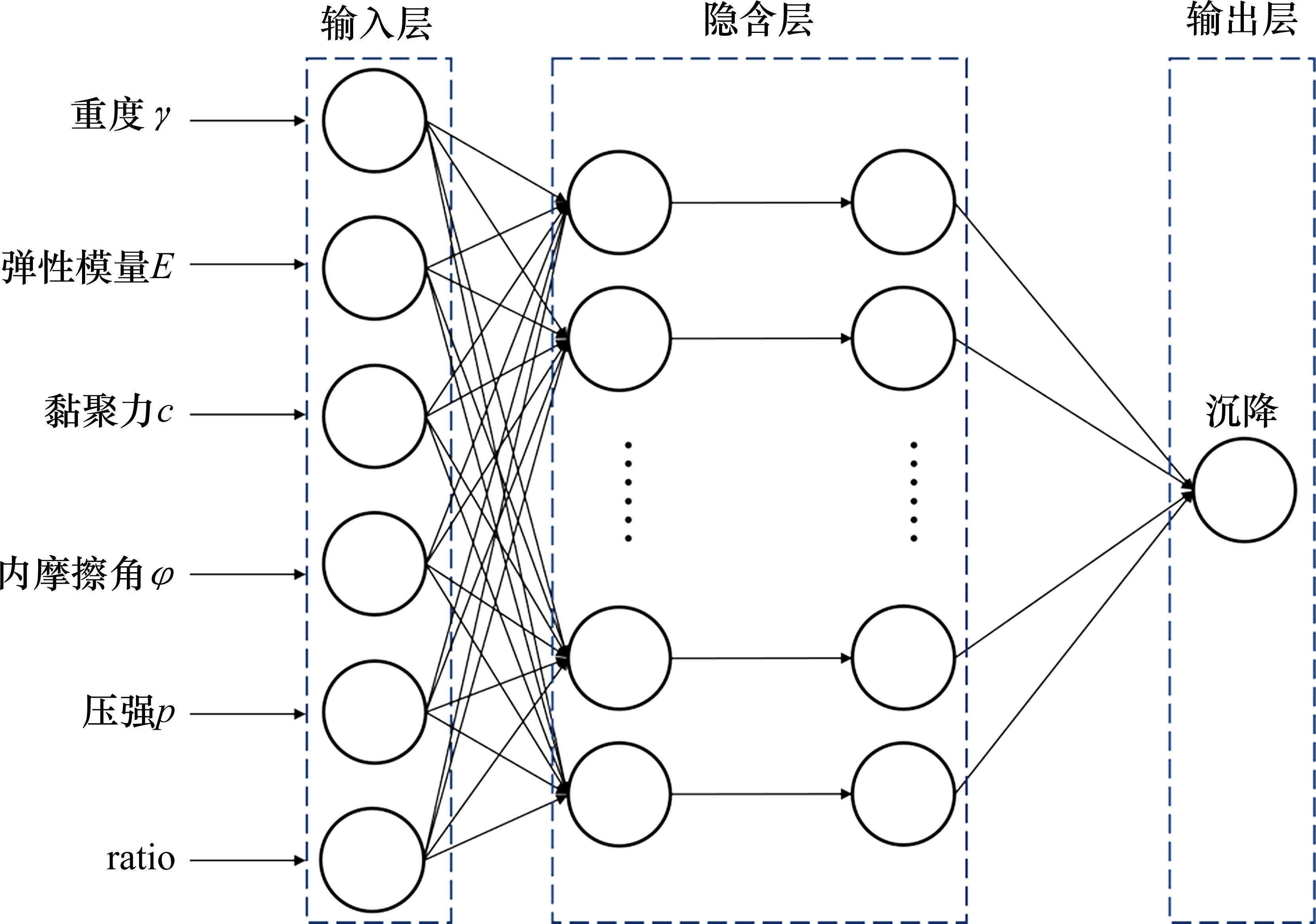
本文以地层岩土体的黏聚力c、内摩擦角φ、重度γ和弹性模量E,以及桩顶荷载压强p和桩-土界面摩擦因数ratio作为输入层,以桥梁基桩的竖向沉降作为输出层,神经网络结构如图2所示。
在由前面基桩沉降数值模拟计算结果构成的样本数据库中选取65个样本(约占总样本的80%)作为训练集,其余16个样本(约占总样本的20%)作为预测集。将训练集样本输入基于BP算法编制的神经网络训练程序,就可训练出桥梁基桩沉降BP神经网络代理模型,模型的拟合效果如图3和表3所示,此外,图3和表3中还列出了所建模型对预测集的预测效果。由表3可知,建立的BP神经网络沉降代理模型在训练集和测试集上的拟合度R2分别是0.994和0.974,这说明模型的拟合精度和预测精度均良好。
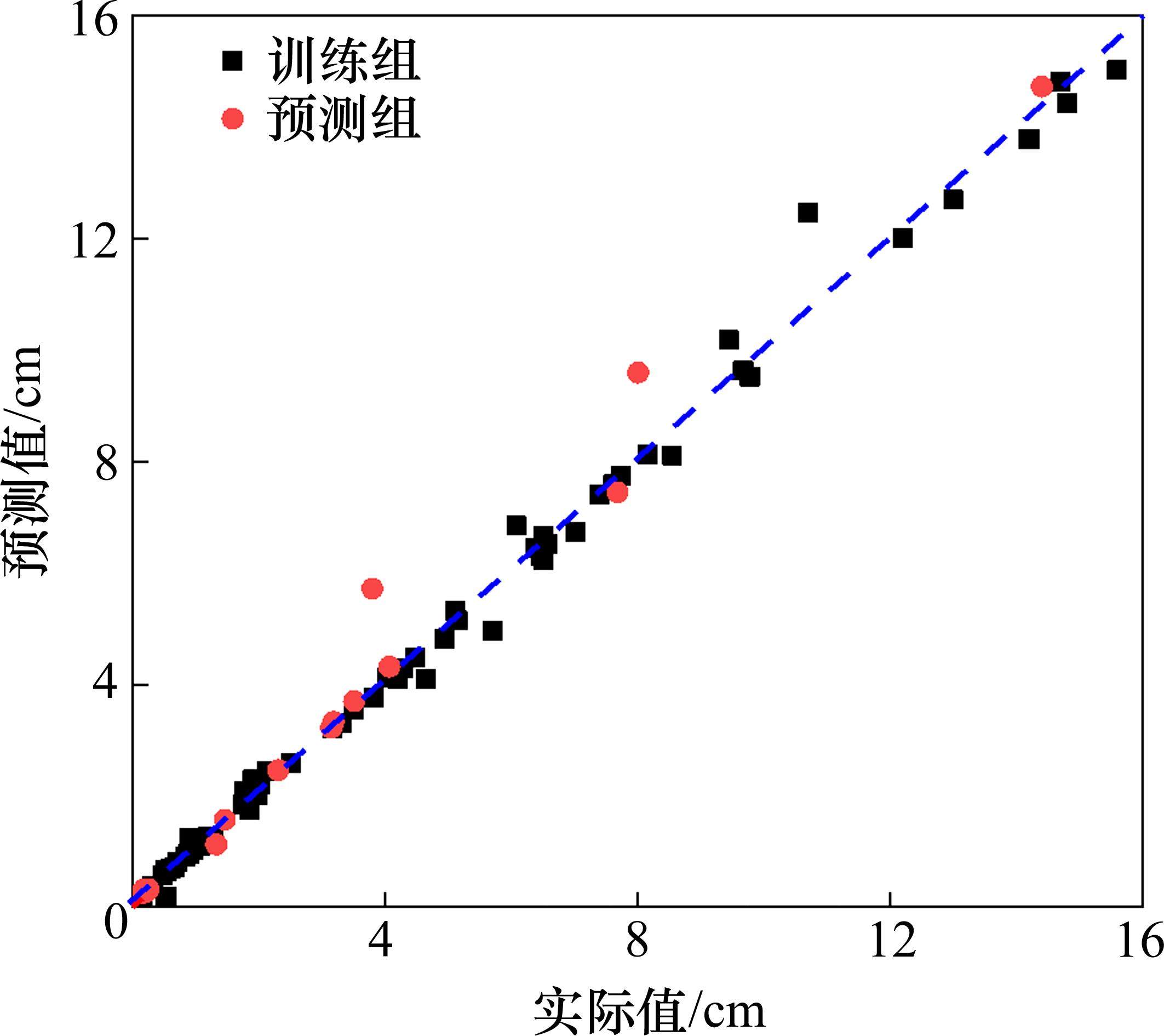
| 样本集 | 可决系 数R2 | 平均绝对 误差δMAE | 平均相对 误差δMAPE | 均方误 差δMSE |
|---|---|---|---|---|
| 训练集 | 0.994 | 0.196 | 0.083 | 7.229 |
| 测试集 | 0.974 | 0.35 | 0.238 | 6.546 |
2.2 ANFIS模糊神经网络沉降代理模型
ANFIS是一种自适应神经网络,这种方法将模糊逻辑和神经元相结合,成为一种新型的模糊推理系统结构[23]。网格分类法和减法聚类法是ANFIS常用的2种训练方法,误差反传学习算法和混合学习算法则是ANFIS常用的2种学习方法。本文基于ANFIS神经网络建立桩基沉降预测模型,同样取c、φ、γ 和E,以及p和ratio共计6个因素作为输入量(图4),并分别赋予其2、2、2、2、4、3个隶属度函数,均为双S和型隶属度函数,输出变量设置为线性函数。选择网格分类法训练模型,算法则选择混合学习算法,该算法具有收敛速度快且不容易陷入局部最优等优点。图4和具体计算步骤如下:
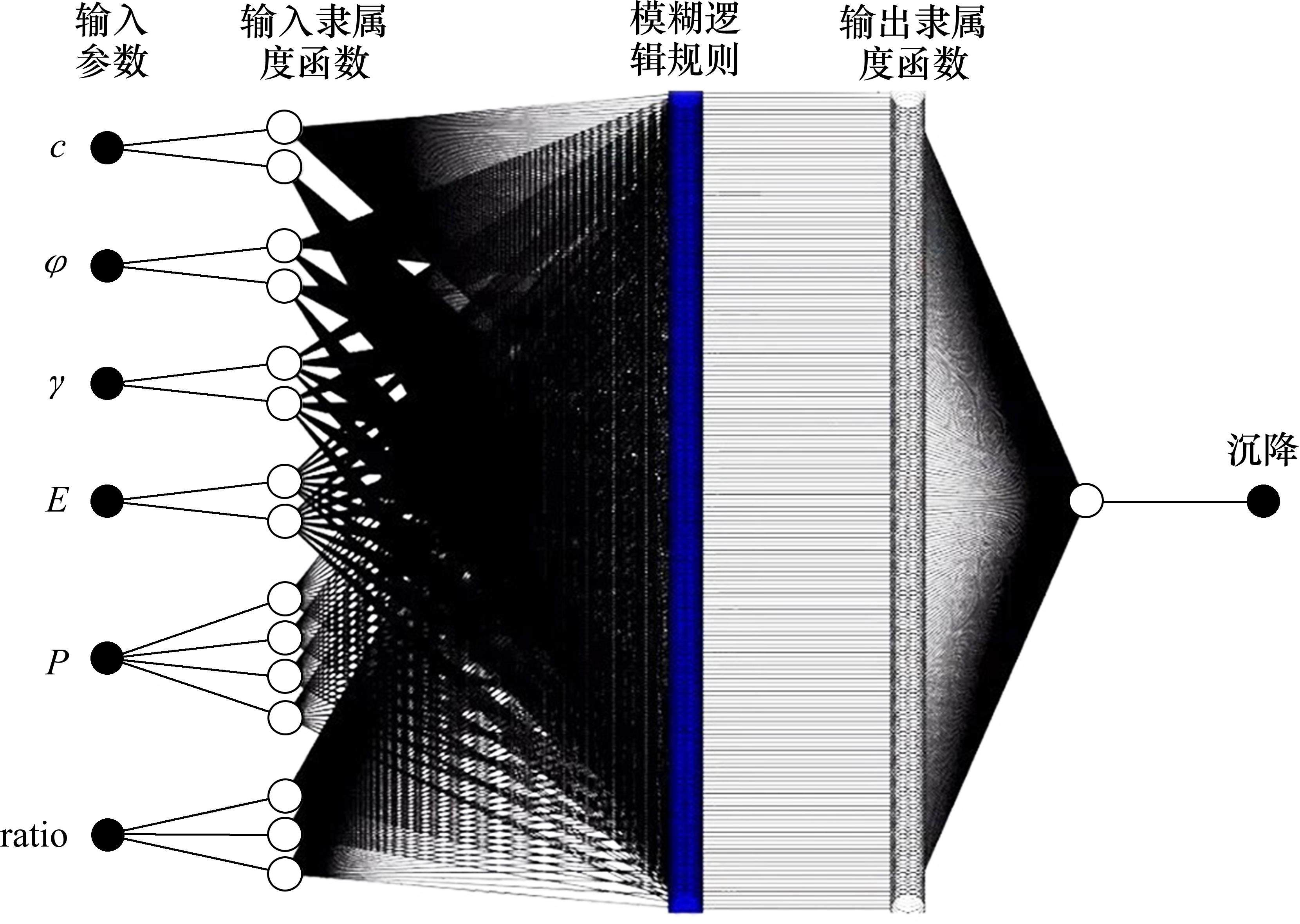
1) 样本组多参数的输入并模糊化;
2) 模糊规则的激励强度计算;
3) 各节点激励强度的归一化计算;
4) 将第3步的结果输入至自适应节点进行计算。
对第4步计算结果求和并输出,表达式为:

式中: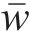
根据上述选取的训练集(65个样本)和测试集(16个样本),首先将训练集样本输入ANFIS模糊神经网络训练程序,可训练得到桥梁基桩沉降ANFIS模糊神经网络代理模型(图4);然后,利用训练得到的ANFIS模糊神经网络代理模型对测试集样本进行预测。模型的拟合和预测效果如图5和表4所示。由表4可知,建立的ANFIS模糊神经网络沉降代理模型在训练集和测试集上的拟合度R2分别是0.999和0.951,这说明模型的拟合精度很好,而预测精度相对较差。
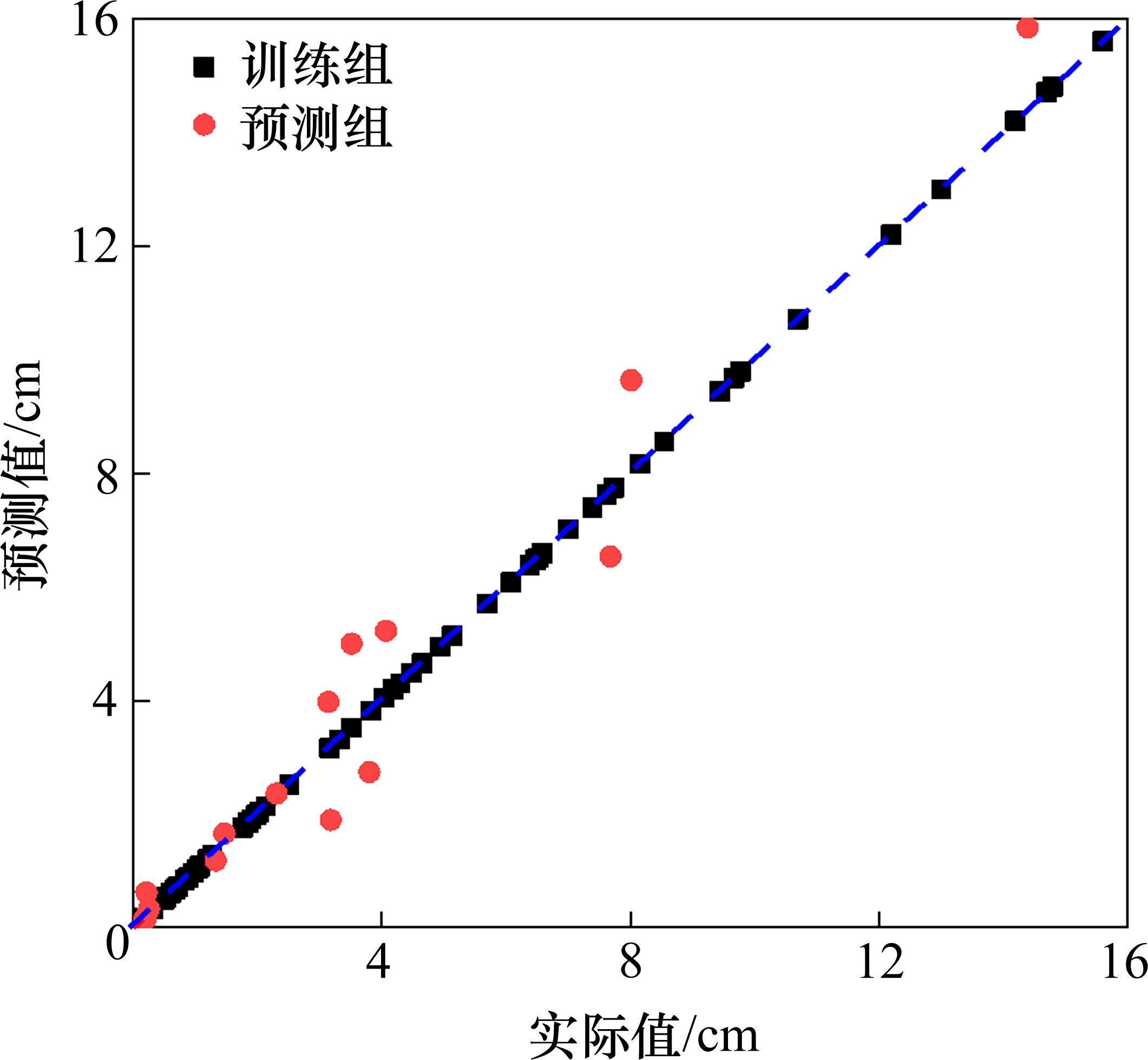
| 样本集 | 可决系数R2 | 平均绝对 误差δMAE | 平均相对 误差δMAPE | 均方误 差δMSE |
|---|---|---|---|---|
| 训练集 | 0.999 | 4.0×10-4 | 0.15×10-3 | 0.106×10-4 |
| 测试集 | 0.951 | 0.690 | 0.344 | 1.327×10 |
2.3 随机森林沉降代理模型
随机森林(Random Forest,RF)使用随机的方式建立一个森林,森林由决策树组成,每个决策树各不相同互不关联,这些决策树就是弱监督学习模型,每一个模型都只能在某一个方面表现良好,通过将这些弱模型进行整合便可以得到一个各方面性能都良好的模型。随机森林具有调节参数少,抗干扰能力高等优点,被广泛应用于解决大样本数据拟合和分类问题[24]。
基桩沉降随机森林代理模型建立步骤为:首先将样本数据库分为训练集(65个样本,占总样本的80%)和测试集(16个样本,占总样本的20%);然后以可决系数R2作为目标函数,利用网格搜索法,选出代理模型中的最佳的参数组合;再将最优参数应用到随机森林模型,并在训练集上训练得到随机森林模型;最后利用测试集进行模型效果评估。随机森林结构框架如图6所示。
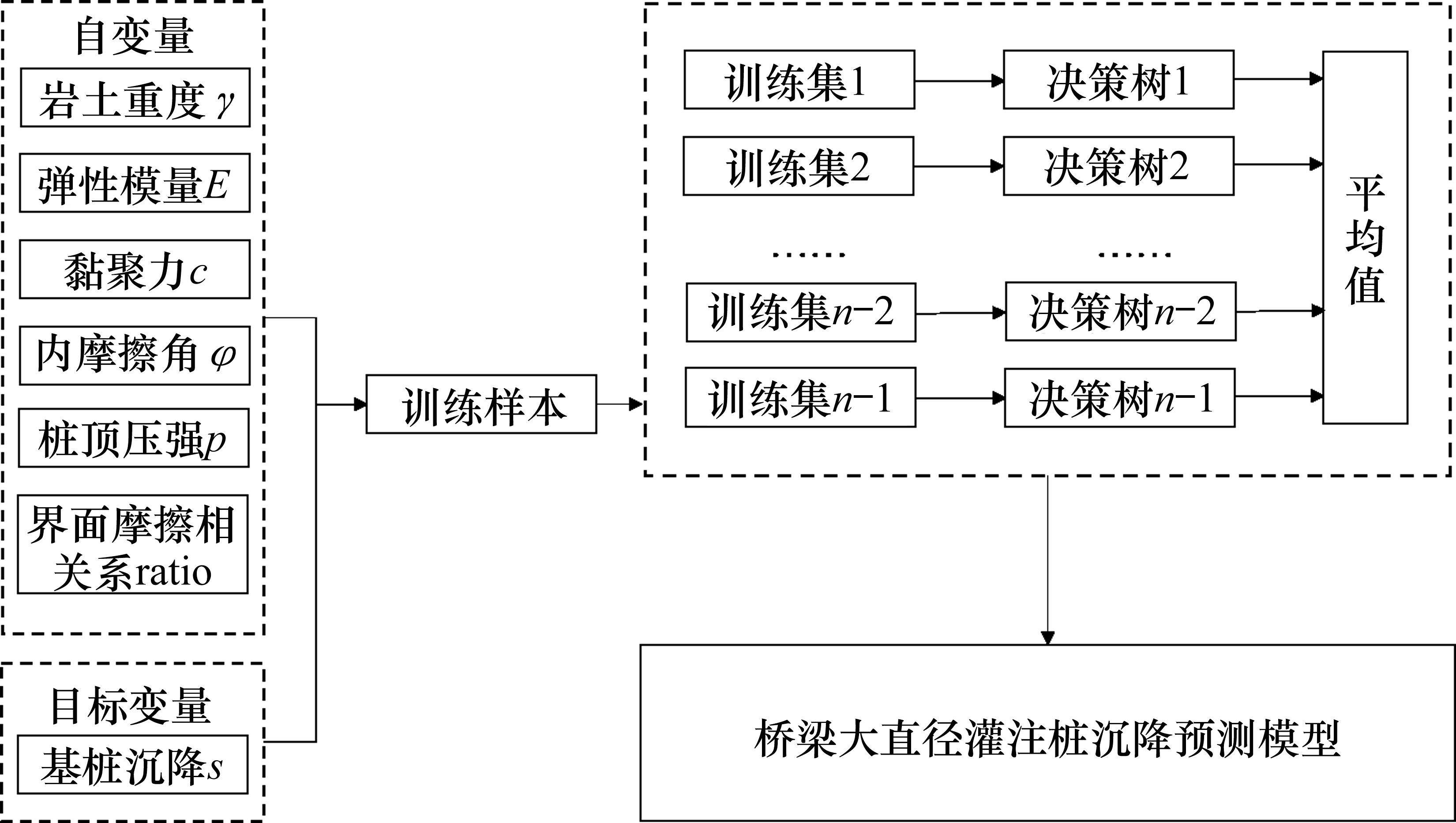
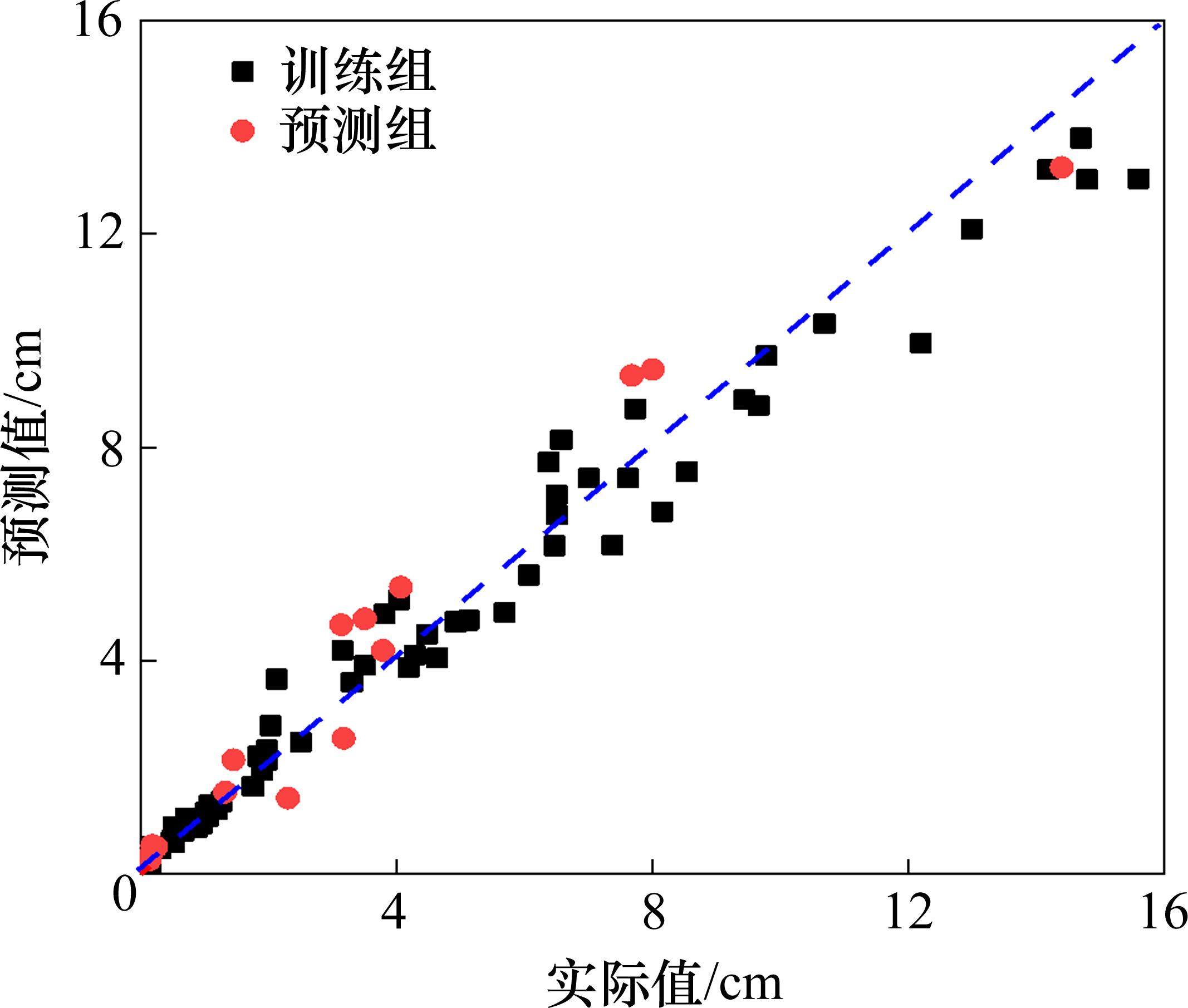
按上述方法建立的基桩沉降随机森林模型的拟合和预测效果如表5和图7所示。由表5可知,随机森林模型在训练集和测试集上的拟合度R2分别是0.959和0.939,这说明该模型的拟合和预测效果均比BP神经网络模型和ANFIS模糊神经网络模型的差。
| 样本集 | 可决系数R2 | 平均绝对 误差δMAE | 平均相对 误差δMAPE | 均方误 差δMSE |
|---|---|---|---|---|
| 训练集 | 0.959 | 0.52 | 0.193 | 38.186 |
| 测试集 | 0.939 | 0.774 | 0.581 | 14.075 |
2.4 沉降代理模型对比分析
通过对上述建立的3种沉降代理模型的可决系数R2、平均绝对误差δMAE、平均相对误差δMAPE和均方误差δMSE(表3~表5)进行对比分析发现:就拟合效果来说,BP神经网络模型和ANFIS模糊神经网络模型相对较好,随机森林模型相对较差;就预测效果来说,BP神经网络模型最好,ANFIS模糊神经网络模型次之,随机森林模型相对较差。BP神经网络具有良好的容错率、非线性映射能力,自学习和自适应能力,很适合建立考虑多变量的非线性预测模型,鉴于上述优点和计算结果,本文选择BP神经网络作为桥梁基桩的沉降代理模型进行后续可靠性分析。
3 基于人工智能(AI)沉降代理模型的基桩可靠性分析
3.1 沉降代理模型对比分析
确立了沉降代理模型,便可以开展桥梁基桩的可靠性分析。由于本文将岩土的重度γ、弹性模量E、内摩擦角φ、黏聚力c以及桩-土界面摩擦因数ratio和桩顶压强p作为随机变量,因此有随机向量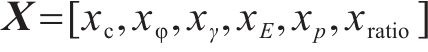
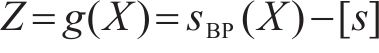
式中: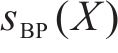
3.2 设计计算参数统计特性
本文在对1.1节所述工程中桥梁基桩进行可靠性分析时,将上述6个参数视为随机变量,随机变量的分布、均值和变异系数根据现场工程条件和勘察资料[26]确定,如表6所示。
| 参数 | 服从分布 | 均值 | 变异系数 |
|---|---|---|---|
| 岩土黏聚力c/kPa | 正态分布 | 35 | 0.3 |
| 岩土内摩擦角φ/(°) | 正态分布 | 25 | 0.1 |
| 岩土重度γ/(kN∙m-3) | 正态分布 | 19.5 | 0.05 |
| 岩土弹性模量E/MPa | 正态分布 | 45 | 0.3 |
| 桩顶压强p/kPa | 正态分布 | 6 500 | 0.2 |
| 摩擦因数ratio | 正态分布 | 0.5 | 0.1 |
3.3 桥梁基桩可靠性分析
本节以1.1节桥梁基桩为研究对象,计算正常使用状态下按沉降控制桥梁基桩的失效概率和可靠性指标,具体计算步骤如下:
1) 按照参数的统计特性,采用蒙特卡洛方法随机抽样NMC次,生成NMC个样本;
2) 将抽取的NMC个样本代入本文建立的基桩沉降代理模型,计算得到NMC个基桩沉降量;
3) 将计算得到的NMC个基桩沉降量批量输入式(6)的极限状态方程,按下式计算失效概率Pf:
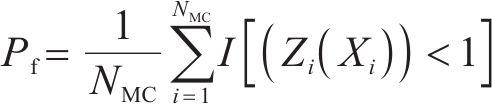
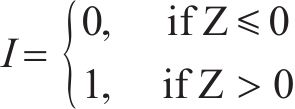
失效概率对应的可靠性指标β 可由下式计算得到:
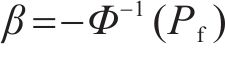
按照上述步骤,采用本文建立的BP神经网络沉降代理模型,随机抽取1 000万组样本数据,计算出不同最大允许沉降值下基桩的沉降失效概率Pf和可靠性指标β,得到了基桩失效概率和可靠性指标随基桩允许沉降的变化规律如图8所示。如图8所示可知,桥梁基桩的失效概率呈现出指数级的下降趋势,失效概率由0.201%迅速降低至0,其变化速率则由-0.41变至-0.008,最后趋于0;可靠性指标β则相反,由2.5迅速增长至5。
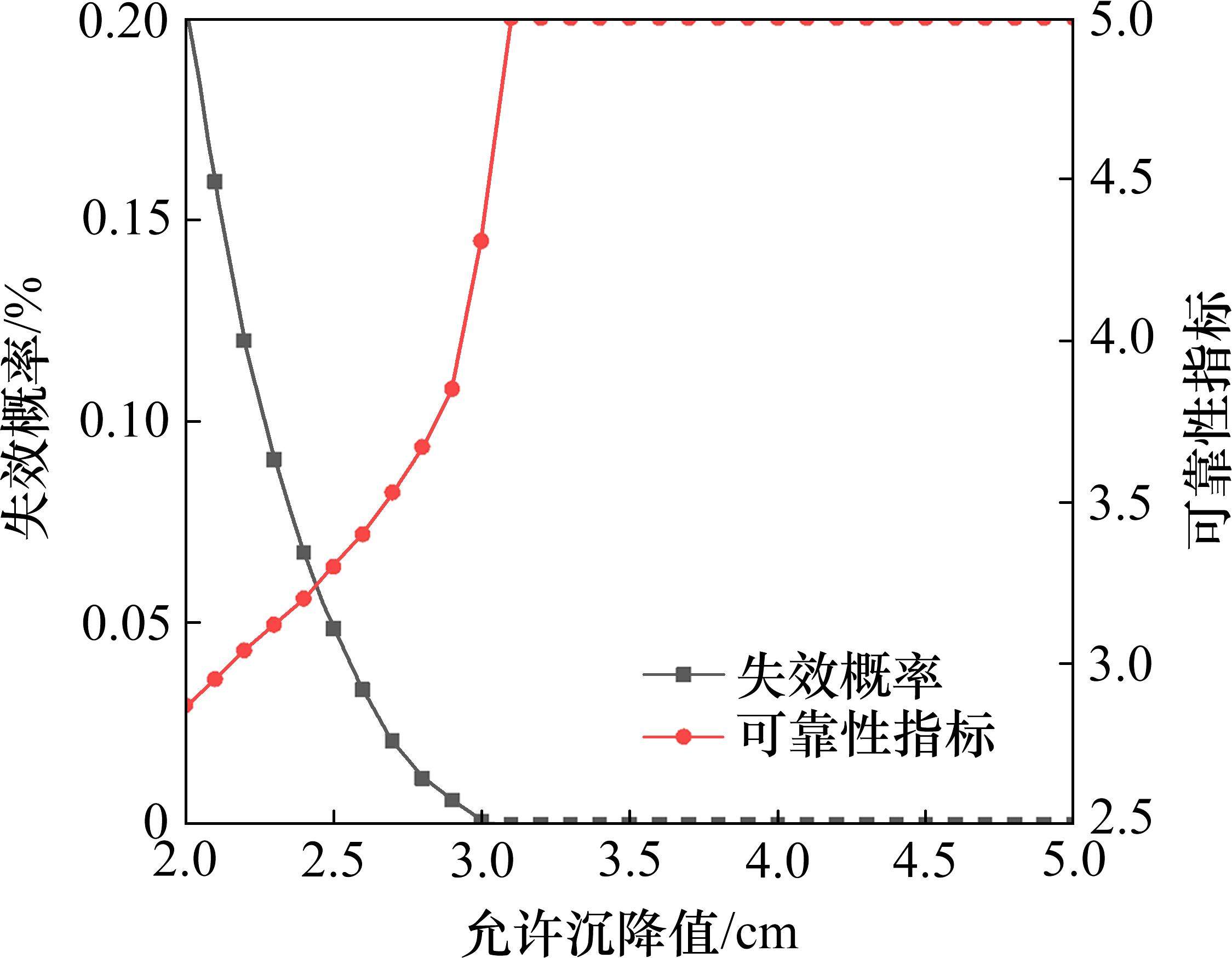
计算结果(图8)表明:若设定桥梁基桩允许沉降分别为2,3,4 和5 cm,本文所研究桥梁基桩的沉降可靠性指标分别为2.87、4.31、5和5。研究成果可为桥梁桩基的设计计算提供更科学的理论支持。
4 结论
1) 正交试验和ABAQUS的前后处理方法提高了建模、提取计算数据的效率,为代理模型的构建提供了高效率、高质量的数据支持;代理模型则提高了桥梁桩基可靠性分析的计算效率。结合上述3种手段提出的基于沉降代理模型桥梁基桩沉降可靠性分析方法,有效地解决了以往繁琐的基桩沉降计算制约可靠性方法应用于桥梁桩基工程的问题。
2) 通过对分别基于BP神经网络、ANFIS模糊神经网络和随机森林建立的3种基桩沉降代理模型进行对比分析发现,BP神经网络基桩沉降代理模型具有最优的预测性能,训练集和测试集上的拟合度R2分别是0.994和0.974,拟合和预测效果均优于ANFIS模糊神经网络和随机森林。
3) 基于蒙特卡洛法和BP神经网络沉降代理模型,计算得到了桥梁基桩的失效概率和可靠性指标随基桩允许沉降的变化规律。当允许沉降值由2 cm增至5 cm时,桥梁基桩的失效概率呈现出指数级的下降趋势,失效概率由0.201%迅速降低至0,其变化速率则由-0.41变至-0.008,最后趋于0,基桩可靠性指标则迅速增加,由2.5迅速增长至5。
极端气候下交通基础设施脆弱性研究综述
[J/OL].西南交通大学学报, 1-18[晏文,唐仁华,王克强等.基于人工智能沉降代理模型的桥梁基桩可靠性分析[J].铁道科学与工程学报,2024,21(11):4588-4598.
YAN Wen,TANG Renhua,WANG Keqiang,et al.Reliability analysis of bridge foundation piles based on artificial intelligence settlement surrogate models[J].Journal of Railway Science and Engineering,2024,21(11):4588-4598.

