盾构具有施工速度快、安全性高、环境影响小[1]等优点,已成为越江跨河交通隧道和引水隧洞建设的主要装备。尤其是水下盾构面临断层错动等复杂地质条件时,易发生盾构下沉、突水突泥、掌子面失稳、地面塌陷等地质灾害。针对隧道穿越断层错动时的结构力学响应特征和破坏机制已开展了一定的研究。张向阳等[2]研究了断层错动作用下隧道衬砌围岩的破坏机理。KIANI等[3]开展正断层下的浅埋盾构隧道离心模型试验,研究了断层倾角以及隧道上覆土层厚度对隧道破坏特征及损伤范围的影响。周光新等[4]通过模型试验,深入研究了走滑断层错动下跨活断层铰接隧洞的破坏形式和破坏机理。马亚丽娜等[5]基于三维离散-连续耦合方法,建立了穿越活动断裂隧洞的三维离散-连续耦合数值分析模型。LIU等[6]通过模型试验研究逆断层黏滑错动引起的山岭隧道破坏模式,并分析了隧道和地层的变形过程及破坏特征。尽管现有研究在一定程度上揭示了断层错动对隧道的影响,但大多是基于给定的断层错动力学参数。由于沉积作用、矿物成分差异和应力历史等[7-9]多种因素影响,整个断层错动存在空间变异性。若忽略岩土体参数的空间变异性,将高估工程的安全性。随机场理论可较好地描述岩土体参数的空间变异性[10-12],并已成功应用于隧道工程变形特征分析。程红战等[13]开展了考虑土体抗剪强度参数的变异性对盾构开挖面稳定性的影响研究,研究表明,内摩擦角的空间变异性对开挖面稳定性有重要影响。LI等[14]分析了参数自相关距离对掌子面破坏概率的影响。王长虹等[15]研究了参数空间变异性对盾构隧道地表变形特征的影响。因此,本文依托向家坝灌区北总干渠一段工程猫儿沱江底盾构隧洞工程,采用FLAC3D软件建立水下隧道地层变形特征分析模型,开展确定性分析研究断层错动对地表沉降的影响。随后,采用基于高斯型自相关函数的随机场理论,构建断层错动力学和水力参数随机场,建立不确定性分析模型。然后,针对断层错动空间变异性对盾构隧道施工引起的地表变形分布规律开展分析,研究不同离散参数、变异系数和自相关距离的影响。最后,采用概率统计方法,分析断层错动内摩擦角的不同变异系数和自相关距离对地表最大沉降和拱顶沉降超出变形阈值概率的影响。
1 随机场理论及其实现
1.1 岩土体空间变异性
岩土体空间变异性是指岩土体在水平和垂直方向上性质存在差异性。随机场理论是研究岩土体参数空间变异性的可靠工具,其最早由VANMARKE[16]提出。其核心内容是利用自相关函数和相关距离来描述研究范围内点与点之间参数的相关性,进而表征整个研究范围内岩土体参数的空间变异性。自相关函数描述了2点的相关系数与距离的关系。鉴于高斯型自相关函数具有良好的连续性和平顺性[17],故选用高斯型自相关函数表征岩土体中任意2点之间的相关性,表达式如式(1):
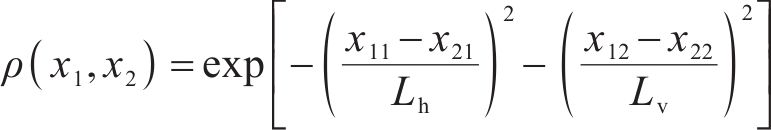
式中:ρ(x1,x2)代表岩土体中任意2点的相关性;x1和x2分别表示空间坐标,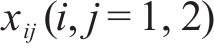
1.2 Karhunen-Loève(KL)级数展开法
岩土体参数的空间平均性质由变异系数Cv和均值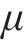
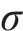
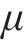
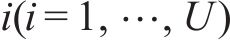
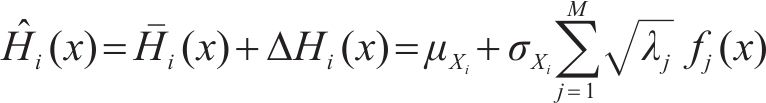
式中: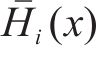
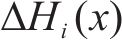
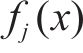
当研究对象为对数正态随机场,则第i(i=1, …, U)个随机场离散公式如式(3):
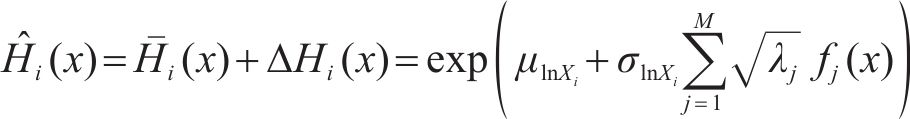
式中: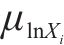
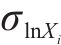
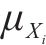
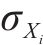
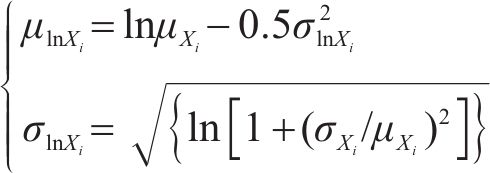
1.3 特征值和特征向量求解
求解自相关函数的特征值和特征向量是随机场离散的关键步骤。此处采用Fredholm二类积分对波动部分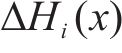
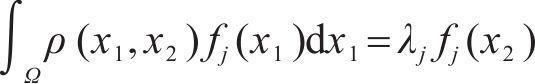
式中:
1.4 级数展开项数确定
在进行随机场离散时,理论上应将展开项数M设置为无穷大。然而,由于计算量的限制,实际上通常只展开一定数量的项数。因此,在保证KL展开法计算精度的情况下,需要合理确定计算项数M。对此,通过逐点均方误差法来求解随机场离散误差,具体表达式如式(6)所示:
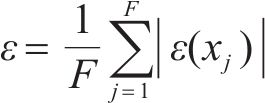
式中:F为随机场离散点数量,ɛ(xj)为随机场中离散点xj的均方误差。其中均方误差ɛ(xj)求解如式(7):
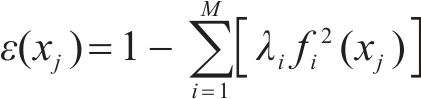
1.5 KL级数展开法离散流程
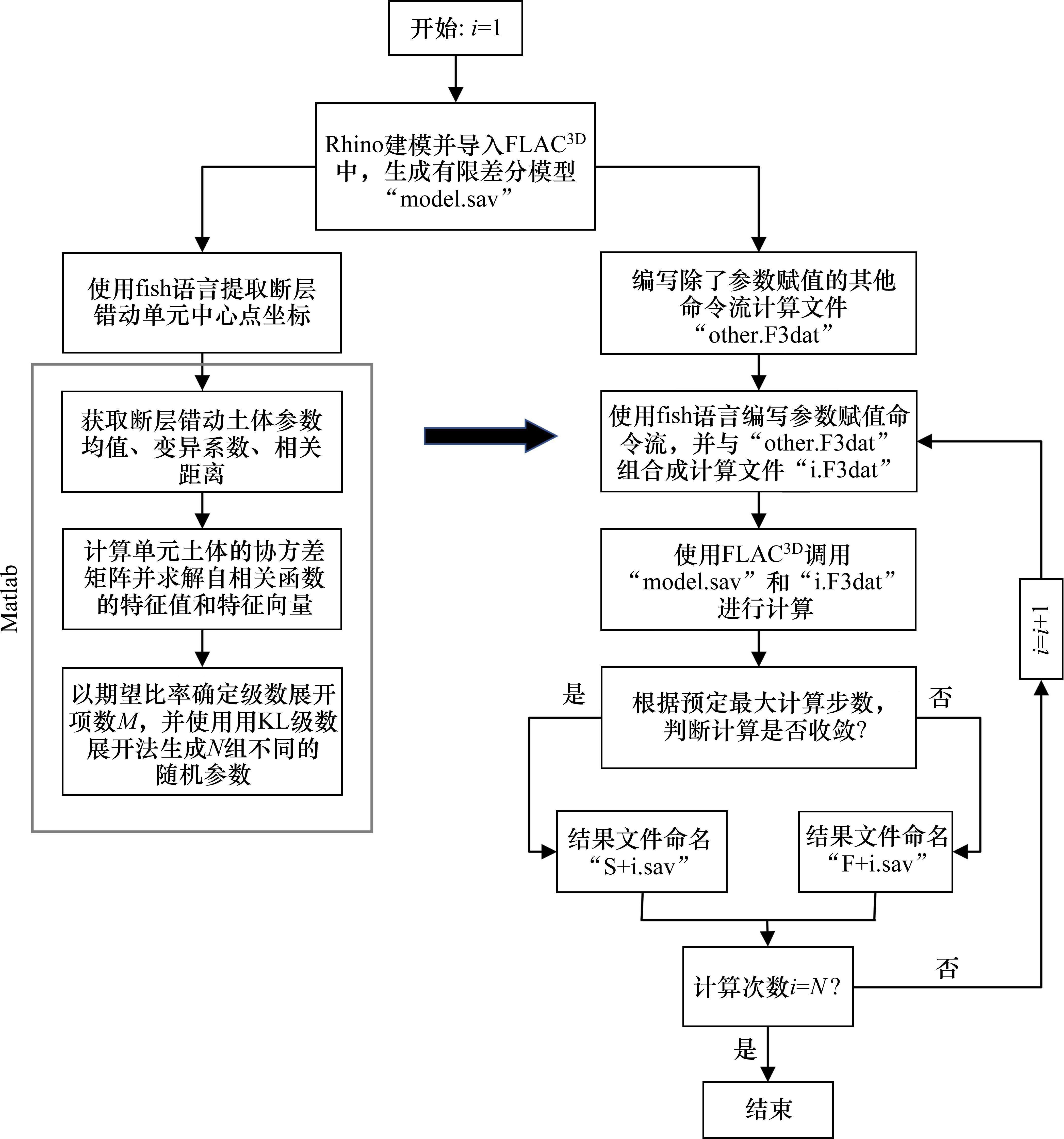
结合KL级数展开法和有限差分模型进行随机场分析的思路如下:首先,在FLAC3D中使用fish语言导出断层错动部分的中心点坐标。然后,在Matlab中利用导出的中心点坐标,采用KL级数展开法生成N组不同的岩土体参数离散数据。接着,通过fish语言将生成的离散数据赋值给断层错动部分。最后,进行计算分析。图1展示了模型建立的整个过程(其中:i为循环变量,初始值为1;N为模拟次数)。
2 盾构施工变形规律分析
2.1 工程背景
向家坝灌区北总干渠一标段猫儿沱江底隧洞工程,隧洞全长1 352.89 m,分为右岸平洞段、下穿岷江段、左岸平洞段和竖井段4部分。下穿岷江段长330.47 m,最小覆土深度约11 m。工程采用一台铁建重工生产的泥水/土压平衡盾构机,盾构机刀盘开挖直径9.2 m,管片外径8.8 m、内径7.9 m。2022年3月18日实测施工段岷江江水深度最大10.081 m。
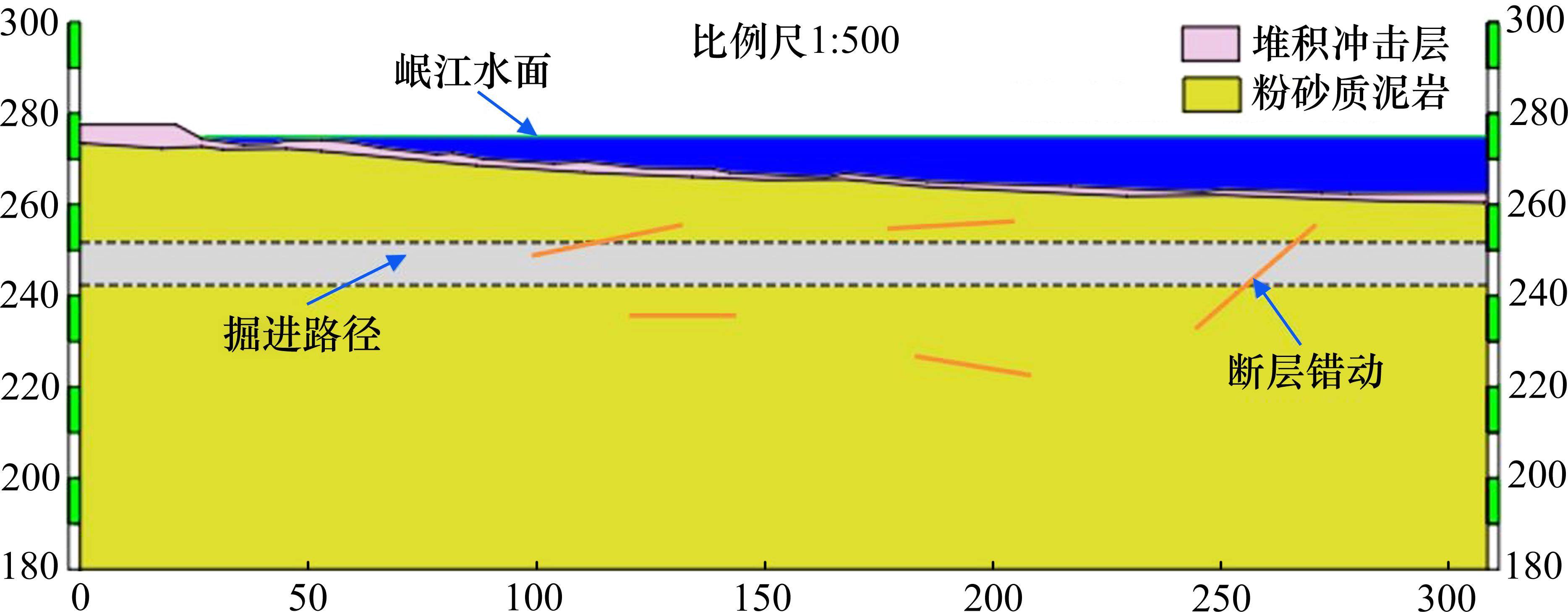
隧洞主要穿越粉砂质泥岩、砂岩及泥岩地层。钻孔压水资料显示,岩层为弱~强透水层,渗透系数为1.43×10-6~1.3×10-5 m/s。图2为下穿岷江段地质纵断面图。勘探揭示,该段中,断层错动构造占48%,断层错动和溶蚀占16%,其余占比32%,这些因素形成了岩体中透水层的复杂分布。且断层错动可能引发盾构下沉、突水突泥、掌子面失稳和地面塌陷等灾害,这些灾害与水下盾构隧道施工引起的地层变形密切相关。本文从断层错动出发,深入探讨了盾构掘进时地层变形规律,为确定双模盾构切换时机提供理论支持。
2.2 数值分析模型
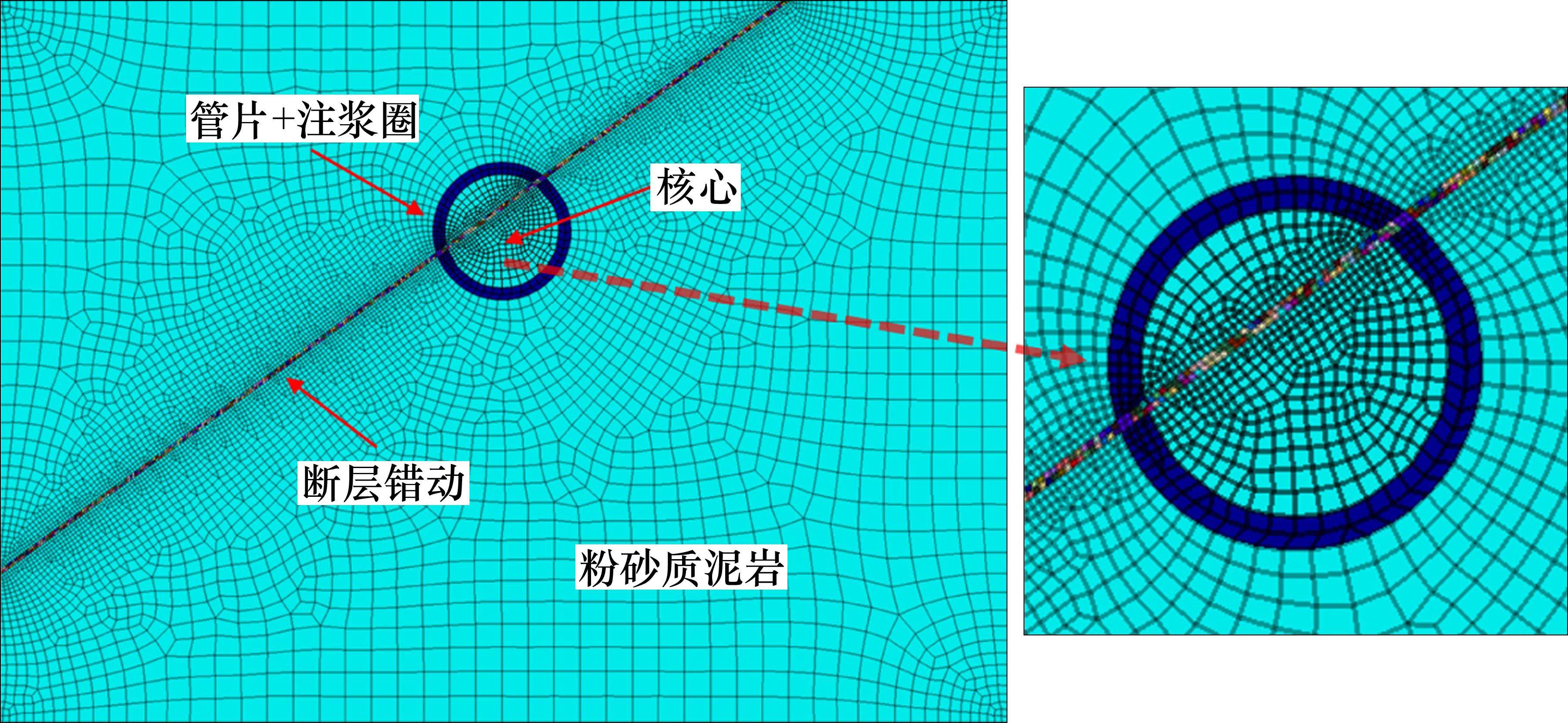
建立考虑断层错动空间变异性的随机场离散模型,研究盾构施工过程中地表和拱顶沉降的规律。管片外径D=8.8 m,管片厚度t1=0.45 m,注浆圈厚度t2=0.5 m,隧道拱顶距地面高度H=11.4 m,模型尺寸为70 m×50 m(宽×高),江面距模型顶面H1=10 m,断层错动倾角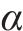
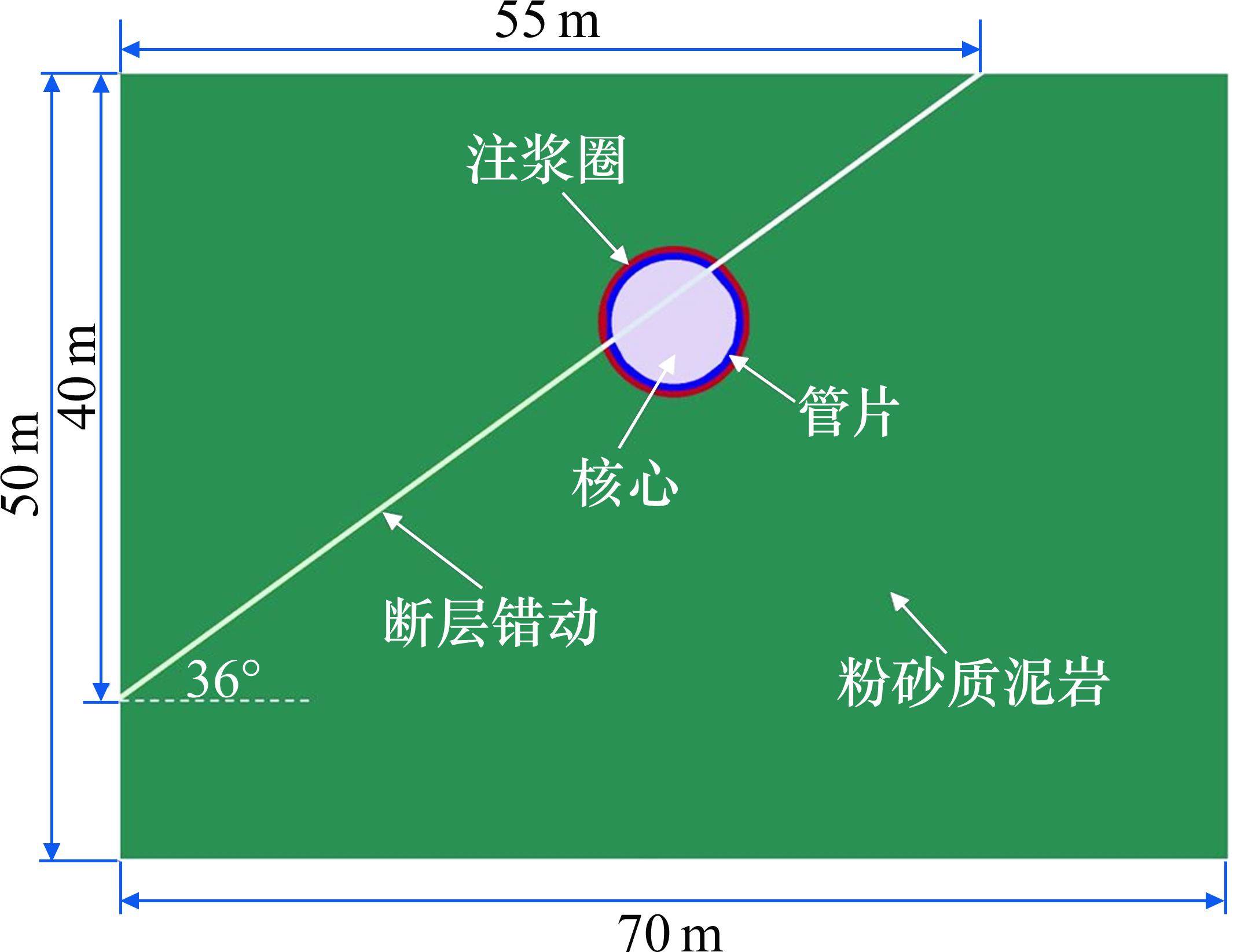
鉴于盾构掘进时全断面均位于粉砂质泥岩地层,为便于研究,建模时将岩土体均设定为粉砂质泥岩。本文研究重点在于考察断层错动对地层变形的影响,故将粉砂质泥岩各项参数均视为常量。粉砂质泥岩和注浆圈采用Mohr-Coulomb模型,管片采用线弹性模型。除了模型上表面外,其余各面均约束法向位移。流体模型为各向同性模型。在底部和四周设置不透水边界,顶部设置透水边界。根据钻孔勘探数据,确定性分析条件下模型各部分材料的取值如表1所示。
| 物理参数 | 密度/(kg∙m-3) | 弹性模量/GPa | 泊松比 | 黏聚力/kPa | 内摩擦角/(°) | 孔隙率 | 饱和度/% | 渗透系数/(m∙s-1) |
|---|---|---|---|---|---|---|---|---|
| 粉砂质泥岩 | 2 010 | 0.3 | 0.35 | 60 | 34 | 0.13 | 100 | 1.2×10-6 |
| 断层错动 | 1 700 | 0.1 | 0.40 | 10 | 20 | 0.20 | 100 | 2.0×10-5 |
| 管片 | 2 500 | 27.6 | 0.20 | — | — | 0.05 | 100 | 9.0×10-10 |
| 注浆圈 | 2 200 | 2.8 | 0.28 | 120 | 35 | 0.15 | 100 | 1.4×10-7 |
2.3 模型的验证
为验证模型的准确性,采用Peck[19]公式对忽略断层错动时地表横向变形结果进行拟合,图4为拟合效果图。由图可以看出,在确定性分析条件下,地表最大沉降值为8.3 mm,而Peck公式的拟合值为8.4 mm,两者的差异很小。变形曲线与Peck公式拟合结果吻合较好,基本符合高斯分布,验证了模型的准确性。
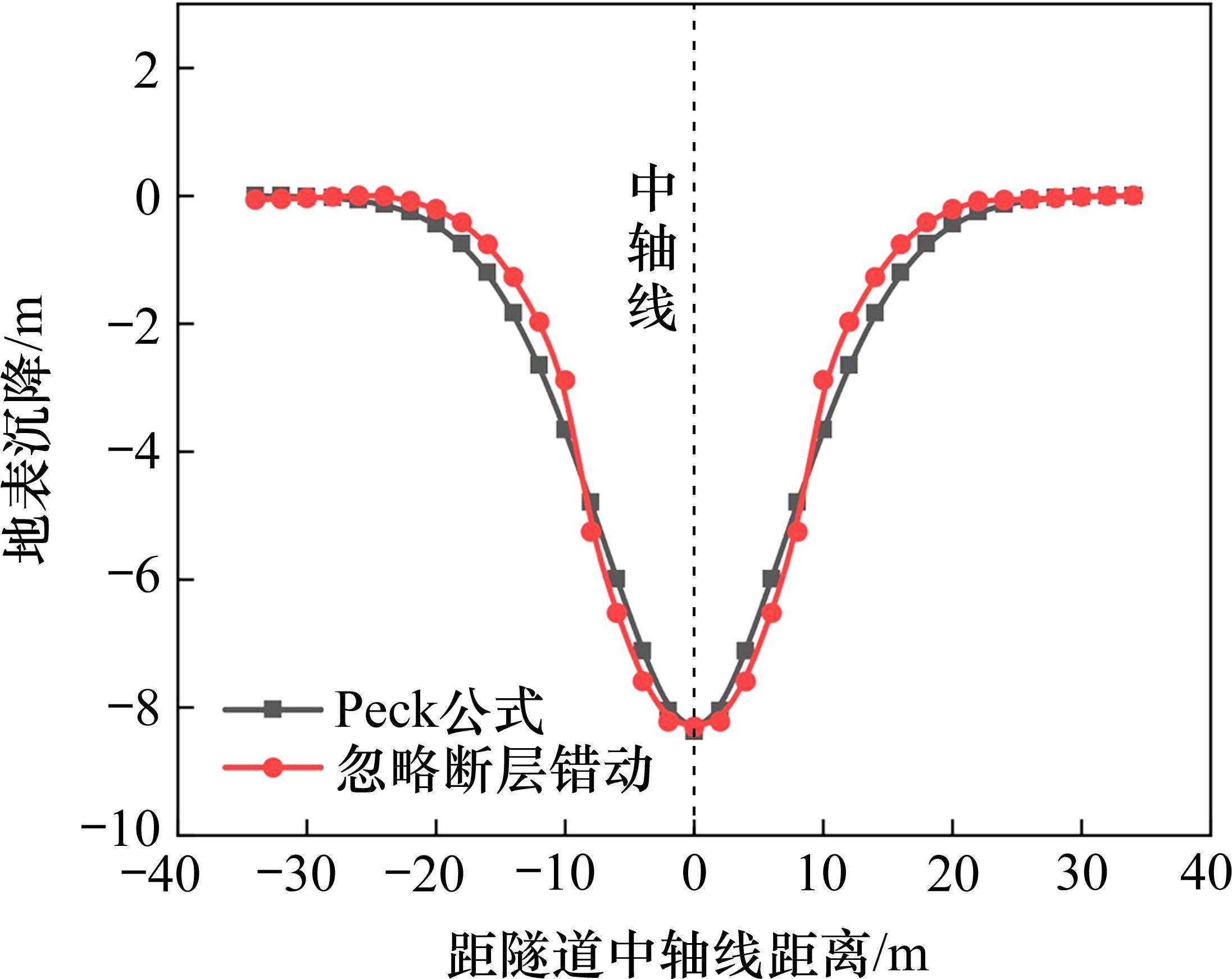
2.4 确定性分析
2.4.1 断层错动影响分析
断层错动对盾构施工安全构成巨大挑战,故设定2种工况,研究在确定性条件下断层错动对地表沉降变形的影响。一种工况不考虑断层错动的影响,另一种工况根据表1为断层错动赋值。图5展示了2种工况的变形曲线。由图可知,忽略断层错动时,地表横向变形呈现出对称形状。而考虑断层错动时,地表横向变形曲线呈现不对称形状,明显不符合高斯分布。具体而言,考虑断层错动时,隧道中轴线一侧沉降显著增加,而另一侧则出现地表隆起。断层错动导致两侧地层发生相对剪切错动,致使地表最大沉降位置发生偏移,从隧道中轴线偏移到距中轴线2 m处,且最大沉降值略有增大。
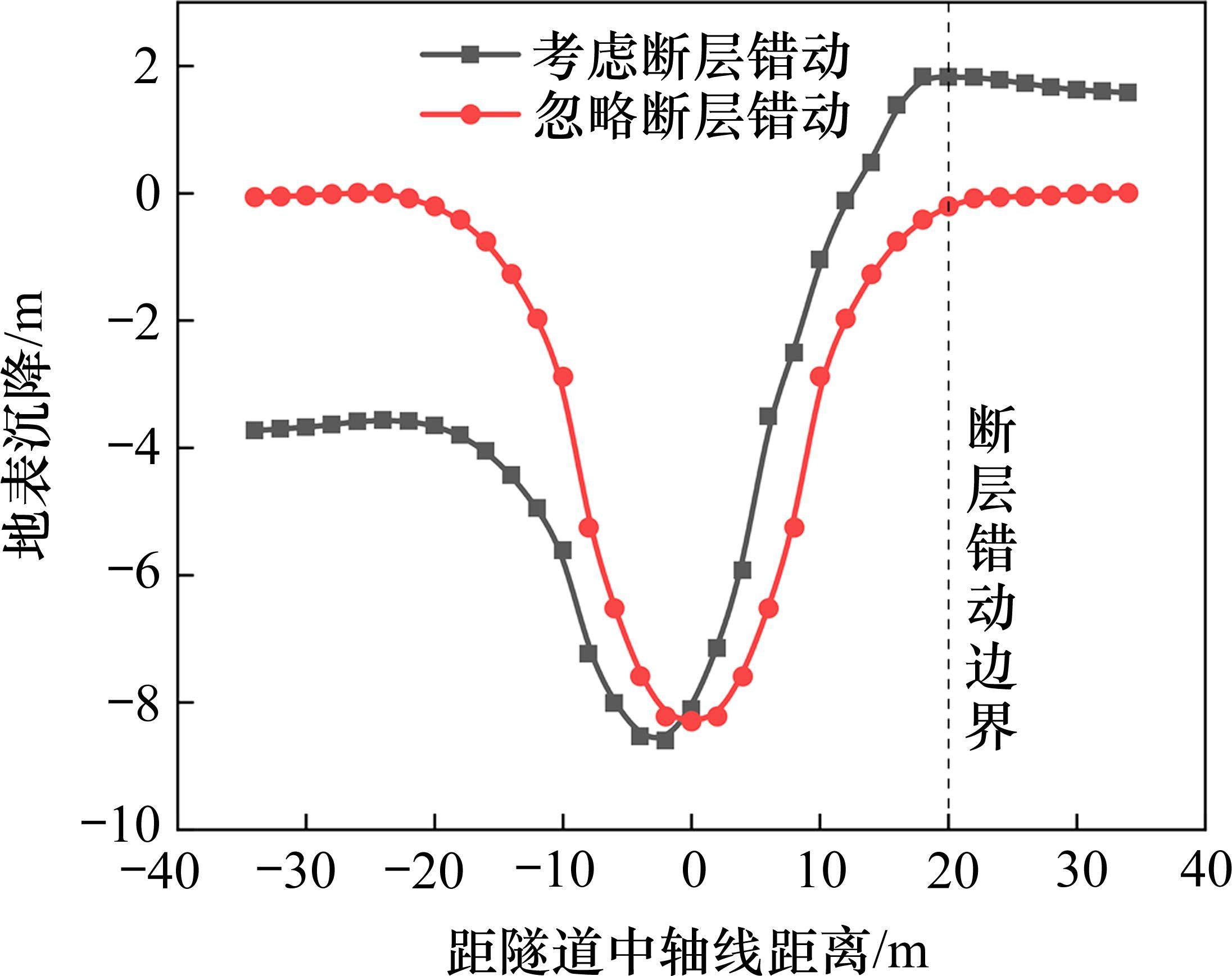
2.4.2 敏感性分析
为分析断层错动参数对地表沉降的影响,选取距离隧道中轴线-2 m位置处的地表沉降值作为观测对象,进行参数敏感性分析。分析时除研究参数外,其余均按表1进行取值。图6为不同参数对沉降的影响曲线。图6(a)中,c=10 kPa,φ=20°。可以看出,随着弹性模量的增加,地表沉降逐渐减小。当E达到100 MPa附近时,沉降值趋于稳定,表明此时E对沉降的影响趋于稳定。渗透系数的变化并没有引起沉降值的大幅波动,表明其对地表沉降的影响较小。图6(b)中,K=2

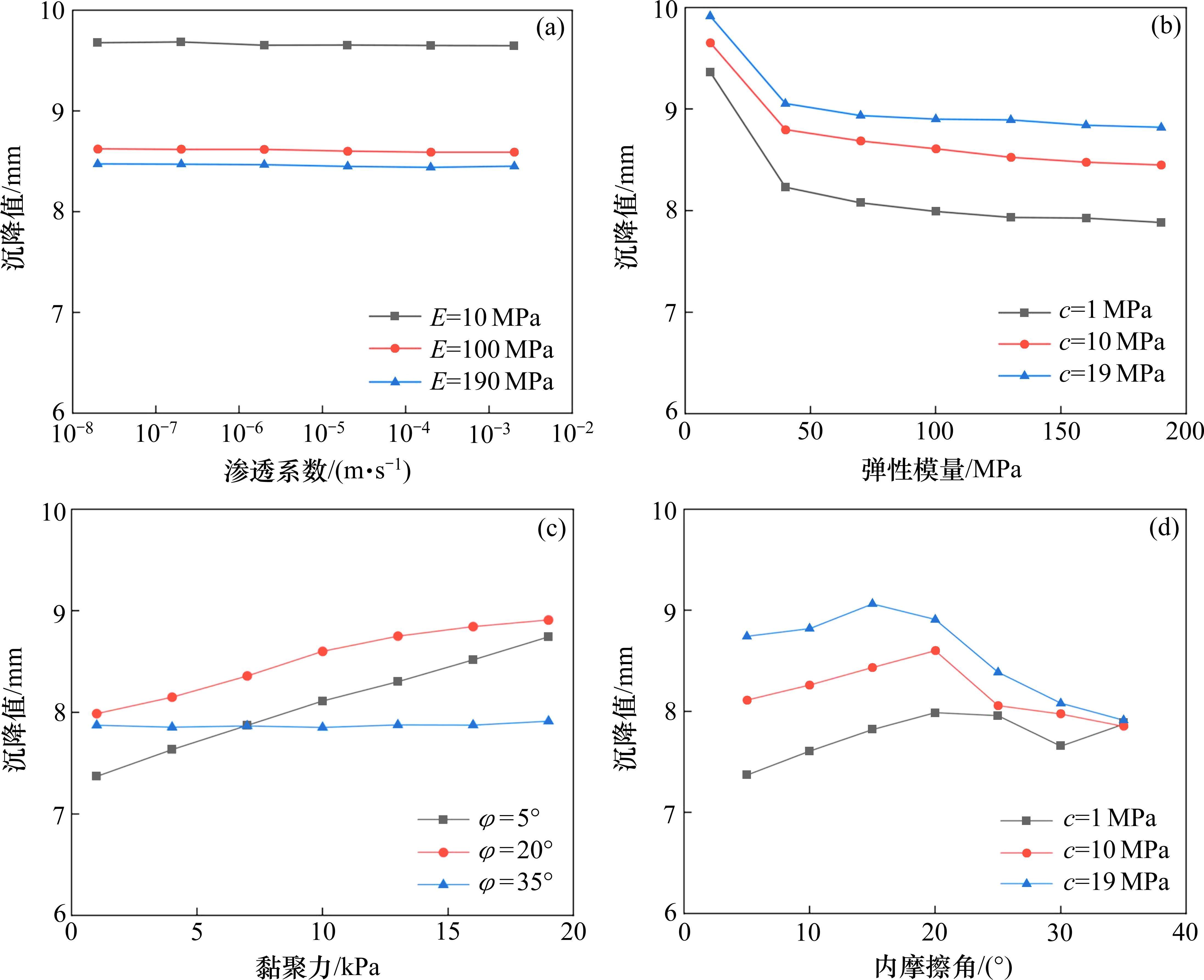
2.5 参数空间变异性分析
2.5.1 不同离散参数影响分析
天然岩土体水平自相关距离Lh通常介于10~80 m,而竖直自相关距离Lv介于1~3 m[20]。本文在设定工况时离散参数的Lh取值范围为10~100 m,Lv取值范围为1~10 m。参考易顺等[12]的研究,变异系数Cv设定为0.1~0.4。详细工况设置如表2所示。
| 工况名称 | 离散化变量 | 离散变量分布类型及自相关函数 | 变异系数CV | 水平波动距离Lh/m | 竖直波动距离Lv/m |
|---|---|---|---|---|---|
| M-K | K | 对数正态分布、高斯型 | 0.2 | 30 | 3 |
| M-E | E | ||||
| M-c | c | ||||
| M-φ | φ | ||||
| M-φ1 | φ | 对数正态分布、高斯型 | 0.1 | 30 | 3 |
| M-φ2 | 0.2 | ||||
| M-φ3 | 0.3 | ||||
| M-φ4 | 0.4 | ||||
| M-h1 | 对数正态分布、高斯型 | 0.2 | 10 | 3 | |
| M-h2 | 30 | ||||
| M-h3 | 50 | ||||
| M-h4 | 100 | ||||
| M-v1 | 对数正态分布、高斯型 | 0.2 | 30 | 1 | |
| M-v2 | 3 | ||||
| M-v3 | 5 | ||||
| M-v4 | 10 |
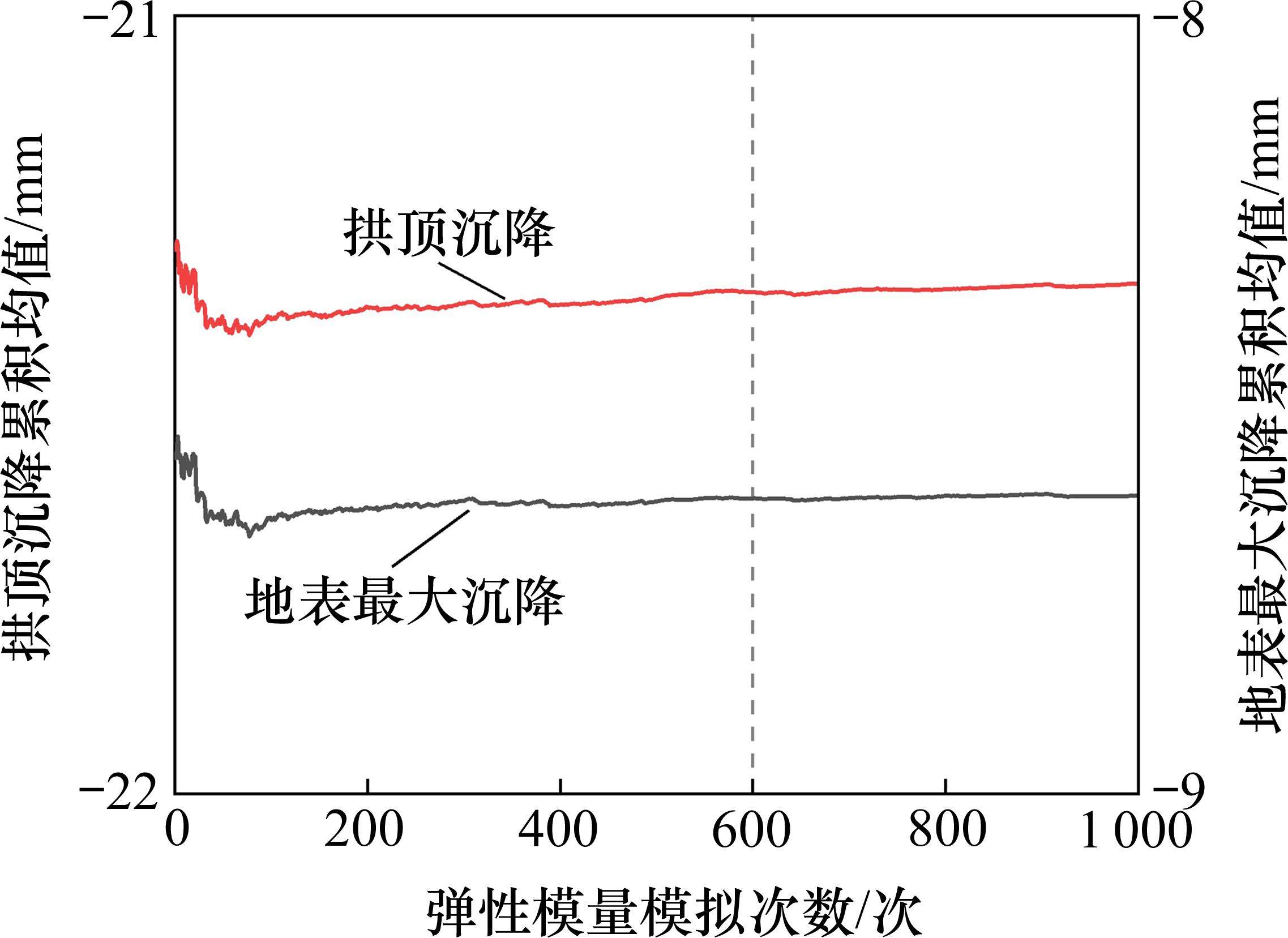
图7展示了盾构未掘进时,通过一次随机模拟得到的断层错动渗透系数K的分布情况。在进行断层错动参数空间变异性分析前,从计算精度和效率等[17]方面对单个工况的模拟次数进行了验证,此处选取弹性模量来确定随机模拟次数。图8表示沉降均值随模拟次数的变化情况。由图8可知,当模拟次数达到600次时,沉降均值均达到稳定。故每种工况模拟600次。
为便于后续分析,定义变形波动量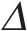
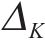
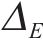

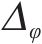
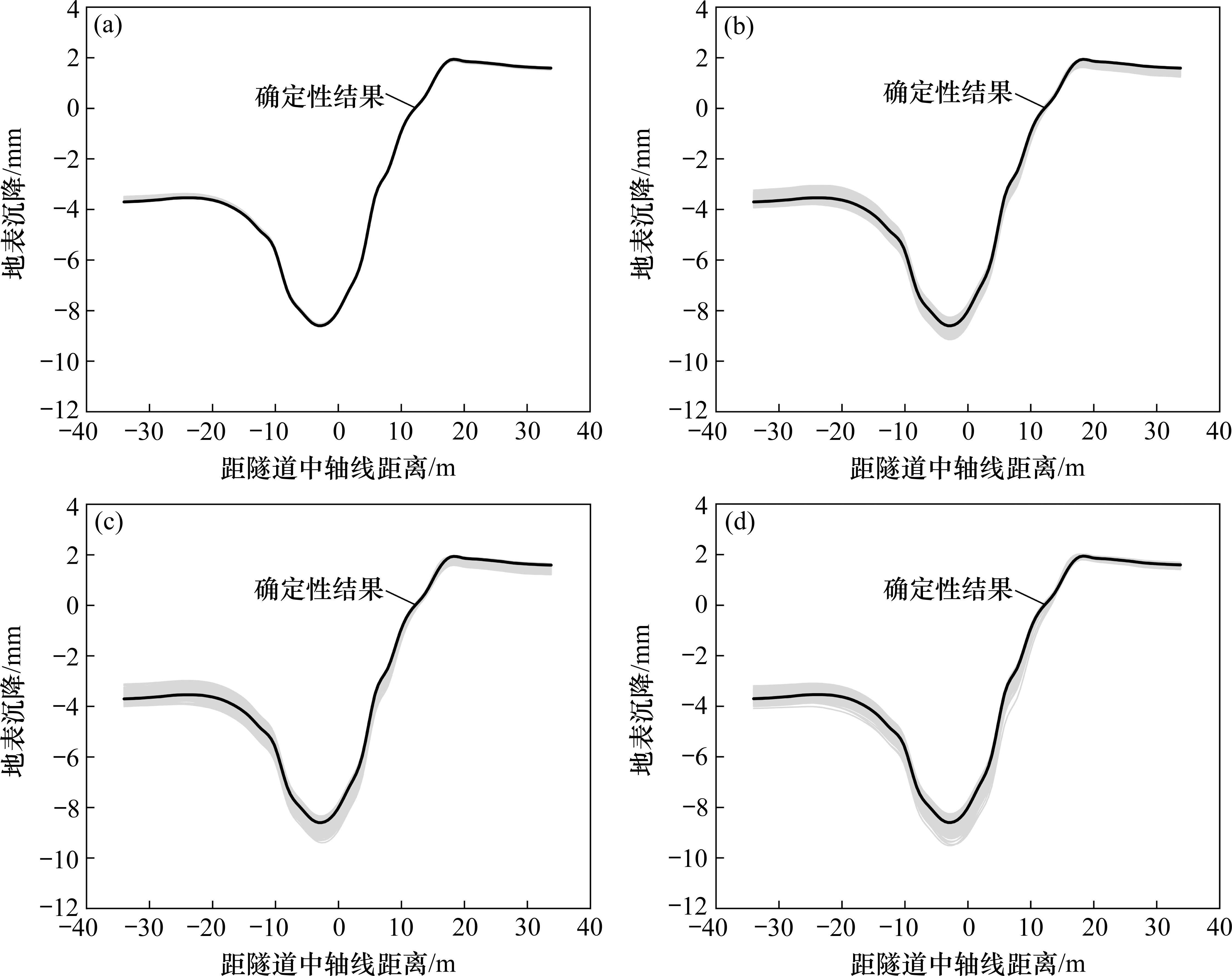
2.5.2 变异系数影响分析
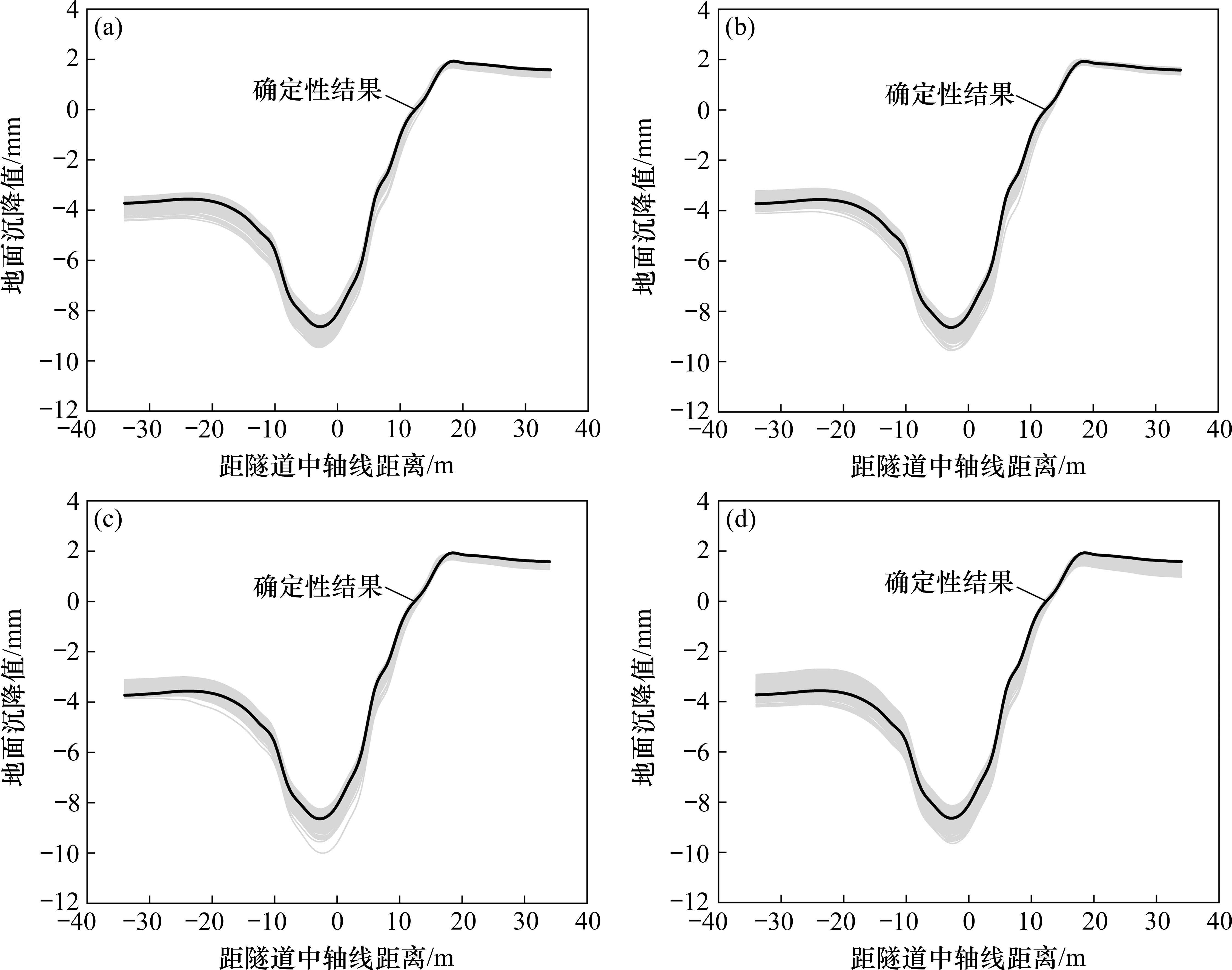
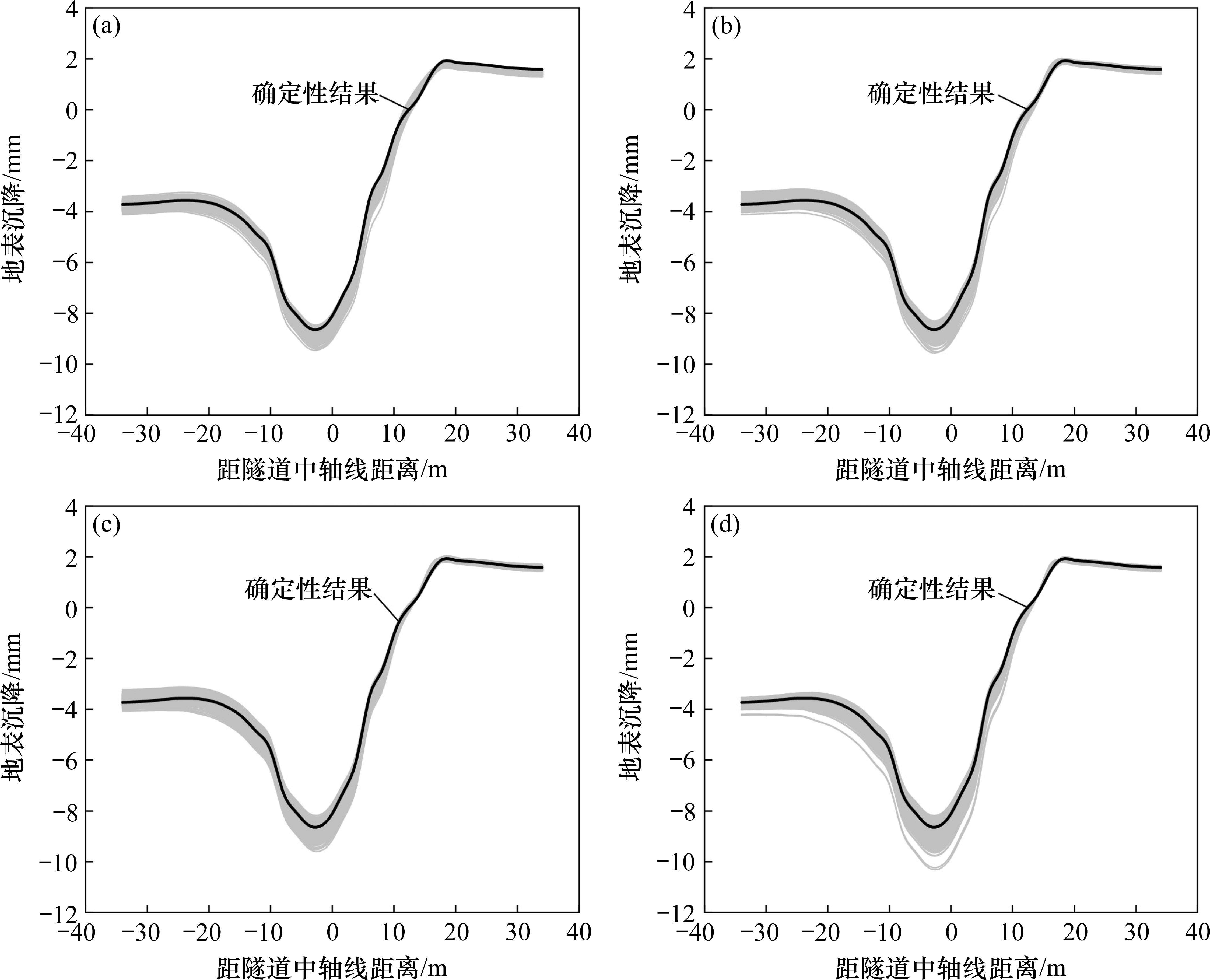
图10为断层错动内摩擦角在不同变异系数Cv下分别进行600次随机模拟的地表变形曲线(M-φ1、M-φ2、M-φ3、M-φ4工况)。观察得知,与确定性结果相比,Cv的变化对地表变形曲线的规律影响较小,但对地表沉降曲线的离散程度影响显著。具体而言,随着Cv的增大,随机模拟得到的部分地表沉降曲线变形规律与确定性结果略有不同,且曲线更为离散。当Cv=0.1时,地表变形曲线呈现高度集中,最大沉降变化范围为-8.91~-8.36 mm,变形波动量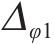
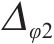
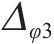
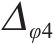
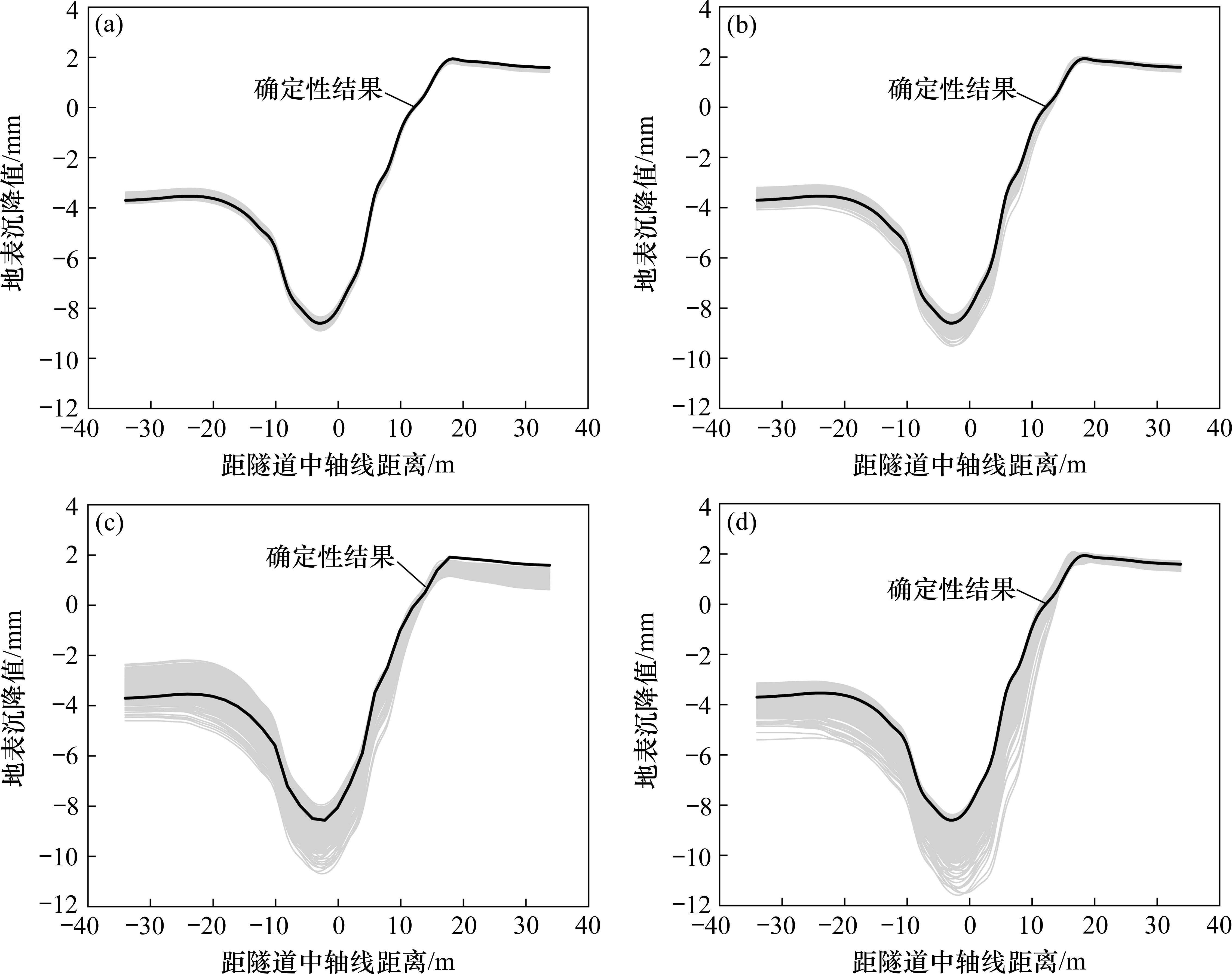
2.5.3 自相关距离影响分析
图11和图12呈现了断层错动内摩擦角在不同自相关距离(Lh和Lv)下随机模拟600次得到的地表变形曲线(M-h1、M-h2、M-h3、M-h4、M-v1、M-v2、M-v3、M-v4工况)。由图可知,Lh、Lv的变化对地表变形曲线的规律影响较小,但对变形曲线的离散程度影响较大。图11中,当Lh=10 m时,地表变形曲线呈较为集中的形态,最大变形范围相对较小,为-8.80~-8.21 mm,变形波动量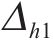
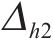
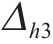
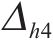
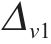
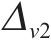
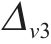
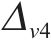
3 变形超出阈值概率分析
工程监测阈值在保障工程安全施工和正常运营方面发挥着关键的预测和警示作用。一旦监测数据超过阈值,就可能暗示工程存在一定的风险,应引起警示,并迅速采取相应的控制措施。类似地,盾构施工中地表变形阈值的重要性也不可忽视。可以通过变形值超过变形阈值的概率来评估隧道工程的安全性。在模拟盾构施工时,每种工况引起的变形值Smax超过变形阈值Slim的概率Pf可定义如式(8)[21]:
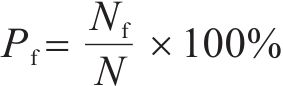
式中:N为每种工况的模拟次数,此处N=600;Nf为每种工况计算中变形值Smax超过变形阈值Slim的次数。
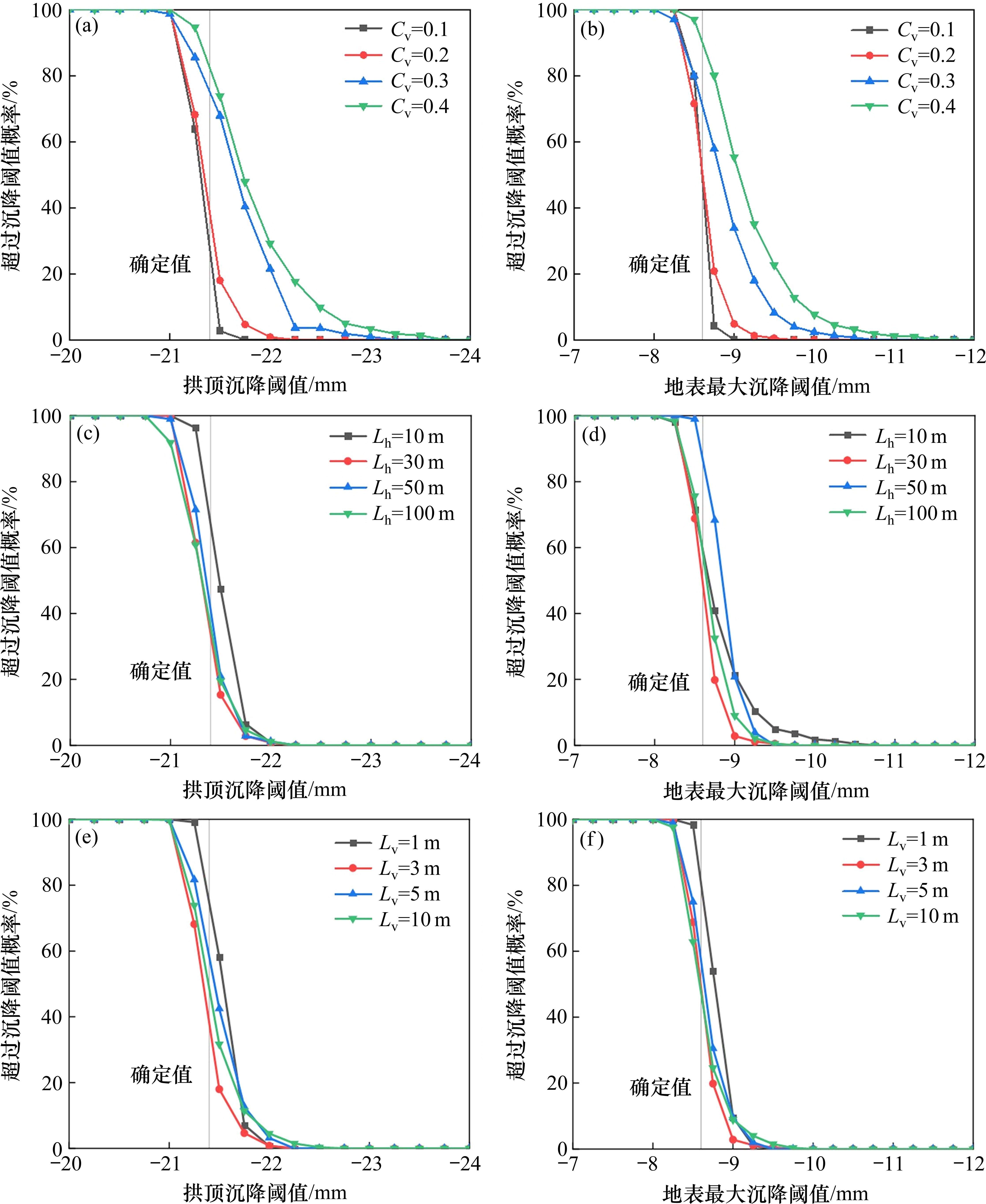
图13展示了断层错动内摩擦角在不同变异系数和自相关距离下拱顶沉降值Smax1和地表最大沉降值Smax2超过变形阈值Slim的概率分布曲线(确定值表示2.4.1节中考虑断层错动所得的变形值)。由图可知,内摩擦角的空间变异性对计算结果的离散性产生显著影响。具体而言,图13(a)和图13(b)的结果显示,随着变异系数的增加,沉降值Smax1和Smax2的分布更加分散。以地表最大沉降为例,当地表最大沉降控制阈值为9 mm(大于确定值)时,Cv分别为0.1、0.2、0.3、0.4时,沉降超过阈值的概率依次为0.2%、4.5%、37.2%、58.3%。值得注意的是,在变异系数较小的情况下(如Cv=0.1),变异系数对拱顶沉降和地表最大沉降值的影响相对较小,这是因为断层错动在较小的变异系数时更趋向于“均质”的材料。图13(c)、图13(d)、图13(e)、图13(f)的结果显示,随着自相关距离(Lh和Lv)的变化,沉降值Smax1和Smax2的分散程度发生一定变化,表明内摩擦角的自相关距离对沉降值超过控制阈值概率的影响不能忽略。综合来看,与自相关距离相比,断层错动的变异系数对工程安全的影响更为显著。
4 结论
1) 确定性分析结果表明,盾构施工受到断层错动的影响,导致地层两侧发生相对剪切移动,并造成地表最大沉降位置偏离中轴线,同时最大沉降值增加,部分地表位置甚至出现隆起。断层错动的渗透系数对地表沉降的影响较小,而内摩擦角的影响则较为显著。表明隧道穿越断层错动时,不能忽视断层错动对施工安全的影响。
2) 采用基于高斯型自相关函数和KL级数展开法的随机场理论,可以在难以勘测且钻孔数据有限的情况下,完整地描述断层错动力学参数和水力参数的空间分布特性,为类似工程在准确表征断层错动空间变异性时提供有益参考。
3) 与黏聚力、弹性模量、渗透系数相比,断层错动内摩擦角的空间变异性对地表变形曲线的离散程度和变形范围影响最大,其次是黏聚力,再次是弹性模量,而渗透系数的影响最小。此外,不同的离散参数均对变形曲线的整体规律和变化趋势影响较小。
4) 随着变异系数和自相关距离的增大,随机分析得到的地表变形曲线表现出更大的离散程度和变形波动量,其中变异系数的影响相较于自相关距离更为显著。基于概率统计方法的拱顶沉降和地表最大沉降超过阈值概率分布图可为隧道穿越断层错动区域前预警最大沉降值提供参考。
黄娟,郑艳林,郑红亮等.考虑断层错动空间变异性的水下盾构隧道地层变形特征研究[J].铁道科学与工程学报,2024,21(11):4599-4611.
HUANG Juan,ZHENG Yanlin,ZHENG Hongliang,et al.Characterizing ground deformation in subaquatic shield tunnels while accounting for spatial variability in fault dislocation[J].Journal of Railway Science and Engineering,2024,21(11):4599-4611.

