在寒区修建隧道,冷风流与隧道壁发生对流换热[1-2],使得含水围岩温度降低而发生冻胀,冻胀力导致衬砌变形、开裂、剥落、渗水、结冰[3],危害极大。明确风流对隧道冻胀力的影响,将是防止冻胀的关键。目前,冻胀力计算模型大多使用适用性高的冻融圈层整体冻胀模型[4],该模型针对衬砌-已冻围岩-未冻围岩系统进行分析,得出了大量的解析解与数值解。首先,将隧道断面简化为圆形且假定围岩冻胀为各向同性的情况下,LAI等[5]根据弹性-黏弹性理论,推导了冻胀力与时间的关系式;GAO等[6]利用连续性方程得到了冻胀力的弹塑性解析解,所求结果未能体现既有非圆形隧道中冻胀力的不均匀分布,李岩松等[7]则利用复变函数理论揭示了这一规律。其次,已有试验[8-9]表明岩石沿冻结方向的冻胀变形大于垂直冻结方向,表现出各向异性冻胀,LÜ等[10]则考虑围岩横向各向同性冻胀,提出了冻胀力的弹塑性解析解。为进一步揭示水分场与温度场带来的影响,学者构建了热水力耦合数值模型,张泽等[11]发现水冰相变潜热对温度场影响较大;李又云等[12]基于实际温度场与水分场计算了冻胀力分布;杨天骄等[13]揭露水分迁移对冻胀力的影响显著;陆许峰等[4]综合考虑非圆形隧道、不均匀冻胀、水分场、温度场对冻胀力的影响,提出了围岩正交各向异性冻胀变形下的冻胀力分布特征。与此同时,谭贤君[14]、郑余朝等[15]、张力杰等[16]分别根据湍流理论、正交试验理论、Laplace变换研究了风流对隧道温度场的显著影响。综上可知,冷风流将对冻胀力有所影响,但机理尚不明确。由此,本文基于冻融圈层整体冻胀理论,考虑风流与衬砌的换热特性,在陆许峰等[4]研究的基础上,建立了风热水力的全过程耦合模型;然后,运用COMSOL Multiphysics 有限元软件进行数值求解,结果与黄继辉等[17]实测数据对比验证了模型的正确性;进而,探究了风流的持续时间、湿度、速度与温度对冻胀力的影响规律,采用正交试验方法,明确了该4个因素对冻胀力的影响敏感性。本研究揭示了冻胀源头(冷风流)对冻胀力的影响机理,可为寒区隧道的保温防冻措施设置提供理论依据。
1 隧道冻胀风热水力耦合模型
1.1 风流参数与对流换热控制方程
风流为具有一定速度的空气,空气中又往往含有水蒸气,为简化计算,本文将风流场浓缩至隧道衬砌边界处,如图1。
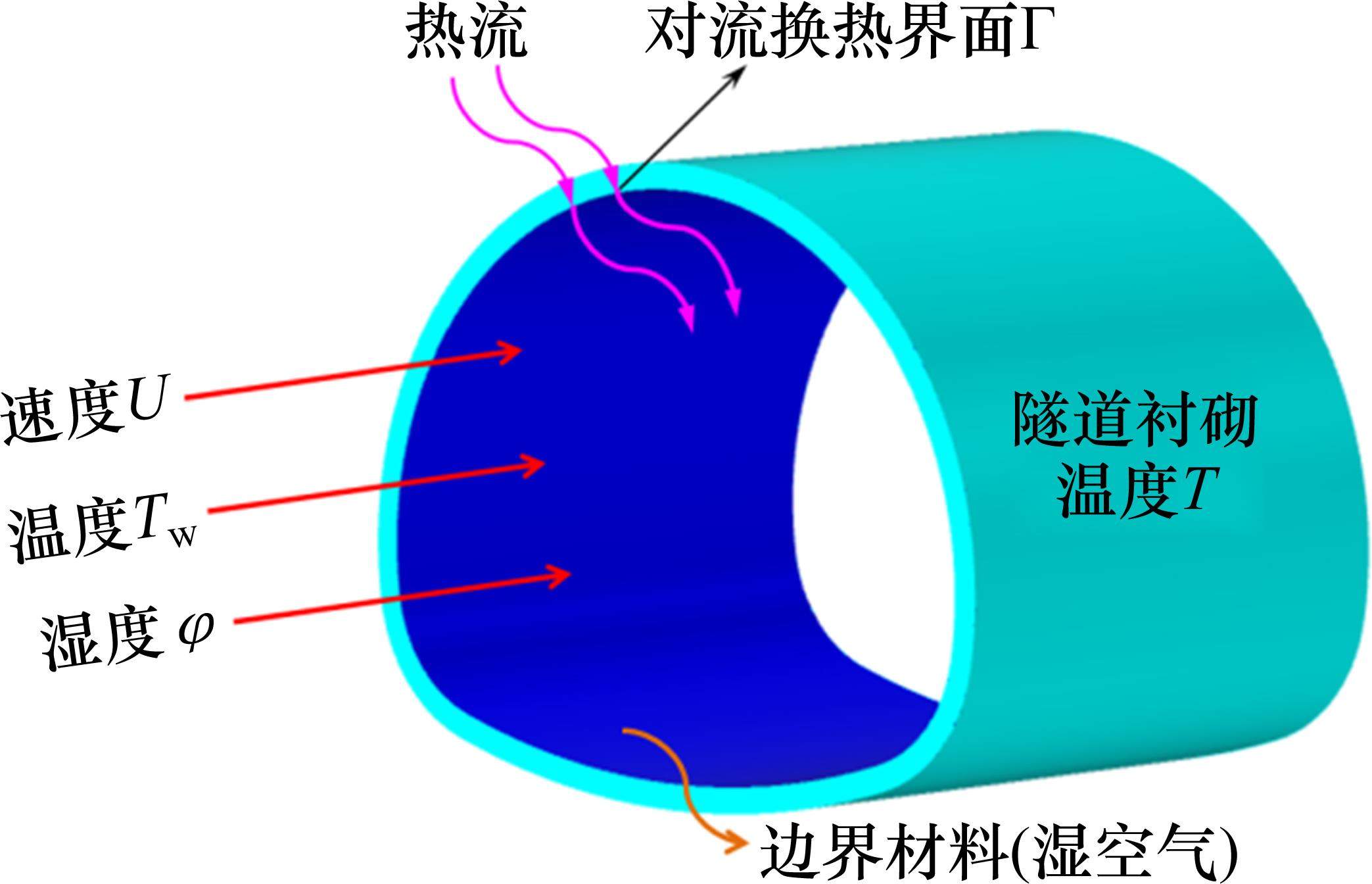
通过定义其温度、湿度、风速、热物性参数进行指代。温度即外界环境温度,湿度为相对湿度,风速为垂直隧道断面的速度。湿空气热物性参数——密度、恒压热容、动力黏度、导热系数分别可由式(1)、式(4)、式(7)、式(10)计算[18]。
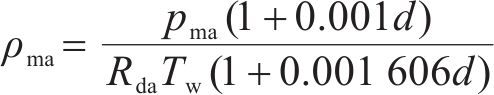
式中:ρma为湿空气的密度,kg/m3;pma为空气总压力,Pa;Rda为干空气的气体常数,在数值上相当于质量为1 kg的干空气在可逆定压加热过程中温度每升高1 K时对外所做的膨胀功,取287 J/(kg∙K);Tw为湿空气的温度,K;d为湿空气的含湿量,g/kg,可表示为:
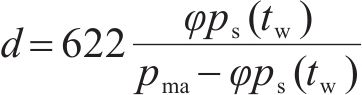
式中:φ为湿空气相对湿度,%;ps(tw)为湿空气摄氏温度tw(℃)时的水蒸气饱和压力:
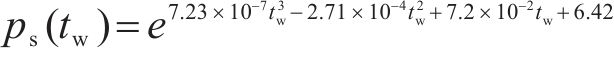
式中: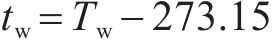
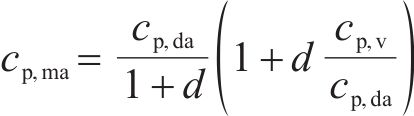
式中:cp,ma为湿空气的定压比热容,J/(kg∙K);cp,da、cp,v分别为干空气和水蒸气的定压比热容,J/(kg∙K),其含义是质量为1 kg的气体在定压条件下温度升高1 K所吸收的热量,由式(5)、式(6)计算。
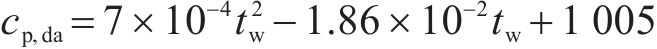
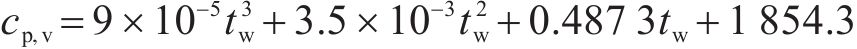
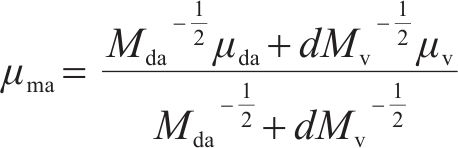
式中:μma为湿空气的动力黏度,kg/(m∙s);Mda、Mv分别为干空气和水蒸气的分子量,取28.97和18.02;μda、μv分别为干空气和水蒸气的动力黏度,kg/(m∙s),由式(8)、式(9)计算。
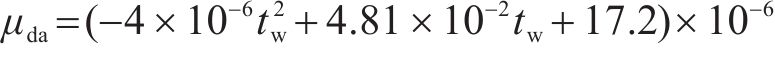
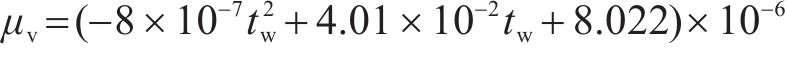
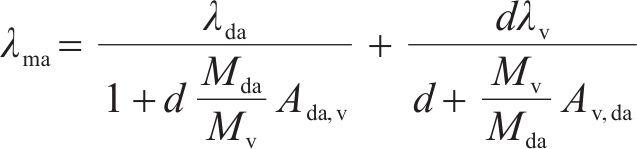
式中:λma为湿空气的导热系数,W/(m∙K);λda为干空气的导热系数,W/(m∙K),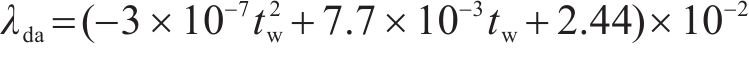
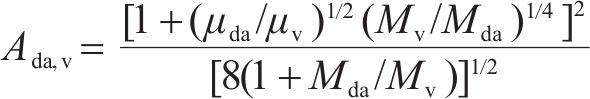
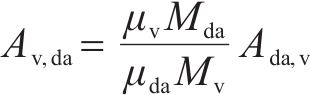
当环境冷空气吹入隧道时,将与衬砌表面发生强烈的对流换热,根据Fourier导热定律、牛顿冷却定律以及能量守恒定律,对流换热控制方程可表示为:
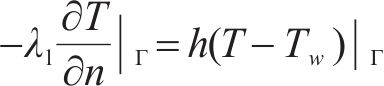
式中:λl为衬砌的导热系数,W/(m∙K);T为衬砌的温度,K;Γ为对流换热界面;∂T/∂n表示T沿边界Γ上的单位外法线方向n的方向导数,K/m;h为对流换热系数,W/(m2∙K)),计算表达式为[19]:
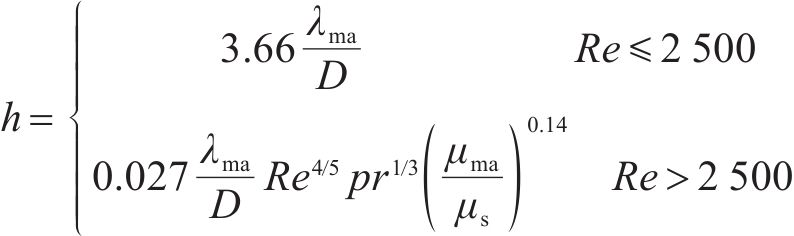
式中:D为水力直径,m;D=4×隧道横截面面积/隧道横截面周长;μs为μma取衬砌壁温计算得到的值;Re为雷诺数,Re=ρmaUD/μma,U为风流速度;pr为普朗特数,pr=μmacp,ma/λma。
1.2 温度场与围岩水分场控制方程
衬砌内部不考虑水分迁移和水冰相变,那么其内能变化量(增加)等于流入的净热量,得到温度控制方程[20]:
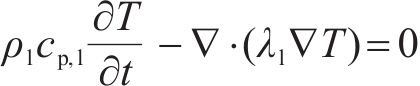
式中:ρl为衬砌的密度,kg/m3;cp,l为衬砌的定压比热容,J/(kg∙K);t为时间,s;
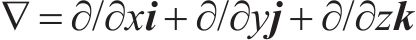
围岩内部因发生水分迁移和水冰相变,其能量方程与含水量和相变潜热有关,同理可得温度控制方程为[20]:
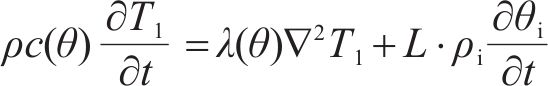
式中:T1为围岩的温度,K;L为水冰相变潜热,取334.56 kJ/kg;ρc(θ)为围岩的体积热容量,J/(m3∙K);λ(θ)为围岩的导热系数,W/(m∙K),其分别可由式(17)、式(18)计算得到[14]。
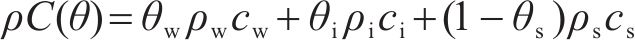
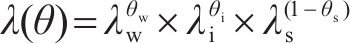
式中:ρw、ρi、ρs分别为水、冰、围岩骨架的密度,kg/m3;cw、ci、cs分别为水、冰、围岩骨架的比热容,J/(kg∙K);θw、θi、θs分别为围岩的体积含水率、含冰率、饱和含水率,%;λw、λi、λs分别为水、冰、围岩骨架的导热系数,W/(m∙K)。
围岩在冻结时,未冻部分中的水分将向冻结面迁移,导致冻结区域内水分增加,假设水分迁移遵循达西定律,根据质量守恒定律,得到围岩水分场控制方程[20]:
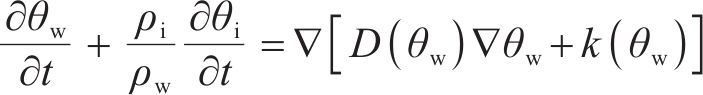
式中:D(θw)为冻土中水的扩散率;k(θw)为重力影响下的非饱和围岩渗透系数,m/s,其表达式分别为:
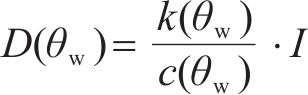
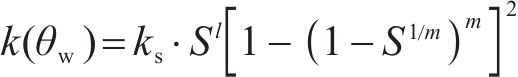
式中:I为冰对水分迁移阻滞作用的阻抗因子,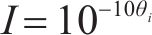
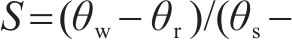
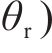
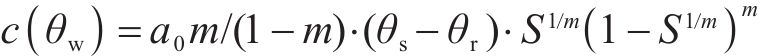
式中:a0、m为模型参数。
为求解上述控制方程,需引入固液比B(T1)的表达式[20],其为围岩中体积含冰率与含水率的比值:
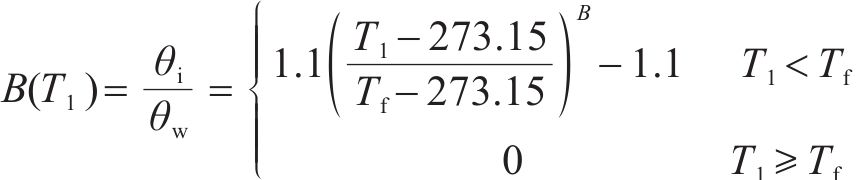
式中:Tf为围岩冻结温度,K;B为常数,与围岩的性质和含盐量有关,徐敩祖根据试验测得砂土取值0.61,粉土取0.47,黏土取0.56。
1.3 隧道冻胀力控制方程
隧道围岩在冻结过程中,由于水分迁移的作用,在垂直热流方向上产生冰透镜体,随着热量的不断流出,冻结锋面向外推移,冰透镜体不断生长,导致热流方向产生的冻胀变形远大于热流正交方向,呈现出正交各向异性冻胀变形的特征,其冻胀应变分量如式[4]。
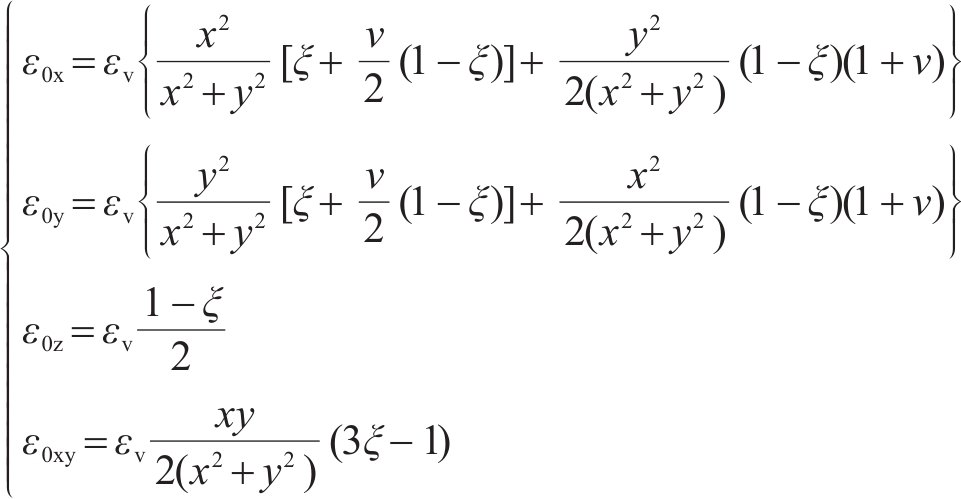
式中:x、y为横纵坐标值;ξ为围岩冻胀变形的正交各向异性系数;ν为围岩泊松比;εv为围岩冻胀体应变,即水变成冰产生的体积应变:
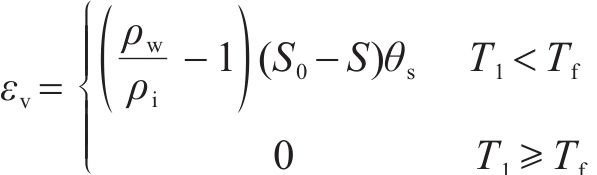
其中,S0为围岩初始相对饱和度。
根据Hooke定律,围岩应力应变关系为:
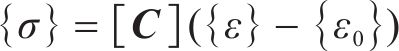
式中:C为弹性矩阵;ε为弹性应变;ε0为冻胀应变。
隧道冻胀力为衬砌与围岩交接处,垂直于接触面的应力[21],其表达式为:
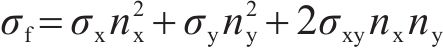
式中:σf为法向应力,取正值为冻胀力;σx、σy、σxy为总应力σ对应的分量;(nx, ny)为衬砌与围岩接触面的单位法向量。
2 模型验证
2.1 几何建模与计算参数
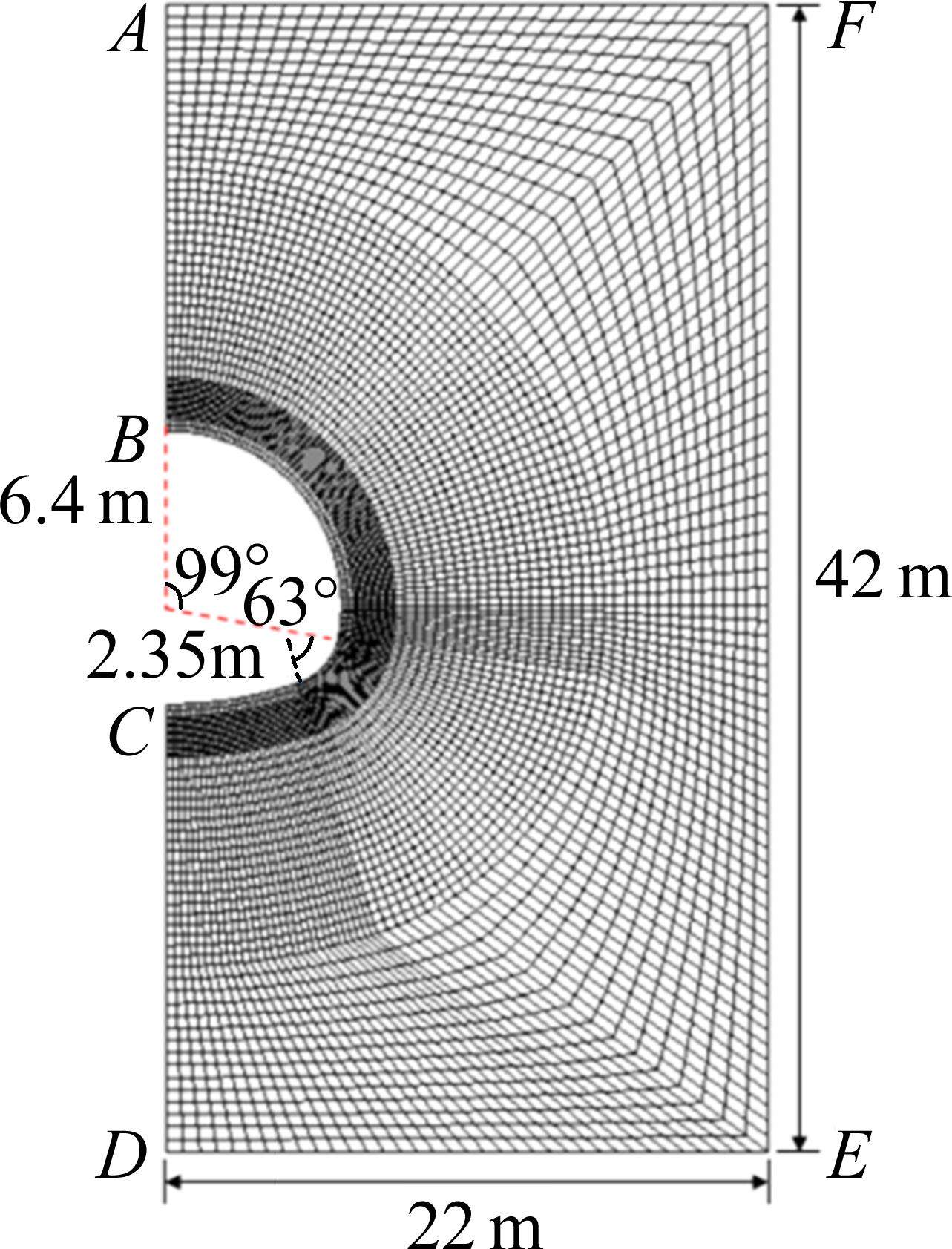
为验证模型的正确性,选取青海省青沙山隧道ZK33+970处的一半断面,进行上述风热水力耦合计算。断面几何如图2,衬砌厚度0.45 m,围岩等级为V级[17],采用COMSOL Multiphysics有限元进行几何建模、划分网格,为保证计算精度的要求,对围岩冻结圈内网格进行了适度加密,网格单元数共7 072个。
计算参数参考相关文献[2, 4, 13-20],如表1所示。
| 参数 | 数值 | 参数 | 数值 |
|---|---|---|---|
| 衬砌密度ρl/(kg∙m-3) | 2 500 | 围岩残余含水率θr/% | 8 |
| 水的密度ρw/(kg∙m-3) | 1 000 | 饱和围岩的渗透系数ks/(m·s-1) | 2×10-8 |
| 冰的密度ρi/(kg∙m-3) | 918 | 模型参数l | 0.50 |
| 围岩骨架密度ρs/(kg∙m-3) | 1 700 | 模型参数a0/m-1 | 2 |
| 衬砌比热容cp,l/(kg∙m-3) | 1 046 | 模型参数m | 0.50 |
| 水的比热容cw/(J∙kg-1∙K-1) | 4 200 | 固液比参数B | 0.55 |
| 冰的比热容ci/(J∙kg-1∙K-1) | 2 100 | 围岩冻结温度Tf/K | 272.97 |
| 围岩骨架比热容cs/(J∙kg-1∙K-1) | 890 | 衬砌弹性模量El/GPa | 28.5 |
| 衬砌导热系数λl/(W∙m-1∙K-1) | 1.85 | 围岩弹性模量Es/GPa | 1.5 |
| 水的导热系数λw/(W∙m-1∙K-1) | 0.63 | 衬砌泊松比vl | 0.2 |
| 冰的导热系数λi/(W∙m-1∙K-1) | 2.31 | 围岩泊松比v | 0.35 |
| 围岩骨架的导热系数λs/(W∙m-1∙K-1) | 1.38 | 围岩变形正交各向异性系数ξ | 0.7 |
| 围岩饱和含水率θs/% | 25 | 围岩初始相对饱和度S0/% | 99.90 |
2.2 边界条件与初始值
根据气象资料,当地年平均风速为1.64 m/s[22],空气湿度为57.8%[23]。由于选取的隧道断面与洞口较近,因此以洞口气温作为本次研究的风流温度,根据文献[24]查得洞口气温为:
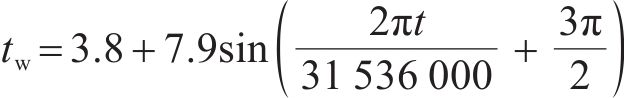
因风流对围岩影响范围有限,忽略围岩初始温度在尺寸上的变化,围岩与衬砌初始温度均为2.9 ℃[4],围岩初始相对饱和度S0取0.999(孔隙中全为水)。图2中AB、CD为对称边界,BC为自由位移边界,AF、EF、DE为温度场与水分场的零通量边界,同时作为力场中的辊轴约束边界。衬砌与围岩之间无水分迁移,接触面设为渗流零通量边界。鉴于力场中重点关注围岩对衬砌的冻胀力,忽略初始地应力、开挖与重力的影响,因此将初始应力场与位移场均设置为0。
2.3 结果对比
针对上述围岩温度场和水分场控制方程组,本文运用COMSOL Multiphysics有限元的系数形式偏微分方程接口进行求解,风流与衬砌对流换热采用固体与流体传热接口,衬砌与围岩接触界面设置狄利克雷边界条件(指定温度),在固体力学中输入冻胀应变,即可实现风热水力耦合的瞬态数值求解,计算容差设置为0.001,步长10 d,共3 650 d。
选取最大深度的冻结圈如图3(a),从衬砌的温度可以看出,此时发生在气温由负温过渡至正温时。冻结圈深度:仰拱>拱顶>拱脚。衬砌温度减小程度与其几何曲率息息相关,曲率越大处,热量传递速率越小,温度变化也越小,便发生了不均匀传热现象,导致冻结圈深度并不一致。冻结圈平均深度1.01 m,此结果与黄继辉等[17]在现场测得的最大冻深1.22 m基本相符。
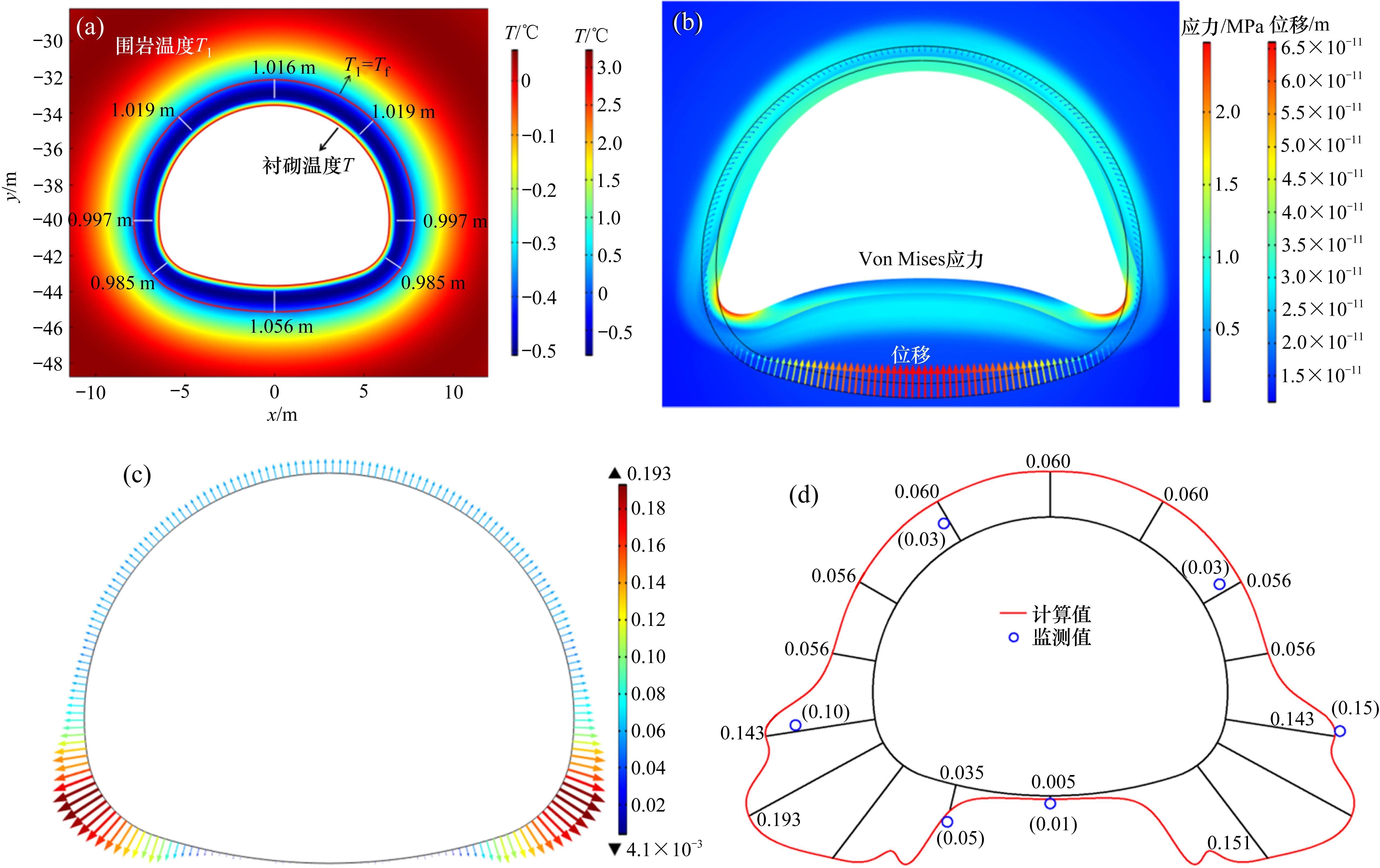
冻结圈深度最大时,冻胀力也达到最大值,文献[7, 21]中的解析解也说明了这一点,提取相应冻胀力如图3(c),冻胀力大小:拱脚>拱顶>仰拱,与黄继辉等[17]在该隧道断面现场监测的数据进行对比(图3(d)),吻合良好。冻胀力如此分布,是因为拱脚传热速率慢,导致拱脚处因温降产生的冻胀力较小,然而拱顶与仰拱因温降产生的冻胀力大,上下挤压衬砌,使拱脚处衬砌向围岩侧挤压(图3(b)),导致拱脚衬砌外边界法向应力变大,拱脚中部尤甚,拱脚上部、下部稍弱,从而在拱脚处形成“凸”字形的冻胀力。仰拱由于其刚度较小,再则温降在此处引起的冻胀力较大,与拱顶、拱腰冻胀共同作用下,变形较大(图3(b)),应力释放较大,导致仰拱最终冻胀力仅0.005 MPa(现场0.01 MPa)。上述计算结果表明,本文所建立的风热水力耦合模型合理可靠,可推广适用于寒区隧道工程。
3 风流对冻胀力的影响
3.1 风流持续时间的影响
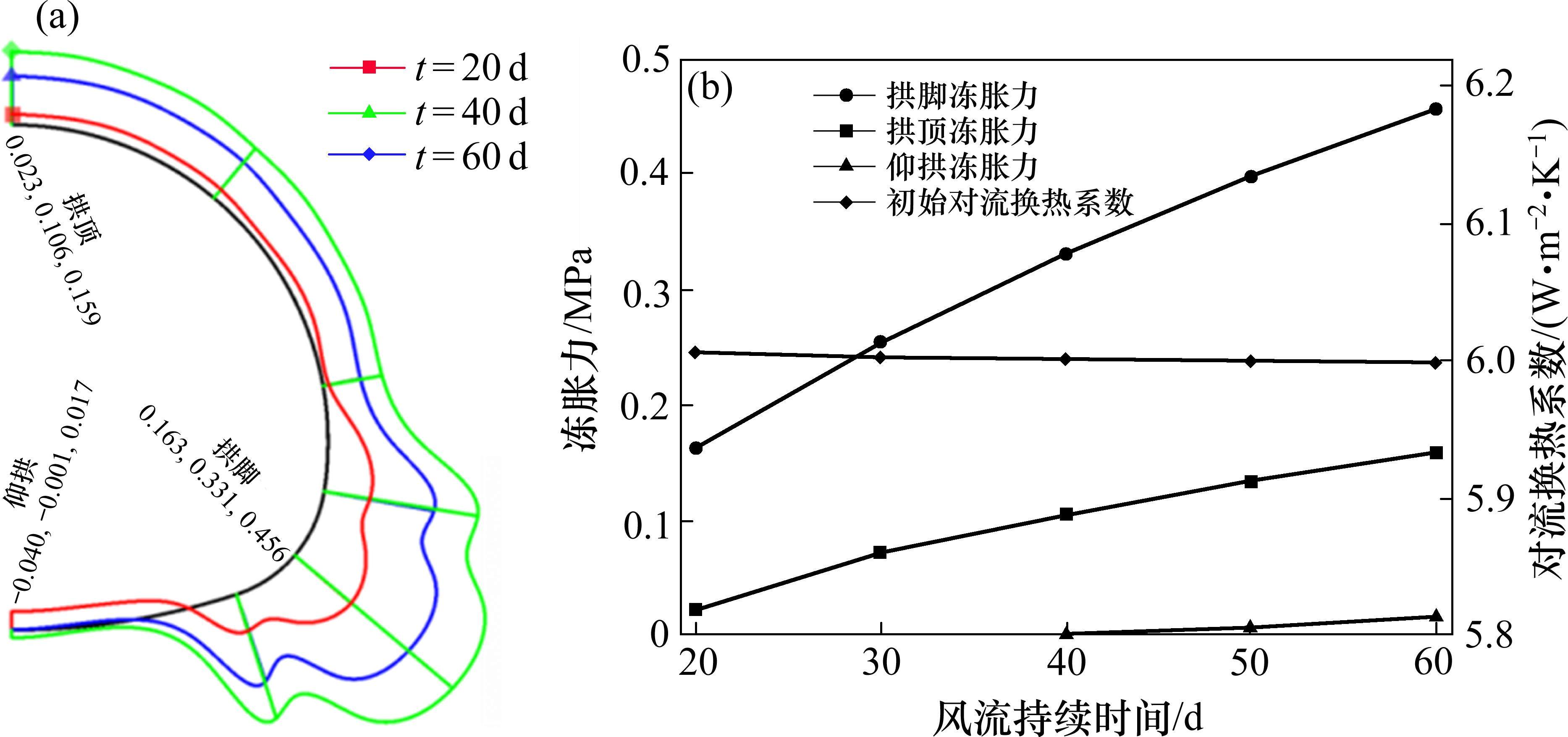
风流持续时间代表着空气与衬砌对流换热的时间长短,为探究其对隧道冻胀力的影响,依旧以青沙山隧道为背景,假定风流湿度、速度、温度分别取定值50%、2 m/s、-10 ℃,计算得到风流持续时间分别为20,40和60 d的温度场、冻结圈、相对饱和度变化量,如图4,衬砌外边界法向应力和拱脚、拱顶、仰拱冻胀力,如图5。
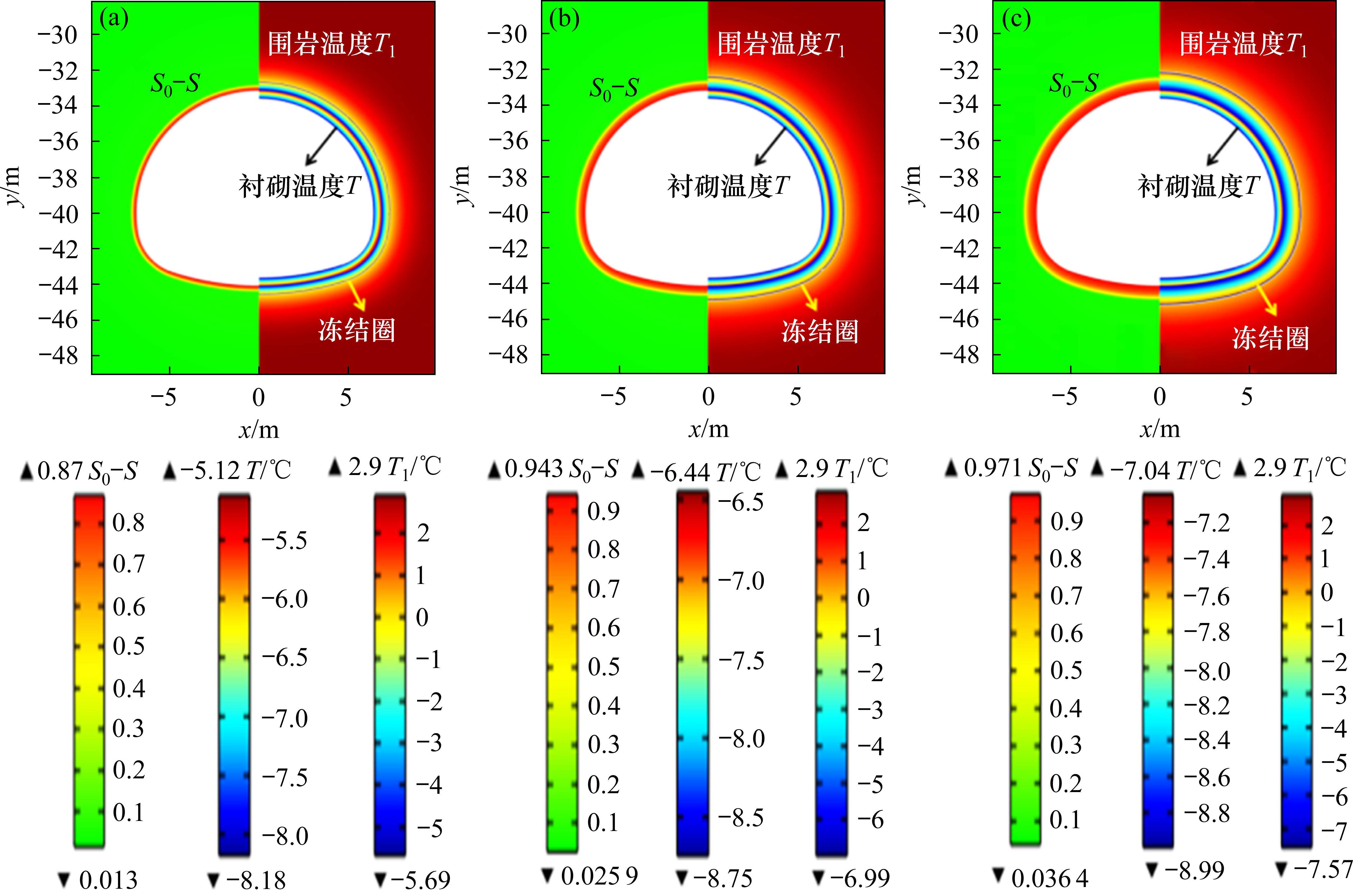
由图4可知,几何曲率带来的不均匀传热现象,风流温度持续在-10 ℃比风温随三角函数变化的情况更加明显,曲率最大的拱脚处温度相对较高。衬砌温度和围岩温度随着时间的增长均在减小,围岩温度影响范围和冻结圈的深度则逐渐增加,随着冻结圈内水分发生冻结,导致了相对饱和度变化量(S0-S)变大,其最大值由20 d时的0.870增至60 d时的0.971,值得注意的是,其最小值也由20 d时的0.013增至60 d时的0.036,这是非冻结区水分向冻结区域迁移导致的结果。
由图5(a)可知,仰拱温降引起的冻胀力不足以弥补其变形带来的应力释放时,将产生负的法向应力(拉应力),如t=20 d时,产生了0.04 MPa的拉应力。法向应力整体表现为:拱脚>拱顶>仰拱。随着风流持续时间的增长,衬砌外边界法向应力均在增加。
衬砌外边界法向应力的正值形成了冻胀力,取不同风流持续时间的拱脚最大冻胀力(后简称拱脚冻胀力)、拱顶冻胀力、仰拱冻胀力得到图5(b),由图5(b)可知,冻胀力:拱脚>拱顶>仰拱,拱脚、拱顶、仰拱冻胀力均随着风流持续时间的增加而增加,冻胀力增长速率:拱脚>拱顶>仰拱,但增长速率均在减小,分析源于对流换热系数随着时间的增长有略微的减小。在20 d至60 d的过程中,拱脚、拱顶冻胀力分别增长了0.293 MPa、0.136 MPa,仰拱冻胀力在第40 d时才开始形成,至60 d时,冻胀力达0.017 MPa。
3.2 风流湿度的影响
为研究风流湿度对冻胀力的影响,假定风流持续时间、速度、温度分别取定值60 d、2 m/s、-10 ℃,同理可得风流湿度分别为0、25%、50%、75%、100%的衬砌外边界法向应力与拱脚、拱顶、仰拱冻胀力,如图6(法向应力展示湿度为25%、50%、75%时的结果)。
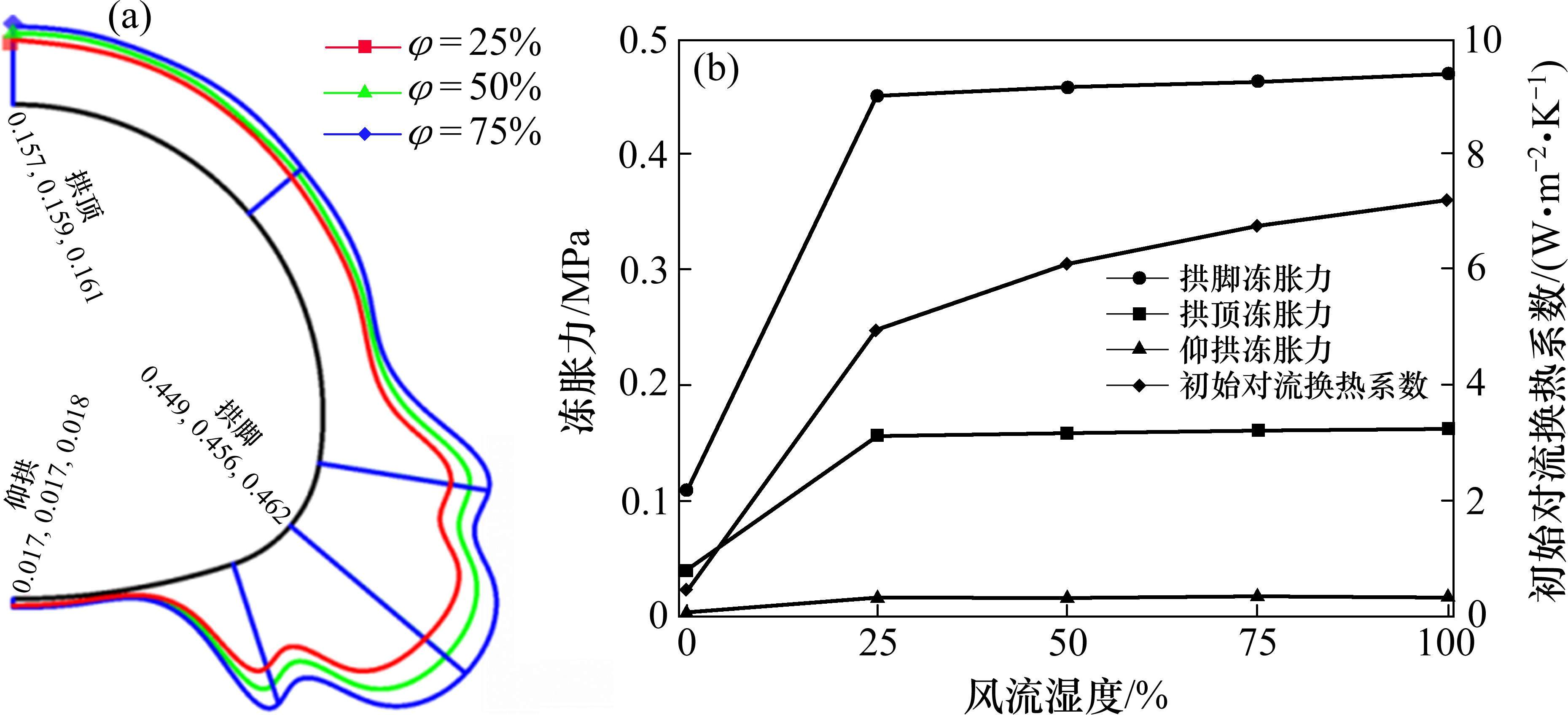
由图6(a)可知,衬砌外边界法向应力均为正值,即为冻胀力,其形状表现及形成原理同2.3节。随着风流湿度的增加,冻胀力随之增加,增加幅度:拱脚>拱顶>仰拱,从图6(b)可知,当湿度为0时,拱脚、拱顶、仰拱冻胀力分别为0.109,0.04和0.004 MPa,冻胀力较小,但当湿度为25%时,拱脚、拱顶、仰拱冻胀力分别迅速增至0.449,0.157和0.017 MPa,而后虽然平稳增加,但增加量极少,湿度为100%时,较25%时增加分别为0.019,0.006和0.001 MPa,这说明当空气含湿度很低时,即可迅速增加冻胀力,这是因为空气含湿迅速改变了其换热系数,而后增加湿度对冻胀力的增加有限。湿度0%~25%,拱脚冻胀力的变化幅度大于其他两处,这是因为此阶段对流换热系数快速增大,换热程度急剧增强,结合2.3节中各处冻胀力形成机理可知,换热程度的增强加剧了拱脚冻胀力的增长。
3.3 风流速度的影响
为研究风流速度对冻胀力的影响,假定风流持续时间、湿度、温度分别取定值60 d、50%、-10 ℃,同理可得风流速度分别为0,1,2,3和4 m/s的衬砌外边界法向应力与拱脚、拱顶、仰拱冻胀力,如图7(法向应力展示速度为1,2和3 m/s时的结果)。
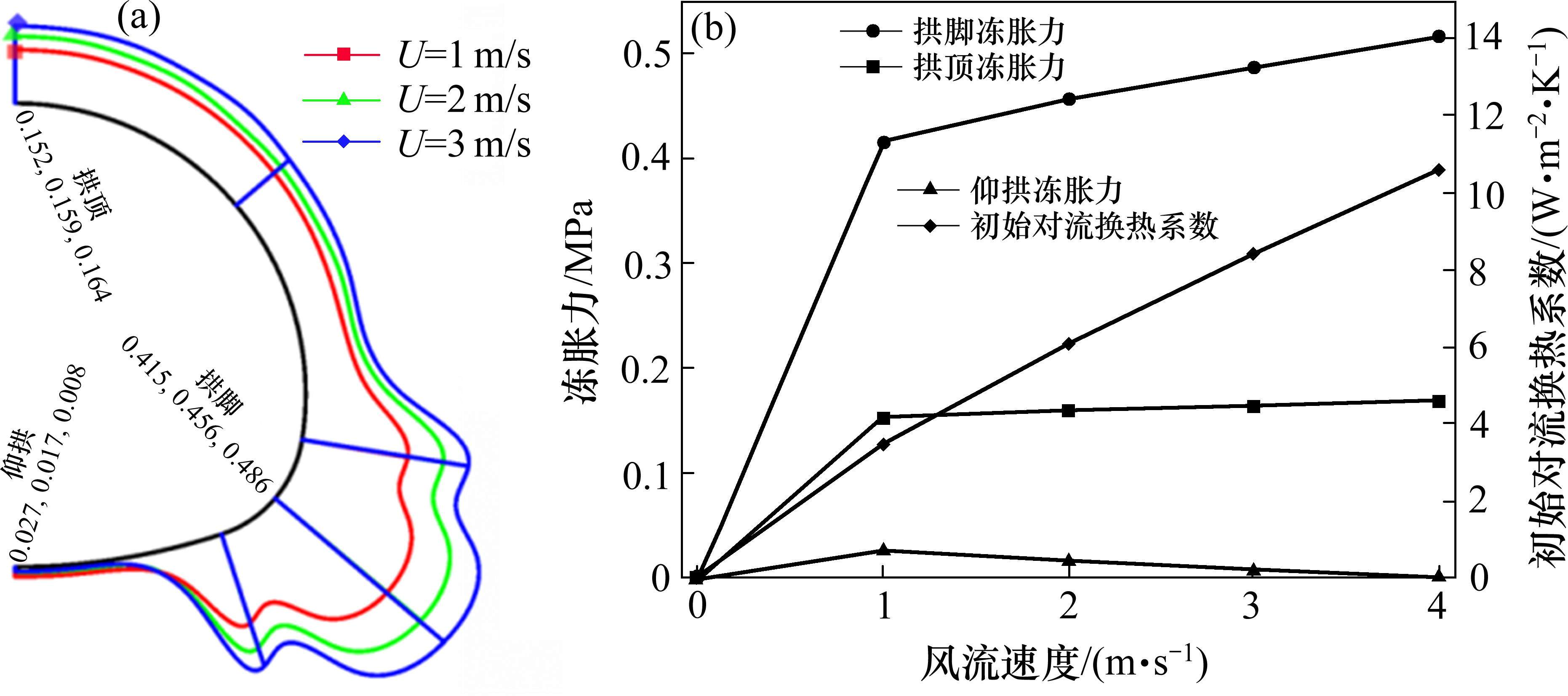
由图7(a)可知,衬砌外边界法向应力的形状表现及形成原理同2.3节,结合图7(b)可知,在风速为0时,冻胀力为0,这是因为此时对流换热系数根据式(14)计算为0.008 W/(m2∙K),60 d内,围岩根本达不到负温。当风速达到1 m/s时,拱脚、拱顶、仰拱冻胀力分别迅速增大为0.415,0.152和0.027 MPa,此阶段对流换热系数上升较快,当风速大于1 m/s时,拱脚、拱顶冻胀力增幅明显减弱,增幅稳定,拱脚增幅依旧大于拱顶增幅,而仰拱由于变形释放冻胀力,使得冻胀力逐渐减小。
3.4 风流温度的影响
为研究风流温度对冻胀力的影响,假定风流持续时间、湿度、速度分别取定值60 d、50%、2 m/s,同理可得风流温度分别为0,-5,-10,-15,和-20 ℃的衬砌外边界法向应力与拱脚、拱顶、仰拱冻胀力,如图8(法向应力展示温度为-5,-10 和-15 ℃时的结果)。
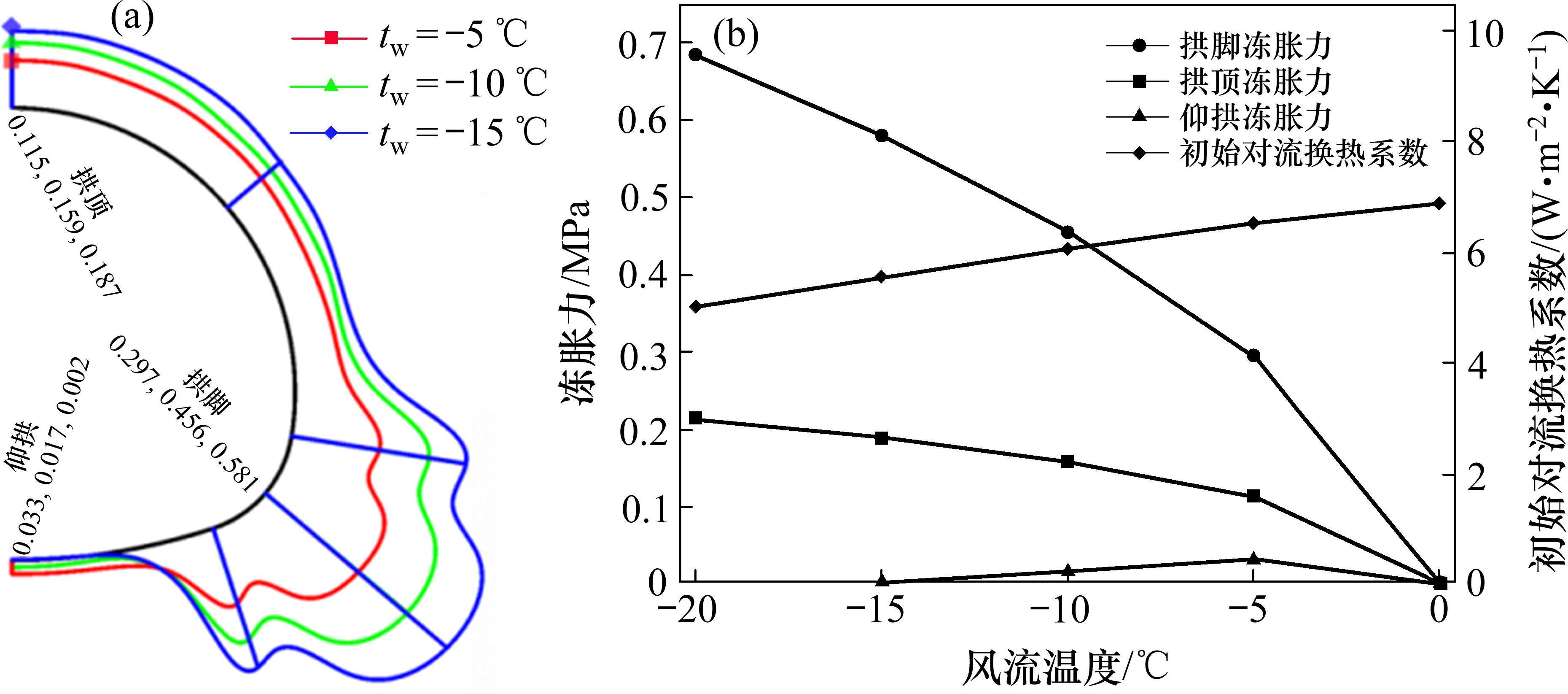
由图8可知,风流温度引起的冻胀力变化与风流速度对冻胀力的影响如出一辙,0 ℃至-5 ℃,冻胀力增幅较大,增幅程度与冻胀力大小:拱脚>拱顶>仰拱。增幅在-5 ℃时出现拐点,明显减小,而后减小温度对拱脚、拱顶冻胀力的增幅影响逐渐减弱,通过式(14)分析,得知温度越低,湿空气导热系数越小,导致换热系数随之减小,从而温度降低对冻胀力增大的作用会略有减弱。
3.5 影响因素敏感性分析
为判定风流持续时间、湿度、速度、温度对冻胀力的影响程度,根据正交试验的原理,选取各因素基础参数值分别为40 d、50%、2 m/s、-10 ℃,然后在基础参数值的基础上上下浮动50%,形成4因素3水平正交表 L9(3×4),以拱脚处的冻胀力最大值作为评价指标,得到正交表设计方案与冻胀力最大值计算结果见表2,极差计算结果见表3。
| 试验序号 | 风流湿度/% | 风流速 度/(m∙s-1) | 风流温度/℃ | 风流持续时间/d | 冻胀力最大值/MPa |
|---|---|---|---|---|---|
| 1 | 25 | 1 | -5 | 20 | 0.061 |
| 2 | 25 | 2 | -15 | 40 | 0.415 |
| 3 | 25 | 3 | -10 | 60 | 0.479 |
| 4 | 50 | 1 | -15 | 60 | 0.551 |
| 5 | 50 | 2 | -10 | 20 | 0.163 |
| 6 | 50 | 3 | -5 | 40 | 0.229 |
| 7 | 75 | 1 | -10 | 40 | 0.302 |
| 8 | 75 | 2 | -5 | 60 | 0.301 |
| 9 | 75 | 3 | -15 | 20 | 0.273 |
| 水平 | 不同影响因素下的冻胀力最大值/MPa | |||
|---|---|---|---|---|
| 风流湿度 | 风流速度 | 风流温度 | 风流持续时间 | |
| 极差 | 0.026 | 0.034 | 0.216 | 0.278 |
| 均值1 | 0.318 | 0.305 | 0.197 | 0.166 |
| 均值2 | 0.314 | 0.293 | 0.413 | 0.315 |
| 均值3 | 0.292 | 0.327 | 0.315 | 0.444 |
由表3可知,隧道冻胀力最大值正交试验结果表明,各影响因素的敏感程度依次为风流持续时间(0.278)、风流温度(0.216)、风流速度(0.034)、风流湿度(0.026)。风流持续时间>风流温度,与文献[15]以背后衬砌温度或冻结深度作为评价指标得出的结果相左,是因为在时间广度上,其增加了水分迁移的数量又影响着温度的分布,双重效应下,对冻胀力影响显著。风流速度与风流湿度对指标的敏感度相对弱一个数量级。
由此可见,风流持续时间与风流温度对隧道冻胀力的影响显著,为防止冻胀产生,应该首先着手控制隧洞内冷空气与隧道壁对流换热的时间,及其导致的水分迁移,同时改变洞内空气温度,已有隔热门、空气幕、深埋排水沟、地下换热器泵技术、电伴热等防冻措施说明了这一点。对于敏感度较低的风流速度与风流湿度控制在较低时,对于减少冻胀力同样效果明显,例如:敷设隔离式保温层,封闭隔离式保温层内空气,内设隔板阻断流通,保持内部空气干燥等。
4 结论
1) 考虑风流与衬砌的换热特性、热-水-力的相互作用与冻胀变形的正交各向异性,建立了风热水力耦合模型,将青沙山隧道冻结圈深度与冻胀力的模拟值与实测值进行对比,数值吻合良好,说明计算模型可靠。冻结圈深度表现为:仰拱>拱顶>拱脚,冻胀力分布为:拱脚>拱顶>仰拱。
2) 基于风热水力耦合模型,采用单因素变量法,得到冻胀力随风流持续时间的增加而增加,增加率在逐渐减小;当湿度为0 ℃时,拱脚冻胀力仅0.109 MPa,当达到25%时,冻胀力有较大提升,而后增加湿度对冻胀力的增大作用非常有限;当速度为0时,冻胀力为0,当达到1 m/s时,冻胀力有很大提升,而后增加速度,拱脚、拱顶冻胀力增幅明显减弱,但增幅稳定;随着温度的降低,拱脚、拱顶冻胀力虽在增加,但增加的速率在减少。增加速率均表现为:拱脚>拱顶>仰拱。
3) 运用正交试验方法,对影响冻胀力的风流4个因素进行了敏感性评价,敏感度依次为:风流持续时间>风流温度>风流速度>风流湿度,风流持续时间不仅降低着围岩的温度,还增长着围岩内的水分迁移,双重效应导致冻胀加剧,保温防冻时应予以重点关注。本文研究成果可为寒区隧道防冻措施的设置提供理论依据。
刘文俊,凌同华,谭嘉诺等.风热水力耦合作用下风流对隧道冻胀力的影响研究[J].铁道科学与工程学报,2024,21(12):5151-5162.
LIU Wenjun,LING Tonghua,TAN Jianuo,et al.Influence of airflow on the frost heaving force in tunnels under windy-thermo-hydro-mechanical coupling[J].Journal of Railway Science and Engineering,2024,21(12):5151-5162.

