人工冻结法作为一种将富水地层中液相水转变为固相,进而提升地层强度及密封性的特殊技术,其冻结媒介多为盐水或液氮,且在静水或低流速状态下发展完善[1-3]。近年来,人工冻结法已被广泛应用于国内外的隧道建设中[4],然而大量工程实践表明,随着地下工程不断扩张,临江沿海地层具有砂层交错、流速大等特点,盐水冻结往往无法使冻结帷幕快速闭合,严重影响施工进度,危及工程安全[5, 6]。相较于盐水冻结,液氮冻结与地层中多孔介质热传导效率快,克服大流速的对流换热能力强。目前,众多学者针对渗流环境下冻结工程进行了大量研究。孙立强等[7]通过研究多因素对冻结温度场的影响规律,提出一种渗流地层盐水冻结壁交圈时间计算方法。张松等[8]建立了基于冻结管温度回升速率与冻结壁厚度关系的冻结管数值模型,并提出了全域温度场求解方法。LI等[9]通过结合随机有限元法和蒙特卡罗模拟(Monte Carlo Simulation,MCS),分析得到热液性质的空间变异性对人工地层冻结法(Artificial Ground Freezing,AGF)的影响。MARWAN等[10]利用蚁群算法(Ant Colony Optimization,ACO)对热-水力耦合冻结模型进行优化,减弱了渗流作用对冻结壁交圈时间的影响。LI等[11]建立了孔隙含冰量与温度的关系方程,提出了一种热渗流耦合数值模拟方法以提高数值模拟计算精度。刘欣等[12]开展不同流速下联络通道冻结模型试验,得到各流速下冻结过程中冻结壁交圈的时间,发现上游侧墙是冻结薄弱区域。王天亮等[13]通过模型试验分析了渗流作用下冻结温度场的分布特征及影响冻结壁交圈的因素。PIMENTEL等[14]开发了一种高渗流速度条件下的AGF大型物理模型,从冷冻时间和冷却功率的角度讨论了渗流情况下AGF封闭形式的解决方案。荣传新等[15]自行研发了大型水-热耦合物理模型试验系统,预测出渗透地层人工盐水冻结的极限流速为12.73 m/d。WANG等[16]采用分段等效法得到不同渗流速度下单根冻结管的温度场,相较于盐水冻结,液氮冻结温度场影响因素更复杂。通过对现有研究成果分析后发现,渗流作用对人工冻结温度场的影响受到越来越多的学者关注。目前的成果基本实现了渗流条件下盐水人工冻结温度场的定性研究,当渗流速度超过一定临界值时,盐水人工冻结无法满足施工要求,而液氮冻结以其超低温、冻结快成为解决大流速下冻结帷幕无法闭合的新方法。但目前仅少数学者对静水条件下液氮冻结温度场进行了分析。由于大渗流地层冻结过程的复杂性及影响参数的多样性[17-20],对于渗流条件下液氮冻结温度场的发展规律至今没有得出一致的研究结论。因此,需要对渗流作用下液氮冻结温度场的发展规律和冻结帷幕形成机制进行定性分析,同时,在液氮冻结过程中,相邻冻结管之间存在的“邻管效应”是影响冻结帷幕交圈时间的重要因素,目前该效应对温度场影响规律的研究尚属空白。鉴于此,基于能量和质量守恒定律建立了水热耦合数值模型,从冻结帷幕交圈时间、冻结帷幕发展规律以及“邻管效应”对渗流作用下地铁隧道液氮冻结温度场的形成机制的影响进行系统的研究。相关研究成果为大流速下液氮地层冻结施工提供有效的指导和帮助。
1 水热耦合模型
1.1 温度场控制方程
取多孔介质单元体作为控制体单元,在渗流场和温度场双重作用下,热量消耗等于控制体积内产生的热量和外部热源造成的能量耗散之和,根据能量守恒:
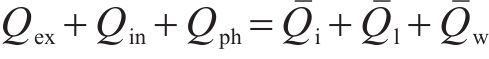
其中,Qex和Qin分别为外部热源提供的热量和控制体内部热源产生的热量;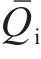
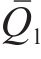
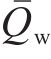
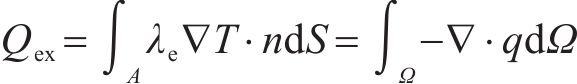
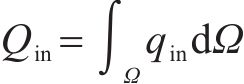
其中,qin为内热源产生的体积热;λe为冻结土体的等效导热系数;q为热流密度矢量;n为外法线方向;S和

由于水在冻结时,控制体内的水逐渐转化成冰是一个动态过程,当负温冻结作用克服了控制体表面势能,地层开始冻结,冻结点是由含水量和温度共同决定的随机值[21]。
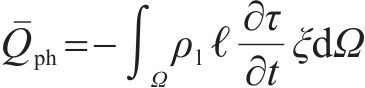
其中,ℓ为水冰相变潜热;τ和ξ分别为冻结砂层的未冻含水量和孔隙度。考虑水的对流换热效应以及单位时间内改变水、冰及固体颗粒状态所需的热量,结合式(1)~(4)得到多孔介质在冻结过程的导热微分方程:
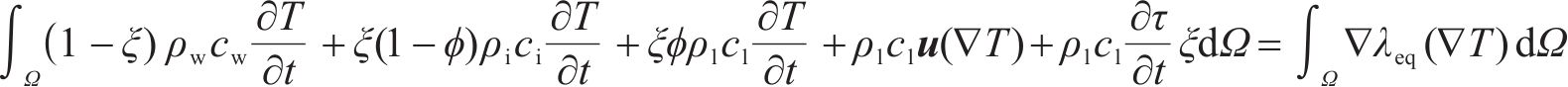
其中,ϕ为冻土中未冻水的体积含量;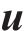
液氮冻结中水冰相变是一个动态平衡且变化迅速的过程,需对结冰温度相变区间进行平滑处理[22]。因此引入sigmoid生长曲线函数并对其优化以满足液氮超低温冻结的需求。假定控制体内的未冻水含量是温度T的函数:
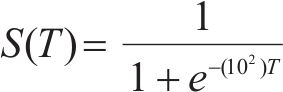
假定未冻水体积含量为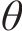
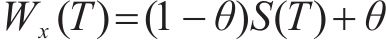
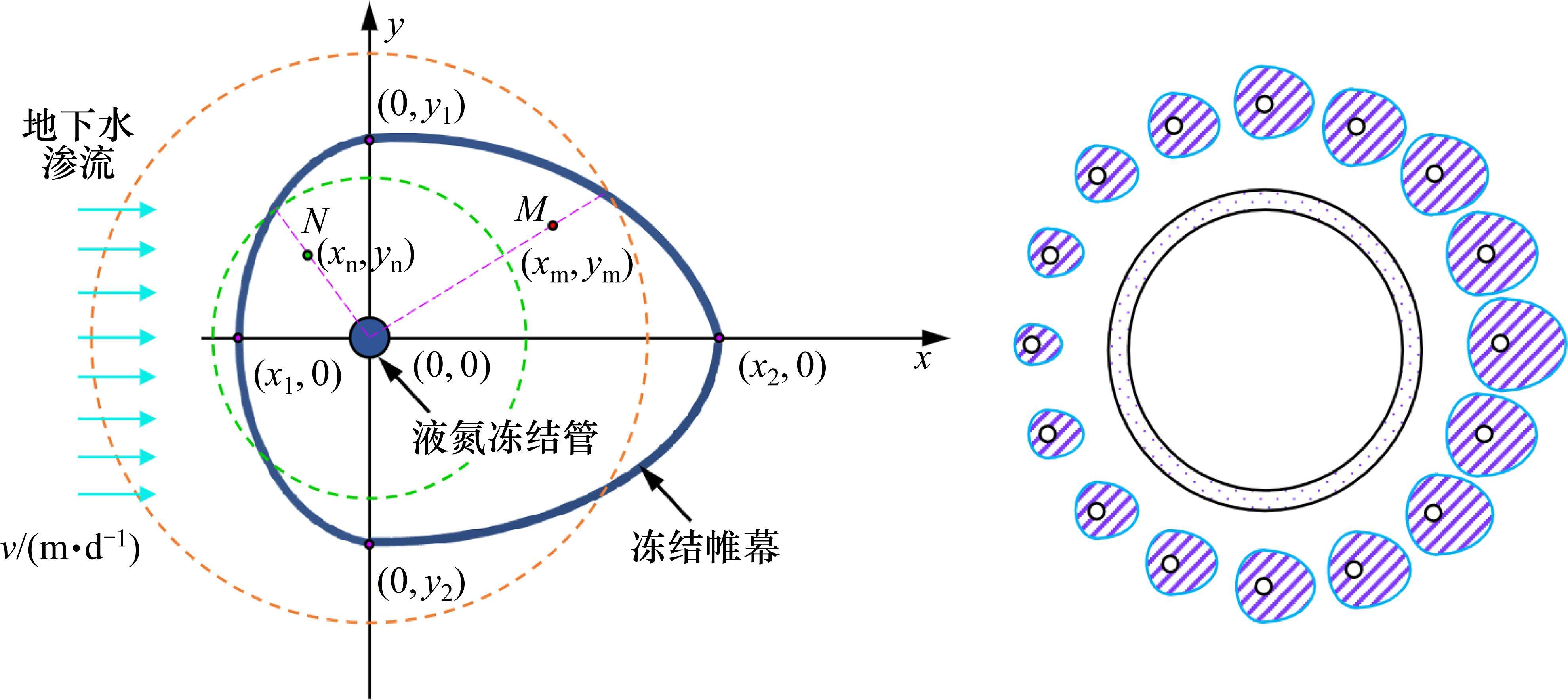
如图1所示,控制体
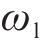
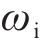
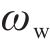
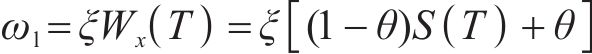
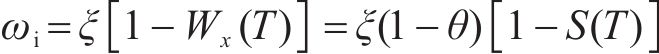
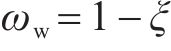
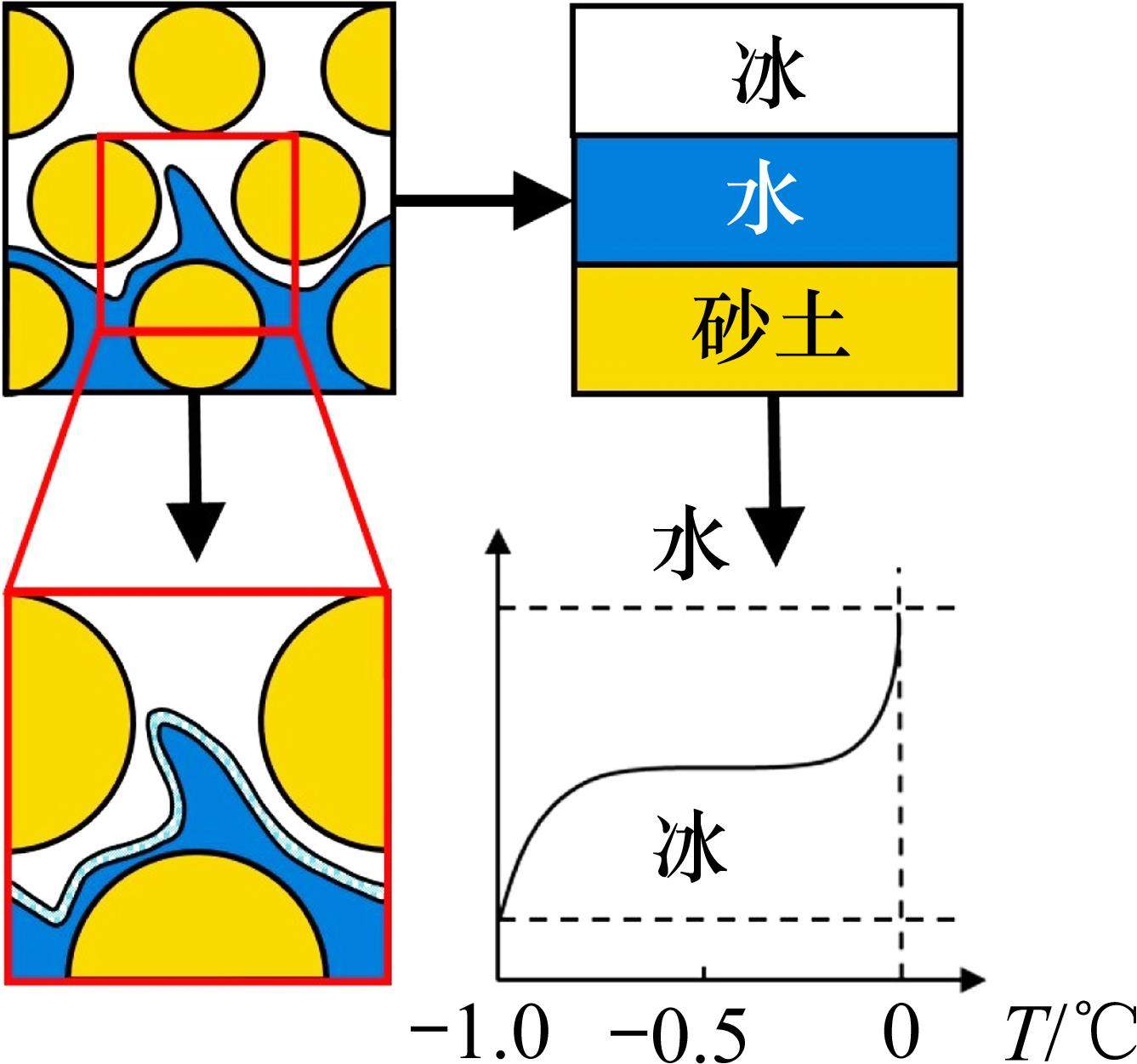
等效热容Ceq代表单位体积介质温度改变1 ℃所需要的热量,可表示为:
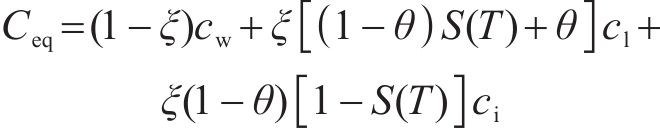
1.2 渗流场控制方程
根据质量守恒定律,假设无外部水源影响,控制体中水/冰质量的变化:
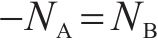
根据散度定理,对任意控制体
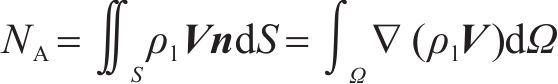
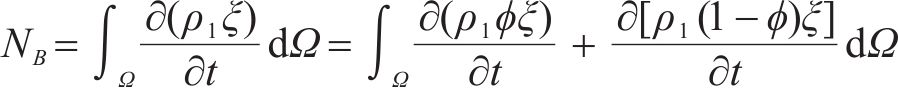
将式(13)、式(14)代入式(12),根据质量守恒定律可得:
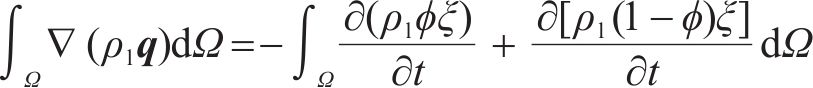
假设渗流场满足达西定律,则在多孔介质中未冻结区域水的渗透速率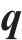
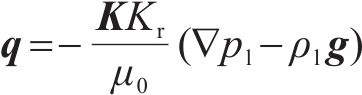
其中,K为固有渗透率矩阵;Kr为与饱和度相关的相对渗透;g为重力加速度矢量;pl为水压力;μ0为凝固点参考黏度[23]。
在多孔介质冻结过程中,冰减缓了液态水流动效应,未冻水饱和度Wx(T)等于达西定律中的水饱和度,因此相对渗透率Kr可表示为[24]:
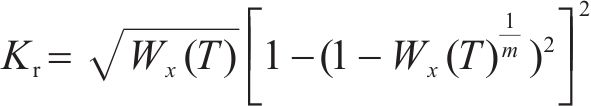
通过相对渗透率表征冻结过程中渗流速度变化机理的方法称为表观热容法。Comsol Multiphysics软件进行水热耦合计算时,表观热容法可更好地反映整个冻结过程的发展规律[25]。将式(16)代入式(15)中,得到渗流场连续方程为:
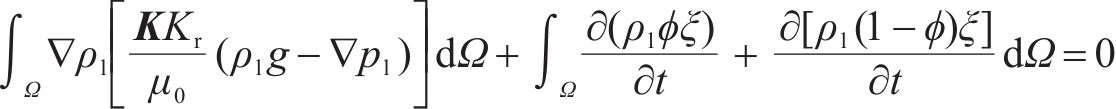
多孔介质在渗流场的作用下,水流通过对流传热改变了整个冻结区的热分布,导致冻结区域温降速率降低,由于水热耦合效应,当冻土柱间的传热为流体传热和固体传热叠加态时,温度场呈不均匀性,导致冻结帷幕呈“类心形”[26],如图2所示。
1.3 数值耦合计算
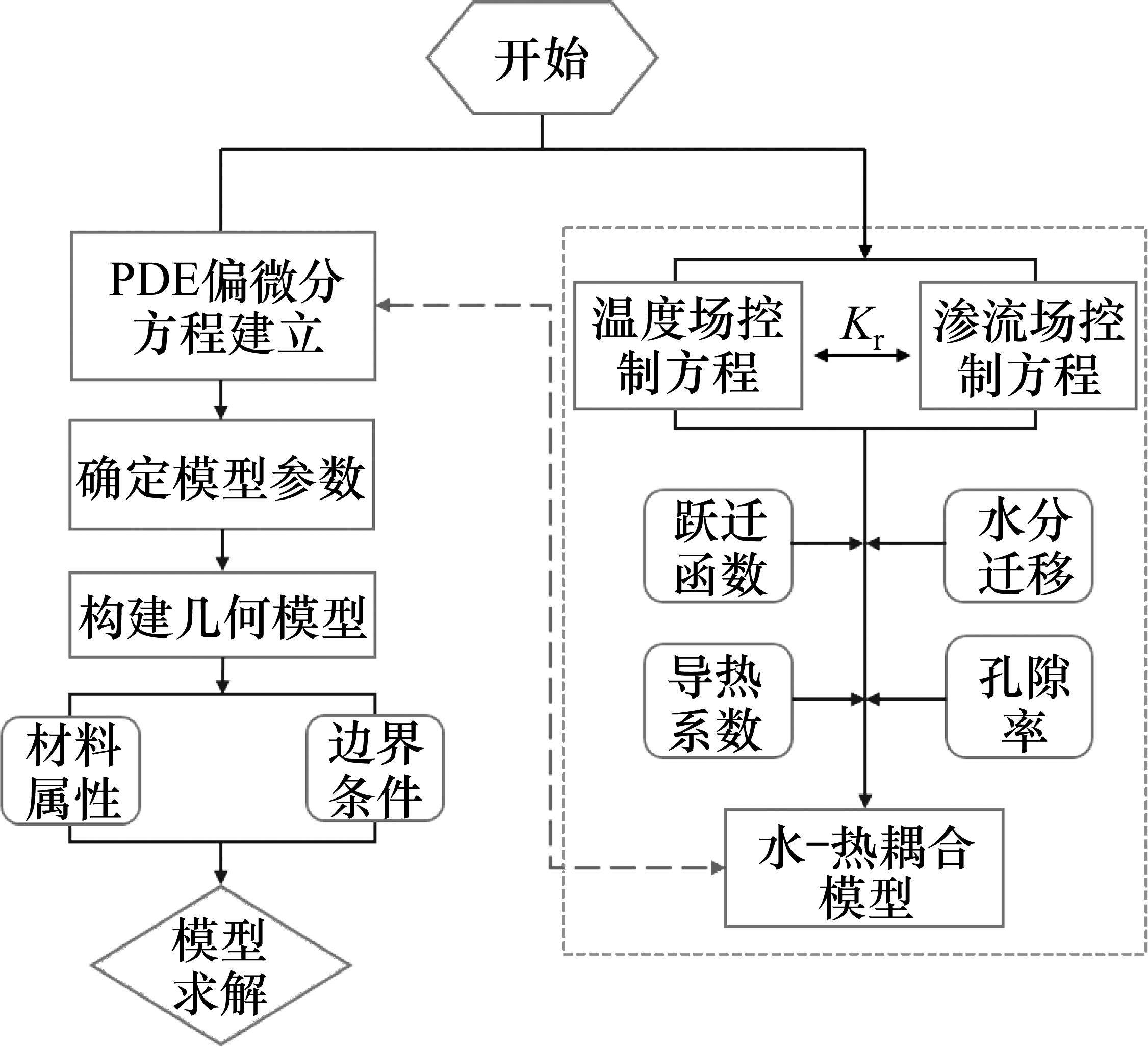
基于COMSOL数值软件,利用中间变量相对渗透率Kr建立了水热耦合数值计算模型,计算流程如图3所示。由于相对渗透率在冻结过程中随冻土含量的变化而变化,当冻土的温度降至冰点时,地层的相对孔隙率接近0,导致渗流速度也几乎为0,将直接影响渗流效应,因此Kr作为一个中间变量将渗流场与温度场耦合。
2 渗流冻结数值模型
2.1 工程概况
以某地铁隧道液氮地层冻结工程为背景,隧道净直径为7 m,开挖断面为圆形,隧道埋深约20 m,位于中粗砂层中,含承压水,含水丰富,渗透系数大,渗流速度达12.76 m/d。根据设计要求,隧道开挖需满足冻结帷幕平均厚度>1.5 m,平均温度<-20 ℃。因地下水渗流速度过大,为保障施工安全,缩短工期,采用液氮水平冻结法对地层加固,沿隧道周围等间距布置一圈Ф89×10 mm冻结管,供液管长18 m,规格为Ф32×3 mm,控制其偏斜率≤1%,确保冻土体能够提供足够的结构支撑和地层稳定性。同时布置8个测温孔C1~C8,其中C1~C6每孔设9个测点,1~9测点分别距开挖面3、5、7、9、11、13、14、15和17 m;C7~C8每孔设6个测点,1~6测点分别距开挖面6、10、12、14、16和18 m。如图4所示。
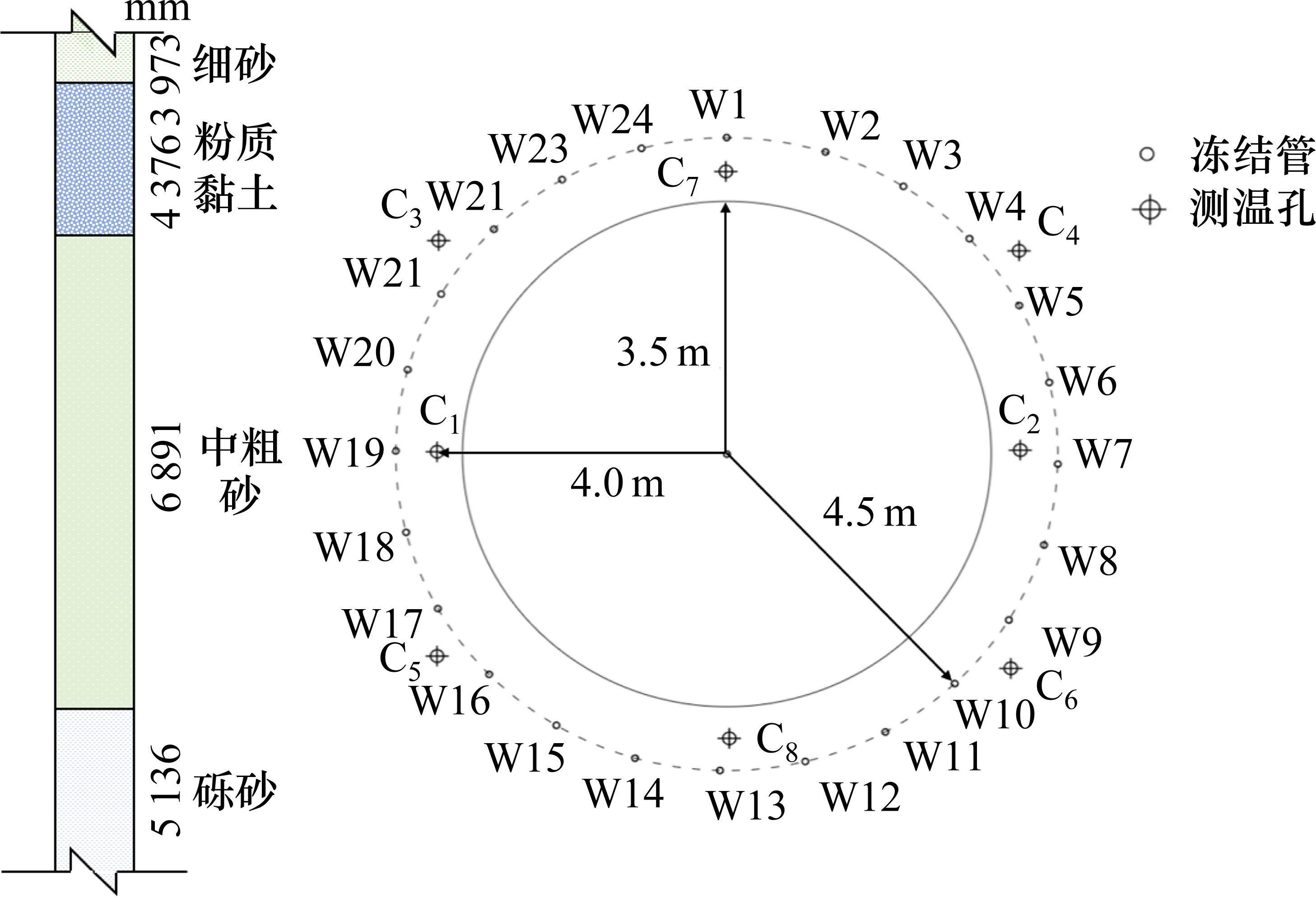
通过对现场土层实地取样,结合室内试验得到多孔介质的热物理参数,如表1所示。其中中粗砂的冰点为-0.48 ℃,受渗流作用影响,冻结帷幕交圈时相邻冻结锋面之间的砂层温度应低于冰点温度,因此将-1 ℃作为温度场中冻结帷幕交圈的温度条件。
| 土层 | 密度/(kg∙m-3) | 孔隙比 | 导热系数/(W∙m-1∙K-1) | 比热容/(kJ∙kg-1∙℃-1) | 冻结温度/℃ | 渗透系数/(m∙d-1) |
|---|---|---|---|---|---|---|
| 细砂 | 1 940 | 0.75 | 1.37 | 1.13 | -0.48 | 15.7 |
| 粉质黏土 | 1 920 | 0.82 | 1.28 | 1.16 | -0.40 | 3.31×10-5 |
| 中粗砂 | 1 990 | 0.71 | 1.46 | 1.35 | -0.48 | 19.6 |
| 砾砂 | 2 030 | 0.68 | 1.72 | 1.01 | -0.50 | 22.7 |
2.2 数值模型
人工冻结法在渗流作用下是一个复杂的水热耦合问题,故作出如下假设:
1) 砂层是各向同性、连续且均匀的饱和多孔介质,在冻结状态下具有独立的热参数;
2) 由于液氮比热容低,反应迅速,导致冻结管壁温度分布不均,因此假设冻结管壁温度为定值;
3) 由于研究过程不涉及冻胀融沉,且砂层中渗流作用符合达西定律,故选取测温点共有断面14 m处作为模型简化后的二维模型,同一断面的测点温度有利于对液氮冻结温度场发展规律的分析;
4) 在热力学计算中,土层骨架孔隙是一个无关参数,流体黏度系数不受环境温度和压力影响,应忽略由传热过程和溶质迁移引起的温度梯度和密度梯度对土壤中未冻水迁移的影响。
考虑到冻结温度影响范围,模型四周设置为纽曼边界,限制模型与外部条件的热量交换,在模型边界给定与地层初始温度20 ℃相同的温度荷载,表示为无穷域的温度条件。模型X方向取[-25 m, 25 m],Y方向取[-25 m, 25 m],在模型两侧设置压力水头边界条件,通过水头差参数方程实现水流由左向右渗流。以-100 ℃恒温狄氏边界条件施加于冻结管边界,作为超低温冷源输出项,设定液氮冻结管的间隔为1.0 m,冻结管直径89 mm,同时以域点探针作为测温孔C1~C8。在渗流冻结薄弱处设立路径1和路径2,以研究液氮冻结温度场的发展规律,其中路径2位于相邻冻结管界面处,属于渗流冻结帷幕交圈的薄弱区,且上游处相邻冻结管间距垂直于水流方向,直接受到高流速水流的冲刷效应,故以此路径下的温度变化作为冻结温度场的重点研究目标。该模型采用自由三角形网格划分绝热边界,并对其进行了精细化处理以适应液氮超低温的温度场,同时将冻结管周围的富水砂层建立为边界层网格,以适应液氮冻结管的热扩散效应,模型包含29 864个域单元和476个边界单元,如图5所示。
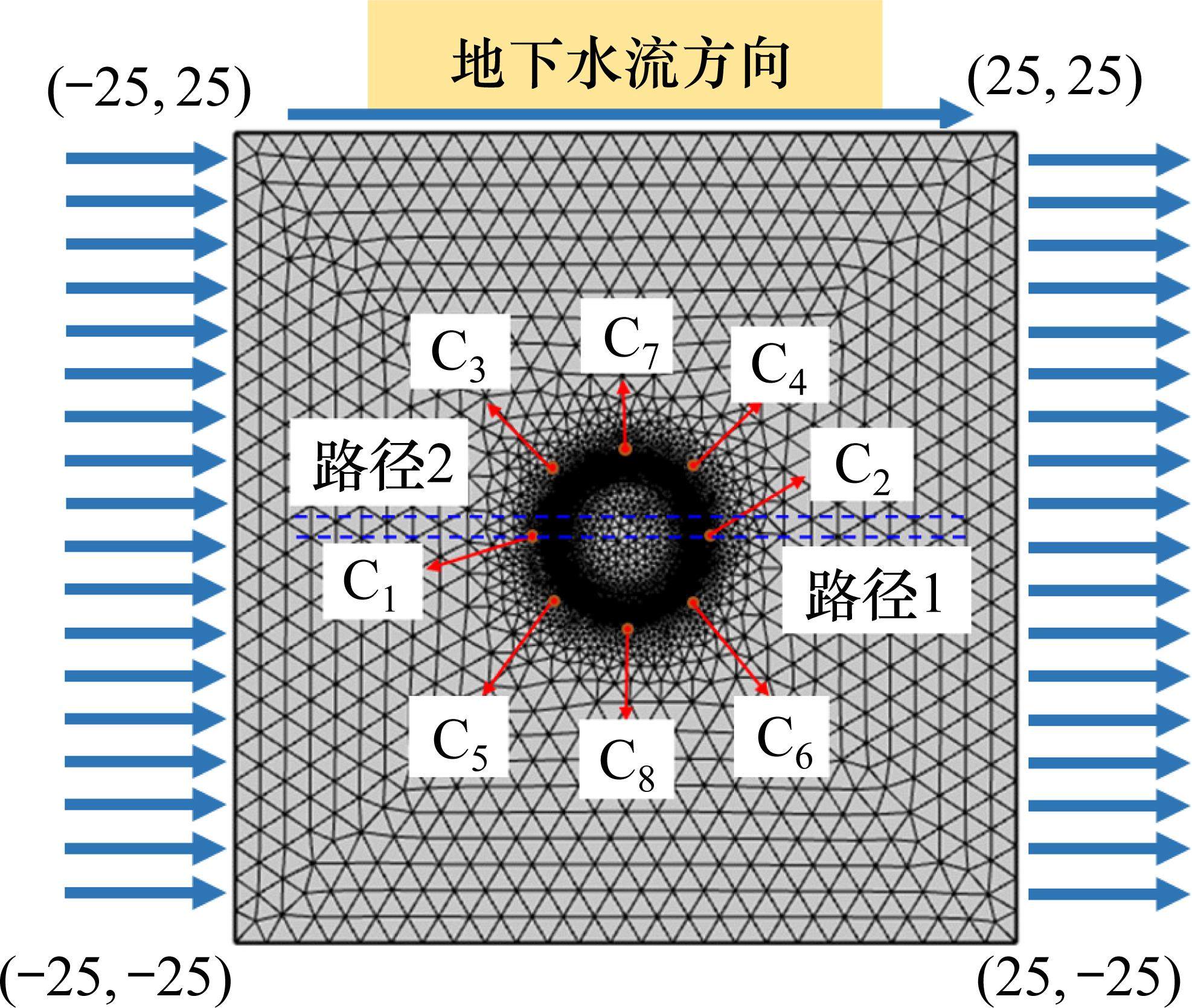
2.3 数值模拟与现场实测对比分析
该隧道实际冻结过程中,积极冻结期为20 d,液氮供液管的温度为-100 ℃。冻结13 d时,通过测温孔C1~C8测得土层平均温度为-21.6 ℃,冻结帷幕平均厚度达1.67m,满足隧道开挖设计要求。积极冻结期内,路径2的温度历时曲线如图6所示。由图6可知,路径2的上游测点的温降速率低于下游,且上游各测点的温度历时曲线的波峰对称性明显低于下游,冻结薄弱处出现在上游处,温度最低点出现在下游冻结管附近,最低温度为-53.5 ℃。说明在液氮人工冻结施工过程中,渗流作用主要影响上游外侧的温度,温度的差异性将直接影响上下游冻结帷幕的发展情况。
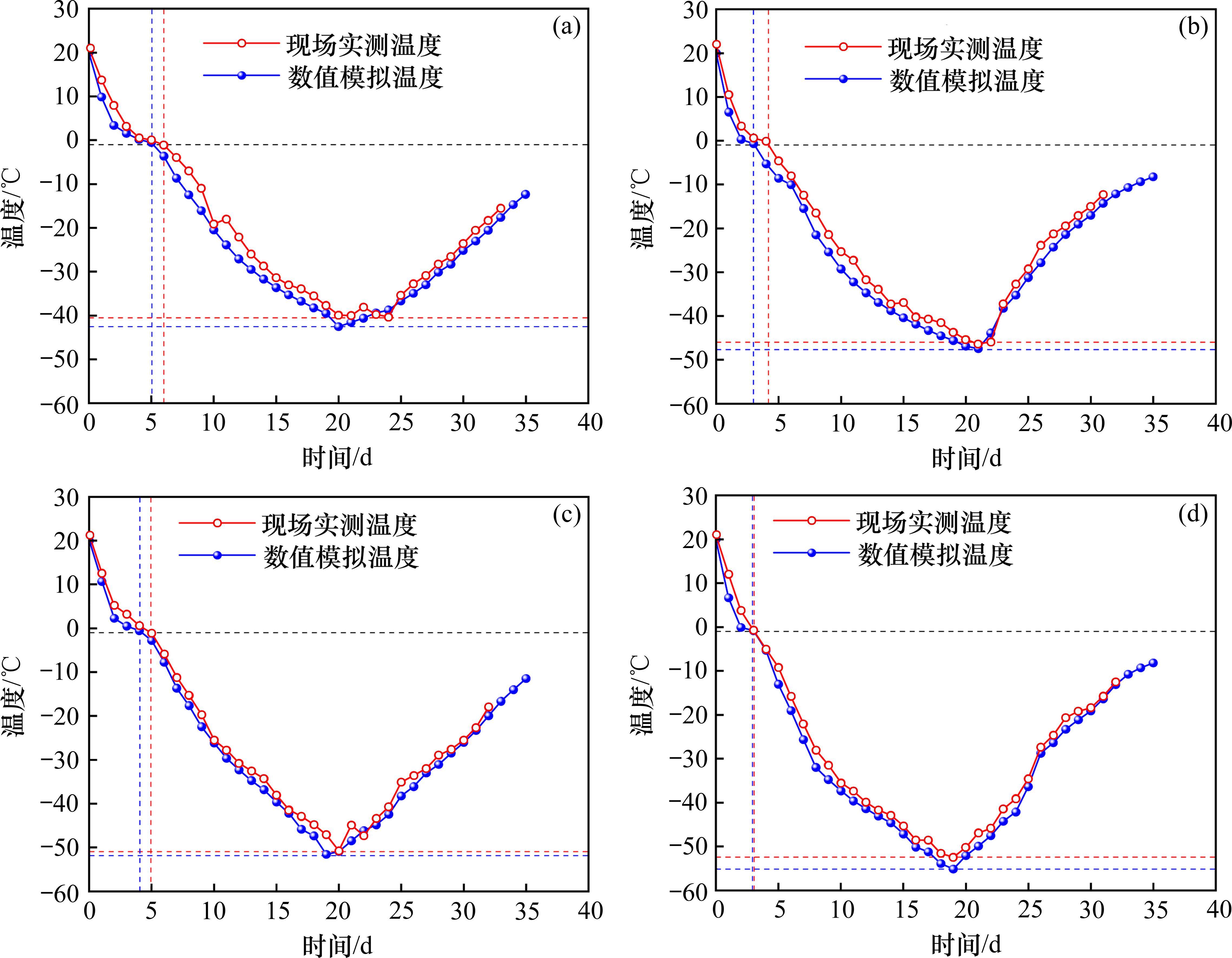
对测温孔C1~C4的现场实测温度与数值模拟温度进行分析,如图7所示。各测温孔的温降趋势基本相同,但上游处的测温孔C1与C3的最低温度要比下游处C2与C4低大约5 ℃,且结冰时间也略晚1~2 d。由于测温孔C3与C4受冷量迁移的影响,整体温度低于测温孔C1与C2。在整个冻结期内,现场实测数据略高于数值模拟结果,这是由于现场施工环境复杂,消耗液氮冷量的因素多。从整体上看,两者数据变化规律一致,最大平均误差为7.28 %,验证了本文提出的数值模型具有良好的可靠性和实用性。
3 渗流作用下液氮冻结温度场演化规律
3.1 不同渗流速度对液氮冻结帷幕交圈时间的影响
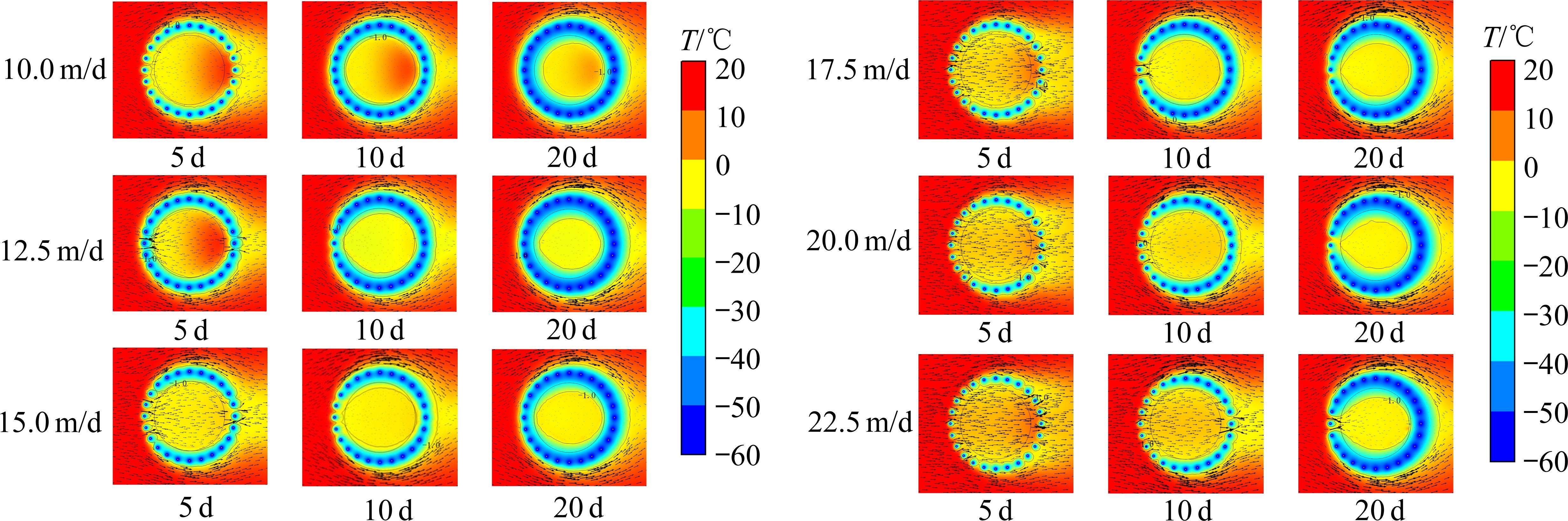
为研究渗流速度与液氮冻结温度场的关系,对不同渗流速度下冻结帷幕发展情况以及温度场变化情况进行统计,如图8所示。通过数值计算得到渗流速度为10、12.5、15、17.5和20 m/d的冻结帷幕交圈时间分别为5.76、6.85、8.31、11.43和18.57 d,极值相差69.0%,当渗流速度大于22.5 m/d时,冻结20 d后冻结帷幕仍无法交圈。由于渗流对上游冻结帷幕产生了“侵蚀”作用,造成上游处的冷量无法凝集,随着渗流速度的不断增加,冷量迁移的速率越来越大,同时促进下游冷势能的叠加。当10 m/d≤v≤15 m/d时,液氮提供的冷量对渗流作用的限制效果较为明显,上下游冻结帷幕发展较为均衡,形状差异并不明显。当v>15 m/d,渗流作用加剧,上游冻结薄弱处的冻结帷幕交圈愈加困难。同时,大部分冷量随水流迁移至下游,使上游冻结帷幕厚度明显小于下游,从而形成了上游薄、下游厚的“类心形”冻结帷幕。当v=22.5 m/d时,渗流作用突破了液氮冻结效果的限制,冻结20 d后上游中心处冻结锋面呈水滴状,且无法与两侧冻土柱形成连接体,导致水流对隧道中心的土层不断冲刷,下游外侧冻结帷幕锋面持续扩展。值得注意的是,随着渗流速度的增加,冻结帷幕的交圈时间不断增加,与此同时已经形成一定冻结帷幕区域的内侧冻结帷幕扩展速度显著大于外侧,印证了冷量叠加效应在冻结帷幕局部区域形成后便可以加速隧道内部土体的降温速率。
通过对数值计算数据进行分析,发现渗流作用下冻结帷幕的交圈时间与渗流速度之间存在近似指数函数关系。采用成长型指数函数ExpGrow对数值结果拟合,拟合结果如图9所示。基于拟合结果,提出渗流作用下冻结帷幕交圈时间的预测公式:
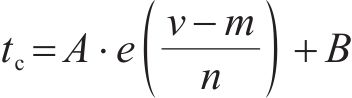
式中:v为渗流速度;A、B、m和n为拟合参数,在本试验中,其数值分别为0.077、3.998、4.981和2.811。
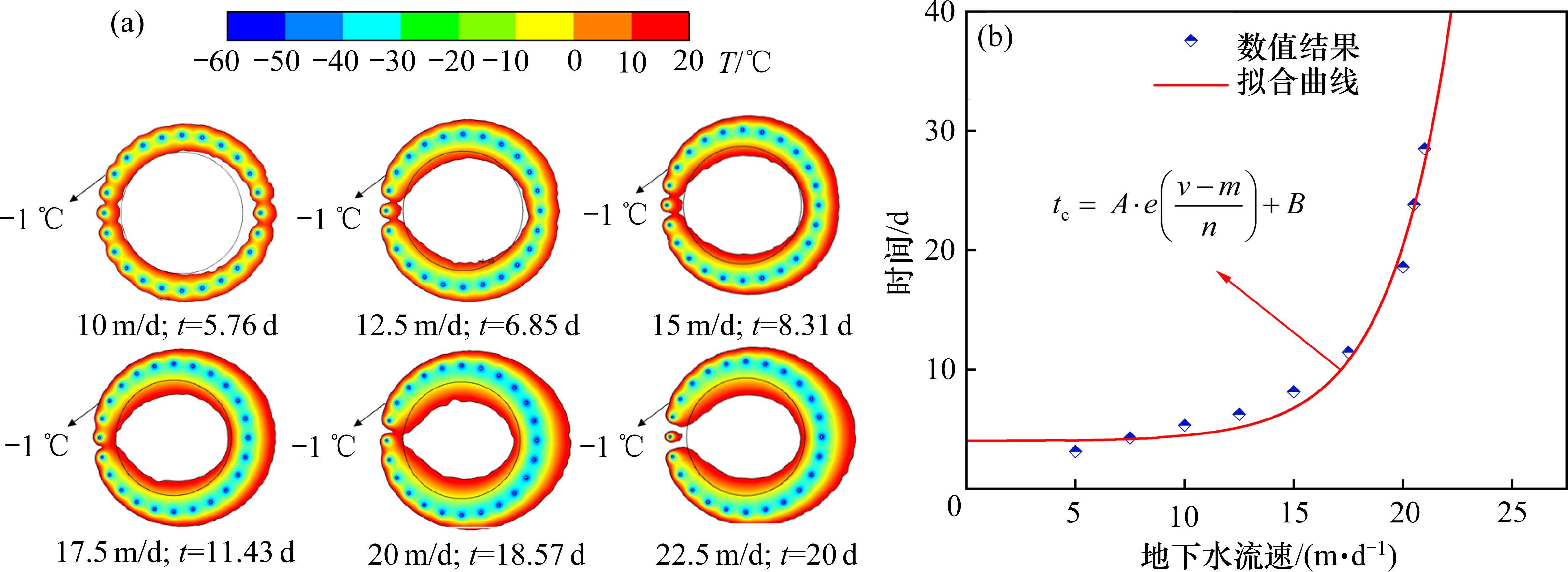
在实际冻结工程中,考虑渗流作用会延长工期在不必要的冻结帷幕扩展上,从而造成施工安全隐患或影响施工进度,若冻结40 d后冻结帷幕仍无法交圈,则认为冻结壁无法交圈,与之对应的渗流速度被定义为极限流速。依据公式(19)可计算出类似渗流冻结工程中冻结帷幕交圈的极限流速为22.26 m/d。
3.2 “邻管效应”对液氮冻结温度场的影响
渗流条件下相邻冻结管之间的“邻管效应”会影响液氮冻结温度场的发展,其中冻结薄弱处的发展过程如图10所示。定义图中液氮冻结管所在轴线两侧的半径分别为Rs和Rx,冻结管间距为d,冻结管圆心的方位角为β,冻结帷幕“窗口”的间距为L,Lj为相邻冻结锋受到邻管效应时的间距临界值。通过几何关系推算:
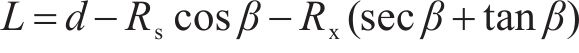
式中:d=1.0 m;β=15°。在液氮冻结温度场发展过程中,当L=0时,代表冻结帷幕交圈。
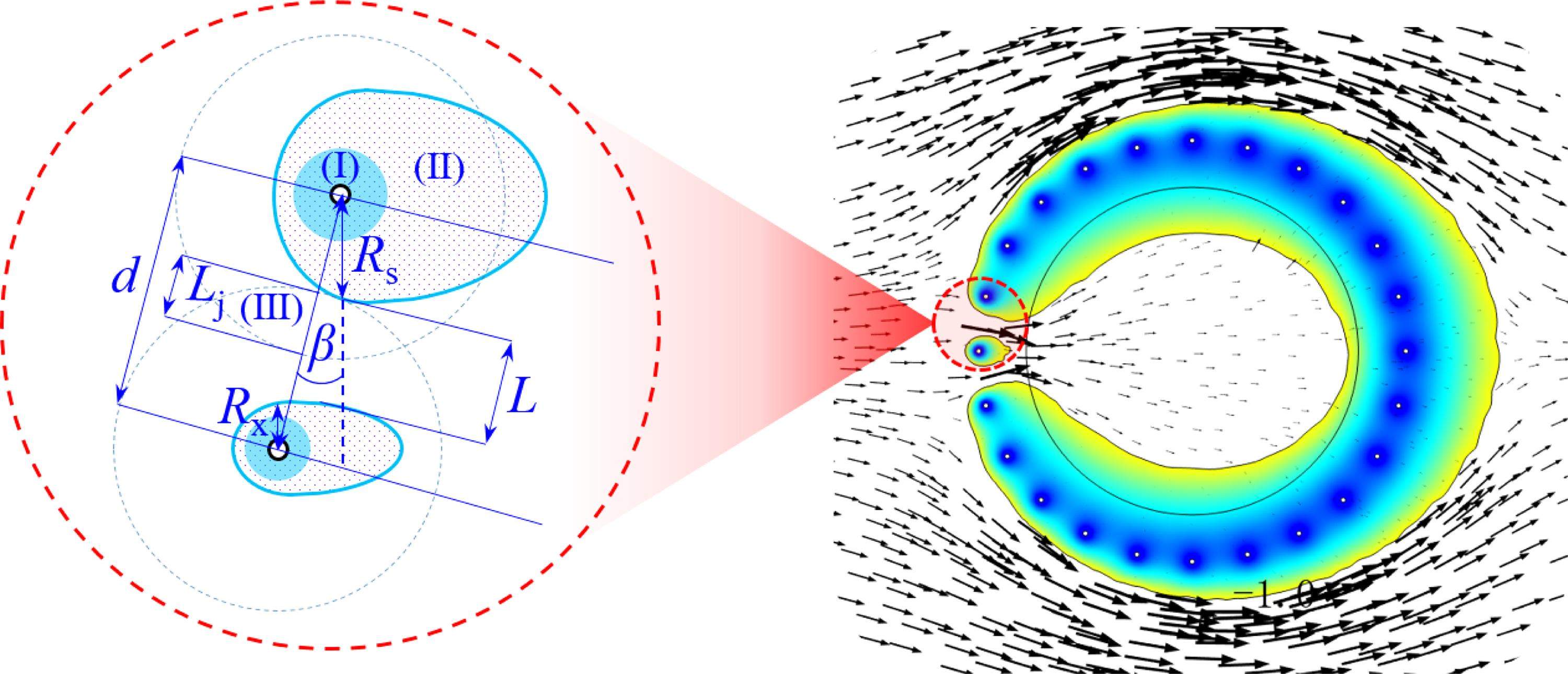
通过对不同渗流速度条件下公式(20)中的变量参数Rs、Rx和L进行分析,得到各变量参数的时间变化曲线,如图11所示。当10.0 m/d≤v≤12.5 m/d时,各组L在前3 d的变化规律差异很小,且L由1 000 mm缩小到0的过程中变化趋势基本保持不变,因此可认为低流速下液氮冻结过程始终受到邻管效应影响。当15.0 m/d≤v≤20.0 m/d时,L随冻结时间变化规律呈阶梯型,冻结2 d后,渗流速度为15.0、17.5和20.0 m/d对应的L分别快速减少为559、578和600 mm,随后L的变化规律出现一段缓慢发展阶段,当L分别减少至389、355和254 mm时,液氮冻结温度场进入二次加速冻结阶段,直至冻结帷幕交圈,因此渗流速度为15.0、17.5和20.0 m/d对应的Lj分别为389、355和254 mm。同样的,Rs随时间的变化规律近似阶梯型,但阶段性并不明显。不同渗流速度的变化曲线拐点发生时间点与参数L变化规律发生转变的时间点基本一致,且Rs的扩展速率始终大于Rx。
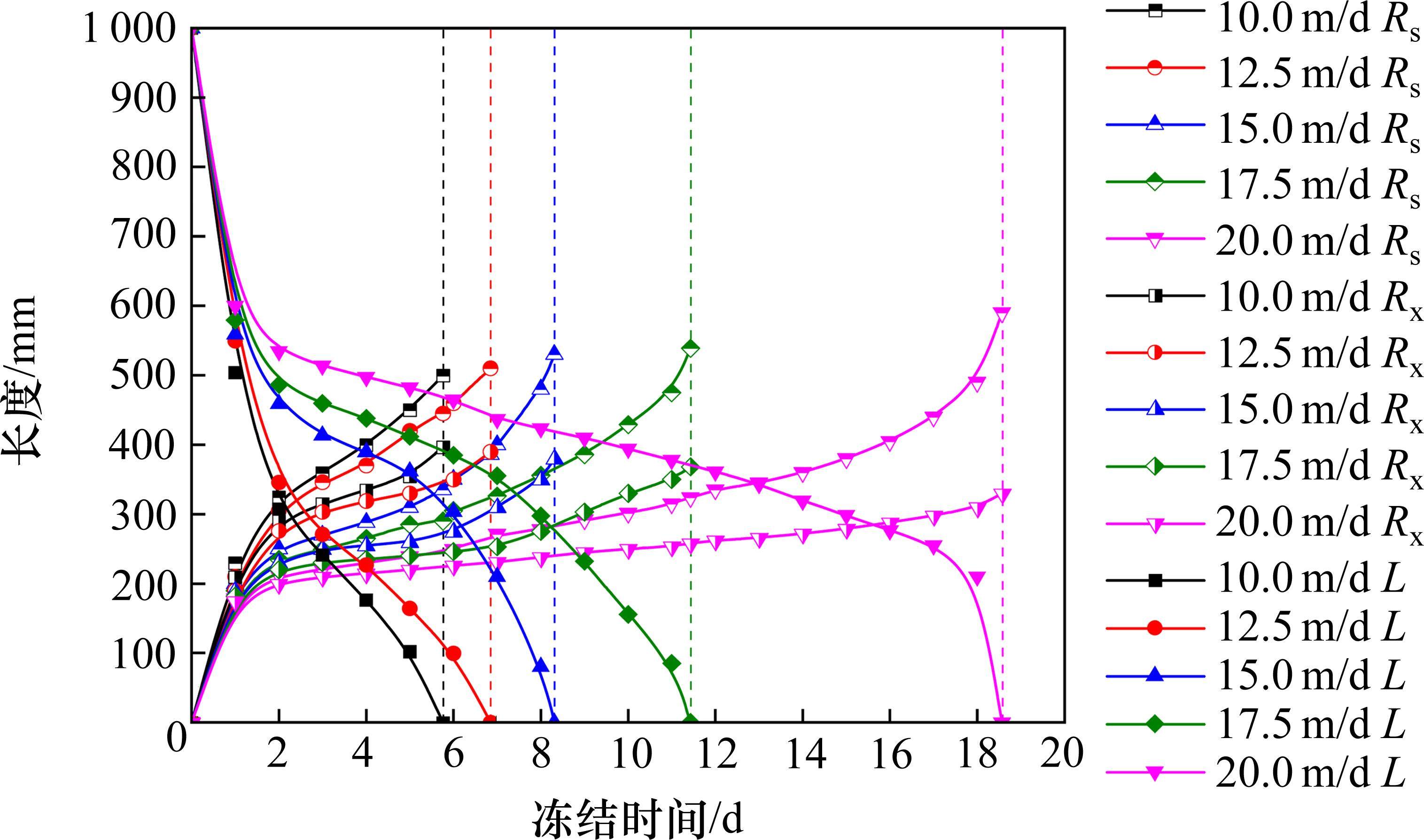
基于模拟结果,可总结出渗流作用下液氮冻结帷幕的发展机制:冻结初期,冻结管附近(区域Ⅰ)多孔介质的热传导迅速发生,水流对流传热效应对冻结锋面的发展影响很小,冻结锋面近似圆形。随着冻结时间增长,冻结区域进一步扩展(区域Ⅱ),由于冻结锋面的推进,多孔介质的热传导效应无法迅速传递至远端,不同位置冻结管的冻结帷幕发展不同,且各冻结管不同位置受水流传热效应的影响程度也不同,渗流速度越大,(Rd/Ru)的值越大,Rs与Rx的差距越明显。当冻结锋面间距达到Lj时,邻管效应促使未冻结区(区域Ⅲ)温度降低,加速冻结帷幕闭合。当冻结帷幕交圈后,隧道内部地层不再受渗流作用影响开始迅速扩展,外侧冻结锋面仍持续受到渗流作用的侵蚀,因此渗流速度越大,冻结帷幕交圈后(Rd/Ru)仍持续增大。
3.3 渗流作用下液氮冻结温度场的分布规律
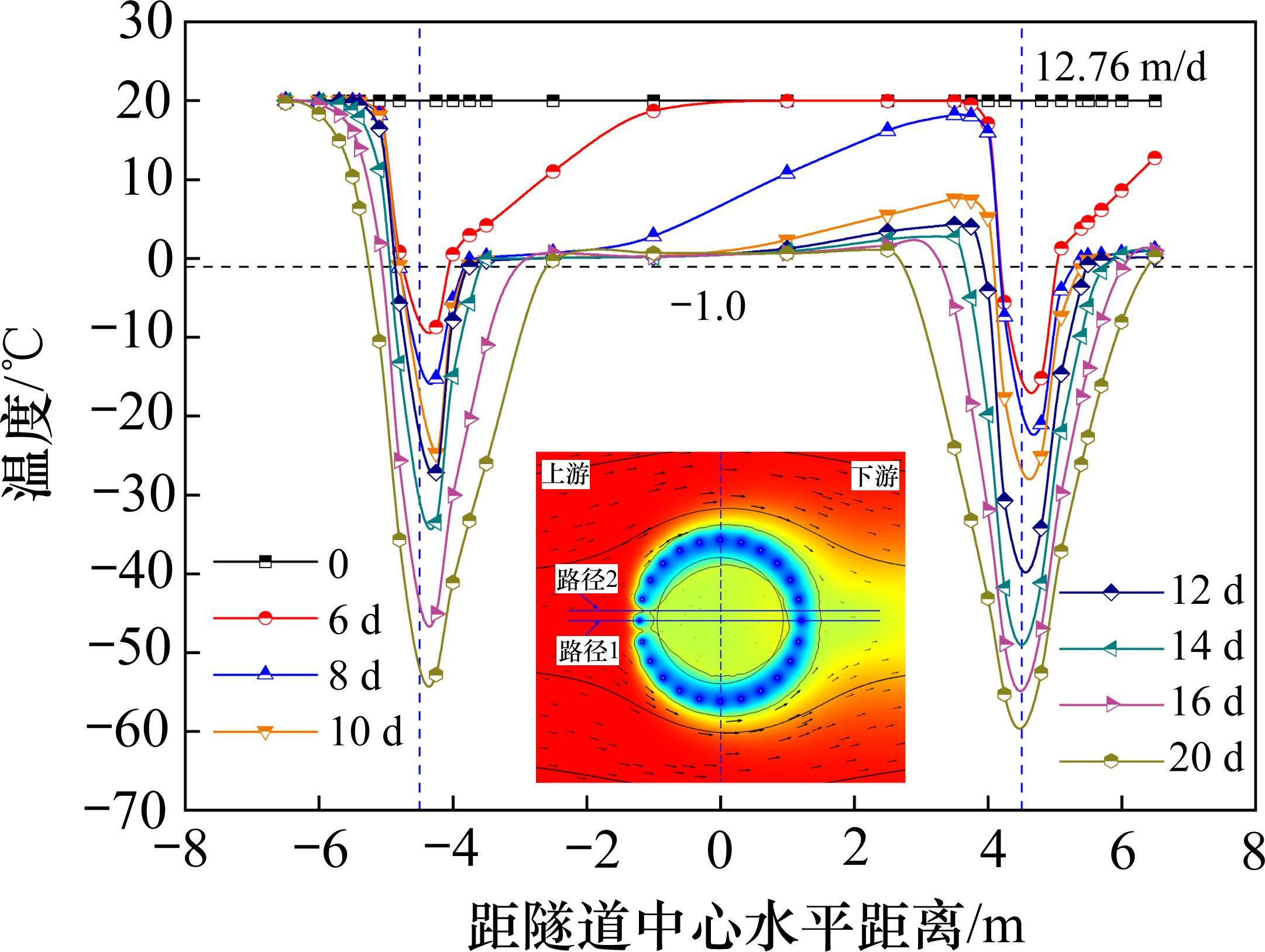
由图12可知,当多孔介质砂层中渗流速度增加时,位于上游的测点温度明显高于以隧道中心轴对称的下游测点温度,并且随着渗流速度的增加,测点的温差逐渐增大。10 m/d≤v≤12.5 m/d时,冻结20 d时上下游测点的最低温度大致相等,当v=15 m/d时,上游测点的最低温度为-52.3 ℃,下游测点的最低温度约为-58.5 ℃,温差为6.2 ℃,当v=17.5 m/d、20 m/d时,上下游测点的最低温度的温差分别为16 ℃和23 ℃。同时,随着渗流速度的增大,隧道内部地层的温降速率逐渐增大。说明在较高的渗流速度影响下,冻结区的热传导途径受到水流对流传热的影响而发生变化,流速越大,对流传热效率越高,进而导致下游区域的平均冻结温度更低。随着渗流速度的不断增加,上下游测点的最低温度的温差逐渐加大,当v=22.5 m/d时,渗流作用使上游测点的温度始终无法降到冰点温度,但下游测点温度变化并不明显。此外,随着渗流速度的逐渐增加,冻结初期隧道内部地层的温降速率随之增加,隧道内部各测温点温度基本保持在冰点温度以上恒定不变。说明流体流动带来的对流传热提高了固体表面的热量传递效率,流速越快,热量传递效率越快,且下游冻结帷幕交圈后各测点的温度变化规律相同,但受大流速的影响,热量传递效率过快会导致上游区域的冷量无法汇集,导致冻结帷幕“窗口”无法关闭,影响冻结施工的效率与质量。
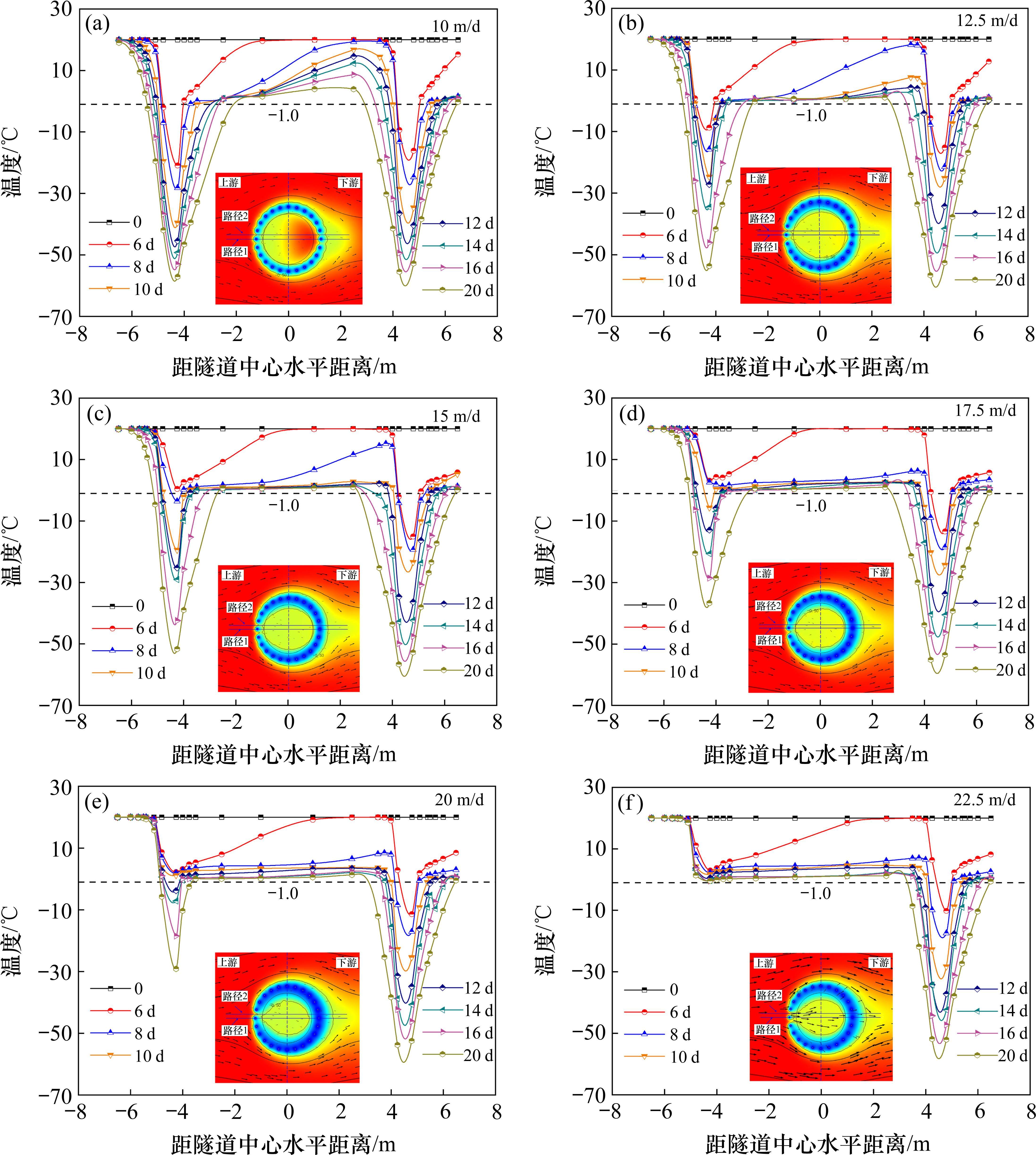
3.4 渗流作用下液氮冻结帷幕变化规律
冻结帷幕厚度是评价冻土强度和稳定性的重要指标[27],利用拉格朗日-高斯积分法对渗流速度为10~20 m/d冻结帷幕的厚度进行计算。将不同渗流速度的下游冻结帷幕拓展的厚度Rd与上游冻结帷幕扩展的厚度Ru进行对比,如图13所示。渗流速度为10、12.5、15、17.5和20 m/d的上游冻结帷幕厚度达到1.5 m时,(Rd/Ru)分别为1.15、1.32、1.42、1.71和2.09;冻结20 d后,(Rd/Ru)分别为1.23、1.35、1.53、1.76和2.12,各组(Rd/Ru)随着冻结时间的增长继续增长。表明冻结帷幕交圈前,受渗流作用影响,冻结帷幕的不均匀性随流速增大而增加,当上游冻结帷幕交圈后,冻结帷幕内侧冻结区域不再受到渗流作用影响,冷量叠加效应加速隧道内部冻结帷幕的扩展速率,使上游冻结帷幕厚度逐渐增加。而由于冻结帷幕外侧的冻结锋面持续受到渗流作用的影响,上游的冷量持续迁移至下游,水流速越大,迁移效果越好,导致下游冻结帷幕外侧冻结锋面不断扩展,同时上游冻结帷幕受“侵蚀”的影响也就越大。
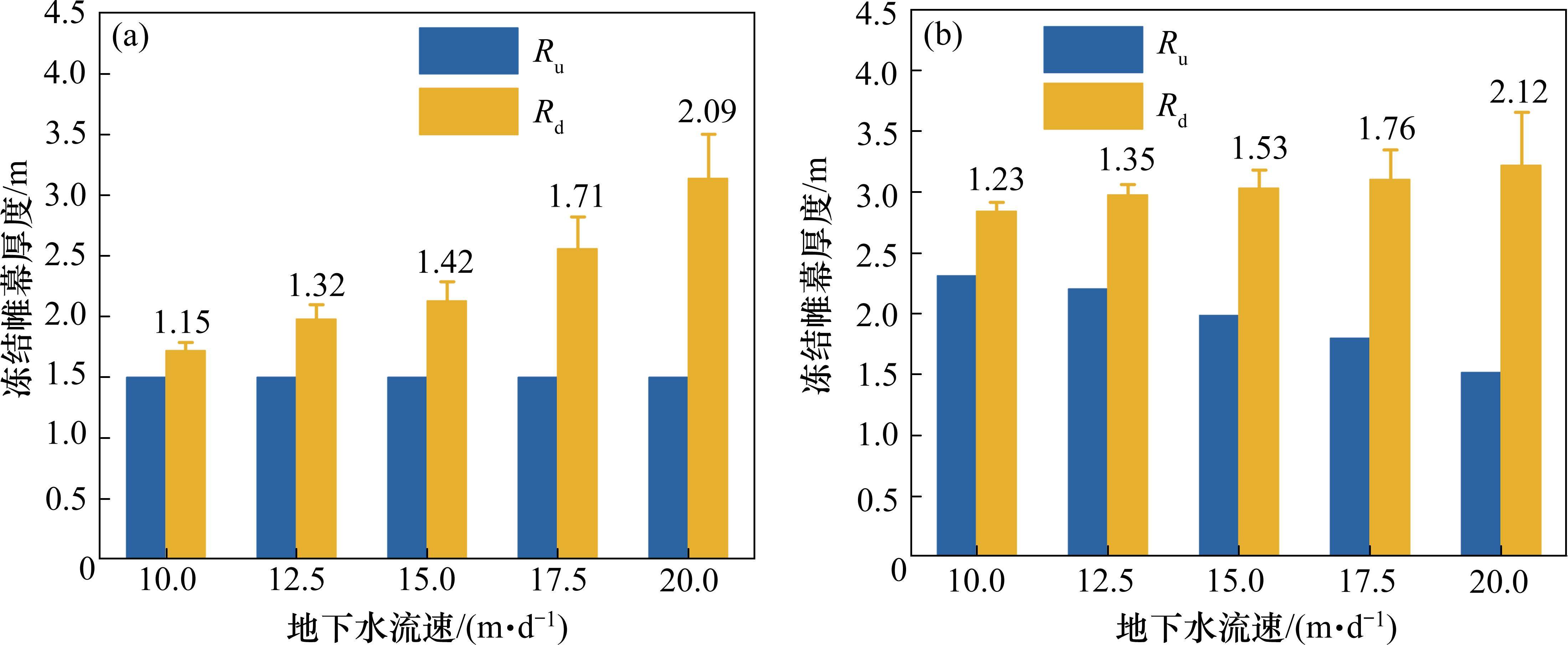
4 结论
1) 在数值模型计算中,v=10、12.5、15、17.5和20 m/d时冻结帷幕交圈时间分别为5.76、6.85、8.31、11.43和18.57 d。通过对数值计算结果拟合,得到渗流作用下地铁隧道液氮冻结帷幕交圈时间的预测公式。基于该公式得到冻结帷幕交圈极限流速为22.26 m/d,随着渗流速度的增加,冻结帷幕交圈时间呈指数型增长,需要考虑在上游区域增加冻结管密度或注浆来降低土层渗透率,从而提高冻结效率。
2) 冻结20 d后,各渗流速度下上游冻结帷幕厚度与下游冻结帷幕厚度之比(Rd/Ru)为1.23、1.35、1.53、1.76和2.12,渗流速度由10 m/d逐渐增大到20 m/d时,冻结帷幕交圈的形状由圆形逐渐转变成“类心形”,同时,隧道内部地层的温降速率随着渗流速度增加而增加,冻结区的热传导途径受到水流对流传热的影响而发生变化,流速越大,对流传热效率越高,导致下游区域的平均冻结温度更低,加剧了冻结帷幕的不均匀性。
3) 通过对地铁隧道相邻冻结管的“邻管效应”分析,发现当相邻冻结锋面的间距减少至临界值Lj后,“邻管效应”开始发挥作用,促使冻结锋面的扩展进入二次加速阶段,缩短了冻结帷幕交圈时间。由于大流速下“邻管效应”受渗流的对流传热影响,Lj会随着渗流速度增加而减小,当渗流速度为15.0、17.5和20.0 m/d,对应的Lj分别为389、355和254 mm。
杨哲,蔡海兵,王彬等.高流速富水砂层地铁隧道液氮冻结温度场演化规律研究[J].铁道科学与工程学报,2025,22(01):307-319.
YANG Zhe,CAI Haibing,WANG Bin,et al.Evolution law of liquid nitrogen freezing temperature field in subway tunnel with high flow rate and water-rich sand layer[J].Journal of Railway Science and Engineering,2025,22(01):307-319.

