在寒冷地区建造的隧道开通后不可避免地受到冷空气的影响,隧道衬砌外围岩石逐渐冻结和隆起,从而引发衬砌裂缝、剥落和挂冰。由此产生的冻害是季冻区隧道安全运行的主要威胁[1],而隧道抗冻设计是防止冻害的重要措施之一。为保证抗冻设计的有效性,关键在于准确评估季冻区隧道运行中的冻胀力荷载和围岩的应力分布特征。针对季冻区隧道的冻胀力和应力分布,主要的研究方法包括物理试验[2]和理论解析[3-4]。相较于物理试验的表象、高成本和特定条件[5],理论解析可从根本上掌握季冻区隧道围岩冻胀破坏的本质[6]。目前,隧道冻胀力的理论计算模型包括含水风化层、衬砌后积水和冻融区整体的冻胀模型。其中,含水风化层冻胀模型假设过于理想且系数难以确定,由此无法反映围岩的真实状态;衬砌后积水冻胀模型适用于计算硬岩隧道局部位置的冻胀力,但其应用存在一定的局限性。冻融区整体冻胀模型鉴于严谨的理论推导,能够反映季冻区隧道衬砌、冻结围岩和未冻结围岩的力学响应,因此有诸多学者从多方面展开了深入研究。基于冻融区整体冻胀模型,FENG等[3]提出了一种适用于寒区隧道衬砌和围岩应力的弹塑性解决方案,但其假设围岩的冻胀为各向同性。XIA等[7]则依据试验研究发现寒区隧道冻胀力产生的关键在于围岩的不均匀冻胀特性[8-9],并以此建立了冻胀力计算模型。在围岩不均匀冻胀特性提出的基础上,LV等[4]和FENG等[10]分别基于Mohr-Coulomb准则和Drucker-Prager准则得到了冻胀力的弹塑性解;张常光等[11]和蒋望涛等[12]则进一步分别引入围岩位移释放系数和围岩损伤程度比值,建立了寒区隧道的应力解答。然而,现有试验结果表明,围岩冻胀与寒区隧道温度场密切相关[13];随围岩靠近寒区隧道洞壁,其温度逐渐降低[14-16]。当围岩温度较低时,围岩冻胀所产生的体积变形更为显著[17-19];随围岩沿径向温度增加,围岩冻胀所引起的体积变形减小[20-21]。由此说明,寒区隧道存在明显的径向温度场所形成的围岩体积冻胀率梯度。特别对于季冻区隧道而言,冻胀主要发生在冻融循环的交替期[22];冻结围岩会经历长期的冻融循环,进而导致岩石力学性质的劣化[23]。此外,在隧道工程中竖直和水平方向的地应力存在明显差异[24],且在隧道出入口处通常受到冷空气的严重影响使其极易发生冻害。衬砌外围不同方位角上的冻胀力和应力分布在非等压隧道中存在差异,但等压隧道因地应力的理想假设使其一致。上述有关冻胀力和应力分布的理论解答均基于等压隧道假设,且未考虑隧道温度场所形成的体积冻胀率梯度和冻融循环下围岩的劣化效应。对于季冻区隧道工程实际而言,采用上述理论进行解答时,会引起冻胀力和应力分布的评估误差。因此,本文针对已有理论解答的应用局限,尝试考虑围岩冻融循环劣化引起的弹性模量和冻胀率的改变;依据试验研究所表明的围岩不均匀冻胀特性,引入寒区隧道温度场所形成的冻胀率径向梯度;采用复变函数映射双向非等压应力边界条件,进而提出一种季冻区非等压隧道的双重不均匀冻胀解析方法。随后,通过围岩双重不均匀冻胀特性、侧压力和冻融循环等参数,进一步探讨季冻区非等压隧道的冻胀力和应力分布特征。
1 考虑冻胀率梯度的季冻区非等压隧道模型
1.1 基本假设
为求解季冻区非等压隧道的应力特征,做如下假设:1) 圆形隧道的衬砌和围岩为连续分布的均质材料,其受力属于平面应变问题;2) 隧道竖直和水平方向的地应力分别为p0和λp0,致使围岩在不同方位角的应力分布存在差异;3) 冻结围岩的体积冻胀率沿径向逐渐变化,且径向冻胀率和环向冻胀率不相等;4) 忽略围岩冻融的过程,即围岩均视为某次冻结的最终状态。
1.2 冻融循环下围岩的双重不均匀冻胀模型
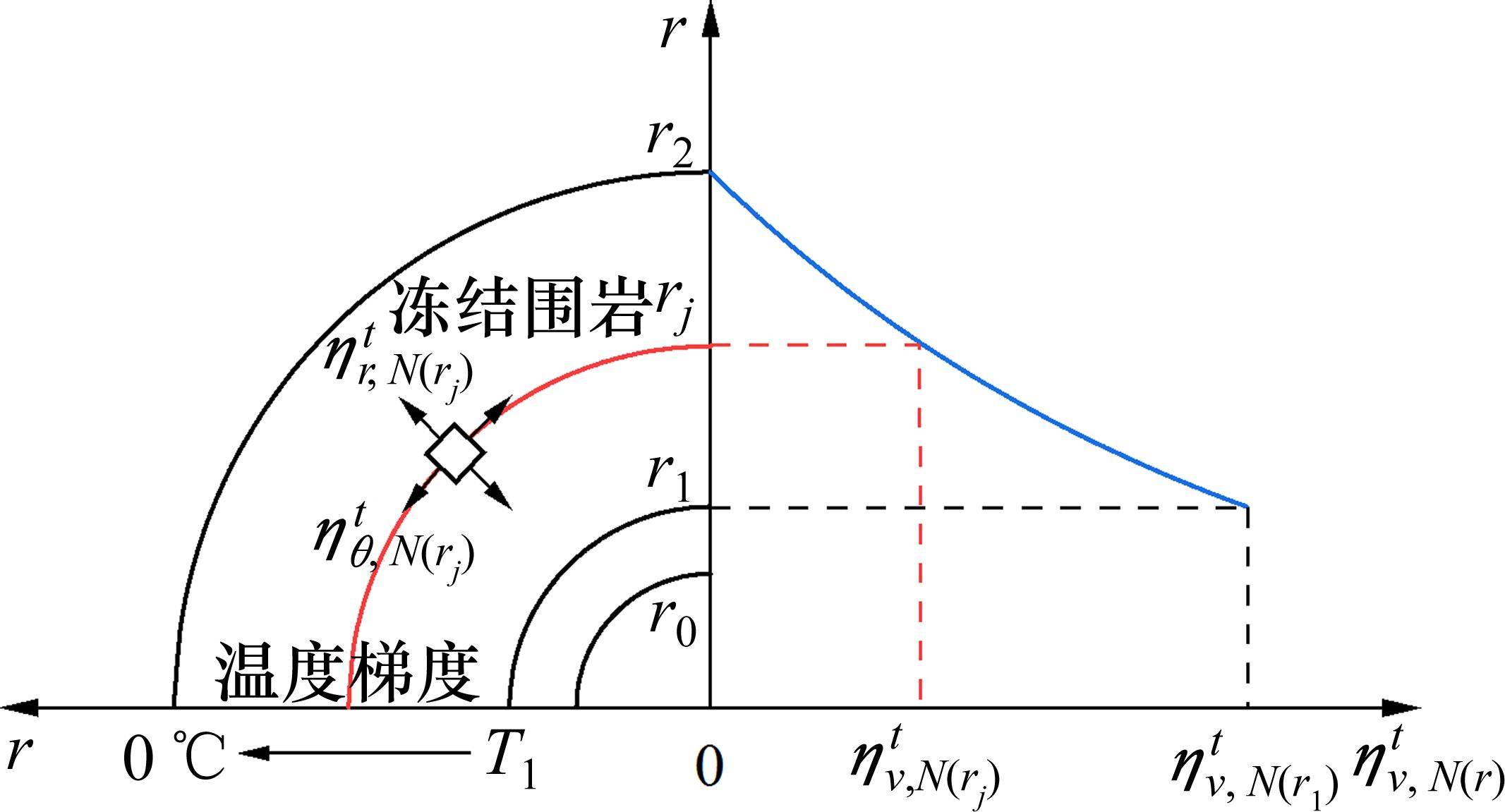
在季冻区隧道开挖后,围岩沿径向和纵向逐渐冻结时存在明显的径向冻结温度梯度。受温度梯度的影响,围岩的双重不均匀冻胀表现在沿径向和环向的不均匀冻胀特性,且随径向梯度分布。考虑第N次冻融循环后围岩的双重不均匀冻胀模型如图1所示。季冻区隧道衬砌外边界r1处的温度为T1,此处围岩的体积冻胀率达到最大值ηtv,N(r1),而在冻结围岩外边界r2处的温度为0 ℃,此处围岩的体积冻胀率为0;位于rj处围岩的体积冻胀率为ηtv,N(rj),且径向冻胀率和环向冻胀率分别为ηtr,N(rj)和ηtθ,N(rj)。围岩不同径向位置的冻胀体积取决于实际温度值T(r)[25],其冻胀率沿径向的梯度分布具体可表示为[6]:
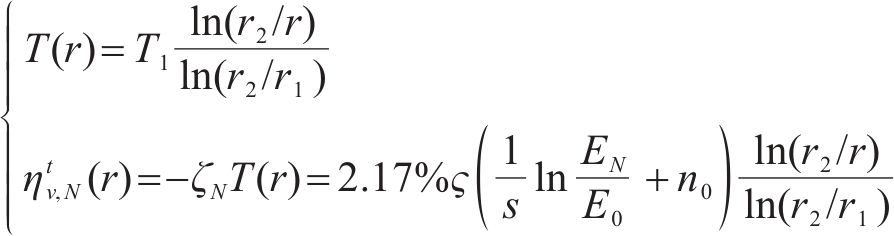
式中:r为计算半径;r1和r2分别为衬砌和冻结围岩的外边界;T1为r1处的温度边界;ηtv,N(r)为体积冻胀率;ζN和T(r)分别为围岩单位温度冻胀系数和实际温度值;ς为水热迁移系数;s为试验拟合参数;n0为冻结围岩孔隙率;E0和EN分别为第0次和第N次围岩冻融循环后的弹性模量。
其中,冻融循环下围岩弹性模量的劣化规律为[6]:
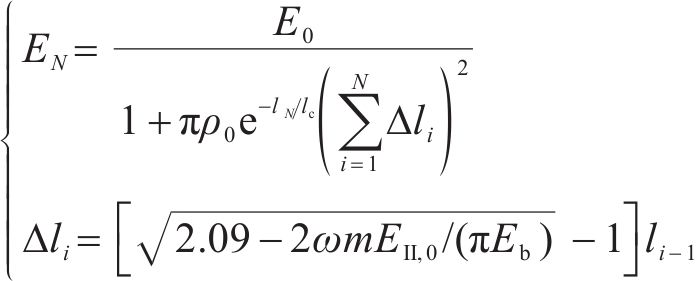
式中:ρ0和lc分别为裂纹密度和分布参数;lN、li-1和Δli分别为N次冻融后、i-1次冻融后和第i次冻融所致的裂纹扩展半长;m和Eb分别为围岩弹性模量放大系数和冰的弹性模量;ω为裂纹长度变化量的比值。
则围岩的径向冻胀率梯度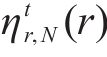
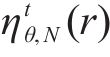
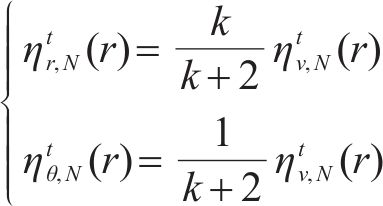
式中:k为围岩的不均匀冻胀系数;对于季冻区隧道而言,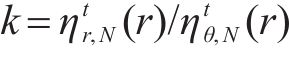
1.3 非等压隧道力学模型
本文隧道模型的平衡状态求解如图2所示,其主要组成包括Ⅰ区衬砌、Ⅱ区冻结围岩和Ⅲ区未冻结围岩。季冻区隧道衬砌外围岩的状态在Ⅱ区冻结围岩和Ⅲ区未冻结围岩之间反复交替,其中某次冻结具体可视为Ⅱ区围岩首先由无约束冻胀引起边界位移(Δ1/Δ2),而后在Ⅰ区衬砌和Ⅲ区围岩约束下达到平衡。由于非等压应力(p0/λp0)的影响,隧道衬砌(Ⅰ区)和冻结围岩(Ⅱ区)最终呈现椭圆形。
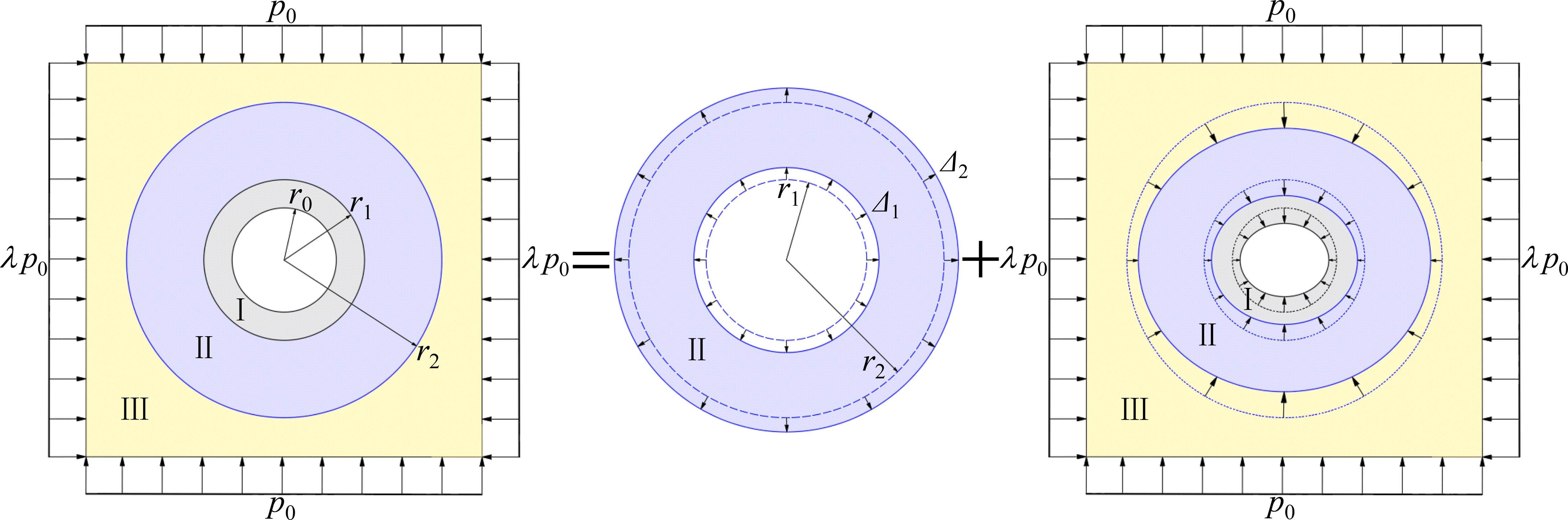
2 理论模型建立与求解
2.1 Ⅱ区围岩无约束冻胀边界位移
季冻区隧道Ⅱ区围岩的应变包括应力应变和冻胀应变,则Ⅱ区冻结围岩的径向应变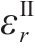
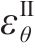
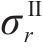
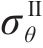
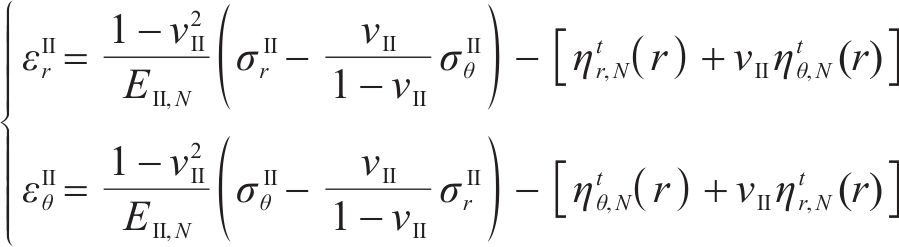
式中: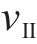
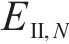
基于围岩的应力平衡方程和几何方程,联立式(1)、式(3)和式(4),并积分可得Ⅱ区围岩径向位移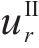
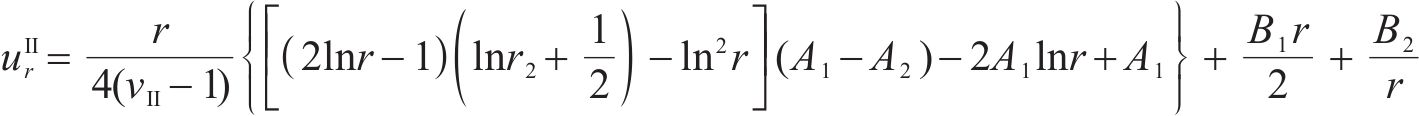
式中:B1和B2为积分常量;A1和A2为冻融循环常量,由Ⅱ区围岩初始弹性模量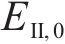
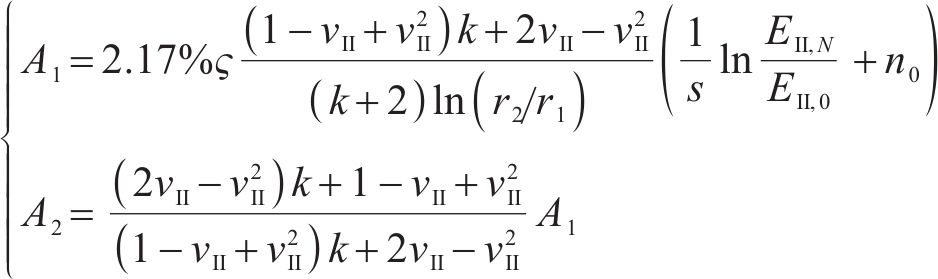
联立式(4)和式(5)以及围岩几何方程可得Ⅱ区围岩的应力分布如下:
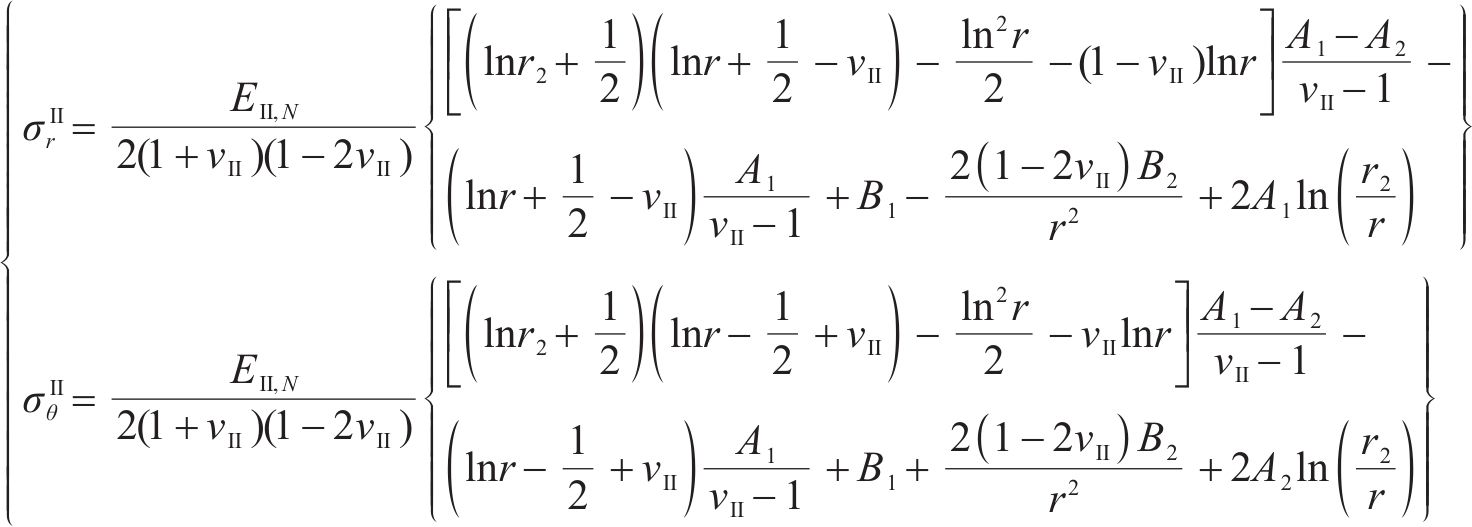
Ⅱ区围岩发生无约束冻胀时,将r=r1和r=r2处径向应力为0的边界条件代入式(7)可得:
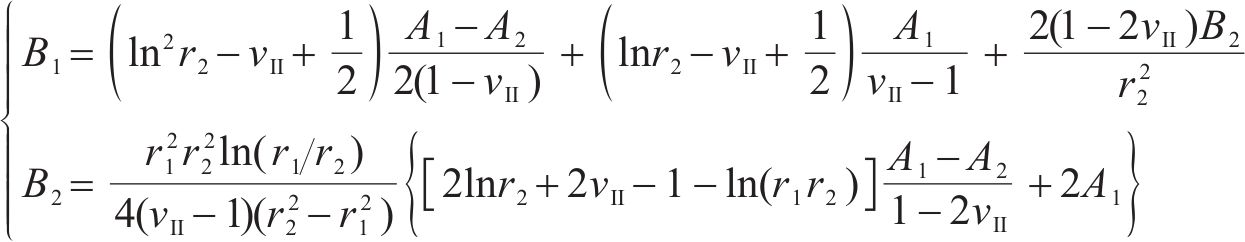
将式(8)代入式(5)中即可得到Ⅱ区围岩在无约束冻胀下,内、外边界处的径向位移为:
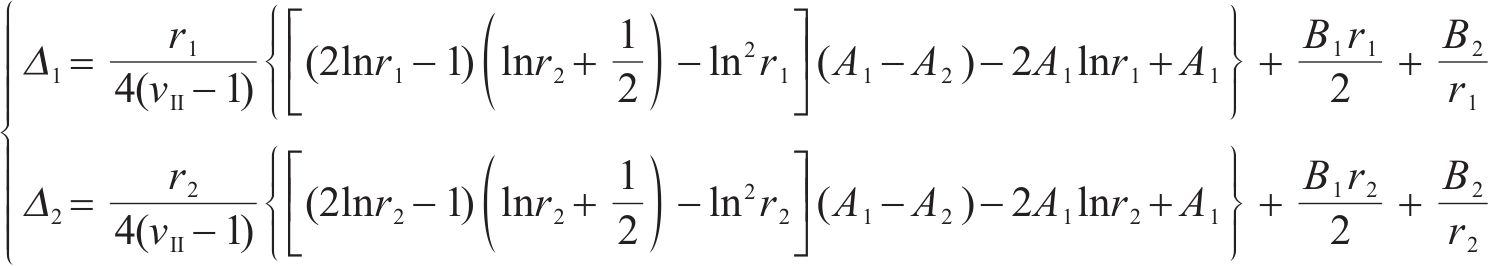
式中:Δ1和Δ2分别为Ⅱ区围岩内边界和外边界处径向位移。
2.2 非等压应力作用下隧道衬砌和围岩力学响应
采用复变函数法求解非等压应力作用下衬砌和围岩的应力和位移,借助极坐标中的解析函数表示如下:
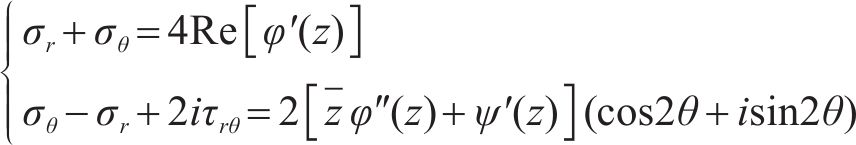
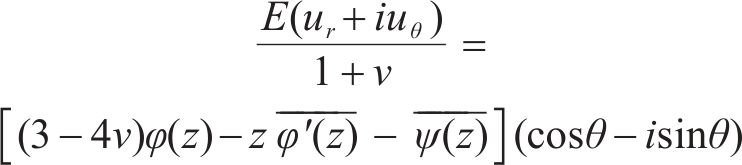
式中:z为复数;i为虚数单位;τrθ为剪切应力;θ为辐角;uθ为环向位移;φ(z)和ψ(z)为分析函数;v和E分别为泊松比和弹性模量。
Ⅰ区衬砌的分析函数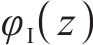
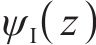
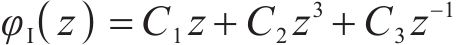
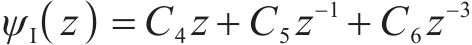
式中:C1、C2、C3、C4、C5和C6为常量。
联立式(10)、式(12)和应力平衡方程可得Ⅰ区衬砌的径向应力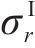
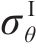
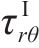
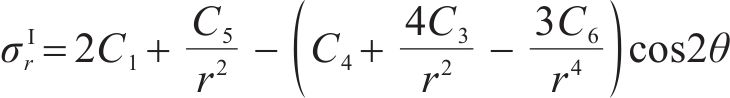
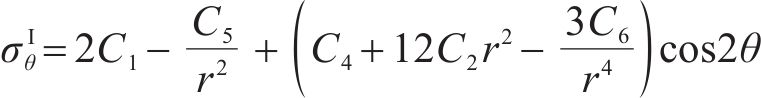
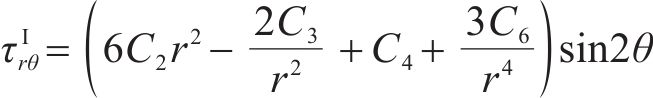
将式(12)代入式(11)中可得Ⅰ区衬砌的径向位移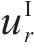
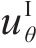
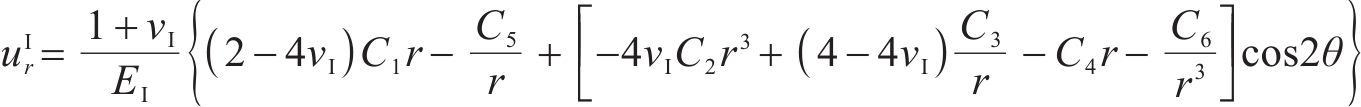
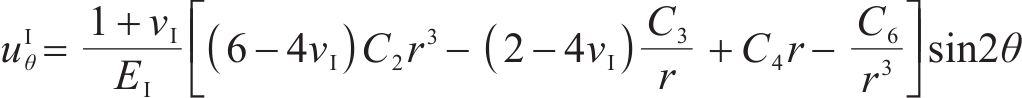
式中: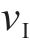
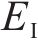
Ⅱ区冻结围岩的分析函数、应力分量和位移分量与Ⅰ区衬砌类似,将式(12)、式(13)和式(14)中C1、C2、C3、C4、C5和C6分别替换为常量D1、D2、D3、D4、D5和D6,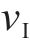
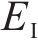
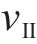
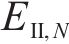
考虑在非等压应力作用下,Ⅲ区未冻结围岩的分析函数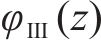
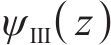
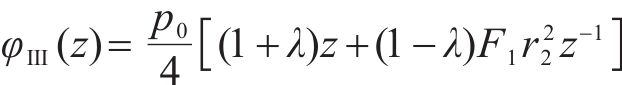
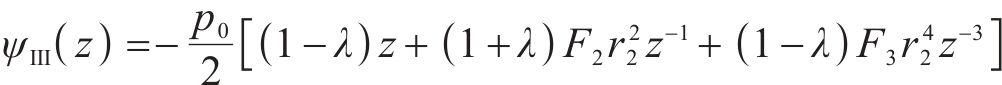
式中:p0为地应力;F1、F2和F3为常量;λ为侧压力系数。
联立式(10)、式(15)和应力平衡方程可得Ⅲ区未冻结围岩的径向应力
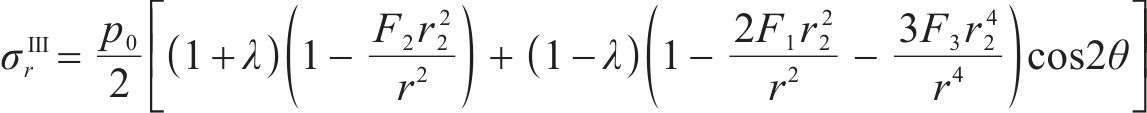
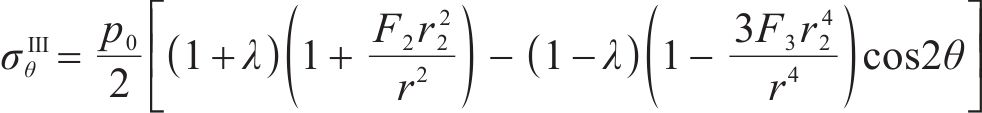
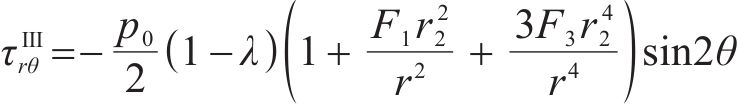
将式(15)代入式(11)中求解Ⅲ区未冻结围岩位移分量时,应当删除初始地应力对位移的影响,即求得径向位移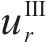
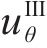
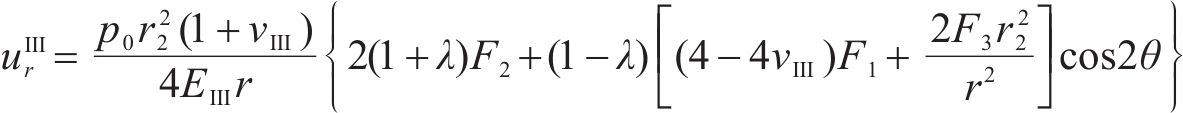
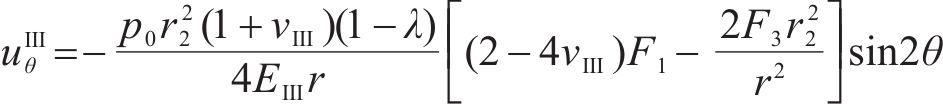
式中: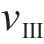
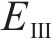
2.3 应力、位移解答
考虑季冻区隧道围岩应力、位移边界的连续性条件,结合Ⅱ区围岩无约束边界冻胀位移和非等压应力作用下隧道应力、位移方程式求解上述常量。围岩发生冻胀时,在r=r0、r=r1和r=r2处的边界条件为:
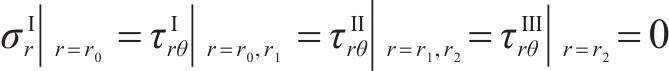
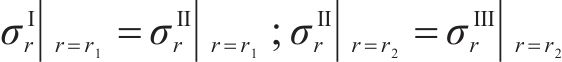
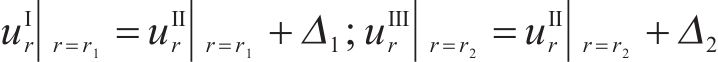
式中:r0为衬砌内边界;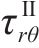
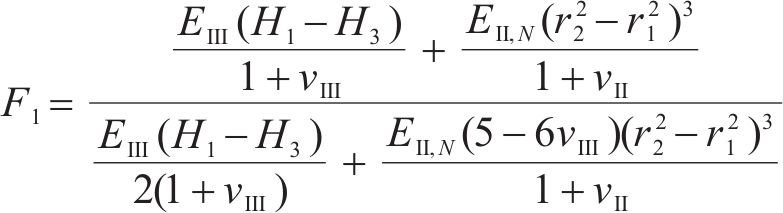
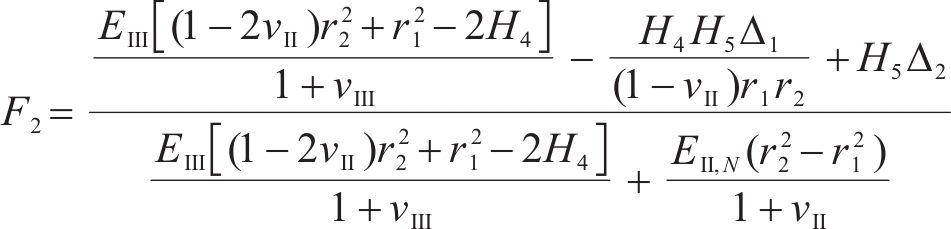
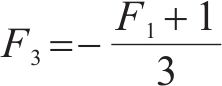
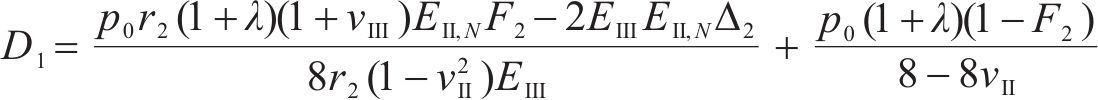
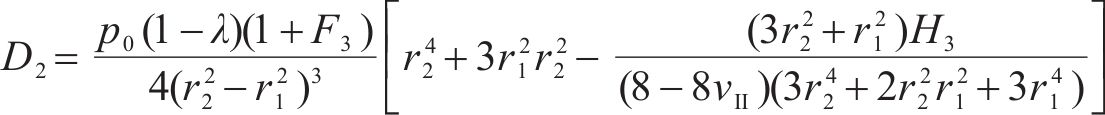
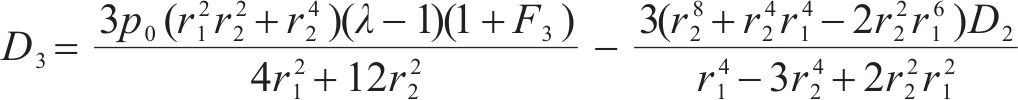
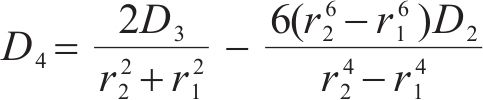
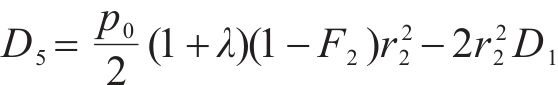
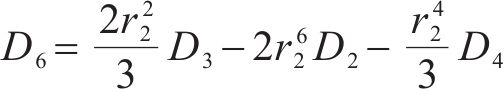
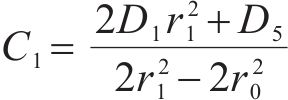
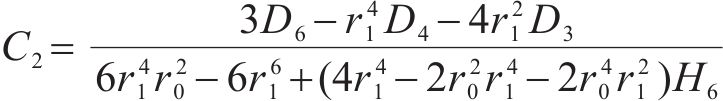
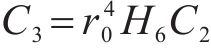
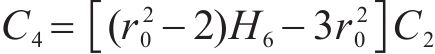
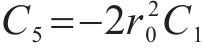
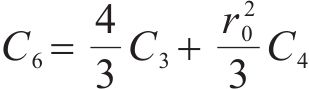
式中:H1、H2、H3、H4、H5和H6为常量,具体可表示为:
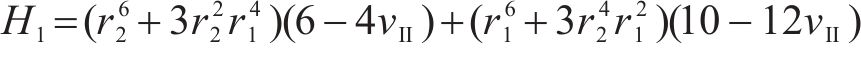
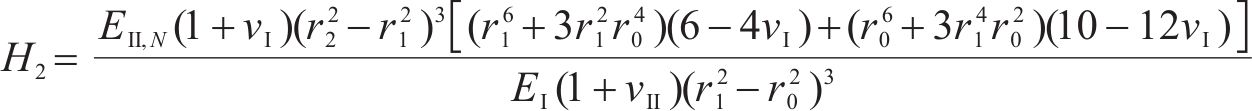
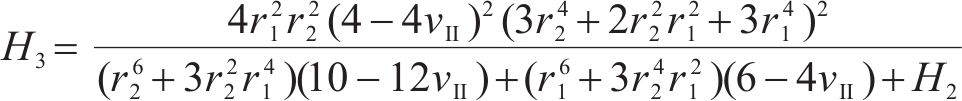
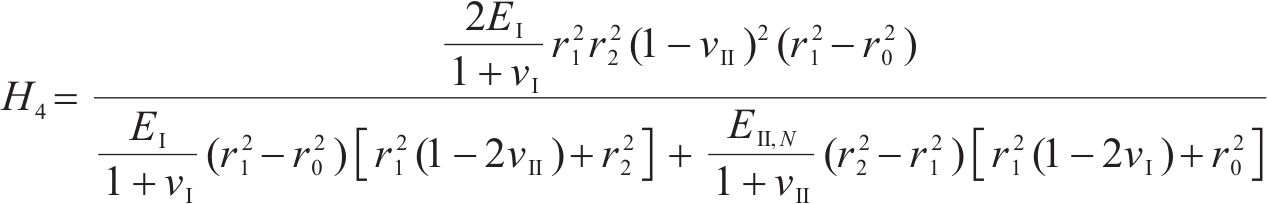
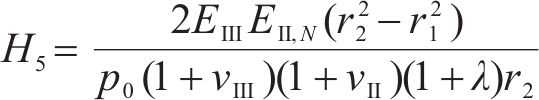
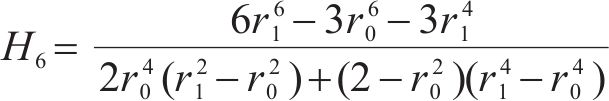
则冻胀力Δp1由式(13(a))计算可得:
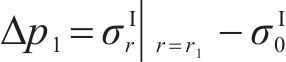
式中: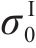
3 模型验证
3.1 围岩冻胀力
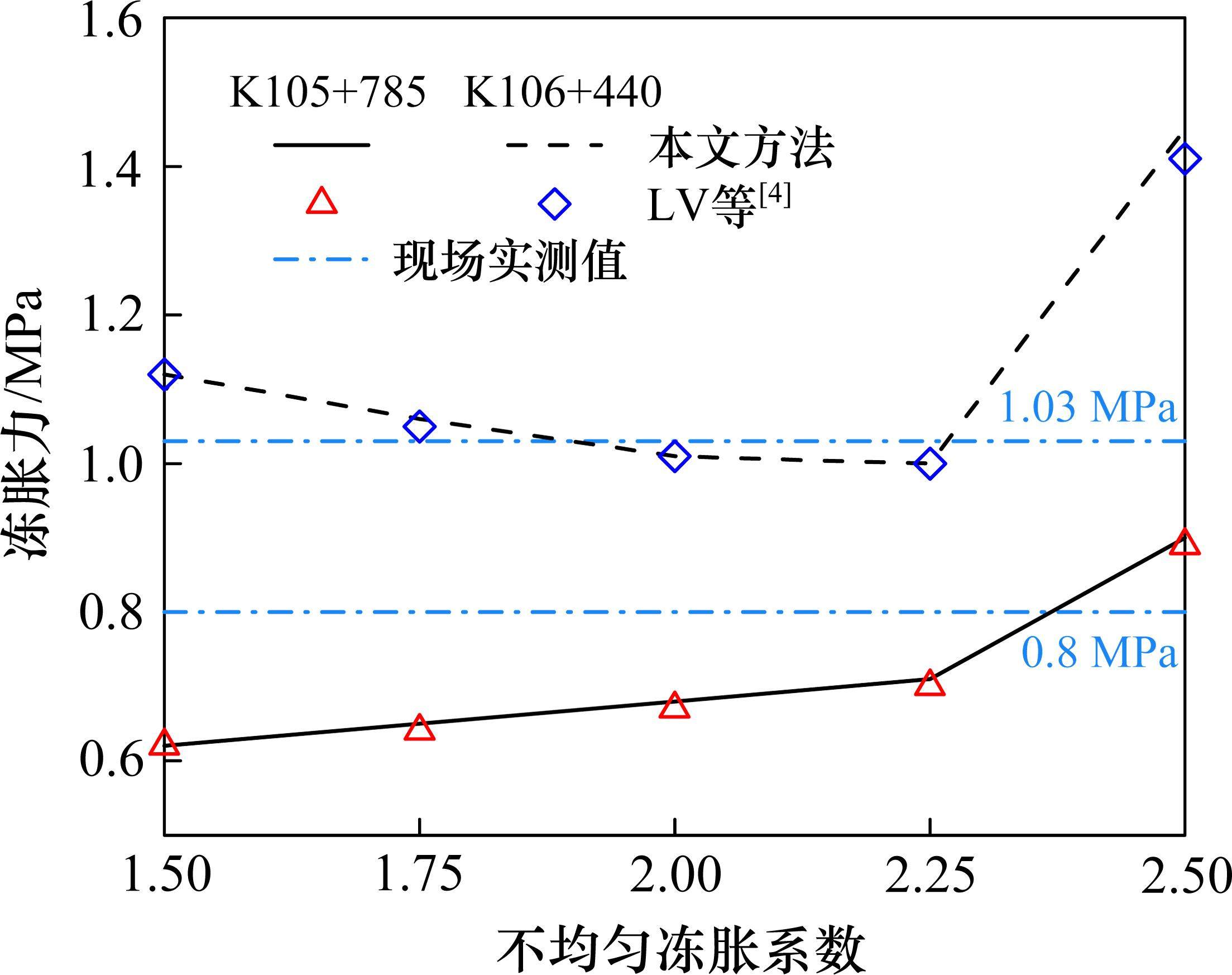
选用文献[4]所提供的寒区隧道模型验证本文方法的有效性,具体参数如表1所示。在地应力为3 MPa的寒区隧道中,随不均匀冻胀系数k增大,对于K105+785段,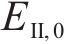
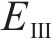
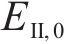
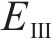
| 里程 | r0/m | r1/m | r2/m | EⅠ/GPa | EⅢ/GPa | vⅠ | vⅡ、vⅢ | ηtv,N(r)/% |
|---|---|---|---|---|---|---|---|---|
| K105+785 | 4.55 | 5.45 | 6.85 | 28.3 | 25.0 | 0.18 | 0.37 | 0.45 |
| K106+440 | 7.55 | 3.3 | 0.25 | 1.35 |
本文方法和文献[4]方法由上述参数计算所得围岩的冻胀力解答如图3所示。对比表明,随不均匀冻胀系数的增大,本文方法和文献[4]方法计算所得冻胀力吻合良好,且本文方法所求解的上/下限包含现场实测冻胀力。由此,可以说明本文方法在围岩冻胀力求解中的有效性。
3.2 隧道应力分布
选用表1所示K106+440段寒区隧道参数,在地应力为3 MPa下,围岩不均匀冻胀系数k为2,
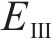
4 参数分析
4.1 双重不均匀冻胀
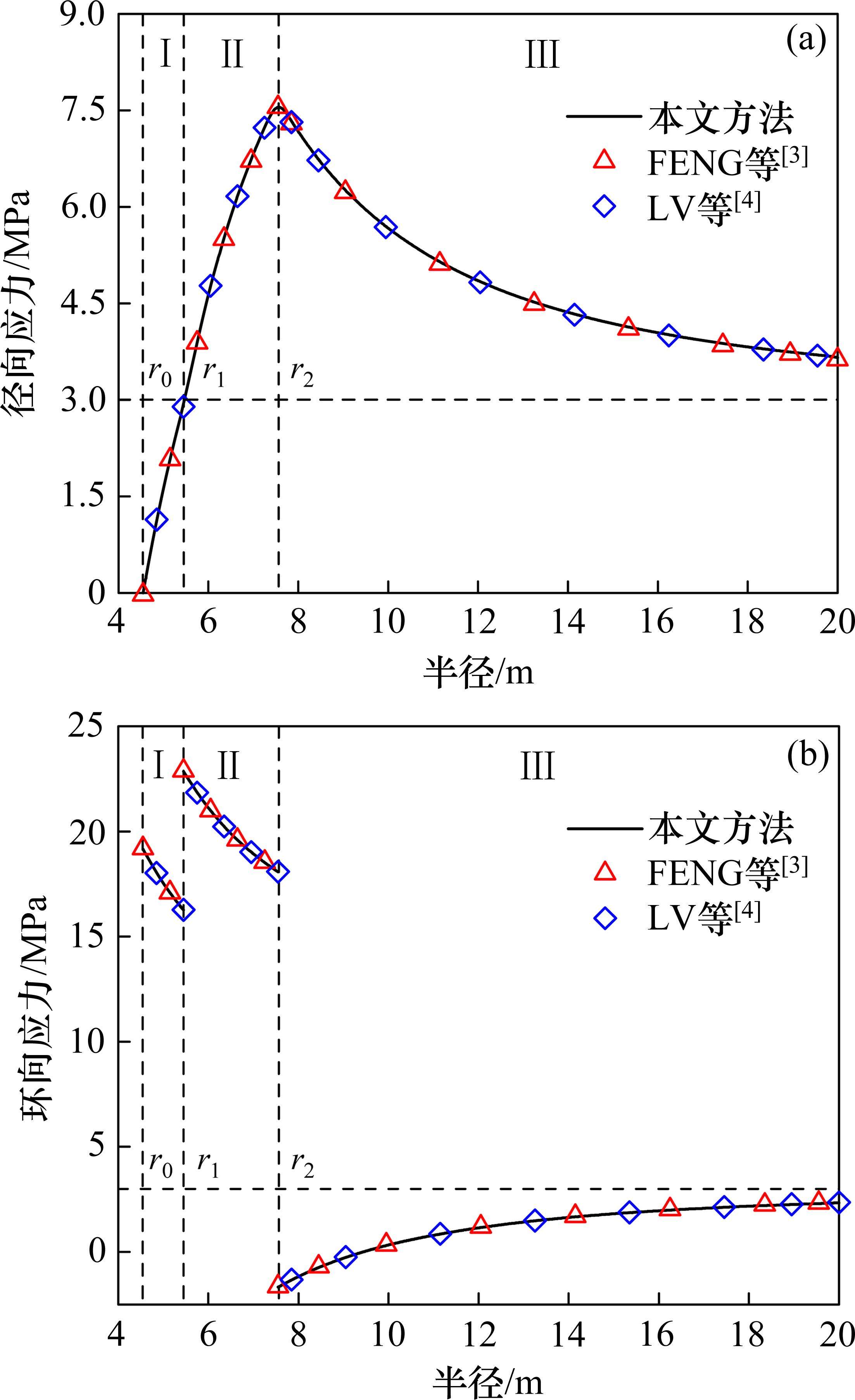
选用3.2节所述模型参数为基本工况,侧压力系数λ设置为0.5。不同计算条件下,考虑有无冻胀率沿径向梯度分布。其中,围岩不均匀冻胀系数k分别设置为2和3,将0°和90°方位角处季冻区隧道的应力分布绘制如图5所示。在图5(a)中,将冻胀率梯度引入基本工况后,相同k值下的径向应力明显减小且峰值降低了39%;随k值增加,Ⅰ区衬砌、Ⅱ区冻结围岩的应力变化速率提高,而在Ⅲ区未冻结围岩内无明显差异;非等压应力作用使得Ⅲ区未冻结围岩在0°方位的应力变化速率高于90°方位,随围岩远离Ⅱ区0°方位的应力变化速率逐渐减缓,从而低于90°方位。由图5(b)可知,随k值增加,冻胀率梯度的引入使得Ⅰ区衬砌的环向应力峰值分别降低了31%和44%,且因围岩环向冻胀特性的减弱使得Ⅱ区冻结围岩的环向应力减小;环向应力的变化速率在Ⅱ区冻结围岩0°方位明显低于90°方位,而在Ⅲ区未冻结围岩内呈现相反变化。如图5(c)所示,隧道不同方位角处的冻胀力因冻胀率梯度的引入而减小,随k值的增加在0°方位分别降低了0.74 MPa和1.73 MPa。综合分析可知,引入冻胀率梯度对季冻区非等压隧道的应力评估具有显著影响,表现为隧道径向应力、环向应力和冻胀力的降低,且随围岩不均匀冻胀特性的增强而明显。
4.2 侧压力
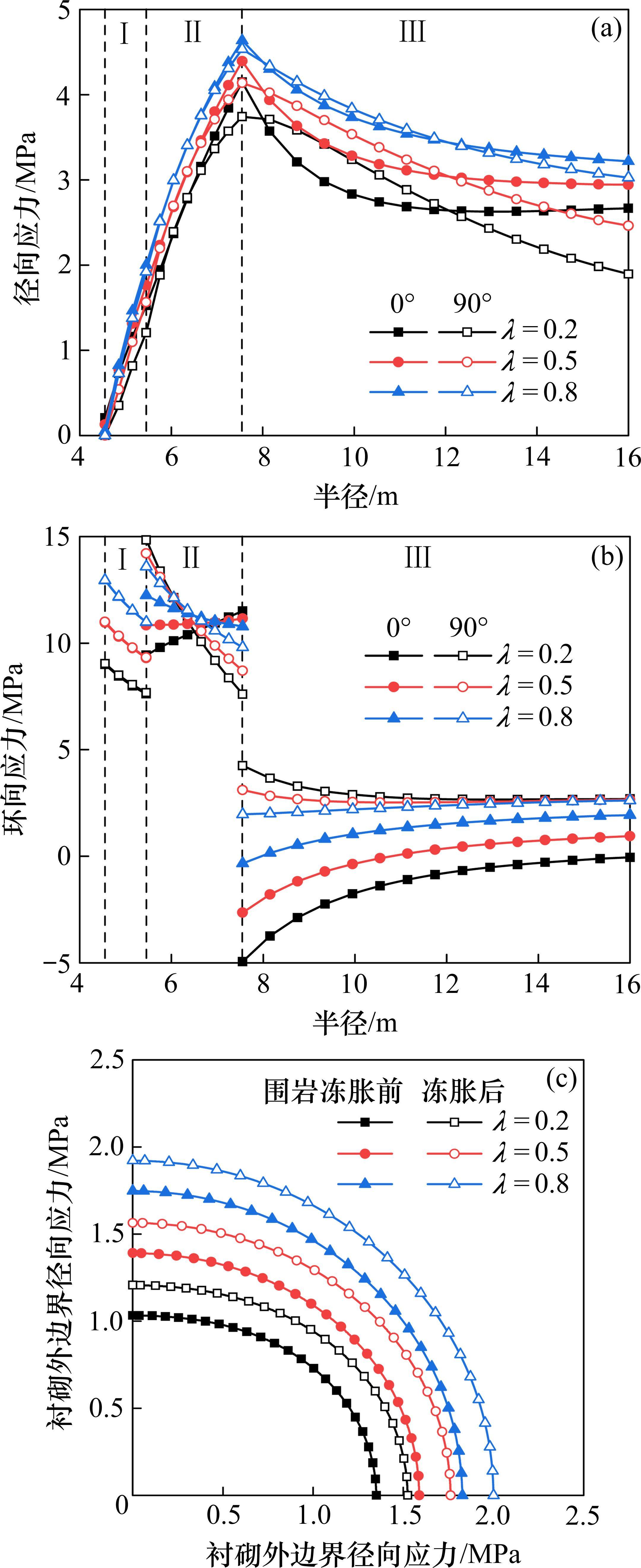
不同计算条件下,侧压力系数λ分别取值为0.2、0.5和0.8,将冻胀率梯度引入基本工况后所得0°和90°方位角处季冻区隧道的应力分布如图6所示。由图6(a)可知,随侧压力的增大,隧道的径向应力逐渐提高,在0°和90°方位角处应力峰值的差值分别为0.41、0.25和0.1 MPa;Ⅲ区未冻结围岩径向应力的变化速率随侧压力的增大而减缓,且在0°和90°方位之间存在的差异逐渐减小。如图6(b)所示,因侧压力的增大,Ⅰ区衬砌的环向应力峰值分别提高了22%和44%,而Ⅱ区冻结围岩、Ⅲ区未冻结围岩的环向应力变化速率在90°方位逐渐降低,但Ⅱ区冻结围岩在0°方位的应力变化速率呈现先减后增的变化趋势。由图6(c)可知,侧压力的增大对隧道不同方位角处的冻胀力无明显影响,而围岩冻胀后作用在衬砌外边界0°和90°方位的径向应力差值分别为0.31、0.2和0.08 MPa。由此分析可知,侧压力会改变季冻区非等压隧道在不同方位角处应力的分布差异,但对隧道冻胀力的影响较小,且围岩冻胀后作用在衬砌外边界不同方位角的径向应力差值随侧压力增大而减小。
4.3 冻融循环
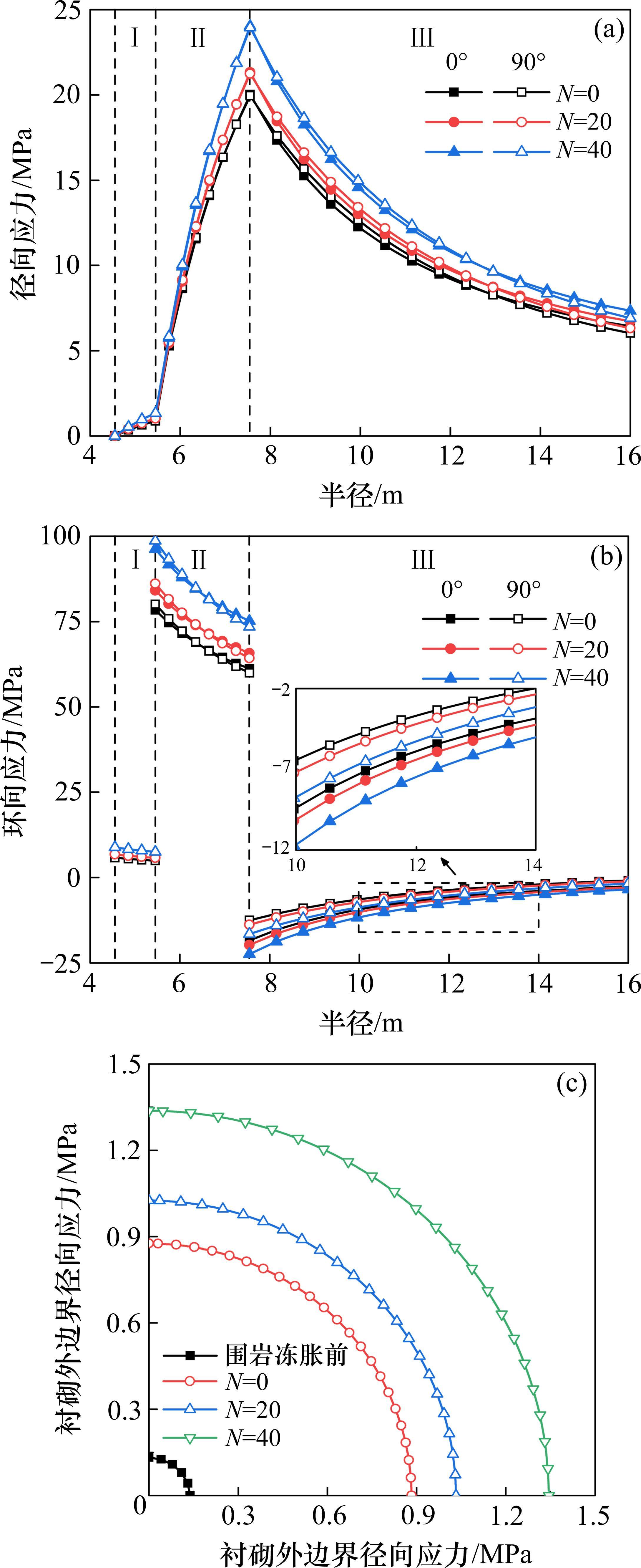
在基本工况中,由本文方法引入冻胀率沿径向的梯度分布,侧压力系数λ=0.5。冻融循环下,基于式(1)和式(2)分别考虑冻结围岩体积冻胀率和弹性模量的改变。其中,围岩冻融参数由文献[6]所提供,具体取值为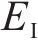
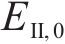
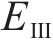
5 结论
1) 基于围岩冻融循环的劣化规律,引入围岩体积冻胀率的径向梯度,进而提出了一种季冻区非等压隧道的双重不均匀冻胀解析方法。将本文模型暂时退化后,得到了工程实例和现有理论方法的有效验证。
2) 引入冻胀率梯度后表明,季冻区隧道的径向应力、环向应力和冻胀力明显减小,且非等压应力作用下隧道在不同方位角的应力变化速率存在差异。随围岩不均匀冻胀特性的增强,引入冻胀率梯度所导致的隧道应力降低逐渐显著。因此,引入冻胀率梯度可实现对季冻区非等压隧道衬砌的适当简化。
3) 侧压力会改变季冻区非等压隧道在不同方位角处应力的分布差异。表现为随侧压力的增大,隧道径向应力和环向应力提高,而隧道应力的峰值和变化速率在不同方位角的差异逐渐减小,且对隧道冻胀力的影响较小。
4) 随着冻融循环次数的增加,季冻区非等压隧道在不同方位角的应力分布差异和应力变化速率大致相同,但将引起围岩体积冻胀率的提高和弹性模量的劣化,进而导致隧道径向应力、环向应力和冻胀力的增大,且隧道应力的增长幅度逐渐明显。由此说明,季冻区非等压隧道在进行抗冻设计时需重视冻融循环对隧道应力分布的影响。
李亮,陈嘉骏,赵炼恒.考虑冻胀率梯度的季冻区非等压隧道不均匀冻胀解析[J].铁道科学与工程学报,2025,22(01):320-331.
LI Liang,CHEN Jiajun,ZHAO Lianheng.Uneven freezing analysis of non-isobaric tunnels in seasonally frozen regions considering gradient of frost heave rate[J].Journal of Railway Science and Engineering,2025,22(01):320-331.

