基础设施建设的快速发展使隧道工程面临着越来越复杂的环境,对隧道的耐久性、承载性能等提出更高的要求[1-3]。为了应对这些挑战,预应力管片逐渐得到研究和技术人员的重视。
日本在20世纪90年代率先开展了预应力管片试验研究[4-5],对盾构隧道张拉施工过程中的预应力损失、横向力学特性进行分析,证明了其在小直径、受内水压隧道中的可行性。在此基础上,国内许多专家也对预应力盾构隧道进行了研究。于宁[6]基于模型试验分析了预应力、偏心距等因素对预应力盾构隧道纵缝接头刚度的影响,据此提出预应力筋的用量及其布置的设计方法。刘丰军[7]在已有盾构隧道等效刚度计算模型[8-9]的基础上提出预应力管片衬砌连续非均匀刚度模型,探究了施加环向预应力时管片纵缝的张角和刚度的计算公式,同时,基于概率极限状态设计方法并结合实际工程给出了预应力管片设计计算的具体步骤。刘鹏[10]通过在管片内部预埋波纹管,进行了预应力筋的张拉试验,验证了预应力的施加效果,得出环形预应力筋张拉过程中,钢绞线摩阻损失率为26.05%~35.2%,偏转器摩阻损失率为8.95%~9.3%,并通过压水试验分析了预应力管片在内水压作用下的力学性能。黄怀宁等[11-12]基于输水隧洞的受力特点,提出使施加的预压应力大于管片的轴拉力的预应力管片衬砌设计思路,并采用理论分析和数值模拟相结合的方法对预应力管片进行了设计计算。贾永刚等[13]采用数值模拟对管片在环向和纵向施加预应力,通过对无预应力、形心预应力以及偏心预应力3种工况的轴力、弯矩以及收敛变形计算结果的比较,得到预应力管片可以显著提高隧道结构的整体性、承载能力、耐久性、抗变形能力。
现有研究主要集中在预应力盾构隧道的设计计算以及横向力学特性分析方面,外加预应力呈环形分布,而鲜少研究纵向预应力盾构隧道的纵向力学特性。然而,由于地质条件的差异、附加荷载变化以及约束条件不同等因素,盾构隧道会产生纵向不均匀变形[14-18],导致环缝间受到剪切和相对变形作用,进一步引起隧道接缝渗漏,对隧道的安全性造成较大威胁,纵向预应力的施加则会避免这一现象[19]。基于此,本文针对完全闭合、部分张开2种环缝接触状态建立纵向预应力盾构隧道的等效刚度梁模型,提出隧道纵向变形控制指标的计算方法,结合某实际工程,基于纵向变形控制确定其最佳预应力,揭示最佳预应力对隧道超限纵向弯矩的影响,这对预应力盾构隧道工程的设计及施工具有重要意义。
1 纵向预应力盾构隧道的环缝接头解析力学模型
1.1 纵向等效刚度梁模型
志波由纪夫等[20]提出了纵向等效刚度梁模型,该模型单独考虑了盾构隧道结构纵向传递的弯矩M作用,给出了盾构隧道中性轴角度和等效抗弯刚度的计算方法。
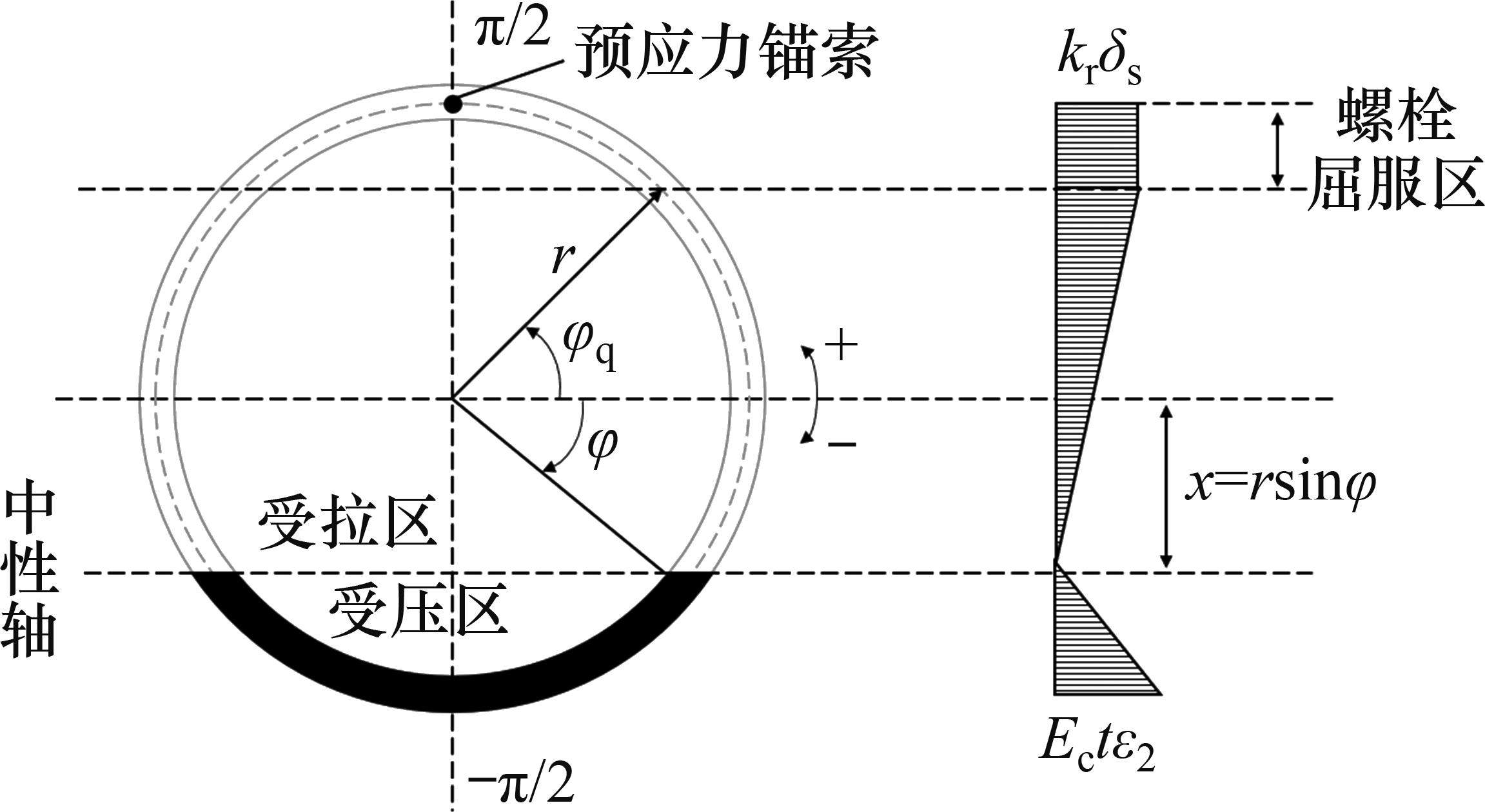
纵向仅受弯矩M作用的盾构隧道变形状态如图1所示,管片环缝面的顶部张开,底部闭合,将相邻两环管片宽度中心线所形成的夹角定义为管片环相对转角θ。隧道中心与管片环受压区域和受拉区域分界线与管片环截面的交点的连线和水平轴线形成的夹角称为中性轴角度φ,如图2所示,图2中,r为管片的计算半径,t为混凝土管片的厚度,α为积分变量。则在分析区域ls内的等效抗弯刚度EIθeq为:
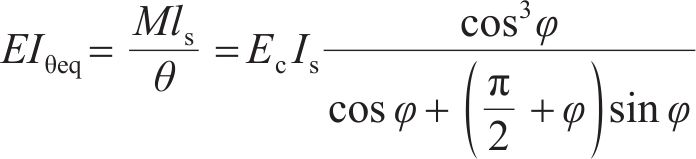
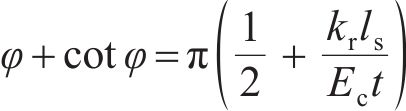
式中:ls为相邻衬砌环宽度中心线之间的长度;Ec为混凝土管片的弹性模量;Is为管片环截面对于几何中心线的惯性矩,Is≈πr3t;kr为纵向螺栓在整个环缝面圆周方向的平均线刚度,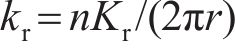
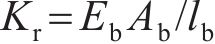
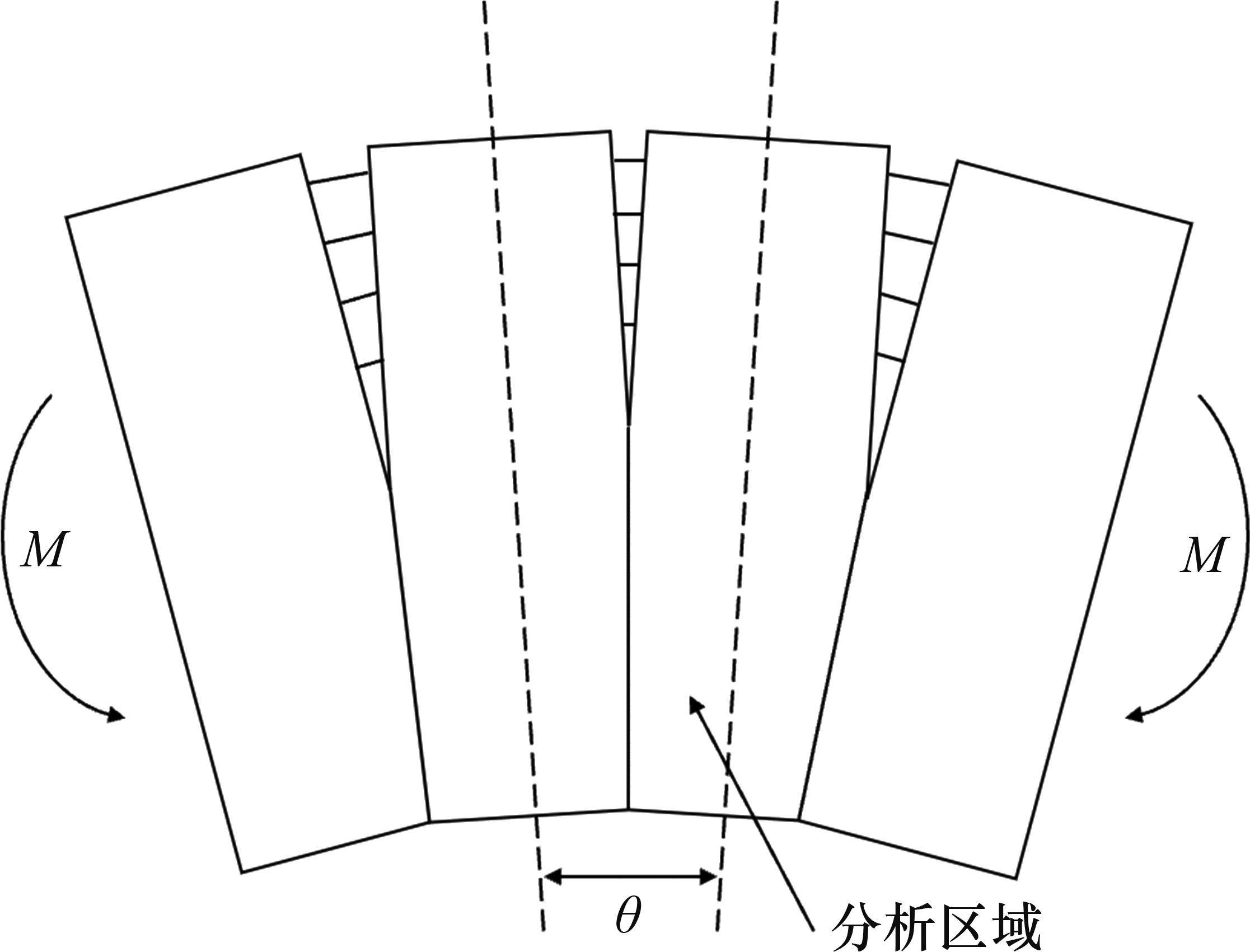
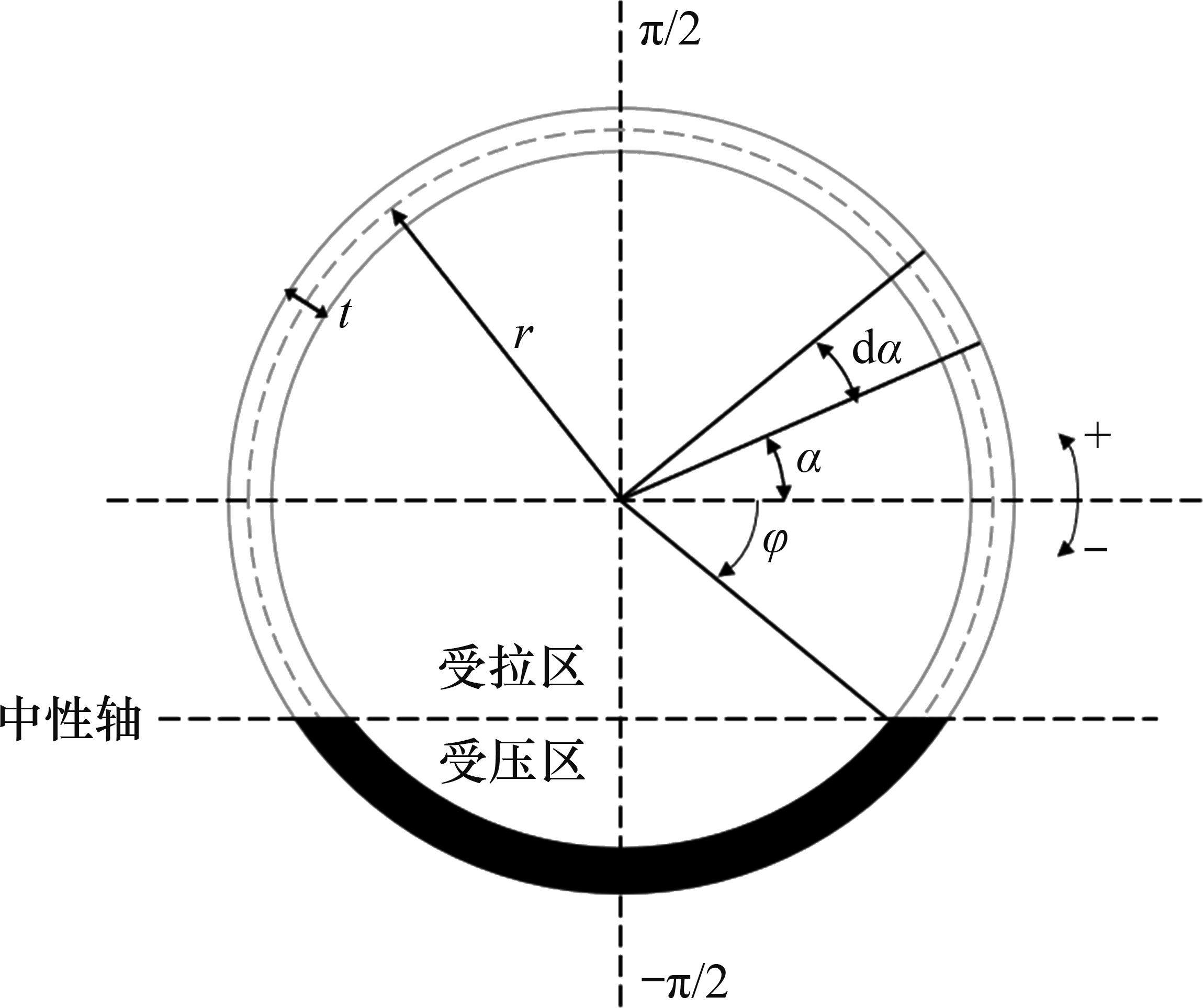
1.2 纵向预应力盾构隧道的等效刚度梁模型
1.2.1 模型基本假定
志波由纪夫等[20]提出的纵向等效刚度梁模型仅单独考虑隧道纵向传递的弯矩作用,而在实际工程中,盾构隧道往往会同时受到纵向轴力、弯矩以及预应力等的复杂作用,因此,使用志波由纪夫等[20]提出的向等效刚度梁模型来计算隧道的抗弯刚度是不够充分的,需要能够考虑复杂荷载同时作用的盾构隧道纵向计算模型。耿萍等[21-22]基于志波由纪夫纵向等效刚度梁模型提出了纵向非线性等效刚度梁模型,该模型同时考虑纵向轴力和纵向弯矩的作用。在此模型基础上,本研究考虑预应力的作用,提出了纵向预应力盾构隧道的等效刚度梁模型。
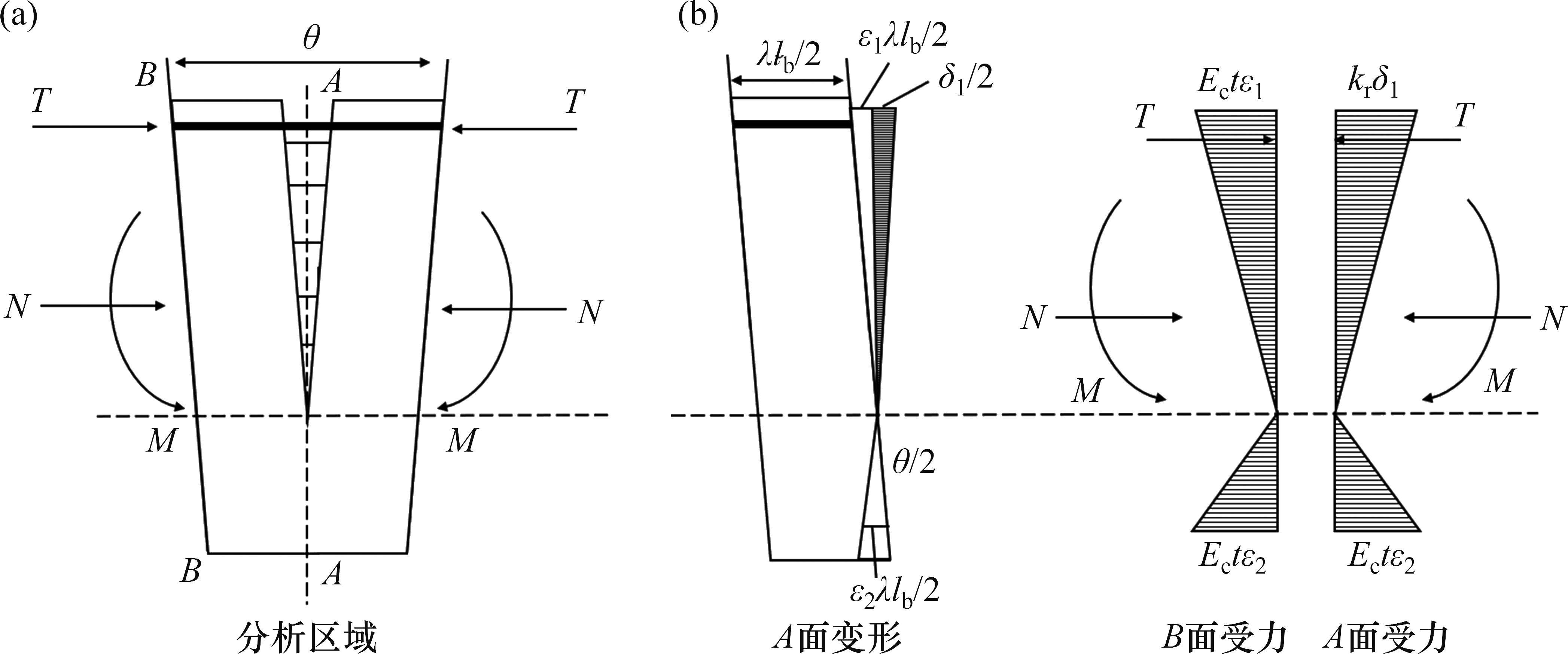
等效刚度的分析区域如图3所示,两管片环所受外力包括预应力T、轴力N以及弯矩M,预应力设置在管片环顶部中心处,其作用点到环面中心距离为e;面1和面2分别为两管片环的中心截面。由于盾构隧道受到轴力、弯矩与预应力的共同作用,在实际工作中,其环缝的接触状态可能有完全闭合、部分张开2种。当纵向预应力T较大,轴力N为较小拉力或为较大压力、弯矩M较小时,管片顶端和底端均发生接触,环面闭合,即a、b点接触,接触状态为完全闭合(接触模式1);当纵向预应力T和轴力N适中、弯矩M较大时,管片顶端张开,底端闭合,即a点未发生接触,b点接触,接触状态为部分张开(接触模式2)。
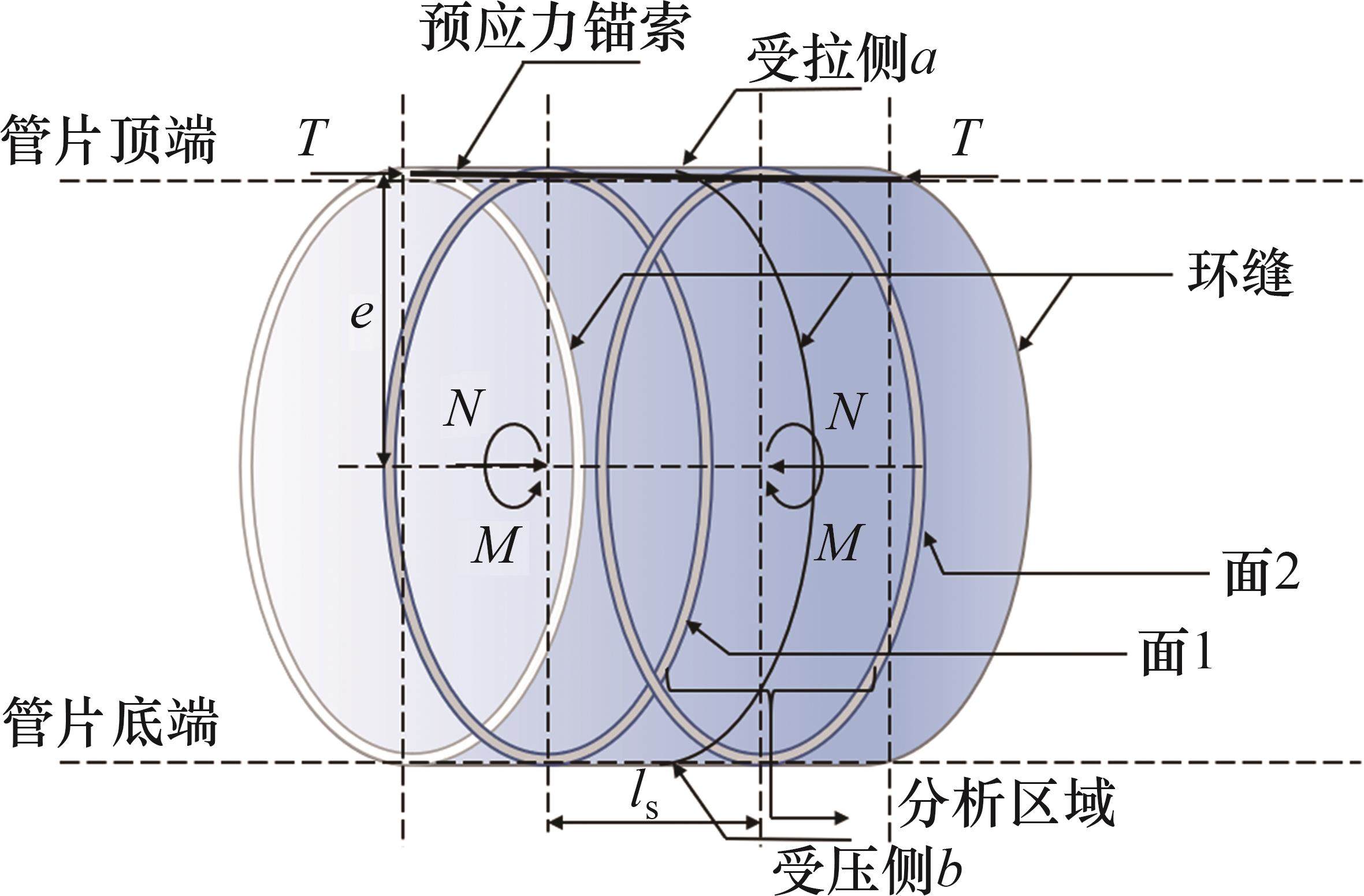
本文规定使管片环顶部受拉底部受压的弯矩为正向弯矩,使管片环顶部受压底部受拉的弯矩为反向弯矩。纵向轴力以拉力为正,压力为负。
该纵向预应力盾构隧道的等效刚度梁模型满足如下假定:
1) 隧道管片的横截面在变形前后保持为平面,横截面上每一点的变形量与该点到中性轴的距离成正比;
2) 中性轴在横断面上的相对位置沿着隧道的纵向不发生改变;
3) 考虑环缝的影响范围,引入环缝长度影响系数λ,当λ≥1时,环缝影响范围长度为lb,当λ<1时,环缝影响范围长度为λlb;
4) 模式2中管片环的应力状态以中性轴为界,一端受拉,另一端受压。在环缝影响范围内(λlb区域内),受压侧压力由混凝土管片承担,受拉侧拉力由管片和纵向螺栓共同承担;在环缝影响范围外(ls-λlb区域内),压力和拉力均由管片承担;
5) 不考虑纵向螺栓连接过程中预先施加的预紧力作用;
6) 将沿管片环向离散布置的纵向螺栓简化为连续均匀分布;
7) 管片和预应力锚索在各个接触模式中均保持弹性状态,而螺栓在接触模式1中一直处于弹性,在接触模式2中考虑塑性变形。
图4所示为环缝影响范围外管片应力和应变的情况,其中,ε1、ε2分别为横断面顶端和底端混凝土管片的纵向应变,受拉时为正,受压时为负。
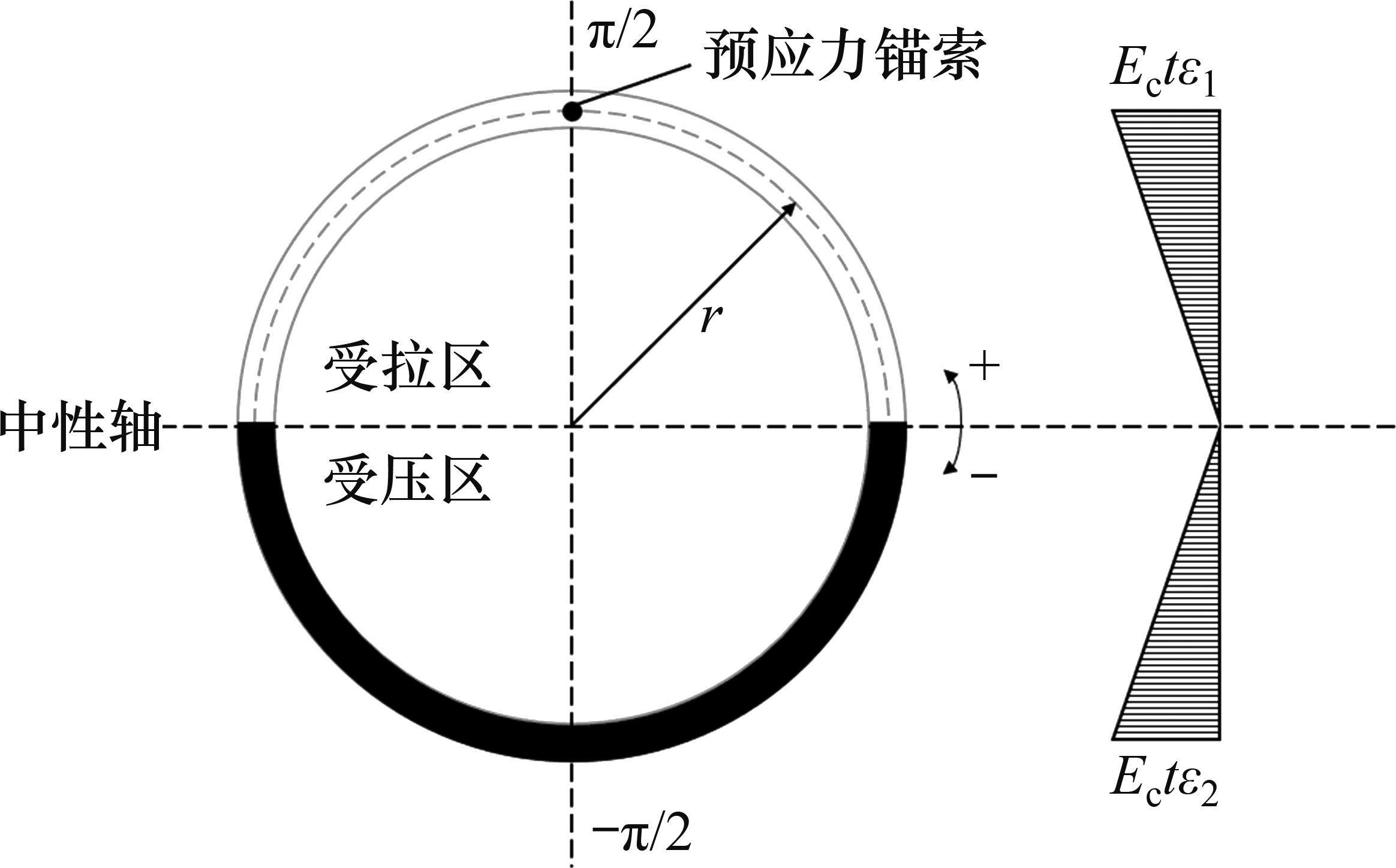
1.2.2 环缝完全闭合(接触模式1)
在模式1的分析区域内,环缝接头发生的弯曲变形如图5(a)所示,管片环之间完全闭合。由于环缝底端压缩量大于顶端,环缝产生了转角θ。转角θ由环缝引起的转角θh和混凝土管片引起的转角θs两部分组成。分析区域的几何尺寸和外力均关于A面对称,因此,选取A面左侧的区域进行受力分析(图5(b))。
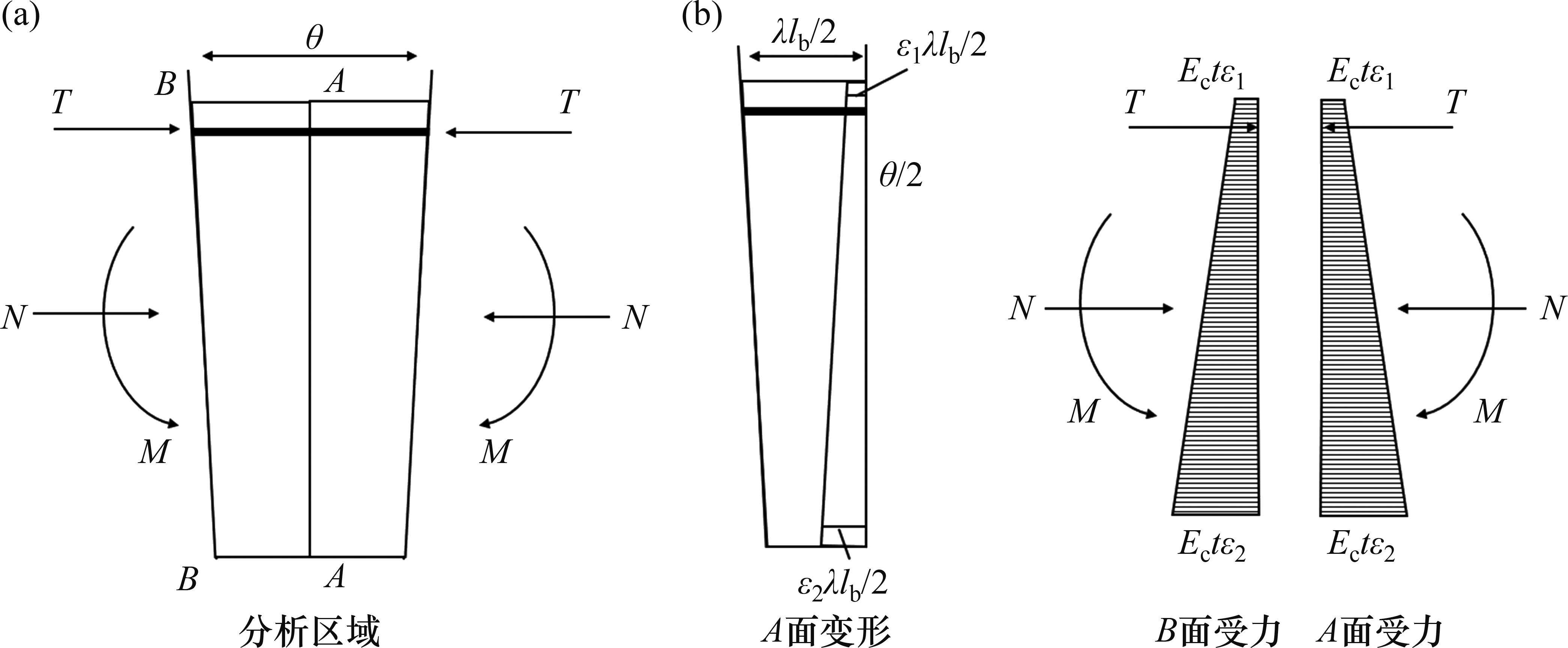
对A面或B面建立平衡方程,可得:
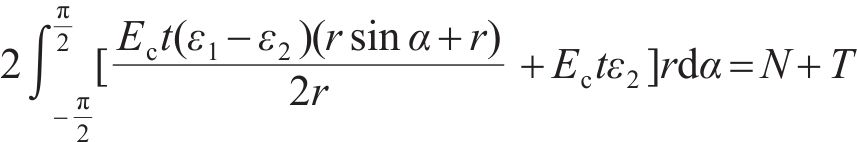
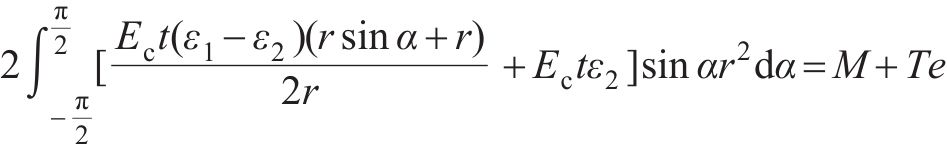
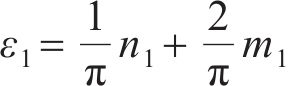
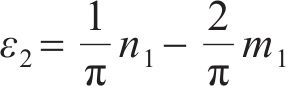
其中:
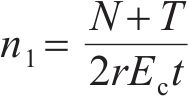
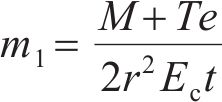
在模式1下,管片环缝面完全闭合,转角θ作用的垂直范围为2r,则环缝引起的转角θh为
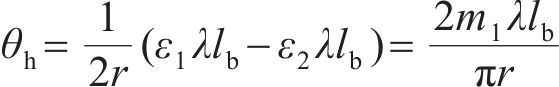
混凝土管片引起的转角θs为
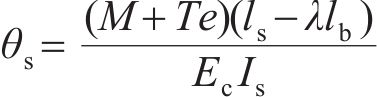
模式1的等效抗弯刚度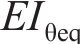
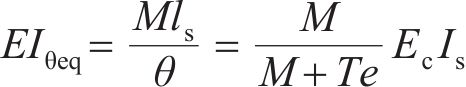
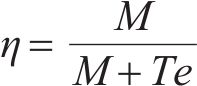
1.2.3 环缝部分张开(接触模式2)
模式2中,管片环缝面顶部张开,底部闭合,环缝产生了转角θ。此时,管片环顶端螺栓与管片一起承受拉力,顶端螺栓变形为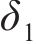
1) 当螺栓处于弹性阶段时,模式2管片环的弯曲变形和受力分布如图6所示。
由变形协调和力的平衡,可得:
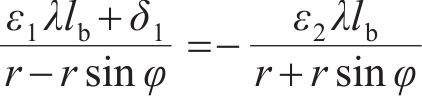
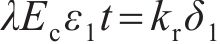
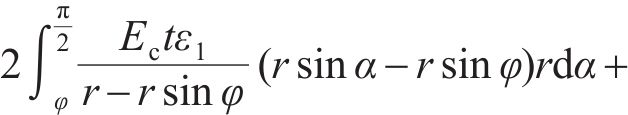
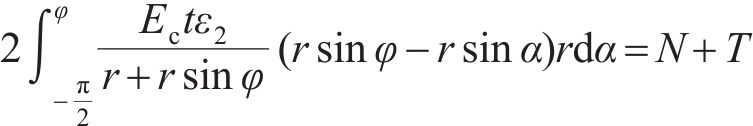
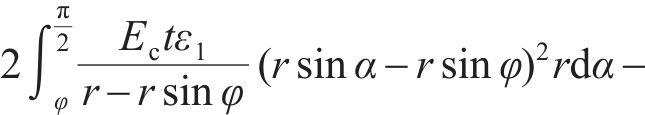
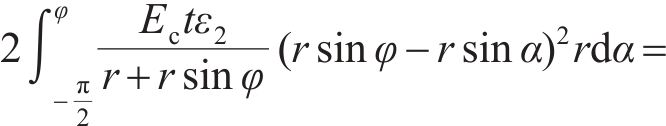
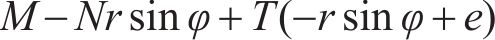
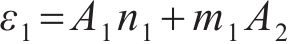
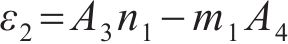
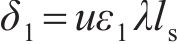
其中:
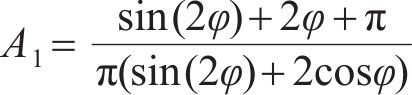
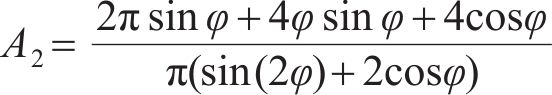
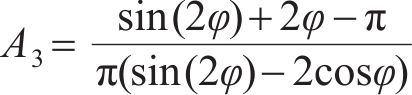
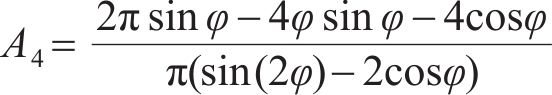
式中:A1、A2、A3、A4在
将式(17)~(19)代入式(13),可得中性轴位置角φ的方程:
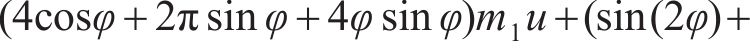
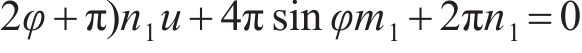
模式2中的环缝面部分张开,其转角θ作用的垂直范围取为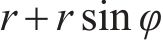
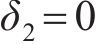
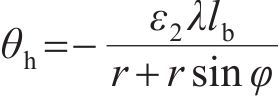
混凝土管片引起的转角θs为
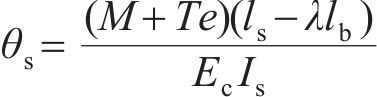
当螺栓呈弹性时,模式2的等效抗弯刚度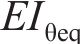
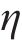
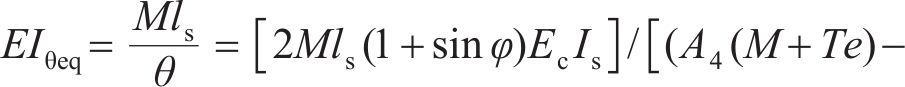
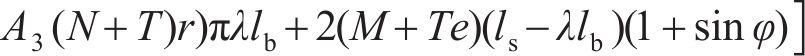
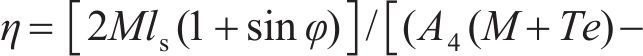
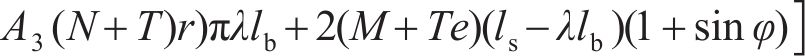
2) 当螺栓处于塑性阶段时,中性轴和螺栓屈服区如图7所示。将隧道中心与屈服螺栓最低水平线和管片厚度中心交界处的连线和水平轴线形成的夹角定义为屈服区位置角度φq。此时,模式2管片环的弯曲变形和受力分布如图8所示。
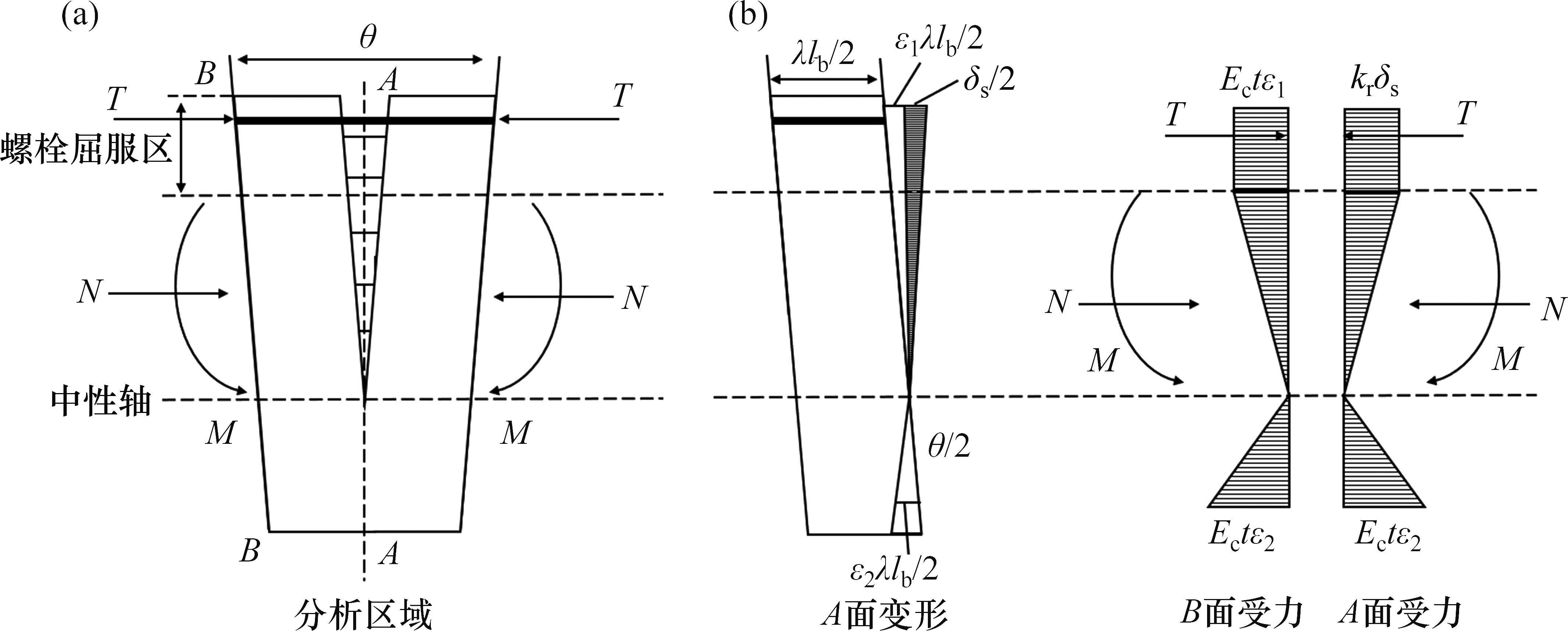
当纵向螺栓达到屈服强度时,其屈服变形量为
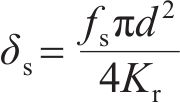
式中: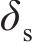
由变形协调和力的平衡,可得:
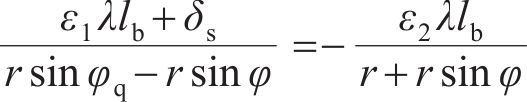
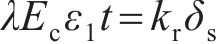
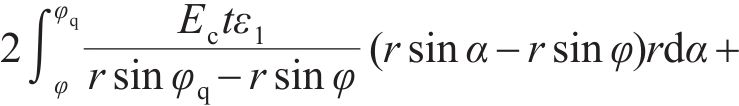
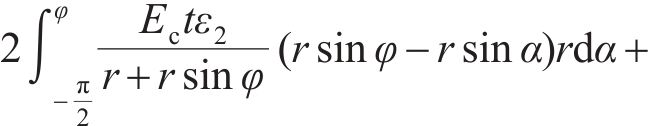
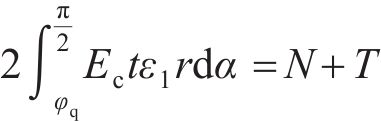
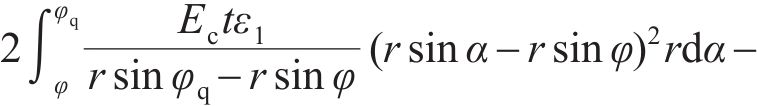
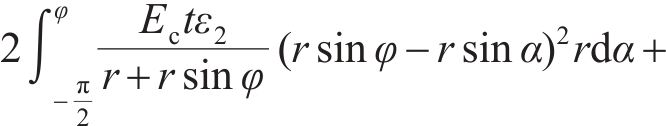
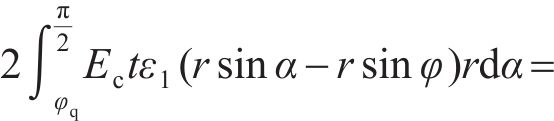
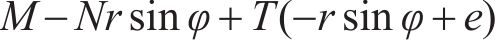
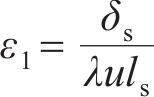
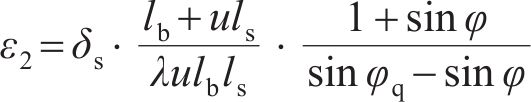
将式(35)~(36)代入式(33)~(34)并整理,可以得到关于中性轴位置角φ和屈服区位置角φq在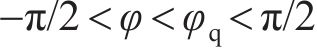
在M、N和T作用下环缝引起的转角θh为
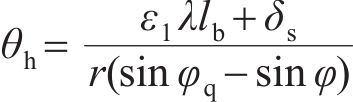
混凝土管片引起的转角θs为
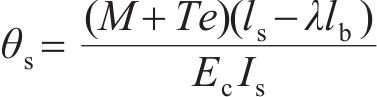
则螺栓为塑性时,模式2的等效抗弯刚度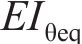
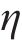
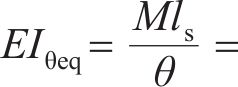
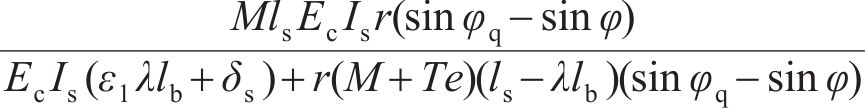
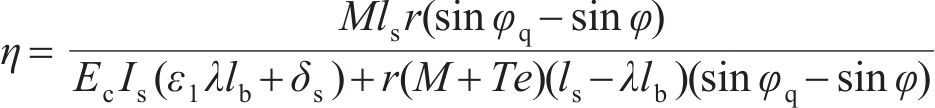
1.3 环缝接头处锚索有效预应力计算
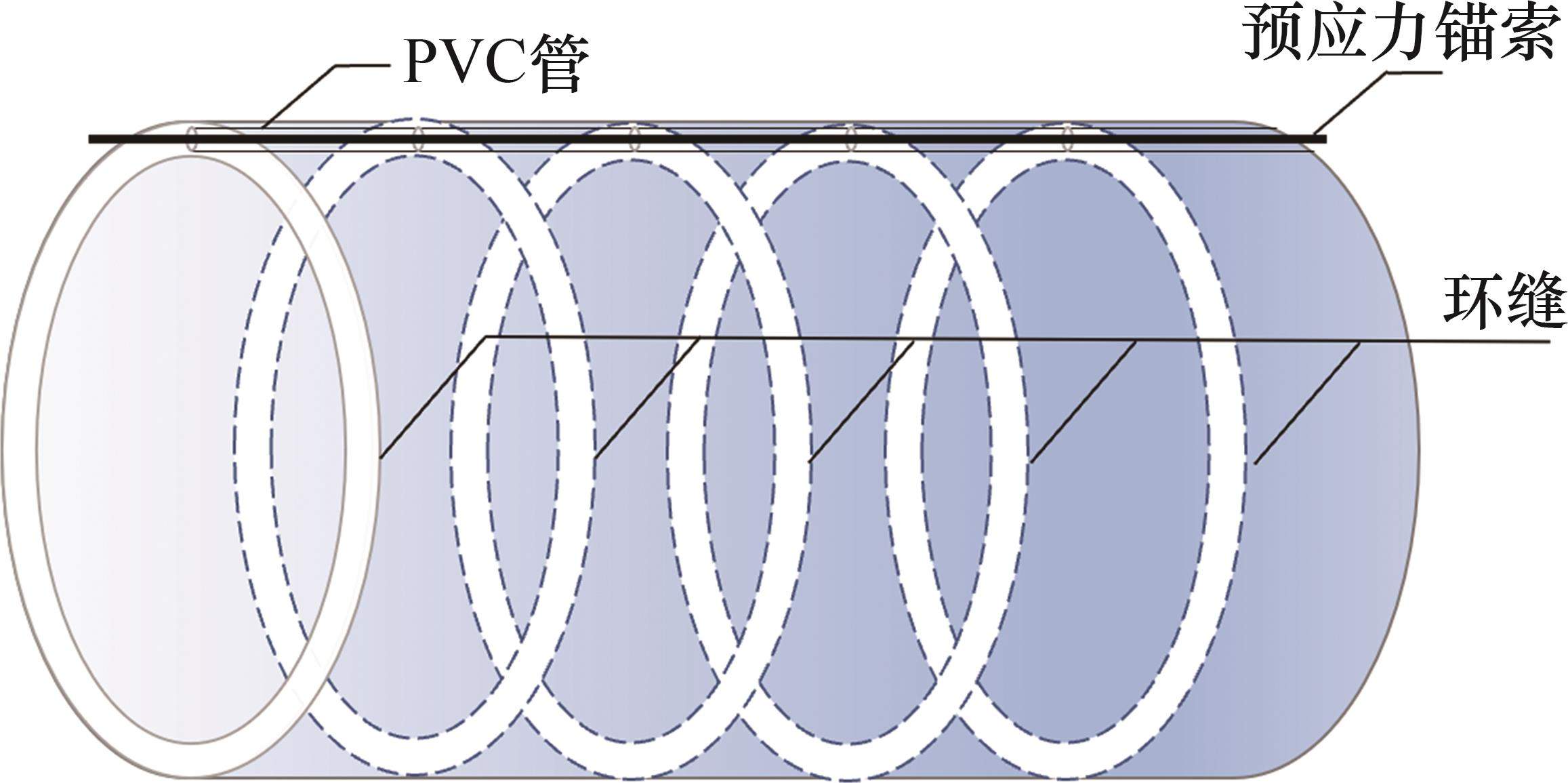
盾构隧道采用的预应力锚索为无黏结形式,如图9所示。具体实施步骤是:在管片混凝土浇筑前,在管片环的厚度中心处预留孔道;管片拼装完成后,先在孔道内穿入PVC管,再将直线形预应力锚索穿入PVC管[23]。纵向预应力锚索在隧道施工完成后进行张拉锚固,可将20环管片作为一个张拉区间,实际区间长度应结合实际工程需要进行调整。
选用公称直径为15.2 mm的无黏结预应力钢绞线,其抗拉强度fptk=1 860 MPa,当采用后张法对锚索进行张拉时,其张拉控制应力允许值[24]为
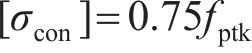
在预应力张拉阶段和运行阶段,锚索的预应力会产生瞬时损失和长期损失。预应力的瞬时损失包括张拉端锚具变形和预应力筋内缩引起的损失、预应力筋沿程摩擦损失;长期损失包括预应力锚索的应力松弛损失、混凝土收缩和徐变以及弹性压缩引起的预应力损失[25-26]。其中,预应力的长期损失要经过数年甚至数十年才能得到,因此,本文主要考虑预应力的瞬时损失。参考规范相关公式[24],将抗拉强度标准值的65%作为单根预应力钢绞线的有效预应力,故计算得出单根预应力钢绞线的有效预应力为0.22 MN,1束含n根钢绞线的锚索的总预应力为0.22n MN。
1.4 纵向预应力等效刚度梁模型可靠性验证
为了验证计算模型的可靠性,将本文计算结果与已有预应力梁[27-28]计算结果进行对比,预应力结构纵向抗弯刚度增率随预应力增量的变化曲线如图10所示。
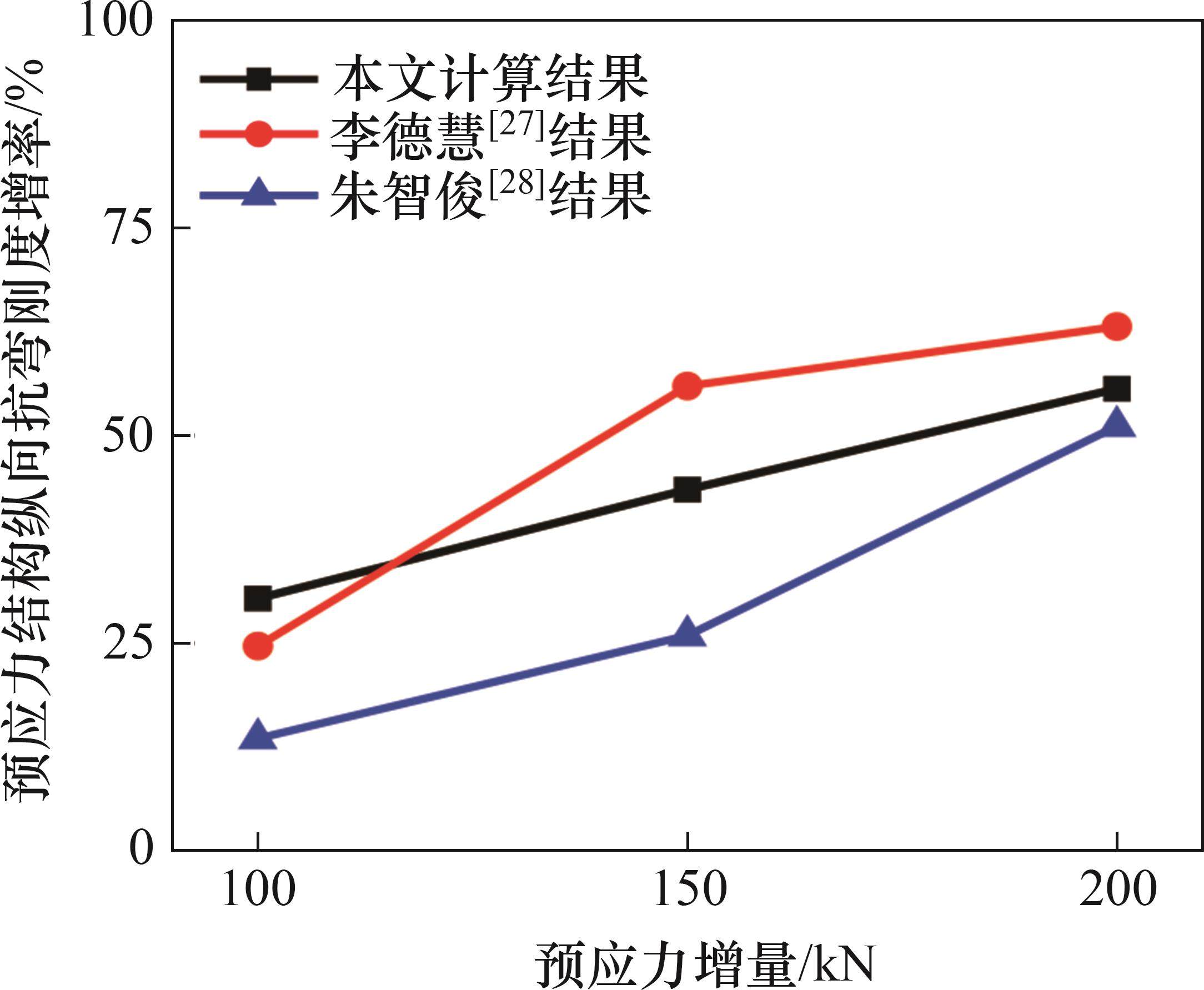
从图10可知:随着预应力的增加,预应力结构纵向抗弯刚度均呈现缓慢递增的趋势,3条曲线变化趋势相近,且3个结构的纵向抗弯刚度增率接近,差值为4.48%~17.56%。上述结果表明,随着纵向预应力的增加,盾构隧道和梁结构的纵向抗弯刚度显著增大,结构抵抗纵向变形的能力随之增强,进而优化结构的纵向受力与变形状态,证明了在纵向施加预应力对提高结构纵向受弯能力是有利的。总体而言,本文基于提出的纵向预应力等效刚度梁模型的计算结果与文献[27-28]中的计算结果接近,变化规律一致,故验证了该计算模型的可靠性,也从侧面证实了将盾构隧道结构在纵向上等效为梁结构的合理性。
2 预应力盾构隧道的纵向变形控制
为了保证纵向预应力盾构隧道的正常运营以及结构安全,研究纵向预应力盾构隧道的纵向变形指标并给出相应的预应力控制方法尤为重要。
2.1 隧道纵向变形指标计算
基于2种环缝接触模式的纵向预应力盾构隧道的等效刚度梁模型,不考虑环缝影响范围,根据材料力学相关原理,结合文献[29],计算盾构隧道纵向变形指标:纵向曲率半径ρ、环缝张开量δ、螺栓最大拉应变εsm、混凝土最大压应力σcm。
1) 模式1环缝完全闭合,各指标的计算公式为:
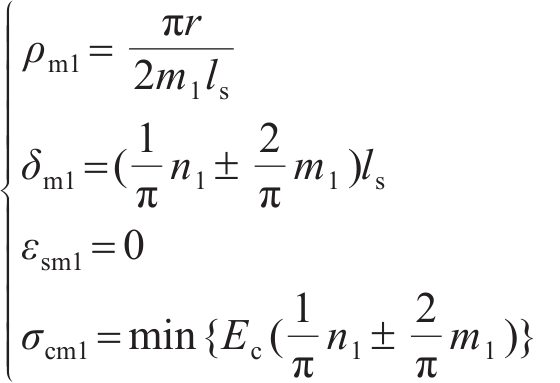
2) 模式2环缝部分张开,螺栓处于弹性状态时,各指标的计算公式为:
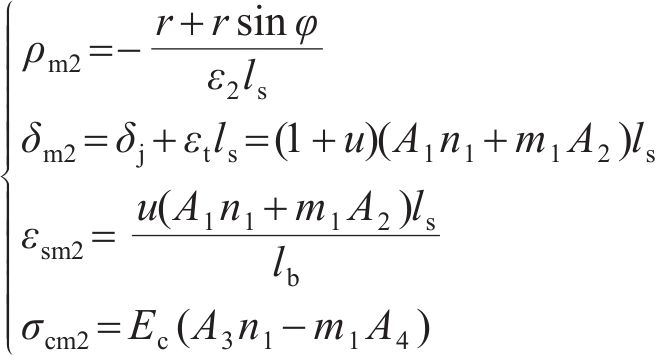
3) 模式2环缝部分张开,螺栓处于塑性状态时,各指标的计算公式为:
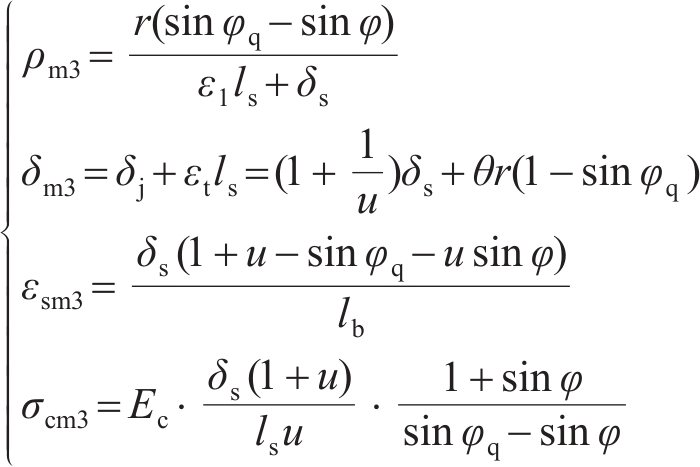
式中:
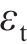
2.2 隧道最佳预应力的确定
基于本文提出的纵向变形指标确定方法,以上海市某越江隧道为例,求解使得隧道超限变形恢复至变形控制值内的最佳预应力。隧道盾构段管片外径为11.36 m,内径为10.4 m,环宽为1.5 m,混凝土强度等级为C50。管片环与环之间用32根5.8级的M30纵向螺栓连接。由于模式2假定螺栓发生塑性变形后,应力保持为屈服应力,故采用螺栓的抗拉变形量即螺栓应力达到抗拉强度时的变形量代替抗拉强度作为控制指标。因此,根据上海市地铁隧道变形的保护控制指标、混凝土管片和螺栓的强度以及预防渗漏水的要求[30],可以确定隧道的7个临界控制指标为纵向曲率半径ρ=15 000 m;受拉螺栓达到屈服应力[σy]=420 MPa;环缝张开量δ=2 mm;密封垫不漏水要求的最大环缝张开量δmax=6 mm;混凝土达到抗压强度设计值[σc1]=23.1 MPa;混凝土达到抗压强度标准值[σc2]=32.4 MPa;受拉螺栓达到抗拉变形[δf]=36.703 mm。
通过调整单束锚索的钢绞线数量改变施加于管片衬砌的预应力,当纵向弯矩M=50 MN·m,即管片内力相同时,不同预应力下纵向变形指标的变化规律如表1所示。
| 单束锚索钢绞线数量/根 | 纵向弯矩/(MN·m) | 抗弯刚度/ (1010 N·m2) | 纵向曲率 半径/m | 环缝张开量/mm | 混凝土压 应力/kPa | 螺栓变形/mm | 螺栓应力/MPa |
|---|---|---|---|---|---|---|---|
| 0 | 50 | 10.54 | 1 405.80 | 7.487 0 | 5 805.32 | 7.462 | 420.000 |
| 27 | 50 | 2 348.66 | 3.13×105 | 0.001 7 | 759.91 | 0.002 | 0.476 |
| 28 | 50 | 2 566.53 | 3.42×105 | -0.032 2 | 743.03 | — | — |
| 40 | 50 | 21 060.00 | 2.80×106 | -0.025 3 | 493.37 | — | — |
| 41 | 50 | 52 520.00 | 7.00×106 | -0.024 7 | 569.14 | — | — |
| 42 | 50 | 106 471.00 | 1.42×107 | -0.024 9 | 573.43 | — | — |
| 43 | 50 | 26 445.00 | 3.53×106 | -0.026 7 | 613.44 | — | — |
由表1可知,当不施加预应力时,管片衬砌的纵向曲率半径和环缝张开量超出了限值,螺栓应力也达到屈服应力。随着单束锚索钢绞线数量的增加,抗弯刚度、纵向曲率半径呈现先增大后减小的趋势,而环缝张开量和混凝土压应力则先减小后增大,各力学指标在预应力的作用下均恢复至控制值内。其中,当钢绞线数量达到28根时,环缝张开量转变为负值,此时,管片衬砌环缝面从部分张开变为完全闭合,环缝面顶端和底端混凝土均受压,螺栓不再提供拉力。此后,随着钢绞线数量继续增加,管片衬砌的抗弯刚度和纵向曲率半径继续增大,混凝土压应力减小。然而,当钢绞线数量达到43根时,管片衬砌抗弯刚度和纵向曲率半径开始下降,混凝土压应力增大,究其原因是,总预应力产生的弯矩远大于截面内力产生的弯矩,出现环缝面顶端压缩量大于底端的压缩量,预应力越大,环缝面顶端和底端的变形量相差越大,纵向曲率半径越小。
上述分析表明,当单束锚索钢绞线数量为42根时,环缝面顶端混凝土和底端混凝土变形量最接近,此时,管片衬砌的抗弯刚度、纵向曲率半径达到最大,环缝变形量绝对值、混凝土压应力、螺栓变形达到最小。因此,在50 MN·m纵向弯矩下,最佳预应力为9.24 MN。与不设置预应力锚索相比,施加最佳预应力后,管片衬砌的抗弯刚度与曲率半径均大幅增加,环缝变形量绝对值减小了99.67%,混凝土压应力减小90.12%。因此,施加纵向预应力可以显著提升结构的纵向受弯能力,明显减少隧道的纵向不均匀变形,环缝张开量也大大降低,对隧道接缝防水有利。
2.3 预应力对超限纵向弯矩的影响
计算无预应力和最佳预应力下管片衬砌达到各指标临界值时的纵向弯矩和变形指标,如表2所示,超限纵向弯矩随变形指标的变化曲线如图11所示。
| 单束锚索钢绞线数量/根 | 超限纵向弯矩/(MN·m) | 抗弯刚度/ (1010 N·m2) | 纵向曲率 半径/m | 环缝张 开量/mm | 混凝土压 应力/kPa | 螺栓变形/mm | 螺栓应力/MPa |
|---|---|---|---|---|---|---|---|
| 0 | 16.73 | 37.64 | 15 000.00 | 0.68 | 1 113.91 | 0.666 | 189 |
| 37.19 | 37.65 | 6 749.00 | 1.51 | 2 475.90 | 1.479 | 420 | |
| 42.88 | 32.81 | 5 102.00 | 2.00 | 3 049.71 | 1.975 | 420 | |
| 49.53 | 12.98 | 1 747.00 | 6.00 | 5 283.63 | 5.975 | 420 | |
| 51.31 | 2.25 | 293.00 | 36.73 | 10 763.30 | 36.703 | 420 | |
| 42 | 113.72 | 255.89 | 15 000.00 | 0.57 | 3 500.78 | 0.564 | 160 |
| 147.52 | 137.47 | 6 212.00 | 1.51 | 5 675.92 | 1.479 | 420 | |
| 158.78 | 113.37 | 4 760.00 | 2.00 | 6 568.16 | 1.975 | 420 | |
| 208.50 | 52.39 | 1 675.20 | 6.00 | 11 380.00 | 5.975 | 420 | |
| 348.55 | 28.04 | 536.30 | 19.28 | 23 100.00 | 19.256 | 420 | |
| 468.00 | 23.75 | 338.20 | 30.76 | 32 400.00 | 30.732 | 420 | |
| 530.06 | 22.56 | 286.75 | 36.73 | 37 160.70 | 36.703 | 420 |
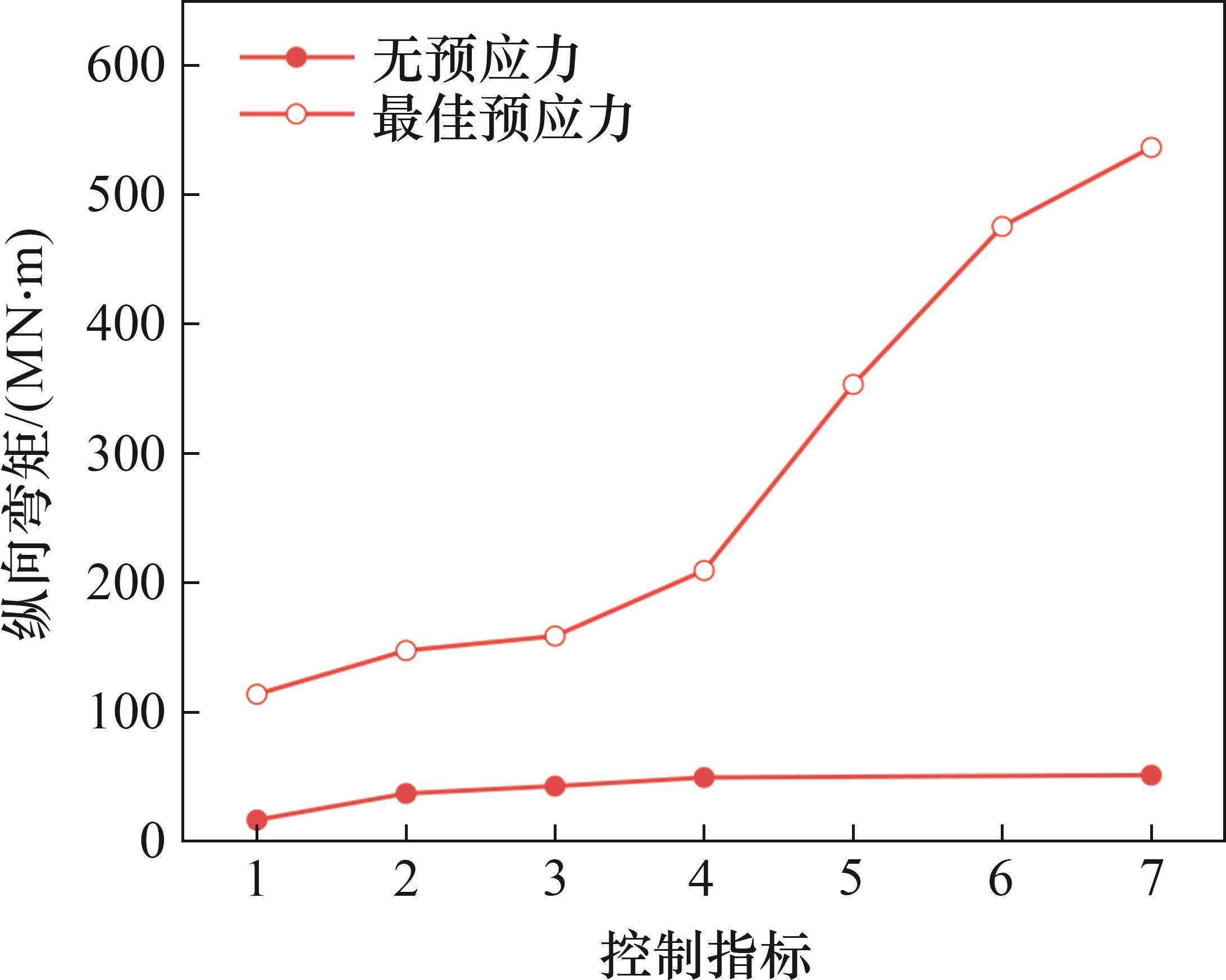
从表2可知,与不设置预应力锚索相比,当最佳预应力管片衬砌的纵向曲率半径达到界限值 15 000 m时,其超限纵向弯矩增大5.80倍,抗弯刚度增大5.80倍,混凝土压应力增大2.14倍,环缝张开量、螺栓应力均减小15.33%;当螺栓应力达到420 MPa时,超限纵向弯矩增大2.97倍,抗弯刚度增大2.65倍,纵向曲率半径减小7.96%,混凝土压应力增大1.29倍,环缝张开量和螺栓变形基本保持一致;当环缝张开量达到界限值2 mm时,超限纵向弯矩增大2.70倍,抗弯刚度增大2.46倍,纵向曲率半径减小6.70%,混凝土压应力增大1.15倍,螺栓变形无明显变化;当环缝张开量达到最大界限值6 mm时,超限纵向弯矩增大3.21倍,抗弯刚度增大3.04倍,纵向曲率半径减小4.11%,混凝土压应力增大1.15倍,螺栓变形无明显变化;当螺栓变形达到界限值36.703 mm时,超限纵向弯矩增大9.33倍,抗弯刚度增大9.03倍,纵向曲率半径减小2.13%,环缝张开量保持一致,混凝土压应力增大2.45倍。
从图11可见未施加预应力时,盾构隧道在纵向弯曲变化过程中达到超限指标的顺序是:先是纵向曲率半径达到界限值15 000 m;然后是螺栓进入屈服状态、环缝张开量依次达到2 mm、6 mm,最后是部分螺栓发生破坏。由此可见,无预应力隧道在螺栓破坏前还没有达到混凝土的抗压强度,混凝土最大压应力保持在较低值。然而,施加最佳预应力后,盾构管片混凝土的压应力增大,在螺栓破坏前达到抗压强度。因此,施加预应力后,应关注混凝土管片的压应力,防止其出现受压破坏。此外,与非预应力管片的隧道相比,管片施加最佳预应力的隧道达到各超限指标时的纵向弯矩和抗弯刚度均更大,表明隧道的承载能力大幅提升,因此,施加最佳纵向预应力对管片的纵向变形具有很好的控制效果。
3 结论
1) 推导了纵向预应力盾构隧道在完全闭合和部分张开两种环缝接触状态下的等效刚度梁模型,模型计算结果与已有研究计算结果非常接近,数值变化规律一致,验证了计算模型的可靠性。
2) 结合某越江隧道工程案例,分析得到隧道的最佳预应力及其对结构纵向受力性能的影响。在最佳预应力9.24 MN下,与非预应力隧道相比,纵向预应力隧道的纵向受弯能力显著提高,纵向不均匀变形明显减少,环缝张开量降低,隧道接缝防水能力提升。其中,环缝变形量绝对值减小了99.67%,混凝土局部弯压应力减小了90.12%。
3) 非预应力盾构隧道在纵向弯曲变化过程中,纵向曲率半径先达到界限值15 000 m,随后部分螺栓进入屈服状态、环缝张开量相继达到2 mm、
6 mm,最后部分螺栓达到抗拉变形量发生破坏,而最佳预应力盾构隧道在螺栓达到抗拉变形量前还会达到混凝土抗压强度。在实际工程中,应该重点关注隧道纵向曲率半径和螺栓应力的变化情况。
4) 当隧道的纵向变形达到各指标控制值时,与非预应力盾构隧道相比,最佳预应力隧道的超限纵向弯矩和抗弯刚度增大2.46~9.33倍,但纵向曲率半径减小2.13%~6.70%,混凝土压应力增大1.15~2.45倍。总体而言,结构纵向的超限承载能力显著增强。
王亚, 廖少明, 马思浩, 等. 预应力盾构隧道的等效刚度梁模型及纵向变形控制研究[J]. 中南大学学报(自然科学版), 2025, 56(2): 610-621.
WANG Ya, LIAO Shaoming, MA Sihao, et al. Research on equivalent stiffness beam model and longitudinal deformation control of prestressed shield tunnel[J]. Journal of Central South University(Science and Technology), 2025, 56(2): 610-621.

